Synchronized spread of COVID-19 in the cities of Bahia, Brazil

Abstract

The COVID-19 pandemic, caused by the highly transmissible SARS-CoV-2 virus, has overloaded health systems in many contexts Conant and Wolfe (2008). Brazil has experienced more than 345,000 deaths, as of April/2021 Conant and Wolfe (2008), with dire consequences for the country’s public and private health systems. This paper aims to estimate the synchronization graph between the cities’ contagion waves from public COVID-19 data records. For this purpose, the Motif–Synchronization method Magwire et al. (2011) was applied to publicly available COVID-19 data records to determine the sequential relationship of occurrence of the waves among Bahia’s cities. We find synchronization between waves of infection between cities, suggesting diffusion of the disease in Bahia and a potential role for inter-city transportation Saba et al. (2018), Saba et al. (2014), Araújo et al. (2018) in the dynamics of this phenomenon McKee and Stuckler (2020), Chinazzi et al. (2020), Tizzoni et al. (2014). Our main contribution lies in the use of the Motif–Synchronization method applied to COVID-19 data records, with the results revealing a pattern of disease spread that extends beyond city boundaries.

1. Introduction

The COVID-19 pandemic has been caused by the SARS-CoV-2 virus, a species of coronavirus (Zhu et al., 2020). Following initial reports in Wuhan Province, China in December 2019, the virus’s spread was declared a Public Health Event of International Concern in January 2020 and a pandemic in March early 2020 by the World Health Organization (WHO) (McKee and Stuckler, 2020). Kristalina Georgieva, director of the International Monetary Fund (IMF), predicted that emerging and developing countries, which are more economically vulnerable than developed economies, would be most affected by the lack of medical supplies (Stubbs et al., 2021).

The year 2020 was marked by the closing of factories and stores, sports arenas, restaurants and entertainment activities, which has highlighted a trade-off between health and the economy. “Stay home” has been the way adopted by some governments to avoid the health system breakdown in many countries, until they reach herd immunity. However, when the economy stops the immediate consequence is the reduction in the circulation of money in the markets, which has led to a negative impact on the government’s resources (McKee and Stuckler, 2020). Accordingly, social welfare in the form of public services is compromised. Once there is no treatment to combat the effects against SARS-CoV-2 virus. Besides early detection, non-pharmaceutical interventions (NPIs), such as hand hygiene, social distancing, facemask use and household quarantine are suggested to be more effective than travel restrictions at mitigating this pandemic (Chinazzi et al., 2020, Saunders-Hastings et al., 2017, Jenness et al., 2021, Ge et al., 2021, Roche et al., 2020, Flaxman et al., 2020, Patiño-Lugo et al., 2020).

This scenario led to an intense worldwide race for an effective vaccine. According to the WHO there are currently more than 50 COVID-19 vaccine candidates in trials (Feynman and Vernon, 1963). Besides, WHO is working in collaboration with scientists, business, and global health organizations to allocate vaccines across different participant countries through the COVAX (McKee and Stuckler, 2020).

This pandemic has been a challenge worldwide, particularly for large and modern cities. Once their population spatial distribution and its behavior, variation in age, mobility system, public facilities that are all directly associated with SARS-Cov-2 virus spread. Modeling the spread of COVID-19 pandemic has been an essential tool for through which the scientific community has contributed to public health decision making (Tizzoni et al., 2014).

Health and economic activities both depend on free mobility. The diffusion of epidemics has been studied as a complex system in the literature. For instance, Self-Organized Criticality (SOC) (Saba et al., 2014a, Nascimento Filho et al., 2018), fractal behaviors (Nascimento Filho et al., 2021, Azevedo et al., 2016), non-linear (Miranda et al., 2021, Macedo et al., 2020), the transportation presents correlations among criticality (Cardoso et al., 2013, Saba et al., 2014b), physical medium of propagation and distribution of epidemics cases (Araújo et al., 2018, Saba et al., 2018). In this sense, analyzing correlation allows us to verify features of the evolution of COVID-19 that are not evident when we use traditional methods. Spatial distribution of the population, variation in age, mobility system and public facilities all may be directly associated with the spread of the SARS-Cov-2 virus.

Here, we use the Motif–Synchronization method to explore synchronicity of COVID-19 epidemic patterns across cities in Bahia State, Brazil. Bahia is the fourth largest state of Brazil in terms of population, with about 15 million inhabitants, which is higher than the estimated population of some European countries, such as Belgium, Greece, Sweden or Portugal (Ohno, 2013). Covering 564,732 km${}^2$ and including 417 cities, Bahia has an extensive road network interconnecting all cities in the state, which providing a potential conduit for the spread of pathogens such as SARS-CoV-2. Thus, this paper aims to evaluate the different roles that mobility between cities plays in the dynamics of the SARS-CoV-2 virus, as its distribution pattern. We conduct a spatio-temporal analysis of the spread of the SARS-CoV-2 virus to health regions in Bahia-Brazil and the apply Motif–Synchronization approach to data sets of SARS-Cov-2 virus cases registered in the year March 2020 through April 2021. Several papers have used a similar approach using the same method in differentcontexts (Saba et al., 2018, Araújo et al., 2018, da Costa et al., 2021, Rosário et al., 2015, Toutain et al., 2021, Toutain et al., 2020, Silva et al., 2019).

2. Material and methods

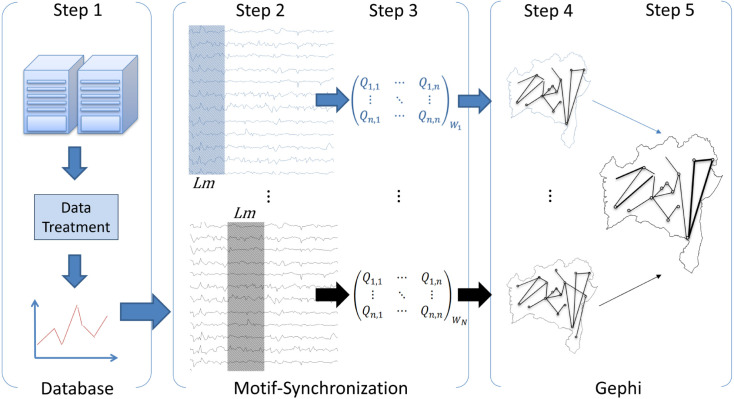
We analyzed the historical series of cases of COVID-19 for 417 cities in the state of Bahia. The series has 860,412 cases reported and confirmed in official health systems. We analyzed the data between 03/01/2020 to 04/24/2021, corresponding to 60 weeks. The data were analyzed by epidemiological week, following the practice adopted by the Ministry of Health of Brazil. Weekly analysis is useful minimize the impact of high variability of daily case numbers (see Fig. 1 Step 01: Database). The original data source used in this paper is available in https://github.com/DataNPAI/motif.

Fig. 1.

The Motif–Synchronization method design - For the time window $T_1$ the method is applied by obtaining a network for the given time instant. By moving the time window along the time series, the process is repeated generating all other networks of the Time Varying Graph ($TVG$) structure.

The Motif–Synchronization algorithm (Flaxman et al., 2020) starts with the codification of the incidence time series in a series of micro patterns known as motifs. Motifs can be identified as slopes, peaks and ditches. For better understanding the methodology of Motif–Synchronization algorithm see Supplementary Information (https://github.com/DataNPAI/motif).

The degree of synchronization is determined by quasi-simultaneous counting of these patterns between the series of incidence for each city pair. The degree of synchronization $Q_{XY}$ between two cities $X$ and $Y$ is given by Eq. (1).

$$Q_{XY}=\frac{max(C_{XY},C_{YX})}{L_m}$$ (1)

$$C_{XY}=max\left(\sum _{i=1}^{L_m}{J}_i^{{\tau }_0},\sum _{i=1}^{L_m}{J}_i^{{\tau }_1},\dots ,\sum _{i=1}^{L_m}{J}_i^{{\tau }_n}\right)\text{and}$$

$$J_i^{\tau }=\left\{\begin{array}{cc}1,\hfill & if{X}_{Mi}=Y_{M_{i+\tau }}.\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\right)$$ (2)

In Eq. (2), $C_{XY}$ represents the maximum amount of the same motif found in both series, between different delay times, ${\tau }_n$ is the longest defined delay, $L_m$ is the box size (Fig. 1 Step 02: Motifs synchronization), and $X_{Mi}$ is the $i$th motif of the X city incidence time series, as shown in Figure (Fig. 1 Step 03: Motifs synchronization).

Assessing the correlation, or the degree of synchronization, between these time series is usually sufficient to obtain epidemiological networks. However, new approaches are needed to understand more deeply the dynamics of the spread of an emerging pathogen in a heterogeneous area such as the state of Bahia. Time varying graphs $\left(TVG\right)$ is the part of Graph theory used to describe networks in which the relationships between their elements are not persistent over time. These time fluctuations are due to the nature of these relationships (i.e. pendulum flow between co-dependent cities), or even through intervention outside the system (i.e. government blockades and decrees to control the pandemic) (Holme and Saramäki, 2013).

TVG can be described mathematically as the set of graphs generated through function $G(V,A,T,\rho ,\zeta )$, where, V and A are edges and vertices of $G,T$ is the total time of the analyzed system, $\rho (A,t)$ e $\zeta (A,t)$ are the functions that indicate the presence and lifetime of each edge (Casteigts et al., 2012). We can describe the whole sequence as $G=G_t$ $t=1,2,\dots ,T$, where each $G_t$ is the configuration of the graph edges in each time $t$ (Tang et al., 2010).

$TVG$ calculates the degree of synchronization between all pairs of cities for an instant of time (Fig. 1 Step 03: Motif–Synchronization). By sliding $L_m$ over the entire time series of incidence, and repeating the previous process, we thus generate a configuration of connections for each instant. We used the sum of cases during the week (7 days) to avoid impact on the evaluation regarding under-reporting on weekends and holidays. All calculations are based on the incidence of disease per week in the patient’s county of residence.

All parameters were determined so that the $L_m$ time window was as small as possible. For a very large window, the method would lose resolution in characterizing the dynamic activity of the system. Thus, the estimated window was 6 weeks ($L_m=6$), and the maximum delay considered to be two weeks (${\tau }_n=2$), an adjustment to represent the incubation period.

Another important parameter is the threshold . This parameter is used to filter out synchronizations that are most likely due to random fluctuation of data. From the determination of its value, we can only consider statistically relevant edges in the process of creating the networks. The threshold value 0.83 used in this work was determined through a surrogate process in order to guarantee that the edges of the networks have at least a 95% chance of not being a product of chance. Details about this surrogate algorithm can be seen in Rosário et al. (2015)

The 83.3% threshold means that the city pair will have an edge considered by the model only when at least 5 of 6 weeks are correlated (Fig. 1 Step 03: Motif–Synchronization). Finally Fig. 1 Steps 04 and 05: Gephi (https://gephi.org/) represent the TVG graphs generated from Motif–Synchronizations. A weighted network in which edge weights and node degrees represent the importance of connections in the dynamics of the analyzed system. Also, the parameters for the construction of the graphs used in this paper are based on the criteria defined in prior paper applied to Dengue cases study (Araújo et al., 2018).

It is essential to choose which association method should be used to establish the functional relationships between its vertices in the construction of $TVGs$. In this study, we used Motif–synchronization (Rosário et al., 2015) to identify the degree of synchronization between the time series of incidence COVID-19 as the criteria for construction of $TVG$ edges.

3. Results

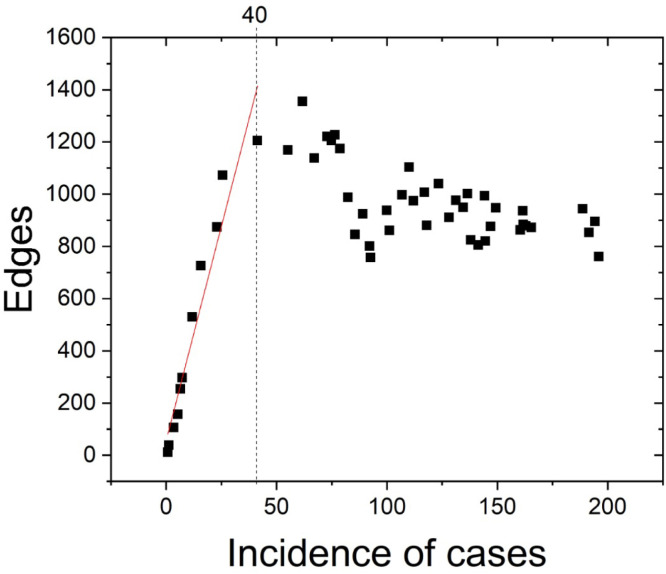
The result of Motif–Synchronization method demonstrate linearity by the increase in the incidence of COVID-19 in the cities of Bahia. Concomitantly, the increase in edges between these cities (until incidence of cases $=$ 40), where this curve represents 27% of the connected nodes in the network (Fig. 2).

Fig. 2.

Correlation between Edges and Incidence of cases in Bahia, the linear adjust (red line) presented $R^2=0.92$ and slope $=$ 32.81. Until incidence of cases equal to 40, the relation between Edges and Incidence of cases is strong. The linear region of the curve represents 27% of the connected nodes in the network (11/41). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

After the execution of the model, the weight of the edges in the found network demonstrates the number of times that a significant synchronization occurred between the incidence time series of the same pair of cities. An edge with a weight equal to 26, for example, indicates that the city presents a correlation in 26 weeks of the 60 weeks analyzed. The edges with a weight greater than or equal to 18 and the distance between the pair of cities are listed in Table 1.

Table 1.

Covid-19 network edge pairs with higher weights in the time series and the distance between the edge cities calculated in latitude and longitude.

Source cities	Target cities	Weight	Distance (km)
SALVADOR	CAMACARI	26	46
CONCEICAO DO JACUIPE	CAMPO FORMOSO	23	317
EUNAPOLIS	ILHEUS	23	249
EUNAPOLIS	SALVADOR	23	529
CONCEICAO DA FEIRA	ILHEUS	22	334
PORTO SEGURO	BRUMADO	22	520
SANTO ANTONIO DE JESUS	FEIRA DE SANTANA	22	117
CACHOEIRA	ITABUNA	21	313
DIAS D’AVILA	EUNAPOLIS	21	639
ITACARE	BRUMADO	21	403
SALVADOR	ITABUNA	21	436
SANTO ANTONIO DE JESUS	JUAZEIRO	21	506
CAMPO FORMOSO	EUCLIDES DA CUNHA	20	173
IBIRAPITANGA	LUIS EDUARDO MAGALHAES	20	977
ILHEUS	BARREIRAS	20	978
ITAJUIPE	SALVADOR	20	420
ITIUBA	SERRINHA	20	208
JUAZEIRO	FEIRA DE SANTANA	20	392
MADRE DE DEUS	PAULO AFONSO	20	443
SALVADOR	FEIRA DE SANTANA	20	116
SAO JOSE DA VITORIA	SANTO ESTEVAO	20	366
SERRINHA	BARREIRAS	20	823
CAMACAN	ILHEUS	19	122
CAMACAN	SEABRA	19	576
CAMPO FORMOSO	GANDU	19	504
EUNAPOLIS	FEIRA DE SANTANA	19	572
EUNAPOLIS	VITORIA DA CONQUISTA	19	322
FEIRA DE SANTANA	ALAGOINHAS	19	80
ITIUBA	CAMPO FORMOSO	19	86
JAGUARARI	BRUMADO	19	648
PAULO AFONSO	IBIRATAIA	19	654
AMARGOSA	NAZARE	18	87
BOM JESUS DA LAPA	IBICARAI	18	576
CACHOEIRA	BELMONTE	18	576
ITABUNA	ILHEUS	18	32
ITIUBA	EUCLIDES DA CUNHA	18	114
JUAZEIRO	ALAGOINHAS	18	444
MUTUIPE	CAMAMU	18	146
PAULO AFONSO	JAGUAQUARA	18	586
TAPEROA	CONCEICAO DO ALMEIDA	18	120
VITORIA DA CONQUISTA	BARREIRAS	18	704

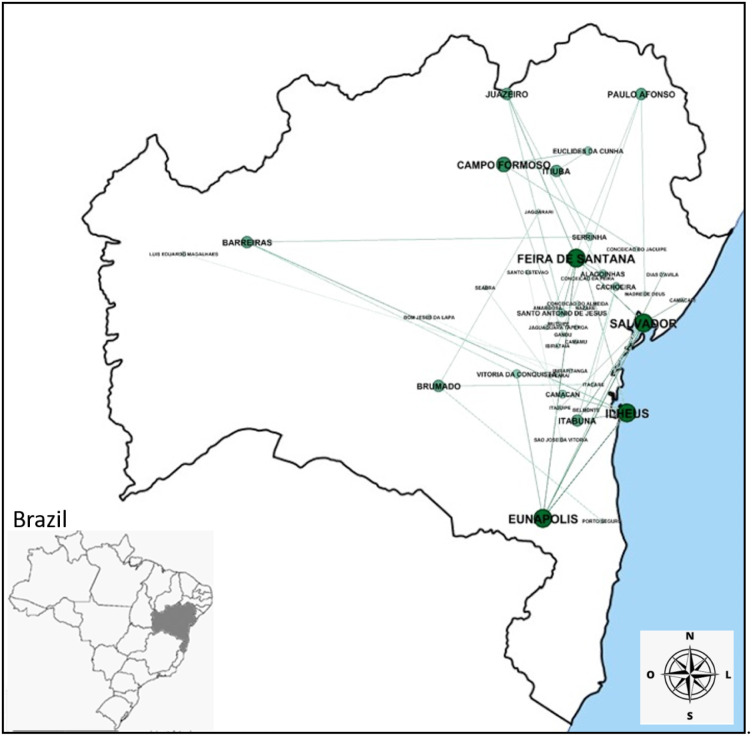
Correlations were observed between the incidence of COVID-19 and the number of edges found in the results may be related to the mechanisms of disease diffusion in Bahia (see Fig. 3). The higher the incidence of COVID-19, the more edges between cities are formed, thus demonstrating similarity in the behavior of increase, decrease or stability of virus diffusion.

Fig. 3.

Network of cities with edges with weight greater than or equal to 18 weeks of correlation.

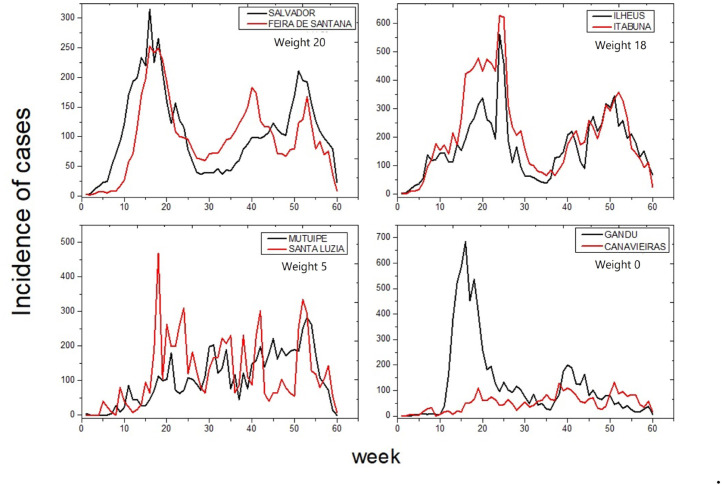
Fig. 4 shows the incidence of COVID-19 between cities with two pairs highly correlated (Salvador and Feira de Santana; Ilhéus and Itabuna); one pairs medium correlated (Mutuípe and Santa Luzia) and one pairs weakly correlated (Gandu and Canavieiras). For instance, Feira de Santana presents a lag for the rise of cases in the first weeks of the analysis with an inversion of this dynamic from the 22nd week, which lasts until approximately the 48nd week, when Salvador becomes the leader again. The pair Ilhéus and Itabuna, the inversion can be seen around 160 week 24. Some of these inversions were noticed in other pairs. In order to compare the pair Mutuípe and Santa Luzia presents weight 5 (general synchronization mean equal to 5.3) and the pair Gandu and Canavieiras presents no synchronizations. The direction of the influence was not evaluated because of this dynamic (inversion of the lead city) found in this pandemic. Once the direction of influence among the municipalities in Bahia suggests a complex system. That may involve several variables, such as neighborhoods between cities, allocation and availability of health facilities, transport networks and scarcity of resources, as observed by Araujo et al. (2022).

Fig. 4.

Time series of dates of first symptom grouped in weeks in the cities. The weights demonstrate the numbers of times that a significant synchronization occurred between the incidence time series of the same pair of cities.

4. Discussions

The linear correlation threshold between incidence and edges for incidence of 40 may be related to the existence of a threshold network where even increasing incidence does not create new synchronization pairs (see Fig. 2). This effect could be explained by the strong relationship between epidemic synchronization networks and the transport network (Saba et al., 2018). Thus, the fixed topology of the transport network would limit the growth of the synchronization network.

Table 1 shows that the distance between cities is not a parameter that defines the spread of COVID-19. The results suggest that inter-city transportation presents similar behavior observed by Saba et al. (2018) and Araújo et al. (2018) about dengue epidemics. Thus, considering the characteristic time and spatial distance, the influence between cities seems to be linked to the transport network (i.e. highways) and airways (i.e. airports). The pair of cities with the shortest distance between them is Ilhéus and Itabuna, with approximately 32 km. The longest distance between two cities analyzed is Ilhéus and Barreiras with 978 km. Both pairs have weights greater than 18, reaffirming that the distance between cities does not represent a barrier to the diffusion of COVID-19.

5. Conclusion

The incidence presents a correlation where it is observed that its growth leads to the formation of more edges. The hypothesis that the COVID-19 epidemic synchronization networks between Bahia cities characterize the disease diffusion process was evaluated, where the effects of the COVID-19 epidemic were measured. The results presented a linear correlation threshold between incidence and edges for incidence of 40, after it occurs behavior change likely due the relationship between epidemic synchronization networks and the transport network as observed in Saba et al. (2018).

The analysis of the network identified the main cities responsible for spreading the disease and the relationships between them. Through the Motif–synchronization it was observed that the cities Salvador, Ilhéus, Feira de Santana and Eunápolis in Fig. 3 demonstrate to be influential in the state of Bahia. Besides, these cities presented the greatest synchronism among the 417 cities evaluated in this study. In order to verify the existence of preferential directions in these relationships, we identified that some pairs of cities exerted mutual influence, since the increased incidence of the disease in one city possibly induced growth in the neighboring city, and vice versa.

We also verified that the high incidence and dynamical similarities found between pairs of cities are not influenced by the spatial distance between them. In this way, priority attention in the different cities (i.e. hubs) can help in public policies, leading to more efficient and targeted actions, as reducing mobility only in specific cities and within a specific time range. These polices could reduce the impact of the pandemic in the state as a whole, reducing the spending velocity and its economic impact. This methodology can be replicated to other States or Countries, to identify the cities that behave as COVID-19 diffusion hubs.

CRediT authorship contribution statement

Hugo Saba: Conceptualization, Research formulation, Methodology, Technical details, Writing – original draft, Supervision, Leadership responsibility for the planning and execution of the research activity. A.S. Nascimento Filho: Conceptualization, Research formulation, Methodology, Technical details, Writing – original draft. José G.V. Miranda: Conceptualization, Research formulation, Methodology, Technical details, Writing – original draft, Supervision, Leadership responsibility for the planning and execution of the research activity. Raphael S. Rosário: Conceptualization, Research formulation, Methodology, Technical details, Writing – original draft. Thiago B. Murari: Conceptualization, Research formulation, Methodology, Technical details, Writing – original draft. Eduardo M.F. Jorge: Resources, Data curation. Elaine C.B. Cambui: Resources, Data curation. Márcia S.P.L. Souza: Resources, Data curation. Ana C.F.N. Silva: Resources, Data curation. Márcio L.V. Araújo: Conceptualization, Research formulation, Methodology, Technical details, Writing – original draft, Resources, Data curation.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.