Abstract
Multispectral and lifetime imaging in turbid media can be mathematically described in two steps, involving spectral or temporal mixing of the fluorophores and the diffuse light transport in the turbid medium. We show that the order of fluorophore mixing and diffuse propagation is reversed in spectral and lifetime multiplexing, resulting in a fundamental difference in their multiplexing capabilities, regardless of the measurement conditions. Using the resolution matrix to define a quantitative measure for inter-fluorophore cross-talk, we show that lifetime multiplexing, using the asymptotic time domain approach, provides zero cross-talk, while spectral multiplexing can achieve zero cross-talk under special conditions. We also compare the performance of spectral and lifetime multiplexing for tomographic inversion of two overlapping fluorophores in a heterogeneous digital mouse atlas.
Keywords: (170.3010) Image reconstruction techniques, (170.6920) Time-resolved imaging, (170.3650) Lifetime-based sensing, (110.4234) Multispectral and hyperspectral imaging
The quantitative separation of multiple fluorophores embedded deep in tissue with spectral and lifetime contrast (“multiplexing”) would enable visualization of parallel biological processes in vivo, and the detection of molecular interactions such as enzyme activation [1] and fluorescence resonance energy transfer [2]. Fluorescence lifetime and multispectral methods have commonly been used in microscopy to unmix multiple fluorophores in thin tissue samples using their unique fluorescence lifetime and spectral signatures [3,4]. Both types of contrast have also been successfully applied to distinguish fluorophores of interest from tissue autofluorescence [5,6]. In microscopy, spectral or lifetime unmixing can be performed directly at each pixel using various fitting techniques [3]. However, in the case of thick turbid samples such as biological tissue, the measurement at the surface of the sample is affected by light propagation through the medium. Therefore, tomographic multiplexing in macroscopic samples requires the consideration of diffuse light transport, in addition to spectral or lifetime unmixing.
In this Letter, we recast the forward problems for multispectral fluorescence tomography (MSFT) and tomographic fluorescence lifetime multiplexing (TFLM) in mathematical forms that explicitly show the reverse order of fluorophore mixing and diffuse light propagation steps in the two techniques. Using the model resolution matrix, we show that this reversal implies a distinct cross-talk performance between MSFT and TFLM. While TFLM can provide zero cross-talk solutions, MSFT can achieve zero cross-talk under two general conditions, regardless of the measurement geometry or other experimental considerations. High cross-talk has been shown to lead to errors in localization, identification, and relative quantification of multiple fluorophores [7,8]. Here, we illustrate the distinct performance of MSFT and TFLM using a simulation model consisting of near-infrared (NIR) fluorophores in a heterogeneous digital mouse atlas. We show that for realistic tissue optical properties, TFLM achieves accurate relative quantitation of the fluorophores, whereas MSFT distorts the relative quantitation due to significant cross-talk.
Consider a turbid medium containing N fluorophores with distinct excitation or emission spectra, bn(λ) and lifetimes , n = 1 … N. The forward problem for MSFT and TFLM takes the following matrix form for V medium voxels, M measurement pairs (number of sources × detectors), and either K wavelengths for MSFT or L time gates for TFLM:
| (1) |
| (2) |
where is the (KM × NV) spectral weight matrix, is the (LM × NV) TD weight matrix, y is a measurement vector with dimensions (LM × 1) for TD and (KM × 1) for spectral data, and is a (NV × 1) parameter vector containing the unknown concentrations for each fluorophore.
Both the spectral and lifetime weight matrices can be factorized into a product of a basis matrix containing either the spectral or lifetime basis functions alone, and a spatially varying matrix representing the diffuse propagation in the medium. For MSFT, the factorized form is
| (3) |
where is a (KV × NV) spectral basis matrix containing Kronecker products of the excitation or emission spectra and the (V × V) identity matrix, I, and is a (KM × KV) block diagonal matrix containing continuous wave (CW) weight matrices for each wavelength. A similar factorization also occurs in TFLM in the decaying or the asymptotic regime [7,8] of the TD fluorescence signal, assuming that , where τD is the intrinsic diffusion time scale for the light transport in the medium [7]:
| (4) |
Here, is a (LM × NM) temporal basis matrix containing Kronecker products of exponential decay functions and the (M × M) identity matrix, I, and is a (NM × NV) block diagonal matrix containing reduced absorption CW weight matrices for each lifetime component. A fundamental difference between the spectral and TD forward problems is immediately clear from Eqs. (3) and (4), as schematically represented in Fig. 1. For spectral multiplexing, the mixing of the unknown fluorophore concentrations occurs at the location of the individual voxels (through AS). The mixed concentrations are then propagated through the medium by wavelength-dependent CW weight matrices . For lifetime multiplexing, the individual concentrations are first propagated through the medium by reduced absorption CW matrices followed by mixing with temporal basis functions ATD).
Fig. 1.
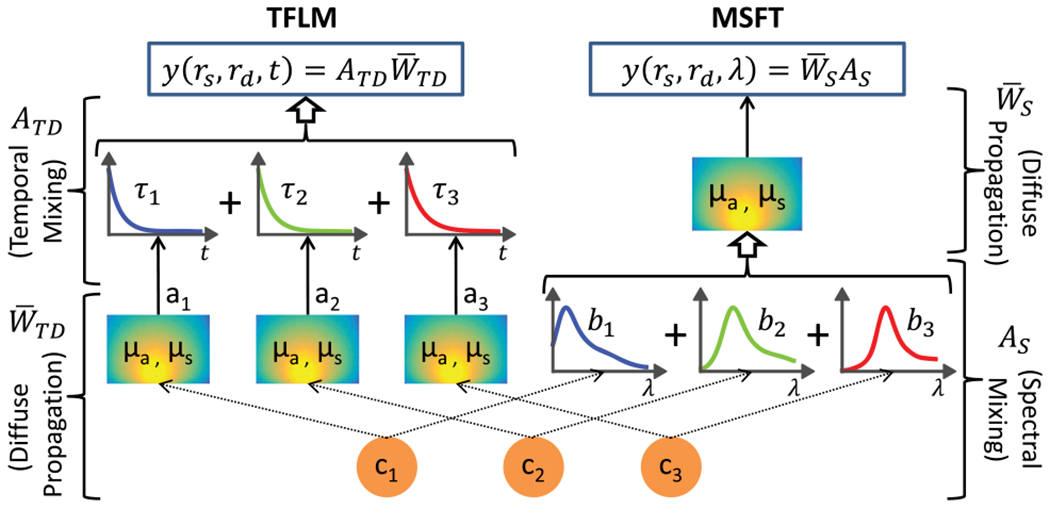
Schematic showing the fundamental difference in the order of the mixing and diffuse propagation steps in TFLM and MSFT forward problems for three fluorophores with concentrations c1, c2, c3, lifetimes τ1, τ2, τ3, and spectral basis functions b1, b2, b3.
We focus on linear inverse operators which allow the reconstructed concentration to be expressed as
| (5) |
where we have introduced the (NV × NV) model resolution matrix, , and n represents the additive noise. We focus on the bias term, Rc [9], assuming that the noise sensitivity term, , can be minimized with appropriate regularization. We first calculate the resolution matrices R of the TD and spectral methods based on both their direct forward problems [Eqs. (1) and (2)] and the corresponding factorized forms [Eqs. (3) and (4)]. Consider first an inversion of the spectral forward problem in Eq. (1), called the direct spectral (DS) method [10,11]. Using Tikhonov regularization [9] for inverting WS and substituting Eq. (3), we get the following resolution matrix for the direct spectral case:
| (6) |
where λ is the Tikhonov regularization parameter. Alternately, Eq. (3) can be used to invert the spectral data in two stages [10,11]. First, is inverted using its Tikhonov-regularized inverse matrix, . Next, due to the well-conditioned nature of AS, it is inverted without regularization by multiplication with its Moore–Penrose pseudoinverse, . The latter step is equivalent to performing a linear fit to the spectral basis functions, bn(λ), at each voxel. The resolution matrix for this indirect spectral (IS) method is given by
| (7) |
where we have again used Eq. (3) for WS.
The inversion of the TD data can also proceed using a direct or a two-step approach. A direct inversion of the TD data in Eq. (2) using Tikhonov regularization and substitution of Eq. (4) leads to the direct TD (DTD) approach, with a resolution matrix [12]:
| (8) |
If we exploit the factorization in Eq. (4), the Moore–Penrose pseudoinverse of ATD can first be applied to the time points in the asymptotic regime resulting in the decay amplitudes, . This step is equivalent to a linear fit of the TD data with exponential decay basis functions. Next, the amplitudes a are inverted using the Tikhonov inverse of , resulting in the asymptotic TD (ATD) resolution matrix [12]
| (9) |
where we have used Eq. (4). A key step in the derivation of the TD resolution matrices is the use of the identity . A similar identity cannot be used in the spectral case due to the reverse order of AS and in Eq. (3).
The cross-talk performance of the direct and indirect MSFT and TFLM problems can now be quantitatively compared using their resolution matrices in Eqs. (6)–(9) [12]. Let the resolution matrix R be divided into N × N blocks, each of the size V × V. Then, the on-diagonal blocks () contain the point spread functions for individual fluorophores, while the off-diagonal blocks () represent the cross-talk between fluorophores with distinct spectra or lifetimes. First, it is clear that all matrices in Eq. (9) are block diagonal since is block diagonal, so that RATD is also block diagonal. This implies that ATD solutions provide zero cross-talk between the cn’s. In the DTD case, the covariance matrix term, , in Eq. (8), results in off-diagonal terms in RDTD, leading to solutions with non-zero cross-talk.
For MSFT, the presence of the non-diagonal spectral basis matrices, AS and , in both Eqs. (6) and (7), implies that, in general, both RDS and RIS are not block diagonal. However, an inspection of Eqs. (6) and (7) reveals that RDS and RIS are block diagonal under certain conditions. Considering the DS case [Eq. (6)] first, and switching to the equivalent overdetermined form of the inverse matrix, we have [using Eq. (3)]
| (10) |
When the basis functions bj(λ) are nonoverlapping [i.e., , for all fluorophore pairs (l, m)], it is clear that the off-diagonal blocks of the term are zero. Hence, RDS also becomes block diagonal. For the IS case, we can rewrite Eq. (7) as
| (11) |
where is a block diagonal matrix with the V × V matrices αj along the diagonal blocks, and we have applied the definition of the Moore–Penrose pseudoinverse for full-column rank matrices, . When the basis functions are nonoverlapping, becomes block diagonal and whose off-diagonal blocks are equal to is also block diagonal. Hence, RIS also becomes block diagonal. Additionally, when the optical properties are wavelength independent, we have , and RIS can be simplified to , which is a NV × NV block diagonal matrix. We can thus summarize the conditions for zero cross-talk in spectral multiplexing as follows:
(1) RIS becomes block diagonal when the blocks along the diagonal of are equal. This occurs when the tissue optical properties (and the .) are wavelength independent.
(2) Both RIS and RDS become block diagonal when the spectral basis functions are nonoverlapping. For biomedical applications, which involve strong wavelength-dependent optical properties and NIR fluorophores that typically exhibit broad and overlapping spectra, both conditions are hard to satisfy.
We note that while the above results employed the Tikhonov form of inversion, the non-existence of a general zero cross-talk estimator for MSFT can be more generally proved based on a recently derived nullity condition for multiplexing (NCM) [12]. The NCM requires that the transpose of the weight matrix be of non-zero nullity for the existence of zero cross-talk estimators. It can be shown that the nullity of the spectral weight matrix, , is generally zero, implying that zero cross-talk solutions do not exist for arbitrary conditions. However, the nullity can become non-zero when the optical properties are wavelength independent or the spectra are nonoverlapping, in agreement with the zero cross-talk conditions specified above. On the other hand, the TD weight matrix [Eq. (4)] has non-zero nullity in the asymptotic region [12], thereby satisfying the NCM and ensuring the existence of zero cross-talk estimators (ATD).
We numerically illustrate these conditions and compare the performance of MSFT with TFLM below. To proceed, we define a measure for cross-talk in terms of the resolution matrix. Let j be the linear index corresponding to voxel (x, y, z). Note that the jth column of R21 represents the cross-talk into the fluorophore 2 channel due to fluorophore 1 located at (x, y, z). The cross-talk of fluorophore 2 into fluorophore 1 can also be defined similarly using the columns of R12. The total cross-talk Cj for the voxel j can be expressed as:
| (12) |
For the simulations, we consider the recently developed NIR fluorescent proteins (iRFP670, iRFP702, and iRFP720) [13] with emission spectra in Fig. 3(a) and lifetimes of 0.68, 0.78, and 0.93 ns [6]. Consider a rectangular slab of size 2 cm × 2 cm × 2 cm with a 1 mm3 voxel size, with 42 sources and 42 detectors located at the z = 0 cm and z = 2 cm planes, respectively. For TD methods, the bulk absorption and reduced scattering were set to μa = 0.6 cm−1 and μS′ = 10 cm−1, respectively. For spectral methods, μa was assumed to linearly increase from 0.6 cm−1 to 1.2 cm−1 across the wavelength range simulated (650–800 nm), while was kept constant at 10 cm−1. The TD data were simulated for 25 time gates separated by 100 ps, while the spectral data consisted of eight wavelengths separated by 20 nm. The TD and the spectral Green’s functions were generated using a Monte Carlo model [8].
Fig. 3.
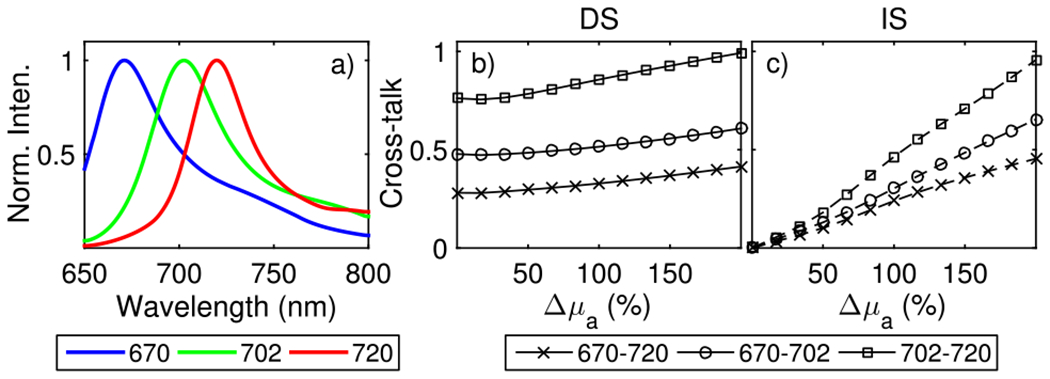
Dependence of cross-talk of the spectral reconstruction methods on the net variation in the bulk absorption across the full spectral range (Δμa). (a) Fluorescence emission spectra for three NIR fluorescent proteins (iRFP670 in blue, iRFP702 in green, and iRFP720 in red) [13]. Total cross-talk [Eq. (12)] for each pair of iRFPs co-localized at the center of a 2 cm thick medium, plotted as a function of Δμa using the (b) DS and (c) IS methods.
Figure 2 illustrates the form of the resolution matrix for TD and spectral methods in Eqs. (6)–(9), for a pair of fluorophores, iRFP702 and iRFP720. To aid in visualization, the rows and columns were binned by a factor of 80. Figure 2 shows that the cross-talk terms for RDS are positive and generally symmetric between the two fluorophores. On the other hand, RIS shows more asymmetry between the two fluorophores with a major portion of the cross-talk being negative. For the TD case, while RDTD contains off-diagonal terms as expected, RATD is a block diagonal matrix with zero cross-talk.
Fig. 2.

Resolution matrices for spectral and lifetime tomography, RDS, RIS, RDTD, and RATD, as given in Eqs. (6)–(9). Each resolution matrix was generated for a 2 cm thick diffuse medium for multiplexing of two NIR fluorophores (iRFP702 and iRFP720). The off-diagonal blocks of each resolution matrix (outlined in red) represent cross-talk between different fluorophores.
We next study the effect of wavelength dependence of the optical properties and the fluorescence spectral overlap on the cross-talk for the MSFT methods, using the same simulation parameters as Fig. 2. Note that the cross-talk in the ATD method is not affected by the optical properties of the medium as the ATD resolution matrix remains block diagonal, regardless of the optical properties. The cross-talk [Eq. (12)] for a voxel at the center of the medium is plotted as a function of the net change in optical absorption, Δμa, across the entire spectral range, for all pairs of the three iRFPs. Δμa was varied from 0% to 200% (from a baseline of μa = 0.6 cm−1), while the bulk scattering was kept constant. Figure 3(c) shows that the cross-talk for IS is zero for all fluorophore pairs when Δμa = 0 and sharply increases for larger Δμa. For the DS method, the cross-talk is significant, even when Δμa = 0 and shows a gradual increase for larger Δμa. Furthermore, the cross-talk increases with increasing spectral overlap for both the IS and DS methods, with the iRFP670/iRFP720 pair showing the least cross-talk. These results are in agreement with the general conditions for zero-cross talk in MSFT presented above. The cross-talk in the IS approach depends on both the spectral overlap and the optical property variation whereas, in the DS case, the cross-talk depends mainly on the spectral overlap.
We next compare the effect of cross-talk on tomographic imaging with MSFT and TFLM (ATD) for a more realistic imaging geometry, using a digital mouse atlas [14] with heterogeneous optical property values [15]. Seventy-two sources were placed beneath, and 72 detectors were placed above a region of the torso covering parts of the skeleton, lung, heart, liver, and kidneys. A fluorescent inclusion (1 mm3) was placed at the centroid of the liver. A 2% shot noise was added to all measurements, and regularization was chosen so that the resolution, measured as FVHM1/3 (FVHM, full volume at half-maximum), reached 5 mm for MSFT and 6 mm for ATD. Figure 4 shows the tomographic reconstructions for the case where the inclusion contained either iRFP670 or iRFP720 alone. While ATD shows negligible cross-talk, the DS shows significant cross-talk for both cases. The IS method showed strong cross-talk into iRFP720 when iRFP670 was used, while the cross-talk from iRFP720 into iRFP670 was minimal. This one-sided cross-talk (also seen in Fig. 2 for the IS case) can be attributed to the redshift of the fluorophore emission spectra due to diffuse propagation [16], which causes the iRFP670 signals to leak into the iRFP720 channel. Finally, we considered the case where both iRFP670 and iRFP720 were simultaneously present (overlapping) in the inclusion, and estimated the ratio of the relative concentration of iRFP670 to iRFP720 using both the MSFT and TFLM methods. The ATD approach resulted in an error of 6.3% in the relative concentration, while the DS and IS methods resulted in significantly higher error rates of 40.5% and 77.9%, respectively, due to cross-talk.
Fig. 4.
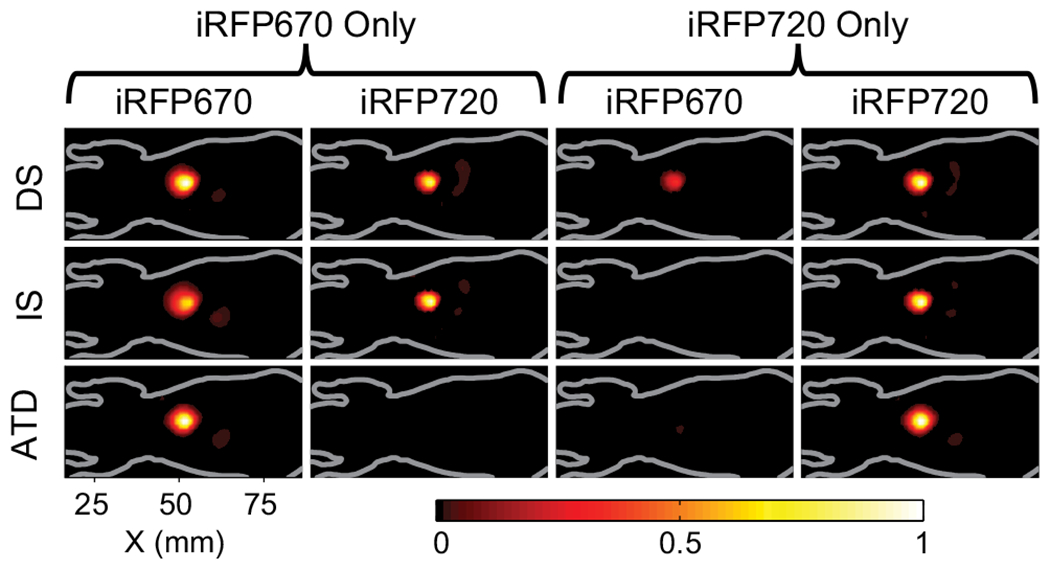
Tomographic reconstructions to compare the cross-talk performance of the DS (top row), IS (middle row), and ATD (bottom row). A single inclusion with either iRFP670 (left two columns) or iRFP720 (right two columns) is located at the centroid of the liver in a digital mouse atlas with heterogeneous optical properties. The images show X–Y slices of the reconstructed concentration averaged over a depth of 6 mm around the inclusion for both iRFP670 and iRFP720 when either alone is present in the inclusion.
In summary, we have presented a comparison of tomographic spectral and lifetime multiplexing using a rigorous mathematical framework based on the model resolution matrix. The actual amount of cross-talk and quantitation error for spectral methods will depend on specific experimental conditions, including spatial and wavelength dependence of the optical properties, the accuracy in optical property estimation, and the degree of spectral overlap. However, the general results of this Letter, namely the superior cross-talk performance of ATD compared to the MSFT methods (due to measurement-level versus voxel-level mixing) and the conditions for zero cross-talk in MSFT are valid, regardless of experimental conditions.
Funding.
National Institute of Biomedical Imaging and Bioengineering (NIBIB) (R01 EB000768, R01 EB015325).
REFERENCES
- 1.Goergen CJ, Chen HH, Bogdanov A, Sosnovik DE, and Kumar AT, J. Biomed. Opt 17, 056001 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Zhao L, Abe K, Rajoria S, Pian Q, Barroso M, and Intes X, Biomed. Opt. Express 5, 944 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Marcu L, French PM, and Elson DS, Fluorescence Lifetime Spectroscopy and Imaging: Principles and Applications in Biomedical Diagnostics (CRC Press, 2014). [Google Scholar]
- 4.Zimmermann T, Rietdorf J, and Pepperkok R, FEBS Lett. 546, 87 (2003). [DOI] [PubMed] [Google Scholar]
- 5.Levenson RM, Lynch DT, Kobayashi H, Backer JM, and Backer MV, ILAR J. 49, 78 (2008). [DOI] [PubMed] [Google Scholar]
- 6.Rice WL, Shcherbakova DM, Verkhusha VV, and Kumar AT, Cancer Res. 75, 1236 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kumar AT, Raymond SB, Boverman G, Boas DA, and Bacskai BJ, Opt. Express 14, 12255 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hou SS, Rice WL, Bacskai BJ, and Kumar AT, Opt. Lett 39, 1165 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bertero M and Boccacci P, Introduction to Inverse Problems in Imaging (CRC press, 1998). [Google Scholar]
- 10.Li A, Boverman G, Zhang Y, Brooks D, Miller EL, Kilmer ME, Zhang Q, Hillman E, and Boas DA, Appl. Opt 44, 1948 (2005). [DOI] [PubMed] [Google Scholar]
- 11.Zhan Y, Eggebrecht AT, Culver JP, and Dehghani H, Biomed. Opt. Express 3, 2036 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hou SS, Bacskai BJ, and Kumar ATN, Opt. Lett 41, 1352 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shcherbakova DM and Verkhusha VV, Nat. Methods 10, 751 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dogdas B, Stout D, Chatziioannou AF, and Leahy RM, Phys. Med. Biol 52, 577 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Alexandrakis G, Rannou FR, and Chatziioannou AF, Phys. Med. Biol 50, 4225 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pera V, Brooks DH, and Niedre M, Biomed. Opt. Express 7, 111 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]


