Identification of Phytoplankton from Flow Cytometry Data by Using Radial Basis Function Neural Networks

Abstract

We describe here the application of a type of artificial neural network, the Gaussian radial basis function (RBF) network, in the identification of a large number of phytoplankton strains from their 11-dimensional flow cytometric characteristics measured by the European Optical Plankton Analyser instrument. The effect of network parameters on optimization is examined. Optimized RBF networks recognized 34 species of marine and freshwater phytoplankton with 91.5% success overall. The relative importance of each measured parameter in discriminating these data and the behavior of RBF networks in response to data from “novel” species (species not present in the training data) were analyzed.

Rapid and accurate identification of vast numbers of phytoplankton cells is essential in aquatic microbial ecology, since these microalgae collectively fuel the marine food web and have been implicated in climate control and some form nuisance blooms. In the past, research has been hampered by the laborious and time-consuming nature of the analysis (usually in the laboratory a long time after sample collection in the field), leading to inaccurate estimates of abundance because of loss due to fixation and storage and to limitations on the number of cells that can be counted. Analytical flow cytometry (AFC), which measures various diffraction, light scatter, and fluorescence parameters, can provide “fingerprints” for individual phytoplankton cells (12, 14). AFC allows easy discrimination of phytoplankton from nonliving particles in seawater (14), and a small number of categories (less than 10) have been distinguished from bivariate scatter plots (12, 14) or by using artificial neural networks (ANNs) (1, 8, 9, 22). In a preliminary study, attempts were made to discriminate 40 microalgal species from each other by using six AFC parameters (2), but half of them were identified with less than 70% success due to the overlap of character distributions. Clearly, the current analytical capacity falls well short of being able to analyze the full taxonomic spectrum in the world’s oceans. For discrimination of large numbers (hundreds) of taxa, different and/or more parameters are required.

Cytometry. Currently available commercial flow cytometers have been designed for use in the laboratory and are able to cope with only a relatively narrow range of particle sizes. For marine use a machine is required that can be used at sea; can cope with a range of cell sizes to include large phytoplankton (>5 μm in diameter), nanoplankton (2 to 5 μm), and picoplankton (<2 μm); is tailored specifically to allow detection of pigments found in phytoplankton; and can sort particles electrostatically or mechanically.

Data analysis problem. AFC yields vast quantities of multivariate data, which present a considerable challenge for data analysis. While multivariate statistical methods have been used (e.g., see references 4 and 6), it can be difficult to find the appropriate technique, and problems may arise if invalid assumptions are made about the data distribution, e.g., assuming normality when data actually have a bi- or multimodal distribution. The use of ANNs is a powerful alternative technique that makes, in general, only minimal assumptions about the nature of the data distribution.

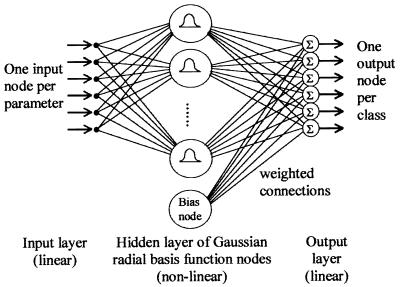
ANNs used for identification generally consist of an interconnected layered structure of simple data-processing elements (nodes): an input layer, which serves merely to distribute input data (one node per identification character); a hidden layer, which models the data distribution; and an output layer, which indicates the identification (one node per taxon) (Fig. 1). When presented with a multivariate data pattern drawn from the probability distribution of one of a number of categories (taxa), ANNs are able to associate the pattern with the category to which it belongs (3, 11). The ANN learns this association in a “training phase,” during which the internal structure is adjusted in response to presentation of a representative sample of data patterns for each of the taxa to be identified, together with information as to their correct identification (the “training data”). Once successfully trained, an ANN can recognize patterns which, although never before presented, are sufficiently similar to the training data to allow the correct association to be drawn. The multilayer perceptron network, also known as the backpropagation network, is the ANN paradigm most commonly applied to biological identification problems, including preliminary studies that use flow cytometry data (1, 2, 8, 9, 22). However, this ANN trains very slowly and may perform poorly if the data distribution is complex (19). Radial basis function (RBF) ANNs, on the other hand, are at least as successful in biological identification as other network types (18, 27, 28), train much more rapidly (28), and allow criteria to be applied to reject as being “unknown” patterns from taxa upon which the network has not been trained (19). Rapid training is important, as when additional taxa are encountered ANNs must be retrained. The ability to recognize unknowns is also essential, since when natural samples are analyzed it is likely that several or many species will be encountered which have not been used for training the network.

FIG. 1.

Schematic diagram of an RBF neural network classifier. Raw data are distributed from the input layer via a “hidden” layer of processing units or nodes to an “output layer” where the network’s decision is formed. The bias node has a constant output value irrespective of input: its use allows output layer nodes to add a constant offset.

RBF neural networks. RBF ANNs model the distributions of the data categories (taxa) to be recognized by superimposing kernels (basis functions) over the data input space. These kernels (implemented by the hidden-layer nodes [HLNs]; Fig. 1) have a defined response to input data that varies depending on the distance of the data point from the center of the kernel. The value of a basis function at any point in the data space is given by a nonlinear function of the scaled distance between that point and the basis function center. A distance scaling parameter for each basis function controls its width or spatial extent.

Training an RBF ANN occurs in two separate stages: determination of the position and size of the basis functions, followed by calculation of the weight coefficients for the output layer nodes (11, 13, 20, 27). The first stage is subdivided into two steps: selection of the basis function centers, followed by selection of the width of each basis function. The second stage is a simple least-mean-squares optimization procedure, either iterative (13) or utilizing a matrix pseudoinverse method (11, 20, 27). Optionally, these may be followed by a third stage of gradient-descent reduction of error, during which the basis functions and weights are simultaneously adjusted to improve classification performance on the training data (11, 16, 25). The training procedure may be varied by changing the algorithm used to select the basis function centers and by changing the form of the basis function around each center. Several factors related to network configuration affect how well an RBF ANN trains, including the number, positioning, shape (radially or non-radially symmetric), and width of basis functions. Optimal configuration must be determined by experiment.

This study reports on successful discrimination of 34 marine and freshwater phytoplankton taxa by using RBF networks trained on 11-parameter AFC data, obtained by using the EurOPA (European Optical Plankton Analyser) (7, 14). The importance of each parameter to the networks in performing this discrimination is assessed, and the ability of RBF ANNs to reject patterns from novel taxa as unknown is examined.

MATERIALS AND METHODS

Phytoplankton cultures.

Eight freshwater species (Table 1) were grown in batch culture in Woods Hole medium (10) for 3 to 4 days at 20°C under a daily 16-h (light)–8-h (dark) regimen (100 microeinsteins m⁻² s⁻²). Five species of cyanobacteria were grown in O-2 medium (24) under the same conditions. Twenty-one marine species (obtained from the Plymouth Culture Collection, Marine Biological Association, United Kingdom) were grown in F/2 enriched seawater medium (10) under continuous illumination at 300 microeinsteins m⁻² s⁻¹ at 17°C.

TABLE 1.

Percent correct identification of test data for all 34 species (400 test patterns per species), after gradient descent optimization procedure, with an RBF ANN having 68 HLNs with Gaussian kernels positioned by the LVQ algorithm

Species	Width (μm)	Length (μm)	% Correct identification	Notesa
Alexandrium tamarensis	25–30	35–45	98.2	m
Anabaena flos-aquae	4–6	10–1,000	96.0	fc1
Aphanizomenon sp.	4–7	30–600	92.5	fc1
Chlamydomonas sp.	10–20	15–30	84.0	f
Chlorella salina	4–6	4–6	82.2	m
Chlorella vulgaris	4–6	4–6	94.2	f
Chroomonas salina	5–7	9–11	99.2	me
Chrysochromulina camella	5–7	6–8	90.8	m
Cryptomonas baltica	7–9	10–15	98.5	me
Cryptomonas calceiformis	7–9	10–15	99.0	me
Dunaliella tertiolecta	6–8	7–9	94.8	m
Emiliania huxleyii	4–6	4–6	96.8	m
Gymnodinium simplex	6–10	6–10	85.5	m
Gyrodinium aureolum	35–45	35–45	96.2	m
Halosphaera russellii	12–15	15–20	84.2	m
Heterocapsa triquetra	15–27	15–27	92.8	m
Microcystis aeruginosa	4–6	4–7	96.8	fc
Nitschia palea	40–70	40–70	89.0	m
Ochromonas sp.	3–12	3–12	94.8	me
Oscillatoria sp.	1–3	10–500	97.0	fc1
Oscillatoria redeckii	1–3	10–500	97.0	fc1
Phaeocystis globosa	3–4	3–4	88.8	m
Porphyridium pupureum	4–6	4–6	98.2	m
Prymnesium parvum	3–4	3–5	95.8	m
Pseudopedinella sp.	8–10	8–10	68.2	m
Pyramimonas obovata	4–8	4–8	87.2	m
Rhodomonas sp.	5–7	10–12	99.0	me
Scenedesmus quadricauda	10–20	20–30	94.2	f2
Scenedesmus subspicatum	3–4	8–12	87.5	f
Selenastrum capricornutum	2–3	6–8	80.8	f
Skeletonema costatum	4–6	6–8	87.2	m
Staurastrum sp.	30–40	35–50	96.8	f
Tetraselmis rubens	5–7	10–12	71.0	m
Thalassiosira rotula	8–10	8–10	97.2	m

^am, marine species; f, fresh water species; c, containing phycocyanin (cyanobacteria); e, containing phycoerythrin. Colony types: 1, filamentous; 2, coenobium of four cells. 

EurOPA flow cytometer and data.

The EurOPA is a compact and easily transportable flow cytometer designed specifically for the analysis of phytoplankton at sea; it was developed during the course of a European Union project in the Marine Science and Technology (MAST-II) programme (7, 14). It allows the simultaneous collection of flow cytometric parameters for particles of up to 500 μm in width and several millimeters in length and uses argon (488-nm) and helium-neon (633-nm) lasers selected to have wavelengths optimal for the excitation of the photosynthetic pigments found in plankton, as well as data acquisition electronics able to cope with a total signal magnitude range of over six decades between the smallest and largest particles encountered during analysis of mixed field samples (14). It also incorporates novel cytometric techniques to improve the capacity for discrimination between species, including a diffraction module (a 5-by-5 square array of photodiode light detectors) which captures particle shape information through polar and azimuthal resolution of the light diffracted at small angles to the beam by particles in flow (5). Pulse-shape analysis of the fluorescence and light scatter signals reveals morphological information about the longitudinal profile of the particles, and a video imaging module allows electronic image capture of particles in flow (26).

Eleven-parameter data (Table 2) were collected for each of 34 marine and freshwater phytoplankton species (Table 1) by using the EurOPA. Seven of the parameters were fluorescence and light scatter measurements, and the other four were from the diffraction module. The data for each species were plotted on two-dimensional scatterplots, on which gates were placed to eliminate clusters corresponding to background noise and contamination. Approximately 1,000 gated events were selected for each species. From these, two independent data sets each containing 400 events were created for each species by random selection without replacement. These were used to create files of training and test data, each containing 400 events per species. The performance of each ANN was assessed by measuring the overall proportion of test patterns that were identified correctly, and a “misidentification matrix” was constructed (3) showing the proportion of the test patterns for each species that were identified by the network as each of the possible classifications. The use of an independent test data set is essential to evaluate the network’s ability to generalize.

TABLE 2.

Parameters measured by the EurOPA instrument

Parameter type and no.	Parameter
Fluorescence-light scatter
1	Time of flight
2	Forward light scatter
3	Perpendicular light scatter
4	Red fluorescence excited at 488 nm
5	Orange fluorescence excited at 488 nm
6	Green fluorescence excited at 488 nm
7	Red fluorescence excited at 630 nm
Diffraction module
8	Vertical bar
9	Horizontal bar
10	Outer ring
11	Inner ring

Computer hardware and software.

All RBF networks were implemented by software written in C by one of the authors (M.F.W.) on a PC.

Optimizing the number of basis functions.

The number of basis functions was varied between one and four for each of the 34 classes. The upper limit of 136 basis functions (i.e., four per taxon) was determined primarily by memory limitations of the computer hardware that restricted the number of HLNs and associated weight values that could be stored (although this is no longer a problem with the increasingly powerful machines now becoming available).

Selecting between nonradially symmetric and radially symmetric basis functions.

The use of the Euclidean distance metric yields hyperspherical (i.e., radially symmetric) basis functions, whereas the Mahalanobis-generalized distance allows networks with hyperelliptical (i.e., non-radially symmetric) basis functions, which can give better modelling of elongated data clusters. All the basis functions used were Gaussian. Radially symmetric basis functions had the following form:

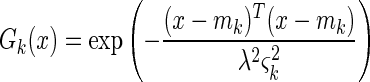where x is the presented pattern and m_k is the center of basis function k, ς_k is the root-mean-square average Euclidean distance between m_k and the cluster of training data patterns associated with it (i.e., those training patterns which are closer to m_k than to any of the other basis function centers), and λ is the distance scaling parameter controlling the basis function width. Non-radially symmetric basis functions had the following analogous form:

where ∑_k is the variance-covariance matrix for the cluster of training patterns around m_k and N is the number of dimensions of the input data.

Optimizing basis function width.

The shape of the Gaussian basis functions can be adjusted by changing the width parameter λ. As λ is decreased, the width of each basis function (the size of the receptive field) decreases, and the functions become more sharply peaked around the center. Broader functions can allow smoother interpolation between basis functions. λ was varied between 1 and 14.

Basis function center selection strategy.

Three methods of center selection were compared: random selection of patterns from the training data set, random selection followed by the K-means algorithm (13, 23), and random selection followed by the Kohonen LVQ algorithm (15, 16).

Use of gradient-descent algorithm.

The gradient descent algorithm was applied after the networks had been trained. The procedure allows simultaneous iterative adjustment of all network parameters (the basis function center positions, the basis function size and shape, and the values of the weighted connections between the hidden and output layers) in order to minimize the identification error on the training data (11, 17, 25).

Construction of optimal RBF network to discriminate 34 species.

After the experiments to determine effects of network configuration on training, an RBF network was trained to discriminate between all 34 species simultaneously. Two non-radially symmetric Gaussian basis functions were used per output class (i.e., 68 HLNs) with a width parameter λ of 1.25, the centers of which were selected through use of the Kohonen LVQ algorithm. This particular architecture was found (see below) to be a good compromise, producing networks which were computationally efficient (necessary for pattern identification at rates comparable with data acquisition rates), yet with near-optimal classification performances (typically within 1% of the optimal performance).

After the training step, the ability of the network to identify the 400 test data patterns correctly for each species was measured. The gradient-descent optimization algorithm was applied to reduce identification error as far as possible on the training data, and the network was tested again to find the extent of the identification performance improvement.

Effect of exclusion of individual parameters.

To investigate whether any of the 11 parameters were redundant in making the identifications, each was removed in turn from the training data patterns, and an RBF network using the above architecture trained on the resulting reduced-dimensionality data. Additionally, networks with the above architecture were trained utilizing the seven fluorescence light scatter-size measurements alone (parameters 1 to 7) and the four diffraction-pattern parameters alone (parameters 8 to 11). After training, the abilities of the networks to identify the test data patterns correctly were compared to the results for a network that used all 11 parameters.

Rejection of data patterns from novel taxa.

An RBF network with the above architecture was constructed and trained to discriminate between 20 species by using all 11 parameters. These 20 species were a randomly selected subset of the 34 species present in the original training data. The network was then used to test two possible criteria for the rejection of data patterns from “novel” taxa, i.e., the 14 species not used for training: (i) rejection if the summed value of all the basis functions (i.e., the sum of the outputs of all the HLNs of the network excluding the bias node) was less than a threshold value θ and (ii) rejection if the output of the closest basis function (i.e., the HLN with the largest output) was less than θ. Two indicators of performance were measured for each criterion: the proportion of the test data patterns for the 20 “known” species that were rejected (incorrectly) and the proportion of test data patterns for the 14 “novel” species that were rejected (correctly). For each criterion, investigation was made of the effect of varying the threshold value θ from 0.0 (i.e., no rejection) upwards on the proportion of test data patterns from the 20 known and 14 unknown species that were rejected.

RESULTS AND DISCUSSION

Optimization of RBF networks.

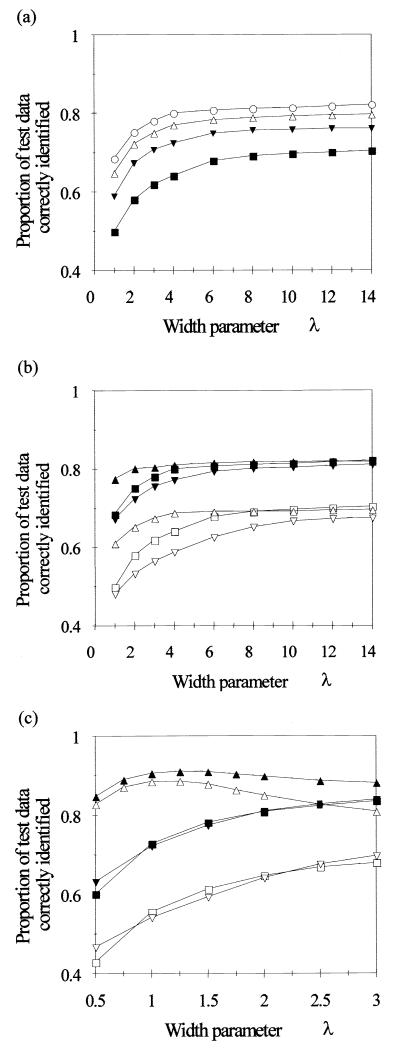
Increasing the number of basis functions (up to the limits imposed by the computer hardware) always improved performance on test data for networks employing radially symmetric (i.e., Euclidean-distance) basis functions (Fig. 2a). Increasing the basis function width parameter improved performance up to a point for such networks, although the value for which the performance approached its maximum was different for the different basis function selection procedures (Fig. 2b). While use of the LVQ-supervised clustering algorithm to adjust the center selection produced networks with much better performance where basis functions were comparatively “narrow,” increasing the width of the basis functions removed this discrepancy, and for wider basis functions the performance of networks employing LVQ to select centers was no better than that of networks employing random centre selection. Use of the K-means algorithm to adjust the center selection was always least successful.

FIG. 2.

Effect of basis function width, shape, and placement strategy on the proportion of test data patterns for 34 species that were identified correctly. (a) Effect of basis function width, for radially symmetric basis functions. Basis function centers were a randomly selected subset of the training data. Curves for four different network sizes are shown: 34 HLNs (■), 68 HLNs (▴), 102 HLNs (▵), and 136 HLNs (○). (b and c) Effect of basis function center selection strategy for radially symmetric basis functions (b) and non-radially symmetric basis functions (c) (formed by using the Mahalanobis distance). Curves for two network sizes (34 HLNs [open symbols] and 136 HLNs [closed symbols]) are shown for three selection strategies: random selection (squares), random selection followed by K-means unsupervised clustering (inverted triangles), random selection followed by LVQ supervised clustering (triangles).

Use of non-radially symmetric basis functions improved performance markedly when the LVQ center selection strategy was employed. The improvement was less for the other center selection strategies (which both gave results comparable to, but generally marginally better than, networks with radially symmetric basis functions with the same width parameter). Increasing the number of HLNs had far less effect on the optimum performance than in the case of radially symmetric basis functions. The optimum width parameter value was approximately 1.25 (Fig. 2c).

Generally, two HLNs per output class, implementing non-radially symmetric basis functions with the centers initially selected by using the LVQ strategy offered a reasonable compromise between performance and computational efficiency. (This is less of a problem with faster machines with more memory.) Doubling the number of HLNs from 68 to 136 marginally improved performance on test data (by 1%) but also doubled the computational effort. The fact that two non-radially symmetric HLNs per class were sufficient for these data may reflect the fact that the class data distributions were generally uni- or bimodal. More complex data distributions would require the use of a larger number of HLNs per class for optimal performance. The LVQ algorithm combines the desirable property of allocating more basis functions to cover densely populated regions with the use of class membership information to produce a set of basis functions that reflect the population densities of each class rather than of the combined density of all classes together. A width parameter λ of 1.25 was optimal with this configuration, though notably this is much wider than recommended in some of the literature (11, 13) by a factor 2.9 (and by 7.0 for Euclidean basis functions).

Performance of optimal network.

The optimal network identified 90.3% of the test data patterns correctly after training. Application of the gradient-descent optimization procedure improved this to 91.5% (Table 1), with the largest single improvement occurring through a reduction in the percentage of Oscillatoria misidentified by the network as Aphanizomenon (from 10.2 to 2.0%). Six species were recognized with 98.0% success or better (Alexandrium tamarensis, Chroomonas salina, Cryptomonas baltica, Cryptomonas calceiformis, Porphyridium pupureum and Rhodomonas). All other species were recognised with at least 80% success, with the exceptions of Tetraselmis rubescens (71.0% success, confused primarily with Gymnodinium simplex and Chlorella salina) and the Pseudopedinella species (68.2% success, confused primarily with Halosphaera russellii but also with Phaeocystis globosa). The excellent performance of the network described here for recognition of 34 species is far superior to the performance of any of the neural networks described previously for identifying phytoplankton (1–4, 9, 16, 22), in terms of the simultaneous recognition of a large number of species with a high recognition accuracy.

Effect of exclusion of parameters.

It is important to know how well phytoplankton can be discriminated if one (or indeed more than one) parameter is missing. For example, if the flow cytometer is being used at sea, parameters may be lost because of problems with optical alignment or failure of one of the lasers in a multilaser instrument such as the EurOPA. The four fluorescence parameters appeared to be the most important (since their individual exclusion resulted in the largest decrease in the proportion of successfully identified test data patterns), although no single parameter decreased performance by more than 5% when excluded (Table 3). Clearly, good identification was achieved even when one parameter was missing, and the effect of the loss of several parameters could be investigated in a similar way.

TABLE 3.

Effect of exclusion of each parameter on the percent correct identification of an RBF ANN trained to discriminate 34 species^a

Parameter omitted	% Correct identification
	Training data	Test data
None	91.9	90.3
Time of flight	90.7	89.0
Forward light scatter	90.8	89.0
Perpendicular light scatter	90.6	89.0
Fluorescence blue-red	86.8	85.2
Fluorescence blue-orange	89.9	88.5
Fluorescence blue-green	89.2	87.4
Fluorescence red-red	87.1	85.4
Vertical bar	92.0	90.4
Outer ring	91.0	89.6
Horizontal bar	91.8	90.3
Inner ring	91.7	90.2
All diffraction module parameters	90.4	88.8
All parameters not belonging to diffraction module	48.6	46.7

^aNetworks used 68 non-radially symmetric Gaussian basis functions (width parameter λ = 1.25), the centers of which were selected by using the Kohonen LVQ algorithm. 

Exclusion of certain parameters adversely affected the identification of some species more than others, revealed by examination of the misidentification matrices (Table 4). This indicates that the particular parameter is an important discriminatory character of the flow cytometric “fingerprint.” For example, in comparison to the network trained by using all parameters, exclusion of parameter 4 (fluorescence blue-red) markedly decreased the identification success of Chrysochromulina camella, Tetraselmis rubens, Gymnodinium simplex, Pseudopedinella spp., Chlorella salina, Selenastrum capricornutum, and Skeletonema costatum. In particular, there was a large increase in the confusion between Chrysochromulina camella and Chlorella salina, with the proportion of the former misidentified as the latter increasing from 1.0 to 12.2% and of the latter misidentified as the former increasing from 0.0 to 15.8%. Parameter 5 (fluorescence red-red) was found to be important in the discrimination of Chrysochromulina camella from Thalassiosira rotula, Pseudopedinella spp. from Halosphaera russellii and Phaeocystis globosa, and Selenastrum capricornutum from Nitschia palea.

TABLE 4.

Percent identification success when single parameters were excluded during training of RBF networks (with architecture as in Table 2) to discriminate 34 plankton species

Species	None	% Identification with excluded parametersa:
		1	2	4	5	6	7	1–7
Chlorella salina	83.0	81.5	79.5	62.8	81.8	79.8	71.5	11.8
Chlorella vulgaris	93.2	93.5	93.0	91.8	93.5	94.0	92.8	79.5
Chrysochromulina camella	91.0	90.5	90.5	65.8	88.5	90.5	70.8	41.5
Cryptomonas baltica	98.5	98.2	98.5	98.5	92.0	96.2	98.8	71.2
Cryptomonas calceiformis	99.0	99.0	98.8	98.8	97.8	98.8	98.8	87.8
Dunaliella tertiolecta	94.0	92.2	93.8	94.8	94.2	91.2	95.2	92.8
Gymnodinium simplex	83.8	83.5	83.8	70.0	79.8	70.2	76.2	32.2
Halosphaera russellii	83.5	63.0	76.2	76.5	81.2	82.2	77.5	51.2
Heterocapsa triquetra	92.0	90.5	90.8	91.0	84.8	90.5	89.8	63.5
Microcystis aeruginosa	95.5	95.2	95.2	95.2	95.0	94.8	95.8	78.2
Oscillatoria sp.	88.8	90.8	89.2	88.5	89.0	89.5	88.8	77.2
Oscillatoria redeckii	96.5	97.0	97.2	97.0	96.8	96.5	96.2	69.5
Prymnesium parvum	95.2	93.8	94.0	94.0	93.8	84.8	93.5	49.8
Pseudopedinella sp.	64.0	63.0	63.0	44.2	65.8	48.0	47.0	23.0
Selenastrum capricornutum	77.2	77.8	76.5	65.0	77.0	79.8	51.8	34.5
Skeletonema costatum	86.5	85.5	84.8	78.8	82.5	75.8	78.2	21.8
Staurastrum sp.	96.2	95.5	95.5	96.0	96.2	96.5	95.8	81.0
Tetraselmis rubens	64.0	61.0	51.0	48.0	62.8	54.5	52.0	10.5

^aOnly parameters and species for which there were marked differences from the network trained on all 11 parameters have been included. Parameter numbers are as presented in Table 2. 

Occasionally, exclusion of a parameter resulted in a slight increase in successful identification of a species (Table 4). This probably only reflects slight differences in the location of decision boundaries and was not accompanied by an increase in overall successful identification.

Addition of the four diffraction parameters to the other seven parameters increased overall performance on the test data by around 1%, in comparison to the network trained by using only the other seven parameters. This indicates that its inclusion gives little advantage for the majority of species. A network using the four diffraction parameters alone only achieved about 47% success overall. However, some species were successfully discriminated solely on the basis of the four diffraction parameters, e.g., Dunaliella tertiolecta (92.8% success), Cryptomonas calceiformis (87.8% success), Staurastrum (81.0% success), Chlorella vulgaris (79.5% success), and Microcystis spp. (78.2% success). Thus, for some species the particle shape is a particularly distinctive feature, and the information gathered by the diffraction module is useful in the discrimination of these species.

Rejection of data patterns from “novel” taxa.

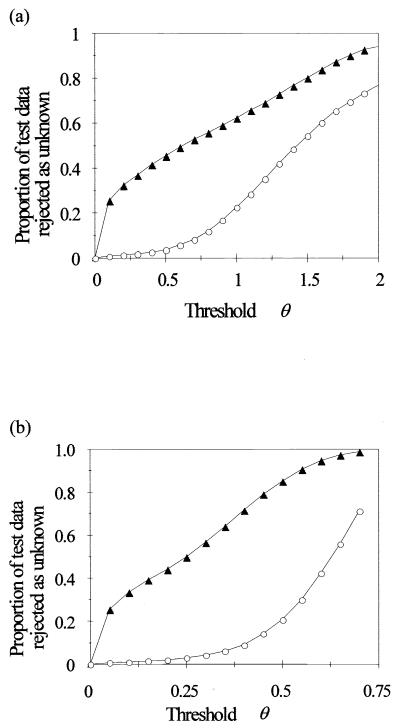
For criterion 1 (a constraint on summed output of all HLNs), as the threshold value was increased, the proportion of rejected data patterns from the 14 novel species initially rose sharply to around 20% and thereafter showed an approximately linear dependence on θ (Fig. 3a). The proportion of rejected data patterns from the 20 known species was quite low for θ values of ≤0.5 but thereafter increased more rapidly than the proportion of rejected patterns from the novel species. Criterion 2 (a constraint on the value of the maximum HLN output) gave a much better ratio between the proportion of novel species rejected against the proportion of known species rejected (Fig. 3b). For example, use of criterion 1 with a θ of 0.7 caused the proportion of correctly identified data patterns for the known species to decrease from 93.8% (no rejection) to 86.8% but successfully rejected 52.8% of the data patterns from the novel species. Use of criterion 2, with a θ value of 0.4, caused virtually the same decrease in the proportion of correctly identified data patterns for the known species but increased the proportion of successfully rejected patterns from the novel species to 71.6% (Table 5). In each case four of the novel species were successfully rejected with 100% accuracy.

FIG. 3.

Use of a threshold parameter θ as a constraint on the summed output of all HLNs (a) and the maximum HLN output value (b) to reject data from “novel” species (not present in the training data). The proportion of test data patterns failing to satisfy the constraint, and therefore rejected as unknown, is shown for the 20 trained species (○) and the 14 novel species (▴).

TABLE 5.

Percentage of test data patterns correctly identified or rejected as “unknown” by each of two criteria for 20 “known” species (on which the network had been trained) and for 14 “novel” species^a

Species	% Test data patternsb
	Criterion 1		Criterion 2
	Correctly identified	Rejected as unknown	Correctly identified	Rejected as unknown
Known
Alexandrium tamarensis	84.8	14.8	87.2	12.8
Aphanizomenon sp.	66.5	31.5	87.0	11.2
Chlorella vulgaris	94.0	2.2	93.5	4.2
Chroomonas salina	86.8	13.2	91.2	8.8
Chrysochromulina camella	89.2	3.0	86.2	7.2
Emiliania huxleyii	96.2	2.5	92.2	7.0
Gymnodinium simplex	90.8	1.2	86.2	6.2
Gyrodinium aureolum	95.0	1.8	88.2	9.5
Halosphaera russellii	82.0	3.0	80.5	7.2
Heterocapsa triquetra	92.5	3.5	87.2	10.2
Microcystis aeruginosa	89.8	10.0	91.5	8.5
Nitschia palea	87.5	11.2	83.5	15.5
Oscillatoria sp.	94.2	4.5	95.5	3.0
Phaeocystis globosa	89.0	1.2	84.2	8.0
Porphyridium pupureum	89.8	10.2	93.5	6.5
Pyramimonas obovata	89.5	2.0	84.5	9.2
Skeletonema costatum	87.8	10.0	87.2	10.5
Staurastrum sp.	79.5	20.5	87.8	12.2
Pseudopedinella	67.5	2.8	62.5	9.8
Thalassiosira rotula	82.8	16.5	85.5	14.0
Avg	86.76	8.28	86.76	9.08
Novel
Anabaena flos-aquae		97.2		87.0
Chlamydomonas		73.8		80.8
Chlorella salina		5.0		30.0
Cryptomonas baltica		100.0		100.0
Cryptomonas calceiformis		100.0		100.0
Dunaliella tertiolecta		1.5		69.2
Ochromonas sp.		34.8		70.8
Oscillatoria redeckii		100.0		100.0
Prymnesium parvum		6.5		59.8
Rhodomonas sp.		100.0		100.0
Selenastrum capricornutum		3.0		27.5
Scenedesmus quadricauda		93.5		97.0
Scenedesmus subspicatum		11.0		26.8
Tetraselmis rubens		12.8		54.0
Avg		52.79		71.64

^aThe network used 40 non-radially symmetric Gaussian basis functions (width parameter = 1.25), the centers of which were positioned by using the Kohonen LVQ algorithm. 

^bCriterion 1, rejection if sum of HLN outputs is <θ, for θ = 0.7; criterion 2, rejection if maximum HLN output is <θ, for θ = 0.4. For comparison, rejection thresholds were selected that gave comparable overall proportions of correctly recognized patterns for the known species. 

Clearly, the best way of achieving good rejection was through use of a threshold value for the maximum HLN output (with rejection of any pattern not close enough to any of the basis function centres to cause any of the HLNs to produce a large enough output value), as was also found in a similar study (19). Since the width of individual basis functions is different (governed by the spread of the training data patterns grouped with the basis function center during the training procedure), the critical distance from each center beyond which patterns are rejected will vary from one basis function to another. Use of the sum of the HLN outputs, while effective for some species, did not allow successful rejection of others. In some regions of the data space surrounded by basis functions, the combined sum may still be large enough to prevent rejection, even for patterns comparatively far from any of the basis function centres.

The ability of the RBF ANN algorithm to detect novel patterns unlike any of the known taxa is likely to be of prime importance in an identifier capable of analyzing “field” samples, which may well contain either novel species or populations of a known species rendered atypical by the environmental conditions.

Future developments.

The approach clearly has considerable potential, but extending it from using pure cultures in the laboratory to mixed populations in natural aquatic environments poses a number of problems. First, it is essential to be able to obtain “good” training data from the environment of interest, since conditions under which cells grow affect their flow cytometric signatures and networks trained on data from cultures may not perform well in identifying field samples. Second, scaling up to a large number of species is nontrivial, and large numbers may make it impractical to train single large networks. Third, though estimating proportions of different species present in mixed samples is straightforward when there is no uncertainty in identification of individual cells, when the identity is equivocal (due to overlapping flow cytometric parameter distributions), recourse to statistical methods is needed in order to place confidence limits on the accuracy of the estimated proportions. These problems are all being addressed currently.