Temperature dependence of ultrasonic attenuation in human calcaneus

Abstract

Ultrasonic attenuation in calcaneus has been shown to be a useful measurement for the diagnosis of osteoporosis. Several studies indicate that this measurement is affected by temperature fluctuations although the fundamental causes for this are currently not well understood. To investigate this phenomenon, six defatted human calcanei were interrogated in vitro at six temperatures ranging from 10°C to 40°C. The temperature-related variation was −0.18 dB/cmMHz°C (95% confidence interval: −0.27 dB/cmMHz°C, −0.10 dB/cmMHz°C). This study reinforces the notion, advanced by other investigators, that temperature-related effects need to be taken into account when performing diagnostic measurements that require high precision (such as monitoring responses to drug intervention), will aid in the interpretation of in vivo experiments designed to investigate temperature-dependent precision limitations, will facilitate comparisons between in vitro studies normally carried out at room temperature with in vivo studies carried out at body temperature, and fills a gap in the compendium of measurements of temperature dependences of acoustic properties of biologic tissues.

Introduction

Bone sonometry is becoming an increasingly popular technique for the diagnosis of osteoporosis. Compared with traditional X-ray methods, ultrasound offers advantages including low cost, lack of ionizing radiation, speed, simplicity, and portability. Many systems measure broadband ultrasonic attenuation (BUA) and/or speed-of-sound (SOS) in the calcaneus. It has been demonstrated that BUA is highly correlated with calcaneal mass density (Langton et al., 1984, Rossman et al., 1989, Tavakoli and Evans, 1991, and Langton et al., 1996). Calcaneal ultrasonic measurements (BUA combined with SOS) have been shown to perform well for prediction of hip fractures in elderly women in prospective (Hans et al., 1996, and Bauer et al., 1997) and retrospective (Schott et al., 1995, Turner et al., 1995, and Glüer et al., 1996) studies.

Measurements of ultrasonic properties may be influenced by many factors other than those of primary concern, i.e. bone mineral density (BMD) and microarchitecture of the calcaneus. Some of these extraneous factors include water bath temperature, foot temperature, degree of edema, heel positioning, and skin preparation (Morris et al., 1997, Barkmann and Glüer, 1998, and Chappard et al., 1999). In particular, attenuation and sound speed are known to depend on temperature in many tissues (Haney and O’Brien, 1986 and Duck, 1990).

Morris and co-workers (1997) measured calcaneal BUA and SOS in a subject as a function of time after switching the foot from a 40°C water bath to a 21°C water bath. They found that BUA decreased by 3.8% while SOS increased by 0.8% over a 30 minute interval. (The opposite direction of these temperature-dependent trends constitutes support for using a linear combination of BUA and SOS to assess density. The two temperature dependences tend to cancel each other out yielding a linear combination with reduced temperature dependence.) Chappard et al. (1999) monitored BUA and SOS in 11 premenopausal women, 10 postmenopausal women, and 10 men as functions of time over a 25 minute interval after immersion into a 30°C water bath. Contrary to Morris et al., Chappard et al. observed BUA to increase by 20.7% (postmenopausal women), 6.8% (premenopausal women), and 2.5% (men) and SOS to decrease by 0.8% in both groups of women and increase by 0.4% in men. Barkmann and Glüer (1998), utilizing a 30°C temperature-stabilized water bath and measuring heel temperature with an infrared sensor in six healthy subjects, have reported temperature dependences of +0.27±0.09 dB/MHz°C (BUA) and −3.6±0.5 m/s°C (SOS).

These findings result from the superposition of many complex phenomena including the temperature dependences of acoustic properties of each of the various tissues in the sound path through the heel. In order to understand the basic mechanisms responsible for the above-mentioned experimental results, it is useful to investigate each of the constituent components of the heel individually. The purpose of the present study was to isolate effects due to the mineralized trabecular bone component. In this investigation, attenuation was measured in six calcaneus samples in vitro at six different temperatures. In addition to the applicability to the development of higher precision methodology and interpretation of calcaneal ultrasonic measurements, this investigation provides additional data to the existing compendium of measurements of temperature dependences of acoustic properties of biologic tissues, nicely compiled by Haney and O’Brien (1986).

Methods

Biological Methods

Six human calcaneus samples (genders and ages unknown) were obtained. They were defatted using a trichloro-ethylene solution. Defatting was presumed not to significantly affect measurements since attenuation of defatted trabecular bone has been measured to be only slightly different from that of bone with marrow left intact (Langton et al., 1996). The cortical lateral layers were sliced off leaving two parallel surfaces with direct access to trabecular bone. The samples were not preserved with formaldehyde. The thicknesses of the samples varied from 14 to 21 mm. The cross sectional areas ranged from 14.7 to 27.0 cm². In order to remove air bubbles, the samples were vacuum degassed underwater in a desiccator.

After vacuum, the samples were allowed to thermally equilibrate for at least 30 minutes in a temperature controlled water bath at the desired temperature prior to ultrasonic interrogation. The temperature was monitored using a digital thermometer. Ultrasonic measurements were performed in distilled water at the same temperature. For measurements below room temperature (approximately 10°C), a Model RU-5 Dip Cooler (Techne Inc., Princeton, NJ) was used. For measurements above room temperature (approximately 25°C, 30°C, 35°C, and 40°C), an immersion heater (Bradshaw International, Santa Fe Springs, CA) was used. Chronologically, the experiments were conducted in the following order: 10°C, 40°C, 20°C, 30°C, 25°C, and 35°C. (This pseudo-random sequence was chosen in order to minimize any potential artifactual apparent trends due to temporally-related drift in measurement procedure).

The relative orientation between the ultrasound beam and the calcanei was the same as with in vivo measurements performed with commercial bone sonometers, in which sound propagates in the mediolateral (or lateromedial) direction. Density of samples was measured from separate measurements of mass and volume. Mass was measured using a balance. Volume was measured by separate measurements of thickness and cross-sectional area. Thickness between the two parallel planar surfaces (cut by machine) was measured using calipers. Cross-sectional areas were measured by computer processing of scanned images of the samples.

Ultrasonic Methods

A Panametrics (Waltham, MA) 5800 pulser/receiver was used. Samples were interrogated in a water tank using Panametrics circular (diameter = 1”), focussed, broadband transducers with center frequencies of 1 MHz. Received ultrasound signals were digitized (8 bit, 10 MHz) using a LeCroy (Chestnut Ridge, NY) 9310C Dual 400 MHz oscilloscope and stored on computer (via GPIB) for off-line analysis.

Attenuation was measured using a standard through-transmission method. Using two opposing coaxially-aligned transducers (one transmitter and one receiver), transmitted signals were recorded both with and without the bone sample in the acoustic path. In the former case, the beam passed through water, then the sample, then water again prior to reception. The bone samples were larger in cross-sectional area than both transducer apertures. The power spectrum was estimated from the average squared magnitude of fast Fourier Transforms of four to eight digitized radio frequency signals. Attenuation coefficient was then estimated using a log spectral difference technique (Kuc and Schwartz, 1979). Due to the high porosity of the bones, the transmission coefficients at the water/bone interfaces were assumed to be approximately one. Attenuation vs. frequency was least-squares fit to a linear function over the range from 0.25 MHz to 1.1 MHz. Attenuation was then characterized by the slope of the resulting line. This parameter is often referred to as “normalized broadband ultrasonic attenuation” (nBUA) in the bone densitometry field (Langton et al., 1996) and “attenuation slope” in the most of the rest of the biomedical ultrasonics field (Kuc and Schwartz, 1979).

In general, this substitution technique can exhibit appreciable error if the speed of sound differs substantially between the sample and the reference (Xu and Kaufman, 1993). However, one investigation indicates that this diffraction-related error is negligible in the calcaneus (Droin et al., 1998). Evidently the speed of sound in the calcaneus, approximately 1475 – 1650 m/s (Droin et al., 1998), is sufficiently close to that of distilled water at room temperature, 1487 m/s (Pierce, 1981), that diffraction-related errors may be ignored.

Results

The densities of the bones examined were 0.42, 0.37, 0.45, 0.36, 0.48, and 0.49 g/ml. The average density was 0.43 g/ml. The standard deviation was 0.05 g/ml.

Measurements for normalized broadband ultrasonic attenuation (nBUA) for the six bone samples and six temperatures are shown in Figure 1. The temperature-related trend is similar for all six samples. Each sample exhibits a trend of decreasing nBUA as temperature is increased. At room temperature (20°C), nBUA was 17.0 ± 3.7 dB/cmMHz (mean ± standard deviation). Near body temperature (35°C), nBUA was 13.5 ± 3.6 dB/cmMHz.

Figure 1.

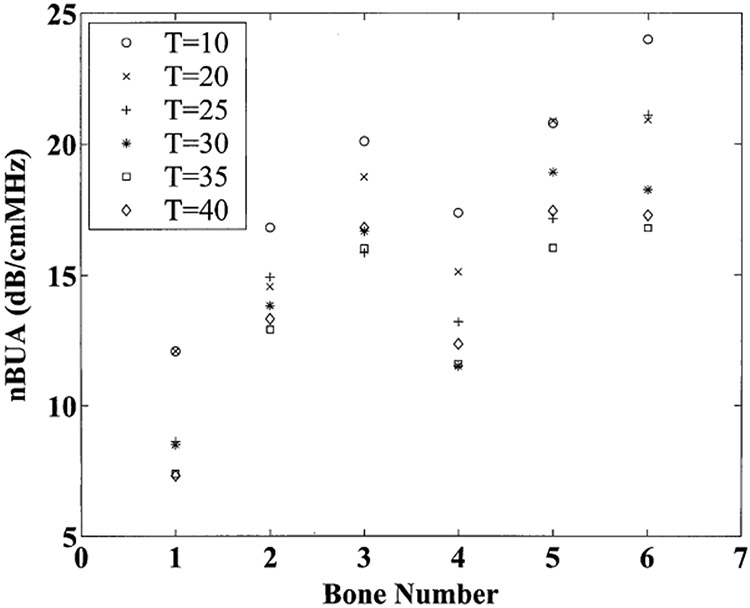
Normalized broadband ultrasonic attenuation (nBUA) for the 6 bone samples at six temperatures: 10°C (circles), 20°C (x’s), 25°C (plus signs), 30°C (asterisks), 35°C (squares), and 40°C (diamonds).

The points in Figure 1 are almost, but not strictly, monotonic with temperature. The departure from strict monotonicity is due to fact that the precision of the measurement is only on the order of about one dB/cmMHz. This level of precision is probably largely influenced by the difficulty in localizing the exact same volume of tissue for each measurement.

Figure 2 shows means and standard errors for changes in nBUA as a function of temperature. Here the change in nBUA for each sample represents the difference between nBUA measured for that sample at a given temperature and the average (over all 6 temperatures) value for nBUA measured for that sample. Again, a general downward trend is apparent. A least-squares linear regression was applied to the data. The correlation coefficient was r = −0.95. The 95% confidence interval for the estimate of the correlation coefficient was (−0.99, −0.58). The slope of the linear fit was found to be −0.18 dB/cmMHz°C. The 95% confidence interval for the estimate of the slope was (−0.27 dB/cmMHz°C, −0.10 dB/cmMHz°C). A parabolic fit was close to the linear fit but suggested a potential slight flattening out near body temperature.

Figure 2.

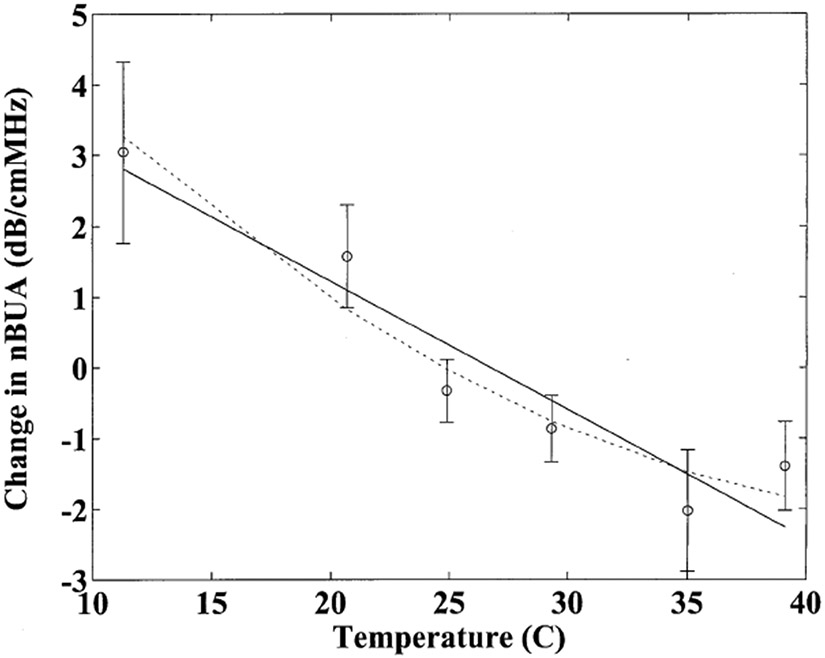
Changes in normalized broadband ultrasonic attenuation (nBUA) about the mean as a function of temperature. Error bars denote standard errors. The linear (solid line) and parabolic (dotted line) fits are also shown.

Figure 3 illustrates potential errors in estimated apparent bone density due to temperature effects. The mapping from nBUA measurements to estimated apparent density was done in a linear fashion. The intercept and slope for the linear mapping were obtained by performing a linear regression of true apparent density (the dependent variable, obtained from independent mass and volume measurements) versus temperature-averaged nBUA (the independent variable). It can be seen that over the full temperature variation range of 30°C, variations of about −0.1 g/ml in estimated apparent density occurred. This corresponds to potential errors of about −0.003 g/ml°C due to mineralized bone effects alone. (Of course, for in vivo measurements, temperature dependences of the other tissues in the heel would also contribute).

Figure 3.

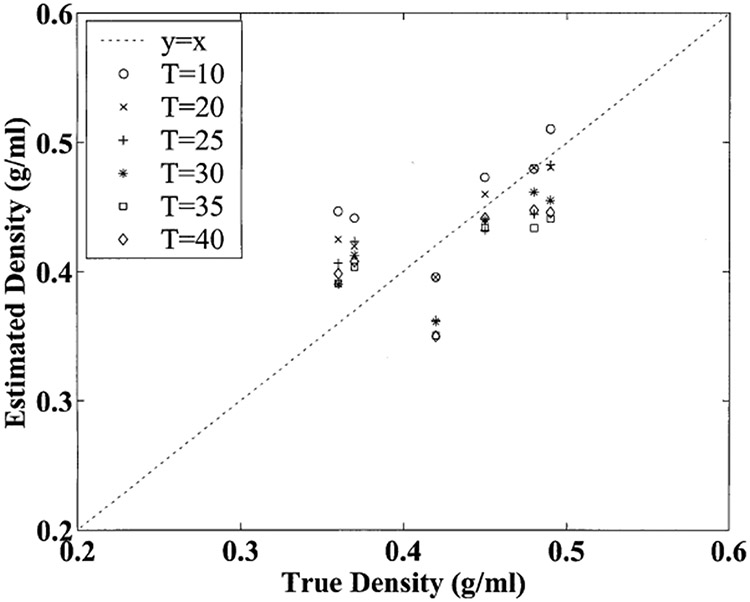
Estimated apparent bone density in g/ml based on attenuation measurements as a function of true apparent density for the six samples at the six temperatures. The dashed line corresponds to the ideal case where estimated apparent density equals true apparent density.

Discussion

Broadband ultrasonic attenuation in calcaneus has been shown to be a practical and valuable measurement for the diagnosis of osteoporosis. Several studies have indicated that this measurement is probably affected by temperature fluctuations. However, the underlying mechanisms responsible for this temperature dependence are currently not well understood. This phenomenon can degrade precision and compromise the ability to monitor small changes in bone density due to interventions such as drug therapy. The present study was conducted in order to investigate the temperature-dependence of ultrasonic attenuation in the trabecular bone component of the heel. Toward this end, 6 defatted human calcanei were investigated in vitro. Broadband ultrasonic attenuation was measured for each of the six samples at six temperatures ranging from 10°C to 40°C. A least-squares linear regression was applied to the data, yielding a negative temperature dependence of −0.18 dB/cmMHz°C. This result reinforces the notion, advanced by other investigators (Morris et al., 1997, Barkmann and Glüer, 1998, and Chappard et al., 1999), that temperature-related effects need to be taken into account when performing diagnostic measurements, especially those that require high precision such as monitoring response to drug intervention.

This study isolates the effects of mineralized bone tissue and excludes the effects of other components of the heel. This will aid in the interpretation of more complicated in vivo experiments designed to investigate precision errors due to fluctuations in temperature (Morris et al., 1997, Barkmann and Glüer, 1998, and Chappard et al., 1999). The results of this investigation will also facilitate future comparisons between in vitro studies normally carried out at room temperature (near 20°C) and in vivo studies carried out at body temperature (near 37°C). Finally, these measurements address a gap in the existing relatively extensive compendium of tabulated measurements of temperature dependences of acoustic properties of biologic tissues (Haney and O’Brien, 1986, and Duck, 1990).