Review of ML and AutoML Solutions to Forecast Time-Series Data

Abstract

Time-series forecasting is a significant discipline of data modeling where past observations of the same variable are analyzed to predict the future values of the time series. Its prominence lies in different use cases where it is required, including economic, weather, stock price, business development, and other use cases. In this work, a review was conducted on the methods of analyzing time series starting from the traditional linear modeling techniques until the automated machine learning (AutoML) frameworks, including deep learning models. The objective of this review article is to support identifying the time-series forecasting challenge and the different techniques to meet the challenge. This work can be additionally an assist and a reference for researchers and industries demanding to use AutoML to solve the problem of forecasting. It identifies the gaps of the previous works and techniques used to solve the problem of forecasting time series.

Introduction

Although research in time series analysis found a place in the past [1, 2], its significance increased recently with the growth of data volumes resulting from users, industries, and markets. The research in time series data has a rich background with pivotal importance in different applications including economic, weather, stock price, business development, and other use cases. Due to this significance, there is an increasing and high demand for robust, scalable, and accurate forecasting tools. The past decade has shown an increase in the number of proposed models to be used in forecasting [3–5]. However, the uncertainty in the time-series data like temperatures, wind speed, network traffic, stock price, etc. makes modeling this type of data a difficult task. We categorize the methods that can be used to forecast time series values into three categories: linear modeling, deep learning (DL), and Automated machine learning (AutoML). Linear models which are the simplest and usually the fastest to execute can perform predictions [6] but might result in low prediction accuracy. DL models can perform better [7] but as with all machine learning methods [8–10], DL requires experience to tweak hyperparameters and set up the model [11]. Moreover, the number of hyperparameters to optimize might become large and require considerable effort to optimizing. AutoML strives to solve this problem by automatically finding a suitable ML model and optimizing it [12]. There are many AutoML frameworks can be utilized to forecast time-series data including EvalML [13], AutoKeras [14], and AutoGluon [15], and others [16, 17]. However, AutoML for time-series is still in the development stage [18] and requires efforts from researchers to reach maturity. Examples of recent significant efforts on reviewing the methods to be utilized in modeling time-series include [19–21]. These works reviewed the usage of machine learning and DL techniques but didn’t discuss the AutoML techniques that appeared recently as a promising tool to facilitate the forecasting process with minimal human intervention and high accuracy. Recent advancements should soon provide the power to deal with time-series data efficiently.

This work is reviewing the research works done recently on time series forecasting using linear modeling, DL, and AutoML. It also reviews the different AutoML frameworks that can be utilized for forecasting. Its key contribution lies in overcoming the problem by reviewing more models, AutoML frameworks, and extending the concept of AutoML. Moreover, it contributes by filling the gap in between the earlier studies conducted in this area of research by exploring more advanced learning approaches. The present paper can act as a reference guide for the growing body of AutoML since it is reviewing different frameworks.

Literature Review

Time-Series Forecasting

The availability of massive amounts of time-series data opens new opportunities for knowledge extraction and decision-making for companies and practitioners. Linear models [22, 23] for time-series forecasting such as ARIMA [24] have been prominent for a long time and many researchers still rely on such models as they can predict efficiently and provide interpretability. However, advances in machine learning research concluded that DL and neural networks can be more powerful models [25], as they can give higher accuracy [7]. Most machine learning algorithms require extensive domain knowledge, pre-processing, feature selection, and hyperparameter optimization to be able to solve a forecasting task with a satisfying result [26]. Analysts with both machine learning and domain expertise are relatively rare, which makes engagement with time series forecasting methods expensive for organizations. This gap fostered a growing demand for frameworks automating the ML pipeline [27]. AutoML provided solutions to build and validate machine learning pipelines minimizing user intervention [28] where analyzing data with limited human intervention became an interest to researchers and industries [29]. However, finding a procedure that automates the entire ML process for forecasting is not yet a mature field of research, and time-series data also have constraints and oddities (e.g., trend, seasonality, outliers, drifts, abrupt changes) and should be handled in special ways [18].

Time-Series Prediction Models

Selecting the prediction model with time-series has a remarkable significance and affects the whole process of prediction, where machine learning models used to predict data behavior can be classified into linear models and non-linear models (including DL) depending on whether the present value forms a linear or non-linear function of preceding values. For example, univariate linear models try to find the future value of a particular time series using the historical performance of a dependent variable and non-linear models try to find complex hidden patterns in the data and non-linear relations between dependent and independent variables.

Machine Learning (Linear Modeling)

The simplest approach to forecast time-series is the linear naive approach [30], in which, forecasting the value at time t + 1 is given as the latest available observation at time t without predictions or adjusting the factors. Another simple approach is the mean model, where the forecast value at time t + 1 is the average of all previous values up to time t. Although the simplicity of linear models, some of which like ARIMA proved efficiency in prediction with high accuracy [31]. The mainly used linear models for time-series data include Auto-Regressive (AR), Moving Average (MA), and Linear Regression (LR). Combining AR and MA models constitute another model called the Auto-regressive Moving Average (ARMA) [32, 33]. Another similar, but more advanced, model to ARMA is the Auto-Regressive Integrated Moving Average (ARIMA) [7, 34]. These five mainly used linear models are elaborated below:

AR Model

AR model calculates the future value of a variable using a linear formula of the historical values of the same variable [32, 33, 35]. The term “auto-regression” indicates regression of the variable against itself, i.e., $y_t=f\left(y_{t-1},,,y_{t-2},,,y_{t-3},,,\dots ,,,y_{t-p}\right).$ The autoregressive model AR(p) that is affected by the ‘p’ of its earlier values is calculated as:

$$y_t=c+{\mathrm{\varphi }}_1{\mathrm{y}}_{t-1}+{\mathrm{\varphi }}_2{\mathrm{y}}_{t-2}+\dots +{\mathrm{\varphi }}_p{\mathrm{y}}_{t-p}+{\mathrm{\epsilon }}_t$$ 1

where ${\mathrm{\epsilon }}_{\mathrm{t}}$ is the error term and p is the parameter that indicates the number of previous values to consider in prediction. When p = 0, AR(0) becomes $y_t=c,$ a constant where no previous values to consider. When p = 1, AR(1) becomes $y_t={\mathrm{\varphi }}_1{\mathrm{y}}_{t-1},$ only one previous value will be considered. And so on for other values of p [32]. We need to find the best value of p for prediction where the model yields optimal prediction. This can be done using ACF and PACF tests.

MA Model

In the MA model, rather than using the earlier values of a variable for prediction, it uses earlier predictions error terms which result when regressing a series from its past values. MA model uses these error terms in the following predictions instead of using the past values. MA(q) is represented as a function of former error terms as:

$${\mathrm{y}}_t=\mathrm{c}+{\mathrm{\epsilon }}_t++{\mathrm{\theta }}_2{\mathrm{\epsilon }}_{t-2}+\cdots +{\mathrm{\theta }}_q{\mathrm{\epsilon }}_{t-q}$$ 2

where q is the number of previous error terms to consider in prediction. It is required to find the optimal value of q for forecasting [32]. This can be done using ACF and PACF tests.

ARMA Model

Autoregressive (AR) and moving average (MA) can be used together to form a new model called the ‘Auto-Regressive Moving Average (ARMA)’, i.e., AR + MA = ARMA [32, 36, 37]. ARMA (p,q) model is given as:

$$y_t=(C+{\varphi }_1{y}_{t-1}+{\varphi }_2{y}_{t-2}+..++{\varphi }_p{y}_{t-p}+{\epsilon }_t)+\left(\mu ,+,{\theta }_1,{\epsilon }_{t-1},+,{\theta }_2,{\epsilon }_{t-2},\cdots ,+,{\theta }_q,{\epsilon }_{t-q},+,{\epsilon }_t\right)$$ 3

where p and q respectively are the number of previous values and the number of previous error terms to consider in prediction. These best values of p and q can also be found using ACF and PACF plots.

ACF and PCF Plots

An important step while selecting a prediction model is to determine its ideal parameters. Plotting the ACF and PACF plots against the successive time lags is a simple method to finding the parameters of the model. ACF and PACF are statistical techniques that indicate the relationship between observations in a time series with one another [38, 39] and aid in determining the parameters of AR and MA models.

ACF [40] is a function that gives values of autocorrelation of any series with its lagged values. ACF plot describes how highly the present value of a series is connected to its past values.

PACF [40] is a partial autocorrelation function where instead of finding correlations of the present with lags, it finds a correlation of the residuals (which remains after removing the effects which are already explained by the earlier lag(s)). In PACF, we correlate the “parts” of $y_t$ and $y_{t-3}$ that are not predicted by $y_{t-1}$ and $y_{t-2}.$

In the case of ‘AR models’, ACF for time series will shrink exponentially, so PACF is plotted to identify the order of ‘p’ [32]. In the case of ‘MA models’, the ‘PACF’ for time-series will shrink exponentially, so ACF is plotted to identify the order of ‘q’ [32].

ARIMA Model

The ARMA model is suitable for stationary time series data. However, most of the time-series data in the real-world show non-stationary behavior. The ARIMA model solves this problem by converting non-stationary data to stationary using the differencing transformation which is the process of replacing the time-series data values with the differences between these values and their preceding values at the previous time steps [32, 33, 41]. The ARIMA equation is a linear equation in which the predictors consist of lags of the dependent variable and/or lags of the error terms and is given as:

$$\text{Predicted value of}Y=a\text{constant and/or a weighted sum of one or more recent values of}Y\text{and/or a weighted sum of one or more recent values of the errors}.$$ 4

The common formula of an “ARIMA model” for $y_t$ is given as:

$$y_t={\mathrm{c}+\mathrm{\varphi }}_1{\mathrm{y}}_{t-1}+{\mathrm{\varphi }}_2{\mathrm{y}}_{t-2}+..++{\mathrm{\varphi }}_p{\mathrm{y}}_{t-p}+{\mathrm{\theta }}_1{\mathrm{\epsilon }}_{t-1}+{\mathrm{\theta }}_2{\mathrm{\epsilon }}_{t-2}+\cdots +{\mathrm{\theta }}_q{\mathrm{\epsilon }}_{t-q}+{\mathrm{\epsilon }}_t,$$ 5

where $y_t$ is a time series and might have been differentiated once or more. This model is called the “ARIMA (p,d,q)” model, where p and q correspondingly refer to p and q of the ARMA model, whereas, d refers to the number of differencing transformations required by the time-series to attain stationarity.

When d = 0, it indicates that the time-series is already stationary and no need to perform differencing. If d = 1, it indicates that the time series is not stationary, and it requires performing the differencing once. If d = 2, it indicates that the time-series requires performing the differencing twice.

To find the best values of the parameters of p, d, and q, a grid search algorithm [42] that tests the performance of ARIMA with all possible values in a range then returns the best combination of values that can be followed. The grid search can also be classified under one of the AutoML techniques for hyperparameters optimization which strives to find optimal hyperparameters for a model.

LR Model

Linear regression [43] is one of the most commonly used prediction models. It predicts the value of a dependent variable given one or more independent variables. It forms an association between the dependent variable and independent variables by fitting a linear line with the data points in such a way that the overall distances of data points from the fitted line are minimized [44]. An example of fitting training data into a line using LR is given in Fig. 1.

Fig. 1.

Linear regression example

The LR, in this case, objected to finding the line that models the data the best and the values of the line to be used in predicting the future. Data is preferred to be stationary when using the LR since it is assumed that the error term is white noise and, therefore, data should be stationary.

Overall, the previous linear models (AR, MA, ARMA, ARIMA, LR) are preferred to be applied to stationary time-series only. The next paragraph elaborates the concepts of stationary and non-stationary data.

Stationary and Non-stationary Data

After collecting and cleaning the time series intending to apply linear models, the next preferable step is to check whether the series is stationary or not. Time series needs to be lacking trend and seasonality to be stationary where the trend and seasonality may affect a time series at different instants and result in inaccurate predictions [45]. ARIMA prediction efficiency relies on the stationarity of the series [24] as it considers the previous values of the time series where modeling a series with regular trends involves uncertainty. An approach to converting non-stationary data into stationary is to compute the differences between consecutive observations. This is referred to as differencing i.e. ($y_t$ –$y_{t-1}$) [32].

Many tests can be used to check whether a time series is stationary or not [46]. One of the most used tests is the Augmented Dickey-Fuller (ADF) tests.

Machine Learning (Deep Learning)

Deep learning is a subordinate field of machine learning that uses artificial neural networks (ANNs) that are inspired by the design and the working mechanism of the biological brain. ANN is built to process and learn a large number of unknown inputs. An ANN contains a set of internally connected neurons that are designed to compute values from inputs like the biological brain neurons [47]. The non-linear nature of ANN makes it useful to calculate complicated relations and patterns between the input and the output [48]. For this reason, it can be used to predict time-series cryptocurrency prices data.

ANN contains parameters and hyperparameters [49] that significantly control the processes of learning, the parameters and hyperparameters affect the whole process of predicting and determining their values significantly influence the model behavior. These parameters and hyperparameters include:

• Number of hidden layers: low number of hidden layers means a fast and well generalized ANN where model designers prefer to keep the ANN as simple as possible but at the same time, the ANN should classify the inputted data properly. More layers mean better accuracy. However, after a particular number of layers, the accuracy will not improve anymore by adding more and layers, thus it might be inconvenient to design a heavy ANN.

• Activation functions: calculate the output of the neuron regarding its input and connections’ weights [50].

• Learning rate: determines the value of change on the model weights each time they are updated. The smaller the learning rate, the longer the training process needed. However, large learning rates cause instability in the training process [51].

• Number of epochs: determines how many times the neural network will train on the whole dataset. More epochs cause better accuracy but at the same time cause longer training time. At some point, further epochs will be futile since each further epoch will cause a very tiny enhancement in the accuracy that doesn’t worth the additional time to be spent on training [52].

• Batch size: determines the number of inputs in each sample of the dataset, to be propagated through the neural network [52].

• Optimizers: algorithms utilized in updating the values of the neural network parameters like weights and learning rate to decrease the loss (difference between the forecasted output and the actual output during the training phase), to provide the most accurate possible results [53].

Examples of the most utilized DL models in modeling time-series data are elaborated below:

Recurrent Neural Network (RNN)

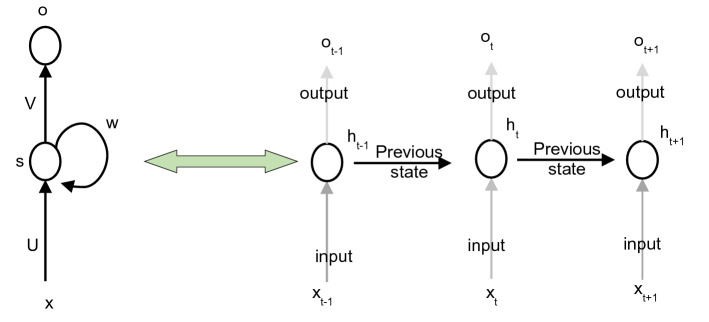
RNN is a neural network that takes input from two sources, from the present and the past. We can say, it has a memory. The input sequence information is stored as a hidden state [54] to be utilized recursively, as it moves forward to deal with a new sample of data. In other words, each RNN hidden layer takes its own previous state at the preceding time-step as an additional input. For this reason, it can be used to model-time series data where it proved efficiency in several cases. The architecture of an RNN is illustrated in Fig. 2.

Fig. 2.

Recurrent neural network architecture

At each given time step, t, a memory state h_t, is computed, depending on the preceding state, h_t−1, at step (t − 1) and the input, x_t, at time step t.

The new state, h_t, is used to predict the output, o_t, at step t.

There are many cases where conventional RNNs are poorly suited. For example, predicting succeeding value in a long context when we don’t only need to know the preceding value to make a strong prediction, but also the values from further back. The traditional RNN will only look at the preceding value, hence giving a reasonably poor prediction, and this is called the “problem of long-term dependencies” [55].

Gated Recurrent Unit (GRU)

It is an enhanced version of the ordinary RNN. It possesses two gates, an update gate and a reset gate, used to determine which information should be pushed to the output. They can be trained to keep time-series data of a long time back, without deleting it through time [56] (Fig. 3).

Fig. 3.

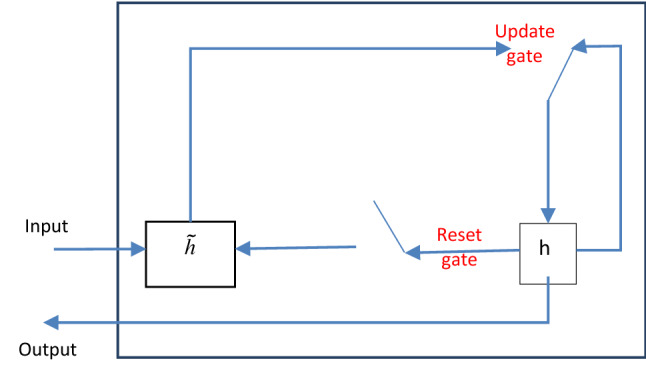
GRU network architecture

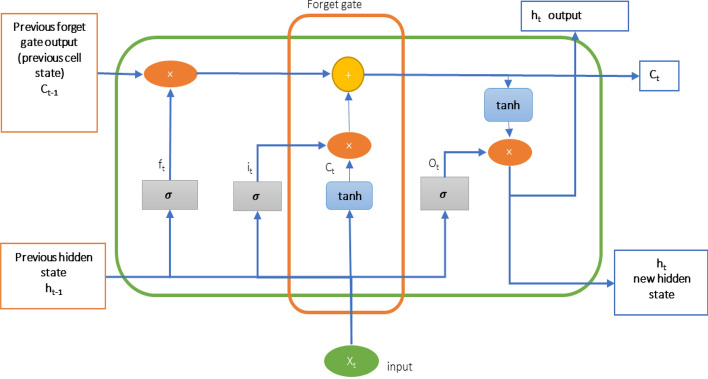
Long Short-Term Memory (LSTM)

It was designed to deal with long-term dependencies using its ability to save the information of a long time back and recall them when needed. It contains several memory cells. Each cell has three gates and a state to adjust the data flow through the cells. In the problem of predicting the value in a context of series, LSTMs perform better than RNN and GRU, due to the memory cell which stores information of a long time back [54, 57]. The architecture of LSTM is given as (Fig. 4):

Fig. 4.

LSTM network architecture

Independently Recurrent Neural Networks (IndRNN)

It was proposed by Li et al. In 2018 [58]. The fundamental IndRNN structure is presented in Fig. 5.

Fig. 5.

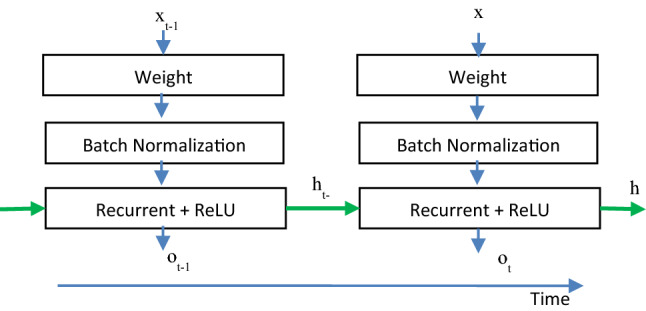
IndRNN architecture

where Weight delineates the input data processing and Recurrent + ReLU delineates the recurrent process with ReLU function, every time-step. Each neuron receives data only from the input and its own hidden state at the previous time step as context data (instead of completely linking with all other neurons in the preceding layer) and thus neurons are independent of each other’s history [59].

AutoML

AutoML refers to solving a machine learning task in an automated way so that none (or very little) manual effort is required [60]. AutoML aims at providing non-experts with the possibility of applying machine learning techniques to address a specific task without requiring prior technical or domain knowledge [61]. The goal of most AutoML approaches is to fully automatize the process of model selection, hyper-parameter optimization, and feature selection [62]. Previously, several approaches and strategies only tackled a subset of this process, whereas in recent years several fully automated approaches arose.

Model Selection

Given a set of machine learning models and a dataset, the goal of model selection is to find models with the highest accuracy when trained and tested on the dataset. AutoML strives to select the best-fit model considering the data without human intervention where AutoML can iterate through different models to be trained on the same input data and select the model that performs best [63].

Hyperparameter Optimization

Setting and tweaking hyperparameters in the right way can—and often will—result in a better-performing model. Research has also shown that a suitable set of hyper-parameters significantly increases the performance of models compared to most default model settings [64, 65].

Hyperparameters refer to the parameters that cannot be updated or fine-tuned during the training process and can be involved in building the structure of the model, such as the number of hidden layers and the activation function, or in determining the efficiency and accuracy of model training, such as the learning rate, batch size, and optimizer [66]. These hyperparameters need tuning and set after selecting a model and the hyperparameters that need optimization differ from one model to another. Hyperparameter optimization (HPO) is a significant process in machine learning and became necessary due to the upscaling of neural networks for enhanced accuracy. The optimization traditionally occurs based on experience, which means a possible set of hyperparameters values becomes necessary due to the upscaling of neural networks for enhanced accuracy requires researchers to have experience in training neural networks. However, with the lack of logical reasoning and the lack of experience, we lack the credibility of experimental values [66].

Common strategies of the automated hyperparameter optimization (HPO) include Grid-Search, Random Search, Bayesian Optimization, Genetic Algorithms, Gradient-Descent, Tree Parzen Estimators, and others:

• Grid search It can be used with ARIMA and other models where it proved efficiency. It tries a set of possible hyper-parameters applied to the task at hand. This brute force approach exhaustively tries every possible combination and returns the best fitting set of hyper-parameters [67–69].

• Random search A random search is a different approach in which the possible hyper-parameters are randomly chosen and not predefined as in the grid search approach. Several studies have proven this approach to be more effective [70].

• Bayesian optimization An approach that gained more attention in the research community. It also runs models with different sets of hyperparameter values, but it evaluates the past model information to select hyperparameter values and build a newer model. Results suggest that hyper-parameter optimizing with this algorithm is more effective than the brute force paradigm of grid search and random search. In some applications, this approach even outperformed manual optimization by domain experts [71].

• Genetic algorithm Genetic Algorithms are a type of search and optimization algorithm which belongs to the class of evolutionary algorithms. This algorithm is biologically inspired by the evolution theory of Charles Darwin [72]. The core idea is that natural selection combined with variation will cause a population to evolve over time. In a search algorithm, a population of possible solutions to a given optimization problem is evolved towards a better solution. In an iterative process, candidate solutions are evaluated and subsequently modified through genetic operators such as selection, crossover, and mutation. This heuristic approach has been proven to work well in large search spaces [27].

• Other strategies for hyper-parameter optimization include Gradient-Descent [73, 74], and Tree of Parzen Estimators (TPE) [75].

Feature Engineering

Another aspect of AutoML search is feature engineering where manual feature engineering is a tedious and repetitive task. Three systems recently introduced to fulfill this task automatically are ExploreKit [76], Data Science Machine [77], and Cognito [78]. The first uses meta-features extracted from previously known datasets and a machine learning-based algorithm to efficiently rank composed features, whereas the data science machines can extract features from relational data sources leveraging deep feature synthesis. Cognito explores various feature construction choices hierarchically and increases model accuracy through a greedy strategy.

AutoML Frameworks

In recent years several systems have been proposed that combine all three aspects of AutoML: model selection, hyper-parameter optimization, and feature engineering. For example: H2O [16], Auto-Sklearn [79], AutoGluon [15], TPOT [17, 80], Auto-Weka [81], TSPO [27], AutoKeras [14], EvalML [13], TransmogrifAI [82], Auto-Pytorch [83], and others. In the following paragraphs, a review of different AutoML frameworks is represented and a comparison between the frameworks.

H2O [16] is a machine learning platform and an AutoML module that covers random forest, extremely randomized trees, generalized linear models, XGBoost, H2O gradient boosting machine, and deep neural networks with an automated target encoding of high dimension categorical variables as a pre-processing technique [18]. H2O trains a Random grid of algorithms using a hyperparameter space. Individual models are tuned using cross-validation. Two stacked ensembles are trained. One contains all the models optimized for model performance, and the other contains only the best-performing model from each algorithm. Then, it returns a sorted leaderboard of all models [16].

Auto-sklearn [79, 84] is a machine learning platform that covers 15 models, 14 feature preprocessing methods, and 4 data preprocessing methods. The models mainly include K-nearest neighbors (KNN), gradient boosting, stochastic gradient descent (SGD), random forest, AdaBoost. It evaluates a set of meta-features over hundreds of datasets and stores the most accurate related configurations [18]. Auto-sklearn starts by extracting dataset meta-feature to find the similarity to the knowledge base relying on meta-learning. Then, Bayesian optimization will try to find and select the outperforming ML pipelines. Finally, it builds the ensemble model based on the best ML workflow in the search space [79].

AutoGluon [15] is an AutoML framework that covers many models including neural networks, LightGBM, CatBoost, random forests, extremely randomized trees, and KNN. Its pre-processing includes model-agnostic pre-processing and model-specific pre-processing techniques. AutoGluon requires labeled input data to perform the preprocessing, feature engineering, and generate models based on the problem. It trains the generated models under different configurations, optimizes hyperparameters, and selects the best of them as the final. The search strategy for the best set of parameters is based on a random search, grid search, or Bayesian optimization [15, 85].

TPOT [17] is a machine learning platform that automatically designs and optimizes ML pipelines using a genetic algorithm. In model selection, it covers the following models: decision tree, random forest, eXtreme gradient boosting (XGBoost), logistic regression, and KNN. In feature selection, it covers techniques like standard scaler, randomized PCA, SelectKBest, and recursive feature elimination. Pipeline design and optimization start by generating 100 tree-base pipelines, evaluating them, and selecting the top 20 on each generation. Each of these 20 pipelines is copied with crossovers or other mutations to produce 5 5 copies and have a total of 100 pipelines again. This process is repeated 100 times until it finally outputs the top-performing models of the last generation [18].

Auto-Weka [81] considers selecting a learning model and setting its hyperparameters simultaneously, going beyond other models that process the two tasks in isolation. Auto-WEKA performs a fully automated approach using the Bayesian optimization approach. It covers Bayes net, naive Bayes, LR, logistic regression, single-layer perceptron, SGD, SVM, KNN, decision trees, random forest, and others [86].

Time Series Pipeline Optimization (TSPO) framework [27] provides an AutoML tool specifically designed to solve time series forecasting tasks. The framework utilizes a genetic algorithm to find an appropriate set of time series features, machine learning models, and suitable hyper-parameters. It is a fully automated time series forecasting tool. It takes a raw time series, automatically decomposes it, extracts time series features for each decomposition and finds a model with a fitting hyper-parameter. It covers XGBoost, random forest, quantile random forest, CatBoost, and feed-forward neural networks.

AutoKeras [14] is an AutoML system that utilizes Keras API. Other than other similar AutoML frameworks, Auto-Keras focuses on DL rather than simple models. It uses a process of searching through neural network architectures to best address a modeling task, referred to as Neural Architecture Search (NAS).

EvalML [13] is an open-source AutoML library written in python that automates a large part of the machine learning process. It builds and optimizes ML pipelines using specific objective functions. It can automatically perform feature selection, model building, hyper-parameter tuning, cross-validation, etc. EvalML handles feature selection with a random forest classifier/regressor. EvalML tunes hyperparameters for its pipelines through Bayesian optimization. EvalML supports different supervised ML problem types: regression, binary classification, multiclass classification, time series regression, time series binary classification, and time series multiclass classification.

TransmogrifAI [82, 87] is another AutoML framework that addresses ML model selection, feature selection and engineering, and hyperparameter optimization. The user has to specify the dataset, the schema, and the target column and the framework automatically discards input features that do not present a predictive value and train a predefined set of algorithms with a predefined set of hyperparameters depending on the type of problem. It covers the following machine learning models: decision trees, gradient boosted trees (GBT), LR, SVM, logistic regression, naïve Bayes, and random forest [82, 87, 88].

A comparison between the different AutoML frameworks is given in Table 1.

Table 1.

AutoML frameworks comparison

AutoML framework	Scope	Working method
H2O [16]	Random forests, extremely randomized trees, generalized linear models, XGBoost, H2O gradient boosting machine, and deep neural networks	Trains a random grid of algorithms using a hyperparameter space. Individual models have been tuned using cross-validation. Two stacked ensembles are trained. One contains all the models optimized for model performance, and the other contains only the best-performing model from each algorithm. Then, it returns a sorted leaderboard of all models [66]
Auto-Sklearn [79]	Covers 15 models, 14 feature preprocessing methods, and 4 data preprocessing methods. The models KNN) gradient boosting, SGD, random forest, AdaBoost, and others	Starts by extracting dataset meta-feature to find the similarity to the knowledge base relying on meta-learning. Then, Bayesian optimization will try to find and select the out-performing ML pipelines. Finally, it builds the ensemble model based on the best ML workflow in the search space [67]
AutoGluon [15]	Covers many models including neural networks, LightGBM boosted trees, CatBoost, boosted trees, random forests, extremely randomized trees, and KNN	Trains a set of generated models under different configurations, optimizes hyperparameters, and selects the best of them. The search strategy for the best set of parameters is based on a random search, grid search, or Bayesian optimization [68, 77]
TPOT [17]	Covers the following models: decision tree, random forest, eXtreme gradient boosting (XGBoost), logistic regression, and KNN	ML model design and optimization start by generating 100 tree-base pipelines evaluating them and selecting the top 20 on each generation. Each of these 20 pipelines is copied with crossovers or other mutations to produce 5 copies. This process is repeated 100 times until it finally outputs the top-performing models of the last generation [18]
Auto-Weka [81]	Bayes net, naive Bayes, linear regression, logistic regression, single-layer perceptron, stochastic gradient descent, SVM, KNN, K-star, decision tree, random forest, and others [78]	Considers selecting a learning model and setting its hyperparameters simultaneously, going beyond other models that process the two tasks in isolation. Auto-WEKA does this fully automated approach using the Bayesian optimization approach
TSPO [27]	XGBoost, random forest, quantile random forest, CatBoost, feed-forward neural networks	Utilizes a genetic algorithm to find an appropriate set of time series features, machine learning models, hyperparameters. It takes a raw time series, automatically decomposes it, extracts time series features for each decomposition and finds a model with a fitting hyper-parameter
AutoKeras [14]	Focuses on deep learning rather than simple modelling	Utilizes Keras API and uses a process of searching through neural network architectures to best address a modeling task, referred to as Neural Architecture Search (NAS)
EvalML [13]	Supports different supervised ML problem types: regression, binary classification, multiclass classification, time series regression, time series binary classification, and time series multiclass classification	Builds and optimizes ML pipelines using specific objective functions. It can automatically perform feature selection, model building, hyper-parameter tuning, cross-validation, etc
TransmogrifAI [82, 87]	Covers the following machine learning models: Decision Trees, Gradient Boosted Trees (GBT), Linear Regression, Linear Support Vector Machines, Logistic Regression, Naïve Bayes, and Random Forest (RF) [82, 87, 88]	The user has to specify the dataset, the schema, and the target column and the framework automatically discards input features that do not present a predictive value and train a predefined set of algorithms with a predefined set of hyperparameters depending on the type of problem

We give a personal recommendation to utilize EvalML to the process of AutoSearch for the best-fitting models concerning the data for the following reasons:

• Domain-specific: A missing feature in most of the AutoML framework where EvalML allows to specify the domain of the problem while searching. For example, we can specify our problem as ‘time-series regression’. Once determining the domain for the business, EvalML can optimize by defining a custom objective function.

• Data checks and warnings: EvalML helps in identifying the problems in data before setting it up for modelling. It can give recommendations on required data pre-processing.

• Pipeline building: EvalML helps in constructing a highly optimized pipeline including state-of-the-art data pre-processing, feature engineering, feature selection, and other modelling techniques.

• Model understanding: EvalML provides a broad level of understanding about the model it builds, for the purpose of presentation.

• Low code interface: EvalML provides a simple easy-to-use low code interface to create a model and use those models to make accurate predictions.

Related Research

Li et al. [48] conducted a review on using AI and artificial neural networks (ANNs) for stock market time-series prediction and found that ANNs are effective forecast tools in financial economics owing to the learning, generalization, and nonlinear behavior properties.

Mitra et al. [89] surveyed machine learning methods to process the textual input from News stories, determine quantitative sentiment scores, and predict abnormal behavior of the time series of stock.

Changqing et al. [90] reviewed the methods that focus on forecasting linear and stationary process presenting a review of the advancements in non-linear and non-stationary time series forecasting models and comparing their performances in real-world manufacturing and health informatics applications. They concluded that there had been an increased interest in nonparametric models for forecasting nonlinear and non-stationary time series, where adapting the principles of nonlinear dynamic systems into nonparametric modeling approaches can provide an attractive means to further advance in forecasting.

Peng et al. [91] used text mining with word embeddings and neural networks to extract information from financial News and detect stocks movements. They demonstrated that the proposed methods improved the accuracy of prediction over the baseline system that uses the historical time-series price information solely.

Many works including Huang et al. [90] and Prosky et al. [92] used sentiment analysis techniques with deep network models to boost the performance of predicting time series stock trends.

Many works compared DL with linear models in predicting time-series data like cryptocurrency and stock market prices. McNally et al. [93], Phaladisailoed et al. [94], Ahmad et al. [7, 95]. The results in all of the four works showed that DL-based models are more accurate compared to linear models.

Yan et al. [97] proposed a time series prediction model to capture complex features such as non-linearity, non-stationary and sequence correlation by combining Wavelet analysis with LSTM neural network. Their results showed that both Wavelet decomposition and reconstruction can improve the generalization ability of the LSTM and the prediction accuracy of long-term dynamic trend.

Ji et al. [96] evaluated various state-of-art DL models to predict time-series Bitcoin prices. Experimental results showed that LSTM-based prediction models slightly outperformed the other models in regressing while deep neural network (DNN) models performed better for classifying and predicting price ups and downs.

Dutta et al. [97], inspected different machine learning models including LSTM and GRU to predict time-series Bitcoin prices. Their results concluded that GRU yielded better accuracy than LSTM in predicting.

Pintelas et al. [98] investigated the efficiency of DL in predicting time-series cryptocurrency prices and whether there is a proper validation method of the prediction models. Their results provided evidence that DL models are not able to solve this problem effectively.

Iqbal et al. [99] used several linear models for cryptocurrency time-series analysis including ARIMAX, FBProphet, and XG Boosting. ARIMAX was found as the best model of forecasting Bitcoin prices with an MAE of 227 while FBProphet and XG Boosting scored an MAE of 323 and 470, respectively.

Hamayel et al. [100] proposed three types of RNN models including GRU, LSTM, and Bi-LSTM to predict the prices of cryptocurrencies. Bi-LSTM performed the lowest compared to the other two models where GRU performed the best yielding the lowest MAPE and RMSE.

Awoke et al. [101, 102] implemented LSTM ad GRU to predict Bitcoin. They concluded that GRU-based models are more efficient in forecasting a highly volatile time series. However, LSTM was better at a sliding window of size 12 or smaller than 7. In other words, when using the prices of the previous 12 days or the previous 7-or-less days to predict the next day price, LSTM performs better.

Several comparative studies on AutoML solutions [103–107] compared various frameworks against each other on standard tasks. The results of these studies showed high variance between models or no significant variance. However, AutoML frameworks did not significantly outperform traditional models or humans in easy classification tasks [18]. Many researchers suggested applications of ML and AutoML techniques and also performed the performance analysis of different models.

Dahl [27] proposed an AutoML system and called it “TSPO”. It outperformed different machine learning benchmarks consisting of statistical benchmarks and ML benchmarks in 9 out of 12 randomly selected time-series datasets in different domains. The results indicated that the proposed TSPO framework can produce accurate forecasts without any human input [108–110]. However, researchers concluded that AutoML and hence TSPO rely on computationally intensive search strategies that require a high computational run-time.

Xu et al. [29] organized an automated time-series regression challenge (AutoSeries) aiming at pushing forward research on automated time series. The challenge used 10 time-series datasets from different domains. Competitors delivered a considered contribution to solving the problem showing efficient models compared to the baseline benchmark model (single LightGBM [111]). Also, showing efficiency in a post-hoc evaluation compared to AutoGluon [87] AutoML framework benchmark where all of the winning solutions outperformed the vanilla AutoGluon technique. Most participants, except the first two winners, used default or fixed hyperparameters. The second winner optimized only the learning rate while the first winner used the hyperparameters optimization techniques of AutoML demonstrating the feasibility and efficiency of automating time series regression.

Paldino et al. [18] evaluated four AutoML frameworks (AutoGluon, H2O, TPOT, Auto-sklearn) against a benchmark of traditional forecasting techniques (naïve, exponential smoothing, Holt-Winter’s) on different time-series forecasting challenges including single variate, multi-variate, single-step ahead, and multi-step ahead with limiting the allowed computational time of AutoML methods to provide a fair comparison. Their results showed that AutoML techniques are not yet mature to address time-series forecasting problems and concluded that this should encourage researchers to a more rigorous validation and work in the field.

Javeri et al. [112] presented a data augmentation method to improve the performance of neural networks and unlock their power on intermediate length time series. The researcher demonstrated that combining data augmentation with AutoML techniques such as Neural Architecture Search (NAS) can help to find the best neural architecture for a given time-series dataset along with significant enhancement in the accuracy. In that work, the accuracies of three neural network-based models for a COVID-19 dataset were enhanced by 21.41%, 24.29%, and 16.42%, respectively.

Table 2 provides a comparison of the relevant efforts in time-series prediction:

Table 2.

Related works comparison

Author(s) and year	Methodologies	Findings	Identified research gaps
Li et al. (2010) [48]	Surveyed the usage of AI and ANNs for time-series stock market prediction	Artificial neural networks are an effective forecast tool in financial economics	Surveyed only basic state-of-art models
Peng et al. (2015) [91]	Text mining techniques with word embeddings and neural networks to extract information from financial News and detect stocks movements	The proposed methods improved the accuracy of prediction over the baseline system that uses time-series historical price information solely	Usage of a simple state-of-art method
McNally et al. (2018) [93], Phaladisailoed et al. (2018) [94], Ahmad et al. (2020) [7], Ahmad et al. (2021) [95]	Compared deep learning with Linear models in predicting time-series data like cryptocurrency and stock market prices	Deep learning-based models gave better accuracy compared to the linear models	Usage of state-of-art prediction models
Ji et al. (2019) [96]	Evaluated various state-of-art deep learning models to predict time-series Bitcoin prices	LSTM-based prediction models slightly outperformed the other models in regressing while deep neural networks (DNN) performed better in classifying price ups and downs	Didn't consider other recent deep learning models, such as transformer networks and few-shot/one-shot learning
Aniruddha Dutta et al. (2020) [97]	Different machine learning models to predict time-series Bitcoin prices including LSTM and GRU	GRU yielded better accuracy than LSTM	Didn’t explore the potential of Convolutional Neural Network (CNN) and the work used a relatively small dataset
Pintelas et al. (2020) [98]	Deep learning in predicting time-series cryptocurrency prices	Deep learning models were not able to solve this problem effectively	Didn't investigate the possibility of some minor information loss due to non-stationarity in the time series
Iqbal et al. (2021) [99]	Linear models including ARIMAX, FBProphet, and XG Boosting in forecasting Bitcoin prices	ARIMAX was found as the best model for forecasting Bitcoin prices	Didn't Hypertune the parameters of the algorithms in order to improve accuracy performance
Hamayel. et al. (2021) [100]	Three types of RNN models including GRU, LSTM, and Bi-LSTM to predict the prices of cryptocurrencies	Bi-LSTM performed the lowest compared to the other two models whereas the GRU model performed the best and yielded the lowest MAPE and RMSE	Didn't study the effect that social media in general and tweets in particular, can have on the price and trading volume of cryptocurrencies
Awoke et al. (2021) [101]	LSTM ad GRU deep learning models to predict Bitcoin with high accuracy in handling its volatility	GRU-based models are more efficient in forecasting a highly volatile time series. However, LSTM was better at a sliding window of size 12 or smaller than 7	Only compared basic deep learning-based models
Dahl (2020) [27]	AutoML system and called it “TSPO”	It outperformed different statistical and ML benchmarks in 9 out of 12 randomly selected time-series datasets in different domains	The current implementation of the proposed system is computationally expensive
Xu et al. (2021) [29]	Organized a challenge to predict time-series data that utilized 10 datasets from different domains	The first winner used the hyperparameters optimization techniques of AutoML demonstrating the feasibility and efficiency of automating time series regression	Some datasets have been too easy or too difficult to model
Paldino et al. (2021) [18]	Compared four AutoML frameworks (AutoGluon, H2O, TPOT, Auto-sklearn) against a benchmark of traditional forecasting techniques (naïve, exponential smoothing, Holt-Winter’s) on different time-series forecasting challenges	AutoML techniques are not yet mature to address forecasting problems and this should encourage researchers to a more rigorous validation and work in the field	AutoML frameworks offer deep customization to improve their performance, which hadn't been considered
Javeri et al. (2021) [112]	A data augmentation method to improve the performance of neural networks and unlock their power on intermediate length time-series data	Combining data augmentation with AutoML techniques such as Neural Architecture Search can help to find the best neural architecture for a given time-series dataset along with significant enhancement in the accuracy	Incorporated only a few deep learning architectures

The previous works used or compared a limited set of models to forecast time-series data. Most papers have used two main techniques to resolve the problem: linear modeling and DL. This problem was solvable to some extent with acceptable accuracy by DL. There were very limited studies on the use of AutoML. Our work, however, aimed to overcome the problems by reviewing more models and AutoML frameworks. It extends and generalizes the concept of AutoML.

Conclusion

The significance of time-series analysis has been growing in the last decade after larger amounts of data were generated calling for robust time-series modeling tools in different applications and disciplines. However, modeling this type of data is a difficult task. Modeling techniques of time series include linear modeling, DL, and AutoML. Linear models are the simplest but might result in inferior prediction accuracy. DL achieves higher but demands experience and patience to design a model and optimize hyperparameters. AutoML automatically finds a reasonable ML model and optimizes it where many AutoML frameworks can be employed to forecast time-series data. However, AutoML for time-series is still in the evolution phase and requires efforts from researchers to become an answer for the problem of modeling time-series. This article introduced different methods to be used to forecast time-series data including AutoML. It also reviewed relevant works conducted to answer the problem. A comparison between different AutoML frameworks and techniques was provided. This work is novel in describing different AutoML frameworks that can be used to model data. However, some study limitations should be acknowledged such as this work didn’t provide an empirical study about the potential of the different methods. The next step should be to conduct an empirical study to compare by experiment with different ML and AutoML techniques to solve the problem of modeling time-series.