Internally generated population activity in cortical networks hinders information transmission

Abstract

How neuronal variability affects sensory coding is a central question in systems neuroscience, often with complex and model-dependent answers. Many studies explore population models with a parametric structure for response tuning and variability, preventing an analysis of how synaptic circuitry establishes neural codes. We study stimulus coding in networks of spiking neuron models with spatially ordered excitatory and inhibitory connectivity. The wiring structure is capable of producing rich population-wide shared neuronal variability that agrees with many features of recorded cortical activity. While both the spatial scales of feedforward and recurrent projections strongly affect noise correlations, only recurrent projections, and in particular inhibitory projections, can introduce correlations that limit the stimulus information available to a decoder. Using a spatial neural field model, we relate the recurrent circuit conditions for information limiting noise correlations to how recurrent excitation and inhibition can form spatiotemporal patterns of population-wide activity.

Spatiotemporal dynamics in spiking neuron networks limit information transmission.

INTRODUCTION

A prominent feature of cortical response to sensory stimuli is that neuronal activity varies substantially across presentation trials (1), even when efforts are taken to control or account for variable animal behavior (2–4). A component of this variability is coordinated among neurons in a brain area, often leading to shared fluctuations in spiking activity (5–7). How stimulus processing is affected by this large, population-wide neuronal variability is a longstanding question in both experimental and theoretical neuroscience communities.

Recording from neuronal populations while simultaneously monitoring an animal’s behavior during a structured task offers a glimpse into how neuronal activity supports computation. Correlations between spike counts from pairs of neurons in response to repeated stimulus, often referred to as noise correlations, are modulated by a variety of cognitive factors that are known to affect task performance (2). For example, noise correlations decrease with animal arousal (8) or task engagement (9). In the visual pathway, noise correlations between neurons in the superficial layer are decreased when spatial attention is directed into the receptive field of a recorded population (10), although the attention-mediated changes in noise correlation depend on cortical layer (11) and task conditions (12). In addition, perceptual learning (13, 14) and visual experience (15) can also result in an attenuation of noise correlations. The common theme in all of these studies is that a reduction in noise correlations co-occurs with cognitive shifts that improve task performance. This supports the often cited idea that shared variability is deleterious to neuronal coding because it cannot be reduced by ensemble averaging (16, 17), and thus, it is expected that its reduction will enhance neural coding.

While the above narrative is appealing, it oversimplifies a long debate in the computational neuroscience community (16, 18–20). It is popular (and pragmatic) to restrict analysis to a linear decoding of neuronal response, where performance is often measured using the linear Fisher information between the estimated and actual stimulus (19, 21–23). Linear Fisher information depends on two components: the set of neuronal tuning curves and the population covariance matrix (19, 21). Whether noise correlations degrade or improve stimulus coding depends on the relationship between these components. For example, while it is true that correlations between similarly tuned neurons limit Fisher information (17), correlations between dissimilarly tuned neurons can actually increase information compared to an asynchronous population (18, 19). Several more recent studies have built upon this idea and shown how stimulus-dependent correlations can also improve linear information transmission (24–26). Last, Moreno-Bote et al. (27) showed that information is only limited by one specific type of correlations, termed differential correlations, which align with population activity in the direction defined by the derivatives of the tuning curves. In all of these varied modeling studies, both tuning curves and covariance structure were assumed and thus had a prescribed relation to one another. In this study, we adopt an alternative modeling approach and consider biophysically grounded population models, where cellular spiking dynamics and synaptic wiring are assumed, and population response and its variability are emergent properties of the circuit.

A serious obstacle in using circuit models to study neuronal coding is the lack of a complete mechanistic theory underlying population-wide variability (28). An often used framework assumes that neuronal fluctuations are inherited from external sources and any circuit wiring filters and propagate this variability throughout the population (29, 30). Along these lines, recent modeling work in a feedforward circuit model of primary visual cortex shows that when such inherited variability originates from a noisy stimulus, then population-wide correlations, which limit information transfer, naturally develop throughout the circuit (31). Neuronal variability can also emerge through recurrent interactions within the network, when synaptic weights are large, and excitation is dynamically balanced by recurrent inhibition (1, 32). However, these networks famously support an asynchronous state (33), making them at the surface ill-suited to probe how internally generated population-wide variability affects neuronal processing. Recent extensions of balanced networks, which include structured wiring, have provided an understanding of how shared variability can emerge through internal mechanics (34–39). These networks are a useful modeling framework to probe how shared variability generated through circuit dynamics affects population coding.

In this work, we study information transmission in spatially ordered networks of spiking neuron models, where a balance between excitation and inhibition produces population-wide variability. We embed a columnar organization of stimulus orientation preference in our model and measure the performance of an optimal estimation of a stimulus from a linear decoding of population activity. In particular, we explore how the spatial scales of feedforward and recurrent wiring influence stimulus estimation. First, we show that both feedforward and recurrent wiring shape population-wide noise correlations within the population, indicating that both aspects of circuitry may affect population coding. However, only the structure of the recurrent network determines whether the network generates information limiting noise correlations, which degrade stimulus estimation. These correlations emerge from pattern-forming dynamics in the recurrent circuit, which prevent a linear model from capturing population-wide variability, and thereby degrade any linear estimation of a stimulus. As we show, inhibition plays a critical, yet complex, role in this pattern-forming dynamics and, hence, in information transmission. Broader lateral inhibition creates patterned network activity, which decreases information, while for spatially narrow inhibition, increasing the mean inhibitory drive stabilizes activity, resulting in increased information transfer. In summary, our work begins to connect the emerging theory of how neuronal circuits produce trial-variable activity with ongoing theories of how population-wide variability affects stimulus representation.

RESULTS

Our study measures the propagation of stimulus information in a two-layer network of spatially ordered neurons. As motivation, our model aims to capture layer (L)4 and L2/3 neurons in the primary visual cortex (V1) (Fig. 1A, see Materials and Methods); however, our model is sufficiently general to capture an arbitrary layered network. We model L4 neuronal spiking activity as a Poisson process with Gabor receptive fields defining the stimulus to firing rate transfer. The orientation preference of L4 neurons is determined from a superimposed pinwheel orientation map [Fig. 1A, bottom right; see (40)]. The Gabor visual images are corrupted by spatially independent noise obeying a temporal Ornstein-Uhlenbeck process; this provides a bound on the stimulus information entering our network. L2/3 is modeled as a recurrently connected network of both excitatory and inhibitory spiking neuron models. The connection probability of all recurrent projections within L2/3 and the feedforward projections from L4 to L2/3 decays with distance with spatial widths α_rec and α_ffwd, respectively [see Materials and Methods and (36) for details]. The spatial size of the network is normalized to be 1 in both x and y directions. The columnar radius is set to be 0.1, and the feedforward and recurrent connection widths vary between 0.05 and 0.2. For comparison, in cat primary visual cortex, the radius of recurrent connection was found to be around 250 μm, and the column radius was approximately 500 μm (41, 42). We assume that the image stimulus is in the receptive field of all neurons, meaning that the image activates the whole network.

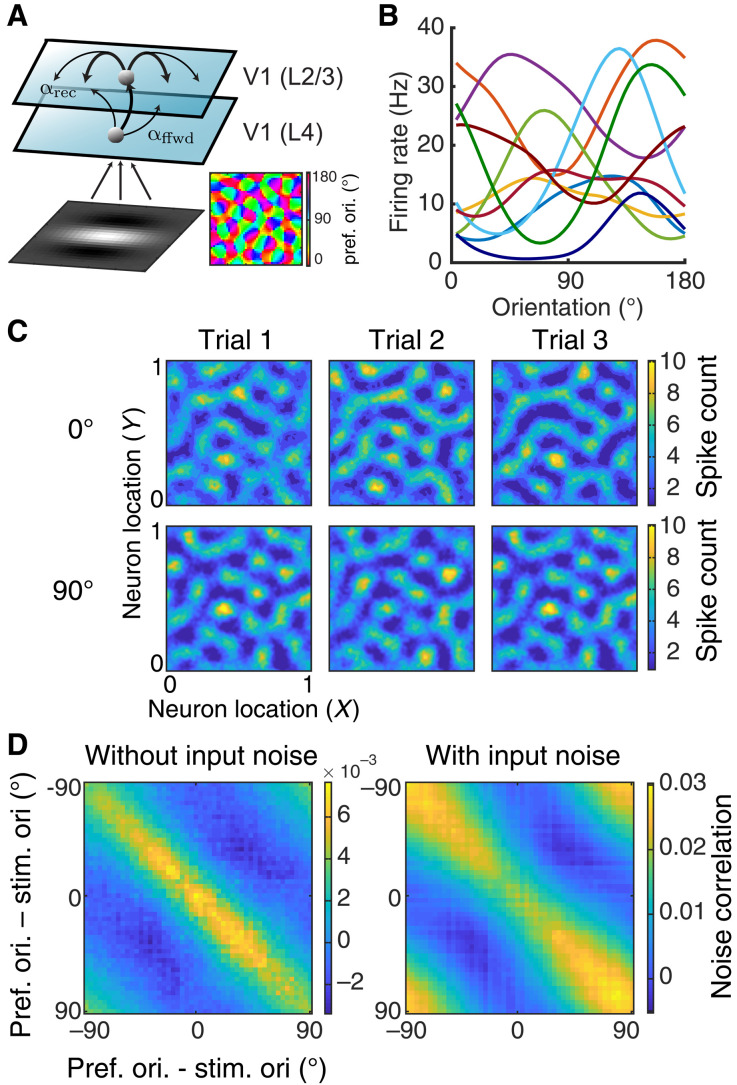
Fig. 1. Spatially ordered balanced networks generate heterogeneous tuning curves and structured trial-to-trial variability.

(A) Model schematic of a two-layer network of spatially ordered spiking neurons modeling L4 neurons and L2/3 neurons, respectively, from visual area V1. The visual input to the model is a Gabor image with orientation θ. The L4 network consists of Poisson units with Gabor receptive fields. The orientation preferences of L4 neurons are assigned according to a pinwheel orientation map (bottom right). The L2/3 network consists of both excitatory and inhibitory neurons modeled with integrate-and-fire dynamics, all arranged on a unit square. The spatial widths of the feedforward projections from L4 to L2/3 and the recurrent projections within L2/3 are denoted as α_ffwd and α_rec, respectively. (B) The L2/3 neurons have heterogeneous orientation tuning curves. Ten examples of tuning curves are shown with different colors representing different neurons (smoothed with a Gaussian kernel of width 9^∘). (C) The model internally generates trial-to-trial variability. Three trials of network spike counts (200 ms time window) are shown from a network with α_ffwd = 0.05 and α_rec = 0.1 in response to a Gabor image of 0° (top) or 90° (bottom). Images are smoothed with a Gaussian kernel of width 0.01. (D) Noise correlation matrix with neurons ordered by their preferred stimulus orientation. Responses were simulated for a Gabor input with orientation at θ = 0^∘ without (left) and with stimulus noise (right).

Networks with large, balanced excitatory and inhibitory connections are an attractive model framework for cortical activity because they capture several aspects of reported in vivo population response. When large synaptic connections are paired with random network wiring, they naturally produce significant heterogeneity in spiking activities across the network (32, 43). In our spatially ordered network, the L2/3 neurons have very heterogeneous tuning curves with various widths and magnitudes (Fig. 1B). This produces a large spread of orientation selectivity across the population (Figs. 1B and 2B), capturing the broad heterogeneity of orientation tuning reported in primary visual cortex (44).

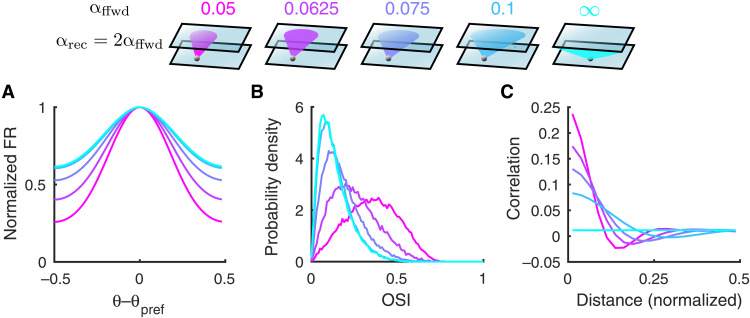
Fig. 2. Both tuning curves and noise correlations change with the feedforward projection width.

(A) The average tuning curve, normalized and centered at the preferred orientation, broadens as the feedforward projection width, α_ffwd, increases (color scheme shown on top). The recurrent width, α_rec, is fixed to be 2α_ffwd. The columnar radius, α_col, is 0.1. The case of α_ffwd = ∞ means the connection probability is independent of distance. (B) The probability density distributions of orientation selectivity indexes (OSI, Eq. 7) of the L2/3 excitatory neurons. (C) Pairwise noise correlations as a function of distance between neuron pairs from the L2/3 excitatory population. The magnitude of pairwise correlations decreases as α_ffwd increases.

Balanced networks produce significant dynamic and trial-to-trial spiking variability through internal mechanisms (32). While balanced networks with disordered connectivity produce asynchronous activity (33), networks with structured wiring can produce correlated variability (34, 35, 37), which, under certain conditions, can be population wide (36). These past models were concerned with the mechanics of neuronal variability and did not model a spatially distributed stimulus to drive network response. In our model, when L4 columnar stimulus structure is enforced, a broad L2/3 columnar activation is recruited, accompanied by significant population-wide trial-to-trial variability (Fig. 1C). Despite the lack of feature-based coupling (i.e., connectivity was determined only by the spatial distance between neurons), there is a clear positive relation between pairwise signal and noise correlations (Fig. 1D), matching diverse in vivo datasets (10, 13, 30, 45). This occurs for two reasons. First, the stimulus has a spatial columnar profile, so any spatial wiring partially overlaps with the signal profile. Second, it is well known that spike count correlations increase with the firing rates of the neuron pair (46), so that when neuron pairs with similar stimulus preference are coactivated, any significant trial-to-trial covariability in their synaptic inputs is better expressed in their output spiking. In our model, the relation between signal and noise correlations occurs in response to Gabor images, which are noiseless (Fig. 1D, left), or those contaminated by sensory noise (Fig. 1D, right). The latter case naturally provides feedforward noise correlations (31) with a columnar spatial scale. These externally imposed correlations are reduced for neuron pairs with a stimulus preference that match the driving stimulus, in agreement with past models where correlations are inherited from outside the circuit (30). In total, our spiking network captures many of the trial-averaged and trial-variable aspects of real cortical population response.

We focus on the network’s ability to discriminate two Gabor images with similar orientations, a paradigm commonly used in experiments (47). Gabor images with orientation θ are presented to the L4 neurons repetitively with an ON interval of 200 ms and an OFF interval of 300 ms (see Materials and Methods). In what follows, we consider a decoder that has access to N model L2/3 pyramidal neurons (randomly chosen from the 4 × 10⁴ L2/3 neurons). We simulate the spiking activities of L2/3 neurons and collect spike counts from the observed population, n = [n₁, …, n_N], during each stimulus presentation (ON interval). The linear Fisher information about θ available from n is defined as

$$I_F=\mathbf{f}\prime {(\mathrm{\theta })}^T{\mathrm{\Sigma }}^{-1}\mathbf{f}\prime (\mathrm{\theta })$$ (1)

where f is the expectation of n conditioned on θ (population tuning curve), ′ denotes differentiation with respect to θ, and Σ is the covariance matrix of n (noise covariance matrix). Fisher information is a useful metric when considering the estimation of orientation θ from n. Let $\widehat{\mathrm{\theta }}$ be the optimal linear estimator of the θ for a given Gabor image, then we have that $I_F=1/\text{Var}(\widehat{\mathrm{\theta }})$ (48). Put more simply, I_F measures the accuracy of the optimal linear estimator of orientation. In practice, we measure the linear Fisher information from the spike counts of the L2/3 excitatory neurons using a bias-corrected estimation [Materials and Methods and Eq. 8; (49)].

The spatial scales of connectivity in our network are key determinants of overall population spiking activity in unstimulated conditions (34–36). In the next sections, we explore how the spatial scales of the feedforward L4 to L2/3 connectivity (α_ffwd; Fig. 1A) and those of the L2/3 to L2/3 recurrent projections (α_rec; Fig. 1A) influence information transfer about stimulus θ within the network.

Narrow feedforward projections increase information saturation rate

Linear Fisher information (Eq. 1) depends on two components: the trial-averaged response gain to stimulus orientation (f′) and the trial-to-trial covariance matrix Σ. As we will show, the joint influence of α_ffwd on gain f′ and covariance Σ sets a conflict between how α_ffwd should ultimately affect I_F.

On the one hand, the population-averaged tuning curve broadens as α_ffwd increases, resulting in reduced orientation gain f′ (Fig. 2A). In agreement, the orientation selectivity index (OSI, Eq. 7) of individual neurons decreases with α_ffwd (Fig. 2B). This reduction in orientation tuning is due to broader spatial filtering of tuned inputs from L4, where the tuning preferences of neurons are spatially clustered in a columnar organization. In particular, when the connection probabilities of all projections are uniform in space (α_ffwd → ∞), the columnar structure is not preserved in L2/3, and neurons are least tuned. Hence, considering these changes in tuning selectivity alone predicts that the I_F about θ from L2/3 neurons decoding would decrease with α_ffwd.

On the other hand, the noise correlations between nearby neurons decrease with increasing α_ffwd (Fig. 2C). Rosenbaum et al. (35) showed that for spatially distributed balanced networks, where α_ffwd < α_rec, an asynchronous solution does not exist. Rather, network activity is organized so that nearby cell pairs have positive noise correlations, while more distant cell pairs have negative correlations (Fig. 2C, pink curves). We remark that while very nearby neurons can have large noise correlations (∼0.25), most pairs are distant, so that mean noise correlation across all pairs remains low (0.01). Previous work on population coding has suggested that positive correlation between similarly tuned neurons can limit information, while between oppositely tuned neurons, it can benefit coding (16–18). Since the tuning preferences of neurons are spatially clustered with a pinwheel orientation map, nearby neurons are likely to share similar tuning. Therefore, in contrast to the effect of the tuning selectivity, which would suggest that I_F could decrease with α_ffwd, the overall reduction in the spatial structure of pairwise noise correlations implies that I_F could increase with α_ffwd.

We divide our analysis of how I_F depends on α_ffwd into two cases: first, when the decoder is restricted to a small (N ∼ 10²) population of neurons and, second, for decoders that have access to large (N ∼ 10⁴) populations. For decoders restricted to small populations, the combined effects of reduced tuning selectivity and correlations with larger α_ffwd result in the linear Fisher information being largely reduced as α_ffwd increases (Fig. 3A). Consistently, the neural thresholds of single neurons, measured as the ratio of the standard deviation of the spike counts and the derivative of the tuning curve function (${\mathrm{\sigma }}_i/f_i^{\prime }$), also increase with α_ffwd (Fig. 3B). In total, the population code is less informative with larger α_ffwd, in line with the single neuron reduction in orientation selectivity (Fig. 2B), despite the associated decrease in pairwise noise correlations (Fig. 2C).

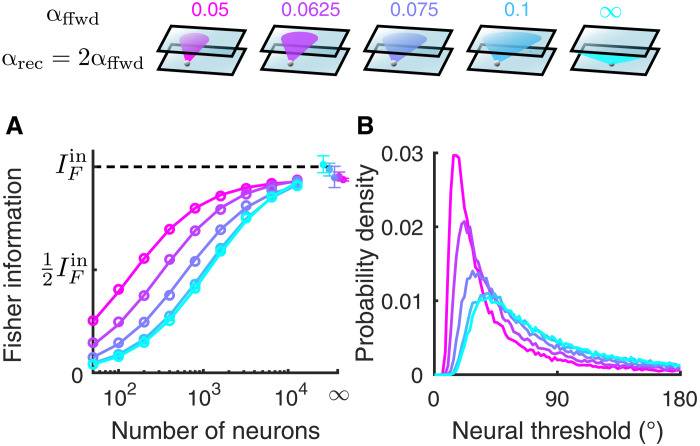
Fig. 3. The linear Fisher information saturates faster with smaller feedforward projection width.

(A) The linear Fisher information (I_F) increases with the number of neurons sampled from the excitatory population in L2/3 (color scheme on top). With a large number of neurons, the linear Fisher information saturates close to the input information bound from the L4 network ($I_F^{\text{in}}$, black dashed line). The asymptotic values of I_F at large N limit (dots at N = ∞) are estimated by fitting Eq. 10 (see Materials and Methods). Solid curves are the fits of I_F (the linear fits shown in fig. S1A). Open circles are the numerical estimation of the linear Fisher information (Eq. 8). Error bars are the 95% confidence intervals. The input noise on the Gabor images is chosen such that $I_F^{\text{in}}$ corresponds to a discrimination threshold of about 1.8°, which is consistent with psychophysical experiments (79) (see Materials and Methods). (B) The probability density distributions of neural thresholds (${\mathrm{\sigma }}_i/f_i^{\prime }$) of the L2/3 excitatory neurons.

The noise in the Gabor image creates shared fluctuations in the L2/3 neurons that cannot be distinguished from signal, limiting the available information about θ that is possible to be decoded ($I_F^{\text{in}}$; Fig. 3A, black dashed line; see Materials and Methods). For decoders that have access to large populations, the linear Fisher information of the L2/3 neurons saturates to a level close to $I_F^{\text{in}}$, regardless of the feedforward projection width (Fig. 3A). It suggests that the network is very efficient at transmitting information. In particular, even networks with spatially disordered connections (α_ffwd → ∞), where neurons are very weakly tuned, still contain most of the information from the input layer.

Moreno-Bote et al. (27) explicitly make the observation that while networks may show significant noise correlations, it is the shared fluctuations that align with the direction of response gain that limit information. In particular, they consider the decomposition of the covariance Σ = Σ₀ + ϵf′f′^T, with ϵ measuring the shared variance along the coding direction (f′). They show that for decoders that have access to a large number of neurons, I_F ∼ 1/ϵ. By assuming that the information of the nonlimiting covariance component (Σ₀) scales linearly with N, we estimated the asymptotic value of I_F at the N → ∞ limit [Fig. 3A, dots, and fig. S1A; (50); see Materials and Methods]. For our network, it is not (to our knowledge) possible to formally decompose Σ into Σ₀ + ϵf′f′^T, meaning we do not have a way of estimating how network interactions contribute to ϵ. However, the fact that the information eventually saturates close to $I_F^{\text{in}}$ for all values of α_ffwd indicates that α_ffwd does not affect the value of ϵ. This is consistent with our network being in a regime where the origin of information limiting correlations stems from strictly external fluctuations, as has been previously studied (31). Recent experiments have found strong evidence supporting the existence of information-limiting correlations in mouse visual cortex in response to grating images (50–52). Information with respect to the orientation of gratings increased sublinearly with the number of decoded neurons and was estimated to approach a plateau with tens of thousands of neurons (50, 51). Consistently, the information in our model typically approaches the asymptotic value with around 10,000 neurons.

Recurrent connections with spatially balanced excitation and inhibition have small effects on information transfer

Next, we study how the spatial scales of recurrent connections (α_rec) affect information transmission. We first consider networks with the same spatial scale of recurrent excitatory and inhibitory projections. A previous study has shown that the relative spatial scale between recurrent and feedforward projections has a large impact on the spatial structure of pairwise noise correlations (35). For fixed α_ffwd and increasing α_rec, pairwise noise correlations become spatially structured with large magnitude (Fig. 4D). In addition, the individual neuron orientation selectivity is higher when α_rec is larger than α_ffwd since the recurrent synaptic current is effectively inhibitory and thus sharpens the tuning curves (Fig. 4C) (34).

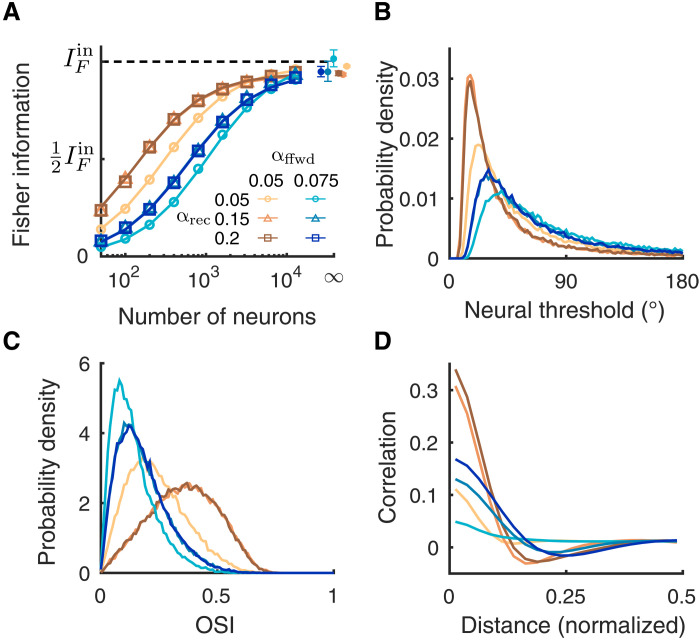
Fig. 4. The recurrent projection width has small effects on the linear Fisher information.

(A) The linear Fisher information is slightly lower when the recurrent projection width (α_rec) is narrower than the feedforward width (α_ffwd) (light shade). When α_rec is broader than α_ffwd, the saturation curve of the Fisher information overlaps (darker shades). Examples of two α_ffwd values are shown (brown, α_ffwd = 0.05; blue, α_ffwd = 0.075). The asymptotic values of I_F at N = ∞ (dots) are estimated by fitting Eq. 10 (see Materials and Methods). Solid curves are the fits of I_F (the linear fits shown in fig. S1B). Open circles are the numerical estimation of the linear Fisher information (Eq. 8). Error bars are the 95% confidence intervals. (B) The probability density distributions of neural thresholds (${\mathrm{\sigma }}_i/f_i^{\prime }$) of the L2/3 excitatory neurons. (C) The probability density distributions of OSI of the L2/3 excitatory neurons. (D) Pairwise noise correlation as a function of the distance between a neuron pair. The excitatory and inhibitory projection widths are set to be equal (σ_e = σ_i = α_rec).

For decoders that consider only small populations (N ∼ 10² to 10³ neurons), we see a clear difference between how α_rec and α_ffwd affect I_F. Specifically, I_F is relatively insensitive to α_rec (the brown curves scanning over α_rec for α_ffwd = 0.05 are clustered in Fig. 4A; similar to the blue curves with α_ffwd = 0.075). Both the distributions of neural thresholds and OSI show similar ordering as the Fisher information (Fig. 4, B and C). By contrast, the spatial structures of pairwise correlations vary in both magnitude and width and do not show a clear relationship with the ordering of the Fisher information curves for finite N (Fig. 4D). In addition, the fact that all I_F saturate at the same value for N → ∞ suggests that the changes in the population correlations do not affect the information-limiting component. Overall, for spatially balanced recurrent excitatory and inhibitory projections, the specific scale of α_rec has much smaller effect than that of the feedforward projections when considering information transfer.

Broad inhibitory projections reduce information

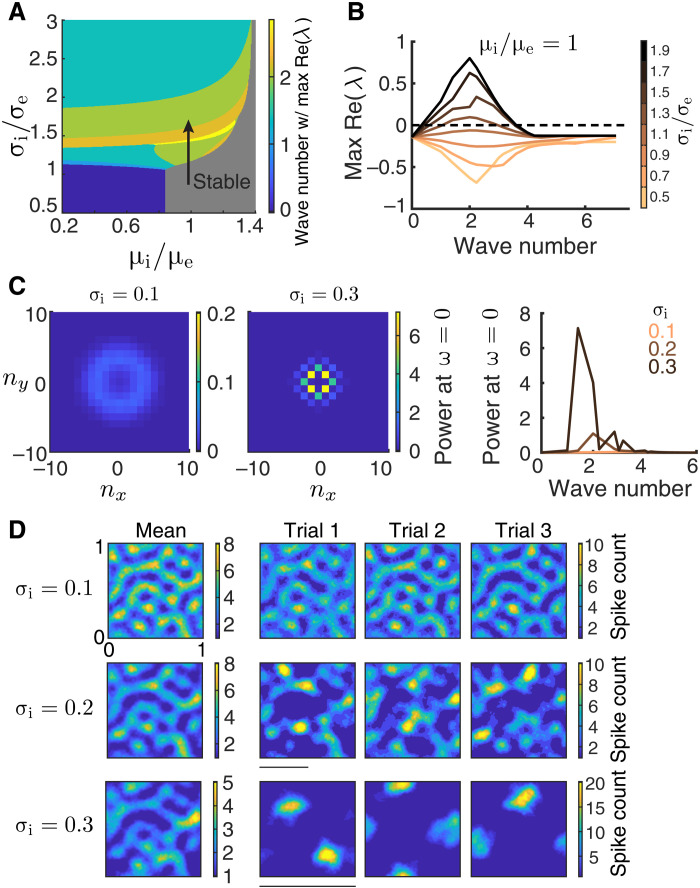
Our cortical network can exist in one of two regimes. The preceding sections consider a regime where circuit parameters are such that the firing rate dynamics across the network are stable despite pairwise correlations being structured. The second regime is where the firing rates are no longer dynamically stable, and large rate fluctuations are produced through internal interactions (as we will formalize below). In past work (36), we showed how model networks in this second regime produced the low-dimensional, population-wide shared variability characteristic of a variety of cortical areas (6, 7, 53, 54). In this section, we consider how networks in this second regime transfer information across layers.

Dynamical networks with spatially ordered coupling can produce rich spatiotemporal patterns of activity (55). To explore how the network circuitry in our cortical model determines its pattern-forming dynamics, we first implement two simplifications. First, we restrict our analysis to an associated firing rate model (56, 57), sharing the same spatial connectivity as our network of model spiking neurons (see Materials and Methods). This greatly simplifies any linear stability analysis, and it provides qualitatively, but not quantitatively, similar macroscopic network firing rates when spiking neuron models are in a fluctuation-driven regime (58). Second, we analyze the dynamics of the network when driven by spatially uniform inputs. This provides a spatial translational symmetry in the network needed for Fourier analysis.

A stable, spatially uniform solution of the firing rate model corresponds to an asynchronous state in the network of spiking neuron models. We linearize the firing rate network dynamics around this uniform solution and obtain a set of eigenvalues and associated eigenmodes. This eigenstructure governs the linearized firing rate dynamics near the uniform solution. Each eigenmode has a wave number indicating its spatial scale across the network; the zero wave number eigenmode describes a spatially uniform solution, while higher wave number eigenmodes contribute to spatially structured solutions (at the spatial period of the wave number). The stability of the solution at each eigenmode is given by the sign of the real component of the associated eigenvalue: Negative (positive) eigenvalues imply that dynamics about that eigenmode are stable (unstable). If all eigenmodes are stable, then we say that the solution is stable. The imaginary component of the associated eigenvalue near the instability indicates the temporal frequency of the unstable solution. A zero imaginary component implies a nonrhythmic solution, while a nonzero imaginary component suggests an oscillatory solution with a characteristic frequency proportional to the imaginary component.

Networks with spatially balanced recurrent excitatory and inhibitory projections (σ_e = σ_i) and strong static inputs to the inhibitory neurons (μ_i) have a stable spatially uniform solution (Fig. 5, A and B, gray region and orange curves, respectively). In this regime, the network dynamics is approximately linear with weak perturbations, meaning that the network fluctuations are linearly related with input fluctuations. Since linear Fisher information is conserved under an invertible linear transformation (see Discussion), a network in a stable regime preserves almost all of its input information. As shown in previous sections, I_F converges to $I_F^{\text{in}}$ for large N decoders, and this convergence is independent of the connectivity scales of both the feedforward and the recurrent pathways (Figs. 3A and 4A).

Fig. 5. Networks with broad inhibitory projections exhibit pattern-forming dynamics.

(A) Bifurcation diagram of a firing rate model (Eq. 6) as a function of the inhibitory projection width σ_i and the depolarization current to the inhibitory neurons (μ_i). The excitatory projection width and the drive to the excitatory neurons are fixed at σ_e = 0.1 and μ_e = 0.5, respectively. Color represents the wave number whose eigenvalue has the largest positive real part, and the gray region is marked stable since all eigenvalues have a negative real part. (B) The maximum real part of eigenvalues as a function of wave number for increasing σ_i (σ_e = 0.1), when μ_i = μ_e. Nonzero wave numbers lose stability as σ_i increases, indicating that the network will exhibit firing rate dynamics with spatial scales of the unstable eigenmodes of the uniform solution. (C) The power spectrum at temporal frequency ω = 0 for different spatial Fourier modes (n_x, n_y) of the spontaneous spiking activity from the spiking neuron networks with σ_i = 0.1 (left, the nonzero spatial frequency power peaks around wave number 3.6.) and σ_i = 0.3 (middle). Right: The average power at ω = 0 across wave numbers ($k=\sqrt{n_x^2+n_y^2}$). The power spectra are computed using a 200-ms time window. (D) Activities of spiking neuron networks with different σ_i when driven by a Gabor image (right, three trials of spike counts within the 200-ms window; left, mean spike counts). The scale bars indicate wavelengths of 0.5 (normalized unit, corresponding to wave number 2; middle) and 1 (normalized unit, corresponding to wave number 1; bottom). The spatial domain of the network is [0,1] × [0,1]. Images are smoothed with a Gaussian kernel of width 0.01. Other parameters for the spiking neuron networks (C and D) are σ_e = 0.1, α_ffwd = 0.05, and feedforward strengths J_eF = 240 mV and J_iF = 400 mV.

When the excitatory and inhibitory projections differ in spatial scale, recurrent connectivity can have a large impact on network dynamics. As the inhibitory projection width (σ_i) increases, the uniform solution in the spatial firing rate model loses stability at a band of nonzero wave numbers (Fig. 5, A and B). This is via a Turing-Hopf bifurcation (55), a pattern-forming transition common to spatially distributed neuronal network models (56, 57). The unstable eigenmodes that emerge from the bifurcation contribute to population dynamics confined to the spatial scale of their wave numbers. The temporal structure of the population dynamics is due to the eigenvalues having nonzero imaginary components at the bifurcation (fig. S2). Similar pattern-forming transitions are also observed in the spontaneous activity of spiking neuron networks (movies S1 to S3) (34, 36, 39). To quantify the spatial scales of population activity, we compute the spatial power of population spiking (at zero temporal frequency) in the spontaneous state. The power at the zero temporal frequency is measured using the same time window (200 ms) as used for Fisher information calculation; therefore, it measures the fluctuations in population activity relevant for the readout information. When σ_i equals σ_e the power spectrum is small (Fig. 5C, right, orange curve) showing a band at a wave number of approximately 3.6 (Fig. 5C, left), reflecting the spatial scale of the feedforward projections [see fig. S3 in (35)]. As σ_i increases, there is a large increase in power at some nonzero wave numbers (Fig. 5C), reflecting large, internally generated fluctuations at nonzero spatial frequencies. The pattern-forming dynamics vary slowly in time, with temporal power concentrating in a frequency band below 5 Hz (fig. S3A). Overall, this suggests that as σ_i increases, the network of spiking neuron models transitions through either a pure Turing instability, where spiking noise causes slow diffusion, or a Turing-Hopf bifurcation.

When the spiking network is driven by a Gabor image, the internal dynamics of the network interacts with the spatial patterns of the feedforward inputs. In the stable regime, where excitation is spatially balanced with inhibition (σ_i = σ_e), the spatial patterns of the network activity are similar across trials and are inherited from the input spatial scale (Fig. 5D, first row). As σ_i increases, the internal pattern-forming dynamics of the network become dominant over the feedforward input patterns (Fig. 5D, top to bottom rows). The spatially periodic patterns of the internal dynamics become evident in the variations of spike counts from the mean (fig. S4). The broad inhibition suppresses significant activity, resulting in only a few stimulus-evoked areas compared to the spatially balanced case. The locations of the evoked areas vary from trial to trial, hence introducing excessive trial-to-trial variability in the population activity patterns. The mean population activity pattern across trials also degrades as σ_i increases (Fig. 5D, left). In total, this suggests that there will be information loss in networks with larger σ_i.

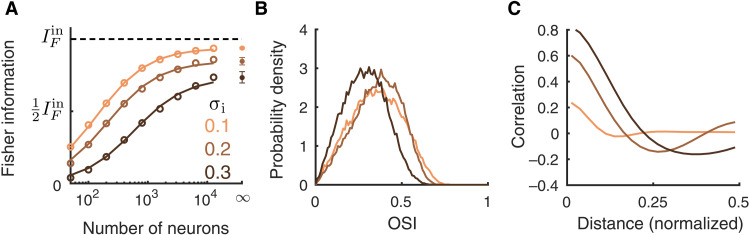
The Fisher information I_F about stimulus θ is markedly reduced when the network loses stability through broader inhibitory projections (Fig. 6A). The orientation selectivity of neurons only changes slightly with σ_i (Fig. 6B), which means that a reduction in tuning selectivity cannot be the primary reason for the decrease in I_F. However, the magnitude of pairwise correlations increases drastically as σ_i increases. Because of the internal pattern-forming dynamics in networks with large σ_i, nearby neurons are strongly correlated, while neuron pairs that are separated by half the distance between active zones are strongly anticorrelated. Consider the decomposition of network covariance Σ = Σ₀ + ϵf′f′^T, recalling that in the limit of large decoded populations (N), we have that the Fisher information I_F ∼ 1/ϵ, so that ϵ measures the strength of information limiting correlations. In the stable regime, I_F converges to the input information $I_F^{\text{in}}$ (Fig. 6A, orange curve), implying that all information-limiting correlations are inherited through the feedforward pathway (as reported earlier in Figs. 3 and 4). However, for broader inhibition, it appears that for large N, the information I_F saturates to a level that is below $I_F^{\text{in}}$. This argues that a component of the internally generated network covariability actually limits information transfer (i.e., contributes to ϵ). While our simulations support this conclusion, we admit that since it is computationally prohibitive to consider N beyond 10⁴ neurons, we cannot verify how I_F truly converges. In total, the pattern-forming dynamics in networks with broad inhibitory projections largely reduce the transmitted information.

Fig. 6. Broad inhibitory projections reduce information flow.

(A) The linear Fisher information from the L2/3 excitatory neurons is largely reduced as the inhibitory projection width (σ_i) increases. The asymptotic values of I_F at N = ∞ (dots) are estimated by fitting Eq. 10 (see Materials and Methods). Solid curves are the fits of I_F (the linear fits shown in fig. S1C). Open circles are the numerical estimation of the linear Fisher information (Eq. 8). Error bars are the 95% confidence intervals. (B) The probability density distributions of OSI of the excitatory neurons from L2/3. (C) Pairwise noise correlations as a function of distance between a neuron pair in L2/3.

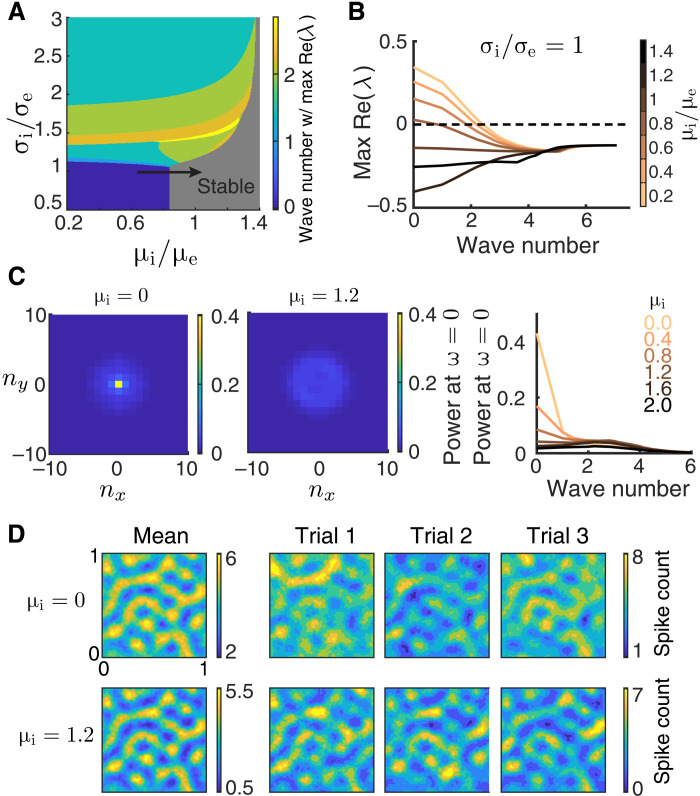
Depolarizing inhibitory neurons improves information flow

Even when excitatory and inhibitory projections are spatially matched, a network can nevertheless have an unstable uniform solution. This occurs when the static input to the inhibitory neurons (μ_i) is low (Fig. 7A, blue region), and the firing rate network is unstable through the eigenmode with zero wave number (Fig. 7B). In this case, the stability of the uniform solution is mediated by a Hopf bifurcation, through which bulk population-wide firing dynamics are produced (Fig. 7A, transition from blue to gray regions; movies S4 and S5), as opposed to the spatially confined dynamics produced via a Turing instability (Fig. 5). The spiking network shows a similar instability; when the static current to the inhibitory neurons is small, the spontaneous activities of spiking neuron networks exhibit large power at zero wave number, indicating large magnitude global fluctuations (Fig. 7C). The global fluctuations exhibit oscillations in the gamma frequency band, with temporal spectra peak around 25 to 50 Hz (fig. S3B). We note that networks in this regime lack fluctuations on the slow time scale as measured in the visual cortex [around 70 to 150 ms; (59, 60)]. Furthermore, the global fluctuations in the spontaneous activities of the spiking neuron network are largely suppressed with more input to the inhibitory neurons (Fig. 7C). In response to a stimulus θ, the population activity patterns show large fluctuations in the overall spiking activity level when μ_i is small (Fig. 7D). However, unlike the case for broad inhibition, since the instability is at zero wave number, then no spatially patterned internal dynamics occur that would compete with the stimulus-evoked spatial patterns. Consequently, the spatial patterns of the evoked activities are similar across trials (Fig. 7D).

Fig. 7. Lack of inhibitory drive gives rise to network-wide fluctuations.

(A) Bifurcation diagram of a firing rate model (Eq. 6) as a function of the inhibitory projection width σ_i and the depolarization current to the inhibitory neurons. The same as Fig. 5A. (B) The real part of eigenvalues as a function of wave number for increasing μ_i (μ_e = 0.5) when σ_i = σ_e. The zero wave number loses stability when μ_i is small, indicating that the network will exhibit network-wide nonlinear dynamics. (C) The power spectrum at temporal frequency ω = 0 for different spatial Fourier modes (n_x, n_y) of the spontaneous spiking activity from the spiking neuron networks with μ_i = 0 (left) and μ_i = 1.2 (middle). Right: The average power at ω = 0 across wave number ($k=\sqrt{n_x^2+n_y^2}$). The power spectra are computed using a 200-ms time window. (D) Activities of spiking neuron networks with different μ_i when driven by a Gabor image (right, three trials of spike counts within the 200-ms window; left, mean spike counts). Images are smoothed with a Gaussian kernel of width 0.01. Other parameters for the spiking neuron networks (C and D) are σ_e = σ_i = 0.1, α_ffwd = 0.05, J_eF = 140 mV, and J_iF = 0 mV, and the tonic current to excitatory neurons is μ_e = 0. This corresponds to an average current of 1.56 to each excitatory neuron.

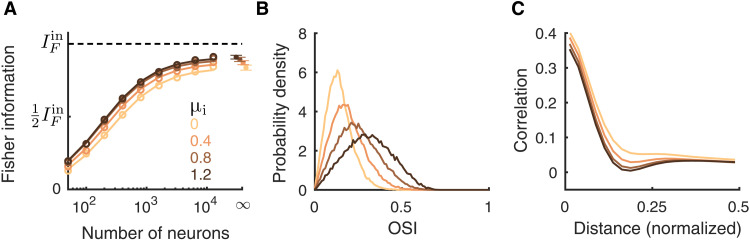
The Fisher information about θ increases with μ_i as the network becomes more stable (Fig. 8A). Once the network is in the stable regime, a further increase in μ_i has little effect on the I_F (Fig. 8A, μ_i = 0.8 compared to μ_i = 1.2). To understand this, we again consider how response gain and population covariability are affected by μ_i. First, as μ_i increases, the tuning curves of the excitatory neurons are sharpened (Fig. 8B). Second, since the unstable dynamics correlate the whole network, they give rise to positive correlations between neurons across long distances. As μ_i increases, these population-wide fluctuations are suppressed, and overall neurons are less correlated (Fig. 8C). This combination could, in principle, conspire to produce the increase in information. However, we note that the impact of global fluctuations upon information transfer is much less than that of the spatially confined fluctuations induced by broad inhibition (compare Figs. 6A and 8A).

Fig. 8. Depolarizing inhibitory neurons improves information flow.

(A) The linear Fisher information increases with depolarizing the inhibitory neurons (μ_i). The saturation curves of the linear Fisher information overlap for μ_i ≥ 0.8. The asymptotic values of I_F at N = ∞ (dots) are estimated by fitting Eq. 10 (see Materials and Methods). Solid curves are the fits of I_F (the linear fits shown in fig. S1D). Open circles are the numerical estimation of the linear Fisher information (Eq. 8). Error bars are the 95% confidence intervals. (B) The probability density distributions of OSI of the L2/3 excitatory neurons. (C) Pairwise noise correlations as a function of the distance between neuron pairs from the L2/3 excitatory population. The feedforward strengths are J_eF = 140 mV and J_iF = 0 mV, and the tonic current to excitatory neurons is μ_e = 0.

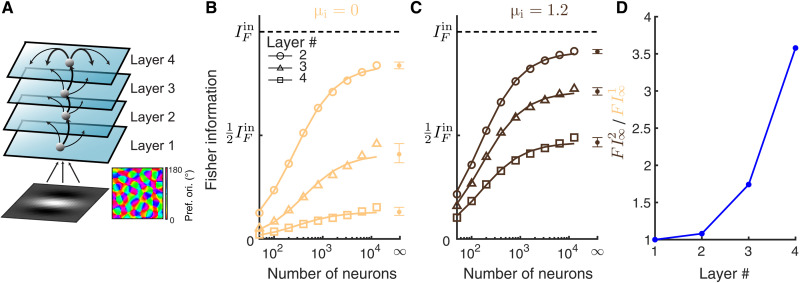
The small improvement in information transfer between two layers can be compounded during multilayer processing. We consider a four-layer network model with the same spatial wiring to model for the processing hierarchy in the visual cortex (Fig. 9A). The first and the second layer are the same as the L4 and L2/3 networks of the V1 area, respectively, in the previous model. The third and fourth layer can be considered as modeling for V2 and V4 areas, respectively. We compare the two networks with different inhibitory biases (μ_i) applied to the neurons in layers 2, 3, and 4. The feedforward strength was adjusted such that the firing rates were similar across layers 2 to 4 (fig. S5C) and between the two conditions of μ_i. As expected, the information about θ decreases as it propagates to higher-order layers (Fig. 9, B and C); this is simply an expression of the data-processing inequality (61). This suggests that information becomes more diffuse in higher-order layers (Fig. 9, B and C); indeed, the pairwise correlations are higher, and the thresholds of single neurons are larger in higher-order layers (fig. S5, A and B). However, the information deteriorates much faster across layers in networks with smaller μ_i (Fig. 9, B and C), not only because of the compounding effect but also because of the increase in spike train synchrony among neurons for small μ_i (fig. S5D). Since the inhibition is insufficient to cancel correlations at each layer, the synchrony builds up as signal propagates to higher-order layers (62). With stronger input to the inhibitory neurons, excitation is more balanced by inhibition, leading to stable asynchronous dynamics (fig. S5D). In total, the improvement in the Fisher information by increasing μ_i markedly increases with the number of processing layers (Fig. 9D).

Fig. 9. Information deteriorates in a multilayer model with internal dynamics.

(A) Schematic of a multilayer model. Layer 2 to 4 are recurrent networks of excitatory and inhibitory neurons, with the same projection widths of both recurrent and feedforward connections (α_rec = 0.1 and α_ffwd = 0.05). Recurrent connections of layer 2 and layer 3 are not shown for better illustration. The layer 1 network is the same as the V1 L4 network in Fig. 1A. (B) The linear Fisher information is much more reduced in the higher-order layers when there is no input to the inhibitory neurons (μ_i = 0). The black dashed line is the total input Fisher information from layer 1 (FI_ctin). The asymptotic values of I_F at N = ∞ (dots) are estimated by fitting Eq. 10 (see Materials and Methods). Solid curves are the fits of I_F (the linear fits shown in fig. S1E). Open circles are the numerical estimation of the linear Fisher information (Eq. 8). Error bars are the 95% confidence intervals. (C) The same as B with larger input to the inhibitory neurons (μ_i = 1.2). The linear fits of 1/I_F versus 1/N are shown in fig. S1F. (D) The ratio between the Fisher information estimated at N = ∞ in networks with μ_i = 1.2 (FI₂) and that with μ_i = 0 (FI₁) across layers. The feedforward strengths are adjusted such that the firing rates are similar between the two conditions of μ_i and are maintained across layers (fig. S5C).

Tuning-dependent connectivity partially mitigates information loss

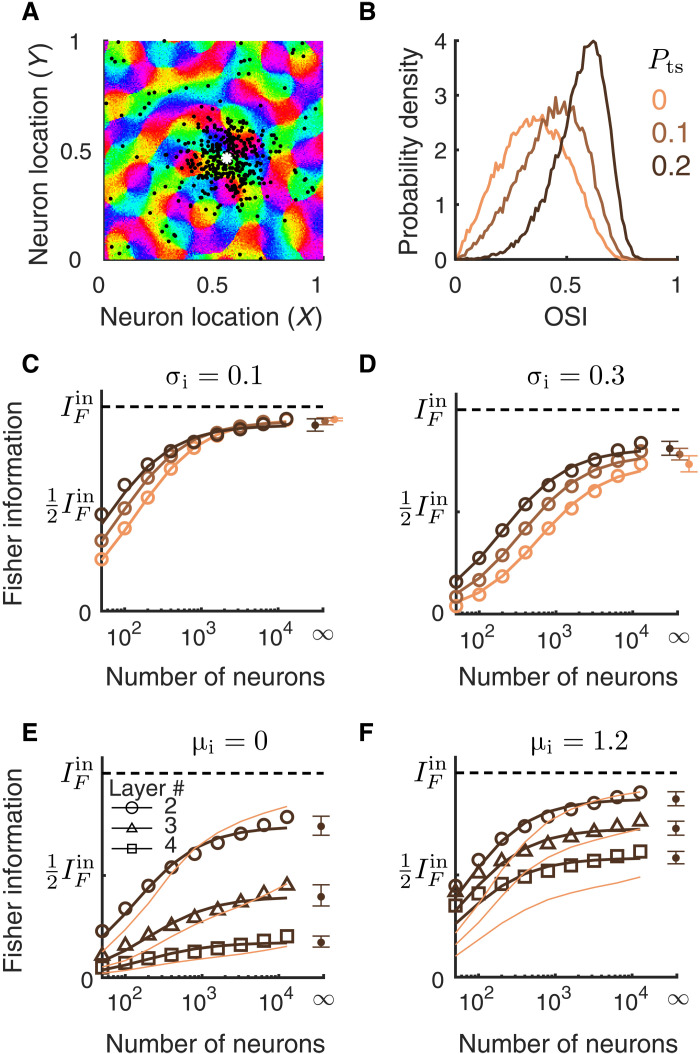
We have, thus far, considered networks with only spatially dependent connections. However, the connection probability between neurons depends not only on the physical distance between them but also on the similarity of their tuning preferences (41, 63, 64). To investigate how tuning-dependent connections shape the information flow, we modified network connectivity by rewiring a percentage of recurrent excitatory connections to be only between similarly tuned neurons (Fig. 10A; see Materials and Methods). This mimics the long-range “patchy” connections found in the visual cortex of cat and tree shrew (41, 63). We denote the percentage of such tuning-dependent connections as P_ts. Networks with P_ts = 0 are the same as those described previously with only spatial-dependent connections.

Fig. 10. Networks with tuning-dependent connectivity.

(A) Locations of postsynaptic excitatory neurons (black dots) of one example presynaptic excitatory neuron (white asterisk). The connection probability is defined similar to the networks described previously, except that a percentage (P_ts) of recurrent excitatory connections were rewired to connect similarly tuned neurons across the whole network (see Materials and Methods). (B) The probability density distributions of OSI of the excitatory neurons from L2/3 for varying the percentage of tuning-dependent connections (P_ts). The network parameters are the same as in (C) with σ_i = σ_e = 0.1. (C to F) The linear Fisher information as a function of the number of neurons sampled from the excitatory population for networks with different P_ts [color scheme the same as in (B)]. The asymptotic values of I_F at large N limit (dots at N = ∞) are estimated by fitting Eq. 10 (see Materials and Methods). Solid curves are the fits of I_F. Open circles are the numerical estimation of the linear Fisher information (Eq. 8). Error bars are the 95% confidence intervals. (C) Networks with σ_i = σ_e = 0.1; (D) networks with σ_i = 0.3 and σ_e = 0.1; (E) multilayer networks with P_ts = 0.2 (dark color) or P_ts = 0 (light color), and μ_i = 0; (F) the same as (E) with μ_i = 1.2. The information curves of networks with P_ts = 0 (light color) in (E) and (F) are the same as those in Fig. 9 (B and C).

We focus on our two identified mechanisms that transition the network between the stable and the pattern-forming dynamical regimes: varying the spatial scale of inhibitory projections (σ_i; Fig. 10, C and D) and the bias current to the inhibitory neurons (μ_i; Fig. 10, E and F). We find that the tuning-dependent connections increase the information encoded in small ensembles of neurons, which is likely due to the large improvement in the orientation selectivity of individual neurons (Fig. 10B). Despite this difference, our main conclusions from previous sections still hold in networks with tuning-dependent connections. First, the addition of tuning-dependent connections does not change the asymptotic information value when networks are in a dynamically stable regime (Fig. 10C). Second, broadening the inhibitory projections largely reduces the total amount of information (Fig. 10D compared with C), although tuning-dependent connections partially mitigate the information loss (Fig. 10D, different colors). Last, depolarizing inhibitory neurons improves the information transmission across the processing layers in multilayer networks (Fig. 10, E and F). Tuning-dependent connections do not have much of an effect on information transmission in networks with smaller μ_i (Fig. 10E), whereas it partially reduces the information loss in higher layers with larger μ_i (Fig. 10F).

DISCUSSION

The performance of a population code depends on the relationship between the individual tuning curves and the shared variability among neurons (18, 20, 21). Previous studies have tacitly assumed a prescribed structure between tuning and variability, allowing a dissection of their respective impacts on population coding (19, 24, 25). While this approach has given some critical insights, an understanding of how the mechanics of a neural circuit affect population coding has remained elusive. It is well known that the trial-averaged (65) and trial-to-trial variability (22, 31, 35, 36) of a population response are shaped by both feedforward and recurrent network connectivity. In this study, we estimated the information available (to a linear decoder) about a simple, one-dimensional stimulus that is contained in the activity of a recurrently coupled network of spatially ordered spiking neuron models. We show that simply understanding how pairwise noise correlations are determined through circuitry is insufficient to predict how information will be transferred across layers. Rather, an analysis of how circuitry determines the stability of network firing activity provides a better understanding of information transfer. Our work reveals in particular the critical role of inhibition in information transmission. Increasing the mean inhibitory drive resulted in better information transmission, while increasing the width of lateral inhibition worsened information transmission.

A central result of our paper is that in the limit of a large number of decoded neurons, the linear Fisher information I_F can either saturate to the input information $I_F^{\text{in}}$ for networks with stable firing rate dynamics (Figs. 3 and 4) or fall short of that bound for networks in a pattern-forming regime (Figs. 6, 8, and 9). To appreciate why this is the case, it is useful to recall a simple fact about how linear systems encode inputs. Consider a one-dimensional stimulus θ that drives a vector of noisy inputs x(θ) = s(θ) + η, where the noise process η has zero mean with covariance matrix Σ_x. Let the output y(θ) be a linear mapping of the input; specifically, we take y(θ) = Lx(θ) for some invertible matrix L. Then, we have that the linear Fisher information available to a decoder from y, termed $I_F^y$, is simply

$$I_F^y(\mathrm{\theta })={\mathbf{y}\prime }^T{\mathrm{\Sigma }}_y^{-1}\mathbf{y}\prime ={\mathbf{x}\prime }^T{L}^T{[L{\mathrm{\Sigma }}_x{L}^T]}^{-1}L\mathbf{x}\prime ={\mathbf{x}\prime }^T{\mathrm{\Sigma }}_{\mathrm{x}}^{-1}\mathbf{x}\prime =I_F^{\mathrm{x}}(\mathrm{\theta })$$ (2)

In other words, deterministic linear mappings do not distort or degrade information transfer (when the decoder is also linear). We remark that $I_F^y(\mathrm{\theta })$ does not depend on the linear mapping L.

When the cortical network is in the stable regime and any input noise is weakly correlated, then we can linearize network dynamics about an operating point (29, 58). In this regime, the noisy spike counts during a trial, n(θ), in response to stimulus θ obey

$$\mathbf{n}(\mathrm{\theta })=G(J\mathbf{n}(\mathrm{\theta })+\mathbf{x}(\mathrm{\theta }))+\mathit{\xi }⟹\mathbf{n}(\mathrm{\theta })={(I-\mathit{GJ})}^{-1}(G\mathbf{x}(\mathrm{\theta })+\mathbf{\xi })$$

Here, G_ij = g_iδ_ij is a diagonal matrix of the neuron response gains (depends on the operating point) and J_ij is the synaptic coupling from neuron j to i. In addition to stimulus noise in x(θ), there is an internal noise process ξ that can reflect any trial fluctuations accrued from the digitization from continuous inputs to spike counts (27) or a “background” noise that is present even when coupling and stimulus are absent (29); in all cases, ξ is independent across neurons. If sufficiently large numbers of neurons are decoded or sufficiently long observation times are used, then the contribution of ξ to population statistics is negligible, and we have that n ≈ (I − GJ)⁻¹Gx, or in other words, the population output is a linear function of the input. Given this linearization and Eq. 2, we would then expect that $I_F\approx I_F^{\text{in}}$, so long as the coupling J and input x provide a stable operating point around which to linearize. In contrast to this stable case, when the network is in a pattern-forming regime, then there is not a stable operating point about which to linearize. This means that Eq. 2 is no longer valid, and we would expect that $I_F<I_F^{\text{in}}$. In total, this argument sketches how an understanding of the network firing rate stability translates quite naturally to an understanding of what circuit conditions will allow the network to faithfully transfer all the information available (to a linear decoder) in an input signal.

Broad inhibitory projections, also referred to as lateral inhibition, are a common circuit structure used to support various neural computations, such as working memory (56, 66), sharpening of tuning curves (22, 65), formation of clustered networks (67), and the periodic spatial receptive fields of grid cells (68). In this work, we show that the pattern-forming dynamics generated by lateral inhibition degrade information transmission, which is consistent with previous results (22). Anatomical measurements of local cortical circuitry in the visual cortex show that excitatory and inhibitory neurons project with similar spatial scales (41, 64). Our results suggest that such spatially balanced excitatory and inhibitory projections are important for maintaining faithful representations of sensory stimuli. Nevertheless, lateral inhibition may be important for transforming sensory information into task-related information in higher-order cortices, such as the prefrontal cortex.

Information transmission in feedforward networks has been studied in several models. Bejjanki et al. (69) show that by improving feedforward template matching of Gabor filters, perceptual learning can increase the information gleaned from a presented image. In our model, the L4 network is similar to such models (31, 69), where information loss depends on the Gabor filters of the L4 neurons. In contrast, the feedforward projections from L4 to L2/3 neurons in our model are random and expansive (meaning there are much more neurons in L2/3 than L4), which is known to minimize information loss (23, 70). Therefore, there is little information loss in the feedforward projections from L4 to L2/3 in our model, regardless of the projection width. Renart and van Rossum (71) and Zylberberg et al. (70) study information transmission with external noise added to the output layer and compute the optimal connectivity and input covariance that maximize the information in the output layer. In our model, there is no external noise imposed on the L2/3 neurons. All the neuronal variability in the L2/3 network is either internally generated or inherited from the feedforward inputs (32, 35, 36).

Our results can potentially explain the improvement in discriminability by selective attention. Spatial attention has been shown to significantly reduce the global fluctuations in cortical recordings and, meanwhile, improve animals’ performance in the orientation change detection task [(10); but see (11, 12)]. However, the magnitude of global fluctuations is found to have little effect on information, and instead, information is only limited by input noise (27, 31). Recently, we developed a circuit model where large-scale wave dynamics give rise to low-dimensional shared variability (36), thus capturing properties of population recordings in the visual cortex (6, 45, 54). By depolarizing the inhibitory neurons, the attentional modulation in our model stabilizes the network and decreases noise correlations. To account for attention-mediated increase in firing rates, the model requires additional mechanisms such as increasing the feedforward projection strengths (72). Our past work suggests that the attention-mediated reduction in noise correlations reflects an increase in the stability of network dynamics. Results from the present study imply that enhanced network stability can increase information flow by quenching the internally generated, turbulent dynamics in the recurrent circuit (Fig. 8A).

In this work, we focused on two types of solutions in spatial networks, each with distinct nonlinear dynamics. In the pattern-forming regime with broad inhibition, networks generate slow fluctuations (below 5 Hz), positive correlations between nearby neuron pairs, and negative correlations for neurons pairs that are half wavelength away. In the regime of wave dynamics, network activity shows gamma rhythms (25 to 50 Hz) and, on average, positive correlations across all distances. Recordings from visual cortex have found fluctuations around the 70- to 150-ms time scale (59, 60) and, on average, positive correlations across long distance (36), which is more consistent with the wave dynamics regime.

In addition to the two types of nonlinear dynamics focused in our work, there are other mechanisms for networks to internally generate shared variability. For example, models with bistability can produce stochastic transitions between active and inactive states (11, 67, 73), which have been commonly observed in anesthetized (73) and awake behaving animals (74). Networks with bistability generate slow fluctuations and large correlations among neurons within the same population (11, 67, 73). The time scale of variability depends on the adaption time constant and input noise strength. A recent spatial network model with local bistability models attention as excitatory inputs and predicts a reduction in the spatial scale of noise correlations by attention (11). In contrast, networks in the wave dynamics regime produce a more spatially uniform shift of correlations (Fig. 8C). A reanalysis of multielectrode recordings from the V4 area shows that noise correlations have a shorter spatial scale in the attended state (fig. S6), which is more consistent with models with local bistability. Despite the differences in mechanisms, models with local bistability also predict that attention improves the stability of the active state of local populations (11). Since the transitions between active and inactive states are internal nonlinear dynamics, results from the present study suggest that they may also reduce information transmission. A more detailed study is needed to compare how different mechanisms of nonlinear network dynamics affect information processing.

Spontaneous dynamics of cortex have been shown to mimic the response patterns evoked by external stimuli (75, 76). It has been hypothesized that the spontaneous dynamics reflect the prior distribution of the stimulus statistics, which is critical for optimal Bayesian inference (76, 77). Our results show that the internal dynamics of recurrent networks do not improve information flow and can reduce it drastically when they are excessive. This is consistent with the correlation between the reduction in global fluctuations in population activity by attention and learning and the improvement in animal’s performance (13, 14). The inclusion of tuning-dependent wiring only partially mitigates the information loss that is due to internal dynamics in some networks. The exact role of spontaneous dynamics in information processing and neural computation remains to be elucidated in future studies.

MATERIALS AND METHODS

Network model description

The network consists of two stages, modeling for the L4 and L2/3 neurons in V1, respectively (Fig. 1A). Neurons on the two layers are arranged on a uniform grid covering a unit square Γ = [−0.5,0.5] × [−0.5,0.5]. L4 population is modeled similarly to the model in (31). There are N_x = 2500 neurons in L4. The firing rate of neuron i from L4 is determined by its Gabor filter F_i acting on the presented image $\tilde{m}(\mathrm{\theta },t)$

$$r_i(\mathrm{\theta },t)={[F_i·\tilde{m}(\mathrm{\theta },t)]}_{+}$$

where ${[x]}_{+}=\{\begin{array}{c}x,x\ge 0\\ 0,x<0\end{array}.\text{denotes half rectification},F_i=F_{(x,y)}({\mathrm{\theta }}_{\text{pref}}^i)\in {\mathcal{R}}^P$ is a Gabor filter, $\tilde{m}(\mathrm{\theta },t)\in {ℛ}^P$ is a Gabor image corrupted by independent additive noise, $\tilde{m}(\mathrm{\theta },t)=m(\mathrm{\theta })+\mathrm{\xi }(t)$, P is the number of pixels in each image, and · is the inner product of two vectors. The noise on each pixel follows the Ornstein-Uhlenbeck process

$${\mathrm{\tau }}_{n}d\mathrm{\xi }=-\mathrm{\xi }\mathit{dt}+{\mathrm{\sigma }}_n\mathit{dW}$$

with τ_n = 40 ms, σ_n = 3.5, and W being a vector of P independent Wiener processes. Spike trains of L4 neurons are generated as inhomogeneous Poisson process with rate r_i(t). The shared stimulus noise generates correlations across L4 neuron pairs and provides an external source of information limiting correlations, as in (31). These correlations are weak, yet nonzero (0.0052 on average) and match the weak values reported in the literature (78).

The Gabor image is defined on Γ with 25 × 25 pixels (Δx = 0.04),

$$m_{(x,y)}(\mathrm{\theta })=\text{exp} (-\frac{x^2+y^2}{2{\mathrm{\sigma }}^2})\text{cos} (\frac{2\mathrm{\pi }}{\mathrm{\lambda }}(x \text{cos} (\mathrm{\theta }\mathrm{\pi })+y \text{sin} (\mathrm{\theta }\mathrm{\pi }))+\mathrm{\varphi })$$

The size of the spatial Gaussian envelope was σ = 0.2, the spatial wavelength was λ = 0.6, and phase was ϕ = 0. The orientation θ is normalized between 0 and 1. The Gabor filters were

$$F_{(x,y)}({\mathrm{\theta }}_{\text{pref}})\propto \text{exp} (-\frac{x^2+y^2}{2{\mathrm{\sigma }}^2})\text{cos} (\frac{2\mathrm{\pi }}{\mathrm{\lambda }}(x \text{cos} ({\mathrm{\theta }}_{\text{pref}}\mathrm{\pi })+y \text{sin} ({\mathrm{\theta }}_{\text{pref}}\mathrm{\pi }))+\mathrm{\varphi })$$

with the same σ, λ, and ϕ as the image. The orientation map was generated using the formula from (40) (Supplementary Materials, eq. S20). The preferred orientation at (x, y) is θ_pref(x, y) = angle(z(x, y))/(2π) and

$$z(x,y)={\displaystyle \sum _{j=0}^{n-1}}\text{exp} (i\frac{2\mathrm{\pi }}{\mathrm{\Lambda }}(l_j(\text{cos} (j\mathrm{\pi }/n)x+\text{sin} (j\mathrm{\pi }/n)y)+{\mathrm{\varphi }}_j)),n=30$$

where Λ = 0.2 is the average column spacing, l_j = ±1 is a random binary vector, and the phase ϕ_j is uniformly distributed in [0,2π].

The L2/3 network consists of recurrently coupled excitatory (N_e = 40,000) and inhibitory (N_i = 10,000) neurons. Each neuron is modeled as an exponential integrate-and-fire neuron whose membrane potential is described by

$$C_m\frac{\mathrm{d}{V}_j^{\mathrm{\alpha }}}{\mathrm{d}t}=-g_L(V_j^{\mathrm{\alpha }}-E_L)+g_L{\mathrm{\Delta }}_T{e}^{(V_j^{\mathrm{\alpha }}-V_T)/{\mathrm{\Delta }}_T}+I_j^{\mathrm{\alpha }}(t)$$ (3)

where superscript α = e, i denotes excitatory and inhibitory neurons, respectively. Each time $V_j^{\mathrm{\alpha }}(t)$ exceeds a threshold V_th, the neuron spikes and the membrane potential is held for a refractory period τ_ref and then resets to a fixed value V_re. Neuron parameters for excitatory neurons are τ_m = C_m/g_L = 15 ms, E_L = −60 mV, V_T = −50 mV, V_th = −10 mV, Δ_T = 2 mV, V_re = −65 mV, and τ_ref = 1.5 ms. Inhibitory neurons are the same except τ_m = 10 ms, Δ_T = 0.5 mV, and τ_ref = 0.5 ms. The total current to each neuron is

$$\frac{I_j^{\mathrm{\alpha }}(t)}{C_m}={\displaystyle \sum _{k=1}^{N_F}}\frac{J_{\mathrm{jk}}^{\mathrm{\alpha }F}}{\sqrt{N}}{\displaystyle \sum _n}{\mathrm{\eta }}_F(t-t_n^{F,k})+{\displaystyle \sum _{\mathrm{\beta }=\mathrm{e},\mathrm{i}}}{\displaystyle \sum _{k=1}^{N_{\mathrm{\beta }}}}\frac{J_{\mathrm{jk}}^{\mathrm{\alpha }\mathrm{\beta }}}{\sqrt{N}}{\displaystyle \sum _n}{\mathrm{\eta }}_{\mathrm{\beta }}(t-t_n^{\mathrm{\beta },k})+{\mathrm{\mu }}_{\mathrm{\alpha }}$$ (4)

where N = N_e + N_i is the total number of neurons in the network. Postsynaptic current is

$${\mathrm{\eta }}_{\mathrm{\beta }}(t)=\frac{1}{{\mathrm{\tau }}_{\mathrm{\beta }d}-{\mathrm{\tau }}_{\mathrm{\beta }r}}\{\begin{array}{cc}{e}^{-t/{\mathrm{\tau }}_{\mathrm{\beta }\mathrm{d}}}-e^{-t/{\mathrm{\tau }}_{\mathrm{\beta }\mathrm{r}}},& t\ge 0\\ 0,& t<0\end{array}$$

where τ_er = 1 ms, τ_ed = 5 ms for excitatory synapses and τ_ir = 1 ms, τ_id = 8 ms for inhibitory synapses. The feedforward synapses from L4 to L2/3 have the same kinetics as the recurrent excitatory synapse, i.e., η_F(t) = η_e(t).

The probability that two neurons, with coordinates x = (x₁, x₂) and y = (y₁, y₂), respectively, are connected depends on their distance measured on Γ with periodic boundary condition

$$p_{\mathrm{\alpha }\mathrm{\beta }}(\mathbf{x},\mathbf{y})={\overline{p}}_{\mathrm{\alpha }\mathrm{\beta }}g(x_1-y_1;{\mathrm{\sigma }}_{\mathrm{\beta }})g(x_2-y_2;{\mathrm{\sigma }}_{\mathrm{\beta }})$$ (5)

Here, ${\overline{p}}_{\mathrm{\alpha }\mathrm{\beta }}$ is the mean connection probability and

$$g(x;\mathrm{\sigma })=\frac{1}{\sqrt{2\mathrm{\pi }}\mathrm{\sigma }}{\displaystyle \sum _{k=-\infty }^{\infty }}{e}^{-{(x+k)}^2/(2{\mathrm{\sigma }}^2)}$$

is a wrapped Gaussian distribution. A presynaptic neuron is allowed to make more than one synaptic connection to a single postsynaptic neuron.

The mean recurrent connection probabilities were ${\overline{p}}_{\text{ee}}=0.01$, ${\overline{p}}_{\text{ei}}=0.04$, ${\overline{p}}_{\text{ie}}=0.03$, and ${\overline{p}}_{\text{ii}}=0.04$, and the recurrent synaptic weights were J_ee = 80 mV, J_ei = −240 mV, J_ie = 40 mV, and J_ii = −300 mV. The feedforward connection probabilities were ${\overline{p}}_{\text{eF}}=0.1$ and ${\overline{p}}_{\text{iF}}=0.05$. The feedforward connection strengths were J_eF = 240 mV and J_iF = 400 mV for Figs. 1 to 6, and J_eF = 140 mV and J_iF = 0 mV for Figs. 7 and 8. The static inputs to inhibitory neurons were μ_i = 0 mV/ms for Figs. 1 to 6, and μ_i = 0,0.4,0.8, and 1.2 mV/ms for Figs. 7 and 8. The static inputs to excitatory neurons were μ_e = 0 mV/ms for all simulations.

The feedforward connection widths, α_ffwd, were 0.05, 0.625, 0.75, 0.1, and ∞, and the excitatory and inhibitory connection widths were fixed to be σ_e = σ_i = 2α_ffwd for Figs. 2 and 3. The inhibitory connection widths σ_i were 0.1, 0.2, and 0.3 for Figs. 5 and 6, and the excitatory and the feedforward connection widths were σ_e = 0.1 and α_ffwd = 0.05, respectively. The feedforward connection width was α_ffwd = 0.05, and the excitatory and inhibitory connection widths were σ_e = σ_i = 0.1 for Figs. 1 and 7 to 9.

In the multilayer network (Fig. 9), the recurrent and the feedforward connections of all layers are α_rec = 0.1 and α_ffwd = 0.05, respectively. The first and the second layer are the same as the L4 and L2/3 networks, respectively, described above. The other layers are modeled the same as the L2/3 network. In the condition when μ_i = 0 mV/ms, the feedforward connection strength from L1 to L2 excitatory neurons is J_eF = 140 mV, and the feedforward connection strengths between other layers are J_eF = 35 mV. In the condition when μ_i = 1.2 mV/ms, the feedforward connection strength from L1 to L2 excitatory neurons is J_eF = 180 mV, and the feedforward connection strengths between other layers are J_eF = 54 mV. The feedforward connection probability from L1 to L2 excitatory neurons was ${\overline{p}}_{\text{eF}}=0.1$, and feedforward connection probabilities to other layers were ${\overline{p}}_{\text{eF}}=0.01$ in both conditions of μ_i. All the feedforward connections to inhibitory neurons and the static inputs to excitatory neurons were set to be zero, i.e., J_iF = 0 mV and μ_e = 0 mV/ms. The feedforward strengths were chosen such that the mean firing rates of L2 to L4 are similar across layers and between the two conditions of μ_i.

In networks with tuning-dependent connections (Fig. 10), P_ts percentages of recurrent excitatory connections are randomly chosen from similarly tuned neurons and do not depend on space. The remaining 1 − P_ts connections are generated according to connection probability that depends only on the physical distance between neurons (Eq. 5). Neurons i and j are called similarly tuned if their preferred orientations, θ_i and θ_j, satisfy condition cos (θ_i − θ_j) > 0.6. The tuning preference of the excitatory neurons are determined by choosing the preferred orientation θ of the estimated feedforward input, h(x, y, θ) = f(x, y, θ) * g(x, y, α_ffwd), where f is the tuning curve function of neurons in the feedforward layer, g is a wrapped Gaussian spatial kernel of width α_ffwd, and * is convolution over space. Other parameters are the same as described above.

All simulations were performed on the High Performance Computing Cluster at the Center for the Neural Basis of Cognition in Pittsburgh, PA. All simulations were written in a combination of C and Matlab (Matlab R 2015a, Mathworks). The differential equations of the neuron model were solved using the forward Euler method with a time step of 0.05 ms.

Neural field model and stability analysis

We use a two-dimensional neural field model to describe the dynamics of population rate (Figs. 4 and 6). The neural field equations are

$${\mathrm{\tau }}_{\mathrm{\alpha }}\frac{\mathrm{\partial }{r}_{\mathrm{\alpha }}(x,t)}{\mathrm{\partial }t}=-r_{\mathrm{\alpha }}+\mathrm{\varphi }(w_{\mathrm{\alpha }e}*r_e+w_{\mathrm{\alpha }i}*r_i+{\mathrm{\mu }}_{\mathrm{\alpha }})$$ (6)

where r_α(x, t) is the firing rate of neurons in population α = e, i near spatial coordinates x ∈ [0,1] × [0,1]. The symbol * denotes convolution in space, μ_α is a constant external input and $w_{\mathrm{\beta }}(x)={\overline{w}}_{\mathrm{\alpha }\mathrm{\beta }}g(x;{\mathrm{\sigma }}_{\mathrm{\beta }})$, where g(x; σ_β) is a two-dimensional wrapped Gaussian with width parameter σ_β, β = e, i. The transfer function is a threshold-quadratic function, $\mathrm{\varphi }(x)={[x]}_{+}^2$. The time scale of synaptic and firing rate responses is implicitly combined into τ_α.

For constant inputs, μ_e and μ_i, there exists a spatially uniform fixed point, $r_{\mathrm{\alpha }}^{*}$. Linearizing around this fixed point in Fourier domain gives a Jacobian matrix at each spatial Fourier mode (34).

$$J(\overrightarrow{n})=\left[\begin{array}{cc}(-1+g_e{\tilde{w}}_{\mathit{ee}}(\overrightarrow{n}))/{\mathrm{\tau }}_e& g_e{\tilde{w}}_{\mathit{ei}}(\overrightarrow{n})/{\mathrm{\tau }}_e\\ g_i{\tilde{w}}_{\mathit{ie}}(\overrightarrow{n})/{\mathrm{\tau }}_i& (-1+g_i{\tilde{w}}_{\mathit{ii}}(\overrightarrow{n}))/{\mathrm{\tau }}_i\end{array}\right]$$

where $\overrightarrow{n}=(n_x,n_y)$ is the two-dimensional Fourier mode, ${\tilde{w}}_{\mathrm{\alpha }\mathrm{\beta }}(\overrightarrow{n})={\overline{w}}_{\mathrm{\alpha }\mathrm{\beta }}\text{exp} (-2\parallel \overrightarrow{n}{\parallel }^2{\mathrm{\pi }}^2{\mathrm{\sigma }}_{\mathrm{\beta }}^2)$ is the Fourier coefficient of w_αβ(x) with $\parallel \overrightarrow{n}{\parallel }^2=n_x^2+n_y^2$, and $g_a={\mathrm{\varphi }}^{\prime }(w_{\mathrm{\alpha }e}*r_e^{*}+w_{\mathrm{\alpha }i}*r_i^{*}+{\mathrm{\mu }}_{\mathrm{\alpha }})$ is the gain. The fixed point is stable at Fourier mode $\overrightarrow{n}$ if both eigenvalues of $J(\overrightarrow{n})$ have negative real part. Note that stability only depends on the wave number, $k=\parallel \overrightarrow{n}\parallel$, so Turing-Hopf instabilities always occur simultaneously at all Fourier modes with the same wave number (spatial frequency).

For the stability analysis in Figs. 5 and 7, μ_i varied from 0.1 to 0.7 with a step size of 0.002, σ_i varied from 0.05 to 0.2 with a step size of 0.0005, and μ_e = 0.5 and σ_e = 0.1. The rest of the parameters were ${\overline{w}}_{\mathit{ee}}=80$, ${\overline{w}}_{\mathit{ei}}=-72$, ${\overline{w}}_{\mathit{ie}}=120$, ${\overline{w}}_{\mathit{ii}}=-90$, τ_e = 5 ms, and τ_i = 8 ms.

Statistical methods

Each simulation was 20 s long consisting of alternating OFF (300 ms) and ON (200 ms) intervals. Image was presented during ON intervals, where the average firing rate of L4 neurons was r_X = 10 Hz. During OFF intervals, spike trains of L4 neurons were an independent Poisson process with rate r_X = 5 Hz. Spike counts from the L2/3 excitatory neurons during the ON intervals were used to compute the linear Fisher information and noise correlations. The first spike count in each simulation was excluded. For each parameter condition, the connectivity matrices were fixed for all simulations. The initial states of each neuron’s membrane potential were randomized in each simulation.

To compute tuning curve functions, the orientation for each ON interval was randomly sampled from 50 orientations uniformly spaced between 0 and 1. There were 9750 spike counts in total for all orientations. Tuning curves were smoothed with a Gaussian kernel of width 0.05. OSI for neuron i is computed as

$${\text{OSI}}_i=\frac{\sqrt{{({\displaystyle {\sum }_{k=1}^{N_{\mathit{th}}}}{r}^i({\mathrm{\theta }}_k)\text{sin} (2\mathrm{\pi }{\mathrm{\theta }}_k))}^2+{({\displaystyle {\sum }_{k=1}^{N_{\mathit{th}}}}{r}^i({\mathrm{\theta }}_k)\text{cos} (2\mathrm{\pi }{\mathrm{\theta }}_k))}^2}}{{\displaystyle {\sum }_{k=1}^{N_{\mathit{th}}}}{r}^i({\mathrm{\theta }}_k)}$$ (7)

where rⁱ(θ) is the tuning curve function of neuron i, and θ_k = k/N_th.

To compute the linear Fisher information and noise correlation, the orientations of the Gabor images during ON intervals were randomly chosen from θ₁ = θ + δθ/2 and θ₂ = θ − δθ/2, where θ = 0.5 and δθ = 0.01. The linear Fisher information of L2/3 neurons is computed using the bias-corrected estimate (49)

$${\widehat{I}}_{\mathit{bc}}=\frac{{({\mathbf{f}}_2-{\mathbf{f}}_1)}^T}{\mathrm{\delta }\mathrm{\theta }}{\left(\frac{Q_1+Q_2}{2}\right)}^{-1}\frac{({\mathbf{f}}_2-{\mathbf{f}}_1)}{\mathrm{\delta }\mathrm{\theta }}\frac{2N_{\text{tr}}-N-3}{2N_{\text{tr}}-2}-\frac{2N}{N_{\text{tr}}\mathrm{\delta }{\mathrm{\theta }}^2}$$ (8)

where f_i and Q_i are the empirical mean and covariance, respectively, for θ_i. N_tr was the number of trials for each θ_i. The number of neurons were N = 50, 100, 200, 400, 800, 1600, 3200, 6400, and 12,800, randomly sampled without replacement from the excitatory population of L2/3.

To estimate the asymptotic value of the linear Fisher information, I_∞, at the limit of N → ∞, we used the fitting algorithm proposed by Kafashan et al. (50). Briefly, the theory of information-limiting correlations (27) shows that the linear Fisher information, I_N, in a population of N neurons can be decomposed into a limiting component, I_∞, and a nonlimiting component I₀(N),

$$I_N=\frac{1}{\frac{1}{I_0}+\frac{1}{I_{\infty }}}$$ (9)

where we assume that the nonlimiting component increases linearly with N, i.e., I₀ = cN. Hence, Eq. 9 can be rewritten as

$$1/I_N=(1/c)(1/N)+1/I_{\infty }$$ (10)

which shows that 1/I_N scales linearly with 1/N with 1/I_∞ as the intercept. Hence, we did a linear fit of 1/I_N versus 1/N, with N varying from 200 to 12,800 and estimated 1/I_∞. A summary of the linear fit is shown in fig. S1.

The linear Fisher information of L4 neurons can be estimated analytically as $I_F^{\text{in}}=f\prime {(\mathrm{\theta })}^T{\mathrm{\Sigma }}^{-1}f(\mathrm{\theta })\prime$ (31), with

$$\begin{array}{c}{f\prime }_i(\mathrm{\theta })={\mathit{TF}}_i·m\prime (\mathrm{\theta }),\\ {\mathrm{\Sigma }}_{\mathit{ij}}(\mathrm{\theta })=F_i·F_j\text{Var}({\mathrm{\xi }}^T)+{\mathrm{\delta }}_{\mathit{ij}}{\mathit{TF}}_i·m\prime (\mathrm{\theta }),\end{array}$$

where ${\mathrm{\xi }}^T(t)={\int }_t^{t+T}\mathrm{\xi }(s)\mathrm{d}s$, T is the time window for spike counts, and δ_ij is a Kroenecker delta, which is 1 if i = j, and 0 otherwise. We can calculate the variance of the integrated noise over time window T as $\text{Var}({\mathrm{\xi }}^T)={\mathrm{\sigma }}_n^2[T-{\mathrm{\tau }}_n(1-e^{-T/{\mathrm{\tau }}_n})]$.

The noise correlation was computed with N = 1600 neurons randomly sampled without replacement from the excitatory population of L2/3. The Pearson correlation coefficients were computed from the average covariance matrix (Q₁ + Q₂)/2.

For the computation of both noise correlations and linear Fisher information, there were 20 sampling of neurons for each N. Neurons of firing rates less than 1 Hz were excluded. There were 117,000 spike counts in total for θ₁ and θ₂.

Supplementary Materials

This PDF file includes:

Figs. S1 to S6

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S5

View/request a protocol for this paper from Bio-protocol.