Medical Image Segmentation Using Transformer Networks

Abstract

Deep learning models represent the state of the art in medical image segmentation. Most of these models are fully-convolutional networks (FCNs), namely each layer processes the output of the preceding layer with convolution operations. The convolution operation enjoys several important properties such as sparse interactions, parameter sharing, and translation equivariance. Because of these properties, FCNs possess a strong and useful inductive bias for image modeling and analysis. However, they also have certain important shortcomings, such as performing a fixed and pre-determined operation on a test image regardless of its content and difficulty in modeling long-range interactions. In this work we show that a different deep neural network architecture, based entirely on self-attention between neighboring image patches and without any convolution operations, can achieve more accurate segmentations than FCNs. Our proposed model is based directly on the transformer network architecture. Given a 3D image block, our network divides it into non-overlapping 3D patches and computes a 1D embedding for each patch. The network predicts the segmentation map for the block based on the self-attention between these patch embeddings. Furthermore, in order to address the common problem of scarcity of labeled medical images, we propose methods for pre-training this model on large corpora of unlabeled images. Our experiments show that the proposed model can achieve segmentation accuracies that are better than several state of the art FCN architectures on two datasets. Our proposed network can be trained using only tens of labeled images. Moreover, with the proposed pre-training strategies, our network outperforms FCNs when labeled training data is small.

I. INTRODUCTION

Image segmentation is needed for quantifying the size and shape of the volume/organ of interest, population studies, disease quantification, and computer-aided treatment and surgical planning. Given the importance and the difficulty of this task in medical applications, manual segmentation by a medical expert is regarded as the ground truth. However, manual segmentation is costly, time-consuming, and subject to inter and intra-observer disagreement. Automatic segmentation methods, on the other hand, have the potential to offer much faster, cheaper, and more reproducible results.

Classical techniques for medical image segmentation include region growing [1], deformable models [2], graph cuts [3], clustering methods [4], and Bayesian approaches [5]. Atlas-based methods are another very popular and powerful set of techniques [6]. With the introduction of deep learning methods for image segmentation [7], [8], these methods were quickly adopted for medical image segmentation. Deep learning methods have achieved unprecedented levels of performance on a range of medical image segmentation tasks [9]–[14]. One can argue that deep learning methods have largely replaced the classical methods for medical image segmentation.

Recent reviews of the main lines of research and recent advancements on the application of deep learning for medical image segmentation can be found in [15], [16]. Most recent studies have aimed at improving the network architecture, loss function, and training procedures. Recent works have shown that standard deep learning models can be trained using small numbers of labeled training images [17], [18]. Despite the large variability in the proposed network architectures, the one common feature in all of these works is that they all use the convolution operation as the main building block. The proposed architectures differ with regard to the arrangement of the convolutional operations, but they all rely on the same basic convolution operation. A few studies have proposed alternative network architectures based on recurrent neural networks [19], [20] and attention mechanisms [21]. There have also been attempts to improve the accuracy and robustness of these methods by modeling the statistical variation in the shape of the organ of interest and incorporating this shape information in the deep learning method [12], [22], [23]. However, all of those models still build upon the convolution operation. Some recent studies have suggested that a basic encoder-decoder-type fully convolutional network (FCN) can handle various segmentation tasks and be as accurate as more elaborate network architectures [24].

The convolution operation is also the main building block of the network architectures that have successfully addressed other central computer vision tasks such as image classification and object detection [25], [26]. These results attest to the effectiveness of the convolution operation for modeling and analyzing images. This effectiveness has been attributed to a number of key properties, including: 1) local (sparse) connections, 2) parameter sharing, and 3) translation equivariance [27], [28]. In fact, a convolutional layer can be regarded as a fully connected layer with an “infinitely strong prior” over its parameters [29].

The properties of the convolution operation that we mentioned above are, in part, inspired by neuroscience of the mammalian primary visual cortex [30]. They give convolutional neural networks (CNNs), including FCNs, a strong and useful inductive bias, which makes them highly effective and efficient in tackling different vision tasks. However, these same properties also put CNNs at some disadvantage. For example, the network weights are determined at training time and subsequently they are fixed. Therefore, these networks treat different images and different parts of an image equally. In other words, they lack a mechanism to change their weights depending on the image content. Furthermore, due to the local nature of convolution operations with small kernel sizes, CNNs cannot easily learn long-range interactions between distant parts of an image.

Attention-based neural network models have the potential to address some of the limitations of convolution-based models. In short, these models aim at learning the relationship between different parts of a sequence [31]. Most importantly, unlike CNNs, in attention-based networks not all network weights are fixed upon training. Rather, only a portion of the network weights are learned from training data and the rest of the weights are determined at test time based on the content of the input. Attention-based networks have become the dominant neural network architectures in natural language processing (NLP) applications. Transformers are the most common attention-based models in NLP [31]. Compared with recurrent neural networks, transformers can learn more complex and longer-range interactions much more effectively. Moreover, they overcome some of the central limitations of recurrent neural networks such as vanishing gradients. They also allow for parallel processing of inputs, which can lead to significantly shorter training time on modern hardware.

Despite the potential advantages of transformer networks, so far they have not been widely adopted in computer vision applications. A recent survey of the relevant works on this topic can be found in [32]. Application of attention-based neural networks for computer vision applications faces several important challenges. The number of pixels in a typical image is much larger than the length of a signal sequence (e.g., number of words) in typical NLP applications. This makes it impossible to directly apply standard attention models to images. The second main reason has been the training difficulty. The strong inductive bias of CNNs that we have mentioned above makes them highly data-efficient. Transformer networks, on the other hand, require much more training data because they incorporate minimal inductive bias. Recent studies have proposed practical solutions to these two challenges. To address the first challenge, vision transformer (ViT) proposed considering image patches, rather than pixels, as the units of information in an image [33]. ViT embeds image patches into a shared space and learns the relation between these embeddings using self-attention modules. It was shown that, given massive datasets of labeled images and vast computational resources, ViT could surpass CNNs in image classification accuracy. One possible solution to the second challenge was proposed in [34], where the authors used knowledge distillation from a CNN teacher to train a transformer network. It was shown that with this training strategy, transformer networks could achieve image classification accuracy levels on par with CNNs using the same amount of labeled training data [34].

In this work, we propose a self-attention-based deep neural network for 3D medical image segmentation. Our proposed network is based on self-attention between linear embeddings of 3D image patches, without any convolution operations. Given the fact that self-attention models generally require large labeled training datasets, we also propose unsupervised pre-training methods that can exploit large unlabeled medical image datasets. We compare our proposed model with several state of the art FCNs on two medical image segmentation datasets.

The specific contributions of this work are as follows:

1. We propose the first convolution-free deep neural network architecture for segmentation of 3D medical images.

2. We show that our proposed network can achieve segmentation performance levels that are better than or at least on par with the state of the art FCNs. Even though prior works have suggested that massive labeled training datasets are needed to effectively train transformer networks for NLP and vision applications, we experimentally show that our network can be trained using datasets of only ~ 20 – 200 labeled images.

3. We propose methods for pre-training our network on large corpora of unlabeled images. We show that when labeled training images are fewer in number, with these pre-training strategies, our network performs better than a state of the art FCN with pre-training.

II. MATERIALS AND METHODS

A. PROPOSED NETWORK

Our proposed transformer network for 3D medical image segmentation is shown in Figure 1. The input to our network is a 3D image block $B\in \text{I}{R}^{W\times W\times W\times c}$, where W denotes the extent of the block (in voxels) in each dimension and c denotes the number of image channels. Working with image sub-blocks is a common approach in processing large volumetric images. It enables processing of large images of arbitrary size on limited GPU memory. Furthermore, it functions as an implicit data augmentation method because during training sub-blocks are sampled from random locations in the training images.

FIGURE 1.

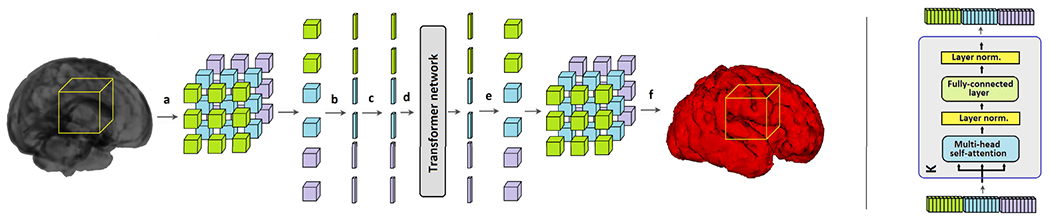
The proposed convolution-free network for 3D medical image segmentation. Left: An overall schematic of the proposed method: (a) an image block is divided into n³ non-overlapping 3D patches, (b) each patch is reshaped into a vector and embedded into a lower dimension, (c) positional encoding is added to the embedding, (d) position-encoded signals go through the transformer network, (e) the output of the network is re-projected back into the shape of the original patches, (f) the network output is the segmentation of the organ of interest for the location corresponding to the location of the extracted block. Right: One of the K stages of the transformer network.

The image block B is divided into n³ non-overlapping 3D patches ${\left\{p_i\in \text{I}{R}^{w\times w\times w\times c}\right\}}_{i=1}^N$, where w = W/n is the side length of each patch and N = n³ denotes the number of patches in the block. In the experiments presented in this paper we choose n ∈ {3, 4, 5}, resulting in N ∈ {27, 64, 125} patches in each block. The proposed transformer network embeds each patch into a lower-dimensional space and predicts the segmentation map corresponding to the image block B based on the self-attention between these embeddings. The steps of the proposed method are described below.

Each of the N patches ${\left\{p_i\right\}}_{i=1}^N$ is first reshaped into a vector of size IR^w3c and embedded into IR^D using a trainable linear mapping $E\in \text{I}{R}^{D\times w^{3}c}$. This step is similar to the first step in the ViT model for image classification. The ViT model appended an extra “class token” to the sequence of embedded patches. This class token is inherited from NLP applications. We did not use such a token in the experiments presented in this work because our preliminary experiments showed that it did not improve the segmentation performance of our network in any way. Hence, the sequence of embedded patches $X^0=\left[E_{p_1};\dots ;E_{p_N}\right]+E_{\mathrm{pos}}$ constitutes the input to our transformer network. The matrix $E_{\mathrm{pos}}\in \text{I}{R}^{D\times N}$, which is added to the embedded patches is intended to learn a positional encoding. This is a common features of self-attention models because the attention mechanism is permutation-invariant. In other words, without such positional information, the transformer network ignores the ordering of the patches in the input sequence. In most NLP applications, the positional encoding has proved to be crucial for achieving optimal results. For 2D image classification with the ViT model, positional encoding resulted in relatively small improvements in performance and a simple 1D raster encoding was as good as more elaborate 2D positional encoding strategies [33]. Because we do not know a priori what type of positional encoding would be useful in the application considered in this work, we leave E_pos as a free parameter to be learned along with the network parameters during training. In Section III, we present the results of experiments with different positional encoding strategies for our network.

As shown in Figure 1, our proposed network includes only the encoder section of the original transformer network proposed in [31]. The network has K identical stages, each consisting of a multi-head self-attention (MSA) and a subsequent two-layer fully-connected feed-forward network (FFN). All MSA and FFN modules include residual connections, ReLU activations, and layer normalization [35]. Starting with the input sequence of embedded and position-encoded patches, X⁰ described above, the k^th stage of the network performs the following operations to map X^k to X^k+1:

1. X^k goes through n_h independent heads in MSA. The i^th head:

   1. Computes the query, key, and value sequences from the input sequence using linear operations:

      $$\begin{array}{l}{Q}^{k,i}=E_Q^{k,i}\text{LN}(X^k),K^{k,i}=E_K^{k,i}\text{LN}(X^k),\\ V^{k,i}=E_V^{k,i}\text{LN}(X^k)\end{array}$$

      where $E_Q,E_K,E_v\in \text{I}{R}^{D_h\times D}$ and LN denotes layer normalization.
   2. Computes the self-attention matrix and then the transformed values:

      $$\begin{array}{l}{A}^{k,i}=\text{Softmax}(Q^{T}K)/\sqrt{D_h}\\ {\mathrm{SA}}^{k,i}=A^{k,i}{V}^{k,i}\end{array}$$

      The above equation highlights one of the central differences between transformer networks and CNNs. It shows that the mapping (A^k,i) used to transform the features from one network layer to the next layer is computed based on the input itself. Hence, this mapping depends on the content of the input at test time, rather than being fixed and the same for all inputs as in CNNs.

2. Outputs of the n_h self-attention heads are stacked together and re-projected back onto IR^D:

   $${\text{MSA}}^k=E_{\text{reproj}}^k{[{\text{SA}}^{k,0};\dots ;{\text{SA}}^{k,n_h}]}^T$$

   where $E_{\text{reproj}}\in \text{I}{R}^{D\times D_h{n}_h}$
3. The output of the current multi-head self-attention module is computed using a residual operation:

   $$X_{\text{MSA}}^k={\text{MSA}}^k+X^k$$
4. $X_{\text{MSA}}^k$ goes through a two-layer FFN to obtain the output of the k^th stage of the network:

   $$X^{k+1}=X_{\text{MSA}}^k+E_2^k\left(\text{ReLU}\left(E_1^k\text{LN}(X_{\text{MSA}}^k)+b_1^k\right)\right)+b_2^k$$

The output of the last stage, X^K, is passed through the final FFN layer that projects it onto $\text{I}{R}^{W^3{n}_{\text{class}}}$. This is then reshaped into $\text{I}{R}^{W\times W\times W\times n_{\text{class}}}$. Here, n_class denotes the number of classes (for binary segmentation, n_class = 2).

$$\widehat{Y}=\text{Softmax}\left(E_{\text{out}}{X}^K+b_{\text{out}})\right).$$

$\widehat{Y}$ is the predicted segmentation map for the block (as shown in Figure 1). Since our network predicts segmentation maps for image sub-blocks, in order to process a test image of arbitrary size, we apply the network in a sliding window fashion on the image.

B. IMPLEMENTATION AND TRAINING

We implemented the network in TensorFlow 1.16 and trained it on an NVIDIA GeForce GTX 1080 GPU on a Linux machine with 120 GB of memory and 16 CPU cores. We compare our model with the following FCN architectures:

• 3D UNet++ [36]. This is a re-design of the UNet model [37]. The main difference between UNet++ and the basic UNet is a set of dense skip connections between the encoder and decoder sections of UNet++.

• Attention UNet [38]. This model is based on attention gates, which are meant to learn to automatically focus on the target organ. These attention gates enable the network to suppress irrelevant features and to learn useful soft region proposals, thereby improving segmentation performance.

• SE-FCN [39]. This network architecture is based on incorporating squeeze & excitation (SE) blocks [40] into FCNs for medical image segmentation. The purpose of SE blocks is to adaptively adjust the importance given to different feature maps, i.e., to promote more useful features and to down-weight less informative features.

• 3D Deeply Supervised Residual Network (DSRNet) [41]. This is an encoder-decoder FCN architecture that uses deep supervision [42] and skip connections between all corresponding encoder and decoder stages.

We trained the networks using a Dice similarity coefficient (DSC)-based loss function [43]:

$$\mathcal{L}(\widehat{Y},Y)=-\frac{{\sum }_i{\widehat{Y}}_i{Y}_i}{{\sum }_i{\widehat{Y}}_i^2+{\sum }_i{Y}_i^2},$$

where Y is the ground truth segmentation map corresponding to the image block B and the index i runs over all voxels in the block. For training of our own network and the competing models we used the Adam optimization algorithm [44] with a batch size of 8. Furthermore, for all models we used blocks of size 24³ voxels. For our own network we used a learning rate of 10⁻⁴. For UNet++ a larger initial learning rate of 3 × 10⁻⁴ was used because that led to the best results with UNet++. For Attention UNet, SE-FCN, and DSRNet we used a learning rate of 10⁻⁴.

C. PRE-TRAINING

Manual segmentation of complex structures such as the brain cortical plate can take several hours of a medical expert’s time for a single 3D image. Therefore, methods that can achieve high performance with fewer labeled training images are highly advantageous. This is especially important for transformer networks. As we mentioned above, transformer networks lack much of the built-in inductive bias that many other networks such as CNNs enjoy merely by the virtue of their architectural design. Therefore, compared with those architectures, transformers typically need much larger labeled training datasets in order to learn the underlying patterns directly from data. In NLP applications, a very common approach is to pre-train the network using unsupervised training on massive unlabeled datasets [45]. In the same spirit, we propose pretext tasks that can be used to train our network on unlabeled 3D medical image datasets.

1). PRE-TRAINING WITH IMAGE DENOISING

In this approach, we add noise to the input image block B and feed the noisy block B_noisy to the network. We train the network to reconstruct the clean image block using an ℓ₂ loss:

$$\mathcal{L}(B_{\text{noisy}},B)={\Vert B_{\text{noisy}}-B\Vert }_2.$$

The noise added to each voxel is independent and identically distributed Gaussian noise with SNR = 10 dB.

2). PRE-TRAINING WITH IMAGE COMPLETION/INPAINTING

In this pre-training approach, we mask 10% of the image voxels at random. This is done by creating a random mask, $M\in {\left\{0,1\right\}}^{W\times W\times W\times c}$, where each element of M is a Bernoulli random variable with p = 0.1 and multiplying M with B in an element-wise fashion. The loss function used in this pre-training approach is similarly:

$$\mathcal{L}(B,M)={\Vert B-M\circ B\Vert }_2.$$

For model pre-training with each of the above two strategies, we use a different output layer (without the softmax operation). In order to fine-tune the pre-trained network for the segmentation task, we introduce a new output layer with the softmax activation and train the network on the labeled data as explained above. We fine-tune the entire network, rather than only the output layer, on the labeled images because we have found that fine-tuning the entire network for the segmentation task leads to much better results.

Pre-training methods are also commonly used for FCNs. Prior studies have shown that pre-training might lead to substantial improvements in segmentation performance of FCNs, especially when the segmentation task is difficult and the size of labeled training data is small [17], [46]. Therefore, we will use the same denoising and inpainting tasks described above to pre-train the FCNs. Moreover, we will also use the semi-supervised FCN training method proposed in [47]. The method of [47] is based on an alternating optimization strategy. It alternately updates the network parameters and the estimated labels for the unlabeled images in parallel.

D. DATASETS AND EVALUATION CRITERIA

Table 1 shows the datasets used for model training and evaluation in this work. The images were randomly split into training and test sets, with no patient data appearing in both training and test sets. The same training/test splits were used for all networks. For each dataset, we used approximately 20% of the training images for initial validation experiments to decide on training settings such as the learning rate for each network. After choosing the training settings, each network was trained on all training images. The only data augmentation was the implicit augmentation via sampling of image blocks from random locations in the training images. Voxel intensities of all images were normalized to have a zero mean and unit standard deviation. Moreover, all images were interpolated using 3D spline interpolation into isotropic voxel sizes shown in the table. The corresponding ground truth segmentations were interpolated using nearest neighbor interpolation. We compare our proposed method with the competing networks in terms of DSC, the 95 percentile of the Hausdorff Distance (HD95), and Average Symmetric Surface Distance (ASSD).

TABLE 1.

Datasets used for experiments in this work.

target organ	image modality	[ntrain, ntest]	image resolution (mm)	source
Brain cortical plate	T2 MRI	[18, 9]	0.80	In-house (Boston Children’s Hospital)
Hippocampus	MRI	[220, 40]	0.75	https://decathlon-10.grand-challenge.org/

III. RESULTS AND DISCUSSION

Table 2 compares the segmentation performance of the proposed method with the competing FCNs on the brain cortical plate and hippocampus datasets. As described in Section II-A, the proposed network includes several hyper-parameters that can influence the segmentation results. The results presented in Table 2 were obtained with: K = 5, W = 24, n = 3, D = 1024, D_h = 256, n_h = 4. These are our default settings for network hyper-parameters that we have used in all experiments reported in the rest of the paper, unless otherwise specified. We arrived at these parameters using cross-validation experiments on the training images in the brain cortical plate and hippocampus datasets as well as other datasets not presented in the paper. We present experimental results on the effects of different hyper-parameters on the segmentation performance below.

TABLE 2.

Comparison of the segmentation performance of the proposed method and several competing FCNs on the brain cortical plate and hippocampus datasets.

Dataset	Method	DSC	HD95 (mm)	ASSD (mm)
Brain cortical plate	Proposed	0.878 ± 0.037 *	0.871 ± 0.141 *	0.271 ± 0.068 *
	UNet++	0.862 ± 0.054	0.938 ± 0.430	0.258 ± 0.082
	Attention UNet	0.831 ± 0.060	1.125 ± 0.337	0.536 ± 0.128
	DSRnet	0.846 ± 0.050	0.978 ± 0.229	0.492 ± 0.135
	SEFCN	0.786 ± 0.076	2.095 ± 0.801	0.641 ± 0.115
Hippocampus	Proposed	0.895 ± 0.020 *	1.035 ± 0.203 *	0.416 ± 0.064 *
	UNet++	0.874 ± 0.027	1.479 ± 1.427	0.533 ± 0.208
	Attention UNet	0.820 ± 0.036	5.850 ± 5.150	1.192 ± 0.597
	DSRnet	0.821 ± 0.038	3.438 ± 3.065	1.395 ± 0.316
	SEFCN	0.716 ± 0.052	8.614 ± 5.230	1.795 ± 0.761

Better results for each dataset/criterion have been marked using bold type. We used paired t-tests to find statistically significant differences;

asterisks denote significantly better results at p < 0.01.)

The results presented in Table 2 show that the proposed network has achieved segmentation performance levels that are superior to the competing FCNs. For each dataset and each of the three criteria, we performed paired t-tests to see if the differences were statistically significant. As shown in the table, segmentation performance of the proposed convolution-free network was significantly better than the four FCNs in terms of DSC, HD95, and ASSD at p < 0.01. Specifically, for paired t-tests between the proposed model and UNet++ on the brain cortical plate dataset the p-values for DSC, HD95, and ASSD were, respectively, 0.0044, 31 × 10⁻⁵, and 0.0082. For the hippocampus dataset, the p-values for these comparisons were, respectively, 20 × 10⁻⁶, 0.0032, and 74 × 10⁻⁶. The results obtained with the proposed method were especially superior in terms of the distance metrics, i.e., HD95 and ASSD. Among the FCN architectures, UNet++ performed substantially better than the other architectures on both datasets, but its segmentation performance was significantly inferior to that of our proposed method.

Figure 2 shows example slices from test images in each dataset and the segmentations predicted by the proposed method and the four FCNs. Visual inspection of the results shows that the proposed network is capable of accurately segmenting fine and intricate structures such as the brain cortical plate. On both datasets, Attention UNet, DSRnet, and SEFCN often resulted in false positive predictions far away from the target organ, which is the reason behind their poor performance in terms of the distance metrics presented in Table 2.

FIGURE 2.

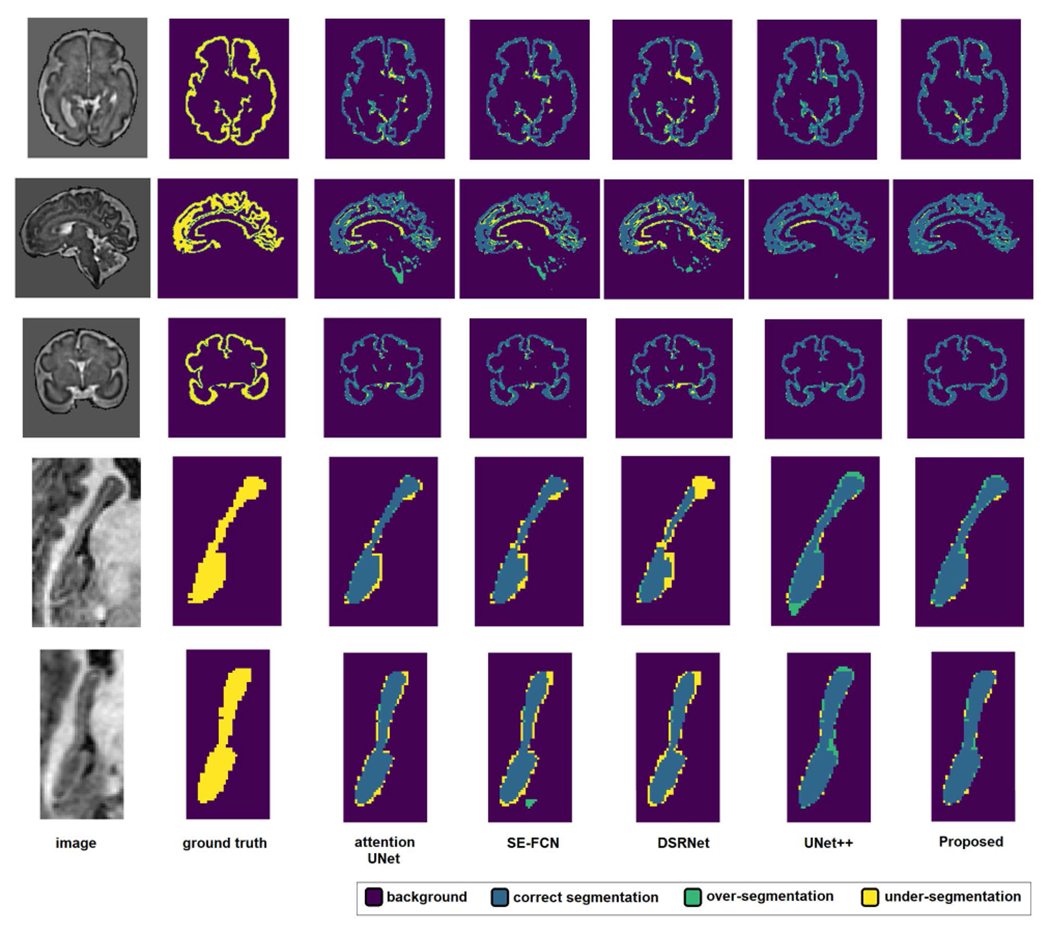
Example segmentations predicted by the proposed method and the four FCNs. The segmentation legend is shown at the top of the figure. Three example slices from the brain cortical plate dataset and two example slices from the hippocampus dataset are shown. In each example, the first row shows the image slice and the ground-truth segmentation map. The second row shows the predictions of the four FCNs and the proposed transformer network.

We further assessed the segmentation performance of our proposed network with reduced number of labeled training images. The goal of this experiment was to investigate if the pre-training tasks proposed in Section II-C could help the network achieve a good segmentation performance with a small number of labeled training images. In this experiment, we compared our model with UNet++, which was more accurate than the other three FCNs in the experiments presented in Table 2. For this experiment, we trained our method and UNet++ using n_train = 5, 10, and 15 labeled training images from cortical plate and hippocampus datasets. We pre-trained our network using either the denoising or the in-painting tasks described in Section II-C. We pre-trained UNet++ using the same denoising and inpainting pre-training tasks and also using the method proposed in [47]. Furthermore, we performed this experiment in two different ways:

1. Pre-training on data with a similar distribution. For brain cortical plate segmentation, we used 500 T2 brain images from the developing Human Connectome Project (dHCP) dataset [14] for pre-training. The subjects in the dHCP dataset range in age between 29 and 44 gestational weeks, which is close enough to the age range of our in-house dataset: between 16 and 39 gestational weeks. For hippocampus segmentation, we used the remaining training images (i.e., 220–n_train) for pre-training.

2. Pre-training on data with a different distribution. Sometimes even unlabeled images with the same distribution are not available. To simulate such a scenario, we used a pool of publicly available computed tomography (CT) images. Specifically, we used 130 liver CT [48] and 300 kidney CT [49] images to pre-train our network and UNet++ for both brain cortical plate segmentation and hippocampus segmentation. As we had done for our target MRI images described above, we also normalized voxel intensities of these CT images to have a zero mean and unit standard deviation.

Figure 3 shows the results of this experiment. The results show that with the proposed pre-training, our convolution-free network achieves significantly more accurate segmentations with fewer labeled training images. As expected, on both datasets there was a drop in the segmentation performance as the number of labeled training images was reduced. However, this drop was smaller for the proposed network than for UNet++. We have observed very similar results with other FCN architectures. For our network as well as for UNet++, the proposed inpainting pre-training leads to slightly better results than the other pre-training methods. Moreover, overall, pre-training on similar images leads to better segmentation performance than pre-training on a dataset of different images. As shown in Figure 3, for both the proposed network and UNet++ the segmentation performance is, slightly but consistently, higher when pre-training is performed on a similar dataset. This indicates that both the proposed network and UNet++ can learn the existing patterns in unlabeled images and leverage this information to achieve better segmentation results.

FIGURE 3.

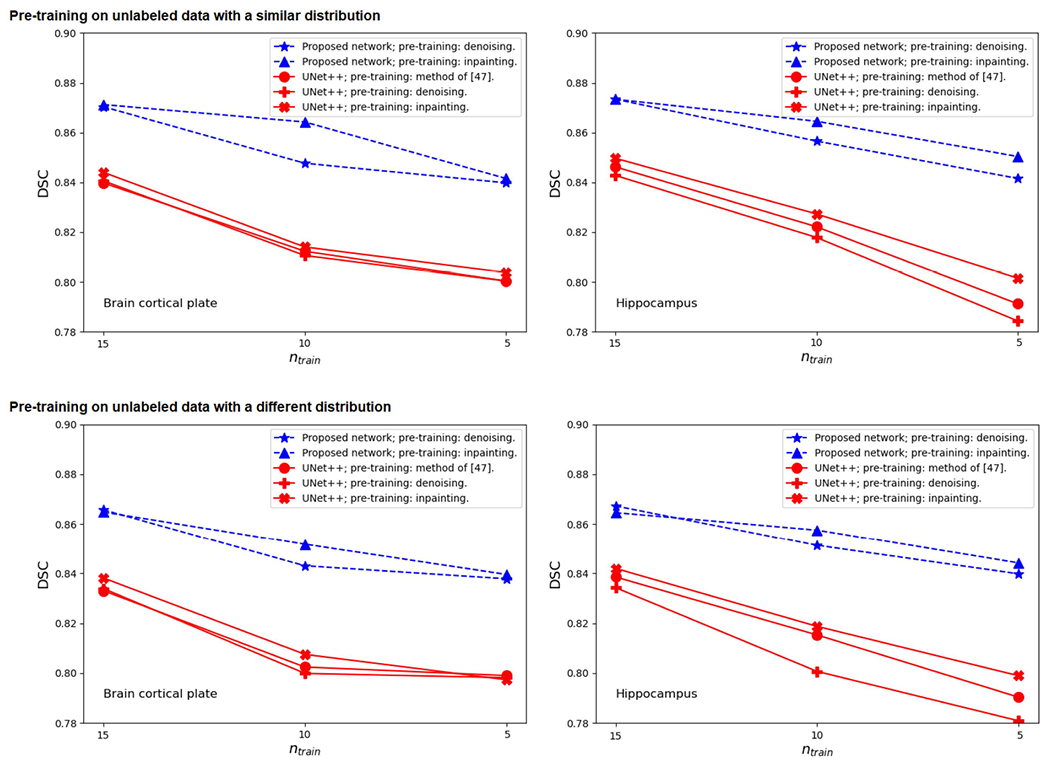
Segmentation performance (in terms of DSC) for the proposed network and UNet++ with reduced number of labeled training images on the brain cortical plate dataset (left) and the hippocampus dataset (right). The top two plots are for the experiment where the images used for pre-training have a distribution that is similar to the target test images. The bottom two plots are for the experiment where the images used for pre-training (liver and kidney CT images) are very different from the target test images.

This is a very interesting and promising observation because it shows that the proposed network can be trained using a handful of labeled images for segmenting complex structures in 3D medical images. This result is even more noteworthy when we consider the results reported by recent image classification studies. As we explained in Section I, image classification studies that used a similar approach (i.e., applying a transformer network on patch embeddings) required massive labeled datasets [33] or relied on knowledge distillation from a CNN teacher model [34]. Our results, on the other hand, show that only a handful of labeled training images are sufficient to train a similar network for 3D medical image segmentation. This can be attributed to several factors: 1) In image classification there are significant variations in relevant image features (even among images that belong to the same class). In the segmentation tasks considered here, on the other hand, there is significant similarity across subjects and even among different patches in the same image. 2) There are far fewer class labels (only two) in the segmentation tasks considered here compared with image classification applications. 3) Working with image sub-blocks acts as a strong data augmentation strategy and enables optimal utilization of labeled training images. As a result, despite their minimal inductive bias, transformer networks appear to be well suited for medical image segmentation tasks.

The experimental results presented above show that the proposed method can achieve segmentation performance on par with or better than FCNs with as few as 10-20 labeled training images. This is an important and encouraging result because in the medical imaging domain manual labels are not easy to obtain. Nonetheless, in order to assess the performance of the proposed method on larger datasets, we conducted another experiment with the newborn brain scans in the developing Human Connectome Project (dHCP) dataset [14]. This dataset includes 558 T2 MRI brain scans with cortical plate segmentation. We randomly selected 58 of these scans as test images. We then trained our model and UNet++ on all 500 remaining images as well as subsets of 100 and 10 images. In addition to the implicit data augmentation caused by sampling patches from random locations in the training images, we applied random flip and rotation and we added random Gaussian noise to the images. We also experimented with random down/up-scaling of the images and random elastic deformation, but these augmentations had a negative impact on segmentation performance because they reduced the accuracy of training labels for fine and complex cortical plate segmentation. Therefore, we did not use these latter augmentation methods. The results of this experiment are presented in Table 3. The results indicate that the proposed method achieves better segmentation results than UNet++ with either 10, 100, or 500 labeled training images. Paired t-tests on the 58 test images showed that, with 500 labeled training images, the proposed method achieved significantly higher DSC (p = 0.0015) and significantly lower ASSD (p = 84 × 10⁻⁶).

TABLE 3.

Results of an experiment to investigate the performance of the proposed network with different numbers of training images. This experiment was performed on brain cortical plate segmentation labels from the dHCP dataset [14].

No. of training images	Method	DSC	HD95 (nun)	ASSD (mm)
ntrain = 10	Proposed	0.910 ± 0.033 *	0.814 ± 0.042	0.231 ± 0.070 *
	UNet++	0.884 ± 0.040	0.816 ± 0.043	0.247 ± 0.065
ntrain = 100	Proposed	0.926 ± 0.030 *	0.806 ± 0.040 *	0.226 ± 0.068 *
	UNet++	0.916 ± 0.032	0.813 ± 0.044	0.241 ± 0.062
ntrain = 500	Proposed	0.928 ± 0.031 *	0.805 ± 0.041	0.221 ± 0.070 *
	UNet++	0.916 ± 0.028	0.805 ± 0.044	0.240 ± 0.057

Asterisks denote statistically significant differences at p = 0.01, computed using paired t-tests.

In Figures 5 and 4, we have shown example attention maps of the proposed network for two different datasets. As mentioned above, in order to process a test image of arbitrary size, we apply our network in a sliding window fashion. To generate the attention maps for the whole image, at each location of the sliding window the attention matrices (which are of size IR^N×N) are summed along their columns to determine the total attention paid to each of the N patches by the other patches in the block. Performing this computation in a sliding window fashion and computing the voxel-wise average gives us the attention maps shown in these figures. They indicate how much attention is paid to every part of the image in the process of generating the segmentation map.

FIGURE 5.

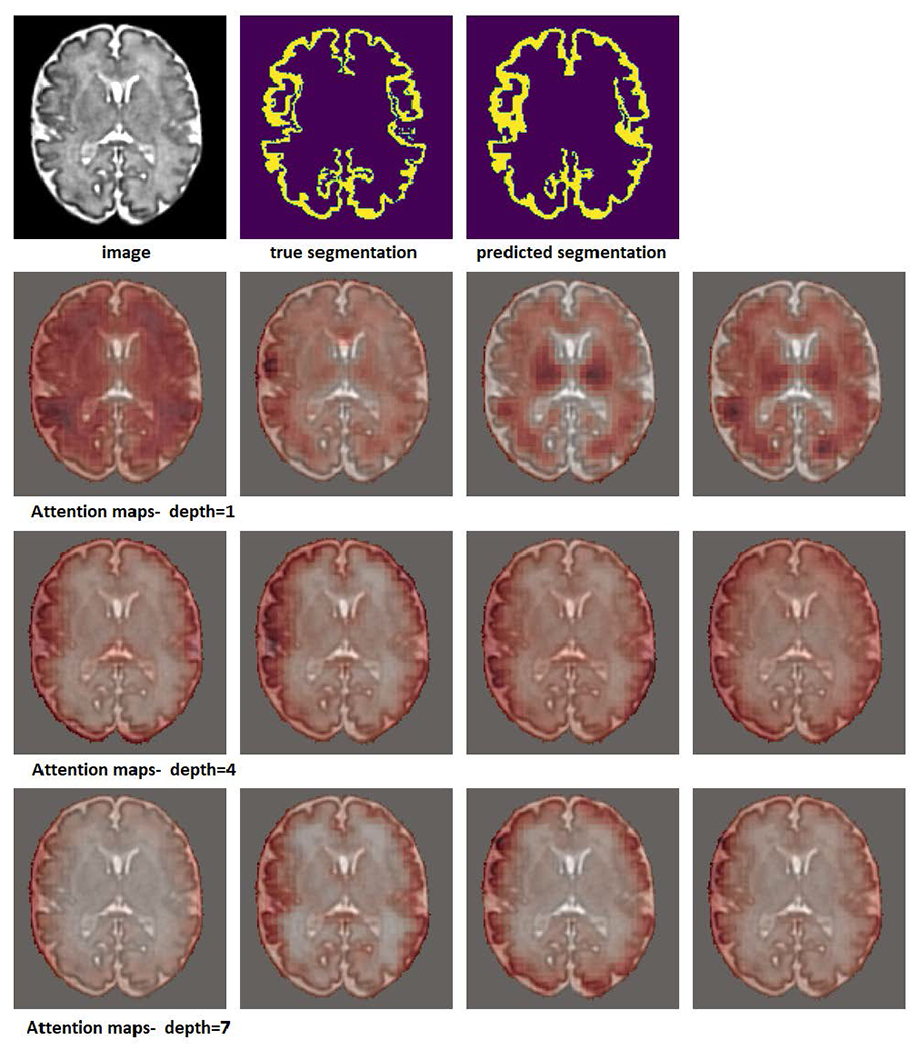
Example attention maps for a cortical plate image. In this experiment, a network with a depth K = 7 was used. Attention maps for depths 1, 4, and 7 are shown. Each row shows the attention map for one of the four heads.

FIGURE 4.

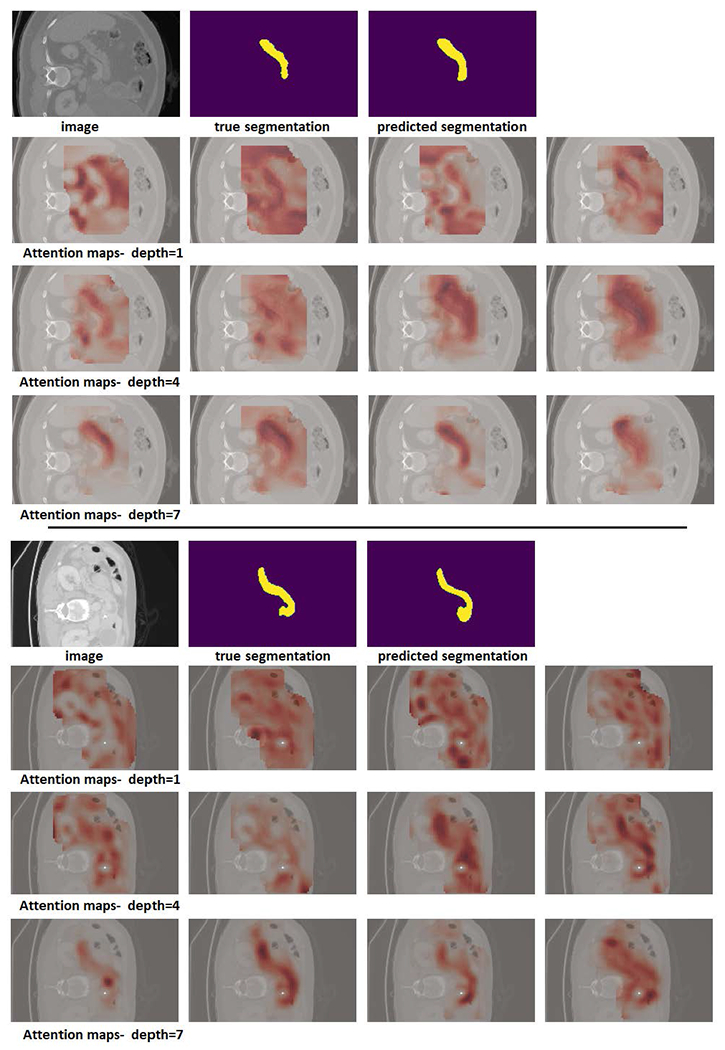
Example attention maps for two pancreas images. In this experiment, a network with a depth K = 7 was used. Attention maps for depths 1, 4, and 7 are shown. Each row shows the attention map for one of the four heads.

The attention maps shown in Figure 4 were generated on pancreas CT images from the Medical Segmentation Decathlon challenge (https://decathlon-10.grand-challenge.org/). The attention maps show that, overall, the early stages of the network have a wider attention scope. They attend to other structures and anatomical features that surround the organ of interest (here, the pancreas). The deeper stages of the network are more focused on the pancreas itself. A rather similar pattern can be observed in the segmentation maps for brain cortical plate segmentation that are shown in Figure 5. In the earlier stages, the network attends to the entire brain, while in the deeper layers the network’s attention tends to be more focused to the regions around the cortical plate.

Another observation from these figures, especially Figure 4, is the variability among the attention patterns of different heads in a multi-head self-attention (MSA) module. In each stage, the four separate heads of the MSA module adopt quite different attention strategies. This may suggest that the multi-head design of the MSA module gives the network more flexibility, enabling it to learn more complex attention patterns that help improve the segmentation performance. The importance of multi-head design is well documented in natural language processing applications [31], and our results show that it is important for 3D medical image segmentation as well. We further show this below by quantifying the effect of the number of attention heads on segmentation performance.

Table 4 shows the results of a set of experiments on the brain cortical plate dataset to investigate the effects of some of the network hyper-parameters on segmentation performance. In this table, the baseline network (first row) corresponds to the settings that we have used in the experiments reported above, i.e., K = 5, W = 24, n = 3, D = 1024, D_h = 256, and n_h = 4. We chose these settings based on preliminary experiments and we have found them to work well for different datasets.

TABLE 4.

Effect of some of the network hyperparameters on the segmentation performance on the brain cortical plate dataset. The baseline network (shown in the first row of this table) corresponds to these settings: K = 5, W = 24, n = 3, D = 1024, D_h = 256, n_h = 4, which are the hyperparameter values that we used in all experiments reported in this paper other than in this table. In the remaining rows of this table, we have changed the hyperparameters, one at a time, and trained the network.

Parameter settings	DSC	HD95 (mm)	ASSD (mm)
baseline	0.878 ± 0.037	0.871 ± 0.141	0.271 ± 0.068
larger blocks, n = 5	0.881 ± 0.033	0.821 ± 0.113	0.257 ± 0.058
larger patches, W = 36	0.865 ± 0.043	0.898 ± 0.155	0.286 ± 0.069
no positional encoding	0.863 ± 0.056	0.904 ± 0.164	0.296 ± 0.077
fixed positional encoding	0.866 ± 0.050	0.881 ± 0.144	0.274 ± 0.060
deeper network, K = 10	0.857 ± 0.070	0.980 ± 0.171	0.301 ± 0.080
shallower network, K = 3	0.869 ± 0.081	1.030 ± 0.176	0.297 ± 0.086
more heads, nh = 8	0.877 ± 0.031	0.864 ± 0.147	0.264 ± 0.060
single head, nh = 1	0.845 ± 0.048	1.112 ± 0.208	0.325 ± 0.084

The results presented in this table show that, overall, the performance of the network is not very sensitive to the hyper-parameter settings. For example, changing the number or the size of the patches typically leads to slight changes in performance. We have also observed that a network depth of K ∈ [5, 7] leads to best results, whereas much deeper or shallower networks were not better. Furthermore, using a fixed positional encoding or no positional encoding slightly reduces the segmentation performance compared with free-parameter/learnable positional encoding. Finally, using a single-head attention significantly reduces the segmentation performance, which indicates the importance of the multi-head design to enable the network to learn a more complex relation between neighboring patches.

Many of the above observations are consistent with the experimental results that have been reported in other applications. For example, our results show that increasing the number of MSA heads (n_h) or the network depth (K) beyond a certain limit has a negative impact on segmentation performance. This observation is similar to some of the experimental results reported in [33], [50], where networks with a larger number of MSA heads and/or larger number of layers resulted in lower image classification accuracy on several datasets. Similar results have been reported in natural language processing applications [51]. For example, one study showed that it was possible to prune 50-72% of the attention heads without a significant reduction in model accuracy in a machine translation application [52]. This is because, depending on the application, a certain number of heads are sufficient to learn the attention patterns between the signals in a sequence (i.e., patch embeddings in our application). Further increasing the number of heads will only increase the number of network parameters without providing any useful capacity to the network.

There may be other factors that can influence the relative advantages of the proposed transformer network compared with FCNs. Some of these factors are image resolution, size of the organ/volume of interest, and patch size. Our experiments show that these factors do not affect the superiority of the proposed method over FCNs. For example, we resampled the brain cortical plate and hippocampus datasets to isotropic voxel sizes of 0.5 mm and repeated our experiments. The results showed that the proposed network achieved significantly higher DSC and significantly lower HD95 and ASSD than UNet++ on both datasets. We also applied UNet++ on larger patch sizes of 48³ and 64³ voxels. This change did not improve the performance of UNet++ on the brain cortical plate dataset. It slightly improved the segmentation performance of UNet++ on the hippocampus dataset (DSC: 0.877±0.029, HD95: 1.448±1.430 mm, and ASSD: 0.502±0.201 mm). However, these were still statistically inferior to those obtained with our proposed network (Table 2). Increasing the input image block size to 48³ or 64³ voxels did not significantly improve the performance of our proposed network either.

Table 5 shows the number of learnable parameters, number of floating point operations (FLOPS), and frames per second (FPS). FLOPS and FPS are reported for processing patches of size 24³ voxels. We computed the FPS for all models on an NVIDIA RTX 2080TI GPU. Overall, the models have relatively similar number of parameters and computational costs. Our proposed network has a slightly smaller number of parameters than the compared FCNs. On the other hand, the number of FLOPS for the proposed network is higher, which is due to the large matrix multiplications involved in the attention modules. In terms of training time, our network converged in approximately 24 hours of GPU time, whereas the FCNs converged in approximately 4 hours of training. This might be due to the fact that transformer networks need additional training time in order to internalize the spatial patterns in the image, whereas FCNs’ architecture makes this learning easier.

TABLE 5.

The number of free parameters (n_param), number of floating point operations (FLOPS), and frames per second (FPS) for each of the FCNs and the proposed network. FLOPS and FPS are computed for processing patches of size 24³ voxels.

Model	nparam × 106	FLOPS ×109	FPS
SEFCN	2.60	4.16	190.3
DSRNet	3.70	3.52	173.2
Attention UNet	2.77	1.83	157.0
UNet++	3.72	4.02	160.2
Proposed	2.49	4.88	144.5

IV. CONCLUSION

The convolution operation has a strong basis in the structure of the mammalian primary visual cortex and it is well suited for developing powerful techniques for image modeling and image understanding. In recent years, CNNs have been shown to be highly effective in tackling various computer vision problems. However, there is no reason to expect that no other model can outperform CNNs on a specific vision task. Medical image analysis applications, in particular, pose specific challenges such as 3D nature of the images and small number of labeled images. In such applications, other models could be more effective than CNNs. In this work we presented a new model for 3D medical image segmentation. Unlike all recent models that use convolutions as their main building blocks, our model is based on self-attention between neighboring 3D patches. Our results show that the proposed network can outperform state of the art FCNs on three medical image segmentation datasets. With pre-training for denoising and in-painting tasks on unlabeled images, our network also performed better than an FCN when only 5-15 labeled training images were available. We expect that the network proposed in this paper should be effective for other tasks in medical image analysis such as anomaly detection and classification.

Biographies

DAVOOD KARIMI received the Ph.D. degree in electrical and computer engineering from The University of British Columbia (UBC), Canada. His Ph.D. dissertation was focused on image reconstruction and enhancement for cone-beam computed tomography. After completing his Ph.D. degree, he worked as a Postdoctoral Research Fellow at UCLA and UBC mostly on projects centered on developing machine learning-based methods for medical image segmentation and cancer detection and grading in digital histopathology. He is currently an Instructor in radiology with the Harvard Medical School, and a Scientist with the Computational Radiology Laboratory, Radiology Department, Boston Children’s Hospital. His research at IMAGINE involves development of new deep learning algorithms for medical image analysis, including improved algorithms and techniques for motion-robust fetal and newborn imaging for the analysis of early brain development.

HAORAN DOU received the B.Eng. degree from Sichuan University, in 2017, and the M.Eng. degree from Shenzhen University. He is currently pursuing the Ph.D. degree with the Center for Computational Imaging & Simulation Technologies in Biomedicine, School of Computing, University of Leeds. His current research interests include medical image segmentation and generative model.

ALI GHOLIPOUR (Senior Member, IEEE) received the B.S. and M.S. degrees in electrical engineering from the University of Tehran, in 2001 and 2003, respectively, and the Ph.D. degree in electrical engineering from the University of Texas at Dallas, in 2008. He is currently an Associate Professor in radiology with the Harvard Medical School and the Director of the Intelligent Medical Imaging Research Group and the Translational Research with the Radiology Department, Boston Children’s Hospital. His research interests include medical imaging and image analysis, in particular on the development of new imaging technologies and methods to study early human brain development.