Sequence-based pangenomic core detection

Summary

One of the most basic kinds of analysis to be performed on a pangenome is the detection of its core, i.e., the information shared among all members. Pangenomic core detection is classically done on the gene level and many tools focus exclusively on core detection in prokaryotes. Here, we present a new method for sequence-based pangenomic core detection. Our model generalizes from a strict core definition allowing us to flexibly determine suitable core properties depending on the research question and the dataset under consideration. We propose an algorithm based on a colored de Bruijn graph that runs in linear time with respect to the number of k-mers in the graph. An implementation of our method is called Corer. Because of the usage of a colored de Bruijn graph, it works alignment-free, is provided with a small memory footprint, and accepts as input assembled genomes as well as sequencing reads.

Graphical abstract

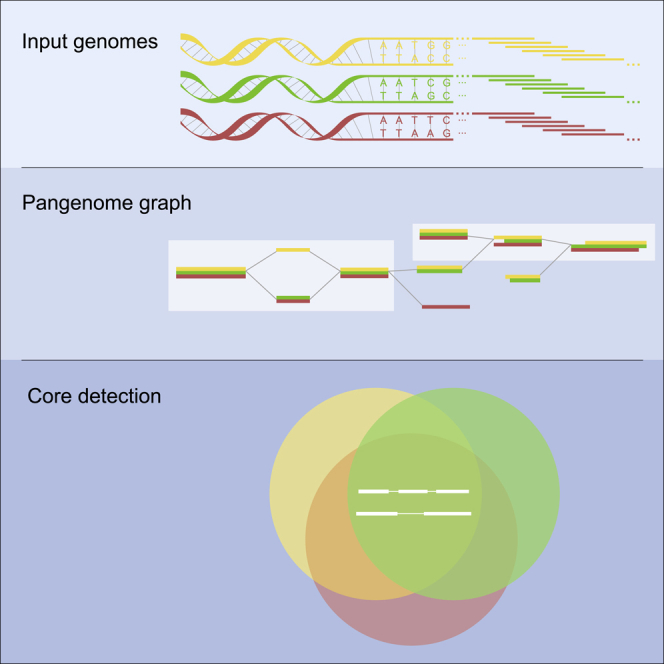
Highlights

• •Pangenomic core detection for large collections of prokaryotes or higher eukaryotes
• •Whole-genome analysis with assemblies or even read data as input
• •Alignment-free, linear time algorithm with small memory footprint
• •Variation tolerance and quorum for flexible core detection

Bioinformatics; Genomics

Introduction

Since the publication of the first bacterial genome sequence at the end of the last century (Fleischmann et al., 1995), the number of sequenced genomes has increased drastically. Not only the number of species has grown for which whole genome data is available, but also the number of individual genomes sequenced per species amounts to hundreds or even thousands in many cases.

Tettelin et al. (2005) were the first to compare intraspecies diversity using multiple genomes of Streptococcus agalactiae as a so-called pangenome. They defined a pangenome as the set of all genes present in a species and found that it can be divided into a set of genes shared by all and sets of genes shared only by some individuals called the core genome and the dispensable genome, respectively. Nowadays, analyzing pangenomes and detecting their core has many different applications. It is performed for prokaryotic and eukaryotic pangenomes and for various taxonomic units like a phylum, an ecotype, or a species (Brockhurst et al., 2019).

Because gene encoding for housekeeping functions and other essential traits are usually contained in the core genome, it represents a valuable source to identify new drug targets. Apart from genetic diversity studies, pangenomic approaches have thus been used, e.g., to identify new antimicrobial drugs (Muzzi et al., 2007). The study of core and dispensable genomes has also been applied to find antigens for the design of new vaccines (Maione et al., 2005). Moreover, analyses of eukaryotic pangenomes are often applied in crop plant breeding where the narrow genetic diversity of crop species is tried to be enriched by desired traits such as disease resistances of wildly occurring relatives (Gao et al., 2019).

A huge variety of software tools provide methods for the detection of a gene-based pangenomic core, e.g., Bayliss et al. (2019); Blom et al. (2009); Chaudhari et al. (2016); Cosentino and Iwasaki (2019); Ding et al. (2018); Fouts et al. (2012); Gautreau et al. (2020); Page et al. (2015); Perrin and Rocha (2021); Sahl et al. (2014); Tonkin-Hill et al. (2020); Zhao et al. (2018, 2012). All of them make use of some kind of fast, approximate alignment calculation to find clusters of homologous genes inside the pangenome first. Thereafter, different methods are applied to filter out false assignments or merge and split clusters. In addition, several tools such as Chaudhari et al. (2016); Ding et al. (2018); Perrin and Rocha (2021); Tonkin-Hill et al. (2020); Zhao et al. (2012) include some preprocessing or postprocessing steps next to the core detection itself or offer other independent functionalities to analyze the pangenome.

Unfortunately, most of these tools are exclusively designed for prokaryotic pangenomes. They also depend on high quality gene annotations to use them for clustering and to provide an accurate core prediction. This is a major drawback because gene predictions, which are usually performed fully automatically, have shown to be strongly error-prone (Denton et al., 2014; Salzberg, 2019).

To avoid gene annotations to bias predictions, core detection needs to be performed on unannotated genomes directly. This was firstly done in Marcus et al. (2014) and requires methods for homology detection. Programs like MUMmer (Kurtz et al., 2004), Mauve (Darling et al., 2004), Multiz (Blanchette et al., 2004), or Mugsy (Angiuoli and Salzberg, 2011) perform such to infer synteny blocks for whole genome alignment. Here, synteny blocks describe large scale genomic fragments often containing several genes that are shuffled between different species because of large scale genome rearrangements occurring during evolution. Panseq (Laing et al., 2010) and PGV (Liang and Lonardi, 2021) make use of these programs to predict pangenomic core features directly from assembled genomes. However, because whole genome alignment of many genome assemblies is costly, these approaches do not scale well to larger amounts of eukaryotic genomes.

Another tool in the context of synteny block detection is Sibelia (Minkin and Medvedev, 2020; Minkin et al., 2013). It uses an iterative de Bruijn graph construction approach for synteny block inference that avoids any explicit alignment calculations and is fast in practice. However, it is not specifically designed for detecting a pangenome’s core.

In this paper we define, for the first time, the sequence-based pangenomic core detection problem. In comparison to previous (gene-based) approaches, it does not rely on gene annotations that can strongly influence the outcome and quality of a core prediction. It also does not depend on alignment calculations, which makes it faster-solvable in practice. Besides, we introduce an algorithm to detect a sequence-based pangenomic core using a colored de Bruijn graph in linear time with respect to the number of vertices in the graph. Working on a de Bruijn graph allows us to consider not only completely assembled genome sequences but also draft assemblies and even sequencing reads. Moreover, our method is able to find core features beyond the gene level and can be applied to prokaryotic as well as eukaryotic datasets.

The remainder of this article is organized as follows. In the next session, we define our model, formally state the problem and describe the algorithmic procedure. Afterwards, we evaluate the performance of our implemented method. Finally, we conclude the text and give a short outlook.

Methods

Basic definitions

A string is a sequence of characters drawn from a finite, non-empty set $\text{Σ}$, the alphabet. For a given string s, we denote its length by $\left|s\right|$, the character at position i by $s\left[i\right]$ and the substring starting at position i and ending at position j by $s\left[i\mathrm{..}j\right]$. A string of length k is called k-mer. For any decomposition $s=xy$ of a given string s, the (potentially empty) substrings x and y are called prefix and suffix of s, respectively.

A genome is a set of strings that can be many millions of short sequencing reads or a few long sequences representing chromosomes or contigs of a complete or draft assembly. Each genome g is identified with a unique color $c\left(g\right)\in C$, where C is a color set and $c\left(g\right)$ is assigned to all strings of g to distinguish between sequences originating from different genomes. For a fixed integer $k\ge 1$ and a genome g, the set $R_k\left(g\right)=\underset{s\in g}{\cup }\left\{r|r\text{ is a }k-\text{mer contained in }s\right\}$ is the k-mer set of g.

A pangenome is a set of genomes. It may be represented as a colored de Bruijn graph.

Colored de Bruijn graphs

Let $k\ge 1$ be a fixed integer, $\text{Σ}$ a finite alphabet and C a color set.

Definition 1 (colored de Bruijn graph (C-DBG))

A colored de Bruijn graph (C-DBG) of dimension k over $\text{Σ}$ and C is a directed graph $G=\left(V,E,c\right)$, where each vertex $v\in V$ is a k-mer, there exists an edge $\left(v,w\right)\in E$ from vertex v to vertex w if and only if the $\left(k-1\right)$ -length suffix of v equals the $\left(k-1\right)$ -length prefix of w, and c assigns a color set $c\left(v\right)\subseteq C$ to each vertex v.

For two vertices $v,w\in V$, vertex v is called predecessor of w if and only if $\left(v,w\right)\in E$. Conversely, w is called successor of v. Note that it is possible to represent any pangenome $p=\left\{g_1,g_2,\dots ,g_n\right\}$ consisting of genomes $g_1,g_2,\dots ,g_n$ as a C-DBG $G=\left(V,E,c\right)$, where $V={\cup }_{g\in p}{R}_k\left(g\right)$, $c\left(v\right)=\left\{c\left(g\right)|g\in p\text{ with }v\in R_k\left(g\right)\right\}$, and E follows directly from the definition of a C-DBG.

Definition 2 (compacted C-DBG)

A compacted C-DBG is obtained from a C-DBG by collapsing all non-branching paths into single vertices called unitigs that are labeled with the concatenated labels of the original path vertices, while considering overlaps only once.

In a compacted C-DBG, color sets are no longer assigned to vertices, but to k-mers, i.e., each k-mer occurring in the label of a unitig may have a distinct color set.

Core and bridging k-mers

A sequence-based pangenomic core should consist of exactly those sequence parts that are shared by all genomes. However, sequencing and assembly quality may vary considerably between members of a pangenome, and low quality genome sequences can lead to substantial core parts being missed. In addition, because genomes are subject to ongoing small changes during evolution, causing e.g., synonymous mutations, some degree of sequence variability should be permitted when determining the core.

Therefore, we introduce two relaxation parameters. A quorum q states the minimum number of genomes a sequence should be shared by, and a variation-tolerance δ determines the maximum amount of sequence variability allowed for sequences of the core. Both are considered by the following definitions.

Definition 3 (core k-mer, bridging k-mer)

Let p be a pangenome with $\left|p\right|=n$ and $G=\left(V,E,c\right)$ a (compacted) C-DBG representing p. Let $q\in [1,n]$ and $\delta \ge 0$ be two integers. A k-mer r is called core k-mer if and only if $\left|c\left(r\right)\right|\ge q$. A k-mer r is called bridging k-mer if and only if it lies on a path π connecting two core k-mers and π contains no more than $\delta +1$ k-mers.

Definition 4 (core genome)

The core genome of a pangenome is defined as the set of all its core and bridging k-mers.

The aforementioned definitions give rise to the following problem formulation.

Problem 1

Given a pangenome $p=\left\{g_1,g_2,\dots ,g_n\right\}$ represented as a C-DBG of dimension $k\ge 1$, let $q\in [1,n]$ and $\delta \ge 0$ be two integers. The Sequence-based Pangenomic Core Detection Problem is to find the core genome of p.

Basic algorithm

Our algorithm to solve Problem one takes as input a C-DBG $G=\left(V,E,c\right)$ of dimension k over the DNA alphabet ${\text{Σ}}_{\text{DNA}}=\left\{A,C,G,T\right\}$ and a color set C representing a pangenome p with $\left|p\right|=n$. In addition, it takes two integers $q\in [1,n]$ and $\delta \ge 0$. It outputs the core genome, i.e., all core and bridging k-mers of p.

The algorithm is based on three steps. First, all core k-mers are identified. Thereafter, vertices are annotated with their distances to the closest core k-mers. In the last step, distance annotations are used to find all bridging k-mers in G.

Step 1 is performed by iterating over all vertices of G and comparing their color sets’ cardinalities to q. This process is possible in $O\left(\left|V\right|\right)$ time assuming that vertices are annotated with their color set cardinalities. Such annotation can easily be generated during graph construction without asymptotically increasing the running time.

In the second step, two integers $d^{pred}$ and $d^{succ}$ are assigned to each vertex $v\in V$ that is at most δ vertices apart from the closest core k-mer. Integer $d^{pred}$ represents the minimum path length, i.e., the distance, from v to any core k-mer in G if only incoming edges are used. Conversely, $d^{succ}$ represents the minimum distance from v to any core k-mer if only outgoing edges are used. If v represents a core k-mer, then $d^{pred}=d^{succ}=0$. For the other k-mers, minimum distances are found and vertices are annotated via a second traversal of vertices that omits an explicit enumeration of all possible paths through the graph. The traversal starts with all core k-mers in G. Next, all vertices that are directly connected to a core k-mer are processed. A vertex that is connected to a core k-mer by an incoming edge is annotated with $d^{pred}=1$. Similarly, a vertex that is connected to a core k-mer by an outgoing edge is annotated with $d^{succ}=1$. The procedure continues by iteratively propagating the distance information to all vertices that are connected to a core k-mer by a path of length 2, then 3, etc. It ends after all vertices with minimum distance δ to some core k-mer have been processed. To ensure that all annotations represent minimum distances, an existing annotation is never updated throughout the whole procedure.

To perform the traversal, a queue Q is maintained, initially containing all core k-mers. Q is successively processed by removing its head vertex v. Let $d_v^{pred}$ be v’s predecessor annotation. Next, all successors of v are queried from G. If a successor w has already a predecessor annotation $d_w^{pred}$, it is ignored. If not, its annotation is set to $d_w^{pred}=d_v^{pred}+1$ and provided $d_w^{pred}<\delta$, w is added at the tail of Q. The procedure works accordingly for a successor annotation of v. It is repeated until Q is empty. At that point, all vertices are annotated with the minimum distance to the closest core k-mer they are connected to by any path π in G if π exists and π contains no more than δ k-mers. Every vertex is annotated with either $d^{pred}$ or $d^{succ}$ before it is added to Q and an annotation is never updated. Thus, a vertex is added to Q at most twice and Step 2 can be executed in $O\left(\left|V\right|\right)$ time.

In the last step of our algorithm, a final iteration over all vertices in G is performed and bridging k-mers are identified. A vertex v is a bridging k-mer if it is annotated with both $d^{pred}$ and $d^{succ}$ and $d^{pred}+d^{succ}\le \delta +1$. The final step is again possible in $O\left(\left|V\right|\right)$ time leading to an overall run time of $O\left(\left|V\right|\right)$. Pseudocode of our algorithm is given in Algorithm 1.

Algorithm 1. Find core genome.

Input C-DBG $G=\left(V,E,c\right)$ of dimension k, integers q and δ

Output set of core k-mers $V^{\prime }$ and set of bridging k-mers $V^{\text{″}}$ in G

• 1:$\begin{array}{ll}{V}^{\text{'}}\leftarrow \left\{v\in V|\left|c\left(v\right)\right|\ge q\right\}& ▷\text{collect core}k-\text{mers in}{V}^{\prime }\end{array}$
• 2:initialize empty queue Q
• 3:$\begin{array}{ll}\mathbf{for}v\in V^{\prime }\mathbf{do}\hfill & ▷\text{set up }Q\text{with core}k-\text{mers}\hfill \end{array}$
• 4: $d_v^{pred}\leftarrow 0$
• 5: $d_v^{succ}\leftarrow 0$
• 6: Q.push(v)
• 7:end for
• 8:$\begin{array}{ll}\mathbf{while}Q\text{not empty}\mathbf{do}\hfill & ▷\text{perform graph traversal}\hfill \end{array}$
• 9: $v\leftarrow Q.\text{pop}\left(\right)$
• 10: ifv annotated with $d_v^{pred}$ then
• 11: for each successor w of v in G not yet annotated with $d_w^{pred}$ do
• 12: $d_w^{pred}\leftarrow d_v^{pred}+1$
• 13: if$d_w^{pred}<\delta$then
• 14: Q.push(w)
• 15: end if
• 16: end for
• 17: end if
• 18: $[\dots ]$ Repeat lines 10–17 for $d^{succ}$ and v’s predecessors
• 19:end while
• 20:$V\text{'}\text{'}\leftarrow \{v\in V\setminus V\text{'}|v$ is annotated with $d_v^{pred}$ and $d_v^{succ}$, and

   $d_v^{pred}+d_v^{succ}\le \delta +1\}$     $▷$ identify bridging k-mers

• 21:return$V^{\prime }$ and $V^{\text{″}}$

Adapted algorithm using the compacted C-DBG

In comparison to the original C-DBG, it is often advantageous to use its compacted variant to represent a pangenome. Because many vertices can usually be merged to form larger unitigs in practice, the number of vertices and edges is often much lower in a compacted C-DBG.

Our algorithm described in the previous section can be modified to work on compacted C-DBGs. Because vertices in compacted C-DBGs are no longer single k-mers but unitigs with labels that may contain several k-mers, Step 1 does no longer iterate over all vertices but iterates over all k-mers in G. As from a practical point of view it might seem counterintuitive at the first glance why this is necessary, be reminded that color sets could change between k-mers from the same unitig because of incomplete assemblies lacking some k-mers or read sets not covering certain regions of the genome. Step 1’s run time therefore changes to $O\left(m\right)$, where $m=\left|{\cup }_{g\in p}{R}_k\left(g\right)\right|$, provided — as before — that during graph construction the value $\left|c\left(r\right)\right|$ is stored for each k-mer r occurring in the input data.

Moreover, vertex annotation has to be adapted slightly. Again, changes are described only for $d^{pred}$ but may be assumed to work accordingly for $d^{succ}$. A vertex v whose label carries a core k-mer r is annotated with $d_v^{pred}=0$ only if r is the last k-mer in v’s label. Otherwise, $d_v^{pred}=i$, where i is the number of k-mers appearing in v’s label behind r. A vertex v whose label does not contain any core k-mer is labeled with $d_v^{pred}=d_{u_{min}}^{pred}+\left|v\right|$, where $u_{min}$ is a predecessor of v with minimal $d^{pred}$ among all predecessors of v and $\left|v\right|$ states the number of k-mers present in the label of v. Furthermore, Q has to be replaced by a priority queue, where $d^{pred}$ is used as key such that priority is given to a vertex v with smallest $d^{pred}$ for annotations of successors with $d^{pred}$ and similarly for annotations of predecessors with $d^{succ}$. Using a binary heap to establish a priority queue raises the run time complexity of Step 2 to $O\left(\left|V\right|log\left(\left|V\right|\right)\right)$, leading to an overall run time of $O\left(m+\left|V\right|log\left(\left|V\right|\right)\right)$ for the adapted algorithm.

Note that, for ease of readability, we omit the following technicalities: (i) the formula used in Step 3 to decide if a k-mer is bridging changes slightly, and (ii) bridging k-mers now may also appear within a unitig label. Neither has an influence on the asymptotic running time.

Choice of parameters

The k-mer length k determines the graph’s dimension. A small k increases the number of core k-mers that may be found between diverged genome sequences and raises the sensitivity of a core detection. However if k is chosen too low, identical k-mers will appear within different genomic contexts just by chance, which decreases the reliability of a core prediction. To find reasonable values for k in our experiments in the next section, we applied an approach presented in Anari et al. (2018). It uses the length of the given sequence and the alphabet size to calculate the smallest k ensuring that the probability for a random k-mer occurrence stays below a desired threshold.

Similar to k, the quorum q also determines a trade-off between sensitivity and specificity. A maximum q that equals the number of individual genomes inside the pangenome complies with the initial definition of a core genome by Tettelin et al. (2005). However, with a growing number of genomes inside the pangenome, a maximum q quickly becomes a strong restriction and significant core parts may be missed, e.g., if only a single genome is of low sequence quality. At the same time, a substring that is present in almost all members of a large pangenome still seems to be a promising core candidate. Therefore, q should be chosen individually with respect to the pangenome under consideration.

The variation-tolerance δ is used to deal with sequence variability among genomes inside pangenomic core parts. Because the change of a single nucleotide character within a DNA sequence may influence up to k vertices in a C-DBG, δ should not be lower than k in order to have an impact on the predicted core. Higher values of δ are also required for pangenomes formed from genomes with larger diversity. The influence of δ is evaluated in the next section.

Results

We implemented the algorithm running on a compacted C-DBG in C++. The underlying graph was realized using Bifrost (Holley and Melsted, 2020). Our tool Corer is available from https://gitlab.ub.uni-bielefeld.de/gi/corer. In the following, we compare it to other related approaches. We evaluate its behavior for an increasing variation-tolerance δ and analyze the quality of its results if using either assembled or raw sequencing data as input for core prediction. Finally, we show its suitability for eukaryotic pangenomes, study what core parts may be found below the level of genes and how varying levels of relatedness change the core.

Comparison to related approaches

We evaluated the performance of our method against different other approaches.

Panaroo (Tonkin-Hill et al., 2020) is a software tool to predict all genes belonging to the core of a prokaryotic pangenome. Thus, it represents a realization of the classical gene-based core detection approach that showed comparable or even advanced performance compared to other state-of-the-art gene-based approaches such as Bayliss et al. (2019); Ding et al. (2018); Gautreau et al. (2020); Page et al. (2015). Panaroo takes as input gene annotations of all genomes and outputs a matrix from which all core genes may be identified. In our experiments, we used version 1.2.8.

Panseq (Laing et al., 2010) (as of November 2017 on Github https://github.com/chadlaing/Panseq) and PGV (Liang and Lonardi, 2021) (as of September 2021 also on Github https://github.com/ucrbioinfo/PGV)) both make use of synteny detection tools to predict core genome fragments as described in the first section. Results of Panseq, however, are not included in this comparison as they were incomparable to the results of any other tool. Panseq’s core predictions were highly conservative for all our datasets. They consisted only of very few sequence fragments that contained only a few hundred or even no genes. Most likely, Panseq would also allow us to find larger cores if default parameters are changed, which we omitted here. PGV was not evaluated because its runs either crashed or produced contradicting results.

SibeliaZ (Minkin and Medvedev, 2020) is another recent too and methodologically very close to our own approach because it also makes use of C-DBG representations of the pangenome. However, its actual purpose is synteny block prediction exclusively. As input, it takes sequence assemblies of all members of the pangenome and outputs coordinates of synteny blocks within them. Thus, to find core fragments, a straightforward postprocessing step is needed in which synteny blocks occurring in at least q distinct genomes are extracted. For our experiments, version 1.2.3 was used.

In our comparisons, we used four prokaryotic pangenomes of different sizes and complexities. Details are shown in Table 1. The smallest pangenome consisted of 18 Bifidobacterium animalis genome assemblies, the largest of 263 assemblies of species Listeria monocytogenes. The pangenomes of B. animalis and Yersinia pestis are considered to be closed, meaning that the number of new gene families per newly sequenced genome is rather small. In contrast, the pangenomes of Enterococcus faecium and L. monocytogenes are considered open, indicating much smaller core genome fractions. Assemblies are available from NCBI (Wheeler et al., 2007).

Table 1.

Pangenome properties

Species	n	Core k-mer fraction	Status
Bifidobacterium animalis	18	0.27	closed (Lugli et al., 2019)
Yersinia pestis	48	0.88	closed (Rouli et al., 2015)
Enterococcus faecium	153	0.09	open (van Schaik et al., 2010)
Listeria monocytogenes	263	0.07	open (Kuenne et al., 2013)

Overview of all prokaryotic pangenomes used in our experiments. The notion core k-mer refers to Definition 3.

All tools were run using default parameters if applicable. In addition, mode strict was selected for Panaroo, and SibeliaZ was run with parameter -n to omit alignment calculations not necessary for our experiment. Following the approach of Anari et al. (2018) to find an optimal k value and rounding to the next uneven integer, $k=17$ was used for Corer for all four pangenomes. The quorum was set to 95% of all members of the pangenome, i.e. $q=⌈0.95·n⌉$, which is the default used by Panaroo. Variation-tolerance was set to $\delta =60$. Exact program calls are documented at https://gitlab.ub.uni-bielefeld.de/gi/corer. Calculations were performed on a virtual machine with 28 cores and 256 GB of RAM.

To allow for a result comparison of all tools, we predicted genes for all assemblies with Prokka (Seemann, 2014) using default parameters. Gene annotations were used as input for Panaroo. To determine which genes were covered by the prediction of Corer, genes were queried from its output on a k-mer basis. A gene was considered to be found if at least half of its k-mers were present in Corer’s predicted core allowing for up to one mismatch per k-mer. On the other hand, synteny blocks reported by SibeliaZ were filtered for an occurrence in at least q individual genomes. Thereafter, sequences of the remaining blocks were queried for all predicted genes using BLAST (Altschul et al., 1990). A gene was considered as found if there was at least one alignment covering half of the gene’s sequence.

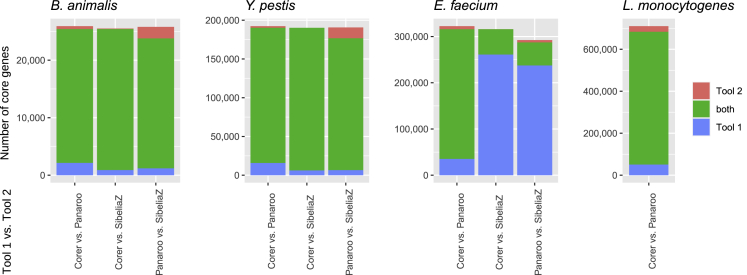
Results are shown in Figure 1. We see that predicted cores of Corer, Panaroo and SibeliaZ agree quite well for the pangenome of B. animalis and even more for that of Y. pestis. Both species are known to have a closed pangenome and their core sequences are well conserved. This can also be seen when calculating the ratio of core k-mers (according to Definition 3) compared to the total number of k-mers present in each respective pangenome. This ratio is 27.1% for B. animalis and 87.8% for Y. pestis. For the open pangenomes of E. faecium and L. monocytogenes, it is only 8.5 and 6.7%, respectively. Nevertheless, Corer and Panaroo also mostly agree for these two pangenomes. SibeliaZ, however, had problems with these datasets. It predicted only very few, short synteny blocks that fulfill the quorum requirement. Most synteny blocks were reported only for smaller subsets of all genomes. This result can be explained by the fact that synteny detection tools like SibeliaZ generally follow a different objective than programs specifically developed for pangenomic core detection. If dealing with larger and rather diverse pangenomes, SibeliaZ seems to favor the detection of larger synteny blocks in fewer genomes that are — thus — not considered as core.

Figure 1.

Result comparison

Result comparison of Corer, Panaroo, and SibeliaZ on four prokaryotic pangenomes. Shown are numbers of genes two tools agree (green) or disagree (blue/red) on. Results of SibeliaZ are not shown for L. monocytogenes because its output did not comprise any gene.

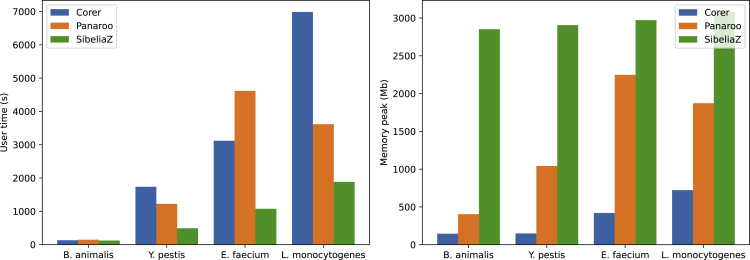
We also compared run times and memory consumption of all tools. Measurements are shown in Figure 2. As can be seen, SibeliaZ was the fastest among all tools on all four pangenomes. Although it uses a similar approach as Corer involving C-DBGs, it ran much faster. We suspect that this might be due to the usage of larger values for k leading to smaller and simpler graphs, but decreasing sensitivity. E.g., already the usage of $k=19$ instead of $k=17$ would reduce Corer’s runtime by one order of magnitude. On the other hand, SibeliaZ consumed by far the most memory. Also Panaroo’s memory requirements strongly increased for the pangenomes of E. faecium and L. monocytogenes. Meanwhile, Corer’s memory usage stayed comparatively low.

Figure 2.

Run time and memory comparison

Run time and memory usage comparison of all three tools.

Influence of δ

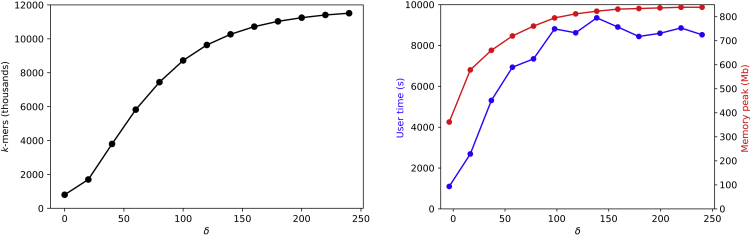
To study the behavior of an increasing variation-tolerance δ on the performance of Corer, we chose the largest and most diverse prokaryotic pangenome of L. monocytogenes to calculate cores for increasing values of this parameter. Core sizes for increasing values of δ are shown in Figure 3.

Figure 3.

Influence of δ

Influence of δ on core sizes (left) and run time and memory consumption for core prediction (right).

A larger variation-tolerance leads to a relaxation of the core definition. Thus, we see an ever growing core size for increasing values of δ. The growth is especially strong in the beginning when many core k-mers can be connected by bridging k-mers that enrich the core. The core size more and more reaches a saturation for larger values of δ, and the predicted core almost stops to grow for $\delta \ge 120$. A similar tendency can be observed for run time and memory usage (Figure 3), which seems to be mostly influenced by the output size.

Beyond bacterial pangenomes

As mentioned in the introduction, pangenomic core analyses are not limited to prokaryotic datasets. Unfortunately, most gene-based approaches are specifically designed for prokaryotic pangenomes and do not cover such applications. This also applies to Panaroo, which expects gene predictions to be performed by Prokka, a pipeline for gene finding in prokaryotes. Thus, we did not test it on eukaryotic pangenomes. Corer and SibeliaZ, however, were evaluated on a plant pangenome consisting of 18 accessions of Arabidopsis thaliana which were first described in Gan et al. (2011). Analyses were performed as for prokaryotic data sets; however, because of the size of the individual genomes, a larger value of $k=21$ was used. Furthermore, gene prediction was performed with Augustus (Stanke et al., 2008) instead of Prokka. The tool was run using default settings.

Most likely because of the larger value of k, Corer was the faster tool this time, taking only $\sim$ 4 h and using 7 GB of RAM. SibeliaZ needed $\sim$ 6 h and required 11 GB of RAM. SibeliaZ’s predicted core comprised 144 million k-mers. The core of Corer was a bit smaller, containing only 140 million k-mers. Both tools agreed in 376,922 genes. 93,740 genes were additionally found by Corer whereas SibeliaZ found 2,189 further genes.

In comparison to bacteria, eukaryotic genomes consist of a much larger ratio of intergenic sequence parts classical gene-based approaches are blind to. To check what can be found in intergenic parts of a core genome, we queried all non-gene related annotations available for our dataset within the predicted cores of Corer and SibeliaZ. Both tools found the vast majority of all annotated noncoding RNAs including all rRNA and tRNA annotations. Furthermore, most annotated pseudogenic transcripts and transposable elements could be found inside the cores. Details are shown in Table 2.

Table 2.

Non-gene core annotations

Element	Total	Fraction in core of
		Corer	SibeliaZ
miRNA	3203	96%	94%
tRNA	11339	100%	100%
ncRNA	8563	90%	79%
ps. transcript	16065	90%	68%
snoRNA	1277	95%	96%
snRNA	234	100%	62%
rRNA	72	100%	100%
tr. elem.	66233	86%	31%

Non-gene related annotations found within the predicted cores of Corer and SibeliaZ from a pangenome of 18 accessions of Arabidopsis thaliana.

Raw vs. assembled data

Next to assembled genome sequences as input data, a C-DBG also allows for the usage of sequencing reads. This does not only allow to avoid bias for pangenomic core prediction caused by erroneous genome assemblies but also omits a potentially time consuming preprocessing step. At the same time, the quorum criteria should make a core prediction on raw sequencing data rather robust against bias introduced by, e.g., sequencing errors or sample contamination. On the downside, a dataset consisting of sequencing reads is usually much larger than its corresponding assembly and may lead to a more complex graph.

To test the influence of unassembled sequencing data on the quality of core prediction, we used again the A. thaliana pangenome. For 17 accessions, Illumina GA-II short read libraries are available next to the assemblies. The remaining accession for which no reads are available was excluded from this experiment. Assemblies and sequencing reads were used to build two independent graphs ($k=21$). In addition, Bifrost’s built-in functionality to filter out k-mers appearing only once was used for the read libraries. Nevertheless, the graph built from reads (read graph) was almost three times larger than its counterpart (assembly graph) built from assemblies (485 million vs. 172 million k-mers). Core prediction using Corer took $\sim$ 11 h using 24 GB of RAM on the read graph and $\sim$ 4 h using 6 GB of RAM on the assembly graph ($q=17,\delta =60$). As expected, the read graph’s core comprised many more k-mers (188 million) than the assembly graph’s core (140 million). Both cores agreed on 131 million k-mers including 63.2 million core k-mers present in the assembly graph. 1.4 million core k-mers could be found exclusively in the assembly graph. We assume these might have been introduced because of read error correction. 1.1 million core k-mers were unique in the read graph and might probably have gotten lost during the assembly process.

To compare both cores on the gene level, we also used the gene predictions from the previous section and queried all genes in both cores using the same k-mer-based approach as above. The vast majority of 438,718 genes present in the assembly graph’s core appeared in the read graph’s core as well. Only 6,621 (1.5%) were not present, whereas 2,019 could be found exclusively in the read graph’s core.

We also performed a BUSCO analysis (Simão et al., 2015) for all predicted genes. We used BUSCO genes present in all members of the taxonomic order Brassicales which also A. thaliana belongs to and thus are expected to be contained in the core. Among all 17 accessions, we could find representatives for only 4,447 of all 4,679 BUSCO genes which either point toward errors in the assemblies or misannotations caused by our automatic gene annotation pipeline. The assembly graph’s core was missing only 15 of 4,447 BUSCO genes, whereas just seven BUSCO genes were not present in the read graph’s core. Only one BUSCO gene found in the assembly graph’s core was absent in the read graph’s core.

Core detection of diverse pangenomes

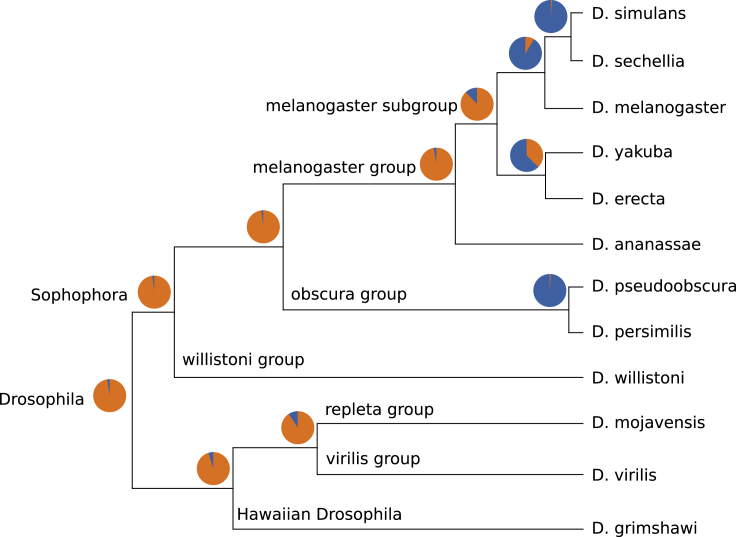
Generally, a core genome’s size should decrease with an increasing phylogenetic distance between pangenome members. To validate this assumption, we ran Corer ($k=21$, $\delta =60$ and 100% quorum) to predict cores of pangenomes built from reference assemblies of different Drosophila species with varying levels of relatedness. Assemblies of 12 Drosophila species were downloaded from FlyBase (Larkin et al., 2021) and assigned to pangenomes each representing an internal node of the genus’s phylogeny, i.e., a pangenome representing internal node v of the tree contained all species below v. Thereafter, genes were queried for each core as above. Results are shown in Figure 4.

Figure 4.

Drosophila core genomes

Phylogenetic tree of genus Drosophila taken from FlyBase (Larkin et al., 2021). Each pie chart represents the ratio of genes inside (blue) and outside (orange) the core of pangenomes built from species’ assemblies below each internal node of the tree.

We see that cores comprise almost all annotated genes in pangenomes of closely related members, e.g., $\sim 99\text{\%}$ of all genes from D. simulans and D. sechellia are part of the core. With an increasing phylogenetic distance, the number of core genes quickly decreases. Only $\sim 2.5\text{\%}$ of all genes are part of the pangenome’s core of all 12 species.

Discussion

We presented the sequence-based pangenomic core detection problem and an algorithm to solve it in linear time. The model we introduced is based on two sets of k-mers and allows us to handle varying degrees of sequence variability. Furthermore, it enables a flexible core definition that can be adapted depending on the dataset and the research question. Unlike methods that predict a core on the gene level, our approach defines the core on the plain genomic sequence, which avoids gene prediction that takes time and may introduce bias. Furthermore, it allows us to detect core features beyond the gene level.

Our algorithm makes use of a colored de Bruijn graph, which notably reduces memory requirements and lets it scale to prokaryotic as well as eukaryotic pangenomes. We showed this in a comparison to other related approaches. It also avoids time consuming alignment calculations and enables us to accept sequence data in all different kinds of states from finished genome assemblies to sequencing reads. Building a graph exclusively from read data raises the complexity of the graph as well as computational costs. Nevertheless, most essential core parts remain preserved. By a BUSCO gene analysis, we even showed that some core genes missing in an assembly-based core may be found if read data is included.

Limitations of the study

Yet, we just started to explore the potential of sequence-based pangenomic core detection, and many open questions remain so far unanswered. E.g., in our experiments we positively evaluated the equivalence of our method to the classical approach based on genes. In addition, we presented a first evaluation of intergenic core parts. However, the potential of what can be found beyond the level of genes deserves a more rigorous investigation. Besides, some first, promising results for core genome analysis including read data motivate for deeper studies. Considering that other core detection methods may not provide completely accurate core predictions, only comparing them does not allow for an overall unbiased evaluation of our findings’ validity. Thus, the usage of simulated data might give us a possibility to find common weaknesses of pangenomic core prediction and to develop further improvements. For instance, a possibility to strengthen our model would be to introduce a core k-mer density constraint to balance the ratio between core and bridging k-mers within core sequences.

Apart from biological questions, our method also allows further extensions that we would like to realize in the future. E.g., one might be able to adapt it to predict dispensable genomes for arbitrary subsets of the pangenome. Furthermore, the design of our algorithm would allow for a simultaneous prediction of several cores using multiple values of δ in a single run. Using this feature, it would be possible to predict a complete hierarchy of different core levels. More practical improvements would comprise efforts to parallelize our algorithm and to reduce its space requirements, e.g., by using an even more sparse graph representation. In addition, our algorithmic approach to find minimum distances between vertices in the graph might also be of value for other applications, e.g., in the context of assembly polishing.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Bifidobacterium animalis genome sequences	NCBI	See Table S1 for a list of accession numbers.
Yersinia pestis genome sequences	NCBI	See Table S1 for a list of accession numbers.
Enterococcus faecium genome sequences	NCBI	See Table S1 for a list of accession numbers.
Listeria monocytogenes genome sequences	NCBI	See Table S1 for a list of accession numbers.
Arabidopsis thaliana accession sequences	Gan et al., 2021	http://mtweb.cs.ucl.ac.uk/mus/www/19genomes/fasta/MASKED/
Arabidopsis thaliana non-gene annotations	Gan et al., 2021	http://mtweb.cs.ucl.ac.uk/mus/www/19genomes/annotations/consolidated_annotation_9.4.2011/gene_models/
Arabidopsis thaliana read datasets	ENA	Study Accession PRJEB2457
Drosophila reference genomes	Larkin et al. (2021)	http://flybase.org
Software and algorithms
Corer software	This paper	https://gitlab.ub.uni-bielefeld.de/gi/corer
Panaroo	Tonkin-Hill et al. (2020)	https://github.com/gtonkinhill/panaroo
SibeliaZ	Minkin and Medvedev (2020)	https://github.com/medvedevgroup/SibeliaZ
Bifrost	Holley and Melsted (2020)	https://github.com/pmelsted/bifrost
Prokka	Seemann (2014)	https://github.com/tseemann/prokka
Augustus	Stanke et al. (2008)	https://github.com/Gaius-Augustus/Augustus
BLAST+	Altschul et al. (1990)	https://ftp.ncbi.nlm.nih.gov/blast/executables/blast+/LATEST/
BUSCO	Simão et al. (2015)	https://gitlab.com/ezlab/busco

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead contact, Jens Stoye (jens.stoye@uni-bielefeld.de).

Materials availability

This study did not generate new unique reagents.

Method details

Experimental workflows

All experiments throughout this paper are documented as a Snakemake workflow (Mölder et al., 2021) at Corer’s code repository (https://gitlab.ub.uni-bielefeld.de/gi/corer). Experiments may be rerun and all results may be reproduced at any time using this workflow.

Published: June 17, 2022

Data and code availability

• •This paper analyzes existing, publicly available data. Genome sequences of prokaryotic genomes can be downloaded from NCBI. Their accession numbers are listed in the key resources table.
• •Download links for all A. thaliana accessions used in this study and their corresponding non-gene annotations are listed in the key resources table as well. Read data sets are available from ENA. The study accession number is stated in the key resources table.
• •Used reference assemblies for all Drosophila species may be downloaded from FlyBase (Larkin et al., 2021). Exact download links are specified inside the key resources table.
• •All original code is publicly available as of the date of publication. It has been deposited at https://gitlab.ub.uni-bielefeld.de/gi/corer.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.