This cohort study investigates the optimal margin width for hepatectomy in patients with colorectal cancer liver metastases.
Key Points
Question
What is the optimal margin width for hepatectomy for colorectal cancer liver metastases and should it be individualized based on patient characteristics?
Findings
In this cohort study of 1843 patients (internal cohort, 965; external cohort, 878), state-of-the-art random forest predictive models were trained; these models had the highest areas under the curve reported in the colorectal cancer liver metastases literature. Artificial intelligence– and game theory–based techniques built on these predictive models inferred that the margin width associated with the maximal decrease in 5-year death probability was 7 mm.
Meaning
This cohort study did not provide evidence for heterogeneous treatment outcomes but rather suggests a single optimal margin width (7 mm) for hepatectomy for KRAS-variant colorectal liver metastases.
Abstract
Importance
In patients with resectable colorectal cancer liver metastases (CRLM), the choice of surgical technique and resection margin are the only variables that are under the surgeon’s direct control and may influence oncologic outcomes. There is currently no consensus on the optimal margin width.
Objective
To determine the optimal margin width in CRLM by using artificial intelligence–based techniques developed by the Massachusetts Institute of Technology and to assess whether optimal margin width should be individualized based on patient characteristics.
Design, Setting, and Participants
The internal cohort of the study included patients who underwent curative-intent surgery for KRAS-variant CRLM between January 1, 2000, and December 31, 2017, at Johns Hopkins Hospital, Baltimore, Maryland, Memorial Sloan Kettering Cancer Center, New York, New York, and Charité–University of Berlin, Berlin, Germany. Patients from institutions in France, Norway, the US, Austria, Argentina, and Japan were retrospectively identified from institutional databases and formed the external cohort of the study. Data were analyzed from April 15, 2019, to November 11, 2021.
Exposures
Hepatectomy.
Main Outcomes and Measures
Patients with KRAS-variant CRLM who underwent surgery between 2000 and 2017 at 3 tertiary centers formed the internal cohort (training and testing). In the training cohort, an artificial intelligence–based technique called optimal policy trees (OPTs) was used by building on random forest (RF) predictive models to infer the margin width associated with the maximal decrease in death probability for a given patient (ie, optimal margin width). The RF component was validated by calculating its area under the curve (AUC) in the testing cohort, whereas the OPT component was validated by a game theory–based approach called Shapley additive explanations (SHAP). Patients from international institutions formed an external validation cohort, and a new RF model was trained to externally validate the OPT-based optimal margin values.
Results
This cohort study included a total of 1843 patients (internal cohort, 965; external cohort, 878). The internal cohort included 386 patients (median [IQR] age, 58.3 [49.0-68.7] years; 200 men [51.8%]) with KRAS-variant tumors. The AUC of the RF counterfactual model was 0.76 in both the internal training and testing cohorts, which is the highest ever reported. The recommended optimal margin widths for patient subgroups A, B, C, and D were 6, 7, 12, and 7 mm, respectively. The SHAP analysis largely confirmed this by suggesting 6 to 7 mm for subgroup A, 7 mm for subgroup B, 7 to 8 mm for subgroup C, and 7 mm for subgroup D. The external cohort included 375 patients (median [IQR] age, 61.0 [53.0-70.0] years; 218 men [58.1%]) with KRAS-variant tumors. The new RF model had an AUC of 0.78, which allowed for a reliable external validation of the OPT-based optimal margin. The external validation was successful as it confirmed the association of the optimal margin width of 7 mm with a considerable prolongation of survival in the external cohort.
Conclusions and Relevance
This cohort study used artificial intelligence–based methodologies to provide a possible resolution to the long-standing debate on optimal margin width in CRLM.
Introduction
In patients with resectable colorectal cancer liver metastases (CRLM), the choice of surgical technique and resection margin are the only variables that are under the surgeon’s direct control and may influence oncologic outcomes. Thus, optimization of these variables may have direct therapeutic implications. This may explain why there have been numerous attempts to identify the optimal margin width. However, there is no consensus on which is optimal.1,2,3,4,5 Furthermore, these studies all recommend a single margin width for all patients with CRLM. This approach assumes that the effect of margin width on survival is independent of other patient characteristics. However, recent studies suggest that margin status may have a variable effect in patient subpopulations.6,7
Until recently, it has been difficult to identify specific characteristics within CRLM subgroups that mandate a specific optimal margin width. In the last few years, progress in artificial intelligence, machine learning, and counterfactual outcomes literature (predicting what would have happened if we had applied other treatments to each patient) has facilitated the development of techniques (eg, causal forests, causal boosting, and causal model-based association test reflecting causal status) that can help develop patient-specific treatment recommendations by estimating the treatment effect in patient subgroups.8,9 However, their main limitation is that they can be only employed when the treatment recommendation is a binary treatment decision (ie, offer a treatment or not), and they have limited interpretability. A new technique called optimal policy trees (OPTs), which was developed by a collaborating group from Massachusetts Institute of Technology, can potentially remedy both deficiencies by allowing clinical interpretability and by assigning several different treatment recommendations to patient subgroups.10 Given that margin width values vary widely, OPT may be particularly suited for estimating the optimal margin width for patient subgroups.
Methods
Patient Selection
Patients who underwent curative intent surgery for CRLM between January 1, 2000, and December 31, 2017, at Johns Hopkins Hospital, Memorial Sloan Kettering Cancer Center, and Charité–University of Berlin were retrospectively identified from institutional databases and formed the internal cohort of the study. The exclusion criteria are illustrated in eFigure 1 in the Supplement. Patients from institutions in France, Norway, the US, Austria, Argentina, and Japan were retrospectively identified from institutional databases and formed the external cohort of the study. The same exclusion criteria applied for this cohort. Patient race and ethnicity information was not available; thus, it was not included in this study. Moreover, there is no evidence to suggest that race and ethnicity play a role in optimal margin width. The study was conducted in accordance with the ethical standards of the participating institutions and was approved by the institutional review board of the leading institution, Johns Hopkins. A waiver of consent was granted by the institutional review board committee owing to no identifiable medical risk and the use of preexisting information in the patient medical record and deidentified patient data.
Definitions and Aim
Patient demographics, clinicopathologic and genetic characteristics, and survival data were obtained from the respective institutional databases. Further details can be found in the eMethods in the Supplement.
We sought to identify the margin width associated with the lowest probability that the patient would die within 5 years after surgery. The end point of 5 years was chosen a priori. The individual patient characteristics included only variables that were known preoperatively or intraoperatively.
First Step: Counterfactual Estimator
Before estimating the counterfactuals, the data set was split into a training and testing set with an 80 to 20 ratio, which has been deemed the optimal split in the literature.11 Next, we split the entire cohort into KRAS variant and wild-type subcohorts because there is evidence that the association of margin status with 5-year death probability differs by this marker of tumor biology (KRAS variant status).12,13
Because it is impossible to find identical patients who have been treated with all possible margin widths, we had to infer what the probability of death at 5 years would have been if a given patient was treated with all possible margin widths (ranging from 0-20 mm). The probabilities of death for a given patient under each margin width (ie, the counterfactual outcomes) were estimated with a regression model (ie, random forests [RFs]). Further details regarding the RF model can be found in the eMethods in the Supplement.
Second Step: OPT
These counterfactual probabilities were used to train a globally optimal decision tree called OPT.14 The OPT then found the optimal margin value for each patient and grouped patients with the same optimal margin width together. It also presented the margin recommendations for each group in an interpretable tree structure. The intensity of the color in each node reflects the difference in quality between the optimal and second-best margin values; in other words, the larger the difference, the stronger the color intensity. Only nodes with the same optimal value can be compared (ie, can have the same color with varying intensities).
Relative Risk Reduction Associated With the OPT Optimal Cutoffs in the Training Data Set
To calculate the associated relative risk reduction (RRR) for a given subgroup if the optimal margin cutoff was applied, we entered the OPT recommended margin values that applied to each patient-specific subgroup and then used the RF model to calculate the 5-year death probability in the training data set. The probabilities of death at 5 years calculated with optimal vs positive margins were compared to determine the RRR associated with the optimal margin value. The probabilities of death at 5 years were also calculated for other margin values between the R1/narrow and the optimal value to assess whether suboptimal margins were still associated with considerable improvement of overall survival. R1 resection was defined as tumor cells at the resection margin (0 mm). A narrow margin group was defined as either margin clearance less than 1 mm or involved margins.
Validation of the OPT Methodology
Shapley additive explanations (SHAP) is a novel methodology developed by Lundberg et al15,16 that can plot the relationship between a variable and an outcome and determine an optimal cutoff for the variable. SHAP plots can be used to estimate the optimal margin width by finding the margin value (x-axis) that is associated with the lowest risk of death (lowest SHAP value on the y-axis). SHAP values for each margin value were calculated using the RF model.
The SHAP method can also assess interactions between predictors by calculating interaction values. Further details can be found in the eMethods in the Supplement.
External Validation
We trained a new RF counterfactual model in the external validation set to evaluate the OPT optimal margins. Specifically, the new RF was used to calculate the probabilities of death at 5 years with optimal (according to the OPT trained in the training cohort) and positive margins and its predictions were compared to calculate the RRR associated with the optimal margin value. The rationale for training a new RF model can be found in the eMethods in the Supplement.
OPT for Liver-Specific Recurrence
A secondary analysis was performed to identify the margin width associated with the lowest probability that the patient will experience an intrahepatic recurrence within 5 years after surgery. Patients who had intrahepatic disease in addition to extrahepatic disease at the time of first recurrence were classified as having intrahepatic disease.17 This analysis was limited by the lack of a proper external validation cohort and is presented in the eResults in the Supplement.
Statistical Analysis
Data processing and analysis were performed on macOS, Windows, and the Massachusetts Institute of Technology Sloan School of Management’s remote engaging cluster. The derived models used the Julia and Python programming languages. For training the RF and OPT models, we used 5-fold cross-validation when estimating rewards and also when fitting those rewards onto the OPTs. Summary statistics were presented as total counts and frequencies for categorical variables and as median values with IQR for continuous variables. The differences of data distribution between data sets for both categorical and continuous variables were assessed by χ2 test and Mann-Whitney U test, respectively. Data were analyzed from April 15, 2019, to November 11, 2021.
Results
Internal Cohort
This cohort study included a total of 1843 patients. The internal cohort included 965 patients. Of these, 386 patients (40%; median [IQR] age, 58.3 [49.0-68.7] years; 200 men [51.8%]; 186 women [48.2%]) had tumors with the KRAS variant and 579 (60%) had tumors that were wild type (eFigure 1 in the Supplement). Of those with the KRAS variant, 302 (78.2%) composed the training data set, and 84 (21.8%) composed the testing data set. Of those with wild-type tumors, 474 (81.9%) composed the training data set, and 105 (18.1%) composed the testing data set. Detailed clinicopathologic characteristics of the training and testing data sets of both patients with the KRAS variant and those with the wild type are presented in Table 1.
Table 1. Patient Characteristics in the Internal Cohort.
| Variable | Entire cohort (n = 965) | |||||
|---|---|---|---|---|---|---|
| KRAS variant | Wild type | |||||
| Train (n = 302) | Test (n = 84) | Entire (n = 386) | Train (n = 474) | Test (n = 105) | Entire (n = 579) | |
| Numerical variables, median (IQR) | ||||||
| Age, y | 58.7 (49.0-68.4) | 55.9 (49.5-68.9) | 58.3 (49.0-68.7) | 59.0 (50.0-67.3) | 54.1 (47.4-66.0) | 58.2 (49.1-67.3) |
| No. of CRLM | 3.0 (1-4) | 2.0 (1-3) | 2.0 (1-4) | 2.0 (1-5) | 2.0 (1-5) | 2.0 (1-5) |
| Diameter of largest CRLM, median (IQR), cm | 2.5 (1.6-4.0) | 2.5 (1.6-4.0) | 2.5 (1.6-4.0) | 2.5 (1.6-4.0) | 2.6 (1.8-3.7) | 2.5 (1.6-4.0) |
| Margin width, mm | 3.0 (1-8) | 2.0 (0.5-7.0) | 3.0 (1.0-8.0) | 3.0 (1.0-8.0) | 3.0 (1.0-8.0) | 3.0 (1.0-8.0) |
| Categorical features total | ||||||
| Sex, No. (%) | ||||||
| Male | 156 (51.7) | 44 (52.4) | 200 (51.8) | 299 (63.1) | 64 (61.0) | 363 (62.7) |
| Female | 146 (48.3) | 40 (47.6) | 186 (48.2) | 175 (36.9) | 41 (39.0) | 216 (37.3) |
| Primary tumor side, No. (%) | ||||||
| Left | 122 (40.4) | 34 (40.5) | 156 (40.4) | 267 (56.3) | 54 (51.4) | 321 (55.4) |
| Right | 131 (43.4) | 41 (48.8) | 172 (44.6) | 108 (22.8) | 26 (24.8) | 134 (23.1) |
| Rectum | 49 (16.2) | 9 (10.7) | 58 (15.0) | 99 (20.9) | 25 (23.8) | 124 (21.4) |
| Primary tumor (T) stage, No. (%) | ||||||
| T0-2 | 37 (12.3) | 10 (11.9) | 47 (12.2) | 76 (16.0) | 19 (18.1) | 95 (16.4) |
| T3-4 | 265 (87.7) | 74 (88.1) | 339 (87.8) | 398 (84.0) | 86 (81.9) | 484 (83.6) |
| Primary tumor nodal status, No. (%) | ||||||
| Yes | 202 (66.9) | 57 (67.9) | 259 (67.1) | 317 (66.9) | 72 (68.6) | 389 (67.2) |
| No | 100 (33.1) | 27 (32.1) | 127 (32.9) | 157 (33.1) | 33 (31.4) | 190 (32.8) |
| Bilobar CRLM, No. (%) | ||||||
| Yes | 159 (52.6) | 44 (52.4) | 203 (52.6) | 263 (55.5) | 51 (48.6) | 314 (54.2) |
| No | 143 (47.4) | 40 (47.6) | 183 (47.4) | 211 (44.5) | 54 (51.4) | 265 (45.8) |
| Extrahepatic disease, No. (%) | ||||||
| Yes | 49 (16.2) | 11 (13.1) | 60 (15.5) | 53 (11.2) | 6 (5.7) | 59 (10.2) |
| No | 253 (83.8) | 73 (86.9) | 326 (84.5) | 421 (88.8) | 99 (94.3) | 520 (89.8) |
| Prehepatectomy chemotherapy, No. (%) | ||||||
| Yes | 190 (62.9) | 49 (58.3) | 239 (61.9) | 307 (64.8) | 70 (66.7) | 377 (65.1) |
| No | 112 (37.1) | 35 (41.7) | 147 (38.1) | 167 (35.2) | 35 (33.3) | 202 (34.9) |
| Intraoperative ablation, No. (%) | ||||||
| Yes | 75 (24.8) | 20 (23.8) | 95 (24.6) | 123 (25.9) | 27 (25.7) | 150 (25.9) |
| No | 227 (75.2) | 64 (76.2) | 291 (75.4) | 351 (74.1) | 78 (74.3) | 429 (74.1) |
| Positive margin, No. (%) | ||||||
| Yes | 40 (13.2) | 15 (17.9) | 55 (14.2) | 73 (15.4) | 11 (10.5) | 84 (14.5) |
| No | 262 (86.8) | 69 (82.1) | 331 (85.8) | 401 (84.6) | 94 (89.5) | 495 (85.5) |
Abbreviation: CRLM, colorectal cancer liver metastases.
Discriminatory Capacity of the RF Counterfactual Models
The area under the curve (AUC) of the RF counterfactual model for patients with KRAS-variant tumors was 0.76 in both the training and testing data set. The AUC of the RF counterfactual model for patients with wild-type tumors was 0.79 in the training data set and 0.57 in the testing data set. The AUC of 0.57 in the testing data set indicates poor discrimination of the model, whereas the higher AUC in the training data set suggests overfitting of the model.18 In turn, we could not be confident about its predictions and elected not to further analyze patients with wild-type tumors.
OPT Optimal Cutoffs
The OPT used to determine the margin width value associated with the maximal reduction of death rate within 5 years of surgery is illustrated in Figure 1. The OPT optimal cutoffs were 6 mm for patient subgroup A, 7 mm for subgroup B, and 7 mm for subgroup D. For subgroup C (diameter of largest CRLM ≥2.85 cm and a left-sided primary tumor), the optimal margin width was 12 mm.
Figure 1. Optimal Policy Trees (OPTs) and Shapley Additive Explanations (SHAP) Plots for Overall Survival in Patients With KRAS-Variant Tumors .
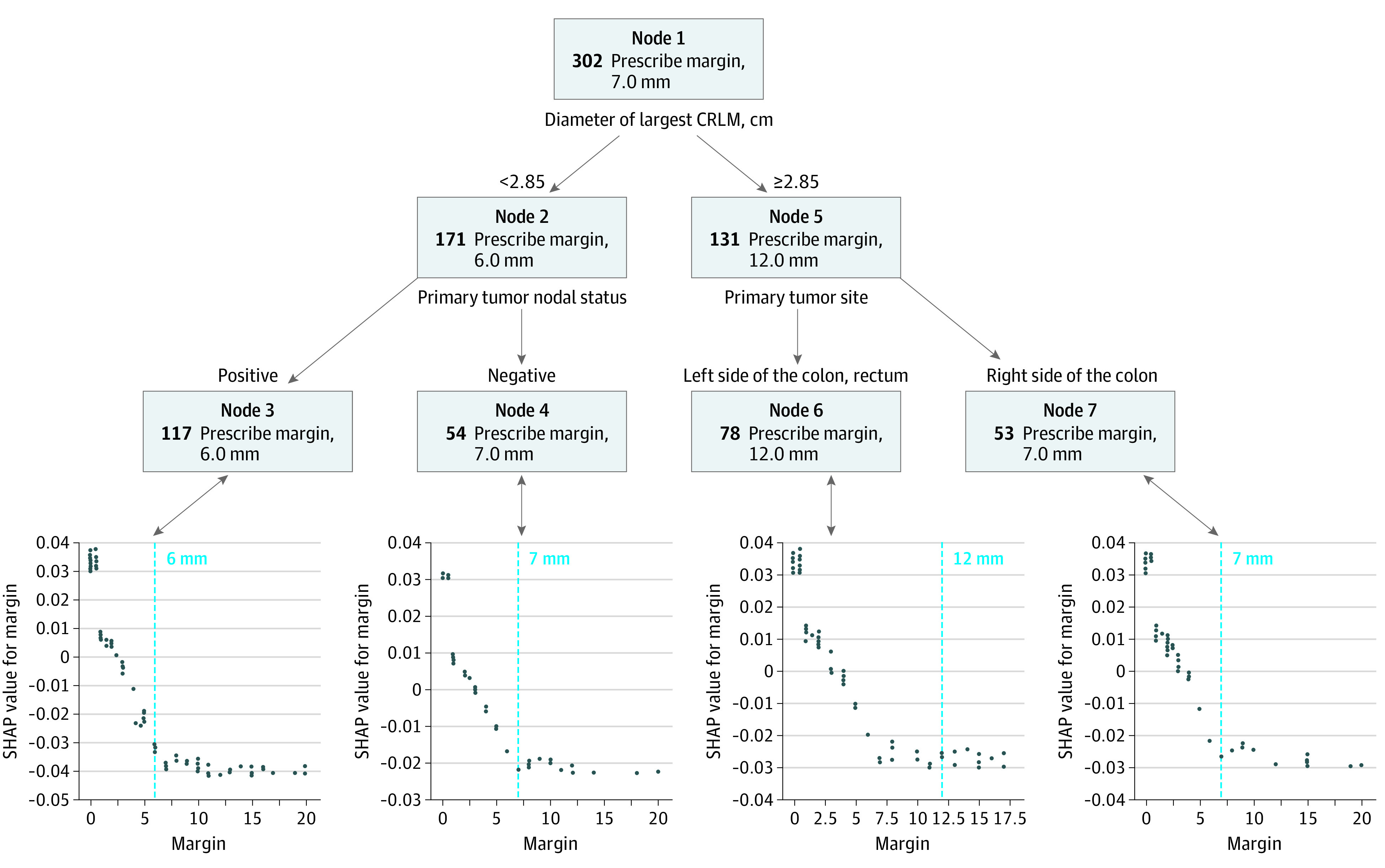
In the upper part of the figure is the OPT analysis (a methodology devised by the collaborating group from Massachusetts Institute of Technology), which suggested optimal margins of 6 to 7 mm, with the exception of group C for which the optimal margin was 12 mm. In the lower part of the figure is the SHAP analysis (a methodology devised by a group from Microsoft), which also suggested optimal margins of 6 to 7 mm (these were the margins associated with the lowest SHAP value and thus the lowest risk of death), with the exception of group C for which the optimal margin was 7 mm. In the SHAP plots, the OPT margin value that was associated with the maximum risk reduction for the specific patient subgroup is depicted by the vertical dashed line. The decrease in risk of death associated with a margin of 7 vs 6 mm is similar in nodes 4 and 7. CRLM indicates colorectal cancer liver metastases.
SHAP Validation Plot and Interaction Analysis
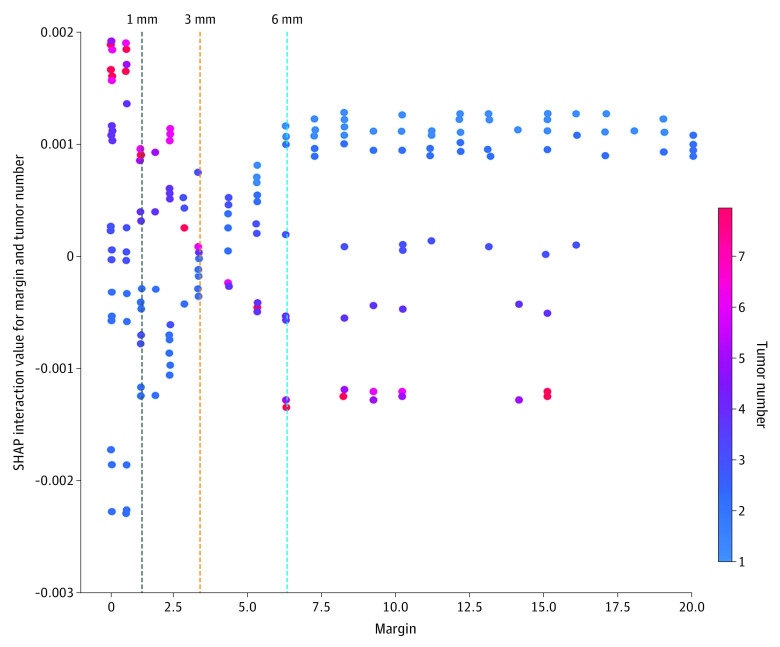
The SHAP plots for each of the subgroups largely confirmed the OPT optimal cutoffs (Figure 1) by suggesting 6 to 7 mm for subgroup A, 7 mm for subgroup B, and 7 mm for subgroup D. However, the exception was the SHAP plot for group C which suggested a margin of approximately 7 to 8 mm, whereas the corresponding OPT recommended a margin of 12 mm. We performed additional analyses to validate the OPT variable selection by constructing separate SHAP dependence plots to examine the association of tumor side and lymph node status with the prognostic impact of tumor size (eFigure 2 in the Supplement). A detailed explanation is provided in the eResults in the Supplement. Figure 2 shows the SHAP interaction values for different margins and number of tumors. A detailed explanation is provided in the eResults in the Supplement.
Figure 2. Shapley Additive Explanations (SHAP) Interaction Values for Different Margins and Number of Tumors.
RRR of Death Rate
The relative reduction of 5-year death risk associated with the OPT margins vs R1 margins as calculated in the training data set would be 12.60%, 13.06%, 10.57%, and 11.75% (Table 2). The probabilities of death at 5 years were also calculated in the training data set for other suboptimal margins (3 and 5 mm) as well as for a wider than optimal margin (10 mm). The results are presented in Table 2.
Table 2. Relative Reduction of 5-Year Death Risk Associated With the Optimal Policy Tree (OPT) Optimal Margins as Calculated in the Patients With KRAS-Variant Tumors.
| Node | Mean predicted probability of death (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| No. of patients | 10.0 mm | 7.0 mm | 5.0 mm | 3.0 mm | 1.0 mm | 0.5 mm | 0.0 mm | RRR (%) | |
| Train data set (n = 302) | |||||||||
| 3 | 117 | 63.89 | 63.66 | 64.12 | 66.68 | 67.43 | 68.85 | 72.84 | 12.60 |
| 4 | 54 | 55.24 | 54.95 | 55.17 | 56.19 | 57.05 | 58.41 | 63.21 | 13.06 |
| 6 | 78 | 65.42 | 65.56 | 66.07 | 67.76 | 68.65 | 69.89 | 73.31 | 10.57 |
| 7 | 53 | 64.44 | 64.33 | 64.94 | 66.90 | 67.74 | 69.10 | 72.90 | 11.75 |
| External validation data set (n = 375) | |||||||||
| 3 | 102 | 57.10 | 56.60 | 57.52 | 57.17 | 57.35 | 58.26 | 60.83 | 6.95 |
| 4 | 85 | 56.14 | 55.79 | 56.82 | 56.55 | 56.69 | 57.52 | 60.03 | 7.06 |
| 6 | 76 | 63.65 | 63.38 | 64.26 | 64.06 | 64.24 | 64.91 | 67.26 | 5.76 |
| 7 | 112 | 58.47 | 57.92 | 58.60 | 58.18 | 58.34 | 59.07 | 61.47 | 5.77 |
Abbreviation: RRR, relative risk reduction.
OPT for Liver-Specific Recurrence
The AUC of the RF counterfactual model for liver-specific recurrence was 0.70 indicating good discriminatory capacity. The OPT used to determine the margin width value associated with the maximal reduction of liver-specific recurrence rate within 5 years of surgery is illustrated in eFigure 3 in the Supplement. The OPT optimal cutoffs were 9 to 11 mm.
External Cohort
The external cohort included 375 patients (median [IQR] age, 61.0 [53.0-70.0] years; 218 men [58.1%]; 157 women [41.9%]) with KRAS-variant tumors. Detailed clinical characteristics of the external validation data set are presented in Table 3.
Table 3. Patient Characteristics in the External Cohort.
| Variable | Entire external cohort (n = 878) | |
|---|---|---|
| KRAS variant | Wild type | |
| Entire (n = 375) | Entire (n = 503) | |
| Numerical features, median (IQR) | ||
| Age, y | 61.0 (53.0-70.0) | 61.0 (52.0-69.0) |
| No. of CRLM | 2.0 (1-3) | 2.0 (1-4) |
| Diameter of largest CRLM, cm | 3.0 (2.0-4.0) | 3.0 (2.0-4.2) |
| Margin width, mm | 5.0 (1-10) | 4.0 (1-10) |
| Categorical variables total, No. (%) | ||
| Sex | ||
| Male | 218 (58.1) | 295 (58.6) |
| Female | 157 (41.9) | 208 (41.4) |
| Primary tumor side | ||
| Left | 95 (25.3) | 179 (35.6) |
| Right | 197 (52.5) | 207 (41.2) |
| Rectum | 83 (22.1) | 117 (23.3) |
| Primary tumor (T) stage | ||
| T0-2 | 77 (20.5) | 93 (18.5) |
| T3-4 | 298 (79.5) | 410 (81.5) |
| Primary tumor nodal status | ||
| Yes | 197 (52.5) | 343 (68.2) |
| No | 178 (47.5) | 160 (31.8) |
| Bilobar CRLM | ||
| Yes | 104 (27.7) | 182 (36.2) |
| No | 271 (72.3) | 321 (63.8) |
| Extrahepatic disease | ||
| Yes | 31 (8.3) | 66 (13.1) |
| No | 344 (91.7) | 437 (86.9) |
| Prehepatectomy chemotherapy | ||
| Yes | 293 (78.1) | 398 (79.1) |
| No | 82 (21.9) | 105 (20.9) |
| Intraoperative ablation | ||
| Yes | 38 (10.1) | 36 (7.2) |
| No | 337 (89.9) | 467 (92.8) |
| Positive margin | ||
| Yes | 51 (13.6) | 92 (18.3) |
| No | 324 (86.4) | 411 (81.7) |
Abbreviation: CRLM, colorectal cancer liver metastases.
Discriminatory Capacity of the RF Counterfactual Model
The AUC of the new RF counterfactual model was 0.78, which indicated very good discriminatory capacity and allowed for a reliable external validation of the OPT-based optimal margin. The external validation was successful as it confirmed the association of the optimal margin width of 7 mm with a considerable prolongation of survival in the external cohort.
RRR of Death Rate if OPT Optimal Cutoffs Were Followed
The relative reduction of 5-year death risk associated with the OPT margins vs R1 margins as calculated using the new RF model in the external cohort was 6.95%, 7.06%, 5.76%, and 5.77% (Table 2). The probabilities of death at 5 years were also calculated in the external validation data set for other suboptimal margins (3 and 5 mm) as well as for a wider than optimal margin (10 mm). The results are presented in Table 2.
Discussion
This cohort study included an internal cohort of 386 patients and an external cohort of 375 patients with KRAS-variant tumors. For the first time, to our knowledge, this study used AI-based methodologies (ie, OPT) to provide a possible resolution to the long-standing debate on optimal margin width in CRLM. OPTs have 2 main advantages compared with conventional biostatistics. They are much more sensitive in optimizing a treatment by detecting even the slightest increase in associated prolongation of survival and can also infer heterogeneous treatment effects for patient subgroups. The OPT was trained based on the estimates of the RF counterfactual model, which had a training and testing AUC of 0.76. These AUCs are the highest reported for a predictive model in CRLM.19 Our findings suggest an average optimal margin width of 7 mm for KRAS-variant tumors, with only slight variation among the subsets, which alludes to a homogeneous treatment outcome. Importantly, a submillimeter/1-mm margin was associated with most of the associated prolongation of survival, and the extension from 1 to 7 mm was associated with a smaller prolongation of survival. The small magnitude of improvement in survival associated with the optimal margin widths is somewhat expected. For example, Sadot et al20 reported that patients with a margin of 10 mm had only a slightly higher median overall survival than those with a margin of 1 to 9 mm (56 vs 53 months, respectively). Similar results were reported in a meta-analysis3 that examined the overall recurrence rates in patients with margins of 1 to 4 mm, 5 to 9 mm, or greater than 10 mm; recurrence rates were 39% vs 41% vs 39%, respectively.
The OPT results were doubly validated. The first validation was performed to assess the robustness of the novel OPT methodology by estimating optimal margin cutoffs with another method (SHAP plots). The cutoffs determined by the SHAP method were almost identical to those determined by OPT (subgroup A, 6-7 mm vs 6 mm; subgroup B, 7 mm vs 7 mm; and subgroup D, 7 mm vs 7 mm). The only exception, which has been discussed in the results section, was subgroup C, with an optimal margin width of 12 mm, as the SHAP plot suggested a margin of 7 to 8 mm. Of note, an analysis of the interaction between margin and tumor number (Figure 2) produced an optimal margin of approximately 6 mm, which is very similar to the average optimal margin width of 7 mm determined by the OPT for KRAS-variant tumors. This further strengthens the overall result of the study that a 7 mm margin is the optimal margin for KRAS-variant tumors. Finally, the OPT trained to identify the margin cutoffs associated with the lowest probability that the patient will experience an intrahepatic recurrence within 5 years from surgery produced similar cutoffs as the overall survival OPT. Specifically, the OPT cutoffs associated with the lowest risk of liver-specific recurrence were 9 to 11 mm, and the optimal margin was on average 9 mm.
The second validation was performed by training a new RF model in an external validation cohort that was fundamentally different from the internal cohort; it differed significantly for 8 of the 13 patient characteristics, likely secondary to its geographically distinct origin. Importantly, the results were reproducible in the external cohort with the optimal margin of 7 mm being associated with a 6% to 7% relative reduction of 5-year death risk compared with R1 resections. Similar to the internal analysis, a submillimeter/1-mm margin was associated with most of the associated prolongation of survival, and the extension from 1 to 7 mm was associated with a much smaller prolongation of survival.
Although dozens of studies and several meta-analyses have aimed to identify the optimal margin width, almost all approached the optimal margin width regardless of the underlying tumor biology, with the exception of a few studies that stratified cohorts by a surrogate of tumor biology before assessing optimal margin widths.2,3,4,21 Specifically, in 2017, a group from Johns Hopkins hypothesized that distinct disease biology dictates different resection extents.22 A similar view was expressed by a group from MD Anderson Cancer Center in Houston, Texas.23 Interestingly, the authors of the Johns Hopkins group reported that “…the group of patients [with KRAS-variant CRLM] with a margin width of 5 to 9 mm tended to have a better overall survival than patients who had an R1 resection.”22(p270) However, this difference was not statistically significant. They ultimately suggested that aggressive tumor biology implied by the presence of a KRAS variant could not be counterbalanced by extensive resection and that even an R1 margin may not seriously affect outcomes in these patients. Hatta et al12 recently reached a similar conclusion. In comparison, the group from MD Anderson Cancer Center suggested that surgeons should strive for aggressive margins of 10 mm or even 15 mm in KRAS-variant CRLM to overcome their underlying biologic aggressiveness.23,24 In light of the evidence provided in the present study, it seems that the truth lies somewhere in between.
Limitations
Although the OPT framework can infer causality, we have elected not to use causal language throughout the article, for 2 reasons.25 First, the causal structure of the clinical problem is not certain, as it is unclear whether margin width is a surrogate of underlying tumor biology or truly a technical issue that can affect survival. In addition, the surgical margin may also depend on variables, such as anatomical distribution of metastases and tumor growth pattern, which may have independent prognostic importance. Thus, it is possible that the observed differences in survival may also depend on other factors that we do not control for or know about (confounders).26 It should be noted that the findings of this study may only apply to patients who are followed up for a significant period of time, as patients who could not maintain follow-up until the time point of interest were censored and thus excluded from the analysis. Also, the RF counterfactual model relied on a relatively small number of predictive variables and thus its predictions are imperfect. Lastly, it should be noted that the OPT methodology does not allow for calculation of the CIs for the AUC of the RF model.
Conclusions
This cohort study used artificial intelligence–based methodologies to provide a possible resolution to the long-standing debate on optimal margin width in CRLM. Our OPT did not provide evidence for heterogeneous treatment effects but rather, results suggest a single optimal margin width (7 mm) for KRAS-variant CRLM, which differs considerably from previous recommendations. Importantly, both the derivation and the internal and external validation of these margin cutoffs were based on state-of-the-art predictive models with the highest AUCs reported in the CRLM literature. Although these relatively wide margins should be attempted when possible, our findings should not be viewed as a recommendation to change operative indications, as submillimeter margin clearance is associated with much of the survival improvement. It should be kept in mind that the presented survival benefits from applying optimal margins is a statistical projection and only prospective validation can determine whether these recommendations can translate into a real survival benefit.
eMethods.
eResults.
eReferences
eFigure 1. Internal Cohort Selection
eFigure 2. SHAP Dependence Plot of Tumor Size vs its SHAP Value in the RF Model
eFigure 3. OPT for Liver-Specific Recurrence in Patients with KRAS-Variant Tumors
References
- 1.Cady B, Stone MD, McDermott WV Jr, et al. Technical and biological factors in disease-free survival after hepatic resection for colorectal cancer metastases. Arch Surg. 1992;127(5):561-568. doi: 10.1001/archsurg.1992.01420050085011 [DOI] [PubMed] [Google Scholar]
- 2.Nuzzo G, Giuliante F, Ardito F, et al. Influence of surgical margin on type of recurrence after liver resection for colorectal metastases: a single-center experience. Surgery. 2008;143(3):384-393. doi: 10.1016/j.surg.2007.09.038 [DOI] [PubMed] [Google Scholar]
- 3.Cucchetti A, Ercolani G, Cescon M, et al. Impact of subcentimeter margin on outcome after hepatic resection for colorectal metastases: a meta-regression approach. Surgery. 2012;151(5):691-699. doi: 10.1016/j.surg.2011.12.009 [DOI] [PubMed] [Google Scholar]
- 4.Margonis GA, Sergentanis TN, Ntanasis-Stathopoulos I, et al. Impact of surgical margin width on recurrence and overall survival following R0 hepatic resection of colorectal metastases: a systematic review and meta-analysis. Ann Surg. 2018;267(6):1047-1055. doi: 10.1097/SLA.0000000000002552 [DOI] [PubMed] [Google Scholar]
- 5.Ekberg H, Tranberg KG, Andersson R, et al. Determinants of survival in liver resection for colorectal secondaries. Br J Surg. 1986;73(9):727-731. doi: 10.1002/bjs.1800730917 [DOI] [PubMed] [Google Scholar]
- 6.Oshi M, Margonis GA, Sawada Y, et al. Higher tumor burden neutralizes negative margin status in hepatectomy for colorectal cancer liver metastasis. Ann Surg Oncol. 2019;26(2):593-603. doi: 10.1245/s10434-018-6830-x [DOI] [PubMed] [Google Scholar]
- 7.McVey JC, Sasaki K, Margonis GA, et al. The impact of resection margin on overall survival for patients with colon cancer liver metastasis varied according to the primary cancer location. HPB (Oxford). 2019;21(6):702-710. doi: 10.1016/j.hpb.2018.11.001 [DOI] [PubMed] [Google Scholar]
- 8.Powers S, Qian J, Jung K, et al. Some methods for heterogeneous treatment effect estimation in high dimensions. Stat Med. 2018;37(11):1767-1787. doi: 10.1002/sim.7623 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wager S, Athey S. Estimation and inference of heterogeneous treatment effects using random forests. J Am Stat Assoc. 2018;113(523):1228-1242. doi: 10.1080/01621459.2017.1319839 [DOI] [Google Scholar]
- 10.Amram M, Dunn J, Zhuo YD. Optimal policy trees. arXiv. Preprint posted online December 3, 2020. doi: 10.48550/arXiv.2012.02279 [DOI]
- 11.Gholamy A, Kreinovich V, Kosheleva O. Why 70/30 or 80/20 relation between training and testing sets: a pedagogical explanation. Accessed November 3, 2021. https://www.cs.utep.edu/vladik/2018/tr18-09.pdf
- 12.Hatta AAZ, Pathanki AM, Hodson J, et al. The effects of resection margin and KRAS status on outcomes after resection of colorectal liver metastases. HPB (Oxford). 2021;23(1):90-98. doi: 10.1016/j.hpb.2020.04.016 [DOI] [PubMed] [Google Scholar]
- 13.Margonis GA, Sasaki K, Kim Y, et al. Tumor biology rather than surgical technique dictates prognosis in colorectal cancer liver metastases. J Gastrointest Surg. 2016;20(11):1821-1829. doi: 10.1007/s11605-016-3198-8 [DOI] [PubMed] [Google Scholar]
- 14.Bertsimas D, Dunn J. Machine Learning Under a Modern Optimization Lens. Dynamic Ideas; 2018. [Google Scholar]
- 15.Lundberg SM, Erion G, Chen H, et al. From local explanations to global understanding with explainable AI for trees. Nat Mach Intell. 2020;2(1):56-67. doi: 10.1038/s42256-019-0138-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lundberg SM, Nair B, Vavilala MS, et al. Explainable machine-learning predictions for the prevention of hypoxaemia during surgery. Nat Biomed Eng. 2018;2(10):749-760. doi: 10.1038/s41551-018-0304-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nishioka Y, Paez-Arango N, Boettcher FO, et al. Neither surgical margin status nor somatic mutation predicts local recurrence after R0-intent resection for colorectal liver metastases. J Gastrointest Surg. 2021. doi: 10.1007/s11605-021-05173-0 [DOI] [PubMed] [Google Scholar]
- 18.Hosmer DW Jr, Lemeshow S, Sturdivant RX. Applied Logistic Regression. 3rd ed. Wiley; 2013. [Google Scholar]
- 19.Mahar AL, Compton C, Halabi S, Hess KR, Weiser MR, Groome PA. Personalizing prognosis in colorectal cancer: a systematic review of the quality and nature of clinical prognostic tools for survival outcomes. J Surg Oncol. 2017;116(8):969-982. doi: 10.1002/jso.24774 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sadot E, Groot Koerkamp B, Leal JN, et al. Resection margin and survival in 2368 patients undergoing hepatic resection for metastatic colorectal cancer: surgical technique or biologic surrogate? Ann Surg. 2015;262(3):476-485. doi: 10.1097/SLA.0000000000001427 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dhir M, Lyden ER, Wang A, Smith LM, Ullrich F, Are C. Influence of margins on overall survival after hepatic resection for colorectal metastasis: a meta-analysis. Ann Surg. 2011;254(2):234-242. doi: 10.1097/SLA.0b013e318223c609 [DOI] [PubMed] [Google Scholar]
- 22.Margonis GA, Sasaki K, Andreatos N, et al. KRAS mutation status dictates optimal surgical margin width in patients undergoing resection of colorectal liver metastases. Ann Surg Oncol. 2017;24(1):264-271. doi: 10.1245/s10434-016-5609-1 [DOI] [PubMed] [Google Scholar]
- 23.Brudvik KW, Mise Y, Chung MH, et al. RAS mutation predicts positive resection margins and narrower resection margins in patients undergoing resection of colorectal liver metastases. Ann Surg Oncol. 2016;23(8):2635-2643. doi: 10.1245/s10434-016-5187-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Brudvik KW, Vauthey JN. Surgery: KRAS mutations and hepatic recurrence after treatment of colorectal liver metastases. Nat Rev Gastroenterol Hepatol. 2017;14(11):638-639. doi: 10.1038/nrgastro.2017.129 [DOI] [PubMed] [Google Scholar]
- 25.Hernán MA. The C-word: scientific euphemisms do not improve causal inference from observational data. Am J Public Health. 2018;108(5):616-619. doi: 10.2105/AJPH.2018.304337 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nielsen K, Rolff HC, Eefsen RL, Vainer B. The morphological growth patterns of colorectal liver metastases are prognostic for overall survival. Mod Pathol. 2014;27(12):1641-1648. doi: 10.1038/modpathol.2014.4 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
eMethods.
eResults.
eReferences
eFigure 1. Internal Cohort Selection
eFigure 2. SHAP Dependence Plot of Tumor Size vs its SHAP Value in the RF Model
eFigure 3. OPT for Liver-Specific Recurrence in Patients with KRAS-Variant Tumors