Abstract
Successful transformation of carbon dioxide (CO2) into value-added products is of great interest, as it contributes in part to the circular carbon economy. Understanding chemical interactions that stabilize crucial reaction intermediates of CO2 is important, and in this contribution, we employ atom centered density matrix propagation (ADMP) molecular dynamics simulations to investigate interactions between CO2– anion radicals with surrounding solvent molecules and electrolyte cations in both aqueous and nonaqueous environments. We show how different cations and solvents affect the stability of the CO2– anion radical by examining its angle and distance to a coordinating cation in molecular dynamics simulations. We identify that the strength of CO2– interactions can be tailored through choosing an appropriate cation and solvent combination. We anticipate that this fundamental understanding of cation/solvent interactions can facilitate the optimization of a chemical pathway that results from selective stabilization of a crucial reaction intermediate.
Introduction
Transforming CO2 into value-added chemicals or fuels is of great interest to create a sustainable carbon neutral cycle to tackle challenges such as climate change.1−3 However, reducing CO2 is a challenging process due to its thermodynamic stability, poor electron affinity, and large kinetic overpotentials. Additionally, as a nonpolar gas, it is only sparingly soluble in water (0.033 M),4 a common solvent for electrochemical reduction of CO2.1 Therefore, it might be advantageous to use nonaqueous (aprotic) solvents due to the higher CO2 solubility, enhanced potential window, as well as lower proton concentrations that can suppress the undesired hydrogen evolution reaction.5−7
The first step of the CO2 reduction reaction (CO2RR) involves the formation of CO2–, and although successful studies have been performed to unravel the mechanism of electrochemical CO2RR,8−17 molecular-level understanding of the dynamics of CO2– interacting with surrounding electrolyte cations and solvents (aqueous vs nonaqueous) remains unclear. Of particular interest is the cation effect,18−24 which was first introduced by Murata and Hori, and it has been better understood that coupling alkali metal cations (M+) with CO2– cocatalyzes the first step25,26 in aqueous solvents, i.e., * + CO2 + M+ + e– → M+···*CO2– by a short-range electrostatic interaction. In nonaqueous solvents, however, alkali metals are known to inhibit CO2 reduction due to the formation of a passivation layer containing carbonate species.27,28 Therefore, electrolyte cations such as NX4+ (X = methyl, ethyl, and butyl groups) are being used, and their catalytic roles were examined.24,29 In aprotic Li–CO2 batteries, it was argued that a LiCO2 intermediate is crucial to tuning CO2RR toward a solution- versus surface-mediated pathway.30
In this contribution, we aim to provide theoretical insights into the fundamental interactions between CO2–, obtained from the electrochemical reduction of CO2 gas, and the supporting electrolyte cations in various solvents, which will help direct the mechanism toward desired products such as CO, formic acid, and/or oxalate, and will lay a foundation to the future study of specific catalyst systems. Here, we focus on the stabilization effect of the CO2– anion radical, as its formation is likely to be the rate-determining step31 for CO2 reduction in some aqueous32−34 and nonaqueous15,35 media, although this is still under debate.1 We compare water and nonaqueous solvents (mainly dimethoxyethane (DME) in this work), as glyme-ether-based solvents have been successfully used for electrochemistry (e.g., metal-air/Mg battery) and gas separation processes capturing CO236,37 but have been rarely studied for CO2 reduction until recently,27 to the best of our knowledge.
To gain understanding of the specific molecular-level interactions, we used ab initio molecular dynamics (AIMD) simulations.38,39 These AIMD simulations show the atomic movement within the system, where the extremes and averages of the oscillations can give detailed information on the stability and other thermodynamic properties. We use the atom centered density matrix propagation (ADMP)40−42 molecular dynamics method, as it gives the accuracy of density functional theory (DFT) and has advantages particularly around handling the dynamics of charged and radical molecular systems.43−47 This approach allows us to gather accurate information on how the CO2– anion radical interacts with cation and solvent species, based on the computed descriptors such as coordination bond distances (cation–CO2) and bond angles to develop a fundamental understanding of the interactions. The shorter coordination distance and/or more decreased bond angle of CO2– indicate that the intermediate complex can be present for prolonged periods and likely undergo subsequent desired reactions such as chelation, charge transfer interactions, and bond cleavage/formation reactions.48,49 We further construct a physics-based model to rationalize the relative contributions of electrostatic and covalent/noncovalent interactions to the stabilization effects of CO2–.
Computational Details
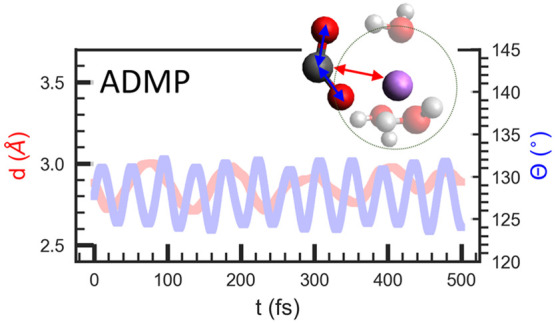
Initial geometry optimizations were performed using Gaussian 16 software50 at the ωb97xD/6-31+G(d,p) level of theory51,52 with ultrafine integration grids and multiple conformers considered.53 The frequencies were calculated at the same level of theory. Upon geometry optimization, trajectories were calculated using ADMP molecular dynamics at the ωb97xD/jun-cc-pVDZ level of theory51,54,55 for 5000 time points (500 fs). ADMP simulations were performed with and without the presence of implicit solvents56,57 (water (H2O), tetrahydrofuran (THF), dimethyl sulfoxide (DMSO), acetonitrile (MeCN), and n,n-dimethylformamide (DMF)). Optimized, maximum, mean, and variation amplitude of the CO2– angle (θ) and the CO2– distance (to the cation, d) were extracted from the AIMD trajectory. As shown in Figure 1a, the CO2– angle (θ) is measured from one oxygen to the other, with the carbon atom as the angle vertex. The CO2–-to-cation distance (d) is measured from the carbon of the CO2– to the center of the cation (either the cation atom or the nitrogen in the ammonium cations). A typical ADMP trajectory is shown in Figure 1b, where CO2– oscillates around its equilibrium position over the course of the simulation. Additional details of the simulations are provided in the Supporting Information (SI).
Figure 1.
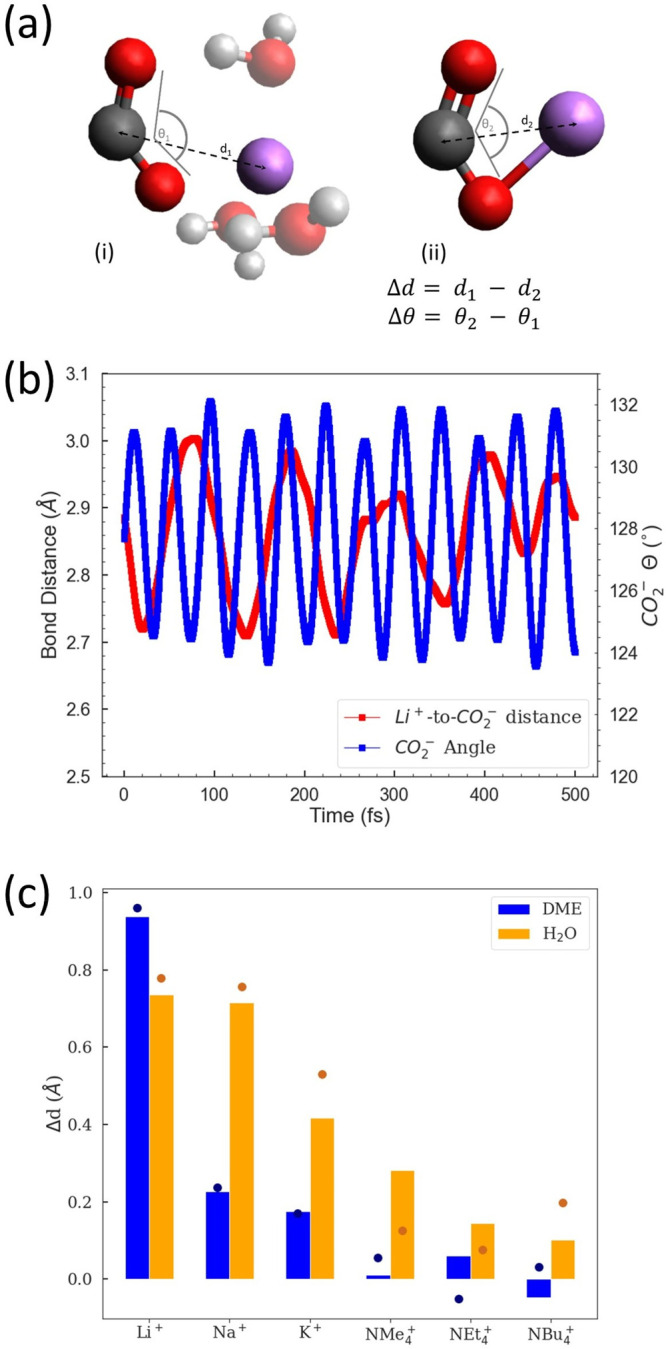
(a) Schematic showing how the change in bond distance (Δd) or change in angle (Δθ) is calculated. Scheme (a) shows a molecular cluster with the dashed black line indicating the bond distance (measured Li+ to CO2– from the center of the cation to the carbon atom) and gray lines showing how the bond angle (θ) is measured (with the carbon as the vertex of the angle). The lithium, carbon, oxygen, and hydrogen atoms are shown in purple, dark gray, red, and light gray, respectively. (b) Computed trajectories of the bond distance (Δd) and CO2– angle (θ) over 500 fs for a Li+–CO2––3H2O molecular cluster. (c) Computed average Δd for various cationic complexes. All complexes in state (i) include three explicit solvent molecules. The dots indicate the difference in bond distances of optimized complexes with and without explicit solvent molecules. Me, Et, and Bu denote methyl, ethyl, and butyl groups, respectively.
Results and Discussion
The interaction strength of two charged particles is inversely related to the separating distance.58 As shown in yellow bars in Figure 1c, based on the simulations, we observe that the interaction of dynamic water molecules increases the cation-to-CO2– distance (Δd) for all cations compared to the gas-phase geometry, which manifests less negative complexation energies and binding energies compared to those in the gas phase (ΔHgas, Table 1). Note that the equations for the complexation enthalpy calculations are provided in the Supporting Information. In the case of the DME solvent system, the chelation of the DME molecule with the alkali metal cation increases the interaction distance for alkali metal cations with the CO2–, while for NX4+ cations (X = Me, Et, and Bu), the difference is minimal (<0.1 Å). This is largely due to the chemical differences between water and DME molecules. Water molecules are strongly polar and have strong ion-dipole interactions with cations and CO2–, as seen from the computed complexation enthalpies (ΔHcomplex) summarized in Table 1. DME is weakly polar and has chelating interactions with alkali metal cations, where the unshielded positive charge can interact closely with the lone pairs on the oxygen atoms of DME. On the basis of the computed enthalpies of complexation (Table 1), the CO2– species itself weakly interacts with DME as compared to water (by 0.50 eV) because DME molecules do not have any strong localized partial positive charges. The NBu4+ positive charge is highly shielded by the butyl arms and as such does not closely interact with the DME oxygen atoms, which also can be seen from our quantum chemical calculations that the difference between ΔHcomplex and ΔHgas for the NBu4+ complex is much smaller than that for alkali metal cations (Table 1). The optimized structures of NBu4+ complexes are shown in Figure S1. The optimized structures of Li+–CO2––solvent with DME and H2O also corroborate the above analysis; i.e., the oxygen atoms of CO2– only bind to Li+ in the DME solvent, as shown in Figure 2a, whereas in water one of the CO2– oxygen atoms binds to Li+, and the other interacts with water to form an O···H hydrogen bond as shown in Figure 2b. Overall, this suggests that the identity of the supporting electrolyte cation, as well as the polarity of solvents, both dictate the strength of interactions of the CO2– anion radical, which primarily consist of (electrostatic) ion-ion and ion-dipole interactions and hydrogen bonds. The different types of interactions will be discussed in more detail.
Table 1. Computed Complexation Enthalpies and Binding Enthalpies (ΔHcomplex and BECO2-, in eV) of CO2–, Li+, Na+, K+, and NBu4+ with Three Explicit H2O or DME Molecules.
| species | ΔHcomplex (3H2O) | BECO2- (3H2O) | ΔHcomplex (3DME) | BECO2- (3DME) | ΔHgas (CO2- + M+) |
|---|---|---|---|---|---|
| CO2– | –1.72 | –1.22 | |||
| Li+ | –3.66 | –5.08 | –5.73 | –3.59 | –6.50 |
| Na+ | –2.73 | –4.96 | –4.65 | –3.51 | –5.66 |
| K+ | –2.03 | –4.82 | –3.55 | –3.49 | –5.00 |
| NBu4+ | –1.17 | –3.65 | –2.03 | –3.28 | –3.84 |
Figure 2.
Gas-phase optimized structures of Li+–CO2––solvent with (a) DME and (b) H2O.
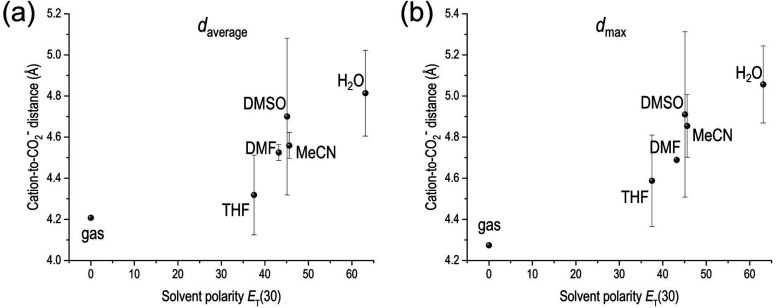
To further explore how the NX4+–CO2– interaction responds to the polarity of the solvent, we carried out ADMP simulations with three explicit solvent molecules (in THF, MeCN, DMSO, DMF, and water) and at the same time included the implicit solvent field of corresponding solvent models in Gaussian 16. For these bulky clusters, we repeated each simulation three times with different initial geometries (randomly generated and subsequently optimized) to make sure that the selection of initial structures have no role in dictating the final results. The average and maximum cation-to-CO2– distances are shown in Figure 3.
Figure 3.
(a) Average cation-to-CO2– distance daverage and (b) maximum cation-to-CO2– distance dmax during simulations in various solvents, as plotted against the polarity (ET(30))62 of solvent. These data points are for clusters of NBu4+, CO2–, three molecules of the solvent in question, and with an implicit solvent field of that solvent. Error bars represent standard deviations of three simulations.
We observe that the strength of interaction between NBu4+ and CO2– decreases with increasing solvent polarity, indicated by the increasing cation-to-CO2– distance, as shown in Figure 3. Such an observation is consistent with the dominant electrostatic interactions and has experimental implications on salt dissociation or formation of ion pairs.25,27 The positive charge on the NBu4+ cation is highly shielded by the bulky and electron donating alkyl chains, which means that changing solvents has a relatively minimal effect on the NBu4+. However, the strength of the interaction between CO2– and NBu4+ is affected by how strongly CO2– is coordinated to the solvent and cationic species. Thus, increasing the polarity of the solvent increases CO2– coordination with the solvent, weakening the bond between CO2– and NBu4+. Similar qualitative trends in CO2RR were also reported by Berto et al.59 and Shi et al.,60 where voltammetric experiments in the presence of NBu4+ electrolytes have shown larger current density values for CO2RR in highly polar DMF and MeCN, as compared to low polarity THF. Here, DMSO has the largest standard deviation (Figure 3), which was also found to exhibit the largest deviation from trends due to coordination via the sulfur atom (as opposed to via the oxygen atom in water and THF) in a study of aprotic solvent (THF, DMF, and DMSO) adsorption on metal surfaces by Nørskov and co-workers.61 In aprotic solvents and NBu4+ salts, tailoring the lifetime of the CO2– will likely depend on solvent, due to the stabilizing influence of more polar solvents.
The foregoing analysis suggests that both solvents and cations play an important role in the stabilization of the CO2– radical,59,60 but the precise effects are less clear. On the basis of our simulations, we hypothesize that inner-sphere solvation effects are the result of electrostatic and covalent/noncovalent interactions based around solvent stabilization and cation binding, and to this end, we sought to rationalize these by constructing a simple physics-based model. Compared to gas-phase CO2–, the introduction of a solvent molecule or a cation reduces the angle of CO2–. In Figure 4a, the largest reductions are observed with cations without solvent molecules, following the trend of Li+ > Na+ > K+ > NX4+ in the gas phase (gray bars), where X = methyl or longer alkyl groups. There is an overall trend of a larger change in the bond angle (Δθ) being associated with more negative complexation enthalpies, as shown in Figure 4b, which also indicates that increased complex stability is associated with a decreased CO2– angle. This decreased angle is due to anion radical stabilization through ion-ion interactions, ion-dipole interactions, and/or hydrogen bonds. Given the computed trends of solvent polarity and complexation enthalpy simultaneously (Figure 3 and Figure 4b) and together with known experiment data, we would be able to provide guidance on the electrolyte environments, e.g., with larger stabilizing effects on CO2–63 toward the desired binding.
Figure 4.
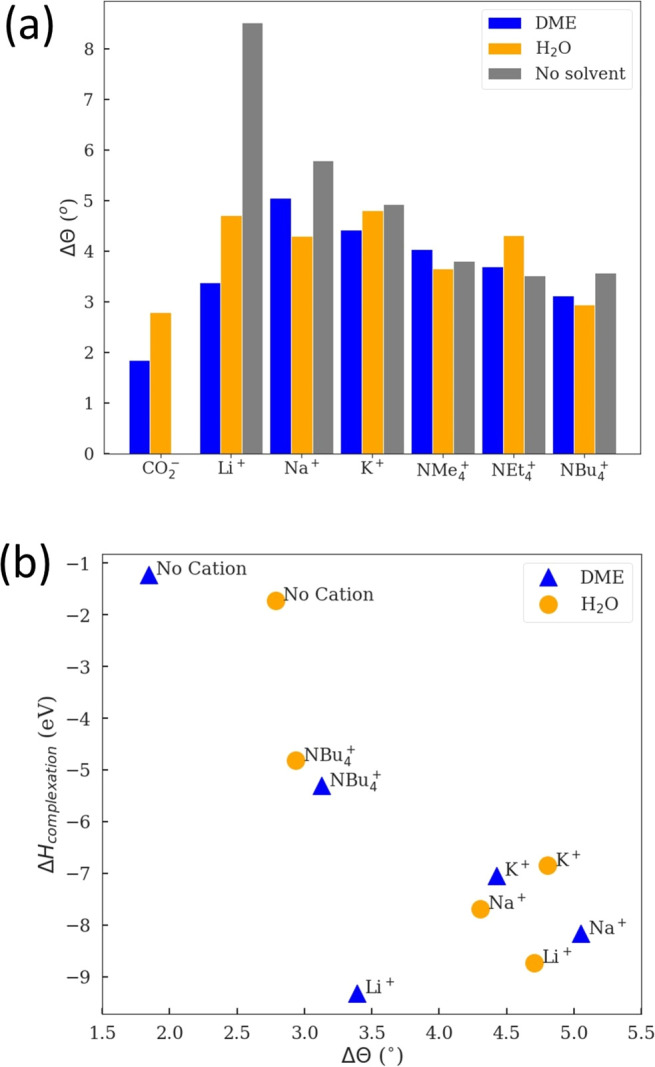
(a) Bar chart of the change in the CO2– angle (Δθ) between the uncomplexed CO2– anion radical in the gas phase and the CO2– angle when complexed with cations and/or three solvent molecules. (b) Computed complexation enthalpy plotted against the change in angle from the gas phase to solvated (by DME or H2O).
To decompose the quantum chemistry-calculated complexation enthalpies into stabilization effects by electrostatic ion-ion interactions and/or ion-dipole interactions explicitly, we have constructed a simple physics-based model (see Supporting Information). This model takes in the geometry of a cluster and computes the different types of interactions based on fundamental physics equations. The model-predicted complexation energies against the known DFT-calculated complexation energies are shown in Figure 5, where red triangles (“ion-CO2–”, e.g., K+–CO2–) represent systems that have only electrostatic ion-ion interactions (also see ΔHgas in Table 1), green squares (“ion-solvent”, e.g. NBu4+–2H2O) represent systems that have ion-dipole and dipole-dipole interactions, and purple circles (“ion-solvent-CO2–”, e.g., Li+–CO2––3DME) represent systems that have ion-ion, ion-dipole, and dipole-dipole interactions. The mean absolute error of the model-predicted complexation energy relative to the DFT-calculated value is about 0.12 eV per ion and solvent molecule in a cluster. For all the “ion-solvent-CO2–” clusters (purple circles), we calculate that on average 73% of the predicted complexation energy results from the electrostatic ion-ion interactions; likewise, the ion-dipole interaction is much stronger than the dipole-dipole interaction. This indicates that CO2 activation could be achieved through electrolyte stabilization of the CO2– anion product due to a stronger interaction with CO2– than the neutral and nonpolar CO2 gas.64,65
Figure 5.
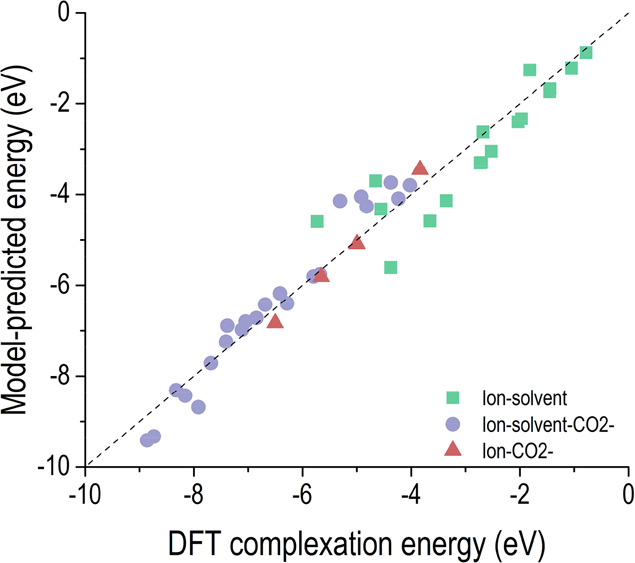
Physics-based model-predicted complexation energy against the known DFT-calculated energy. The dashed line indicates a perfect agreement between the model-predicted complexation energy and the known DFT-calculated complexation energy.
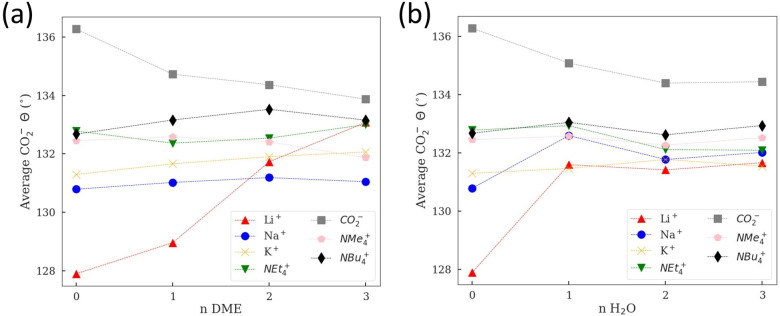
Finally, we show the average CO2– bond angles in DME and water as a function of the number of solvent molecules (Figure 6) from our simulations. The average cation-to-CO2– distances are shown in Figure S2. Here, a small and computationally tractable number of solvent molecules could be used to simulate a reasonable solvation behavior,66,67 where key interactions between cation/anion and solvent (ion-dipole) are captured. We note that there is a different behavior for Li+–CO2––nDME where the CO2– angle keeps increasing as we increase the number of solvent molecules (Figure 6a). Specifically, for Li+–CO2––3DME, only one CO2– oxygen binds to Li+ (Figure 2a), resulting in a weak interaction and thus increased angle and increased Li+-to-CO2– distance (by 0.9 Å, see Table 2 and Figure 1c). Such a weakening interaction from bidentate to monodentate geometry is also captured by the physics model. For Li+–CO2––nH2O the increased angle and Li+-to-CO2– distance is rather minimal (Table 2 and Figure 6b). These observations are important to keep in mind, as fully solvated systems indicate that the Li+–CO2– interaction is the weakest among alkali metal cations in DME but the strongest in water (Figure S4). However, we know that hard shell Li+ cation coordinates poorly to an adsorbed CO2 on the surface,26 and thus we also compare the relative stability of two configurations of Li+–CO2––4H2O (Figure S6) as a function of the partial charge of CO2, assuming the dominant interaction comes from the electrostatic interaction. We find that for a partial charge of −1e, Li+ preferably coordinates with CO2–, but only within about 0.16 eV compared to the other configuration according to DFT. As the charge of CO2 is decreased to −0.6e, which mimics its charge state on the surface, we find that Li+ now preferably coordinates with 4H2O according to our physics-based model (Figure S6).
Figure 6.
Average CO2– angle of different cation–CO2––solvent (DME or H2O) systems from AIMD simulations: (a) cation–CO2––nDME and (b) cation–CO2––nH2O (n = 0, 1, 2, 3).
Table 2. Computed Li+ Coordination Distances for Complexes with O Atoms (of DME/H2O) and C Atoms (of CO2–).
| d(Li–Osolvent)/Å | d(Li–CCO2–)/Å | |
|---|---|---|
| Li+–CO2– | 1.92 | |
| Li+–CO2––1DME | 2.00 | 2.19 |
| Li+–CO2––2DME | 2.09 | 2.39 |
| Li+–CO2––3DME | 2.20 | 3.07 |
| Li+–CO2––1H2O | 1.86 | 2.63 |
| Li+–CO2––2H2O | 1.93 | 2.76 |
| Li+–CO2––3H2O | 2.01 | 2.89 |
Conclusions
We have used ADMP simulations to investigate the interactions of the CO2– anion radical in various chemical environments, including both aqueous and nonaqueous electrolytes. Simulations show the effect of cations and solvent molecules on the fundamental properties of bond distance and angle of CO2, e.g., DME solvation increases the interaction distance for small cations with CO2–, while for NX4+ cations the difference is minimal. This correlates well with the complexation enthalpy of CO2–, offering a guide to which combinations of solvent and supporting electrolyte may provide the desired experimental conditions. Moreover, we have shown that the identity of the supporting electrolyte cation will likely matter more in polar solvents than in solvents of less polarity. Therefore, we can tailor the strength of interactions between CO2– and supporting electrolytes through the judicious choice of electrolyte cations and solvents. Our simulation and physics-based model provides a general and suitable approach to studying solvation effects particularly in an aprotic electrolyte environment, and it was shown that the electrochemical CO2RR activity could be correlated to the bulk solvation properties in DME and DMSO.27 We note the limitation of our model not yet including the electrode surface as well as the pH effect at the interface,68 and future experimental and computational efforts are necessary to elucidate the interactions of the CO2 anion radical with the electrode surface.
Acknowledgments
This work was supported by funding from The University of Chicago Center for Data and Computing (CDAC) program and the Data Science Institute. R.S.A. and C.L. would like to acknowledge Consortium for Computational Physics and Chemistry (CCPC), which is supported by the Bioenergy Technologies Office (BETO) of Energy Efficiency & Renewable Energy (EERE). C.V.A. acknowledges support from the University of Chicago and the Neubauer Family Assistant Professors program. We gratefully acknowledge the computing resources provided on “Bebop”, a 1024-node computing cluster operated by the Laboratory Computing Resource Center at the Argonne National Laboratory. We also acknowledge the computational resources from the Center for Nanoscale Materials, an Office of Science user facility, which was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357. The submitted manuscript has been created by UChicago Argonne, LLC, Operator of Argonne National Laboratory (“Argonne”). Argonne, a U.S. Department of Energy Office of Science laboratory, is operated under Contract No. DE-AC02-06CH11357. The U.S. Government retains for itself, and others acting on its behalf, a paid-up nonexclusive, irrevocable worldwide license in said article to reproduce, prepare derivative works, distribute copies to the public, and perform publicly and display publicly, by or on behalf of the Government.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c01733.
Details of computational methods and analysis, details of quantum chemical calculations and physics-based model, list of systems simulated using ADMP, and trend of cation-to-CO2– bond distances and CO2– angles (Table S1 and Figures S1–S6) (PDF)
Author Present Address
⊥ Schrödinger, Inc., New York, NY 10036
Author Contributions
§ M.M.C. and C.L. contributed equally to this work.
The authors declare no competing financial interest.
Supplementary Material
References
- Birdja Y. Y.; Pérez-Gallent E.; Figueiredo M. C.; Göttle A. J.; Calle-Vallejo F.; Koper M. T. M. Advances and Challenges in Understanding the Electrocatalytic Conversion of Carbon Dioxide to Fuels. Nature Energy 2019, 4 (9), 732–745. 10.1038/s41560-019-0450-y. [DOI] [Google Scholar]
- De Luna P.; Hahn C.; Higgins D.; Jaffer S. A.; Jaramillo T. F.; Sargent E. H.. What Would It Take for Renewably Powered Electrosynthesis to Displace Petrochemical Processes? Science 2019, 364 ( (6438), ). 10.1126/science.aav3506. [DOI] [PubMed] [Google Scholar]
- Whipple D. T.; Kenis P. J. A. Prospects of CO2 Utilization via Direct Heterogeneous Electrochemical Reduction. J. Phys. Chem. Lett. 2010, 1 (24), 3451–3458. 10.1021/jz1012627. [DOI] [Google Scholar]
- Dean J. A.Lange’s Handbook of Chemistry, 15th ed.; Dean J. A., Ed.; McGraw-Hill, 1999. [Google Scholar]
- Tomita Y.; Hori Y. Electrochemical Reduction of Carbon Dioxide at a Platinum Electrode in Acetonitrile-Water Mixtures.. Stud. Surf. Sci. Catal. 1998, 114, 581–584. 10.1016/S0167-2991(98)80826-4. [DOI] [Google Scholar]
- Ikeda S.; Takagi T.; Ito K. Selective Formation of Formic Acid, Oxalic Acid, and Carbon Monoxide by Electrochemical Reduction of Carbon Dioxide. Bull. Chem. Soc. Jpn. 1987, 60, 2517–2522. 10.1246/bcsj.60.2517. [DOI] [Google Scholar]
- König M.; Vaes J.; Klemm E.; Pant D. Solvents and Supporting Electrolytes in the Electrocatalytic Reduction of CO2.. iScience 2019, 19, 135–160. 10.1016/j.isci.2019.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Resasco J.; Chen L. D.; Clark E.; Tsai C.; Hahn C.; Jaramillo T. F.; Chan K.; Bell A. T. Promoter Effects of Alkali Metal Cations on the Electrochemical Reduction of Carbon Dioxide. J. Am. Chem. Soc. 2017, 139 (32), 11277–11287. 10.1021/jacs.7b06765. [DOI] [PubMed] [Google Scholar]
- Murata A.; Hori Y. Product Selectivity Affected by Cationic Species in Electrochemical Reduction of CO2 and CO at a Cu Electrode. Bull. Chem. Soc. Jpn. 1991, 64, 123–127. 10.1246/bcsj.64.123. [DOI] [Google Scholar]
- Thorson M. R.; Siil K. I.; Kenis P. J. A. Effect of Cations on the Electrochemical Conversion of CO 2 to CO. J. Electrochem. Soc. 2013, 160 (1), F69–F74. 10.1149/2.052301jes. [DOI] [Google Scholar]
- Singh M. R.; Kwon Y.; Lum Y.; Ager J. W.; Bell A. T. Hydrolysis of Electrolyte Cations Enhances the Electrochemical Reduction of CO2 over Ag and Cu. J. Am. Chem. Soc. 2016, 138 (39), 13006–13012. 10.1021/jacs.6b07612. [DOI] [PubMed] [Google Scholar]
- Cheng T.; Fortunelli A.; Goddard W. A. Reaction Intermediates during Operando Electrocatalysis Identified from Full Solvent Quantum Mechanics Molecular Dynamics. Proc. Natl. Acad. Sci. U. S. A. 2019, 116 (16), 7718–7722. 10.1073/pnas.1821709116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma M.; Liu K.; Shen J.; Kas R.; Smith W. A. In Situ Fabrication and Reactivation of Highly Selective and Stable Ag Catalysts for Electrochemical CO2 Conversion. ACS Energy Letters 2018, 3 (6), 1301–1306. 10.1021/acsenergylett.8b00472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schreier M.; Yoon Y.; Jackson M. N.; Surendranath Y. Competition between H and CO for Active Sites Governs Copper-Mediated Electrosynthesis of Hydrocarbon Fuels. Angewandte Chemie - International Edition 2018, 57 (32), 10221–10225. 10.1002/anie.201806051. [DOI] [PubMed] [Google Scholar]
- Gennaro A.; Isse A. A.; Severin M. G.; Vianello E.; Bhugun I.; Savéant J. M. Mechanism of the Electrochemical Reduction of Carbon Dioxide at Inert Electrodes in Media of Low Proton Availability. Journal of the Chemical Society - Faraday Transactions 1996, 92 (20), 3963–3968. 10.1039/FT9969203963. [DOI] [Google Scholar]
- Ludwig T.; Singh A. R.; Nørskov J. K. Acetonitrile Transition Metal Interfaces from First Principles. J. Phys. Chem. Lett. 2020, 11 (22), 9802–9811. 10.1021/acs.jpclett.0c02692. [DOI] [PubMed] [Google Scholar]
- Cao L.; Raciti D.; Li C.; Livi K. J. T.; Rottmann P. F.; Hemker K. J.; Mueller T.; Wang C. Mechanistic Insights for Low-Overpotential Electroreduction of CO2 to CO on Copper Nanowires. ACS Catal. 2017, 7 (12), 8578–8587. 10.1021/acscatal.7b03107. [DOI] [Google Scholar]
- Kyriacou D.; Jahngen E. G. E. An Electrogenerative Acidobasic Cell Utilizing Biomass for the Generation of Electricity and Molecular Hydrogen. J. Appl. Electrochem. 1993, 23 (11), 1196–1198. 10.1007/BF00625595. [DOI] [Google Scholar]
- Moura de Salles Pupo M.; Kortlever R. Electrolyte Effects on the Electrochemical Reduction of CO 2. ChemPhysChem 2019, 20 (22), 2926–2935. 10.1002/cphc.201900680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim H.-Y.; Choi I.; Ahn S. H.; Hwang S. J.; Yoo S. J.; Han J.; Kim J.; Park H.; Jang J. H.; Kim S.-K. Analysis on the Effect of Operating Conditions on Electrochemical Conversion of Carbon Dioxide to Formic Acid. Int. J. Hydrogen Energy 2014, 39 (29), 16506–16512. 10.1016/j.ijhydene.2014.03.145. [DOI] [Google Scholar]
- Ringe S.; Clark E. L.; Resasco J.; Walton A.; Seger B.; Bell A. T.; Chan K. Understanding Cation Effects in Electrochemical CO 2 Reduction. Energy Environ. Sci. 2019, 12 (10), 3001–3014. 10.1039/C9EE01341E. [DOI] [Google Scholar]
- Gunathunge C. M.; Ovalle V. J.; Waegele M. M. Probing Promoting Effects of Alkali Cations on the Reduction of CO at the Aqueous Electrolyte/Copper Interface. Phys. Chem. Chem. Phys. 2017, 19 (44), 30166–30172. 10.1039/C7CP06087D. [DOI] [PubMed] [Google Scholar]
- Verma S.; Lu X.; Ma S.; Masel R. I.; Kenis P. J. A. The Effect of Electrolyte Composition on the Electroreduction of CO 2 to CO on Ag Based Gas Diffusion Electrodes. Phys. Chem. Chem. Phys. 2016, 18 (10), 7075–7084. 10.1039/C5CP05665A. [DOI] [PubMed] [Google Scholar]
- Berto T. C.; Zhang L.; Hamers R. J.; Berry J. F. Electrolyte Dependence of CO2 Electroreduction: Tetraalkylammonium Ions Are Not Electrocatalysts. ACS Catal. 2015, 5 (2), 703–707. 10.1021/cs501641z. [DOI] [Google Scholar]
- Shin S.-J.; Choi H.; Ringe S.; Won D. H.; Choi C. H.; Kim H.. Alkali Cation Effect on CO2 Electroreduction to CO: A Local Colligative Property. ChemRxiv 2021, 10.26434/chemrxiv-2021-x0msb-v2 [DOI] [Google Scholar]
- Monteiro M. C. O.; Dattila F.; Hagedoorn B.; García-Muelas R.; López N.; Koper M. T. M. Absence of CO2 Electroreduction on Copper, Gold and Silver Electrodes without Metal Cations in Solution. Nature Catalysis 2021, 4 (8), 654–662. 10.1038/s41929-021-00655-5. [DOI] [Google Scholar]
- Gomes R. J.; Birch C.; Cencer M. M.; Li C.; Son S.; Bloom D.; Assary R. S.; Amanchukwu C. V.. Probing Electrolyte Influence on CO 2 Reduction in Aprotic Solvents. ChemRxiv 2021, 10.26434/chemrxiv-2021-17zmv. 10.26434/chemrxiv-2021-17zmv [DOI] [Google Scholar]
- Xie Z.; Zhang X.; Zhang Z.; Zhou Z. Metal-CO2 Batteries on the Road: CO2 from Contamination Gas to Energy Source. Adv. Mater. 2017, 29 (15), 1605891. 10.1002/adma.201605891. [DOI] [PubMed] [Google Scholar]
- Lamy E.; Nadjo L.; Saveant J. M. Standard Potential and Kinetic Parameters of the Electrochemical Reduction of Carbon Dioxide in Dimethylformamide. Journal of Electroanalytical Chemistry and Interfacial Electrochemistry 1977, 78 (2), 403–407. 10.1016/S0022-0728(77)80143-5. [DOI] [Google Scholar]
- Zhao Z.; Wang E.; Wang J.; Liu C.; Peng Z. Kinetics of the CO 2 Reduction Reaction in Aprotic Li-CO 2 Batteries: A Model Study. Journal of Materials Chemistry A 2021, 9 (6), 3290–3296. 10.1039/D0TA11281J. [DOI] [Google Scholar]
- Wuttig A.; Yaguchi M.; Motobayashi K.; Osawa M.; Surendranath Y. Inhibited Proton Transfer Enhances Au-Catalyzed CO2-to-Fuels Selectivity. Proc. Natl. Acad. Sci. U. S. A. 2016, 113 (32), E4585–E4593. 10.1073/pnas.1602984113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verma S.; Hamasaki Y.; Kim C.; Huang W.; Lu S.; Jhong H. R. M.; Gewirth A. A.; Fujigaya T.; Nakashima N.; Kenis P. J. A. Insights into the Low Overpotential Electroreduction of CO2 to CO on a Supported Gold Catalyst in an Alkaline Flow Electrolyzer. ACS Energy Letters 2018, 3 (1), 193–198. 10.1021/acsenergylett.7b01096. [DOI] [Google Scholar]
- Dunwell M.; Luc W.; Yan Y.; Jiao F.; Xu B. Understanding Surface-Mediated Electrochemical Reactions: CO2 Reduction and Beyond. ACS Catal. 2018, 8 (9), 8121–8129. 10.1021/acscatal.8b02181. [DOI] [Google Scholar]
- Zhang B. A.; Ozel T.; Elias J. S.; Costentin C.; Nocera D. G. Interplay of Homogeneous Reactions, Mass Transport, and Kinetics in Determining Selectivity of the Reduction of CO2 on Gold Electrodes. ACS Central Science 2019, 5 (6), 1097–1105. 10.1021/acscentsci.9b00302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amatore C.; Savéant J. M. Mechanism and Kinetic Characteristics of the Electrochemical Reduction of Carbon Dioxide in Media of Low Proton Availability. J. Am. Chem. Soc. 1981, 103 (17), 5021–5023. 10.1021/ja00407a008. [DOI] [Google Scholar]
- Vardar G.; Smith J. G.; Thompson T.; Inagaki K.; Naruse J.; Hiramatsu H.; Sleightholme A. E. S.; Sakamoto J.; Siegel D. J.; Monroe C. W. Mg/O2 Battery Based on the Magnesium-Aluminum Chloride Complex (MACC) Electrolyte. Chem. Mater. 2016, 28 (21), 7629–7637. 10.1021/acs.chemmater.6b02488. [DOI] [Google Scholar]
- Gutiérrez A.; Atilhan M.; Aparicio S. Molecular Modeling Analysis of CO2 Absorption by Glymes. J. Phys. Chem. B 2018, 122 (6), 1948–1957. 10.1021/acs.jpcb.7b10276. [DOI] [PubMed] [Google Scholar]
- Kohn W.; Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140 (4A), A1133. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
- Hohenberg P.; Kohn W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136 (3B), B864. 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
- Iyengar S. S.; Schlegel H. B.; Millam J. M.; Voth G. A.; Scuseria G. E.; Frisch M. J. Ab Initio Molecular Dynamics: Propagating the Density Matrix with Gaussian Orbitals. II. Generalizations Based on Mass-Weighting, Idempotency, Energy Conservation and Choice of Initial Conditions. J. Chem. Phys. 2001, 115 (22), 10291–10302. 10.1063/1.1416876. [DOI] [Google Scholar]
- Schlegel H. B.; Iyengar S. S.; Li X.; Millam J. M.; Voth G. A.; Scuseria G. E.; Frisch M. J. Ab Initio Molecular Dynamics: Propagating the Density Matrix with Gaussian Orbitals. III. Comparison with Born-Oppenheimer Dynamics. J. Chem. Phys. 2002, 117 (19), 8694–8704. 10.1063/1.1514582. [DOI] [Google Scholar]
- Schlegel H. B.; Millam J. M.; Iyengar S. S.; Voth G. A.; Daniels A. D.; Scuseria G. E.; Frisch M. J. Ab Initio Molecular Dynamics: Propagating the Density Matrix with Gaussian Orbitals. J. Chem. Phys. 2001, 114 (22), 9758–9763. 10.1063/1.1372182. [DOI] [Google Scholar]
- McDonnell M.; Laforge A. C.; Reino-González J.; Disla M.; Kling N. G.; Mishra D.; Obaid R.; Sundberg M.; Svoboda V.; Díaz-Tendero S.; Martín F.; Berrah N. Ultrafast Laser-Induced Isomerization Dynamics in Acetonitrile. J. Phys. Chem. Lett. 2020, 11 (16), 6724–6729. 10.1021/acs.jpclett.0c01344. [DOI] [PubMed] [Google Scholar]
- Barreiro-Lage D.; Bolognesi P.; Chiarinelli J.; Richter R.; Zettergren H.; Stockett M. H.; Carlini L.; Diaz-Tendero S.; Avaldi L. smart Decomposition” of Cyclic Alanine-Alanine Dipeptide by VUV Radiation: A Seed for the Synthesis of Biologically Relevant Species. J. Phys. Chem. Lett. 2021, 12 (30), 7379–7386. 10.1021/acs.jpclett.1c01788. [DOI] [PubMed] [Google Scholar]
- Esteban-Gómez D.; Cassino C.; Botta M.; Platas-Iglesias C. 17O and 1H Relaxometric and DFT Study of Hyperfine Coupling Constants in [Mn(H2O)6]2+. RSC Adv. 2014, 4 (14), 7094–7103. 10.1039/c3ra45721d. [DOI] [Google Scholar]
- Iyengar S. S. Dynamical Effects on Vibrational and Electronic Spectra of Hydroperoxyl Radical Water Clusters. J. Chem. Phys. 2005, 123 (8), 084310. 10.1063/1.2006674. [DOI] [PubMed] [Google Scholar]
- Zhang Y.; Xu Z.; Zhao Y.; Zhang X. Ab Initio Molecular Dynamics Simulation Study of Dissociation Electron Attachment to Lactic Acid and Isomer. Sci. Rep. 2019, 9 (1), 1–11. 10.1038/s41598-019-56019-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chernyshova I. V.; Somasundaran P.; Ponnurangam S. On the Origin of the Elusive First Intermediate of CO2 Electroreduction. Proc. Natl. Acad. Sci. U. S. A. 2018, 115 (40), E9261–E9270. 10.1073/pnas.1802256115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jestilä J. S.; Denton J. K.; Perez E. H.; Khuu T.; Aprà E.; Xantheas S. S.; Johnson M. A.; Uggerud E. Characterization of the Alkali Metal Oxalates (MC2O4-) and Their Formation by CO2 Reduction: Via the Alkali Metal Carbonites (MCO2-). Phys. Chem. Chem. Phys. 2020, 22 (14), 7460–7473. 10.1039/D0CP00547A. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A. V.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams-Young D.; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M. J.; Heyd J. J.; Brothers E. N.; Kudin K. N.; Staroverov V. N.; Keith T. A.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A. P.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.. Gaussian 16, Revision A.03; Gaussian Inc.: Wallingford, CT, 2016. [Google Scholar]
- Chai J. Da; Head-Gordon M. Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10 (44), 6615–6620. 10.1039/b810189b. [DOI] [PubMed] [Google Scholar]
- Petersson G. A.; Bennett A.; Tensfeldt T. G.; Al-Laham M. A.; Shirley W. A.; Mantzaris J. A Complete Basis Set Model Chemistry. I. The Total Energies of Closed-Shell Atoms and Hydrides of the First-Row Elements. J. Chem. Phys. 1988, 89 (4), 2193–2218. 10.1063/1.455064. [DOI] [Google Scholar]
- Martínez L.; Andrade R.; Birgin E. G.; Martínez J. M. PACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations. J. Comput. Chem. 2009, 30 (13), 2157–2164. 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
- Papajak E.; Zheng J.; Xu X.; Leverentz H. R.; Truhlar D. G. Perspectives on Basis Sets Beautiful: Seasonal Plantings of Diffuse Basis Functions. J. Chem. Theory Comput. 2011, 7 (10), 3027–3034. 10.1021/ct200106a. [DOI] [PubMed] [Google Scholar]
- Woon D. E.; Dunning T. H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. V. Core-Valence Basis Sets for Boron through Neon. J. Chem. Phys. 1995, 103 (11), 4572–4585. 10.1063/1.470645. [DOI] [Google Scholar]
- Cossi M.; Rega N.; Scalmani G.; Barone V. Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model. J. Comput. Chem. 2003, 24 (6), 669–681. 10.1002/jcc.10189. [DOI] [PubMed] [Google Scholar]
- Barone V.; Cossi M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102 (11), 1995–2001. 10.1021/jp9716997. [DOI] [Google Scholar]
- Lindgren E. B.; Chan H. K.; Stace A. J.; Besley E. Progress in the Theory of Electrostatic Interactions between Charged Particles. Phys. Chem. Chem. Phys. 2016, 18 (8), 5883–5895. 10.1039/C5CP07709E. [DOI] [PubMed] [Google Scholar]
- Berto T. C.; Zhang L.; Hamers R. J.; Berry J. F. Electrolyte Dependence of CO2 Electroreduction: Tetraalkylammonium Ions Are Not Electrocatalysts. ACS Catal. 2015, 5 (2), 703–707. 10.1021/cs501641z. [DOI] [Google Scholar]
- Shi J.; Shen F. x.; Shi F.; Song N.; Jia Y. J.; Hu Y. Q.; Li Q. Y.; Liu J. x.; Chen T. Y.; Dai Y. N. Electrochemical Reduction of CO2 into CO in Tetrabutylammonium Perchlorate/Propylene Carbonate: Water Effects and Mechanism.. Electrochim. Acta 2017, 240, 114–121. 10.1016/j.electacta.2017.04.065. [DOI] [Google Scholar]
- Ludwig T.; Singh A. R.; Nørskov J. K. Nonaqueous Solvent Adsorption on Transition Metal Surfaces with Density Functional Theory: Interaction OfN,N-Dimethylformamide (DMF), Tetrahydrofuran (THF), and Dimethyl Sulfoxide (DMSO) with Ag, Cu, Pt, Rh, and Re Surfaces. J. Phys. Chem. C 2021, 125 (40), 21943–21957. 10.1021/acs.jpcc.1c05724. [DOI] [Google Scholar]
- Cerõn-Carrasco J. P.; Jacquemin D.; Laurence C.; Planchat A.; Reichardt C.; Sraïdi K. Solvent Polarity Scales: Determination of New ET(30) Values for 84 Organic Solvents. J. Phys. Org. Chem. 2014, 27 (6), 512–518. 10.1002/poc.3293. [DOI] [Google Scholar]
- Monteiro M. C. O.; Dattila F.; Hagedoorn B.; García-Muelas R.; López N.; Koper M. T. M. Absence of CO2 Electroreduction on Copper, Gold and Silver Electrodes without Metal Cations in Solution. Nature Catalysis 2021, 4 (8), 654–662. 10.1038/s41929-021-00655-5. [DOI] [Google Scholar]
- Li G.; Wang B.; Resasco D. E. Water-Mediated Heterogeneously Catalyzed Reactions. ACS Catal. 2020, 10 (2), 1294–1309. 10.1021/acscatal.9b04637. [DOI] [Google Scholar]
- Sato S.; Saita K.; Sekizawa K.; Maeda S.; Morikawa T. Low-Energy Electrocatalytic CO 2 Reduction in Water over Mn-Complex Catalyst Electrode Aided by a Nanocarbon Support and K + Cations. ACS Catal. 2018, 8 (5), 4452–4458. 10.1021/acscatal.8b01068. [DOI] [Google Scholar]
- Mills J. N.; McCrum I. T.; Janik M. J. Alkali Cation Specific Adsorption onto Fcc(111) Transition Metal Electrodes. Phys. Chem. Chem. Phys. 2014, 16 (27), 13699–13707. 10.1039/C4CP00760C. [DOI] [PubMed] [Google Scholar]
- Nie X.; Luo W.; Janik M. J.; Asthagiri A. Reaction Mechanisms of CO2 Electrochemical Reduction on Cu(1 1 1) Determined with Density Functional Theory.. J. Catal. 2014, 312, 108–122. 10.1016/j.jcat.2014.01.013. [DOI] [Google Scholar]
- Ayemoba O.; Cuesta A. Spectroscopic Evidence of Size-Dependent Buffering of Interfacial PH by Cation Hydrolysis during CO2 Electroreduction. ACS Appl. Mater. Interfaces 2017, 9 (33), 27377–27382. 10.1021/acsami.7b07351. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.