A human-specific modifier of cortical connectivity and circuit function

Abstract

The cognitive abilities characterizing humans are thought to emerge from unique features of cortical circuit architecture of the human brain, including increased cortico-cortical connectivity. However, the evolutionary origin of these changes in connectivity and how they impacted cortical circuit function and behavior is currently unknown. The human-specific gene duplication SRGAP2C emerged in the ancestral genome of the Homo lineage prior to the major phase of increase in brain size^1,2. SRGAP2C expression in mouse increases the density of excitatory (E) and inhibitory (I) synapses received by layer 2/3 pyramidal neurons (PNs)^3–5. Here we show that the increased number of E synapses received by layer 2/3 PNs induced by SRGAP2C expression, originates from a specific increase in local and long-range cortico-cortical connections. Mice humanized for SRGAP2C expression in all cortical PNs display a shift in the fraction of layer 2/3 PNs activated by sensory stimulation and an enhanced ability to learn a cortex-dependent sensory discrimination task. Computational modeling revealed that the increased layer 4 to layer 2/3 connectivity induced by SRGAP2C expression explains some of the key changes in sensory coding properties. These results suggest that the emergence of SRGAP2C at the birth of the Homo lineage contributed to the evolution of unique structural and functional features of cortical circuits in the human cortex.

In recent years, a growing number of human-specific genetic modifiers have been identified, such as human-specific gene duplications (HSGDs)^6,7, that could induce human-specific traits of brain development. The first experimental test of this idea came from studies of the HSGD affecting the ancestral gene Slit-Robo GTPase Activating Protein 2A (SRGAP2A). Duplication of SRGAP2A specifically in the human lineage led to the emergence of the human-specific paralog SRGAP2C^3,4. When expressed in mouse cortical pyramidal neurons (PNs) in vivo, SRGAP2C inhibits the functions of its ancestral SRGAP2A, a postsynaptic protein regulating E and I synapse maturation and density in cortical pyramidal neurons. Because of the truncation of the last 49 amino-acid of its F-BAR domain, SRGAP2C is intrinsically unstable but remains able to dimerize with SRGAP2A and thereby reduces SRGAP2A levels through proteasome-dependent degradation^5,8. Expression of human-specific SRGAP2C in mouse layer 2/3 PNs induces changes in synaptic development mimicking those characterizing human cortical PNs. These include strikingly similar increases in the density of both E and I synapses received by layer 2/3 PNs, and neotenic features of E and I synaptic development^3–5. These findings indicate that mouse cortical PNs expressing SRGAP2C receive an increased number of synaptic inputs, similar to what is observed in human PNs^9,10. SRGAP2C may therefore act as a human-specific modifier of cortical connectivity in the human brain.

Here, using a novel humanized mouse model expressing SRGAP2C in all cortical glutamatergic neurons together with quantitative monosynaptic rabies tracing, in vivo 2-photon Ca²⁺ imaging, computational modeling approaches and a new behavioral paradigm, we sought to investigate how humanization of SRGAP2C expression modifies cortical circuit connectivity and function as well as behavioral performance.

Mapping of connectivity in SRGAP2C mice

We developed a novel transgenic mouse line (Rosa26-loxP-STOP-LoxP-SRGAP2C-HA knockin) allowing for spatial and temporal control of SRGAP2C expression in a Cre-dependent manner (Extended Data Figure 1). To determine the origin of increased connectivity received by layer 2/3 PNs upon expression of SRGAP2C, we devised a strategy using sparse in utero cortical electroporation (IUCE) combined with monosynaptic rabies tracing^11,12 (Fig. 1a–b). IUCE experiments were performed with a low amount of plasmid encoding Cre recombinase (see Methods), which led to a sparse expression of SRGAP2C in a small number of layer 2/3 cortical PNs in the primary somatosensory cortex (barrel cortex; S1) that were primed for RABV infection (‘starter’ neurons). Adult mice (>P65) were stereotactically injected with RABV (Fig. 1a). Whole mouse brains were digitally reconstructed and the anatomical position of each traced neuron was mapped onto a reference atlas based on the Allen Institute Common Coordinate Framework¹³ (Fig. 1c–e, Extended Data Fig. 2a and Supplementary Video 1).

Figure. 1. Sparse monosynaptic tracing in layer 2/3 PNs humanized for SRGAP2C expression.

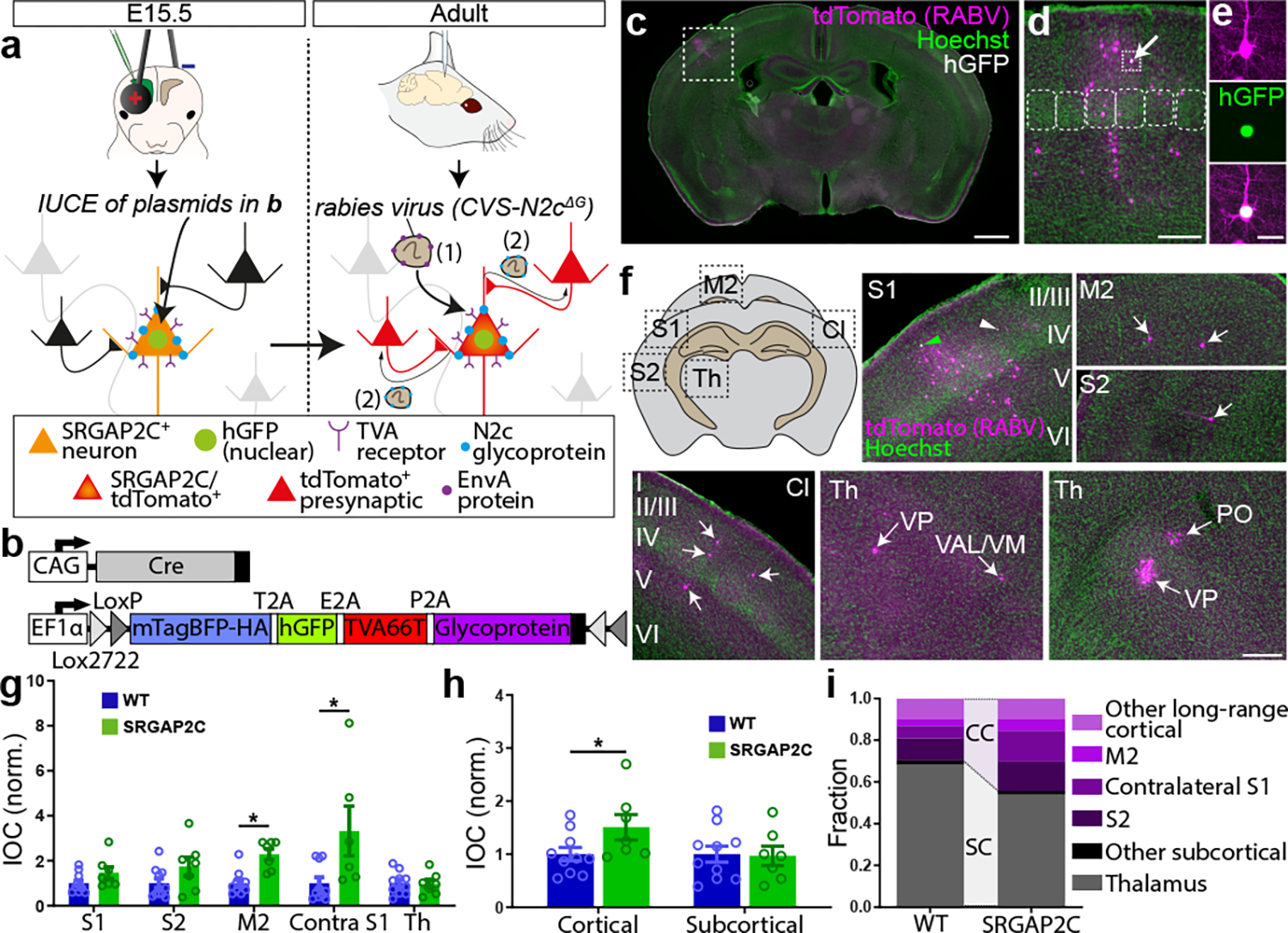
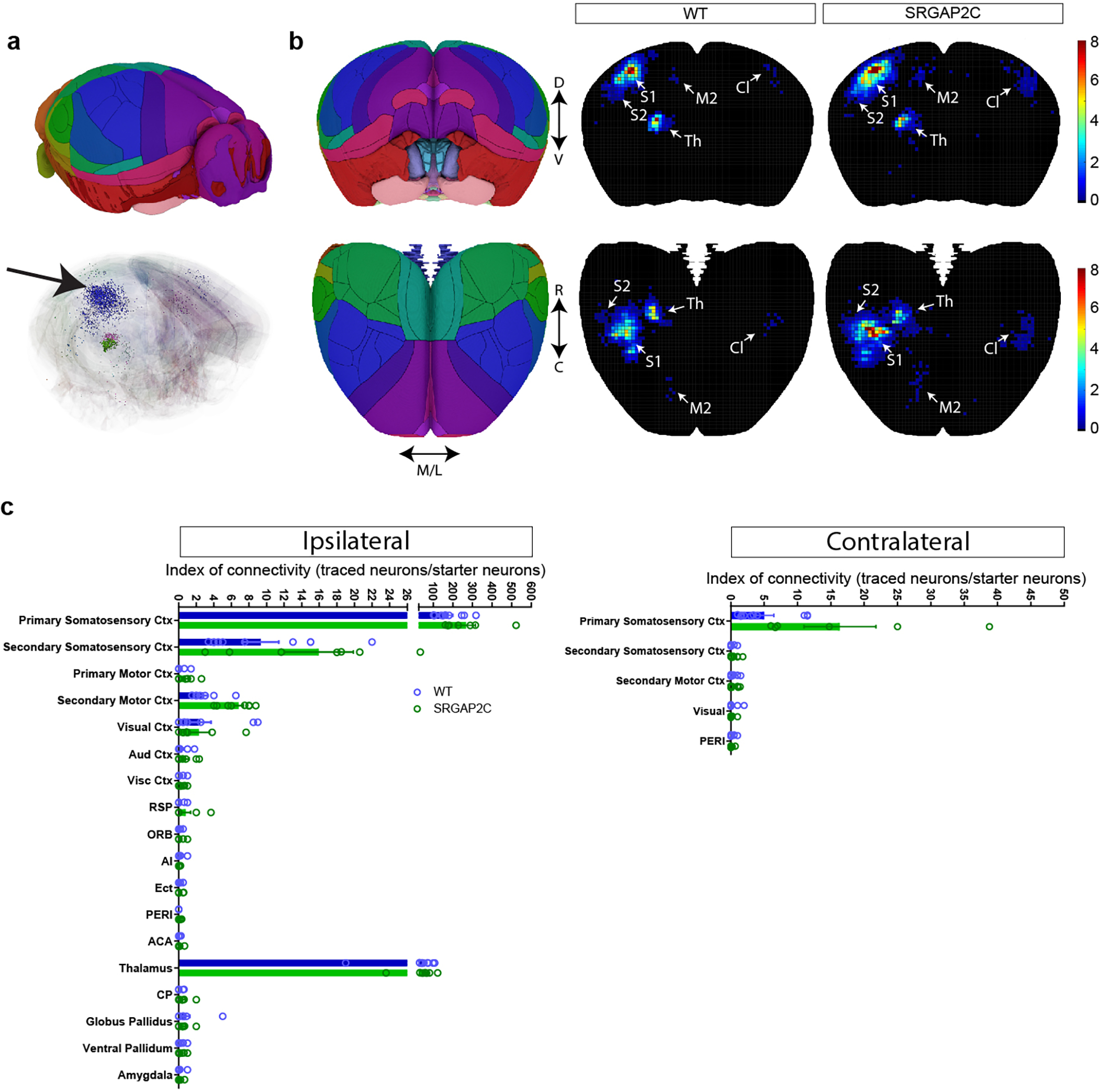
(a) The BHTG construct (see b), together with Cre recombinase, is targeted to layer 2/3 cortical PNs in S1 by in utero electroporation (IUCE) at E15.5. Stereotactic injection of RABV in adult mice leads to infection of starter neurons (1), after which it spreads to presynaptically connected neurons (2). (b) BHTG and Cre constructs. (c) Coronal section stained for Hoechst (green) showing location of a starter neuron (dashed white box) in the barrel field of the primary sensory cortex (S1). Scale bar, 1 mm. (d) Higher magnification of dashed white box area in (c). Starter neuron indicated by white arrow. Rounded boxes indicate barrels in layer 4. Scale bar, 200 μm. (e) High magnification of starter neuron. Scale bar, 25 μm. (f) Anatomical location of RABV traced neurons. Green arrowhead in S1 indicates RABV infected starter neuron. White arrowheads mark non-infected, electroporated neurons. White arrows mark RABV traced neurons. Roman numbers identify cortical layers. Scale bar, 250 μm. (g) Index of connectivity (IOC) for brain regions in (f), relative to control. P = 2.54 × 10⁻² for M2 and P = 1.56 × 10⁻² for contralateral S1. *P < 0.05, Kruskal-Wallis test. (h) IOC relative to control for cortical and subcortical inputs. P = 3.33 × 10⁻² for cortical and P = 0.98 for subcortical. Bar graphs plotted as mean ± s.e.m. Open circles in bar graphs indicate individual mice (n = 10 for WT and n = 7 for SRGAP2C mice), *P < 0.05, two-sided Mann-Whitney test. (i) Fraction of inputs for all RABV traced long-range inputs.

A large fraction of the traced neurons was found surrounding the starter neuron in ipsilateral S1 (Fig. 1f, and Extended Data Fig. 2b–c, n = 10 for WT littermate controls and n = 7 for SRGAP2C mice). We consistently observed traced neurons in the secondary motor cortex (M2), secondary somatosensory cortex (S2), and S1 cortex contralateral to the starter neurons. We also traced presynaptic neurons from subcortical regions located almost exclusively in thalamic nuclei, such as the ventral-anterior lateral/medial (VAL/VM), ventral posterior (VP) and posterior (PO) nuclei (Fig. 1f–g and Extended Data Fig. 3a). Together, these five brain regions (ipsilateral S1, S2, M2, contralateral S1 cortex, and ipsilateral thalamus) contained over 95% (95.8% ± 1.5% for WT, 96.3% ± 1% for SRGAP2C, mean ± s.e.m.) of traced neurons.

Increased connectivity in SRGAP2C mice

We next quantified the number of inputs received by WT or SRGAP2C-expressing layer 2/3 cortical PNs by calculating the Index of Connectivity (IOC), i.e. the number of traced neurons normalized by the number of starter neurons. Long-range cortico-cortical feedback projections were significantly increased in SRGAP2C mice without a corresponding change in subcortical inputs (Fig. 1g–i). Connectivity originating in M2 was increased equally for both supra- and infragranular layers, maintaining the relative proportion between supra- and infragranular inputs (Fig. 2a and Extended Data Fig. 3b). In contrast, inputs from contralateral S1 onto SRGAP2C-expressing layer 2/3 PNs were more balanced between supra- and infragranular layers compared to WT neurons (Fig. 2b and Extended Data Fig. 3c). For S2 we found a significant increase for inputs originating in layer 4 (Fig. 2c and Extended Data Fig. 3d), a projection that has recently been described as a non-canonical cortical feedback pathway between S2 and S1¹⁴. Increased connectivity was not caused by differences in cortical depth or number of starter neurons between the two genotypes (Extended Data Fig. 4).

Figure. 2. SRGAP2C expression increases cortical inputs onto layer 2/3 PNs.

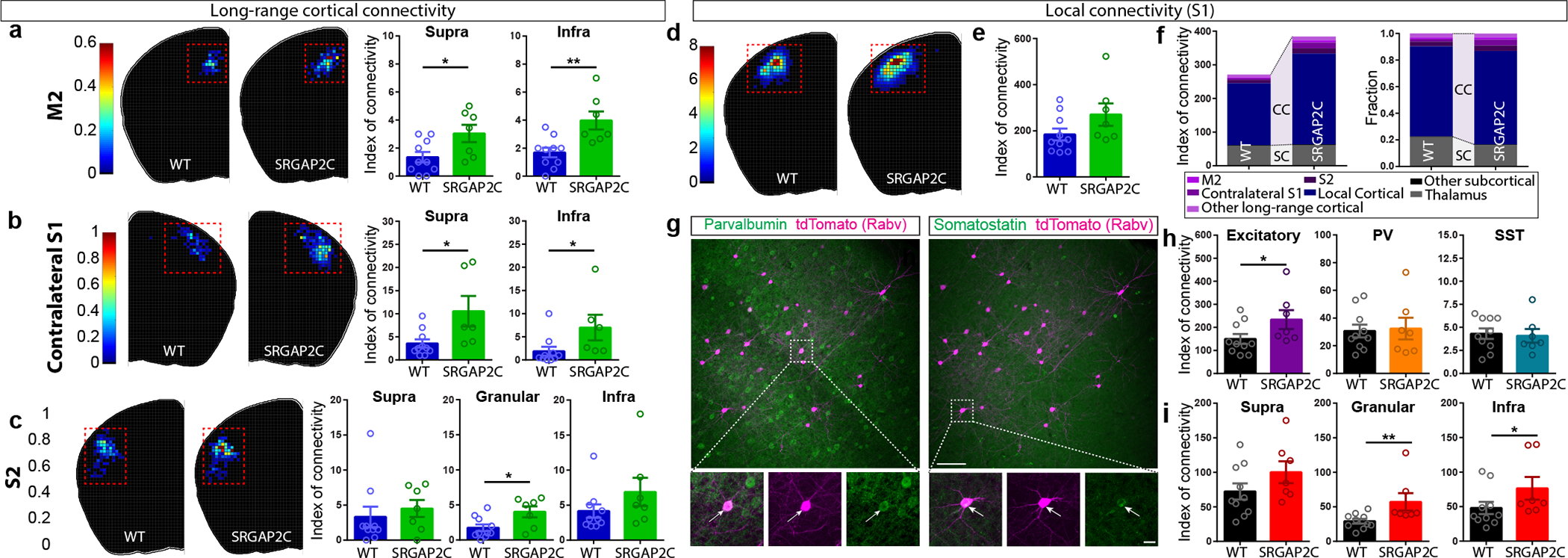
(a-c) Index of connectivity (IOC) for M2, contralateral S1, and S2. Left: distribution of traced neurons. Colors in density plot indicate IOC. Right: IOC. M2: P = 2.99 × 10⁻² for supragranular and P = 4.1 × 10⁻³ for infragranular; Contralateral S1: P = 1.77 × 10⁻² for supragranular and P = 1.39 × 10⁻² for infragranular; S2: P = 2.63 × 10⁻² for granular; two-sided Mann-Whitney test. (d) Distribution of locally traced neurons in S1, colors indicate IOC. (e) IOC for S1. P = 0.109, two-sided Mann-Whitney test. (f) IOC (left) and fraction (right) for all RABV traced inputs, including local cortical inputs originating in S1. (g) Double immunohistochemistry of the same RABV traced brain section for PV (top) and SST (bottom). Bottom panels represent higher magnification of area indicated by dashed boxes. Scale bar large panel, 200 μm. Scale bar small panel, 20 μm. (h) IOC for excitatory, PV-positive, and SST-positive RABV traced neurons in S1. P = 3.3 × 10⁻² for excitatory, two-sided Mann-Whitney test. (i) IOC for excitatory neurons in supragranular, granular, and infragranular layers of S1. P = 6.8 × 10⁻³ and P = 4.31 × 10⁻² for excitatory neurons in the granular and infragranular layer, respectively. Bar graph plotted as mean ± s.e.m. Open circles in bar graphs indicate individual mice (n = 10 for WT and n = 7 for SRGAP2C mice), *P < 0.05, **P < 0.01, two-sided Mann-Whitney test.

Focusing on local connectivity within S1, we noticed a trend toward an increased IOC in SRGAP2C mice compared to WT mice (Fig. 2d–e). Local inputs onto layer 2/3 PNs consist of excitatory inputs from other PNs and inhibitory inputs from interneurons, the majority (~80%) of which expresses either parvalbumin (PV; fast-spiking large Basket cells) or somatostatin (SST; dendrite-targeting interneurons). We performed post hoc immunofluorescent staining for PV and SST and quantified IOC for these two subtypes (Fig. 2g–h). Since PV and SST expressing interneurons provide the majority of inhibitory inputs onto layer 2/3 PNs, we classified RABV traced cells negative for these markers as excitatory¹⁵. Based on previous work, layer 1 neurons were classified as inhibitory irrespective of whether they were positive for PV or SST¹⁶. No differences were observed for the IOC or distribution of inhibitory interneurons (Fig. 2h and Extended Data Fig. 5e–h). In contrast, the fraction of RABV-traced excitatory neurons from granular (L4) and infragranular layers (L5/6) was significantly increased for SRGAP2C-expressing layer 2/3 PNs (Fig. 2h–i and Extended Data Fig. 5b–d). The spatial distribution of locally traced neurons was not changed, indicating that the increased inputs received by SRGAP2C-expressing layer 2/3 PNs originated from the same local cluster of neurons (Extended Data Fig. 5a–b). Together, these results show that SRGAP2C expression specifically increases the number of local excitatory feedforward (in particular increased layer 4 to layer 2/3 connections) and long-range feedback inputs received by layer 2/3 PNs.

This selective increase in cortico-cortical feedforward and feedback connectivity may arise from changes in synaptic density localized to specific dendritic domains. Our previous work focused on the analysis of apical oblique dendrites, but did not examine whether SRGAP2C expression affects synaptic development in other dendritic compartments^3,4. Using our newly developed SRGAP2C mouse line, we found that spine density was increased in the apical oblique and distal tuft segment of adult SRGAP2C-expressing neurons compared to WT, but we observed no increase for basal dendrites (Extended Data Fig. 6a–c). Spine size was similar between WT and SRGAP2C animals, suggesting that E synapses reached maturation in SRGAP2C-expressing neurons after P65 (Extended Data Fig. 6d) as previously reported^3,4.

Response reliability in SRGAP2C mice

Selectively increasing cortico-cortical connectivity may modify how layer 2/3 PNs process sensory information. To test this, we performed in vivo 2-photon Ca²⁺ imaging in SRGAP2C mice crossed with Thy1-GCaMP6f¹⁷ and Nex^Cre mice and WT littermate controls (n = 4 WT and n = 3 SRGAP2C mice). This approach enabled us to image neuronal activity in layer 2/3 PNs (n = 962 neurons for WT and n = 618 for SRGAP2C) while ensuring that all imaged PNs express SRGAP2C¹⁸. We confirmed that this approach leads to an increase in synaptic density in distal and oblique dendritic domains of layer 2/3 cortical PNs, similar to sparse manipulation of layer 2/3 PNs (Extended Data Fig. 6 and Extended Data Fig. 7a).

Whisker stimulation was performed on awake mice for 5 seconds per trial and repeated 24 times separated by 25 seconds inter-trial interval (Fig. 3a–c and Extended Data Fig. 7b). Neuronal responses were either time-locked to the onset of the stimulus (ON), occurred during progression of the stimulus, time-locked to the offset of the stimulus (OFF), or were negative (Extended Data Fig. 7d). Transients that were not time-locked to the onset or offset of the stimulus but occurred during the 5-second stimulus window (referred to as Sustained responses) had overall longer response durations compared to ON or OFF responses (Extended Data Fig. 7e).

Figure. 3. SRGAP2C increases probability and selectivity of neuronal responses to sensory stimulation.

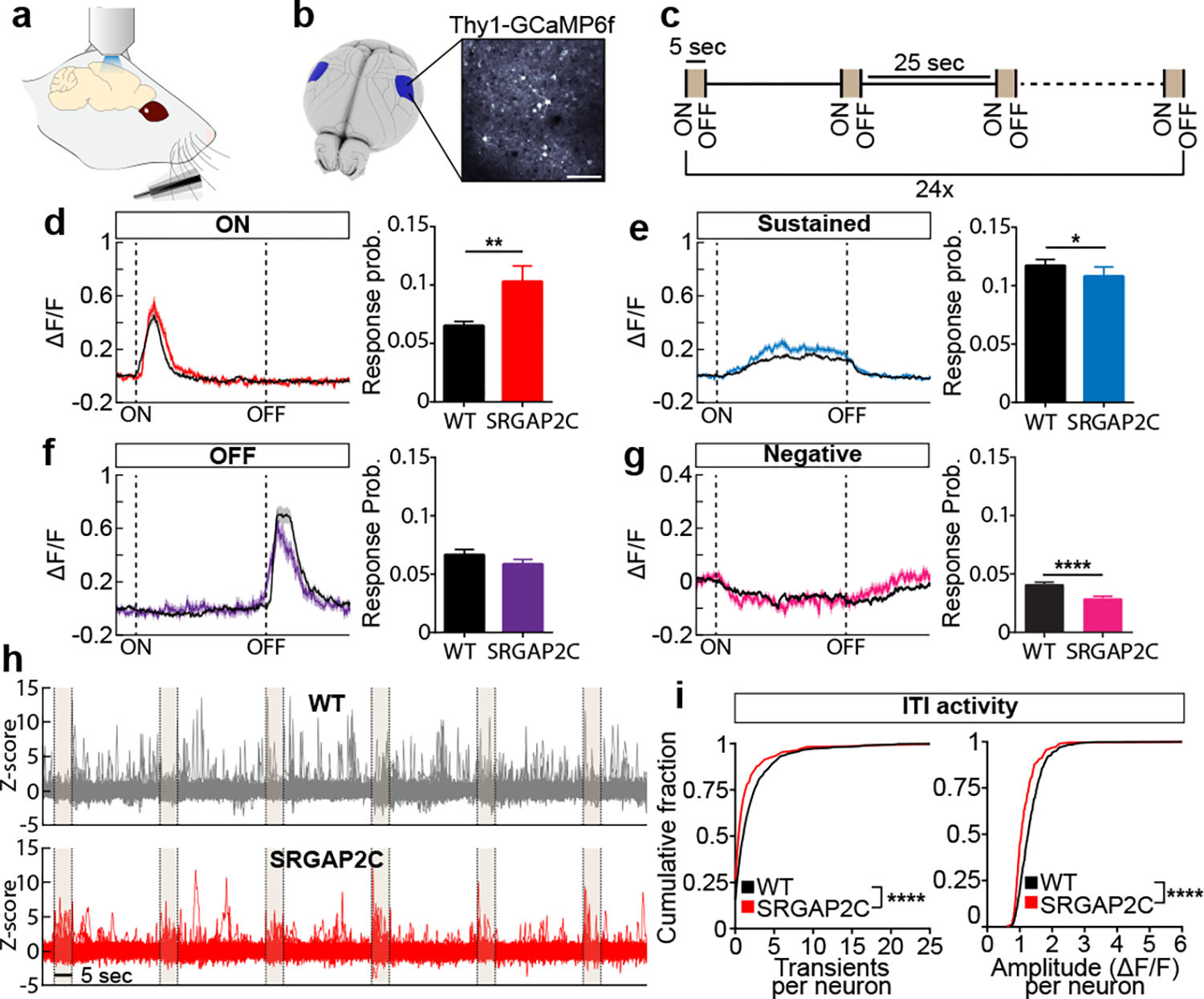
(a-c) Schema of experimental approach. (d-g) Left panels: average calcium traces (ΔF/F) for indicated response types. Shaded area indicates s.e.m. Right panels: response probability expressed as fraction of stimuli leading to a response. P = 6.4 × 10⁻³ for ON, P = 4.31 × 10⁻² for Sustained, and P = 3.21 × 10⁻¹ for OFF. Bar graph plotted as mean ± s.e.m. *P < 0.05, **P < 0.01, ****P < 0.0001, two-sided Mann-Whitney test. (h) 150 randomly chosen Z-scored example traces showing activity during six consecutive stimuli (shaded) and corresponding ITIs. (i) Cumulative probability distribution of Ca²⁺ transient number and amplitude during intertrial interval (ITI). ****P < 0.0001, Kolmogorov-Smirnov test (n = 580 neurons for WT and n = 277 neurons for SRGAP2C).

We measured the response probability for each neuron by calculating the fraction of trials that led to a response (ON, Sustained, or OFF), excluding neurons for which no responses were observed for any trials. Overall sensory-evoked response probabilities were low with a long-tail distribution in WT layer 2/3 PNs (Extended Data Fig. 7c). In contrast, SRGAP2C expressing neurons displayed a significantly higher response probability specifically for ON responses, with a small but significant reduction in response probability for Sustained responses (Fig. 3d–f). While the overall probability of negative responses was low, the probability of these responses was decreased for SRGAP2C neurons (Fig. 3g). In addition, the duration of Sustained responses was significantly longer in SRGAP2C mice (Extended Data Fig. 7e–g). During the ITI, neuronal activity was reduced in SRGAP2C neurons for both the number of transients and transient amplitude (Fig. 3h–i, P < 1 × 10⁻⁴, Kolmogorov-Smirnov test), which was not explained by differences in behavioral activity, such as whisking or grooming (Extended Data Fig. 7h–i). Together with a higher response probability for the onset of the stimulus, this led to activity patterns that were more restricted to sensory stimulus epochs, resulting in an increase in response selectivity of SRGAP2C expressing layer 2/3 PNs (Fig. 3h).

Increased probability and selectivity of sensory-evoked neuronal responses suggests that SRGAP2C-expressing neurons encode sensory inputs more reliably. To determine this, we trained a linear support vector machine (SVM) to classify for each time point whether the stimulus was ON or OFF. Accuracy of the classifier was significantly higher when using responses from SRGAP2C neurons, with a significant increase in predicting stimulus onset as well more accurately predicting continuation of the stimulus until stimulus offset (Extended Data Fig. 7j–k). Together, these results show that SRGAP2C expression in layer 2/3 PNs improves the accuracy of sensory coding by increasing response reliability and selectivity to whisker inputs.

An important feature underlying increased response probability is an increase in the ratio between evoked and spontaneous activity (Fig. 3d–i). To further investigate this, we analyzed neuronal response properties by computing stimulus-triggered average fluorescence responses (Extended Data Fig. 8a–b and Extended Data Fig. 9a). We found that the fraction of neurons with positive evoked responses was larger in SRGAP2C mice (196 out of 581 or 33.7% of layer 2/3 PNs increased their activity following whisker stimulation in SRGAP2C mice compared to 222 out of 960 cells or 23.1% in WT mice). On the other hand, only 14.5% showed a significant decreased evoked response in SRGAP2C mice following whisker stimulation compared to 27.7% in WT (P < 0.05, Two-sample t-test). Changes in GCaMP6f fluorescence following sensory stimulation could reflect either actual changes in spiking frequency or changes in sub-threshold events reflecting depolarization or hyperpolarization at the soma level¹⁹. To more accurately estimate if the change in GCaMP6f fluorescence leads to changes in evoked spiking frequency, we applied spike deconvolution on GCaMP6f traces with sufficient signal-to-noise ratio. We again observed a significantly larger fraction of neurons with positive responses to whisker stimuli in the SRGAP2C mice (40 out of 72, or 55.6%, of cells had a significant decrease in response, while 20.8% had a significant increase in response, P < 0.05, Two-sample t-test) compared to WT mice (Extended Data Fig. 8b, 129 out of 377, or 34.2%, of cells had a significant decrease in responses, while 8.8% had a significant increase in response, P < 0.05, Two-sample t-test). This difference was robust to selecting different thresholds of signal-to-noise ratio for cell selection (Extended Data Fig. 9b). Together, this analysis revealed that SRGAP2C expression in PNs significantly modifies the neural population response dynamics by increasing the ratio between evoked responses and spontaneous activity (Extended Data Fig. 8c).

To test the hypothesis that increased cortico-cortical connectivity is sufficient to drive some of the changes in sensory-evoked response properties, we used a computational modeling approach. We focused on the impact of increased connectivity between layer 4 and layer 2/3 PNs because of the well-documented effect this feedforward connection has on driving layer 2/3 PNs responses to whisker stimulation²⁰. We developed a computational model of the layer 2/3 local network with input from layer 4 (Extended Data Fig. 8d). The model considered only the total number of connections and was agnostic on whether the increase in connections originated from an increased number of presynaptic neurons or from an increased number of connections per connected pair. In a broad parameter regime, an increase in strength of these two connections (thicker black lines in SRGAP2C of Extended Data Fig. 8d) led to an increase in layer 2/3 PNs mean spiking activity for any input strength, by a factor that increased with increasing input strength (Extended Data Fig. 8e–f and h). Accordingly, the ratio of evoked to spontaneous excitatory mean activity increased monotonically with an increase in the strength of the two connections (Extended Data Fig. 8g). Thus, in the model as in the data, spontaneous and sensory evoked mean activity, as well as the ratio of evoked to spontaneous mean activity, all increase in SRGAP2C mice. Parameter sets that reproduced these effects had excitatory-to-excitatory connections as the weakest and inhibitory-to-inhibitory connections as the strongest among the four sets of connections strengths.

We also modelled the distribution of activity across the excitatory neuronal population. In the model (Extended Data Fig. 8i), as in the data (Extended Data Fig. 8c), both WT and SRGAP2C layer 2/3 PNs populations included neurons that increased and neurons that decreased their activity in response to a stimulus (stimulation of layer 4 activity), relative to spontaneous activity, and SRGAP2C mice had a higher fraction of neurons increasing their activity in response to activation of layer 4 (stimulus). We also found that the standard deviation of the response distribution increased with the strength of the stimulus and the strength of the connections (Extended Data Fig. 8j and Extended Data Fig. 9d–f), consistent with the data (Extended Data Fig. 9c). This effect depended on variability both in the recurrent weights and in the presynaptic inputs from layer 4. Our model demonstrates that the observed increase of excitatory layer 4 to layer 2/3 PNs connections is sufficient to account for some of the key observed changes in response properties in layer 2/3 PNs in SRGAP2C mice relative to WT mice.

Sensory discrimination in SRGAP2C mice

To test if increased feedforward and feedback cortico-cortical connectivity together with improved sensory coding accuracy in SRGAP2C mice affects behavioral performance, we tested the ability of WT littermate control and Nex^Cre-SRGAP2C mice to learn a whisker-based texture discrimination task previously shown to rely on cortical processing^21–23. We trained mice in a two-alternative forced choice (2AFC) task to discriminate two different rough textures (Fig. 4a–b, and Supplementary Video 2), which is a more difficult task than smooth versus rough texture discrimination²³. Performance was whisker-dependent and improved over sessions (50 days) for both WT and SRGAP2C mice (Fig. 4c and Extended Data Fig. 10a–b, n = 20 mice for WT and n = 18 for SRGAP2C mice, pooled from two independent cohorts).

Figure. 4. Humanized SRGAP2C mice display increased ability to learn a texture discrimination task.

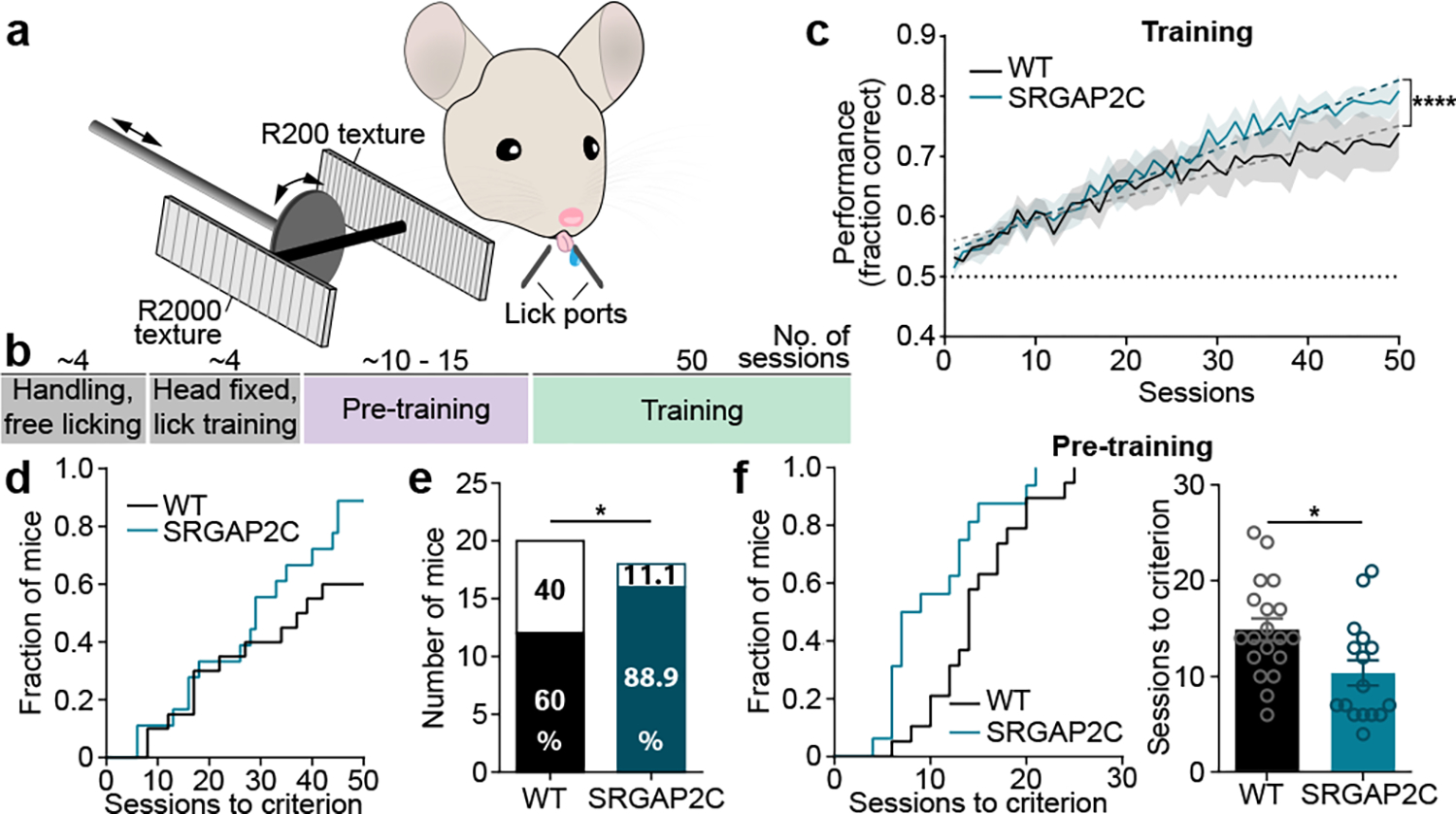
(a-b) Schematic of whisker-based texture discrimination task. Distance between laser cut grooves for R200 and R2000 textures is 200 and 2000 μm, respectively. Scale bar, 100 μm. (c) Behavioral performance shown as fraction of correct trials over sessions of training (1 session / day). Shaded area indicates s.e.m. Linear regression indicated by dashed lines. Dotted horizontal line indicates chance level performance (50% correct). Linear regression, slope WT = 0.0039, slope SRGAP2C = 0.0057. ****P < 0.0001, linear regression F-test. (d) Cumulative histogram for number of sessions to learning criterion (75% correct). (e) Number of learners (mice that reached 75% correct responses) and non-learners (mice that never reached 75% correct responses). Numbers in bar graphs indicate percentage of total number of mice tested. P = 0.043, Chi-Square test. (f) Left: cumulative histogram for number of sessions to learning criterion during pre-training (75% correct responses). Right: number of sessions to reach criterion. P=0.0135, two-sided Mann-Whitney test. Bar graphs plotted as mean ± s.e.m. Open circles in bar graphs indicate individual mice (n = 19 for WT and n = 16 for SRGAP2C mice), *P < 0.05.

As a group, SRGAP2C-expressing mice displayed an increased learning rate, which was evident from a difference in slope of the performance curve (Fig. 4c). Due to the difficulty of the task, each group consisted of learners (>75% correct) and non-learners (Fig. 4d). SRGAP2C mice were more likely to learn the task than WT mice (Fig. 4e), an effect that was consistent for both independently tested cohorts (Cohort 1 learners: 62.5% for WT and 88.9% for SRGAP2C. Cohort 2 learners: 58.3% for WT and 90.9% for SRGAP2C). These results were neither explained by a difference in the number of sessions or trials the mice performed during the training stage, nor by a difference in number of sessions or trials run for pre-training (Extended Data Fig. 10c). We also observed no difference in overall water intake, suggesting no increased motivation due to potential higher thirst levels (Extended Data Fig. 10d).

We wondered whether improved learning performance of SRGAP2C mice was due to an enhanced ability to perceive texture differences. To assess this, we analyzed lick responses of naïve and expert learners (Extended Data Fig. 10e–i). Naïve mice extensively licked even before the texture was within reach of the whiskers (sampling window, see Extended Data Fig. 10e). In contrast, expert mice restricted their licking to the sampling window. While we observed no difference between naïve WT and SRGAP2C mice, we found that expert SRGAP2C mice increased their lick frequency earlier in the sampling window (Extended Data Fig. 10g–h). This earlier lick response corresponded with a trend for SRGAP2C mice to respond with higher accuracy earlier in the sampling window (Extended Data Fig. 10i). To further investigate this, we analyzed behavioral performance during the pre-training phase. Here, mice are required to alternate their lick responses between left and right while they are presented with the corresponding texture. During this ‘forced-alternation’ phase, mice can learn the rule of the task independent of texture information, i.e. even without presentation of the textures, the mice can learn the alternation rule by keeping track of which side the reward was presented on the previous trial. However, given that the textures provide a clue about which side the reward will be located, the textures themselves provide additional context for mice to learn the rule of the task during the pre-training period. Interestingly, SRGAP2C mice required significantly fewer sessions than WT mice to reach criterion during pre-training (Fig. 4f).

DISCUSSION

The results presented in this study demonstrate that expression of the human-specific gene duplication SRGAP2C in cortical PNs alters cortical circuit connectivity by increasing the number of local and long-range cortical inputs received by layer 2/3 PNs, increases the probability of sensory-evoked responses by layer 2/3 PNs, and enhances sensory learning in a cortex-dependent texture discrimination task.

To perform this texture discrimination task correctly, mice must learn to (1) discriminate two textures using their whiskers and (2) to learn an abstract association between each texture and the correct lick port for reward. Strikingly, only 60% of wild-type mice learned this task after 50 training sessions, illustrating that this behavior is cognitively demanding for wild-type mice. Increased cortico-cortical connectivity and increased reliability of sensory coding may offer one potential explanation for this improvement in behavioral performance, but several other possible contributing factors could participate. These include more synchronous dendritic and/or somatic inhibition recently shown to shape response selectivity in multiple circuits^24,25. Furthermore, how local and long-range cortical projections work together to facilitate increased sensory learning remains to be determined. One possibility is that increased local connectivity from layer 4 enhances sensory coding in S1, as our modeling data suggests. This may allow for more reliable detection of subtle differences between textures. In turn, increased long-range cortico-cortical connectivity, facilitating more effective communication between cortical regions such as M2 and S1, could subsequently propagate this more reliable signal to other cortical regions for a more effective association of the texture with appropriate behavioral output.

In summary, we propose that our results identify a new substrate for human brain evolution: the emergence of SRGAP2C approximately 2–3 million years ago at the birth of the Homo lineage, but before the main phase of brain volume increase¹, led to increased cortico-cortical connectivity, enhanced sensory coding by layer 2/3 PNs and improved behavioral performance required to solve complex cognitive tasks involving associative learning.

METHODS

Mice

All animals were handled according to protocols approved by the institutional animal care and use committee (IACUC) at Columbia University, New York. All mice used in experiments were adults (>P65), heterozygous for indicated transgenes, and were maintained on a 12h light/dark cycle at 20 to 22 °C and humidity between 30 to 70%. Nex^Cre (NeuroD6^tm1(cre)Kan) mice¹⁸ were obtained through Jax and induce recombination in dorsal telencephalic-derived postmitotic neurons giving rise to all pyramidal neurons throughout the cortex, hippocampus and amygdala but not in astrocytes, interneurons or microglial cells in these structures. Thy1-GCaMP6f mice¹⁷ were obtained through Jax (C57BL/6J-Tg(Thy1-GCaMP6f)GP5.17Dkim/J) and stochastically express GCaMP6f in a subset of excitatory pyramidal neurons in various brain regions, including cortex and hippocampus.

Conditional SRGAP2C expressing mice were generated using homologous recombination in C57BL/6J mouse ES cells (see Extended Data Fig. 1 for details) in collaboration with genOway (France). A targeting vector containing a CAG promoter, SRGAP2C-3xHA cDNA, rabbit-globin poly-A, a LoxP-STOP-LoxP and neomycin selection cassette, and homology arms consisting of sequences between exon 1 and exon 2 of the Rosa26 locus was constructed. In addition, Diptheria Toxin A (DTA) cDNA was placed downstream of the 3’ homology arm for negative selection of non-recombined ES cell clones. Southern blot analysis was used to confirm homologous recombination of the targeting vector in ES cell clones. Recombined ES cell clones were injected into C57BL/6J blastocysts and re-implanted into OF1 pseudo-pregnant females to generate chimeric males. Male chimeras were subsequently bred with wild-type C57BL/6J females to generate an F1 population of SRGAP2C mice. Heterozygous mice (Rosa26^SRGAP2C(F/+)) were confirmed carriers of the transgene by genomic PCR and Southern blot analysis (Extended Data Fig. 1). Wild-type and SRGAP2C alleles are identified with PCR of genomic DNA using the following primers: 5’-CAATACCTTTCTGGGAGTTCT-3’ and 5’-CTGCATAAAACCCCAGATGAC-3’ for detection of the WT allele, and 5’-CATGGGGGATATGGCTTCC-3’ and 5’-GGAACATCGTATGGGTAAGCG-3’ for detecting the presence of Rosa26 targeted SRGAP2C. For in utero electroporation experiments, mice were crossed once with the outbred strain 129S2/SvPasCrl mice (obtained from Charles River) to produce F1 hybrids females used to generate timed-pregnant females by crossing with Rosa26^SRGAP2C(F/+) heterozygous males (on pure C57BL/6J). In this study, we will refer to SRGAP2C mice as animals that are heterozygous for the Rosa26^SRGAP2C(F/+) allele.

Western Blot

Cre-dependent expression of SRGAP2C-HA protein was analyzed by crossing SRGAP2C mice with Nex-Cre mice¹⁸ to induce expression of SRGAP2C in all excitatory forebrain neurons. Cortical hemispheres were dissected and homogenized in ice-cold homogenization buffer (N-PER Neuronal Protein Extraction Reagent (ThermoFisher Scientific) with complete Protease Inhibitor Cocktail (Roche), 10 μM MG-132 (Sigma-Aldrich), and Benzonase (EMD Millipore)) using a disposable Biomasher II (Kimble Chase). After homogenization, samples were incubated for 30 min at 4°C in homogenization buffer and subsequently centrifuged at 10,000 g for 30 min in a cooling centrifuge at 4°C. Samples were prepared in Laemmli buffer (Bio-Rad) containing 10% 2-Mercaptoethanol and boiled at 95°C for 5 min. Using SDS-PAGE, proteins were separated and then transferred to a polyvinylidene difluoride (PVDF) membrane (Immobilon-FL, EMD Millipore). Western blotting was performed using anti-HA primary (1:1000, Anti-HA.11 901513, Biolegend) and anti-actin (1:5000, MAB1501, Millipore) together with goat-anti-mouse IgG conjugated to IRDye 800CW (1:10,000, Li-Cor) and goat-anti-mouse IgG conjugated to IRDye 680RD (1:40,000). Imaging of immunoblots was performed on an Odyssey CLx Imaging System (Li-Cor).

DNA constructs

The BHTG construct was generated by subcloning mTagBFP-3xHA, histone-GFP, TVA66T and the N2c glycoprotein together with 2A self-cleaving peptide sequences (see Fig. 1b for details) in between NheI and AscI cloning sites of the pAAV-Ef1a-DIO eNpHR 3.0-EYFP plasmid (Addgene plasmid # 26966) using Gibson assembly cloning. pCAG-Cre was generated in the Polleux lab, as previously described²⁶.

In utero cortical electroporation

In utero cortical electroporation (IUCE) was performed at E15.5 on isoflurane anaesthetized timed-pregnant SRGAP2C or control female mice as previously described²⁷, with the following modifications. Endotoxin-free DNA containing 1μg/μl of BHTG plasmid and 10–20 ng/μl Cre plasmid, 1μg/μl mRuby-Cre plasmid (for Extended Data Fig. 1), or a Flp-dependent version of the BHTG plasmid with 10–20 ng/μl FlpO plasmid (for Extended Data Fig. 7a), was injected into the ventricles of E15.5 embryos using a heat-pulled capillary. Electroporation was performed by applying 5 pulses of 42 V for 50 ms with 500 ms intervals using a 3 mm diameter platinum tweezer electrode (Nepa Gene) and a square wave electroporator (ECM 830, BTX). After placing embryos back into the abdominal cavity, the incision was closed using sutures and the mouse allowed to recover on a heating plate.

Virus injection

Adult mice were anaesthetized using isoflurane and placed in a stereotactic frame (Stoelting). A small burr hole was drilled over the barrel field of the primary sensory cortex (1.3 mm posterior and 3 mm lateral to Bregma²⁸) using a high-speed dental drill. A glass pipette (Drummond Scientific) was heat-pulled (Narishige PC-10) to produce a tip of approximately 10 μm in diameter. It was then filled with viral vector solution containing CVS-N2c^Δg [EnvA] RABV-tdTomato and lowered into the brain to a depth of 200–300 μm. Virus was subsequently injected at bouts of 25 nl at 2 nl/s with a 20s interval until a total volume of 400–500 nl was injected. The glass injection pipette was left for 2 min after the injection was completed after which it was slowly removed. The skin was closed using sutures and the mouse was allowed to recover on a heating plate. Mice were left for 7 days to allow enough time for RABV-tdTomato to reach sufficient levels of expression in both starter neurons and presynaptic inputs.

Sparse monosynaptic rabies tracing and whole brain reconstruction

Tissue preparation

After 7 days of RABV tracing, mice were anaesthetized with isoflurane and intracardiac perfusion was performed using 4% paraformaldehyde (Electron Microscopy Sciences) in PBS. Brains were isolated and incubated overnight in a 4% paraformaldehyde in PBS solution at 4°C. The following day, brains were washed in PBS and sectioned along the coronal plane at 100 μm using a vibrating microtome (Leica VT1200S). Approximately 100 sections were collected spanning the most rostral part of the cortex to the cerebellum. Sections were stained using Hoechst 33258 (Sigma-Aldrich) and subsequently mounted on glass slides in Fluoromount-G aqueous mounting medium (ThermoFisher Scientific).

Image acquisition

Sections were first imaged on a Nikon SMZ18 stereo microscope with automatic stage using a SHR Plan Apo 1X at a zoom magnification of 4x. Stitching was performed directly after imaging using Nikon NIS-Elements software. Sections containing both tdTomato and hGFP positive cells were subsequently imaged by collecting Z-stacks on a Nikon A1 confocal microscope using a 10x Plan Apo NA 0.45 objective (Nikon) for identification of RABV starter neurons, which we identified by co-expression of hGFP and tdTomato. Additional confirmation of starter neurons was done by imaging these neurons again using a 40x Plan Apo NA 0.95 (Nikon) objective.

Section alignment and registration to atlas

Imaged sections were aligned using rigid body alignment in StackReg (ImageJ plugin) and when necessary manual adjustments were made using Adobe Photoshop. Neurons were subsequently counted and annotated using a Cell Counter plugin (Fiji-ImageJ) after which sections and coordinates were imported into 3ds Max (Autodesk). Landmarks were then manually placed at multiple anatomical locations (113 anatomical landmarks) corresponding to landmarks we assigned to a 3D mouse brain atlas imported from the Allen Brain Institute (Common Coordinate Framework 3). Landmarks were placed at anatomical regions easily identified in imaged sections, such as the first section containing hippocampus or the first section where the corpus callosum forms a continuous bundle. In addition, a single landmark indicating the point at which both cortical hemispheres meet was assigned to each section (designated as midline landmark). Using these assigned landmarks, together with custom-written scripts in MAXScript, the 1) section stack was resized to match the reference brain size, 2) based on the midline landmark each section was aligned along the dorsal/ventral axis of the reference brain, and 3) using anatomical landmarks each neuron was assigned to the corresponding location in the reference brain. Finally, in order to assign proper cortical depth to each neuron, the pial surface was traced and reconstructed for each section and the distance to the pial surface for each neuron was measured along the line that intersects the pial surface perpendicularly. Neurons were color coded according to their assigned brain region or their calculated cortical depth to manually confirm proper alignment to the reference brain. Finally, the 3D position and assigned brain region for each neuron was exported for subsequent analysis.

Identification of interneurons

Tissue sections were washed in PBS and subsequently blocked overnight at 4°C in blocking buffer (PBS containing 1% Triton X-100 (Sigma-Aldrich) and 5% goat serum (Gibco)). The following day, sections were washed 3x for 1 h in PBS containing 0.5% Triton-X100. Next, sections were incubated with primary antibody in PBS containing 0.5% Triton-X100 and 0.5% goat serum for 4 days at 4°C. Sections were then washed 3× 1 h in PBS containing 0.5% Triton-X100 after which they were incubated with secondary antibodies conjugated to Alexa Fluor-488, 546, and 647 of appropriate species (1:500, ThermoFisher Scientific). After several washes in PBS sections were mounted on glass slides and mounted in Fluoromount-G. Z-stacks were collected by imaging on a Nikon A1 confocal microscope using a 10x Plan Apo NA 0.45 objective (Nikon) to identify neuronal identity for Rabv-traced neurons. Primary antibodies used were mouse anti-HA (1:1000, Anti-HA.11, Biolegend), rat anti-somatostatin (1:100, MAB354, Millipore), guinea pig anti-parvalbumin (1:200, 195004, Synaptic Systems), and rabbit anti-DsRed (1:500, 632496, Takara Bio).

Data analysis

Index of connectivity (IOC) was calculated for each animal by dividing the number of traced neurons by the number of starter neurons. Average IOC density maps showing the distribution of traced neurons across the brain were generated in MATLAB (Mathworks) by generating IOC density maps per animal and subsequently combining these maps to calculate an average IOC density map per genotype. For density maps showing distribution of neurons relative to their closest starter neuron, we determined, per animal, the closest starter neuron for each traced neuron in the primary sensory cortex (S1). We then calculated the relative medial-lateral and rostro-caudal position of each traced neuron with respect to the closest starter neuron. The majority of traced neurons in S1 form a dense cloud closely around the starter neuron. However, this approach may misclassify which starter neuron belongs to which traced neurons when multiple starter neurons are in close proximity to each other. Differences in the distance between starter neurons in a single brain for WT and SRGAP2C mice could therefore obscure a potential change in the distribution of traced neurons between WT and SRGAP2C mice. We therefore analyzed the minimum distance between starter neurons for brains with more than 1 starter neurons. We found no difference in the distribution of starter neurons between WT and SRGAP2C mice (distance from starter neuron to nearest other starter neuron: 300.4 μm ± 55.92 for WT and 357.1 μm ± 74.19 for SRGAP2C, mean ± sem). Furthermore, when we analyzed brains with only 1 starter neuron (n = 3 for WT and n = 2 SRGAP2C) we similarly did not observe a difference in the spatial distribution of traced neurons (data not shown).

Dendritic spine analysis

Dendritic spine quantification.

Tissue sections were washed in PBS and subsequently blocked for 3 h at room temperature in blocking buffer (PBS containing 0.2% Triton X-100 (Sigma-Aldrich) and 5% goat serum (Gibco)). Next, sections were incubated with primary antibody in PBS containing 0.2% Triton-X100 and 5% goat serum overnight at 4°C. The next day, sections were washed 3x for 30 min in PBS containing 0.2% Triton-X100. Sections were then incubated for 1 h with secondary antibodies conjugated to Alex Fluor-546 or 647 of appropriate species (1:500, ThermoFisher Scientific). After several washes in PBS sections were mounted on glass slides using Fluoromount-G. Imaging of dendritic spines was performed using a Nikon A1 confocal microscope. First, low magnification Z-stack images were collected using a 20x Plan Apo NA 0.75 objective (Nikon) to visualize the entire dendritic tree of optically isolated neurons. Next, appropriate terminal branches were selected for distal, apical oblique, and basal dendritic segments, for which we collected Z-stack images using a 100x H-TIRF, NA 1.49 objective (Nikon).

Data analysis

Nikon NIS-Elements was used to generate a z-stack maximum intensity projection of selected dendritic branches. We then quantified spine density and head size by tracing the dendritic segment to measure the dendritic length and drawing ROIs around the spine head as visualized by the mTagBFP-HA filler signal.

Two-photon calcium imaging

Surgery and image acquisition

Adult mice were anaesthetized using isoflurane and injected with buprenorphine (0.1 mg/kg body weight), after which the dorsal skull was exposed and cleaned with a razor blade. A craniotomy was performed, and a glass window was placed over the barrel field of the primary sensory cortex. The window was glued in place using cyanoacrylate glue, after which a custom head plate was secured onto the skull using both cyanoacrylate glue and dental acrylic cement. Mice were allowed to recover for a minimum of 7 days, after which imaging in awake mice (n = 4 WT and n = 3 SRGAP2C) was conducted on a Bergamo II two-photon microscope (Thorlabs) running ThorImage LS and Thorsync, using a 16× 0.8 NA objective (Nikon) and 920-nm wavelength Ti-Sapphire laser (Coherent). Imaging was performed 150 – 250 μm below the pial surface at 30 Hz and 512 × 512 pixels covering 830 μm × 830 μm. For whisker stimulation trials a transparent acrylic rod was placed next to the right whisker pad at a fixed distance of 2 mm. Every stimulus trial consisted of a 10 second pre-stimulus, 5 second stimulus, and 15 second post-stimulus period. Six trials were grouped into a single run, separated by 25 second intertrial interval, and 4 runs were performed per session (total 24 stimuli). Whisker stimuli were applied by vibrating the bar at 25Hz, a speed of more than 100 mm/s, and an amplitude of over 1 mm. To identify the responding region in the barrel field of primary sensory cortex contralateral to the stimulated whisker pad, we first performed a wide-field imaging experiment in which the entire region under the cranial window was imaged during multiple stimulus trials. The hemodynamic component was calculated and the neural signal was isolated, as previously described²⁹. Subsequent two-photon imaging was performed on 2 to 3 non-overlapping fields of view per mouse within the center of the activated area. Activity of the animal during imaging was monitored using an infrared camera.

Image processing and analysis

Non-rigid motion correction of acquired images was performed using NoRMCorre, as previously described³⁰. Regions of interest (ROIs) were manually drawn over soma of individual neurons. All subsequent analyses were done using custom-written MATLAB code, which is available upon request. Time-courses were calculated as the mean of all pixels within the ROI. Neuropil signal was estimated by dilating neuronal ROIs by 4 pixels to form a ring-shaped neuropil ROI around the soma of each neuron. To remove neuropil contamination, we subtracted the ΔF/F neuropil signal from the ΔF/F neuronal signal. To avoid subtraction of signal not considered neuropil contamination, we excluded pixels in the neuropil ROI that contained transients exceeding two times the standard deviation of the difference between the neuropil and neuronal signals, as previously described³¹. To identify the response type per stimulus for each neuron, we aligned all time-courses to their respective stimulus onset and performed K-means clustering with 60 clusters and correlation as the distance metric. Common time-courses were identified by running K-means 200 times with random initialization. The resulting outputs of the repeated K-means were clustered a final time to obtain a set of representative responses. Clusters with responses where the onset time was time-locked with the start or end of the whisker stimulus were determined to be an on- or off-type response, respectively. Those occurring during the duration of stimulus were grouped as Sustained-type responses. Neuronal responses were subsequently assigned to a cluster by evaluating the Pearson’s correlation between the time-course and each basis time-course. The highest correlation value greater than 0.4 was determined to be the representative time-course. Duration of Sustained responses were calculated as the time where z-scored time-courses were greater than 1. To characterize activity during the inter-trial interval (ITI), transients were identified by finding the local maxima during ITI periods. Peaks were constrained to having widths of at least two frames, a minimum ΔF/F of 0.5, and a relative increase in ΔF/F of 6 times the standard deviation compared to the preceding local minimum. A frame-to-frame sliding window correlation analysis of webcam images was done to determine periods and duration of active behavior, such as whisking or grooming.

Support vector machine classification

Time courses for all neurons were z-scored, after which for each field of view (FOV) a random number of 10 neurons were selected to train a linear support vector machine (SVM) to classify between the presence (ON) and absence (OFF) of a whisker stimulus. For each FOV, the SVM was performed 50 times, each time with a new randomly selected group of 10 neurons. Each iteration was performed with 5-fold cross validation using 80% of time points for training and the remaining 20% for testing. Accuracy was calculated as the average across all 50 iterations. We repeated this procedure by progressively increasing the number of neurons per FOV used for the SVM by 5. In order to calculate accuracy of the SVM across time, we calculated the average accuracy for each time point across all 24 stimuli. This generated an average accuracy value for each time point of the time course. We grouped these results for WT and SRGAP2C FOVs to generate an average accuracy across genotypes and normalized the results to the maximum (set to 1) and minimum (set to 0) values. All SVM analyses were performed using custom written MATLAB code (Mathworks).

Stimulus triggered responses

To compute the stimulus-triggered response of each neuron, we first subtracted the raw neuropil signal F_n from the raw ROI signal F_r using a neuropil factor of α = 0.7, consistently with an earlier study on Thy1-GCaMP6 mice¹⁷, such that the signal considered was F_s = F_r − αF_n. Then we computed ΔF/F₀ by estimating F₀ as the lower 5^th percentile of the whole trace F_s and then computing $\frac{\Delta F}{F_0}=\frac{F_s-F_0}{F_0}$. For every stimulus repetition, we considered a period starting from 5 s before the stimulus onset and ending 15 s after the stimulus offset for a total period of 25 s, with a stimulus duration of 5 s. We then averaged the corresponding fluorescence traces across all repetitions to obtain a stimulus triggered fluorescence average for each neuron. For visualization purposes in Extended Data Fig. 8a, we first z-scored the traces and then subtracted the average z-score activity during the 5 s prior to the stimulus. We performed a paired t-test between the average activity during 5 s prior to the stimulus and 5 s of stimulation and so obtained a p-value p_i for each neuron. We then sorted the neurons according to their p-values p_i and the sign of their responses (depending on whether the activity increased or decreased from spontaneous to evoked) such that neurons at the top (resp. bottom) of the colormap corresponded to those with the more robust increase (resp. decrease) of activity.

We performed spike deconvolution using the method MLspike³². We used as a calcium indicator time constant τ = 0.167 s which was consistent with the one reported for GCaMP6f¹⁷. We noticed that the spike deconvolution was suboptimal for very noisy traces. We used as a proxy for high-signal-to noise ratio the skewness of the trace, since a trace with strong relative noise will have a distribution of ΔF/F₀ close to gaussian and therefore a skewness close to 0. We selected neurons with a skewness equal to or above 1.5 for most of the analyses. We checked the robustness of our results and found that evoked activity was much larger than spontaneous activity in SRGAP2C relatively to WT for the whole range of skewness threshold considered (Extended Data Fig. 8d).

Modelling neural responses

We implemented a recurrent circuit model with a population of excitatory cells and a population of inhibitory cells representing neurons in L2/3, following the dynamical equations below (see supplementary material):

$$\tau \frac{d\mathit{e}}{dt}=-\mathit{e}+{⌊W_{ee}\mathit{e}-\xi W_{ei}\mathit{i}+\xi {\omega }_{eh}\mathit{h}+b_{e}1⌋}_{+}^2$$

$$\tau \frac{d\mathit{i}}{di}=-\mathit{i}+{⌊W_{ie}\mathit{e}-W_{ii}\mathit{i}+{\omega }_{ih}\mathit{h}+b_{i}1⌋}_{+}^2$$

Here, the vectors e and i correspond to the neural activity of excitatory and inhibitory neurons, respectively, while the vector h represents the activity of input neurons from L4; ${⌊x⌋}_{+}^2$ represents a rectified quadratic function applied to the scalar x; W_αβ is the matrix of recurrent connections from population β to population α with α,β∈{e,i}; the scalars ω_αh represent the strength of feedforward connections from L4 to population α; τ is the membrane time constant; and ξ is the factor giving the increase in connection strengths in the SRGAP2C mouse (ξ = 1.8 in 2C, ξ = 1.0 in WT). The vector 1 is the vector whose elements are all 1, and the scalars b_e and b_i are the strengths of background (stimulus-independent) inputs. The elements of the matrices W_αβ are randomly drawn and i.i.d., with mean $〈W_{\alpha \beta }〉={\omega }_{\alpha \beta }/n_{\beta }$ and $Var\left[W_{\alpha \beta }\right]={\sigma }_{\alpha \beta }^2/n_{\beta }$, where n_β is the number of presynaptic connections from population β. The scalars ω_αh represent the feedforward connection strengths from the L4 excitatory neurons to the L2/3 population α. The elements of the vector h are randomly drawn with mean $〈h_j〉={\mu }_h$ and $Var\left[h_j\right]={\varsigma }_h^2$. The various parameters are fit as described below. We selected a quadratic input/output function because power laws phenomenologically describe neurons in mouse V1^33–35 and because our previous work has demonstrated that neurons with such i/o functions capture many properties of cortical circuits^36,37. Note that a rectified quadratic power law was able to capture the distribution of firing rates across different conditions, while this would not have been possible with a linear transfer function which could only generate gaussian distributions (see discussion in Supplementary material).

We optimized the parameters ω_αβ,σ_αβ,ω_αh,μ_h(stimulus= spont.), μ_h(stimulus = evoked) ς_hb_α following a two-step procedure. First, similarly to Keller et al. (2020)³⁸, we optimized the parameters other than σ_αβ and ς_h in a two-unit population model described by the following equations:

$$\tau \frac{d{\mu }_e}{di}=-{\mu }_e+{\lfloor {\omega }_{ee}{\mu }_e-\xi {\omega }_{ei}{\mu }_i+\xi {\omega }_{eh}{\mu }_h+b_e\rfloor }_{+}^2$$

$$\tau \frac{d{\mu }_i}{di}=-{\mu }_i+{\lfloor {\omega }_{ie}{\mu }_e-{\omega }_{ii}{\mu }_i+{\omega }_{ih}{\mu }_h+b_i\rfloor }_{+}^2$$

We independently generated N_p = 1,000,000 different values of ω_αβ and of ω_αh from gamma distributions of mean and standard deviation equal to 2. Similarly, we generated N_p different values of b_α from a gaussian distribution of mean 0 and standard deviation 1. Then, we generated μ_h(spon.) and μ_h(evoked) from two gamma distributions of mean 0.5 and 1 for spontaneous and evoked activity respectively. If for a set of parameters μ_h(s = spon.) > μ_h(s = evoked), we switched the two. We fixed τ = 10 ms and evolved the dynamical equations using an Euler scheme. Finally, when the system converged to a stable fixed point, we compared the rates to the data by minimizing

$$Err={\sum }_{\xi \in \mathrm{1,1.8}}{\sum }_{s\in spon.,evoked}{\left[{\mu }_e^{model}(\xi ,s)-{\mu }_e^{data}(\xi ,s)\right]}^2+{\lambda }_1{\sum }_{\alpha \gamma }{\omega }_{\alpha \gamma }^2+{\lambda }_2{\sum }_{\alpha \gamma }{⌊-\log {\omega }_{\alpha \gamma }⌋}_{+}$$

where γ represent either one of the two layer 2/3 populations e and i or the layer 4 input h and with λ₁ = 0.1 and λ₂ = 5 · 10⁻⁵, which ensured the weights were neither too close to 0 nor too large³⁸. We selected the 20 parameter sets with the minimum value of Err after removing solutions not satisfying:

$$y:=\frac{{\mu }_e^{model}(\xi =2c,s=ev.)}{{\mu }_e^{model}(\xi =2c,s=sp.)}/\frac{{\mu }_e^{model}(\xi =wt,s=ev.)}{{\mu }_e^{model}(\xi =wt,s=sp.)}>1$$

In these top 20 solutions, the excitatory-to-excitatory connections were typically weak, and they were the weakest of the recurrent connections (16 out of 20 solutions). On the other hand, inhibitory-to-inhibitory connections were typically the strongest of the recurrent connections (14 out of the 20 solutions). Although not all solutions satisfy y>1, we find that the more closely the generated parameter sets match the activity of WT mice, the higher the proportion of solutions satisfying y>1. To demonstrate this, we generated 10,000,000 parameter sets as before and discarded all unstable solutions (44.6%). Among the stable solutions, we considered the solutions with error on the WT activity below a given threshold and varied the threshold (so that the lower the threshold, the fewer the number of solutions considered). We observe that the lower the error threshold (the more closely the solutions matched WT activity), the more solutions satisfied y>1 (Extended Data Fig. 8h). In particular, when considering the 2,000 solutions that best fit the WT data, 78.8% satisfied y>1.In the second step we tested 15 different values of noise in the recurrent connection strengths σ_αβ ∈ [0,7ω_αβ] (including the factor ξ, when appropriate) and 11 different values of noise in the inputs ς_h ∈ [0,0.035] with a grid search using, for the other parameters, the 20 top solutions generated from the first step. Among the resulting solutions, we selected the one which was most robust in reproducing the data in terms of variation of σ_αβ and ς_h, as follows. We selected the one for which (1) the Wasserstein distance between the probability distribution of responses (evoked – spontaneous activity) in the model and in the data (summed over WT and SRGAP2C mice) was smaller than 1.5 and (2) the difference between responses (evoked – spontaneous activity) was on average the closest to the data for the largest range of σ_αβ and ς_h: defining Δμ = μ_e(stimulus = spont.) − μ_e(stimulus = evoked), we chose the solution that satisfied (1) and satisfied $\left|\left({\mathrm{\Delta }\mu }_{2c}^{model}-{\mathrm{\Delta }\mu }_{wt}^{model}\right)-\left({\mathrm{\Delta }\mu }_{2c}^{data}-{\mathrm{\Delta }\mu }_{wt}^{data}\right)\right|/std\left(\left\{{\mathrm{\Delta }\mu }_{2c}^{data},{\mathrm{\Delta }\mu }_{wt}^{data}\right\}\right)<0.5$) for the largest number of combinations of σ_αβ and ς_h. We generated the values of W_αβ by sampling over gamma distributions and the values of h by sampling over gaussian distributions. Finally, for the chosen solution, we selected the values of σ_αβ and ς_h that maximized the following function:

$$\left(1-\frac{N_{2c}+N_{wt}}{2}\right)+{\lambda }_3\left(\frac{N_{2c}-N_{wt}}{2}\right)$$

with λ₃ = 10, where N_wt and N_2c are the fraction of neurons increasing their responses from spontaneous to evoked activity in the WT or SRGAP2C mice, respectively. This ensured that the fraction of neurons increasing their responses, summed over SRGAP2C and WT mice, was as small as possible (because it was difficult in the model to have as many neurons decreasing their response as in the data, so this pushed the model in the direction of having more neurons decreasing their response) and that the difference between the SRGAP2C and WT mice in the number of neurons increasing their responses was as large as possible, with the second weighted 10 times more strongly than the first. For a fixed set of parameters these properties were robust across different initializations of the random weights (see below).

The selected model had the following parameters (approximately): n_γ = 1,000, ω_ee = 0.34, ω_ei = 0.76, ω_ie = 0.39, ω_ii = 4.27, σ_αβ = 0.045 · ω_αβ for the recurrent connections; ω_eh = 0.69, ω_ih = 1.97; μ_h(s = spon.) = 0.50, μ_h(s = evoked) = 0.81, ς_h = 0.37; b_e = 0.15, and b_i = − 0.34. We ran 100 simulations with different random seeds and N_2c was larger than N_wt in all of them. The network would reproduce qualitatively the effects described in the main text for a reasonable range of parameters, for example when varying σ_αβ and ς_h while fixing all other parameters. Simulations were performed with Python, Matplotlib, NumPy, SciPy, and sklearn.

Texture-discrimination task

Surgeries

Adult mice were anaesthetized using isoflurane and injected with meloxicam, after which the dorsal skull was exposed and cleaned with a scalpel. A custom-designed steel head plate (Wilke Enginuity) was subsequently secured onto the skull using Metabond (Parkell).

Behavior setup

The behavioral apparatus was contained within a black box (Foremost) with a light-blocking door. A stepper motor (Pololu) rotated custom-designed textures in position after which they were advanced into the final stimulus position within approximately 1 cm of the right whisker pad of the mouse using a linear actuator (Actuonix L12-30-50-6-R). Textures were laser cut from acrylic sheets to a dimension of 16 × 33 mm. Vertical grooves of approximately 500 μm deep and 350 μm wide were laser cut into the acrylic textures at a spacing of 200 or 2000 μm apart. These were identified as R200 and R2000, respectively. Rewards (~5 μL of water) were delivered by opening a solenoid valve (The Lee Co. LFAA1209512H) that allowed water to flow from a reservoir to the lick port, which was made of a stainless-steel tube (McMaster). Two lick ports were positioned in front and slightly to the left and right of the mouse’s mouth, and licking was registered using capacitive touch sensors (Sparkfun MPR121). Between trials, a white light (LE LED 1800016-WW-US) was activated to prevent mice from fully dark-adapting. This prevented mice from using visual cues in performing the task. A computer fan (Cooler Master 80 mm Silent Fan) blew air over the texture away from the mouse, preventing the mouse from picking up olfactory cues. In addition, the textures were regularly cleaned with 70% ethanol. We never observed mice exploiting auditory or vibrational cues from the motors and thus no masking noises were necessary.

All aspects of the task were controlled by an Arduino Uno. A desktop PC chose the stimulus and correct response and logged all events read from the Arduino to disk using custom Python code. The training parameters for each mouse were stored in a custom-written Django database and updated manually or semi-manually by the experiments depending on each mouse’s progress.

Mouse training and testing

Experimenters were blind to the genotype of mice during every step of training and testing. Mice were denied water access in the home cage and learned to receive their water during behavioral training. For each mouse we closely monitored water intake, weight, and general health to ensure they did not suffer from dehydration. Ad libitum water was provided as necessary to prevent adverse effects on health. Mouse training was performed according to the following pipeline (also see Fig. 4b). 1) Handling and free licking. During this stage, mice were handled to become familiar with the experimenters. By placing mice in the set up without head-fixing and allowing them to drink freely from the water pipes, they also became familiar with the behavioral set up. This stage required on average 4 sessions. 2) Head-fixed lick training. Mice were head-fixed directly in front of a single lick pipe and received a water reward for every lick. Next, mice were presented with two lick pipes on the left and right side of their mouth and learned to lick alternatively from each of them. This lick training started with mice alternating after every ten licks and was gradually decreased to a single lick on each side. This stage required on average 4 sessions. 3) Pre-training. Here, mice were presented with the complete trial structure for the first time, i.e. textures were presented and mice were only rewarded for correct responses. Incorrect responses were punished with a timeout. Presentation of the same texture was repeated until mice responded correctly, after which the other texture was presented. Thus, mice could perform at 100% by alternating responses from trial to trial. The timeout was initially 2 s and gradually increased to 9 s as mouse performance increased. This stage required between 10 – 15 sessions. 4) Training. Each session began with 45 trials of pre-training (as in step 3) to verify mice were able to lick both lick ports. After these initial pre-training trials, presentation of textures was randomized. The software continuously monitored mouse performance for biases, where mice stopped alternating between lick pipes and focused on one lick pipe only. When a strong bias was detected, presentation of the textures stopped being random and were presented to counteract the bias: if mice responded ≥20% more on one side than the other, the software would deliver only trials opposite to the biased side. If mice showed a significance perseverative bias (P < 0.05, ANOVA), the software would deliver alternating trials. For analysis, non-randomized trials were excluded, and only randomized trials were used to assess performance.

Finally, to assess that mice relied on their whiskers to discriminate between textures, whiskers facing the texture side were fully trimmed. If performance did not fall to chance (<60% correct), mice were excluded from analysis. One mouse was excluded based on this criterion.

Statistics and Reproducibility

Statistical analysis was performed using Prism v6, v8 and v9 (Graphpad Software). Normality was checked using Kolmogorov-Smirnov test. A non-parametric test (Kruskal-Wallis with post-hoc Dunn’s multiple comparison test or Mann-Whitney U test) was used when distribution deviated significantly from normality. A test was considered significant when P < 0.05. For RABV tracing, 10 WT littermate controls and 7 SRGAP2C mice were obtained from a minimum of four independent litters. For in vivo spine analysis, data was obtained from at least six animals from a minimum of three independent litters. For two-photon microscopy experiments, 4 WT littermate controls and 3 SRGAP2C mice were obtained from two independent litters. For the texture-discrimination task, 20 WT littermate controls and 18 SRGAP2C mice were tested across two separate cohorts from a minimum of four independent litters. Significance was tested using a chi-squared test. Independent data points shown denote data from individual animals. Each experiment was repeated at least three times with similar results.

Data availability

The reagents, mouse line, datasets generated and/or analyzed during the current study are available from the corresponding author on request.

Extended Data

Extended Data Figure 1. Generation of an inducible, humanized SRGAP2C transgenic mouse line.

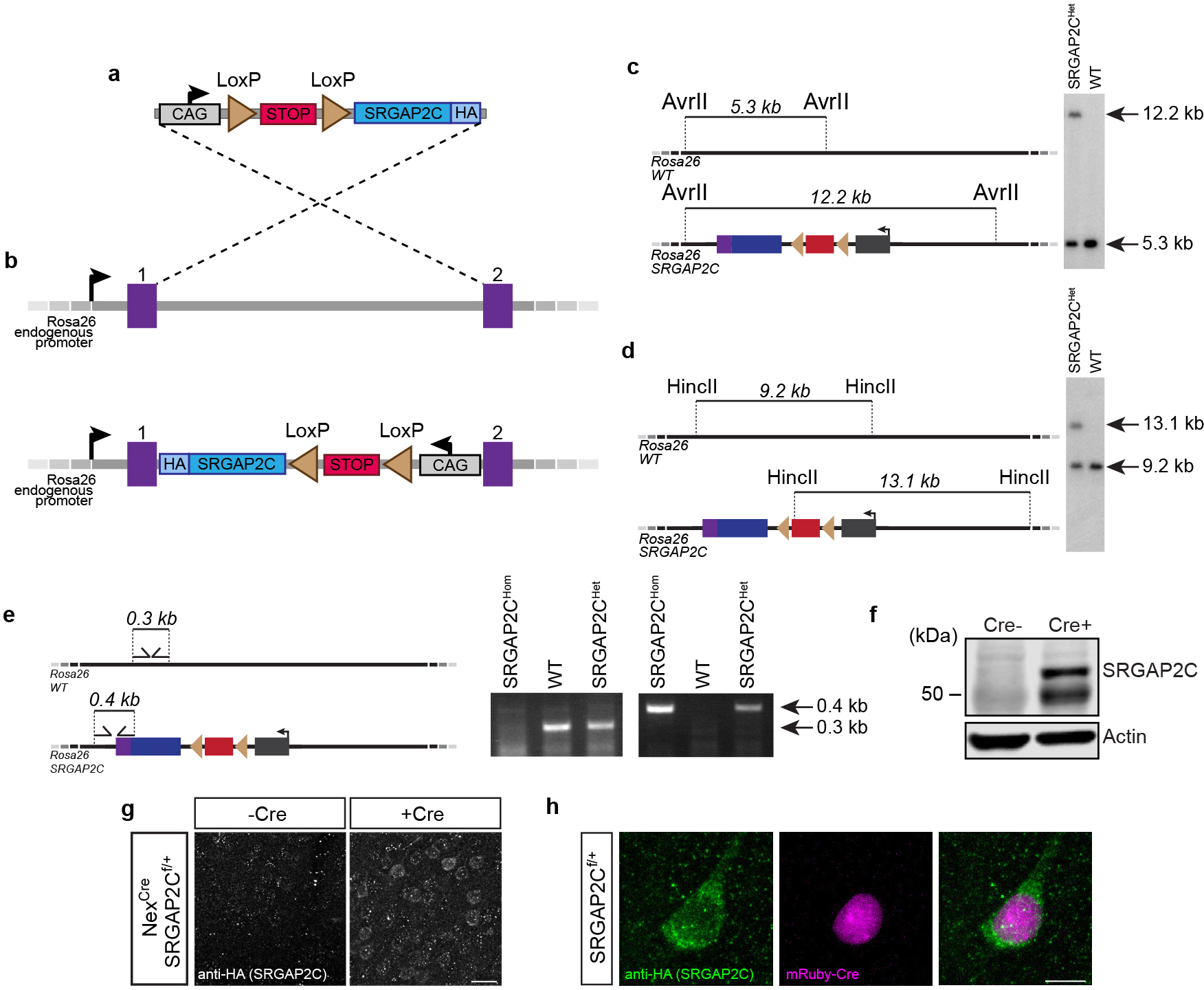
(a-b) Design strategy for generating SRGAP2C conditional knock in mice. 3x HA tagged SRGAP2C was inserted into a Rosa26 targeting vector (a), which contains a CAG promoter, a floxed STOP-Neomycin cassette, and Rosa26 homology arms. Image not to scale. Using homologous recombination, the targeting vector was inserted between exon 1 and 2 of the Rosa26 locus (b). (c-d) Verification of SRGAP2C targeting in mouse embryonic stem cells using Southern blot analysis with probes that distinguish the targeted allele (12.2 kb in (c), 13.1 kb in (d)) from the wild-type allele (5.3 kb in (c), 9.2 kb in (d)). (e) Mice were genotyped by genomic PCR using the forward and reverse primers indicated that distinguish the WT Rosa26 allele or the SRGAP2C allele. (f) Western blot probed with anti-HA antibody of adult (P30) cortex isolated from SRGAP2C heterozygous conditional knock-in mice crossed with heterozygous Nex^Cre/+ mice (Cre+) or wild-type littermate (Cre-). The presence of Cre induces SRGAP2C-HA expression. Without Cre, no SRGAP2C was detected. Anti-Actin antibody was used as loading control. (g) Immunohistochemistry for HA on cortical brain sections from adult SRGAP2C heterozygous conditional knock-in mice crossed with heterozygous Nex^Cre/+ mice (Cre+) or wild-type littermate control (Cre-). Scale bar, 25 μm. (h) Same as g, on sections from SRGAP2C heterozygous conditional knock-in mice in which mRuby-Cre was sparsely expressed using in utero cortical electroporation. Scale bar, 10 μm.

Extended Data Figure 2. Brain regions containing RABV traced neurons.

(a) Reference brain (top) based on Allen Reference Atlas. Digital reconstruction of RABV traced brain and registration onto reference brain. Black arrow indicates location of starter neurons in barrel field of S1. (b) Density plots showing distribution of traced neurons in WT and SRGAP2C mice. Colors in density plot indicate index of connectivity (IOC): number of traced neurons / number of starter neurons). (c) IOC for brain regions ipsilateral and contralateral to the injection site. RSP, retrosplenial area, ORB, Orbital cortex, Ai, Agranular Insular cortex, Ect, Ectorhinal cortex, PERI, Perirhinal cortex, ACA, Anterior Cingulate cortex, CP, Caudate-putamen. Bar graphs plotted as mean ± s.e.m. Open circles in bar graphs indicate individual mice (n = 10 for WT and n = 7 for SRGAP2C mice).

Extended Data Figure 3. Distribution of RABV traced neurons.

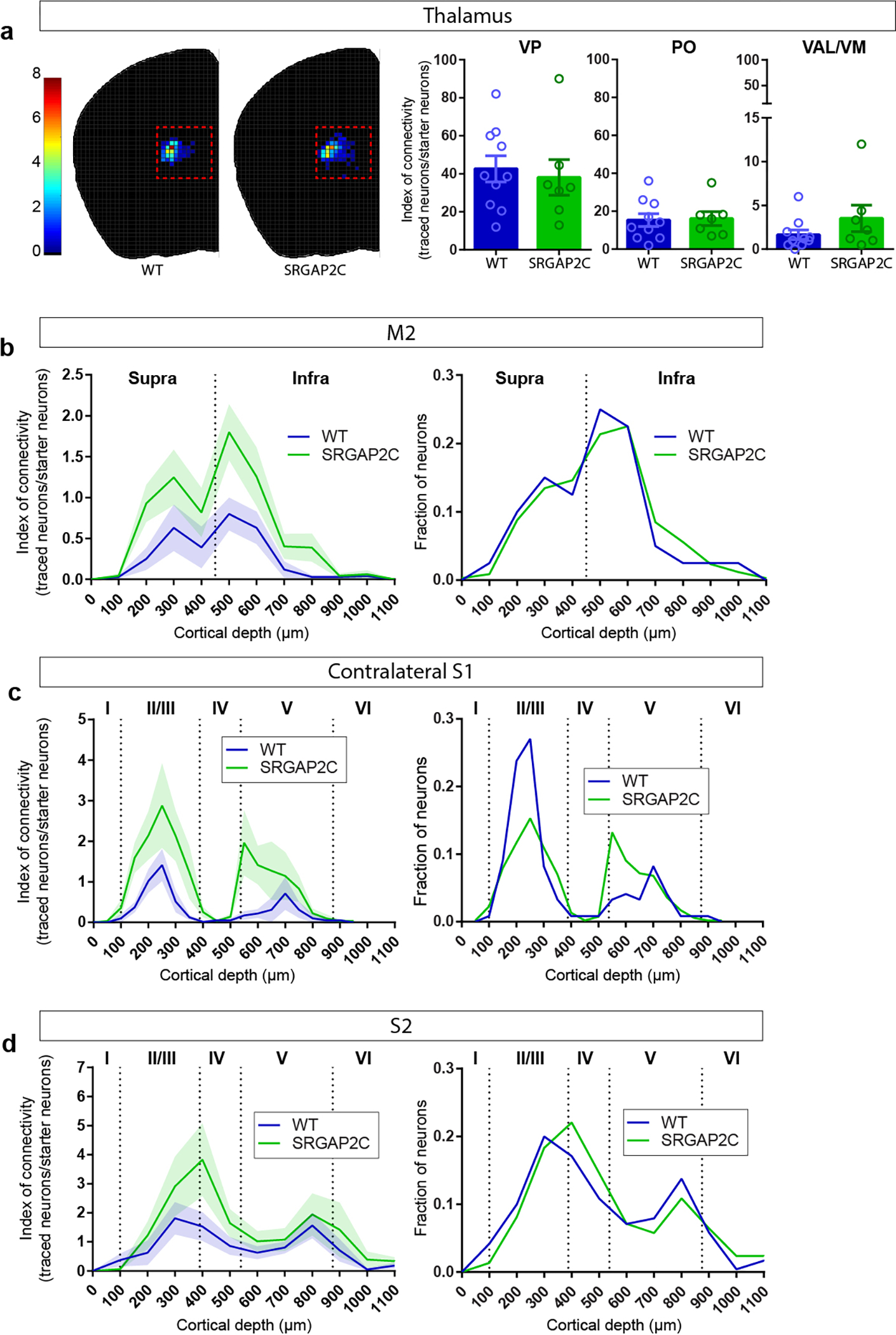
(a) Index of connectivity (IOC, number of traced neurons / number of starter neurons) for traced neurons in the thalamus. No difference was observed between WT and SRGAP2C mice (two-sided Mann-Whitney test). Left: distribution of traced neurons in WT and SRGAP2C, colors indicate IOC. Right: IOC for Ventralanteriorlateral/medial (VAL/VM), Ventralposterior (VP), and Posterior (PO) thalamic subnuclei. Bar graphs plotted as mean ± s.e.m. Open circles in bar graphs indicate individual mice (n = 10 for WT and n = 7 for SRGAP2C mice). (b-d) Distribution of traced neurons as a function of their cortical depth. Left: IOC, right: fraction. Shaded area indicates s.e.m.

Extended Data Figure 4. Connectivity changes are not caused by differences in cortical depth or number of starter neurons.

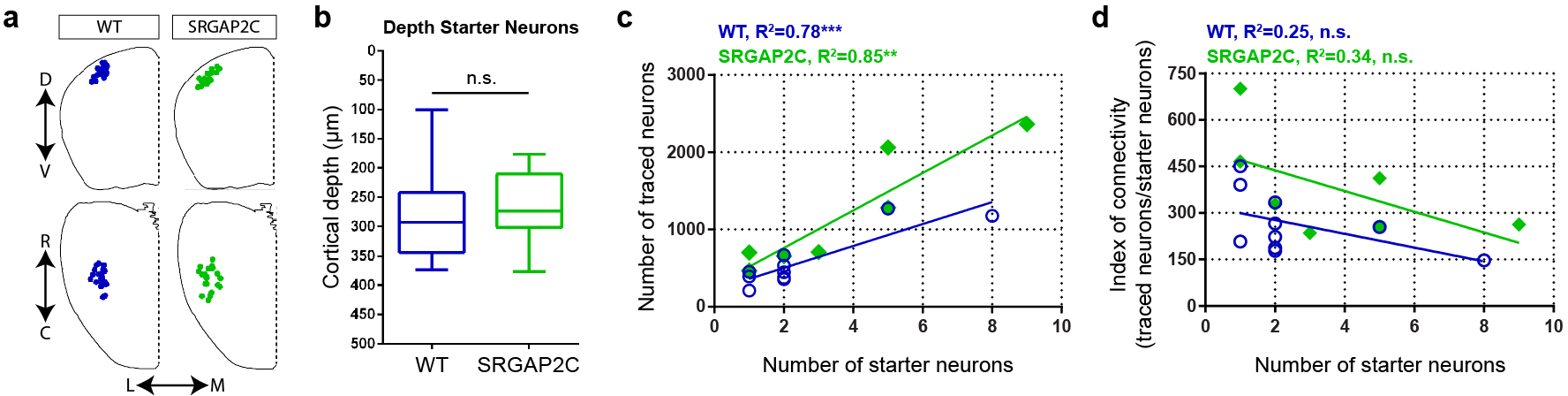
(a) Anatomical location of starter neurons. (b) Cortical depth of starter neurons measured as distance from pial surface is not different between WT and SRGAP2C mice, two-sided Mann-Whitney test. Data shown as box-and-whisker plots. Center line indicates median, box edges represent first and third quartiles, and whiskers represent minimum and maximum values (n = 26 starter neurons from 10 WT mice and n = 26 starter neurons from 7 SRGAP2C mice). (c) Correlation between number of RABV infected starter neurons and RABV traced neurons (Pearson’s correlation coefficient r = 0.88, P = 7 × 10⁻⁴ for WT, and r = 0.92, P = 3.2 × 10⁻³ for SRGAP2C). (d) No correlation was observed between IOC and number of RABV infected starter neurons per brain (Pearson’s correlation coefficient r = −0.5, P = 0.14 for WT, and r = −0.58, P = 0.17 for SRGAP2C).

Extended Data Figure 5. Distribution of RABV traced neurons locally in S1.

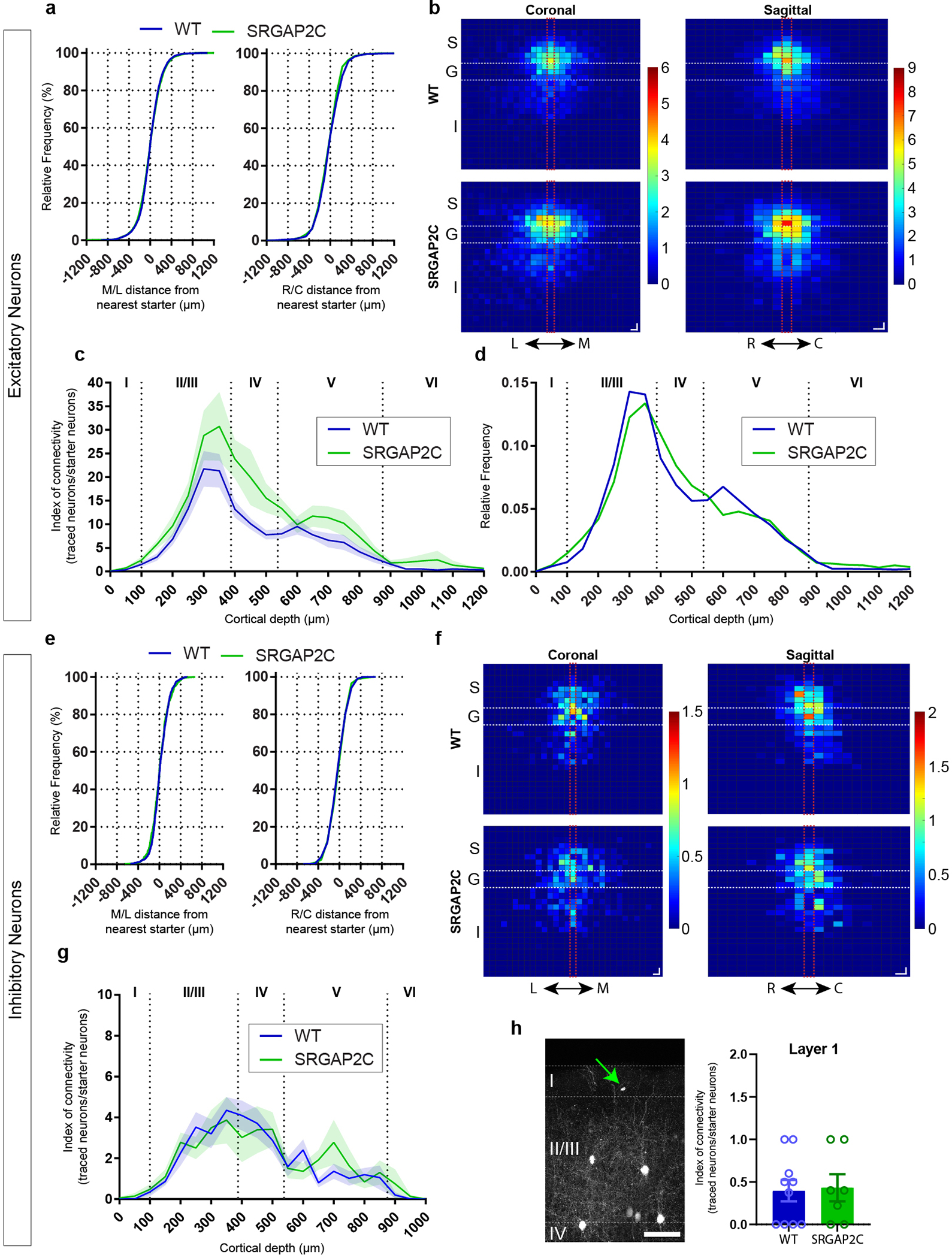
(a) Distance between RABV traced excitatory neurons in S1 and their closest starter neuron along the medial/lateral (M/L) or rostral/caudal (R/C) plane. No difference was observed between WT and SRGAP2C mice (Kolmogorov-Smirnov test). Data shown as relative frequency distribution. (b) Density plots showing distribution of traced excitatory neurons relative to their closest starter neuron for coronal (left, L and M indicate lateral and medial orientation, respectively) and sagittal view (right, R and C indicate rostral and caudal orientation, respectively). Center bins aligned with relative position of starter neuron are indicated by red dashed lines. S, supragranular, G, granular, I, infragranular layers. For coronal, bin size = 50×50 μm. For sagittal, bin size = 50×100 μm. Colors in density plots indicate IOC. (c) Cortical layer distribution of RABV traced excitatory neurons in S1 shown as Index of connectivity (IOC, number of traced neurons / number of starter neurons). Shaded are indicates s.e.m. (d) Fraction of RABV traced neurons across cortical layers in S1. Dashed lines indicate borders between layers. Roman numbers identify cortical layers. (e) Same as (a), for inhibitory neurons. For analysis of interneurons, Parvalbumin-positive and Somatostatin-positive were grouped together. (f) Same as (b), for inhibitory neurons. (g) Same as in (c), for inhibitory neurons. Shaded are indicates s.e.m. (h) RABV traced neurons in layer 1. Left: Coronal section showing location of a layer 1 traced neuron (green arrow) in the barrel field of the primary sensory cortex (S1). Right: IOC for layer 1 traced neurons. No difference was observed between WT and SRGAP2C mice (Mann-Whitney test). Scale bar, 100 μm. Bar graphs plotted as mean ± s.e.m. Open circles in bar graphs indicate individual mice (n = 10 for WT and n = 7 for SRGAP2C mice).

Extended Data Figure 6. SRGAP2C expression selectively increases synaptic density on apical dendrites.

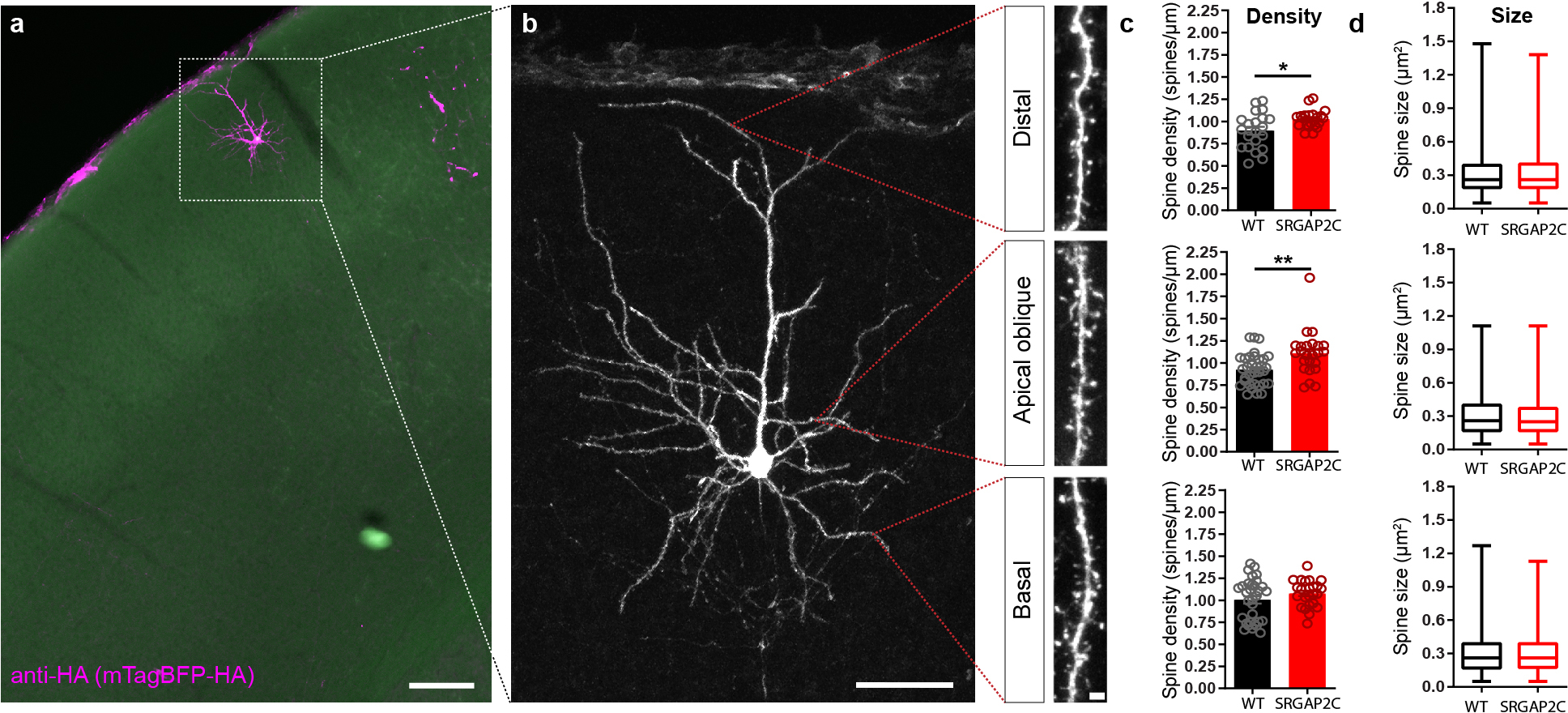
(a) Coronal section stained for HA showing sparse labeling of a layer 2/3 cortical pyramidal neuron in the barrel field of the primary somatosensory cortex. Scale bar, 150 μm. (b) Higher magnification of neuron in (a). Red dotted lines indicate approximate location where spine density and size were quantified for distal, apical oblique, and basal dendritic compartments. Panels on right show high magnification images of dendritic segments on which spines can clearly be identified. Left panel scale bar, 50 μm. Right panel scale bar, 2 μm. (c) Spine density is increased for distal, and apical but not basal dendritic segments. (P = 1.92 × 10⁻² for distal, P = 1.5 × 10⁻³ for apical oblique, P = 0.3 for basal; distal: n = 21 segments for WT and SRGAP2C, apical oblique: n = 33 segments for WT and n = 24 segments for SRGAP2C, basal: n = 32 segments for WT and n = 24 segments for SRGAP2C). Bar graph plotted as mean ± s.e.m. *P < 0.05, **P < 0.01, two-sided Mann-Whitney test. (d) Spine size is not significantly changed in adult SRGAP2C expressing layer 2/3 cortical pyramidal neurons. Data shown as box-and-whisker plots. Center line indicates median, box edges represent first and third quartiles, and whiskers represent minimum and maximum values (distal: n = 1273 spines for WT and n = 1083 spines for SRGAP2C, apical oblique: n = 2401 spines for WT and n = 1650 spines for SRGAP2C, basal: n = 2286 spines for WT and n = 1448 spines for SRGAP2C).

Extended Data Figure 7. Neuronal responses following whisker stimulation.

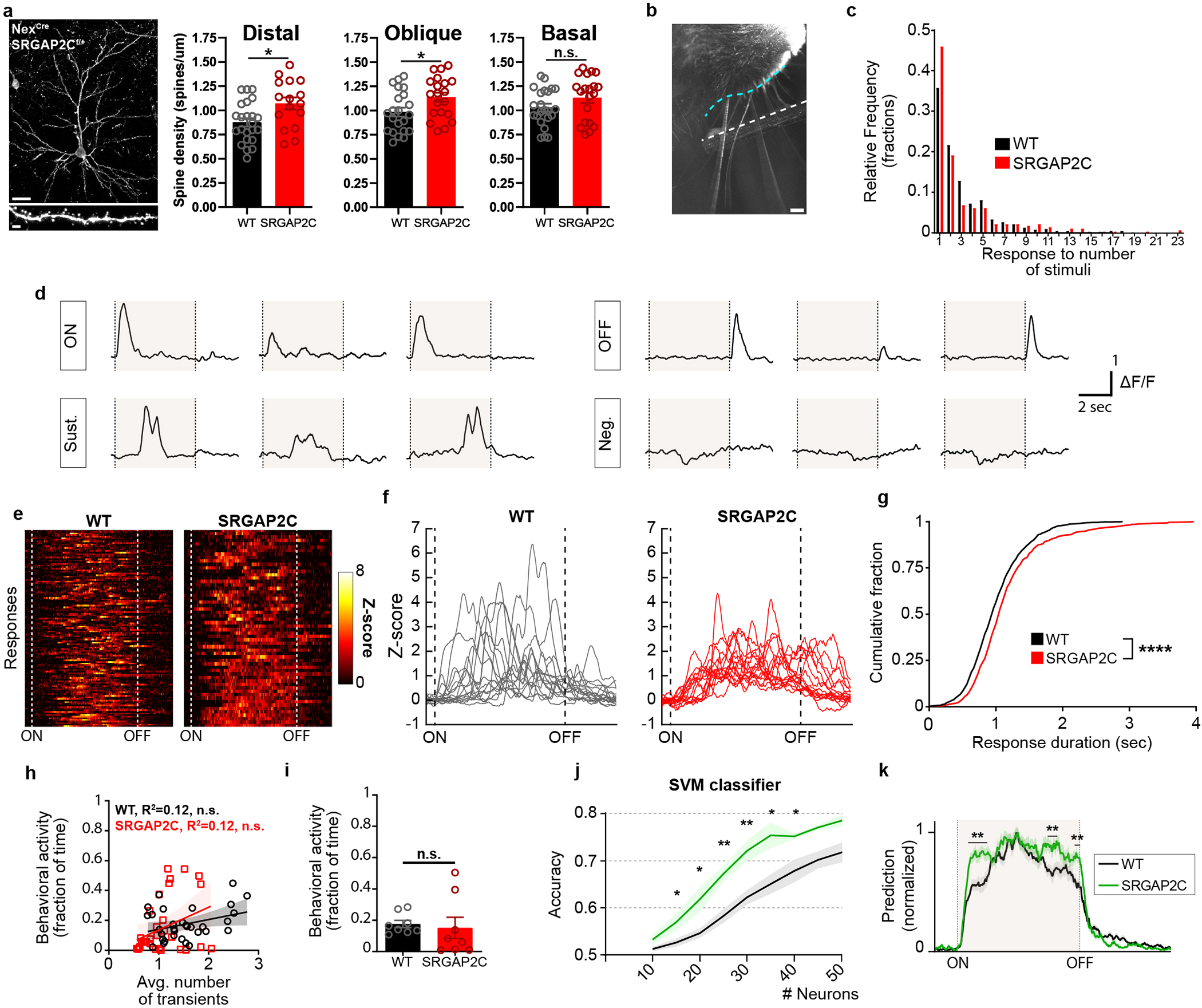
(a) Left: Coronal section stained for HA showing sparse labeling of a layer 2/3 cortical pyramidal neuron in the barrel field of the primary somatosensory cortex with high magnification (bottom) of dendritic segment in which spines can clearly be identified. Scale bar top, 25 μm. Scale bar bottom, 2 μm. Right: Spine density quantification in SRGAP2C heterozygous conditional knock-in mice crossed with heterozygous Nex^Cre/+ mice. Spine density is increased for distal and apical but not basal dendritic segments (P = 1.34 × 10⁻² for distal, P = 2.47 × 10⁻² for apical oblique, P = 0.117 for basal; distal: n = 23 segments for WT and n = 16 for SRGAP2C, apical oblique: n = 22 segments for WT and n = 20 segments for SRGAP2C, basal: n = 23 segments for WT and n = 20 segments for SRGAP2C). Bar graph plotted as mean ± s.e.m. *P < 0.05, two-sided Mann-Whitney test. (b) Top-down view of placement of stimulating rod (white dashed line, 2mm away from the whisker pad) next to right whisker pad (cyan dashed line). Scale bar, 1mm. (c) Frequency distribution of response fraction for neurons responding to either onset, sustained phase, or offset of the stimulus. (d) Singe-trial example responses. Shaded area indicates whisker stimulation. (e) Ten percent of single trial Sustained responses with longest sustained activity converted to Z-scores and sorted by duration of response. ON and OFF dashed lines indicate stimulus onset and offset, respectively (f) Bottom 15 responses shown in (e). (g) Cumulative probability distribution of Sustained response durations (time that Z-score was greater than 1). P < 1 × 10⁻⁴, Kolmogorov-Smirnov test. (h) Correlation between behavioral activity and average number of transients (n = 32 runs for 8 FOVs from 4 WT mice and n = 32 runs for 8 FOVs from 3 SRGAP2C mice). (i) Fraction of time during which behavioral activity was observed (n = 8 FOVs from 4 WT and n = 8 FOVs from 3 SRGAP2C mice). Bar graph plotted as mean ± s.e.m., two-sided Mann-Whitney test. (j) Support vector machine (SVM) accuracy in classifying presence or absence of whisker stimulus. Shaded area indicates s.e.m. (k) Normalized SVM prediction accuracy across time from stimulus ON to stimulus OFF for 25 neurons per field of view. Shaded area indicates stimulus time. Multiple t-test with multiple comparison correction using false-discovery rate Benjamini-Hochberg method (q < 0.05), *P < 0.05, **P < 0.01.

Extended Data Figure 8. Computational modeling of increased layer 4 to layer 2/3 connectivity explains observed SRGAP2C neuronal response properties.

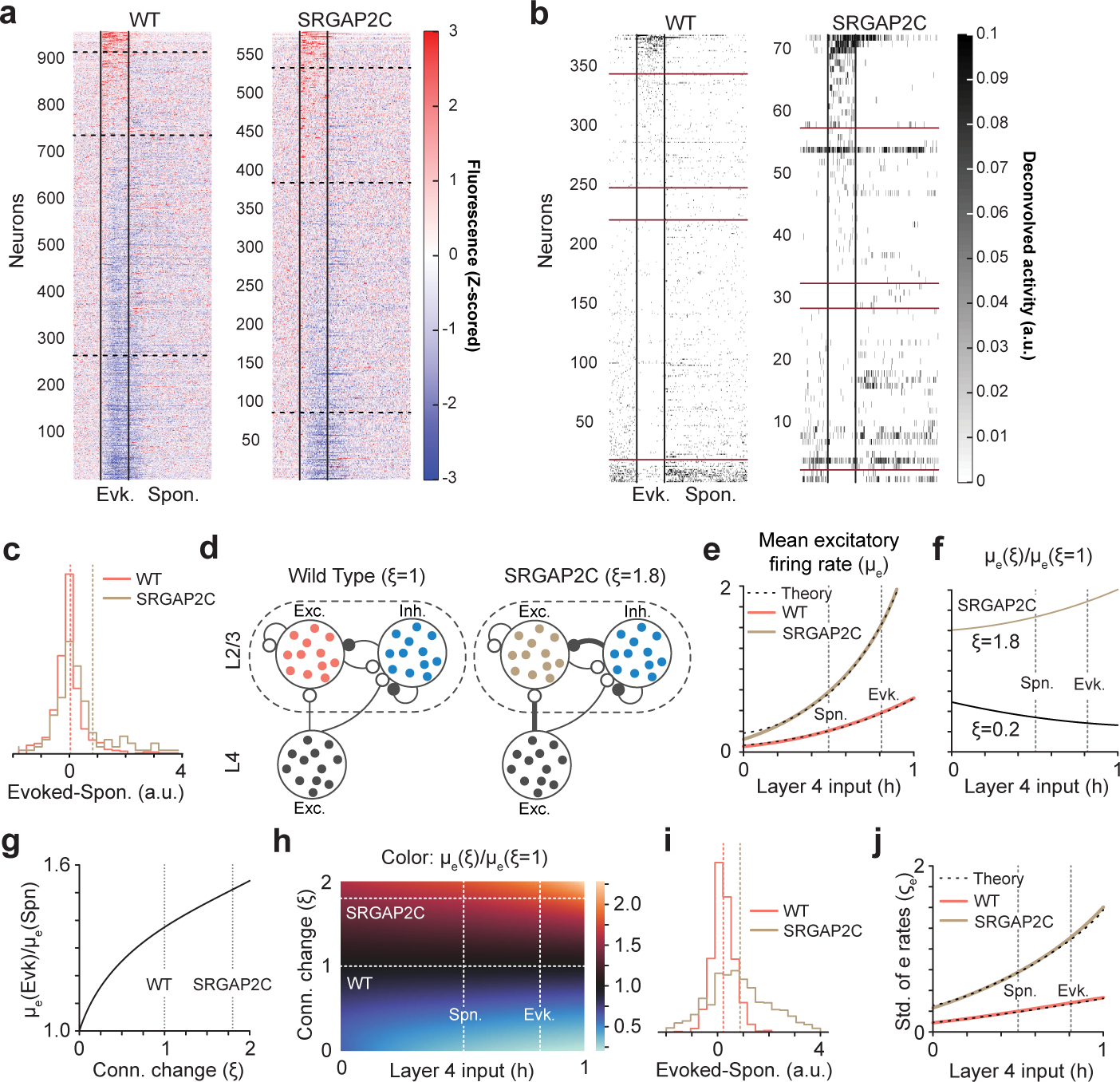
(a) Stimulus-triggered average fluorescence for all neurons recorded in WT and SRGAP2C mice. Fluorescence has been Z-scored and average activity during the 5 s prior to the stimuli have been subtracted. Horizontal dashed lines correspond to the separation between neurons that significantly increase (top) or decrease (bottom) their activity during evoked activity. Vertical solid lines correspond to stimulus onset and offset. Layer 2/3 PNs have been sorted according to the robustness of their signed response to the stimulus. (b) Stimulus-triggered average neural activity (after deconvolving fluorescence) for neurons with high signal-to-noise ratio. Horizontal red lines correspond to the separation between neurons that significantly increase (top) or decrease (bottom) their activity during evoked activity. Neurons between the middle horizontal red lines had an equal average response during spontaneous and evoked activity (typically 0). Neurons have been sorted according to the strength of their signed response to the stimulus. (c) The normalized distributions of firing rate differences between whisker stimulation and spontaneous activity. Dashed vertical lines indicate means of the distributions. (d) The model considers a population of excitatory neurons in layer 4 (gray) projecting to populations of inhibitory (blue) and excitatory (red, brown) neurons in cortical layer 2/3 of barrel cortex. The strength of the projections targeting layer 2/3 PNs and coming from layer 4 excitatory and layer 2/3 inhibitory neurons is assumed to be larger in SRGAP2C mice than WT mice by a factor ξ, as indicated. All neurons are modelled with a quadratic I/O transfer function. (e) The mean rate of simulated excitatory units (μ_e) in SRGAP2C mice (brown) are higher and increase at a higher rate than those in WT mice (red) as a function of the mean excitatory input h from layer 4. This is particularly true for the rates at the input levels we model as spontaneous and evoked activity (left and right gray vertical dashed lines, respectively). A mathematical approximation (black dashed lines; Supplementary Material) agrees to an excellent degree with the simulations. (f) The model ratio of mean excitatory rates between SRGAP2C mice (ξ = 1.8, top black curve) or mice with a hypothetical decrease in connection strength (ξ = 0.2, bottom black curve) and WT mice. (g) The model ratio between the mean excitatory rate during evoked vs. spontaneous activity monotonically increases with the change in connectivity relative to WT mice. (h) The model ratio of mean excitatory rates between mice with an arbitrary change in connection strength and WT mice. (i) The normalized distributions of firing rate differences between evoked and spontaneous mean input in the model. As in the experimental data (panel c), both model SRGAP2C and model WT mice contain subgroups of neurons that increase and subgroups that decrease their activity in going from spontaneous to evoked stimulation; and the fraction of neurons increasing their activity is higher in SRGAP2C mice than WT mice. (j) As for the mean rates (panel e), the variances of excitatory units in model SRGAP2C mice (brown) are higher, and increase at a higher rate as a function of the mean excitatory input from layer 4, than those in model WT mice (red).

Extended Data Figure 9. Modeling of layer 2/3 PN response properties in WT and SRGAP2C mice.

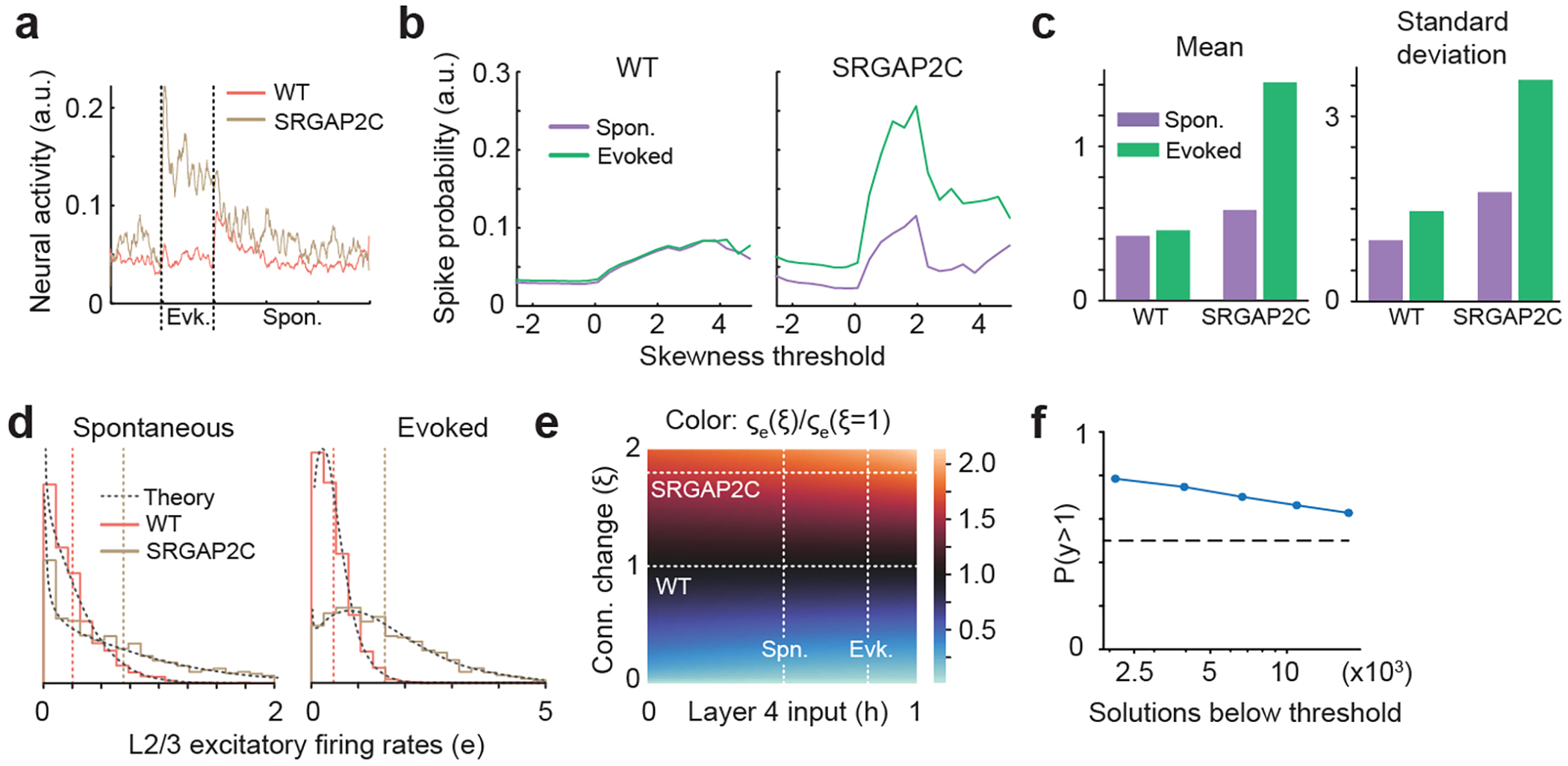
(a) Population stimulus-triggered-average neural activity obtained by averaging over all neurons in Extended Data Figure 8b. Vertical dashed lines correspond to stimulus onset and offset. (b) Average neural activity computed during the 5 s before the stimulus (Spon.) or during the 5 s of stimulation (evoked; stimulus is applied at time 0) across all selected neurons and trials as a function of the skewness threshold used to select neurons. The threshold in (a) is 1.5. (c) Mean and standard deviation of the deconvolved traces in Extended Data Figure 8b during both stimulus conditions. (d) The normalized distributions of simulated excitatory rates in both SRGAP2C (brown) and WT (red) mice and during spontaneous and evoked mean input illustrate the increase in the mean and variance discussed in the main text. The shapes of the distributions agree with their mathematical approximations (dashed black line) discussed in Supplementary Material. (e) The ratio of the standard deviation of excitatory rates between mice with an arbitrary change in connection strength and WT mice. This demonstrates that the effects are robust to the specific choice of parameters. (f) Probability of solutions with y>1 as a function of the number of solutions with a fit error of the firing rates of the wild type mouse below a certain threshold, where y = [mu(2c,evoked)/mu(2c,spont)]/[mu(wt,evoked)/mu(wt,spont)] and mu corresponds to the mean firing rate of the excitatory population.

Extended Data Figure 10. Whisker-based texture discrimination task.

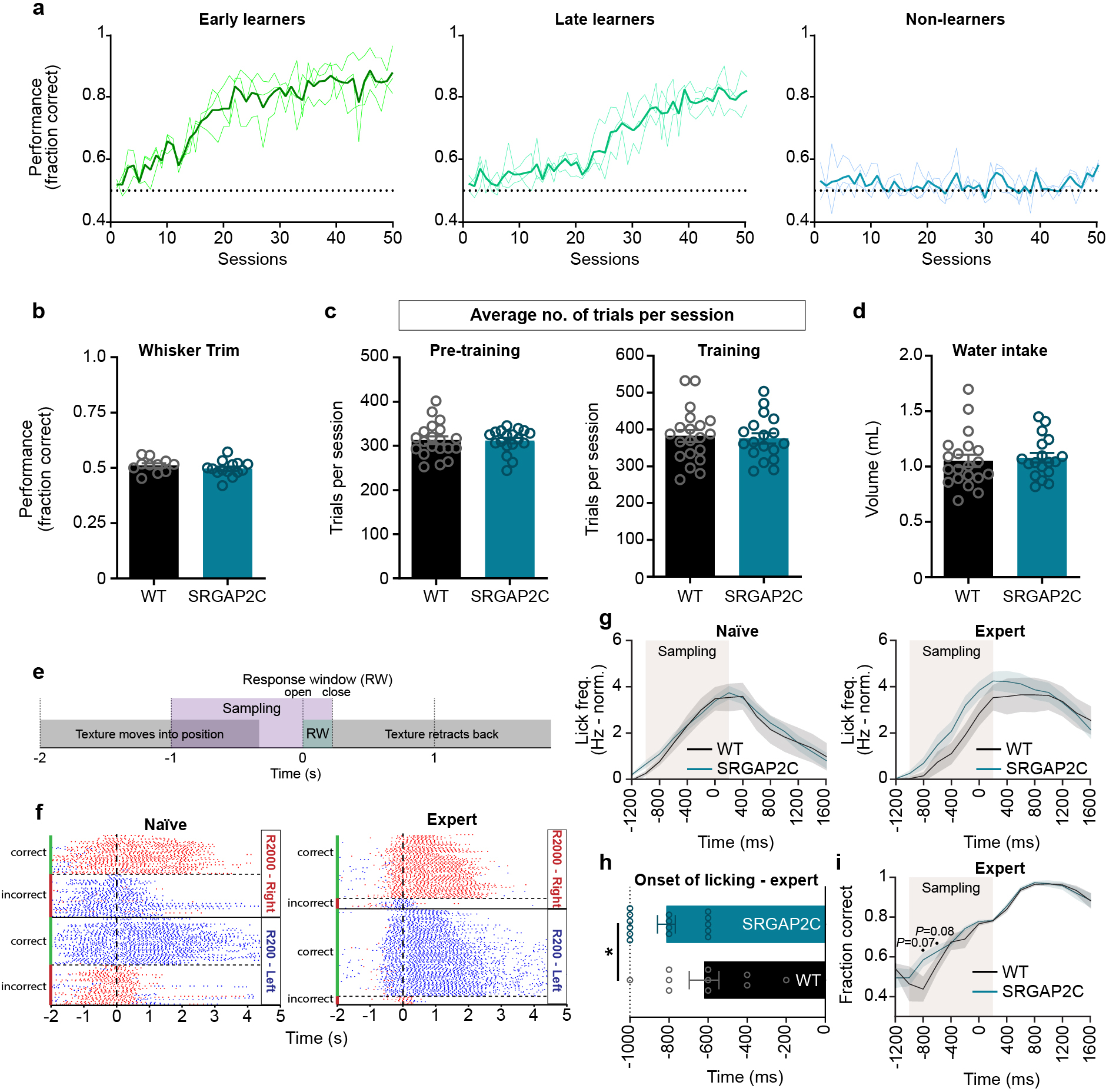
(a) Example learning curves (lighter shades) of three individual mice. Mean learning curve is shown in darker shade (b) Performance (fraction correct) after whiskers facing texture were trimmed dropped to chance level, showing that mice needed their whiskers to perform this task (n = 11 for WT and n = 14 for SRGAP2C mice). (c) Average number of trials per session for pre-training and training phase (n = 20 for WT and n = 18 for SRGAP2C mice). (d) Mean water intake per session (n = 20 for WT and n = 18 for SRGAP2C mice). Bar graphs plotted as s.e.m. (e) Schema showing structure of single trial. Textures rotate and move into position 2 s before opening of the response window (RW). Approximately 1 s before RW opening the texture is within reach of the whiskers, allowing mice to sample the texture while it moves further into position. Upon opening of the RW, correct lick responses lead to a water reward, while incorrect lick responses cause to a time-out. Following RW closure the texture retracts back out of reach of the whiskers. (f) Example raster plot of an individual mouse showing the distribution of individual licks (red dot for right licks, blue dot for left licks) relative to opening of the response window before (naïve) and after (expert) learning of the task. Correct licks are either right licks (red) for the R2000 texture, or left licks (blue) for the R200 texture. (g) Lick frequency plot for naïve and expert mice. Lick frequency was normalized for each individual mouse to the mean lick frequency before the sampling window. Shaded area around curves indicates s.e.m. (h) Average timing of licking onset in expert mice relative to opening of the response window (P = 4.91 × 10⁻²; n = 10 for WT and n = 15 for SRGAP2C mice). Bar graph plotted as mean ± s.e.m. *P < 0.05, two-sided Mann-Whitney test. (i) Fraction of licks from expert mice that are correct relative to opening of the response window. Shaded area around curves indicates s.e.m., two-sided Mann-Whitney test.

Data and materials availability:

Reagents and other materials will be available upon request to F.P.