Skip to main content
PMC home page
HHS Author Manuscripts logoLink to HHS Author Manuscripts
. Author manuscript; available in PMC: 2022 Jun 2.
Published in final edited form as: Ultrasound Med Biol. 2000 May;26(4):641–646. doi: 10.1016/s0301-5629(99)00172-6

Measurements of Phase Velocity and Group Velocity in Human Calcaneus

Keith A Wear 1
PMCID: PMC9161808  NIHMSID: NIHMS1808126  PMID: 10856627

Abstract

Ultrasonic velocity in calcaneus correlates highly with bone mineral density which is a good predictor of osteoporotic fracture risk. Several commercial bone sonometers perform a velocity measurement based on the transit time of a broadband pulse to assess skeletal status. This approach is somewhat problematic however as several authors have reported ambiguities in measurements in calcaneus. Phase velocity is an alternative that may be less dependent on device spectral characteristics. In addition, dispersion (the frequency dependence of phase velocity) is a fundamental property worth investigating in order to increase understanding of interaction between ultrasound and bone. In order to compare two group velocity measurement methods and one phase velocity measurement method, a polycarbonate sample (for method validation) and 24 human calcanei were investigated in vitro. Phase velocity in calcaneus at 500 kHz was 1511 m/s ± 30 m/s (mean ± standard deviation). Average phase velocity decreased approximately linearly with frequency (−18 m/sMHz). The two group velocity measurements were comparable and tended to be slightly lower than phase velocity. The magnitude of dispersion showed little correlation with bone mineral density.

Keywords: calcaneus, trabecular bone, cancellous bone, velocity, dispersion, osteoporosis

Introduction

Bone sonometry is now accepted as an effective tool for diagnosis of osteoporosis. One ultrasonic feature, speed of sound in calcaneus, has been demonstrated to be highly correlated with calcaneal bone mineral density (Rossman et al., 1989, Tavakoli and Evans, 1991, Zagzebski et al., 1991, Njeh et al., 1996, Laugier et al., 1997, Nicholson et al., 1998, Hans et al., 1999, H. Trebacz, and A. Natali, et al., 1999) which is in turn an indicator of systemic osteoporotic fracture risk (Cummings et al., 1993). Calcaneal ultrasonic measurements (sound speed combined with broadband ultrasonic attenuation) have been shown to be predictive of hip fractures in women in prospective (Hans et al., 1996, and Bauer et al., 1997) and retrospective (Schott et al., 1995, Turner et al., 1995, Glüer et al., 1996, and Thompson et al., 1998) studies.

It is important to recognize potential differences among phase velocity (the velocity of a single-frequency component), group velocity (the velocity of the center of a pulse), and signal velocity (the velocity of the front of a pulse) (Morse and Ingard, 1986). In performing transit-time-based measurements of sound speed, many investigators employ a marker (such as a zero crossing) somewhere between the leading edge and the center of the pulse, yielding a value between signal and group velocity. Ambiguities associated with transit-time methods for estimation of velocity in bone have been reported by several researchers (Laugier et al., 1993, Nicholson et al., 1996, Strelitzki and Evans, 1996a). These inconsistencies have been qualitatively attributed to distortions in pulse waveforms due to spectral changes arising from frequency-dependent attenuation and dispersion. This problem has led some investigators to suggest measurement of phase velocity, which is measured in the frequency domain, as an alternative to transit-time methods. (Kaufman et al., 1995, Nicholson et al., 1996, Strelitzki and Evans, 1996a, Droin et al., 1998). Since the majority of clinical validation studies of speed of sound as a diagnostic tool are based on transit-time-based velocity measurements, however, both measurement techniques are currently of high interest.

The principal goal of this paper is to provide a direct comparison between phase velocity measurements and group velocity measurements in calcaneus. Group velocity is chosen because transit-time measurements based on the pulse center exhibit less variability due to frequency-dependent attenuation than measurements based on other markers in nondispersive (Ragozzino, 1981) and weakly-dispersive (Wear, 2000) media. A secondary objective is to measure velocity dispersion in calcaneus, previously reported by others (Nicholson et al., 1996, Strelitzki and Evans, 1996a, and Droin, Berger, and Laugier, 1998). The paper is organized as follows. First, biological methods and the methodology for measuring group and phase velocities are described. Two methods of measuring group velocity are presented. One method assesses group velocity directly using a standard transit-time-based approach. The other method extracts group velocity from dispersion measurements and a formula that relates group velocity to phase velocity and dispersion. The three velocity measurement methods are then validated using a polycarbonate sample. Finally, the velocity measurements in human calcaneus are presented and discussed.

Methods

Biological Methods

Twenty four human calcaneus samples (both genders, ages unknown) were obtained. They were defatted using a trichloro-ethylene solution. Defatting was presumed not to significantly affect measurements since speed of sound of defatted trabecular bone has been measured to be only slightly different from that of bone with marrow left intact (Alves et al., 1996, and Njeh and Langton, 1997). The cortical lateral layers were sliced off leaving two parallel surfaces with direct access to trabecular bone. The thicknesses of the samples varied from 12 to 21 mm. In order to remove air bubbles, the samples were vacuum degassed underwater in a desiccator. After vacuum, samples were allowed to thermally equilibrate to room temperature prior to ultrasonic interrogation. Ultrasonic measurements were performed in distilled water at room temperature. The temperature was measured for each experiment and ranged between 19.1°C and 21.2°C. The relative orientation between the ultrasound beam and the calcanei was the same as with in vivo measurements performed with commercial bone sonometers, in which sound propagates in the mediolateral (or lateromedial) direction.

Density of samples was assessed from separate measurements of mass and volume. Apparent density, the ratio of the dehydrated, defatted tissue mass to the total specimen volume (Langton et al., 1996) was employed. Mass was measured using a balance. Volume was computed from separate measurements of thickness and cross-sectional area. Thickness between the two parallel planar surfaces (cut by machine) was measured using calipers. Cross-sectional areas were measured by computer processing of scanned images of the samples.

Ultrasonic Methods

In addition to interrogation of bone samples, measurements were performed on a 25.8 mm thick polycarbonate sample in order to test the measurement methodology. Two group velocity measurement methods were checked for consistency. Dispersion measurements were compared with measurements of frequency-dependent phase velocity in polycarbonate previously published by Droin, Berger, and Laugier (1998).

A Panametrics (Waltham, MA) 5800 pulser/receiver was used. Samples were interrogated in a water tank using pairs of coaxially-aligned Panametrics 1” diameter, focussed, broadband transducers with center frequencies of 500 kHz (polycarbonate sample and bone samples) and 1 MHz (polycarbonate sample). Received ultrasound signals were digitized (8 bit, 10 MHz) using a LeCroy (Chestnut Ridge, NY) 9310C Dual 400 MHz oscilloscope and stored on computer (via GPIB) for off-line analysis.

The phase velocity of propagating wave, cp, is a function of angular frequency, ω, and is given by (Morse and Ingard, 1986, and Duck, 1990)

cp(ω)=ωk(ω) (1)

where ω=2πf, f is the frequency, k = 2π/λ, and λ is the wavelength. The group velocity of a broadband pulse, cg, is given by (Morse and Ingard, 1986, and Duck, 1990)

cg=cpc1−ωccpc(∂cp∂ω)ω=ωc (2)

where cpc is the phase velocity at the center frequency of the pulse, ωc.

To measure group velocity, arrival times of received broadband pulses were measured with and without the sample in the water path. Group velocity, cg, was computed from

cg=cw1+cwΔtd (3)

where d is the thickness of the sample, Δt is the difference in arrival times, and cw is the temperature-dependent speed of sound in distilled water given by (Kaye and Laby, 1973)

cw=1402.9+4.835T−0.047016T2+0.00012725T3m/s (4)

where T is the temperature in degrees Celsius. Each arrival time was computed as follows. First, the digitized received pulse was bandpass filtered (pass bands: 150 – 800 kHz for the 500 kHz transducers and 300 kHz – 1.6 MHz for the 1 MHz transducers). Then the signal envelope was computed using the Hilbert transform. The arrival time was then taken to the average of the two zero crossing times immediately prior and immediately after the maximum in the signal envelope.

Following Strelitzki and Evans (1996a), a second group velocity measurement was performed by measuring phase velocity over a range of frequencies, as described below, and using Equation (2).

Phase velocity was computed using

cp(ω)=cw1+cwΔϕ(ω)ωd (5)

where Δϕ(ω) is the difference in unwrapped phases of the received signals with and without the sample in the water path. The unwrapped phase difference, Δϕ(ω), was computed as follows. The Fast Fourier Transform (FFT) of the digitized received signal was taken. The phase of the signal at each frequency was taken to be the inverse tangent of the ratio of the imaginary to real part of the FFT at that frequency. Since the inverse tangent function yields principal values between −π and π, the phase had to be unwrapped by adding an integer multiple of 2π to all frequencies above each frequency where a discontinuity appeared. Following Droin, Berger, and Laugier (1998), dispersion was characterized by the velocity dispersion magnitude (VDM),

VDM=cp(600kHz)−cp(200kHz) (6)

These substitution techniques can potentially exhibit appreciable error if the speed of sound differs substantially between the sample and the reference (Kaufman et al., 1993). However, one study indicates that this diffraction-related error is negligible in calcaneus (Droin et al., 1998). Apparently, the sound speed in calcaneus, ranging approximately from 1475 m/s to 1650 m/s (Droin et al., 1998), is sufficiently close to that of distilled water at room temperature, 1487 m/s (Kaye and Laby, 1973) that diffraction-related errors may be ignored for an experimental geometry such as the one used here. The relevant dimensions involved were transducer diameter (29 mm for Droin et al., 25.4 mm in the present study), focal length (40 mm for Droin et al., 38.1 mm for the present study), ultrasound propagation distance (80 mm for Droin et al., 76.2 mm for the present study) and calcaneal sample thickness (12.5 mm for Droin et al., 12-21 mm for the present study).

Results

The two methods for group velocity estimation yielded similar results in the polycarbonate sample. The direct method - measurement of arrival times from pulse waveforms and using Equation (3) – produced group velocity estimates of 2198 ± 4 m/s at 500 kHz and 2205 ± 5 m/s at 1 MHz. The indirect method - estimation of group velocity using the measurement of frequency-dependent phase velocity and Equation (2) – resulted in group velocity estimates of 2207 ± 7 ms at 500 kHz and 2220 ± 7 m/s at 1 MHz. The discrepancies for the two methods were 9 m/s (0.4%) at 500 kHz and 15 m/s (0.7%) at 1 MHz.

Measurements of phase velocity in the polycarbonate sample are depicted in Figure 1. For comparison, measurements performed by Droin, Berger, and Laugier (1998) are also shown. The frequency dependence of phase velocity is essentially the same for both experiments. The difference in absolute level of sound speed (about 15 m/s) may be attributable to minor compositional differences in the two different samples and temperature effects. Note that the group velocities listed in the previous paragraph were higher than the corresponding phase velocities (see Figure 1) as would be expected from Equation 2 for a medium with positively sloped dispersion.

Figure 1.

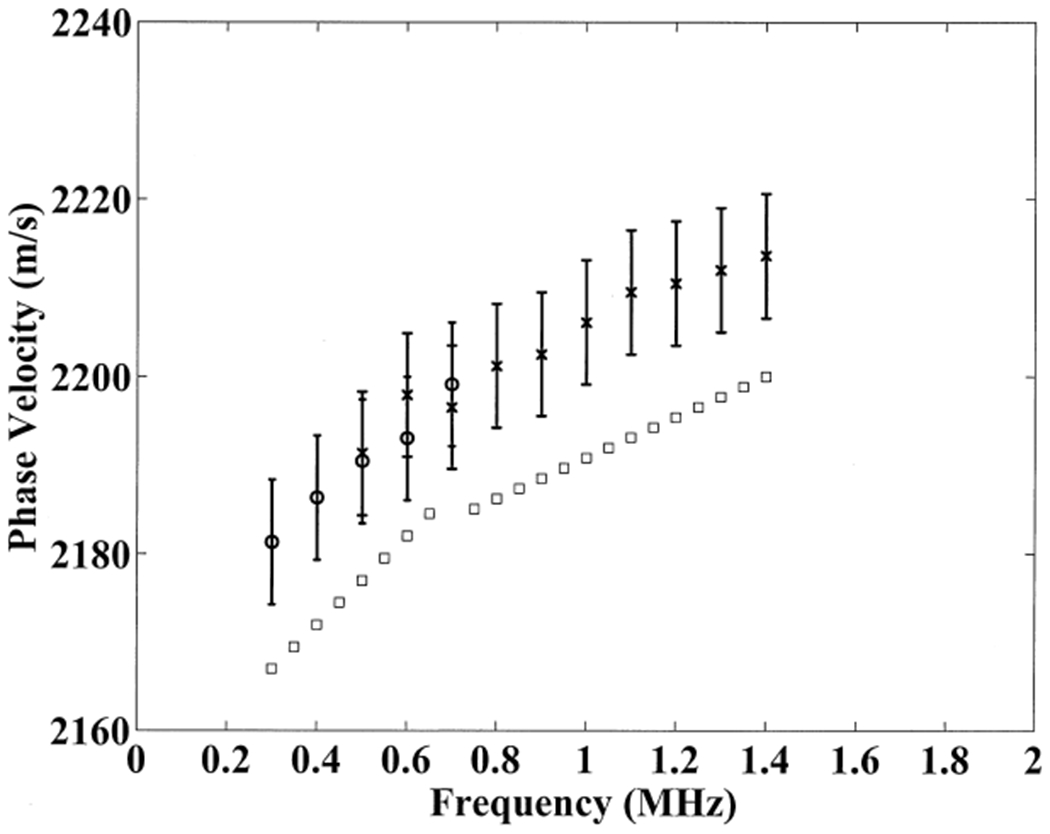
Figure 1.

Open in a new tab

Phase velocity measurements versus frequency for the polycarbonate slab (25.8 mm thickness). Measurements were performed with 500 kHz (circles) and 1 MHz (x’s) broadband transducers. The error bars denote standard deviations for measurements. Measurements reported by Droin, Berger, and Laugier (1998, squares) are also shown (30 mm polycarbonate cylinder).

Droin, Berger, and Laugier (1998) published results of a computer simulation that demonstrated that for a pair of planar transducers with radius equal to 12.5 mm and separated by 8 cm, the diffraction-related sound-speed error (discussed in the previous section) for a 30 mm thick polycarbonate cylinder may become significant (10 m/s or more), but only for frequencies below about 400 kHz. Polycarbonate is much more susceptible to diffraction-related sound-speed errors than trabecular bone because the disparity in sound speeds (and therefore wavelengths) between polycarbonate and water is much greater than that for trabecular bone and water. The fact that the measurements shown in Figure 1 (which were not corrected for diffraction-related errors) exhibited the same trend as the measurements reported by Droin, Berger, and Laugier (which were corrected for diffraction-related errors) suggests that diffraction-related errors were minimal in the present study both above and below 400 kHz. This difference may be largely attributable to differences in transducer properties in the two studies, which would lead to different beam diffraction properties. In the present study, 25.4 mm diameter focussed transducers were used. Droin and co-workers used 12.5 mm planar transducers for polycarbonate experiments. In addition, the sample used in the present study was slightly thinner (25.8 mm) than that used by Droin et al. (30 mm), which would be expected to reduce the magnitude of diffraction-related errors.

The average phase velocity as a function of frequency for the 24 bone samples is shown in Figure 2. Phase velocity shows an approximately linear decreasing relationship with frequency. The average phase velocity at 500 kHz was 1511 m/s. The standard deviation was 30 m/s. The slope of the phase velocity versus frequency relationship was −18 m/sMHz. The physical mechanisms underlying measurements of negative dispersion in trabecular bone, also reported by others (see Table 1), are currently not well understood but a thorough analysis of potential explanations is provided by Droin et al. (1998).

Figure 2.

Figure 2.

Open in a new tab

Average phase velocity measurements versus frequency for the 24 human calcaneus samples. The error bars denote standard errors. A least-squares linear regression to the data is also shown.

Table 1.

Estimates of dispersion in human calcaneus from the present paper, Nicholson et al. (1996, Table 1), Strelitzki and Evans (1996, Table 2), and Droin, Berger, and Laugier (1998, Table 1).

Author(s) N Frequency Range (kHz) Dispersion (mean ± standard deviation) (m/sMHz)
Wear 24 200 – 600 −18 ± 15
Nicholson et al. 70 200 – 800 −40
Strelitzki and Evans 10 600 – 800 −32 ± 27
Droin, Berger, and Laugier 15 200 – 600 −15 ± 13
Open in a new tab

Figure 3 compares the two methods for group velocity estimation. The direct measurements tended to be slightly greater by an average of 11.4 m/s (standard deviation: 7.0 m/s) or about 0.76%. A least squares linear regression between the two yielded a correlation coefficient of 0.98 (95% confidence interval: 0.96 – 0.99).

Figure 3.

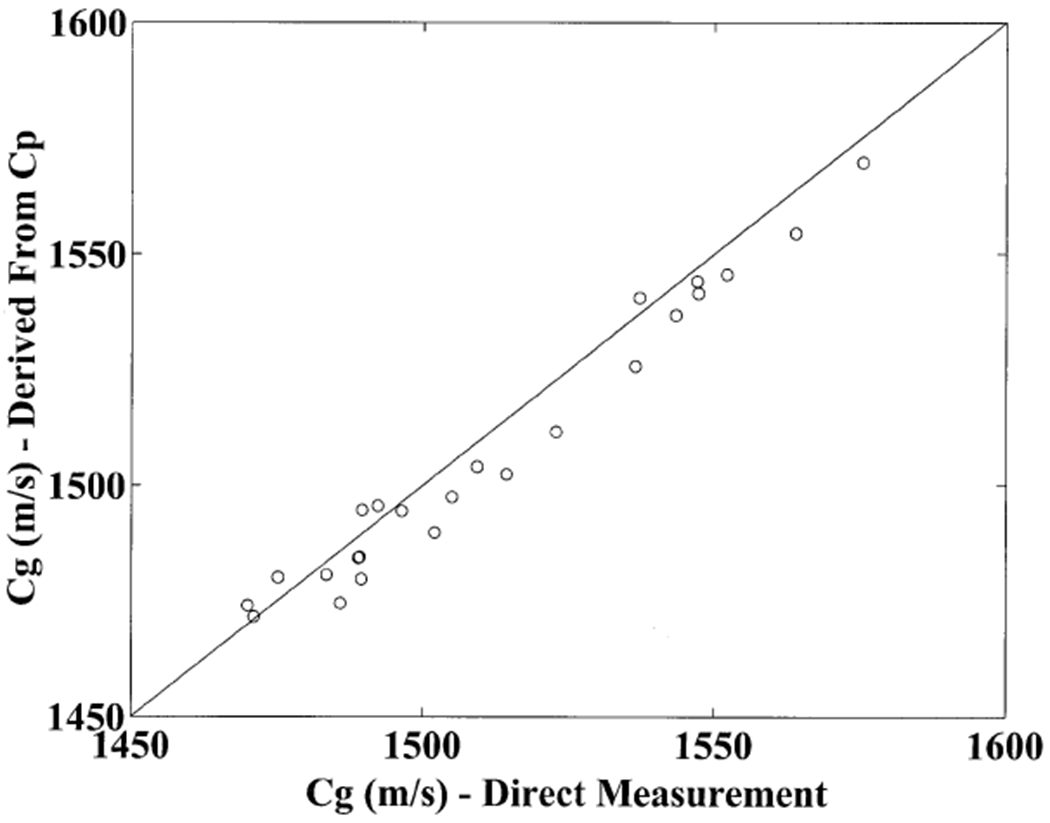
Figure 3.

Open in a new tab

Group velocity estimates derived from frequency-dependent phase velocity measurements and Equation 2 versus direct group velocity estimates obtained from transit time measurements and Equation 3 in 24 human calcaneus samples. A line corresponding to hypothetical equality between the two is also shown.

Figure 4 illustrates that phase velocity (at 500 kHz) and direct group velocity measurements were similar for the 24 bone samples. Group velocities tended to be slightly lower than phase velocities, as expected from Equation 2 and the negative sloping dispersion shown in Figure 2. A least squares linear regression between the two yielded a correlation coefficient of 1.00 (95% confidence interval: 0.99 – 1.00). This suggests that, in this experiment, the direct group velocity and phase velocity measurements would have the same effectiveness for predicting bone mineral density or any other feature.

Figure 4.

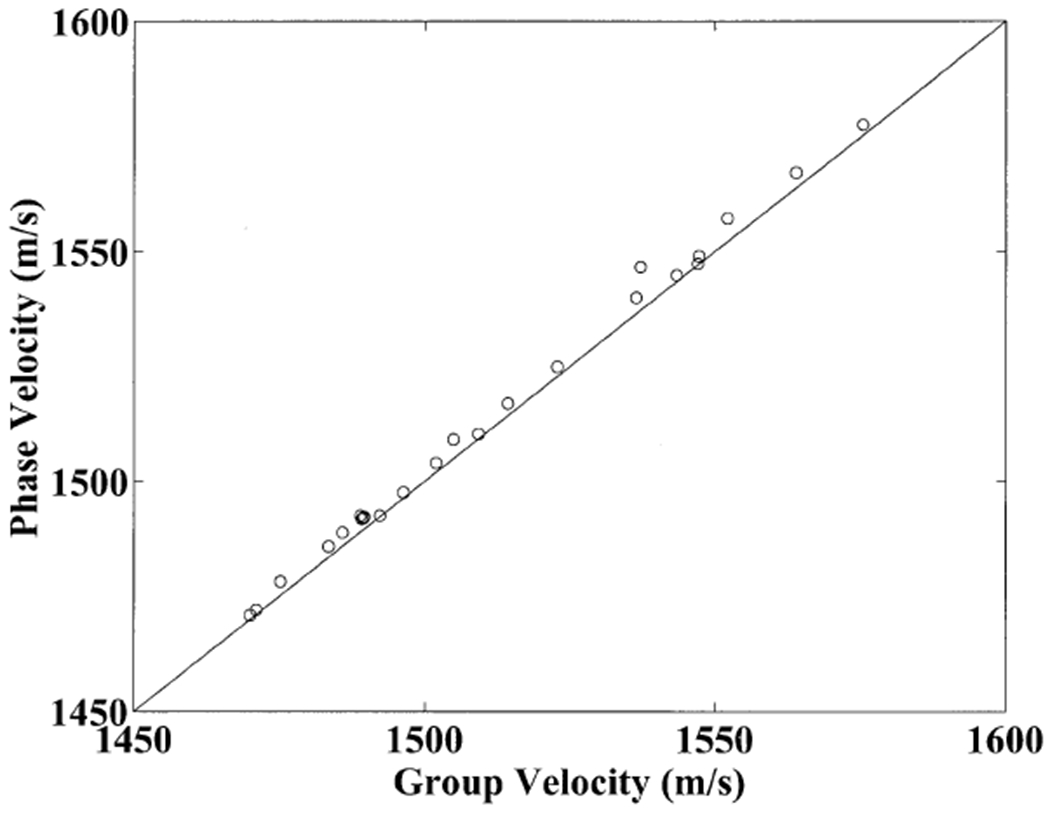
Figure 4.

Open in a new tab

Phase velocity measurements at 500 kHz versus direct group velocity measurements for the 24 human calcaneus samples. A line depicting hypothetical equality of phase velocity with group velocity is also shown.

Figure 5 shows a scatter plot of the velocity dispersion magnitude versus bone mineral density for the 24 human calcaneus samples. Similar to the findings of Droin, Berger, and Laugier (1998), VDM could be positive or negative but was usually negative and was almost independent of bone mineral density. The average VDM was −7 m/s with a standard deviation of 6 m/s

Figure 5.

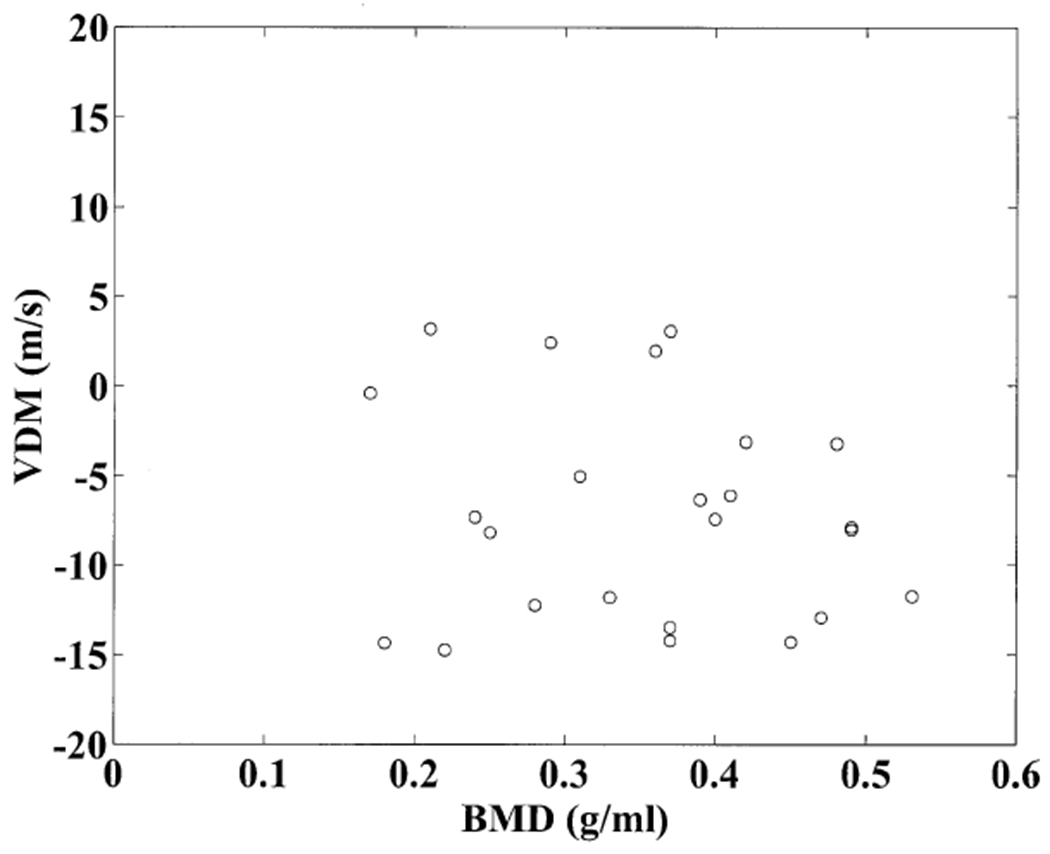
Figure 5.

Open in a new tab

Velocity dispersion magnitude measurements plotted versus bone mineral density for the 24 human calcaneus samples. The correlation between the two is low.

Discussion

Ultrasonic velocity in calcaneus has been demonstrated to correlate highly with bone mineral density which has been demonstrated to be a good predictor of osteoporotic fracture risk. Several existing commercial bone sonometers either use velocity alone or in combination with broadband ultrasonic attenuation to assess skeletal status. Usually a transit-time-based measurement of velocity is used. Several investigators have suggested a frequency-domain-based phase velocity measurement as a possible alternative (Kaufman et al., 1995, Nicholson et al., 1996, Strelitzki and Evans, 1996a, Droin et al., 1998).

In order to study and compare group and phase velocity measurements, 24 human calcanei were investigated in vitro using broadband ultrasound with center frequency of 500 kHz. The methods were first validated using a polycarbonate sample. Two group velocity measurement methods exhibited excellent consistency in both polycarbonate and bone. Phase velocity measurements in bone showed an approximately linear decreasing relationship with frequency. Phase velocity at 500 kHz and group velocity measurements were highly correlated for the 24 bone samples although group velocity measurements tended to be slightly lower. The measured magnitude of dispersion showed little correlation with bone mineral density.

Some authors (Laugier et al., 1993, Nicholson et al., 1996, Strelitzki et al., 1996b, and Wear, 2000) have demonstrated that time-domain velocity estimates can depend greatly on which marker (e.g. zero crossing) in the pulse waveform is designated for measurement of transit times. This inconsistency has been attributed to pulse spreading due to frequency-dependent attenuation and distortion due to dispersion. In the present study, the direct group velocity measurement (time-domain method using Equation 3) showed good agreement with the indirect group velocity measurement (which does not require choice of a marker as it is derived from frequency-dependent phase velocity and Equation 2) for both polycarbonate and bone. This suggests that it may be advisable to choose a marker near the middle of the waveform as was done in the present study rather than near the leading edge as has been done in other studies. A theoretical basis for this choice has been provided for nondispersive (Ragozzino, 1981) and dispersive (Wear, 2000) media. It has been shown that substantial variations in sound-speed estimates, on the order of 40-50 m/s, may be obtained in human trabecular bone from variations in marker location (Laugier et al., 1993, and Wear, 2000).

Generally speaking, when comparing measurements performed using different systems, phase velocity at a specified frequency may provide a more standard, less variable, measurement than group velocity. This is due to the fact that a group velocity measurement will exhibit some dependence on the spectral content of the broadband pulse. This spectrum will be a function of the frequency-dependent electromechanical response functions of the transducers as well as the system frequency-dependent diffraction properties (which are determined by size, shape, focussing properties, and separation distance of the transmitting and receiving transducers). Changes in these properties (which may vary substantially among different commercial systems) would be expected to produce changes in group velocity measurements. Phase velocity measurements at a specified frequency, on the other hand, would be expected to be much less sensitive to system electromechanical and diffraction properties.

Table 1 summarizes measurements of velocity dispersion reported in four papers. The values measured in the present study are comparable to those reported by Droin, Berger, and Laugier (1998) and somewhat lower than those reported by Strelitzki and Evans (1996a) and Nicholson et al. (1996).

Recent studies suggest that the standard ultrasonic measurements of velocity and attenuation correlate highly with bone mineral density (BMD) but unfortunately provide little or no histomorphometric information (trabecular size, separation, number density, etc.) beyond that predicted by BMD (Laugier et al., 1997, Nicholson et al., 1998, Hans et al., 1999). These microarchitectural properties have definite relationships with bone strength and fracture risk. The magnitude of dispersion, on the other hand, was found to be virtually independent of BMD in this experiment (see Figure 5). If the magnitude of dispersion is related to histomorphometric properties of trabecular bone, as has been postulated (Droin, 1998), then this measurement could convey important structural information not already contained in BMD, sound speed, or broadband ultrasonic attenuation.

Acknowledgements

The author is grateful for funding provided by the US Food and Drug Administration Office of Women’s Health.

References

  1. Alves JM, Ryaby JT, Kaufman JJ, Magee PP, and Siffert RS. Influence of marrow on ultrasonic velocity and attenuation in bovine trabecular bone. Calc. Tissue. Int 1996; 58:362–367. [DOI] [PubMed] [Google Scholar]
  2. Bauer DC, Glüer CC, Cauley JA et al. Broadband ultrasound attenuation predicts fractures strongly and independently of densitometry in older women, Arch. Intern, Med 1997; 157:629–634. [PubMed] [Google Scholar]
  3. Cummings SR, Black DM, Nevitt MC, et al. Bone density at various sites for prediction of hip fractures. Lancet. 1993; 341,72–75. [DOI] [PubMed] [Google Scholar]
  4. Droin P, Berger G, and Laugier P. Velocity dispersion of acoustic waves in cancellous bone. IEEE Trans. Ultrason. Ferro. Freq. Cont 1998; 45,581–592. [DOI] [PubMed] [Google Scholar]
  5. Duck FA. Physical properties of tissue. Cambridge, UK: University Press, 1990. [Google Scholar]
  6. Glüer CC, Cummings SR, Bauer DC et al. , Osteoporosis: Association of recent fractures with quantitative US findings, Radiology. 1996; 199:725–732. [DOI] [PubMed] [Google Scholar]
  7. Hans D, Dargent-Molina P, Schott AM et al. , Ultrasonographic heel measurements to predict hip fracture in elderly women: the EPIDOS prospective study, Lancet. 1996; 348:511–514. [DOI] [PubMed] [Google Scholar]
  8. Hans D, Wu C, Njeh CF et al. Ultasound velocity of trabecular cubes reflects mainly bone density and elasticity. Calcif. Tissue Intl 1999; 64:18–23. [DOI] [PubMed] [Google Scholar]
  9. Kaufman JJ, Xu W, Chiabrera AE, and Siffert RS, Diffraction effects in insertion mode estimation of ultrasonic group velocity, IEEE Trans. Ultrason. Ferroelectr. Freq. Contr, 1995; 42:232–242. [Google Scholar]
  10. Kaye GWC, and Laby TH. Table of Physical and Chemical Constants. London, UK: Longman, 1973. [Google Scholar]
  11. Langton CM, Njeh CF, Hodgskinson R, et al. , Prediction of Mechanical Properties of the Human Calcaneus by Broadband Ultrasonic Attenuation. Bone.1996; 18:495–503. [DOI] [PubMed] [Google Scholar]
  12. Laugier P, Giat P, Droin P, Saied A, and Berger G. Ultrasound images of the os calcis: a new method of assessment of bone status. Proc. 1993 IEEE Ultrasonics Symp., vol.2, 989–92. [Google Scholar]
  13. Laugier P, Droin P, Laval-Jeantet AM, and Berger G. In vitro assessment of the relationship between acoustic properties and bone mass density of the calcaneus by comparison of ultrasound parametric imaging and quantitative computed tomography. Bone. 1997; 20:157–165. [DOI] [PubMed] [Google Scholar]
  14. Morse PM and Ingard KU. Theoretical Acoustics. Princeton, NJ. Princeton University Press, 1986, chapter 9. [Google Scholar]
  15. Nicholson PHF, Lowet G, Langton CM, Dequeker J, and Van der Perre G, Comparison of time-domain and frequency-domain approaches to ultrasonic velocity measurements in trabecular bone, Phys. Med. Biol 1996; 41:2421–2435. [DOI] [PubMed] [Google Scholar]
  16. Nicholson PHF, Müller R, Lowet G, et al. Do quantitative ultrasound measurements reflect structure independently of density in human vertebral cancellous bone? Bone. 1998; 23:425–431. [DOI] [PubMed] [Google Scholar]
  17. Njeh CF, Hodgskinson R, Currey JD, and Langton CM. Orthogonal relationships between ultrasonic velocity and material properties of bovine cancellous bone. Med. Eng. Phys, 1996; 18:373–381. [DOI] [PubMed] [Google Scholar]
  18. Njeh CF and Langton CM. The effect of cortical endplates on ultrasound velocity through the calcaneus: an in vitro study. Brit. J. Radiol 1997; 70:504–510. [DOI] [PubMed] [Google Scholar]
  19. Ragozzino M Analysis of the error in measurement of ultrasound speed in tissue due to waveform deformation by frequency-dependent attenuation. Ultrasonics. 1981; 19:135–138 [DOI] [PubMed] [Google Scholar]
  20. Rossman P, Zagzebski J, Mesina C, Sorenson J, and Mazess R, Comparison of Speed of Sound and Ultrasound Attenuation in the Os Calcis to Bone Density of the Radius, Femur and Lumbar Spine, Clin. Phys. Physiol. Meas, 1989; 10:353–360. [DOI] [PubMed] [Google Scholar]
  21. Schott AM, Weill-Engerer S, Hans D, et al. , Ultrasound discriminates patients with hip fracture equally well as dual energy X-ray absorptiometry and independently of bone mineral density. J. Bone Min. Res, 1995; 10:243–249. [DOI] [PubMed] [Google Scholar]
  22. Strelitzki R, and Evans JA, On the measurement of the velocity of ultrasound in the os calcis using short pulses, Eur. J. Ultrasound 1996; 4:205–213. [Google Scholar]
  23. Strelitzki R, Clarke AJ, and Evans JA, The measurement of the vlocity of ultrasound in fixed trabecular bone using braodband pulses and single-frequency tone bursts, Phys. Med. Biol 1996; 41:743–753. [DOI] [PubMed] [Google Scholar]
  24. Tavakoli MB and Evans JA. Dependence of the velocity and attenuation of ultrasound in bone on the mineral content. Phys. Med. Biol, 1991; 36:1529–1537. [DOI] [PubMed] [Google Scholar]
  25. Thompson P, Taylor J, Fisher A, and Oliver R, Quantitative heel ultrasound in 3180 women between 45 and 75 years of age: compliance, normal ranges and relationship to fracture history, Osteo. Int’l 1998; 8:211–214. [DOI] [PubMed] [Google Scholar]
  26. Trebacz H, and Natali A. Ultrasound velocity and attenuation in cancellous bone samples from lumbar vertebra and calcaneus. Osteo. Int’l, 1999; 9:99–105. [DOI] [PubMed] [Google Scholar]
  27. Turner CH, Peacock M, Timmerman L, et al. Calcaneal ultrasonic measurements discriminate hip fracture independently of bone mass, Osteo. International, 1995; 5:130–135. [DOI] [PubMed] [Google Scholar]
  28. Wear KA. The effects of frequency-dependent attenuation and dispersion on sound speed measurements: applications in human trabecular bone. IEEE Trans. Ultrason. Ferro. Freq. Cont, 2000; in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Zagzebski JA, Rossman PJ, Mesina C, Mazess RB, and Madsen EL. Ultrasound transmission measurements through the os calcis. Calcif Tissue Int. 1991; 49:107–111. [DOI] [PubMed] [Google Scholar]

RESOURCES