Modeling the invasion and establishment of a tick-borne pathogen

Abstract

We develop a discrete-time tick–host–pathogen model to describe the spread of a disease in a hard-bodied tick species. This model incorporates the developmental stages for a tick, the dependence of the tick life-cycle and disease transmission on host availability, and three sources of pathogen transmission. We first establish the global dynamics of the disease-free system. We then apply the model to two pathogens, Borellia burgdorferi and Anaplasma phagocytophila, using Ixodes ricinus as the tick species to study properties of the invasion and establishment of a disease numerically. In particular, we consider the basic reproduction number, which determines whether a disease can invade the tick-host system, as well as disease prevalence and time to establishment in the case of successful disease invasion. Using Monte Carlo simulations, we calculate the means of each of these disease metrics and their elasticities with respect to various model parameters. We find that increased tick survival may help enable disease invasion, decrease the time to disease establishment, and increase disease prevalence once established. In contrast, though disease invasion is sensitive to tick-to-host transmission and tick searching efficiencies, neither disease prevalence nor time to disease establishment is sensitive to these parameters. These differences emphasize the importance of developing approaches, such as the one highlighted here, that can be used to study disease dynamics beyond just pathogen invasion, including transitional and long-term dynamics.

1. Introduction

Worldwide, ticks are one of the most important vectors of human diseases. In the United States, they account for 95% of vector-borne diseases reported annually (Rochlin and Toledo, 2020; Sonenshine, 2018; Troughton and Levin, 2007). In recent decades, geographical expansions of tick populations, as well as local abundances in both pre-existing and newly established locations, have increased dramatically (Sonenshine, 2018). These increases have been attributed to reforestation and the coinciding expansions of deer populations, such as in northeastern United States, and to climate change (Ogden et al., 2014; Ostfeld and Brunner, 2015; Sonenshine, 2018; Troughton and Levin, 2007). Concurrent to this range expansion has been an increase in the incidence of tick-borne diseases including Lyme disease and human ehrlichiosis in the United States, and tick-borne encephalitis and haemorrhagic fever in Europe and Asia (Rochlin and Toledo, 2020). Understanding the complexities involved in the emergence and establishment of tick-borne diseases is crucial for mitigating the impacts of these emerging disease threats.

In epidemiological modeling, the next-generation-matrix approach is used to calculate the basic reproduction number R₀ from an SIR-type compartmental model in which individuals are classified according to infection status, such as susceptible, infected, or recovered. The next generation matrix describes how much an individual of a particular infection status contributes to new infections and the basic reproduction number R₀ is calculated as the dominant eigenvalue of this matrix. This quantity provides a single threshold value that determines whether the introduction of an infectious individual into an entirely susceptible population will result in an epidemic (Allen and Van den Driessche, 2008). Calculation of R₀ relies on a system of equations that gives the densities over time of the various ecological and epidemiological states involved in the disease spread. Previously, this approach has been applied to calculate R₀ for continuous-time, ordinary differential equation models of tick-borne pathogens (Norman et al., 1999; Rosa et al., 2003; Rosa and Pugliese, 2007). A major emphasis of these models has been to understand how the presence of a non-competent host impacts disease invasion. More detailed models, which include features such as temperature and seasonal activity, have also been investigated numerically using the software program STELLA, see for instance (Ogden et al., 2005, 2007, 2013, 2014). These models have been used to explore how seasonal asynchrony in immature questing and climate change may affect tick and disease dynamics.

Modeling of tick-borne diseases can be quite complicated since it involves multiple species, multiple transmission routes, and dependence on life-stage specific differences in transmission (Hartemink et al., 2008). To circumvent these difficulties, an alternative next-generation-matrix approach has been developed that computes the next generation matrix directly from biological principles and does not rely on developing a system of model equations to describe time series dynamics (Davis and Bent, 2011; Hartemink et al., 2008; Matser et al., 2009). This approach has the advantage of being easily modified to account for additional factors, such as including additional host types. It also provides a threshold value R₀ that is more biologically meaningful than the quantity obtained via a modeling approach (Hartemink et al., 2008). However, while this approach provides information about disease invasion, it cannot be used to understand what happens after a disease has invaded.

In this paper, relying on fundamental biological principles of the disease, we develop an explicit, discrete-time tick–host–pathogen model to study the spread of a tick-borne infection in a hard-bodied tick population. This model incorporates the developmental stages for a tick – egg, larva, nymph, and adult – as well as the dependence on obtaining a blood meal for transitions between these stages to occur. It also includes three sources of transmission: systemic transmission, non-systemic (co-feeding) transmission, and transovarial transmission. Unlike many of the previously developed models (e.g., Norman et al., 1999; Rosa et al., 2003; Rosa and Pugliese, 2007), here we use a discrete time step to model the tick–host–pathogen interaction and include an egg stage. Though the egg stage does not contribute to the pathogen dynamics, since the time to hatching can take weeks or months (Padgett and Lane, 2001; Randolph, 2004), the inclusion of the egg stage helps to better capture the tick developmental dynamics.

The model developed here presents some advantages in contrast with the alternative next-generation-matrix approach and continuous-time models. Unlike the alternative next-generation-matrix approach, the model is described by a discrete-time dynamical system that can be used to generate disease dynamics in the form of time-series. This allows for the understanding of specific pre-disease dynamics and post-invasion disease dynamics, and thus presents a tool to examine different disease metrics and study control strategies and scenarios. In comparison with continuous-time models in the form of differential equations, it is much easier and faster to solve computationally a discrete-time system to generate time-series dynamics and does not require efficient numerical solvers. This is important when it comes to studying sensitivity and elasticity analysis, parameter estimation, and control problems associated with such diseases which usually involve solving the model many times until an optimal control or parameter is found.

We use this model to examine three disease metrics: pathogen invasion, prevalence, and time to establishment. Given the uncertainty surrounding tick ecology and pathogens, as well as the dependence of both the tick life-cycle and disease prevalence on environmental factors (Halos et al., 2010; Sonenshine, 2018), rather then working with point estimates for model parameters here we follow Matser et al. (2009) and instead consider ranges for parameter values. Specifically, we apply Monte Carlo simulations in which parameters are chosen uniformly from specified intervals. We apply this approach to two tick pathogens Borellia burgdorferi and Anaplasma phagocytophila using Ixodes Ricinus, a major vector of these diseases in Europe, as the tick species. We calculate means of the three disease metrics as well as the elasticity of these metrics to various model parameters.

In order to test whether the established model produces biologically reasonable predictions, we compare estimates for R₀ and its elasticities to those obtained in Matser et al. (2009) using the alternative next-generation-matrix approach. We find that, though not all assumptions used in these two fundamentally different modeling approaches are the same, they produce similar results. All together, these calculations help identify which biological processes may be driving disease invasion and establishment.

2. Model development

In this section we provide a detailed derivation of the tick–host–pathogen model. We first present a discrete-time, stage-structured tick model in which biological processes depend on obtaining a blood meal from a host. We then derive expressions for systemic and non-systemic pathogen transmission before giving the full model.

2.1. Baseline tick model without disease

We describe a female hard-tick population using a discrete-time, stage-structured model consisting of fours developmental stages: egg E, larva L, nymph N, and adult A. A female tick that survives to reproduce will consume three blood meals in its lifetime. We assume that the tick species is a three-host species meaning that each of these blood meals will occur on a different host individual. The three host-seeking developmental stages (larva, nymph, and adult) often have different host preferences, with the immature stages feeding on smaller hosts such as lizards, birds and small to medium-sized mammals and the adult stage feeding on a larger hosts such as hedgehogs, hares, deer and domestic livestock (Gray et al., 2016). Here we assume two distinct host classes with the larvae and nymphs feeding on a small host h and the adults feeding on a large host H. These assumptions are appropriate for some species of hard tick from the genera Amblyomma spp., Dermacentor spp., Ixodes spp., Ornithodoros spp., and Rhipicephalus spp..

With the exception of the egg stage, in order for a tick individual to transition to the next developmental stage or reproduce, it must both reach developmental maturity and obtain a blood meal. Let γ_j denote the probability of a stage j tick reaching developmental maturity conditioned it has obtained a blood meal. We assume that this quantity, which accounts for the delay between feeding in one developmental stage and actively questing in the next, is equivalent to the probability of a stage j individual feeding from a host conditioned it has encountered a host. Define $e^{-a_{j}k}$ to be the probability a stage j tick does not encounter a host of type K, where the proportionality constant a_j may be interpreted as representing the searching efficiency of stage j. Then the probability of a tick transitioning to the next developmental stage (or an adult reproducing) is the probability of the tick reaching developmental maturation and having at least one host encounter ${\gamma }_j\left(1-e^{-a_{j}k}\right)$. Meanwhile, if both of these events do not occur, $1-{\gamma }_j\left(1-e^{-a_{j}k}\right)$, then the tick does not mature to the next developmental stage and may remain in its current stage. In either case, in order for a tick to be present in the next time unit, it must also survive the current time interval, as is determined by the survival probability s_j. We note that the nonlinearity $e^{-a_{j}k}$ may arise if, for instance, it is assumed that encounters follow a Poisson distribution.

The model equations are given by

$$\begin{gathered} E\left(t+1\right)\hspace{1em}=\beta \left[{\gamma }_A\left(1-e^{-a_{A}H\left(t\right)}\right)A\left(t\right)\right]s_A{\gamma }_A\left(1-e^{-a_{A}H\left(t\right)}\right)A\left(t\right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+s_E\left(1-{\gamma }_E\right)E\left(t\right), \\ L\left(t+1\right)\hspace{1em}=s_E{\gamma }_{E}E\left(t\right)+s_L\left(1-{\gamma }_L\left(1-e^{-a_{L}h\left(t\right)}\right)\right)L\left(t\right), \\ N\left(t+1\right)\hspace{1em}=s_L{\gamma }_L\left(1-e^{-a_{L}h\left(t\right)}\right)L\left(t\right)+s_N\left(1-{\gamma }_N\left(1-e^{-a_{N}h\left(t\right)}\right)\right)N\left(t\right), \\ A\left(t+1\right)\hspace{1em}=s_N{\gamma }_N\left(1-e^{-a_{N}h\left(t\right)}\right)N\left(t\right)+s_A\left(1-{\gamma }_A\left(1-e^{-a_{A}H\left(t\right)}\right)\right)A\left(t\right), \\ h\left(t+1\right)\hspace{1em}=\frac{{\beta }_{h}h\left(t\right)}{1+c_{h}h\left(t\right)}+s_{h}h\left(t\right), \\ H\left(t+1\right)\hspace{1em}=\frac{{\beta }_{H}H\left(t\right)}{1+c_{H}H\left(t\right)}+s_{H}H\left(t\right), \end{gathered}$$ (1)

where we take the unit of time to be one month. We define the tick fecundity β as the Beverton–Holt nonlinearity

$$\beta \left(x\right)=\frac{{\beta }_0}{1+cx},$$

where β₀ is the inherent (density-independent) fecundity and c > 0 is an intraspecific competition coefficient. This is the equivalent of logistic growth for discrete-time models. Since reproduction occurs on hosts and after a blood meal, we have assumed that the density effect is a function of feeding adults rather than all adults. Notice that a female tick will only reproduce once in its lifetime, with death following. We assume that fecundity for each of the host species is defined in an equivalent manner and that each host has a density-independent survival probability s_k.

2.2. The disease model

To incorporate the pathogen, we assume that individuals in each developmental stage may be in one of two disease states, either susceptible S or infectious I, where the disease state is indicated by a subscript. Thus L_S and L_I denote the densities of susceptible and infectious larvae, respectively. Similarly, both hosts types are assumed to be competent hosts and are also assigned disease states S or I. Once infected, ticks are assumed to remain infected with 100% transstadial transmission. Thus, once a tick is infected it remains infected until death. The hosts, meanwhile, recover from infection with recovery determined by the average length of infection.

For the tick population, we consider three types of infection: systemic infection from a susceptible tick feeding on an infected host, non-systemic co-feeding infection from susceptible and infectious ticks feeding on a host at the same time, and transovarial transmission (i.e., infected adults laying infected eggs). For hosts, the only type of infection considered is systemic infection arising from an infected tick feeding on a susceptible host.

Before giving the complete model, we first provide a detailed description of how each of these sources of infection are derived for the model. To simplify the discussion, we describe infection in the larva stage, with equivalent terms for the other stages defined in a similar manner.

2.2.1. Systemic infection: host to tick

Consider the larva stage. A mature larva individual has two options: to feed on a susceptible small host h_S or an infected small host h_I. Since a larva individual will only feed once, we assume that a fraction ϕ_h of the mature larvae will to feed on h_I hosts and the remaining fraction (1 – ϕ_h) will to feed on h_s hosts. A similar formulation was used in van den Driessche and Yakubu (2020) to define a situation in which only one type of infectious encounter, either with an infected juvenile or an infected adult, was allowed per unit time. Unlike van den Driessche and Yakubu (2020), rather than assuming ϕ_h is constant, we define ϕ_h as

$${\varphi }_h={\varphi }_h^0+\left(1-{\varphi }_h^0\right)\frac{h_I}{h_C},$$

where ${\varphi }_h^0\approx 0$ and h_c is the small host carrying capacity. Thus, ${\varphi }_h\approx 0$ when infected hosts are rare and ${\varphi }_h\approx 1$ when they dominate the host population.

We note that a more natural definition for ϕ_h might be

$${\varphi }_h=\frac{h_I}{h_S+h_I}.$$

However, defining ϕ_h in this manner creates a technical issue when applying the basic reproduction number theory. Specifically, we require that the Jacobian matrix formed from the disease states evaluated at the disease-free equilibrium is irreducible (Allen and Van den Driessche, 2008). Since this does not hold in this case, the basic reproduction number R₀, at least as calculated using the next-generation-matrix approach, does not correctly predict the invasion of a disease. Heuristically, the issue that arises is that evaluation of the Jacobian matrix at zero disease density should represent what happens at ‘‘low disease density’’ but, by defining ϕ_h in this manner, the first derivative of the infection terms describing infection in ticks by hosts in model (2) when evaluated at zero disease density vanishes. See for instance the first term in the equation N_I of model (2).

Following the same assumptions as the disease-free model, the probability that a mature susceptible larva successfully encounters a susceptible host is $\left(1-e^{-a_L{h}_S}\right)$ and the probability a mature susceptible larva successfully encounters an infectious host is $\left(1-e^{-a_L{h}_I}\right)$. All together we have $\left(1-e^{-a_L{h}_S}\right)\left(1-{\varphi }_h\right){\gamma }_L{L}_S$ susceptible larvae feed on h_s and $\left(1-e^{-a_L{h}_I}\right){\varphi }_h{\gamma }_L{L}_S$ feed on h_I. Defining p_L to be the probability that a meal on an infected host results in infection, we have that feeding results in $p_L\left(1-e^{-a_L{h}_I}\right){\gamma }_L{\varphi }_h{L}_S$ infections. Each of the transition terms (either maturation, or maturation and infection) is multiplied by a probability s_L that a larva survives a unit of time. Here we make the simplifying assumption that survival is not impacted by infection state.

Alternatively, a larva may remain in the larva stage if it does not obtain a blood meal. The number of susceptible larvae that do not feed but survive to the next time unit is given by

$$s_L\left(\left(1-{\varphi }_h\right)\left(1-{\gamma }_L\left(1-e^{-a_L{h}_S}\right)\right)+{\varphi }_h\left(1-{\gamma }_L\left(1-e^{-a_L{h}_I}\right)\right)\right)L_S$$

and an equivalent term may be defined for the infectious larvae. Since we assume 100% transstadial transmission, an infectious larva may become an infectious nymph if it feeds and survives molting, which is given by

$$s_L\left(\left(1-{\varphi }_h\right){\gamma }_L\left(1-e^{-a_L{h}_S}\right)+{\varphi }_h{\gamma }_L\left(1-e^{-a_L{h}_I}\right)\right)L_I.$$

Equivalent terms may be defined for the nymph and adult stages, where adults are assumed to feed on the larger hosts H.

2.2.2. Systemic infection: tick to host

Define v_j to be the probability a bite from an infectious tick of stage j results in an infection in a host individual. Assuming an individual small host has on average $a_L{L}_I$ encounters with infectious larvae per time unit, the probability that a host does not become infected from encounters with L_I is ${\left(1-v_L\right)}^{a_L{L}_I}$. Similarly, the probability a host does not become infected from encounters with N_I is ${\left(1-v_N\right)}^{a_N{N}_I}$. Thus overall, the probability a small host does not become infected is

$${\left(1-v_L\right)}^{a_L{L}_I}{\left(1-v_N\right)}^{a_N{N}_I}=\exp \left[-\left(a_L{\omega }_L{L}_I+a_N{\omega }_N{N}_I\right)\right],$$

where ${\omega }_j=\left|\ln \left(1-v_j\right)\right|$. A similar term may be defined for large hosts H, where infection is assumed to occur due to encounters with infected adults ticks.

Infection was defined in this manner in Lewis et al. (2006), which considered a single infectious state. Alternatively, to define infection from multiple infectious states, in Allen and Van den Driessche (2008) it was assumed that the probability of infection follows a Poisson distribution with the weights ω_i defining the impacts of the different stages. This leads to the probability of no infection for an individual h_s being the same form as we have here, $e^{-a_L{\omega }_L{L}_I-a_N{\omega }_N{N}_I}$. However, the above derivation allows for a direct biological interpretation of weights ω_i. Notice that systemic infections in hosts are assumed to follow from density-dependent (mass action) incidence rates, motivated by the assumption that higher tick densities will lead to higher tick burdens.

2.2.3. Non-systemic infection: Co-feeding transmission

Define η_ji to be the probability that a susceptible stage j tick is infected from co-feeding on a host with an infected tick of stage i. Then the probability a stage L_S tick is not infected due to co-feeding with infectious individuals on a small infected host is given by

$${\left(1-{\eta }_{LL}\right)}^{\frac{{\varphi }_h\left(1-e^{-a_L{h}_I}\right)L_I}{k_L{h}_I}}{\left(1-{\eta }_{LN}\right)}^{\frac{{\varphi }_h\left(1-e^{-a_N{h}_I}\right)N_I}{k_L{h}_I}}$$

where ${\varphi }_h\left(1-e^{-a_L{h}_I}\right)L_I$ and ${\varphi }_h\left(1-e^{-a_L{h}_I}\right)N_I$ are the number of infectious larvae and nymph ticks, respectively, that feed on infected hosts in the given time period. This quantity is divided by k_Lh_I to account for individuals feeding on different hosts and at different days during the time interval. Here k_L is the average number of larval feedings that can occur in one unit time and is obtained by dividing 30 days by the average number of days that larvae feed. This may be rewritten in the equivalent form

$$e^{-\frac{1}{k_L{h}_I}\left({\lambda }_{LL}{\varphi }_h\left(1-e^{-a_L{h}_I}\right)L_I+{\lambda }_{LN}{\varphi }_h\left(1-e^{-a_N{h}_I}\right)N_I\right)},$$

where ${\lambda }_{ik}=\left|\ln \left(1-{\eta }_{ik}\right)\right|$. Meanwhile, the probability a stage L_S tick is not infected due to co-feeding with infectious individuals on a small susceptible host is given by

$${\left(1-{\eta }_{LL}\right)}^{\frac{\left(1-{\varphi }_h\right)\left(1-e^{-a_L{h}_S}\right)L_I}{k_L{h}_S}}{\left(1-{\eta }_{LN}\right)}^{\frac{\left(1-{\varphi }_h\right)\left(1-e^{-a_N{h}_S}\right)N_I}{k_L{h}_S}}.$$

Similar terms may be defined for co-feeding infection in nymphs and adults, where nymphs may be infected through co-feeding with infected larvae or nymphs but adults may be infected only through co-feeding with infected adults since we have assumed that the adults do not feed on the same hosts as the immature stages.

2.2.4. The full model

The full tick–host–pathogen model is defined as follows:

$$\begin{gathered} E_S^{\prime }=\beta \left[{\gamma }_A{\Phi }_{A}A\right]s_A{\gamma }_A[\left(1-{\varphi }_H\right)\left(1-e^{-a_A{H}_S}\right){\Psi }_{AS}{A}_S \\ \hspace{1em}\hspace{0.17em}+\left(1-r_A\right)\left(1-{\varphi }_H\right)\left(1-e^{-a_A{H}_S}\right)\left(1-{\Psi }_{AS}\right)A_S+\left(1-p_A\right) \\ \hspace{1em}\hspace{0.17em}\times {\varphi }_H\left(1-e^{-a_A{H}_I}\right){\Psi }_{AI}{A}_S \\ \hspace{1em}\hspace{0.17em}+\left(1-r_A\right)\left(1-p_A\right){\varphi }_H\left(1-e^{-a_A{H}_I}\right)\left(1-{\Psi }_{AI}\right)A_S \\ \hspace{1em}\hspace{0.17em}+\left(1-r_A\right)p_A{\varphi }_H\left(1-e^{-a_A{H}_I}\right)A_S+\left(1-r_A\right){\Phi }_A{A}_I] \\ \hspace{1em}\hspace{0.17em}+s_E\left(1-{\gamma }_E\right)E_S, \\ {L}_S^{\prime }=s_E{\gamma }_E{E}_S+s_L{\Gamma }_L{L}_S, \\ {N}_S^{\prime }=s_L\left(1-{\varphi }_h\right){\gamma }_L\left(1-e^{-a_L{h}_S}\right){\Psi }_{LS}{L}_S+s_L\left(1-p_L\right){\varphi }_h{\gamma }_L\left(1-e^{-a_L{h}_I}\right) \\ \hspace{1em}\hspace{0.17em}\times {\Psi }_{LI}{L}_S \\ \hspace{1em}\hspace{0.17em}+s_N{\Gamma }_N{N}_S, \\ {A}_S^{\prime }=s_N\left(1-{\varphi }_h\right){\gamma }_N\left(1-e^{-a_N{h}_S}\right){\Psi }_{NS}{N}_S+s_N\left(1-p_N\right){\varphi }_h{\gamma }_N\left(1-e^{-a_N{h}_I}\right) \\ \hspace{1em}\hspace{0.17em}\times {\Psi }_{NI}{N}_S \\ \hspace{1em}\hspace{0.17em}+s_A{\Gamma }_A{A}_S, \\ {h}_S^{\prime }=\frac{{\beta }_{h}h}{1+c_{h}h}+s_h{e}^{-a_L{\omega }_L{L}_I-a_N{\omega }_N{N}_I}{h}_s+s_h{\gamma }_h{h}_I, \\ {H}_S^{\prime }=\frac{{\beta }_{H}H}{1+c_{H}H}+s_H{e}^{-a_A{\omega }_A{A}_I}{H}_s+s_H{\gamma }_H{H}_I, \\ {E}_I^{\prime }=\beta \left[{\gamma }_A{\Phi }_{A}A\right]s_A{\gamma }_A[r_A\left(1-{\varphi }_H\right)\left(1-e^{-a_A{H}_S}\right)\left(1-{\Psi }_{AS}\right)A_S \\ \hspace{1em}\hspace{0.17em}+r_A\left(1-p_A\right){\varphi }_H\left(1-e^{-a_A{H}_I}\right)\left(1-{\Psi }_{AI}\right)A_S \\ \hspace{1em}\hspace{0.17em}+r_A{p}_A{\varphi }_H\left(1-e^{-a_A{H}_I}\right)A_S+r_A{s}_A{\Phi }_A{A}_I]+s_E\left(1-{\gamma }_E\right)E_I, \\ {L}_I^{\prime }=s_E{\gamma }_E{E}_I+s_L{\Gamma }_L{L}_I, \\ {N}_I^{\prime }=s_L{p}_L{\varphi }_h{\gamma }_L\left(1-e^{-a_L{h}_I}\right)L_S+s_L\left(1-p_L\right){\varphi }_h{\gamma }_L\left(1-e^{-a_L{h}_I}\right)\left(1-{\Psi }_{LI}\right)L_S \\ \hspace{1em}\hspace{0.17em}+s_L{\gamma }_L{\Phi }_L{L}_I+s_L\left(1-{\varphi }_h\right){\gamma }_L\left(1-e^{-a_L{h}_S}\right)\left(1-{\Psi }_{LS}\right)L_S+s_N{\Gamma }_N{N}_I, \\ {A}_I^{\prime }=s_N{p}_N{\varphi }_h{\gamma }_N\left(1-e^{-a_N{h}_I}\right)N_S+s_N\left(1-p_N\right){\varphi }_h{\gamma }_N\left(1-e^{-a_N{h}_I}\right) \\ \hspace{1em}\hspace{0.17em}\times \left(1-{\Psi }_{NI}\right)N_S \\ \hspace{1em}\hspace{0.17em}+s_N{\gamma }_N{\Phi }_N{N}_I+s_N\left(1-{\varphi }_h\right){\gamma }_N\left(1-e^{-a_N{h}_S}\right)\left(1-{\Psi }_{NS}\right)N_S+s_A{\Gamma }_A{A}_I, \\ {h}_I^{\prime }=s_h\left(1-e^{-a_L{\omega }_L{L}_I-a_N{\omega }_N{N}_I}\right)h_s+s_h\left(1-{\gamma }_h\right)h_I, \\ {H}_I^{\prime }=s_H\left(1-e^{-a_A{\omega }_A{A}_I}\right)H_s+s_H\left(1-{\gamma }_H\right)H_I, \end{gathered}$$ (2)

where A = A_I + A_S, ℎ = ℎ_S + h_I, and H = H_S + H_I. To reduce notation we use prime ′ to denote the next iterate and take the unit of time to be one month. The terms ${\Phi }_j$ and ${\Gamma }_j$ are defined as

$${\Phi }_j=\left(1-{\varphi }_h\right)\left(1-e^{-a_j{h}_S}\right)+{\varphi }_h\left(1-e^{-a_j{h}_I}\right),j=L,N,$$

$${\Gamma }_j=\left(1-{\varphi }_h\right)\left(1-{\gamma }_i\left(1-e^{-a_j{h}_S}\right)\right)+{\varphi }_h\left(1-{\gamma }_j\left(1-e^{-a_j{h}_I}\right)\right),j=L,N,$$

$${\Phi }_A=\left(1-{\varphi }_H\right)\left(1-e^{-a_A{H}_S}\right)+{\varphi }_H\left(1-e^{-a_A{H}_I}\right),$$

$${\Gamma }_A=\left(1-{\varphi }_H\right)\left(1-{\gamma }_A\left(1-e^{-a_A{H}_S}\right)\right)+{\varphi }_H\left(1-{\gamma }_A\left(1-e^{-a_A{H}_I}\right)\right),$$

and the co-feeding infection terms are defined using the quantities

$${\Psi }_{jS}=e^{-\frac{1}{k_j{h}_S}\left({\lambda }_{jL}\left(1-{\varphi }_h\right)\left(1-e^{-a_L{h}_S}\right)L_I+{\lambda }_{jN}\left(1-{\varphi }_h\right)\left(1-e^{-a_N{h}_S}\right)N_I\right)},j=L,N,$$

$${\Psi }_{jI}=e^{-\frac{1}{k_j{h}_I}\left({\lambda }_{jL}{\varphi }_h\left(1-e^{-a}{L}^{h}I\right)L_I+{\lambda }_{jN}{\varphi }_h\left(1-e^{-a_N{h}_I}\right)N_I\right)},j=L,N,$$

$${\Psi }_{AS}=e^{-\frac{1}{k_A{H}_S}\left({\lambda }_{AA}\left(1-{\varphi }_H\right)\left(1-e^{-a}{A}^{H}S\right)A_I\right)},$$

$${\Psi }_{AI}=e^{-\frac{1}{k_A{H}_I}\left({\lambda }_{AA}{\varphi }_H\left(1-e^{-a_A{H}_I}\right)A_I\right)}.$$

Here the tick parameters s_j, γ_j, and a_j and the nonlinearity β are defined the same as in the baseline model (1), as are the host parameters β_k, s_k, and c_k. Parameter r_A gives the probability of transovarial transmission, that is, it is the fraction of infected eggs produced by an infected adult. Notice that a susceptible adult that becomes infected during its third and last blood meal (either by systemic or non-systemic infection) may pass on the infection to her eggs. The meanings of the remaining parameters are provided in Tables 1 and 2. A schematic of model (2) is given in Fig. 1.

Table 1.

Life history parameter estimates for Ixodes ricinus and hosts based on a one-month time unit. Small host parameters are based on mice, while large host parameters are based on deer.

Parameter	Description	Estimate	Citation
β 0	Fecundity of an adult tick	750–1250	Matser et al. (2009)
c	Negative density-dependent coefficient	0.001–0.05	Estimated
${\tilde{s}}_E$	Egg survival probability	0.04–0.17	Matser et al. (2009)
${\tilde{s}}_L$	Larva survival probability	0.04–0.17	Matser et al. (2009)
${\tilde{s}}_N$	Nymph survival probability	0.04–0.17	Matser et al. (2009)
${\tilde{s}}_A$	Adult survival probability	0.1–0.17	Matser et al. (2009)
γE	Transition probability from egg to larva	1/4–1	Padgett and Lane (2001) and Randolph (2004)
γL	Transition probability from larva to nymph	1/14–1/10	Padgett and Lane (2001) and Randolph (2004)
γN	Transition probability from nymph to adult	1/12–1/6	Padgett and Lane (2001) and Randolph (2004)
γA	Transition probability from adult to reproduction	1/12–1/6	Padgett and Lane (2001) and Randolph (2004)
aL	Searching efficiency of larva	0.1–1	Estimated
aN	Searching efficiency of nymph	0.1–1	Estimated
aA	Searching efficiency of adult	0.1–1	Estimated
kL	Number of larva feedings that can occur in one time unit	7.5–15	Matser et al. (2009)
kN	Number of nymph feedings that can occur in one time unit	5–10	Matser et al. (2009)
kA	Number of adult feedings that can occur in one time unit	15/7–5	Matser et al. (2009)
βh	Fecundity of small hosts	0.75–1.5	Aguilar (2011)
βH	Fecundity of large hosts	0.108–0.15	DelGiudice et al. (2007)
hC	Carry capacity of small hosts	400–600	Estimated
HC	Carry capacity of large hosts	40–60	Estimated
sh	Small host survival probability	0.9167–0.9444	Aguilar (2011)
SH	Large host survival probability	0.9667–0.9722	Dewey (2003)
${\varphi }_h^0$	Proportion of immature ticks feeding on infected hosts	0.0001	Estimated
${\varphi }_H^0$	Proportion of adult ticks feeding on infected hosts	0.0001	Estimated

Table 2.

Pathogen-specific parameter estimates for B. burgdorferi and A. phagocytophila based on a one-month time unit. All estimates are obtained from Matser et al. (2009). Note, however, that estimates for p_A and v_A provided in Matser et al. (2009) assume that same host species for all tick stages.

Parameter	Description	Borellia burgdorferi	Anaplasma phagocytophila
rA	Transovarial transmission probability	0–0.01	0–0.01
pL	Probability of systemic transmission from small host to larva	0.1–0.9	0.2–0.83
pN	Probability of systemic transmission from small host to nymph	0.1–0.9	0.015–0.2
pA	Probability of systemic transmission from small host to adult	0	0.01–0.6
vL	Probability of systemic transmission from larva to small host	0.6–0.99	0.041–0.2
vN	Probability of systemic transmission from nymph to small host	0.6–0.99	0.041–0.2
vA	Probability of systemic transmission from adult to large host	0	0.041–0.2
η	Co-feeding transmission probability	0.2–0.8	0.01–0.211
γh	Recovery probability for small hosts	1/40–6/7	1/67–6/7
γH	Recovery probability for large hosts	–	1/67, 6/7

Fig. 1.

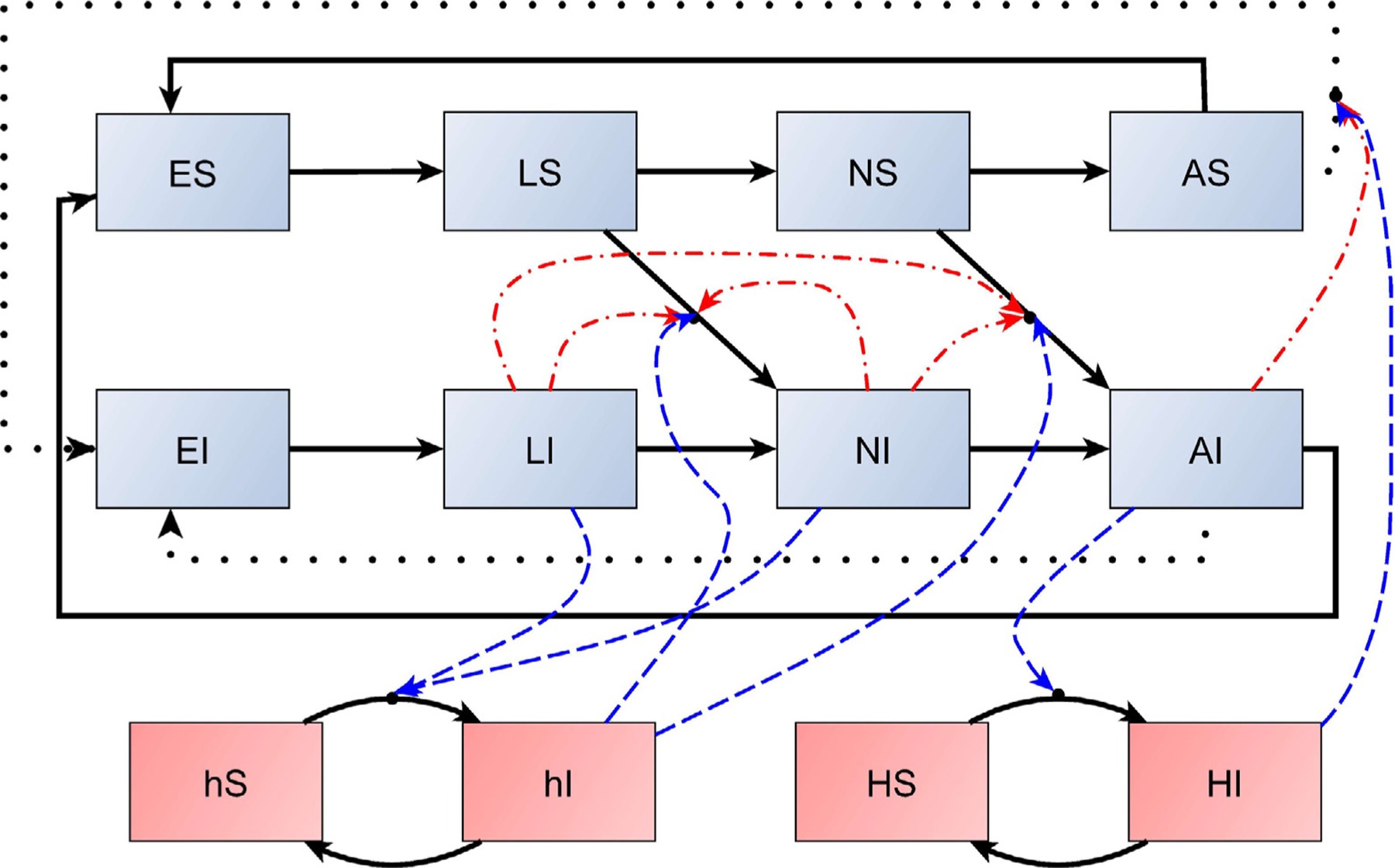
A schematic of model (2). Solid black lines denote developmental and disease-state transitions, dotted black lines denote transovarial transmission, dashed blue lines denote potential sources of systemic infection, and dashed–dotted red lines denote sources of co-feeding transmission. For example, after obtaining a blood meal a susceptible larva individual L_S may either mature to N_S if it escapes infection or mature to N_I if it becomes infected. Here there are two ways that infection may occur: either systemic infection from feeding on an infected host h_I, as indicated by a blue dashed line, or non-systemic infection by co-feeding with other infected larvae or nymphs, as indicated by the red dashed–dotted lines.

3. Persistence and global dynamics of the tick-host model

In this section we present a complete characterization of the global dynamics of the tick-host model, including the existence, uniqueness and global stability of the interior equilibrium of model (1). An understanding of the dynamics of model (1) is essential for studying the full tick–host–pathogen model as these describe the dynamics of model (2) in the absence of the disease. Omitted proofs of the statements below are provided in the Appendix.

First note that the difference equation system (1) can be written in the matrix form

$$x\left(t+1\right)=P\left(x\left(t\right)x\left(t\right)\right),$$ (3)

where $x\left(t\right)={\left(E\left(t\right),L\left(t\right),N\left(t\right),A\left(t\right),h\left(t\right),H\left(t\right)\right)}^{⊺}$ is a column vector containing the densities of the different stages and the projection matrix P has the form

$$P\left(x\right)=\left(\begin{array}{cc}{P}_1\left(x\right)& \mathbf{0}\\ \mathbf{0}& P_2\left(x\right)\end{array}\right),$$

where P₁(x) is given in Box I and

$$P_2\left(x\right)=\left(\begin{array}{cc}\frac{{\beta }_h}{1+c_{h}h}+s_h& 0\\ 0& \frac{{\beta }_H}{1+c_{H}H}+s_H\end{array}\right).$$

Next, observe that the equation for host h is decoupled from the rest of the system and the same is true for the equation for host H. It is not hard to show that for k = h, H if β_k + s_k > 1 and k(0) > 0, then each host population converges to its carrying capacity,

$$\underset{t\to \infty }{\lim }k\left(t\right)=k_C=\frac{{\beta }_k-\left(1-s_k\right)}{c_k\left(1-s_k\right)}.$$ (4)

Box I.

$$P_1\left(x\right)=\left(\begin{array}{cccc}{s}_E\left(1-{\gamma }_E\right)& 0& 0& \beta \left[{\gamma }_A\left(1-e^{-a_{A}H}\right)A\right]s_A{\gamma }_A\left(1-e^{-a_{A}H}\right)\\ s_E{\gamma }_E& s_L\left(1-{\gamma }_L\left(1-e^{-a_{L}h}\right)\right)& 0& 0\\ 0& s_L\left(1-{\gamma }_L\left(1-e^{-a_{L}h}\right)\right)& s_N\left(1-{\gamma }_N\left(1-e^{-a_{N}h}\right)\right)& 0\\ 0& 0& s_N\left(1-{\gamma }_N\left(1-e^{-a_{N}h}\right)\right)& s_A\left(1-\left(1-{\gamma }_A\left(1-e^{-a_{A}H}\right)\right)\right)\end{array}\right)$$

Thus, for the rest of this section we focus on establishing a global stability result for the interior equilibrium of the model

$$x_1\left(t+1\right)=P_1\left(x_1\left(t\right),h_C,H_C\right)x_1\left(t\right)$$ (5)

where $x_1\left(t\right)={\left(E\left(t\right),L\left(t\right),N\left(t\right),A\left(t\right)\right)}^{⊺}$. Then, we lift up the global stability to the model (1) by utilizing results on asymptotically autonomous systems and (4). To this end, first note that it is not difficult to verify that

$$x_1\le y_1,\hspace{0.17em}\text{implies}\hspace{0.17em}{P}_1\left(y_1,h_C,H_C\right)\le P_1\left(x_1,h_C,H_C\right),$$ (6)

where x ≤ y denotes the usual, component-wise partial order on ${ℝ}^n$. Next, following Caswell (2000) and Cushing (1998) define $\widehat{T}$ as given in Box II and

$$\widehat{F}=\left(\begin{array}{cccc}0& 0& 0& {\beta }_0{s}_A{\gamma }_A\left(1-e^{-a_A{H}_C}\right)\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right).$$

Note that the inherent projection matrix of the nonlinear system for the tick sub-model (5) is

$$P_1\left(0\right)=\widehat{F}+\widehat{T}.$$

Thus, the inherent net reproductive number ${\widehat{R}}_0$, Which gives the expected number of offspring produced by a female throughout its life-time in the absence of density dependence, is the positive, simple and strictly dominant eigenvalue of $\widehat{F}{\left(I-\widehat{T}\right)}^{-1}$, where I denotes the identity matrix. A simple calculation shows that

$${\widehat{R}}_0=\frac{{\beta }_0{s}_E{s}_L{s}_N{s}_A{\gamma }_E{\gamma }_L{\gamma }_N{\gamma }_A\left(1-e^{-a_L{h}_C}\right)\left(1-e^{-a_N{h}_C}\right)\left(1-e^{-a_A{H}_C}\right)}{\left(1-s_E\left(1-{\gamma }_E\right)\right){\Pi }_{j=L,N}\left(1-s_j\left(1-{\gamma }_j\left(1-e^{-a_j{h}_C}\right)\right)\right)\left(1-s_A\left(1-{\gamma }_A\left(1-e^{-a_A{H}_C}\right)\right)\right)}.$$

By Theorem 1.1.3 in Cushing (1998) the inherent net reproductive number is on the same side of one as the spectral radius of P₁(0). Thus, we make use of ${\widehat{R}}_0$ in establishing the local and global dynamics of model (1). We now have the following result:

Box II.

$$\widehat{T}=\left(\begin{array}{cccc}{s}_E\left(1-{\gamma }_E\right)& 0& 0& 0\\ s_E{\gamma }_E& s_L\left(1-{\gamma }_L\left(1-e^{-a_L{h}_C}\right)\right)& 0& 0\\ 0& s_L{\gamma }_L\left(1-e^{-a_L{h}_C}\right)& s_N\left(1-{\gamma }_N\left(1-e^{-a_N{h}_C}\right)\right)& 0\\ 0& 0& s_N{\gamma }_N\left(1-e^{a_N{h}_C}\right)& s_A\left(1-{\gamma }_A\left(1-e^{-a_A{H}_C}\right)\right)\end{array}\right)$$

Lemma 3.1. Suppose ${\widehat{R}}_0<1$. Then the origin E₀ = (0, 0, 0, 0) is a globally asymptotically stable fixed point of system (5).

Next, we establish the existence, uniqueness and local stability of an interior fixed point.

Theorem 3.2. Suppose ${\widehat{R}}_0>1$. Then (5) has a unique interior fixed point ${\overline{x}}_1=\left(\overline{E},\overline{L},\overline{N},\overline{A}\right)$ which is locally asymptotically stable.

Lemma 3.3 establishes boundedness of solutions uniformly in the parameters.

Lemma 3.3. Let $\xi \stackrel{>}{\approx }0$. Define $K=\left[0,\widehat{{\rm E}}\right]\times \left[0,\widehat{L}\right]\times \left[0,\widehat{N}\right]\times \left[0,\widehat{A}\right]$, where

$$\widehat{{\rm E}}=\frac{{\beta }_0{s}_A}{c\left(1-s_E\left(1-{\gamma }_E\right)\right)}\left(1+\xi \right),$$

$$\widehat{L}=\frac{s_E{\gamma }_E}{1-s_L\left(1-{\gamma }_L\left(1-e^{-a_L{h}_C}\right)\right)}\widehat{{\rm E}}\left(1+\xi \right),$$

$$\widehat{N}=\frac{s_L{\gamma }_L\left(1-e^{a_L{h}_C}\right)}{1-s_N\left(1-{\gamma }_N\left(1-e^{-a_N{h}_C}\right)\right)}\widehat{L}\left(1+\xi \right),$$

$$\widehat{A}=\frac{s_N{\gamma }_N\left(1-e^{a_N{h}_C}\right)}{1-s_A\left(1-{\gamma }_A\left(1-e^{-a_A{H}_C}\right)\right)}\widehat{N}\left(1+\xi \right).$$

Then every forward solution of (5) enters K in finite time and remains in K forever after.

Next we show that if the net reproductive number is greater than one, then the origin is unstable and system (5) is uniformly persistent.

Theorem 3.4. Suppose ${\widehat{R}}_0>1$, then (5) is uniformly persistent.

Finally, we establish the global stability of the interior fixed point. The proof of this result relies on the following lemma from Ackleh and DeLeenheer (2008). Consider a map $G:{ℝ}^n\to {ℝ}^n$. We say that G is monotone if x ≤ y implies that G(x) ≤ G(y).

Lemma 3.5 (Ackleh and DeLeenheer, 2008). Let $G:{ℝ}^n\to {ℝ}^n$ be a continuous, monotone map and a ≤ b be points in ${ℝ}^n$. If a ≤ G(a) and G(b) ≤ b, and if G has a unique fixed point x∗in the ordered interval $\left[a,b\right]:=\left\{x\in {ℝ}^n|a\le x\le b\right\}$, then every solution sequence of the discrete system

$$x\left(t+1\right)=G\left(x\left(t\right)\right),$$ (7)

starting in [a, b], converges to x∗.

Theorem 3.6. Suppose that ${\widehat{R}}_0>1$. Then every solution of (5) starting in ${ℝ}_{+}^4\backslash \left\{\left(0,0,0,0\right)\right\}$ converges to the unique interior equilibrium. This equilibrium is globally asymptotically stable.

Proof. First observe that every solution starting on the boundary of ${ℝ}_{+}^4$, but not in (0, 0, 0, 0), enters the positively invariant set $\mathrm{int}\left({ℝ}_{+}^4\right)$. Therefore, it is enough to establish the theorem for solutions in $\mathrm{int}\left({ℝ}_{+}^4\right)$. To this end, pick $x_1\left(0\right)=\left(E\left(0\right),L\left(0\right),N\left(0\right),A\left(0\right)\right)\in \mathrm{int}\left({ℝ}_{+}^4\right)$. In fact, by Lemma 3.3 it suffices to consider $x_1\left(0\right)\in \mathrm{int}\left({ℝ}_{+}^4\right)\cap K$. The unique positive fixed point clearly belongs to K. Define $b=\left(\widehat{{\rm E}},\widehat{L},\widehat{N},\widehat{A}\right)$ (the maximal element in K). Then, by Lemma 3.3 we have that G(b) ≤ b (where G(x) denotes the right hand side of (5)). Clearly, G is monotone since the Jacobian of G, Gʹ(x), is a nonnegative matrix for all x. Since P₁(0) is an irreducible non-negative matrix, its spectral radius r (which we know is larger than 1 because ${\widehat{R}}_0>1$) is an eigenvalue with a corresponding positive eigenvector υ:

$$P_1\left(0\right)\upsilon =r\upsilon .$$

In addition, for all ϵ > 0 sufficiently small, it holds that

$$G\left(ϵ\upsilon \right)=rϵ\upsilon +o\left(ϵ\right)\ge ϵ\upsilon ,$$

since r > 1. Now for a given $x_1\left(0\right)\in \mathrm{int}\left({ℝ}_{+}^4\right)\cap K$, we can pick a sufficiently small ϵ > 0 such that

$$a=ϵ\upsilon \le x_1\left(0\right)\hspace{0.17em}\text{and}\hspace{0.17em}\le G\left(a\right).$$

It follows from an application of Lemma 3.5 that every solution of (5) starting in ${ℝ}_{+}^4\backslash \left\{\left(0,0,0,0\right)\right\}$ converges to the unique interior equilibrium.

The global asymptotic stability of the unique interior fixed point now follows from the local asymptotic stability in Theorem 3.2 together with the global attractivity established above. □

Next we establish the global stability of the interior equilibrium for the full model (1). To prove this theorem we rely on theory for asymptotically autonomous discrete dynamical systems in D’Aniello and Elaydi (2020) and Mokni et al. (2020).

Theorem 3.7. Suppose that ${\widehat{R}}_0>1$ and s_k + β_k > 1 for k = h, H. Then every solution of (1) with initial condition $int\left({ℝ}_{+}^4\right)\backslash \left(0,0,0,0\right),h\left(0\right)>0$ and H(0) > 0 converges to the unique interior equilibrium $\left(\overline{E},\overline{L},\overline{N},\overline{A},h_C,H_C\right)$.

Proof. By Theorem 3.2 in Mokni et al. (2020) it is sufficient to show that assumptions (A1) and (A2) in that paper are satisfied. Since, H(t) → H_C and h(t) → h_C exponentially due to the global asymptotic stability, then G_t defined by the right hand side mapping of the first four equation of (1) converge uniformly to G the map defined by the right-hand side of (5). Hence, (A1) is satisfied. As for (A2), this is clearly satisfied as it is easily seen that G_t maps $\mathrm{int}\left({ℝ}_{+}^4\right)\to \mathrm{int}\left({ℝ}_{+}^4\right)$. □

4. Case study: Borellia burgdorferi and Anaplasma phagocytophila in Ixodes ricinus

In this section, we apply model (2) to study two tick-borne pathogens: Borellia burgdorferi and Anaplasma phagocytophila. We use the hard-bodied tick species Ixodes Ricinus which is one of the primary vectors of these pathogens in Europe. I. ricinus is a three-host tick with immature stages preferring small hosts such as lizards, birds and small to medium-sized mammals and adult ticks preferring larger hosts such as hedgehogs, hares, deer and domestic livestock (Gray et al., 2016).

Estimates for life-history parameters and pathogen-specific parameters are provided in Tables 1 and 2. Tick and pathogen estimates primarily come from Matser et al. (2009). Since we model female ticks only, fecundity is estimated as half of the values provided in Matser et al. (2009). Survival probabilities in model (2) are estimated using $s_j={\tilde{s}}_j^{1/T_j}$ where ${\tilde{s}}_j$ is the stage-to-stage survival probability provided in Matser et al. (2009) and T_j is the average length of stage j. Meanwhile, we estimate the probability a stage j tick reaches maturation as the inverse of the average length of stage j, ${\gamma }_i=\frac{1}{T_j}$ (Caswell, 2000). Following Matser et al. (2009), we assume the same co-feeding transmission η for all tick stage. We base parameter estimates for small and large hosts on mice and deer, respectively. Note that, while deer are not competent reservoir for B. burgdorferi, they may be competent reservoirs for A. phagocytophila (Svitálková et al., 2015).

4.1. The basic reproduction number: Disease invasion

We first apply the next-generation-matrix approach to calculate the basic reproduction number R₀ which gives the expected number of secondary infections produced by a primary infection in a totally susceptible population (Allen and Van den Driessche, 2008). This quantity determines whether a pathogen will be able to invade the tick-host system. Specifically, a pathogen is able to invade the system if and only if R₀ > 1. Note that, in comparison, ${\widehat{R}}_0$ determines whether a tick population can invade a given location.

To calculate R₀ we follow Allen and Van den Driessche (2008). Namely, we first linearize the projection matrix of system (2) around the disease-free equilibrium $\left(\overline{E},\overline{L},\overline{N},\overline{A},h_C,H_C,0,0,0,0,0,0\right)$ of model (2) which is equivalent to the positive equilibrium of model (1) when ${\varphi }_h^0={\varphi }_H^0=0$ Recall that, in order for a non-trivial disease-free equilibrium exist we must have the inherent net reproductive number greater than one. This results in a block triangular matrix with the 6 × 6 lower right block corresponding to the Jacobian matrix for the disease states. We then decompose this 6 × 6 block matrix into a matrix F describing new infections and a matrix T containing all other types of transitions. The basic net reproduction number is calculated as the dominant eigenvalue of the next generation matrix defined as F (I −T )⁻¹, where I is the identity matrix. In many disease models, F is a low rank matrix which makes it possible to obtain an exact expression for the dominant eigenvalue of the matrix F (I − T )⁻¹. However, for model (2), since there are many sources of new infections, this is not the case and R₀ is a zero of a high degree polynomial for which solutions are not generally tractable. Therefore, we instead calculate R₀ numerically in MATLAB, using the built-in eig() function to calculate the dominant eigenvalue.

In addition to calculating R₀, we also consider the elasticity of R₀ with respect to changes in model parameters. The elasticity of R₀ with respect to parameter ξ is defined as

$$\frac{\zeta }{R_0}\frac{\partial R_0}{\partial \zeta },$$ (8)

and gives the proportional change in R₀ given a proportional change in the input ξ (Caswell, 2000). Elasticity calculations indicate which processes may be key drivers of disease invasion and can help identify important information gaps in parameter estimates.

Given both the variability and uncertainty surrounding tick ecology and pathogens, we choose to work with interval estimates rather than point estimates for the model parameters. Therefore, we compute R₀ for 20,000 sets of parameters chosen randomly from uniform distributions defined on the intervals given in Tables 1 and 2. For each simulation, R₀ is calculated as well as its elasticity with respect to proportional changes in the disease transmission parameters. All derivatives are calculated numerically using the standard forward difference approximation with step size 0.01. Approximately 1% of the simulations (238 and 239 for B. burgdorferi and A. phagocytophila, respectively) resulted in ${\widehat{R}}_0$ values less than one. Since this means the tick population dies out, these simulations were removed.

A histogram of the obtained R₀ estimates is provided in Fig. 2(a) for B. burgdorferi. Since the distribution is skewed, we applied a logarithmic transformation, shown in Fig. 2(b), to obtain the 95% confidence interval. In Figs. 2(c)–2(d), we also provide normal probability plots for this logarithmic transformation. We observe that, after dropping 500 of the largest and smallest R₀ estimates, R₀ appears to follow a log-normal distribution. Similar results (not shown) were also obtained for A. phagocytophila. The estimated mean basic reproduction number R₀ and the 95% confidence intervals for both diseases are given in Table 3. When compared to the estimates obtained in Matser et al. (2009), also provided in Table 3, we observe that for B. burgdorferi the R₀ estimate obtained from model (2) is larger, as is the confidence interval, while the opposite is true for A. phagocytophila. However, relative to the length of the confidence intervals from Matser et al. (2009), these R₀ estimates are within 14.3% and 8.9%, respectively, of the estimates provided in Matser et al. (2009). We find the level of agreement between these two complementary approaches promising given the complicated nature of tick–host–pathogen systems, as well as the existing uncertainty surrounding the many tick species and their pathogens.

Fig. 2.

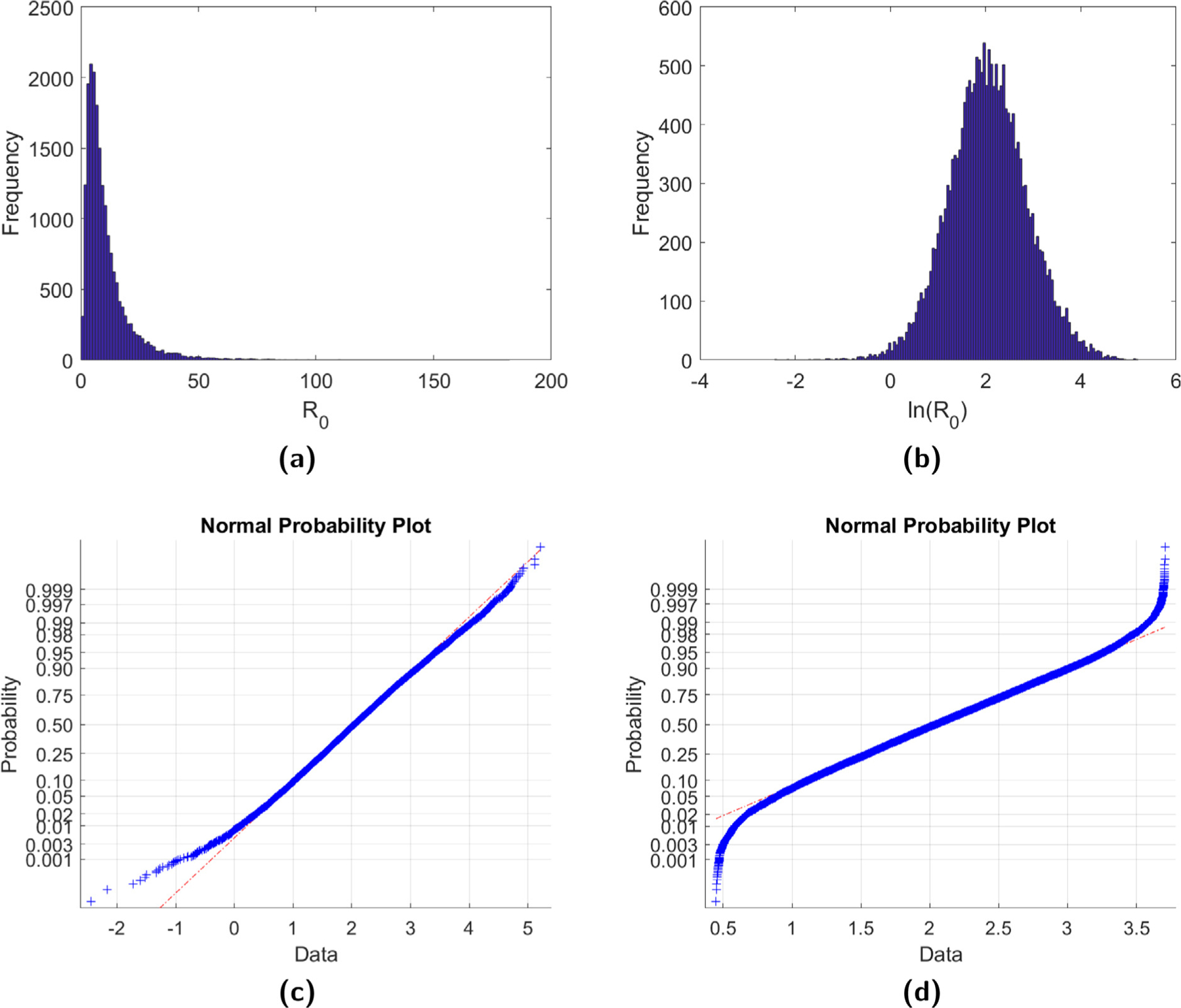
(a) A histogram of the R₀ estimates for B. burgdorferi obtained from 20,000 sets of parameters chosen randomly from uniform distributions after removing all cases where ${\widehat{R}}_0<1$. (b) The natural logarithmic transformation of the R₀ estimates. Graphs (c) and (d) give the normal probability plot for ln(R₀), with (d) obtained after removing the 500 largest and 500 smallest R₀ values.

Table 3.

Estimated mean R₀ and 95% confidence intervals obtained from simulation. Estimates in column 2 are from 20,000 iterations minus the simulations that result in ${\widehat{R}}_0<1$. Estimates in column 3 drop the 500 smallest and the 500 largest R₀ values from these simulations.

	Full simulation	Truncated	Estimate from Matser et al. (2009)
Borellia burgdorferi
Mean R0 95% Confidence interval	11.01 (1.55, 39.22)	9.99 (1.96, 31.12)	8.25 (1.93, 21.18)
Anaplasma phagocytophila
Mean R0 95% Confidence interval	3.01 (0.45, 10.48)	2.74 (0.56, 8.36)	3.90 (0.74, 10.76)

The elasticities of R₀ for B. burgdorferi with respect to the six disease transmission parameters from each of the 20,000 simulations (minus the 500 largest and 500 smallest values and those simulations resulting in ${\widehat{R}}_0<1$) are provided in Fig. 3. We observe that R₀ is most sensitive to changes in parameters describing systemic transmission. Meanwhile, it is less sensitive to changes in transovarial transmission. The elasticities of R₀ for A. phagocytophila (not shown) follow similar trends. These results are in agreement with the results from Matser et al. (2009) which also found that R₀ for both diseases was most sensitive to changes in systemic infection parameters. Mean elasticities for both diseases are provided in Table 4.

Fig. 3.

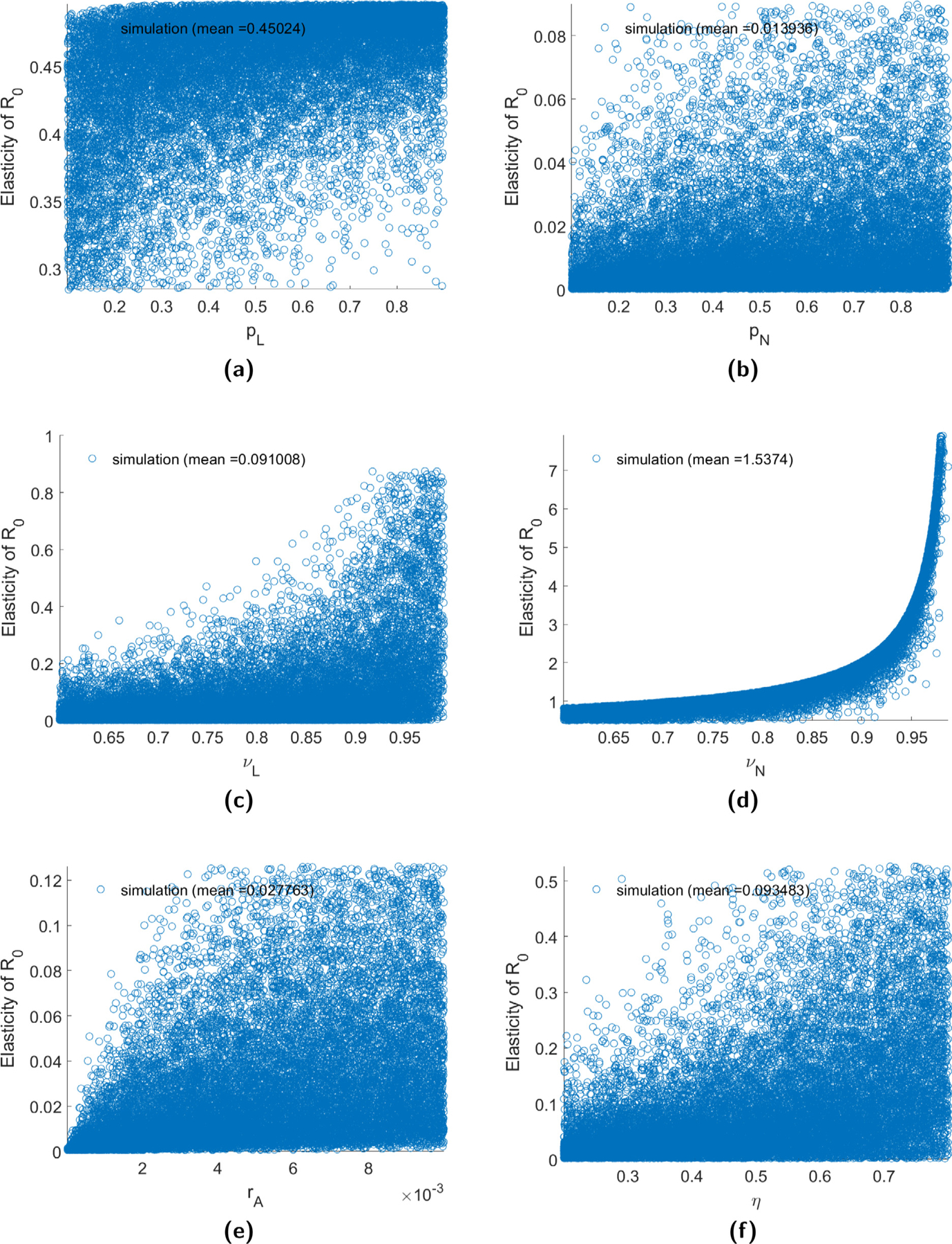
The elasticity of R₀ with respect to the disease transmission parameters for B. burgdorferi. Elasticities are obtained from 20,000 sets of parameters chosen randomly from uniform distributions after first removing all sets that result in ${\widehat{R}}_0<1$, and then removing the 500 largest and 500 smallest values.

Table 4.

Mean elasticity of R₀ with respect to pathogen parameters and coefficients of determination when data is fit to a linear regression.

Parameter	Borellia burgdorferi		Anaplasma phagocytophila
	Elasticity	R 2	Elasticity	R 2
pL	0.4502	0.1612	0.4699	0.0507
pN	0.0139	0.0716	0.0038	0.0962
pA	–	–	0.0016	0.0391
rA	0.0278	0.1731	0.0226	0.1768
η	0.0935	0.2307	0.0292	0.1893
vL	0.0910	0.2308	0.0216	0.0522
vN	1.5374	0.8030a	0.4799	0.3563
vA	–	–	0.0015	0.0210

^aDenotes a fit to a quadratic regression.

In Table 4, we also provide the coefficient of determination when these elasticities are fit to a linear regression in order to observe which parameters are correlated with R₀. Since each of the 20,000 simulations are obtained by first choosing model parameters uniformly from their respective intervals, and thus each simulation is based a different set of parameter values, in general we should not expect to see a significant correlation between changes in a single model parameter and changes in R₀. In this case, the only correlation we observe is with v_N in B. burgdorferi which is quadratically correlated. This correlation is also in agreement with what is known about the transmission of these pathogens. Specifically, for B. burgdorferi, since the likelihood of transovarial transmission is small resulting few infected larvae, nymphs are the primary drivers of this pathogen (Van Duijvendijk et al., 2015). Hence, the strong correlation of R₀ with the infection of hosts from infected nymphs v_N. We hypothesize that the nonlinear relationship with v_N is likely due to the fact that an infection in a host may lead to multiple tick infections.

Though host abundance is an important factor in the establishment and survival of tick populations, Ixodes ticks spend a majority of their life-cycle off hosts (Cheng et al., 2017). Therefore, abiotic environmental factors play a crucial role in tick survival and development (Cheng et al., 2017; Sonenshine, 2018). In fact, recent studies on the effect of climate change on tick population expansion have found that increasing temperature, leading to increased survival rates, can help enable tick invasion into new environments (Cheng et al., 2017; Hamer et al., 2010). In order to understand how these parameters may contribute to disease invasion, in Table 5 we provide the elasticity of R₀ with respect to tick life-cycle parameters and host carrying capacities. We observe that R₀ tends to be more sensitive to changes in life-history parameters, such as survival probabilities, than to changes in the pathogen parameters. These elasticity results suggest that increased temperatures may also help enable disease invasion. With respect to the survival of the different tick stages, we observe that R₀ is most sensitive to the survival of the larva stage. This is in agreement with previous studies which found survival from the larva to the nymph stage is critical for R₀ in both tick-borne encephalitis and Lyme borreliosis (Ostfeld and Brunner, 2015).

Table 5.

Mean elasticity of R₀ with respect to tick life-history parameters and coefficients of determination when data is fit to a linear regression.

Parameter	Borellia burgdorferi		Anaplasma phagocytophila
	Elasticity	R 2	Elasticity	R 2
sE	0.9537	0.0007	0.9160	0.2189
sL	3.3186	0.0420	3.1846	0.0404
sN	1.9047	0.1269	1.8271	0.1269
sA	1.5827	0.0232	1.4837	0.0130
γE	0.7075	0.2032	0.6786	0.1924
γL	0.5520	0.0024	0.5343	0.0019
γN	0.1115	0.0056	0.0907	0.0070
γA	0.1933	0.0011	0.1885	0.0016
β 0	0.8431	0.0316	0.8092	0.0403
c	−0.3744	0.7550	−0.3628	0.7785
aL	0.4737	0.2266	0.4904	0.3275
aN	0.4557	0.2387	0.4572	0.2459
aA	0.0001	0.1446	0.0026	0.0436
kL	−0.0245	0.0166	−0.0121	0.0059
kN	0.0010	0.0002	0.0016	0.0001
kA	−0.0213	0.0130	−0.0064	0.0070
hc	0.6758	0.0007	0.6824	0.0000
Hc	−0.0036	0.0001	0.0136	0.0008

For both diseases, we observe in Table 5 that the tick competition coefficient c is correlated with R₀. Notice that larger c values result in smaller tick populations, thus R₀ is positively correlated with larger tick densities. The correlation of R₀ with the competition coefficient highlights an important data gap as intraspecific density-dependent effects in ticks are difficult to estimate. For example, though estimates of questing ticks obtained through blanket dragging or flagging methods can be used to measure epidemiological risk, they cannot yield information on absolute tick population sizes unless host assemblages and densities are also known (Randolph, 2004). In addition, these methods only capture a minority of active ticks and, thus, tick abundance estimates may be biased downward (Nyrhilä et al., 2020).

4.2. Beyond R₀: Disease establishment

While R₀ is a useful quantity for determining whether a pathogen can invade a tick-host system, it does not provide any information about what happens after invasion occurs. This fact is highlighted in Fig. 4 which gives the disease prevalence in the tick population against R₀ for cases when invasion occurs (i.e. R₀ > 1). Specifically, we define disease prevalence to be the proportion of ticks in host-seeking tick stages (larva, nymph, and adult) that are infected. As can be seen in this figure, the same disease prevalence may be obtained for a wide range of R₀ values. In this section, we use model (2) to examine two important disease metrics once invasion has occurred: disease prevalence and time to disease establishment. We define the establishment time to be the amount of time it takes the number of host-seeking infected ticks to reach some proportion of the total disease equilibrium density. For simulation purposes, here we choose the proportion to be 50%.

Fig. 4.

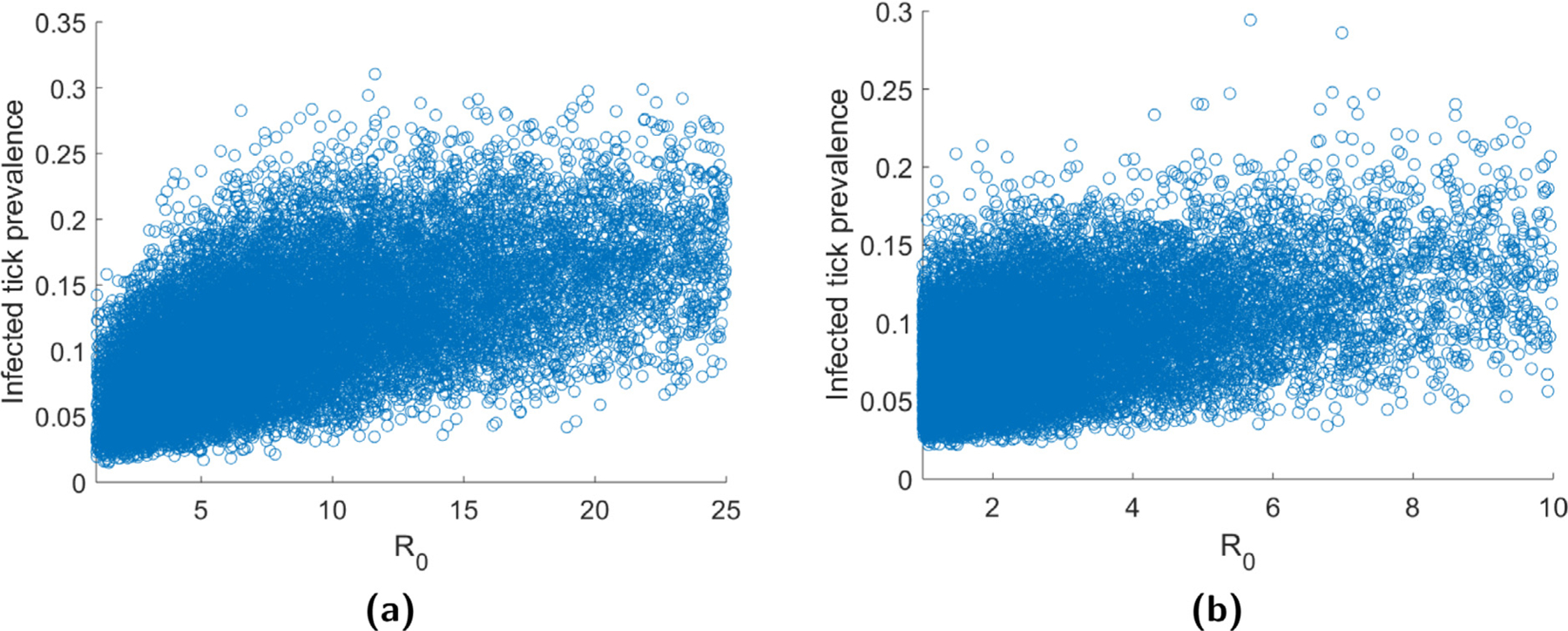
Disease prevalence in ticks against R₀ for (a) B. burgdorferi and (b) A. phagocytophila.

For all numerical simulations of model (2) generated with parameter values selected from Tables 1 and 2, we observed the system converge to a stationary equilibrium. This was confirmed numerically by verifying that the final-time densities for each of the tick stages was sufficiently close (here we used 10⁻⁸) to the nine previous values. Thus, the infection prevalence in the long run is essentially constant and may be found by numerically simulating model (2) for sufficiently long time.

Histograms for the disease prevalence and time to disease establishment for B. burgdorferi generated from 20,000 Monte Carlo simulations are provided in Fig. 5. Table 6 provides the means and confidence intervals for the two disease metrics for both diseases. Both a logarithmic and square root transformation of the calculated histograms result in distributions that are approximately normal, thus we provide confidence intervals obtained from each of these transformations. Meanwhile, Tables 7 and 8 give elasticities of these two metrics with respect to changes in the model parameters. Reported values in Tables 6–8 were calculated from 20,000 Monte Carlo simulations after removing all cases where R₀ < 1 and then removing the 500 largest and 500 smallest values. Simulations for time to disease establishment were initialized with a single individual in each of the infected states.

Fig. 5.

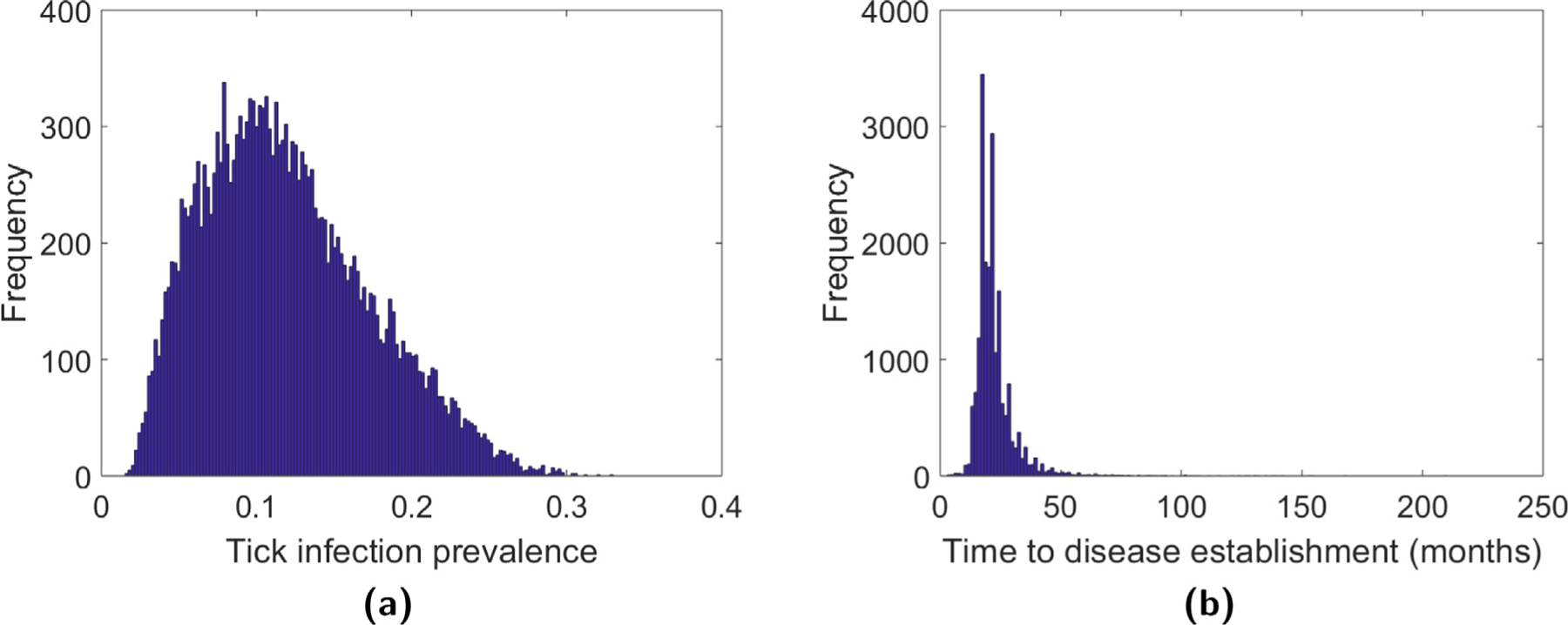
Histogram of disease prevalence and time to disease establishment for B. burgdorferi. The histograms were generated using 20,000 Monte Carlo simulations and then removing all cases where R₀ < 1.

Table 6.

Estimated mean and 95% confidence intervals (CI) for disease prevalence and time to disease establishment obtained from Monte Carlo simulation.

	Borellia burgdorferi	Anaplasma phagocytophila
Disease prevalence
Mean	11.85%	9.00%
95% CI (logarithmic)	(4.65%, 25.34%)	(4.11%, 16.83%)
95% CI (square root)	(3.39%, 24.02%)	(3.68%, 15.55%)
Disease establishment time
Mean	21.77 months	20.84 months
95% CI (logarithmic)	(13.49, 33.24)	(13.49, 30.76)
95% CI (square root)	(12.57, 32.72)	(12.75, 30.31)

Table 7.

Mean elasticity of the tick infection prevalence with respect to pathogen and tick parameters and coefficients of determination when data is fit to a linear regression.

Parameter	Borellia burgdorferi		Anaplasma phagocytophila
	Elasticity	R 2	Elasticity	R 2
pL	0.5221	0.0170	0.8662	0.0125
pN	0.0751	0.0909	0.0270	0.2860
pA	–	–	0.0053	0.1511
rA	0.0502	0.4474	0.0427	0.6326
η	0.3444	0.1842	0.0912	0.1590
vL	0.0000	0.0001	0.0000	0.0001
vN	0.0000	0.0000	0.0000	0.0037
vA	–	–	0.0000	0.0213
sE	0.3743	0.0590	0.1443	0.0543
sL	2.0476	0.0311	1.2489	0.0217
sN	2.4788	0.3790	1.9980	0.6052
sA	1.1744	0.1733	0.7007	0.3565
γE	0.2640	0.0019	0.0980	0.0043
γL	0.9726	0.0021	0.8289	0.0070
γN	0.0816	0.0668	0.0125	0.1593
γA	−0.0130	0.0293	−0.0393	0.0750
β 0	0.3200	0.0021	0.1201	0.0056
c	−0.1462	0.0059	−0.0454	0.0867
aL	0.0000	0.0219	0.0000	0.0002
aN	0.0000	0.0253	0.0000	0.0194
aA	0.0000	0.0384	−0.0004	0.3096
kL	−0.1862	0.0095	−0.0632	0.0139
kN	−0.0212	0.0139	−0.0154	0.0164
kA	−0.0045	0.0009	−0.0044	0.0088
hc	−0.2083	0.0022	−0.0792	0.0042
Hc	−0.0045	0.0001	−0.0050	0.0070

Table 8.

Mean elasticity of time to disease establishment with respect to pathogen and tick parameters and coefficients of determination when data is fit to a linear regression.

Parameter	Borellia burgdorfer		Anaplasma phagocytophila
	Elasticity	R 2	Elasticity	R 2
pL	−0.3723	0.0743	−0.4396	0.0905
pN	−0.0658	0.0215	−0.0159	0.0456
pA	–	–	−0.0298	0.0170
rA	−0.0149	0.8080	−0.0238	0.7836
η	−0.2708	0.3239	−0.0706	0.2983
vL	0.0000	–	−0.0026	0.0221
vN	0.0000	–	−0.0038	0.0232
vA	–	–	−0.0004	0.0175
sE	−0.9545	0.7426	−0.8774	0.6636
sL	−2.8468	0.0268	−2.5091	0.0181
sN	−2.0950	0.0753	−1.8238	0.0791
sA	−2.2779	0.0732	−1.9902	0.0714
γE	−1.0628	0.3737	−0.9063	0.3560
γL	−0.4445	0.1898	−0.3866	0.1239
γN	−0.3475	0.1202	−0.3065	0.0861
γA	−0.3689	0.0672	−0.3170	0.0382
β 0	0.0000	–	0.0000	–
aL	0.0000	–	0.0000	–
aN	0.0000	–	−0.0008	0.0295
aA	0.0000	–	0.0000	0.0045
kL	0.0167	0.0038	0.0000	–
kN	0.0000	–	0.0000	–
kA	0.0000	–	0.0000	–
hc	0.0000	–	0.0000	–
Hc	0.0000	–	0.0000	–

The mean disease prevalence was found to be 11.85% for B. burgdorferi and 9.00% for A. phagocytophila. Though previous studies have shown that disease prevalence may be highly variable in different habitat types, these estimates fall within prevalence ranges reported in the literature, see for example (Ogden et al., 2013; Reye et al., 2010; Schorn et al., 2011). A metaanalysis of 154 European studies found that 13.7% of I. ricinus were infected with Borrelia spp., but prevalence varied from 2% to 49% depending on the region (Reye et al., 2010). In Luxembourg, the mean prevalence was found to be 11.3% for B. burgdorferi with highest and lowest observed prevalences of 21.9% and 2.8%, respectively (Reye et al., 2010). A study of the prevalence of B. burgdorferi in I. scapularis for different locations in Canada found similar prevalences which ranged from 9.8% to 14.1% (Ogden et al., 2013). In Luxembourg, the mean prevalence for A. phagocytophilum in I. ricinus was 1.9% with highest and lowest observed prevalences of 4.5% and 0.8%, respectively (Reye et al., 2010). However, in Bavarian public parks in Germany higher prevalences of A. phagocytophilum were found with a mean prevalence of 11.6%, and ranges from 8.1% to 20.1% (Schorn et al., 2011). Notably, it is remarked in Schorn et al. (2011) that the prevalence of A. phagocytophilum appears to be lower in woodland areas.

With respect to the elasticity calculations, we continue to observe that, as with disease invasion, disease prevalence is also sensitive to the tick survival probabilities. However, infection of hosts and tick searching efficiency have no impact on infection prevalence. In addition, there are no significant correlations.

The mean time to disease establishment was found to be 21.77 months for B. burgdorferi, and 20.84 months for A. phagocytophila. For comparison, it was found that it takes the pathogen B. burgdorferi three to five years to invade following the invasion of the tick I. scapularis in central and eastern Canada, respectively (Ogden et al., 2013). However, these estimates are based on the time since the tick, rather than the pathogen, first invades a region and disease establishment is defined as the first time that the disease prevalence increases. In Table 8, we observe that there are a number of model parameters that the time to disease establishment is not sensitive to. However, as with the previous metrics, it is sensitive to the tick survival probabilities. We also observe that the transovarial transmission probability r_A and egg survival probability s_E are correlated with disease establishment time. Since increases in the parameter c decreases tick density and, thus, may make it possible that the infection never reaches establishment as defined here, we do not include elasticity calculations for c in Table 8.

5. Discussion

The tick–host–pathogen system involves many complex interactions that depend on both abiotic conditions, such as temperature and humidity, and biotic factors, such as availability of hosts (Gray et al., 2016; Randolph, 2004). Clearly, not all of these factors have been included in model (2). In this section, we briefly discuss how the model framework developed here may be extended to incorporate some of these elements.

Since tick development and questing is temperature-dependent, variation in seasonal tick dynamics may occur in different geographic regions which may have significant impacts on pathogen transmission (Randolph, 2004). For example, maintenance of B. burgdorferi in I. scapularis depends heavily on the timing of seasonal activity in the immature stages since efficient infection of the larva stage from reservoir hosts requires that larvae feed after infected nymphs (Gatewood et al., 2009). Though model (2) does not include seasonality, this may be easily incorporated by making the search efficiencies a_j a function of time. Given the one-month time unit, this would mean that, rather than a disease-free equilibrium, the model would possess a disease-free p-cycle for some 1 < p ≤ 12. In this case, R₀ is calculated as the dominant eigenvalue of

$$\prod _{i=1}^p{F}_1{\left(I-T_i\right)}^{-1},$$

where matrices F_i and T_i describe new infections and other transitions, respectively, evaluated at each point of the p-cycle (Cushing and Ackleh, 2012; van den Driessche and Yakubu, 2019). Similarly, it is also possible to define the survival probabilities to be functions of temperature, as is commonly done in STELLA models.

Model (2) also does not account for all of the possible complicated interactions between ticks and host species. For example, ticks often feed on multiple host types, with only a portion of these hosts being reservoirs for the pathogen. Depending on the specific biological population under consideration, it may be appropriate to incorporate additional host types into model (2), such as a non-competent host for the immature stages. In addition, it has been observed that ticks have a tendency to aggregate on hosts. For example, a study of I. ricinus on rodents in Slovakia found that 20% of hosts fed 74% of nymphs and 61% of larvae (Randolph et al., 1999). Accounting for this aggregation can be particularly important for pathogens such as tick-borne encephalitis where short infection durations in reservoir hosts mean that co-feeding is a major source of transmission. This aggregation tendency may be incorporated into model (2) following the arguments developed in Rosa et al. (2003). Specifically, suppose the distribution of stage j ticks on hosts follows a negative binomial distribution with the shape parameter σ_j determining the degree of aggregation. Then the average numbers of infected larvae and nymphs feeding with a susceptible larva individual on a susceptible host become

$$\begin{gathered} \frac{{\varphi }_h\left(1-e^{-a_L{h}_S}\right)L_I}{k_L{h}_S}\left(1+\frac{1}{{\sigma }_L}\right),\hspace{0.17em}\text{and} \\ \frac{{\varphi }_h\left(1-e^{-a_N{h}_S}\right)L_I{N}_I}{k_L{h}_S}\left(1+\frac{{\rho }_{LN}}{\sqrt{{\sigma }_L{\sigma }_N}}\right), \end{gathered}$$

respectively, where p_LN is a correlation coefficient for larvae and nymphs. Thus, the probability that a susceptible larva feeding on a susceptible host does not become infected through co-feeding is now given by

$${\Psi }_{LS}=e^{-\frac{1}{k_L{h}_S}\left({\lambda }_{LL}{\varphi }_h\left(1-e^{-a_L{h}_S}\right)\left(1+\frac{1}{{\sigma }_L}\right)L_1+{\lambda }_{LN}{\varphi }_h\left(1-e^{-a_N{h}_S}\right)\left(1+\frac{{\rho }_{LN}}{\sqrt{{\sigma }_L{\sigma }_N}}\right)N_I\right)},$$

with the other co-feeding terms defined similarly.

Finally we note that the two pathogens considered in this paper were chosen because of the long durations of infection in competent hosts. For other diseases in which host infection lasts for only a matter of days, such as tick-borne encephalitis, the one-month time unit used in model (2) means that the contribution of infected hosts to disease transmission becomes exaggerated. However, this one-month time unit allows us to take a more coarse-grain approach to modeling the tick population by only distinguishing between different developmental stages and not different tick activity states (e.g., questing larvae versus feeding larvae), as has been done in other models such as (Norman et al., 1999; Rosa et al., 2003; Rosa and Pugliese, 2007). Since questing and feeding may last for weeks or days, respectively, reducing the unit of time to a week or a day to account for shorter durations of infection would mean that these different activity states should also be included. An extension of model (2) that includes these states is currently being developed by the authors and, in future work, we intend to examine how these differences in scales may affect model predictions.

6. Conclusion

In this paper, we developed a tick–host–pathogen system to study the invasion and establishment of tick-borne diseases. This discrete-time model incorporates different developmental stages of the tick, variable host preference based on developmental stage, and three forms of pathogen transmission. Since model (2) describes changes in densities over time, it is possible to study disease metrics beyond the basic reproduction number R₀, such as disease prevalence and time to establishment. A consistent pattern we observed for all three disease metrics considered here is that the tick survival probabilities play an important role in both disease invasion and establishment. Since increased temperatures have been shown to result in increased tick survival rates, this supports previous findings that climate change may facilitate the expansion of both tick populations and their associated pathogens (Cheng et al., 2017; Hamer et al., 2010). In contrast, though disease invasion is sensitive to tick-to-host transmission v_j and tick searching efficiency a_j, neither disease prevalence nor time to disease establishment are sensitive to these parameters.

Though model (2) does not include some biological features of the tick–host–pathogen system, as described above, we find that the model is still able to produce results similar to those found using the alternative next-generation-matrix approach applied in Matser et al. (2009), as well as results obtained from field studies. In future work we aim to incorporate at least some of these additional aspects into our model framework. Model (2) will serve as a benchmark for understanding the effects of these added factors since comparisons of the two model outputs may help to identify which characteristics cause fundamental changes in the predictions of disease transmission and, thus, are important to include when studying tick-borne pathogens. Understanding what enables the successful invasion of ticks into new geographic locations and coinciding pathogen invasions is essential for controlling the expansion of tick-borne diseases. Variations of models (1) and (2) will also be used to gain further insights into this issue. In these studies, invasion and time to extinction for ticks and their pathogens will be studied by extending the models developed here to include demographic stochasticity and Allee effects, both of which are be particularly important for small populations, as well as spatial structure and host movement.

Appendix

We first establish the global dynamics for the two host equations and show that, if either host population converges to zero, then the tick population dies out.

Lemma A.1. Consider the host equation

$$k\left(t+1\right)=\frac{{\beta }_{k}k\left(t\right)}{1+c_{k}k\left(t\right)}+s_{k}k\left(t\right)=f\left(k\left(t\right)\right).$$ (9)

1. If β_k + s_k < 1, then the extinction equilibrium $\overline{k}=0$ is globally asymptotically stable.

2. If β_k + s_k > 1, then there exists a unique positive equilibrium $\overline{k}=k_C$ that is globally asymptotically stable.

Proof. Eq. (9) has two equilibria, 0 and k_C, as defined by Eq. (4). Clearly, the positive equilibrium exists if and only if β_k + s_k > 1. Moreover, we have 0 < x < f (x) when β_k + s_k < 1. Thus, the extinction equilibrium is globally asymptotically stable when β_k + s_k < 1 (Theorem 2.5, Allen (2007)). When β_k + s_k > 1, we have x < f (x) < k_C for 0 < x < k_C and k_C < f (x) < x for x > k. It follows that the positive equilibrium is globally asymptotically stable when it exists (Theorem 2.8, Allen (2007)). □

Lemma A.2. If either h_C = 0 or H_C = 0, then the origin E₀ = (0, 0, 0, 0) is a globally asymptotically stable fixed point of system (5).

Proof. If h_C = 0 or H_C = 0, then P₁(0) is triangular and its spectral radius r, 0 < r < 1, is the largest diagonal entry. By relationship (6), it follows that for any x(0) ≥ 0 we have

$$0\le x\left(t\right)={\prod }_{i=0}^{t-1}{P}_1\left(x\left(i\right)\right)x\left(0\right)\le P_1^t\left(0\right)x\left(0\right)\to \text{0}\hspace{0.17em}\text{as}\hspace{0.17em}t\to \infty .\hspace{1em}\square$$

For all remaining results, we assume that β_k + s_k > 1 for k = h, H so that $\overline{k}=k_C$.

Proof of Lemma 3.1. Since P₁(0) is non-negative and irreducible, it has a positive, simple, strictly dominant eigenvalue r. By Theorem 1.1.3 in Cushing (1998), we have r < 1 if and only if ${\widehat{R}}_0<1$. Thus, the extinction equilibrium E₀ is locally asymptotically stable if ${\widehat{R}}_0<1$. Moreover, following the same argument as in Lemma A.2, we have that, for any x(0) ≥ 0, x(t) → 0 as t → ∞ whenever ${\widehat{R}}_0<1$. Thus, the extinction equilibrium is globally asymptotically stable for ${\widehat{R}}_0<1$. □

Proof of Theorem 3.2. An interior equilibrium is a positive solution to equilibrium equations

$$E=\beta \left[{\gamma }_A\left(1-e^{-a_A{H}_C}\right)A\right]s_A{\gamma }_A\left(1-e^{-a_A{H}_C}\right)A+s_E\left(1-{\gamma }_E\right)E,$$ (10a)

$$L=s_E{\gamma }_{E}E+s_L\left(1-{\gamma }_L\left(1-e^{-a_L{h}_C}\right)\right)L,$$ (10b)

$$N=s_L{\gamma }_L\left(1-e^{-a_L{h}_C}\right)L+s_N\left(1-{\gamma }_N\left(1-e^{-a_N{h}_C}\right)\right)N,$$ (10c)

$$A=s_N{\gamma }_N\left(1-e^{-a_N{h}_C}\right)N+s_A\left(1-\left(1-{\gamma }_A{e}^{-a_A{H}_C}\right)\right)A.$$ (10d)

We solve these equations by first reducing the system down to a single equation in terms of A. Solve Eq. (10a) for E, Eq. (10b) for L, and Eq. (10c) for N, and then substitute these into (10d) to get an equation that only depends on A. This equation has exactly one non-zero solution $\overline{A}$. Substituting this solution back into the remaining equations, we find a unique interior fixed point ${\overline{x}}_1\left(\overline{E},\overline{L},\overline{N},\overline{A}\right)$ defined by

$$\overline{A}\frac{{\widehat{R}}_0-1}{c{\gamma }_A\left(1-e^{-a_A{H}_C}\right)},$$

$$\overline{E}\frac{s_A{\gamma }_A\left(1-e^{-a_A{H}_C}\right)}{1-s_E\left(1-{\gamma }_E\right)}\overline{A}\beta \left[{\gamma }_A\left(1-e^{-a_A{H}_C}\right)\overline{A}\right],$$

$$\overline{L}\frac{s_E{\gamma }_E}{1-s_L\left(1-{\gamma }_L\left(1-e^{-a_L{h}_C}\right)\right)}\overline{E},$$

$$\overline{N}\frac{s_L{\gamma }_L\left(1-e^{-a_L{h}_C}\right)}{1-s_N\left(1-{\gamma }_N\left(1-e^{-a_N{h}_C}\right)\right)}\overline{L}.$$

Clearly this fixed point is positive for ${\widehat{R}}_0>1$.

Next, to establish local stability, note that the Jacobian of system (5) evaluated at the interior fixed point is given by

$$\mathcal{J}=\widehat{T}+\overline{F},$$

where $\widehat{T}$ is the same matrix as defined for P₁(0) and

$$\overline{F}=\frac{1}{{\left(1+c{\gamma }_A\left(1-e^{-a_A{H}_C}\right)\overline{A}\right)}^2}\widehat{F}\ge 0.$$

Since $\overline{F}$ satisfies the conditions of Theorem 1.1.3 in Cushing (1998), it follows that the interior fixed point is locally asymptotically stable if and only if ${\overline{R}}_0<1$ where ${\overline{R}}_0$ is the spectral radius of $\overline{F}{\left(I-\widehat{T}\right)}^{-1}$. Calculation shows that

$${\overline{R}}_0=\frac{{\widehat{R}}_0}{{\left(1+c{\gamma }_A\left(1-e^{-a_A{H}_C}\right)\overline{A}\right)}^2}=\frac{1}{{\widehat{R}}_0}.$$

Since the fixed point exists for ${\widehat{R}}_0>1$, we conclude that it is locally asymptotically stable. □

Proof of Lemma 3.3. It is clear that ${ℝ}_{+}^4$ is forward invariant. Moreover, any non-negative initial condition in ${ℝ}_{+}^4\backslash \left\{\left(0,0,0,0\right)\right\}$ enters $\mathrm{int}\left({ℝ}_{+}^4\right)$ in at most three time units. Let $x_1\left(0\right)=\left(E\left(0\right),L\left(0\right),N\left(0\right),A\left(0\right)\right)>0$. Then for

$$t\ge t_1=\ln \left(\frac{{\beta }_0{s}_A}{c\left(1-s_E\left(1-{\gamma }_E\right)\right)E\left(0\right)}\xi \right)/\left|\ln \left(s_E\left(1-{\gamma }_E\right)\right)\right|$$

we have

$$\begin{gathered} E\left(t\right)\le \frac{{\beta }_0{s}_A}{c}+s_E\left(1-{\gamma }_E\right)E\left(t-1\right) \\ \hspace{1em}\hspace{1em}\le \frac{{\beta }_0{s}_A}{c\left(1-s_E\left(1-{\gamma }_E\right)\right)}+{\left(s_E\left(1-{\gamma }_E\right)\right)}^{t}E\left(0\right) \\ \hspace{1em}\hspace{1em}\le \frac{{\beta }_0{s}_A}{c\left(1-s_E\left(1-{\gamma }_E\right)\right)}\left(1+\xi \right). \end{gathered}$$

It follows that

$$\begin{gathered} L\left(t\right)\le s_E{\gamma }_E\widehat{E}+s_L\left(1-{\gamma }_L\left(1-e^{-a_L{h}_C}\right)\right)L\left(t-1\right) \\ \hspace{1em}\hspace{1em}\le \frac{s_E{\gamma }_E\widehat{E}}{1-s_L\left(1-{\gamma }_L\left(1-e^{-a_L{h}_C}\right)\right)}+{\left(s_L\left(1-{\gamma }_L\left(1-e^{-a_L{h}_C}\right)\right)\right)}^{t}L\left(0\right), \\ \hspace{1em}\hspace{1em}\le \frac{s_E{\gamma }_E\widehat{E}}{1-s_L\left(1-{\gamma }_L\left(1-e^{-a_L{h}_C}\right)\right)}\left(1+\xi \right), \end{gathered}$$

for t ≥ t₁ + t₂ where

$$\begin{gathered} t_2=\ln \left(\frac{s_E{\gamma }_E\widehat{E}}{\left(1-s_L\left(1-{\gamma }_L\left(1-e^{-a_L{h}_C}\right)\right)\right)L\left(0\right)}\xi \right) \\ \hspace{1em}\hspace{1em}\hspace{1em}/\left|\ln \left(s_L\left(1-{\gamma }_L\left(1-e^{-a_L{h}_C}\right)\right)\right)\right|. \end{gathered}$$

Following similar arguments, we may also bound N (t) and A(t). It follows that the solution x₁(t) enters the set K in at most t = t₁+t₂+t₃+t₄ time steps where

$$\begin{gathered} t_3=\ln \left(\frac{s_L{\gamma }_L\left(1-e^{-a_L{h}_C}\right)\widehat{L}}{\left(1-s_N\left(1-{\gamma }_N\left(1-e^{-a_N{h}_C}\right)\right)\right)N\left(0\right)}\xi \right) \\ \hspace{1em}\hspace{1em}/\left|\ln \left(s_N\left(1-{\gamma }_N\left(1-e^{-a_N{h}_C}\right)\right)\right)\right|, \end{gathered}$$

$$\begin{gathered} t_4=\ln \left(\frac{s_N{\gamma }_N\left(1-e^{-a_N{h}_C}\right)\widehat{N}}{\left(1-s_A\left(1-{\gamma }_A\left(1-e^{-a_A{H}_C}\right)\right)\right)A\left(0\right)}\xi \right) \\ \hspace{1em}\hspace{1em}/\left|\ln \left(s_A\left(1-{\gamma }_A\left(1-e^{-a_A{H}_C}\right)\right)\right)\right|. \end{gathered}$$

Next we show that the set K is invariant. Let $x_1\left(t\right)\in K$. Then we have

$$\begin{gathered} E\left(t+1\right)\le \frac{{\beta }_0{s}_A}{c}+s_E\left(1-{\gamma }_E\right)E_t\le \frac{{\beta }_0{s}_A}{c}+s_E\left(1-{\gamma }_E\right)\widehat{E} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=\frac{{\beta }_0{s}_A}{c\left(1-s_E\left(1-{\gamma }_E\right)\right)}\left(1+s_E\left(1-{\gamma }_E\right)\xi \right)<\widehat{E}, \end{gathered}$$

$$\begin{gathered} L\left(t+1\right)\le s_E{\gamma }_E\widehat{E}+s_L\left(1-{\gamma }_L\left(1-e^{-a_L{h}_C}\right)\right)\widehat{L} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=\frac{s_E{\gamma }_E}{1-s_L\left(1-{\gamma }_L\left(1-e^{-a_L{h}_C}\right)\right)}\widehat{E}\left(1+s_L\left(1-{\gamma }_L\left(1-e^{-a_L{h}_C}\right)\right)\xi \right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}<\widehat{L}, \end{gathered}$$

$$\begin{gathered} N\left(t+1\right)\le s_L\left(1-{\gamma }_L\left(1-e^{-a_L{h}_C}\right)\right)\widehat{L}+s_N\left(1-{\gamma }_N\left(1-e^{-a_N{h}_C}\right)\right)\widehat{N} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=\frac{s_L\left(1-{\gamma }_L\left(1-e^{-a_L{h}_C}\right)\right)}{1-s_N\left(1-{\gamma }_N\left(1-e^{-a_N{h}_C}\right)\right)}\widehat{L}\left(1+s_N\left(1-{\gamma }_N\left(1-e^{-a_N{h}_C}\right)\right)\xi \right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}<\widehat{N}, \end{gathered}$$

$$\begin{gathered} A\left(t+1\right)\le s_N\left(1-{\gamma }_N\left(1-e^{-a_N{h}_C}\right)\right)\widehat{N}+s_A\left(1-{\gamma }_A\left(1-e^{-a_A{H}_C}\right)\right)\widehat{A} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=\frac{s_N\left(1-{\gamma }_N\left(1-e^{-a_N{h}_C}\right)\right)}{1-s_A\left(1-{\gamma }_A\left(1-e^{-a_A{H}_C}\right)\right)}\widehat{N}\left(1+s_A\left(1-{\gamma }_A\left(1-e^{-a_A{H}_C}\right)\right)\xi \right) \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}<\widehat{A}.\hspace{1em}\square \end{gathered}$$

Proof of Theorem 3.4. To establish uniform persistence we follow similar arguments to those in Ackleh and DeLeenheer (2008) that rely on an application of Theorem 4.1 in Hofbauer and So (1989). First note that, since ${\widehat{R}}_0>1$, it follows from Theorem 1.1.3 in Cushing (1998) that P₁(0) has a positive strictly dominant eigenvalue r > 1. Hence, (0, 0, 0, 0) is unstable. Now, using similar notation as in Hofbauer and So (1989), we let $\mathcal{H}={ℝ}_{+}^4$, $\mathcal{Y}=\text{bd}\left({ℝ}_{+}^4\right)$, and f denote the map on the right hand side of (5). Then clearly $f\left(\mathcal{H}\backslash \mathcal{Y}\right)\subset \mathcal{H}\backslash \mathcal{Y}$ since $\mathrm{int}\left({ℝ}_{+}^4\right)$ is positively invariant for the system (5). By Theorem 2.1 in Hale and Waltman (1989) and using Lemma 3.3, it follows that there exists a global attractor X in $\mathcal{H}$. Let M be the maximal compact invariant set in $\mathcal{Y}$. Here, M = {(0, 0, 0, 0)}. Uniform persistence follows if we can prove that (1) M is isolated in X and (2) $W^s\left(M\right)\subset \mathcal{Y}$(here, W ^S(M), the stable set of M, denotes the set of points whose solution sequence for (5) converges to M). In fact, next we prove a stronger result that M is a repeller which by Theorem 2.1 in Hofbauer and So (1989) is equivalent to showing (1) M is isolated in $\mathcal{H}$ and (2) $W^s\left(M\right)\subset M$.

Utilizing Corollary 2.2 in Hofbauer and So (1989), we can prove that M is a repeller by constructing a continuous function $Q:{ℝ}_{+}^4\to {ℝ}_{+}$ which satisfies (1) Q(x) = 0 for $x\in M$ and (2) there is a neighborhood U of M such that for all $x\in U\backslash M$, there exists a t > 0 where Q(f ^t(x)) > P₁(x)x. To this end, since P₁(0) is non-negative and irreducible, its dominant eigenvalue r > 1 has a corresponding left eigenvector p > 0, i.e., $p^{⊺}{P}_1\left(0\right)=r{p}^{⊺}$. Pick $r^{\ast }\in \left(1,r\right)$ such that $p^{⊺}{P}_1\left(0\right)-r^{\ast }{p}^{⊺}>0$. Then by continuity of P₁(x), there exists a neighborhood U of M in $\mathcal{H}$ such that

$$p^{⊺}{P}_1\left(x\right)-r^{\ast }{p}^{⊺}>0.$$

Now, define $Q:{ℝ}_{+}^4\to {ℝ}_{+}$ as follows:

$$Q\left(x\right)=p^{⊺}x.$$

Then, Q(x) = 0 for $x\in U\hspace{0.17em}\text{iff}\hspace{0.17em}x\in M$, and is positive everywhere else in U. Moreover,

$$Q\left(f\left(x\right)\right)=p^{⊺}{P}_1\left(x\right)x>r^{\ast }{p}^{⊺}x>Q\left(x\right),\hspace{0.17em}\forall x\in U\hspace{0.17em}\backslash M.$$

This proves that the system (5) uniformly persistent, i.e. there is some η > 0, such that,

$$\underset{t\to \infty }{\lim \inf } E\left(t\right),L\left(t\right),N\left(t\right),A\left(t\right)\ge \eta$$

for any solutions with nonzero initial conditions in ${ℝ}_{+}^4$. □