Abstract
The newly developed finite element (FE) modeling at the atomic scale was used to predict the static and dynamic response of the α-helix (AH) and tropocollagen (TC) protein fragments, the main building blocks of the spike of the SARS-CoV-2. The geometry and morphology of the spike’s stalk and its connection to the viral envelope were determined from the combination of most recent molecular dynamics (MD) simulation and images of cryoelectron microscopy. The stiffness parameters of the covalent bonds in the main chain of the helix were taken from the literature. The AH and TC were modeled using both beam elements (wire model) and shell elements (ribbon model) in FE analysis to predict their mechanical properties under tension. The asymptotic stiffening features of AH and TC under tensile loading were revealed and compared with a new analytical solution. The mechanical stiffnesses under other loading conditions, including compression, torsion, and bending, were also predicted numerically and correlated with the results of the existing MD simulations and tests. The mode shapes and natural frequencies of the spike were predicted using the built FE model. The frequencies were shown to be within the safe range of 1–20 MHz routinely used for medical imaging and diagnosis by means of ultrasound. These results provide a solid theoretical basis for using ultrasound to study damaging coronavirus through transient and resonant vibration at large deformations.
Significance
The outbreak of SARS-CoV-2 has significantly impacted the whole world. Most of research is focused on vaccines development and targeted to specific mutations and variants. The concept of ultrasound induced resonant vibration to kill coronavirus will provide an innovative alternative to prevention and treatment. The approach is not affected by mutation. This paper successfully predicts natural frequencies and mode shapes of spike protein of SARS-CoV-2, which consists of alpha-helices and tropocollagen molecules. The mechanical properties of spike’s stalk are simulated in FE analysis, which is well correlated with a new analytical solution and existing results of MD simulation on TC. This research shows great promise of using FE analysis to study mechanical properties of proteins at the atomic level.
Introduction
In the spring of 2020 the world was watching with anticipation the development of vaccines and other innovative techniques against COVID-19 (1). At the same time, we asked ourselves a question: are there ways of deactivating the virus other than promoting the immune response? We were encouraged by mounting evidence that ultrasound can selectively kill some types of cancer cells. Ultrasound is a safe and proven technique in medicine for imaging and diagnosis. It has also been used for treatment, by the shattering of kidney stones of millimeters in size and for killing some types of cancer cells the size range of micrometers (2,3). We are putting forward the hypothesis that ultrasound could damage some proteins in the virus so that it loses the ability to multiply.
We would like first to place the present paper in the context of the general objective of our COVID-inspired research. This paper resolves only one piece of the four-piece puzzle. Determination of forces exerted by an ultrasound wave on the virus was covered in our previous paper (4) in which rigorous structural acoustics equations were solved. The harmonic wave was shown to induce vibrations of the viral shell as well as spikes. The present article is focused on the resonant vibration of spikes. As a continuation of this line of research, the transient vibrations are currently studied by applying frequencies of ultrasound harmonic wave equal to or close to the resonant frequencies. This will be followed by the design of the most damaging ultrasound pulse.
The diameter of the coronavirus family is 100 nm and the spikes are about 20 nm in length. Several deadly viruses, including SARS-CoV-2 and influenza A viruses, belong to this family. This is three orders of magnitude smaller than the diameter of cancer cells. It was shown that because of such a small size, the magnitude of the scattered pressure is negligible and the viral shell feels only the incident pressure, which is known and could be controlled. The problem of free and transient vibrations of the viral envelope was also formulated in the same article (4). Depending on the combination of the ultrasound frequencies in the range of 1–100 MHz and pressure intensities of 0.1–10 MPa, the viral shell developed the resonant vibrations with increasing amplitude within nanoseconds. Much higher natural frequencies (>100 MHz) were predicted by other researchers using a similar modal analysis approach but with different geometries (5).
The next logical question to be asked is whether such large vibration amplitudes could damage the virus and thus break its deadly reproductive cycle. In this paper, the term damage is understood either as rupturing of the bilayer lipid envelope or by inflicting mechanical permanent deformation to the sequence of proteins in the spike that control the binding process. The present paper is concerned with the second scenario of the inactivation of spikes. Because of the large degree of flexibility, the spike’s job of searching and attaching to the host cells can be performed more easily (6, 7, 8, 9, 10). By the same token, spikes may easily be put into different vibration modes when suitably disturbed. The spike is connected to the viral envelope by a slender structure—the stalk. Careful studies using molecular dynamics (MD) simulation and cryoelectron microscopy (cryo-EM) revealed that the stalk of SARS-CoV-2 is composed of three twisted α-helices, forming the tropocollagen molecules, the building blocks of all living organisms (8,11,12). The work of Casalino’s team (12) stands out because it provides an extremely high resolution and complete information on the atomistic shape of the main skeleton and side chains of the spike of SARS-CoV-2.
The next step was to select a methodology for solving the problem of resonant and transient vibration of a spike. The main computational tool to study the interaction between atoms and formation of molecules and proteins is MD. Its fundamental axiom is that forces and the corresponding displacements between atoms are related through potential functions. Mathematically it can be described by defining the atomic potential energy of a given protein. There is an array of formulation of interatomic potentials to study biological materials at different length scales from fully blown models consisting of hundreds of millions of atoms (13), to simplified ones such as a coarse grain model (14), for example the CHARMM model (15) and the Martini model (16). We refer readers to a more extensive review article on the assumptions and results of MD techniques (17). An up-to-date perspective on the biological modeling and simulation was offered by Schlick and colleagues (18, 19, 20). The progress in this key area is enormous and new tools, such as knowledge-based and machine-learning methods, are now added to the available arsenal of computational tools.
While the MD simulation technique started a revolution in microbiology, it was found to be unsuitable for the task at hand because if its limitations to handle large displacement vibration problems. Instead, the finite element (FE) method is ideally suited for this purpose. The general-purpose FE codes already have built-in packages for performing modal analysis and can easily handle forced vibrations with a minimum number of input parameters. Both MD simulation and FE simulation are based on a similar set of assumptions. Atoms interact with forces and displacement rather than stresses and strain. It is here that structural mechanics offers a convenient tool for studying the response of several biological structures. Structural mechanics operates with the concepts of generalized loads (moments, torques, and tensile and compressive forces) and corresponding generalized deformations (displacements, curvatures, and rotations). These concepts are compatible with the coarse grain methods of MD and will be pursued in the present study. The quadratic terms in the expression for the potential energy of covalent bonds are retained. It was found to be more convenient from the computational point of view to account for the long-range van der Waals (vdW) and electrostatic force by introducing additional linear or nonlinear beam elements between the individual strands of the tropocollagen (TC) molecules. Such a simplification is possible for slender molecules forming the stalk of the spike. The beam elements also prevent the interpenetration of atoms.
The application of the FE technique for studying structures on the atomistic scale goes back to the discoveries of graphene and nanotubes. Graphene sheets consist of one layer of atoms arranged in a hexagonal pattern. Of course polymers and graphene are not biological materials, but at the level of a covalent bond there is no distinction between living and inorganic matter. The forces between atoms obey the same rules. Graphene and nanotubes were for decades modeled using MD tools (21). Following the seminal work by Odegard and colleagues (22,23), a number of FE models were developed for graphene and nanotubes (24, 25, 26, 27, 28). Fracture of graphene sheets was formulated in a series of papers by Xiao and Belytschko (29). An excellent review of the state of the art was published by Couto and Silvestre (30). These authors were the first to point out that the continuum mechanics concept of stress and the elasticity constants measured in pressure unit (i.e., MPa) does not make sense for structures as thin as the atom diameter. Instead, the axial, bending, and torsional stiffness must be treated as an independent material/structural property. In the present study of biological structures, we are adopting the FE modeling strategy of nanomaterials. Nonetheless, the hexagonal symmetry of graphene and nanotubes, lack of side chains, and torsional resistance make the FE analysis of such man-made structures simple. The three-dimensional (3D) geometries of the α-helices and TC molecules are very complex, and such models still need to be developed.
There is limited information in the literature on application of ultrasound to disarm viruses that was found helpful in the present investigation, even though the keyword “ultrasound” was used in hundreds of papers. Chrysikopoulos et al. and Yang et al. presented a very thorough study on acoustic vibration of viruses induced by microwaves (31,32). Dykeman et al., in a series of papers, promoted the application of Raman spectroscopy for studying the vibration spectrum of M13 bacteriophage subjected to laser excitations (33, 34, 35, 36). Their results apply to the family of icosahedral viruses that form viral capsids. The family of coronaviruses embodies enveloped viruses. The concept of the possible destruction of HIV by ultrasound energy was first put forward by Babincová et al. (37). Several authors followed up on this concept (38, 39, 40), but with no progress in explaining the mechanisms of virus’ response to ultrasound, this concept was not taken seriously by the medical community. An example of the undocumented claim is the 2008 patent by Microsoft on “Utilizing ultrasound to disrupt pathogens” (41). Recently, the resonant vibration of the envelope was solved using elasticity, but the predicted natural frequency was unrealistically high (5).
Real progress in understanding the merits of using ultrasound as a weapon against viruses was made by the drug-delivery industry. The literature on this subject is enormous, and two excellent papers reviewing the state of the art in this field were published in 2009 and 2014 (40,42). It was found that ultrasound helps to create an opening in the viral shell in order to deliver medication to the designated location. This observation provides additional proof on the safe application of ultrasound to interfere with SARS-CoV-2. The present model is not competing with MD simulation but rather complementing it, and extends it further into large deformation and much longer simulation times.
In this paper, two FE models are developed: the beam model, as the “wire” representation of the coils spring, and the more realistic shell model, representing the “ribbon.” Next, the stiffness of a bundle of three α-molecules, forming a familiar TC, is studied by analytical and numerical methods. The advantage of such a formulation is that one FE model describes the coupled axial, torsional, and bending vibration modes of the spike. The results will provide the necessary input data for the transient vibration analysis of the spike, which is the subject of the current study.
The present paper is divided into several sections. The next section (“Geometry and molecular structure of spikes”) defines the geometry of the virus and the spike protein. The analytical solution for the geometrically perfect α-helix (AH) subjected to tensile load, based on minimization of the total potential energy, is derived in “Modeling of the α-helix.” This section also includes calibration of the stiffness parameters and comparison with the worm-like chain (WLC) closed-form solution. The new numerical load-extension relation of the AH subjected to tensile load, together with comparison with the analytical solution, is covered in “Finite element simulation of the single α-helix.” The FE simulation of TC subjected to tension, compression, bending, and torsion is described in “Finite element simulation of the tropocollagen stalk.” Differences in the prediction of the beam and shell model, as well as explicit and implicit integration schemes, are discussed at length in the same section. In addition, a comparison with the known MD simulation and limited test data for the TC under tension is presented. Information on the stiffnesses of the stalk of the spike is then used in the subsequent section (“The resonant vibrations of spikes”) to run eigenvalue analysis and determine the six lowest vibration modes and the corresponding resonant frequencies. In the final section, we briefly describe the ongoing work in transient vibrations induced by the ultrasound wave and present some new ideas for future microbiology research.
The world is watching with fear the emergence of new strains and strain variants and the declining effectiveness of the existing vaccines. At the time of writing, the number of COVID cases has started again to grow exponentially in the United States and Europe. There is extensive discussion concerning a vaccine that can treat all variants that could be available within the next few years. Looking at alternative solutions to combat the present pandemic has thus become more urgent than ever. We have predicted that resonant (the potentially damaging) vibrations of the viral spikes are in the range of vibration routinely used in medicine for imaging and diagnosis. Furthermore, the vibration spectrum does not depend on the type of mutations, whether it be Delta, Gamma, Omicron, or a new one yet to appear. This finding opens the way for designing the most damaging ultrasound pulse to possibly deactivate the spikes of SARS-CoV-2 and thereby interrupt once and for all its deadly reproductive cycle. As a by-product of the present research, the first step in developing the FE model at the atomistic scale applicable for complex proteins has already been made.
Geometry and molecular structure of spikes
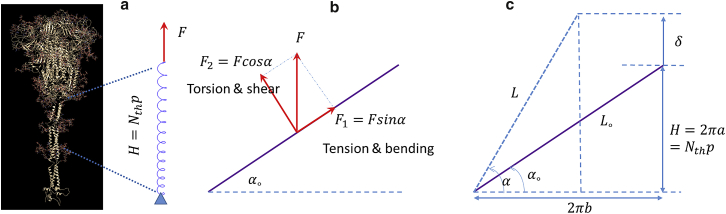
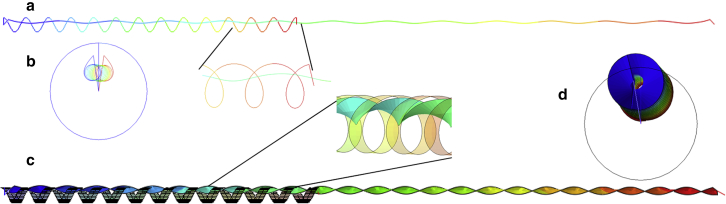
The topology of spike-decorated viruses was discussed in the previous paper of the investigating team (4). For predicting the correct vibration modes and frequencies of the virus, it is important to determine the exact shape of spikes and the way they are attached to the lipid bilayer and to the membrane (M) protein below. Compared with the diameter of the virus, spikes are small but compact structures, resembling a hot-air balloon from the side view and a triangle or a clown leaf from above. The early photographs published by Beniac et al. (43) and Neuman et al. (7) were too crude to serve as prototypes of computational models. The review article by Dyson (44) offered an interesting perspective on the folding of molecules into complex structures. A more precise geometry of the SARS-CoV-2 spike is reconstructed on the basis of recent images provided by cryo-EM and MD simulation (8,9,11,12) (Fig. 1 a–c). The spikes are composed of a more solid head in the shape of an inverted cone and a slender stalk connecting the head with the envelope. It is acknowledged that in the present formulation, the head consisting of thousands of atoms is treated as a solid homogeneous elastic material. In a still magnified view, it can be broken into several subunits that will move on their own with respect to each other. The MD simulation of such a detailed model was reported by Hu and Buehler (45) and others.
Figure 1.
(a) Most spikes are inclined to the local normal axis, as shown by the cryo-EM picture from Turoňová et al. (8). (b) Turoňová et al. (8) introduced the nomenclature of ankle, knee, and hip where most bending deformations are concentrated. (c) MD simulation of molecular structure of the S protein showing detailed features of α-helices and tropocollagen from Casalino et al. (12) and Yu et al. (11). (d) Overall geometry of the spike with a slender stalk and a solid head. The values of the main parameters were determined by averaging the dimension of the MD simulation taken from several most recent papers, mentioned in the above discussion, including Yu et al. (11). To see this figure in color, go online.
The present geometry, as shown in Fig. 1 d, was decided on by averaging the measured parameters , , , and taken from several aforementioned papers, and are gathered in Table 1. The length of the stalk is 7 nm, and its diameter is estimated to be around 0.84 nm. The 21 nm total height of the spike served as a reference scale in finding all other dimensions. In the zoomed-in pictures of the spike shown by Casalino et al. (12) and Yu et al. (11), the spike is much longer but it includes the root embedded in the lipid bilayer envelope.
Table 1.
Input parameters of the present FE static, explicit, and modal analyses
| 26 | 14 nm | 7 nm | 0.42 nm | 1.94 nm | 4 nm |
| P0 | |||||
| 5.82 nm | 0.1–1.0 MPa | 1300 kg/m3 | 0.45 | 3 GPa | 26.5° |
Modeling of the α-helix
The AH and TC are two fundamental building blocks of all biological materials. The two recently published cryo-EM photographs (8) and the MD simulation on the SARS-CoV-2 spikes (12) revealed that the stalk is composed of three interwound AHs forming one TC molecule, often referred to as the coiled coil (see Fig. 1 c and (11,46)). Furthermore, each strand of the TC is not a single spiral but is formed by three shorter collagen helices connected in series. This type of molecular structure gives an appearance of a three-hinge model, proposed in (8). The model with three hinges, which is conceptually appealing but practically difficult to quantify, is not considered in this article. Instead, a single longer and uniform helix was assumed in the analytical and numerical solution. In other words, each strand is approximated by one longer spiral. Attention is focused first on properties and response of a single helical structure subjected to mechanical loading. For brevity this will be called the AH throughout the paper, even though the proper term is the collagen helix. To develop a realistic mechanics model of the stalk, one must go down to the atomistic and molecular level.
Geometry and deformation of the α-helix under tension
The main chain of atoms forms a backbone of the helix that branches into the side chains called the residues. The main resistance to mechanical loading is offered by the covalent bonds. There are 3.6 residues per one turn. Assuming that there are three atoms between the residue corner atoms, there are 10.8 atoms per one full turn. The diameter of hydrogen atom is 0.106 nm and oxygen atom 0.074 nm. If the atoms just touch one another, the length of the backbone, called the contour length, should be about 1.1 nm per one turn. The backbone of the helix is assumed as a mathematically smooth curve, which approximates reality. The complex 3D scaffold-like structure of the SARS-CoV-2 spike, consisting of repeated sequences of the oxygen and nitrogen atoms, was determined by Casalino et al. (12). The skeleton is stabilized by the long-range electrostatic and vdW interaction between atoms in the side chains. The 3D geometry of this complex structure can be visualized by connecting the atoms (see the sketch in Fig. 2 a). One can distinguish relative rotations, twists, and displacements between the adjacent atoms that form a basis for constructing the energy function needed for the MD and FE simulations. The backbone exhibits complex deformation and failure sequence during unwinding of the helix. With applied external forces, the relative distance between the atoms changes and resistance develops on unwinding the AH. A given atom interacts with all other atoms in the neighborhood through the atomistic potentials, including the long-range electrostatic and vdW interactions. The latter two forces are orders of magnitude smaller than the covalent bonds. Because they act as long “arms” of the side chains, their contribution to the torsional and bending moments is implicitly taken into account during model calibration for simplicity.
Figure 2.
(a) An α-helix fragment “isolated” from the stalk’s tropocollagen and subjected to a tension load , (b) Free body diagram of a tensile force acting on the coil, which is decomposed to two components. (c) Definitions of the geometrical parameters of an α-helix. To see this figure in color, go online.
In the present analytical and numerical solution, the AH is considered as a mathematically perfect spiral curve. The diameter of an AH is approximately nm with a pitch of nm, and the initial pitch angle . The main chain has a contour length each turn/thread. For the long stalk, there will be turns of the helix (see Fig. 2 a). An AH’s outside radius is , and the coil “radius” is set as (in this paper), which is about the radius size of a carbon’s covalent bond. The backbone chain of atoms can be visualized as a coil made of a wire or a ribbon. There are numerous similarities between the discrete atomistic model and the present structural model. The mathematical helix resembles a circle from above, while the real helix looks like an octagon. If we remove all atoms except the ones forming the main skeleton, these atoms will be distributed around the perfect helix with an average eccentricity distance. By bringing this distance to zero, the atoms will fall into the smooth helix. Still, the contour length of the actual chain of atoms and their projection onto the helix will be very similar. The interaction forces between the atoms are now defined by the bending stiffness , torsional stiffness , and axial tensile stiffness , much in the same way as the corresponding terms in the atomistic energy potential. For the sake of a calibration from test data and a parametric study, shape and size of the cross section must be assumed to be the same as in the FE analysis. We are aware that such a cross section of the spiral curve does not exist in reality, and one can calculate the second moment of inertia , the polar moment of inertia , and the cross-section area . The dimension of the cross section will be chosen when constructing the beam and shell models of the AH. Two papers (47,48) were found to be helpful in this task.
A free body diagram of force components when an AH is subjected to tension is presented in Fig. 2 b. The total force can be decomposed to along the coil (resulting in tension and bending on the coil) and perpendicular to the coil (resulting in torsion and shear loadings on the coil). Consider a spiral on an imaginary cylinder. By cutting and flattening the cylinder, the spiral maps into the triangle with a pitch , perimeter length , and total contour length (Fig. 2 c). The curvature and twist, and contour length of the helix are defined by
| (1) |
in terms of the pitch angle . The above definitions can be rewritten as
| (2) |
and their ratio depends only on the pitch angle ,
| (3) |
The pitch angle is related to the end displacement () of the helix,
| (4) |
Suppose that the helix is stretched by increasing the pitch angle. Initially, the curvature is equal to the inverse of the cylinder radius , as it should be. The twist is zero. At the end, at the helix becomes a straight line, the curvature vanishes, and the twist maximizes. Even more interesting is that the curvature and twist are not independent kinematic variables but are related through the pitch angle. This general geometrical property reduces the problem to one degree of freedom, which enormously simplifies the analytical and numerical solutions.
The everyday experience with winding and unwinding a watering hose illustrates a complex interaction between tension and torsion. When one pulls the hose from the coiled configuration, torsion develops, and poor-quality hoses start to develop loops and kinks. To prevent kinking, one must simultaneously twist the hose while pulling, one full turn per pitch. Inversely, by twisting a straight hose, the hose develops loops after onset of torsional buckling. This phenomenon has been extensively studied in the literature in relation to DNA looping.
Analytical solution of the α-helix under tension
We present here a simple derivation of the force-extension relationship using the energy method. A closed-form solution will help interpret several features of the numerical simulation. We follow the formulation similar to that of the coarse grain MD approach whereby the total potential energy consists of several components. The main contribution comes from the tensile, bending, and torsional resistance of covalent bonds. The electrostatic forces and vdW forces acting between atoms in the side chains provide additional contribution to . The long-range interaction forces are implicitly accounted for in the numerical solution (through model calibration) but are neglected in the analytical derivation. The stiffnesses in bending, torsion, and tension are denoted by , , and , respectively. The expression for the elastic strain energy of the AH is then reduced to four terms, whereby the three stiffnesses of covalent bonds subtract the work of external force ,
| (5) |
Here, the total vertical elongation (see Fig. 2 c) results from both the unwinding and the extension of the main skeleton . The formula of is defined by Eq. 4 by substituting . In structural mechanics, the axial, bending, and torsional stiffnesses of a cross section are defined as , , and , where is the cross-sectional area of a slender structure, is the second moment of inertial of the cross section, and is the polar moment of inertia. The stiffness coefficients are specified in “Correlation with the worm-like chain model” based on the information in the literature. The change of curvature and twist (per length) from the initial state is
| (6) |
The axial strain is . The axial stiffness of the helix is much larger than the bending and torsional stiffness. and it is only at the very end of the process of unwinding that the contour length changes from into . There are two degrees of freedom, the pitch angle and the displacement . For the system to be in equilibrium, the first variation of the total potential energy must be zero, , which leads to the following two simultaneous equations:
| (7) |
| (8) |
where . The above system together with Eq. 4 represents a parametric form of the solution. Eliminating between Eqs. 7 and 8 provides a unique relation between the axial displacement due to unwinding and the change of length of the contour length. It should be noted that both the displacement describing unwinding of the AH (Eq. 6) and extension of the contour length (Eq. 7) are per one turn. The distance between atoms in bending and torsion does not change, but they twist or rotate.
Many special cases can be obtained from the above general solution. For example, assuming zero initial pitch angle (), Eq. 7 reduces to
| (9) |
The small pitch angle approximation yields
| (10) |
where . The ratio of bending to torsion stiffness is for Poisson ratio . Here, is the diameter of a coil. Note that in the theory of elasticity, the shear modulus is related to the Young’s modulus by . A standard textbook solution is recovered for the spring (zero initial pitch angle ), or , with the spring coil stiffness (for one turn). The first term in Eq. 10 is the contribution of bending, which blows up to infinity at when the helix is fully straight. The second term in Eq. 10 is the torsion contribution, which increases linearly with displacement. The above solution was derived by assuming a full fixity of the helix against rotation at the ends. When the relative end rotation is allowed, the second term vanishes.
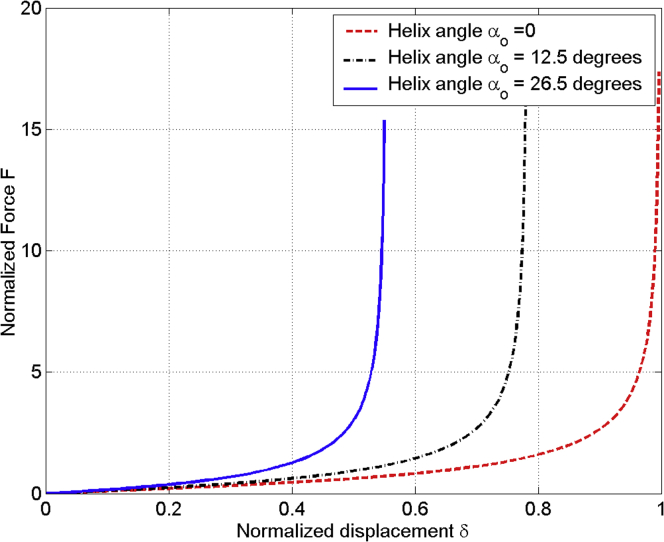
The nondimensional plots of force versus displacement are shown in Fig. 3 for three values of the pith angle, = 0°, 12.5°, and 26.5°. The features of a linear relationship at initial deformation and rapid nonlinear increase of force at the highly stretched ranges are well captured (similar to hyperelasticity). One can discern that an AH with higher initial helix angle is stiffer and reaches its fully stretched length earlier.
Figure 3.
A plot of Eq. (7) and Eq. (4) for normalized force () versus normalized displacement () under three different initial helix angles, in which an AH with is subjected to tension. To see this figure in color, go online.
Compression, bending, torsion, and buckling of the α-helix
The stiffnesses of bending, torsion, and buckling response are calculated numerically for TC later in “Other loading conditions in addition to tension.” For the sake of saving space the analytical solution is not presented here, although it would be a straightforward task. It is worth noting that in all cases the solution depends on the initial pitch angle parameter. For example, at zero pitch angle, the subsequent turns are in contact and the compressive force is infinite. For the real AH with the pitch angle , the maximum compressive displacement causing the bottoming up of the spring is . The value of the dimensionless force should theoretically be for the case of . Before this value is reached, the AH may buckle. Upon bending, the change of the pitch angle is very small, and the axial stiffness depends on the parameter and the initial configuration. The FE simulation confirms the above observations.
Calibration of elastic and fracture properties of the spike
In the closed-form solution of Eqs. 7, 8, 9, and 10, there are three stiffness parameters representing elastic properties of covalent bonds. The value of these parameters is taken from the literature. At the same time the mechanical properties of isotropic elastic bodies are fully defined by two parameters, the Young’s modulus and the Poisson ratio . It is interesting to see how the three material constants can be reduced to two parameters without losing the amount of information.
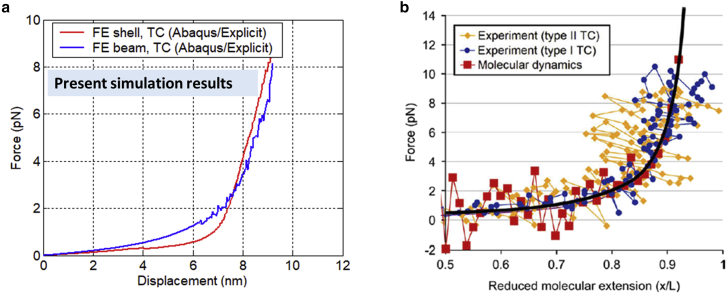
The underlying assumption is that the spike proteins obey initially the elasticity law. This is consistent with the main assumption of the atomistic model, in which atoms are interacting through elastic potentials. The calibration of the present model can be made by comparing the solution with the direct experimental results or the MD simulation. Results of tensile simulation of the AH were reported by Buehler et al. (17). The initial response is linear, up to a sudden rupture. By roughly estimating the MD simulation of a TC (see Fig. 8 b), the slope is 0.7 pN at 0.7 normalized displacement. Note that the stiffness of an AH approximately takes one-third of a TC. The stiffness of an AH coil with one turn is because of (as a simplification). Here, one turn of coil takes a length of . The value of the torsional stiffness of the of the backbone spiral is . There are many combinations of and that gives this value. Taking , the shear modulus is estimated as . Young’s modulus then becomes 3 GPa (assuming Poisson ratio ). The magnitude of torsional stiffness found from tests agrees with the values given in the literature, for example Odegard’s work (22,23). In particular the ratio of the axial stiffness and bending stiffness given in the above references is . In the present formulation, this ratio is . The agreement is remarkably close.
Figure 8.
(a) FE predicted tensile forces versus displacement for the TC of a spike leg of SARS-Cov-2. Both present simulation results of beam model and shell model are included, which are in the range of a few pN. Note that the displacement is not normalized (initial length = 7 nm). (b) Some available testing and MD data on other TC (17,60, 61, 62) as a comparison. Note that these data are normalized by a TC’s initial length. To see this figure in color, go online.
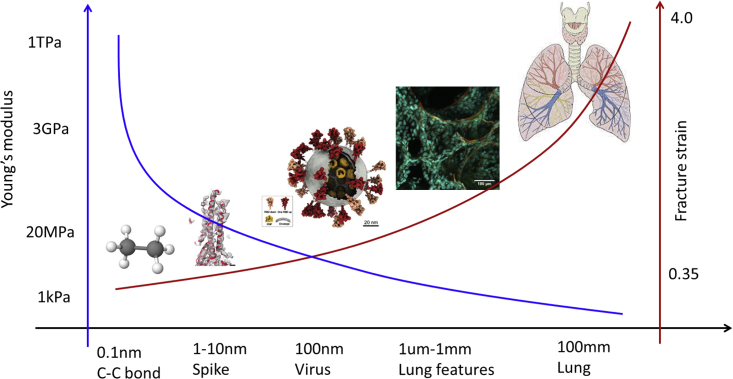
For the head of the spike, and the Young’s modulus drops to . These values are used in the present FE simulations. The qualitative dependence of the elastic modulus on the size of proteins from the simplest to more complex is shown in Fig. 4. In solid mechanics of engineering materials, the size effect is explained by the Weibull statistics of material imperfection. The interpretation for proteins and soft tissues are different due to different deformation mechanisms.
Figure 4.
An illustration of the size effect in biological structures, from the simple and small to the complex and large. The Young’s modulus and fracture strain properties are on an opposite trend. To see this figure in color, go online.
A review article by Buehler and Yung (49) provided a wealth of information on deformation and failure of protein materials in general, with no reference to the viral envelope and/or spike S-protein. At the same time the actual microscopic strain in the helix strand due to bending and torsion is initially very small but grows exponentially as the strand assumes a fully straightened position. At this stage, the distance between the hydrogen atoms forming the covalent bond starts to increase and could be broken at a defined but small critical displacement Rupture of covalent bonds is accounted for by the reactive force field method (50). Fracture at this length scale must then be formulated in terms of displacements, or more precisely the critical value of the total strain energy . To break the covalent bond, one must provide the external energy equal to the energy of the bond, which is known. More research should be carried out to determine fracture properties of the α-helices and TC. The general formulation of fracture and fracture analysis of the spike are left to a subsequent publication.
Correlation with the worm-like chain model
The WLC model of large displacement of the AH and DNA helix, often referred to as the Kratky-Prod model (51), has been developed in (52, 53, 54). The force-extension relation derived for small and moderately large displacement is of the form
| (11) |
where is the Boltzmann constant, is the temperature in Kelvin, and is the persistence length. At room temperature the Boltzmann constant is . The initial solution by Marko and Siggia (55) was subsequently improved by several authors, and the comparison of all these theories with the tests reported by Bozec and Horton (56) was presented by Hillgärtner et al. (57). On the comparison plots, each solution was adjusted by selecting a different value of the persistence length in the range of . The force blows up at infinity when the end shortening reaches the contour length . By comparing the WLC solution with Eq. 10, it is apparent that the two terms in Eq. 11 represent the contribution to bending and torsion, respectively, in agreement with the present solution.
In the enormous literature on the WLC model, no mention is made of the original shape of the AH. The lack of defining the original configuration of the WLC model is the most severe drawback of this widely accepted approach. Nonetheless, the WLC solution can be used as a cross-calibration of the present solution. For small displacement, equating Eqs. 10 and 11 provides the following relation for the torsional stiffness of the helix:
| (12) |
Assuming , , Eq. 12 gives the following estimate: . Any combination of and should be equal to this value. For example, taking , the shear modulus closely becomes , and (assuming Poisson ratio ). This result is consistent with the estimation in the preceding section.
Finite element simulation of the single α-helix
In the following two sections, FE models will be developed for the AH and TC representing the stalk of the SARS-CoV-2 virus at the atomistic scale. Different loading conditions (including tension, compression, bending, and torsion) will be considered in the FE simulations. For convenience, the unit system used in current FE simulations is as follows: nm (length), kg (mass), s (time), GPa (pressure), and nN (force).
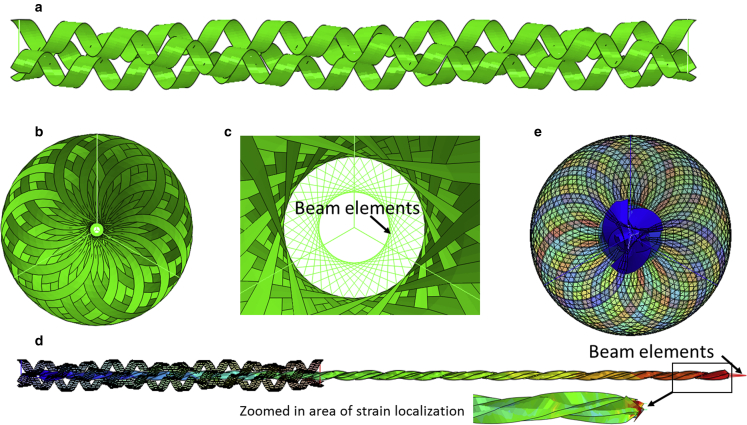
Beam elements and shell elements are two common structural level elements in FE analysis for large-scale simulations. From covalent bonds of two carbon atoms to a whole long chain of AH protein, 3D beam element (B31) and shell elements (S3 and S4) in Abaqus (58) are good choices to simulate its mechanical properties. The geometry information of AH is listed in Table 1 and the above section on Geometry and deformation of the α-helix under tension. The input of the FE model requires selecting the mesh size. To capture the response at such a small scale, the mesh size is assumed to have the order of the diameter of an atom. This assumption defines the cross section of the helix, even though the cross section of a single chain of atoms does not exist. The cross section can be a circular, giving rise to a “wire” model (called the beam model) or a rectangular cross section visualized as a “ribbon” (called the shell model). A ribbon model is a better representation of the distribution of atoms around the skeleton helix line than the wire model, but neither of the two describes it perfectly. The bulk of the microbiology literature portrays the α-helices as ribbons. The ribbon model can provide some additional insight into the anisotropic strength of the AH, which develops resistance to in-plain shear and twist.
The FE wire mesh was generated by a customized MATLAB code, and the result is shown in Fig. 5 a and b. The same coil dimensions were used to build a shell element-based ribbon-type AH model. The ribbon width and shell element thickness were set as and , respectively, giving the aspect ratio of 4. The shell mesh is shown in Fig. 5 c and d. For an AH model with beam elements there are about 500 elements, and each FE simulation takes about half an hour on a laptop computer. For an AH model with shell elements there are about 1000 elements, and each FE simulation takes just a few minutes on a laptop computer. This proves that the FE simulations with a mesh size of 0.03 nm are significantly faster than MD simulations, which usually need supercomputers.
Figure 5.
(a) Finite element mesh of a beam AH model, where before and after tensile loading are superimposed. (b) Top view of the beam model, where the blue circle is the original coil circle and the colored circle is the deformed one. (c) FE mesh of a shell AH model (representing DNA ribbon) superimposing initial and deformed configurations. (d) Top view of the shell model, where the outside black circle is the original shape. To see this figure in color, go online.
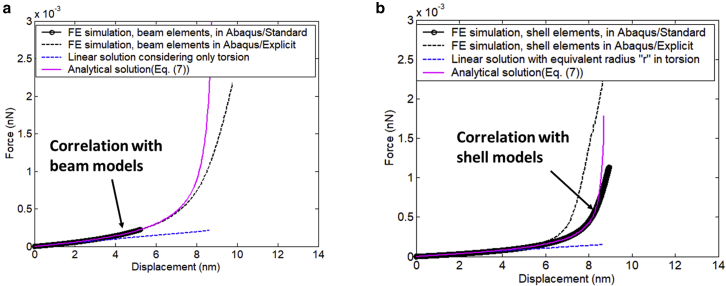
Both the beam model and shell model were run under the Abaqus/Standard (static) solver and the Explicit solver. The AH beams were highly stretched under tension, which resulted in decreasing AH radius, as illustrated in Fig. 5 b and d. The Standard (static) solver usually runs well up to moderately large deformation of AH but comes across significant reduction of time incremental and some convergence issues. Fortunately, the Abaqus/Explicit solver always runs up to very large deformations, as specified. Both solvers gave the same results for the beam model in terms of force response (Fig. 6 a), but predicted slightly different results for the shell model after 4 nm deformation (Fig. 6 b). In the initial stage of tensile loading, torsion along coil is the most important deformation mode, so the initial stiffness can be estimated using the coil spring formula. The results are also plotted in Fig. 6 for comparison. Generally speaking, the analytical solutions (Eqs. 4, 7, and 8) give an excellent correlation with FE results of the Abaqus/Standard solver. From Fig. 6, one can deduce that the predicted tensile force for an individual AH up to large deformation (100% stretch at stalk length of 7 nm) is about .
Figure 6.
(a) FE simulation results of AH under tension using beam elements. The predicted force-displacement curves are identical between Abaqus Explicit and Standard solvers. Analytical solution (Eqs. 4, 7, and 8) gives an excellent correlation with FE results of Standard solver. (b) FE results of shell models. There are some differences between the two Abaqus solvers. The analytical solution gives an excellent correlation with the result of Abaqus Standard solver up to 8 nm. To see this figure in color, go online.
Finite element simulation of the tropocollagen stalk
The TC molecule consists of three left-handed AHs intertwined in an overall right-handed coil. Compared with the twist of each AH, the global twist is small, less than one turn per the length of the stalk. For the TC molecule one can distinguish the diameter of the wire and the diameter of the helix . In the present model, the distance between symmetry axes of individual helices must be equal to to avoid interpenetration. Three strands interact through side chains, so the atoms break and develop new bonds. The effect of residues was accounted for in the present structural model by introducing the interface between the AHs. With no cross-links between the individual AH, the tensile strength of the TC is three times larger than the strength of a single AH. The interaction of the side chains of the AHs was studied by Wolgemuth and Sun (59). In compression, a single AH will buckle due to a very low bending stiffness. The aspect ratio of the TC is much larger, so the TC molecule will compress and crumple instead of buckling. It is possible to solve this problem analytically, but numerical solution is more straightforward.
The TC stalk is modeled by assembling three AHs with a right-handed coil angle, which was set as one turn () for a whole stalk. The radius of an AH is , and three AHs attached together as an equilateral triangle for their centers result in an outer radius of . Since the beam and shell elements are modeled in their middle axis/plane with a radius/thickness of 0.05 nm, the resulting overall stalk radius is about 0.42 nm, which is listed in the geometrical parameters (Table 1). In this section, results of both beam TC model and shell TC model under tension will be presented. The results of shell model under other typical loadings will also be included.
Beam (wire) model
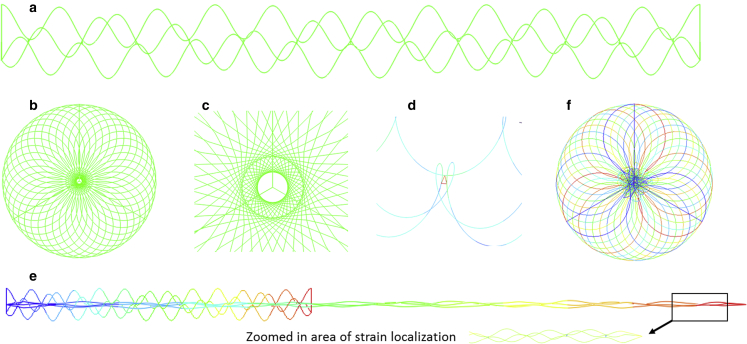
A MATLAB code was written to create the FE meshes by given key controlling parameters. Fig. 7 a shows the mesh of beam before and after tensile loading. To apply the prescribed boundary displacement on the three AHs, a tripod consisting of three beam elements is linked to the ends of three AHs. The side view of an AH coil is a circle, but it shows a beautiful flower shape after introducing the right-handed coiled angle (Fig. 7 b). The interaction between three AHs is very complex due to the vdW and electrostatic forces between atoms. Contact forces develop during deformation that may lead to interpenetration of the skeleton atoms between different strands. This is a challenge when searching contact surfaces for coiled structures in the current FE solvers. Three short beam elements at the nearest three AHs are introduced to mimic the long-range as well as contact interaction between respective atoms (Fig. 7 c and d).
Figure 7.
(a) Initial configuration of the spike leg is modeled by beam elements as a TC. (b) Top view of the TC model where its coiled-coil structure shows a periodic feature. (c) Zoom-in view of the center showing the connected beam elements for three AH coils. (d) Further zoom-in view shows the connected three close AHs by triple beam elements, which simulates their interactions. (e) Deformation of a TC under tension up to very large stretching. The local strain concentration at the tip is zoomed-in. (f) Top view of the TC superimposing the original and deformed configurations. To see this figure in color, go online.
Fig. 7e and f shows the predicted deformation of TC under tensile loading up to over 100% stretching ratio. The contour color shows the total displacement. One can see the significant reduction of radii of AHs and TC. The local stress/strain of linked beams among AHs can be larger (see Fig. 7 d), but their contribution to the total strain energy is negligible. The predicted force-displacement curve is plotted in Fig. 8 a. Results shown here are taken from Abaqus/Explicit for very large deformation. The predicted range of tensile force is about . The real test data of SARS-CoV-2 spikes are not available and probably will be too difficult to obtain experimentally. However, tensile tests of several different TCs have been reported in open literature. One example of tensile force from experiments and MD simulations (17,60) are included in Fig. 8 b, where the authors used optical tweezer experiments (61,62). One can observe that both the curve trend (quickly stiffening up at large stretching) and the force range are well correlated. This helps to validate the FE modeling.
Shell (ribbon) model
The second method of modeling TC by means of shell elements (called hereafter the ribbon model) is also presented in addition to the wire model (Fig. 9 a–c). One can easily visualize the left-handed feature of AH and the right-handed appearance of TC in Fig. 9 a. In the numerical simulation, the program must search for the self-contact between the respective strands, a very difficult task for such a complex geometry. Like in the wire model, the interfacial beam elements are used to connect the three AHs and link them for mimicking contacts during deformation, which can be seen (shown by an arrow) inside the TC (Fig. 9 c) and in the right end of a TC (Fig. 9 d). The interface beam elements are utilized in the present simulation only to prevent interpenetration. The same beam elements can model the long-range vdW and electrostatic forces as well as the interaction forces exerted by side chains, following the information from the work of Wolgemuth and Sun (59). This has not been done here.
Figure 9.
(a) Initial configuration of the spike leg is modeled by shell elements as a TC, where an AH is left-handed and the TC is right-handed for one turn. (b) Top view of the TC shell model where its coiled-coil structure shows a periodic feature. (c) Zoom-in view of the center showing the connected beam elements for three AH ribbon coils, which simulates their interactions. (d) Deformation of a shell TC under tension up to very large stretching. Three short artificial beam elements are used to eliminate interpenetration between α-helices. The contour colors represent their amount of displacement. The local strain concentration at the tip is zoomed-in. (e) Top view of the TC superimposing the original and deformed configurations. To see this figure in color, go online.
The deformed configurations under tensile loading are shown in Fig. 9 d and e. The periodic feature of a coiled coil creates a beautiful pattern when seen from above. The contour colors represent the amounts of displacement. The predicted tensile force is presented in Fig. 8 a and compared with the beam models. The predicted force from the shell model is a slightly smaller than that of the beam model in the beginning, due to a selected relatively small shell thickness, which affects its bending rigidity and torsion rigidity. The force in the shell model picks up more quickly at the large deformation, which ends up with a result similar to that of the beam model. Both models correlate with reported literature data of other TCs. It is not easy to establish uniquely the equivalence of the two types of the FE elements at the atomistic scale because neither the wire nor ribbon contains all atoms in the side chains. The shell model is more realistic, and the AHs are always represented by ribbons in the microbiology literature.
Other loading conditions in addition to tension
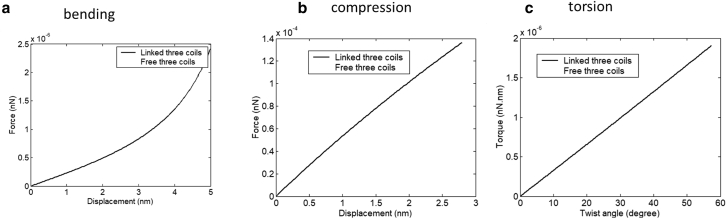
In a real situation of SARS-CoV-2 spike subjected to ultrasound loading, other typical loading conditions occur in addition to simple tension. With a fixed boundary at the base of the spike (on the left-hand side of a TC), FE simulations of bending, compression, and torsion are shown in Fig. 10. The predicted reaction force and reaction moments are plotted in Fig. 11. The compression of TC predicts the same initial stiffness as in tension around the neutral position. There is no buckling under compression if three AHs are linked. However, column buckling will occur if individual AHs are left freely in a TC. From Fig. 11 a, one can deduce that the bending force is at the level of about three orders of magnitude smaller than that of tensile loading, in accord with the calibration of stiffness described in “Calibration of elastic and fracture properties of the spike.” Based on the classical beam theory, the “equivalent” tensile rigidity, bending rigidity, and torsion rigidity of a TC can be calculated.
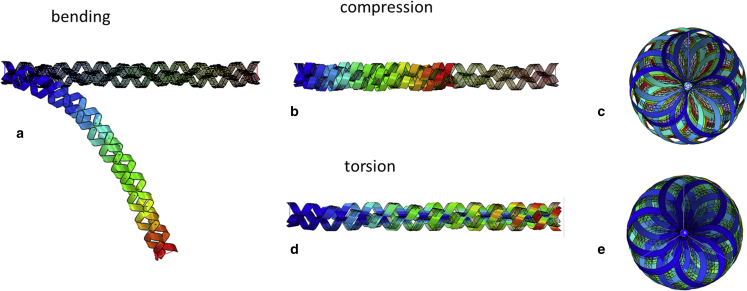
Figure 10.
FE simulations of a TC using shell elements for other loading conditions, where both initial and deformed configurations are illustrated: (a) cantilever beam bending, (b and c) compression, (d and e) torsion. (c) and (e) are top views. The contour color represents displacement. To see this figure in color, go online.
Figure 11.
FE predicted force or moment for other loading conditions for TC: (a) cantilever beam bending, (b) compression, (c) torsion.
The resonant vibrations of spikes
This paper concludes with the modal analysis of the spike. The natural vibration modes and corresponding frequencies are the property of a structure, and the eigenvalue analysis does require the definition of the forces exerted by the ultrasound waves. Those forces are known and were determined by the present team in (4). The solution of transient vibration will require the running of many cases with different frequencies and amplitudes. Besides, the presence of coupled vibration modes combined with material and structural imperfections calls for design of the optimum ultrasound pulse with frequency modulation in time. The results of this ongoing study will be summarized in a subsequent publication.
The ultimate objective of the present research program is to answer the question stated in the introduction: under what conditions the ultrasound can induce resonant vibration of the spike and in the end inflict permanent damage to SARS-CoV-2 so that it will lose the ability to multiply. The FE simulation technique at the atomistic scale, developed in this paper, is the most critical step on the path to answer this question. It has the main advantage of MD simulation and is free of the timescale limitation of the MD technique. In other words, it can be considered as the second stage of the MD where the multiatomic discrete system of individual atoms is replaced by beam and shell elements that can undergo large strains and displacements. The general-purpose FE code Abaqus instantly provides a natural vibration spectrum and is ideal for running the transient vibration problems. Additionally, it requires orders of magnitude smaller resources in terms of computer power as compared with the MD technique. With a total number of elements needed to model the entire spike on an order of or less, it can be run on personal computers within minutes. A full all-atom MD simulation with a comparable accuracy involving millions of atoms must be run on supercomputers. Furthermore, the method can be easily extended to cover damped as well as random vibrations. Many nonlinear FE software packages can be used for such a purpose, all of which will require the same input data.
Numerical solutions
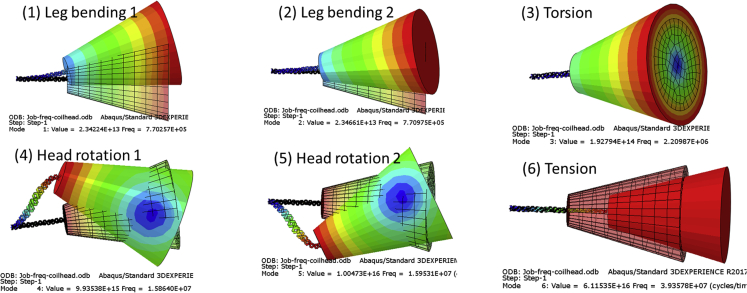
For the purpose of the modal analysis, the stalk of the spike is represented by the TC shell model and the spike head is represented as an elastic solid, modeled by solid elements (C3D8R) in Abaqus. The geometry and mass distribution are defined in Fig. 1 and Table 1. The fundamental mode shapes and natural frequencies are illustrated in Fig. 12 and Table 2. The mode shapes are superimposed on initial shapes for visualization. The mass of the spike is not a point mass but a distributed mass. It has its translation and rotation degrees of freedom, and responses of two different bendings, three different rotations, and one tension are generated. The predicted first two bending modes (in y and z directions) have the same frequency of 0.77 MHz. The frequency of the first torsion mode is about 2.2 MHz, and the other two spike head rotation modes have a frequency of around 16 MHz. The frequency of the first tension/compression mode of 39 MHz is the highest of all, but because of structural imperfections it will seldom be observed in a real virus. Note that these values are much lower than those previously determined in (4) for a much cruder and stiffer spike. We believe that the predicted values of resonant vibrations are this time correct, given the great care in modeling the geometry and mechanical properties of the AHs and TC forming the stalk of the spike. These values are within the range of frequencies used in medicine for imaging and diagnosis (2–20 MHz), thus removing any concerns about the safety of the proposed approach.
Figure 12.
FE predicted first mode shapes and frequencies of a SARS-CoV-2 spike under a cantilever boundary condition. To see this figure in color, go online.
Table 2.
FE predicted first six natural frequencies and mode shapes of SARS-CoV-2 spikes
| Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | Mode 6 | |
|---|---|---|---|---|---|---|
| Frequency (MHz) | 0.7703 | 0.7710 | 2.2099 | 15.864 | 15.953 | 39.358 |
| Mode type | bending-1 | bending-2 | torsion | rotation-1 | rotation-2 | tension |
Analytical solutions
The model of the spike with a known stiffness of the stalk and the mass moments of the head is sufficient to determine resonant frequencies of a selected modal shape. For example, a textbook solution for the frequency of the tension/compression mode (mode 6 in Fig. 12) is
| (13) |
where is the initial stiffness of the of the stalk TC and is the mass of the spike’s head. Substituting values of the stiffness ( is given by Eq. 10, and number of turns is discussed in “Geometry and deformation of the α-helix under tension”) and the mass , the tension/compression frequency becomes 43.9 MHz. This value correlates well with the numerical solution (mode 6 in Table 2). The frequencies in torsion and bending could also be calculated in a similar way based on results in “Other loading conditions in addition to tension.” It should be noted that the resonant frequencies determined by the modal analysis correspond to small amplitude vibrations. Because the TC’s stiffness is increasing with larger displacements, the spikes subjected to ultrasound excitation will undergo nonlinear vibrations. Also, in this paper the natural frequencies were determined in air. Extension to the water environment was derived in (4) using the added mass concept. The frequencies then become 50% lower.
Conclusion
The mathematical model of any biological or man-made structure requires definition of 1) the initial geometry, 2) time- and space-dependent loading, 3) the boundary, and 4) the initial conditions. A virus is a tiny structure that obeys the Newton equations and the elasticity law, all the way to the size of atoms. The loading was determined in the previous paper of the investigating team (4) where the solution of the structural acoustics was developed for a virus floating either in water or the air. On the relatively solid head of the spike, the uniform incident pressure is fully equilibrated so that the ultrasound wave does not directly induce spike vibration. However, the viral shell responds to the uniform pressure by developing a multitude of vibration modes. The lowest mode is the so-called bouncing mode in which the ratio of the vertical and horizontal displacements depends on the azimuth angle. It is the harmonic variation of these two displacements that sets the bottom of the stem and thereby the whole spike into the various modes of vibrations.
In this paper an effort was made to identify only the first-order effects, leaving many factors for future improvement. First, a more rigorous description of the long-range electrostatic and vdW forces should be formulated. In the current model these forces are transmitted by short elastic beams that also prevent local interpenetration of atoms in the three separate strands. For the task of predicting the global structural response, the long-range forces between all atoms could be lumped together by a much smaller number of interfacial beams with a cutoff value to include only the strongest interactions.
The most important contribution of this paper is the determination of the coupled tensile, compressive, bending, and torsional stiffness of the AH and TC and, on that basis, calculation of a spectrum of the six lowest vibration frequencies and modes of the spike. Those frequencies were found to be within the safe range routinely used for medical imaging and diagnosis by means of ultrasound. In other words, these results provide a solid theoretical basis for using ultrasound to damage the coronavirus (1–40 MHz) through transient and resonant vibration at large deformations. The results of the transient vibration analysis will be the subject of ongoing work.
Modal analysis already provides some clues regarding possible damage to the spike. By increasing the amplitude of the bending modes, our preliminary simulation indicates that the head of the spike will eventually hit the viral shell and bounce back. The repeated impact could damage proteins at the outer core of the head, responsible for opening the channels between the virus and the invaded cell. At the same time the rotational mode will impose both bending and extension of the spike and may damage or fracture one or more strands in the stalk. During tensile simulations the maximum tensile strain occurs at the two fixed ends (tips) of the TC, with an approximate local tensile strain of 0.40 (see Figs. 7 e and 9 d). Compared with the estimated fracture strain of TC in “Calibration of elastic and fracture properties of the spike,” it is highly possible to break (or damage) the stalk of the spikes during resonant vibration at large deformations.
Jiménez-Zaragoza et al., (63) observed that spikes were detached from the viral outer shell after only a few frames of the high-speed camera. In either case, the deadly life cycle of SARS-CoV-2 will be interrupted. To make this critical step, a new failure criterion of the covalent bonds subjected to simultaneous tension, torsion, and bending under monotonic loading and/or nanofatigue must be formulated. This will be the subject of continuing research. It is noted that there is AH-to-β-sheet transition in mechanical pulling of TC proteins (64, 65, 66), which was not considered in the current study. Our studies were focused on predicting the spike stalk protein’s elastic modulus and its structure’s natural frequencies, which will guide how to damage/fracture virus using ultrasound pulses. In fact the α-to-β transition can also be one of the failure modes, which needs further study in the future.
Finally, we would like to bring the issue of nanofatigue to the attention of the microbiology community. At the frequency of 1.0 MHz there will be 106 vibration cycles in 1 s. This calls for looking at the progressive damage in nanofatigue. Repeated static nanoindentation tests under atomic force microscopy (AFM) by Jiménez-Zaragoza et al. (63) and Kiss et al. (67) have demonstrated that the strength of the viral shell diminished with each loading and unloading cycle up to only 100 cycles. The experimental results by Kiss et al. (67) referred specifically to SARS-CoV-2. This effect could be dramatically magnified up to millions of cycles and could be the key factor in the quest to deactivate the virus. Biological materials have an ability to heal. The final outcome of external loading is the result of the interplay between damage and healing. The effect of nanofatigue should be a new and important theme for biomedical research.
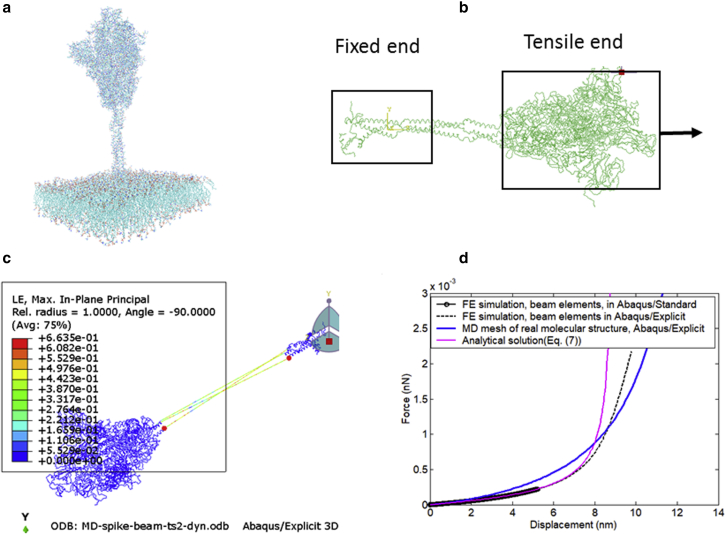
Another effort by the authors is to use the developed FE simulation methodology for the real molecular structure of SARS-CoV-2 virus. A detailed MD model developed by Casalino et al. (12) was converted to an FE model using beam elements that link the backbone carbon atoms of the spike protein (Fig. 13 a–c). A tensile loading condition is applied to the stalk within a similar length of 7 nm. The same beam cross section and material properties (calibrated in “Calibration of elastic and fracture properties of the spike” and “Finite element simulation of the tropocollagen stalk”) are used, and the predicted force-displacement curve is shown in Fig. 13 d. This result is very close to the current beam model of TC, which uses “isolated” AH and TC protein fragments for analysis. This part of our work could represent a new line of research in microbiology.
Figure 13.
Tension simulation of spike protein’s stalk TC using beam mesh transferred from an MD model. (a) Detailed molecular structures of the SARS-CoV-2 virus. (b) FE beam element model setup for spike protein subjected to tension. (c) Predicted deformation shape in Abaqus/Explicit. (d) Predicted force-displacement curve and comparison with previous beam models and analytical solutions. To see this figure in color, go online.
It is noted again that there is thermodynamic stability of the spikes and possible transition from AH to β-sheets. This possible transition will not change the overall geometry of the spikes. They are physical objects, seen on photographs provided by cryo-EM of the coronavirus family, and they were also predicted by MD simulation. However, the resolution of the cryo-EM technique is insufficient to discriminate the composition of the spike, and specifically its stalk. All-atomic MD simulation assures local equilibrium in a neighborhood of any atoms. Such an approach is equivalent to seeking global minimization of the potential energy of a system. Since we are using the information on the molecular structure of TC, from the all-atom MD simulation performed by Casalino et al. (12) the stalk of the spike must be in a state of thermodynamic stability. Under ultrasound excitation, the work of external forces is converted to kinetic energy, ensuring dynamic equilibrium. The transition between AH and β-sheets would require the formation of additional lateral hydrogen bonds between N–H groups in the individual strands. Such a transition could indeed provide additional stiffness. It is impossible to experimentally prove whether such a transition occurs by X-ray crystallography in the time span of nanoseconds. Therefore, the issue of transition under dynamic loading at about 2–20 MHz ultrasound waves must remain only a hypothetical question. At the same time, the present FE technique opens the possibility of introducing the effect of additional covalent bonds between strands through the concept of energy interpenetration.
The ultimate proof of concept should be provided by the laboratory experiments. To this end, we are working closely with two of the world’s leading teams on the application of the AFM technique. We believe that FE modeling and computational experiments will prove to be an important tool in the fight against the present pandemic. Furthermore, the same methodology can be applied to other viruses with similar nanostructures as summarized by Zandi et al. (68). Their resonant frequencies are expected to be within a similar range. The door is open for the microbiology community to contribute to the experimental verification of the present findings.
Author contributions
T.W. designed the research. Y.B. conducted the FE simulations. T.W. and Y.B. both contributed to analytical solutions and wrote the article.
Acknowledgments
Insightful discussions from Aida Nonn from OTH Regensburg, Thomas Tancogne-Dejean from ETH, and Albert Cerrone from Notre Dame are greatly appreciated. Gregory Odegard of the Michigan Technological University, Miklos Kellermayer of Semmelweis University, Siewert-Jan Marrink of the University of Groningen, and Roger D. Kamm of MIT provided us with very valuable comments on the atomistic formulation in molecular mechanics. Y.B. would also like to acknowledge the Abaqus (Simulia) software license support from Dassault Systems.
Declaration of interests
The authors declare no competing interests.
Editor: Elizabeth Rhoades.
Contributor Information
Tomasz Wierzbicki, Email: wierz@mit.edu.
Yuanli Bai, Email: bai@ucf.edu.
References
- 1.Rosales-Mendoza S., Comas-García M., González-Ortega O. Academic Press; 2021. Biomedical Innovations to Combat COVID-19. [Google Scholar]
- 2.Mittelstein D.R., Ye J., et al. Gharib M. Selective ablation of cancer cells with low intensity pulsed ultrasound. Appl. Phys. Lett. 2020;116:013701. doi: 10.1063/1.5128627. [DOI] [Google Scholar]
- 3.Heyden S., Ortiz M. Oncotripsy: targeting cancer cells selectively via resonant harmonic excitation. J. Mech. Phys. Solid. 2016;92:164–175. doi: 10.1016/j.jmps.2016.04.016. [DOI] [Google Scholar]
- 4.Wierzbicki T., Li W., Zhu J., et al. Effect of receptors on the resonant and transient harmonic vibrations of Coronavirus. J. Mech. Phys. Solid. 2021;150:104369. doi: 10.1016/j.jmps.2021.104369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Yao M., Wang H. A potential treatment for COVID-19 based on modal characteristics and dynamic responses analysis of 2019-nCoV. Nonlin. Dyn. 2020;106:1425–1432. doi: 10.1007/s11071-020-06019-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ke Z., Oton J., et al. Briggs J.A.G. Structures and distributions of SARS-CoV-2 spike proteins on intact virions. Nature. 2020;588:498–502. doi: 10.1038/s41586-020-2665-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Neuman B.W., Adair B.D., et al. Buchmeier M.J. Supramolecular architecture of severe acute respiratory syndrome coronavirus revealed by electron cryomicroscopy. J. Virol. 2006;80:7918–7928. doi: 10.1128/jvi.00645-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Turoňová B., Sikora M., et al. van Zandbergen G. In situ structural analysis of SARS-CoV-2 spike reveals flexibility mediated by three hinges. Science. 2020;370:203–208. doi: 10.1126/science.abd5223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wrapp D., Wang N., et al. McLellan J.S. Cryo-EM structure of the 2019-nCoV spike in the prefusion conformation. Science. 2020;367:1260–1263. doi: 10.1126/science.abb2507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yao H., Song Y., et al. Cheng L. Molecular architecture of the SARS-CoV-2 virus. Cell. 2020;183:730–738.e13. doi: 10.1016/j.cell.2020.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yu A., Pak A.J., et al. Voth G.A. A multiscale coarse-grained model of the SARS-CoV-2 virion. Biophys. J. 2021;120:1097–1104. doi: 10.1016/j.bpj.2020.10.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Casalino L., Gaieb Z., et al. Fadda E. Beyond shielding: the roles of glycans in the SARS-CoV-2 spike protein. ACS Cent. Sci. 2020;6:1722–1734. doi: 10.1021/acscentsci.0c01056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Vashishta P., Kalia R.K., Nakano A. Large-scale atomistic simulations of dynamic fracture. Comput. Sci. Eng. 1999;1:56–65. doi: 10.1109/5992.790588. [DOI] [Google Scholar]
- 14.Bond P.J., Holyoake J., et al. Sansom M.S. Coarse-grained molecular dynamics simulations of membrane proteins and peptides. J. Struct. Biol. 2007;157:593–605. doi: 10.1016/j.jsb.2006.10.004. [DOI] [PubMed] [Google Scholar]
- 15.Brooks B.R., Brooks C.L., et al. Caflisch A. CHARMM: the biomolecular simulation program. J. Comput. Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Souza P.C.T., Alessandri R., et al. Kroon P.C. Martini 3: a general purpose force field for coarse-grained molecular dynamics. Nat. Methods. 2021;18:382–388. doi: 10.1038/s41592-021-01098-3. [DOI] [PubMed] [Google Scholar]
- 17.Buehler M.J., Keten S., Ackbarow T. Theoretical and computational hierarchical nanomechanics of protein materials: deformation and fracture. Prog. Mater. Sci. 2008;53:1101–1241. doi: 10.1016/j.pmatsci.2008.06.002. [DOI] [Google Scholar]
- 18.Schlick T., Portillo-Ledesma S. Biomolecular modeling thrives in the age of technology. Nat. Comput. Sci. 2021;1:321–331. doi: 10.1038/s43588-021-00060-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Schlick T., Portillo-Ledesma S., et al. Liang E. Biomolecular modeling and simulation: a prospering multidisciplinary field. Annu. Rev. Biophys. 2021;50:267–301. doi: 10.1146/annurev-biophys-091720-102019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Schlick T., Zhu Q., et al. Yan S. Structure-altering mutations of the SARS-CoV-2 frameshifting RNA element. Biophys. J. 2021;120:1040–1053. doi: 10.1016/j.bpj.2020.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cranford S., Sen D., Buehler M.J. Meso-origami: folding multilayer graphene sheets. Appl. Phys. Lett. 2009;95:123121. doi: 10.1063/1.3223783. [DOI] [Google Scholar]
- 22.Odegard G.M., Gates T.S., et al. Siochi E.J. Constitutive modeling of nanotube–reinforced polymer composites. Compos. Sci. Technol. 2003;63:1671–1687. doi: 10.1016/s0266-3538(03)00063-0. [DOI] [Google Scholar]
- 23.Odegard G.M., Gates T.S., et al. Wise K.E. Equivalent-continuum modeling of nano-structured materials. Compos. Sci. Technol. 2002;62:1869–1880. doi: 10.1016/s0266-3538(02)00113-6. [DOI] [Google Scholar]
- 24.Rouhi S., Ansari R. Atomistic finite element model for axial buckling and vibration analysis of single-layered graphene sheets. Phys. E Low Dimens. Syst. Nanostruct. 2012;44:764–772. doi: 10.1016/j.physe.2011.11.020. [DOI] [Google Scholar]
- 25.Chandra Y., Chowdhury R., et al. Scarpa F. Elastic instability of bilayer graphene using atomistic finite element. Phys. E Low Dimens. Syst. Nanostruct. 2011;44:12–16. doi: 10.1016/j.physe.2011.06.020. [DOI] [Google Scholar]
- 26.Georgantzinos S., Katsareas D., Anifantis N. Graphene characterization: a fully non-linear spring-based finite element prediction. Phys. E Low Dimens. Syst. Nanostruct. 2011;43:1833–1839. doi: 10.1016/j.physe.2011.06.037. [DOI] [Google Scholar]
- 27.Scarpa F., Adhikari S., Srikantha Phani A. Effective elastic mechanical properties of single layer graphene sheets. Nanotechnology. 2009;20:065709. doi: 10.1088/0957-4484/20/6/065709. [DOI] [PubMed] [Google Scholar]
- 28.Cao G., Chen X. Buckling of single-walled carbon nanotubes upon bending: molecular dynamics simulations and finite element method. Phys. Rev. B. 2006;73:155435. doi: 10.1103/physrevb.73.155435. [DOI] [Google Scholar]
- 29.Xiao S., Belytschko T. A bridging domain method for coupling continua with molecular dynamics. Comput. Methods Appl. Mech. Eng. 2004;193:1645–1669. doi: 10.1016/j.cma.2003.12.053. [DOI] [Google Scholar]
- 30.Couto R., Silvestre N. Finite element modelling and mechanical characterization of graphyne. J. Nanomater. 2016;2016:1–15. doi: 10.1155/2016/7487049. [DOI] [Google Scholar]
- 31.Yang S.-C., Lin H.C., et al. Sun C.K. Efficient structure resonance energy transfer from microwaves to confined acoustic vibrations in viruses. Sci. Rep. 2015;5:18030. doi: 10.1038/srep18030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chrysikopoulos C.V., Manariotis I.D., Syngouna V.I. Virus inactivation by high frequency ultrasound in combination with visible light. Colloids Surf. B Biointerfaces. 2013;107:174–179. doi: 10.1016/j.colsurfb.2013.01.038. [DOI] [PubMed] [Google Scholar]
- 33.Dykeman E.C., Sankey O.F. Normal mode analysis and applications in biological physics. J. Phys. Condens. Matter. 2010;22:423202. doi: 10.1088/0953-8984/22/42/423202. [DOI] [PubMed] [Google Scholar]
- 34.Dykeman E.C., Sankey O.F. Atomistic modeling of the low-frequency mechanical modes and Raman spectra of icosahedral virus capsids. Phys. Rev. 2010;81:021918. doi: 10.1103/physreve.81.021918. [DOI] [PubMed] [Google Scholar]
- 35.Dykeman E.C., Sankey O.F. Low frequency mechanical modes of viral capsids: an atomistic approach. Phys. Rev. Lett. 2008;100:028101. doi: 10.1103/physrevlett.100.028101. [DOI] [PubMed] [Google Scholar]
- 36.Dykeman E.C., Sankey O.F. Theory of the low frequency mechanical modes and Raman spectra of the M13 bacteriophage capsid with atomic detail. J. Phys. Condens. Matter. 2008;21:035116. doi: 10.1088/0953-8984/21/3/035116. [DOI] [PubMed] [Google Scholar]
- 37.Babincová M., Sourivong P., Babinec P. Resonant absorption of ultrasound energy as a method of HIV destruction. Med. Hypotheses. 2000;55:450–451. doi: 10.1054/mehy.2000.1088. [DOI] [PubMed] [Google Scholar]
- 38.Burkhartsmeyer J., Wang Y., et al. Gordon R. Optical trapping, sizing, and probing acoustic modes of a small virus. Appl. Sci. 2020;10:394. doi: 10.3390/app10010394. [DOI] [Google Scholar]
- 39.Talati M., Jha P.K. Erratum: acoustic phonon quantization and low-frequency Raman spectra of spherical viruses [Phys. Rev. E 73, 011901 (2006)] Phys. Rev. 2008;77:029904. doi: 10.1103/physreve.77.029904. [DOI] [PubMed] [Google Scholar]
- 40.Sirsi S.R., Borden M.A. State-of-the-art materials for ultrasound-triggered drug delivery. Adv. Drug Deliv. Rev. 2014;72:3–14. doi: 10.1016/j.addr.2013.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Heckerman D.E., Mercer S.J., et al. Horvitz E.J. Google Patents; 2010. Utilizing Ultrasound to Disrupt Pathogens. [Google Scholar]
- 42.Schroeder A., Kost J., Barenholz Y. Ultrasound, liposomes, and drug delivery: principles for using ultrasound to control the release of drugs from liposomes. Chem. Phys. Lipids. 2009;162:1–16. doi: 10.1016/j.chemphyslip.2009.08.003. [DOI] [PubMed] [Google Scholar]
- 43.Beniac D.R., Andonov A., et al. Booth T.F. Architecture of the SARS coronavirus prefusion spike. Nat. Struct. Mol. Biol. 2006;13:751–752. doi: 10.1038/nsmb1123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Dyson H.J. Expanding the proteome: disordered and alternatively folded proteins. Q. Rev. Biophys. 2011;44:467–518. doi: 10.1017/s0033583511000060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hu Y., Buehler M.J. Comparative analysis of nanomechanical features of coronavirus spike proteins and correlation with lethality and infection rate. Matter. 2021;4:265–275. doi: 10.1016/j.matt.2020.10.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Shoulders M.D., Raines R.T. Collagen structure and stability. Annu. Rev. Biochem. 2009;78:929–958. doi: 10.1146/annurev.biochem.77.032207.120833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Dym C.L. Consistent derivations of spring rates for helical springs. J. Mech. Des. 2009;131 doi: 10.1115/1.3125888. [DOI] [Google Scholar]
- 48.Brokaw C.J. California Institute of Technology; 2002. Torsion, Twist, and Writhe: The Elementary Geometry of Axonemal Bending in Three Dimensions. [Google Scholar]
- 49.Buehler M.J., Yung Y.C. Deformation and failure of protein materials in physiologically extreme conditions and disease. Nat. Mater. 2009;8:175–188. doi: 10.1038/nmat2387. [DOI] [PubMed] [Google Scholar]
- 50.Buehler M.J. Atomistic and continuum modeling of mechanical properties of collagen: elasticity, fracture, and self-assembly. J. Mater. Res. 2006;21:1947–1961. doi: 10.1557/jmr.2006.0236. [DOI] [Google Scholar]
- 51.Kratky O., Porod G. Diffuse small-angle scattering of X-rays in colloid systems. J. Colloid Sci. 1949;4:35–70. doi: 10.1016/0095-8522(49)90032-x. [DOI] [PubMed] [Google Scholar]
- 52.Marko J.F., Siggia E.D. Stretching dna. Macromolecules. 1995;28:8759–8770. doi: 10.1021/ma00130a008. [DOI] [Google Scholar]
- 53.Smith S.B., Finzi L., Bustamante C. Direct mechanical measurements of the elasticity of single DNA molecules by using magnetic beads. Science. 1992;258:1122–1126. doi: 10.1126/science.1439819. [DOI] [PubMed] [Google Scholar]
- 54.Bustamante C., Bryant Z., Smith S.B. Ten years of tension: single-molecule DNA mechanics. Nature. 2003;421:423–427. doi: 10.1038/nature01405. [DOI] [PubMed] [Google Scholar]
- 55.Marko J.F., Siggia E.D. Statistical mechanics of supercoiled DNA. Phys. Rev. 1995;52:2912–2938. doi: 10.1103/physreve.52.2912. [DOI] [PubMed] [Google Scholar]
- 56.Bozec L., Horton M. Topography and mechanical properties of single molecules of type I collagen using atomic force microscopy. Biophys. J. 2005;88:4223–4231. doi: 10.1529/biophysj.104.055228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Hillgärtner M., Linka K., Itskov M. Worm-like chain model extensions for highly stretched tropocollagen molecules. J. Biomech. 2018;80:129–135. doi: 10.1016/j.jbiomech.2018.08.034. [DOI] [PubMed] [Google Scholar]
- 58.ABAQUS . Simulia; 2017. User's Manual of ABAQUS Version 6.17. [Google Scholar]
- 59.Wolgemuth C.W., Sun S.X. Elasticity of α-helical coiled coils. Phys. Rev. Lett. 2006;97:248101. doi: 10.1103/PhysRevLett.97.248101. [DOI] [PubMed] [Google Scholar]
- 60.Buehler M.J., Wong S.Y. Entropic elasticity controls nanomechanics of single tropocollagen molecules. Biophys. J. 2007;93:37–43. doi: 10.1529/biophysj.106.102616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Sun Y.-L., Luo Z.P., et al. An K.N. Direct quantification of the flexibility of type I collagen monomer. Biochem. Biophys. Res. Commun. 2002;295:382–386. doi: 10.1016/s0006-291x(02)00685-x. [DOI] [PubMed] [Google Scholar]
- 62.Sun Y.-L., Luo Z.P., et al. An K.N. Stretching type II collagen with optical tweezers. J. Biomech. 2004;37:1665–1669. doi: 10.1016/j.jbiomech.2004.02.028. [DOI] [PubMed] [Google Scholar]
- 63.Jiménez-Zaragoza M., Yubero M.P., et al. Rodriguez J.M. Biophysical properties of single rotavirus particles account for the functions of protein shells in a multilayered virus. Elife. 2018;7:e37295. doi: 10.7554/elife.37295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Zhmurov A., Kononova O., et al. Weisel J.W. Mechanical transition from α-helical coiled coils to β-sheets in fibrin (ogen) J. Am. Chem. Soc. 2012;134:20396–20402. doi: 10.1021/ja3076428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Chen M., Zheng W., Wolynes P.G. Energy landscapes of a mechanical prion and their implications for the molecular mechanism of long-term memory. Proc. Natl. Acad. Sci. U S A. 2016;113:5006–5011. doi: 10.1073/pnas.1602702113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Qin Z., Buehler M.J. Molecular dynamics simulation of the α-helix to β-sheet transition in coiled protein filaments: evidence for a critical filament length scale. Phys. Rev. Lett. 2010;104:198304. doi: 10.1103/PhysRevLett.104.198304. [DOI] [PubMed] [Google Scholar]
- 67.Kiss B., Kis Z., et al. Kellermayer M.S. Topography, spike dynamics, and nanomechanics of individual native SARS-CoV-2 virions. Nano Lett. 2021;120:15a–2680. doi: 10.1016/j.bpj.2020.11.361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Zandi R., Dragnea B., et al. Podgornik R. On virus growth and form. Phys. Rep. 2020;847:1–102. doi: 10.1016/j.physrep.2019.12.005. [DOI] [Google Scholar]