Validating markerless pose estimation with 3D X-ray radiography

ABSTRACT

To reveal the neurophysiological underpinnings of natural movement, neural recordings must be paired with accurate tracking of limbs and postures. Here, we evaluated the accuracy of DeepLabCut (DLC), a deep learning markerless motion capture approach, by comparing it with a 3D X-ray video radiography system that tracks markers placed under the skin (XROMM). We recorded behavioral data simultaneously with XROMM and RGB video as marmosets foraged and reconstructed 3D kinematics in a common coordinate system. We used the toolkit Anipose to filter and triangulate DLC trajectories of 11 markers on the forelimb and torso and found a low median error (0.228 cm) between the two modalities corresponding to 2.0% of the range of motion. For studies allowing this relatively small error, DLC and similar markerless pose estimation tools enable the study of increasingly naturalistic behaviors in many fields including non-human primate motor control.

Summary: Evaluation of DeepLabCut, a markerless pose estimation tool, compared with marker-based 3D X-ray radiography (XROMM), by processing marker trajectories using Anipose and characterizing the effect of parameter choices on accuracy.

INTRODUCTION

As the study of motor neuroscience progresses toward an emphasis on naturalistic, unconstrained behavior, kinematics must be captured accurately and efficiently. Past research has relied on marker-based systems tracking markers attached to an animal's skin (such as Vicon, OptiTrack and PhaseSpace) or surgically implanted radiopaque beads (XROMM; Brainerd et al., 2010). However, these systems are expensive and often impractical with smaller species such as mice or marmosets, especially for tracking free or semi-constrained behavior. To solve this problem, multiple groups have developed markerless pose estimation tools that use deep learning to apply digital markers to recorded video. The most widely used is DeepLabCut (DLC; Mathis et al., 2018), but alternatives exist (Dunn et al., 2021; Graving et al., 2019; Pereira et al., 2019; Wu et al., 2020 preprint). These enable the study of a wider range of behaviors by allowing free movement without the disturbance of physical markers. Furthermore, these tools alleviate the bottleneck of semi-automatic tracking; a well-trained network labels video with an accuracy comparable to that of human labelers (Mathis et al., 2018) and requires minimal hands-on time for subsequent datasets. DLC has been used in many contexts, including tracking eye movements, pupil dilation and hand movements in mice (Sauerbrei et al., 2020; Siegle et al., 2021; Steinmetz et al., 2019), estimating 3D pose of freely moving macaques (Bala et al., 2020), and even on XROMM video to increase throughput (Laurence-Chasen et al., 2020).

DLC accuracy has not been compared with that of marker-based tracking in the context of close-up forelimb tracking that is common in motor control studies. Dunn et al. (2021) tested DLC and a geometric deep learning tool (DANNCE) against a rat motion capture dataset, but recording from a small number of cameras in this unconstrained context with significant environment and self-occlusion is beyond the intended use for DLC unless many cameras are used as in Bala et al. (2020). Thus, a comparison in the semi-constrained context with a small number of cameras is crucial to confirm whether DLC reliably tracks kinematics with an accuracy comparable to that of human labelers and existing marker-based systems. XROMM provides a useful comparison, as we have shown that the system tracks radiopaque markers with submillimeter precision (Walker et al., 2020). To this end, we collected simultaneous recordings with XROMM and RGB video as common marmosets engaged in naturalistic foraging, then reconstructed 3D reaching kinematics in a shared coordinate system. We performed filtering, triangulation and optimization steps with Anipose (Karashchuk et al., 2021) and present the effect of parameter choices on tracking quality. We found that optimized DLC+Anipose tracks position with a median absolute error of 0.228 cm (mean absolute error 0.274 cm), corresponding to 2.0% of the range of marker positions.

MATERIALS AND METHODS

Subjects

These experiments were conducted with two common marmosets, Callithrix jacchus (Linnaeus 1758) (an 8 year old, 356 g male designated TY and a 7 year old, 418 g female designated PT). All methods were approved by the Institutional Animal Care and Use Committee of the University of Chicago.

Data collection

The two marmosets were placed together in a 1 m×1 m×1 m cage with a modular foraging apparatus attached to the top of the cage, as previously described by Walker et al. (2020). The marmosets were allowed to forage voluntarily throughout recording sessions that lasted 1–2 h. Recordings of individual trials were triggered manually with a foot pedal by the experimenters when the marmosets appeared ready to initiate a reach. The manual trigger initiated synchronized video collection by the XROMM system (Brainerd et al., 2010) and two visible light cameras, as described in further detail below. We retained all trials recorded on 14–15 April 2019 that captured right-handed reaches. Marmoset TY produced four useful reaching events containing five total reaches and marmoset PT produced 13 reaching events containing 17 reaches.

XROMM

Bi-planar X-ray sources and image intensifiers (90 kV, 25 mA at 200 frames s⁻¹) were used to track the 3D position of radiopaque tantalum beads (0.5–1 mm, Bal-tec) placed subcutaneously in the arm, hand and torso. Details of bead implants can be found in Walker et al. (2020), in which the authors also report estimating XROMM marker tracking precision equal to 0.06 mm based on the standard deviation of inter-marker distances during a recording of a calibration specimen. Marker locations were chosen to approximate the recommendations given by the International Society of Biomechanics for defining coordinate systems of the upper limb and torso in humans (Wu et al., 2005). These recommendations were adapted to the marmoset and constrained by surgical considerations. The positions of 13 beads were tracked using a semi-automated process in XMALab (Knorlein et al., 2016) following the procedure described there and in the XMALab User Guide (https://bitbucket.org/xromm/xmalab/wiki/Home). Two beads implanted in the anterior torso were ignored for comparison with DLC because corresponding positions on the skin were occluded in nearly every frame captured by visible light cameras.

DeepLabCut

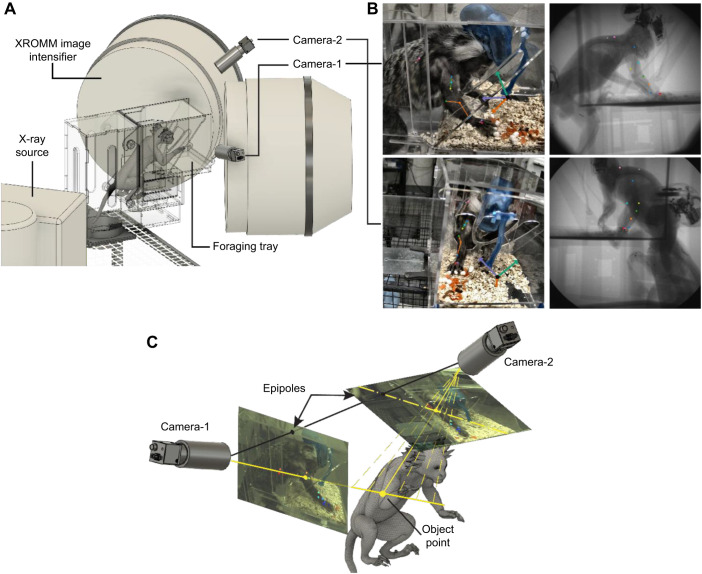
Two high-speed cameras (FLIR Blackfly S, 200 frames s⁻¹, 1440×1080 resolution) were used to record video for analysis by DLC. The cameras were positioned to optimize visibility of the right upper limb during reaching behavior in the foraging apparatus and to minimize occlusions, while avoiding the path between the X-ray sources and image intensifiers (Fig. 1A). The cameras were triggered to record continuous images between the onset and offset of the manual XROMM trigger, with the series of images later converted to video for DLC processing. All videos were brightened using the OpenCV algorithm for contrast limited adaptive histogram equalization (CLAHE) prior to labeling. We labeled 11 body parts in DLC: two labels on the torso and three on each of the upper arm, forearm and hand (Fig. 1B; Table S1). Locations of each label were chosen to be as close as possible to the approximate location of XROMM beads, although concessions had to be made to ensure the location was not occluded consistently in the recordings. We used DLC 2.2 with in-house modifications to produce epipolar lines in image frames that were matched between the two cameras (Fig. 1C), which significantly improved human labeling accuracy by correcting gross errors and fine-tuning minor errors. We did not train a network on labels produced without the aid of epipolar lines and therefore cannot evaluate 3D error reduction using epipolar lines. However, we note that labels applied without epipolar lines on the torso were grossly inaccurate – these labels were adjusted by an average of 63 pixels and 57 pixels in camera-1 and camera-2, respectively, after implementation. The other nine labels were adjusted by an average of <1 pixel in camera-1 and 11 pixels in camera-2. This modification has been added as a command line feature in the DLC package (a guide for using epipolar lines can be found at https://deeplabcut.github.io/DeepLabCut/docs/HelperFunctions.html). Aside from this and related changes to the standard DLC process, we followed the steps outlined in Nath et al. (2019).

Fig. 1.

Recording apparatus, markers and labeling with epipolar lines. (A) Marmosets used their right forelimb to forage. Blackfly-S cameras and XROMM recorded foraging behavior simultaneously. (B) Left: video frames from camera-1 (top) and camera-2 (bottom). Markers were applied by DLC+Anipose. The coordinate system is shown in green (x), orange (y) and purple (z). Right: corresponding XROMM frames. Subcutaneous tantalum beads were overlaid with colors to match corresponding DLC+Anipose labels. (C) Epipolar lines improve labeling accuracy. A vector projects from camera-1 through the applied label into 3D space, where it intersects with possible vectors from camera-2 (a subset is shown by the dashed yellow lines). The epipolar line (dot-dash line) passes through the epipole in camera-2 and each of the points at which a vector intersects the image plane. A correct label applied along the epipolar line produces accurate triangulation to the object point (correct labels and camera-2 vector shown by solid yellow lines).

In the first labeling iteration, we extracted 100 total frames (50 per camera) across the four events for marmoset TY and 254 frames (127 per camera) across seven of the 13 events for marmoset PT, which produced a labeled dataset of 354 frames. These were chosen manually to avoid wasting time labeling frames before and after reaching bouts during which much of the marmoset forelimb was entirely occluded in the second camera angle. An additional 202 frames (101 per camera) were extracted using the DLC toolbox with outliers identified by the ‘jump’ algorithm and frame selection by k-means clustering. We chose the number of frames to extract for each video based on visual inspection of labeling quality and chose the start and stop parameters to extract useful frames that captured reaching bouts. In all cases, frame numbers of extracted frames were matched between cameras to enable the use of epipolar lines. This refinement step resulted in an error reduction of 0.046 cm and an increase in the percentage of frames tracked of 14.7% after analysis with the chosen Anipose parameters. The final dataset consisted of 278 human-labeled time points from 15 of the 17 events and 10,253 time points from all 17 events labeled by the network only.

We used the default resnet-50 architecture for our networks with default image augmentation. We trained three shuffles of the first labeling iteration with a 0.95 training set fraction and used the first shuffle for the label refinement discussed above. We trained 15 total networks after one round of label refinement: three shuffles each with training fractions of 0.3, 0.5, 0.7, 0.85 and 0.95. Each network was trained for 300,000 iterations starting from the default initial weights. We evaluated each network every 10,000 iterations and selected the snapshot that produced the minimum test error across all labels for further analysis.

We chose the network to use in subsequent analyses by finding the smallest training set size that reached the threshold of human labeling error (discussed next). We then chose the median-performing network of the three shuffles at this training set size for all further analysis.

Human labeling error

We selected 134 frames (67 per camera) across three events from the same marmoset and session to be relabeled by the original, experienced human labeler and by a second, less experienced labeler. We used the error between the new and original labels to evaluate whether the networks reached asymptotic performance, defined by the experienced human labeling error.

Calibration

A custom calibration device was built to allow for calibration in both recording domains (Knorlein et al., 2016; instruction manual for a small Lego cube is located in the XMALab BitBucket). The device was constructed to contain a 3D grid of steel beads within the structure and a 2D grid of white circles on one face of the cube. Calibration of X-ray images was computed in XMALab and calibration of visible light images was computed with custom code using OpenCV. This integrated calibration device, along with the PCA-based alignment procedure described below, ensures that DLC and XROMM tracked trajectories in a common 3D coordinate system. DLC videos were accurately calibrated, with 0.42 pixels and 0.40 pixels of intrinsic calibration error for camera-1 and camera-2, respectively, and 0.63 pixels of stereo reprojection error. XROMM calibration was similarly accurate, with an average intrinsic calibration error equal to 0.81 pixels and 1.38 pixels for the two cameras.

Trajectory processing with Anipose

We used Anipose to analyze videos, filter in 2D, triangulate 3D position from 2D trajectories, and apply 3D filters (see Karashchuk et al., 2021, for details). For 2D filtering, we chose to apply a Viterbi filter followed by an autoencoder filter because the authors demonstrate this to be the most accurate combination of 2D filters. For triangulation and 3D filtering, we enabled optimization during triangulation and enabled spatial constraints for each set of three points on the hand, forearm and upper arm, and for the pair of points on the torso. We identified six Anipose parameters and one post-processing parameter that may affect the final accuracy of DLC+Anipose tracking and ran a parameter sweep to find the optimal combination. In 2D filtering, we varied the number of bad points that could be back-filled into the Viterbi filter (‘n-back’) and the offset threshold beyond which a label was considered to have jumped from the filter. We varied four parameters in 3D processing, including the weight applied to spatial constraints (‘scale_length’) and a smoothing factor (‘scale_smooth’), the reprojection error threshold used during triangulation optimization, and the score threshold used as a cutoff for 2D points prior to triangulation. We also varied our own post-processing reprojection error threshold that filtered the outputs of DLC+Anipose. We tested 3456 parameter combinations in total, the details of which will be discussed below. We generally chose parameter values centered on those described in the Anipose documentation and in Karashchuk et al. (2021).

Post-processing of DLC+Anipose trajectories

To process the 3D pose outputs from Anipose, we first used the reprojection error between cameras provided by Anipose to filter out obviously bad frames. We tested two thresholds, 10 and 20 pixels, for 15 of 17 events. We tested much higher thresholds, 25 and 35 pixels, for the final two events of 14 April 2019 because the calibration was poor in these events – we suspect one of the cameras was bumped prior to these events. Next, we deleted brief segments of five or fewer frames and stitched together longer segments separated by fewer than 30 frames. Importantly, we did not have to do any further interpolation to stitch segments together, as Anipose produces a continuous 3D trajectory. Together, these steps remove portions of trajectories captured when the marmoset was chewing or otherwise disengaged from the foraging task and outside of the usable region of interest in camera-2 and combined segments during foraging bouts that were separated only by brief occlusions or minor tracking errors. All steps were performed independently for each label and event.

DLC labels could not be applied to the upper limb and torso in spots corresponding exactly to XROMM bead locations because those locations would often be obstructed from view by the marmoset's own body in one of the camera angles. We therefore applied labels as close as possible to the correct spots and subtracted the average position from each label and bead during post-processing. This removes a constant offset that should not be included in the DLC error calculations.

Despite our best efforts to place DLC and XROMM in the same 3D coordinate system through the calibration process described above, we found the two systems to be slightly misaligned. To fix this, we computed the three principal components across good frames for all DLC+Anipose labels and separately for all XROMM markers, then projected the mean-subtracted DLC+Anipose and XROMM trajectories onto their respective principal components. We found that this brought the coordinate systems into close alignment, such that we could no longer identify any systematic error that could be attributed to misalignment.

Finally, we found that there was a brief delay ranging from 0 to 10 frames between the pedal-triggered onset of the XROMM event and the corresponding pedal-triggered TTL pulse initiating the start of the event for the FLIR cameras (and for the pulse ending the event). To adjust for the timing difference, we iterated over a range of possible sample shifts separately for each event to find the shift that minimized the mean absolute error between the DLC+Anipose and XROMM trajectory. We visually inspected each trajectory after the adjustment to ensure the shift was qualitatively accurate.

Evaluation of DLC performance

We computed the median and mean absolute error between matched trajectories from DLC+Anipose and XROMM for all body parts across all reaching events. We also computed the percentage of motion tracked across all labels and all active segments of reaching events. To define active segments, we manually inspected the videos for the first and last frames in each event for which the marmoset was engaged in the task; as mentioned before, the position of camera-2 prevented accurate human labeling when the marmoset was positioned well behind the partition and the vast majority of these frames were discarded by Anipose and in post-processing.

Statistical tests

As the error distributions were right-skewed with long tails of large errors, we used the median error to describe the center of each distribution and a two-tailed Mann–Whitney U-test to assess statistical significance. The P-values computed with this method are artificially low as a result of the large sample size (e.g. between 27,630 samples for the three upper arm markers and 11,480 samples for the two torso markers), so we report the correlation effect size defined by the rank-biserial correlation to describe statistical differences between distributions. According to convention, we consider r<0.20 to be a negligible effect (Cohen, 1992).

In order to determine which of the Anipose and post-processing parameters from the parameter sweep significantly affected either the median error or percentage of frames tracked, we created two linear regression models using the seven parameters and a constant as independent variables and either error or percentage of frames tracked as the dependent variable. We tested the effect of individual parameters by calculating the log likelihood ratio Chi-squared test statistic (LR) between the full model and each nested model created by leaving one parameter out at a time (such that each nested model had a constant term and six parameter terms). We computed the P-value of each comparison using a Chi-squared test with two degrees of freedom.

We also created a full interaction model with the seven individual parameter terms and all possible first-order interaction terms. We tested the significance of each term by the same method.

Normalized error and fraction of variance accounted for

To compute normalized error, we divided the position error by the maximum range of motion for each marker across the dataset. To compute the fraction of variance accounted for (FVAF), we used the following equation:

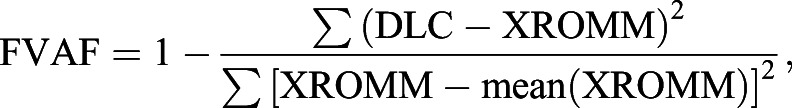(1)

which normalizes the sum of squared DLC error by the XROMM variance and subtracts from one.

RESULTS AND DISCUSSION

Human versus DLC error

We found that each network reached asymptotic performance within 300,000 iterations (Fig. S1A). DLC error on training images was similar across set sizes, but test error decreased with set size until reaching an asymptote at the 85% training fraction (472 images, 236 per camera), with mean error of 7.38 pixels (Fig. S1B). This error matches that of the experienced human labeler (7.53 pixels) and is better than that of the inexperienced labeler (14.24 pixels). For subsequent analysis, we used the median-performing shuffle of the 85% training set networks. As further confirmation of asymptotic performance, we found that the median error of frames that passed the post-processing reprojection error threshold remained constant across training set size while the percentage of frames tracked reached an asymptote at the 85% split (Fig. S1C).

Anipose parameter selection

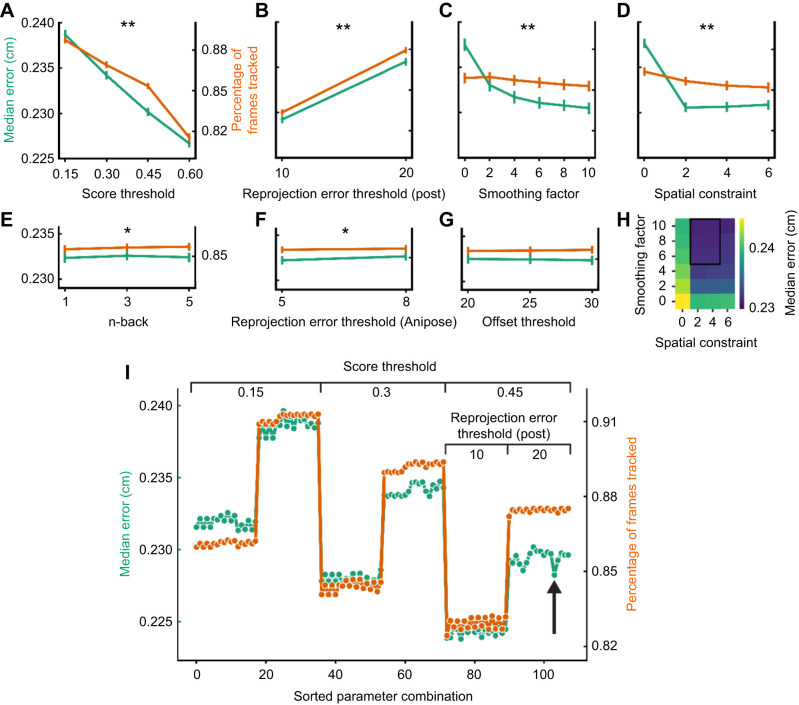
By sweeping through a total of 3456 combinations of six Anipose parameters and one post-processing parameter, we identified four with large, significant effects on the median error linear regression model (P<0.05 and log-likelihood ratio LR>>50): pre-triangulation score threshold (LR=4666), post-processing reprojection error threshold (LR=3098), spatial constraint (LR=1881), and smoothing factor (LR=1634; Fig. 2A–D). Error decreased linearly with score threshold without reaching an asymptote. It decreased monotonically with smoothing factor until reaching 6 then continued to decrease at a small, constant rate. Error was lowest for spatial constraint=2. Anipose reprojection error threshold was technically significant with a comparatively modest effect (LR=23.3). The remaining parameters were not significant (Fig. 2E–G).

Fig. 2.

Anipose parameter sweep. (A) Median error (green) and percentage of frames tracked (orange) versus score threshold, averaged across the other parameters. Plots show mean±95% confidence interval of median errors. (B–G) Same for each of the tested parameters: post-processing reprojection error threshold (B), smoothing factor (C), spatial constraint (D), n-back (E), Anipose reprojection error threshold (F) and offset threshold (G). Plots are labeled with asterisks to indicate a large effect on both error and percentage of frames tracked (**log likelihood ratio Chi-squared statistic LR>>50, P<0.05) or a modest effect on one or the other (*LR<50, P<0.05). (H) Median error, represented by cell color, versus smoothing factor and spatial constraint. The combinations with lowest error are boxed. (I) Median error and percentage of frames tracked for 108 parameter sets with smoothing factor and spatial constraint set to 6 and 2, respectively. Results are sorted along the x-axis by score threshold first, post-processing reprojection error threshold second and n-back third. The arrow indicates the parameter set selected for further analysis.

We identified the same four parameters with large, significant effects on the percentage of frames tracked model: score threshold (LR=4689), post-processing reprojection error threshold (LR=4085), spatial constraint (LR=261) and smoothing factor (LR=81.7; Fig. 2A–D). The percentage of frames tracked decreased linearly with score threshold until dropping steeply at 0.6 and decreased slightly with spatial constraint and smoothing factor. n-back showed a modest effect (LR=8.75) with a slightly higher percentage of frames tracked for n-back>1, and the remaining parameters were not significant (Fig. 2E–G).

The model incorporating first-order interaction terms provided limited information. Significant interaction terms were combinations of significant individual parameters and we found no evidence of non-linear interactions (Fig. S2). However, the interaction between spatial constraint and smoothing factor helped us choose 2 and 6 for their respective values; these were the smallest weights in the region of negligible error differences highlighted in Fig. 2H.

We visualized the effect of score threshold, post-processing reprojection error threshold and n-back by plotting median error and percentage of frames tracked for each parameter set with spatial constraint=2 and smoothing factor=6, sorted by score threshold first, post-processing reprojection error threshold second and n-back third (Fig. 2I). We found that score threshold=0.45 and post-processing reprojection error threshold=20 provided a balance of low error and high percentage of frames tracked, and that n-back>1 improves percentage of frames tracked for some combinations. We selected the parameter set that minimized error under these constraints and performed subsequent analyses with score_threshold=0.45, post_reprojection_error_threshold=20, scale_smooth=6, scale_length=2, n_back=5, reproj_error_threshold=8 and offset_threshold=20. We excluded 0.6 from the score threshold because of the large drop in percentage of frames tracked and unstable interactions with other parameters (Fig. S2J).

Tracking examples

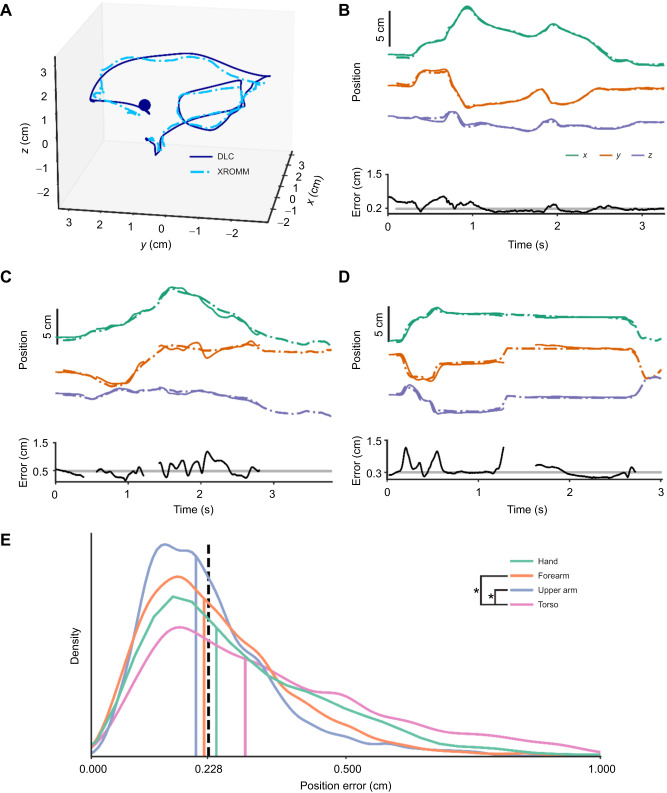
Qualitatively, DLC+Anipose and XROMM forelimb trajectories were nearly identical for most time points and reaches (Fig. 3A,B). The 3D view illustrates DLC tracking the overall motion of a foraging bout consisting of a long reach and a shorter secondary reach faithfully, with some loss of fine details due to the smoothing factor (Fig. 3A). Breaking out x–y–z components demonstrates a low position error (median 0.179 cm; Fig. 3B).

Fig. 3.

Tracking position with DLC+Anipose and XROMM. (A,B) Example of accurate DLC tracking. (A) 3D position of a distal hand marker with DLC+Anipose (dark blue, solid line) and XROMM (light blue, dot-dash line). The movement begins at the blue dot. (B) Top: position split into x–y–z coordinates colored to match the axes in Fig. 1B, with DLC+Anipose represented by solid lines and XROMM by dot-dash lines. Bottom: error at each time (black) overlaid on the median error for the event (gray). (C,D) Examples of DLC+Anipose tracking errors. (E) Distribution of errors for the markers of each body segment. Colored vertical lines show the median error for each segment and the dashed black line shows the median error across all markers. Significant differences between distributions are marked by asterisks in the inset (rank biserial correlation, r>0.2, n_hand=24,605, n_forearm=24,403, n_upperarm=27,007, n_torso=11,083).

Some reaches were not tracked with the same accuracy. Fig. 3C shows the medial forearm marker during a reach through the left-hand arm hole, resulting in three brief occlusions, the first two of which were removed by the post-processing reprojection error threshold. In the third, the marker gets ‘stuck’ on the occluding part of the partition around 2 s, manifesting as a position oscillation after filtering and smoothing. Fig. 3D shows a reach in which a hand marker was occluded by the marmoset's other hand in camera-2 around 1.25 s, resulting in brief large errors before an untracked gap. It also shows errors early in the reach resulting from a non-optimal lag adjustment, which could happen if large errors in another label (the torso labels in this case) biased the optimal lag for the event.

Aggregate error results

Error distributions were right-skewed with a long tail of large errors, so we used median error as the measure of accuracy. We found that DLC tracked position with a median error of 0.228 cm across all markers (Fig. 3E). We found that position errors on the torso (median 0.302 cm) were significantly larger than errors on the forearm (0.222 cm, r=0.26) and upper arm (0.206 cm, r=0.319). We found no significant difference between the median error of 278 time points corresponding to the training set and that of the remaining data which were labeled by the network only (test).

Median error was equivalent to 2.0% of position range when normalized by the maximum range for each marker. Viewed another way, DLC+Anipose accounted for 97.2% of XROMM position variance. We also computed the pixel error between reprojected trajectories and labeled frames and found the median error to be 3.42 pixels (mean 4.58 pixels), suggesting that Anipose improved on the 7.38 pixels of error present in the original un-processed network.

The level of DLC+Anipose error demonstrated here is sufficient for many purposes, and there is reason to treat this as an upper error bound for well-trained DLC networks.

Assessment of errors and limitations

The primary limitation in this study is the viewing angle of DLC camera-2 (Fig. 1), which would ideally have been placed in the center of the XROMM image intensifier. The angle resulted in occlusion of torso markers in approximately 34% of relevant time points and occlusion of hand markers when the wrist was supinated. We approximated label positions for the supinated hand to maximize percentage of frames tracked, but this certainly increased the error. The second limitation is that marker positions were chosen as a compromise between proximity to XROMM bead positions and ease of labeling; for example, the medial forearm marker was placed in a muscular spot where the visual landmark was often ambiguous and resulted in poor re-labeling precision (12.2 pixel error for the experienced labeler), while the upper arm markers were easily located (5.96 pixels). There is also unquantified XROMM error from soft-tissue artifacts as well as skin deformation affecting DLC relative to subcutaneous XROMM beads. The final limitation is the use of only two cameras – adding more would increase the percentage of frames tracked and improve 3D optimization in Anipose.

Improving accuracy

DLC is open-source and actively maintained, with frequent implementation of new features. We have contributed one such feature by incorporating epipolar lines to improve labeling precision across cameras for 3D projects (Fig. 1C). Epipolar lines simplify the identification of the same landmark in different camera angles, particularly for ambiguous landmarks.

Multiple tools supplement DLC, including Anipose (Karashchuk et al., 2021), Pose3d (Sheshadri et al., 2020), OpenMonkeyStudio (Bala et al., 2020) and a tool developed by Bolaños et al. (2021). Anipose and Pose3d implement optimizations for 3D pose estimation in Python and MATLAB, respectively. OpenMonkeyStudio and the Bolaños et al. (2021) method are data augmentation tools – the former uses labels on a subset of 62 camera views to reproject labels on remaining views, while the latter animates a 3D model to render synthetic DLC training data.

Optimal Anipose parameters for our data may not generalize perfectly to different settings. We propose that readers without access to a marker-based system could optimize parameters by minimizing error between reprojected trajectories and held-out human-labeled data. Errors can also be reduced through manual frame-by-frame error correction of DLC-labeled video in XMALab or a similar toolbox.

Comparing DLC and XROMM workflows

This dataset required 45–50 h to produce a well-trained network to label 10,531 frames from 17 events (Fig. S3A,B). This compares favorably with the approximately 34–51 h required for semi-automated XROMM tracking of the same events (Fig. S3C). While XROMM scales poorly to larger datasets, a robust DLC network may label such data with little or no manual intervention. For example, six events that were excluded from the initial set of labeled events required only the ∼5 h refinement process, much less than ∼15 h of XROMM tracking. Time requirements will depend on context, but the difference in scalability is evident. For work requiring both the precision of XROMM and improved scalability, we suggest the procedure described by Laurence-Chasen et al. (2020) to apply DLC directly to XROMM data.

Applicability to other pose estimation tools

There are a few alternative pose estimation tools. LEAP (Pereira et al., 2019) and DeepPoseKit (Graving et al., 2019) use different network architectures to reduce training and inference time. Deep Graph Pose (DGP; Wu et al., 2020 preprint) uses a similar architecture to DLC with temporal and spatial constraints to eliminate marker jumps. We suspect DGP attenuates high-error frames resulting from marker jumps but would not affect error for well-tracked frames. Based on advances in 3D human pose estimation (Iskakov et al., 2019; but see He et al., 2020, and Reddy et al., 2021, for subsequent state-of-the-art developments), DANNCE (Dunn et al., 2021) trains a network on 3D image volumes rather than triangulating and optimizing outputs from a network trained on 2D images (as in DLC+Anipose). DANNCE demonstrates higher accuracy than DLC for the same small number of cameras when applied to unconstrained settings in which 3D information is crucial for dealing with occlusions. However, we suspect DANNCE would perform similarly to DLC in semi-constrained settings such as ours with just a few cameras. Thus, we expect DLC errors reported here to be representative for existing tools, at least for well-tracked frames in semi-constrained environments.