Ti₃C₂T _x /MoS₂ Self‐Rolling Rod‐Based Foam Boosts Interfacial Polarization for Electromagnetic Wave Absorption

Abstract

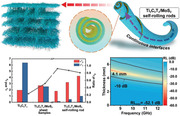
Heterogeneous interface design to boost interfacial polarization has become a feasible way to realize high electromagnetic wave absorbing (EMA) performance of dielectric materials. However, interfacial polarization in simple structures such as particles, rods, and flakes is weak and usually plays a secondary role. In order to enhance the interfacial polarization and simultaneously reduce the electronic conductivity to avoid reflection of electromagnetic wave, a more rational geometric structure for dielectric materials is desired. Herein, a Ti₃C₂T _x /MoS₂ self‐rolling rod‐based foam is proposed to realize excellent interfacial polarization and achieve high EMA performance at ultralow density. Different surface tensions of Ti₃C₂T _x and ammonium tetrathiomolybdate are utilized to induce the self‐rolling of Ti₃C₂T _x sheets. The rods with a high aspect ratio not only remarkably improve the polarization loss but also are beneficial to the construction of Ti₃C₂T _x /MoS₂ foam, leading to enhanced EMA capability. As a result, the effective absorption bandwidth of Ti₃C₂T _x /MoS₂ foam covers the whole X band (8.2–12.4 GHz) with a density of only 0.009 g cm⁻³, at a thickness of 3.3 mm. The advantages of rod structures are verified through simulations in the CST microwave studio. This work inspires the rational geometric design of micro/nanostructures for new‐generation EMA materials.

A more rational geometric structure for dielectric materials, i.e., a self‐rolling rod‐based foam structure is proposed, which can not only remarkably enhance the interfacial polarization loss but also simultaneously reduce the electronic conductivity to avoid reflection of electromagnetic wave. This work will inspire the rational geometric design of micro/nanostructures for new‐generation electromagnetic wave absorbing materials.

1. Introduction

Spatial electromagnetic (EM) wave pollution has been an unavoidable issue in daily life with the rapid development of electronic technology. To reduce EM wave interference, extensive studies about EM wave absorbing (EMA) materials have been propelled.^{[ 1 ]} Generally, the rational design of heterogenous interface in dielectric EMA materials can optimize the impedance match conditions (Table S1, Supporting Information).^{[ 2 ]} As a result, the optimal heterogeneous interface design has become a mainstream way to realize high EMA performance.^{[ 3 ]}

2D material Ti₃C₂T _x MXene is often used to carry on interface design due to its high specific surface areas and solution‐processibility.^{[ 4 ]} However, the pristine Ti₃C₂T _x possesses high electrical conductivity (higher than 10 000 S cm⁻¹), leading to impedance mismatch and showing EM interference (EMI) shielding performance.^{[ 5 ]} For instance, Ti₃C₂T _x foam with a density of 5.5 mg cm⁻³ shows shielding effectiveness of 54.8 dB.^{[ 6 ]} To optimize the impedance match condition, heterogeneous interface design based on Ti₃C₂T _x has been carried out, such as Ti₃C₂T _x /SiC, Ti₃C₂T _x /NiCo₂O_4, and so on.^{[ 7 ]} Although the EMA performances have been improved to some extent in these structures, the interfacial polarizations are still weak in these traditional sheet structures. Due to the limit of sheet structures, it is hard to increase the number of interfaces between two sheets. Recent research verifies that the rod structure is one of the most effective structures to enhance polarization loss, such as core–shell or core–sheath.^{[ 8 ]} Nevertheless, in these structures, the interface structure between core and shell is very simple. Self‐rolling rod structures without cores are expected to overcome the above problems and realize the great increase of interfaces between two materials. The interfaces between two materials will increase greatly with the decrease of the diameter of this self‐rolling rod structure. Furthermore, the electronic conductivity of Ti₃C₂T _x will decrease rapidly due to the composition with the second phase such as semiconductor in the self‐rolling rod structure, which could optimize the impedance match conditions. However, there are still synthetic methodological challenges to the implementation of self‐rolling rod structures for Ti₃C₂T _x .

Except for microstructure, macroscopic foam structures are usually adopted as one of the most promising structures for EMA materials, whose high porosity facilitates the entry and transmission of EM wave inside samples and is beneficial to the dissipation of EM wave energy.^{[ 1} , ⁸ , ^{9 ]} Self‐rolling rod structures with a high aspect ratio are expected to efficiently construct EMA foams, due to the formation of intertwined networks during the process of the freeze‐drying method.^{[ 10 ]} Therefore, self‐rolling rod structures are not only helpful for constructing foam structures but also good for the formation of massive heterogeneous interfaces between two phases. Based on the above analysis, it is an efficient way to realize lightweight and high EMA capability by constructing MXene‐based foam with self‐rolling rod structures.

In this work, the 3D foams composed of Ti₃C₂T _x /MoS₂ self‐rolling rods were prepared through the unidirectional freeze‐drying method (Figure 1 ). Ammonium tetrathiomolybdate (ATM) was used as the precursor of MoS₂. The different surface tension directions of ATM and Ti₃C₂T _x would induce the self‐rolling of Ti₃C₂T _x /MoS₂.^{[ 11 ]} There is a big jump in the number of interfaces after the self‐rolling process and the interfaces between Ti₃C₂T _x and MoS₂ are utilized to increase the interfacial polarization. As a result, the ratio of polarization loss remarkably reaches above 80% and the impedance match condition is greatly improved. The effective absorption bandwidth (EAB) covers the whole X band and can cover C and Ku bands according to simulation results. To investigate the influence of the ratio of Ti₃C₂T _x /MoS₂, three Ti₃C₂T _x /MoS₂ self‐rolling rod samples named S1–S3 were prepared by adjusting the contents of Ti₃C₂T _x and MoS₂. The EMA mechanisms of Ti₃C₂T _x /MoS₂ self‐rolling rod structures are studied through simulation in the CST microwave studio.

Figure 1.

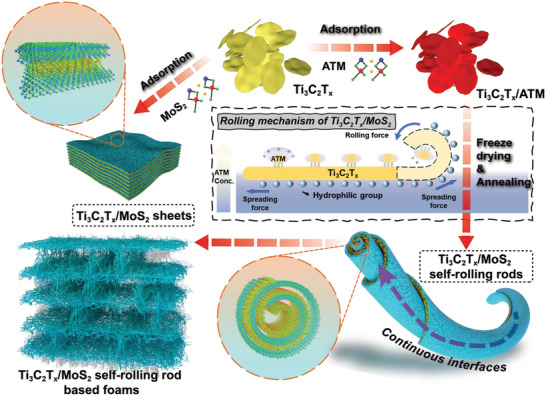
Schematic illustration of the fabrication process of Ti₃C₂T _x /MoS₂ sheets and self‐rolling rods and rolling mechanism of Ti₃C₂T _x /MoS₂ self‐rolling rods.

2. Results and Discussion

2.1. Formation Mechanism and Micro/Nanostructure

Figure 1 illustrates the fabrication process and rolling mechanism of Ti₃C₂T _x /MoS₂ foam. Ti₃C₂T _x sheets were prepared through in situ fluohydric acid (HF) etching and hand‐shaking method.^{[ 4c ]} The abundant surface groups (—F, —O, and —OH) on the Ti₃C₂T _x sheets make them good dispersion properties in an aqueous solution.^{[ 12 ]} Thus, the surface tension of Ti₃C₂T _x sheets tends to flatten themselves (spreading force). However, the dispersion property of the ATM in the aqueous solution is poor. The surface tension of ATM tends to curl the droplets from the edge to achieve minimum surface energy (rolling force).^{[ 11b ]} As a result, after attachment with Ti₃C₂T _x through Van der Waals' force, the rolling force derived from the surface tension of ATM would induce the self‐rolling of Ti₃C₂T _x sheets (Figure 1 and Figure S1, Supporting Information). Figure S2 in the Supporting Information shows that a change in pH value does not result in morphological changes of Ti₃C₂T _x sheets, further proving that the surface tension is critical to the rolling of Ti₃C₂T _x . In addition, a temperature gradient existed along the vertical direction, benefiting from the fine control of the freezing process. While the aqueous suspension was frozen, the ice crystals grew along the vertical direction and expelled Ti₃C₂T _x /ATM rod to the gaps between ice crystals. The orderly lamellar foam structure was constructed after the ice sublimation under vacuum. After annealing at 350 °C for 2 h, the MoS₂ was formed by the decomposition of the ATM. The thermogravimetry (TG) curve and decomposition equations of ATM are given in Figure S3 in the Supporting Information, which indicates that about 25% of weight loss during annealing, caused by the escape of NH₃.^{[ 13 ]} To demonstrate the advantages of self‐rolling rod structure, the Ti₃C₂T _x /MoS₂ sheets were also prepared. The ATM was annealed at first to obtain MoS₂ and then mixed with Ti₃C₂T _x followed by the same unidirectional freezing process.

Figure 2a shows the X‐ray diffraction (XRD) patterns of MoS₂, Ti₃C₂T _x , and Ti₃C₂T _x /MoS₂. For the MoS₂, the peak around 15° represents the (002) crystal plane of MoS₂, which verifies the decomposition of ATM.^{[ 14 ]} The peak at 7.4° is the characteristic peak of Ti₃C₂T _x , representing the (002) plane of Ti₃C₂T _x .^{[ 15 ]} After heat‐treatment of the Ti₃C₂T _x ‐ATM sample, the characteristic diffraction peaks of MoS₂ appear. It is noted that the peak of the (002) plane of Ti₃C₂T _x shifts from 7.4° to 6.8°, which means that the d‐spacing of the (002) plane increased from 11.70 to 12.97 Å, which is consistent with the interlayer spacing of Ti₃C₂T _x in Figure 3g. It can be concluded that the MoS₂ sheets were in situ formed in the interlayer of Ti₃C₂T _x flakes, leading to the enlarged interlayer space. Raman spectra of MoS₂, Ti₃C₂T _x , and Ti₃C₂T _x /MoS₂ are shown in Figure 2b. Consistent with previous studies, three broad peaks of Ti₃C₂T _x are shown at ≈202, 378, and 605 cm⁻¹.^{[ 16 ]} The broad peak at 605 cm⁻¹ represents the existence of —OH groups.^{[ 17 ]} After binding with MoS₂, the peak of —OH groups disappeared, which means that the ATM attaches with Ti₃C₂T _x through —OH groups.

Figure 2.

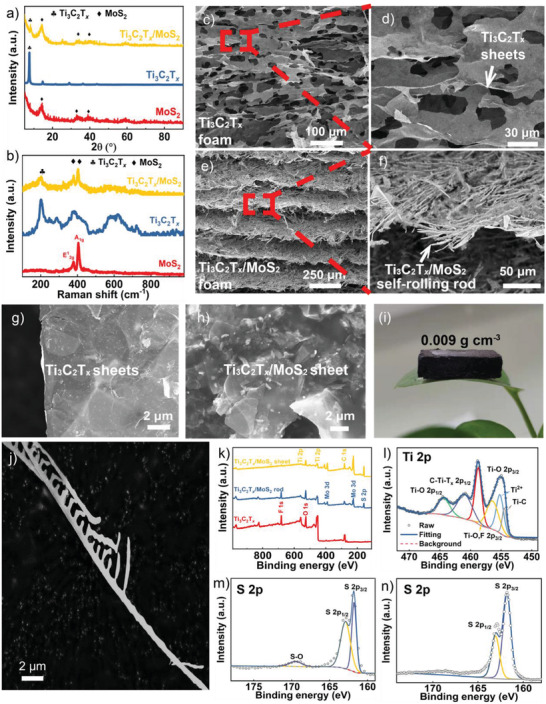
a) XRD and b) Raman patterns of MoS₂, T₃C₂T _x , and Ti₃C₂T _x /MoS₂. Cross‐sectional scanning electron microscope (SEM) images of c,d) Ti₃C₂T _x foam and e,f) Ti₃C₂T _x /MoS₂ foam. SEM image of g) Ti₃C₂T _x sheets and h) Ti₃C₂T _x /MoS₂ sheets. i) The optical photos of Ti₃C₂T _x /MoS₂ self‐rolling rod‐based foam. j) SEM image of single Ti₃C₂T _x /MoS₂ self‐rolling rod. k) X‐ray photoelectron spectroscopy (XPS) spectra of Ti₃C₂T _x , Ti₃C₂T _x /MoS₂ self‐rolling rod structure, and Ti₃C₂T _x /MoS₂ sheet structure. l) High‐resolution of Ti 2p spectrum of Ti₃C₂T _x /MoS₂ self‐rolling rod structure. m,n) High‐resolution of S 2p spectrum of Ti₃C₂T _x /MoS₂ self‐rolling rod structure and Ti₃C₂T _x /MoS₂ sheet structure, respectively.

Figure 3.

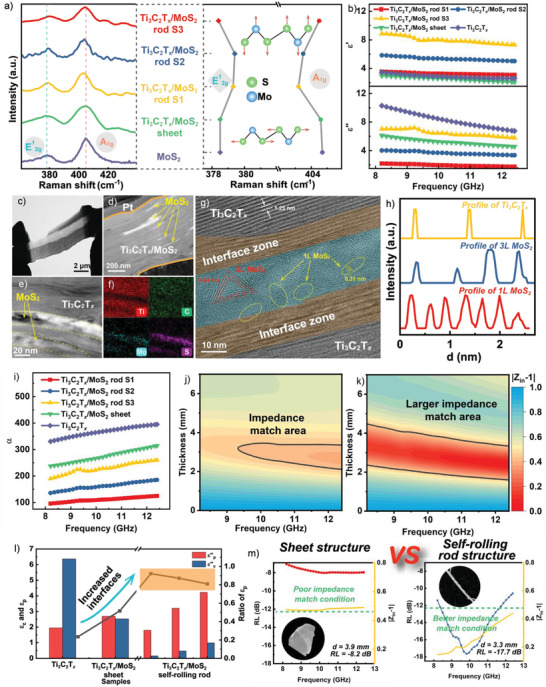
a) E¹ _2g mode and A_1g mode of Raman spectra of MoS₂, Ti₃C₂T _x /MoS₂ sheet, and Ti₃C₂T _x /MoS₂ self‐rolling rod. b) The real and imaginary part of permittivities of all samples. c) The cross‐sectional sample of Ti₃C₂T _x /MoS₂ self‐rolling rod prepared by FIB technique and d) its corresponding transmission electron microscope (TEM) images. e,f) The high‐magnification TEM image and its corresponding energy disperse spectroscopy (EDS) mapping images. g) The interface between Ti₃C₂T _x and MoS₂. h) The intensity profiles of 1L MoS₂, 3L MoS_2, and Ti₃C₂T _x . i) Attenuation constants of Ti₃C₂T _x , Ti₃C₂T _x /MoS₂ sheets, and Ti₃C₂T _x /MoS₂ self‐rolling rods. |Z _in  − 1| contours of j) Ti₃C₂T _x /MoS₂ sheets and k) Ti₃C₂T _x /MoS₂ self‐rolling rods. l) The conductive and polarization loss of Ti₃C₂T _x , Ti₃C₂T _x /MoS₂ sheets, and Ti₃C₂T _x /MoS₂ self‐rolling rods. m) Comparation of EMA performances for Ti₃C₂T _x /MoS₂ sheets and Ti₃C₂T _x /MoS₂ self‐rolling rods, revealing the superiority of self‐rolling rod structure for enhancing EM wave absorption and impedance match condition.

The SEM images in Figure 2c–f show that both Ti₃C₂T _x and Ti₃C₂T _x /MoS₂ foams are similar layered structures. The layer spacing of Ti₃C₂T _x foam is only 30 µm and the layer spacing of Ti₃C₂T _x /MoS₂ foam is 200 µm. The larger layer spacing is propitious to the entry of EM waves into Ti₃C₂T _x /MoS₂ foam. According to the high magnification SEM images, the layer arrangements of Ti₃C₂T _x /MoS₂ and Ti₃C₂T _x are different. The layer of Ti₃C₂T _x foam is composed of 2D Ti₃C₂T _x sheets and there are some holes on the surface (Figure 2d). The layer of Ti₃C₂T _x /MoS₂ foam is composed of crossed rods (Figure 2f). Compared with Ti₃C₂T _x and Ti₃C₂T _x /MoS₂ sheets, the Ti₃C₂T _x /MoS₂ self‐rolling rods cross each other and show a rough surface (Figure 2g,h). The N₂ sorption isotherms at 77 K and pore‐size distribution derived from Barrett–Joyner–Halenda method are shown in Figure S4 in the Supporting Information. The specific surface areas of Ti₃C₂T _x /MoS₂ sheets and Ti₃C₂T _x /MoS₂ self‐rolling rods are 5.2327 and 3.7463 m² g⁻¹, respectively. The self‐rolling structure leads to the decrease of specific surface areas, due to a lot of surfaces being used to construct heterogeneous interfaces. The pore size distributions of Ti₃C₂T _x /MoS₂ sheets and Ti₃C₂T _x /MoS₂ self‐rolling rods are similar. However, the pore volume of Ti₃C₂T _x /MoS₂ self‐rolling rods is 0.016 cm³ g⁻¹, which is higher than 0.013 cm³ g⁻¹ of Ti₃C₂T _x /MoS₂ sheets. A larger pore volume is beneficial to the impedance match condition. To better observe the morphology of Ti₃C₂T _x /MoS₂ self‐rolling rods, a single Ti₃C₂T _x /MoS₂ self‐rolling rod was obtained through sonication (Figure 2j). The length of a single rod can reach tens of micrometers and there are some synapses‐like structures along the rod, which are beneficial to the construction of Ti₃C₂T _x /MoS₂ foams. These flexible rods are interconnected through synapses (Figure S5a, Supporting Information), which are like bridges, leading to the formation of stable foam structures (Figure 2i and Figure S9, Supporting Information). The foam structures composed of Ti₃C₂T _x /MoS₂ self‐rolling rods facilitate the entry and transmission of EM wave inside samples and are propitious to the consumption of EM wave energy through heat dissipation.^{[ 18 ]}

The XPS survey in Figure 2k demonstrates four main elements, including Ti, C, O, and F in Ti₃C₂T _x . After attaching with MoS₂, the signal of S and Mo can be detected. The XPS spectrum of Ti 2p in pure Ti₃C₂T _x foam shows four predominant peaks of Ti—O 2p_1/2 (464.3 eV), Ti—O 2p_3/2 (458.8 eV), Ti—C 2p_3/2 (455.1 eV), and C—Ti—T _x 2p_1/2 (461.1 eV) bonds. These chemical states are caused by the chemical etching process of Ti₃AlC₂ using HCl and LiF, which can introduce many functional groups.^{[ 19 ]} The preparation of MoS₂ is confirmed by the Mo 3d and S 2s peaks. In the S 2p spectrum, the two conspicuous peaks of S 2p_1/2 and S 2p_3/2 at 162.9 and 161.8 eV represent the S²⁻ of MoS₂.^{[ 20 ]} It is worth noting that there is a small peak at about 169.5 eV for Ti₃C₂T _x /MoS₂ self‐rolling rod structure, which can be assigned to S—O bonds, indicating the combination of MoS₂ and —O groups of Ti₃C₂T _x .^{[ 21 ]} The S 2p spectrum of Ti₃C₂T _x /MoS₂ shows that there is no S—O bond, which means MoS₂ and Ti₃C₂T _x are just mixed simply. As a result, the signal of O 1s is stronger in Ti₃C₂T _x /MoS₂ compared with pure Ti₃C₂T _x due to the partly oxidized MoS₂ layer on the surface of Ti₃C₂T _x .

The Raman spectra of MoS₂ show two dominant peaks around 400 cm⁻¹, which are assigned to E¹ _2g and A_1g mode of S—Mo—S.^{[ 22 ]} The frequency difference of E¹ _2g and A_1g peaks can be used to evaluate the property of MoS₂ and the distance of Mo—S bonds (Figure 3a). The frequency differences between E¹ _2g and A_1g peaks are about 26 cm⁻¹ for both MoS₂ and Ti₃C₂T _x /MoS₂ sheets, which are consistent with bulk MoS₂.^{[ 23 ]} For Ti₃C₂T _x /MoS₂ self‐rolling rods, the frequency differences between E¹ _2g and A_1g peaks decrease to about 24 cm⁻¹, which are consistent with few‐layer MoS₂. Apart from that, the E¹ _2g mode exhibits a slight blueshift from Ti₃C₂T _x /MoS₂ sheet to Ti₃C₂T _x /MoS₂ self‐rolling rod, suggesting a decrease of Mo—S distance.^{[ 24 ]} Moreover, the A_1g mode exhibits an obvious redshift, which is related to the carrier doping effect, meaning the strong combination of Ti₃C₂T _x and MoS₂ in self‐rolling rod structure.^{[ 17} , ^{25 ]} All these results show that MoS₂ are formed between the layers of Ti₃C₂T _x , which can induce the rolling of Ti₃C₂T _x sheets through a strong combination.

To directly observe the interface of Ti₃C₂T _x and MoS₂, a single Ti₃C₂T _x /MoS₂ self‐rolling rod was chosen to prepare a cross‐sectional TEM sample through the focus ion beam (FIB) “lift‐out” technique.^{[ 26 ]} A TEM sample with a length of about 8 µm was cut by FIB along the axis of the Ti₃C₂T _x /MoS₂ self‐rolling rod (Figure 3c). The detailed preparation process is shown in Figure S10 in the Supporting Information. A typical layered structure can be seen clearly from the cross‐sectional TEM image of the Ti₃C₂T _x /MoS₂ self‐rolling rod, compared with 2D Ti₃C₂T _x and 2D Ti₃C₂T _x /MoS₂ sheets (Figure 3d and Figures S6 and S7, Supporting Information). The MoS₂ layers alternate with Ti₃C₂T _x layers with a bending feature, suggesting the rolling of Ti₃C₂T _x /MoS₂ (Figure 3e,f). The thickness of the MoS₂ layer is about 10 nm and there are typical triangle MoS₂ crystals with single layer property, which is consistent with the difference of E¹ _2g and A_1g modes of Ti₃C₂T _x /MoS₂ self‐rolling rod structures in Raman spectra (Figure 3h). An interface zone can be seen clearly between Ti₃C₂T _x and MoS₂, where can be found lattice stripes of both MoS₂ and Ti₃C₂T _x . This means the tight combination of Ti₃C₂T _x and MoS₂. The alternation of MoS₂ and Ti₃C₂T _x would provide abundant nanoheterogeneous interfaces, which can enhance the interfacial polarization loss. The area of heterogeneous interfaces can be calculated according to the number of rolling layers of the Ti₃C₂T _x /MoS₂ self‐rolling rod structure. In an ideal situation, it is an exponential function (Figure S11, Supporting Information). The area can be doubled at maximum, which can realize the full utilization of surface areas of Ti₃C₂T _x .

2.2. Electromagnetic Response Behavior and EMA Performance

The enhancement of interfacial polarization loss can influence the permittivity of corresponding samples. Generally, the ε′ represents the ability to store charge, which is related to the multipolarizations. The ε′′ represents the ability to attenuate EM wave energy, which is associated with both polarization loss and conductive loss. As shown in Figure 3b, the ε′ of Ti₃C₂T _x and Ti₃C₂T _x /MoS₂ sheets are the lowest due to weak interfacial polarization.^{[ 27 ]} For Ti₃C₂T _x /MoS₂ self‐rolling rods, the ε′ increased about two times which is corresponding to the strong interfacial polarization. As to ε′′, the trend is the opposite with ε′. The ε′′ of Ti₃C₂T _x and Ti₃C₂T _x /MoS₂ sheets are the highest due to high conductive loss. For Ti₃C₂T _x /MoS₂ self‐rolling rods, the conductive network of Ti₃C₂T _x would be interrupted by MoS₂ inevitably, leading to the decrease of ε′′. Also, the electrical conductivity decreased due to the broken conductive network (Figure S16, Supporting Information). It is noted that the ε′′ values rise at 9–10 GHz in Ti₃C₂T _x /MoS₂ self‐rolling rods. This is caused by the dielectric relaxation originating from interfacial polarization. The Cole‐Cole circles of Ti₃C₂T _x /MoS₂ self‐rolling rod S2 (Figure S14, Supporting Information) reveal that the polarization loss at 9–10 GHz is the strongest. Figure 3i shows the attenuation constant of all samples, which can represent the overall EM loss capacity of the material. It can be found that Ti₃C₂T _x /MoS₂ sheet has a higher EM loss capacity than the Ti₃C₂T _x /MoS₂ self‐rolling rod. However, according to Figures 3j,k, the self‐rolling rod structure shows a larger impedance match area. To better understand this phenomenon, the polarization loss and conductive loss are calculated based on Debye theory (Figure 3l, detailed information is shown in the Supporting Information). The conductive loss plays a primary role in Ti₃C₂T _x and Ti₃C₂T _x /MoS₂ sheets due to the high conductivity of Ti₃C₂T _x . After the rolling process, the polarization loss increases about two times and plays a primary role with a better impedance match. The better impedance condition of Ti₃C₂T _x /MoS₂ self‐rolling rod structures leads to better EMA performance, compared with Ti₃C₂T _x /MoS₂ sheets in Figure 3m.

The EMA performances of these foams are evaluated by the wave‐guide method, which ensures the structural integrity of the foam structures. The test direction is vertical to the layer of foams, as shown in Figure S12 in the Supporting Information. This direction maximizes the effect of the layer‐by‐layer structure constructed in the unidirectional freeze‐drying process. Strong reflection of the EM wave caused by the highest ε′′ makes Ti₃C₂T _x foams show EMI shielding performance (Figure S13, Supporting Information). The downward trend of ε′′ with frequency increasing agrees well with the decrease of SE_R. With the addition of MoS₂, the EMA performances are improved substantially. The reflection loss (RL) contours of the Ti₃C₂T _x /MoS₂ sheet are shown in Figure 4a. The minimum reflection loss (RL_min) is −8.2 dB. Although its absorption of EM wave energy reached more than 84%, the narrow absorption band still cannot meet the requirement. In contrast, when Ti₃C₂T _x /MoS₂ sheets are rolled into rods, the RL_min can reach −52.1 dB and the EAB can cover the whole X band (Figure 4b,c). More detailed RL curves with different thicknesses are shown in Figure S15 in the Supporting Information. The corresponding frequency of RL_min shifts to a lower frequency with increased thickness. This effect is caused by the quarter‐wavelength model.^{[ 28 ]} Due to the excellent absorption of Ti₃C₂T _x /MoS₂ self‐rolling rod‐based foams at the X band, the EMA performance at 2–18 GHz was also simulated by the CST microwave studio suite based on the standard finite difference time domain method. The EAB is 6.5 GHz and can cover C, X, and Ku bands (4–18 GHz) with varied thicknesses (Figure S17, Supporting Information). The Ti₃C₂T _x /MoS₂ self‐rolling rod‐based foams can satisfy the application requirements of “thin, light, strong, and broad” for EMA materials. Certainly, the EMA performance could be further improved through tuning the properties of the self‐rolling rod, such as diameters and rolling methods.

Figure 4.

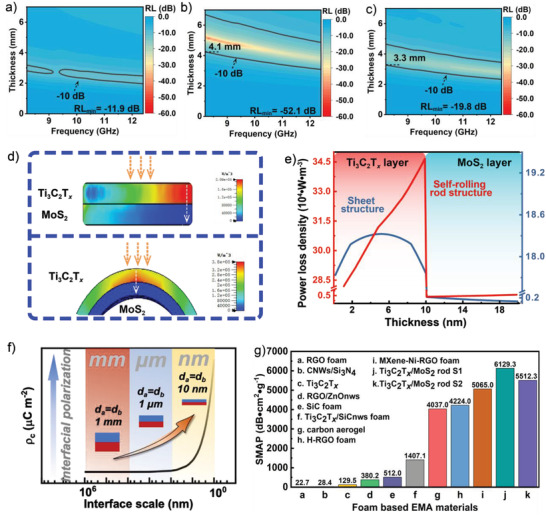
The 2D contours of reflection coefficient versus frequency and thickness (0–7 mm) of a) Ti₃C₂T _x /MoS₂ sheet, b) Ti₃C₂T _x /MoS₂ self‐rolling rod S1, and c) Ti₃C₂T _x /MoS₂ self‐rolling rod S2. d) The distribution of power loss density of sheet structure and rod structure on the heterogeneous interface. e) The value difference of power loss density for sheet structure and rod structure extracted from the white line. f) The relationship of interface scale and interfacial polarization loss (the abscissa axis is logarithm). g) Comparison of the SMAP of the Ti₃C₂T _x /MoS₂ foams in this work with the reported foam‐based EMA materials.

2.3. EMA Mechanism and Physical Model

To further reveal the advantage of self‐rolling rod structure, the Ti₃C₂T _x /MoS₂ sheet structure and Ti₃C₂T _x /MoS₂ self‐rolling rod structure models are constructed in the CST microwave studio (Figure S20, Supporting Information). The power loss density (PLD) is used to evaluate the EMA absorption ability in different structures. Two lines passing through the highest values of PLD are chosen as representatives. Compared with sheet structure, the self‐rolling rod structure shows higher EMA absorption ability at the heterogeneous interface area (Figure 4e and Figure S18, Supporting Information). Apart from that, the PLD values of the self‐rolling rod structure are much higher than the sheet structure, which can lead to better EMA performance. The Maxwell–Wagner theory also can be used to describe the interfacial polarization loss (Figure S19, Supporting Information).^{[ 29 ]} The intensity of interfacial polarization loss can be expressed by interfacial charge accumulated density ρ(t)(μCm⁻²)^{[ 30 ]}

$$\rho (t)=\frac{{\epsilon }_{\mathrm{A}}{\sigma }_{\mathrm{B}}-{\epsilon }_{\mathrm{B}}{\sigma }_{\mathrm{A}}}{{\sigma }_{\mathrm{A}}{d}_{\mathrm{B}}+{\sigma }_{\mathrm{B}}{d}_{\mathrm{A}}}{U}_0(1-e^{-\frac{t}{\tau }})$$ (1)

$$\tau =\frac{d_{\mathrm{A}}{\epsilon }_{\mathrm{B}}+d_{\mathrm{B}}{\epsilon }_{\mathrm{A}}}{d_{\mathrm{A}}{\sigma }_{\mathrm{B}}+d_{\mathrm{B}}{\sigma }_{\mathrm{A}}}$$ (2)

where ε _A and ε _B are permittivity of A phase with low conductivity and B phase with high conductivity, d _A and d _B are the thickness of A and B phases, U ₀ is the activation energy and τ is the relaxation time. When d _A = d _B, Equation (2) can be simplified to the following equation

$$\tau =\frac{{\epsilon }_{\mathrm{B}}+{\epsilon }_{\mathrm{A}}}{{\sigma }_{\mathrm{B}}+{\sigma }_{\mathrm{A}}}$$ (3)

Higher ρ(t) means stronger interfacial polarization loss. For two certain kinds of materials with similar thickness, the ρ(t) is only related to interfacial thicknesses d _A and d _B. As a result, the thinner the interface, the higher the interfacial polarization loss. For the Ti₃C₂T _x /MoS₂ self‐rolling rod structure, the thickness of interfaces was only about 10 nm, which lead to the remarkable improvement of polarization loss. Apart from that, the work functions can affect the accumulation of charges at heterogeneous interfaces, which is related to interfacial polarization loss. The work function difference between Ti₃C₂T _x and few‐layer MoS₂ is higher than bulk MoS₂ (Figure S21, Supporting Information), which indicates the interfacial polarization loss of Ti₃C₂T _x /MoS₂ self‐rolling rod structure is stronger than sheet structure.^{[ 31 ]} The work function of few‐layer MoS₂ is higher than Ti₃C₂T _x , which means that the polarized charges will flow to MoS₂ from Ti₃C₂T _x . As a result, the ratio of ε _p′′ is higher than 80%, which surpasses other EMA materials (Table S2, Supporting Information). The high ratio of ε _p′′ endow our samples with superior EMA performance. For a more comprehensive evaluation, the specific EM absorption performance (SMAP), which includes RL, density, and thickness at the same time, is used to evaluate the performance of our samples. The SMAP of Ti₃C₂T _x /MoS₂ foams is higher than 6100 dB cm² g⁻¹, due to highly ordered structure and effective interfacial polarization loss after the addition of MoS₂. Besides, other foam‐based EMA materials with EAB at X band are summarized and their corresponding SMAP is shown in Figure 4g and Table S3 in the Supporting Information. The SMAP of Ti₃C₂T _x /MoS₂ self‐rolling rod foams is superior to these reported foam‐based materials,^{[ 7} , ^{32 ]} demonstrating the advantages of self‐rolling rod structures.

3. Conclusions

In this work, the different surface tension directions of ATM and Ti₃C₂T _x derived from the varied hydrophilic properties induce the self‐rolling of Ti₃C₂T _x /MoS₂ rod structures. According to the simulation and Maxwell–Wagner theory, interfacial polarization loss significantly increases in self‐rolling rod structures. Based on the calculation results of Debye theory, the polarization loss plays a primary role with a ratio of higher than 80% in Ti₃C₂T _x /MoS₂ rod structures. In other words, the interfacial polarization loss is more important than its conduction loss for EMA performance in this system. As a result, the Ti₃C₂T _x /MoS₂ rod structures show better EMA performance compared with Ti₃C₂T _x /MoS₂ sheets, which can realize effective absorption at the whole X band. The SMAP is higher than 6100 dB cm² g⁻¹ with a density of 0.009 g cm⁻³. A self‐rolling rod structure based on Ti₃C₂T _x /MoS₂ was proposed to realize high interfacial polarization loss for obtaining high‐performance EMA materials. This work provides a new insight to design excellent foam‐based EMA materials with self‐rolling rod structures.

4. Experimental Section

Preparation of Ti₃C₂T _x MXenes

Ti₃C₂T _x was prepared according to an in situ acid‐etching method. Typically, LiF (1 g, Aladdin materials, China) and HCl (10 mL, 9 m, Aladdin materials, China) were mixed. 2 g of Ti₃AlC₂ powder (Jilin 11 technology, China) was added into the mixed solution slowly, following stirring at 40 °C for 24 h. Then, the etching products were collected through centrifugation at 3500 rpm until the supernatant became clear. After that, the mixture was washed about ten times with handshaking, until the supernatant became black. The black Ti₃C₂T _x supernatant was collected. The concentration of the suspension was evaluated through the vacuum filtration method.

Preparation of Ti₃C₂T _x /MoS₂ Foam

Firstly, the concentration of the Ti₃C₂T _x suspension was concentrated to 3, 4, and 5 mg mL⁻¹, respectively. Then, 0.03 g ATM (Aladdin materials, China) was added to the above solution and sonicated for 30 min for uniform dispersion. After that, the solution was freeze‐dried for 48 h to form the porous structure.^{[ 33 ]} Finally, the as‐prepared foams were calcined for 2 h at 350 °C under 90% Ar and 10% H₂. The samples were named S1, S2, and S3, corresponding to the concentration of 3, 4, and 5 mg mL⁻¹, respectively. The pure Ti₃C₂T _x foam was 5 mg mL⁻¹. The Ti₃C₂T _x /MoS₂ foams composed of Ti₃C₂T _x /MoS₂ sheets were also prepared. Typically, the ATM were annealed at first and then mixed with Ti₃C₂T _x suspension of 5 mg mL⁻¹, followed by the same unidirectional freezing and annealing processes.

Microstructure Characterization

The structures of foams were characterized by tabletop microscopes (TM400plus, Hitachi, Japan). The morphology of the Ti₃C₂T _x /MoS₂ rod was characterized by SEM (Sigma 300, Zeiss, Germany). The preparation TEM sample through FIB proceeded on FIB (Helios G4 CX, FEI, USA). The distribution of MoS₂ on the Ti₃C₂T _x sheets was observed by Double Cs Corrector TEM (Themis Z, FEI, USA). XRD (D8 Advance, Bruker, Germany) and Raman (He‐Ne laser, λ = 532 nm Renishaw, UK) were exploited to analyze the phase compositions. The chemical bonds were characterized by XPS (K‐Alpha, Waltham, Thermo Scientific, USA). TG curves of ATM were obtained on simultaneous thermal analysis (STA 449F3, Netzsch, Germany) in the temperature range of 30–400 °C under Ar.

Measurement and Calculation of EMA Performance

The S‐parameters and permittivity of the final foams were obtained through the wave‐guide method (ASTM D5568‐14) at a frequency range of 8.2–12.4 GHz. Based on the permittivity, the RL (dB) was obtained through the following equations

$$Z_{\mathrm{in}}=\sqrt{\frac{\mu }{\epsilon }}\tanh \left[j\left(\frac{2\pi fd}{c}\right)\sqrt{\mu \epsilon }\right]$$ (4)

$$\mathrm{RL}=20\mathrm{lo}{\mathrm{g}}_{10}\left|\frac{Z_{\mathrm{in}}-1}{Z_{\mathrm{in}}+1}\right|$$ (5)

where Z _in is the normalized impedance, and μ,ε, c, f, and d are permeability, permittivity, speed of light in vacuum, frequency of the EM wave, and the thickness of the test samples. The corresponding frequency range of RL lower than −10 dB is called EAB. The SMAP is adopted as one evaluation index, integrating with density, thickness, RL values, and effective bandwidth. The SMAP values are calculated by the following equation

$$\mathrm{SMAP}(\mathrm{dB}\mathrm{c}{\mathrm{m}}^2{\mathrm{g}}^{-1})=\frac{\left|{\int }_{f_{\mathrm{a}}}^{f_{\mathrm{b}}}\mathrm{RL}\mathrm{d}f\right|}{f_{\mathrm{b}}-f_{\mathrm{a}}}/(\rho ·d)$$ (6)

where f _a is the start frequency (8.2 GHz) andf _b is the stop frequency (12.4 GHz), d is the thickness, and ρis the bulk density of the foam.

Conflict of Interest

The authors declare no conflict of interest.

Supporting information

Supporting Information

Li M., Zhu W., Li X., Xu H., Fan X., Wu H., Ye F., Xue J., Li X., Cheng L., Zhang L., Ti₃C₂T x /MoS₂ Self‐Rolling Rod‐Based Foam Boosts Interfacial Polarization for Electromagnetic Wave Absorption. Adv. Sci. 2022, 9, 2201118. 10.1002/advs.202201118

Data Availability Statement

Research data are not shared.