A brain atlas of axonal and synaptic delays based on modelling of cortico-cortical evoked potentials

Abstract

Epilepsy presurgical investigation may include focal intracortical single-pulse electrical stimulations with depth electrodes, which induce cortico-cortical evoked potentials at distant sites because of white matter connectivity. Cortico-cortical evoked potentials provide a unique window on functional brain networks because they contain sufficient information to infer dynamical properties of large-scale brain connectivity, such as preferred directionality and propagation latencies.

 Here, we developed a biologically informed modelling approach to estimate the neural physiological parameters of brain functional networks from the cortico-cortical evoked potentials recorded in a large multicentric database. Specifically, we considered each cortico-cortical evoked potential as the output of a transient stimulus entering the stimulated region, which directly propagated to the recording region. Both regions were modelled as coupled neural mass models, the parameters of which were estimated from the first cortico-cortical evoked potential component, occurring before 80 ms, using dynamic causal modelling and Bayesian model inversion. This methodology was applied to the data of 780 patients with epilepsy from the F-TRACT database, providing a total of 34 354 bipolar stimulations and 774 445 cortico-cortical evoked potentials. The cortical mapping of the local excitatory and inhibitory synaptic time constants and of the axonal conduction delays between cortical regions was obtained at the population level using anatomy-based averaging procedures, based on the Lausanne2008 and the HCP-MMP1 parcellation schemes, containing 130 and 360 parcels, respectively. To rule out brain maturation effects, a separate analysis was performed for older (>15 years) and younger patients (<15 years). In the group of older subjects, we found that the cortico-cortical axonal conduction delays between parcels were globally short (median = 10.2 ms) and only 16% were larger than 20 ms. This was associated to a median velocity of 3.9 m/s. Although a general lengthening of these delays with the distance between the stimulating and recording contacts was observed across the cortex, some regions were less affected by this rule, such as the insula for which almost all efferent and afferent connections were faster than 10 ms. Synaptic time constants were found to be shorter in the sensorimotor, medial occipital and latero-temporal regions, than in other cortical areas. Finally, we found that axonal conduction delays were significantly larger in the group of subjects younger than 15 years, which corroborates that brain maturation increases the speed of brain dynamics.

To our knowledge, this study is the first to provide a local estimation of axonal conduction delays and synaptic time constants across the whole human cortex in vivo, based on intracerebral electrophysiological recordings.

Lemaréchal et al. model cortico-cortical evoked potentials to estimate axonal conduction delays, axonal velocity and synaptic time constants across the entire human cortex in vivo. By applying the methods to data from a large cohort of patients with epilepsy, they generate an atlas of dynamic cortical parameters.

Introduction

The transmission of neuronal activations in the brain results from the propagation of electrical currents through a series of distinct neuronal mechanisms. In short, the release of neurotransmitters into a synaptic junction gives rise to local changes of transmembrane potential in a post-synaptic neuron (depolarization or hyperpolarization). These post-synaptic variations propagate along the dendritic tree and are integrated into a global (excitatory or inhibitory) post-synaptic potential, with specific dynamics that can be summarized into a synaptic time constant.¹ When exceeding a given threshold, an action potential is triggered near the soma of the neuron and propagates along its axon towards the next synapse, with a conduction delay ranging from tenths to tens of milliseconds.² These neuronal delays play a key role in the dynamics of the brain, considered as a distributed and integrative network which can be modelled in a biologically plausible way by local neural assemblies connected through long-range connections.^3,4 Knowing these delays is necessary to decipher causal interactions between brain areas.⁵ Many techniques can be used to measure neuronal delays in animal models.⁶ Intracellular patch-clamp, optogenetics⁷ or dense arrays of microelectrodes in combination with spike sorting techniques⁸ now provide very high spatio-temporal resolution to track membrane potential changes and propagation of action potentials along axonal arborization of single neurons. In contrast, so far, human studies only allowed indirect inference of axonal conduction velocity from the morphology of white matter fibres,² characterized with electron microscopy⁹ or myelin g-ratio,¹⁰ thus lacking direct experimental evidence.

In this study, we focused on the direct cortico-cortical connections mediated by the excitatory projections of the axons of pyramidal cell populations and propose the in vivo estimation of the synaptic time constants and of the axonal conduction delays between distant brain regions of the human cortex based on dynamic causal modelling (DCM) of cortico-cortical evoked potentials (CCEPs). CCEPs were obtained in the context of clinical neurophysiological procedures used for the resective surgery of pharmaco-resistant focal epilepsies, based on the use of intracerebral depth electrodes (stereoelectroencephalography, SEEG) for characterizing the seizure onset zone and the epileptogenic networks.^11,12 During the SEEG procedure, low-frequency (typically 1 Hz) bipolar direct electrical stimulation (DES), by passing a current between two adjacent contacts located in a specific brain region, is repeated 10–40 times to trigger evoked responses at distant locations, which are recorded by the other implanted electrodes. CCEPs generally consist of a first sharp peak (10–50 ms), the N1 component, followed by a slow wave (80–250 ms), the N2 component. Please note that this N1/N2 terminology is a simplification of the complexity of CCEPs, which also includes positive components, but for simplicity we will refer only to ‘N1’ when discussing early CCEP components and to ‘N2’ for the late CCEP components. The analysis of the CCEPs elicited by single-pulse DES is particularly relevant to infer the properties of large-scale brain connectivity.¹³ In the F-TRACT project (f-tract.eu), we gathered CCEPs from several hundreds of patients worldwide to develop a probabilistic atlas of functional tractography by extracting the characteristics of each CCEP individually (i.e. peak significance and latency of the N1 component).^14,15

Here, we built on the assumption that the first early N1 component is generated via a direct cortico-cortical pathway between the stimulation and the recording site, mainly because we have previously shown that the peak delay of the N1 component linearly increases with distance, which suggests direct cortico-cortical pathways, assuming constant propagation speed.¹⁵ In addition, we did not primarily consider indirect cortico-subcortico-cortical pathways that would rather be implicated in the later N2 component.¹⁶ To characterize the direct connection underlying the N1 component, we applied the DCM approach to all significant responses available from the F-TRACT database that occurred during the first 80 ms following the stimulation (774 445 CCEPs). Based on local neural mass models embedded in a global model of effective connectivity,^17,18 DCM implements an efficient Bayesian inversion to estimate the parameters of a generative neuronal model, including neuronal delays, which minimize the error prediction of the model. Finally, projecting the DCM estimation of axonal conduction delays and synaptic time constants from all the patients into a common anatomical space allowed us to build an atlas of these key neuronal delays at the group level based on existing parcellation schemes.

Materials and methods

General information

In this study, we used the data from 780 patients with epilepsy (387 females; age at evaluation from 2 to 61 years old; mean age 24 ± 14) explored with SEEG in 25 epilepsy surgery centres (see consortium details in Appendix 1 and Supplementary material) and included in the F-TRACT protocol. As part of a presurgical evaluation of their drug-resistant epilepsy, each patient signed a written informed consent to undergo invasive recordings and low-frequency stimulation. In accordance with the Declaration of Helsinki, they also agreed, either prospectively or retrospectively, for their data re-use for the F-TRACT protocol validated by the International Review Board at INSERM (protocol number: INSERM IRB 14–140), which adhered to the ethical procedures for conducting international multicentre post-processing of clinical data. The CCEPs were recorded using local clinical practice, following 1-Hz stimulations (99.5% of CCEPs), or rarely 2 or 3 Hz (0.5% of CCEPs), between two contiguous contacts located either in the grey matter (61% of contacts) or white matter (39% of contacts), using either monophasic (20% of CCEPs) or biphasic (80% of CCEPs) electrical pulses. The number of pulses in a row were up to 40 and only stimulation runs with at least 3 pulses were considered (see Trebaul et al.¹⁵ for an analysis on the influence of the number of pulses for CCEP quantification). Other stimulation parameters were rather homogeneous across the population (mean pulse intensity: 3.4 ± 1.1 mA, mean pulse duration: 1.0 ± 0.4 ms and mean pulse charge: 3.5 ± 1.8 μC; see Supplementary Fig. 10A for distribution analysis). On average, the patients were implanted with 320 ± 85 contacts (min: 60, max: 618) and were stimulated 58 ± 48 times (min: 1, max: 257).

Processing and selection of cortico-cortical evoked potentials

The multicentre F-TRACT database (f-tract.eu) comprises CCEPs induced by low-frequency bipolar stimulations. Extensive details on the anatomical and functional preprocessing steps used to compute the CCEPs are available in two previous studies.^14,15 In brief, with regard to anatomy, electrode and contact positions extracted from the post-implantation CT scan were first co-registered to the pre-implantation 3D T₁ MRI of the patient and their tissue classification was determined according to a grey/white matter segmentation of the MRI. Then, spatial normalization with DARTEL—as implemented in SPM12 (www.fil.ion.ucl.ac.uk/spm)—projected the contacts of each patient in the MNI referential. In addition, in order to formally cluster, summarize and present the extracted CCEPs’ characteristics at the group level, we computed parcel labels with respect to a series of neuroanatomical atlases for each contact. The full neuroanatomical preparation of the data was performed with the IntranatElectrodes software.¹⁹

The slow early components of CCEPs, which are only considered here, are thought to be less affected by the pathology than the late ones, even for stimulating or recording electrode contacts located in either the epileptogenic or the propagation zone.^20,21 However, to minimize a potential bias in our findings due to epileptogenic processes, we removed from our analysis the data recorded by electrode contacts suspected to present a pathological activity. To do so in an unsupervised manner, we computed the interictal spiking rate of each contact from prestimulation period recordings using Delphos software (Detector of Electro Physiological Oscillations and Spikes).^22,23 Given that no direct relationship is commonly accepted in SEEG between epileptogenicity and interictal spiking rate, we defined a rejection threshold on the interictal spiking rate from the results of a retrospective study.²⁴ In this study, the data from 100 patients with focal epilepsy and implanted with ECoG and SEEG electrodes were collected. The authors reviewed recorded seizures and epileptiform spikes and concluded that the majority of electrodes were located in non-epileptic tissue (82%) and that sites with pathological activity were clustered in a few electrode contacts. Based on these observations, we decided to keep a similar proportion (80%) of electrode contacts for analyses, which corresponded to a maximum interictal spiking rate of 8.4 spikes per minute (the estimation and the thresholding of the spiking rates across contacts and CCEPs are detailed in Supplementary Fig. 2).

Following this initial selection step, stimulation runs (series of maximum 40 single electrical pulses at low frequency, i.e. in 99.5% of cases at 1 Hz) were first automatically detected in the raw data based on the stimulation artefacts caused by the electrical stimulation. Bad channels were first pre-identified with a machine learning approach,²⁵ which was then followed by visual inspection by SEEG experts for final classification and data were re-referenced with a bipolar montage of adjacent contacts, to retain only focal activities. This procedure allowed us to avoid selecting saturating responses in channels very sensitive to electrical artefacts or when acquisition procedures were not performed in optimal conditions. Transient stimulation artefacts were corrected using a piecewise cubic Hermite interpolation of the [−3 6] ms window surrounding the artefact peak and continuous data were band-pass filtered between 1 and 45 Hz. Epochs were defined on a [−200 800] ms interval around the stimulation pulse. Importantly, epochs containing (and following) the presence of after discharges were removed from the analysis. A robust-averaging procedure was also used to track and exclude epochs showing spiking activity and/or transient artefacts.¹⁴ Finally, CCEPs were z-scored with respect to a [−200 −10] ms baseline interval preceding the stimulation pulse. The evoked response was considered significant if its absolute value reached the threshold of z = 5 during the first 200 ms post-stimulation onset. This condition indicated the presence of a functional link between the stimulation and the recording sites. The software suite used to perform these processing steps are open-source tools available from the F-TRACT project at f-tract.eu/software.

For the ensuing DCM analysis, only significant CCEPs with a peak latency comprised in the first 80 ms were selected, in order to limit the analysis to the early N1 component. We made the explicit assumption that the N1 is primarily due to cortico-cortical propagation as demonstrated by us¹⁵ and other authors.¹⁶ In our previous study,¹⁵ we showed that the N1 peak latency linearly increases with the distance between stimulated and recorded areas, which is highly suggestive of cortico-cortical propagation as a major cause of observed delays in the N1 response.

Finally, unless specified otherwise, CCEPs were not selected based on the tissue classification of their contacts, in order to maximize the number of data for having optimal spatial coverage. We elaborate on this choice in the ‘Impact of contacts tissue classification’ section of the Discussion. The selection of data resulted in a total of 774 445 CCEPs, spread across 34 354 stimulations from 780 patients. The complete selection process of the CCEPs, along with the number of CCEPs remaining after each step, is detailed in Supplementary Fig. 3.

Estimation of axonal conduction delays and synaptic time constants

Architecture of the DCM model

The DCM architecture used to fit the CCEPs of a given stimulation comprised one region for the stimulation site and one region for each of the recording sites, connected together by a single forward connection (Fig. 1A). Each region was modelled with an event-related potential (ERP) neural mass model,²⁶ which is reproduced (along with the equations defining the dynamics) for clarity purposes in the Supplementary material and Supplementary Fig. 1. Because electrode contacts at the stimulation site were used to inject the current, no CCEP was recorded at this location. The first region was therefore modelled as a hidden region, observed indirectly through its causal interactions with the second region,²⁷ where CCEPs were recorded and observed directly. Consequently, the DCM observation model was reduced to the activity of the pyramidal cells of the second region. The DES pulse was modelled as a transient input entering the first region.

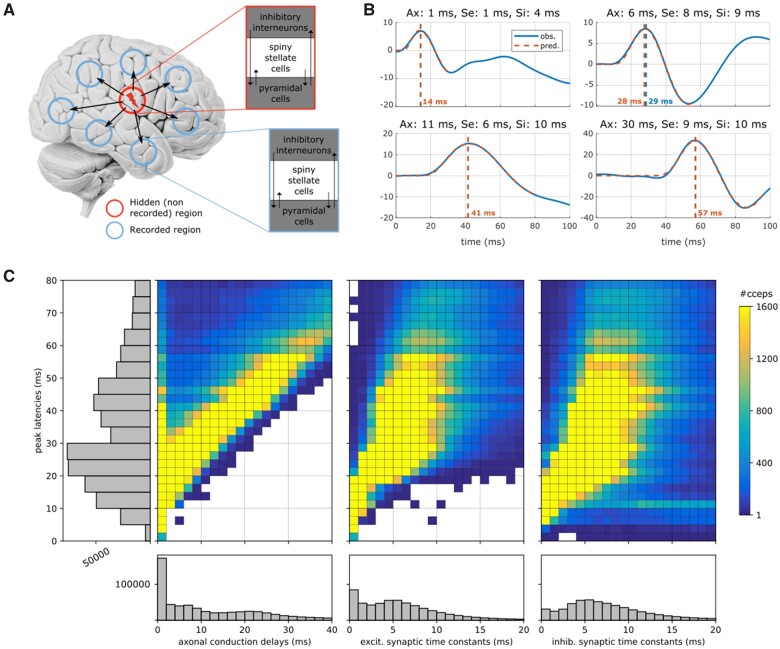
Figure 1.

Estimation of CCEPs neuronal parameters at the individual level. (A) Architecture of the generative model underlying the early N1 component of CCEPs. Each of the stimulation (red circle) and recording (blue circles) sites are modelled with local neural mass models. Following a transient bipolar stimulation and for a sufficient charge level (product of pulse intensity and duration), action potentials initiated in the stimulated region propagate via orthodromic projections to connected regions, where significant responses are recorded. (B) Model predictions (red) of CCEP observations (blue) for increasing N1 peak latencies (vertical line). Estimated axonal conduction delays (Ax), excitatory (Se) and inhibitory (Si) synaptic time constants are indicated on top of each panel. (C) Distribution of the estimated neuronal delays. The main panels (coloured 2D histograms) represent the joint distribution of the axonal conduction delays (left), excitatory (middle) and inhibitory (right) synaptic time constants (horizontal axes) according to the N1 peak latency (vertical axis). White colour indicates an absence of data. The side panels (grey 1D histograms) show the marginal distributions of the N1 peak latencies (vertical plot on the left) and of each neuronal parameter (horizontal plots at the bottom).

Fit of the N1 component

The eventually large number of significant CCEPs recorded for any given stimulation site (mean = 27) resulted in very high dimensionality of the parameter space. It was therefore computationally intractable to take into consideration all recording sites at once in a single model. Indeed, the running time required for the Bayesian inversion of such a DCM with more than 10 regions could exceed 12 h (quadratic with respect to the number of regions). Computational time was also very much increased, compared to standard DCM code implementation, by the precise integration scheme required to estimate axonal delays²⁸ (see the ‘Technical implementation’ section). Therefore, we implemented an equivalent practical solution in which the CCEPs of a given stimulation were estimated separately from each other using a series of simple reduced models, where the first region, corresponding to the stimulated region, was artificially duplicated (Supplementary Fig. 4). To guarantee the uniqueness of the neuronal parameters of the stimulated region across the CCEPs, the estimation was then performed in two steps. During the first step, the n reduced models were fully estimated independently (input and neuronal parameter estimation). The estimates of the parameters of the first (stimulated) region (input u, synaptic time constants and gains, intrinsic coupling) were then averaged across the n reduced models using a posterior variance-weighted averaging procedure.²⁹ During the second step, the averaged posteriors of the stimulated region parameters were used as fixed parameters and only the connectivity parameters and the neuronal parameters of the second region were estimated (i.e. the strength of the forward connection, the axonal conduction delay and the local synaptic parameters). This iterative two-step procedure refers to an empirical Bayes approach, in which the empirical prior distributions for the second step are derived from first step posterior distributions and thus estimated from the data. By reducing the number of parameters in each reduced model and iteratively setting the priors, the Bayesian inversion was less prone to the problem of local minima in both steps and therefore provided a robust estimation of the model parameters.³⁰ After the completion of the second step, only accurate fits were selected for further analyses, according to the following conditions: (i) a goodness of fit (ratio of the explained variance to the total variance) above 70%; and (ii) an absolute difference in the alignment of the N1 peak latencies between observation and prediction smaller than 5 ms. The two-step approach undertaken had the advantage of giving us the possibility to consider the variability of the N1 peak latencies across recording sites and to adjust the time window of the fit separately for each CCEP for optimizing computational duration. The time interval used to fit the data was set to $\left[t_0{t}_1\right]$, where $t_0=0$ corresponded to the stimulation onset and $t_1=\mathit{peak}\mathit{latency}+2\times \mathit{duration}$, with $\mathit{duration}$ being the time duration during which the response exceeded the significance threshold of z = 5.¹⁵ In addition, $t_1$ was constrained to be smaller than $\mathit{peak}\mathit{latency}+40ms$. This ensured that DCM estimation focused on the N1 component, without being biased by the presence of an N2 component, usually carrying a higher level of energy and for which the biological plausibility of the DCM was very much reduced.

Technical implementation

The technical implementation made use of the generic code of DCM as provided in the official SPM software (SPM12, version r6732, fil.ion.ucl.ac.uk/spm). In particular, the definition of the ERP neural mass model was left unchanged (Supplementary material and Supplementary Fig. 1). Yet, some adjustments were necessary. First, the model was equipped with a numerical integration scheme based on Runge–Kutta techniques to generate neural time series using an accurate integration of the system of delay differential equations describing brain dynamics.²⁸ Second, the DCM priors of the neuronal model parameters were modified from their default values, to account for the specific context of DES, which induced faster evoked responses than usually observed from EEG during standard cognitive tasks.³¹ In particular, for the first step, the excitatory (respectively, inhibitory) synaptic time constant was set to 1 ms (respectively, 2 ms) for the first region. This reflected the fast activation of the hidden region, right after stimulation onset. With regard to the axonal delays between the two regions and the synaptic time constants of the second region, the prior means were initialized based on simulations. A series of CCEPs was generated with the previously described DCM (Supplementary Fig. 4) by varying axonal conduction delays between [1 and 40] ms and excitatory synaptic time constants between [1 and 8] ms, and the peak latency of the response was reported for each combination of parameters (Supplementary Fig. 5). Priors were then selected so that the peak latency of the model prediction, generated during the first iteration of the fit procedure, would coincide with the peak latency of the observation. This adaptive simple heuristic revealed both necessary and very efficient for fitting the model to any response that occurred within the first 80 ms. The synaptic gains were adjusted accordingly in order to preserve the power of the synaptic convolution kernel.¹⁷ The prior variance of each of these modified parameters was set to 1 (instead of the default value 1/16).¹⁷ Such an uninformative prior offered the parameters the possibility to easily depart from their initial value. Prior means and variances of all other parameters were left to their default values.

Group-level analysis

Parcellations

To present the estimation of neuronal delays at the group level, we clustered all contacts according to their parcel label (see the ‘Processing and selection of CCEPs’ section) based on two established parcellation schemes: Lausanne2008³² and HCP-MMP1.³³ Lausanne2008 is a cortical parcellation based on anatomical landmarks. In short, an average brain, manually labelled with regions of interest (ROIs), is registered to the anatomy of each subject during the individual segmentation procedure performed by Freesurfer (surfer.nmr.mgh.harvard.edu). By successively subdividing each region of interest, the parcellation is available at resolutions 33, 60, 125 and 250 (identified as Lausanne2008-resolution), which include 84, 130, 235 and 464 parcels, respectively. Lausanne2008-60 was chosen in this study to map the axonal delays at the group level, because it offered the best compromise between its spatial resolution and the repartition density of the F-TRACT data across brain regions at the moment. At this resolution, each hemisphere is partitioned into 57 cortical parcels, hippocampus and amygdala and other subcortical areas of no interest here because they were not sampled by SEEG electrodes. In addition, we used the HCP-MMP1 parcellation scheme³³ to map the synaptic time constants at the group level. The HCP-MMP1 parcellation scheme was produced from multimodal acquisitions from 210 healthy subjects of the Human Connectome Project. By detecting reproducible ‘sharp changes in cortical architecture, function, connectivity, and/or topography’,³³ this semi-automated approach identified 180 areas per hemisphere.

Distance between contacts

To assess the axonal conduction velocities, distances between stimulating and recording contacts were measured along the white matter fibres supposedly connecting them. Because the diffusion tensor imaging data were not available for the patients of F-TRACT, we used the ARCHI database built from 79 healthy subjects, aged between 18 and 40, at the Neurospin centre.³⁴ We registered each patient anatomy on the ARCHI DTI atlas and computed the distance as the average path length of the database bundles running close (within 5 mm) to both contacts.

Data availability

Raw data cannot be distributed because of personal data-protection sensitive issues. Fully processed data at the group level are available for download on the atlas page F-TRACT website (f-tract.eu/atlas). Additionally, fully anonymized CCEPs time series have been made available on the website of the Human Brain Project (search for ‘CCEP database’ on ebrains.eu).

Results

Individual data fitting

Typical examples of fitted CCEPs are presented (Fig. 1B) for increasing peak latencies (14, 29, 41 and 57 ms), along with the estimated neuronal delays. In addition to the variability of the waveforms, these examples illustrate the face validity of the approach, namely the ability of the DCM model to provide accurate predictions of the observed N1 components. The complete set of 774 445 CCEPs was fitted with an average goodness of fit (ratio of the explained variance to the total variance) of 87% and an average difference of the N1 peak alignment between observations and predictions of 1.9 ms. By requiring a minimum goodness of fit of 70% and a N1 peak alignment error smaller than 5 ms, poorly estimated CCEPs were identified and eliminated. This resulted in 78% of the CCEPs (representing a total of 602 154) to be considered in the subsequent analysis at the group level. Here, it is important to mention that pooling these CCEPs was also justified by the fact that the stimulation parameters used to trigger these 602 154 significant responses, similarly to the stimulation parameters used in the whole initial set of CCEPs (see ‘General information’ section), were still particularly homogeneous across patients (mean pulse intensity: 3.5 ± 1.0 mA, mean pulse duration: 1.0 ± 0.3 ms and mean pulse charge: 3.5 ± 1.6 μC; Supplementary Fig. 10B).

Group-level estimation of neuronal delays

Among the parameters of the DCM neuronal model, we focused on the estimates of the axonal conduction delays between the two regions and of the synaptic time constants of the second region. We computed the joint distribution for each of these parameters with the corresponding peak latency (Fig. 1C), as well as their marginal distribution. In general, the earliest N1 responses required both short axonal delay and short excitatory synaptic time constant while longer N1 peak latencies were explained by an increase of both axonal delays and synaptic time constants. Interestingly, while the CCEP peak latency naturally imposed an upper bound on axonal delays and excitatory synaptic time constants (Fig. 1C, large white regions under the diagonal of the left and middle panels), this was not necessarily the case for the inhibitory synaptic time constants (Fig. 1C, right panel), which could exhibit large values (from 6 to 20 ms) for both short and long N1 peak latencies. Marginal distributions revealed peaks for the shortest delays, particularly marked for axonal conduction delays. Indeed, 29% of axonal delays were estimated below 2 ms and 55% below 10 ms. It is also worth noting that both excitatory and inhibitory synaptic time constants exhibited a second mode around 4–6 ms.

Mapping of axonal conduction delays

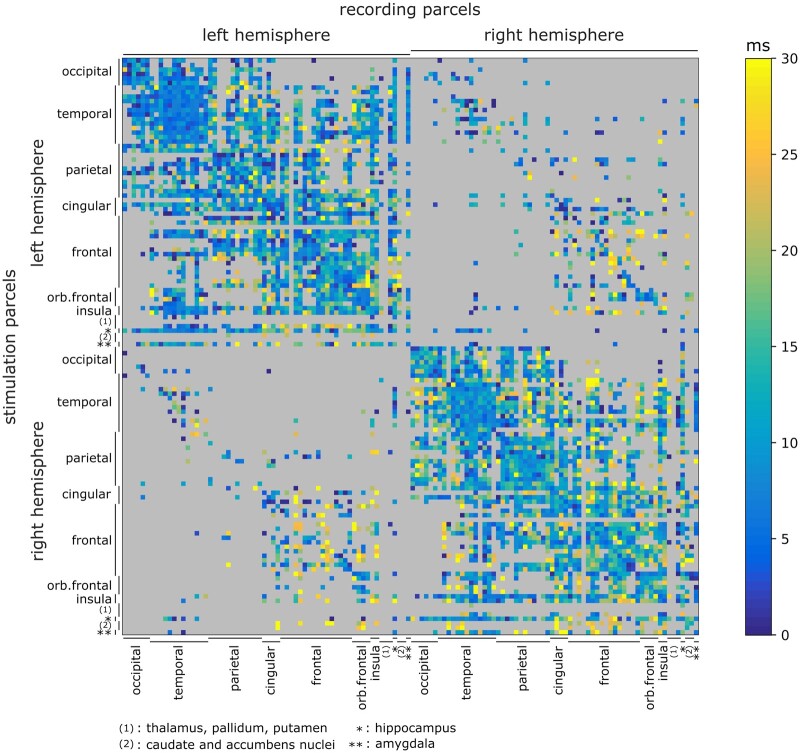
Because of changes in conduction properties (myelination, axonal growth, synaptic plasticity) during development,³⁵ we used the age of 15 years as a boundary to split the subject sample into a younger (min: 2 years, max: 15 years, mean: 9 years, 274 patients) and an older group (min: 15 years, max: 60 years, mean: 32 years, 506 patients). For each group, estimated neuronal parameters were spatially clustered using brain parcellation to provide an insight into their distribution across (pairs of) brain areas. In this study, parcellation schemes were chosen to offer the best compromise between their spatial resolution and the repartition density of the data provided by F-TRACT at the moment. Thus, we used Lausanne2008-60,³² which partitions each hemisphere into 57 cortical parcels and also includes subcortical structures, i.e. hippocampus and amygdala (see ‘Group-level analysis’ section). To limit the presence of outliers in the parameter estimates, the median delay was assigned to a given parcel pair when at least five significant CCEPs were accurately fitted for this parcel pair; otherwise, it remained undocumented. Results are presented for the older group in a matrix form where each row corresponds to a stimulated parcel and each column corresponds to a recording parcel (Fig. 2A and Supplementary Fig. 6 for the number of CCEPs used in each estimation, along with the median absolute deviations). Estimated delays were colour-coded from 0 to 30 ms, while grey-coloured entries corresponded to connections for which it was not possible to provide an estimation of the neuronal parameters (due to the absence of a significant connection, or to an insufficient number of accurate fits). Given the Lausanne2008-60 parcellation scheme, 54% of intrahemispheric connections and 8% of interhemispheric connections were estimated.

Figure 2.

Estimation of axonal conduction delays between brain regions. Results are presented for the older group (>15 years) based on the Lausanne2008-60 parcellation scheme. The matrix presents median axonal delays for this group, between stimulating (vertical axis) and recording (horizontal axis) parcels based on the Lausanne2008-60 parcellation scheme. Grey-coloured entries indicate the absence of direct connections (or an insufficient number of significant responses fitted with accuracy).

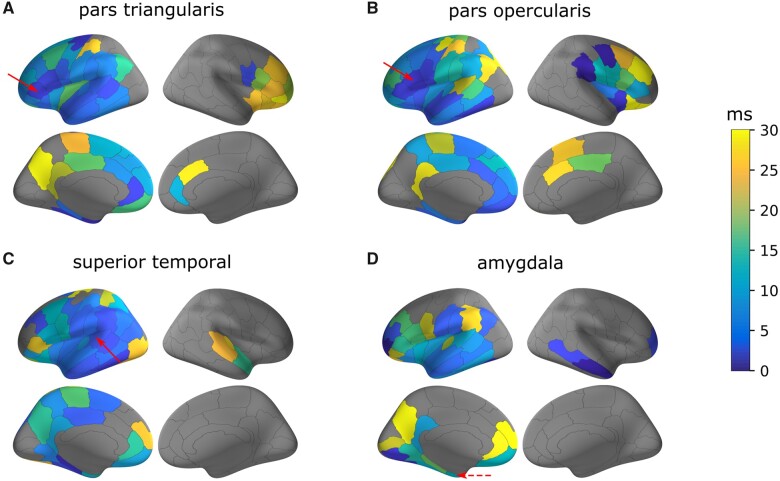
The mapping of neuronal parameters at group-level on a parcellated brain allows several properties of axonal delays in the human brain to be highlighted. First, it showed a gradient pattern whereby axonal delays increased along with the distance between the stimulated and the recording parcels. Delays shorter than 1 ms were found when recordings occurred within the stimulated parcel and no longer than 5 ms for the parcels just next to the stimulated parcel. Delays greater than 10 ms corresponded to more distant connected regions, located in either the ipsilateral (Fig. 3A: 17 ms between the left pars triangularis and the left inferior parietal region) or the contralateral (Fig. 3A: 26 ms between the left pars triangularis and the right lateral orbitofrontal region) hemisphere with respect to the stimulation. Moreover, while results were qualitatively similar for the stimulation of the amygdala (Fig. 3D), the delays estimated from this subcortical region turned out to be slightly longer than following neocortical stimulation and ranged from 6–10 ms for the nearby temporal regions to 20–25 ms for the orbitofrontal and frontal regions. Finally, some regions such as the right insula presented an idiosyncratic pattern of dynamic functional connectivity, which shows, except for a few prefrontal regions, spatially uniform conduction delays less than 6–8 ms throughout the ipsilateral hemisphere (Fig. 4A).

Figure 3.

Brain mapping of axonal conduction delays. Median axonal conduction delays are presented for the efferent connections from one stimulated parcel (pointed by a red arrow) to the rest of the brain. Here, the series of stimulated parcels have been chosen in the left hemisphere: (A) the pars triangularis, (B) the pars opercularis, (C) the superior temporal gyrus and (D) the amygdala. Results are presented for the older group (>15 years) based on the Lausanne2008-60 parcellation scheme.

Figure 4.

Brain mapping of axonal conduction delays for the right insula. (A) Efferent connections: the insula is stimulated and CCEPs are recorded in other regions. (B) Afferent connectivity: insula is recording CCEPs when stimulation is performed in other regions. Results are presented for the older group (>15 years) based on the Lausanne2008-60 parcellation scheme. The red arrow indicates the right insula.

An intrinsic advantage of investigating the brain functional connectivity with CCEPs is the ability to characterize directed connections and assess the asymmetry of reciprocal connections. As a practical example, we considered the axonal conduction delays between the pars opercularis (Fig. 3B) and the posterior superior temporal gyrus (Fig. 3C), two parcels comprising, respectively, Broca’s and Wernicke’s areas involved in the language processing network. The axonal delay from the pars opercularis to the superior temporal gyrus was estimated around 5.1 ms (from 275 stimulations), whereas it was estimated around 6.2 ms (from 261 stimulations) for the reciprocal connection. Considering now the pars triangularis (Fig. 3A), anterior to the pars opercularis (and also part of the Broca area) and the superior temporal gyrus, the axonal delay was estimated to be 6.6 ms (159 stimulations) and 8.3 ms (213 stimulations) for the reciprocal connections.

Finally, instead of focusing on the efferent connectivity from one stimulated area, as we did until now, an alternative approach is to examine the afferent connectivity to one recorded area. This showed, for example, regarding the insula that the axonal conduction delays of afferent connections (Fig. 4B) were very similar to the ones of efferent connections (Fig. 4A).

Mapping of axonal conduction velocities

For each estimated CCEP and given the white matter path length between the stimulating and the recording contacts computed from the ARCHI database³⁴ (see ‘Group-level analysis’ section), we produced two measures of conduction velocity, first based on N1 peak latency and second based on estimated axonal conduction delay. These velocity estimates were then extended at the group level using the same parcellation scheme previously described. The distributions across parcels pairs of the Lausanne2008-60 parcellation scheme were computed for N1 peak latencies (median: 37.0 ms, Fig. 5A), axonal conduction delays (median: 10.2 ms, Fig. 5B), distances between contacts (median: 42.9 mm) and for the conduction velocities derived from the N1 peak latencies (median: 1.1 m/s, Fig. 5C) and from the axonal conduction delays (median: 3.9 m/s, Fig. 5D), respectively. The same measures were also estimated for the younger group of patients (<15 years). As expected, it indicated a general slowdown of conduction, as compared to the older group (Table 1 and Supplementary Fig. 7), observed for N1 peak latencies (median: 37.5 ms), axonal conduction delays (median: 11.0 ms) and the corresponding velocities (median: 0.9 m/s and 3.1 m/s), despite overall shorter distances between contacts (median: 34.9 mm).

Figure 5.

Estimation of conduction velocities. Results are presented for the older group (>15 years) based on the Lausanne2008-60 parcellation scheme. Distributions of (A) N1 peak latencies (median: 37.0 ms), (B) axonal conduction delays (median: 10.2 ms), and conduction velocities based on (C) N1 peak latencies (median: 1.1 m/s) and (D) axonal conduction delays (median: 3.9 m/s). Distances between stimulating and recording contacts were measured along white matter fibres, using the ARCHI DTI atlas (see ‘Group-level analysis’ section).

Table 1.

Comparison of neuronal characteristics between age groups

Neuronal characteristic	Median ± MAD		P-value
	<15 years	>15 years
Peak latency, ms	37.5 ± 14.5	35.0 ± 10.8	<10−10
Axonal conduction delay, ms	11.0 ± 8.2	9.5 ± 5.5	<10−10
Distance between parcels, mm	34.0 ± 15.7	34.2 ± 14.5	<10−6
Peak latency velocity, m/s	0.9 ± 0.4	1.0 ± 0.3	<10−10
Axonal conduction delay velocity, m/s	3.1 ± 2.0	3.5 ± 1.8	<10−6
Excitatory synaptic time constant, ms	5.8 ± 1.2	5.6 ± 1.0	0.2
Inhibitory synaptic time constant, ms	7.3 ± 1.1	7.3 ± 0.7	0.9

Median values and median absolute deviations (MAD) are provided separately for the younger (<15 years, 274 patients) and the older (>15 years, 506 patients) group. The first five characteristics were estimated based on the Lausanne2008-60 parcellation scheme and Wilcoxon signed rank tests were performed across parcels pairs (total of 2712) estimated conjointly in the two groups. The last two characteristics were estimated based on the HCP-MMP1 parcellation scheme and Wilcoxon signed rank tests were performed across parcels (total of 327) estimated conjointly in the two groups. Please note that, because of the joint estimation, median values reported here slightly differed from median values.

Mapping of synaptic time constants

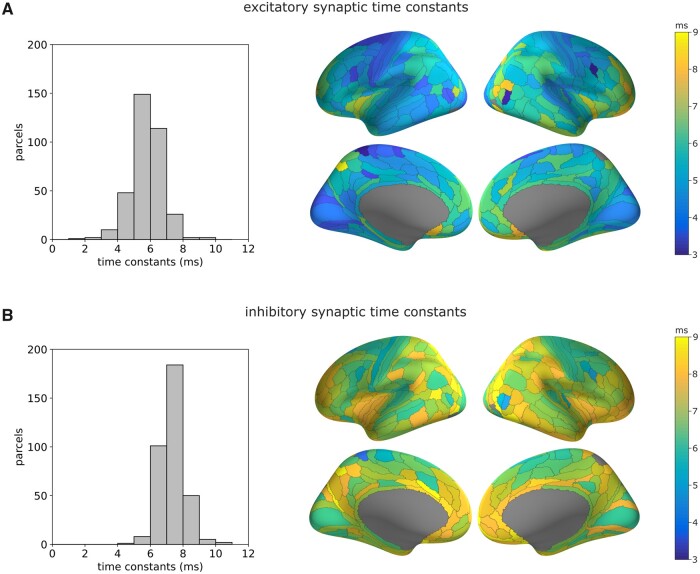
Whereas the axonal conduction delays were estimated for each parcel pair, the synaptic time constants were considered as intrinsic neuronal properties of each parcel and were computed from all the CCEPs having their recording contact in that parcel, whatever the stimulated parcel. We assigned the median value of the synaptic time constants to each parcel for which a minimum of five significant CCEPs were accurately fitted by the model. The number of data was sufficient to provide an estimation for almost all parcels in each hemisphere, using the functional HCP-MMP1³³ parcellation scheme (360 parcels, see ‘Group-level analysis’ section). Considering the whole group of patients, the distributions exhibited globally shorter excitatory (median: 5.8 ms, Fig. 6A) than inhibitory (median: 7.3 ms, Fig. 6B) synaptic time constants (Wilcoxon signed-rank test, P < 1 × 10⁻⁵). Mapping the synaptic time constants on the cortex also pointed out some interesting properties. There was a statistically significant linear correlation of synaptic time constants between each hemisphere, both for excitatory (slope = 0.51, r = 0.48, P < 1 × 10⁻¹⁰; Supplementary Fig. 8A) and inhibitory (slope = 0.46, r = 0.55, P < 1 × 10⁻¹⁴; Supplementary Fig. 8B) time constants, indicative of a certain level of interhemispheric symmetry. Furthermore, the distribution of the synaptic time constants showed heterogeneity across the cortical brain regions. Sensorimotor, medial occipital and lateral temporal regions exhibited shorter synaptic time constants than did frontal, anterior insular, parietal or cingulate regions. Interestingly, regions belonging to the default mode network seemed to show slower synaptic time constants. This was also confirmed for the different spatial resolutions of the Lausanne2008 parcellation scheme (Supplementary Fig. 9). When considering the synaptic time constants for the younger versus the older group, no significant difference was found (Table 1).

Figure 6.

Estimation of synaptic time constants. Results are presented for the whole group based on the 360 parcels of the HCP-MMP1 parcellation scheme. (A) Distribution (left) and brain mapping (right) of excitatory synaptic time constants. (B) Distribution (left) and brain mapping (right) of inhibitory synaptic time constants. For a very few grey-coloured cortical regions, the estimation was not possible, due to an insufficient amount of data.

Discussion

In this study, a biologically informed ERP neural mass model was fitted to the early N1 component of CCEPs to provide estimates for axonal conduction delays and synaptic time constants throughout the human brain, from a large series of 774 445 CCEPs obtained in 780 patients with epilepsy. Although the involvement of indirect cortico-subcortico-cortical or even cortico-cortico-cortical connections cannot be completely excluded, we grounded our modelling approach on results from previous studies^15,16 (see ‘Processing and selection of CCEPs’ section) and assumed that the N1 components of the CCEPs were generated by direct cortico-cortical connections between the stimulating and the recording sites. This allowed us to put in light different properties of the dynamical functional properties of the brain. The brain mapping at the group level revealed that the axonal propagation delays were globally short (median: 10.2 ms for the older group). Although an increase of these delays with the distance between the stimulation and the recording site was an overall general rule across the cortex and recorded subcortical structures, some regions were less submitted to this rule, such as the insula (Fig. 4), for which almost all ipsilateral efferent and afferent connections were faster than 10 ms. This fits with the view of the insula as a region at the crossroad of multiple functional networks.³⁶ Moreover, the spatial distribution of synaptic time constants pointed out an interesting interhemispheric symmetry as well as local cortical specificities. While primary areas (sensory, motor, auditory, visual) exhibited the fastest dynamics, other regions (medial prefrontal cortex, anterior insula, cingulate cortex, precuneus, temporoparietal junction, medial temporal lobe) reminiscent of the default mode network³⁷ showed slower ones. Moreover, within the younger group (<15 years), axonal delays were significantly increased (Table 1). This result indicates that the dynamics of CCEP are sufficiently sensitive to indirectly track brain maturation mechanisms, like the degree of myelination at the origin of axonal velocity changes. In this regard, the ambition of the present study was very limited and the simple comparison between two age ranges was used as an internal validation step. Another limitation of the present analysis is that we used structural connectivity pathways obtained in adults (the ARCHI database was built with subjects aged between 18 and 40) to estimate axonal conduction velocity at all ages. More sophisticated analyses should be considered in the future to evaluate better the interest of CCEPs for addressing developmental questions.

Effect of the cortico-cortical evoked potential selection

One of the main difficulties when generating different CCEP-based atlases is to select the CCEPs with a good compromise between the quantity and the accuracy of the estimations, while reaching a sufficient spatial resolution for a whole-head coverage. We discuss below important parameters.

Effect of the contact tissue classification

In previous work,¹⁵ we demonstrated how the stimulation parameters influence the connectivity estimated from CCEPs, i.e. fewer remote responses are detected for low levels of injected electrical charges.³⁸ A similar effect can be anticipated here, but its precise quantification was outside of the scope of this study. For completeness, we provide in Supplementary Fig. 10 the distributions of stimulation parameters.

Effect of the contact tissue classification

To maximize the biological plausibility of the model, we could have selected only CCEPs for which both stimulating and recording contacts were located in the grey matter, because when contacts are located in white matter, the direct stimulation of axons can make it difficult to clearly distinguish between the stimulation and the recording sites.³⁹ However, we did not consider this option in the main report, because it would have dramatically decreased the number of available data as 39% of contacts of the F-TRACT database are located in white matter; we preferred to prioritize statistical robustness of reported effects. In the Supplementary material we elaborate further on this issue and provide additional data on the influence of tissue classification (grey or white matter) of CCEPs contacts on the estimations of neuronal parameters.

Effect of the spiking rate threshold

Even if the early N1 slow component of the CCEPs may be unaffected by the hyper-excitability of the recording region,²⁰ we used a threshold to detect and reject contacts with highest interictal spiking activity. To keep 80% of the contacts, this (default) threshold was set to 8.4 spikes/min according to the output of the DELPHOS software with default parameters (see ‘Processing and selection of CCEPs’ section). To study the potential impact of this threshold, estimations of neuronal delays based on three more restrictive thresholds (respectively, 1, 2 and 4 spikes/min) were performed and compared to the estimations based on the default threshold (Supplementary Fig. 12). Results demonstrated that a higher number of data increases the convergence of the estimations across the different thresholds. With a higher threshold of 8.4 spikes/min, the greater presence of potentially pathological CCEPs was counterbalanced and attenuated by a higher number of CCEPs, which enabled us to almost provide whole-brain estimates.

Effect of the parcellation scheme

Parcellation schemes were used in the present study as a practical solution for presenting the results at the whole-brain level and for estimating differences between conditions (age of patients, tissue classification of contacts or spiking rate threshold). A parcellation scheme is optimal when its spatial resolution is sufficient to reflect the spatial variability present in the data and when adding new data has no more effect on the results (a stationary distribution is reached). In the present study, it also needs to adapt to the inhomogeneous spatial density of the recordings (see ‘Group-level analysis’ section). In this respect, the multimodal and functional HCP-MMP1 parcellation scheme was in good agreement with the resolution of our data for the mapping of synaptic time constants. This was evaluated by using two high resolutions of the multilevel Lausanne2008 parcellation, including, respectively, 235 and 464 parcels (Supplementary Fig. 9C and D), which showed results very similar to those obtained with the HCP-MMP1 parcellation, including 360 parcels (Fig. 6). For the mapping of axonal conduction delays, which uses number of parcels times more values than the mapping of synaptic time constants, the spatial resolution of the Lausanne2008-60 is already sufficient, in particular to study the influence of different conditions which systematically reduces the quantity of data available in each condition. Indeed, using a parcellation scheme with a higher resolution such as Lausanne2008-125 or HCP-MMP1 would imply having, respectively, nearly 3 and 7 times more parcel pairs to estimate than for Lausanne2008-60. The consequence of such a transition would be a reduction of the number of values available for each estimate, resulting in an increase of undocumented estimates and a loss of their precision. Thus, we have chosen to display in this report the data in the most appropriate parcellation schemes for a general presentation, but it should be noted that the F-TRACT atlas maps have been generated in multiple parcellation schemes that can be downloaded at f-tract.eu. For an appropriate use of the atlases, it is important to remember that, at the group level, a connection with a small probability (number of significant responses/number of stimulations), e.g. 0.2 or below, is indicative of an absence of connection.¹⁵ Axonal conduction parameter estimates in that case are thus likely to be less robust because they are estimated from fewer responses than in cases where connection probability is high.

Comparison with other approaches

Until recently, the standard way to estimate axonal velocities was to measure axonal diameters. Electron microscopy of histological sections has indeed proven to be efficient to characterize in vitro the distribution of axonal diameters both within non-human⁴⁰ and human⁹ brains. Based on anatomical and diffusion MRI and validated with histology, an alternative non-invasive methodology has been developed to characterize in vivo the geometrical properties of white matter fibres: axonal diameter,⁴¹ tract length⁴² and g-ratio.¹⁰ The accuracy of this technique mainly depends on reliable local estimates of axonal diameter, given its higher spatial variability compared to the g-ratio.⁴³ This approach estimated the axonal velocities in the human corpus callosum between 8 and 41 m/s (median: 14 m/s), which is compatible with our results at whole-brain level (Fig. 5). Even if these anatomy-based methods are very precise, they do not rely on the dynamics directly observed in brain signals. Measures from information theory are thus also relevant to characterize communication between brain regions. By extending the measure of transfer entropy between a source and a target, interaction delays can be taken into account during the causal modelling of the time series.⁴⁴ In turn, they can be precisely recovered, even from complex interacting conditions (reciprocal connections, multiple delays). This general formulation is particularly attractive because it can be applied to non-invasive electrophysiological signals, such as waveforms resulting from cortical MEG source reconstruction.⁴⁵ However, it lacks the important physiological distinction between axonal and synaptic propagation. It is important to underline that, here, although different neural models could have been suitably used,⁴⁶ we assumed a simple but robust three-population, convolution-based, neural mass model.¹⁷ Our aim was to adopt a compromise between biological realism and computational efficiency. However, given the uniqueness of the F-TRACT database, such modelling issues as the development and comparison of neural model architectures will undoubtedly be the matter of dedicated studies in the future.

Extension to the healthy population

Even if all CCEPs exhibiting epileptic activity (high interictal spiking rate, after discharges) were removed from our analysis (see ‘Processing and selection of CCEPs’ section), a crucial question is whether the estimation of neuronal parameters carried out on data from patients with epilepsy is valid for the healthy brain. Indeed, it remains unclear to what extent whole-brain long-range connectivity profiles (and axonal conduction delays) are affected. Using diffusion MRI tractography, a general decrease of structural connectivity in the connectome of patients with epilepsy was observed, while the connections intrinsic to the epileptogenic network, which are the ones mostly represented in our data, were spared.⁴⁷ A recent multimodal study embedded a neuronal model in the individual connectome of a patient with epilepsy in order to predict the spatio-temporal structure of seizure propagations.⁴⁸ It showed that, although the general topology of the connectivity matrix was very important, predictions were not significantly improved when the structural information was extracted from control subject’s anatomy instead. This indicated that the contained alterations of structural properties observed across patients with epilepsy, while still preserving the essential features intact, should not be considered as an obstacle to the extension of the present results to healthy subjects. From a neurophysiological point of view, some authors found that the early slow wave N1 component of CCEPs was not significantly altered in epileptogenic zones of hyper-excitability,²⁰ while other authors concluded that epilepsy could indeed affect the early part of the CCEP response, but only in the high-frequency domain.²¹ Local changes in cortical excitability (through synaptic properties) could, however, induce an increase in the amplitude of CCEPs recorded in ictal-onset regions while leaving the latencies unchanged.⁴⁹ Changes of functional connectivity are also not spread across all cortical connections, but are restricted to the epileptogenic zone and do not affect the propagation zone when compared to healthy tissue.⁵⁰ In addition, investigating fronto-temporal functional connections with 1-Hz electrical stimulation in a cohort of 51 patients with epilepsy, no difference was found between epileptogenic and non-epileptogenic hemispheres.⁵¹ The important (and still growing) number of patients included in the present work, the fact that a majority of the contacts may be located in non-epileptic tissues²⁴ and the variability in the localization of their epileptic foci should in principle also reduce the functional effects of the pathology. However, the question of an eventual impact of the pathology on the estimated neuronal parameters is an important one and we are currently investigating it in our group. Based on a similarity analysis of CCEPs characteristics, this dedicated study aims for an automatic detection (and removal) of abnormal contacts. This identification could in turn provide some hints about the structural and functional reorganization which occurred, with respect to the onset of the pathology. In our case, because we provided median values of neural parameters, the impact of outliers in parameter distributions was very limited.

Implications for neuronal modelling

Axonal and synaptic delays are essential for the emergence of (large-scale) synchronized oscillations, although their respective roles are not well understood.^52,53 When modelling the whole brain at a macroscale, both attributes of the space–time coupling (along with noise) are required to predict the functional connectivity and the spectral properties observed during resting state in EEG and blood oxygen level-dependent signals.^5,54 Similarly, in models of epileptic activity, the neuronal delays within implicated regions are determining factors for the spatial propagation and synchronization of fast oscillations at the seizure onset⁵⁵ or for the frequency of characteristic ictal patterns.⁵⁶ While axonal delays between brain areas are usually taken as discrete values (length of fibre × a constant uniform velocity), several studies have emphasized the importance of considering distributed axonal velocities in mean field models for a better prediction of spectral densities⁵⁷ and long-range propagation of cortical activity.⁵⁸ Likewise, a recent modelling study pointed out the key role of regional heterogeneity in excitatory and inhibitory synaptic properties to account for the wide repertoire of brain dynamics.⁵⁹ The estimation of neuronal delays that we provided in this study should therefore improve not only the physiological ground and validity of brain modelling approaches, but also the comprehension of neuronal mechanisms occurring during large-scale integration both in healthy and pathological conditions. In order to further progress in the understanding and characterization of the governing principles of brain network dynamics, future work should investigate how the different synaptic dynamics revealed by the present study are related to the hierarchical principles of a distributed brain organization, from the spatial heterogeneity of gene expression underlying cytoarchitecture, microcircuitry and functional segregation,⁶⁰ to the integration mechanisms taking place at the macroscale level. The F-TRACT atlas has been updated with the proposed methodology and provides dynamical information of human brain large scale connectivity at an unprecedented precision level. It can be downloaded from f-tract.eu/atlas and is regularly updated with novel data. It is in the process of being integrated to the Human Brain Project atlas on the EBRAINS platform as an interactive tool, offering the unique opportunity to be compared and integrated with other multimodal brain atlases (https://ebrains.eu/service/human-brain-atlas).

Funding

The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP/2007–2013)/ERC Grant Agreement No. 616268 F-TRACT, the European Union’s Horizon 2020 Framework Programme for Research and Innovation under Specific Grant Agreement No. 785907 and 945539 (Human Brain Project SGA2 and SGA3) and from the French ‘Investissements d’avenir’ programme under grant numbers ANR-11-INBS-0006 and ANR-10-IAIHU-06. P.H. was supported by Swiss National Science Foundation grant #CRSII5_170873.

Competing interests

The authors declare no conflict of interest.

Supplementary material

Supplementary material is available at Brain online.

Glossary

Abbreviations

CCEP

cortico-cortical evoked potential

DCM

dynamic causal modelling

SEEG

stereoelectroencephalography

Appendix 1

Full details are available in the Supplementary material.

F-TRACT consortium members: Claude Adam, Vincent Navarro, Arnaud Biraben, Anca Nica, Dominique Menard, Milan Brazdil, Robert Kuba, Jitka Kočvarová, Martin Pail, Irena Doležalová, François Dubeau, Jean Gotman, Philippe Ryvlin, Jean Isnard, Hélène Catenoix, Alexandra Montavont, Sylvain Rheims, Fabrice Bartolomei, Agnès Trébuchon, Aileen McGonigal, Wenjing Zhou, Haixiang Wang, Sinclair Liu, Zhang Wei, Zhu Dan, Guo Qiang, Hu Xiangshu, Li Hua, Hua Gang, Wang Wensheng, Mei Xi, Feng Yigang, Rima Nabbout, Marie Bourgeois, Anna Kaminska, Thomas Blauwblomme, Mercedes Garcés, Antonio Valentin, Rinki Singh, Liisa Metsähonkala, Eija Gaily, Leena Lauronen, Maria Peltola, Francine Chassoux, Elizabeth Landré, Philippe Derambure, William Szurhaj, Maxime Chochois, Edouard Hirsch, Maria Paola Valenti, Julia Scholly, Luc Valton, Marie Denuelle, Jonathan Curot, Rodrigo Rocamora, Alessandro Principe, Miguel Ley, Neurology Department, University Emergency Hospital, Bucharest, Romania: Ioana Mindruta, Andrei Barborica, Stefano Francione, Roberto Mai, Lino Nobili, Ivana Sartori, Laura Tassi, Louis Maillard, Jean-Pierre Vignal, Jacques Jonas, Louise Tyvaert, Mathilde Chipaux, Delphine Taussig, Philippe Kahane, Lorella Minotti, Anne-Sophie Job, Véronique Michel, Marie de Montaudoin, Jérôme Aupy, Viviane Bouilleret, Ana Maria Petrescu, Pascal Masnou, Claire Dussaule, Marion Quirins, Delphine Taussig, Carmen Barba, Renzo Guerrini, Matteo Lenge and Elisa Nacci.