Missing the trees for the forest: most subgroup analyses using forest plots at the ASCO annual meeting are inconclusive

Abstract

Background:

Oncologists often refer to forest plots to determine which patient subgroups may be more likely to benefit from a therapy tested in a randomized clinical trial (RCT). We sought to empirically determine the information content of subgroup comparisons from forest plots of RCTs.

Methods:

We assessed all forest plots from RCTs of therapeutic interventions presented orally at the American Society of Clinical Oncology Annual Meetings in 2020 and 2021. Subgroups were considered as showing evidence of treatment effect heterogeneity in forest plots when their confidence intervals (CIs) did not overlap with the vertical line corresponding to the main effect observed in the overall RCT cohort. Subgroups were considered as showing evidence of treatment effect homogeneity in forest plots when their CIs did not meaningfully differ, within 80–125% equivalence range, with the values compatible with the main effect. All other subgroups were considered as inconclusive.

Results:

A total of 99 forest plots were presented, and only 24.2% contained one or more subgroups suggestive of treatment effect heterogeneity. A total of 81 forest plots provided enough information to evaluate treatment effect heterogeneity and homogeneity. These 81 forest plots represented a total of 1344 individual subgroups, of which 57.2% were inconclusive, 41.1% showed evidence of treatment effect homogeneity, and 1.6% yielded evidence suggestive of treatment effect heterogeneity.

Conclusion:

The majority of subgroup comparisons were inconclusive in this empirical analysis of forest plots used in oncology RCTs. Different strategies should be considered to improve the estimation and representation of subgroup-specific effects.

Introduction

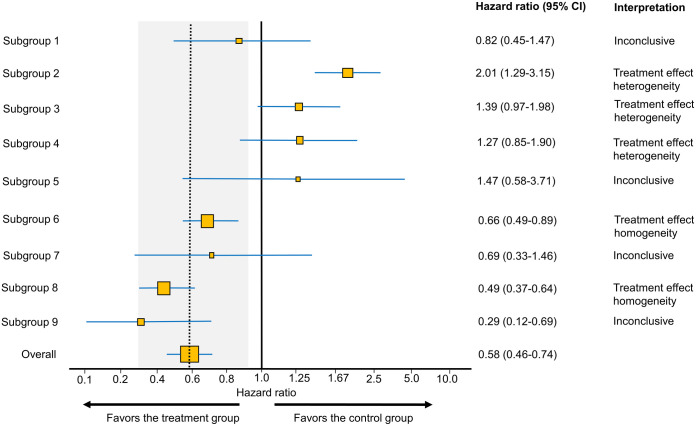
Oncologists are regularly tasked to make individualized recommendations for their patients using evidence derived from clinical trials. ¹ A key step toward this goal is to determine whether the estimated treatment effect in the overall trial cohort, also known as the ‘main effect’, varied in the subset of trial participants most relevant to the patient seen in the clinic. ² Forest plots are a commonly used tool to visualize and facilitate such subgroup comparisons in oncology clinical trials.^1,3 A common mistake when interpreting forest plots is to conclude that the treatment effect is not significant for subgroups with confidence intervals (CIs) that cross the vertical line corresponding to the null point of no effect, that is, 1.0 when the hazard ratio (HR) relative scale is used.^1,4,5 However, crossing the null point only means that the data for these subgroups were statistically compatible with no effect; the data may be equally or more compatible with many other values (Figure 1).^4,6

Figure 1.

Example forest plot looking at subgroup differences in hazard ratio (HR) estimates from a hypothetical randomized controlled trial of a new treatment versus control. The dotted vertical line highlights the overall treatment effect point, also known as the ‘main effect’. For each group of interest, the size of the yellow squares corresponds to the sample size, whereas the blue horizontal lines represent the 95% confidence interval (CI). The area shaded in gray represents the ‘indifference zone’ for the overall treatment effect, assuming that treatment effects between 80% and 125% of the 95% CI for the main effect do not represent clinically meaningful differences between each subgroup and the main effect. In this example, the 95% CI for the main effect HR is 0.46–0.74 corresponding to an indifference zone of 0.368–0.925. Accordingly, all subgroups with 95% CI that are only compatible with values within the indifference zone show treatment effect homogeneity. Subgroups with 95% CI that do not overlap with the dotted vertical line (main effect) show evidence of treatment effect heterogeneity. All other subgroups are inconclusive.

To facilitate interpretation of forest plots, Cuzick ⁵ proposed to de-emphasize the no-effect point and instead focus on the vertical line corresponding to the point estimate for the main effect. This is because the question clinicians are interested in when looking at forest plots is whether the treatment effect in a particular subgroup differs from the reported main effect. If the CIs of a subgroup do not cross the vertical line corresponding to the main effect, then this can serve as a signal of treatment effect heterogeneity that may merit further exploration.^1,3,5 More comprehensive subgroup analyses may include tests for treatment-by-subgroup interactions to formally determine whether the relative treatment effect, commonly expressed by HRs in oncology, varies across subgroups.^3,7–9 However, some guidelines recommend against the presentation of p values of treatment-by-subgroup tests for interaction in forest plots due to the risk of misinterpretation and type I error inflation from multiple comparisons. ¹⁰ However, the same concerns apply for the crude visualization of subgroup point estimates and their CIs in forest plots, with the added limitation that forest plots are less informative and less sensitive to potential signals of exploratory subgroup differences than full modeling for treatment-by-subgroup interaction effects. ³ Motivated by these considerations, we empirically evaluated the information content of forest plots in studies presented at the Annual Meeting of the American Society of Clinical Oncology (ASCO).

Methods

Study design and outcome definitions

We focused on the most recent ASCO Annual Meetings, 2020 and 2021, and evaluated all oral presentations (Plenary Sessions, n = 30, or Oral Abstract Sessions, n = 646). Presentations were included if they reported the results of a randomized clinical trial (RCT) that evaluated any therapeutic intervention (n = 147). We initially screened each presentation that met inclusion criteria for the presence of a forest plot, and if present, we descriptively characterized the forest plot using consistent terminology (Figure 1 and Supplemental File 1).

Although forest plots are based on refutational metrics naturally suited toward demonstrating treatment effect heterogeneity,^5,6,11 readers often seek to determine evidence of treatment effect homogeneity (i.e. lack of treatment effect heterogeneity) from forest plots. To facilitate this task, we developed a simple approach (see section on ‘Assessing treatment effect homogeneity in forest plots’ below for additional details) and calculator (Supplemental File 2) to estimate an ‘indifference zone’ of no clinically meaningful difference between the main effect and each subgroup visualized by a forest plot (Figure 1). We used indifference limits of 80–125% corresponding to the commonly used thresholds for bioequivalence and clinical equivalence. ¹² A subgroup comparison represented by a forest plot was accordingly deemed informative if it either (1) provided a signal of subgroup treatment effect heterogeneity compared with the main effect as evidenced by the subgroup CIs not overlapping with the main effect ⁵ (e.g. subgroups 2, 3, and 4 in Figure 1), or (2) indicated subgroup treatment effect homogeneity compared with the main effect as evidenced by the subgroup CIs being only compatible with values within the indifference zone (e.g. subgroups 6 and 8 in Figure 1). Forest plots providing no evidence of treatment effect heterogeneity or homogeneity were deemed inconclusive (e.g. subgroups 1, 5, 7, and 9 in Figure 1).

Assessing treatment effect homogeneity in forest plots

Theoretical considerations

In the frequentist approach most commonly used in forest plots, the point estimate is the value that the data are most compatible with the background statistical modeling assumptions. ¹¹ The subgroup CIs include all other values compatible with the data under the background assumptions at the specified confidence level, which is usually set at 95% confidence, corresponding to hypothesis tests at the 0.05 type I error alpha level.^11,13 The higher statistical uncertainty inherent in subgroup analyses can yield wide CIs that may include values compatible with favoring the treatment or control group and may include the null point. No meaningful conclusions can be drawn when the wide CIs of a subgroup cover divergent treatment effects. Conversely, a common error known as ‘second-order nullism’ is to conclude consistency of treatment effect between a subgroup and the overall cohort when the CIs of the subgroup do cross the vertical line at the main effect level. ¹⁴ This ‘absence of evidence is not evidence of absence’ fallacy is a more intricate, but equally incorrect version of first-order nullism whereby a large p value is thought to provide evidence in support of no treatment effect.^6,15 The wide CIs of patient subgroups may include treatment effect values that are not compatible with those included in the typically more narrow CIs of the overall trial cohort. Thus, accepting the null hypothesis of no difference between a subgroup and the overall cohort based on the lack of a statistical signal in noisy data obscured by random error may mislead researchers into failing to capture subtle, but real signals of treatment effect heterogeneity.^6,15,16 It is therefore more prudent to deem the results of such subgroups with wide CIs represented by forest plots as ‘inconclusive’.^1,4,14,17,18

First- and second-order nullism arise because frequentist metrics are naturally refutational and are thus well-suited to detecting signals of incompatibility with the tested hypothesis (usually the null hypothesis), such as the absence of treatment effect homogeneity.^6,11,19,20 Refutation of the null hypothesis of treatment effect homogeneity suggests the presence of treatment effect heterogeneity. On the other hand, determining the presence of treatment effect homogeneity is a more indirect task that typically requires first the specification of equivalence or noninferiority margins and then to show that the CIs of the subgroup of interest lie within these margins.^21,22 However, no such approach has been developed to date for forest plots of subgroup differences in RCTs, despite the clinical interest in this setting to detect signals of treatment effect homogeneity between subgroups and the main effect. To address this need, we developed a practical approach and calculator (Supplemental File 2) based on the estimation of indifference margins defining an ‘indifference zone’ of no clinically meaningful difference between the main effect and each subgroup visualized by a forest plot.

Indifference zone estimation

All indifference zone estimations are performed in the log-scale (additive scale) because modeling of relative treatment effect estimates, such as HRs, in RCTs is always done in this scale. The indifference zone can be specified based on clinically plausible indifference limits. For example, treatment effects that differ within 80–125% of each other are commonly considered to be clinically equivalent. At the HR scale, this corresponds to a HR for the main treatment effect being clinically meaningful when it is less than 0.8 or greater than 1.25. Note that the inverse of 0.8 (1/0.8) = 1.25 and thus specifying the lower indifference limit (e.g. 80%) will automatically yield the corresponding upper indifference limit (e.g. 125%). The 80–125% criterion is also typically used as the bioequivalence limit by the World Health Organization and the United States Food and Drug Administration. ¹² We accordingly used this limit to define the indifference zone used in the present study.

The point estimate and CIs of the overall group define the main treatment effect values that are most compatible with the observed data at the specified confidence level, which is usually set at 95% confidence. This defines the confidence margin that includes all values compatible with the data for the main treatment effect at the specified confidence level. The indifference zone is used to determine the treatment effect values that differ within 80–125% (or any other specified indifference limit) from the confidence margin of the main treatment effect. The specified indifference level i (e.g. 0.8, corresponding to 80%) and its inverse (e.g. 1/0.8 = 1.25, corresponding to 125%) is logarithmically transformed to the additive scale (log_e(i) and log_e(1/i), respectively). Log_e(i) is then added to the log-transformed lower bound of the main treatment effect CI to obtain the lower bound of the indifference zone, whereas log_e(1/i) is added to the log-transformed upper bound of the main treatment effect CI to obtain the upper bound of the indifference zone. The estimated lower and upper bounds of the indifference zone can then be exponentiated from the additive scale to the relative treatment effect scale commonly presented in forest plots.

Indifference zone calculator

We provide a simple calculator (Supplemental File 2) for readers to estimate the lower and upper bounds of the indifference zone for the main treatment effect presented in forest plots. The calculator allows the specification of the indifference level i (e.g. 80%) for relative treatment effect reduction and then estimates the corresponding indifference level 1/i (e.g. 125%) for relative treatment effect increase. The lower and upper bounds of the CI for the main treatment effect shown in the forest plot can then be inputted, and the calculator estimates the corresponding lower and upper bounds of the indifference zone, highlighted in red.

Results

The results are summarized in Table 1, and the detailed extracted features of each abstract are provided in Supplemental File 1. Almost half of the studies used forest plots for subgroup analyses, with some studies displaying more than one forest plot (31.4%). Most forest plots (85.9%) did not include a vertical line at the overall effect point estimate. Out of the 99 forest plots presented, only 24.2% showed one or more subgroups with evidence of treatment effect heterogeneity. Treatment effect homogeneity was not evaluable in 18/99 (18.2%) of forest plots presented, primarily because CI numerical values were not provided. Out of the 1344 individual subgroups presented in the 81 forest plots where both treatment effect heterogeneity and homogeneity were evaluable, 769 were inconclusive (57.2%), 553 indicated treatment effect homogeneity (41.1%), and only 22 yielded a signal suggestive of treatment effect heterogeneity (1.6%).

Table 1.

Descriptive analysis of forest plots presented at the 2020 and 2021 American Society of Clinical Oncology Annual Meeting.

Forest plot in presentation
Yes	70
No	77
Number of forest plots per presentation
1	48
2	17
3	3
4	2
Total number of forest plots analyzed	99
Treatment effect heterogeneity in any subgroup shown in each of the 99 forest plots (%)
Yes	24 (24.2)
No	75 (75.8)
Treatment effect heterogeneity in each individual subgroup shown in the 99 forest plots (%)
Yes	36 (2.2)
No	1576 (97.8)
Total number of forest plots evaluable for treatment effect homogeneity	81
Interpretation of each individual subgroup shown the 81 forest plots evaluable for homogeneity (%)
Homogeneity present	553 (41.1)
Heterogeneity present	22 (1.6)
Inconclusive	769 (57.2)
p-Values for interaction shown (%)
Yes	29 (29.3)
No	70 (70.7)
Vertical line at overall effect point estimate (%)
Yes	14 (14.1)
No	85 (85.9)
Statistical approach used (%)
Frequentist	99 (100)
Bayesian	0 (0)
Specified confidence level (%)
95%	95 (96.0)
Other	4 (4.0)
95% CI numerical value shown (%)
Yes	85 (85.9)
No	14 (14.1)
Forest plot endpoint (%)
OS	39 (39.4)
PFS	35 (35.4)
DFS	17 (17.2)
Other	8 (8.1)
Relative outcome scale (%)
HR	98 (99.0)
OR	1 (1.0)
Disease setting (%)
Metastatic	72 (72.7)
Adjuvant	24 (24.2)
Neoadjuvant	3 (3.0)
Type of intervention (%)
Immune checkpoint therapy	37 (37.3)
Targeted therapy	30 (30.3)
Chemotherapy	25 (25.3)
Hormone	3 (3.0)
Other	3 (3.0)
Procedural intervention	1 (1.0)
Cancer type (%)
Breast	18 (18.2)
NSCLC	15 (15.2)
Colorectal cancer	12 (12.1)
Other GI	12 (12.1)
Genitourinary	8 (8.1)
Malignant heme	8 (8.1)
Melanoma	6 (6.1)
SCLC	5 (5.1)
Gynecologic	5 (5.1)
HNSCC	4 (4.0)
Sarcoma	4 (4.0)
CNS	1 (1.0)
Other	1 (1.0)

CI, confidence interval; CNS, central nervous system; DFS, disease-free survival; GI, gastrointestinal; HNSCC, head and neck squamous cell carcinoma; HR, hazard ratio; NSCLC, non-small cell lung cancer; OR, odds ratio; OS, overall survival; PFS, progression-free survival; SCLC, small cell lung cancer; heme, hematology.

Discussion

Our results suggest that forest plots are commonly inconclusive when used to determine subgroup differences or similarities in treatment effect in oncology RCTs. This is despite the fact that our study used very lenient definitions for treatment effect heterogeneity and homogeneity. More specifically, we considered as positive any signal of treatment effect heterogeneity evidenced by the subgroup CIs not overlapping with the main effect ⁵ and defined our indifference zone for treatment effect homogeneity using the bioequivalence limits of 80–125% commonly used by the World Health Organization and the United States Food and Drug Administration and corresponding to the clinically meaningful HR limits of 0.8–1.25 typically used in RCTs. ¹² More strict definitions of treatment effect heterogeneity or more narrow bioequivalence limits would have yielded even higher numbers of inconclusive forest plots.

The statistical power of forest plots is reduced by the smaller sample sizes of each subgroup compared with the overall trial population. Given that the subgroup comparisons presented by forest plots are typically underpowered and often inconclusive, cautious interpretation in oral or written presentations should be promoted by journals, professional organizations, and regulatory bodies. In addition to the increased type II error probability due to low power, scanning through multiple subgroups in forest plots also increases type I error.^8,9 To reduce type I error, analyses for treatment effect heterogeneity should instead focus on prespecified biologically and clinically plausible subgroups. Statistical power can be improved by full treatment effect modeling that accounts for mediator-outcome confounding and preserves all information from continuous variables by flexibly incorporating them into the analysis model using approaches such as cubic splines.^1,17,23,24 Interpretation of forest plots can be facilitated by consistently including the vertical line corresponding to the point estimate for the main effect, ⁵ and by showing the indifference zone for treatment effect homogeneity using prespecified commonly accepted indifference limits such as 80–125%.

Limitations

We focused our analysis on studies presented at the last two annual ASCO meetings. The ASCO annual meeting is the largest multidisciplinary cancer conference where practice-changing findings from large RCTs are often first presented. Although physical attendance was limited by the COVID-19 pandemic, the 2020 and 2021 ASCO Annual Meetings were highly attended oncology gatherings, and the studies presented are reflective of contemporary oncology practice. Nevertheless, it is possible that the information content was different in forest plots used in previous years, other oncology meetings, journal publications, or different medical fields.

Conclusion

We have performed the first empirical analysis of the information content of forest plots used for subgroup comparisons of treatment effect heterogeneity or homogeneity and have found the majority of forest plots to be inconclusive. Different strategies may therefore be preferable to investigate treatment effect heterogeneity across trial participants.