Synchronous spiking of cerebellar Purkinje cells during control of movements

Significance

The information that one region of the brain transmits to another is usually viewed through the lens of firing rates. However, if the output neurons could vary the timing of their spikes, then, through synchronization, they would spotlight information that may be critical for control of behavior. Here we report that, in the cerebellum, Purkinje cell populations that share a preference for error convey, to the nucleus, when to decelerate the movement, by reducing their firing rates and temporally synchronizing the remaining spikes.

Abstract

The ability of the brain to accurately control a movement depends on the cerebellum. Yet, how the cerebellar neurons encode information relevant for this control remains poorly understood. The computations that are performed in the cerebellar cortex are transmitted to its nuclei via Purkinje cells (P cells), which are inhibitory neurons. However, if the spiking activity within P cell populations were temporally synchronized, that inhibition would entrain nucleus neurons, making them fire. Do P cells transmit information by synchronously timing their spikes? We simultaneously recorded from multiple P cells while marmosets performed saccadic eye movements, and organized the neurons into populations that shared a complex spike response to error. Before movement onset, this population of P cells increased their simple spike activity with a magnitude that depended on the velocity of the upcoming saccade, and then sharply reduced their activity below baseline at saccade onset. During deceleration, the spikes became temporally aligned within the population. Thus, the P cells relied on disinhibition, combined with spike synchronization, to convey to the nucleus when to decelerate and potentially stop the movement.

To understand how neurons in a region of the brain contribute to control of behavior, we typically search for correlates of the sensory and motor variables in the patterns of spikes. These patterns are usually quantified via average firing rates of neurons. However, there can be additional information in the timing of each spike, as exemplified by the independent rate and temporal codes in the hippocampus (1), the thalamus (2), and the somatosensory cortex (3). A central question is whether neurons use spike timing to transmit functionally relevant information from one region of the brain to another.

A special form of temporal coding is synchronization of spikes among a group of neurons. For example, synchronization among glutamatergic thalamic neurons increases the efficiency of driving postsynaptic neurons in the somatosensory cortex (4). Unlike the thalamus, the sole output from the cerebellar cortex is via GABAergic Purkinje cells (P cells). As a result, asynchronous activity of P cells inhibits the cerebellar nucleus neurons. Previous analysis of spike timing in individual P cells did not find evidence that timing of spikes affected the ongoing movement (5). Yet, there are specialized mechanisms in the cerebellar cortex that promote synchronization of nearby P cells (6). Indeed, ataxia and other cerebellar disorders may arise not because there are changes in the average firing rates of P cells (7, 8), but because there are disruptions in the timing of spikes. Does the cerebellum rely on spike timing within specific populations of P cells to transfer information from its cortex to its nuclei?

In principle, when a population of P cells synchronizes their spikes, they can drive cerebellar output in a way that is not possible via asynchronous spiking (9). For example, when P cells are synchronously stimulated (in slice, and anesthetized preparations), they entrain the downstream nucleus cell, transforming their inhibitory influence into production of spikes (10, 11). This raises the possibility that, analogous to the thalamic input to the cerebral cortex, P cells that belong to a specific population may rely on synchronization to convey information to the nucleus, possibly affecting a critical part of the ongoing movement (12).

Here, we focused on saccadic eye movements, because they are so brief as to preclude the possibility of sensory feedback, requiring the brain to rely entirely on its internal predictions (13–15). These predictions depend critically on the cerebellum (16, 17). For example, firing rates of populations of P cells, but not individual cells, predict the direction and velocity of the ongoing saccade (18, 19). However, to check for synchrony, we needed to simultaneously record from multiple P cells during saccades, something that, to our knowledge, had not been accomplished in any primate species.

Results

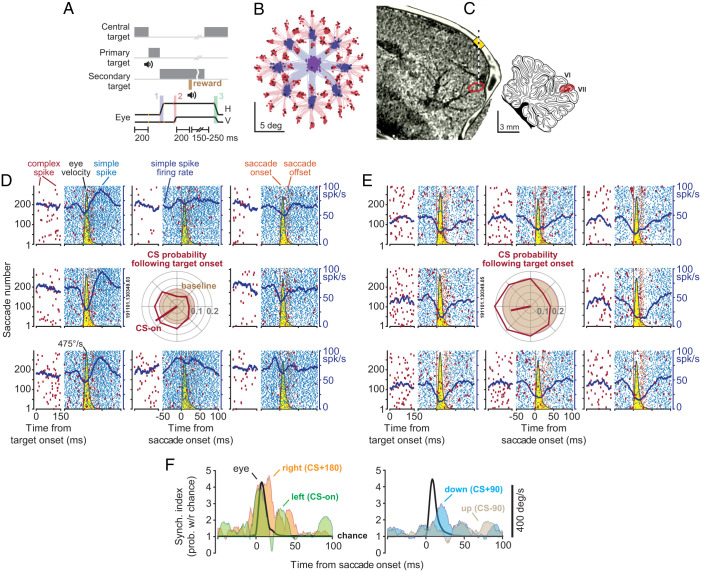
We focused on marmosets, a primate that, like macaques and humans, relies on saccadic eye movements to explore its visual scene, but is a fraction of the size of macaques, thus making it possible to record from the cerebellum using short, multichannel probes. We used MRI and CT-aligned maps of each animal’s cerebellum (20) to guide electrodes and recorded from P cells in lobules VI and VII of the vermis (Fig. 1C). Because there were no previous electrophysiological data from the marmoset cerebellum, we searched for saccade-related activity and found that P cells in the posterior part of lobule VI and the anterior part of lobule VII produced simple spikes (SSs) that were modulated during saccades. Thus, we focused on these regions and recorded from n = 149 well-isolated P cells (SI Appendix, Fig. S1 provides characteristics of the entire dataset). Crucially, our data included n = 42 pairs of simultaneously isolated P cells that were recorded from separate channels.

Fig. 1.

P cells synchronized their SSs during saccades. (A) Experimental paradigm. Marmosets were trained to make saccades to visual targets that appeared randomly at one of eight directions. Onset of the primary saccade (labeled 1 in the lowest trace) resulted in the replacement of the primary target with a secondary target, also at a random direction. Following the secondary saccade (labeled 2), and a fixation period, reward was delivered, and the center target was displayed, resulting in a centripetal saccade (labeled 3). (B) Eye position for the primary (blue) and secondary (red) saccades in a typical experiment. (C) We used the MRI and CT images of each animal to guide the electrodes to lobule VI or VII of the cerebellar vermis. (D and E) SCs (blue) and CSs (red) in two simultaneously recorded P cells during saccades to various directions. Eye velocity is shown in yellow. The CSs are also aligned to the onset of the visual target. Both cells exhibited a reduction in SSs during saccades, with a modulation pattern that lasted much longer than the saccade. CS probability during the 200 ms following target onset is quantified via the center subplot. Baseline CS probability is shown by the brown circle. The target direction that produced the highest CS probability (CS-on) is estimated by the red line. (F) Synchronization index during saccades to various directions. This index quantified the probability of synchronization with respect to chance at 1-ms time bins. Eye velocity is indicated by the black curve. Probability of synchronization is greatest for saccades in direction CS+180, reaching a peak at around saccade deceleration.

We trained the animals to fixate a central target and make a saccade to a primary target that appeared at random in one of eight directions (Fig. 1 A and B). At the onset of the primary saccade, the target was erased and replaced with a secondary target, also at a random location. Following a random period of fixation and delivery of reward, the secondary target was erased, the central target was displayed, and the trial restarted. Whereas production of saccades accompanied modulation of SSs, the random nature of the visual stimuli produced sensory prediction errors, promoting modulation of complex spikes (CSs) (18, 19, 21, 22).

Data from a pair of simultaneously recorded P cells are shown in Fig. 1 D and E. Despite their proximity (50 μm), one cell tended to pause its SS activity with saccades, while the neighboring cell tended to pause, then burst. Indeed, in both cells, the SSs remained modulated long after the saccade ended. However, when the target appeared to the left of the fovea, both P cells responded with an increased probability of CSs (Center Subplot of Fig. 1 D and E), and, when the target appeared to the right, both decreased their CS probability. Production of a CS in one P cell was followed by 10- to 20-ms suppression of SSs in that cell but not the neighboring cell (SI Appendix, Fig. S2 B and D). Interestingly, the SSs shared a degree of temporal coordination: The probability of observing an SS in P cell 2 in a 1-ms window of time increased by 39.3% if P cell 1 happened to generate an SS during the same period (SI Appendix, Fig. S2C).

To quantify spike coordination during saccades, we measured the probability of synchronization with respect to chance (6, 23). The synchronization index quantified the probability that both cells fired an SS during a 1-ms interval of time, corrected for the independent probabilities of spiking in each cell (all probabilities were conditioned on a saccade to a specific direction at time 0). Thus, the index determined whether there was greater synchrony than expected, where chance was quantified from the saccade-related changes in the average firing rates of each neuron.

Remarkably, while both cells reduced their firing rates during saccades, their spikes became more synchronized (Fig. 1F). Moreover, the probability of synchronization depended on the direction of the saccade: It was greatest when the saccade was toward the direction for which CSs were least likely (CS+180). In these two P cells, the probability of SS synchronization reached a maximum around the time when the saccade decelerated and came to a stop.

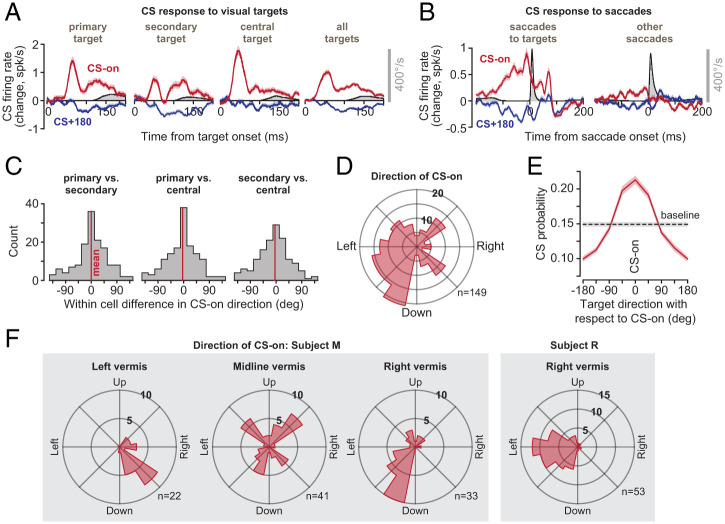
To analyze the data in our population, we began by measuring the CS response of each P cell to the various visual events (primary, secondary, or central target). For each event, we estimated the target direction that produced the largest CS probability (CS-on; Fig. 2A). We found that the direction of CS-on remained consistent across the various visual events (Fig. 2C; within-cell comparison of direction of CS-on in response to visual event type, primary vs. secondary target 0.1° ± 5.4° [SEM], t(148) = 0.03, P = 0.98; primary vs. central target −3.7° ± 5.2°, t(148) = −0.71, P = 0.48, secondary vs. central target −3.8°±5.3°, t(148) = −0.72, P = 0.47). Thus, we combined the CS response for all three visual events and used the results to define the CS-on direction of each P cell (Fig. 2A; all targets).

Fig. 2.

CSs were tuned with respect to the direction of the target, and this tuning was anatomically organized. (A) CS response aligned to target onset. For each target type, the direction of stimulus that produced the greatest probability of CS was labeled as CS-on. Eye velocity is shown in gray. (B) CS response aligned to saccade onset. Modulation of CS response was present before saccades that were visually instructed. The response was muted before other saccades. (C) Within-cell difference between CS-on directions as computed following the onset of the primary target, the secondary target, and the central target. We found no systematic differences in the estimate of CS-on between various types of targets, and thus combined the response for all targets to compute the CS-on of each P cell. (D) Distribution of CS-on across the population of P cells. (E) CS tuning function. (F) Distribution of directions of CS-on in various regions of the vermis in two animals. Error bars are SEM.

The distribution of CS-on directions across the P cells varied widely (Fig. 2D). However, the CS-on direction was not random. Rather, it varied with the location of the cell in the vermis: P cells in the left vermis tended to have rightward CS-on, while P cells on the right had leftward CS-on (Fig. 2F). When target directions were represented with respect to CS-on, the result was a unimodal tuning function that described the CS response of P cells following presentation of a visual target (Fig. 2E). The probability of CSs increased by 43.5 ± 2.6% (mean ± SEM) above baseline when the stimulus was presented in direction CS-on but decreased by 34.6 ± 1.7% below baseline when it was presented in direction CS+180.

Because each target instructed a saccade, we wondered whether the CS response was due to the sudden onset of the stimulus or associated with the movement that followed. Although our experiment was not designed to specifically answer this question, we made an interesting observation. Saccades that were made in response to visual targets were preceded with large changes in CS firing rates (Fig. 2B; saccades to targets). However, saccades that were not instructed by a target, but were in the same direction and amplitude, were preceded by significantly smaller modulation of CS firing rates (Fig. 2B; “other saccades,” average CS firing rate 50 ms before saccade onset in direction CS-on, paired t test, t(296) = 6.4, P = 5 × 10⁻¹⁰, direction CS+180, t(296) = −2.8, P = 0.005). Thus, CSs were modulated primarily in response to sensory events that instructed movements. This modulation was weak or missing when similar movements were made spontaneously.

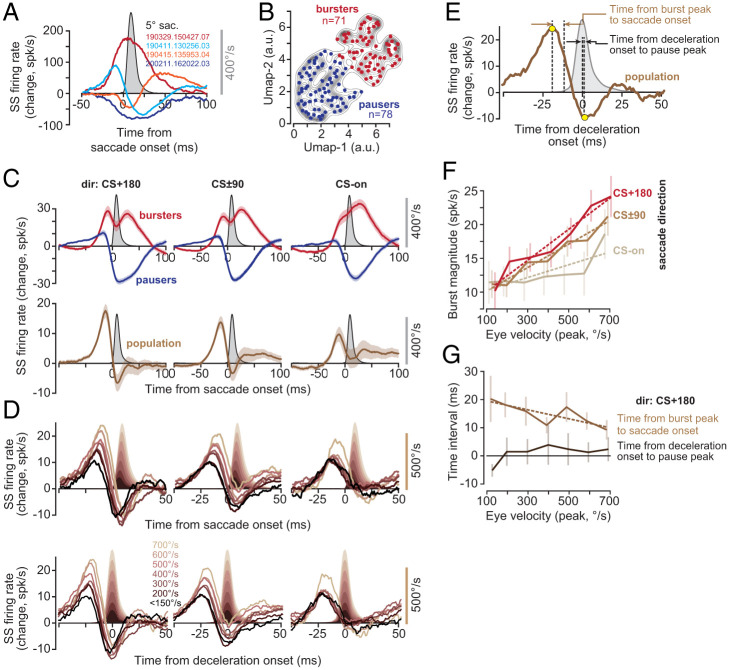
The SSs exhibited a variety of patterns during saccades: Some P cells increased their activity, some decreased their activity, while others produced more complicated patterns (Fig. 3A). Indeed, for some directions, a P cell might burst; for another direction, it might pause; and, for a third, it might produce a combination of the two. Regardless, in all cases, the modulation pattern continued long after the movement ended (SI Appendix, Fig. S3C). The activity patterns, averaged across all directions, did not separate the cells into clusters but rather formed a continuum (Fig. 3B). For the sake of labeling, we divided the P cells into two groups: pausers and bursters; 48% of our cells were bursters, while 52% were pausers. To quantify how well their activities were modulated during saccades, for each P cell, we measured the change in SS rates aligned to saccade onset and computed a z score (SI Appendix, Fig. S3A). Indeed, the P cell SS rates were modulated strongly during the movements (SI Appendix, Fig. S3B; z score 7.5 ± 0.3, mean ± SEM).

Fig. 3.

Population response of SSs encoded saccade direction, peak velocity, and the onset of deceleration. (A) Average change in the firing rates of four representative P cells with respect to baseline, during saccades (data collapsed across all directions). (B) Clustering of saccade-aligned change in firing rates for all P cells, using the algorithm UMAP (70). Separating the data into two clusters produces bursters (red) and pausers (blue). (C) Activities of the bursters and pausers during saccade in various directions. The population response is the sum of firing rates in all P cells. Top: Activities of the bursters and pausers during saccades in various directions. Bottom: The population response, i.e., the sum of the firing rate in all P cells. (D) Population response aligned to saccade onset and deceleration onset. The burst tends to grow with saccade velocity and shifts forward in time, but the pause remains invariant with respect to the onset of deceleration. (E) Quantification of the population response with respect to saccade kinematics. (F) Magnitude of the burst before saccade onset as a function of saccade peak velocity in various directions. (G) Timing of the burst with respect to saccade onset decreased with increased velocity. However, despite a sevenfold change in peak velocity, the timing of the pause with respect to deceleration onset remained invariant.

We next organized the P cells based on a computational model that incorporated an important anatomical feature of the cerebellum: P cells that have similar CS tuning not only receive similar olivary inputs, but they also are likely to be part of a single olivocerebellar module (24–29). To estimate activity of a population of P cells that belonged to an olivocerebellar module, we computed saccade direction with respect to the CS-on of each P cell. By using this coordinate transformation, we estimated the population SS response in a hypothetical olivocerebellar module when saccades were in direction CS-on, CS+90, etc. (Fig. 3C).

Activities of the bursters and pausers were modulated long after the saccade ended (Fig. 3 C, Top). However, when the activities across all cells were organized into a population and summed, the response exhibited a remarkable pattern: There was a burst that preceded saccades in all directions, followed by a modulation that ended near the conclusion of the saccade. For example, for direction CS+180, the burst was followed by a pause that ended as the saccade came to a stop (Fig. 3 C, Bottom). This burst–pause pattern was somewhat weaker for saccades in direction CS±90, and weaker still for saccades in direction CS-on.

The burst magnitude increased with the velocity of the impending saccade (Fig. 3D). However, the rate of increase as a function of velocity was direction dependent, showing the greatest gain for saccades in direction CS+180 (Fig. 3F; dir CS+180, F(1, 5) = 88.3, P = 0.0002). This pattern is called a gain field, confirming earlier findings in the macaque cerebellum (18). Thus, before saccade onset, the P cells appeared to inhibit the nucleus with a magnitude that depended on the velocity and direction of the forthcoming saccade.

In direction CS+180, the magnitude of the burst increased with saccade velocity, but its timing shifted forward: The period from the peak of the burst to the onset of the saccade (Fig. 3E) became smaller as saccade velocity increased (Fig. 3G; r² = 0.65, F(1, 5) = 9.4, P = 0.027). As the saccade started toward direction CS+180, the activity changed from a burst to a pause (Fig. 3D). However, unlike the burst that preceded the saccade, the pause magnitude and timing remained invariant with respect to saccade velocity (Fig. 3G, time of deceleration onset to pause peak as a function of velocity, F(1, 5) = 2.4, P = 0.18; Fig. 3D, rate of pause as a function of velocity, F(1, 5) = 1.1, P = 0.34). Critically, despite a sevenfold change in velocity, the timing of the maximum pause was unchanged with respect to the onset of saccade deceleration (Fig. 3G). Thus, with increased saccade velocity, the burst magnitude increased, and its timing shifted forward. However, regardless of saccade velocity, the pause that followed the burst was time-locked to the onset of saccade deceleration.

This invariant relationship between the timing of the pause in firing rates and the onset of saccade deceleration (in direction CS+180) raised the possibility that the P cells were signaling when the nucleus cells should fire, presumably stopping the saccade. However, entraining the nucleus neurons would be far more efficient if the P cells not only reduced their firing rates below baseline (disinhibiting the nucleus) but also synchronized their spikes (9, 10). To test this hypothesis, we computed the probability of synchronized firing in our population of simultaneously recorded P cells.

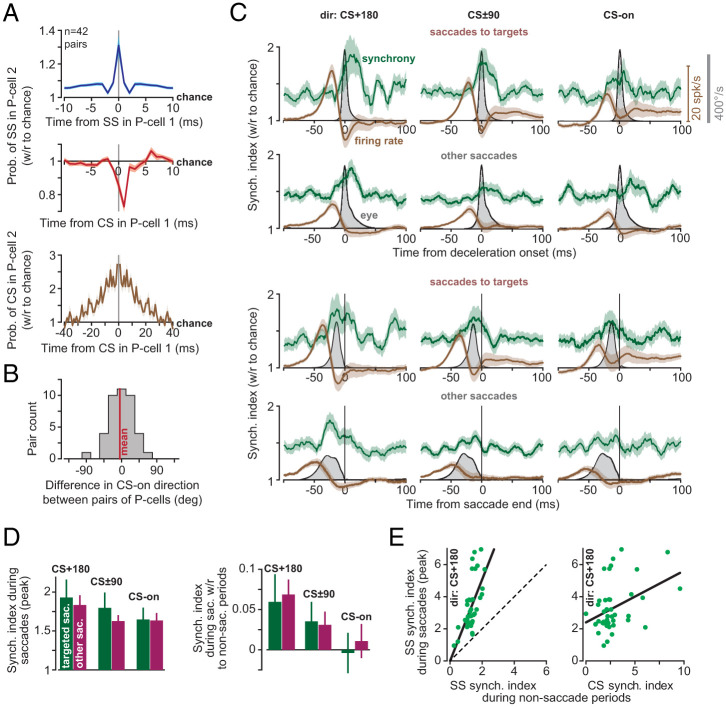
Our dataset included 33 recording sessions in which we simultaneously isolated two P cells, and 3 sessions in which we simultaneously isolated three P cells. These P cells were recorded by contacts that were within 100 μm of each other. Production of an SS in a P cell was associated with 31% increase in the probability (with respect to chance) that there would be a simultaneous (1-ms window) SS in another P cell (Fig. 4 A, Top). Similarly, production of a CS in a P cell increased the probability of observing a CS in another P cell at ±5-ms latency by 227% with respect to chance (Fig. 4 A, Bottom) (30). Finally, production of a CS in one P cell reduced the probability of SS in another P cell at 1-ms latency by 27% (Fig. 4 A, Middle). All of these observations are consistent with earlier findings in mice, demonstrating not only that nearby P cells share a degree of spike synchrony (6), but that a CS in one P cell can briefly suppress SSs in another P cell (31). The simultaneously recorded P cells tended to have very similar CS-on directions (Fig. 4B; between-cell difference −4.4° ± 6.3°). However, did the P cells synchronize their SSs during saccades?

Fig. 4.

P cells synchronized their spikes during saccade deceleration. (A) Probability of spike synchronization in pairs of P cells during the entire recording (41 ± 2 min, mean ± SEM). (Top) Probability of SS in P cell 2 at time point t (with respect to chance), given that an SS occurred in P cell 1 at time 0. (Middle) Probability of SS in P cell 2, given that a CS was produced in P cell 1 at time 0. (Bottom) Probability of CS in P cell 2 given that a CS was produced in P cell 1 at time 0. Bin is 1 ms. (B) Difference in CS-on directions among pairs of simultaneously recorded P cells. (C) Synchronization index (green) and firing rates (brown) for targeted saccades and other saccades. In the first and second rows, data are aligned to deceleration onset. In the third and fourth rows, data are aligned to saccade end. Firing rate is the population response. Bin size is 1 ms. (D) SS synchronization index during saccades (peak value) as a function of direction. (E) (Left) SS synchronization index during saccades (peak value) in direction CS+180, with respect to synchronization index as measured during nonsaccade periods. Dashed line is identity. (Right) Synchronization index during saccades with respect to CS synchronization index as measured during nonsaccade periods (1-ms bin for SS, and 10-ms bin for CS). Error bars are SEM.

Before saccade onset, there was a burst in the P cell population response. Despite this burst of activity, the probability of synchronization remained at baseline (Fig. 4C; note that before saccade onset synchronization was greater than chance because, at baseline, the neighboring P cells were more synchronous than chance). As the saccade started and then began to decelerate (in direction CS+180), the firing rates fell below baseline, but the synchronization index increased, reaching its peak probability after deceleration onset but before saccade end (2.3 ± 3.5 ms after deceleration onset and 5.2 ± 4.1 ms before saccade end). The synchronization index, averaged across the population, reached its peak value 13 ms before saccade end (Fig. 4 C, Third Row). That is, during saccade deceleration, the few spikes that remained were significantly more likely than chance to be synchronized.

Synchronization varied with the direction of the saccade: The greatest synchronization occurred in direction CS+180 (Fig. 4D; repeated measure ANOVA, significant effect of direction, F(2, 82) = 1,269.0, P = 0.021). As a result, the synchronization pattern was strongest in the direction in which the visual stimulus had the least probability of producing a CS.

We next considered task-irrelevant, spontaneous saccades that were not in response to the onset of a visual stimulus. In these saccades, the SS firing rates also exhibited a burst before saccade onset, with a magnitude that was largest for direction CS+180. The task-irrelevant saccades exhibited a synchronization that peaked around 20 ms before saccade end (Fig. 4 C, Fourth Row), with a probability that was largest for direction CS+180 (Fig. 4D). Thus, while CSs showed strong modulation before targeted saccades but not task-irrelevant saccades, SSs were modulated during all saccades. Indeed, regardless of whether saccades were target driven or not, SSs reached their greatest probability of synchrony as the movement decelerated and came to a stop.

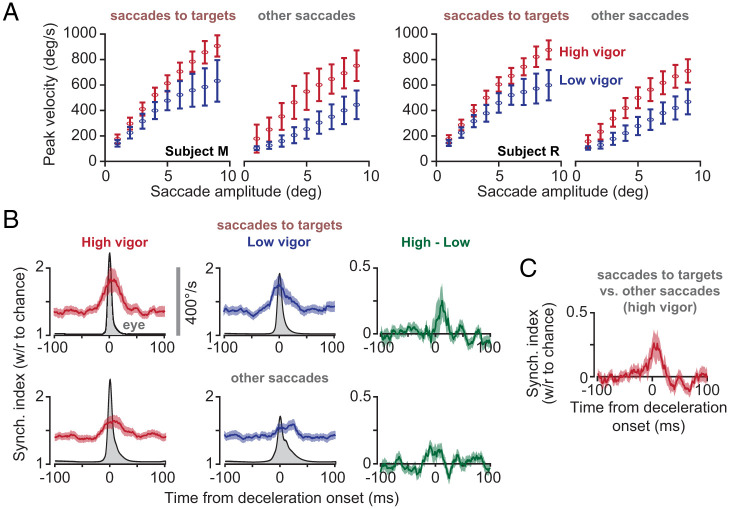
If synchronization of SSs is intended to entrain the nucleus neurons and is associated with saccade deceleration, then we would expect that there should be greater probability of synchronization for movements that required greater deceleration. To check for this, we separated high-velocity and low-velocity saccades, while normalizing for their amplitudes. We did this by fitting a hyperbolic function to the velocity–amplitude relationship, thus separating the high-vigor (i.e., high velocity) from the low-vigor saccades, while simultaneously controlling for amplitude (32–34) (Fig. 5A). We found that, both for saccades to targets and for spontaneous saccades, movements that exhibited greater velocity exhibited a small increase in probability of synchronization (Fig. 5A; within P cell pair change in synchronization index, targeted saccades, t (41) = 1.97 P = 0.055; spontaneous saccade, t (41) = 2.52 P = 0.016). Notably, the velocity-dependent change in synchronization index was present near the onset of deceleration.

Fig. 5.

Probability of synchronization increased with saccade velocity, and synchronization was more likely for saccades to targets. (A) For each animal and each type of saccade, we separated the movements based on their peak velocity and amplitude into high and low vigor. Error bars are SD. (B) High-vigor saccades exhibited a greater probability of SS synchrony than low-vigor saccades. Error bars are SEM. (C) A comparison of high-vigor saccades to targets vs. high-vigor other saccades. Amplitudes and velocities were larger for other saccades, yet saccades to targets were more likely to exhibit synchronization of SSs. Error bars are SEM.

While saccades toward visual targets had an inherent accuracy requirement, spontaneous saccades did not. Thus, we wondered whether the probability of synchronization was greater when the movement was aimed toward a visual target. High-vigor targeted saccades had smaller velocities and amplitudes than high-vigor other saccades (targeted: 4.2 ± 1.9° at 512 ± 185°/s; other: 5.7 ± 3.4° at 527 ± 239°/s, mean ± STD), yet the targeted saccades had a greater probability of synchronization (Fig. 5C; t (41) = 2.83, P = 0.0072).

Finally, we found that pairs of P cells that had greater CS synchrony, as measured during nonsaccade periods, tended to have greater SS synchrony during saccades (Fig. 4E; F(1, 40) = 7.6, P = 0.009). Pairs of P cells that had greater SS synchrony during nonsaccade periods also exhibited greater SS synchrony during saccades (Fig. 4E; F(1, 40) = 29.0, P = 3 × 10⁻⁶). However, the gain of the relationship between saccade period synchrony and general synchrony was significantly greater than one (F(1, 40)=10.7, P = 0.002). Thus, although the timing of SSs among nearby P cells was generally coordinated, during saccades, this coordination was greatly enhanced, especially during deceleration.

Control Studies.

To check whether the increased synchronization during saccades could be an artifact of the change in firing rates, we performed a simulation of spiking neurons that burst and paused like the cells in our population, but had independent probabilities of spike timing. This control condition produced a synchronization index that remained at chance during saccades (SI Appendix, Fig. S4), suggesting that changes in firing rates alone could not produce the observed increase in the synchronization index.

However, if there is a noise source that is common to both P cells, then there is a real risk that we will misestimate the amount of synchrony. In such a scenario, we record from neurons $S_1$ and $S_2$, but our recordings $\widetilde{S_1}$ and $\widetilde{S_2}$ are also picking up spikes generated by a third neuron $N$ (SI Appendix, Fig. S5A). If the P cells are well isolated, then this noise will be small. An empirical measure of this quality is $\text{Pr}(SS(t)|SS\left(0\right))$, which we plotted in SI Appendix, Fig. S5C for the n = 74 P cells that composed the n = 42 pairs. The probability of a spike at 1 ms is an estimate of the size of the noise. In our dataset, the median probability of noise that was common among pairs of simultaneously recorded P cells was 0.2 Hz. To check how this noise could have affected our estimate of synchronization index, we next performed a theoretical analysis.

We theoretically derived the relationship between the estimated synchronization index that we reported and the actual synchronization index. Suppose that the probability of spiking (in a 1-ms bin) for neurons $S_1$ and $S_2$ is $\alpha$ and $\beta$, and the probability of a spike from a noise source $N$ confounding both measurements is $\pi$. The estimated synchronization index $\widetilde{SI}$ is related to the actual index $SI$ via the following equality:

$$\widetilde{SI}=\frac{\left(1-\pi \right)\alpha \beta \times SI+\pi }{\left(\left(1-\alpha \right)\left(1-\pi \right)-1\right)\left(\left(1-\beta \right)\left(1-\pi \right)-1\right)}.$$ [1]

This equation predicts that, as the firing rates of neurons $S_1$ and $S_2$ decrease, presence of a common noise source will increase the estimated synchronization index (SI Appendix, Fig. S5B). This is alarming because, during saccades, as the firing rates fell below baseline, our estimated synchronization index increased above baseline. However, the theory also predicts that, as the firing rates of the two neurons increase, then the presence of the common noise source should reduce the estimated synchronization index (SI Appendix, Fig. S5D). Remarkably, before saccade onset, firing rates increased, but the synchronization index remained at baseline. This result was consistent for all directions of saccade. Thus, the crucial clue is that the increased firing rates before saccade onset did not produce a significant change in the synchronization index, providing evidence against the possibility of a significant source of common noise.

Discussion

In describing symptoms of cerebellar damage, Holmes (35) noted that “the most obvious errors are seen toward the end of the movement [during which] the speed of the affected limb is often unchecked until the object is reached or even passed.” For example, during an outward reach, many interposed nucleus neurons of the cerebellum produce their greatest discharge during deceleration, with spiking activity that plays a causal role in stopping the movement (36). Similarly, following inactivation of the fastigial nucleus, extraocular motoneurons that act as saccade agonists produce an abnormally large amount of activity during the deceleration period of ipsilateral movements (37), resulting in saccades that overshoot the target (38, 39). Thus, the computations that are performed by the cerebellar cortex are critical for monitoring the ongoing motor commands and predicting when the movement should be stopped. Yet, P cell SSs are often modulated long after the movement ends (40–44).

Here we found that, if P cells were organized based on their CS response to visual stimuli, their SSs as a population produced a burst–pause pattern that started before saccade onset and ended with saccade termination. The magnitude of the burst encoded the dynamics of the upcoming saccade: The burst became larger, and its timing shifted later, for larger velocity and greater amplitudes. However, the burst ended near saccade onset, and the firing rates sharply fell below baseline, arriving at a minimum value as the saccade began to decelerate. Even though, during this point in the movement, the P cells were producing fewer spikes than at baseline, these spikes were roughly twice as likely to be synchronized within the population. The resulting inhibition–disinhibition pattern of firing rates, coupled with spike synchronization, suggested that, following the onset of deceleration, the P cells attempted to entrain the nucleus neurons (9, 11, 45), potentially signaling when to stop the movement.

What is the behavioral consequence of this synchronization? The synchronization probability was greatest for saccades that were in the direction that coincided with the least probability of CSs (CS+180). For many types of behaviors, including eye lid conditioning, saccades, and limb movements, the CS tuning of a P cell is likely aligned with the direction of action of the downstream nucleus neuron (19, 46, 47). For example, in saccadic eye movements, trial-to-trial analysis of the effects of CSs on SSs and behavior suggests that P cells that have CS-on tuning for leftward end point errors project to nucleus neurons that have a downstream direction of action that indirectly promotes production of leftward forces (19), thus correcting for those errors. This implies that, during a saccade in direction CS+180, the increased synchrony combines with disinhibition (peak pause) to entrain the nucleus neurons during deceleration (9), producing downstream forces that are aligned with the CS-on of the parent P cells. As a result, the effect of synchronization of P cells, coupled with disinhibition of the nucleus, is likely to produce forces that oppose the direction of movement, bringing it to a stop.

One earlier work reported increased spike synchrony among P cells during movements. Using multiunit signals (i.e., not single unit isolation of spikes), Heck et al. (12) found increased covariance between P cells during reaching movements in rats. The authors reported that synchrony was most prominent as the hand approached the target, that is, during deceleration. Here, we found that P cell firing rates and spike synchrony were coordinated specifically in populations that shared a common CS tuning.

Our results were obtained in the marmoset, a New World primate that, like macaques and humans, relies on saccades to explore its environment. Like macaques, individual P cells in lobules VI and VII of marmosets produced SSs that were bursting, pausing, or a combination of the two, with no obvious relationship to the direction of the saccade or its velocity. However, following the onset of a visual stimulus, the P cells received information from the olive regarding the location of the stimulus with respect to the fovea, producing CSs that were tuned to the direction of the target. In both species, this tuning was anatomically organized, with P cells in the right vermis showing highest CS probability for targets to the left. A similar anatomical representation of contralateral stimuli/movements of the arm has recently been noted in the vermis of mice (48).

When we organized P cells based on their CS tuning, the SSs of P cells in both macaques and marmosets exhibited a consistent encoding of direction and velocity of movement (18, 19). Before saccade onset, the P cells produced a burst that increased with the velocity of the forthcoming saccade, with a gain that was highest when saccades were in direction CS+180. In both species, as the saccade started in direction CS+180, firing rates sharply fell below baseline, and then the modulation ended as the movement came to a halt. The consistency of these results across species suggests that viewing P cell activity through the lens of population coding (29), that is, a lens in which the climbing fibers organize the P cells into olivo-cerebellar modules (47, 49), may provide a key for unlocking the language with which the cerebellar cortex makes predictions.

How does SS synchronization arise during a specific phase of a movement? P cells that show elevated synchrony in their CSs also tend to fire more synchronous SSs (50, 51). We observed that P cells with greater CS synchrony in nonsaccade periods tended to have greater SS synchrony during saccades. In addition, we found that, following a CS in one P cell, after a 1-ms delay, there was a 1- to 2-ms period of SS suppression in the neighboring P cell, confirming recent findings in mice (31). This raises the possibility that P cells that receive a common input from the olive generate a synchronized CS, leading to SS suppression, which may then be followed by a synchronized resumption of SS firing (52). Indeed, in anesthetized animals, nearby P cells exhibit greater synchrony among SSs that start or end a pause period (53). However, we found that SS synchrony was greatest in direction CS+180, that is, the direction for which there was the smallest probability of CSs. Furthermore, whereas SSs showed synchronization for both targeted and task-irrelevant saccades, CSs were modulated only in response to target presentation. Thus, while P cells that exhibited CS synchrony also tended to have greater SS synchrony, we did not find evidence that, during saccades, CSs played a role in synchronizing SSs.

SS synchrony is present in P cells that are likely to have a common parallel fiber input (on-beam) but different climbing fibers (12, 54). Indeed, here we found not only that nearby P cells had greater than chance levels of synchrony but that cells with greater SS synchrony during nonsaccade periods had much greater than expected SS synchrony during saccades. Thus, it is possible that SS synchrony arises from a shared input from ascending granule cell axons that are positioned directly beneath the P cells and receive inputs from the same mossy fibers (12). However, how this synchrony is focused during the deceleration phase, particularly for saccades in direction CS+180, remains unknown.

Because granule cells also recruit molecular layer interneurons (55), synchronization of P cell SSs may be due to a network-wide organization in the cerebellar cortex that involves basket and stellate cells (56). The fact that, during saccades, SS synchronization is most likely when the P cell firing rates are suppressed below baseline suggests that, during deceleration, the molecular layer interneurons are playing a critical role in both reducing the P cell firing rates (57–61) and synchronizing the few remaining SSs (62). Molecular layer interneurons do play a critical role in controlling the timing of P cell SSs (61–63), but, to test whether they play a role in synchronizing P cells, it will be essential to record simultaneously from P cells and molecular layer interneurons during goal-driven movements such as saccades or reaching.

There are hints that major symptoms of cerebellar disease may be associated with disordered timing of P cell spikes. For example, in a form of ataxia that is caused by a genetic mutation in voltage-gated calcium channels, the average SS firing rates are unchanged, but spike timing is altered (8), particularly during visuomotor tasks (7). Drugs that help patients who suffer from nystagmus do not change average firing rates of P cells, but appear to restore spike timing (64).

In a typical artificial neural network, information transfer from one layer to the next is via firing rates of neurons. In these networks, learning modifies synaptic weights to change the activity of each neuron and minimize error in the output layer. The cerebellum resembles a three-layer network where learning is partially guided by climbing fibers (29, 65). Our results demonstrate that the information that is transmitted from the P cells to the nucleus is encoded in an exquisite coordination of firing rates and synchronization. This implies that, when there is an error, cerebellar learning cannot simply focus on changing the P cell firing rates. Rather, learning must also alter population-wide synchronization, perhaps through the interaction of climbing fibers with molecular layer interneurons (59, 66, 67). We speculate that, following an error, a CS should promote learning not only via suppression in the activity of individual P cells (19, 68, 69) but also via enhancement of synchronization among the population of P cells that share the same preference for error.

How does SS synchronization arise during movements? Is ataxia partly due to disruption of synchronization? Does learning from error cause changes in synchronization? These are some of exciting new directions for future research.

Methods

Neurophysiological data were collected from two marmosets (Callithrix Jacchus, male and female, 350 g to 370 g, subjects M and R, 6 y old). The marmosets were born and raised in a colony that Xiaoqin Wang has maintained at the Johns Hopkins School of Medicine since 1996. The procedures on the marmosets were evaluated and approved by the Johns Hopkins University Animal Care and Use Committee in compliance with the guidelines of the US NIH.

Data Acquisition.

Following recovery from head-post implantation surgery, the animals were trained to make saccades to visual targets and rewarded with a mixture of applesauce and laboratory diet (20). Visual targets were presented on an LCD screen (Curved MSI 32” 144 Hz, model AG32CQ) while binocular eye movements were tracked using an EyeLink-1000 eye tracking system (SR Research). Timing of target presentations on the video screen was measured using a photodiode.

We used the MRI and CT imaging data for each animal and designed an alignment system that defined trajectories from the burr hole to various locations in the cerebellar vermis, including points in lobules VI and VII. We used a piezoelectric, high-precision microdrive (0.5-μm resolution) with an integrated absolute encoder (M3-LA-3.4-15 Linear smart stage, New Scale Technologies) to advance the electrode.

We recorded from the cerebellum using four types of electrodes: quartz insulated four-fiber (tetrode) or seven-fiber (heptode) metal core (platinum/tungsten 95/05) electrodes (Thomas Recording), and 64-channel checkerboard or linear high-density silicon probes (M1 and M2 probes, Cambridge Neurotech). We connected each electrode to a 32- or 64-channel head stage amplifier and digitizer (RHD2132 and RHD2164, Intan Technologies), and then connected the head stage to a communication system (RHD2000 Evaluation Board, Intan Technologies). Data were sampled at 30 kHz and band-pass filtered (2.5 kHz to 7.6 kHz). We used OpenEphys (70), an open-source extracellular electrophysiology data acquisition software, for interfacing with the RHD2000 system and recording of signals. We used P-sort (71) to identify the SSs and CSs in the heptodes and tetrodes recordings, and used Kilosort and Phi (72) to identify the spikes for the silicon probes.

Behavioral Protocol.

Each trial began with fixation of a center target for 200 ms, after which a primary target (0.5° × 0.5° square) appeared at one of eight randomly selected directions at a distance of 6.5°. Onset of the primary target coincided with presentation of a distinct tone. As the animal made a saccade to this primary target, that target was erased, and a secondary target was presented at a distance of 2° to 2.5°, also at one of eight randomly selected directions. The subject was rewarded if, following the primary saccade, it made a corrective saccade to the secondary target, landed within 1.5° radius of the target center, and maintained fixation for at least 200 ms. Onset of reward coincided with presentation of another distinct tone. Following an additional 150- to 250-ms period (uniform random distribution), the secondary target was erased, and the center target was displayed.

Data Analysis.

All saccades, regardless of whether they were instructed by presentation of a visual target or not, were identified in the behavioral data using a velocity threshold. Saccades to primary, secondary, and central targets were labeled as targeted saccades, while all remaining saccades were labeled as task-irrelevant, “other saccades.” For the targeted saccades, we computed the neurophysiological response to the presentation of the visual stimulus, as well as the response to the onset of the saccade. To compute the visual response to the secondary target, we aligned the data to the offset of the preceding primary saccade, thus producing the data in Fig. 2A (secondary target). For other saccades, there were no visual targets, and thus the response was aligned only to saccade onset.

SS and CS baseline firing rates were computed by dividing the total number of spikes by the duration of the entire recording. SS and CS instantaneous firing rate were calculated from perievent time histograms with 1-ms bin size. Events of interest included visual events (target onset), saccade onset, deceleration onset, and saccade offset. We used a Savitzky–Golay filter (second order, 31 datapoints) to smooth the traces for visualization purposes.

CS tuning was computed by measuring the CS probability following target onset as a function of target position with respect to the actual position of the eyes. We counted the number of CSs after target onset up to saccade onset or a fixed 200-ms window, whichever happened first. This approach ensured that the CSs during saccades or after saccade offset were not included in the measurements. Dividing the spike count by the number of events resulted in the CS probability in each direction.

Suppression duration of SSs following a CS (SI Appendix, Fig. S1C) was computed by measuring the period during which the SSs recovered 63% of their precomplex spike firing rate.

To compute population response during saccades, we began by computing the change in SS firing rate of each P cell with respect to its baseline. Next, we labeled each saccade by measuring its direction of movement with respect to the CS-on of the recorded P cell. Finally, we summed the activities in all P cells (i.e., changes with respect to baseline) for saccades in direction CS-on, CS+45, etc., using a bin size of ±25°.

Analysis of the Simultaneously Recorded P Cells.

Multichannel electrodes allowed for analysis of simultaneously recorded neurons. However, spiking activity in one neuron can easily influence the data recorded by two nearby channels, thus giving an illusion that the two channels are picking up two distinct neurons. To guard against this, after we sorted the data in each channel, we waveform triggered the data recorded by channel A by the spikes recorded on channel B. This identified the waveform of the neuron recorded by channel B on the spike recorded on channel A. We compared this cross-channel triggered waveform with the within-channel triggered waveform generated by the spikes recorded by channel A. The cross-channel triggered waveform must produce a different cluster of spikes in A than the main neuron isolated by A. If there were spikes that occurred within 1 ms of each other on channels A and B, we used these coincident-spike events to trigger the waveform in A. The spikes in A that were identified to be coincident with B should look approximately the same as the noncoincident spikes in A. Examples of this approach are provided in Sedaghat-Nejad et al. (20).

To quantify coordination between activities of two P cells, we computed joint probabilities, corrected for chance (6, 23). We computed$\mathrm{Pr} (S2\left(t\right),S1\left(0\right))/(\mathrm{Pr} \left(S2\right)\mathrm{Pr} \left(S1\right))$, which is equal to $\mathrm{Pr} (S2\left(t\right)|S1\left(0\right))/(\mathrm{Pr} \left(S2\right))$. This quantified whether the occurrence of an SS on channel 1 at time 0 altered the probability of SSs on channel 2 at time t, corrected for probabilities expected from their average firing rates. Because channel labels 1 or 2 are interchangeable, we considered the average of the two cases as the corrected conditional probability for a pair of P cells. We implemented a similar analysis to quantify the coordination between CSs in two cells, or CSs in one cell and SSs in another cell.

To compute the probability of synchronization of SSs during saccades, we began by computing the joint probability of spiking at time t, given that a saccade took place at time 0 in a particular direction, $\mathrm{Pr} (S1\left(t\right),S2\left(t\right)|\mathit{sac}\left(0\right))$. To correct for the fact that firing rates changed during the saccade, we divided the joint probability by the independent probabilities of spike production in each cell, measured when a saccade took place in the given direction at time 0. Thus, the synchronization index was defined, for each saccade direction, as

$$SI=\frac{\text{Pr}\left(S1\left(t\right),S2\left(t\right)\mid sac(0)\right)}{\mathrm{Pr} \left(S1\left(t\right)\text{|}\mathit{sac}\left(0\right)\right)\text{Pr}(S2(t)|\mathit{sac}\left(0\right))}.$$ [2]

Sensitivity Analysis of Synchronization Index to Confounding Noise.

An important concern regarding synchrony analysis is its sensitivity to erroneous spike sorting. The main source of misattributed synchrony comes from a confounding source of noise from a third cell contaminating spike sorting of a pair of cells. In such a scenario, we record from neurons $S_1$ and $S_2$, but our recordings $\widetilde{S_1}$ and $\widetilde{S_2}$ are also picking up spikes generated by a third neuron $N$ (SI Appendix, Fig. S5A). We performed empirical and theoretical analysis to quantify the size of this common noise source in our data, and then estimated how much this noise might have affected our measurement of synchrony.

As we will see below, there is a real danger that we will overestimate synchrony when firing rates fall. However, the empirical data on the goodness of cell isolation, coupled with the fact that synchrony did not change when firing rates increased, provided some assurance that our estimates of synchrony were close to the truth.

Let binary random variables $S_1,S_2$ represent occurrence of spikes in P cell 1 and P cell 2, respectively. Now let an independent source of spiking noise $N$ confound both P cells. Our contaminated measurements are described as

$$\widetilde{S_1}=S_1\vee N$$ [3]

$$\widetilde{S_2}=S_2\vee N.$$ [4]

In the above expression, the operator $\vee$ represents the logical OR. Now let $\mathrm{Pr} \left(N=1\right)=\pi$, $\mathrm{Pr} \left(S_1=1\right)=\alpha$, and $\mathrm{Pr} \left(S_2=1\right)=\beta$. We are interested in describing the effects of the noise source $N$ on corrupting the real synchronization index $SI$ to produce our estimated synchronization $\widetilde{SI}$.

We can compute the probability of assigning a spike to neuron 1, that is, $\mathrm{Pr} \left(\widetilde{S_1}=1\right)$, as a function of its probability of spiking, plus the probability of spiking in the noise source,

$$\begin{array}{c}\mathrm{Pr} \left(\widetilde{S_1}=1\right)=\mathrm{Pr} \left( S_1=1,N=1\right)+\mathrm{Pr} \left( S_1=0,N=1\right)+\mathrm{Pr} \left( S_1=1,N=0\right)\\ \mathrm{Pr} \left(\widetilde{S_1}=1\right)=\alpha \pi +\left(1-\alpha \right)\pi +a\left(1-\pi \right)\\ \mathrm{Pr} \left(\widetilde{S_1}=1\right)=\left(1-\pi \right)\alpha +\pi .\end{array}$$ [5]

Similarly, we can compute the probability of assigning a spike to neuron 2.

$$\mathrm{Pr} \left(\widetilde{S_2}=1\right)=\left(1-\pi \right)\beta +\pi .$$ [6]

The joint probability of these spikes is defined as either that the noise source produced a spike or that there were spikes in both recorded neurons,

$$\mathrm{Pr} \left(\widetilde{S_1}=1, \widetilde{S_2}=1\right)=\left(1-\pi \right)\mathrm{Pr} \left(S_1=1,S_2=1\right)+\pi .$$ [7]

We can describe the estimated synchrony index $\widetilde{SI}$ as a function of the true synchronization index $SI$,

$$\widetilde{SI}=\frac{\left(1-\pi \right)\alpha \beta \times SI+\pi }{\mathrm{Pr} \left(\widetilde{S_1}=1\right)\mathrm{Pr} \left(\widetilde{S_2}=1\right)}.$$ [8]

SI Appendix, Fig. S5B illustrates how the estimated synchronization index $\widetilde{SI}$ will change for common ranges of SS rates as a function of noise probability. The results illustrate that the estimated synchrony has high sensitivity to noise probability. Importantly, this sensitivity is higher for lower values of SS rate. Thus, when there is common noise, the estimated synchrony will, in general, be greater than the actual synchrony. As a sanity check, we find that

$$\begin{array}{c}\underset{\pi \to 0}{\lim }\widetilde{SI}=SI,\\ \underset{\pi \to 1}{\lim }\widetilde{SI}=1.\end{array}$$

How much noise did we have in our dataset? The confounding noise probability ($\pi$) is bounded by the goodness of isolation of each P cell. This contamination in each P cell can be estimated using the samples violating the refractory period in the autocorrelogram plots (SI Appendix, Fig. S5C). The noise probability $\pi$ is the joint probability of contamination in the pair, and is bounded by the smaller contamination probability. To estimate the confounding noise for each pair, we bounded $\pi$ as follows:

$$\begin{array}{c}{\text{π}}_1=\mathrm{Pr} \left(\widetilde{S_1}\left(t\le 1ms\right)=1\text{|}\widetilde{S_1}\left(0\right)=1\right)\\ \pi \le \text{min}({\pi }_1,{\pi }_2).\end{array}$$

Because our P cells were well isolated, we observed a very small amount of contamination noise (median ± median absolute deviation [MAD]: 0.19 ± 0.17 Hz). SI Appendix, Fig. S5C shows the average and SD of cross-probability of 74 P cells forming 42 pairs and the distribution of the defined bound on the probability of the confounding noise. The median of the noise firing rate was less than 0.2 Hz.

Next, we used the theoretical result in Eq. 8 to test the validity of our claim regarding low noise levels. We had found that, prior to saccade deceleration, the P cell population had exhibited an increase in firing rates. Critically, this change in firing rates did not accompany a change in the synchrony index (Fig. 4C). We evaluated Eq. 8 for $SI=1.5$ and firing rates in the range 50 Hz to 100 Hz in the presence of varying amounts of confounding noise. We found that, for confounding noise as small as 1 Hz, an increase in the rate of firing in P cells must lead to a significant decrease in $\widetilde{SI}$, which is intuitive in a manner that an increase in the P cell rate ($S_1$) reduces the effect of confounding noise ($N$) on the observed spike ($\widetilde{S_1}$). Hence, if the increase in the synchrony index during deceleration phase was due to significant confounding noise, we must also see a decrease in the synchrony index prior to the deceleration phase due to the increase in firing rates. However, this decrease was not observed. This observation was consistent in all saccade directions, despite the significant increase in the SS rate (Fig. 4). Thus, the empirical data, combined with theoretical analysis, provided evidence that the increase in synchrony observed during deceleration was unlikely to be have been due to a common noise source.

Modulation of Synchrony as a Function of Saccade Velocity.

We asked whether the probability of synchronization differed between high- and low-velocity saccades. However, to compare saccades, we first had to normalize for saccade amplitude. To do this, we relied on previous work that defined high- and low-vigor movements as a function of movement amplitude (32–34, 73, 74). If saccade amplitude is $x$ and the peak velocity of that saccade is $v$, then, for each subject, the relationship between the two variables is

$$v=\alpha \left(1-\frac{1}{1+\beta x}\right).$$ [9]

In the above expression, $\alpha ,\beta \ge 0$ and are subject-specific parameters. These parameters are reported in SI Appendix, Fig. S6 for each animal. The scaling parameter $\alpha$ was not significantly different for saccades to targets vs. other saccades, while parameter $\beta$ was significantly larger for saccades toward targets, indicating that saccades to targets had an overall higher vigor.

For a saccade with amplitude $x$, its vigor was defined as the ratio of the expected value of its peak velocity with respect to the actual peak velocity, that is, $E\left[v(x)\right]/v$. When vigor was greater than one, the saccade had a peak velocity that was higher than the mean value associated with this amplitude. Thus, we defined high-vigor saccades as those that had a vigor greater than one. This procedure divided saccades into groups of high vigor and low vigor (percentage of high-vigor saccades: saccades to targets, 48.25 ± 1.07%; other saccades, 49.4 ± 2.34% for n = 42 pairs). By design, the amplitudes of the low- and high-vigor saccades were comparable (saccades to targets: high vigor, 4.25 ± 0.45°, vs. low vigor, 3.95 ± 0.36°; other saccades: high vigor, 5.34 ±0.88°, vs. low-vigor, 5.13 ± 0.76°).

Because estimation of synchrony index required a large number of trials, we combined all saccade directions, divided them into high and low vigor, and then evaluated the synchrony index for pairs of simultaneously recorded P cells (Fig. 5). We ensured that this division into low and high vigor did not produce a preference for saccades toward one direction or another.

Can Changes in Synchrony Be due to Changes in Firing Rates?

To check whether the increased synchronization index during saccades was an artifact of the change in firing rates of P cells, we performed a simulation of spiking neurons that burst and paused like cells in our population but had independent probabilities of spike timing. We predefined the firing rate pattern for 11 hypothetical neurons all with a 60 spike per s baseline firing rate (SI Appendix, Fig. S4A) and then added a 130-ms duration modulation. The result produced a population response firing pattern that mimicked the firing rate pattern of P cells in our dataset (SI Appendix, Fig. S4B). Using a Bernoulli process and predefined waveform of firing rates, we simulated the spiking activity for the 11 hypothetical neurons for 1,000 trials. Next, we used the methods described above to compute the estimated firing rate of each cell and the population response (SI Appendix, Fig. S4B). Finally, we computed the joint probability as well as the synchronization index between 55 (two choose 11) pairs of cells. Our results confirmed that the joint probability was modulated according to the change in firing rates in the population of cells. However, because the spike timing in our simulation was independent for each neuron, the synchronization index stayed at chance level.

Data Availability

Neurophysiology and behavior data have been deposited in Open Science Framework (https://osf.io/xhbya/, DOI 10.17605/OSF.IO/XHBYA).