Significance
The endoplasmic reticulum (ER) and the microtubule (MT) cytoskeleton form a coextensive, dynamic system that pervades eukaryotic cells. The shape of the ER is generated by a set of evolutionarily conserved membrane proteins that are able to control ER morphology and dynamics independently of MTs. Here we uncover that the molecular machinery that determines ER network dynamics can influence the subcellular distribution of MTs. We show that active control of local ER tubule junction density by ER tethering and fusion is important for the spatial organization of the combined ER–MT system. Our work suggests that cells might alter ER junction dynamics to drive formation of MT bundles, which are important structures, e.g., in migrating cells or in neuronal axons.
Keywords: endoplasmic reticulum, microtubules, cellular organization, microtubule bundles
Abstract
The dynamic distribution of the microtubule (MT) cytoskeleton is crucial for the shape, motility, and internal organization of eukaryotic cells. However, the basic principles that control the subcellular position of MTs in mammalian interphase cells remain largely unknown. Here we show by a combination of microscopy and computational modeling that the dynamics of the endoplasmic reticulum (ER) plays an important role in distributing MTs in the cell. Specifically, our physics-based model of the ER–MT system reveals that spatial inhomogeneity in the density of ER tubule junctions results in an overall contractile force that acts on MTs and influences their distribution. At steady state, cells rapidly compensate for local variability of ER junction density by dynamic formation, release, and movement of ER junctions across the ER. Perturbation of ER junction tethering and fusion by depleting the ER fusogens called atlastins disrupts the dynamics of junction equilibration, rendering the ER–MT system unstable and causing the formation of MT bundles. Our study points to a mechanical role of ER dynamics in cellular organization and suggests a mechanism by which cells might dynamically regulate MT distribution in, e.g., motile cells or in the formation and maintenance of neuronal axons.
The microtubule (MT) cytoskeleton is essential for cellular organization. Interphase MTs are critical for membrane traffic, cellular morphology, and cell polarity (1, 2). MTs are also actively involved in distributing membrane-bound organelles, including the endoplasmic reticulum (ER), mitochondria, and the Golgi apparatus (3). To fulfill these important functions in the dynamic organization of the cell, the position of the MT cytoskeleton needs to be actively controlled. While nucleation at the MT organizing center (MTOC), MT growth dynamics, and the interaction with other cytoskeletal elements as well as with components of the polarity machinery are well understood, it remains largely unknown how cells are able to exert control over the organization of polymerized MTs during interphase. In particular, it remains largely unexplored whether and how the physical interplay with large membrane-bound organelles such as the ER plays a role in the spatial distribution of the MT system.
The peripheral ER is a continuous network of membrane tubules and sheets that spans the cytoplasm of eukaryotic cells and is physically connected with MTs (4–7). The high membrane curvature seen in cross-section of ER tubules and sheet edges is stabilized by members of the reticulon and REEP protein families (8–10), and the tubules are connected at three-way junctions (3WJs). In metazoans, membrane tethering and fusion during 3WJ formation is mediated by ER resident dynamin-like GTPases called atlastins (ATL1 to ATL3) (11–13). Newly generated 3WJs appear to be stabilized by lunapark (LNP), yet another evolutionarily conserved ER membrane protein (11–13). Loss of ATL function leads to a reduction in 3WJs and the formation of long unbranched ER tubules (14, 15) and results in a pronounced change of ER distribution in the cell.
The initial understanding of mechanisms determining ER morphology has to a large extent been based on in vitro work with Xenopus egg extracts (10, 16–19). Over the past decade, ER network reconstitution experiments with purified components (20–25) have provided key insights into the function of the proteins that are involved in network formation and maintenance (23–30). A central result of these studies indicates that ER network formation is possible with a minimal set of ER membrane proteins and that the cytoskeleton is not strictly necessary (23).
Within living cells, the ER is an extremely dynamic organelle, and its shape is continuously remodeled (5, 31–35). In this context, the ER shaping machinery is obviously required, but the interaction with the MT cytoskeleton is equally important. For example, new ER tubules can be formed by ER sliding, when motor proteins pull on the ER along MTs (34). In addition, ER tubules are pulled out by attaching directly to the growing plus-ends of MTs, which are marked by the evolutionarily conserved plus-end tracking proteins (+TIP) called end binding proteins (EB1 to EB3) (34, 36–38). Finally, a vast number of ER factors have been shown to interact with the MT cytoskeleton, including some of the ER tubule and sheet stabilizing proteins, such as members of the REEP family and CLIMP-63, respectively (39–41). Therefore, the MT cytoskeleton exerts a considerable mechanical influence on the ER and has an important role in the dynamic distribution of this elaborate membrane system in the cell (7, 42).
Given the extensive mechanical coupling between the ER network and the MTs, independent modulation of ER structure by the ER-shaping proteins may arguably have an important reciprocal effect on the cytoskeleton and might contribute to the organization of MTs. The cellular distribution of the combined system may in fact result from a concerted interplay between both structures and is conceivably not only determined by the action of MTs alone. The mechanisms by which the ER influences the state of the combined MT–ER system and how ER shape contributes to the control of MT distribution in the cell are largely unknown.
Increasing evidence pointing at a role for the ER in controlling MT organization exists mainly from work in neurons, for instance, showing codependent accumulation of the ER and MTs at the tips of regenerating axons in fly (43). The ER is also important in establishing polarity of mammalian neurons and stabilizes MTs within axons (44). Depletion of ATLs perturbs the interdependent localization of the ER and MTs, resulting in a significant reduction of axon repair after injury (43). Additionally, altering ER localization within the cell as shown by elegant anchor away experiments in neurons perturbs the mechanisms of axon initiation. Specifically, removal of the ER from axons by anchoring it in the neuronal cell body changes the stability and dynamics of axonal MTs (44). Moreover, it has been found that loss of ATL function in Caenorhabditis elegans results in retraction of the ER network from distal dendritic elements, leading to destabilization of the MTs in high-order dendritic branches (45). Consistent with these observations, mutations in human ATLs are linked to neurodegenerative diseases such as hereditary spastic paraplegia and hereditary sensory and autonomic neuropathy (HSAN), in which aberrant ER shape and dynamics lead to atrophy of neuronal axons (46). While these are highly complex diseases, accumulating evidence suggests that impaired ER tethering and fusion result in profound changes in both neuronal ER shape and MT biology (22, 40, 44, 47). Recent three-dimensional (3D) EM reconstructions of the ER in primary HSAN patient fibroblasts reinforce this concept and add the notion that aberrant ER shape after loss of ATL function is accompanied by a drastic change in subcellular distribution of the ER network (48). The mechanisms by which inhibition of ATL-mediated ER tethering and fusion might influence the position of the ER in the cell and the role of the interaction with MTs in this process remain, however, largely mysterious.
Here we have explored the physical interplay between MT organization and ER morphology. We have used quantitative, automated confocal fluorescence microscopy to show that perturbation of ER network dynamics by inhibition of homotypic ER tethering and fusion leads to drastic changes in MT distribution within the cell. A theoretical model that relates the elastic properties of the tubular ER network to the local density of 3WJs recapitulated the experimental findings and predicted that the kinetics of formation, resolution, and mobility of ER junctions are critical for the spatial organization of MTs within mammalian cells. Quantitative live cell imaging confirmed the central theoretical predictions. Specifically, depletion of the ER fusion machinery led to a significant reduction in the rates of ER junction equilibration and promoted the local bundling of the ER–MT system. Our work identifies ER network dynamics as a core process contributing to the mechanisms that control MT distribution in mammalian cells.
Results
Automated Analysis of ER Network Structure.
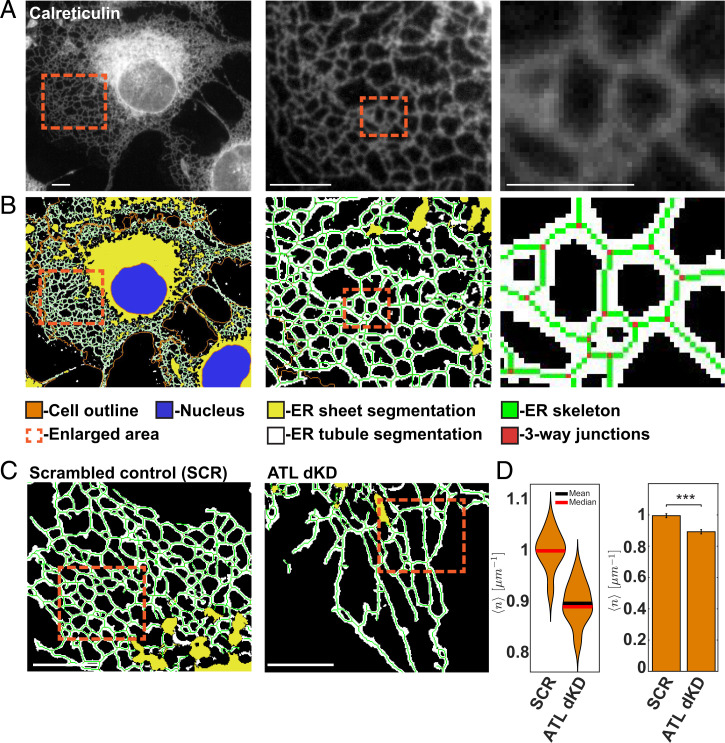
To quantitatively assess ER morphology in an unbiased manner, we used an automated computer vision approach facilitating the quantitative assessment of ER shape in large populations of single cells. We first imaged the ER by immunofluorescence with antibodies to endogenously expressed calreticulin (CRT), a luminal ER protein found in all subdomains (Fig. 1A). We then automatically segmented DAPI-stained nuclei and used low concentrations of fluorescent N-hydroxysuccinimide to determine the outline of individual cells (Fig. 1B). To segment the ER and separate it from the cytoplasm, we trained a supervised random forest-based pixel classifier with intensity and texture features of the CRT signal (Fig. 1B). In order to focus our analysis on the tubular ER network, we additionally segmented ER sheets and excluded them from further analysis (Fig. 1B). Comparison of the automated sheet classification with the localization of endogenously expressed CLIMP-63, a known ER sheet protein, validated this approach (SI Appendix, Fig. S1 A and B).
Fig. 1.
Automated analysis of ER morphology. (A) COS7 cells were analyzed by immunofluorescence with antibodies to the luminal ER protein CRT. The boxed areas are enlarged and are shown on the right. (Scale bar, 10 µm.) (B) As in A but ER tubules (white) and sheets (yellow) were automatically segmented by user-supervised pixel classification trained with features of the CRT signal. The skeleton of the ER network is shown in green, and 3WJs between tubules are red. Nuclei (blue) and cell outlines were segmented using DAPI and NHS-647. (C) As in B but ATL2 and ATL3 were depleted by RNAi (ATLdKD), or COS7 cells were treated with scrambled control small interfering (si) RNAs (SCR). (Scale bar, 1 µm.) (D) Automated quantification of 3WJs per tubule length (number per micrometer). Statistical significance was assessed using Welch's test (***P < 0.001). n = 186 control (SCR) cells, and n = 170 ATL-depleted cells (ATLdKD).
To parameterize the shape and structure of the peripheral ER, we skeletonized the network segmentation and determined the localization of 3WJs (Fig. 1B). Subsequently, we extracted characteristic network properties, such as the number of 3WJs per ER tubule length (number per micrometer), as well as higher-order features, such as the geometry of network polygons that are bounded by the ER tubules (Fig. 1 D and E).
Perturbation of ER Tethering and Fusion Leads to Changes in Subcellular Distribution of the ER.
To perturb the morphology of the ER, we acutely depleted both atlastin isoforms that are expressed in COS7 cells (ATL2 and ATL3) by RNA interference (RNAi) and confirmed their efficient removal using automated single-cell–based fluorescence microscopy (SI Appendix, Fig. S1C). Quantitative analysis showed that the change of structural ER parameters was consistent with previous work, revealing a significant reduction of 3WJ density and longer ER tubules (Fig. 1 C and D).
Apart from these expected changes, we observed a pronounced change in the subcellular distribution of the ER network when compared to wild-type (WT) or control cells (Fig. 1C and S1E). Specifically, the ER tubules of cells lacking ATLs appeared more parallel to one another, and the ER polygons bounded by ER tubules seemed narrow and elongated. Quantification of the polygon shape corroborated this visual impression showing a significant increase of the polygonal eccentricity, consistent with the elongation along one axis of the fitted ellipsoid (Fig. S1E). Although the basic structure of the remaining 3WJs that connect tubules did not change when we measured the angles between the axes of the converging tubules (Fig. S1F), the ER seemed to be stretched into the cellular periphery (Fig. 1C and S1E).
Taken together, these observations indicate that ATL depletion not only reduces the degree of network connectivity but additionally affects the subcellular distribution of the ER. The mechanisms that lead to the altered ER distribution under these conditions are so far unclear but likely involve the cytoskeleton.
Perturbation of ER Morphology Influences MT Distribution.
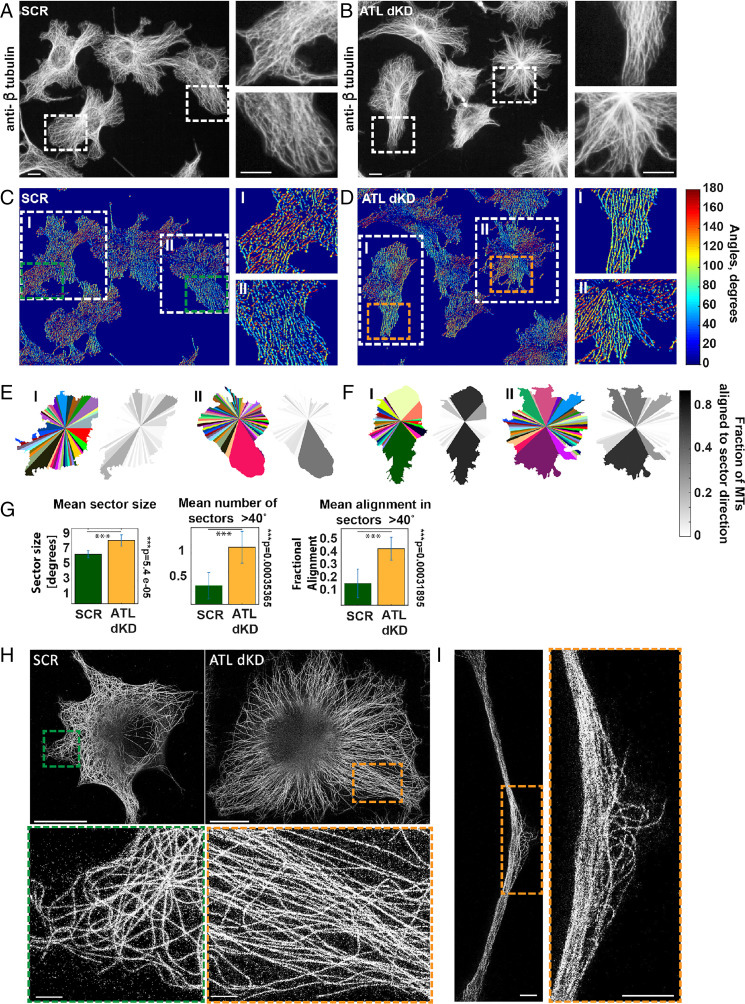
To explore this possibility, we visualized the MT cytoskeleton by immunofluorescence. As expected, the MTs spread evenly throughout the cytoplasm of control cells and the MT axes were distributed isotropically (Fig. 2A). In the absence of ATLs the MTs often clustered (Fig. 2B). Interestingly, the distribution of actin remained largely unaffected (SI Appendix, Fig. S2 A and B), with no apparent change in the cellular actin content or any accumulation of stress fibers compared to controls (SI Appendix, Fig. S2C). In addition, many cells appeared elongated and formed pronounced protrusions that were filled with tightly packed MT bundles (Fig. 2B and SI Appendix, Fig. S2B). In these bundles, we sometimes observed a slight increase of actin and the intermediate filament vimentin (SI Appendix, Fig. S2 B and D). In addition to MT bundling, the MTs were also differently organized around the nucleus, showing strong accumulation at the MTOC (Fig. 2 A and B). Remarkably, the shape of the nucleus turned into a multilobed structure, resembling a flower (Fig. 2B and SI Appendix, Fig. S2B).
Fig. 2.
The distribution of MTs changes upon ATL depletion. (A) COS7 cells treated with scrambled siRNAs were analyzed by immunofluorescence with antibodies to β-tubulin staining MTs. The boxed areas are enlarged and are shown on the right. (Scale bar, 10 µm.) (B) As in A but ATL2 and ATL3 were depleted. (C) As in A but the images were processed with a rotated elongated Gaussian kernel as described in Materials and Methods to build a MT angle map of each cell. The MT angle is visualized in color. (D) As in C but ATL2 and ATL3 were depleted. (E) The cells were divided into 100 sectors, which were unified when the MT direction and angle distribution were similar as described in Materials and Methods. Each sector has a different color. The grayscale images indicate the fractional directionality of all MTs within each sector aligned with the sector axes. The two example cells shown correspond to regions I and II in C boxed in white. (F) As in E but ATL2 and ATL3 were depleted. (G) Quantification of mean size of sectors, the number of sectors larger than 40°, and the mean fractional alignment of MTs with the sector axes in SCR or ATL2- and ATL3-depleted cells. (n = 22 SCR cells, and 23 ATLdKD cells.) (H) MTs were visualized by superresolution imaging with STED, after immunofluorescence with antibodies to β-tubulin. Cells were treated with control (SCR) or ATL2 and ATL3 siRNAs (ATLdKD). (Scale bars, 10 µm and 1 µm in the zoomed-in images.) (I) As in H but a long cellular protrusion formed after ATL2 and ATL3 depletion is shown. (Scale bars, 10 µm and 1 µm in the zoomed-in image.)
In order to quantify the change of MT distribution in individual cells, we applied an image processing method, which has been previously developed to assess the direction of stress fibers in stem cells (49). The analysis is based on convolving the MT fluorescence images with a rotated anisotropic Gaussian kernel, resulting in maximal intensity for each pixel when the rotational angle of the kernel is aligned with the local direction of the MTs. A maximum intensity projection results in a MT angle map of the cell, in which the MT direction is visualized in color (Fig. 2 C and D).
Next, we systematically analyzed the extent of MT isotropicity by dividing the cell into 100 radial sectors and merged neighboring sectors when the MTs within them had similar mean radial direction (≤12°) and MT angle distribution (SD ≤ 36°). As expected, the random distribution of MT orientation in control cells resulted in many small sectors (Fig. 2E, cell I), in which MTs were arranged in various different directions. In ATL-depleted cells the mean sector size increased significantly (Fig. 2 F and G), indicating a more regular arrangement of MTs over larger areas in the cell. Indeed, the number of sectors with a size larger than 40° doubled in ATL-depleted cells (Fig. 2F, cell I and II, and Fig. 2G). Interestingly, within these large sectors of ATL-depleted cells, a substantial fraction of the MTs were coaligned with the sector axis, i.e., pointing radially into the periphery of the cell. Occasionally, control cells also contained large sectors (Fig. 2E, cell II), but the MTs within these were poorly aligned with the axis of the sector and were not oriented radially (Fig. 2E, cell II). Quantification of these observations revealed that the fraction of radially aligned MTs increased fourfold in ATL-depleted cells compared to controls and therefore served as an additional quantitative indicator of the MT bundling phenotype (Fig. 2F, grayscale images, and Fig. 2G).
In contrast, when we depleted the 3WJ-stabilizing protein LNP (SI Appendix, Fig. S2 E and F) and the ER sheets expanded as previously reported, the MTs did not bundle at all (SI Appendix, Fig. S2G). In fact, the distribution of MTs in LNP-depleted cells appeared even more random than in controls (SI Appendix, Fig. S2H), suggesting that the controlled, local accumulation of 3WJs might be involved in the formation of MT bundles.
Taken together, these results indicate that the bundling of MTs is a specific effect of ATL removal and suggest that perturbation of 3WJ formation results in an extensive redistribution of MTs in the cell.
Superresolution stimulated emission depletion (STED) microscopy images confirmed the ordered distribution and bundling of MTs in cells lacking ATLs (Fig. 2H). Additionally, these experiments revealed that the tightly packed MTs within long cellular protrusion often had sudden kinks and appeared to buckle (Fig. 2I), possibly indicating a change in the mechanical load and stability of MTs within the bundles.
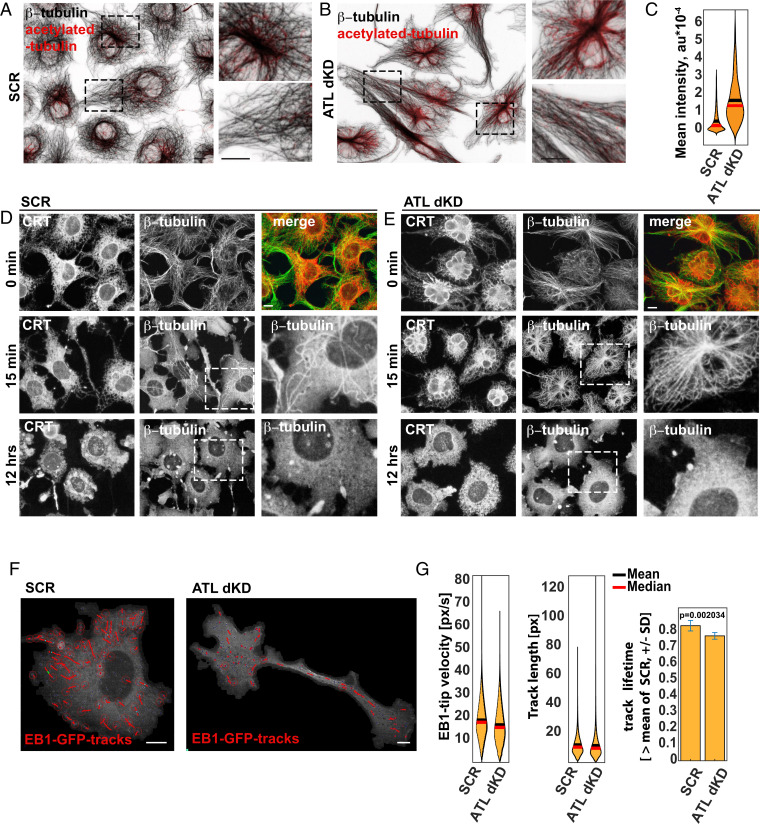
ATL Depletion Increases MT Acetylation and Stability.
To investigate this possibility, we quantified the extent of α-tubulin acetylation, (50, 51). Acetylated MTs are more elastic and protected against mechanical damage (52). Fig. 3 A–C show that acetylation is indeed increased when ATLs were depleted. As expected, the acetylated MTs were also more stable. A 15-min-long treatment with the MT depolymerization drug colchicine removed most of the MTs in controls (Fig. 3D) but did not depolymerize MTs in ATL-depleted cells (Fig. 3E). Several hours after drug addition, the MTs were depolymerized in all conditions (12 h; Fig. 3 D and E).
Fig. 3.
ATL depletion leads to increased acetylation and stability of MTs but does not change +TIP dynamics. (A) COS7 cells treated with scrambled siRNAs (SCR) were analyzed by immunofluorescence with antibodies to β-tubulin and to α-tubulin acetylated at K40. The boxed areas are enlarged and shown on the right. (Scale bar, 10 µm.) (B) As in A but ATL2 and ATL3 were depleted (ATLdKD). (C) The mean intensity of acetylated α-tubulin is determined in SCR and ATLdKD cells, which are segmented as described in Fig. 1B. (D) COS7 cells treated with SCR siRNAs were treated with the MT depolymerization drug colchicine for 0 min, 15 min, and 12 h, and MTs and the ER were visualized with antibodies to β-tubulin and CRT, respectively. (Scale bar, 10 µm.) (E) As in D but ATL2 and ATL3 were depleted (ATLdKD). (F) COS7 cells were transfected with EB1-GFP marking the +TIPs of growing MTs. Live cell imaging of control and ATL-depleted cells (SCR and ATLdKD, respectively) was performed to track the movement of +TIPs. (Scale bars, 10 µm.) (G) Quantification of +TIP velocity and track length as well as track lifetime. (N = 8,684 +TIP tracks in 11 SCR cells; n = 4,021 +TIP tracks in 16 ATLdKD cells.)
Interestingly, ATL-depleted cells also contained enlarged MTOCs, (SI Appendix, Fig. S3 A and B). However, the cellular content of γ- tubulin, which contributes to the nucleation of MTs at the MTOC, remained unchanged (SI Appendix, Fig. S3 A and C), and the number of centrosomes were the same as in control cells (SI Appendix, Fig. S3D).
Since anomalous centrosome structure is often indicative of perturbations in the cell cycle (53), we considered the possibility that the observed MT-bundling phenotype might be an indirect effect of aberrant cell cycle progression (54). We therefore assessed the cell cycle stages in large populations of fixed, single cells (55). While ATL depletion slightly reduced the total cell number, consistent with previous work (56), the cells, surprisingly, progressed efficiently through the cell cycle (SI Appendix, Fig. S3E). In addition, we found that the dramatic change in nuclear shape was not a cell cycle–dependent effect In contrast to controls, most nuclei in interphase of ATL-depleted cells were not spherical, and the measured solidity of the nuclear outline was significantly decreased, regardless of the cell cycle phase (SI Appendix, Fig. S3F). Strikingly, after MT depolymerization, the nuclei relaxed into spherical shapes, and the ER completely lost its typical structure but remained evenly distributed throughout the entire cell (SI Appendix, Fig. S3 G and H) consistent with previous observations (57).
Given that the MTs were more stable in ATL-depleted than in control cells, we expected a decrease in MT growth dynamics. However, quantitative analyses of MT dynamics after ATL depletion did not reveal any detectable effect (Fig. 3 F and G). We tracked GFP-EB1, a +TIP protein that specifically associates with growing plus-ends of MTs, by live cell imaging. In contrast to our expectation, the velocity of EB-1–labeled tips and the lifetime of tip tracks remained quantitatively similar under all conditions (Fig. 3 F and G).
In summary, the most prominent changes in MT organization of ATL-depleted cells is the formation of closely packed, acetylated MT bundles that either point radially toward the periphery of the cells or form pronounced bundles that even have an impact on the overall shape of the cell.
Fluctuations in ER Junction Density Control MT Distribution.
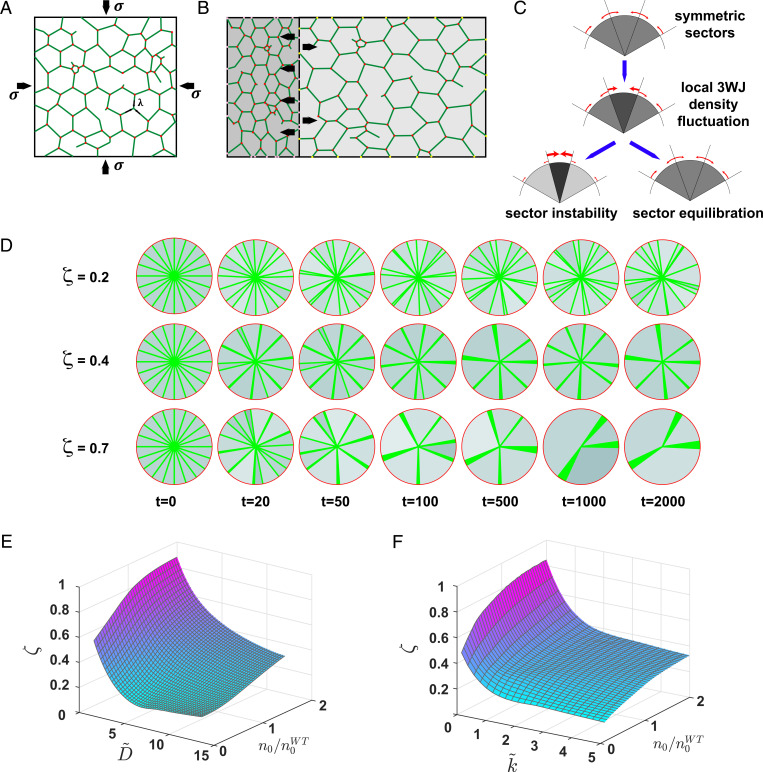
In order to gain better insight into the processes by which ATL activity causes changes in MT distribution in the cell, we developed a physics-based model of the coextensive MT–ER system. As in previous work (8, 13), we represented the tubular ER as a network of 1D line segments, corresponding to the axes of cylindrical membrane tubules that are connected by 3WJs. The area, , that is covered by such a planar network consisting of tubules with a total length and connected at symmetric junctions is given by
| [1] |
where for an ideal triangular lattice. Since ER tubules are not perfectly straight and some tubule tips are unconnected, we tested the validity of this representation by relating the junction area density, , to the junction length density (i.e., the number of junctions per unit length of the tubules), . Using a skeletonized version of the segmented ER network, we indeed find that , thus validating the form of Eq. 1 (SI Appendix, Fig. S4A; see SI Appendix for details).
Although ER tubules do not seem taut, quantitative analysis of ER tubule motion has revealed a residual longitudinal tension in the tubule network, (58). As a result of such a line tension, a network patch with the area will generate an inward-directed 2D pressure, , acting effectively as a contractile force on the surrounding MTs (Fig. 4A). At mechanical equilibrium, the line tension and 2D pressure are related by
| [2] |
Fig. 4.
Model for MT bundling by dynamic remodeling of the ER network. (A) Cartoon representation of a patch of ER network. ER tubules are represented by green lines, and 3WJs are represented by red dots. The patch is bounded by MTs (black lines). (B) Cartoon showing the effect of uneven 3WJ distribution. The density of 3WJ in the left network patch (dark gray) is higher than the density in the right network patch (light gray). Black arrows indicate pulling forces that act on the MT. (C) Onset of bundling by inhomogeneous 3WJ distribution across MT-bound regions. (Top) Homogenous junction density (light gray). Red arrows indicate forces acting on MTs. (Middle) Increased junction density in one sector (medium gray). If the equilibration and redistribution of ER junctions are rapid in comparison to MT dynamics, the force balance is restored (Bottom Right); otherwise, the high-density region contracts (Bottom Left), leading to increased inhomogeneity of junction densities (dark gray). (D) Simulation instances of MT distributions (green lines) at different time points. ER junction density is indicated by grayscale (darker shades indicate higher density). (Top) , (Middle) , and (Bottom) . (E) Simulated bundling parameter,, vs. dimensionless junction diffusion, , and equilibrium junction density, . Each point in the phase space represents the average of 500 simulation instances taken at steady state. . (F) Simulated bundling parameter, , vs. dimensionless junction equilibration rate, , and equilibrium junction density, . Each point in the phase space represents the average of 500 simulation instances taken at steady state. .
Based on Eqs. 1 and 2 we find that each ER network patch will develop an effective 2D pressure that is proportional to its junction density, :
| [3] |
An immediate consequence of this model is that an imbalance between the junction densities of neighboring ER regions will generate a net pressure on the MTs delimiting these regions, (Fig. 4B). As long as the imbalance in junction densities persists, the net 2D pressure would contract regions with a high junction density and expand adjacent regions with a lower junction density (Fig. 4 B and C). Such a 2D pressure is equivalent to a normal bundling force acting on the MTs. We find that the magnitudes of the maximal bundling forces acting on radial MTs are in the range of 10 to 20 pN and therefore fall within the scale of relevant intracellular forces (SI Appendix). In addition to the direct pulling forces on MT that arise from the longitudinal stress within ER tubules, we hypothesize that the local ER junction density may further affect MT bundling indirectly by binding and local enrichment of MT binding proteins that additionally promote MT bundling. As this contribution scales linearly with the junction density, , the shape of Eq. 3 remains unaltered. We may therefore represent the combined direct and indirect contributions to the bundling 2D pressure by an effective tension, .
At the experimental time scales, the movement of the MTs and the associated ER network patch is largely limited by viscous drag. The area of a given network patch will therefore shrink at the rate
| [4] |
where is the effective friction coefficient of the combined system. Since the ER membranes redistribute much faster than the moving MTs (59, 60), the line tension, , is taken to be uniformly distributed throughout the ER. The total tubule length within each ER sector, , is therefore considered to be at quasi–steady state, following Eq. 1. Consequently, contraction of a sector will result in a further increase in its junction density (Fig. 4C), as given by
| [5] |
In addition to the motion of MTs and ER tubules, our model further considers the movement of 3WJs themselves. At the subminute time scale, it was recently shown that 3WJs redistribute with subdiffusion dynamics (61). We, however, consider motion of 3WJs across MT boundaries, which occurs at longer time scales, and therefore model this process as simple Brownian diffusion with an effective diffusion coefficient, . Moreover, the number of 3WJs in the tubular ER constantly changes by ATL-mediated ER fusion, as well as 3WJ resolution by ring closure or the release of tethered junctions (12, 30, 33, 62). The combined kinetics of these processes results in the steady-state junction density, . The junction equilibration rate, , at which the steady-state density is maintained reflects the capacity of the system to counteract local density changes. Finally, we account for random fluctuations in junction densities as geometric random noise with an amplitude .
Taken together, the overall rate of change in 3WJ density is a combination of area contraction (Eqs. 3–5), junction remodeling, junction diffusion, and noise. The complete dynamics of the MT–ER system are then described by the equations
| [6a] |
| [6b] |
where denotes the differential form of a Wiener process (a stochastic noise term).
The distribution of the ER network and the repositioning of the MTs are determined by numerically solving the stochastic differential equations in Eqs. 6a and 6b. However, the onset of MT bundling may be understood qualitatively by considering an initial system with equally sized MT-bounded regions having the area and a homogeneous junction density . We next introduce a small fluctuation in the junction density of one region, . The time evolution of the density fluctuation, according to Eq. 6, is
| [7] |
where we define and as dimensionless parameters.
According to Eq. 7, fluctuations increasing the local junction density result in positive feedback, leading to a further increase in junction density and additional contraction of the region’s area. In WT cells, the junction mobility and the junction equilibration process efficiently restore local ER junction density to a stable steady-state value (second and third terms in the parentheses in Eq. 7; Fig. 4C, sector equilibration). Defects in junction density reequilibration across the ER ultimately cause instability of the MT-bound ER sectors, and the feedback between junction density and ER contraction may lead to MT bundling (Fig. 4C, sector instability). Eq. 7 shows that the fluctuation will be amplified if .
To study the temporal development of junction heterogeneities across the ER of an entire cell, we implemented our model as a numerical simulation (Fig. 4D and SI Appendix, Extended Theory). We represent MT-bound regions by radial sectors of varying angles, , and quantify the extent of MT bundling by the bundling parameter, , defined as
where increasing values of correspond to states of high bundling.
The results of the simulation obtained with different levels of network dynamics (Fig. 4 E and F) confirm our qualitative considerations above. The data show that a reduction of junction movement between sector boundaries, , or a decrease in the equilibration rate, , enhances MT bundling (Fig. 4 E and F). At low levels of network dynamics, when and approach zero, the system displays a sharp transition to a state with highly bundled MTs, characterized by high values of the bundling parameter .
Remarkably, our model unexpectedly predicts that a large global decrease in the junction density, , relative to the WT (), diminishes the tendency of MT bundling (Fig. 4 E and F). This result indicates that the experimentally observed bundling of the MT system after depletion of ATLs is not driven by the overall reduction in the global level of ER junctions but is rather due to the impaired kinetics of junction dynamics upon ATLs removal.
ATL Depletion Alters ER Tubule Dynamics and the 3WJ Equilibration Rate.
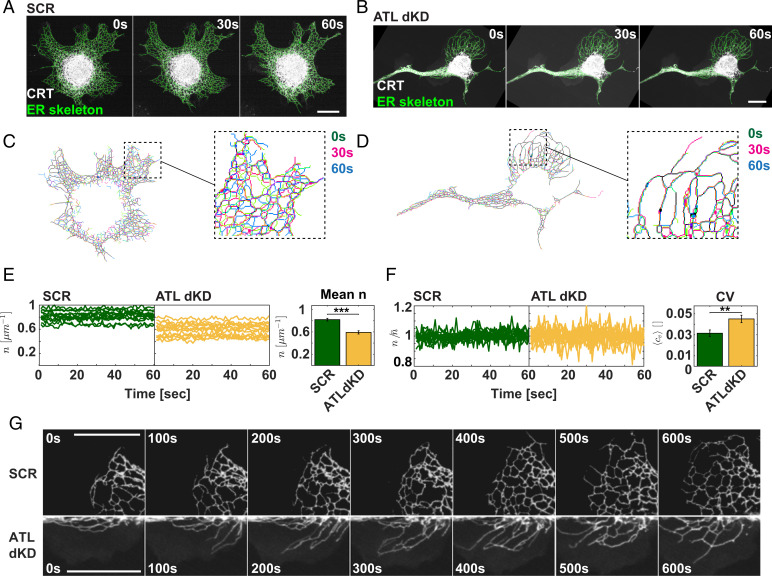
In order to investigate the theoretically predicted changes of ER dynamics in ATL-depleted cells, we turned to live cell imaging. We visualized the ER with an mCherry carrying the signal sequence of CRT at the N terminus and an ER retention signal at the C terminus (ss-mCherry-KDEL). We then segmented the ER (Fig. 5 A and B) in each frame of the movies.
Fig. 5.
ER tubule junction dynamics is reduced in ATL-depleted cells. (A) COS7 were transfected with ss-mCherry-KDEL, treated with scrambled siRNAs (SCR), and subjected to live cell imaging. Movies with 1-s frame rate were acquired, and the ER was segmented as described for fixed cells in Fig. 1 A and B. Example frames of the movie are shown at the indicated time points. (Scale bar, 10 µm.) (B) As in A but the cells were treated with siRNAs to ATL2 and ATL3. (C) The skeletonized ER network obtained after processing the images of the movie shown in A was superimposed at the indicated time points. (D) As in C but the ER skeletons were obtained from movies shown in B. (E) The total 3WJ number density per ER skeleton length (n) was determined in each frame of the movies and plotted over time for the indicated conditions (SCR, control; ATLdKD). (Right) Quantification of the mean 3WJ number of all movies analyzed. (N = 13 SCR cells, and 14 ATLdKD cells *** indicates statistical significance P < 0.001 determined by Welch's test.) (F) As in E but the equilibration rate was determined for each movie by calculating the ratio between the number of 3WJs and the mean over all time points. (Right) The mean coefficient of variation (CV) was determined over all movies analyzed. (N = 13 SCR cells and 14ATLdKD cells. ** indicates statistical significance P < 0.01 determined by Welch's test.) (G) Example frames from 10-min-long movies demonstrating the difference in network dynamics in newly forming ER areas between SCR and ATLdKD cell. (Scale bar, 10 µm.)
Next, we superimposed the skeletonized ER networks acquired at the start (0 s), with frames recorded at 30 and 60 s of the movies. The overlay provided evidence that the ER was indeed less dynamic in ATL-depleted cells than in controls, qualitatively confirming one of the predictions made by the model (Fig. 5 C and D). In agreement with the results in fixed cells (Fig. 1D), the 3WJ density per ER length, , was reduced only modestly by around 27% (Fig. 5E). Interestingly, our model predicted that a stronger reduction of the total number of 3WJs relative to WT or controls would lead to a decrease of the MT bundling parameter , which means that MT bundling would be less favorable (Fig. 4 E and F; values for ). However, simulations with up to 30% reduction in 3WJs density did not result in a considerable decrease in , demonstrating that MT bundling is not influenced by the experimentally observed drop in the overall 3WJ density in the cells. Our results therefore rather support the possibility that the role of the ER in controlling MT bundling is connected to a change in dynamic ER features instead of being determined by steady-state features of the ER network.
To further test these predictions, we quantified the effect of ATL depletion on the movement of 3WJs. To this end, we extracted the 3WJs from the time series and calculated the average mean-square displacement (MSD) of each track (SI Appendix, Fig. S5 A and B). By fitting the MSDs to a power law function we determined the diffusion exponent characterizing the 3WJ movement at the subminute time scale (see SI Appendix for details). In agreement with previous work, our data show that the diffusion exponent in control cells is below 1 (SI Appendix, Fig. S5C), indicating subdiffusive behavior.
Upon ATL depletion, the diffusion exponent indeed decreased (SI Appendix, Fig. S5C), indicating a reduced mobility of 3WJs in ATL-depleted cells as predicted by the theory. Despite being highly significant, the change was, however, not pronounced, suggesting that the small reduction in 3WJ movement must be accompanied by an additional alteration in ER network behavior, in order to explain the formation of MT bundles.
We therefore additionally considered the effect of ATL depletion on the rate of junction equilibration, , which reflects the ability of the ER to actively counterbalance local variability of tubule junction density restoring a uniform distribution of 3WJs across the ER. Our model predicts that a decrease in leads to an increase of the MT bundling parameter (Fig. 4F), raising the expectation that cells bundle their MTs when the mechanisms underlying 3WJ density equilibration are impaired. To assess the 3WJ equilibration rate we examined the fluctuation of the global junction density in the entire cell over time. According to our model, a high rate of 3WJ equilibration is critical to maintain a constant steady-state junction density. A reduction in the rate of 3WJ equilibration, , would be reflected in an increase of the temporal fluctuation of the global cellular junction density (see Fig. 5E and SI Appendix for additional details). To quantify the 3WJ density fluctuations in live cells, we measured the global 3WJ density per cell in each time frame, , and divided it by the time-averaged density, . The calculated coefficient of variation () indeed shows that the distribution of the cellular junction densities over time is considerably broader in ATL-depleted cells than in controls. These results demonstrate that the ER network of control cells is much more efficiently equilibrated than in cells lacking ATLs, confirming the second major prediction of our model.
Finally, longer movies acquired with control and ATLdKD cells visually confirm the interpretation that ATL depletion leads to impaired 3WJ kinetics. In control cells the ER network expands symmetrically by rapidly forming new junctions between tubules. In ATL-depleted cells the network expands more slowly, and fewer junctions are formed. Tubules are frequently pulled out by MTs but remain often untethered and do not fuse readily with partner tubules (Fig. 5G).
Taken together, these data indeed suggest that a combination of impaired 3WJ mobility and reduction of 3WJ equilibration rate underlies the instability of MT-bounded ER sectors as predicted by our theoretical considerations. Consistent with the model, this change in ER dynamics would explain a contraction of some ER sectors in ATL-depleted cells, leading to the local accumulation of the ER–MT system causing MT bundle formation.
MT Bundles Form at Regions of High ER Density.
To explore the principal prediction that dense regions of the ER lead to localized MT bundling, we costained MTs and the ER in ATL-depleted cells and tested whether the ER membranes accumulate in regions with bundled MTs (Fig. S6A). As expected, the MTs were often bundled, and a number of cells show long cellular protrusions that were densely packed with MTs and ER. To display MT distribution within these cells in a systematic fashion, we generated a MT angle map (Fig. S6B) as described above (Fig. 2 C and D). In areas with parallel MTs pointing into the cell periphery (as in cell I and cell III in Fig. 6B), the ER accumulated in the center of the bundle. In regions with tight MT bundles within cells or in cellular protrusion (see cell II in Fig. S6B), the ER accumulated even more drastically, confirming the localization predicted by the model.
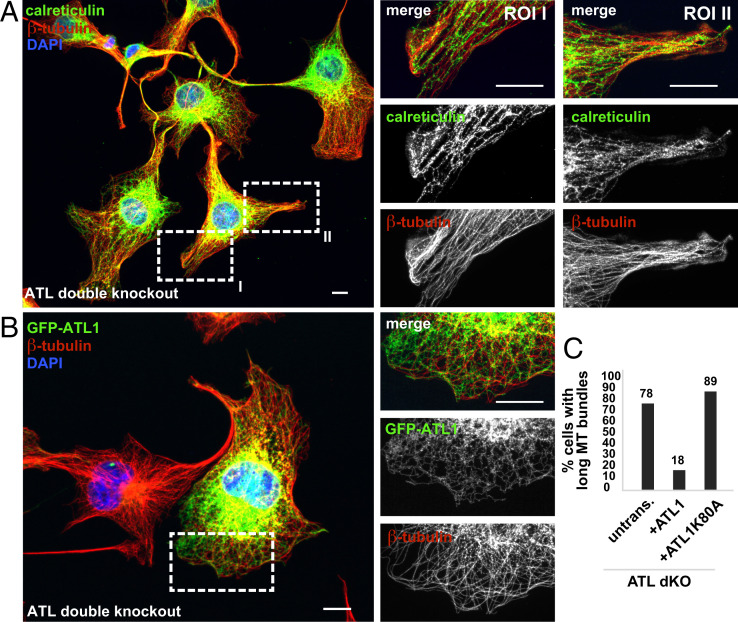
Fig. 6.
MTs and the ER cocluster in bundles of ATL 2,3 CRISPR double knockout cells. (A) ATL2 and ATL3 were knocked out in COS7 cells using CRISPR. Zoomed-in images were processed with the Olympus super resolution (OSR) software using the standard filter mode (see details in Materials and Methods). Scale bar, 10 µm. (B) As in A but the ATL2 and ATL3 double knockout cells were transfected with ATL1 tagged at its N terminus with GFP (GFP-ATL1). (C) Quantification of the results in B. Untransfected, n = 223; +ATL1, n = 65; +ATL1K80A, n = 28 (see ATL1K80A expressing double knockout cell in Fig. S6D). Scale bar, 10 µm. The ATL double knockout cells were stained with antbodies specific to calreticulin and β-tubulin.
ATL1 Rescues Formation of MT Bundles in ATL Double Knockout Cells.
Finally, we validated the MT bundling phenotype in ATL2 and ATL3 double knockout cells (15). Consistent with ATL depletion by RNAi, ATL2 and ATL3 double knockout by CRISPR resulted in long cellular protrusions that were filled with bundled MTs and dense ER (Fig. 6A). The parallel-oriented MTs pointed unidirectionally toward the periphery of the cell (Fig. 6A and ROI I) and locally accumulated together with the ER in bundles (Fig. 6A, and ROI II). Importantly, expression of GFP-ATL1 rescued the normal MT morphology, reducing the percentage of cells showing long MT bundles fourfold (Fig. 6 B and C). Consistently, ATL1 K80A, which is a dominant negative, GTPase-deficient ATL mutant led to the formation of MT bundles when overexpressed in COS7 cells (SI Appendix, Fig. S6A) and was not able to rescue the phenotype in ATL double knockout cells (Fig. S6D).
Taken together, our data suggest that ER network dynamics play an important role in the cellular distribution of MTs. In WT or control cells the ER is efficiently remodeled, and the 3WJs are rapidly equilibrated across the entire ER by processes involving junction movement, tubule tethering, and fusion, as well as junction resolution. Conversely, we found that reduction in 3WJ equilibration rates and junction mobility after ATL depletion promote inhomogeneous distribution of the ER network. The MT cytoskeleton is surprisingly sensitive to such changes in ER network dynamics and responds to a local increase in ER junction density by MT bundling. As shown in Fig. 6 and Fig. S6, both the ER and the MTs accumulate in regions of MT bundles. In general, ATL is necessary to spread MTs efficiently.
Discussion
The ability to control the distribution of the MT cytoskeleton in interphase cells is critical for a wide spectrum of cellular processes ranging from the organization of membrane traffic to establishing cell polarity. While it is widely accepted that the MT cytoskeleton is critical for the cellular distribution of the ER, a reciprocal effect of the ER on the position of MTs has not been explored extensively. Accumulating evidence in neurons indicates that the ER might indeed be important for MT biology. Specifically, it appears that the ER influences MT organization during axon initiation and maintenance (43–45, 48). From a physical perspective it remains, however, unclear how the soft ER membranes are able to influence the position of the rigid MT cytoskeleton. Here we have revealed that ER network dynamics and particularly the dynamic equilibration of ER tubule junctions across the ER are critical for positioning MTs in the cell.
To test whether alterations in ER network structure would have an effect on MT distribution, we perturbed ER tethering and fusion by depleting ATLs. Unbiased quantification of ER features indicated a relatively modest decrease in the global number of 3WJs. Initially, these findings seemed to contradict previous observations showing that loss of ATL caused a drastic reduction of 3WJs. Analysis of the spatial distribution of the remaining 3WJs within ATL-depleted cells revealed, however, that they were often clustered in compact ER regions. As a result, the 3WJs outside of the clustered regions were distributed over larger cellular areas that showed sparse ER with low junction density. The visual impression created by these images possibly suggested a stronger decrease in 3WJs than that which had in fact occurred.
Additionally, we observed that the MTs accumulated as closely packed bundles within ATL-depleted cells. One explanation would have been an involvement of other cytoskeletal elements that affect MT bundling. However, our control experiments visualizing the actin cytoskeleton, stress fibers, and the intermediate filament vimentin indicated that the observed changes of the cytoskeleton were specific to MTs.
In order to understand the ER-dependent MT bundling better, we next developed a physics-based model of the ER–MT system and simulated the effect of changes in ER connectivity on MT distribution. The simulations recapitulated the experimental findings showing that inhibition of ER junction formation causes strong MT bundling. In addition, our theoretical model predicted that an actively maintained, uniform distribution of 3WJs across the ER is critical for an isotropic and homogeneous distribution of the MTs in the cell. Our theory showed that low, residual tension in the ER leads to an effective contractile force proportional to the junction density within an ER network patch which acts on the bordering MTs. An uneven distribution of 3WJs between ER regions results in mechanical instability of the ER–MT system contracting the junction-dense regions at the expense of neighboring areas. Consequently, the ER–MT system locally accumulates and forms densely packed MT bundles.
In contrast to our initial assumptions, the model showed that the global decrease of 3WJs is not the main driving factor for MT bundling. In fact, our simulations indicated that a reduction of total 3WJs by more than 30% would even counteract bundling. Instead, our simulations revealed that ER dynamics, and in particular the dynamic equilibration of ER tubule junctions across the ER, plays a major role in controlling MT bundling. We confirmed these predictions by quantitative live cell imaging showing that both the mobility of 3WJs and the rate of 3WJ equilibration through formation and release of 3WJs are reduced upon ATL depletion. Inhibiting tubule tethering and fusion by depletion of ATLs reduced the ability of the system to rapidly equilibrate 3WJs across the ER leading to a local increase in 3WJ density and bundling of MTs.
Interestingly, a reduction of the 3WJ equilibration rate implies that both the processes of junction formation and junction resolution become slower upon ATL depletion. While this notion is consistent with a function of ATL in ER fusion, it is not readily understandable how ATLs are involved in resolution of 3WJs. One possible explanation might be found in long-lasting ATL dependent tethering of 3WJs that precedes membrane fusion (30, 62). Reversible tethering of 3WJs might facilitate a much more rapid equilibration of junction density across the ER than formation and resolution of fused junctions. The lack of tethered junctions may in fact specifically result from ATL depletion and might account significantly for the reduction of 3WJ equilibration rates. This possibility might explain the long, reversible tethering during ATL-mediated membrane fusion justifying the seemingly futile GTP consumption in this state.
Moreover, our theoretical considerations for the 3WJ density-dependent contractility of ER patches may in general explain local aggregation of ER junctions in MT-free regions. Future applications of our findings may therefore elucidate the mechanisms that form different types of ER morphologies, such as highly fenestrated sheets (63) or tubular matrices that consist of closely packed and rapidly remodeling 3WJs (35).
The effects of ATL-mediated ER remodeling on MT distribution and their stability might further be important in the molecular understanding of axonal atrophy that is caused by mutations in ATLs leading, e.g., to hereditary spastic paraplegia or hereditary sensory and autonomic neuropathy (14, 46, 64). It is possible that ATL-dependent distribution and stabilization of MTs are operating in concert with the mechanism that rearranges the ER–MT system during axon initiation and maintenance (43–45).
Importantly, our study is indicative of residual membrane tension in the ER network. Although the cross-sectional curvature of ER tubules is stabilized by curvature generating proteins, rather than by surface tension, we found that the minimal membrane tension that has recently been measured in the ER within cells produces appreciable forces that can lead to bundling of MTs. Additionally, our model indicates that ER-generated pulling forces may be augmented by MT interacting ER proteins (44, 65). Such indirect contributions may indeed have significant impact on the effective bundling forces experienced by the MTs and possibly explain the importance of MT-binding proteins for the stability of axonal MTs (44).
Proteins that mediate the physical coupling between MTs and the ER are obviously a necessary prerequisite for the reciprocal interaction between the two structures. Whether their localization is systematically affected by the distribution of ER junctions is still to be investigated. Various posttranslational modifications of tubulin were recently shown to underlie the specificity of MT binding of several ER membrane proteins and constitute another layer of possible regulation controlling the interplay between the ER and MTs (65).
Finally, changes in ER dynamics are presumably only one factor of a larger machinery that is important for controlling the distribution of MTs in the cell. Future work is necessary in order to explain the full mechanistic underpinnings of the functional interaction between these two major cellular systems. Our data provide, however, strong evidence that dynamic ER network remodeling by the ER shaping machinery is a central mechanism in the spatial organization of the ER–MT system.
Materials and Methods
Cell Culture.
COS7 cells were a kind gift from Tom Rapoport (HHMI, Harvard Medical School, Cambridge, MA). ATL2 and ATL3 dKO cells were a kind gift from Junjie Hu (Chinese Academy of Sciences, Beijing, China) and Yusong Guo (The Hong Kong University of Science and Technology, Hong Kong, China).
All cells were cultured at 37 °C and 5% CO2 in Dulbecco’s modified eagle medium with 10% fetal bovine serum.
Immunofluorescence.
The cells were fixed with PBS, 4% paraformaldehyde, permeabilized, and incubated with primary and secondary antibodies as described in SI Appendix.
Image Analyses.
Image analysis was performed using CellProfiler (CP), with inbuilt CP modules, or custom MATLAB-based modules. Typical CP pipelines are described in SI Appendix.
Segmentation of Nuclei and Single Cells.
The nuclei were identified by thresholding of the DAPI signal, and the segmented objects were subsequently used as seeding points to identify the cell outline based on the fluorescent N-hydroxy succinimidylester signal. The datasets were additionally filtered for border cells crossing imaging sites and mitotic and polynuclear cells as described in SI Appendix.
Automated ER Segmentation.
The ER segmentation was performed using a random forest pixel classifier in Ilastik. The resulting probability map was segmented in Cell profiler and subsequently skeletonized in MATLAB. After that the polygon shape parameters of ER tubule bound areas, the tubule branch points and open-end points of unfused tubules were extracted using MATLAB as outlined in SI Appendix.
Automated Determination of MT Orientation by Building MT Angle Maps.
MT segmentation and directionality analysis was based on work presented in ref. 63, 66, 67 as described in SI Appendix.
Measuring the Fractional Alignment of Cellular MTs with Cell Sector Axes.
To evaluate to which extent the MTs that localize to unified sectors were aligned with the sector axes, the ratio of all pixels marking MTs in a certain sector and the pixels having the same orientation angle as the sector angle was determined and the ratio was calculated.
Supplementary Material
Acknowledgments
We thank Junjie Hu (Chinese Academy of Sciences, Beijing, China) and Yusong Guo (The Hong Kong University of Science and Technology, Hong Kong, China) for the generous gift of ATL2 and ATL3 dKO cells and Craig Blackstone, Massachussetts General Hospital, Harvard Medical School, for mycATLK80A. We thank Paulina Volz for initial work on ATL RNAi experiments and all members of the R.W.K., T.S., and Pelkmans laboratories for discussion and suggestions. R.W.K wishes to thank Lucas Pelkmans (University of Zürich [UZH], Zürich, Switzerland), for sharing critical resources. R.W.K. was supported by the Swiss National Science Foundation (Grant 31003A_159793), the Helmut Horten Foundation, and a grant from the Funds for Support of young investigators from the UZH. This work was additionally supported by funding from the Biotechnology and Biological Sciences Research Council (UK Research and Innovation) (Grant BB/T008784/1). M.S.T. was recipient of a PhD fellowship “Forschungskredit” by the UZH. T.S. acknowledges support from the Israel Science Foundation (Grant 921/15).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2104309119/-/DCSupplemental.
Data Availability
All study data are included in the article and/or SI Appendix.
The probability maps of ER segmentation and the live cell data which were used for statistical assessment are deposited at Zenodo: https://zenodo.org/record/6369232#.YjTsFy0RoWo.
References
- 1.Booth A. J. R., Blanchard G. B., Adams R. J., Röper K., A dynamic microtubule cytoskeleton directs medial actomyosin function during tube formation. Dev. Cell 29, 562–576 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Meiring J. C. M., Shneyer B. I., Akhmanova A., Generation and regulation of microtubule network asymmetry to drive cell polarity. Curr. Opin. Cell Biol. 62, 86–95 (2020). [DOI] [PubMed] [Google Scholar]
- 3.Barlan K., Gelfand V. I., Microtubule-based transport and the distribution, tethering, and organization of organelles. Cold Spring Harb. Perspect. Biol. 9, a025817 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hu J., Prinz W. A., Rapoport T. A., Weaving the web of ER tubules. Cell 147, 1226–1231 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Guo Y., et al. , Visualizing intracellular organelle and cytoskeletal interactions at nanoscale resolution on millisecond timescales. Cell 175, 1430–1442.e17 (2018). [DOI] [PubMed] [Google Scholar]
- 6.Baumann O., Walz B., Endoplasmic reticulum of animal cells and its organization into structural and functional domains. Int. Rev. Cytol. 205, 149–214 (2001). [DOI] [PubMed] [Google Scholar]
- 7.Terasaki M., Chen L. B., Fujiwara K., Microtubules and the endoplasmic reticulum are highly interdependent structures. J. Cell Biol. 103, 1557–1568 (1986). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shibata Y., et al. , Mechanisms determining the morphology of the peripheral ER. Cell 143, 774–788 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Shibata Y., Hu J., Kozlov M. M., Rapoport T. A., Mechanisms shaping the membranes of cellular organelles. Annu. Rev. Cell Dev. Biol. 25, 329–354 (2009). [DOI] [PubMed] [Google Scholar]
- 10.Voeltz G. K., Prinz W. A., Shibata Y., Rist J. M., Rapoport T. A., A class of membrane proteins shaping the tubular endoplasmic reticulum. Cell 124, 573–586 (2006). [DOI] [PubMed] [Google Scholar]
- 11.Chen S., Novick P., Ferro-Novick S., ER network formation requires a balance of the dynamin-like GTPase Sey1p and the Lunapark family member Lnp1p. Nat. Cell Biol. 14, 707–716 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chen S., et al. , Lunapark stabilizes nascent three-way junctions in the endoplasmic reticulum. Proc. Natl. Acad. Sci. U.S.A. 112, 418–423 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shemesh T., et al. , A model for the generation and interconversion of ER morphologies. Proc. Natl. Acad. Sci. U.S.A. 111, E5243–E5251 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hu J., et al. , A class of dynamin-like GTPases involved in the generation of the tubular ER network. Cell 138, 549–561 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Niu L., et al. , Atlastin-mediated membrane tethering is critical for cargo mobility and exit from the endoplasmic reticulum. Proc. Natl. Acad. Sci. U.S.A. 116, 14029–14038 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dreier L., Rapoport T. A., In vitro formation of the endoplasmic reticulum occurs independently of microtubules by a controlled fusion reaction. J. Cell Biol. 148, 883–898 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Allan V., Vale R., Movement of membrane tubules along microtubules in vitro: Evidence for specialised sites of motor attachment. J. Cell Sci. 107, 1885–1897 (1994). [DOI] [PubMed] [Google Scholar]
- 18.Allan V. J., Vale R. D., Cell cycle control of microtubule-based membrane transport and tubule formation in vitro. J. Cell Biol. 113, 347–359 (1991). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dabora S. L., Sheetz M. P., The microtubule-dependent formation of a tubulovesicular network with characteristics of the ER from cultured cell extracts. Cell 54, 27–35 (1988). [DOI] [PubMed] [Google Scholar]
- 20.Moss T. J., Andreazza C., Verma A., Daga A., McNew J. A., Membrane fusion by the GTPase atlastin requires a conserved C-terminal cytoplasmic tail and dimerization through the middle domain. Proc. Natl. Acad. Sci. U.S.A. 108, 11133–11138 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pendin D., et al. , GTP-dependent packing of a three-helix bundle is required for atlastin-mediated fusion. Proc. Natl. Acad. Sci. U.S.A. 108, 16283–16288 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bian X., et al. , Structures of the atlastin GTPase provide insight into homotypic fusion of endoplasmic reticulum membranes. Proc. Natl. Acad. Sci. U.S.A. 108, 3976–3981 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Powers R. E., Wang S., Liu T. Y., Rapoport T. A., Reconstitution of the tubular endoplasmic reticulum network with purified components. Nature 543, 257–260 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hu J., et al. , Membrane proteins of the endoplasmic reticulum induce high-curvature tubules. Science 319, 1247–1250 (2008). [DOI] [PubMed] [Google Scholar]
- 25.Crosby D., et al. , Reconstitution of human atlastin fusion activity reveals autoinhibition by the C terminus. J. Cell Biol. 221, e202107070 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Byrnes L. J., et al. , Structural basis for conformational switching and GTP loading of the large G protein atlastin. EMBO J. 32, 369–384 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.O’Donnell J. P., et al. , Timing and reset mechanism of GTP hydrolysis-driven conformational changes of Atlastin. Structure 25, 997–1010.e4 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Byrnes L. J., Sondermann H., Structural basis for the nucleotide-dependent dimerization of the large G protein atlastin-1/SPG3A. Proc. Natl. Acad. Sci. U.S.A. 108, 2216–2221 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Anwar K., et al. , The dynamin-like GTPase Sey1p mediates homotypic ER fusion in S. cerevisiae. J. Cell Biol. 197, 209–217 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Liu T. Y., et al. , Cis and trans interactions between Atlastin molecules during membrane fusion. Proc. Natl. Acad. Sci. U.S.A. 112, E1851–E1860 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Terasaki M., Dynamics of the endoplasmic reticulum and golgi apparatus during early sea urchin development. Mol. Biol. Cell 11, 897–914 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ungricht R., Klann M., Horvath P., Kutay U., Diffusion and retention are major determinants of protein targeting to the inner nuclear membrane. J. Cell Biol. 209, 687–703 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pawar S., Ungricht R., Tiefenboeck P., Leroux J.-C., Kutay U., Efficient protein targeting to the inner nuclear membrane requires Atlastin-dependent maintenance of ER topology. eLife 6, 911 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Friedman J. R., Webster B. M., Mastronarde D. N., Verhey K. J., Voeltz G. K., ER sliding dynamics and ER-mitochondrial contacts occur on acetylated microtubules. J. Cell Biol. 190, 363–375 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Nixon-Abell J., et al. , Increased spatiotemporal resolution reveals highly dynamic dense tubular matrices in the peripheral ER. Science 354, aaf3928 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Honnappa S., et al. , An EB1-binding motif acts as a microtubule tip localization signal. Cell 138, 366–376 (2009). [DOI] [PubMed] [Google Scholar]
- 37.Rodríguez-García R., et al. , Mechanisms of motor-independent membrane remodeling driven by dynamic microtubules. Curr. Biol. 30, 972–987.e12 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wang S., Romano F. B., Field C. M., Mitchison T. J., Rapoport T. A., Multiple mechanisms determine ER network morphology during the cell cycle in Xenopus egg extracts. J. Cell Biol. 203, 801–814 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Schlaitz A.-L., Thompson J., Wong C. C. L., Yates J. R., Heald R., REEP3/4 ensure endoplasmic reticulum clearance from metaphase chromatin and proper nuclear envelope architecture. Dev. Cell 26, 315–323 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Park S. H., Zhu P.-P., Parker R. L., Blackstone C., Hereditary spastic paraplegia proteins REEP1, spastin, and atlastin-1 coordinate microtubule interactions with the tubular ER network. J. Clin. Invest. 120, 1097–1110 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nikonov A. V., Hauri H.-P., Lauring B., Kreibich G., Climp-63-mediated binding of microtubules to the ER affects the lateral mobility of translocon complexes. J. Cell Sci. 120, 2248–2258 (2007). [DOI] [PubMed] [Google Scholar]
- 42.Terasaki M., Song J., Wong J. R., Weiss M. J., Chen L. B., Localization of endoplasmic reticulum in living and glutaraldehyde-fixed cells with fluorescent dyes. Cell 38, 101–108 (1984). [DOI] [PubMed] [Google Scholar]
- 43.Rao K., et al. , Spastin, atlastin, and ER relocalization are involved in axon but not dendrite regeneration. Mol. Biol. Cell 27, 3245–3256 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Farías G. G., et al. , Feedback-driven mechanisms between microtubules and the endoplasmic reticulum instruct neuronal polarity. Neuron 102, 184–201.e8 (2019). [DOI] [PubMed] [Google Scholar]
- 45.Liu X., et al. , Atlastin-1 regulates morphology and function of endoplasmic reticulum in dendrites. Nat. Commun. 10, 568 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Blackstone C., O’Kane C. J., Reid E., Hereditary spastic paraplegias: Membrane traffic and the motor pathway. Nat. Rev. Neurosci. 12, 31–42 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Behrendt L., Kurth I., Kaether C., A disease causing ATLASTIN 3 mutation affects multiple endoplasmic reticulum-related pathways. Cell. Mol. Life Sci. 76, 1433–1445 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Krols M., et al. , Sensory-neuropathy-causing mutations in ATL3 cause aberrant ER membrane tethering. Cell Rep. 23, 2026–2038 (2018). [DOI] [PubMed] [Google Scholar]
- 49.Zemel A., Rehfeldt F., Brown A. E. X., Discher D. E., Safran S. A., Optimal matrix rigidity for stress fiber polarization in stem cells. Nat. Phys. 6, 468–473 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Portran D., Schaedel L., Xu Z., Théry M., Nachury M. V., Tubulin acetylation protects long-lived microtubules against mechanical ageing. Nat. Cell Biol. 19, 391–398 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Janke C., Bulinski J. C., Post-translational regulation of the microtubule cytoskeleton: Mechanisms and functions. Nat. Rev. Mol. Cell Biol. 12, 773–786 (2011). [DOI] [PubMed] [Google Scholar]
- 52.Xu Z., et al. , Microtubules acquire resistance from mechanical breakage through intralumenal acetylation. Science 356, 328–332 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Nigg E. A., Raff J. W., Centrioles, centrosomes, and cilia in health and disease. Cell 139, 663–678 (2009). [DOI] [PubMed] [Google Scholar]
- 54.Mikule K., et al. , Loss of centrosome integrity induces p38-p53-p21-dependent G1-S arrest. Nat. Cell Biol. 9, 160–170 (2007). [DOI] [PubMed] [Google Scholar]
- 55.Gut G., Tadmor M. D., Pe’er D., Pelkmans L., Liberali P., Trajectories of cell-cycle progression from fixed cell populations. Nat. Methods 12, 951–954 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Zhao G., et al. , Mammalian knock out cells reveal prominent roles for atlastin GTPases in ER network morphology. Exp. Cell Res. 349, 32–44 (2016). [DOI] [PubMed] [Google Scholar]
- 57.Schroeder L. K., et al. , Dynamic nanoscale morphology of the ER surveyed by STED microscopy. J. Cell Biol. 218, 83–96 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Georgiades P., et al. , The flexibility and dynamics of the tubules in the endoplasmic reticulum. Sci. Rep. 7, 16474 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Gauthier N. C., Fardin M. A., Roca-Cusachs P., Sheetz M. P., Temporary increase in plasma membrane tension coordinates the activation of exocytosis and contraction during cell spreading. Proc. Natl. Acad. Sci. U.S.A. 108, 14467–14472 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Fogelson B., Mogilner A., Computational estimates of membrane flow and tension gradient in motile cells. PLoS One 9, e84524 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Speckner K., Stadler L., Weiss M., Anomalous dynamics of the endoplasmic reticulum network. Phys. Rev. E 98, 012406 (2018). [DOI] [PubMed] [Google Scholar]
- 62.Saini S. G., Liu C., Zhang P., Lee T. H., Membrane tethering by the atlastin GTPase depends on GTP hydrolysis but not on forming the cross-over configuration. Mol. Biol. Cell 25, 3942–3953 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Zucker B., Kozlov M. M., Mechanism of shaping membrane nanostructures of endoplasmic reticulum. Proc. Natl. Acad. Sci. U.S.A. 119, e2116142119 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Goyal U., Blackstone C., Untangling the web: Mechanisms underlying ER network formation. Biochim. Biophys. Acta Mol. Cell Res. 1833, 2492–2498 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Zheng P., et al. , ER proteins decipher the tubulin code to regulate organelle distribution. Nature 601, 132–138 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Wang S., Tukachinsky H., Romano F. B., Rapoport T. A., Cooperation of the ER-shaping proteins atlastin, lunapark, and reticulons to generate a tubular membrane network. eLife 5, 209 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Rismanchi N., Soderblom C., Stadler J., Zhu P.-P., Blackstone C., Atlastin GTPases are required for Golgi apparatus and ER morphogenesis. Hum. Mol. Genet. 17, 1591–1604 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or SI Appendix.
The probability maps of ER segmentation and the live cell data which were used for statistical assessment are deposited at Zenodo: https://zenodo.org/record/6369232#.YjTsFy0RoWo.