Significance
Understanding how humans process time series data is more pressing now than ever amid a progressing pandemic. Current research draws on some fifty years of empirical evidence on laypeople’s (in-)ability to extrapolate exponential growth. Yet even canonized evidence ought not to be trusted blindly. As a case in point, I review a seminal study that is still highly (even increasingly) cited, although seriously flawed. This case serves as both a reminder of how readily even experienced, well-meaning researchers underestimate exponential dynamics, and an admonition for subsequent researchers to critically read and evaluate the research they cite in order to catch and correct errors quickly rather than carry them forward over decades.
Keywords: exponential growth, prediction task, experiment, extrapolation, cognitive bias
Abstract
Scientists prominently argue that the COVID-19 pandemic stems not least from people’s inability to understand exponential growth. They increasingly cite evidence from a classic psychological experiment published some 45 years prior to the first case of COVID-19. Despite—or precisely because of—becoming such a canonical study (more often cited than read), its critical design flaws went completely unnoticed. They are discussed here as a cautionary tale against uncritically enshrining unsound research in the “lore” of a field of research. In hindsight, this is a unique case study of researchers falling prey to just the cognitive bias they set out to study—undermining an experiment’s methodology while, ironically, still supporting its conclusion.
In 1973, a young but well-published Dutch psychologist named Willem Albert Wagenaar visited Pennsylvania State University as an adjunct associate professor on a Fulbright grant. He conducted research together with a student named Sabato D. Sagaria (later an associate professor of psychology himself), and both of them ended up inspiring an entire field of research through a pioneering publication, for which Willem turned William, in 1975 (1).
Fast forward 45 years, the world is in a state of emergency, and Wagenaar and Sagaria’s findings are now more prominent than ever (1). Their study enjoys newfound popularity and has become a standard reference of sorts—cited wherever researchers lament people’s inability to understand and extrapolate time series that grow exponentially, which many say lies at the heart of our current COVID-19 pandemic (e.g., refs. 2–5).
There is just one hitch with Wagenaar and Sagaria’s seminal study: It was wrong all along. Their inventive experimental setup was plagued by three critical design flaws. Rather than document erroneous reasoning on the part of their participants, their study effectively turned the cognitive bias mirror on researchers themselves. With hundreds of other professors and PhDs citing the study while failing to appreciate and discuss its flaws, the experiment eventually became self-fulfilling of sorts—turning subsequent authors into unwitting participants in a metaexperiment that did fully accomplish what Wagenaar and Sagaria (1) had had in mind: to demonstrate dramatically how difficult and error fraught exponential extrapolation really is.
In a global pandemic where policies should rest on the best available evidence, this case should remind us of the diligence and critical scrutiny required in the face of even the most accepted canonical evidence. Therein lies, after all, a lasting value of Willem Wagenaar’s Pennsylvania stint—and a lesson to remember in subsequent research (not just) on COVID-19.
Background: Wagenaar and Sagaria’s Pollution Prediction Task
Imagine being shown the following sequence of numbers: 3, 7, 20, 55, and 148. Authorities tell you that this is a pollution index, measuring “pollution in the upper air space” in each of the years 2010 to 2014, respectively. What is your intuitive prediction, they ask you, for the pollution index in 2019? (Feel encouraged to pause for a moment to come up with your own prediction.)
This was the puzzle that Wagenaar and Sagaria (1) put to Penn State psychology students in their now classical experiment—except for the years being 1970 to 1974 rather than 2010 to 2014. The experiment tested other index progressions as well, but the authors disclosed no details, which explains why every follow-up study (e.g., 5–9) and even critics (e.g., 10, 11) have all zeroed in on just this example. How then would you continue the series after its fifth value, 148?
The researchers had generated their series using the simplest exponential function: f(t) = et, where f(t) is the pollution index, e is the base of the natural logarithm, and t is the number of years since 1969. Using this formula on each of the years 1970 to 1974 returns the values 2.72, 7.39, 20.09, 54.60, and 148.41, which round to exactly the sequence cited earlier. Extrapolating to 1979 (the tenth year in the series) yields e10, which the researchers called the “value prescribed by exponential extrapolation” or normative value for short. This was the prediction target for 1979 that they expected their participants to report.
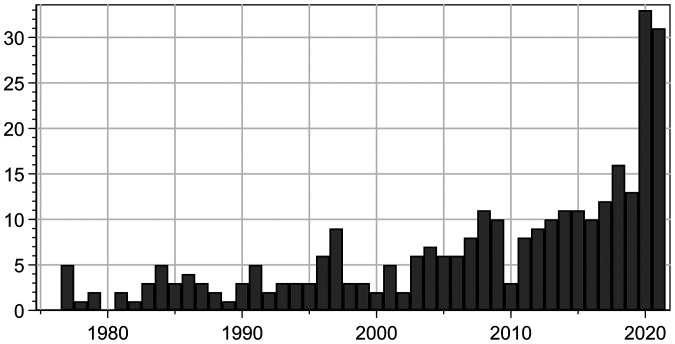
Looking at their experimental data, however, the authors were surprised and alarmed to discover that “[n]inety percent of the subjects estimated below half of the normative value” (1). Later researchers were likewise alarmed and cited the study at least 320 times (not counting many books), with seemingly exponential growth since the onset of COVID-19 (Fig. 1).
Fig. 1.
Citations to Wagenaar and Sagaria (1) each year since 1975 using Google Scholar data from 4 January 2022.
Despite some early (and limited) criticism (10, 11), Wagenaar and Sagaria’s study (1) was commended as “a fundamental reference” (12) and “a famous experiment” (13)—thus gradually becoming a canonical citation, even in an anthology on “the right way of doing psychology” (14). Recently, the study met with approval not just within some of the most reputable academic journals (2–4) and a growing number of popular science books (5, 15, 16) but also in normative analyses by legal scholars (12, 17, 18) and even policy documents such as the World Economic Forum’s COVID-19: The Great Reset (13). It seems to be almost everywhere these days.
Discussion: Three Critical Flaws in the Experiment’s Design
As is often the case with canonical literature, Wagenaar and Sagaria’s study (1) has accrued fame to a point where it probably gets cited more often than read. Despite its immense (and still growing) popularity, a closer look at the study’s design reveals three critical flaws that were never adequately addressed in any subsequent literature.
Flaw 1: Miscalculation of the Normative Value.
As the benchmark for their participants’ predictive performance, the authors stated a prediction target for 1979 (“normative value”) of 25,000 (1). This value appears to have never been questioned but instead, reiterated on faith by subsequent authors, who asserted simply that “[t]he correct answer is 25,000” (5, 8). Yet, this “correct answer” had, in fact, no basis in (correct) mathematics. Computing the 10th power of Euler’s number (e10) actually yields not 25,000 but merely 22,026. Thus, Wagenaar and Sagaria’s normative value was inflated by 13.5% right from the start—conversely lowering the share of their participants who actually did underestimate any growth process (1).*
Flaw 2: Misspecification of the Growth Process.
More critically, the authors relied on an unstated assumption about the functional dynamics of air pollution. They expected (but did not cue) their participants to extrapolate the series exponentially, instead of assuming noisy data from an underlying quadratic or other polynomial growth process. As an earlier critic noted, “There are an infinity of possible extrapolations, and choice between them can only be made on the basis of a hypothesis concerning the process that generated the numbers” (10). So, unless we assume pollution to beget more pollution, it should accumulate at the same rate by which polluters on the ground multiply. This may be exponential but need not be at all. In fact, pollution and similar phenomena “often do not demonstrate exponential growth” in practice because of ecological resilience; countervailing forces “would normally intervene to prevent unabated exponential growth” (10).
These are not merely theoretical objections. Even at the time of the experiment, contemporary research noted “the limited use […] by local air pollution control agencies” of exponential models, and recommended—as a best practice—to extrapolate air pollution based on a linearized calculation (19). Even researchers already used linear extrapolation (as when CO2 emissions were “predicted by using a 4%/y and a 3.5%/y growth rate”, ref. 20), since empirical data at the time suggested nothing like exponential growth. For any ten-year interval between 1940 and 1970, emission growth of various pollutants was reported at between –26 and +44% in total (20).
These estimates—no matter how accurate in hindsight—would have shaped contemporary assumptions, including those of the participants studied by Wagenaar and Sagaria (1). There was then—and is now—no atmospheric pollutant known to humanity that (even at a retention rate of 100%) would accumulate more than 7,000-fold in nine years, as a progression from 3 to 22,026 in the years 1970 to 1979 would have implied. The experiment’s participants would, therefore, have been well advised to assume subexponential growth given that neither theoretical nor empirical reasons suggested otherwise.
One might debate exactly which implicit function would have guided participants in the experiment; an earlier critic suggested polynomial extrapolation (10). For the present exposition, it suffices to show that there are indeed alternatives that do not require any exponential term. For instance, consider the polynomial f(t) = 0.04 × t5 + 3 × t. For years 1 through 5, this function would yield pollution indices of 3, 7, 19, 53, and 140—almost identical to the series cited earlier. Yet, extrapolating further would yield a wildly different prediction for year 10. Under polynomial growth, the process would arrive at 4,030 rather than 22,026.
Therefore, all that the experiment may have demonstrated are different assumptions about how air pollution accumulates. Given very few observations and a plausible subexponential mechanism, people may tend (justifiably) not to assume exponential growth. If, in contrast, the researchers did, then whose “misperception” did they really document?
Flaw 3: Misperception of Exponential Growth.
A third flaw is both the most intricate and most instructive. If you (dear reader) did actually pause earlier to extrapolate the series of five numbers cited in the Background section, how did you proceed?
Without guidance on the functional form, the most practical approach would be to compute the rate of change from one year to the next and to extrapolate on that basis. Consider the first five powers of Euler’s number cited earlier: 2.72, 7.39, 20.09, 54.60, and 148.41. The rate of change from 2.72 to 7.39 is +172%. The rate of change from 7.39 to 20.09 is +172%. So is the rate of change for each of the next steps in the series—which is mathematically trivial because adding 172% is exactly the same as multiplying by 2.72, the base (e) of our exponential process. If we continued to extrapolate by adding 172% to the 1974 value (148.41) and each of the subsequent values until 1979, we would obtain 22,096—off the normative value e10 = 22,026 by merely 70 units: a rounding error of 0.3%.
Note, however, this rounding error. What would happen if instead of computing the rate of change from numbers with two-digit precision, we computed it from rounded whole numbers, like those provided by Wagenaar and Sagaria (1)? In their series of 3, 7, 20, 55, and 148—despite each value being rounded correctly—we find a rate of change from the first year to the second of +133%; from the second to the third, +186%; from the third to the fourth, +175%; and from the fourth to the fifth, +169%. In other words, attentive participants observed four different rates of change between 133 and 186%. Since they could hardly be expected to compute an overall annual growth rate (165%) on the fly, they may have reasonably used a conservative extrapolation strategy. Using the initial growth rate (or the lowest of four; i.e., 133%), they might have determined 1979 pollution to come out at just 148 × 2.335 = 10,163.
Three Flaws—Three Prediction Strategies.
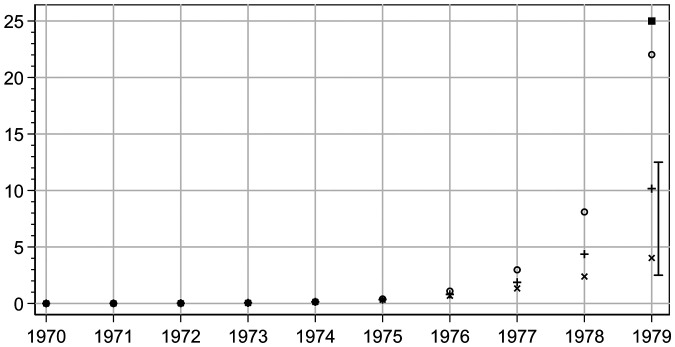
Given the three flaws we observed, we should indeed be surprised if any participant had estimated 1979 pollution at the supposed “normative value” of 25,000. Instead, accounting for each flaw in turn, we describe three different prediction strategies, which Fig. 2 illustrates.
Fig. 2.
Prediction strategies for the pollution index (y-axis; in 1,000) per year (x-axis).
To make sense of Fig. 2, first look at its right-most edge. At the very top sits the normative value of 25,000 expected by Wagenaar and Sagaria (1). Below it, the range plot (I) indicates the range within which, according to the experiment’s empirical findings, roughly a quarter of participants’ predictions fell. Ten percent of predictions fell above the higher end of the range, and two-thirds fell below the lower end; the authors were alarmed that the entire range was far removed from their expected normative value.
Now consider the three time series (+, x, and o). All start with almost identical values in the first five years—their markers overlap indistinguishably. This means that participants seeing these five values simply cannot know (absent additional information) which of three trajectories to follow: the exponential trend imagined by the researchers (o), a plausible polynomial alternative (x), or an extrapolation of the year by year growth rate under a conservative assumption (+).† Seeing that two of these trends end up, after ten years, well within the range of at least a third of Wagenaar and Sagaria’s participants, there may have been much less reason for alarm than the authors made out (1).
Conclusion: Turning the Cognitive Bias Mirror on Ourselves
The experiment by Wagenaar and Sagaria (1), albeit cited frequently, contained serious design flaws that undercut their analysis that “[n]inety percent of the subjects estimated below half of the normative value.” However, to the same extent that these flaws undermined the study’s design, its conclusion may, ironically, have gotten stronger still.
To see this, consider the third and most consequential flaw in Wagenaar and Sagaria’s design (1). They rounded 2.72 to 3.00 for the initial value of their series of ten. In other words, the very first value of their exponential progression was off from the true value by more than one-tenth. Such a difference of 10.4% in step 1 alone accumulates to a deviation of 168% in the tenth step of the progression. Had the researchers themselves properly appreciated the dynamics of exponential growth, they should never have rounded so liberally.
Why should this cognitive lapse concern us even fifty years later? The study’s first author has been dead for ten years, so this story would hardly be interesting if it was just about an honest mistake once made, a mere historical curiosity. After all, subsequent research by the same (e.g., 21) and other authors (e.g., 22) did document a tendency to underestimate exponential growth using more convincing experimental designs. The fact, however, that even today policy makers and lawyers continue to perceive the 1975 study as meaningful—or even exclusive—empirical evidence may teach us a broader lesson:
Time and again, flawed studies are cited uncritically, gradually building up “misinformation in and about science” (23), which solidifies with each additional citation. Conversely, the probability that researchers in a given field recheck earlier methods may decline over time as a paper becomes canonized in what Robert Abelson (24) once called “the lore of that field.” So, even with no reason to suspect that Wagenaar and Sagaria (1) erred in anything but the best of faith, decades of subsequent research should not have overlooked (or acquiesced to) their critical mistakes (notwithstanding rare but equally overlooked exceptions such as refs. 10, 11).
What their study therefore truly (and impressively) demonstrates is that even hundreds of professors and PhDs routinely underestimate the effect of a seemingly minor mathematical manipulation (such as rounding to the nearest integer) on subsequent exponential growth. This is a striking case study adding to a growing literature on “bias bias”. Researchers have a “tendency to spot biases even when there are none” (25) and to overstate biases because of their own cognitive limitations. For instance, a provocative study once asked, “Are we overconfident in the belief that probability forecasters are overconfident?” (26, 27). More recent analyses of another bias suggest that “the hot hand fallacy itself can be viewed as a fallacy,” committed by its very proponents themselves (28). In a similar vein, we can conclude that Wagenaar and Sagaria (1) devised a study not as much of their participants as of their academic peers—a fifty-year-long metaexperiment on the efficacy of scientific error correction with unfortunately rather bleak results.
This is why even today, almost five decades later, we should mind Wagenaar and Sagaria’s prescient conclusion: “Underestimation appears to be a general effect which is not reduced by daily experience with growing processes” (1). This is at once a timeless finding and an apt reminder to anyone in statistical practice—as well as a note of caution to policy makers relying on time-honored research to contain the exponential spread of a global pandemic.
Footnotes
The author declares no competing interest.
This article is a PNAS Direct Submission.
*Unfortunately, Wagenaar and Sagaria (1) did not document the raw data needed for an exact reanalysis (as would be best practice nowadays).
†Participants were in a position like major league baseball hitters facing top pitchers like Yu Darvish, whose pitches have been shown—by video overlay—to produce a wide range of deliveries from indistinguishable initial moves (https://www.youtube.com/watch?v=jUbAAurrnwU). I thank Carl Bergstrom for this instructive simile.
Data Availability
All study data are included in the article.
References
- 1.Wagenaar W. A., Sagaria S. D., Misperception of exponential growth. Percept. Psychophys. 18, 416–422 (1975). [Google Scholar]
- 2.Lammers J., Crusius J., Gast A., Correcting misperceptions of exponential coronavirus growth increases support for social distancing. Proc. Natl. Acad. Sci. U.S.A. 117, 16264–16266 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hutzler F., et al. , Anticipating trajectories of exponential growth. R. Soc. Open Sci. 8, 201574 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ritter M., Ott D. V. M., Paul F., Haynes J. D., Ritter K., COVID-19: A simple statistical model for predicting intensive care unit load in exponential phases of the disease. Sci. Rep. 11, 5018 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Eysenck M. W., Eysenck C., AI vs Humans (Routledge, 2022), pp. 253–256. [Google Scholar]
- 6.Svenson O., Time perception and long-term risks. INFOR Inform. Systems Oper. Res. 22, 196–214 (1984). [Google Scholar]
- 7.Mullet E., Cheminat Y., Estimation of exponential expressions by high school students. Contemp. Educ. Psychol. 20, 451–456 (1995). [Google Scholar]
- 8.O’Donnell P., Arnott D., “An experimental study of the impact of a computer-based decision aid on the forecast of exponential data” in Proceedings of the Pacific Asia Conference on Information Systems—PACIS (1997), p. 279. https://aisel.aisnet.org/pacis1997/29. Accessed 25 March 2022.
- 9.María T. M. S., Mullet E., Evolution of the intuitive mastery of the relationship between base, exponent, and number magnitude in high-school students. Math. Cogn. 4, 67–77 (1998). [Google Scholar]
- 10.Jones G. V., A generalized polynomial model for perception of exponential series. Percept. Psychophys. 25, 232–234 (1979). [DOI] [PubMed] [Google Scholar]
- 11.Jones G. V., Perception of inflation: Polynomial not exponential. Percept. Psychophys. 36, 485–489 (1984). [DOI] [PubMed] [Google Scholar]
- 12.Reifner U., Schroeder M., Usury Laws: A Legal and Economic Evaluation of Interest Rate Restrictions in the European Union (Books on Demand, 2012). [Google Scholar]
- 13.Schwab K., Malleret T., COVID-19: The Great Reset (Forum Publishing, 2020). [Google Scholar]
- 14.Rainer H., Über die Richtige Art, Psychologie zu Betreiben: Klaus Foppa und Mario von Cranach zum 60, Grawe K., Hänni R., Semmer N., Eds. (Verlag für Psychologie Hogrefe, 1991), p. 254. [Google Scholar]
- 15.Pinker S., Rationality: What It Is, Why It Seems Scarce, Why It Matters (Viking, 2021). [Google Scholar]
- 16.Azhar A., The Exponential Age: How Accelerating Technology Is Transforming Business, Politics and Society (Diversion Books, 2021). [Google Scholar]
- 17.Hermstrüwer Y., Informationelle Selbstgefährdung (Mohr Siebeck, Tübingen, Germany, 2016), pp. 290–291. [Google Scholar]
- 18.Zamir E., Teichman D., “Mathematics and law: The legal ramifications of the exponential growth bias” (Legal Research Paper 21-11, Hebrew University of Jerusalem, Jerusalem, Israel, 2021). https://web.archive.org/web/20210723073612/law.huji.ac.il/sites/default/files/law/files/zamir.teichman.egb_.pdf. Accessed 25 March 2022.
- 19.Ott W. R., Thom G. C., A critical review of air pollution index systems in the United States and Canada. J. Air Pollut. Control Assoc. 26, 460–470 (1976). [DOI] [PubMed] [Google Scholar]
- 20.Bach W., . Global air pollution and climatic change. Rev. Geophys. 14, 429–474 (1976). [Google Scholar]
- 21.Wagenaar W. A., Timmers H., The pond-and-duckweed problem: Three experiments on the misperception of exponential growth. Acta Psy. 43, 239–251 (1979). [Google Scholar]
- 22.Banerjee R., Bhattacharya J., Majumdar P., Exponential-growth prediction bias and compliance with safety measures related to COVID-19. Soc. Sci. Med. 268, 113473 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.West J. D., Bergstrom C. T., Misinformation in and about science. Proc. Natl. Acad. Sci. U.S.A. 118, e1912444117 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Abelson R. P., Statistics as Principled Argument (Psychology Press, 1995), p. 105. [Google Scholar]
- 25.Gigerenzer G., The bias bias in behavioral economics. Rev. Behav. Econ. 5, 303–336 (2018). [Google Scholar]
- 26.Pfeifer P. E., Are we overconfident in the belief that probability forecasters are overconfident? Org. Behav. Hum. Dec. Proc. 58, 203–213 (1994). [Google Scholar]
- 27.Erev I., et al. , Simultaneous over- and underconfidence: The role of error in judgment processes. Psy. Rev. 101, 519–527 (1994). [Google Scholar]
- 28.Miller J. B., Sanjurjo A., Surprised by the hot hand fallacy? A truth in the law of small numbers. Econometrica 86, 2019–2047 (2018). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All study data are included in the article.