Predicting relative efficiency of amide bond formation using multivariate linear regression

Significance

Given the ubiquity of amide coupling reactions, understanding the factors which influence the success of the reaction and having means to predict the reaction rate would streamline synthetic efforts. This study outlines a data science–based workflow for effective statistical modeling with sparse experimental data. We demonstrated informed substrate selection, collection of rate data and interpretable molecular descriptors, and statistical model development for amide coupling rates. The resulting statistical models illuminate substrate features that impact rate and allow for the prediction of untested amide coupling rates.

Abstract

Amides are ubiquitous in biologically active natural products and commercial drugs. The most common strategy for introducing this functional group is the coupling of a carboxylic acid with an amine, which requires the use of a coupling reagent to facilitate elimination of water. However, the optimal reaction conditions often appear rather arbitrary to the specific reaction. Herein, we report the development of statistical models correlating measured rates to physical organic descriptors to enable the prediction of reaction rates for untested carboxylic acid/amine pairs. The key to the success of this endeavor was the development of an end-to-end data science–based workflow to select a set of coupling partners that are appropriately distributed in chemical space to facilitate statistical model development. By using a parameterization, dimensionality reduction, and clustering protocol, a training set was identified. Reaction rates for a range of carboxylic acid and primary alkyl amine couplings utilizing carbonyldiimidazole (CDI) as the coupling reagent were measured. The collected rates span five orders of magnitude, confirming that the designed training set encompasses a wide range of chemical space necessary for effective model development. Regressing these rates with high-level density functional theory (DFT) descriptors allowed for identification of a statistical model wherein the molecular features of the carboxylic acid are primarily responsible for the observed rates. Finally, out-of-sample amide couplings are used to determine the limitations and effectiveness of the model.

Amide bonds are ubiquitous in proteins, commercial drugs, and biologically active molecules. In fact, amide bond–forming reactions account for approximately a quarter of all reactions performed in drug discovery programs and are an attractive disconnection due to the ease of compound diversification and the variety of conditions that can be utilized (1). This functional group is most commonly introduced by reacting amines with carboxylic acids, which although thermodynamically favorable, does not readily occur under mild conditions. Thus, activating reagents are routinely used to form reactive intermediates (e.g., acid chlorides, mixed anhydrides, carbonic anhydrides, and activated esters) that serve as acyl electrophiles for nucleophilic attack by the amine (2).

Despite the prevalence of amide coupling reactions, identifying the optimal conditions for a specific target can be challenging due to the number of reaction parameters (e.g., activating reagent, solvent, temperature, stoichiometry, mode of addition, etc.) that can be varied (3). Furthermore, in multistep synthesis, an amide coupling can be implemented at various stages, requiring the exact identity of the acid and amine components to be considered, since different structural features can influence the overall success of a coupling reaction. Typically, multiple iterations of high-throughput experimentation (HTE) are used to explore many activating reagents and conditions for a given set of reaction partners, but insights from one screen are not always transferable when the acid or amine component is modified. Given that HTE is well precedented at exploring different reaction parameters for a set of reaction partners, we sought to develop a statistical model to understand how structural features of the acid and amine fragments contribute to the success of a given amide coupling.

In this context, predicting rates is a task that chemists routinely perform, though often only in a relative sense for cases where significant steric or electronic differences exist (e.g., substrate A will be faster than substrate B). De novo prediction of absolute bimolecular rate constants (k) is a challenging problem, even when high-level ab initio computational methods are employed. In cases where multiple steric and/or electronic factors are in competition, we hypothesized that even relative comparisons would be difficult for trained chemists (1). Simply stated, considering the diversity of possible amide couplings, it is not easy to intuitively determine which substrate features impact the rate of a given amide coupling reaction. To probe this hypothesis, we designed a survey (see SI Appendix for details) that asked participants to order the relative rates of five amide couplings performed under identical conditions but with a unique acid and amine fragment for each reaction. The results revealed that no consensus was achieved for predicting rates, even among expert synthetic chemists (SI Appendix, Fig. S1). Notably, out of >65 chemists surveyed, not a single participant successfully ordered the rates of all five reactions.

The ubiquity of amide-forming reactions and the results of this survey indicated to us that there is a general need for methods that provide greater insight into the structural features of the acid and amine fragments that contribute to the rate of the desired coupling reaction. Such methods could serve to streamline time- and resource-intensive HTE screens by avoiding substrate combinations that show poor reactivity. They could also prove useful in early development and medicinal chemistry when quantities (and time) are limited, providing insight into reaction conditions with the least number of iterations. Additionally, this type of tool would be especially beneficial when implemented in the late stages of multistep syntheses, where complex precursors are not readily available for screening in large quantities, or to derisk proposed synthetic routes during brainstorming efforts.

To inform these goals, we surmised that a method to predict the observed second order rate constant (k) for a hypothetical combination of acid and amine partners would provide the necessary insight into how the molecular features of each component contributed to the overall reaction. The k for a reaction is not directly related to the overall yield; however, it is proportional to the activation energy and therefore provides information on the overall ease of bringing the two species together. From a practical perspective, working at concentrations of 0.5 M, any k below 0.01 M⁻¹·min⁻¹ is less attractive, as it would take over 24 h to reach 90% conversion. While multiple studies exploring kinetic analysis of amide couplings have been reported, such studies lack the systematic and simultaneous variation of both coupling components that would encompass the reaction space necessary for predictive capacity (4, 5). Given that literature data are highly biased toward positive results and do not ensure chemical diversity of the substrates, we elected to collect experimental rate data for our statistical model–building efforts under a standardized set of conditions.

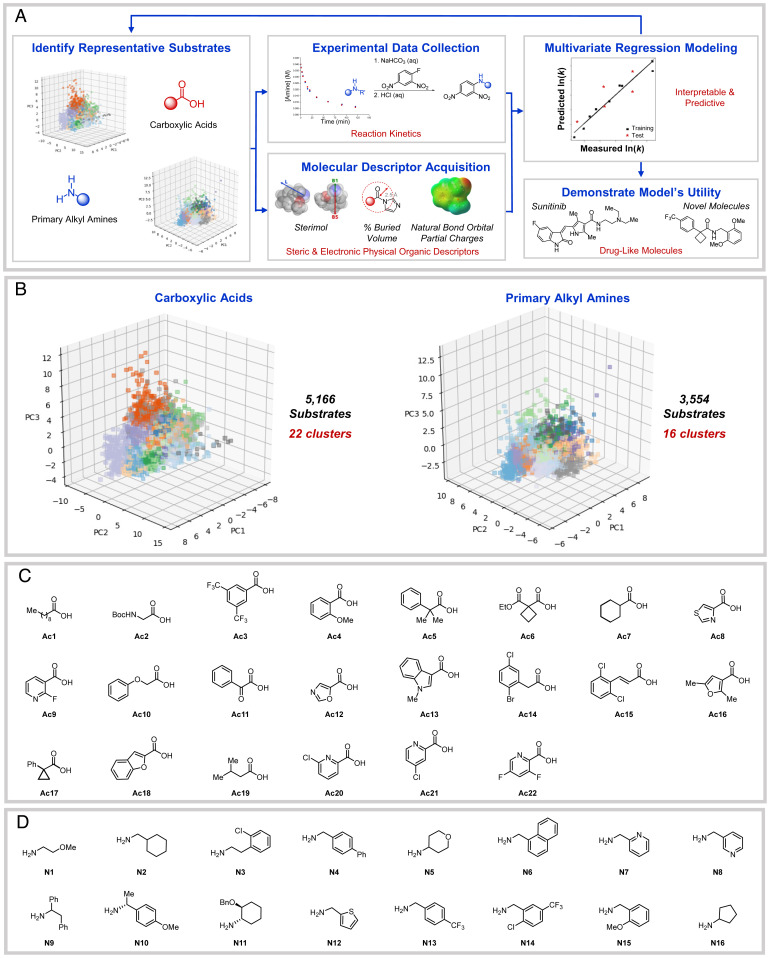
The project workflow consists of five key steps (6) (Fig. 1A): 1) dataset design (7–10), 2) measurement of reaction kinetics (11), and 3) acquisition of molecular descriptors (6), followed by 4) development of a statistical model correlating the kinetic outputs with physical organic molecular descriptors (6) and 5) model implementation to predict outcomes of untested amide coupling reactions (11, 12). This data science workflow was employed to develop quantitative structure-property relationships that provide insight to the reaction rates of carboxylic acid/amine pairs that have not been tested. Additionally, use of interpretable molecular descriptors allows the model to extend beyond predicting reaction rates and provide chemists with a general understanding of the important structural features that govern the rate of a given amide coupling. Through application of this workflow, we have developed a model that predicts the rate of amide couplings for previously unseen substrates within reasonable error.

Fig. 1.

(A) Project workflow. (B) PCA plots showing clusters by color for carboxylic acids in 22 clusters and primary alkyl amines in 16 clusters. Three PCs describe 57.2% (72.6% in 5 PCs) of the variance in the acids and 59.5% (78.1% in 5 PCs) of the variance in the amines. (C) Selected carboxylic acids and (D) primary alkyl amines for training set substrates.

Results and Discussion

Substrate Selection.

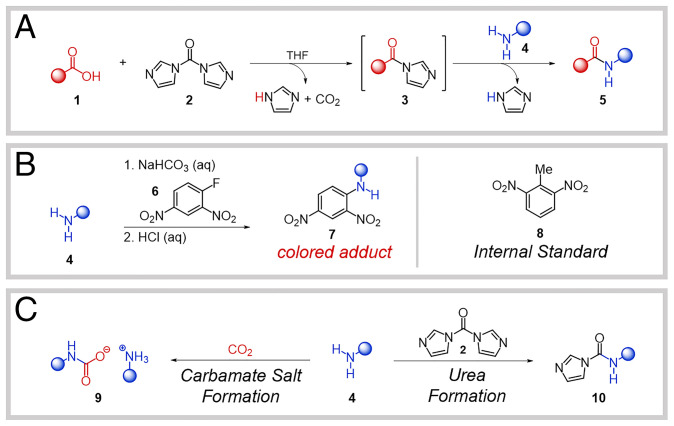
Given the number of commercially available carboxylic acids and amines, collecting kinetic data for even a portion of the possible coupling combinations would not be feasible. Thus, we implemented a workflow to select a representative subset of substrates that would reduce the number of measurements necessary while maintaining the diversity crucial to ensuring the system is amenable to statistical modeling (9, 13, 14). The system chosen for study utilized coupling reactions between commercially available carboxylic acids and primary alkyl amines, with carbonyldiimidazole (CDI) as the coupling reagent and tetrahydrofuran (THF) as the solvent (Fig. 2A). Primary alkyl amines were selected for this initial demonstration to narrow the substrate scope while still being ubiquitous in amide couplings. CDI was chosen as the coupling reagent as it is synthetically easy to work with, generates readily removable byproducts, does not require an additional base, and is commonly employed in industrial settings (3).

Fig. 2.

(A) Reaction under study. (B) Amine-quenching reaction, noting colored amine adduct 7 and internal standard (8, 2,6-dinitrotoluene). (C) Alternative amine consumption pathways by CO₂ and CDI.

For substrate selection, the web platform Reaxys was used to identify a list of commercially available carboxylic acids and primary alkyl amines. Additional filtering of the results was performed to limit molecular weight to <500 g/mol (to avoid peptides) and eliminate incompatible functional groups (e.g., diamines, diacids, hydroxyl groups, compounds that contain both an acid and an amine, etc.). The remaining compounds encompassed >5,000 carboxylic acids and >3,500 amines to evaluate for training set selection. Of note, the number of possible amine and acid combinations is still greater than 10⁷, which far exceeds experimental viability.

Developing a comprehensive model requires a system that provides a wide range of descriptor values and experimental reaction outputs (i.e., variance in reaction rate: fast, moderate, and slow) (15). In order to select representative carboxylic acid and amine substrates, chemical space was first defined using the dimensionality reduction technique of principal component analysis (PCA) (16–21). Molecular descriptors [i.e., Sterimol values, natural bond orbital (NBO) partial charges, and minimum electrostatic potential (22)] used for PCA were obtained by submitting the filtered substrates to a molecular mechanics (MM) gas-phase conformational search using the OPLS3e force field (23). The lowest energy conformer identified was submitted for a Gaussian density functional theory (DFT) single-point calculation [B3LYP/6-31G*, SMD(THF)]. Fig. 1B is a representative depiction of the acid and amine substrates plotted in three-dimensional principal component (PC) space (21).

K-means clustering (24, 25) was employed on five-dimensional PC space for both the carboxylic acids and amines. The number of clusters defined was largely informed by considering future experimental work that would demand a feasible number of substrates for rate collection. We also strived to include a proportionate number of clusters from the possible acids and amines and to employ the elbow method (SI Appendix, Fig. S2) to provide insight into the optimal number of clusters (26). As a result, we hypothesized that 22 acids (Fig. 1C) and 16 amines (Fig. 1D) would provide adequate diversity for statistical modeling and practicality for experimental work. From the identified clusters, substrates were selected to maximize the diversity in the sample set by picking one substrate from each cluster based on its proximity to the centroid (i.e., cluster center), cost of the material, and assay compatibility.

Experimental Data Collection.

The k (in M⁻¹·min⁻¹) of the coupling reaction between the amine 4 and the activated acid 3 was selected as the reaction output. Though yield could be employed as the measured output, meaningful measurements of low-yielding reactions would be difficult, and yields would not distinguish between rapid reactions with low barriers and slow reactions with high barriers. By contrast, reaction rate can reliably be measured across many orders of magnitude. A reaction k at a given temperature and known initial reactant concentrations can be used to determine yield at different timepoints when side reactions are mitigated and the product is stable. The ability to predict reaction rate (even as a range of values due to model uncertainty) has benefits in terms of kinetic modeling, as well as practical considerations for experimentalists (i.e., what concentration/temperature and how long a reaction should be performed) (27).

Reaction rates were collected by monitoring the concentration of remaining amine 4 upon addition to the pregenerated activated acid 3 at 25 °C (Fig. 2A). Amide couplings can often proceed with near-stoichiometric conversion due to the lack of side reactions; however, reactions that are inherently slow allow other pathways to compete. In our assay, the unreacted amine was quenched with 2,4-dinitrofluorobenzene (6, Sanger’s reagent) to yield the colored adduct 7 (Fig. 2B), which was quantified by ultra-performance liquid chromatography (UPLC) coupled to a photodiode array detector and normalized against an internal standard (8, 2,6-dinitrotoluene) (28).

Mitigation of amine side reactions is necessary in order to ensure meaningful reaction rate measurements were collected. In some cases, we observed unexpectedly high amine conversion after 1 min, which we attributed to either reaction of certain amines with carbon dioxide to form ammonium carbamate salts (4→9) (29, 30) or the presence of unreacted CDI, resulting in formation of urea-type products (4→10) (31) (Fig. 2C). Since CO₂ is generated during acid activation Fig. 2A and is known to impact the rate of amide couplings (30), we utilized three freeze-pump-thaw cycles following activation to remove any CO₂ from the system. For acid activation, control studies using ¹H-NMR showed that a modified protocol using a more concentrated reaction mixture (0.2 M) for an extended time (18 h) consistently showed complete activation for a variety of substrates. While exhaustive mass balance analysis was not performed for every coupling, experiments that showed unexpectedly high initial amine conversion or a premature plateau in amine consumption were repeated to obtain reliable kinetic values. The product for each combination of acid and amine was also isolated and characterized to confirm that the desired amide coupling occurred (SI Appendix).

The sheer number of acid/amine combinations (352 in total) precluded exhaustive rate measurements of each combination. We therefore pursued further curation to a sufficient number of diverse couplings representative of reactivity, with the goal of ultimately predicting behavior for substrates outside of the training set. Our objective was twofold: collect as few rates as possible while ensuring 1) every acid and amine in the training set was represented in the dataset and 2) the collected rates spanned a wide range. This was achieved by collecting 44 absolute rates in duplicate, which spanned five orders of magnitude. For reference, assuming a reaction performed at 0.5 M, this span in rates translates to the difference between requiring 5 min vs. 4 d to achieve 97% conversion. This rate range suggests that the training set encompasses the range of chemical space presumably required for model development.

Molecular Descriptor Acquisition.

Physical organic molecular descriptors serve to quantify steric and electronic substrate features using mathematical relationships (6, 32). In turn, reaction rate can be correlated to interpretable molecular descriptors. Our approach exploits descriptors from either the acid or amine component individually, which allows for a mix-and-match approach to subsequent rate predictions rather than requiring descriptors be calculated for each specific combination of substrates. Computational analysis of both acid 1 and amine 4 are key variables, but the acid also assumes several other forms during the course of the reaction, such as a carboxylate (deprotonated 1) and acyl imidazole 3. Thus, we obtained molecular descriptors for these four critical reaction components (1, carboxylate form of 1, 3, and 4). This was accomplished through modification of the computational procedure initially used for PCA. We employed a higher level of theory and included conformational flexibility, since many molecular descriptors can differ considerably as a function of conformation (33). A MM gas-phase conformational search using the OPLS3e force field produced a representative ensemble of conformers (23). All conformations within 3 kcal/mol of the lowest energy conformer were subjected to DFT optimization [B3LYP/6-311++G(d,p)] and single-point energy [M062X/6-311++G(d,p), SMD(THF)] calculations using Gaussian. Molecular descriptors appropriate for the various forms of the substrates were determined, and from the optimized structures for all conformers of a given substrate, the molecular descriptors were extracted. Molecular descriptors (SI Appendix and Dataset S2) acquired include NMR chemical shifts, infrared (IR) frequencies, NBO partial charges, bond lengths, bond angles, dihedral angles, percent buried volume (%V_bur), and Sterimol values (6). Each descriptor was calculated as the Boltzmann weighted average to convey the dynamic nature of experimental chemistry, combatting the static picture of a single conformer. The maximum/minimum values for each descriptor, as well as the descriptor values from the lowest energy conformer, were also collected.

Model Development.

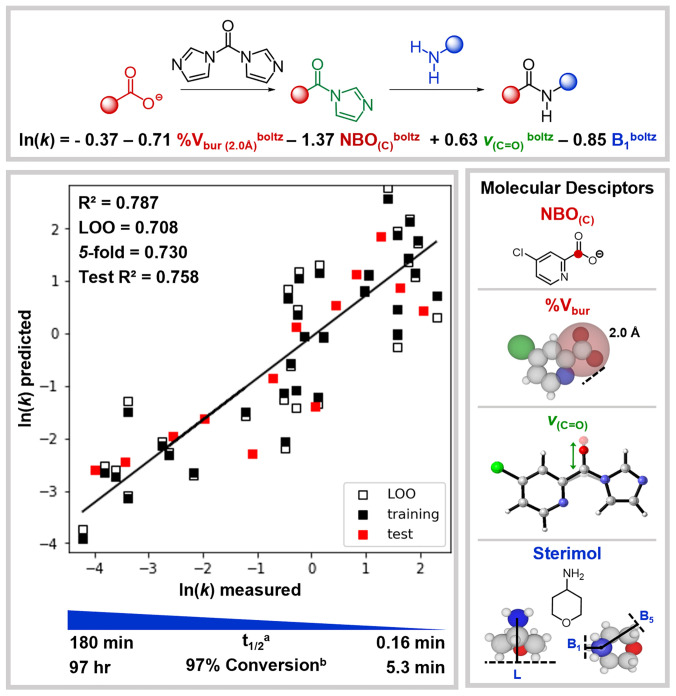
Multivariate linear regression (MLR) analysis using a forward stepwise algorithm was performed by regressing the DFT-derived molecular descriptors to the measured ln(k), as it is proportional to the Gibb's free energy of activation (ΔG^‡) (6). The original 44 couplings were split 70:30 into training (31 couplings, black squares) and test (13 couplings, red squares) sets using a pseudorandom automated process in the algorithm. Model candidates were subsequently evaluated using statistical metrics: [R², leave one out (LOO), k-fold (k = 5)] (6). While data collection was in progress, preliminary models were utilized to predict couplings not yet included in the dataset, allowing us to identify acid and amine combinations that would provide rate data in regions where experimental data were sparse (10).

A model for the coupling of carboxylic acids and primary alkyl amines with CDI using Boltzmann averaged descriptors is shown in Fig. 3. Models using descriptors from the lowest energy conformer, maximum and minimum descriptor values, and Boltzmann averaged descriptors are statistically similar and are presented in SI Appendix. Given that descriptors are first normalized, the relative signs and magnitudes of equation coefficients can be analyzed to indicate the relative importance of such features. We have presented the model using Boltzmann averaged descriptors as it is hypothesized to most accurately reflect the relevant species involved in the amide bond–forming step (34). In this model, the carboxylate NBO partial charge at the carbonyl carbon (Fig. 3, red) has the largest contribution to determining the reaction rate. It reveals that a more positive partial charge results in a slower reaction. While this may seem counterintuitive, the same dependence on NBO charge for the acyl imidazole intermediate is also observed. We interpret this to indicate that while a greater positive charge on the central carbon may be more susceptible to attack from the amine, it is also less prone to expulsion of the imidazole leaving group as required by the mechanism. The amine Sterimol B₁ (Fig. 3, blue) refers to the minimum distance perpendicular to the primary L axis, which was defined along the N‒C_α bond. This steric descriptor indicates that the bulkier the amine, the slower the reaction will proceed. The amine B₁ term also classifies the amine as α-branched or not, which affects both the steric and electronic nature of the coupling partner. A steric descriptor for the acid component also arises, indicating that the greater %V_bur within a 2.0 Å sphere about the carbonyl carbon of the carboxylate (Fig. 3, red) reduces the rate. Lastly, the higher the carbonyl stretching frequency of the activated acid (Fig. 3, green), the faster the reaction rate. This describes the amine attack of the activated acid to form the tetrahedral intermediate, which is likely rate determining.

Fig. 3.

MLR equation and model plotted as predicted vs. measured ln(k) and representations of the molecular descriptors used in the model. Reaction half-life (t_1/2) calculated for second-order kinetics and time to 97% conversion (denoted with superscript letters a and b, respectively) for reactions with initial amine and CDI concentrations of 0.5 M.

Notably, three terms in the model equation describe the acid component, whereas only one term describes the amine. This suggests that the rate is largely dictated by the molecular features of the acid coupling partner. Examination of experimental rates reveals that the acid component largely determines the magnitude of the rate and the amine has only a modest impact. For a chemical system to be amenable to statistical modeling, overlapping structural features must be present to provide a means to compare reactions (e.g., carboxylic acid functional group, primary amine functional group, and CDI as a coupling agent). Thus, we hypothesize that the subtle differences in rate that arise from the various primary alkyl amines do not merit a significant contribution to the model. More dramatic amine differences (i.e., primary vs. secondary amines and aryl amines) would likely cause other amine terms to be required in model construction. Of note, some of the least hindered amines show the slowest overall rate, which further reinforces that for primary amines, the size of this component is not a major contributor to the overall rate. Regarding the statistical metrics, we obtained reasonable values for R², LOO, and k-fold even though our training set comprised <10% of the possible combinations of amines and acids (31 out of 352), which further highlights the success of our PCA and clustering protocols.

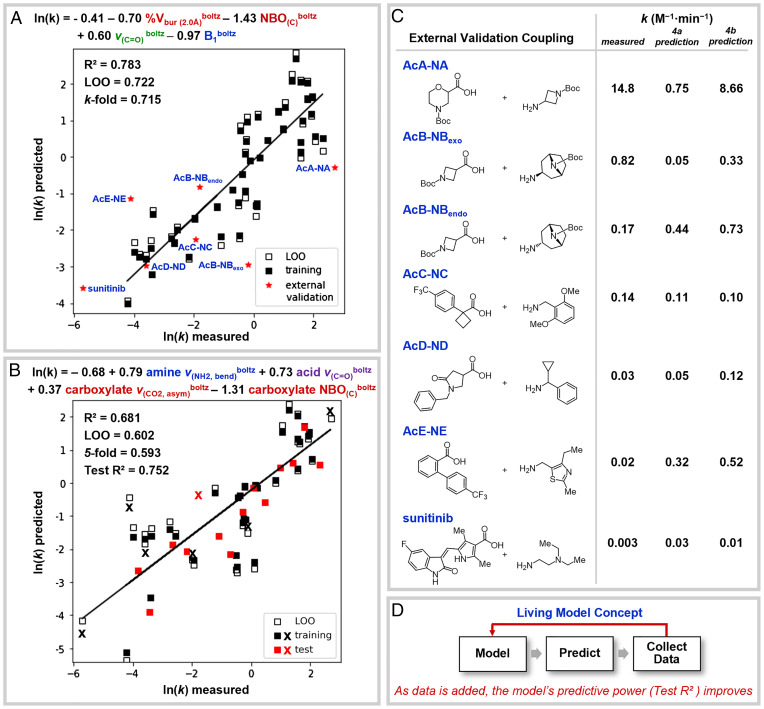
The effectiveness of the model was further explored by external validation. A set of substrates with motifs that are commonly found in pharmaceuticals and that were structurally unique from those in the original training set were selected to probe the model’s ability to make predictions for diverse couplings. The DFT-derived molecular descriptors of the external validation amine and acid fragments are computed. These descriptor values are then inserted into the MLR model (Fig. 4A) to predict the rate of the untested reaction. The model in Fig. 4A is fit using all the training set data by no longer withholding a test set, ensuring the model is provided as much data as possible to make accurate out-of-sample predictions. The updated model utilizes the same general features, albeit with slightly different coefficients. This model is used in conjunction with the unseen substrates’ molecular descriptors to predict the external validation coupling rates (red stars).

Fig. 4.

(A) MLR model, using the same descriptors as the Fig. 3 model, used to predict rates of external validation amide couplings. (B) Model retrained on all training and external validation data (pseudorandom 70:30 training/test split), where x indicates a coupling previously in the external validation set. (C) External validation couplings with their measured rates and predicted rates based on the MLR model in A and B. (D) Living model concept schematic.

The evaluation of several external couplings (Fig. 4A, red stars) demonstrates the utility and limitations of the model. A total of seven reactions (Fig. 4C) using acid and amine substrates not provided for the initial model construction were evaluated. Overall, the predictions were found to be consistent within one order of magnitude of the measured value, with a few exceptions. Compared to the experimental rates, the relative ordering of predicted rates is in agreement for five out of seven external validation couplings. It should be noted that amine substrates similar to those used in couplings AcC-NC and AcE-NE are found in the training set, but as stated earlier, the amine component has less impact on the reaction rate. Coupling AcC-NC was predicted well, but coupling AcE-NE fails to be predicted within a reasonable degree of error. The differences in the model’s predictive capacity for these two couplings can be explained by the nature of the training set. There are α-tertiary carboxylic acids (i.e., Ac6 and Ac17) included in the training set that resemble the acid substrate used in coupling AcC-NC. In contrast, there are no ortho substituents on the acid larger than a methoxy group in the training set. Thus, the model has not been trained to anticipate the impact of larger groups, namely, the ortho-phenyl group from the acid, used in coupling AcE-NE. The modest performance of predictions involving amine diastereomers NB_endo and NB_exo is consistent with the low sensitivity given to amine sterics by the current model. Perhaps of most consequence, the CDI-mediated amide coupling used in the synthesis of sunitinib, a U.S. Food and Drug Administration (FDA)-approved cancer drug, was effectively predicted (29). The model was able to predict this coupling rate within one order of magnitude. This is particularly significant as the measured rate falls outside the range of the training set, requiring the model to extrapolate in order to make the prediction.

As the model utilizes sparse data in its construction, one can envision feeding this model more data as they are obtained. In short, we intend to build a living model to which data can be added for continuous improvement through retraining of the model (Fig. 4D). To demonstrate the value of doing so, the collective training set and external validation set data were combined to generate another model (Fig. 4B). This is an added benefit of our training set design approach, as it allows any identified shortcomings in the model to be trained in using the next iteration of substrates. Fig. 4B shows that while the retrained model’s general mechanistic features are similar, the subtle differences in the selected descriptors can better incorporate what were previously outliers from the external validation set (Fig. 4B, x; predictions tabulated in Fig. 4C), resulting in an improvement to the test R² from 0.715 to 0.752.

Conclusion.

In summary, we have demonstrated the ability to use a rationally designed series of carboxylic acids and primary alkyl amines under standardized conditions to construct interpretable, mechanistically insightful, and predictive statistical models for the rate of amide couplings. The molecular features important to determining reaction rate were elucidated, indicating electronic descriptors are necessary to explain the acid component, and steric descriptors for both reaction components are required. The dataset design results in coupling rates that span five orders of magnitude, which allows our MLR model to predict untested coupling reaction rates within a large range using substantially fewer data points than would be required by HTE. We report most rate predictions of previously unseen couplings within one order of magnitude. Further expansion of the training set to include more diverse substrates, as well as additional substrate classes such as secondary amines, will improve accuracy and offer greater insight into the factors controlling these ubiquitous reactions. We believe these results validate our data science–based workflow for creating a predictive model to cover a diverse chemical space while minimizing extensive data collection and believe that this strategy can be applied to other classes of reactions that are of interest to chemists.

Materials and Methods

Substrate and activated acid conformational searches were performed using MM gas-phase computations implemented via MacroModel (35). All DFT-level molecular descriptors were extracted from Gaussian (36) output files using an in-house Python script. PCA was performed on DFT molecular descriptors at the B3LYP/6-31G*, SMD(THF) level of theory (Dataset S1). DFT descriptors from a geometry optimization [B3LYP/6-311++G(d,p)] and single-point energy [M062X/6-311++G(d,p), SMD(THF)] calculation were used to for model generation (Dataset S2). Kinetic data were collected by monitoring unreacted amine quenched with 2,4-dinitrofluorobenzene to yield a colored adduct, which was quantified by UPLC coupled to a photodiode array detector and normalized against an internal standard (2,6-dinitrotoluene). Beginning with a set of molecular descriptors hypothesized to have mechanistic significance for the selected training set substrates, stepwise linear regression was performed using in-house Python scripts. Statistical models identified were evaluated for robustness by both cross- and external validation. Greater detail for PCA, the experimental procedure for rate determination, computational methods used to obtain molecular descriptors, and the model development process are provided in SI Appendix.

Data Availability

All study data are included in the article and/or supporting information.