Pure nematic quantum critical point accompanied by a superconducting dome

Significance

The notion of the quantum critical point (QCP) is at the core of modern condensed matter physics. Near a QCP of the symmetry-breaking order, associated quantum-mechanical fluctuations are intensified, which can lead to unconventional superconductivity. Indeed, dome-shaped superconducting phases are often observed near the magnetic QCPs, which supports the spin fluctuation–driven superconductivity. However, the fundamental question remains as to whether a nonmagnetic QCP of electronic nematic order characterized by spontaneous rotational symmetry breaking can promote superconductivity in real materials. Here, we provide an experimental demonstration that a pure nematic QCP exists near the center of a superconducting dome in nonmagnetic FeSe${}_{1-x}$ Te_x. This result evidences that nematic fluctuations enhanced around the nematic QCP can boost superconductivity.

Abstract

When a symmetry-breaking phase of matter is suppressed to a quantum critical point (QCP) at absolute zero, quantum-mechanical fluctuations proliferate. Such fluctuations can lead to unconventional superconductivity, as evidenced by the superconducting domes often found near magnetic QCPs in correlated materials. Experimentally, however, it remains much less clear whether the superconductivity can be promoted around QCPs of the electronic nematic phase, characterized by rotational symmetry breaking. Here, we demonstrate from systematic elastoresistivity measurements that nonmagnetic FeSe${}_{1-x}$ Te_x exhibits an electronic nematic QCP showing diverging nematic susceptibility. This finding establishes two nematic QCPs in FeSe-based superconductors with contrasting accompanying phase diagrams. In FeSe${}_{1-x}$ Te_x, a superconducting dome is centered at the QCP, whereas FeSe${}_{1-x}$ S_x shows no QCP-associated enhancement of superconductivity. We find that this difference is related to the relative strength of nematic and spin fluctuations. Our results in FeSe${}_{1-x}$ Te_x present the unprecedented case in support of the superconducting dome being associated with the QCP of pure electronic nematic order, which does not intertwine with any other long-range orders.

In unconventional superconductors, the interplay between superconductivity (SC) and a quantum critical point (QCP), defined as the point of continuous phase transition at absolute zero temperature, has been one of the central topics for decades. At the QCP, the ground state becomes a scale-invariant critical state, in which quantum-mechanical fluctuations are substantially enhanced (1). These enhanced quantum fluctuations couple with the low-energy quasiparticle excitations near the Fermi energy, which causes the non-Fermi liquid power law behavior of the physical quantities and sometimes leads to the formation of Cooper pairs. In particular, the focus of interest has been on the antiferromagnetic QCPs found in many classes of unconventional superconductors, such as heavy-fermion and iron-pnictide superconductors (2, 3). The phase diagrams of these materials show a dome-shaped superconducting phase near the vanishing point of the antiferromagnetic phase, which implies that strong spin fluctuations near the antiferromagnetic QCP can mediate the superconductivity with high critical temperature $T_{\text{c}}$ (4).

In recent years, several kinds of unconventional superconductors have also been found to exhibit electronic nematic orders, which break rotational symmetry of the underlying lattice, close to the superconducting phase (5–7). It is then important to investigate whether such nematic fluctuations can promote unconventional superconductivity or not. Theoretical studies have pointed out that they can enhance the critical temperature $T_{\text{c}}$ (8–10). Indeed, recently, nematic fluctuations in Ba${}_{1-x}$ Sr_x Ni₂ As₂ have been shown to contribute to an increase of $T_{\text{c}}$ (11), and the drastic suppression of $T_{\text{c}}$ under the uniaxial strain in Ba(Fe${}_{1-x}$ Co_x)₂ As₂ (12) is in line with the nematicity-mediated superconductivity predicted in the theory (13). However, the nematic orders in these materials coexist with other intertwined spin or charge orders, which makes it challenging to experimentally establish that nematic fluctuations themselves can strengthen the superconducting pairing.

The iron-chalcogenide superconductor FeSe is an ideal system to address this issue. This compound exhibits an electronic nematic phase below the tetragonal to orthorhombic structural transition temperature $T_{\text{s}}$ $\sim 90$ K, but unlike most iron-based superconductors, it does not show any long-range magnetic order down to zero temperature (14). By applying hydrostatic pressure, $T_{\text{s}}$ of FeSe is rapidly suppressed, but before the vanishing of nematic order, a pressure-induced antiferromagnetic order sets in. This magnetic phase shows a dome shape in the pressure phase diagram, whereas $T_{\text{c}}$ exhibits a fourfold increase from 9 K at ambient pressure up to ∼37 K when the antiferromagnetism is suppressed at high pressure (15). In contrast, the isovalent S substitution for Se can suppress $T_{\text{s}}$ to zero temperature without stabilizing the magnetic order, but $T_{\text{c}}$ is found to show an abrupt decrease across the end point of the nematic phase (16). Thus, experimentally, there is no evidence in S-substituted FeSe that nematic fluctuations enhanced at the end point of $T_{\text{s}}$ promote superconductivity.

The Se site of FeSe can also be substituted by isovalent Te. Previously, the single-crystal studies of FeSe${}_{1-x}$ Te_x were almost limited to the high Te–composition side ($x\mathrm{\gtrsim }0.50$), which had shown that FeSe${}_{0.5}$ Te${}_{0.5}$ does not exhibit nematic order with $T_{\text{c}}$ as high as 14 K (17, 18). Although elastoresistivity measurements in FeSe${}_{0.4}$ Te${}_{0.6}$ single crystals grown by the flux method show that the nematic susceptibility diverges toward $\sim -10$ K (19, 20), its evolution to FeSe has not been clarified. Recent advances in the single-crystal growth of FeSe${}_{1-x}$ Te_x by the flux method under the temperature gradient conditions (21) and the chemical vapor transport (CVT) technique (22) have enabled the systematic tracing of the nematic and superconducting transition temperatures with Te substitution by overcoming the phase separation issue previously reported for $0.10\mathrm{\lesssim }x\mathrm{\lesssim }0.30$ (23). It has been found that $T_{\text{s}}$ of the CVT-grown single crystals is monotonically suppressed with increasing Te concentrations and disappears around x = 0.50, whereas $T_{\text{c}}$ first decreases, reaches its minimum at $x\sim 0.30$, and then, turns to increase (22), as reproduced in Fig. 1B, Lower.

Fig. 1.

Nonmagnetic nematic quantum critical points in FeSe-based superconductors. (A) S and Te composition dependence of the a-axis length (Bottom), c-axis length (Middle), and the height of the chalcogen from the Fe plane (Top). Closed pentagons and open diamonds are from refs. 22 and 37, respectively. (B) Combined phase diagram of FeSe${}_{1-x}$ S_x and FeSe${}_{1-x}$ Te_x, which includes $T_{\text{s}}$ determined by the resistivity (yellow squares) and X-ray diffraction experiments (orange squares) (22), $T_{\text{c}}$ (blue triangles), the transition temperature to the antiferromagnetic (AFM) phase $T_{\text{N}}$ (red squares) (31), and T₀ obtained from the analysis of $2m_{66}$ data (red circles). The data of closed symbols are from the single crystals grown by the CVT technique (22), and the data of open symbols in the highly Te substituted region are taken from the study of single crystals synthesized by the flux method (31). The magnitude of $2m_{66}$ is shown as a color plot. $T_{\text{c}}$ has a two-dome structure, which contains two nematic QCPs ($x_{\text{c,S}}$ and $x_{\text{c,Te}}$), and the superconducting state can be separated into three regions (SC1, SC2, and SC3), whose properties are considered to be different.

The increase in $T_{\text{c}}$ toward the end point of $T_{\text{s}}$ points to a potential link between suppressed nematicity and enhanced superconductivity in FeSe${}_{1-x}$ Te_x. However, this increasing trend of $T_{\text{c}}$ with vanishing $T_{\text{s}}$ stands in marked contrast to the phase diagram of FeSe${}_{1-x}$ S_x, which raises the fundamental question of the origin of this difference. To discuss the above issues, it is essential to clarify how nematic fluctuations evolve with Te substitutions compared with the S-substitution case and whether we have a nematic QCP in the phase diagram of FeSe${}_{1-x}$ Te_x. Here, by performing systematic elastoresistivity measurements on FeSe${}_{1-x}$ Te_x single crystals to quantify the nematic susceptibility, we demonstrate that FeSe${}_{1-x}$ Te_x is an unprecedented system whose nematic QCP lies near the center of the superconducting dome in isolation from any other long-range orders. Comparisons between the results in FeSe${}_{1-x}$ Te_x and FeSe${}_{1-x}$ S_x imply that the dominance of nematic fluctuations over antiferromagnetic fluctuations is the key to enhancing $T_{\text{c}}$ around the nonmagnetic nematic QCP.

Results

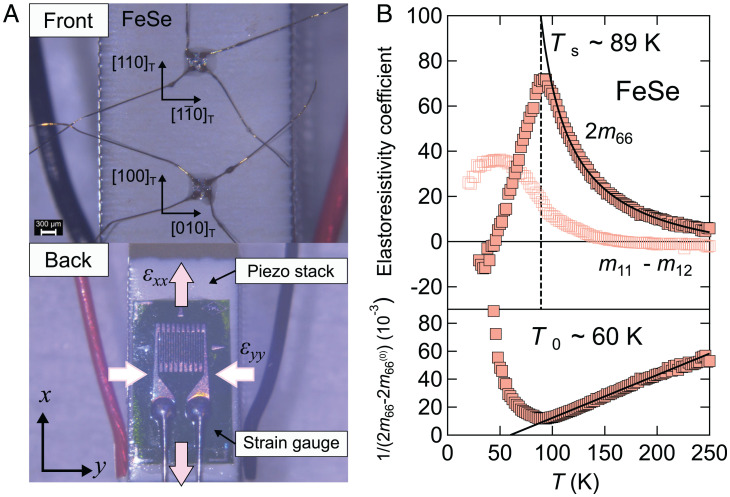
Nematic order is characterized by rotational symmetry breaking, and thus, its order parameter can be expressed by the anisotropy of physical quantities, such as electrical resistivity (5). Since the uniaxial strain works as a conjugate field to the nematic order parameter, the nematic susceptibility above the transition temperature $T_{\text{s}}$ can be obtained from the electronic anisotropy induced by the strain applied to the system as a perturbation. In our elastoresistivity measurements, we assume the in-plane resistivity anisotropy as an order parameter of the nematic phase, and the anisotropic biaxial strain is applied using the piezoelectric device (Materials and Methods) (24). As shown in Fig. 2A, for the resistivity measurements along two directions on a single sample, we apply the Montgomery method to the square-shaped crystals. The samples are directly glued on the surface of the piezo stack, and the strain is controlled by applying the voltage to the device and monitored by the strain gauge attached on the other side.

Fig. 2.

$B_{1g}$ and $B_{2g}$ nematic susceptibilities of FeSe measured by elastoresistivity technique. (A) Photographs of the elastoresistance measurement setup. The square-shaped samples with electric contacts on four corners were directly glued on the piezo stack. On the back side, the strain gauge was attached to measure the amount of the applied strain. For the $B_{2g}$ and $B_{1g}$ nematic susceptibility measurements, the samples are aligned along the ${[110]}_{\text{T}}$ and ${[100]}_{\text{T}}$ directions, respectively. B, Upper shows the temperature dependence of the two elastoresistivity coefficients of FeSe. The black line represents the Curie–Weiss fit for $2m_{66}(T)$. B, Lower displays the inverse of $2m_{66}-2m_{66}^{(0)}$, where $2m_{66}^{(0)}$ is determined by the Curie–Weiss fitting.

In the tetragonal FeSe-based materials with the $D_{4h}$ point group, there are two candidates for the in-plane nematic order. One is along the adjacent Fe–chalcogen direction with $B_{1g}$ irreducible representation, and the other is along the Fe–Fe direction with $B_{2g}$ symmetry (here, we use the experimental two-Fe unit cell notation). Nematic susceptibility for each symmetry channel can be measured by applying the strain along its corresponding direction and by using the elastoresistivity tensor defined as $m_{ij}={(\mathrm{\Delta }\rho /\rho )}_i/{\epsilon }_j$, where ${(\mathrm{\Delta }\rho /\rho )}_i$ is the relative change of resistivity against the strain ${\epsilon }_j$, with subscripts i and j represented by the Voigt notation ($1=xx,2=yy,3=zz,4=yz,5=zx,6=xy$); the $B_{1g}$ and $B_{2g}$ components can be expressed as $m_{11}-m_{12}$ and 2m₆₆, respectively (19).

Fig. 2B exhibits the temperature dependence of the two nematic susceptibilities for an FeSe single crystal. Above $T_{\text{s}}$, 2m₆₆ displays a strong temperature evolution with much larger magnitude compared with $m_{11}-m_{12}$, confirming the $B_{2g}$ Ising nematic order of FeSe. Furthermore, in the disordered state above $T_{\text{s}}$, 2m₆₆ obeys the Curie–Weiss law:

$$2m_{66}(T)=\frac{a}{T-T_0}+2m_{66}^{(0)},$$ [1]

where a and $2m_{66}^{(0)}$ are temperature-independent constants. The Curie–Weiss temperature T₀ gives the bare nematic transition temperature in the absence of nematoelastic coupling in the system. However, the presence of finite coupling shifts the thermodynamic nematic transition from T₀ to $T_{\text{s}}$ ($>T_0$). Inside the ordered phase below $T_{\text{s}},\hspace{0.17em}2m_{66}(T)$ no longer follows the Curie–Weiss law, as shown in Fig. 2B. The Curie–Weiss temperature dependence of the nematic susceptibility above $T_{\text{s}}$ in FeSe has also been reported in the previous measurements of the elastoresistivity, Young modulus, and Raman scattering (25–28).

Next, we discuss the evolution of nematic susceptibility with Te substitution. Single crystals of FeSe${}_{1-x}$ Te_x used in this study were grown by the CVT technique, which can tune the lattice parameters continuously (Fig. 1A). The CVT-grown crystals show homogeneous distributions of Te ions (SI Appendix, Fig. S1) with no resistivity upturn (22), which is caused by the localization effects due to excess Fe as reported in crystals synthesized by the Bridgman method for $x\mathrm{\gtrsim }0.50$ (20, 29). As depicted in Fig. 3, our systematic measurements in a wide range of Te composition $0\le x\le 0.51$ reveal that with increasing x, the $B_{2g}$ nematic susceptibility 2m₆₆ exhibits a continuous evolution with a gradual decrease in $T_{\text{s}}$. For all Te compositions with finite $T_{\text{s}}$, the temperature dependence of 2m₆₆ above $T_{\text{s}}$ can be reasonably described by the Curie–Weiss function, evidencing their continuous nematic transitions (SI Appendix has the protocol of Curie–Weiss analysis). The Curie–Weiss temperature dependence can be also seen at low temperatures in the tetragonal $x=0.51$, but here, we find a clear deviation from the Curie–Weiss behavior at high temperatures $T\mathrm{\gtrsim }150$ K. The magnitude of 2m₆₆ becomes largest at x = 0.38, in which the Curie–Weiss temperature becomes T₀ $\sim 0$ K. For comparison, we have also measured the $B_{1g}$ nematic susceptibility $m_{11}-m_{12}$, which is found to be much less significant than 2m₆₆ even in the tetragonal x = 0.51 (SI Appendix, Fig. S2), demonstrating that the large signal in 2m₆₆ solely comes from the $B_{2g}$ nematic response covering the entire Te composition range of the present study. The observed much weaker temperature dependence of $m_{11}-m_{12}$ contrasts with the case of FeTe, in which $m_{11}-m_{12}$ shows a diverging behavior toward the onset temperature of the double-stripe magnetism (30), while 2m₆₆ is much less temperature dependent (20). This implies that spin fluctuations associated with the double-stripe magnetic order are almost negligible for $x\le 0.51$.

Fig. 3.

Evolution of elastoresistivity coefficients $2m_{66}$ in FeSe${}_{1-x}$ Te_x. Temperature dependence of $B_{2g}$ nematic susceptibilities (Upper) and their Curie–Weiss analyses (Lower) for x = 0.06 (A), 0.12 (B), 0.20 (C), 0.28 (D), 0.34 (E), 0.36 (F), 0.38 (G), 0.40 (H), 0.46 (I), and 0.51 (J). In each panel, the structural transition temperatures $T_{\text{s}}$ are shown by the vertical dashed lines, except for x = 0.51 with no structural transition. Black lines represent the Curie–Weiss fitting, and the obtained Curie–Weiss temperatures T₀ are indicated in Lower.

From the elastoresistivity measurements, we map out the magnitude of 2m₆₆ in the phase diagram of FeSe${}_{1-x}$ Te_x (Fig. 1B). The Curie–Weiss temperature T₀ decreases almost monotonically with increasing Te composition and crosses the zero temperature line around x = 0.38, where the magnitude of 2m₆₆ is strongly enhanced. Since there have been no reports for long-range magnetic order up to $x\sim 0.90$ (31), the observed diverging $B_{2g}$ nematic susceptibility toward 0 K evidences if the electron subsystem was not under the lattice environment, we would have the nonmagnetic nematic QCP around x = 0.38. Note that the intensity of 2m₆₆, which measures the dynamic nematic susceptibility, should become strongest at T₀ $\sim 0$ K because it sees the scale of the bare nematic transition temperature (32, 33). The thermodynamic QCP, in which the continuous electronic nematic transition takes place at zero temperature, is shifted to the end point of $T_{\text{s}}$ due to the inevitable finite nematoelastic coupling.

The obtained set of nematic susceptibility data can be compared with the x dependence of $T_{\text{c}}$, combined with the previous reports for $x\mathrm{\gtrsim }0.60$ (Fig. 1B), which clearly indicates that the nematic QCP in this system locates near the center of the superconducting dome. This implies a close correlation between the nematic quantum phase transition and enhanced superconductivity. Our results are consistent with the recent study for the Te-rich side using Bridgman crystals, which shows the smooth suppression of 2m₆₆ for $x\mathrm{\gtrsim }0.50$ (20).

Our results on FeSe${}_{1-x}$ Te_x indicate that the isovalent Te substitution for Se, which may be considered as a negative chemical pressure effect (Fig. 1A), affects the superconductivity in a completely different way from the S substitution corresponding to a positive chemical pressure. To gain more insights into the difference between the Te and S substitution effects, we also performed the elastoresistivity measurements for FeSe${}_{1-x}$ S_x in the same experimental setup (SI Appendix, Fig. S4) and plotted the intensities of $2m_{66}$ on the same scale with that of FeSe${}_{1-x}$ Te_x in the combined phase diagram shown in Fig. 1B. As previously reported (25), 2m₆₆ of FeSe${}_{1-x}$ S_x also follows the Curie–Weiss temperature dependence, and its T₀ changes sign around x = 0.17 with a strong enhancement of the magnitude of nematic susceptibility, demonstrating the $B_{2g}$ nematic QCP (SI Appendix, Fig. S4). Furthermore, the singular behavior in 2m₆₆ at the QCP of FeSe${}_{1-x}$ S_x is found to be quite similar to that of FeSe${}_{1-x}$ Te_x (Fig. 4A), suggesting that the underlying nematic quantum critical behavior is essentially the same between the two systems.

Fig. 4.

Similarities of nonmagnetic $B_{2g}$ nematic quantum criticality in FeSe${}_{1-x}$ Te_x and FeSe${}_{1-x}$ S_x. (A) The temperature dependence of $2m_{66}$ for FeSe${}_{1-x}$ Te_x with x = 0.38 (purple squares) from Fig. 3G is compared with that for FeSe${}_{1-x}$ S_x with x = 0.18 (blue circles) from SI Appendix, Fig. S4D. (B) Strength of nematoelastic coupling $r_0=(T_{\text{s}}-T_0)/T_{\text{F}}$ in FeSe (orange square), FeSe${}_{1-x}$ Te_x (purple squares), and FeSe${}_{1-x}$ S_x (blue circles) as a function of the structural transition temperature. The purple and blue lines represent the linear fitting for the r₀ values of FeSe${}_{1-x}$ Te_x and FeSe${}_{1-x}$ S_x, and their shades correspond to the uncertainties of the fitting.

Discussion

Although diverging behavior of 2m₆₆ around the nematic QCP of FeSe${}_{1-x}$ S_x is almost identical to that of FeSe${}_{1-x}$ Te_x, $T_{\text{c}}$ of FeSe${}_{1-x}$ S_x exhibits a sudden decrease across the quantum phase transition, which is in sharp contrast to the superconducting dome in FeSe${}_{1-x}$ Te_x. As illustrated in Fig. 1 B, Lower, the dependence of $T_{\text{c}}$ on S concentration inside the nematic phase of FeSe${}_{1-x}$ S_x shows a broad peak structure, which is connected continuously to that in FeSe${}_{1-x}$ Te_x across x = 0 (FeSe), forming a superconducting dome (SC2). In this SC2 region of FeSe${}_{1-x}$ S_x, several bulk probes and surface-sensitive techniques have provided evidence that their superconducting gap structures have strong momentum dependence (14, 34, 35). Recent NMR experiments revealed that antiferromagnetic fluctuations with the $(\pi ,\pi )$ wave vector are enhanced inside the nematic phase of FeSe${}_{1-x}$ S_x, which appears to be in correspondence with the $T_{\text{c}}$ dome (36). Moreover, high-pressure studies in FeSe${}_{1-x}$ S_x demonstrated that $T_{\text{c}}$ is enhanced around the end points of the pressure-induced antiferromagnetic phase (37). These results imply the close relationship between antiferromagnetic fluctuations and enhanced superconductivity in the SC2 region.

In FeSe${}_{1-x}$ Te_x, the x dependence of $T_{\text{c}}$ shows a minimum at $x\sim 0.30$, above which another superconducting dome emerges around the nematic QCP found in this study. This nonmonotonic $T_{\text{c}}(x)$ in FeSe${}_{1-x}$ Te_x strongly suggests that the superconducting state (SC3) in the $x\mathrm{\gtrsim }0.30$ region has a different mechanism from that in SC2. Indeed, the full-gap superconductivity, which is quite different from the strongly momentum-dependent gap structures found in the SC2 region, has been reported by scanning tunneling spectroscopy in optimally substituted FeSe${}_{1-x}$ Te_x (38). Although Raman spectroscopy revealed that in FeSe${}_{0.4}$ Te${}_{0.6}$, the strength of electron–phonon coupling is insufficient to give $T_{\text{c}}$ $=14$ K (39), no significant $(\pi ,\pi )$ antiferromagnetic fluctuations are detected in the NMR experiments (40), which is consistent with the recent high-pressure study in FeSe${}_{1-x}$ Te_x showing that the pressure-induced antiferromagnetic order fades away above $x\sim 0.14$ (22). These results can preclude that the superconducting dome at $x\mathrm{\gtrsim }0.30$ is associated with magnetic fluctuations and further support that the enhancement of critical temperature in the SC3 region comes from the nematic quantum critical fluctuations observed in our elastoresistivity measurements.

Although several theories have shown that nematic fluctuations can enhance $T_{\text{c}}$, most of these theories consider pure electronic systems (8, 9), which do not include the coupling to the underlying lattice inevitably present in real materials. Recently, however, it has been pointed out that this nematoelastic coupling plays a crucial role in the nematic quantum criticality (32). Through the coupling to the lattice, the divergence of the correlation length at the nematic QCP is restricted only along the two high-symmetry regions, and the criticality can be cut off. Consequently, the strength of nematoelastic coupling becomes an important parameter at the nematic QCP, and this is closely related to the parameter $r_0=(T_{\text{s}}-T_0)/T_{\text{F}}$, where $T_{\text{F}}$ is the Fermi temperature. According to this theory, in FeSe-based materials with small Fermi energy, the effect of nematoelastic coupling can be particularly significant compared with other iron-based superconductors (SI Appendix, SI Text and Fig. S6). To compare the strength of the coupling with the lattice in FeSe${}_{1-x}$ S_x and FeSe${}_{1-x}$ Te_x, we plot in Fig. 4B the r₀ parameters estimated from the obtained $T_{\text{s}}$ and T₀ values as a function of structural transition temperature. Here, we assume that the Fermi energy is independent of composition and set to 20 meV for simplicity. We find that r₀ values of these two systems are close to each other, and moreover, their strengths at thermodynamic nematic QCP [$r_0(T_{\text{s}}\to 0)$] are also similar. The almost identical r₀ parameters between FeSe${}_{1-x}$ S_x and FeSe${}_{1-x}$ Te_x mean that the nematoelastic coupling is equally important to discuss the nematic quantum criticality in both systems.

It has been suggested from recent studies that the absence of the $T_{\text{c}}$ enhancement around the QCP in FeSe${}_{1-x}$ S_x is related to this nematoelastic coupling effect (41, 42). However, our above analysis reveals that even in the presence of sizable coupling to the lattice, the superconductivity can be enhanced around the nematic QCP in FeSe${}_{1-x}$ Te_x. The origin of this distinct difference between FeSe${}_{1-x}$ S_x and FeSe${}_{1-x}$ Te_x is an intriguing issue that deserves further investigation, but the recent phenomenological theory (33) may offer a qualitative explanation. This theory predicts that the enhancement of $T_{\text{c}}$ near the nematic QCP is expected only when the nematoelastic coupling parameter r₀ is much smaller than the ratio ${(U/V)}^2$, where U and V are the phenomenological parameters representing the nematic and magnetic pairing interactions, respectively (33). Although our observations of identically diverging nematic susceptibility around the two nematic QCPs (Fig. 4A) and similar strengths of nematoelastic coupling (Fig. 4B) imply that the nematic interaction U and coupling parameter r₀ are similar in FeSe${}_{1-x}$ S_x and FeSe${}_{1-x}$ Te_x, the spin interaction term V is considered quite different between them, as revealed by NMR measurements (36, 40). Namely, FeSe${}_{1-x}$ S_x with no enhancement of $T_{\text{c}}$ exhibits relatively strong spin fluctuations, leading to a small ${(U/V)}^2$ parameter, which may be unable to satisfy the $r_0\ll {(U/V)}^2$ relation; however, FeSe${}_{1-x}$ Te_x, in which no significant antiferromagnetic fluctuations are found and thus, a larger ${(U/V)}^2$ is expected, exhibits a clear superconducting dome near the thermodynamic nematic QCP.

Before concluding, we point out that the two superconducting domes (SC2 and SC3) studied here may have some similarities with the phase diagram of hole-doped high-$T_{\text{c}}$ cuprate superconductors under high magnetic fields, which also has two peaks in underdoped and slightly overdoped regions (43). While the center of one dome locates near the end point of the short-range antiferromagnetic order, the other with higher $T_{\text{c}}$ is around the critical doping at which the enigmatic pseudogap phase terminates. Recent studies showed that significant electronic anisotropy develops inside the pseudogap phase (44, 45), and there is evidence for enhanced nematic fluctuations at its critical point (6, 46). This similarity in the systems with quite different electronic structures may imply that nematic fluctuations can enhance superconductivity more strongly than previously thought, which stimulates further investigation.

In summary, the present systematic elastoresistivity measurements in FeSe${}_{1-x}$ Te_x single crystals provide strong evidence for the nonmagnetic pure nematic QCP accompanied by the superconducting dome. The enhancement of critical temperature in this material can be ascribed to the quantum critical fluctuations of the electronic nematic phase, which can offer a unique route to high-temperature superconductivity. We note that this is further supported by the recent high-field experiments in FeSe${}_{1-x}$ Te_x, which have revealed that the superconducting dome straddles the nematic QCP quite robustly even when the dome shrinks by applying the magnetic field (47).

Materials and Methods

Single Crystals.

Single crystals of FeSe${}_{1-x}$ S_x and FeSe${}_{1-x}$ Te_x were grown by the CVT technique (22, 37). The samples of FeSe${}_{1-x}$ Te_x measured in this study are from the same batches used in ref. 22. Fe, Se, and S (Te) powders were mixed with AlCl₃ and KCl transport agents and sealed in evacuated quartz ample. Temperatures of the source and sink sides were set at 420 ${}^{°}$C and 250 ${}^{°}$C for FeSe${}_{1-x}$ S_x and FeSe${}_{1-x}$ Te_x with $x\mathrm{\lesssim }0.25$ and 620 ${}^{°}$C and 450 ${}^{°}$C for FeSe${}_{1-x}$ Te_x with $x\mathrm{\gtrsim }0.25$, respectively.

The actual Te and S compositions were determined for each sample before the elastoresistivity measurements by the c-axis length measured by X-ray diffraction (Fig. 1A). For all the samples, homogeneous distributions of chalcogen ions were confirmed by energy-dispersive X-ray spectroscopy (SI Appendix, Fig. S1).

Elastoresistance Measurements.

For the systematic measurements of nematic susceptibility, we adopt the elastoresistivity measurement technique using the piezoelectric device. In this technique, we measure the strain-induced in-plane resistivity anisotropy. The experimental setup is shown in Fig. 2A. The samples are cut into square shapes, and the resistivity along the x and y directions (ρ_xx and ρ_yy) is measured by the Montgomery method. One advantage of this method is that we can measure both ρ_xx and ρ_yy in a given sample. To discuss the systematic dependence of the magnitude of the nematic susceptibility, we set the lateral sample size approximately fixed to 250 × 250 μm to minimize the possible size dependence.

After making the electrical contacts on the prepared samples, we glued them on the piezo stacks. The strain was transmitted to the sample via orthorhombic distortion of the device and controlled in situ by applying the voltage to the piezo stack. The amount of the strain ${\epsilon }_{xx}$ was measured by a strain gauge attached on the backside of the device, and the orthogonal strain ${\epsilon }_{yy}$ was calculated by the Poisson’s ratio of piezo stacks calibrated beforehand.

Data Availability

All study data are included in the article and/or SI Appendix.