Accounting for perception, placebo and unmasking effects in estimating treatment effects in randomised clinical trials

Abstract

There is a rich literature on the role of placebos in experimental design and evaluation of therapeutic agents or interventions. The importance of masking participants, investigators and evaluators to treatment assignment (treatment or placebo) has long been stressed as a key feature of a successful trial design. Nevertheless, there is considerable variability in the technical definition of the placebo effect and the impact of treatment assignments being unmasked. We suggest a formal concept of a ‘perception effect’ and define unmasking and placebo effects in the context of randomised trials. We employ modern tools from causal inference to derive semi-parametric estimators of such effects. The methods are illustrated on a motivating example from a recent pain trial where the occurrence of treatment-related side effects acts as a proxy for unmasking.

1. Introduction

Masking of participants and investigators has long been used in randomised clinical trials to prevent the measurement of research outcomes from being influenced by either the placebo effect or observer bias associated with knowledge of treatment assignment. This is of particular importance in clinical trials with a subjective patient response. During the course of blinded clinical trials, some patients, however, might be inadvertently unmasked to their assigned treatment, or at least grow to believe they are in a specific arm for several reasons. For instance, patients who receive treatment may believe they are on treatment as a result of experiencing documented treatment-related side effects, and/or placebo patients may believe that they are on placebo due to a lack of efficacy or worsening of their condition. Such ‘unmasking’ may subsequently affect outcome reporting. In these clinical trials, the investigator may be interested in the average causal effect of treatment in the target population, had unmasking not occurred with the patient’s perception of treatment assignment remaining at a fixed baseline level. In this article, we use methodology from the causal inference/semiparametric estimation literature to formally define and estimate perception, placebo and masking effects as theoretical interventions in a graphical model. We define causal treatment effects (after removal of unmasking effects) in terms of type I and type II direct effects based on a counterfactual framework¹ and estimate these effects using two semi-parametric estimation methods: maximum likelihood estimation (MLE) and targeted maximum likelihood estimation (TMLE). To motivate our discussion, these definitions and estimation methods will be applied to data from a recent clinical trial that was conducted to study the effect of the drug gabapentin for treatment of painful neuropathy among diabetic patients.

One of the most discomforting symptoms among diabetic patients is pain associated with peripheral neuropathy, estimated to affect about 45% of diabetic patients.² Backonja et al.³ published results of a randomised double-blind clinical trial, which was conducted to evaluate the effect of a drug called gabapentin (or Neurontin) on pain among patients with either type I or type II diabetes. The study consisted of a 7-day screening phase, followed by an 8-week double-blind phase, with 165 participants randomised to treatment or placebo groups. Baseline covariates such as age, height, weight, race, sex, baseline pain and sleep scores were measured during the screening phase, prior to randomisation. Treatment dosage was gradually titrated to a maximum tolerated dosage during the first 4 weeks of the double-blind phase, and it remained fixed thereafter. The main outcome measure was daily pain severity, recorded by patients on a 11-point Likert scale (0–10) in daily diaries, and the primary end point was calculated as the mean score for the last seven recorded diary entries.³

Using an intent-to-treat analysis, the investigators had reported that patients who received gabapentin had a significantly lower (p < 0.001) mean end point daily pain score than patients who received placebo with the treatment difference estimated to be a decline of 1.2 points. In what follows, we reanalyse the gabapentin trial data considering patients’ perceptions and unmasking. For all our analysis, we will use data on 164 participants (83 and 81 in the gabapentin and placebo groups, respectively) as one individual had reported no pain scores.

2. Non-specific effects of treatment and the placebo effect

Although our focus is on the effects of perception on estimation of an average causal treatment effect, it is worth beginning with a precise definition and brief discussion of the placebo effect. Beecher first quantified this phenomenon in 1955. He observed that in 15 trials studying different diseases, 35% of all 1082 patients were satisfactorily relieved by a placebo.⁴ Many researchers have subsequently studied the placebo effect and have claimed significant improvements in patients’ outcome due to this effect. However, a recent meta-analysis of clinical trials, including placebo and no-treatment groups, has questioned the significance of the placebo effect. Hrobjartsson and Gotzsche⁵ performed a meta-analysis of 114 randomised trials on 40 different clinical conditions comparing treatments, placebo controls and no-treatment controls. Their goal was to investigate whether patients assigned to placebo had a better outcome than those assigned to no treatment. The study found no significant placebo effect on binary or continuous objective outcomes. The only consistent placebo effect was observed for continuous subjective outcomes. Among the 40 conditions, only trials with subjective pain score assessments as an outcome displayed a significant average placebo effect.

In earlier literature, the placebo effect is referred to a variety of responses that occur when patients are being treated with inactive placebo that in theory should have no therapeutic effect. This definition of a placebo effect is what we refer to as the placebo response (i.e. the outcome of a patient receiving a placebo) and is different than how a placebo effect is defined in more recent literature. Turner et al.⁶ define the placebo effect as the non-specific effects of treatment attributable to factors other than specific active components. These non-specific effects include ‘physician attention, interest and concern in a healing setting; patient and physician expectations of treatment effects; the reputation, expense and impressiveness of the treatment; and characteristics of the setting that influence patients to report improvement’. The latter definition may be thought of as the difference in a patient’s outcome had he received a placebo compared with no treatment at all. These two differing definitions of the placebo effect have long been confused. Miller and Rosenstein⁷ note that progress in understanding and estimating the placebo effect has been hampered by a lack of conceptual clarity, some of which has been due to confusion of the placebo effect with the placebo response.

Consider the following hypothetical experiments: in a first experiment, a group of patients with a headache are observed without their knowledge. These patients receive neither a placebo nor any treatment. Any improvement in their condition must be solely due to the individual mechanisms of their bodies and/or interactions of the latter with a personalised environment. In a second experiment, a group of patients with a headache are given placebos by clinicians (with at least some expectation of a therapeutic effect as occurs when patients assume that there is some chance of receiving an active treatment), and their response is observed. Improvements in patients’ condition for this experiment are due to factors such as internal patient mechanisms, physician attention and patients’ expectation regarding their assigned therapy. The natural healing of the body cannot be attributed purely to the placebo effect as at least components of the effect are also present in the first experiment where patients do not receive a placebo. The placebo response is due to a combination of the placebo effect and internal patient mechanisms and must be distinguished from the placebo effect. As Miller and Rosenstein⁷ conclude, placebo-controlled trials are inadequate for elucidating the placebo effect, and to do so, we need no-treatment control groups.

Formally, we define the placebo effect for an individual as the difference in the outcome if an individual received a placebo when compared with no treatment at all. Although the presence of an active treatment does not directly factor into the definition, it is necessary for a placebo effect to exist. We return to this point further in the next section that discusses the impact of unmasking of treatment assignment.

Quantification of specific and non-specific effects of treatment has received considerable attention in recent years. Petkova et al.⁸ consider three hypothetical treatment scenarios of no treatment, placebo and active treatment, combined with the counterfactual framework to separate specific and non-specific effects of treatment. To estimate the placebo effect, they compare the outcome of the placebo group with the baseline measurements of the outcome variable for all the patients, implicit from certain model assumptions.⁸ Still, this remains unsatisfactory in situations where measurements on patients at baseline may not be exchangeable for those arising later in a ‘no-treatment’ group, as time itself is often an important factor influencing outcome assessment (as in the gabapentin trial).

3. Perception, unmasking and side effects as a proxy

Masking patients in clinical trials prevents them from knowing certain information about the trial, including the treatment group to which they are randomised. However, participants may develop a perception about their assigned treatment. Patients may either believe they are more likely to be on placebo, or more likely to be on treatment, or they may have no opinion about their treatment. In a more general sense, we may think of the patients assigning a degree of certainty to receiving a specific active treatment. In a single treatment/placebo trial, a low degree of certainty would imply that the patient is leaning towards placebo and a high degree would mean that the patient is on treatment. We refer to this random variable of degree of certainty as a patient’s perception, P, where P = 1 indicates that a patient is certain that he or she has been assigned the active treatment; at the other end of the scale, P = 0 indicates that a patient is certain that he or she is receiving the placebo.

In the extreme case where the investigator informs a patient about her treatment group, the patient would automatically have P = 1 or P = 0, depending on her original treatment assignment; such patients may be considered unmasked. We do not directly allow the variable P to distinguish here between the case where full unmasking has occurred and where an individual may be convinced that he or she is on active treatment (or placebo), although this perception is incorrect. However, interaction effects between P and T allow differentiation of these two scenarios.

In almost all cases, we do not observe the patient’s perception on a continuous scale, nor directly observe P. For simplicity, we focus on a discrete approximation. In particular, we consider observation of the following three-level variable, P, indicating perception, extending the simple version of P introduced above

$$P=\{\begin{array}{cc}1& \text{ patient believes she is on treatment }\hfill \\ 0& \text{ patient has no knowledge of assignment }\hfill \\ -1& \text{ patient believes she is on placebo }\hfill \end{array}$$

In double-blind studies, experimenters are also masked (in addition to patients) to prevent patient outcomes from being influenced by the experimenter’s expectations or interest. In such trials, data may be collected on experimenter’s perception in a similar fashion. Although our focus is on perception and unmasking of the patients, it is straightforward to expand our discussion to include perception/unmasking of investigators.

During the course of the gabapentin trial, some of the patients in both treatment and placebo arms developed a wide variety of side effects, many of which were known to be associated with active treatment. Backonja et al.³ acknowledge that since the study end point is subjective, the occurrence of adverse events may result in unmasking of some patients, potentially, biasing the results of their efficacy analysis. The authors circumvented this problem by separately excluding patients with dizziness and somnolence, ‘the two most frequent adverse events, and also, the two with the largest difference in incidence between the treatment and the placebo groups’.³ After excluding patients with dizziness, the estimated mean end point pain score for the gabapentin group remained 1.2 (p = 0.002) points lower than the placebo group. Effectively, this stratifies participants by occurrence of this particular side effect and considers the results solely in the group who do not experience these adverse events. By a similar stratified analysis, when patients who reported somnolence were excluded, the treatment–placebo difference dropped to 0.81 points (p = 0.03). By analysing side effects one-by-one, this approach neither addresses the simultaneous impact of all treatment-related side effects nor does it account for the effect of potential confounding variables, which will be discussed in section 6.

As in most clinical trials, patients in the gabapentin trial were not questioned on their perception regarding the treatment they received. It is likely, however, that the occurrence of any treatment-related side effects may have led patients to believe that they had been assigned to active treatment (incorrectly in some cases), the concern raised by the investigators leading to the naive analysis above that excluded patients with a single such side effect. We thus use the occurrence of any treatment-related side effects as a proxy for perception P being set to P = 1. The list of treatment-related side effects includes amnesia, ataxia, depersonalisation, insomnia and nervousness. A total of 43 patients, 31 in the gabapentin group and 12 patients in the placebo group, experienced at least one of these side effects during the 8-week period, the imbalance reflecting the anticipated association of these side effects with treatment. Patients who did not experience any side effects consisted of those who had no knowledge of the treatment assignment and those who believed they were receiving placebo. For our analysis, we label this group as P = 0, keeping in mind that it is a combination of the P = −1 and P = 0 groups introduced earlier. This point will be discussed further in the discussion section.

4. Type I and type II direct effects

Consider three possible treatment ‘conditions’ that may be assigned to all members of a population: (0) assigned to placebo, (1) assigned to active treatment and (2) assigned to neither treatment nor placebo. Such assignments may not be ethical in some experiments with a major outcome, and we only consider them here as a hypothetical experiments. For each individual, define Y_j to be the (possibly counterfactual) value of the outcome for individuals exposed to the jth treatment (j = 0, 1, 2). Then, the ‘causal’ placebo effect could be defined as ψ_placebo = E[Y₀ − Y₂] = E[Y₀] – E[Y₂], i.e. the population outcome mean when everyone receives the placebo in the experiment minus the outcome mean when all individuals receive neither treatment nor placebo. Note that for the placebo effect to occur, it is important that all individuals assigned to either treatment or placebo believe it is possible that they may receive active treatment. It is plausible and likely that the placebo effect, if it exists, depends on the perceived likelihood of receiving treatment.

One may argue that the no-treatment control group is already unmasked by knowing they are not receiving a treatment, or any attempt to measure their outcome may affect the outcome itself, and therefore, it is not possible to estimate the placebo effect. However, it may still be possible to estimate the placebo effect indirectly. For instance, consider cancer patients who visit their physician weekly to receive chemotherapy. At every visit, the patients are asked to rate their pain on a scale of 0–10 as part of a routine. The physician could (possibly) randomise some of these patients to a pain treatment group, some to a placebo group and some to a no-treatment control group. The patients who are assigned to either treatment or placebo groups will be informed that they are part of a pain treatment study. The placebo group may experience a placebo effect since they are aware of the possibility of being treated for pain, and they have a perceived likelihood of receiving the active treatment. Since the no-treatment group has no knowledge of the study or any expectations for improvement in their pain, and since their interaction with the clinicians is solely for cancer treatment, they may not experience a placebo effect.

Typically, it is not feasible to observe a single individual in more than one experimental setting and so the chosen treatment (j = 0, 1, 2) is randomly assigned to all individuals in the sample, and in principle, this removes the potential for confounding and allows population causal treatment and placebo effects to be estimated without bias. We now turn to the more common experiment where patients are solely allocated to either an active treatment or a placebo, so that the ‘no-treatment or placebo’ group (j = 2) is not evaluated.

For a variety of reasons, individuals may vary on their perception, P, of their assigned treatment, as defined in its approximate form at the end of section 3. Consider an ideal experiment in which the investigator measures the effect of a treatment A (1 = treatment, 0 = placebo) on the outcome by holding all patients’ perception at a fixed level P = p. In this ideal experiment, the direct effect of a treatment on an individual is defined as the difference in the counterfactual outcome if the individual received treatment with her perception fixed at level P = p when compared with the counterfactual outcome if she received placebo with her perception again fixed at the same level P = p. Using standard notation, the type I direct effect of a treatment on an individual can thus be written as Y_1,p − Y_0,p, where Y_a,p denotes an individual’s counterfactual outcome fixing both treatment and perception. The population direct effect of treatment at fixed perception level P = p is thus ψ_a(p) = E[Y_1,p − Y_0,p] = E[Y_1,p] − E[Y_0,p]. Usually, in experiments where full blinding can be achieved and maintained, interest focuses on this mean with P = 0.

In the rest of the article, although our focus will be on type I direct effects, it is worth mentioning the alternative type II direct effects. In the simple example above, a type II direct effect could be defined as the difference in the counterfactual outcome if an individual received placebo when compared with her counterfactual outcome if she received treatment, with her perception held fixed at its counterfactual level under placebo. In the population, the mean type II direct effect may thus be defined as ${\psi }_a\left(P_0\right)=E\left[Y_1,P_0-Y_{0,P_0}\right]$. In this case, P₀ is the perception level of the individual (possibly counterfactual) if she received placebo.¹ Note that a type I direct effect of a treatment is defined at a fixed level of perception for everyone in the population. On the other hand, for a type II direct effect of a treatment, the perception levels may vary from one individual to another. In the definition of a type II direct effect, although the perception levels vary among the patients, what patients have in common is that each individual’s perception is fixed at what her perception would have been had she received a placebo (for more information on type II direct effects, see Petersen et al.^1,9).

One advantage of using a type II direct effect is that it yields a single treatment/placebo comparison, whereas with type I direct effects potentially different comparisons exist for each fixed level of P. For instance, considering a binary treatment A = 0, 1 and a binary perception P = 0, 1, there are two possible type I direct effects of the treatment at fixed levels of perception, namely, ψ_a(1) = E[Y_1,1 − Y_0,1], and ψ_a(0) = E[Y_1,0 − Y_0,0], whereas the type II direct effect is given by ${\psi }_a\left(P_0\right)=E\left[Y_{1,p_0}-Y_{0,p_0}\right]$. However, the definition of a type II direct effect implied by a particular graph can be represented as a weighted average of the type I direct effects across the different strata of P.⁹ Thus, a type II effect may obscure the variation of different type I direct effects across the strata of perception levels.

In the following sections, we discuss estimation of the type I direct effects of treatment holding the post-randomisation variable, perception, fixed. A general discussion of causal inference in the analysis of the impact of post-randomisation factors can be found in Lynch et al.¹⁰ A similar causal structure (see section 6) in a quite different setting can be found in Rosenblum et al.,¹¹ where the post-randomisation factor is of use of a secondary treatment or intervention that is not randomised.

5. Additional parameters of interest

In addition to treatment effects at various levels of fixed perception, we may also be interested in the perception effects at a particular fixed treatment level. For example, the perception effect for placebo patients may be defined as the difference in the average outcome had everyone received placebo and was masked (i.e. P = 0) when compared with everyone receiving placebo but being unmasked (i.e. P = −1). In general, we define perception effects based on two distinct perception levels p_i, p_j for i ≠ j. The perception effect on the outcome, due to having perception P = p_i compared with P = p_j, at fixed treatment level a may be defined as ${\psi }_p\left(p_i,p_j,a\right)=E\left[Y_{a,p_i}\right]-E\left[Y_{a,p_j}\right]$; thus, ${\psi }_p\left(p_i,p_j,0\right)=E\left[Y_{0,p_i}\right]-E\left[Y_{0,p_j}\right]$ for placebo patients and ${\psi }_p\left(p_i,p_j,1\right)=E\left[Y_{1,p_i}\right]-E\left[Y_{1,p_j}\right]$ for treated patients. This framework naturally lends itself to organising the researchers’ thoughts by defining the parameter of interest as the one they could have estimated when they could have performed any theoretical experiment of interest and thus observed any set of counterfactuals of interest.

6. Estimation of type I direct effects

The marginal effects of treatment and perception may be estimated using non-parametric or semi-parametric estimators (depending on the complexity of the involved covariates). Semi-parametric estimators for these marginal effects include the maximum likelihood estimator,¹² the inverse probability of treatment weighted (IPTW) estimator,^13,14 the double robust inverse probability of treatment weighted (DR-IPTW) estimator^15–17 and the targeted maximum likelihood estimator.^18,19 We focus on the MLE and TMLE estimators, as the former is the simplest of the above estimators, and the TMLE estimator satisfies the properties of the most robust of these estimators (possessing the so-called double robust property discussed below). The TMLE estimator also has the property that guarantees a proper model for the parameter of interest, as well as the observed data-generating distribution, which is not a guaranteed property of the estimating equation approaches (IPTW and DR-IPTW), and it is easy to implement in this case using standard software.

Let A denote treatment assignment, P denote perception and Y be the outcome (as above). In addition, let W represent a vector of baseline (pre-randomisation) covariates. We have alluded to causal graph theory above, but now we discuss the consequences of assuming a particular direct acyclic graph (DAG), one that describes one set of possible causal relationships between A, P, W and Y. A DAG is a directed graph formed by a collection of nodes (variables) and directed edges, each edge connecting one node to another.²⁰ The acyclic property of DAGs imposes a restriction on a directed graph such that no direct path can form a closed loop that starts from a node and returns to that node.²⁰ Figure 1 illustrates a potential DAG that allows for (i) differing levels of perception across treatment groups, (ii) an effect of perception on the outcome and (iii) a set of covariates that effect both perception and outcome. Note that since W is measured prior to treatment randomisation, none of its components can lie on the causal pathway between A and Y.

Figure 1.

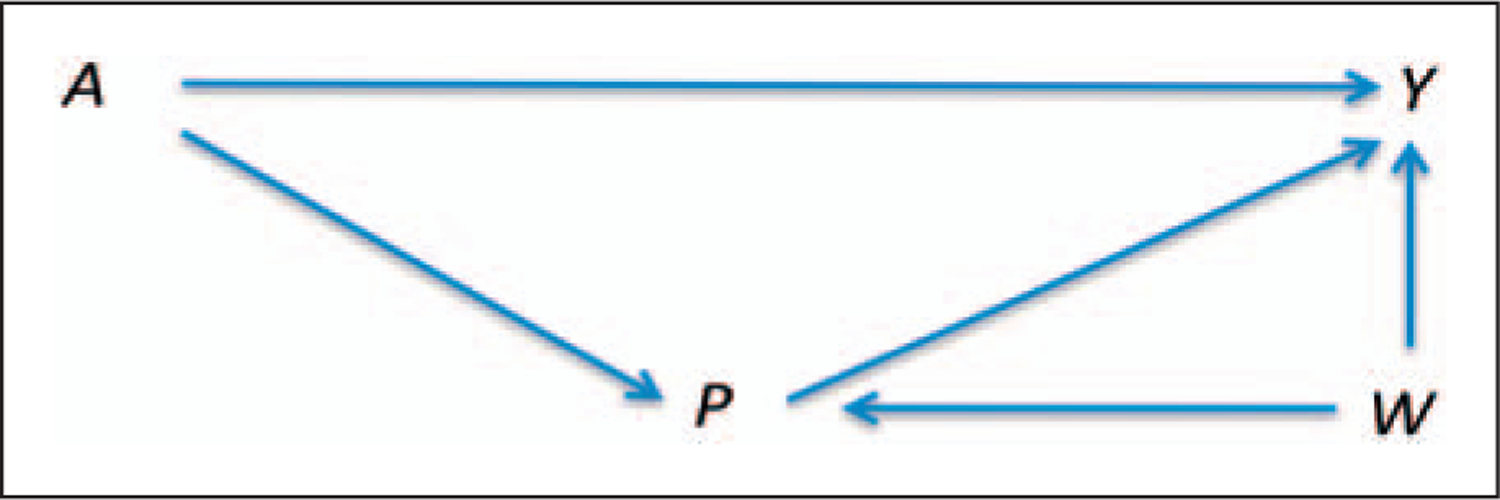
A direct acyclic graph linking treatment (A), perception (P), and covariates (W) to an outcome variable (Y).

It is tempting to estimate the direct effects of treatment, controlling for perception, via simple stratification on P. However, Fig. 1 and the rules developed for DAGs show that simply stratifying on perception, ignoring the covariates W, results in a biased estimate since this ‘introduces’ confounding of the direct effect of treatment on the outcome. This arises since P is a collider in the DAG, being caused by both A and W. In graphical models, a variable on a path is called a collider if it is caused by two or more variables, since the arrows of the causing variables appear to collide on that node, blocking that path.²⁰ Stratifying on colliders may result in new pathways being opened between the causing variables. Thus, if stratification/regression methods are to be used, it is necessary to adjust for both P and W. For further discussion of these issues, see chapter 3 in Pearl⁹ or chapter 9 in Jewell.²⁰ Conditioning on W raises new difficulties if the set of covariates W is high dimensional.

Returning to our general discussion, we note that the causal parameters defined in previous sections are defined in terms of all counterfactuals. However, we only observe one counterfactual for every subject. These parameters may still be estimated from observed data, however, if we make relevant assumptions. Different counterfactual outcomes are denoted as Y_a,p for every value of A = a and P = p, with the full data defined as X^FULL = (W, Y_a,p, a ∈ A, p ∈ P), where we use A and P to denote the set of possible values of treatment and perception, respectively. First, we assume that the observed data for a subject can be treated as a random draw (according to some mechanism) of one of the counterfactuals from a theoretically defined full data, i.e. the observed data are assumed to be n i.i.d. copies of O = (W, A, P, Y_A,P) or a censored version of the theoretical full data consisting of all possible counterfactuals, X^FULL (the so-called consistency assumption, closely related to the stable unit treatment value assumption (SUTVA)).^21,22 Second, we assume that conditional on the potential confounding variables W, treatment assignment and perception are independent of the outcome (A, P ⊥ Y_a,p | W, ∀a, p). This assumption is referred to as the ‘randomisation assumption’ or the ‘no unmeasured confounding assumption’ so that W is assumed to contain all variables that cause both P and Y. Finally, we assume that each treatment/perception combination (a, p) is possible for all the members of the target population, i.e. P(A = a, P = p | W) > 0 ∀W. This last condition is referred to as the ‘experimental treatment assignment’ assumption or the positivity assumption.^23,24

Given the graph in Fig. 1, the likelihood of an observed data observation can be factorised as: l(O) = P(W)P(A | W)P(P | A, W)P(Y | A, W, P) = P(W)g(A, P, W)Q(Y, A, P, W), where g(A, P, W) ≡ P(A | W)P(P | A, W and Q(A, P, W) ≡ E[Y | A, W, P].

7. Maximum likelihood estimation

The MLE works specifically with the term Q(A, P, W), which may be estimated using an appropriate regression model; this approach does not require estimates of distributions defined by the terms that determine treatment and perception distribution. Counterfactual distributions of the data under specific interventions are defined by the G-computation formula. The name, G-computation, stands for graphical computation and has roots in graphical modelling. Assuming a particular causal graph, the likelihood can be factorised, and the G-computation formula is obtained by carrying out a specific intervention on the likelihood. The obtained formula represents the counterfactual distribution the data would have had under the specific intervention. The MLE estimator is sometimes referred to as the G-computation estimator.

$$\text{Pr}\left(Y_a<y\right)=\int \text{Pr}(Y<y\mid A=a,P=p,W)dF(W)$$

Using the G-computation formula, estimates of the relevant population counterfactual means are E[Y_a,p]= E_W[E[Y | A = a, P = p, W]], and thus our counterfactual means of interest can be estimated by $\widehat{E}\left[Y_{a,p}\right]=\frac{1}{n}{\sum }_{i=1}^n\widehat{E}\left[Y\mid A=a,P=p,W_i\right]$, where i indexes participants, i = 1, …, n. Each comparison defined in sections 4 and 5 may be estimated by first estimating each of two defining marginal expectations and then taking their difference. For instance, for a dichotomous treatment variable, A, ψ_a(p) = E[Y_1,p] − E[Y_0,p] may be estimated by

$${\widehat{\psi }}_a(p)=\widehat{E}\left[Y_{1,p}\right]-\widehat{E}\left[Y_{0,p}\right]=\frac{1}{n}\sum _{i=1}^n\widehat{Q}\left(A=1,P=p,W_i\right)-\frac{1}{n}\sum _{i=1}^n\widehat{Q}\left(A=0,P=p,W_i\right)$$ (1)

The MLE estimator $\widehat{Q}(A,P,W)\equiv \widehat{E}[Y\mid A,W,P]$ can be based on a parametric model; however, the consistency of this estimator relies on the consistency of the regression. Given that non-parametric approaches are not feasible if W is high dimensional, we suggest use of a machine-learning algorithm that allows the user to specify the degree of flexibility in regression terms and includes model selection. In particular, in the example of section 7, we employ the deletion substitution algorithm (DSA)²⁵ to choose the final regression form. DSA is a data-adaptive model selection algorithm based on cross-validation. The algorithm selects from a set of candidate generalised linear models that consist of polynomials of the covariates and their tensor products. The candidate models are produced by three different moves: deletions, substitutions and additions. A deletion step removes a term from the model, a substitution step replaces a variable with another and an addition step adds a variable to the model. The final model selected by the DSA minimises the empirical risk on the learning set.²⁵ The algorithm limits the search for the best model through user-specified parameters for the space of candidate models such as the maximum sum of powers for the variables and the maximum order of interaction between them. Standard errors (and confidence intervals) that account for data-driven levels of flexibility in the regression model can be based on the bootstrap. The hope for using this model and a simple plug-in estimator for our parameter of interest is that the optimisation in the balance between bias and variance in the estimate of the regression model using this approach will translate to a close to optimal variance-bias trade-off for the parameter estimate of interest.²⁶ However, in section 8, we will discuss a generalisation of this approach that more directly targets this model selection towards estimating the parameter of interest.

For the gabapentin trial, parameters of sections 4 and 5 were estimated using MLE of the G-computation formula, which requires modelling of the end point pain score on treatment, perception and baseline covariates, E[Y | A, P, W]. The model was selected using the machine-learning, DSA algorithm with perception, treatment and the interaction between the two forced into the model, with the rest of the terms selected from basis functions of the following measured confounding variables: sex, age, race, height, weight, baseline pain score and baseline sleep score. The covariates selected in the model were restricted to no higher than second-degree terms and, similarly, only allowed for two-way interactions. Five-fold cross-validation was used within the DSA algorithm for model comparison and selection.

Once the regression model has been fit, the marginal mean E[Y_a,p] is estimated by using the final fitted regression model to predict, for each individual, their outcome keeping the covariates as observed, but fixing treatment at A = a and perception at P = p; this yields, for the ith observation, the ‘predicted’ value $\widehat{E}\left[Y\mid A=a,P=p,W_i\right]$. These predicted outcomes were then averaged over individuals (and thus over the empirical distribution of W) to give $\widehat{E}\left[Y_{a,p}\right]\equiv {\widehat{E}}_W[\widehat{E}[Y\mid A=a,P=p,W]]$ as discussed in section 6. Finally, to estimate the marginal effect E[Y_a,p] − E[Y_a′,p′], we simply subtracted $\widehat{E}\left[Y_{a^{\prime },p^{\prime }}\right]$ from $\widehat{E}\left[Y_{a,p}\right]$. Bootstrap standard errors were estimated by re-sampling the observations with replacement 5000 times, performing model selection using DSA for every bootstrap sample, and finally, estimating the desired parameters as above. Visual checks on the bootstrap distributions showed symmetric distributions of the bootstrap estimates around the full-data estimate, suggesting that the variability introduced by the model selection is of second order; note that examination of the bootstrap distribution provides an informal diagnostic on whether the estimate has the desired sampling distribution. For each parameter, the estimated standard error was used to calculate a two-sided Wald test statistic and a subsequent p-value.

For the original data, the following variables were selected by DSA for the estimator (in addition to perception, treatment and their interaction, which were forced into the model): baseline pain score, baseline sleep score and the second power of baseline sleep score. We note that the chosen model for any flexible machine-learning algorithm with a relatively small sample size is unstable in its ‘choice’ of included covariates, and so one can conclude very little about the relative importance of variables from a single fit.

Table 1 shows the resulting MLE estimates for four comparisons: the treatment effects at both levels of perception and the perception effects at both levels of treatment. For example, based on these results, the average effect of gabapentin on end point pain scores, with P fixed at no knowledge of treatment or placebo (i.e. in this case, no side effects), is estimated to ${\widehat{\psi }}_a(0)=0.71$ points, with an associated 95% confidence interval of (−0.14, 1.56). The estimated effect of gabapentin with perception set to P = 1 (i.e. everyone had side effects) is ${\widehat{\psi }}_a(1)=2.50$ points, with a 95% confidence interval of (1.15, 3.84).

Table 1.

Estimated parameters using MLE and the corresponding 95% confidence intervals

Parameter	G-comp estimate (SE)	p	95% CI
ψa(0) = E[Y0,0] – E[Y1,0]	0.71 (0.44)	0.10	(−0.14, 1.56)
ψa(1) = E[Y0,1] – E[Y1,1]	2.50 (0.69)	0.0002	(1.15, 3.84)
ψp(0) = E[Y0,0] – E[Y0,1]	−0.59 (0.64)	0.35	(−1.83, 0.65)
ψp(1) = E[Y1,0] – E[Y1,1]	1.18 (0.51)	0.02	(0.18, 2.17)

The average perception effect with treatment fixed at A = 0 (placebo) is ${\widehat{\psi }}_p(0)=-0.59$ with a 95% confidence interval of (−1.83, 0.65), and conversely, the estimate of the perception effect with treatment fixed at A = 1 (gabapentin) is ${\widehat{\psi }}_p(1)=1.18$ with a 95% confidence interval of (0.18, 2.17). The results imply that, contrary to fact, had everyone received the treatment, patients with treatment-related side effects are estimated to report significantly greater pain reduction than if they had no side effects. This in turn suggests that treated patients who believe that they are receiving active treatment report significantly greater pain reduction, on average, than treated individuals who have no opinion about their treatment.

In summary, we estimate about 40% of the naive estimated treatment effect (ignoring treatment-related side effects) disappears if no one would have experienced side effects and presumably remained unbiased in reporting their pain scores. After accounting for perception, the estimated mean differences suggest that gabapentin does not have a statistically significant effect on pain reduction had no individual experienced a treatment-related side effect during the trial: the estimated treatment effect with P fixed at 0 is no longer significant. However, the treatment effect among those with side effects is much higher and highly statistically significant. There are several possible explanations for this result that are all consistent with the data. The obvious explanation is that unmasking creates the very bias that blinding is designed to protect against; an alternative hypothesis is that the occurrence of treatment-related side effects is an indication or proxy that the drug is efficacious, and it is exactly this group of individuals who experience pain reduction. Unfortunately, the data cannot possibly distinguish between these two alternative interpretations. However, given that masking in subjectively scored pain trials is considered so key to obtaining unbiased results, it would be inappropriate in our view to assign the entire treatment effect when P = 1 to a therapeutic effect of the drug.

Some participants were lost to follow-up before the end of the study (14 and 18 patients in the gabapentin and placebo groups, respectively). We followed the investigators in using the average of the last seven pain measurements as indicated, the so-called ‘carry-forward’ method. In both treatment and placebo groups, there is a tendency for the pain scores to decline over the 8-week follow-up period. This means that the ‘carry-forward’ approach to missing data for those lost to follow-up tends to lead to overestimates of the mean end point pain scores in both treatment and placebo groups. To investigate the sensitivity of the findings to this form of imputation, we did an equivalent analysis using only participants who remained under follow-up the entire 8 weeks. Effectively, this assumes that the data for individuals lost to follow-up are missing at random. Although the standard errors are necessarily higher, there is a marked difference in the estimated average treatment effects at both levels of P. Specifically, we now estimate ${\widehat{\psi }}_a(0)=-0.05$ points and ${\widehat{\psi }}_a(1)=1.53$. Thus, the entire treatment effect is now erased when unmasking (i.e. occurrence of side effects) is accounted for; in fact the treated patients are very slightly worse off than those on placebo when we set P = 0. The estimated treatment effect among the unmasked participants (P = 1) is still notable but smaller than when the carry-forward method is employed, ${\widehat{\psi }}_a(1)=2.50$.

8. Targeted maximum likelihood estimation

We discussed an MLE estimator in the previous section, but there also exist estimating equation approaches for these types of parameters in semi-parametric models. Specifically, the IPTW estimator^13,14 represents a different approach to estimation of the causal parameters of interest here; this approach requires estimation of the treatment/perception assignment mechanism as determined by g(A, P, W). In addition, this estimator can be augmented such that the new estimator is double robust (so-called DR-IPTW estimator^15–17). The virtue of this estimator is that it is consistent if either the outcome regression model or the treatment/assignment mechanism is correctly specified. In addition, the estimator is locally efficient, so it achieves (under assumptions) maximal efficiency among competing estimators in a semi-parametric model. However, often these estimating equation approaches have very poor finite sample performance, which for instance may result in the estimator not necessarily being bounded between the natural limits of the parameter of interest (e.g. probability differences < −1 or > 1). Optimally, one would like the asymptotic properties of the DR-IPTW estimator, but with the finite sample virtues of the MLE estimator. This is achieved by TMLE.

What machine-learning approach alone lacks is that the algorithm is not optimised towards the parameter of interest; whereas it might provide an optimal estimator of the prediction of Y, given A, P, W, it may be a poor estimator for a particular parameter that is a function of this model.¹⁸ Typically, a plug-in estimator for the parameter of the density estimator will be biased due to model mis-specification (unless the estimate is non-parametric) as noted above for the MLE estimator. The standard criteria for model improvement (by making it more flexible) usually focus on the model and not the ultimate parameter of interest. In such cases, the TMLE directly addresses the bias issue by carrying out a subsequent clever parametric maximum likelihood fit that is directly tailored to remove bias for the target parameter of interest, treating the initial MLE estimator as an offset. In particular, the TMLE modifies MLE in a way that yields a plug-in estimator with the influence curve equal to the efficient influence curve;¹⁸ the resulting estimator will also be double robust (in fact, it will be so-called collaboratively double robust – see van der Laan and Gruber²⁷). Practical consequences could be that covariates that are potential confounders (W) for the association of interest might be dropped by a model selection procedure for estimating Q as we are simply trying to get the best density estimate of Y given A, W, P (rather than estimation of regression coefficients). To retrieve robustness, TMLE works by augmenting the original fit of this density (i.e. the conditional distribution of Y, given A, W) by adding an appropriate ‘clever’ covariate (the choice of this covariate, relative to the choice of the models for Q and g, is discussed in van der Laan and Rubin¹⁸).

As noted, the estimator is consistent if either Q (A, P, W) or g (A, P, W) is consistently estimated. A model selection algorithm such as the DSA²⁵ may be used for finding the initial estimate $Q_n^0$ as before. Given this initial estimate, the updated Q is given by (in the linear model)

$$Q_n^{*}(A,P,W)=Q_n^0(A,P,W)+\epsilon h(A,P,W)$$ (2)

where the derived covariate h(A, P, W) is a function of g(A, P, W).²⁷ Here ε is estimated using maximum likelihood (e.g. least squares), where $Q_n^0$ is treated as an offset, as further discussed below. For the defined mean parameters E[Y_a,p] of sections 4 and 5, h(A, P, W) is equal to $\frac{I(A=a,P=p)}{p(A=a\mid W)P(P=p\mid A=a,W)}$. If one wishes to solely target a difference such as E[Y_1,p – Y_0,p], one can use the difference of the two corresponding clever covariates as a single clever covariate. To implement TMLE, we have to estimate the denominator of h(A, P, W). For the first term, P(A = a | W), we use the fact that A is randomised (independent of W) and substitute either the known treatment assignment probabilities, or, to gain efficiency,¹⁸ the estimated empirical treatment assignment proportions ignoring W. The second term requires estimation through some form of binary (such as logistic) regression as perception presumably varies by treatment group and possibly the added covariates W; model selection can be employed here to allow as much flexibility in estimation as supported by the data. In observational studies for which treatment A is not randomised, the treatment mechanism may also be modelled using a logistic regression similar to the model for perception.

Once the h term is approximated, the coefficient ε is estimated using maximum likelihood for the regression model equation (2) assuming Gaussian errors; here $Q_n^0$ is a fixed offset in the model and ε is the coefficient to be estimated. The magnitude of the estimated ε depends on the amount of residual confounding (for estimation of the targeted mean parameter) along the direction of h(A, P, W). This process is iterated until convergence. In our simple case, convergence is achieved in one step (see van der Laan and Rubin).¹⁸

This estimator is identical to estimator given in equation (1) except that it uses the updated Q*, instead of Q, with the consequence that bias is reduced by directly targeting the desired mean and double robustness is attained. Estimation of each mean requires separately updated ${\widehat{Q}}^{*}s$, e.g. one for $\widehat{Q}(A=1,P=p,W)$ and another for $\widehat{Q}(A=0,P=p,W)$. Each of the updated ${\widehat{Q}}^{*}s$ is obtained by plugging in the corresponding choice of A = a, P = p to determine the appropriate ‘clever covariate’. Under regularity conditions, the TMLE estimator is a consistent and asymptotic linear estimator.¹⁸ Consequently, for inference and testing, we may use ${\widehat{\psi }}_a~N\left({\psi }_a,{\Sigma }_0\right)$, where ψ_a is the true population parameter, and Σ₀ is the variance of the efficient influence curve. The latter variance can be estimated via the sample variance of a plug-in estimate of the efficient influence curve, or more safely by using the bootstrap as illustrated in the following section.

Any combination of the mean parameters can then be directly estimated from the TMLEs of the individual components. For example, of most interest, the average causal effect of treatment had everyone’s perception remained at a fixed level P = p can be estimated by

$${\widehat{\psi }}_a(p)=\widehat{E}\left[Y_{1,p}\right]-\widehat{E}\left[Y_{0,p}\right]=\frac{1}{n}\sum _{i=1}^n{\widehat{Q}}^{*}\left(A=1,P=p,W_i\right)-\frac{1}{n}\sum _{i=1}^n{\widehat{Q}}^{*}\left(A=0,P=p,W_i\right)$$ (3)

A TMLE estimator for a specific mean comparison can be computed, specifically targeting this parameter of interest. We do not pursue this further here as we wish to examine several mean comparisons simultaneously.

Following our earlier analysis of the gabapentin trial, we used TMLE as an augmentation to the MLE with the possibility of minimising bias due to model mis-specification, as well as reducing the variability of estimation. As the first step in estimating each of the four means, E[Y_a,p], we used the MLE estimator of section 7. To approximate the ‘clever’ covariate, the empirical proportion of treated patients was used instead of using 0.5 for probability of treatment P(A = a). The probability that P = 1 was modelled based on treatment and the baseline covariates as discussed in earlier, the DSA algorithm was used to fit a logistic regression model with treatment forced into the model. Once again, predictors were restricted to second degree, and interaction terms restricted to two-way terms, with five-fold cross-validation used for model comparison and selection. Subsequently, we used precisely the same plug-in estimator, with the model of E[Y | A, P, W] augmented by the clever covariate noted in section 6.1. As discussed above, we ‘targeted’ each of the estimated marginal means $\widehat{E}\left[Y_{0,0}\right]$, $\widehat{E}\left[Y_{0,1}\right]$, $\widehat{E}\left[Y_{1,0}\right]$ and $\widehat{E}\left[Y_{1,0}\right]$ separately. As above, the marginal difference E[Y_a,p] − E[Y_a′,p′] was simply estimated by subtracting $\widehat{E}\left[Y_{a^{\prime },p^{\prime }}\right]$ from $\widehat{E}\left[Y_{a,p}\right]$. Bootstrap standard errors were calculated by repeating the TMLE fit to each of 5000 bootstrap samples. For each bootstrap sample, the clever covariate was formed separately based on the treatment mechanism model (g) selected for that particular sample. Regression models for each sample (Q) were augmented by the corresponding clever covariates, the responses were predicted for each individual and the marginal means estimated as before. Once again, a two-sided Wald test was used to calculate p-values.

Table 2 provides the analogous estimates to Table 1, but now using TMLE. The estimates are generally similar to the unaugmented results, reflecting little residual bias with respect to the observed covariates in the latter method. There are increases in the standard errors associated with TMLE results, possibly due to finite sample issues with regards to the method used to estimate g. With regard to the latter point, for a few levels of W, the model predicts small probabilities for perception (= 1), given treatment, thereby inflating the variance of the ‘clever’ covariate and, subsequently, the predicted pain scores. Although beyond the scope of this article, one can construct the ‘clever’ covariate in a manner that can ameliorate this problem.²¹ In summary, the approach here confirms the results and interpretation achieved through MLE approach.

Table 2.

Estimated parameters using TMLE and the corresponding 95% confidence intervals

Parameter	TMLE estimate (SE)	p	95% CI
ψa(0) = E[Y0,0] – E[Y1,0]	0.78 (0.58)	0.18	(−0.35, 1.91)
ψa(1) = E[Y0,1] – E[Y1,1]	1.98 (0.99)	0.04	(0.04, 3.91)
ψp(0) = E[Y0,0] – E[Y0,1]	−0.07 (0.81)	0.93	(−1.64, 1.50)
ψp(1) = E[Y1,0] – E[Y1,1]	1.12 (0.62)	0.07	(−0.09, 2.32)

An additional efficiency enhancement could result from methods used to properly constrain models to predict the outcomes within a known limited range (as here where the pain score must lie between 0 and 10). Specifically, one can transform the dependent variable to lie between 0 and 1 and use a TMLE logistic regression approach that guarantees that all predicted scores fall within the known range,²⁸ although we do not pursue this further here. One thus has several tools at their disposal that can help to optimise finite sample performance.

9. Discussion

It is important to note an asymmetry in our analysis regarding the use of observable treatment-related side effects as a proxy for treatment perception or unmasking, i.e. we have not accounted for the possibility that some participant’s perception changes to P = −1 (convinced they are on placebo) during the course of the trial. This might occur because an individual feels no benefit from treatment, thereby becoming convinced that they are on placebo and possibly biasing their subjective end point pain scores upwards, i.e. there is no analogue of the potential unmasking side effect in the other direction. It is possible that adjusting for this additional unmasking effect might increase treatment efficacy estimates were unmasking maintained (P = 0) although this is impossible to determine in the absence of further information.

This observation and the fact that we cannot disentangle a significant perception effect from a stronger treatment effect for those who had the relevant side effects suggest the need for collecting data on patients’ perception in randomised trials with subjectively recorded outcomes, previously suggested by other authors including Turner et al.²⁹ We note that in some vaccine efficacy trials, investigators have been concerned about patients’ increased risk behaviour due to their treatment perception and have suggested collecting data on perception. In a hepatitis B vaccine efficacy trial, placebo recipients were at a higher risk of hepatitis B infection after their final injection. This higher risk of infection suggested that some placebo recipients may have assumed they were protected and increased their risk behaviour.³⁰ Similarly, Bartholow et al.³¹ investigated sexual risk behaviour of participants in an HIV vaccine efficacy trial and found that among younger (<30) men who have sex with men, a perceived assignment to vaccine, was associated with an increased probability of unprotected sex.

As we demonstrated in the gabapentin trial, investigators may estimate and remove some adverse post-randomisation confounding factors of the effect of treatment using the causal inference framework. Suitable definition of appropriate parameters and the use of semi-parametric machine-learning techniques allow investigators to obtain less biased and more interpretable estimates. In particular, TMLE of parameters defined by the G-computation formula improves upon the MLE approach by reducing bias and improving efficiency of estimators, with additional enhancements available to improve finite sample performance. In the example, the methods demonstrate that the naive approaches to accommodate treatment-related side effects and using carry-forward to impute missing data both considerably distort the assessment of treatment efficacy.

In this article, we focused on placebo, perception and unmasking effects. However, any other measurable non-specific effect of the treatment may also be estimated using the same framework. Perception effects are non-specific effects of treatment and therefore a component of the placebo effect. As an alternative to adjusting for perception effects in subjective outcome clinical trials, we suggest conducting (i) randomised trials with no-treatment control groups to estimate the placebo effect as a whole (in possible settings) and/or (ii) small unmasked randomised trials parallel to the main trial to allow direct estimation of the masking effect.

We note that the desired parameters of interests, and appropriate estimation techniques, become more complex when components of W are on the direct causal pathway describing the effect of treatment on the outcome. This is not the case for any covariates in the gabapentin example discussed in section 7. Targeted maximum likelihood has been recently extended to accommodate this situation.^32,33

The methods and analysis proposed do not exploit the particular time when side effects and possible unmasking occur during the conduct of the trial. Longitudinal observations provide such additional information and can be used to refine the techniques outlined here. Further work will demonstrate how the suggested methods can be extended to the analysis of longitudinal information on unmasking.