Distinct but correlated latent factors support the regulation of learned conflict-control and task-switching

Abstract

Cognitive control is guided by learning, as people adjust control to meet changing task demands. The two best-studied instances of “control-learning” are the enhancement of attentional task focus in response to increased frequencies of incongruent distracter stimuli, reflected in the list-wide proportion congruent (LWPC) effect, and the enhancement of switch-readiness in response to increased frequencies of task switches, reflected in the list-wide proportion switch (LWPS) effect. However, the latent architecture underpinning these adaptations in cognitive stability and flexibility – specifically, whether there is a single, domain-general, or multiple, domain-specific learners – is currently not known. To reveal the underlying structure of control-learning, we had a large sample of participants (N = 950) perform LWPC and LWPS paradigms, and afterwards assessed their explicit awareness of the task manipulations, as well as general cognitive ability and motivation. Structural equation modeling was used to evaluate several preregistered models representing different plausible hypotheses concerning the latent structure of control-learning. Task performance replicated standard LWPC and LWPS effects. Crucially, the model that best fit the data had correlated domain- and context-specific latent factors. Thus, people’s ability to adapt their on-task focus and between-task switch-readiness to changing levels of demand was mediated by distinct (though correlated) underlying factors. Model fit remained good when accounting for speed-accuracy trade-offs, variance in individual cognitive ability and self-reported motivation, as well as self-reported explicit awareness of manipulations and the order in which different levels of demand were experienced. Implications of these results for the cognitive architecture of dynamic cognitive control are discussed.

1. Introduction

Reading this paper likely required you to select a link in a table-of-contents from among several other links competing for your attention; subsequently, you had to shift your mental set from searching through article titles to opening and reading this particular text. Getting here has thus involved the use of several “cognitive control” processes.

Cognitive control (which we here use interchangeably with “executive function”) is an umbrella term that denotes a collection of cognitive mechanisms allowing us to impose internal goals on how we process stimuli and select responses (Egner, 2017; Miller & Cohen, 2001). While there is no universally accepted ontology of cognitive control (Lenartowicz et al., 2010), the example above involves two broadly agreed-upon, and much-investigated, core capacities: (1) the ability to selectively focus attention on task-relevant stimuli in the face of competition from conflicting, task-irrelevant stimuli (conflict-control, also known as interference resolution, supporting cognitive stability, Botvinick et al., 2001); and (2) the ability to switch between different sets of rules (“task sets”) that guide how stimuli are evaluated and responded to (task-switching, supporting cognitive flexibility, e.g., Monsell, 2003).

Crucially, adaptive behavior not only requires that we have the basic capacity for resolving conflict from distracters and for changing task sets, but also that these abilities be deployed strategically, i.e., in a context-sensitive manner. For instance, we need to adjust our level of attentional focus in line with changing traffic density during the morning commute, and we need to be more or less ready to switch between multiple tasks during different phases of our workday. Accordingly, the question of how functions like conflict-control and task-switching are dynamically regulated to meet changing demands – which we here refer to as the process of control-learning – has been the focus of a burgeoning literature over the past two decades (for reviews on regulating conflict-control, see Abrahamse et al., 2017; Bugg, 2017; Bugg & Crump, 2012; Chiu & Egner, 2019; Egner, 2014; for reviews on regulating task-switching, see Braem & Egner, 2018; De Baene & Brass, 2014; Dreisbach & Fröber, 2019).

The most fundamental insight derived from this literature is that humans learn about the statistics of their environment, such as changes in demand over time or in relation to contextual cues, and accordingly adapt the degree to which they engage different control processes. Consider, for example, performance on the Stroop task (Stroop, 1935), a classic probe of conflict-control, where participants are asked to name the ink color of printed color words where the meaning can be congruent (e.g., the word BLUE in blue ink) or incongruent (e.g. the word RED in blue ink) with that color. Participants are asked to ignore the word meaning, but they display reliably slower and more error-prone responses to incongruent than congruent stimuli (the “congruency effect”), reflecting a behavioral cost of conflicting word information (reviewed in MacLeod, 1991). Importantly, many studies have documented that people are better at overcoming interference from conflicting (incongruent) distracter stimulus features in blocks of trials where incongruent distracters are frequent than in blocks where they are rare – an effect known as the list-wide proportion congruent (LWPC) effect (e.g., Bejjani, Tan, et al., 2020; Bugg & Chanani, 2011; Logan & Zbrodoff, 1979; reviewed in Bugg & Crump, 2012; Bugg, 2017). This suggests that people learn about the likelihood of encountering conflicting distracters and regulate their attentional selectivity (focusing more or less strongly on the target feature) to match demands, with more frequent conflict leading to a higher level of conflict-control (Botvinick et al., 2001; Jiang et al., 2014).

Similar evidence for learning processes guiding the titration of control settings has also been obtained in the context of task-switching studies. Here, the measure of interest is the “switch cost,” the canonical finding of slower and more error-prone responses on trials where participants are cued to switch from one task to another as opposed to repeating the same task (reviewed in Kiesel et al., 2010; Monsell, 2003; Vandierendonck et al., 2010). Switch costs are reliably reduced in blocks of trials where switching is required frequently than in blocks where switching is rare (Bejjani et al., 2021; Dreisbach & Haider, 2006; Monsell & Mizon, 2006; Siqi-Liu & Egner, 2020). This list-wide proportion switch (LWPS) effect has been attributed to people learning about the relative likelihood of encountering task switches (or repetitions) in a given context or task, and accordingly adjusting their readiness to switch (Braem & Egner, 2018; Dreisbach & Fröber, 2018).

Thus, substantial literatures have provided support for control-learning processes in the domains of on-task conflict-control (the LWPC effect) and between-task-switching (the LWPS effect). However, it is not presently known how these learning phenomena relate to each other. For example, given the basic similarity of the data patterns between the LWPC and LWPS effects, adapting to the frequency of conflicting distracters and to the frequency of cued task switches may be mediated by a single, domain-general learning mechanism. On the other hand, conflict-control and task-switching serve distinct functions – protecting an ongoing task set from distraction versus changing to another task set – which have often been conceptualized as antagonistic to each other (that is, as promoting either cognitive stability or flexibility; Dreisbach & Wenke, 2011; Goschke, 2003). This antagonistic relationship may suggest that contextual adaptations of these functions would likely be supported by distinct underlying learning mechanisms. In order to address the fundamental question of how the dynamic regulation of on-task focus and readiness to switch tasks is organized, the current study aimed to elucidate the latent structure of control-learning. In particular, we pursued this goal by applying structural equation modeling of several preregistered models on a large online sample of participants (N=950) performing both a LWPC and a LWPS protocol, both of which were designed to isolate confound-free markers of dynamic control-learning (Braem et al., 2019).

1.1. Latent Variable Research on Cognitive Control

Previous individual difference research in this area has focused on exploring the nature of executive function (EF) by using structural equation modeling to determine latent factors underlying performance on a variety of tasks assumed to require some form of control. This literature has primarily been concerned with the questions of which executive functions there are (Friedman et al., 2004, 2008; Miyake et al., 2000, 2002; Miyake & Friedman, 2012), whether a specific assumed executive function, such as inhibition, is really a unitary construct (e.g., Rey-Mermet et al., 2018), and to what degree specific executive control constructs correlate with conceptually closely related constructs, with a particular focus on the relationship between attentional control and working memory capacity (e.g., Rey-Mermet et al., 2019; reviewed in Kane et al., 2008). The first line of work has focused on modeling individual differences in performance on a wide range of tasks thought to tap into cognitive control processes (including the Stroop task, an N-back task, a set-shifting task, etc.), and identifying common sources of variance that help explain associations between tasks. This research suggests that executive function tasks share enough common variance to be organized into different domains such as the shifting of mental sets, the monitoring and updating of working memory representations, and the inhibition of prepotent responses. Specifically, these three latent factors were identified as having separable, diverse components associated with their specific domains, but also sharing variance via a unifying common EF factor that potentially reflected the same underlying mechanisms or cognitive ability. These factors display high heritability, and reliable individual differences in neural activation, gray matter volume, and connectivity (Friedman & Miyake, 2017). Research into these cognitive control domains has been widespread (reviewed in Karr et al., 2018), including clinical studies aiming to identify deficits in different control domains relating to individual differences in mental health (Friedman et al., 2020) and developmental studies aiming to identify the stability of the domains across the lifespan (Friedman et al., 2016).

The current study pursues a question that is complementary to this prior work. Specifically, we adopt the basic insight from the above models and the theoretical literature at large – that conflict-control and task-switching represent different basic control functions – and we build on it by asking the question of how the dynamic, contextual regulation (control-learning) of these functions is organized. This can be thought of as investigating the nature of meta-control, the strategic nudging up or down of control processes. Thus, we are here not seeking to detect commonalities among different probes of cognitive control (for a recent review, see Bastian et al., 2020), but to assess the relationship between the learning mechanisms that drive adaptation in two core control domains. Some prior work has pursued related questions within the domain of conflict-control, by assessing whether trial-by-trial adjustments in control (“conflict adaptation effects”, reviewed in Egner, 2007) correlate across different conflict tasks (e.g., Keye et al., 2009; Whitehead et al., 2019), and/or by applying structural equation modeling to conflict task data (e.g., Keye et al., 2009, 2013). The latter latent variable analyses suggested that response time variance in these tasks could be attributed to three sources, general response speed, conflict, and context, which here refer to the congruency of the previous trial (i.e., conflict adaptation) (Keye et al., 2009; 2013). However, as noted previously (Meier & Kane, 2013), these results cannot be interpreted unambiguously because they stem from task designs that confounded trial-wise adjustment to conflict with overlapping stimulus features and responses across trials (“feature integration effects”, see Hommel, 2004) and may thus have tapped into mnemonic binding rather than conflict-control processes. In the present study, by contrast, we (a) assess list-wide (rather than trial-by-trial) effects of context, and (b) relate these effects across control domains (conflict-control vs. switching), while (c) fully controlling for typical confounds related to memory and learning effects. Moreover, in pursuing this question, the present study also seeks to mitigate a few critical issues that have been raised in relation to the approach taken by Miyake, Friedman, and colleagues.

First, at the level of measurement, researchers have highlighted that it can be problematic to use difference scores as dependent measures when evaluating individual differences (see review by Draheim et al., 2019). For example, when modeling the common variance within inhibition or attentional control tasks, such as the Stroop task (Stroop, 1935), researchers typically use the congruency effect (the difference between incongruent and congruent trial performance) as a dependent measure. As a difference score (i.e., incongruent – congruent), this metric may result in more unstable and thus less reliable scores than raw performance measures. Poorer reliability has been argued to result in poorer replicability (cf. Draheim et al., 2021; Thomas & Zumbo, 2012). To address this concern, in the present study we employ condition-specific response time (RT) as indicators; for instance, we use both congruent and incongruent trial RT, separately. However, to facilitate comparison with previous work and mitigate concerns over conceptual validity, we also used other metrics, including difference scores, in additional control analyses.

Second, it has recently been argued that determining how cognitive control “skills” are being employed in a goal-directed, context-sensitive fashion is a more fruitful way of accounting for individual differences and development than focusing on executive function components per se (Doebel, 2020). In other words, the assumption that individual differences in control can be satisfactorily captured by “static”, context-insensitive measures, such as a mean congruency effect, has been drawn into question. The present study naturally mitigates this concern, because we are here interested in evaluating the structure of precisely such context-guided, dynamic adaptation in how cognitive control functions are being deployed, as represented by the LWPC and LWPS effects.

1.2. Models of Control-Learning

How exactly participants learn context-appropriate attentional control-states and bring about strategic processing adjustments remains debated. For instance, with respect to adapting conflict-control in line with changing demands, some models have simulated the LWPC performance pattern by assuming a learning mechanism that monitors and predicts the level of conflict (or control demand) experienced on each trial, and nudges top-down attention to the relevant task features up or down as a function of whether conflict was higher or lower than expected (Botvinick et al., 2001; Jiang et al., 2014). These models can account for the temporal signature of control-learning findings, such as the LWPC effect, but face difficulty in explaining “item-specific” effects, whereby particular stimuli can become cues of control (Bugg & Hutchison, 2013; Chiu & Egner, 2017; Jacoby et al., 2003; Spinelli & Lupker, 2020), because these models do not take into consideration the particulars of the stimuli involved and only consider the level of conflict caused by the stimuli. In response, other models have assumed that control regulation involves the binding of attentional control states to specific stimuli (e.g., an incongruent Stroop stimulus), whose reoccurrence reinstates those control states (Blais & Verguts, 2012; Verguts & Notebaert, 2008, 2009). These models can thus accommodate findings of item-specific control-learning, but have difficulty explaining LWPC effects obtained in the absence of any stimulus feature repetitions (e.g., Spinelli et al., 2019).

More recently, these perspectives have been melded by theories that propose control-learning can operate at a stimulus-independent level (where it is guided by the temporal or episodic context) but that control settings are also bound to specific stimulus or event features, whereby stimuli that frequently occur in situations requiring control become bottom-up cues for retrieving control (Abrahamse et al., 2016; Egner, 2014). Here, all event features, such as task-relevant and -irrelevant stimulus characteristics and motor responses, become bound in an associative network with goal representations and control settings that are co-activated during the event, allowing for contextually appropriate recruitment of control (Abrahamse et al., 2016; Braem & Egner, 2018). Based on the broader literature on key characteristics of associative learning, this perspective results in three primary predictions about control-learning: one, that control-learning is context-specific, via the binding of any active task-relevant and task-irrelevant representations in an associative network; two, that these associations can develop outside of explicit awareness and that control-learning is primarily implicit, but can also occur when participants are explicitly aware; and three, that control-learning is sensitive to reward.

The latter two, in particular, refer to the grounding of cognitive control in reinforcement learning principles, a shared feature among control-learning models (Botvinick et al., 2001; Blais et al., 2007; Verguts & Notebaert, 2008; Jiang et al., 2014). A basic reinforcement learning problem involves a set of environmental states, a set of actions taken at these states, a transition function that maps how actions will cause the transition to another state, and a reward function that indicates the amount of reward available at each state (Sutton & Barto, 1998). The typical assumption is that agents learn a set of actions, or a policy, that maximizes overall reward. When applying reinforcement learning models to cognitive control data, researchers assume that instead of learning the likelihood of reward, participants implicitly learn the likelihood of contextual control-demand and update their expectancies based on the control-demand they experience on each trial (for use of this modeling approach in neuroscience studies of control-learning, see Chiu et al., 2017; Jiang et al., 2015; Muhle-Karbe et al., 2018). This process is then sensitive to implicit or explicit reward, because reward is thought to reinforce these learned associations.

A major question arising from this prior work into control-learning and latent variable analysis of control then is whether the underlying learning processes governing adaptations in conflict-control and task-switching are mediated by a domain-general control learner or whether control-learning in different domains relies on distinct abilities. The aforementioned models are agnostic to this question, as the formal modeling work was typically conducted in a single domain (e.g., conflict-control, but see Brown et al., 2007), and thus did not address the issue of domain-specific versus domain-general learning mechanisms. The broader cognitive control literature offers examples of both domain-general proposals, like Norman and Shallice’s (1986) classic “supervisory attention system”, as well as domain-specific proposals (e.g., Egner, 2008) and hybrid approaches (e.g., Miyake & Friedman, 2012). Moreover, as noted above, plausible theoretical arguments can be made in favor of either possibility, due to, for example, the pattern similarities versus functional distinctions between the LWPC and LWPS effects. In the present study, our aim was therefore to adjudicate empirically between different possible structural models of control-learning, which we lay out in detail below.

1.3. The Current Study

In the current study, participants performed consecutive LWPC and LWPS paradigms. Thus, the proportion of difficult (incongruent, task-switch) and easy (congruent, task-repeat) trials varied temporally over blocks of trials while participants identified the color in which color-words were printed (in a Stroop task assessing the LWPC effect) or were cued to categorize either letters as consonants or vowels or digits as odd or even (in a task-switching protocol assessing the LWPS effect). We refer to the block-level manipulation of the proportion of easy-to-hard trials as creating a “context”, such that “context-specificity” in our modeling reflects people’s sensitivity to the proportion manipulation. By contrast, “domain-specificity” refers to sensitivity to the different task goals or control demands (i.e., the Stroop task or the task-switching protocol). We chose task-switching and conflict-control as target domains of cognitive control, and the list-wide manipulation as a means of measuring contextual control-learning, for several reasons. One, these two domains (conflict-control, task-switching) are, by some distance, the most well studied with respect to control-learning (reviewed in Abrahamse et al., 2016; Bugg & Crump, 2012; Bugg, 2017; Braem & Egner, 2018; Dreisbach & Froeber, 2019). Two, the specific control-learning paradigms we employ here have produced results that have been replicated in multiple studies (Bejjani et al., 2021; Bejjani & Egner, 2021; Siqi-Liu & Egner, 2020). Three, these studies have also shown these paradigms to have acceptable reliability, with test-retest reliability documented in Bejjani and colleagues (2021) and reliability across and within blocks identified in Bejjani and Egner (2021). Finally, the list-wide proportion paradigms we employ incorporate means of dissociating “pure”, block-level control-learning effects from item-specific contributions.

The latter is achieved by distinguishing between “inducer” and “diagnostic” stimuli in the design of our tasks (Braem et al., 2019; cf. Bugg et al., 2008). Specifically, in the LWPC task, half of the blocks consist mostly of congruent stimuli (MC blocks) and the other half mostly of incongruent stimuli (MI blocks). Correspondingly, in the LWPS task, half of the blocks consist mostly of task-repeat trials (MR blocks) and the other half mostly of task switch trials (MS blocks). Crucially, the manner in which these proportion-biased blocks (or contexts) are created involves splitting up the stimulus sets, with one half of the stimuli being frequency-biased (“inducer” items), serving to create the block-level bias, and the other half frequency-unbiased (“diagnostic” items), serving to measure the effect of the block-level bias. For instance, in the LWPC task, the biased, inducer stimuli are congruent 90% of the time in the MC blocks and 10% of the time in the MI blocks, whereas – importantly – the unbiased, diagnostic items are presented as congruent and incongruent stimuli 50% of the time in both the MC and MI blocks. These frequency-unbiased, diagnostic stimuli are thus influenced by the global control-demand context (i.e., being presented in the context of an “easy” or “difficult” block), but are not biased at the item level, and this controls for frequency-based stimulus-response learning confounds when interpreting control-learning effects (cf. Braem et al., 2019; Somasundaram et al., 2021). Including these frequency-unbiased stimuli is particularly important because another explanation for proportion congruent (and related) effects has been based on the learning of event frequency rather than the modulation of control per se (e.g., Schmidt & Besner, 2008).

In modeling control-learning using these paradigms, our indicators were defined by domain (the LWPC and LWPS protocols), context (MC, MI, MR, MS blocks), trial type (congruent, incongruent, repeat, switch), and context phase (first versus second half of each context). In particular, within each of these conditions, we used mean RT for the frequency-unbiased, diagnostic stimuli as reflective indicators, so as to capture generalizable, list-wide control-learning free from frequency confounds. These means are reflective indicators, because changes in statistical learning of the proportion constructs cause or are manifest in changes of the indicators (Hoyle, 2012). We make two additional assumptions. First, we assume that participants can adjust their control either by relaxing control on easy trials or increasing control on difficult trials (or both), but in either case these adjustments are an expression of control-learning. This codifies state-based assumptions in costs-benefit frameworks of control (e.g., Kool & Botvinick, 2018; Shenhav et al., 2013), where participants learn whether relaxing or increasing control is worth the pay-off of the mental effort exerted. Second, we assume that adjusting control early (e.g., first MI block) or late (e.g., second MI block) within a given context is similar, because participants generally form strong expectations of upcoming control-demand early on in a given context yet maintain control-learning effects across the experiment (Abrahamse et al., 2013; Bejjani, Tan, et al., 2020; Bejjani & Egner, 2021). While attention inevitably drifts within blocks (cf.1 Dey & Bugg, 2021), we have found strong correlations between participant response times on early versus late blocks (Bejjani & Egner, 2021), supporting this assumption of consistent learning and application of control over time.

To evaluate the latent structure of control-learning, we estimate six preregistered models. We first estimate a one-factor model that assumes one domain-general latent variable can explain the common variance among the LWPS and LWPC. We then estimate a two-factor model that assumes one domain-general latent variable per task goal – that is, there is no context-sensitivity (no proportion latent variables), but there is correlated domain-sensitivity, with one variable for conflict-control and one for task-switching. Afterwards, we estimate a four-factor model that assumes correlated domain- and context-sensitivity, with each latent variable tuned to the MI, MC, MS, and MR contexts. The next three models test the strength of the within and across domain correlations for these latent variables. Based on prior research, we expected the model with correlated domain- and context-sensitivity to yield the best (and a good) model fit.

2. Method

2.1. Sample Size

Bejjani and Egner (2021) reported η_p² = 0.06 (RT) for the repeated-measures ANOVA interaction between congruency and proportion congruent context. With a power of 0.8, Type I error of 0.05 and similar experimental procedure, we thus needed to recruit 126 participants to detect a mean control-learning effect.

The most restricted of our preregistered latent variable models of control-learning had 98 degrees of freedom, suggesting that for 80% power, the sample size required to reject RMSEA (a measure of omnibus fit) less than 0.05 if the true RMSEA is 0.08 is 134 participants. The median sample size for structural equation modeling (SEM) studies is about 200 participants (Shah & Goldstein, 2006), which is appropriate for normally distributed continuous data estimated with maximum likelihood. Together these a priori estimates indicated the need for at least 200 participants.

Notably, we expected our control-learning metrics to violate assumptions such as multivariate nonnormality, and there have been concerns over the reliability of cognitive control metrics (Whitehead et al., 2019; but see also Bejjani et al., 2021; Bejjani & Egner, 2021). We also wanted to ensure that we could efficiently estimate model parameters, detect model misspecification (i.e., a sufficient chi-square test statistic and accurate fit statistics), and have no model estimation problems, so we had to recruit more than the median sample size in SEM studies. With this knowledge in mind, and because no prior studies have performed structural equation modeling of control-learning and this was not the primary purpose of our preregistered project, we assumed a target sample size of at least two hundred participants per level of the between-participants block order group, attempting to recruit close to a thousand participants.

2.2. Participants

One thousand four hundred and ninety-five Amazon Mechanical Turk (MTurk) workers consented to participate for $15.60¹ with the potential for a $3 bonus if they achieved greater than 80% accuracy on both cognitive tasks. Sixty-six MTurk workers were excluded for poor accuracy (<70%) on the LWPC task, 190 for poor accuracy on the LWPS task, and 222 for poor accuracy on both tasks. 26 participants were excluded for missing the attention check embedded within the Qualtrics (Provo, Utah) questionnaire. An additional 24 workers were excluded for being older than 50, since the age eligibility criterion was between 18 and 50, and 10 were excluded for having IP addresses outside of the United States, despite the Location Qualification filter set to the U.S. on MTurk.

These preregistered exclusions resulted in a final sample size of 957 MTurk workers (mean age = 31.56 ± 6.35; gender: 427 Female, 524 Male, 1 Nonbinary, 1 Nonbinary Femme, 4 Trans*; Hispanic origin: 105 Hispanic/Latino (11.0%), 839 Non-Hispanic/Latino, 13 Do Not Wish to Reply; race (N = 852 who didn’t reply Hispanic/Latino): 9 American Indian/Alaska Native (1.1%), 1 Arab-American/Middle Eastern (0.1%), 93 Asian (10.9%), 85 Black/African American (10.0%), 1 Hebrew American (0.1%), 18 Multiracial (2.1%), 1 Native Hawaiian/Other Pacific Islander (0.1%), 640 White/Caucasian (75.1%), 4 Do Not Wish to Reply). Of these 957 participants, 716 earned the bonus.

MTurk is a web-based platform where experimenters crowdsource paid participants for online studies. A large research literature has documented that as long as standard practices are followed to ensure good data quality² (e.g., having ways of excluding inattentive participants), effect sizes in cognitive psychology tasks like the ones employed here are similar to what they are with in person, lab participants (Bauer et al., 2020; Buhrmester et al., 2018; Crump et al., 2013; Hauser et al., 2019; Hunt & Scheetz, 2018; Mason & Suri, 2012; Robinson et al., 2019; Stewart et al., 2017).

2.3. Overall Procedure

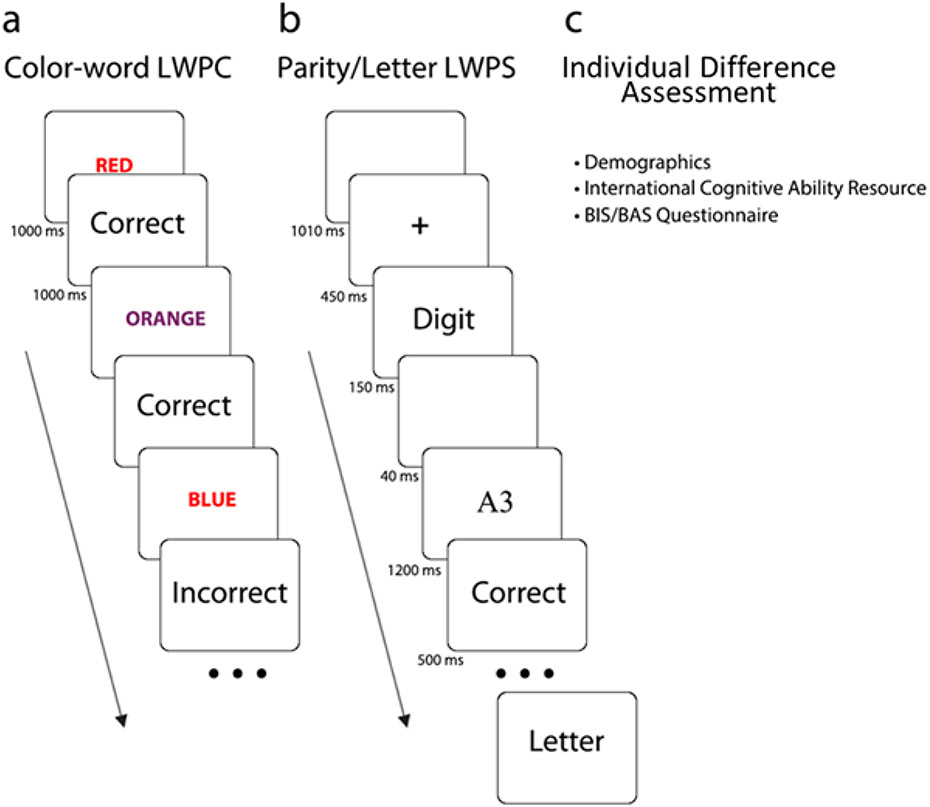
The experimental procedure (Figure 1) consisted of consecutive list-wide proportion congruent and switch paradigms (Bejjani, Tan, et al., 2020; Bejjani et al., 2021; Bejjani & Egner, 2021; Siqi-Liu & Egner, 2020), followed by a post-task questionnaire.

Figure 1. Experimental protocol.

Participants performed a color-word Stroop task (A), which involved a list-wide proportion congruent (PC) manipulation. Next, they completed a cued parity/letter task-switching paradigm, which also involved a list-wide proportion switch (PS) manipulation (B). Finally, participants answered mental health questions and demographics prompts, and responded to explicit awareness questions and personality questionnaires (C).

2.3.1. List-wide proportion congruent (LWPC) task

The first block of the color-word LWPC (Bejjani, Tan, et al., 2020; Bejjani & Egner, 2021) involved a practice set of 120 congruent trials to ensure that participants learned the stimulus-response mappings for the six color-words (red, orange, yellow, green, blue, and purple). Participants categorized the color in which the color-words were printed by pressing the z, x, and c keys with their left ring, middle, and index fingers and the b, n, and m keys with their right index, middle, and ring fingers. Notably, these trials were split such that the first 30 trials involved the buttons for the left hand, followed by 30 trials for the buttons associated with the right hand, with response mappings provided on-screen as a reminder. The last 60 trials were still split into two blocks of 30 trials each, but the response mappings were no longer on-screen. This design was inspired by remote moderated usability testing with participants, addressing concerns about the difficulty of learning six response mappings. Performance feedback (correct/incorrect; response time-out: respond faster) lasted 1000 ms, following the 1000 ms response window for the color-word stimuli. Response mappings were constant, with only four of six mappings relevant per block after the practice block.

After the practice block, participants were told that the color in which color-words were printed may no longer match the meaning of the color-words. On the 108 trials in each of the main four blocks (Figure 1a; Table 1), timing remained the same as in the practice block. Critically, we included a proportion congruent (PC) manipulation: four color-words were more often congruent (PC-90) or incongruent (PC-10) (“biased” or “inducer” items), while two color-words were not biased at the stimulus level (PC-50) and could only be influenced by the context in which they were presented (“unbiased” or “diagnostic” items). Specifically, each block included 61 trials of the frequent type and 7 trials of the rare type for the biased items and 20 of each trial type for the unbiased items. The PC-90 and PC-10 items thus created an overall list-wide bias of PC-75/25, whereby half of the blocks of trials were mostly congruent (MC), using the 2 PC-50 and 2 PC-90 items, and the other half mostly incongruent (MI), using the 2 PC-50 and 2 PC-10 items. Note that the PC-90 and PC-10 items were subject to a combination of potential control-learning effects and stimulus-response contingency learning confounds, because they occur more frequently for each of their respective trial types and are biased by the context in which they are presented. However, the PC-50 items provided a pure index of list-level control-learning effects (cf. Braem et al., 2019), because they occurred with the same frequency in the MC and MI contexts and had no item-specific biases. Each PC-90 item was only incongruent with the other PC-90 item (e.g., if blue and purple were PC-90 items, BLUE was incongruent only in purple), and the same was true for the PC-50 and PC-10 items. We randomized color-word assignment to the proportion congruent contexts (thus also randomizing response mappings) and ensured that at least one color-word of each PC probability was mapped to each hand (e.g., z, x, and c represented either PC 90, 50, or 10).

Table 1.

Trial counts across the LWPC and LWPS within a single task block and across all blocks by proportion context manipulation.

	MC	MI	MR	MS
Biased Items
Congruent	61 (122)	7 (14)
Incongruent	7 (14)	61 (122)
Unbiased Items
Congruent	20 (40)	20 (40)
Incongruent	20 (40)	20 (40)
Biased Items
Task-Repeat			32 (128)	8 (32)
Task-Switch			8 (32)	32 (128)
Unbiased Items
Task-Repeat			10 (40)	10 (40)
Task-Switch			10 (40)	10 (40)

2.3.2. List-wide proportion switch (LWPS) task

After completing the color-word LWPC, participants performed a cued, digit/letter LWPS paradigm (Figure 1b) (Bejjani et al., 2021; Siqi-Liu & Egner, 2020). On each trial, participants were cued to perform either a letter classification task (cues: Letter, Alphabet), indicating whether a given letter stimulus was a vowel or consonant, or a digit classification task (cues: Digit, Number), indicating whether a given digit was odd or even. A 2:1 cue-to-task mapping was employed to avoid any exact cue repetitions over successive trials (Mayr & Kliegl, 2003). Thus, the cue word always changed from one trial to the next. Responses were given via the d and k keys on a QWERTY keyboard, and response mappings were counterbalanced across sessions and task rules. Each trial began with a blank screen for 1010 ms, followed by a fixation cross for 450 ms, a task cue of 150 ms, another blank interval for 40 ms, and then the task stimulus (one letter and one digit) for 1200 ms. Performance feedback was then displayed for 500 ms. To become familiar with the task demands, participants first performed a 61-trial practice block with an equal likelihood of task-repeat and switch trials and no predictive relationship between any stimuli and switch-likelihood.

Critically, the subsequent main task involved a LWPS manipulation: four blocks were comprised mostly of task-switch trials (mostly switch (MS) or 70% proportion switch (PS-70)), while the other four were comprised mostly of task-repeat trials (mostly repeat (MR) or 30% proportion switch (PS-30)). As in the LWPC protocol, we created this block-wise manipulation of task-switch likelihood with a biased and unbiased stimulus set. The biased stimulus set (4 digits and 4 letters) drove the overall list-wide switch proportion by being predictive of task-switches (when presented in the PS-70 blocks) and task-repetitions (when presented in the PS-30 blocks), while the unbiased stimulus set (4 digits and 4 letters) was associated with an equal number of task repetitions and switches in every block. Unlike the LWPC, the biased stimuli predicted the proportion of task-switches only in the current block: in PS-70 blocks, the biased items occurred more often as switch trials. In the PS-30 blocks, the same biased items occurred more often as repeat trials instead. A pseudorandom stimulus sequence ensured that, within PS-30 blocks, the eight biased items were presented four times as repeat trials and once as switch trials, while the eight unbiased items were presented once each as repeat and switch trials, except for two stimuli that were presented twice as each trial type. Thus, while the overall switch likelihood was 30% (i.e., 18:42 switch:repeat trials), the biased stimuli were associated with switch trials 20% of the time (8:32) and the unbiased stimuli was equally associated with switch and repeat trials (10:10). The corresponding manipulation was applied for the PS-70 blocks.

The eight main task blocks consisted of 61 trials each, ensuring participants encountered every stimulus item as both a task-repeat and switch trial at least once within each block. Moreover, each task was presented an equal number of times across blocks, whereby each categorization task was presented 9 times and 21 times as switch and repeat trials, respectively, within the PS-30 blocks, and vice versa for the PS-70 blocks. As with the LWPC protocol, all four blocks of each PS context were presented consecutively.

With both the LWPC and LWPS, we counterbalanced for block order, since participants in LWPC studies have been found to display larger control-learning effects when they switch from an easy, mostly congruent context to a difficult, mostly incongruent context than when those block orders are switched (Abrahamse et al., 2013; Bejjani, Tan, et al., 2020; Bejjani & Egner, 2021). Although this effect is not present in the LWPS (Bejjani et al., 2021), we nonetheless ensured that there were approximately equal numbers of participants between the four block orders: MC (2 blocks) – MI (2) – MR (4) – MS (4); MC (2) – MI (2) – MS (4) – MR (4); MI (2) – MC (2) – MR (4) – MS (4); MI (2) – MC (2) – MS (4) – MR (4). Notably, participants always completed the LWPC before the LWPS. This was done because of potential response congruency concerns (Kiesel et al., 2007), and it was also expected to reduce irrelevant variance between participants (Goodhew & Edwards, 2019). Note that the LWPC and LWPS have slightly different contingencies for the biased stimuli (PC-90, PC-10, PS-80, PS-20) and thus overall proportion contexts (PC-75, PC-25, PS-70, PS-30) because of consistency with prior work (Bejjani et al., 2021; Bejjani and Egner, 2021). All stimuli and feedback were presented in the center of the screen on a white background.

2.3.3. Post-test questionnaire

After completing both the LWPC and LWPS tasks, participants filled out a post-test questionnaire (Figure 1c). First, they answered basic demographic questions (gender, age, ethnicity, race, and highest education attained). They then were told that we would ask about the task where they categorized color-words, and they answered a series of questions designed to assess explicit awareness of the LWPC manipulations and repeated this process for the LWPS manipulation (see Explicit Awareness section below and in Appendix A, with the Supplementary Text). Afterwards, they were told that we would ask about a series of cognitive puzzles and they should not use a calculator to solve any of the problems. Here, participants filled out the International Cognitive Ability Resource (ICAR; Condon & Revelle, 2014), a sixteen-item public domain intelligence questionnaire with four questions each devoted to verbal reasoning, letter and number judgments, matrix reasoning, and three-dimensional rotation, the presentation of which were randomized and counterbalanced across participants (α = 0.78, 95% CI [0.76, 0.80]). Note that counterbalancing of these items may introduce some additional error variance, but that reliability overall for the scales was acceptable to good.

Next, participants were asked about their personal and family history of mental health symptomatology and other mental health symptoms, which are not the focus of the current study.³ Here, we also presented an attention check where we attempted to identify which participants were not paying attention to how they were responding. Participants were asked to select a specific response during the loop of symptom questions, ensuring they were not button-mashing. Afterwards, participants filled out, in a counterbalanced and randomized order, the 10-item Emotion Regulation scale (Gross & John, 2003) and the 24-item Behavioral Inhibition System (BIS) – Behavioral Activation System (BAS) scale (Carver & White, 1994) (BIS subscale: α = 0.87, 95% CI [0.85, 0.88]; BAS reward subscale: α = 0.78, 95% CI [0.76, 0.80]). Finally, participants were asked about their experience with MTurk, the Stroop task, and task-switching paradigms as well as whether they would want to be recontacted for a possible followup study and what their Perceived Stress was over the past year (4-item; Cohen et al., 1983). Because the current paper is focused on the latent structure of control-learning, we only report and analyze data related to the main tasks, the explicit awareness questions, the ICAR task, and the BIS/BAS questionnaire.

2.4. Data Analysis

We analyzed reaction time (RT) data for correct trials in the main task blocks that were neither a direct stimulus repetition from the previous trial within the LWPC task nor the first trial of the block within the LWPS task, nor excessively fast (< 200 ms) or slow (feedback time-out: > 1000 ms). For the LWPS task, we also removed trials following an incorrect response, and for both tasks, we excluded outlier responses in the sample that were not within 1.5 times the interquartile RT range of the remaining sample. Finally, participants who had fewer than ten trials per cell for the Proportion Context × Trial Type interactions were excluded from learning analyses (N = 2 for LWPS; N = 5 for LWPC), to avoid unstable estimates and control for missing data. Readers interested in standard repeated-measures ANOVAs of LWPC and LWPS task data can find these in Appendix A with the Supplementary Text. Briefly, these ANOVAs detected all the expected effects, most importantly, main effects of congruency and switching, and the modulation of congruency and switch costs by the proportion congruent/switch factors for unbiased/diagnostic stimuli across RT and accuracy data.

We planned to test several candidate models that represent different plausible hypotheses concerning the latent variable structure of control adaption to changing demands. For these models, we treated condition-specific mean RT for the unbiased, diagnostic stimulus items as reflective indicators of the latent factors of interest. By using the unbiased items as our indicators, we avoided the instability of difference scores and controlled for potential frequency-based confounds, since the unbiased items are PC-50 and PS-50 and all the trial types are presented equally often. Because these data were expected to be continuous but multivariate nonnormal, we selected the maximum likelihood estimator with robust standard errors and Satorra-Bentler scaled test statistics when evaluating model fit (Satorra & Bentler, 1988). We also fixed the variances of the latent factors within our models to 1 so that the models are identified, factor measurements are scaled, and any relationships between the factors are essentially standardized correlations.

To evaluate model fit, we used several indices: incremental fit indices such as the comparative fit index (CFI; Bentler, 1990) and the Tucker-Lewis Index (TLI; Tucker & Lewis, 1973), root mean square error of approximation (RMSEA; Steiger & Lind, 1990), and the standardized root mean square residual (SRMR; Hu & Bentler, 1999). Incremental fit indices compare misfit against a baseline model that only estimates variance, whereas RMSEA indicates absolute model misfit per degrees of freedom and SRMR is the average of squared values in the residual correlation matrix. We considered good or excellent fit to be CFI and TLI values of 0.95 or higher; RMSEA values of 0.05 or lower; and SRMR values less than 0.06. Adequate fit is indicated by CFI and TLI values above 0.90 and RMSEA of less than 0.08. We also report χ², which is overpowered in large samples and not usually considered an appropriate measure of model fit, because it would validly mark model fit only if the specified model is the true model in the population, an assumption that cannot be verifiably proven. Finally, we selected between competing models using nested model comparisons.

For the final model, we formally tested measurement invariance with respect to the between-participant multi-group factor of block order, which was collapsed to either mostly congruent (MC) or mostly incongruent (MI) first. The first level of measurement invariance, configural invariance, tests whether the groups have the same factor structure (i.e., number of factors and pattern of path loadings). The final model must be configurally invariant to be comparable for all block order groups. After configural invariance, metric invariance tests whether the constructs have the same meaning by constraining the factor loadings (i.e., slopes) across groups. At least partial metric invariance (Byrne et al., 1989) is necessary for meaningful comparisons between block order groups. Following metric invariance, scalar invariance tests whether the groups have similar baseline responses (and their latent means can be compared meaningfully) by constraining the intercepts across groups. Finally, a more restrictive form of invariance is strict invariance, with item residual variances constrained across all groups. To evaluate these forms of invariance, we used change in CFI when moving from weaker to stronger invariance. Differences in CFI of less than 0.01 were interpreted as evidence of no reduction in fit when additional invariance constraints are added (Cheung & Rensvold, 2002).

One concern with respect to cognitive control domains has been the extent to which the latent structure reflects the ability to perform well on cognitive tasks at large rather than anything specific to the constructs in question. Therefore, in the next analysis, we ran regression models where each indicator was separately predicted by ICAR (our measure of general intelligence) and extracted the residuals as a measure of variance that was not shared by ICAR (cf. Robinson & Tamir, 2005). We interpret these residualized scores to indicate learned control after accounting for baseline intelligence or ability. If model fit noticeably decreased for our final model, this would suggest that the constructs we modeled do not reflect learned control alone. To account for concerns around processing speed, we also estimate a bifactor model with correlated specific factors and a general factor meant to represent speed, subsequently examining what the addition of the general factor does to path loadings and the across domain correlations.

In addition to examining model fit, we also tested whether participants were explicitly aware of the PC manipulations via a series of t-tests and ANOVAs. Analyses were performed in a Python Jupyter notebook, via the pandas (Reback et al., 2020) and seaborn (Waskom, 2021) packages, and RStudio (R version 3.5.1; R Core Team, 2018), via the lavaan (Rosseel, 2012), semTools (Jorgensen et al., 2021), and semPlot (Epskamp, 2015) packages, as well as other data manipulation, analysis, and visualization related packages (e.g., dplyr, Wickham et al., 2021; ggplot2, Wickham et al., 2020; afex, Singmann et al., 2021). All analyses, unless otherwise indicated as exploratory, were preregistered, with the preregistration plan transparently edited at the OSF repository as we respecified candidate models (https://osf.io/nmwhe/). This plan includes information relevant to the mental health symptomatology not mentioned here. All materials (e.g., analysis and experimental code, data) are available online at this OSF repository.

3. Results

Behavioral metrics across the list-wide proportion congruent (LWPC) and list-wide proportion switch (LWPS) tasks largely look as expected: we observe larger congruency effects and switch costs when incongruent trials and task-switching (PC-25, PS-70) are more frequent (vs. PC-75, PS-30) (Table 2; see Supplementary Tables 1-8 for traditional ANOVA analyses). Table 2 includes descriptive statistics for RT and additional RT measures corrected for accuracy (e.g., inverse efficiency (IE) and linear integrated speed accuracy scores (LISAS)) as well as RT difference scores, though only analyses with IE were preregistered. Here, with split-halves reliability around acceptable levels for the primary RT metric, we replicate our prior work: Bejjani and colleagues (2021) reported a test-retest reliability for the LWPS RT conditions used within the current study between 0.69 and 0.76 as well as 0.47 for RT switch costs, which, unlike the current study, had been collapsed across biased and unbiased items for greater trial counts. Bejjani and Egner (2021) additionally reported reliability for the LWPC RT conditions between 0.67 and 0.72, similar to what is reported in the current study.

Table 2.

Descriptive behavioral metrics (RT, IE, LISAS, and RT difference scores) across the LWPC and LWPS.

Reaction Time (ms)
Metric	Mean	Lower 95% CI	Upper 95% CI	Skew	Kurtosis	Reliability
eMCC	652	648	656	0.70	1.07	ρ(947) = 0.69
eMCIC	717	712	722	0.18	0.05	ρ(938) = 0.63
eMIC	656	652	660	0.72	1.21	ρ(946) = 0.63
eMIIC	709	705	713	0.23	0.17	ρ(943) = 0.67
lMCC	641	637	645	0.75	1.32	ρ(948) = 0.68
lMCIC	696	692	701	0.23	0.16	ρ(948) = 0.66
lMIC	640	636	644	0.85	1.70	ρ(948) = 0.70
lMIIC	685	681	689	0.50	0.84	ρ(948) = 0.67
eMRR	725	720	730	0.07	0.09	ρ(948) = 0.72
eMRS	754	749	759	−0.19	0.12	ρ(947) = 0.68
eMSR	736	731	741	−0.12	0.07	ρ(947) = 0.70
eMSS	750	744	755	−0.22	0.36	ρ(948) = 0.65
lMRR	713	708	718	0.21	0.19	ρ(948) = 0.72
lMRS	743	737	748	−0.19	0.13	ρ(948) = 0.69
lMSR	727	722	732	0.05	0.17	ρ(948) = 0.72
lMSS	740	735	746	−0.10	0.04	ρ(947) = 0.69
Inverse Efficiency (ms)
Metric	Mean	Lower 95% CI	Upper 95% CI	Skew	Kurtosis	Reliability
eMCC	769	756	782	3.05	14.85	ρ(947) = 0.63
eMCIC	1109	1064	1154	5.33	41.62	ρ(938) = 0.64
eMIC	782	767	796	5.03	48.73	ρ(946) = 0.58
eMIIC	1001	971	1032	5.68	52.82	ρ(943) = 0.61
lMCC	731	721	741	2.46	10.40	ρ(948) = 0.52
lMCIC	882	864	900	5.39	56.86	ρ(948) = 0.56
lMIC	721	713	729	1.78	5.10	ρ(948) = 0.53
lMIIC	837	825	849	1.89	5.84	ρ(948) = 0.53
eMRR	850	839	860	1.70	6.25	ρ(948) = 0.54
eMRS	955	939	970	6.98	113.34	ρ(947) = 0.41
eMSR	858	849	868	1.02	2.08	ρ(947) = 0.47
eMSS	934	921	947	1.72	7.06	ρ(946) = 0.45
lMRR	810	801	819	1.12	2.40	ρ(948) = 0.50
lMRS	921	909	933	1.27	2.50	ρ(948) = 0.50
lMSR	830	821	840	1.59	5.68	ρ(948) = 0.51
lMSS	899	887	911	1.28	3.39	ρ(947) = 0.51
LISAS (ms)
Metric	Mean	Lower 95% CI	Upper 95% CI	Skew	Kurtosis	Reliability
eMCC	689	684	694	0.67	0.33	ρ(947) = 0.69
eMCIC	795	789	802	0.39	−0.01	ρ(938) = 0.66
eMIC	695	690	700	0.61	0.37	ρ(946) = 0.64
eMIIC	778	772	783	0.35	−0.08	ρ(943) = 0.66
lMCC	673	668	678	0.71	0.86	ρ(948) = 0.61
lMCIC	749	744	755	0.24	−0.25	ρ(948) = 0.64
lMIC	670	665	675	0.66	0.85	ρ(948) = 0.63
lMIIC	733	728	738	0.37	0.12	ρ(948) = 0.62
eMRR	769	764	775	0.14	0.06	ρ(948) = 0.65
eMRS	820	814	826	−0.13	0.05	ρ(947) = 0.57
eMSR	780	774	786	−0.04	−0.15	ρ(947) = 0.61
eMSS	811	805	817	−0.17	0.06	ρ(946) = 0.60
lMRR	749	743	754	0.19	−0.06	ρ(948) = 0.63
lMRS	802	796	808	−0.03	0.01	ρ(948) = 0.61
lMSR	764	759	770	0.11	0.13	ρ(948) = 0.64
lMSS	794	788	800	−0.01	−0.11	ρ(947) = 0.62
RT Difference Scores divided by overall RT
Metric	Mean	Lower 95% CI	Upper 95% CI	Skew	Kurtosis	Reliability
eMCcong	0.10	0.09	0.10	0.05	2.09	ρ(948) = 0.20
eMICcong	0.08	0.07	0.08	0.12	0.44	ρ(947) = 0.12
lMCcong	0.08	0.08	0.09	0.21	−0.16	ρ(948) = 0.20
lMICcong	0.07	0.06	0.07	0.15	0.23	ρ(948) = 0.18
eMRswi	0.04	0.03	0.04	−0.09	0.55	ρ(947) = 0.13
eMSswi	0.02	0.01	0.02	0.14	0.33	ρ(948) = 0.01
lMRswi	0.04	0.04	0.05	0.07	0.03	ρ(948) = 0.11
lMSswi	0.02	0.01	0.02	0.51	3.31	ρ(947) = 0.05

Reliability refers to split-halves reliability, which was calculated by correlating the mean condition-specific measures that result from alternating 0s and 1s across trials within all blocks of each respective task.

A number of tables are displayed in Appendix A for interested readers. Tables 3 and 9-11 display the correlation matrices for the behavioral metrics of interest in Table 2, and Tables 12-15 display the path loadings associated with all the Models estimated within the study using those metrics. Finally, Table 16 displays the reliabilities for the final latent factor models and Table 17 includes fits from an exploratory analysis on the timescales of learning between tasks.

Table 3.

Omnibus fit statistics across behavioral metrics (RT, IE, LISAS, difference scores)

	Model 1 – One (domain-general) factor
	χ 2	df	CFI	TLI	RMSEA	SRMR
RT	5024.97	104	0.618	0.559	0.245 [0.239, 0.250]	0.184
IE	1119.27	104	0.644	0.590	0.155 [0.147, 0.164]	0.124
LISAS	4225.99	104	0.615	0.556	0.217 [0.211, 0.222]	0.162
RT Difference Scores	158.87	20	0.712	0.597	0.090 [0.077, 0.103]	0.072
	Model 2 – Two factors (Conflict and Switch domains)
	χ 2	df	CFI	TLI	RMSEA	SRMR
RT	1366.69	103	0.914	0.900	0.117 [0.111, 0.122]	0.037
IE	583.50	103	0.849	0.824	0.102 [0.094, 0.110]	0.063
LISAS	1529.18	103	0.872	0.851	0.125 [0.120, 0.131]	0.052
RT Difference Scores	45.78	19	0.946	0.921	0.040 [0.025, 0.055]	0.033
	Model 3 – Four fully correlated proportion context factors (PC/PS)
	χ 2	df	CFI	TLI	RMSEA	SRMR
RT	748.52	98	0.956	0.946	0.086 [0.080, 0.092]	0.028
IE	444.51	98	0.895	0.872	0.087 [0.079, 0.095]	0.054
LISAS	972.63	98	0.923	0.905	0.100 [0.094, 0.106]	0.042
RT Difference Scores	16.71	14	0.995	0.989	0.015 [0.000, 0.037]	0.019
	Model 4 – Four domain-only correlated proportion context factors (PC/PS)
	χ 2	df	CFI	TLI	RMSEA	SRMR
RT	1036.39	102	0.937	0.925	0.101 [0.095, 0.106]	0.272
IE	557.79	102	0.863	0.838	0.098 [0.090, 0.106]	0.167
LISAS	1226.50	102	0.901	0.883	0.111 [0.105, 0.117]	0.232
RT Difference Scores	35.13	18	0.966	0.947	0.032 [0.016, 0.048]	0.037
Model 5 – One higher-order factor (domain-general context) predicted by proportion context factors (PC/PS)
	χ 2	df	CFI	TLI	RMSEA	SRMR
RT	1607.58	100	0.898	0.877	0.129 [0.123, 0.135]	0.146
IE	572.19	100	0.856	0.827	0.101 [0.093, 0.109]	0.094
LISAS	1587.97	100	0.870	0.843	0.129 [0.123, 0.134]	0.125
RT Difference Scores	n/a	n/a	n/a	n/a	n/a	n/a
Model 6 – Two higher-order factors (domain-specific context) predicted by proportion context factors (PC/PS)
	χ 2	df	CFI	TLI	RMSEA	SRMR
RT	749.30	99	0.956	0.946	0.085 [0.080, 0.091]	0.028
IE	442.52	99	0.896	0.873	0.086 [0.078, 0.095]	0.054
LISAS	972.66	99	0.923	0.906	0.099 [0.094,0.105]	0.042
RT Difference Scores	n/a	n/a	n/a	n/a	n/a	n/a

3.1. Correlated Domain- and Context-Specificity of Control-Learning

The first model we considered for control-learning harkens back to traditional theories of control as a general supervisory system (e.g., Norman & Shallice, 1986): one factor that controls attention and might explain all the variance in the behavioral metrics. However, Model 1 fit poorly (χ²(104, N = 950) = 5024.97, CFI = 0.618, TLI = 0.559, RMSEA = 0.245, 90% CI = [0.239, 0.250], SRMR = 0.184). Path loadings (see Supplementary Table 12 in Appendix A) were positive and high (LWPS: range [0.81, 0.87]; LWPC: range [0.52, 0.60]), but uniquenesses on the indicators within the LWPC task remained high (0.64-0.73), highlighting that variance was not well explained by this model. See Table 2 for descriptive statistics on the metrics in this section and Supplementary Table 16 for the reliabilities of the final latent factors.

Next, we considered a model in which there was one factor per domain, akin to prior “diversity” models of cognitive control (Friedman et al., 2008; Miyake et al., 2000; Miyake & Friedman, 2012), and these first-order latent variable domains were allowed to correlate. Model 2 fit was adequate (χ²(103, N = 950) = 1366.69, CFI = 0.914, TLI = 0.900, RMSEA = 0.117, 90% CI = [0.111, 0.122], SRMR = 0.037) and improved from the one factor supervisory model (Δχ²(1) = 281.8, p < 0.001). Path loadings were again high and positive (LWPS: range [0.83, 0.88]; LWPC: range [0.76, 0.87]), and domain factors were moderately correlated (r = 0.54). This suggests that a model accounting for domain (conflict-control vs. task-switching) fits well and domain is a significant source of common variance in control-learning.

We then tested whether model fit could be improved by accounting for context-specificity in the form of the proportion manipulations within the conflict and task-switching protocols (Egner, 2014). We allowed these first-order latent variables to correlate within and across domains, without any constraints. Model 3 fit was good (χ²(98, N = 950) = 748.52, CFI = 0.956, TLI = 0.946, RMSEA = 0.086, 90% CI = [0.080, 0.092], SRMR = 0.028) and improved from the correlated, two factor domain-specific model (Δχ²(5) = 597.64, p < 0.001). Again, path loadings were strong and positive (LWPS: range [0.87, 0.90]; LWPC: range [0.79, 0.89]). Interestingly, supporting the domain-specificity suggested by the previous model, within domain correlations (0.90, 0.92) were much higher than across domain correlations (0.52, 0.51, 0.52, 0.51). However, theoretical accounts of control-learning do not typically make strong assumptions about how, for example, adapting control within the easier, mostly congruent context would relate to adapting control within the harder, mostly task-switch context. The attentional states typically are not theorized to be similar across these contexts, nor are the specific task goals. Ultimately, this model poses little question of causality, since all of the proportion contexts were allowed to freely correlate as first order latent variables, so we next tested whether these across domain correlations between context-specific proportion latent variables improve model fit and matter to construct understanding.

In the fourth model, we fixed to 0 the across domain correlations between the context-specific proportion latent variables. Model 4 fit was still adequate (χ²(102, N = 950) = 1036.39, CFI = 0.937, TLI = 0.925, RMSEA = 0.101, 90% CI = [0.095, 0.106], SRMR = 0.272), but decreased from the third model (Δχ²(4) = 302.81, p < 0.001). We next tested whether there was one second-order, across domain statistical learning latent variable that accounted for the correlation between the first-order proportion congruent and switch context latent variables. Here, Model 5 fit was no longer adequate (χ²(100, N = 950) = 1607.58, CFI = 0.898, TLI = 0.877, RMSEA = 0.129, 90% CI = [0.123, 0.135], SRMR = 0.146) and significantly decreased from the third model (Δχ²(2) = 1095.3, p < 0.001). Because model fit decreased with the fourth and fifth models, these results suggest that the across domain correlations observed under model three are important to understanding the constructs, and that statistical learning of control demand cannot bridge the gap across domains or task goal on its own.

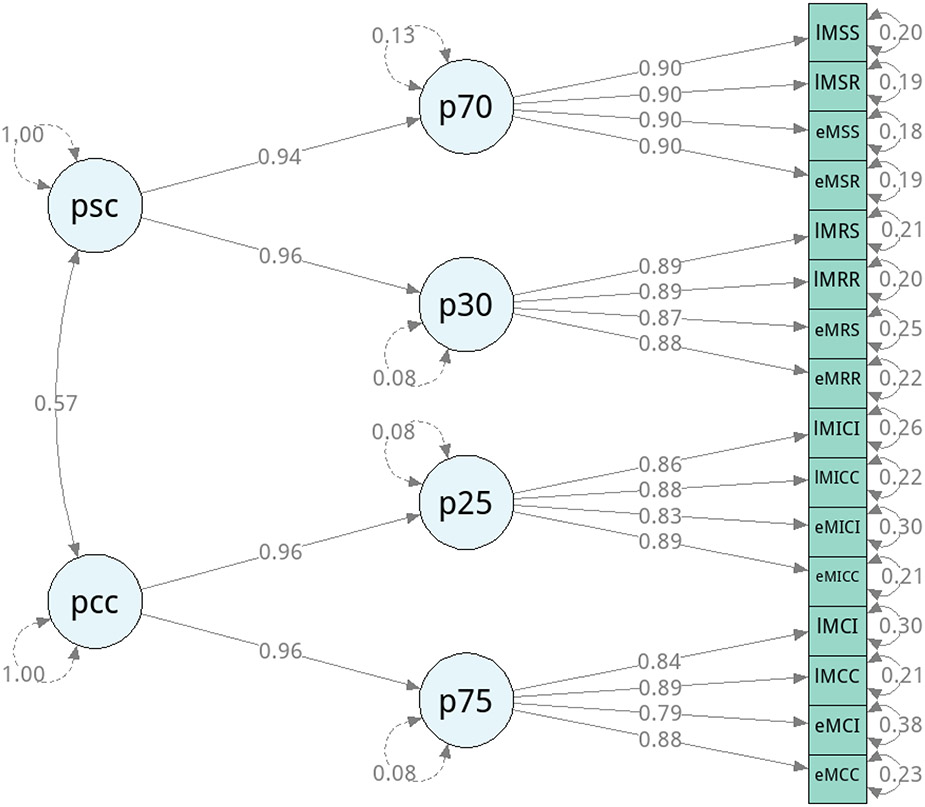
Finally, we tested whether adding two second-order, correlated domain-specific factors that were predicted by their respective proportion context variables would improve model fit. Model 6 fit was good (Figure 2; χ²(99, N = 950) = 749.30, CFI = .956, TLI = 0.946, RMSEA = 0.085⁴, 90% CI = [0.080, 0.091], SRMR = 0.028) and did not differ from the third model (Δχ²(1) = 0.60, p = 0.438). Although Model 6 is nearly equivalent to Model 3, where all correlations between proportion latent variables were unconstrained, on statistical grounds, Model 6 is more parsimonious (with an additional degree of freedom) and fits just as well as Model 3, suggesting that Model 6 ultimately yields the best fit. However, the theoretical interpretations differ substantially. Since Model 3 allows for unconstrained correlations among the proportion latent variables, an explanation for the pattern of correlations is not specified. Here, with Model 6, by specifying second-order domain-specific factors, we suggest that these factors explain the within-domain correlations between PS-70 and PS-30 as well as PC-25 and PC-75, and we then do not specify a latent source to explain the correlation among domain-specific adaptation. We thus argue that Model 6 is also more representative of the current theoretical understanding of control-learning, whereby participants learn the current difficulty of each proportion context, learned adaptation of control is specific to the task goal at hand (i.e., the Stroop or task-switching protocol), and adapting learned control across domains is distinct yet correlated. Nonetheless, whether via Model 6 or Model 3, these results at large support the idea of correlated domain- and context-specificity of learned control.

Figure 2. Control-Learning Structural Equation Model.

Mean Reaction Times (ms) within condition-specific variables for unbiased (PC-50/PS-50) items are modeled to reflect their respective context-specific proportion latent variables, which then reflect correlated domain-specificity. The path diagram above was produced with the semPlot package and displays the standardized estimates after model estimation. E = Early, L = Late within context. MC = Mostly Congruent (PC-75), MI = Mostly Incongruent (PC-25), MR = Mostly Repeat (PS-30), MS = Mostly Switch (PS-70) contexts. C = Congruent, I = Incongruent, R = Repeat, S = Switch trial. P70 = PS-70, P30 = PS-30, P25 = PC-25, P75 = PC-75, PSC = Proportion Switch Contexts, PCC = Proportion Congruent Contexts.

To bolster evidence for Model 6, we inspected its associated reliability statistics, which were not all preregistered, but would provide support for the stability of the data. Altogether these reliability metrics were high (e.g., range [0.91, 0.94] for the coefficient alpha; see Supplementary Table 16 in Appendix A for model reliability), suggesting that the final model was stable and that the second-order factors were justifiable. We also examined whether the model assumptions held by examining the correlation matrix for the observed variables (Table 3). Early indicators were indeed highly correlated with late indicators; across domain correlations were smaller than within domain correlations; and proportion context variables typically hung together. Thus, although the path loadings were similar for each second-order domain latent variable as predicted by the first-order proportion variables, the underlying data suggest that these constructs were noticeably different.

Finally, in the preregistration, we initially proposed including a bifactor model with a general factor to account for additional common variance, potentially attributable to trait individual differences like working memory capacity (Hutchison, 2011) that were independent of control adaptation. However, second-order and bifactor models are mathematically closely related (Yung et al., 1999), which makes model selection difficult (van Bork et al., 2017), and bifactor models with a general factor must justify that the data are not unidimensional (Rodriguez et al., 2016), since model fit statistics are biased towards bifactor models (Morgan et al., 2015; Murray & Johnson, 2013). Therefore, rather than proposing that a bifactor model is the best representation of the data, in the present application of a bifactor model, we were primarily concerned about the extent to which processing speed played a role in our results.

Because Model 6 included a second-order factor, variance would likely not be parsed correctly with a general factor, so we here include a general factor with Model 3, which was statistically similar to Model 6, and examine whether the path loadings and covariances between latent variables decrease as a result of adding the general factor. As expected, this bifactor model fit better than Model 3 without a general factor (χ²(82, N = 950) = 409.51, CFI = 0.977, TLI = 0.967, RMSEA = 0.067, 90% CI = [0.061, 0.073], SRMR = 0.015). Importantly, however, while the path loadings decreased for the specific factors (range on conflict specific factors: [0.43, 0.85], switch specific factors: [0.78, 0.85]; range on general factor for conflict indicators: [0.43, 0.79], for switch indicators [0.30, 0.41]; see Figure 2 for comparison and Supplementary Table 12), the correlations also decreased (range for within domain: [0.79, 0.88]; range for across domain: [0.35, 0.37]), but remained modest in strength across domains, supporting the conclusion of correlated, but distinct latent factors. Additionally, we again note the worse fit of Model 5 relative to Models 3 and 6: Model 5 included a higher-order factor that was predicted by the proportion context latent factors, presumably to represent a frequency-based learner across domains that controlled context adaptation, which would certainly be sensitive to differences in processing speed, were they the sole explanation of the data. Moreover, the path loadings were not equal across domains – what we might expect if this all represented processing speed – and were strong. Taken together with the results of the bifactor model, we believe that this bolsters evidence for correlated but distinct latent factors in learning cognitive control even when accounting for processing speed.

In sum, we found support for theoretical proposals that learning to adapt cognitive control in the conflict and task-switching domains, while controlling for general processing speed, is best explained by modeling correlated domain- and statistical context-sensitivity, and that factors in this model are highly reliable. In other words, correlated but domain-specific statistical learning processes underpin the abilities to adapt to changes in conflict versus switch demand.

3.2. Addressing Speed-Accuracy Trade-offs and Conceptual Validity

Similar to the prior analysis with the bifactor model, while using aggregate reaction time data for the indicators has advantages related to reliability (as discussed in the Introduction), it can be argued that they run the risk of undermining conceptual validity, in that raw RT variance may indicate commonality between factors due to generic processing speed rather than the learned adaptation in specific control operations we intend to capture. Thus, we here examined further whether processing speed may have driven the conclusion of correlated but distinct latent factors, by estimating the specified models with metrics that control for processing speed.

We use inverse efficiency scores (Townsend & Ashby, 1983), which reflect RT in a given condition divided by accuracy in that condition, as well as linear integrated speed accuracy score (LISAS) (Vandierendonck, 2017), representing the overall standard deviation of RT divided by the overall standard deviation of the proportion of errors, which is subsequently multiplied by the proportion of errors in a specific condition and added to the reaction time in that condition. To preview, while these accuracy-corrected reaction time scores decrease omnibus model fit statistics because of the variability in accuracy, correlations among the latent variables remain similar in magnitude (see Supplementary Tables 9 and 10 for the correlation matrices and Tables 13 and 14 for the inverse efficiency and LISAS path loadings, respectively).

Inverse Efficiency (IE) largely followed the same pattern as RT (Table 4), except that fit of Model 6 was not acceptable, meeting our a priori criteria only for SRMR (vs. Model 3: Δχ²(1) = 0.07, p = 0.787). LISAS followed the same pattern as inverse efficiency, but with better fit: Model 6 had acceptable fit (vs. Model 3: Δχ²(1) = 0.00, p = 0.984).

Table 4.

Omnibus fit statistics when accounting for Block Order between-participant groups.

	χ 2	df	CFI	TLI	RMSEA	SRMR
Configural	894.46	198	0.953	0.943	0.088	0.030
Metric	925.61	212	0.952	0.946	0.086	0.037
Scalar	1008.27	222	0.948	0.943	0.088	0.040
Strict	1080.34	238	0.943	0.943	0.088	0.039

With all three metrics (RT, IE, LISAS), the correlations between domains at the higher-order proportion context latent factors were either 0.56 or 0.57, and the path loadings on these factors were all strong (range [0.82, 0.96]). In short, even using corrected speed metrics, the control factors were still distinct and correlated moderately with each other.

Finally, to align with previous literature, we estimated the specified models with RT difference scores (congruency effect, switch cost) that were divided by their respective overall task reaction times as a baseline (cf. Bejjani et al., 2018). Using difference scores involved a total of eight, not sixteen, indicators, which subsequently meant that we were unable to estimate Models 5 and 6, because they include a higher-level factor that results in model misidentification (see path loadings at Supplementary Table 15). As with the bifactor model analysis, we use the fit of Model 3 as an estimate for how Model 6 would fare, since these models are statistically similar, although we previously mentioned reasons for why we believe Model 6 to better represent control-learning theories.

As with RT, Model 3 fit using difference scores was excellent (vs. Model 2: Δχ²(5) = 28.64, p < 0.001). Interestingly, with Model 3 for difference scores, the across domain correlations were all non-significant except for PC-75 to PS-30, i.e., the correlation between the two “easy” context latent factors, which were moderately correlated (0.28). We view the lack of multiple cross-domain correlations in two ways: first, it may stem in part from unreliability due to the nature of difference scores (Tables 2, 16). Accordingly, the two factors with the highest reliabilities within their domains (PC-75, PS-30) had a significant across domain correlation with each other, and the second highest across domain correlation was also with PC-75, which had the highest split-halves reliability (Table 2). Thus, this explanation seems plausible and in line with what prior research has reported on difference scores (e.g., Draheim et al., 2019). Second, given the converging evidence from RT, LISAS, and IE as well as the bifactor model that shows distinct but correlated latent factors, it is also possible that variance shared across control domains primarily stems from how participants relax control in the easier contexts (cf. Bugg et al., 2015). This is consistent with our prior work (Bejjani & Egner, 2021) where we found stronger correlations across time regulating congruency differences for the mostly congruent context than the mostly incongruent context.

3.3. Timing of Control-Learning Effects

In an exploratory analysis that resulted from the revision process, we reexamined assumptions around the early/late indicator designation. We thus re-estimated Models 3 and 6 with RT, IE, and LISAS collapsed across the early/late metrics, collapsed only for the switch task, and collapsed only for the conflict task (see Supplementary Table 17). Because these models are non-nested and trained on different sets of indicators, we looked at differences in AIC and BIC as well as the omnibus fit statistics for model comparison. As stated in the preregistration, per established guidelines (Kass & Raftery, 1995; Schwarz, 1978), weak evidence is typically qualified as a BIC difference between 0-2, good evidence between 2-6, strong evidence between 6-10, and very strong for 10+, and with respect to the omnibus fit statistics, we primarily looked for patterns in the data about model fit.

Of all the models, reaction time difference scores for Model 3 have the smallest AIC and BIC values and best omnibus fit statistics. Next are the collapsed early/late models across all metrics, but the RMSEA for these models is well outside the acceptable bounds, indicating some level of misfit despite the reduced degrees of freedom. In fact, what produces the best model fit among the corrected speed metrics (IE, LISAS) – beyond RT difference scores, which cannot be collapsed across time due to model misidentification – is the model that includes early and late indicators for the task-switching paradigm, but collapses across time for the conflict-control paradigm. Here, AIC and BIC values are lower than those of the models discussed in the above, and RMSEA values are much closer to the acceptable criterion. RT shows a similar pattern, but for the models where early and late indicators are present for the conflict-control paradigm and collapsed for the task-switching paradigm.

Of note, we do not believe these results are particular to our experimental design, that is, because participants performed the LWPC before the LWPS. Task order is unlikely to fully explain these differences because early and late meant early and late within a proportion context: if a person experienced the mostly switch context first, early would mean the first half of that context and late would mean the second half of the context, and the same definition would occur for the mostly repeat context. We would expect the effects of exhaustion or fatigue to impact the latter four blocks (i.e., a whole context) rather than selectively impact halves of each, and we did not find measurement invariance due to block order (see the next section, Section 3.4).

Together these results suggest an intriguing possibility that the two domains could also be learned on different timescales.

3.4. Measurement Invariance across Block Order

Here, we tested whether the context that participants experienced first (e.g., MC or MI first) systematically shifted the way in which participants learned. In terms of measurement invariance across block order groups, the fit of the configural model was good (Table 2; χ²(198, N = 950) = 894.46, CFI = .953, TLI = 0.943, RMSEA = 0.088, SRMR = 0.030). When factor loadings were constrained to equality across groups, CFI barely decreased (0.952), resulting in a CFI difference of 0.001, well below the cutoff (0.01), suggesting full metric invariance across block order groups. For the sake of completeness, we report the model fit statistics for the tests associated with metric (constrained slopes), scalar (constrained intercepts), and strict (constrained item residual variances) invariance in Table 4, which do not fall within the CFI decision criterion and therefore suggest measurement invariance across block order groups. In sum, for Model 6, the factor structure, loadings, intercepts, and item residual variances were equivalent across block order groups, allowing for means to be compared between groups without concern for whether they represent the same construct.

3.5. Specificity of Control-Learning

Here, we tested whether the good model fit for the final model reflects a bias in our indicators for participants performing well on cognitive tasks, rather than being specific to the control-learning constructs we specified. To this end, we residualized our indicators on ICAR, our measure of general intelligence, and reran the model estimation.

Model fit, using the residualized indicators, remained good (χ²(99, N = 950) = 733.85, CFI = 0.957, TLI = 0.947, RMSEA = 0.084, 90% CI = [0.079, 0.090], SRMR = 0.027), with strong path loadings (LWPS: range [0.88, 0.90]; LWPC: range [0.79, 0.88]) and a moderate correlation across control domains (r = 0.57).

Another question is the extent to which self-reported motivation or trait individual differences might also have driven the good model fit for the final model. We therefore repeated the same process that we used to residualize indicators on ICAR, but with participant scores on the BIS (thought to reflect punishment sensitivity) and the BAS reward responsiveness subscale. Thus, the residualized indicators are now residualized on both ICAR and reward and punishment sensitivity. Although we preregistered our intent to residualize indicators on ICAR, we did not preregister this analysis with BIS/BAS, and this is therefore an exploratory analysis.

Model fit was again good (χ²(99, N = 950) = 727.46, CFI = 0.957, TLI = 0.948, RMSEA = 0.084, 90% CI = [0.078, 0.090], SRMR = 0.027), with strong path loadings (LWPS: range [0.87, 0.90]; LWPC: range [0.79, 0.89]) and a moderate correlation across control domains (r = 0.56).

In sum, we found good model fit for the final control-learning model, with correlated domain- and context-specificity, even when accounting for individual differences in performance on intelligence tasks and self-reported reward and punishment sensitivity.

3.6. Explicit Awareness as a Learning Signal

The extent to which explicit awareness plays a role in control-learning remains debated (Abrahamse et al., 2016). Here, we assessed explicit awareness of the proportion context manipulations with a variety of questions; these results are fully reported in Appendix A with the Supplementary Text for interested readers. In short, participants did not accurately estimate the causal strength of the item-specific and list-wide proportion manipulations, but they could explicitly identify the temporal difficulty associated with blocks and the item-specific difficulty associated with biased items. Combined with the fact that participants misidentified the difficulty of unbiased items, these results may suggest that intermixing biased with unbiased items causes an increased awareness of difficulty that may then act as a learning signal for generalization of control within a temporal context (cf. Bugg & Dey, 2018).

3.7. Measurement Invariance across Explicit Awareness

We also ran an exploratory analysis testing whether there is measurement invariance across participants who self-report different levels of explicit awareness on these tasks. We therefore created a new subgroup of participants who self-reported noticing that some blocks of trials were harder than others, when categorizing both color-words and digits/letters (N = 278 for “Yes” to both, i.e., level 1, versus N = 672, i.e., level 2). One caveat is that self-report delineated this group. It is also possible that participants said “yes” simply due to response bias. However, participants could select “Don’t Know”, and only about 46% of participants who reported awareness for the LWPC blocks reported awareness on the LWPS blocks, suggesting some level of discriminability.

We found little support for differences in model fit due to explicit awareness or lack thereof. Model fit for the configural model remained good (χ²(198, N = 950) = 876.37, CFI = 0.953, TLI = 0.943, RMSEA = 0.087, SRMR = 0.028), and differences in CFI never exceeded the 0.01 decision criterion (Table 5). In sum, we found evidence that factor structure, loadings, and intercepts, as well as item residual variances, do not differ as a function of explicit awareness, suggesting that explicit awareness of the task statistics does not influence the meaning of the latent sources of influence in learned control adaptation.

Table 5.

Omnibus fit statistics when accounting for Explicit Awareness between-participant groups.

	χ 2	df	CFI	TLI	RMSEA	SRMR
Configural	876.37	198	0.953	0.943	0.087	0.028
Metric	918.82	212	0.952	0.946	0.085	0.036
Scalar	929.10	222	0.952	0.948	0.083	0.036
Strict	913.82	238	0.952	0.951	0.081	0.037

4. General Discussion

The current study aimed to examine the latent structure of control-learning underlying contextual adaptations of control processes in the domains of cognitive stability (conflict-control) and flexibility (task switching). Participants performed consecutive list-wide proportion congruent (LWPC) and switch (LWPS) paradigms, which manipulated the proportion of difficult trials over blocks. Within each block, there were inducer, frequency-biased stimuli that were either predictive of difficult (incongruent/task-switch) or easy (congruent/task-repeat) trials as well as diagnostic, frequency-unbiased stimuli that were equally associated with either difficult or easy trials and were thus only influenced by the block-wide context. We modeled the frequency-unbiased stimuli as reflective indicators that changed as a function of their causal latent variables. We evaluated one- and two-factor models that included domain-general adaptation of control, accounting for the commonality among categorization task goals, as well as models that also accounted for context-sensitivity and the role of learning. According to established standards for structural equation modeling, model fit was good for the model that included correlated domain- and context-specific latent factors, exceeding most of the other models against which it was compared. This final model continued to fit the data well even after we accounted for processing speed and individual variance in performance on a measure of general intelligence, as well as self-reported scores on measures of reward and punishment sensitivity. Moreover, we found measurement invariance across self-reported explicit awareness of the task manipulations and the order in which participants experienced the more difficult blocks. Finally, a series of additional model fits using inverse efficiency scores, LISAS, and difference scores, all of which control for the potential confound of individual differences in generic processing speed driving the results, corroborated the conclusions based on raw RT data. Together these results provide evidence for domain-specific but correlated learners of contextual control demands, and this control-learning architecture was minimally impacted by motivation, awareness, and cognitive ability.

4.1. Caveats

One major caveat inherent in statistical modeling is that our conclusions are necessarily limited to the set of models we considered. We believe that the models we compared represent the most common and plausible assumptions in this literature, and we respecified hypothesized models in our preregistration as our thinking on the topic evolved, but we nonetheless have not estimated all possible models that could fit the control-learning data reported here. Other caveats are specific to the experimental procedures deployed. For instance, consistent with past research (see review at Stewart et al., 2017), the MTurk sample recruited shows a slight underrepresentation of Black/African-American participants and participants with Hispanic origin relative to the U.S. population as a whole.

Because participants only performed list-wide paradigms, with temporal manipulations of control-learning, we also do not know the extent to which the final model applies to other manipulations of control-learning, such as the context-specific and item-specific proportion paradigms or other, shorter-scale control adjustments like the congruency sequence effect (Gratton et al., 1992; reviewed in Egner, 2007) or post-error slowing (Rabbitt, 1966; reviewed in Wessel, 2018). While current theories largely assume learning in these paradigms should work similarly (Abrahamse et al., 2016; Egner, 2014), this has yet to be tested, particularly since control application may differ depending on whether participants anticipate or react to demand in the moment (Bejjani, Tan, et al., 2020; Bugg, 2017); that is, whether control is deployed proactively or reactively (Braver, 2012). Since the present results also imply some level of differences in learning by timescale, this question is particularly relevant.

Here, the reflective indicators were aggregate RT means from specific conditions, which means that they all had the same measurement error (though error due to unreliability, i.e., random error, was minimal). This measurement error would also manifest in the latent variables, making it impossible for us to discern, for example, the extent to which arousal (cf. Verguts & Notebaert, 2009) may have played a role in learning. This is especially true given the fact that the LWPC and LWPS tasks differed slightly in overall block-wide contingency strength (75:25 versus 70:30), and no work has yet addressed whether the degree of contingency impacts the strength of pure frequency-unbiased relative to frequency-biased control-learning⁵.

Because both the LWPC and LWPS protocols involved stimulus categorization-oriented tasks, it is possible that the correlation between the second-order latent variables reflects this mutualism, whereby strength in categorization ability would boost the shared variance between domains. However, we largely discount this interpretation because of the correlation strengths (path loadings) of the unconstrained third model and the fact that the LWPS protocol involves more categorization tasks than the LWPC protocol. Unbiased items are equally associated with difficult and easy trials, but in the LWPS protocol, although the two tasks (parity and letter) are presented an equal number of times as switch and repeat trials across the paradigm, the list-wide manipulation nonetheless involves task-level bias. That is, tasks that occur in low PS blocks are necessarily presented more often as repeat than switch trials in those blocks and tasks in high PS blocks are necessarily presented more often as switch than repeat trials in those blocks. For example, in one PS-30 block where the switch:repeat trial ratio is 18:42, 9 of the total 18 switch trials will be task A while 9 will be task B. Likewise, 21 of the 42 total repeat trials will be task A while 21 will be task B. Overall, task A and B were presented 30 times each, but both have been associated with switch trials 9 times and repeat trials 21 times. As such, both task A and task B become associated with low-switch likelihood in a PS-30 block (Siqi-Liu & Egner, 2020). Thus, if categorization ability provided the commonality between the two domains, we should have observed differences in the across domain path loadings for the PS-70 versus PS-30 variables, where the task-level bias would have manifested. We did not, which suggests that the common theme of stimulus categorization was not what determined the common variance between the conflict-control and task-switching domains.

A final limitation of the present study is that while we have demonstrated discriminant validity of our factors with respect to their independence from general intelligence and motivation measures, it would arguably have been desirable to also show (expected) positive relationships with some independent measures of related constructs. For instance, a number of previous studies have shown that performance on conflict-control tasks correlates positively with complex working memory span (Hutchison, 2011; Kane & Engle, 2003; Meier & Kane, 2013; Unsworth et al., 2009; but see Rey-Mermet et al., 2019). Accordingly, one would anticipate that the control-learning factor in the present study would account for significant variance in working memory performance. However, given that this relationship has been found to be quite context-specific (e.g., Kane & Engle, 2003; Meier & Kane, 2013) and that other studies have found little evidence for short-scale adjustments in conflict-control to relate to working memory span (e.g., Keye et al., 2013; Meier & Kane, 2013; Unsworth et al., 2012; Wilhelm et al., 2013), it is not entirely clear whether observing or not observing this type of relationship in the current study would really provide a conclusive test of convergent validity. Nonetheless, combining the control-learning probes employed in the present paper with complex span tasks would undoubtedly be of interest for further studies, in particular since there seems a be a dearth of studies relating adjustments in switch readiness to working memory capacity. Having said that, based on the fact that a substantial number of prior studies have shown that individual differences in performance on some classic working memory tasks (e.g., a variant of the n-back task) and task switching protocols (e.g., the classic number/letter switch task; Rogers & Monsell, 1995) load on distinct latent factors (“updating” vs. “shifting”, respectively) (e.g., Friedman et al., 2006, 2008, 2020; Miyake et al., 2000; Seer et al., 2021; Snyder et al., 2021; Vaughan & Giovanello, 2010), it appears unlikely that the types of adjustment in switch readiness probed in the present study would be closely related to working memory capacity.

4.2. Correlated Domain-Specificity

In this study, we found evidence of good fit for a model that included correlated domain- and context-specific latent factors. Put another way, people learn to adapt control settings to changing contexts, and this ability is underpinned by distinct but correlated mechanisms when it comes to adapting to changes in demand on shielding a current task set from distracters versus changes in demand on switching from one task set to another. This finding is in line with the assumption that regulating on-task focus and between-task switching are related, but are neither mediated by a unitary supervisor nor fully reciprocal processes. Critically, this model was derived using only frequency-unbiased items that are free of most confounds that plagued earlier research on control-learning (Braem et al., 2019). While the idea of a single, domain-general learner is discounted by the current findings, the moderate correlation (0.56-0.57) between adaptations in the conflict-control and task-switching domains across all behavioral metrics suggests some commonality in how domain-specific learning takes place, that is, that some underlying mechanisms may be similar. Results from various studies support this notion: for example, researchers have found support for episodic contributions to learned control across both conflict-control (Brosowsky & Crump, 2018; Spinelli et al., 2019) and task-switching (Whitehead et al., 2020) domains. However, despite a potentially similar learning source, each domain still retains its own unique properties: we found tighter potential coupling between the proportion switch than proportion congruent contexts, but also less stable individual differences when using switch costs compared to congruency effects.

To explicitly probe for the source of commonalities and test the role of learning, researchers could follow the lead of prior latent variable studies on cognitive control (Friedman & Miyake, 2017; Miyake & Friedman, 2012) and examine the overlap between brain regions or neural mechanisms that are involved between domains as well as the separable components specific to each domain. For example, Chiu and Egner (2019) suggested that a subcortical learning machinery centered on the dorsal striatum, typically associated with reward learning (e.g., Bejjani et al., 2019), mediates the learning of stimulus-control associations (in conjunction with frontoparietal cortex). This proposal was based on model-based neuroimaging of conflict-control learning (Jiang et al., 2015; Chiu et al., 2017), and it naturally raises the question of whether the striatum may play a similar role across other control domains, in particular within the domain of task switching (cf. De Baene & Brass, 2013). Importantly, this “unity and diversity” research approach should nonetheless yield findings that differ from copious prior neuroimaging research on conflict-control and task switching, since it is concerned with dynamic adjustments of control rather than modeling static differences in control metrics. Moreover, the final model identified here yielded highly reliable path loadings and composite reliability, an improvement on prior research with difference scores that sometimes yielded strong common variance among indicators and sometimes did not (Draheim et al., 2019).

Finally, another possibility for investigating the source of commonality among tasks is to impose similar demands across the learning paradigms and simply test for domain-specific contributions to control-learning. For example, Bugg and colleagues (2015) used a cued LWPC protocol to show that participants typically relax control when they have foreknowledge of upcoming demand. This is similar to cued LWPS studies, where most adjustments occur in response to the easier, task-repeat trials (e.g., Bejjani et al., in press; Siqi-Liu & Egner, 2020) than in response to the harder, task-switch trials. Here, this commonality may arise from awareness or from relaxing control because of learned expectations (cf. Bejjani, Dolgin, et al., 2020) or both, which may impact the timing of how people adjust control. Research that more explicitly teases apart the implications of a shared learning framework along these lines is needed (Abrahamse et al., 2016).

4.3. Timescales of Learning Control

One intriguing possibility suggested by the current data set is that people might learn to adjust control in different domains on different timescales. Specifically, exploratory model comparison showed that separating out early and late indicators for the task-switching, but not conflict-control, domain yielded the smallest AIC and BIC values as well as good omnibus model fit. This could suggest two, not mutually exclusive possibilities: that people are less consistent over time in their recruitment of conflict-control and thus the collapsed metrics are needed to reflect their ongoing expectations, or that people learn probabilistic changes in switch likelihood more easily than changes in conflict likelihood and thus the timescale of adjustments is more rapid for the former.

With respect to the latter possibility, memory effects for associations between specific stimuli and task-switching demands are potentially of shorter duration than those of conflict-control. For example, studies that have used one-shot control-learning paradigms, in which participants are shown trial-unique images that are associated with the need to recruit different levels of control, have found conflict-control effects that last longer than those for task-switching (Bejjani et al., 2021; Brosowsky & Crump, 2018; Whitehead et al., 2020). These differences in duration may be caused in part by a difference in how attention is allocated to target stimuli under conflict as compared to task switching. Specifically, there is some evidence that conflict, presumably by refocusing attention on task-relevant information (Egner & Hirsch, 2005), can lead to enhanced memory for target information (Krebs et al., 2015; Rosner et al., 2015; Rosner & Milliken, 2015; see also Davis et al., 2019), whereas task-switching may cause memory impairment for target stimuli (Richter & Yeung, 2012), perhaps due to the need to relax task-set shielding during task set updating (e.g. Dreisbach & Wenke, 2011). Outside of longer-term adjustments, item-specific control effects may also have smaller effect sizes within the task-switching domain (Chiu & Egner, 2017) than in the conflict-control domain (Bejjani, Tan, et al., 2020), although a formal meta-analysis to that effect has not yet been conducted. Nonetheless, within the task-switching domain, we have found control-learning to be insensitive to long-term memory consolidation (Bejjani et al., 2021), with effect sizes that are larger earlier on in the task than later. Finally, time-bound differences in learning may also stem from the nature of specific task statistics in the present study: to form stable associations between stimuli, contexts, tasks, and task-set learning, we ensured biased stimuli were both PS-80 and PS-20, whereas the item-specific manipulation within conflict-control meant that biased stimuli were either PC-90 or PC-10 (Bejjani et al., 2021). This could result in weaker overall relationships – although this is contradicted by the effect sizes noted in Appendix A – or a deeper emphasis on earlier learned expectations that may dissipate more over task blocks until the context shift.

With respect to the possibility that people may recruit conflict-control less consistently across time, we suggest a few explanations. For example, an asymmetrical list shifting effect (Abrahamse et al., 2013; Bejjani, Tan, et al., 2020; Bejjani & Egner, 2021), in which congruency effects are more reduced when participants shift from a harder, mostly incongruent context to a mostly congruent context than in the other order, is present for the conflict-control domain, but not the task-switching domain (Bejjani et al., 2021). This potentially signals that conflict-control is more volatile (Jiang et al., 2015) on a short-term scale and sensitive to contextual demands that may make collapsing across metrics necessary to understand broader adjustments in control. We do not believe that including collapsed metrics means necessarily less reliability, given that the AIC, BIC, and model fit statistics were not much poorer with collapsed task-switching indicators, early/late indicators were well correlated within the conflict-control paradigm, and scores on the latent variables were higher for conflict-control than task-switching (see Table 16). Given task-specific demands, however, and hints of differences across domains (e.g., in the awareness data), it is possible each involves different learning sensitivity.

Ultimately, because collapsing the indicators within the early/late timescales results in fewer indicators, we cannot estimate models with higher order factors or bifactor models because of model misidentification. Thus, future research will have to determine more precisely the time course of learning conflict-control relative to switch-readiness. All of the above hint at intriguing possibilities for understanding both the unity and diversity within learning to adjust control across different contextual demands.

4.4. Individual Differences in Control-Learning

One key finding within the current study was that residualizing the indicators on our measure of general cognitive ability (i.e., ICAR) and self-reported reward and punishment sensitivity (i.e., BIS-BAS) had little impact on model fit. First, this suggests that the kind of learning modeled here does not simply result from participants being good at doing cognitive tasks at large; while we do exclude participants for poorer accuracy on the control tasks, we did not do so for their performance on the ICAR, so exclusion biases should not impact this conclusion.

Second, this suggests a larger distinction between state-based and trait-based individual differences in control-learning, with some support for state-based and not trait-based adjustments. One core assumption we made was that participants could either relax or increase their degree of control on easy or hard trials, respectively, which allows for the role of intra-individual differences (Braver, 2012) in deciding whether recruiting control is worth the effort, given the current context (Kool & Botvinick, 2018; Shenhav et al., 2013). This fits with Bejjani, Dolgin, and colleagues (2020), for instance, where it was found that participants only adjusted their control in response to precues when they understood both what the precues meant in terms of upcoming control-demand – i.e., the value of the precues – and could consciously perceive the precues. This supports the state-based idea that individuals adjust control in accordance with their context and evaluation of the mental effort involved and that individual differences in this type of control-learning are stable enough for the structural equation modeling used here. On the contrary, trait-based individual differences in control-learning do not seem well supported within the current framework. This is consistent with a recent study by Bejjani and Egner (in press), which investigated the learning of stimulus-control associations through incidental memory of reinforcement (feedback) events and found little evidence for trait-based motivational contributions to control-learning. In the current study, the uniquenesses (error terms of the indicators) ranged from 0.19 to 0.38 (LWPC: 0.21-0.38; LWPS: 0.19-0.25), indicating that there is little variance left to explain. When we accounted for individual variance on a trait-level costs-benefits framework (reward vs. punishment sensitivity), model fit nonetheless remained good. Because our model assumptions codified state-based adjustments in control, we cannot suggest definitive support for these (as opposed to say, an inherent limitation to the model itself), but the results of the current study do suggest a much smaller impact of trait-based individual differences in control-learning.

4.5. Automaticity in Control-Learning

Interestingly, generalization of learning from frequency-biased to frequency-unbiased items may be relatively automatic, as supported by the pattern of results we observed with respect to explicit awareness. About two in three participants reported awareness that some blocks were harder when they were categorizing the color of color-words, and of those participants, about one in three also reported awareness that some blocks were harder when they were categorizing digits and letters. However, model fit was estimated to be similar for factor loadings (slopes), structure (construct), and intercepts (baseline values) as well as item level residual variances across participants who self-reported awareness about block difficulty on these list-wide paradigms and those who self-reported having less explicit awareness of the task manipulation. This thus suggests that participants who are explicitly aware do not necessarily show more control-learning, and that the latent variables represent similar constructs across different levels of self-reported explicit awareness. Similarly, post-test questions revealed that while participants could identify the temporal difficulty associated with blocks and the item-specific difficulty associated with frequency-biased items, they were not accurately estimating the causal strength of the proportion manipulations and they misidentified the difficulty of frequency-unbiased items. We interpreted this to mean that frequency-biased items increase explicit awareness in participants about the current difficulty level, which serves as a learning signal that causes the generalization of attention from frequency-biased (inducer) items to frequency-unbiased (diagnostic) items in a relatively automatic fashion. Thus, what researchers have termed intentionality (e.g., Brosowsky & Crump, 2016) or even strategic adjustments may instead reflect increased awareness of task manipulations that can provoke automatic adjustments in control.

4.6. Contextual Adaptations of Control

In addition to observing measurement invariance for explicit awareness groups, we also observed measurement invariance across block order groups, or participants who experienced the mostly congruent context first relative to those who experienced the mostly incongruent context first. Previous studies have found larger mean congruency differences for participants who experience the MC context first and then switch to the MI context compared to the other way around (Abrahamse et al., 2013; Bejjani, Tan, et al., 2020; Bejjani & Egner, 2021), indicating another contextual adaptation of control, whereby initial learned expectations dictate subsequent participant responding. Because we observed measurement invariance across factor structure, loadings, and intercepts as well as item residual variances, this provides support for the idea that these block order groups do not differ in terms of latent sources of influence in control-learning (e.g., the rate of learning (slopes), latent structure (construct), or baseline differences (intercepts)). This then allows the means for the two groups to be compared and provides further support for the idea that the constructs are the same, or have the same meaning, across block order groups. Bejjani and Egner (2021) speculated that participants strongly anchor their expectations of control-demand to the context they experienced first. Within a learning framework of control, this is thus possible without the meaning of the latent variables differing between groups: that is, individuals may develop learned expectations that thus cause varying scores on those second-order variables, without the constructs themselves changing.

Of note, we could rule out differences in construct meaning because of our methodological approach. Most control-learning studies use basic repeated-measures ANOVA analyses to infer learning of different specific attentional states (see Appendix A with Supplementary Text). However, within the current study, we instead focused on the variance-covariance matrix. Future studies should also consider increasing their sample sizes or pooling together relevant samples and shifting away from repeated-measures ANOVAs to more sensitive analyses as a means of accounting for individual differences, such as the modeling of reinforcement learning variables (Chiu et al., 2017; Jiang et al., 2015; Muhle-Karbe et al., 2018), Gaussian Process models accounting for latent learning (McDonald et al., 2019), hierarchical modeling (Rouder & Haaf, 2019), exploratory network analysis (Epskamp et al., 2018), or latent growth curve models that estimate growth trajectories for repeated measures of dependent variables (Kim-Spoon et al., 2021). These analytical approaches may more accurately take the learning process into account than the more commonly used analyses focusing on aggregate measures of performance as indicators of learning.

5. Conclusions

The current study examined the cognitive architecture of learning to dynamically adjust control across different contexts. Participants performed a conflict-control and task-switching paradigm in which the difficulty of trials was manipulated temporally across blocks of trials, with inducer, frequency-biased stimuli that were predictive of either difficult or easy trials as well as diagnostic, frequency-unbiased stimuli that were equally associated with difficult and easy trials. Modeling these frequency-unbiased stimuli as reflective indicators of control-learning, we found support for a model that included correlated domain- and context-specific latent variables, and this model was not impacted by individual variance in cognitive ability, motivation, or explicit awareness of the task manipulations. This suggests that the ability to adapt control settings to changing demands is mediated by distinct but correlated mechanisms in the domains of cognitive stability (conflict-control) and flexibility (task-switching).

Highlights:

• We examine the latent structure of learning to adjust cognitive control

• We manipulate the proportion of congruency and task-switching over blocks of trials

• Model fit is best with correlated domain- and context-specific latent factors

• Model fit does not decrease when accounting for awareness, ability, and motivation

• Learned conflict-control and switch-readiness may depend on distinct abilities