Repurposing FDA approved drugs as possible anti-SARS-CoV-2 medications using ligand-based computational approaches: sum of ranking difference-based model selection

Abstract

The worldwide burden of coronavirus disease 2019 (COVID-19) is still unremittingly prevailing, with more than 440 million infections and over 5.9 million deaths documented so far since the SARS-CoV-2 (severe acute respiratory syndrome coronavirus 2) pandemic. The non-availability of treatment further aggravates the scenario, thereby demanding the exploration of pre-existing FDA-approved drugs for their effectiveness against COVID-19. The current research aims to identify potential anti-SARS-CoV-2 drugs using a computational approach and repurpose them if possible. In the present study, we have collected a set of 44 FDA-approved drugs of different classes from a previously published literature with their potential antiviral activity against COVID-19. We have employed both regression- and classification-based quantitative structure–activity relationship (QSAR) modeling to identify critical chemical features essential for anticoronaviral activity. Multiple models with the consensus algorithm were employed for the regression-based approach to improve the predictions. Additionally, we have employed a machine learning-based read-across approach using Read-Across-v3.1 available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home and linear discriminant analysis for the efficient prediction of potential drug candidate for COVID-19. Finally, the quantitative prediction ability of different modeling approaches was compared using the sum of ranking differences (SRD). Furthermore, we have predicted a true external set of 98 pharmaceuticals using the developed models for their probable anti-COVID activity and their prediction reliability was checked employing the “Prediction Reliability Indicator” tool available from https://dtclab.webs.com/software-tools. Though the present study does not target any protein of viral interaction, the modeling approaches developed can be helpful for identifying or screening potential anti-coronaviral drug candidates.

Supplementary information

The online version contains supplementary material available at 10.1007/s11224-022-01975-3.

Introduction

The enormity of the pandemic caused by severe acute coronavirus 2 (SARS-CoV-2) has encouraged the repurposing of several drugs to control the disease’s rate of spread and death [1, 2]. Drugs with proven human safety can be reprocessed to treat new diseases using the “repurposing” approach as a fast and effective therapeutic choice. As a rapid response to the sudden outburst of COVID-19, intensive research has been conducted worldwide to develop a potential drug candidate to combat SARS-CoV-2.

The repurposing approach targets finding new indications in existing drugs, thereby diminishing the challenges faced during the drug development process. Drug repurposing has been estimated to have a success rate of 30 to 75% over the past few years [3]. However, for any new disease condition, the overall success rate is considerably low [3]. Repurposing can happen unintentionally or through serendipity, such as the indication of thalidomide in treating multiple myeloma and sildenafil in erectile dysfunction [4]. Till today, there is no proven therapeutic agent available for COVID-19 treatment; however, many candidates have been found to provide supportive care. In combination, antiviral drugs such as oseltamivir, ganciclovir, lopinavir, and ritonavir have shown good efficacy under clinical trials [4]. Cytotoxic agents like etoposide and methotrexate and immunomodulators like imatinib have shown effects against COVID-19 [5]. Chloroquine and its analogs were initially developed as an antimalarial agent, and also showed activity against SARS-CoV-2 [6].

The drug repurposing algorithm is designed differently from the conventional method of the drug development process. For COVID-19, the repurposing technique involves certain steps: identification of target compound, compound attainment, compound development, and Food and Drug Administration (FDA) approval after post-marketing surveillance [7]. With the advancement of computational approaches, there has been an immense improvement in drug repurposing or repositioning methods, helping accelerate scientific research. These techniques are effective and practical approaches in quantifying different biological interactions of ligand-receptor complex [8]. Computational approaches such as quantitative structure–activity relationship (QSAR) [9] and read-across [10] are promising methods where resources are limited and animal experimentation is not feasible. The major advantages of these computational methods are mainly (a) cost effective, (b) reduce animal experimentation, and (c) accelerate the drug development process.

The present work is an amalgamation of various in silico-based studies involving regression- and classification-based modeling along with read-across predictions. The current research aims at predicting the antiviral activity against SARS-CoV-2 virus in both a quantitative and qualitative manner and assuring the modeling reproducibility. Data of 44 FDA-approved drugs were procured from previously published data [11] which was segregated in a modeling set and a validation set. The modeling set was exclusively used for model generation using various methods like (a) partial least squares-regression followed by consensus predictions and (b) linear discriminant analysis for classification modeling. We have also performed a machine learning-based read-across predictions. The reliability of the generated models was checked using strict validation criteria. The present study also reports the best model with the most effective discriminating ability by using sum of ranking difference (SRD) analysis to exterminate any model ambiguity. Furthermore, we have predicted 94 marketed pharmaceuticals as well as 4 drug candidates which are under clinical trial for their anti-SARS-CoV-2 activity. The developed models can be used as promising tools for the identifying and screening potential anti-SARS-CoV-2 candidates irrespective of their mode of action.

Materials and methods

Collection of the dataset

The antiviral activity of 44 compounds against SARS-CoV-2 was retrieved from the previously published literature [11]. The dataset involved diverse classes of heterocyclic compounds of varied pharmacological importance. The IC₅₀ (nM) values of various categories of FDA-approved drugs calculated from normalized activity dataset-fitted curves (dose–response curve) by immunofluorescence were reported in the literature. For the purpose of QSAR model development, we have converted the experimental IC₅₀ values into a negative logarithmic scale (pIC₅₀). The molecules were represented in MarvinSketch software (https://chemaxon.com/products/marvin). The molecules in the dataset were curated by applying the KNIME software (https://www.knime.com/downloads) using a chemical curation workflow developed by Roy et al. [18] (https://sites.google.com/site/dtclabdc/).

Molecular descriptors calculation and dataset division for QSAR model

We have used a selected class of two-dimensional descriptors in the present research using the AlvaDesc software (https://www.alvascience.com/alvadesc/). The descriptor pool constitutes of topological indices, topological indices, connectivity indices, 2D-matrix-based descriptors, functional group counts, atom centered fragments, atom-type E-state indices, extended topochemical atom (ETA) indices, 2D atom pairs, and molecular property descriptors. Prior to the model development, descriptors with constant/near-constant/missing values or intercorrelated descriptors are passed to the data pre-treatment process using software available at http://dtclab.webs.com/software-tools. The final pool used for modeling consisted of 460 descriptors. This descriptor set is then used for dataset division into training and test sets. Data division was done using the k-medoids clustering technique into training (70%) and test (30%) sets using modified k-medoids [12] using a software available at https://dtclab.webs.com/software-tools.

Feature selection and regression-based QSAR model development

The present study aimed at developing a well-validated QSAR model with the best features predicting the anti-SARS-CoV-2 activity of selected FDA-approved drugs. Critical selection of structural attributes in the form of descriptors is vital in the QSAR model development process. Prior to the model development, we pooled 17 descriptors used for final model development using the best subset selection (BSS) (https://dtclab.webs.com/software-tools) method. To diminish the possibility of correlation between descriptors, we have further improved the model using partial least square regression modeling [13]. The present study also highlights the importance of consensus models [14] for the QSAR-derived predictions for drug repurposing against coronavirus.

Read-across-based predictions

In the present research, we have applied a machine learning approach for read-across predictions based on similarity measures [10]. The predictions were made using the tool, Quantitative Read Across v4.0 (available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home) which uses Euclidean distance, Gaussian kernel function, and Laplacian kernel function-based similarity estimation. The method requires optimization of various hyperparameters (sigma and gamma values; distance and similarity threshold), which is accomplished by dividing the training set into sub-training and sub-test sets into different combinations. This follows read-across predictions with “n” number of sub-training and sub-test sets using various settings of the hyperparameters. The best setting is then utilized for the original training and test division.

Development of the classification-based QSAR model

Classification-based QSAR modeling was performed by employing linear discriminant analysis (LDA) [15] using STATISTICA software (STATISTICA 7.1, STATSOFT Inc. USA. http://www.statsoft.com/). We have kept the training and test set division the same as the regression-based model. The compounds in the training and test sets were classified into two classes (0 and 1) by taking the median of the response value of the training set. Compounds that fall in class “1” are higher active compounds, and those in class “0” are lower actives. We have then selected a pool of descriptors for LDA by using certain measures explained below:

1. The training and test sets descriptor values were standardized using the MINITAB software (https://www.minitab.com/en-us/).

2. The training set compounds were divided into two classes (active and inactive).

3. The mean of all descriptors (standardized values) was separately calculated for high actives (HA_mean) and low actives (LA_mean).

4. The absolute differences of the mean value of the descriptors for all high and low active compounds were calculated (AbsDiff =| HA_mean- LA_mean|).

5. A total of 60 descriptors were pooled observing the highest absolute difference of the mean of high and low active compounds.

These selected descriptors were then used for LDA model development using forward stepwise selection method keeping the stepping F-criteria of inclusion (F to enter = 3.0) and exclusion (F to remove = 2.9) in STATISTICA software.

Statistical validation metrics

Statistical validation of any QSAR model is an essential measure ensuring the model’s predictive ability, robustness, and reliability. Regression-based validation criteria included statistical metrics like determination coefficient ($R^2$), adjusted determination coefficient ($R_{\mathit{adj}}^2$), and leave-one-out squared correlation coefficient ($Q_{\mathit{LOO}}^2$) for internal validation [16]. External validation included calculation of parameters like $R_{\mathit{pred}}^2$ or $Q_{F1}^2$, $Q_{F2}^2$, and concordance correlation coefficient (CCC) [17]. Error-based parameters like mean absolute error (MAE) and root mean square error (RMSE) were also reported [18]. For read-across predictions, regression-based external validation metrics like $Q_{F1}^2$, $Q_{F2}^2$ along with error-based metrics like MAE and RMSE were reported.

A classification-based model can serve as a primary filtering tool for categorizing the dataset compounds into “highly active” and “less active.” For validation purpose, several measures were used to judge the quality of the developed LDA models. The statistical validation metrics includes Wilks’ λ statistic [19], probability-level (p), canonical index (Rc) [20], Matthews correlation coefficient (MCC) [21, 22], Cohen’s κ [23], and chi-square (χ2) [24]. The discriminating ability of the classification model was obtained from the receiver operating characteristic (ROC) plot [25]. Besides these, other parameters like sensitivity, specificity, F-measure, G-means (geometric means), precision, and accuracy were also performed to check the classification ability of the model classifiers [25].

Sum of ranking differences (SRD) analysis

It is always challenging to choose the “best” model because of the bias-variance problem. In certain cases, the model with the best performance does not provide an easy understanding of the features responsible for the endpoint. In such incidents, a discriminating approach called the “sum of ranking differences (SRDs)” can be used for good discrimination and ranking of model-derived predictions in a methodical manner [26]. In this approach, the data should be arranged in a matrix with datapoints (here test compounds) in the rows and variables (here the methods or models: predicted pIC₅₀ values) which is to be compared are kept in the columns. For each method or model, the results are then ranked based on the ranking of known or reference values (here the observed pIC₅₀ values of the test compounds). Then the absolute difference between the standard reference and individual method ranks are deduced and summed for each method. In this manner, the sum of ranking difference (SRD) values is calculated for each method. An SRD value closer to zero (i.e., the closer is the ranking to the reference value) signifies that the metric is better. We have validated the method using leave-one-out (LOO) cross-validation. The scaled SRD values between 0 and 100 were calculated using the software named CRRN_DNA (downloaded from http://knight.kit.bme.hu/CRRN).

Results and discussion

In the present work, we have reported both regression-based and classification-based QSAR studies to recognize the structural features associated with the inhibitory activity of common FDA-approved drugs against SARS-CoV-2. We have also tried to provide a mechanistic interpretation along with the identification of structural features responsible for anti-SARS CoV-2 activity. The models developed passed the stringent validation criteria of robustness and internal and external stability.

Regression-based PLS modeling

Here, we present simple and statistically significant 2D QSAR models to predict the anti-SARS CoV-2 activity of FDA-approved drugs by applying DCV-GA for feature selection and applying the PLS method to descriptors selected using the best subset selection method (BSS). The PLS models derived are given below:

Model M1:

$$\begin{array}{cc}\hfill {\mathit{pIC}}_{\mathbf{50}}=& 5.327+0.233\times \mathit{nROR}+0.060\times \mathit{F}\mathbf{06}\left[C,-,C,l\right]\hfill \\ \hfill & -0.407\times \mathit{N}\mathit{s}\mathit{N}\mathit{H}\mathbf{2}-0.194\times {\mathit{V}\mathit{E}\mathbf{1}\mathit{s}\mathit{i}\mathit{g}\mathit{n}}_{Dz(p)}\hfill \end{array}$$

$$\begin{array}{cc}\hfill N_{\mathit{train}}& =33,R^2=0.672,Q_{\mathit{LOO}}^2=0.612,\overline{r_{m(train)}^2}\hfill \\ \hfill & =0.487,{\mathrm{\Delta }r}_{m(train)}^2=0.203,{\mathit{MAE}}_{\mathit{LOO}}\hfill \\ \hfill & =0.163,Predictionquality=Moderate\hfill \end{array}$$

$$\begin{array}{cc}\hfill N_{\mathit{test}}& =11,Q_{F1}^2=0.831,Q_{F2}^2=0.831,\overline{r_{m(test)}^2}\hfill \\ \hfill & =0.668,{\mathrm{\Delta }r}_{m(test)}^2=0.110,{CCC=0.906,MAE}_{\mathit{Test}}\hfill \\ \hfill & =0.139,Predictionquality=Good\hfill \end{array}$$

Model M2:

$$\begin{array}{cc}\hfill {\mathit{pIC}}_{\mathbf{50}}=& 5.265+0.242\times \mathit{nROR}+0.062\times \mathit{F}\mathbf{06}\left[\mathit{C}\mathbf{-}\mathit{C}\mathit{l}\right]\hfill \\ \hfill & -0.367\times \mathit{N}\mathit{s}\mathit{N}\mathit{H}\mathbf{2}-0.097\times \mathit{nRCOOR}\hfill \end{array}$$

$$\begin{array}{cc}\hfill N_{\mathit{train}}& =33,R^2=0.663,Q_{\mathit{LOO}}^2=0.607,\overline{r_{m(train)}^2}\hfill \\ \hfill & =0.474,{\mathrm{\Delta }r}_{m(train)}^2=0.250,{MAE}_{\mathit{LOO}}\hfill \\ \hfill & =0.194,Predictionquality=Good\hfill \end{array}$$

$$\begin{array}{cc}\hfill N_{\mathit{test}}& =11,Q_{F1}^2=0.834,Q_{F2}^2=0.834,\overline{r_{m(test)}^2}\hfill \\ \hfill & =0.675,{\mathrm{\Delta }r}_{m(test)}^2=0.109,{CCC=0.907,MAE}_{\mathit{Test}}\hfill \\ \hfill & =0.157,Predictionquality=Good\hfill \end{array}$$

Model M3:

$$\begin{array}{cc}\hfill {\mathit{pIC}}_{\mathbf{50}}=& 4.937+0.226\times \mathit{nROR}+0.065\times \mathit{F}\mathbf{06}\left[\mathit{C}\mathbf{-}\mathit{C}\mathit{l}\right]\hfill \\ \hfill & -0.351\times NsNH2-0.074\times \mathit{V}\mathit{E}\mathbf{1}\mathit{\_}\mathit{B}\mathbf{(}\mathit{e}\mathbf{)}\hfill \end{array}$$

$$\begin{array}{cc}\hfill N_{\mathit{train}}& =33,R^2=0.668,Q_{\mathit{LOO}}^2=0.608,\overline{r_{m(train)}^2}\hfill \\ \hfill & =0.480,{\mathrm{\Delta }r}_{m(train)}^2=0.218,{MAE}_{\mathit{LOO}}\hfill \\ \hfill & =0.189,Predictionquality=Moderate\hfill \end{array}$$

$$\begin{array}{cc}\hfill N_{\mathit{test}}& =11,Q_{F1}^2=0.839,Q_{F2}^2=0.839,\overline{r_{m(test)}^2}\hfill \\ \hfill & =0.706,{\mathrm{\Delta }r}_{m(test)}^2=0.100,{CCC=0.912,MAE}_{\mathit{Test}}\hfill \\ \hfill & =0.154,Predictionquality=Good\hfill \end{array}$$

Model M4:

$$\begin{array}{cc}\hfill {\mathit{pIC}}_{\mathbf{50}}=& 4.975+0.232\times \mathit{nROR}+0.066\times \mathit{F}\mathbf{06}\left[\mathit{C}\mathbf{-}\mathit{C}\mathit{l}\right]\hfill \\ \hfill & -0.353\times NsNH2-0.062\times \mathit{V}\mathit{E}\mathbf{1}\mathit{\_}\mathit{H}\mathbf{2}\hfill \end{array}$$

$$\begin{array}{cc}\hfill N_{\mathit{train}}& =33,R^2=0.665,Q_{\mathit{LOO}}^2=0.604,\overline{r_{m(train)}^2}\hfill \\ \hfill & =0.477,{\mathrm{\Delta }r}_{m(train)}^2=0.209,{\mathit{MAE}}_{\mathit{LOO}}\hfill \\ \hfill & =0.187,Predictionquality=Moderate\hfill \end{array}$$

$$\begin{array}{cc}\hfill N_{\mathit{test}}& =11,Q_{F1}^2=0.826,Q_{F2}^2=0.826,\overline{r_{m(test)}^2}\hfill \\ \hfill & =0.705,{\mathrm{\Delta }r}_{m(test)}^2=0.104,{CCC=0.906,MAE}_{\mathit{Test}}\hfill \\ \hfill & =0.153,Predictionquality=Good\hfill \end{array}$$

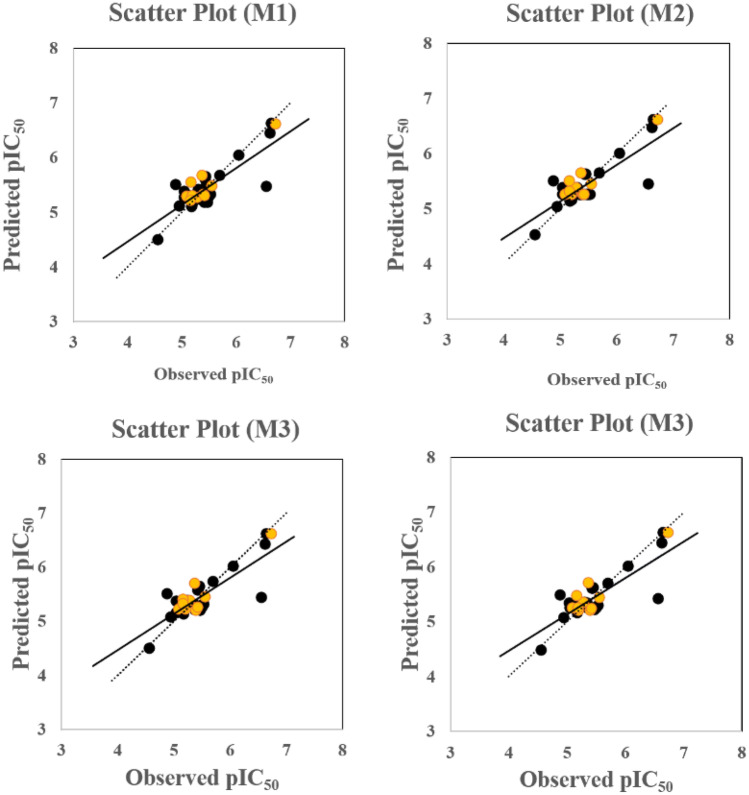
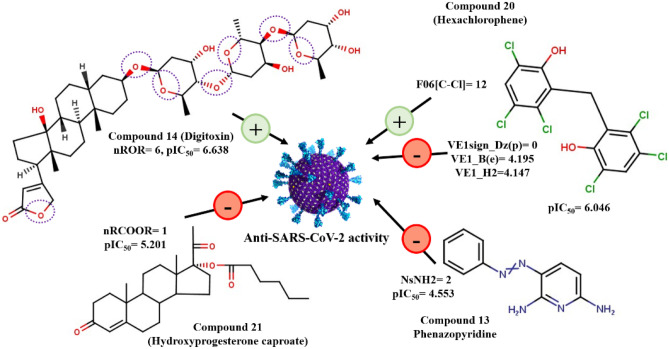
The models reported here show “Good” to “Moderate” prediction quality for the training sets and “Good” prediction quality for all the test sets. The observed versus predicted pIC₅₀ plot is shown in Fig. 1. The $R^2$ value ranges from 0.663 to 0.672, the $Q_{\mathit{LOO}}^2$ value ranges from 0.604 to 0.612, and that of $Q_{F1}^2$ ranges from 0.826 to 0.839. The descriptors appearing in the models are of two major types: (a) positively correlated: nROR and F06[C–Cl]; (b) negatively correlated: NsNH2, VE1sign_Dz(p), nRCOOR, $\mathbf{V}\mathbf{E}1\_\mathbf{B}(\mathbf{e})$, and VE1_H2. Table 1 shows the actual meaning of the descriptors, their number of occurrences in the developed models, and their correlation with pIC₅₀. It was observed that the presence of aliphatic esters as implied by nROR descriptor and the presence of carbon-chlorine fragment at the topological distance 6 (F06[C–Cl]) accentuate the antiviral activity against SARS-CoV-2. Compounds like Digitoxin (compound 14) and Salinomycin (compound 23) contain six and five aliphatic ester groups, respectively, showing high anti-SARS-CoV-2 activity. It was also found that higher active compounds like Niclosamide (compound 4) and Hexachlorophene (compound 20) contain a higher number of C–Cl fragments at distance 6 (3 and 12, respectively). The effect of different positively contributing features toward anti-SARS-CoV-2 activity is depicted in Fig. 1.

Fig. 1.

The observed versus predicted pIC₅₀ plots of all four PLS models

Table 1.

Descriptors appearing in the four PLS models

Descriptor	Type	Definition	Contribution to pIC50	Number of occurrences
nROR	Functional group counts	Number of aliphatic ether groups	Positive	4
F06[C–Cl]	2D atom pairs	Frequency of C – Cl at topological distance 6	Positive	4
NsNH2	Atom-type E-state indices	Number of atoms of type sNH2	Negative	4
VE1sign_Dz(p)	2D matrix-based descriptors	Coefficient sum of the last eigenvector from Barysz matrix weighted by polarizability	Negative	1
nRCOOR	Functional group counts	Number of aliphatic esters	Negative	1
VE1_B(e)	2D matrix-based descriptors	Coefficient sum of the last eigenvector (absolute values) from Burden matrix weighted by Sanderson electronegativity	Negative	1
VE1_H2	2D matrix-based descriptors	Coefficient sum of the last eigenvector (absolute values) from reciprocal squared distance matrix	Negative	1

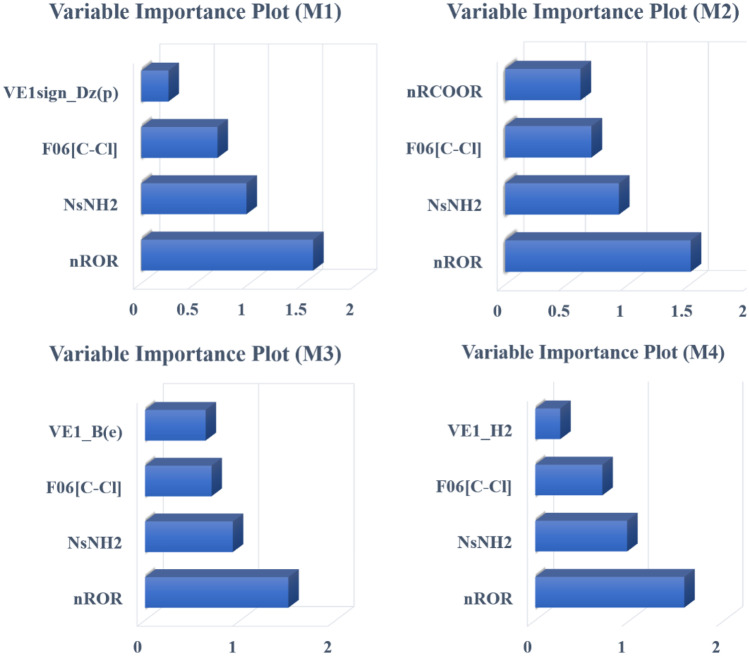
Among the negatively contributing features, NsNH2 is the most important one, as it appears in all four selected models. It denotes the number of atoms of type sNH2 (-NH2), i.e., the number of uncharged amino groups. The higher the number of this fragment, the lower will be the antiviral activity, as observed in Phenazopyridine (compound 13) and Gliteritinib (compound 38). These two compounds contain two and one -NH₂ fragment, respectively, and have antiviral activity in the lower range. Other negatively correlated descriptors affecting the anti-SARS-CoV2: VE1sign_Dz(p), nRCOOR, VE1_B(e), and VE1_H2 appear only a single time in models M1, M2, M3, and M4 respectively. These descriptors decrease the anti-SARS-CoV-2 with an increase in their value (Fig. 2). The variable importance plots [27] for all four models are given in Fig. 2. This plot signifies the importance of descriptors towards the variable. Concerning Fig. 3, we can conclude that ROR (ether linkage) is the most significant group affecting the anti-SARS-CoV-2 activity since its VIP is always greater than 1 in all the four models. The loading plot explains the relationship between the X-variable and the Y-response [28]. Figure 4 provides knowledge about the relationship between the descriptors appearing in all the four models with anti-SARS-CoV-2 activity. The model randomization was performed using the Y-randomization method to ensure that the model is not an outcome of chance correlation [29]. The randomization plots are shown in the Supplementary Section S1.

Fig. 2.

Features increasing or decreasing the antiviral activity against SARS-CoV-2

Fig. 3.

Variable importance plot of four PLS models (M1–M4)

Fig. 4.

Loading plots of all four PLS models (M1–M4)

Applicability domain of PLS models

The theoretical region in the chemical space as surrounded by both the model response and independent variables is termed as the applicability domain (AD) [30]. The distance to model in X-space (DModX) approach was implemented to check the model’s AD at 99% confidence interval. The AD analysis (Supplementary Section S1) showed that in all the four models (M1 to M4), there was neither any outlier in the training set nor any compound outside the AD in the test set.

Development of multiple PLS models and intelligent consensus modeling

In QSAR modeling, a single model cannot guarantee the best prediction since a particular set of features may not be able to characterize a query compound accurately. Thus, multiple modeling techniques with various consensus approaches is introduced to achieve a lower degree of predicted residuals for query compounds. In the study, we have selected four PLS models through a feature selection method and the best subset selection method, as discussed in the previous section in Eqs. M1 to M4. These models were further subjected to the development of “intelligent” consensus models using the “Intelligent Consensus Prediction” tool developed by Roy et al. [31] with the prime objective to reduce prediction errors thereby enhancing the prediction quality. Individual QSAR models include a number of variables that can reflect distinct aspects of molecular structure, but they may overemphasize some features or understate others if used in isolation, and in many cases, they can neglect others. Generating consensus models can overcome these limitations and offer a wider applicability domain with increased accuracy in prediction. Roy et al. [14] described four different methods of consensus approach, viz., CM0 — the simple average of predictions from all individual models, CM1 — the average of predictions from all individual “qualified” models, CM2 — the weighted average prediction (WAP) from all qualified individual models, and CM3 — the compound-wise best selection of predictions from qualified individual models. Consensus predictions, mainly from CM2 and CM3, outperformed individual models in terms of both external validation metrics $Q_{F1}^2$ and $Q_{F2}^2$ as well as there was a considerable decline in the mean absolute error (both ${\mathit{MAE}}_{100\%}$ and ${\mathit{MAE}}_{95\%}$) as observed in CM3. Thus, the predictive ability of individual models was boosted using consensus modeling thereby upsurging the reliability of the models [32]. Table 2 reports the consensus models highlighting the best one along with the values of validation metrics.

Table 2.

Statistical qualities of all four PLS models along with their consensus predictions (the best metric values are shown in bold)

Model	Training set					Test set
	${\mathit{R}}^{\mathbf{2}}$	${\mathit{Q}}_{\mathit{L}\mathit{O}\mathit{O}}^{\mathbf{2}}$	$\overline{{\mathit{r}}_{\mathit{m}\mathbf{(}\mathit{t}\mathit{r}\mathit{a}\mathit{i}\mathit{n}\mathbf{)}}^{\mathbf{2}}}$	${\mathbf{\Delta }\mathit{r}}_{\mathit{m}\mathbf{(}\mathit{t}\mathit{r}\mathit{a}\mathit{i}\mathit{n}\mathbf{)}}^{\mathbf{2}}$	$\mathit{M}\mathit{A}{\mathit{E}}_{\mathit{L}\mathit{O}\mathit{O}}$	${\mathit{Q}}_{\mathit{F}\mathbf{1}}^{\mathbf{2}}$	${\mathit{Q}}_{\mathit{F}\mathbf{2}}^{\mathbf{2}}$	$\overline{{\mathit{r}}_{\mathit{m}\mathbf{(}\mathit{t}\mathit{e}\mathit{s}\mathit{t}\mathbf{)}}^{\mathbf{2}}}$	${\mathbf{\Delta }\mathit{r}}_{\mathit{m}\mathbf{(}\mathit{t}\mathit{e}\mathit{s}\mathit{t}\mathbf{)}}^{\mathbf{2}}$	$\mathit{M}\mathit{A}{\mathit{E}}_{\mathbf{100}\mathbf{\%}}$	$\mathit{M}\mathit{A}{\mathit{E}}_{\mathbf{95}\mathbf{\%}}$	CCC
IM1	0.672	0.612	0.487	0.203	0.184	0.831	0.831	0.668	0.110	0.139	0.114	0.906
IM2	0.663	0.607	0.474	0.250	0.194	0.834	0.834	0.675	0.109	0.157	0.138	0.907
IM3	0.668	0.608	0.480	0.218	0.189	0.839	0.839	0.706	0.100	0.154	0.135	0.912
IM4	0.665	0.604	0.477	0.209	0.187	0.826	0.826	0.705	0.104	0.153	0.132	0.906
CM0	-	-	-	-	-	0.838	0.838	0.691	0.103	0.151	0.133	0.910
CM1	-	-	-	-	-	0.838	0.838	0.691	0.103	0.151	0.133	0.910
CM2	-	-	-	-	-	0.843	0.843	0.702	0.099	0.148	0.131	0.913
CM3	-	-	-	-	-	0.879	0.879	0.782	0.074	0.126	0.110	0.934

Chemical read-across analysis

Read-across is quite a similarity-based method for predicting an endpoint of a chemical referred to as a “target” compound by using the information of the same endpoint from other similar “source” compounds. The method has gained enormous importance owing to its non-testing approach, supporting data gap filling issues. The present research has implemented similarity-based quantitative read-across predictions using the same training and test set combinations as used in QSAR modeling. The present method applies three different similarity-based measures: Euclidean distance-based (ED), Gaussian kernel similarity-based (GK), and Laplacian kernel similarity-based (LK) predictions, and after hyperparameter optimization, it was found that for all four descriptor combinations corresponding to models M1–M4, read-across predictions were better compared to the results obtained from the individual regression-based QSAR models. Table 3 shows a comparison table between the classical QSAR models and their corresponding read-across predictions. According to our results, local similarity-based approaches yield better results than model-derived predictions based on the entire set of training data.

Table 3.

Comparison between classical QSAR models and their corresponding read-across predictions (the best metric values are shown in bold)

Feature combination	Hypothesis	Hyperparameters					${\mathit{Q}}_{\mathit{F}\mathbf{1}}^{\mathbf{2}}$	${\mathit{Q}}_{\mathit{F}\mathbf{2}}^{\mathbf{2}}$	MAE	RMSEP
		σ	γ	CTC	Distance threshold	Similarity threshold
M1	PLSR	-	-	-	-	-	0.831	0.831	0.139	0.179
	RA-ED	1.5	1.5	10	0.5	0.0	0.879	0.878	0.127	0.152
	RA-GK						0.893	0.893	0.121	0.143
	RA-LK						0.909	0.909	0.118	0.132
M2	PLSR	-	-	-	-	-	0.834	0.834	0.157	0.178
	RA-ED	1	1	10	0.6	0.0	0.870	0.870	0.135	0.152
	RA-GK						0.916	0.916	0.121	0.143
	RA-LK						0.911	0.911	0.119	0.132
M3	PLSR	-	-	-	-	-	0.839	0.839	0.154	0.175
	RA-ED	0.75	1.5	10	0.5	0.0	0.862	0.862	0.142	0.162
	RA-GK						0.912	0.912	0.114	0.130
	RA-LK						0.892	0.892	0.132	0.144
M4	PLSR	-	-	-	-	-	0.826	0.826	0.153	0.182
	RA-ED	0.75	1.75	10	0.6	0.0	0.722	0.722	0.163	0.230
	RA-GK						0.931	0.931	0.100	0.115
	RA-LK						0.932	0.932	0.104	0.114

Sum of ranking differences (SRD)

To understand the discriminating ability of different modeling approaches, i.e., simple PLS modeling, consensus modeling, and read across predictions, we have applied the method of sum of ranking differences as described by Héberger and Kollár‐Hunek [26]. The method ranks the difference between the reference (here observed pIC₅₀) and variables (predicted values from different models or hypotheses) under study, and variables having the least total rank (low sum of ranking differences) and farthest to maxSRD value will have more significance. Furthermore, the results were graphically analyzed by plotting the % SRD data (Fig. 5) for each modeling technique in a random environment, i.e., random ranking given to each data input for each method to generate all possible random sum of ranking differences. The SRD plot signifies the different modeling techniques arranged in ascending order of their SRD values: M1_LK < M2_ED, M2_GK, M2_LK < M1_GK < M1_ED, M3_GK < M1_PLS, CM3, M3_LK, M4_LK < M3_ED, M4_GK < M4_ED < M2_PLS, M3_PLS < CM0, CM1, CM2 < M4_PLS. From the SRD plot, one can identify that M1_LK is the most significant having the least SRD even in randomized conditions. The critical threshold XX1 signifies the region of randomness with p < 0.05 (i.e., probability of randomness less than 5%), Med denotes 50% randomness, and XX19 signifies 95% randomness. M1_LK being the most significant modeling technique falls under XX1 region, hence, the confidence for the method is greater than 95% (p < 0.05). Similarly, other techniques such as M2_ED, M2_GK, M2_LK, M1_GK, M1_ED, and M3_GK also fall under XX1 region with less than 5% randomness. We have also performed leave-one-out cross-validated SRD, where a series of SRD was obtained using leave-one-out technique. In each iteration, one compound was removed and all possible SRDs were generated, and this method is continued for all iterations. Finally, the SRDs were arranged in ascending order and the median values for all the modeling methods were determined. After plotting the maximum, minimum, and median SRD values (in Supplementary Section S1) in Fig. 6, we can conclude that M1_LK has the lowest cross-validated SRDs (maximum, minimum and median). This observation corroborates with the previous study and explains the significance of the M1_LK approach.

Fig. 5.

Comparative plot of the scaled SRD values of the different modeling approaches

Fig. 6.

Cross-validated SRD plotting: maximum, minimum, and median SRD values for all the modeling approaches

Classification-based modeling

A classification model aims to segregate the compounds of the dataset into two groups (high anti-SARS-CoV-2 activity and low anti-SARS-CoV-2 activity) by deducing the relationship between molecular descriptors and qualitative response. The developed model of four descriptors H-048, Me, MaxssO, and C-029 was characterized by reliable values of Wilks’ lambda (λ = 0.425) and canonical correlation coefficient ($R_c$ = 0.758). We have also determined the chi-square (χ²) distribution parameter and Fisher-distribution (F-value) to determine whether the groups are separated properly, and a good level of discrimination is attained.

$$\begin{array}{cc}\hfill DF=& -1449.23+12.30\times \mathit{H}-\mathbf{048}+2882.03\times \mathit{M}\mathit{e}\hfill \\ \hfill & +11.79\times \mathit{M}\mathit{a}\mathit{x}\mathit{s}\mathit{s}\mathit{O}-18.66\times \mathit{C}-\mathbf{029}\hfill \end{array}$$

$$N_{\mathit{train}}=33,N_{\mathit{test}}=11,p-value=0.0001,Wilks{}^{\prime }\lambda =0.425,Eigenvalue=1.354,{\chi }^2=24.827,R_c=0.758,F\left(4,28\right)=9.478,AURO{C}_{\mathit{train}}=0.875,AURO{C}_{\mathit{test}}=1$$

Depending on the anti-SARS-CoV-2 activity threshold value (i.e., the median value) of 5.333, the developed LDA model could predict and correctly classify 14 (82.4%) out of 17 highly active compounds and 14 (87.5%) out of 16 less active compounds in the training set. In case of the test set, the model could correctly predict 3 (60%) out of 5 highly active compounds and all 6 (100%) less active compounds. Table 4 contains the results confusion matrix for training and test sets. In addition, an appreciable high value of G-means for both training (84.89%) and test (77.46%) sets suggests that the model is proficient in discriminating between highly active and less active anti-SARS-CoV-2 agents. The discriminating ability of the variables obtained in the LDA models is understood through the ROC curve, and to support our model, both the ROC curve for training and test sets gave promising results (Supplementary Sect. S1).

Table 4.

Qualitative validation parameters for the training and test sets for LDA model

Set	No. of compounds	Sensitivity	Specificity	Accuracy	Precision	F-measure	G-means	MCC	Cohen’s κ
Training	33	0.824	0.875	0.848	0.875	0.848	0.849	0.699	0.697
Test	11	0.60	1	0.818	1	0.750	0.775	0.671	0.621

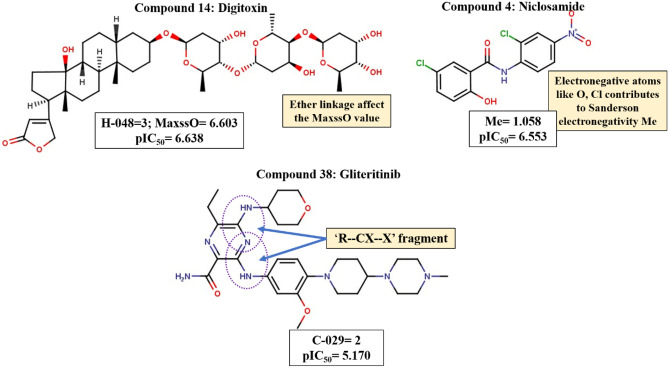
We have also tried to interpret the descriptors (Fig. 7) obtained in the classification model and how they can classify the anti-SARS-CoV-2 agents into higher and lower active compounds. The descriptor H-048 indicates the number of hydrogens attached to C2(sp3)/C1(sp2)/C0(sp) atoms. The descriptor’s positive correlation corroborates that compounds having such hydrogens are highly active (for example, Digitoxin) and fall above the threshold applied while classification. The next positively correlated descriptor is Me, which denotes mean atomic Sanderson electronegativity (scaled on carbon atom). The Me value increases with electronegative atoms like O, Cl, etc. as is observed in compounds like Niclosamide (compound 4) thereby increasing the pIC₅₀ value. Another positively correlated descriptor that increases the DF value is MaxssO denotes the maximum atom type E-state of “-O-” fragment (ether linkage). This descriptor has a similar meaning to the nROR descriptor obtained in the PLS regression models (M1–M4) signifying the importance of ether linkage in increasing the pIC₅₀ value against the SARS-CoV-2 virus (as seen in compound 14, i.e., Digitoxin). The descriptor C-029 is an atom-centered fragment descriptor describing “R–CX—X” fragment where R is any group linked through a carbon atom, X is an electronegative atom (O, N, S, P, Se, halogens), and “–” is an aromatic bond as in benzene or delocalized bonds such as the N–O bond in a nitro group. The negative correlation coefficient indicates that such fragments decrease the anti-SARS-CoV-2 activity. All the compounds containing such fragments are grouped as lower active compounds according to the threshold calculated.

Fig. 7.

Features contributing to the anti-SARS-CoV-2 activity according to the classification model

True external set predictions

The purpose of any QSAR modeling is to use the model for future prediction of new and untested compounds. On this note, we have tried to predict two sets of compounds: (a) External Data1: consisting of four anti-SARS-CoV-2 drugs which are under trial; and (b) External Data2: consisting of 94 FDA approved drugs [33] where many of which are under trial for the treatment of COVD-19, using all four PLS models. Furthermore, we have tried to analyze the predictive reliability of the models using “Prediction Reliability Indicator (PRI)” tool [34] available from https://dtclab.webs.com/software-tools. The analysis suggested that all the compounds under trial, i.e., compounds from External Data1 are within the AD of all four models with a “Good” predictive score. Again, most of the compounds in External Data2 are within the AD of the all four models with a few exceptions mentioned in the Supplementary Sect. S2 Excel file.

Conclusion

The alarming rate of occurrence of COVID-19 over the past 2 years in different countries emphasizes the pressing need for effective treatments. The FDA has approved several drugs used for other diseases that can be repurposed for SARS-CoV-2 based on clinical trials. These include antivirals, antimalarials, antibiotics, ACEIs, ARBs, statins, and monoclonal antibodies. The present study aims at developing a 2D-QSAR model for a series of compounds approved by the FDA acting as anti-SARS-CoV-2 agents and studying the structural features of those molecules controlling their antiviral activity. The prime features observed controlling the antiviral activity were (i) the presence of an ether linkage, (ii) the presence of electronegative atoms like chlorine and oxygen, and (iii) the presence of amino group (decreases antiviral activity). The predictive ability of the PLS models developed was further enhanced by “intelligent” consensus modeling. Similarity-based read-across predictions [10, 35] superseded both individual PLS models as well as consensus prediction. Furthermore, the SRD analysis gave an idea about the modeling approach’s discriminating ability. The results showed that the Laplacian-kernel similarity function for model M1 gave the best prediction. Finally, we have predicted a set of compoun ds inten ding to repurpose them, and the prediction quality was analyzed using the “Prediction Reliability Indicator (PRI)” tool. We assume that the different modeling approaches will help in anti-COVID activity data gap filling and repurposing potential candidates.

Supplementary Information

Below is the link to the electronic supplementary material.

Author contribution

PD: computation, analysis, and initial draft. VK: analysis and initial draft. SK: analysis and editing. KR: conceptualization, editing, supervision, and funding. JL: analysis, editing, and funding.

Funding

Funding is provided by ICMR, New Delhi (PD & VK), SERB, New Delhi (KR), National Science Foundation (JL).

Availability of data and material

Some of the data and materials are available in Supplementary Materials of this paper. Additional data are available from the authors on request.

Code availability

DTC Lab software tools are available from http://teqip.jdvu.ac.in/QSAR_Tools/.

Declarations

Conflict of interest

The authors declare no competing interests.