Abstract
Introduction
Rather than generating 1 transplant by directly donating to a candidate on the waitlist, deceased donors (DDs) could achieve additional transplants by donating to a candidate in a kidney paired donation (KPD) pool, thereby, initiating a chain that ends with a living donor (LD) donating to a candidate on the waitlist. We model outcomes arising from various strategies that allow DDs to initiate KPD chains.
Methods
We base simulations on actual 2016 to 2017 US DD and waitlist data and use simulated KPD pools to model DD-initiated KPD chains. We also consider methods to assess and overcome the primary criticism of this approach, namely the potential to disadvantage blood type O-waitlisted candidates.
Results
Compared with shorter DD-initiated KPD chains, longer chains increase the number of KPD transplants by up to 5% and reduce the number of DDs allocated to the KPD pool by 25%. These strategies increase the overall number of blood type O transplants and make LDs available to candidates on the waitlist. Restricting allocation of blood type O DDs to require ending KPD chains with LD blood type O donations to the waitlist markedly reduces the number of KPD transplants achieved.
Conclusion
Allocating fewer than 3% of DD to initiate KPD chains could increase the number of kidney transplants by up to 290 annually. Such use of DDs allows additional transplantation of highly sensitized and blood type O KPD candidates. Collectively, patients of each blood type, including blood type O, would benefit from the proposed strategies.
Keywords: deceased donor, exchange chain, kidney exchange program, kidney paired donation, living donor, nondirected donor
Graphical abstract
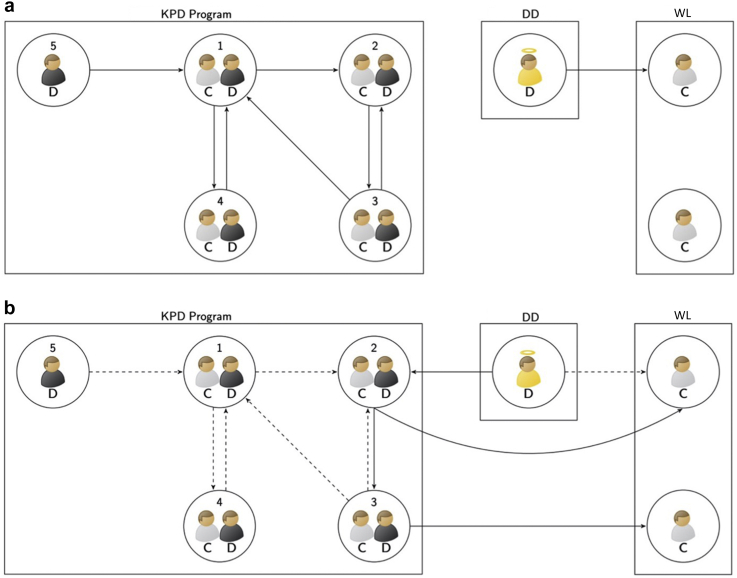
KPD circumvents incompatibilities between potential LD and their intended recipients.1, 2, 3, 4, 5, 6, 7, 8 As in Figure 1a, a KPD pool comprises pairs made up of kidney transplant candidates and their associated incompatible donor(s) and nondirected LDs who are willing to donate a kidney to a not yet identified KPD candidate. Transplants are done by chains or cycles also as illustrated in Figure 1a. A chain is initiated by a nondirected LD followed by a sequence of pairs, with each LD donating to the candidate in the next pair, except the donor in the last pair, who may become a bridge donor and act as a nondirected donor for a future chain or alternatively may donate to a candidate on the DD waitlist.9, 10, 11, 12 In contrast, in a cycle, the donor of the first pair donates to the candidate of the second pair and so on until the cycle ends with the donor of the last pair completing the cycle by giving to the candidate of the first pair. Transplants are determined via match runs that select nonoverlapping cycles and chains consisting of possibly viable transplants.13,14 If a selected transplant is shown to be nonviable, any proposed cycle containing that transplant is also nonviable and any chain containing that transplant breaks at that point.15, 16, 17, 18
Figure 1.
Illustrations of a KPD program and DD-initiated chains. Simulated kidney transplantation candidates are indicated by gray shirts and “C” labels and simulated LDs by black shirts with “D” labels. The donor indicated by the yellow shirt could provide a DD-chain–initiating kidney. A circle with only one candidate is a candidate on the DD WL. A circle with only one LD is a nondirected donor. A circle with one candidate and one donor is a pair in a KPD pool. An arrow indicates a possible transplant from the donor in the starting circle to the candidate in the ending circle. (a) The left graph is an illustration of a KPD program. Kidney transplants in this simulated KPD pool may move forward with cycles, chains, or a combination of cycles and chains. In this example, potential chains are 5 → 1, 5 → 1 → 2, 5 → 1 → 4, and 5 → 1 → 2 → 3. Potential cycles are 1 → 4 → 1, 1 → 2 → 3 → 1, and 2 → 3 → 2. Assuming viability of all of the matches described, the optimal chains and cycles without overlap that maximize the total number of transplants would be the cycle 2 → 3 → 2 plus the chain 5 → 1 → 4. The right graph illustrates the usual donation of a DD kidney to a candidate on the WL. (b) An illustration of DD-initiated chains. Potential DD chains are illustrated by solid arrows: DD → 2 → WL and DD → 2 → 3 → WL. Dotted arrows indicate other potential transplants within the KPD pool. DD, deceased donor; KPD, kidney paired donation; LD, living donor; WL, waitlist.
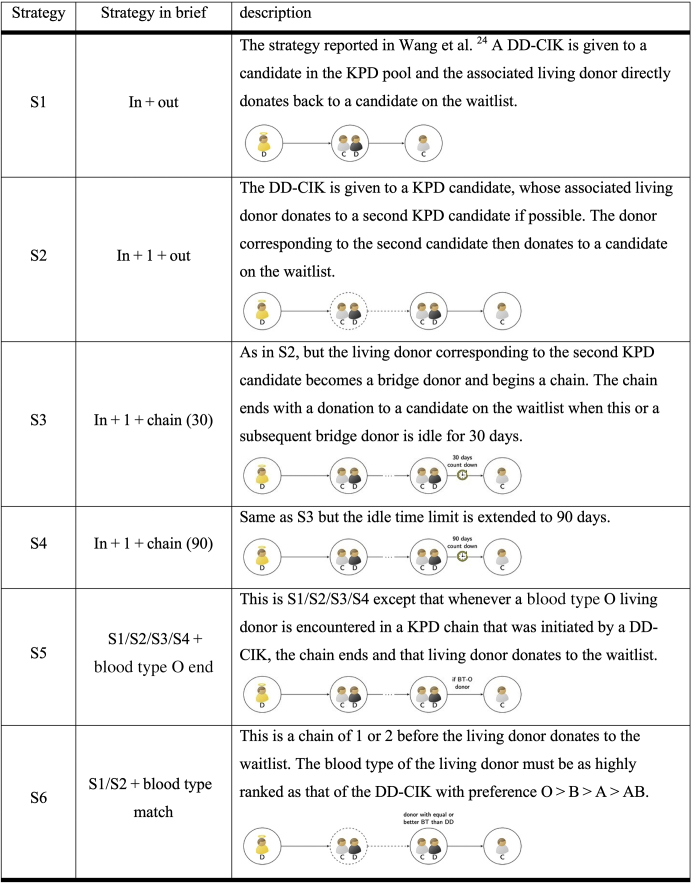
Several authors have suggested using DDs to initiate chains in a KPD pool as illustrated by Figure 1b.19, 20, 21, 22, 23 Wang et al.24 presented the first detailed simulation study evaluating a simple strategy whereby fewer than 3% of DDs donate to a candidate in a KPD pool whose incompatible donors would immediately donate to a candidate on the DD waitlist, as illustrated by strategy S1 in Figure 2. This strategy could increase the national number of kidney transplants by hundreds per year. In an accompanying editorial, Turgeon25 reviewed much of the previous literature and called for an active discussion of the policy implications arising from potential use of DD-chain–initiating kidneys (DD-CIKs), citing an often stated concern that this approach could disadvantage blood type O candidates on the waitlist but not in the KPD pool. One of our purposes in this article is to evaluate this concern. We show an overall advantage for blood type O candidates on the waitlist and reveal only modest additional wait times for blood type O candidates long on the waitlist but not in the KPD pool.
Figure 2.
Illustration of strategies for simulating DD-initiated chains. See the discussion in the “Methods” section for additional details. People in gray shirts and with “C” labels are candidates in need of a kidney transplant. People in black shirts and with “D” labels are living donors. People in yellow shirts with “D” labels are DDs. A circle with only one candidate is a candidate on DD kidney transplant waitlist. A circle with only one living donor is a nondirected donor. A circle with one candidate and one donor is a pair in a KPD pool. An arrow indicates a negative virtual crossmatch from the donor in the starting circle to the candidate in the ending circle. Dotted circles and arrows are optional pairs and transplants in the strategy. Edges with ellipsis indicate one or more transplants in the chain. DD, deceased donor; DD-CIK, deceased donor chain–initiating kidney; KPD, kidney paired donation.
Following previous work in this field, 3 natural questions are whether longer DD-initiated chains can: (i) produce more transplants; (ii) reduce the number of DD-CIKs; (iii) and balance the number of blood type O DD-CIKs and LDs returning to the waitlist. In this article, we evaluate more general approaches that permit the DD-CIKs to create longer chains of various lengths, as shown by strategies S2 to S4 in Figure 2. We also investigate strategies that might improve access to blood type O LDs for candidates on the waitlist, as demonstrated by strategies S5 and S6 in Figure 2.
Methods
This study uses data from the Scientific Registry of Transplant Recipients, which includes information on all DDs, waitlisted candidates, and transplant recipients in the United States as submitted by the members of the Organ Procurement and Transplantation Network. The Health Resources and Services Administration, an agency of the US Department of Health and Human Services, provides oversight to the activities of the Organ Procurement and Transplantation Network and Scientific Registry of Transplant Recipients contractors. The data used were on DDs and waitlisted candidates from 2016 to 2017. Furthermore, the Alliance for Paired Kidney Donation provided data on 2068 incompatible candidate-donor pairs and 156 nondirected donors.
Each simulation begins with the creation of a “mature” KPD pool, which, similar to most of real-world KPD pools, has large proportions of highly sensitized and/or blood type O candidates. The mature KPD pool is created as follows: pairs and nondirected donors are sampled with replacement from the Alliance for Paired Kidney Donation data and arrive at average rates of 30 per month and 1 per month, respectively. Match runs are simulated as if they were performed every 30 days. Pairs and nondirected donors are removed as they are transplanted or donated. This process continues until the sum of the number of pairs, nondirected donors and bridge donors, following a match run is at least 400.
As described in Table 1, once the initial KPD pool is constructed, pairs and nondirected donors join the KPD pool at constant average rates. Untransplanted pairs withdraw from the pool with a predesignated probability. Nondirected donors and bridge donors are subject to unavailability and renege rates each time they are called on to begin a new chain segment or donate to the waitlist. Different delay times before a candidate in a KPD pool becoming eligible to be allocated a DD-CIK are evaluated.
Table 1.
Simulation parameter specifications: parameter settings in the simulations
| Simulation setting parameter | Parameter range |
|---|---|
| Initial pool size | 400 |
| Pair arrival rate (# per day) | 2 |
| Nondirected donor arrival rate (# per month) | 0, 2, 5 |
| Withdrawal probability (per day) | 0.0005, 0.0015 |
| Match run frequency (day) | 5, 10 |
| Pair/nondirected donor/bridge donor unavailability probability | 0.1, 0.15 |
| Nondirected donor/bridge donor renege probability | 0.01 |
| Delay time (day) | 0, 30, 60, 90, 180 |
#, number.
In total, there are 120 distinct settings and 6 runs are performed at each setting.
A potential transplant from a donor to a candidate is determined by a virtual crossmatch, which in these simulations requires both identical ABO blood type and human leukocyte antigen compatibility.1, 2, 3, 4 Transplants with a negative virtual crossmatch result may still be nonviable based on a predesignated probability. Table 2 gives the probability that a proposed transplant is nonviable depending on the candidate’s calculated panel-reactive antibodies (cPRAs).
Table 2.
Simulation parameter specifications: match failure rates are considered in the simulations
| cPRA level | Match failure rate |
||
|---|---|---|---|
| BLa | Living donor transplant (BL + 0.1) | DD-CIK transplantb (BL + 0.2) | |
| 75–100 | 0.5 | 0.6 | 0.7 |
| 50–74 | 0.35 | 0.45 | 0.55 |
| 25–49 | 0.2 | 0.3 | 0.4 |
| 0–24 | 0.05 | 0.15 | 0.25 |
BL, baseline; cPRA, calculated panel-reactive antibody; DD-CIK, deceased donor-chain–initiating kidney.
Include a baseline probability or rate that depends on cPRA plus an additional 0.1 for living donor transplant offers or 0.2 for DD-CIK transplant offers.
Baseline values are taken from Ashalgi et al.9
Exception: BL + 0.5 for a blood type A candidate with cPRA <75% and a blood type O donor. This exception reflects the fact that such candidates may be unwilling to accept a deceased donor when a living donor exchange will likely eventually be open to them.
LD transplants within the KPD pool are arranged through regular match runs as in Wang et al.24 Briefly, in these simulations, a match run generates virtual transplants by selecting nonoverlapping cycles and nondirected donor- or bridge donor-initiated chains of length 3 or less. Details are given in Table 3
Table 3.
An outline of the match run rules in a simulated “mature” KPD pool which are used in the simulations
| Outline of the match run procedures | |
|---|---|
| a | Enumerate cycles and nondirected donor- or bridge donor-initiated chains (segments) of length 3 or less. |
| b | Select nonoverlapping cycles and chains so as to maximize the expected number of transplants achieved. |
| c | Apply the predesignated match failure rates to the selected cycles and chains to identify all remaining viable potential transplants. Carry out a set of viable nonoverlapping cycles and chains that maximizes the number of transplants. |
| d | All pairs, nondirected donors or bridge donors, in the selected cycles or chains are simulated to be “inactive, awaiting transplant” for 9 days, after which untransplanted pairs and unutilized nondirected donors or bridge donors return to the KPD pool. |
| e | The living donors at the end of the chains carried out in step c return to the KPD pool as bridge donors and participate in the next match run or donate to a candidate on the deceased donor kidney waitlist. |
KPD, kidney paired donation.
As in Wang et al.,24 we simulate a new allocation category in the current DD kidney allocation system that is inserted into the 21 to 35 Kidney Donor Profile Index range just before local allocation. DDs arrive in the actual sequence of DDs for the calendar years 2016 to 2017. Each eligible DD with a Kidney Donor Profile Index between 21 and 35 donates at most 1 DD-CIK to the KPD pool. A DD kidney is ineligible to be used as a DD-CIK if in real life it was discarded, transplanted “en bloc” or simultaneously with another organ, or transplanted to a candidate with medical urgency, a 0-ABDR mismatch, a cPRA ≥98%, or of age under 18 years. Eligible recipients of DD-CIKs are KPD candidates with cPRA <98% who have participated in the KPD pool for a specified “delay time” as described in Table 1.
Figure 2 describes the strategies, labeled S1 to S6, that we consider. Strategy S1 is the simple “in+out” strategy (S1) proposed in Wang et al.24 That approach results in 2 kidney transplants with a donation by a DD to a KPD candidate and that candidate’s paired LD to a candidate on the waitlist. Strategies S2 to S4 extend DD-CIK chains to various lengths beyond strategy S1. In strategies S1 to S4, eligible candidates (and pairs) are ranked by the blood type of their associated LDs based on a precedence of O > B > A > AB, and a DD-CIK is allocated to the top-ranked viable KPD candidate of the same blood type as the DD. Ties are broken using the point score from the current Organ Procurement and Transplantation Network DD Kidney Allocation System.26 If the chain can be extended with a second KPD transplant in strategies S2 to S4, viable options are sorted in the same manner as the first transplant; otherwise, the first LD donates to a candidate on the waitlist. In strategy S2, the second LD, if any, immediately donates to the waitlist. In strategies S3 and S4, the second LD becomes a bridge donor and participates in match runs in future KPD simulation. This bridge donor or any subsequent bridge donor in this chain will donate to the waitlist if that bridge donor remains unutilized for an idle time limit of 30 (S3) or 90 (S4) days. A shorter idle time limit results in an earlier return of a transplant to the waitlist, whereas a longer idle time limit increases the opportunity to find transplants in the KPD pool, but with a higher risk of a renege by a bridge donor.
A feature of strategies S1 to S4 is that many more blood type O DDs donate to the KPD pool than blood type O LDs donate to a candidate on the waitlist. To address this imbalance, we considered adding a constraint to strategies S1 to S4 to create S5, whereby the DD-CIK chain concludes with a donation to the waitlist whenever a blood type O LD is encountered. A more aggressive version is strategy S6, in which a restriction is added to S1 and S2, whereby the blood type of the LD returning to the waitlist must be ranked no lower than the blood type of the DD-CIK with a precedence of blood type O > B > A > AB. For example, in strategy S6, a blood type B DD-CIK must result in a LD donation to a candidate on the waitlist of blood type O or B. Thus, in strategy S6, we enumerate DD-CIK chains of length one or two satisfying this restriction and proceed with the best viable chain according to the following rules: longer chains are better than shorter chains; for two chains of the same length, the one with the higher ranked blood type of the final LD is preferred; for two chains of the same length and same blood type of the final LD, the one with higher total Organ Procurement and Transplantation Network DD Kidney Allocation System point score of all involved KPD candidates is preferred.
A daily simulation procedure for “KPD + DD” and “KPD only” is given in Table 4. In Table 5, Table 6, Table 7, we compare simulated numbers of transplants using DD-CIKs (labeled as “KPD + DD”) to those not using DD-CIKs (identified as “KPD only”). Table 1 indicates other parameters varied in the simulations. For each combination of strategies and parameters, 6 replicates are simulated.
Table 4.
The entries in this table describe the steps taken each day in the simulation of KPD only or KPD + DD strategies
| Simulated daily procedures | |
|---|---|
| a | Some pairs withdraw from KPD pool. |
| b | New pairs and nondirected donors arrive in KPD pool. |
| c | If method “KPD only” is adopted, skip this step. Otherwise, if a DD is eligible to be a DD-CIK, assign one DD kidney to a KPD pair by one of the strategies described in Figures 2, S1–S6. |
| d | Remove transplanted KPD candidates from the KPD pool and convert the living donor at the end of the DD-initiated chains to a bridge donor. |
| e | When a match run is due, conduct one as in Table 3. |
| f | Execute viable transplants selected in previous match runs and return the untransplanted pairs, nondirected donors, and bridge donors to the KPD pool. |
| g | Allocate bridge donors to a DD candidate on the waitlist if the bridge donor’s idle time surpasses a specified time limit. |
DD, deceased donor; DD-CIK, deceased donor chain-initiating kidney; KPD, kidney paired donation.
Table 5.
Comparison of strategies to extend deceased donor chains
| KPD only |
KPD + DD |
KPD + DD minus KPD only |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Method name (see Figure 2) | KPD cand tx | Living donor to WLa | KPD cand tx | Living donor to WLa | DD-CIK | Blood type O DD-CIK | Blood type O living donor to WL | Extra total txb | Extra blood type O txb |
| S1: in + out | 659 (12.60) | 63 (2.10) | 1202 (12.96) | 776 (8.94) | 719 (9.77) | 588 (8.28) | 142 (2.25) | 536 (8.16) | 52 (3.37) |
| S2: in + 1 + out | 659 (12.58) | 63 (2.09) | 1237 (13.60) | 695 (7.75) | 635 (9.28) | 546 (9.41) | 100 (2.23) | 574 (8.95) | 68 (3.16) |
| S3: in + 1 + chain (30) | 659 (12.59) | 63 (2.09) | 1254 (13.21) | 605 (6.69) | 554 (8.18) | 481 (8.20) | 28 (0.59) | 582 (8.16) | 71 (3.10) |
| S4: in + 1 + chain (90) | 659 (12.59) | 63 (2.09) | 1261 (13.16) | 570 (6.95) | 538 (8.14) | 471 (8.10) | 18 (0.63) | 571 (8.70) | 71 (3.05) |
| S5: S4 + blood type O end | 659 (12.59) | 63 (2.09) | 1227 (13.26) | 744 (7.95) | 695 (9.00) | 626 (9.38) | 193 (2.74) | 554 (8.20) | 59 (3.24) |
| S6: S1 + blood type match | 659 (12.59) | 63 (2.09) | 732 (11.78) | 248 (6.04) | 185 (4.23) | 116 (2.48) | 134 (2.67) | 73 (4.18) | 66 (2.55) |
| S6: S2 + blood type match | 659 (12.59) | 63 (2.09) | 754 (11.65) | 255 (5.72) | 192 (3.97) | 128 (2.27) | 133 (2.21) | 94 (3.92) | 69 (2.47) |
DD, deceased donor; DD-CIK, deceased donor chain-initiating kidney; cand, candidates; KPD, kidney paired donation; KPDP, kidney paired donation program; Tx, transplant; WL, waitlist.
For each strategy indicated in the first column, the next 7 columns report results for “KPD only” and “KPD + DD” averaged over all other variables. The final two columns report the average numbers of extra transplants and extra blood type O transplants achieved in “KPD + DD” compared with “KPD only.”
These living donor transplants to the waitlist reflect donations by nondirected donors or bridge donors from the KPDP.
The extra total number of transplants in column 9 is obtained as fourth column plus fifth column minus sixth column minus second column minus third column. This follows because the total number of transplants in the KPD only method is the second column plus the third column plus the actual number of deceased donor transplants in 2016 to 2017. In the “KPD+DD” method, the total number of transplants is the fourth column plus the fifth column plus the actual number of deceased donor transplants in 2016 to 2017 minus the sixth column. Extra blood type O transplants are obtained in a similar way, although not all data required for this calculation are included in this table.
Table 6.
Deceased donor chain length for different methods
| Method name (see Figure 2) | Number of deceased donor chains of different lengths and number of transplants in deceased donor chains of different lengths |
||||||
|---|---|---|---|---|---|---|---|
| Length = 1 | Length = 2 | Length = 3 | Length = 4 | Length = 5 | Length ≥6 | Total | |
| S1: in + out | 719 (9.73) 719 (9.73) |
— | — | — | — | — | 719 (9.73) 719 (9.73) |
| S2: in + 1 + out | 375 (7.32) 375 (7.32) |
260 (4.31) 520 (17.25) |
— | — | — | — | 635 (9.43) 895 (12.7) |
| S3: in + 1 + chain (30) | 333 (6.96) 333 (6.96) |
112 (2.01) 225 (8.05) |
64 (1.22) 191 (11.00) |
28 (0.66) 113 (10.53) |
11 (0.34) 54 (8.42) |
6 (0.54) 41 (3.79) |
554 (8.13) 957 (11.14) |
| S4: in + 1 + chain (90) | 327 (6.68) 327 (6.68) |
82 (2.42) 164 (9.69) |
64 (1.33) 192 (11.94) |
32 (0.52) 127 (8.37) |
16 (0.37) 82 (9.35) |
16 (0.49) 110 (3.80) |
538 (8.09) 1003 (9.74) |
| S5: S4 + blood type O end | 547 (7.10) 547 (7.10) |
101 (4.22) 202 (16.87) |
29 (0.34) 88 (3.03) |
11 (0.37) 45 (5.84) |
4 (0.23) 22 (5.77) |
2 (0.37) 16 (2.41) |
695 (9.14) 919 (10.39) |
| S6: S1 + blood type match | 185 (4.22) 185 (4.22) |
— | — | — | — | — | 185 (4.22) 185 (4.22) |
| S6: S2 + blood type match | 125 (4.03) 125 (4.03) |
67 (0.97) 133 (3.86) |
— | — | — | — | 192 (4.00) 258 (4.19) |
KPD, kidney paired donation.
For each method indicated in the first column, the next 7 columns report the number of deceased donor chains of various lengths and the number of transplants to KPD candidates, averaged over all other parameters. Note that deceased donor chain length is defined as the number of KPD transplants involved excluding the final donation to the waitlist. The numbers in parentheses are standard errors.
Table 7.
Average of simulation results from strategies S1 to S5
| KPD only |
KPD + DD |
KPD + DD minus KPD only |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| Parameter | Value | KPD cand tx | Living donor to WL | KPD cand tx | Living donor to WL | DD-CIK | Blood type O DD-CIK | Blood type O living donor to WL | Extra total txa | Extra blood type O txa |
| Withdrawal probability (per day) | 0.0005 | 681 (12.32) | 64 (2.06) | 1265 (13.69) | 731 (7.70) | 679 (8.90) | 586 (8.83) | 128 (1.81) | 572 (8.01) | 60 (3.24) |
| 0.0015 | 637 (12.88) | 63 (2.13) | 1192 (12.81) | 688 (7.90) | 635 (9.08) | 548 (8.83) | 119 (1.64) | 545 (8.77) | 61 (3.42) | |
| Nondirected donor arrivals (# per year) | 0 | 606 (12.80) | 21 (1.88) | 1222 (13.29) | 700 (7.14) | 693 (7.96) | 593 (7.82) | 128 (2.23) | 602 (6.75) | 63 (3.55) |
| 24 | 663 (13.19) | 55 (3.15) | 1228 (12.58) | 703 (8.08) | 658 (9.64) | 570 (9.46) | 124 (1.71) | 556 (10.01) | 60 (3.29) | |
| 60 | 709 (12.22) | 114 (2.58) | 1236 (14.07) | 725 (8.50) | 619 (10.05) | 539 (9.45) | 120 (1.33) | 518 (9.25) | 60 (3.38) | |
| Match run frequency (day) | 5 | 661 (12.28) | 63 (2.05) | 1229 (13.23) | 703 (7.82) | 651 (9.04) | 563 (8.78) | 120 (1.65) | 557 (8.02) | 60 (3.17) |
| 10 | 657 (12.92) | 64 (2.14) | 1228 (13.23) | 715 (7.73) | 662 (8.89) | 571 (8.81) | 127 (1.79) | 560 (8.69) | 62 (3.31) | |
| Delay time (day) | 0 | 659 (12.59) | 63 (2.10) | 1316 (14.69) | 998 (8.20) | 948 (9.08) | 738 (10.23) | 226 (3.55) | 644 (10.09) | 74 (3.71) |
| 30 | 659 (12.60) | 63 (2.09) | 1271 (14.56) | 739 (9.83) | 687 (11.06) | 605 (11.18) | 128 (1.68) | 600 (9.71) | 68 (3.33) | |
| 60 | 659 (12.58) | 63 (2.10) | 1236 (13.43) | 672 (9.27) | 619 (10.36) | 556 (9.34) | 106 (2.28) | 566 (8.74) | 61 (3.31) | |
| 90 | 659 (12.59) | 63 (2.09) | 1203 (12.94) | 624 (8.65) | 570 (9.72) | 517 (8.57) | 92 (2.44) | 534 (8.15) | 57 (3.26) | |
| 180 | 659 (12.59) | 63 (2.09) | 1115 (11.04) | 514 (5.96) | 459 (7.31) | 421 (6.98) | 67 (1.58) | 448 (5.67) | 45 (2.76) | |
#, number; DD, deceased donor; DD-CIK, deceased donor chain-initiating kidney; cand, candidate; KPD, kidney paired donation; Tx, transplant; WL, waitlist.
For each fixed parameter value as indicated in the first two columns, the next 7 columns report average results for “KPD only” and “KPD + DD” (except strategy S6). The final two columns report the average numbers of extra transplants and extra blood type O transplants achieved in “KPD + DD” compared with “KPD only.”
The extra total number of transplants in column 9 is obtained as the fifth column plus the sixth column minus the third column minus the fourth column minus the seventh column. This follows because the total number of transplants in the KPD-only method is the third column plus the fourth column plus the actual number of deceased donor transplants in 2016 to 2017. In the “KPD + DD” method, the total number of transplants is the fifth column plus the sixth column plus the actual number of deceased donor transplants in 2016 to 2017 minus the seventh column. Extra blood type O transplants are obtained in a similar way, although not all data required for this calculation are included in this table.
Results
Table 5 reports the total number of LD transplants for candidates on the waitlist and LD and DD transplants for candidates within the KPD pool for both the “KPD only” and “KPD + DD” approaches and then presents differences in the final 2 columns. Strategy S1 replicates the results reported in Wang et al.24 and gives rise over two years to 536 additional transplants, including 52 additional blood type O transplants. This can be compared with 582 additional transplants with strategy S3, which generates the largest number of extra transplants. Because strategy S4 has longer bridge donor idle time (90 days) leading to longer chains and more reneges, it yields 11 fewer transplants than S3.
In strategy S1, 588 DD-CIKs of blood type O donate to a blood type O candidate in a KPD pool. In addition, 142 LDs of blood type O donate to the waitlist. Similar effects are seen in strategies S2 to S4 increasing the number of transplants of blood type O candidates by 68 to 71. When compared with S1, strategies S3 and S4 use fewer blood type O DD-CIKs, but also direct fewer blood type O LDs to the waitlist.
Strategy S5 is identical to S4 except that a DD chain stops when it encounters a blood type O LD. It aims to increase blood type O LD donations to the waitlist, but in this regard, it is only partially successful. Compared with S4, S5 increases the overall number of blood type O LD transplants of candidates on the waitlist but not in the KPD pool from 18 to 193, but generates fewer overall transplants, requires 157 more DD-CIKs, and decreases the total additional blood type O transplants from 71 to 59.
Strategy S6 requires that the blood type of the LD returned to the waitlist be at least as favorable as the blood type of the DD-CIK, which greatly restricts the number of possible matches. Compared with “KPD only,” S6 is the only strategy that increases the number of blood type O kidneys offered to candidates on the waitlist but not in the KPD pool. This increase occurs because every DD-CIK of blood type O results in the allocation of a LD of blood type O to a candidate on the waitlist and some of the DD-CIKs of blood type other than O also result in the offer of a LD of blood type O a waitlisted candidate. Compared with strategy S4, S6 results in 477 to 498 fewer transplants over two years. Therefore, although this approach assures that waitlisted blood type O candidates with no LD are not disadvantaged by DD-CIK chains, it also incurs a steep penalty in overall transplants achieved. Note that, when compared with strategies S1 to S4, strategy S6 substantially reduces the overall number of blood type O kidney transplants that could be performed.
Table 6 gives detail on the distribution of length of DD chains, which is the number of KPD pairs involved in the DD chain. As shown in Figure 2, strategy S1 is limited to a chain length of one by the conditions of the simulation. Strategy S2 extends to a second transplant approximately 41% of the time, whereas, S3 to S5 can generate longer chains, with mean chain lengths of 1.73, 1.86, and 1.32, respectively.
Corresponding to each parameter value in Table 7 is the average result of all simulations involving that value across all strategies and other parameters. First, a withdrawal probability of 0.0015/d (approximately 14% per 100 days) results on average in 45 (KPD only) or 72 (KPD + DD) fewer transplants over two years compared with a withdrawal probability of 0.0005/d (approximately 5% per 100 days). This is because the higher departure rate results in a smaller KPD pool and fewer transplant opportunities. Second, when the nondirected donor arrival rate increases from 0 to 60 per year, the average total number of transplants in the KPD pool and waitlist over two years increases by 196 for the KPD only method, but only by 113 for the “KPD + DD” method. In addition, in the “KPD + DD” method, the number of DD-CIKs is reduced by 74, as the 120 nondirected donors substitute for some of the DD-CIKs. Third, higher match run frequency (every 5 days instead of 10 days) has little effect on the simulation results. Last, lengthening the delay time (from 0 to 180 days) reduces the total number of transplants for the “KPD + DD” methods by 196 and the number of DD-CIKs by 489. Intuitively, the longer delay time results in pairs participating in more KPD match runs, so fewer pairs are eligible to receive DD-CIKs because of withdrawal or transplantation. More than 75% of the reduction in number of transplants resulting from lengthening delay time occurs in the first year, whereas the reduction in DD-CIKs is more evenly distributed over the two years. When compared with no delay in eligibility for DD-CIK, delay times of 30 or 60 days or more limit the number of DD-CIKs used, albeit at the price of substantial penalties in the total number of extra transplant performed.
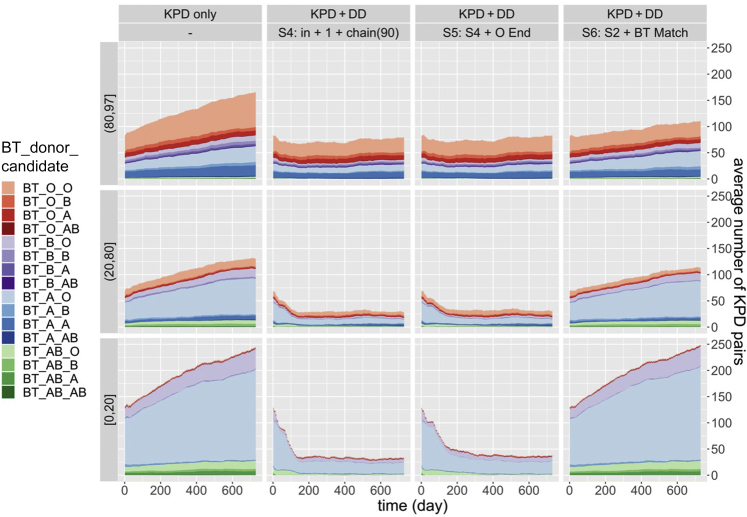
Figure 3 displays the distribution of cPRA and candidate/donor blood type in the KPD pool over time. In “KPD only,” almost all pairs with a candidate cPRA <80% are blood type incompatible (indicated by the paler shades) and most of these blood type incompatible pairs are blood type O candidates with a blood type A donor (identified by the pale blue coloring). In contrast, as candidate cPRA increases, the frequency of sensitized blood type compatible pairs increases. For each cPRA group, donor-candidate blood type combinations reach a steady state in strategies S1 to S5, whereas in S6, the number of pairs with a blood type O candidate and blood type A, B, or AB donor increases over time. Strategy S6 prevents blood type incompatible pairs from participating in DD-initiated chains, unless a blood type compatible but not identical pair is also in the chain.
Figure 3.
The graphs show the distribution of cPRA and BT of donor-candidate pairs in a KPD pool over two years. In each column, parameters are fixed as described in the top two rows and pairs in three cPRA categories define the three graphs in each column. BTs of donors in pairs are indicated by colors and those of candidates in pairs by shades. Pairs with cPRA ≥98% are omitted because they are not eligible to receive chain-initiating deceased donor kidneys in these simulations. BT, blood type; cPRA, calculated panel-reactive antibody; DD, deceased donor; KPD, kidney paired donation.
For pairs of varying cPRAs and blood types, Figure 4 shows the probability that a candidate in the KPD pool is transplanted as a function of time since arrival to the pool. In “KPD only,” the probability of transplant is lower for blood type incompatible pairs than for blood type compatible or identical pairs. S4 and S5 both efficiently transplant blood type incompatible pairs and substantially reduce their disadvantage seen in KPD only. The blood type requirements in S6 greatly reduce the number of transplants to blood type incompatible pairs.
Figure 4.
The probability that a candidate in the KPD pool is transplanted by a time point since arrival in the KPD pool. The nondirected donor arrival rate is 2 per month, withdrawal probability is 0.0005, match run frequency is every 10 days, pair/nondirected donor/bridge donor unavailability probability is 0.1, and delay time is 90 days. With the parameters at the top of each column and cPRA group specifying the rows, graphs are given for 3 blood type categories of pairs. Pairs with cPRA ≥98% are omitted because in these simulations they are not eligible to receive DD-CIKs. BT, blood type; cPRA, calculated panel-reactive antibody; DD, deceased donor; DD-CIK, deceased donor chain-initiating kidney; KPD, kidney paired donation.
Discussion
Kidney paired exchange enables more transplants to be accomplished and could grow even more if DD kidneys were used to stimulate chain formation. However, some ethicists have criticized this proposal because they worry that waitlisted patients, particularly those with blood type O, will be disadvantaged. Our simulations evaluate this criticism, and we find that DD-initiated chains actually increase the overall number of transplants for blood type O patients on the waiting list—some of whom are concomitantly in a KPD pool.
All proposed strategies S1 to S6 are designed with a view to ease of implementation, and in each case, fewer than 3% of the total national number of DD kidneys are allocated to the KPD pool. Strategies S1 and S2 require only a relatively quick settlement of exchanges. For the longer DD-CIK chains (strategies S3–S6), the LD remaining after the second transplant becomes a bridge donor and can potentially begin a new chain through participation in future match runs along with other nondirected donors and bridge donors. Thus, bridge donors resulting from extended chains only need to be monitored for an idle time. When a predetermined idle time limit is exceeded, the bridge donor donates to the waitlist.
Our current microsimulation model only simulates the activity within the KPD pool and does not follow in detail effects on specific waitlisted candidates. A more comprehensive model, currently under development, would also simulate the effects of policy changes on candidates on the waitlist, including those with blood type O, minorities, or members of other candidate groups.
Candidates of all blood types benefit from the proposed policies; however, we expect that there could be some disadvantage to blood type O patients with no LD who have been long on the waitlist, many of whom will have high cPRA of 80% to 97%, as discussed in Turgeon23,25 and in earlier assessments of list exchange contexts.27, 28, 29 Evaluating the degree of such potential disadvantage is important in examining the ethical issues involved. One way to measure the possible disadvantage because of implementation of these policies is based on the change in the waiting time distribution for a randomly chosen candidate, from a given group of candidates. A simple calculation can give insight for the estimated proportional effect on the mean additional waiting time for a compatible kidney of a hypothetical randomly selected blood type O candidate with substantial accrued waiting time, and with a given cPRA of 95% (say). The average additional waiting time depends on the size of the candidate’s “local area.”
The local area for organ allocation priority was previously defined as corresponding to the boundaries of the Donor Service Area in which the kidney was recovered and is more recently defined as the collection of transplant facilities within 250 nautical miles of the donor hospital.26 We assume that the local area of the random candidate of interest generates 2% of the national pool of DDs. We compare the expected number of blood type O donors arriving in the local area in one year, with which the candidate would have a negative virtual crossmatch under the current kidney allocation system and under strategies S1 to S4.
There are approximately 16,000 kidney-alone DD transplants performed in the United States each year.30 Of these, 20% are judged to be the kidneys with the highest potential for long-term graft function and are allocated to candidates with the longest expected post-transplant survival, which would not include this candidate. Of the remaining organs, 44% are blood type O, and approximately 15% of those are allocated to a 0-ABDR mismatch with a waitlisted candidate or match a cPRA ≥98% candidate.31 There are then approximately 4800 blood type O kidneys left for allocation at the local level, and strategies S1 to S4 reduce the number of blood type O kidney offers to the waitlist by approximately 225 (Table 5), leaving 4575 blood type O kidneys. Because this candidate has a cPRA of 95% and comes from a local area that generates 2% of the DDs, there are 4800 × 0.05 × 0.02 = 4.8 kidneys per year on average that arrive at this local area under the current allocation system and are virtually compatible with the candidate. Under strategies S1 to S4, there would be 4575 × 0.05 × 0.02 = 4.6 such kidneys.
The candidate’s expected average additional waiting time to the next compatible kidney is 365/4.8 = 76 days under current policies and 79.3 days under strategies S1 to S4. Thus, there is an increase in the average additional waiting time to the next virtually compatible DD kidney of approximately 3.3 days (or 4.3%). There is, of course, an additional chance that when such a donor arrives, a positive laboratory crossmatch result or other issues may prevent the candidate from receiving the transplant. With different cPRA and different local area size, the disadvantage could be more or less, but always there is a 4.3% increase in average waiting time. This approximation could be verified through simulation in an extended microsimulation model that includes the waitlist. This is a relatively small disadvantage compared with the extra blood type O transplants overall, which would suggest an advantage for all blood type O candidates over the long run.
Another concern is that DD-CIKs prioritize KPD pool candidates with an associated LD.23,25 Such candidates tend to be White and to come from higher socioeconomic groups, and this additional benefit is perhaps at the expense of someone less advantaged. Nevertheless, by reducing somewhat the pressure on the waitlist, DD-CIKs may tend to advantage most waitlist candidates regardless of participation in the KPD pool or not. Moreover, the final LDs of DD chains might be used to help address equity issues by donation to a child or a minority waitlist candidate. A more comprehensive microsimulation would allow assessment of these important equity issues and ideas.
There are some potential weaknesses of these simulations and results. We use a finite set of donors and candidates from a KPD pool in the simulations, and this will not completely cover the diversity that arises in a real-world application. We have also done many simulations creating donors by drawing human leukocyte antigens from the National Marrow Donor Program database,32 conditional on the sex and race of the selected donor. These simulations have led invariably to similar results. The results that we obtain are specific to the US transplant system, and generalization to other countries should be done with care. In the United States, there are many operating KPD programs. The approach in strategies S1 or S2 would easily extend to this situation, but S3 and S4 would work less well if confined to smaller local KPD pools, and the expected number of additional transplants obtained through these more general approaches would be reduced.
In conclusion, this study simulates the use of DD-CIKs and suggests several new strategies that can further increase the total number of kidney transplants, the number of blood type O transplants, the number of transplants from within the KPD pool, and the number of transplants for candidates on the DD waitlist. These strategies would also make available LD kidneys to candidates who are waitlisted for DD transplantation, but who otherwise are without such access. These strategies follow established practices of providing access to kidney transplantation ahead of local allocation for some categories of candidates, but unlike these existing priorities (multiorgan transplants involving a kidney, 0-ABDR mismatch between the donor and recipient, pediatric patients, cPRA ≥98%), the use of DD-CIKs would increase the overall number of transplants.
Disclosure
MAR has an ownership interest in Rejuvenate Healthcare, LLC, and is the uncompensated CEO of the Alliance for Paired Kidney Donation. All the other authors declared no competing interests.
Acknowledgments
The authors thank the Alliance for Paired Kidney Donation and Mr. Jonathon Kopke for sharing data on candidate-donor pairs and nondirected donors that were used in these simulations. The Scientific Registry of Transplant Recipients data used here have been supplied by the Hennepin Healthcare Research Institute as the contractor for the Scientific Registry of Transplant Recipients. The interpretation and reporting of these results are the responsibility of the authors and in no way should be treated as an official policy of or interpretation by the Scientific Registry of Transplant Recipients or the US Government. This study was partly supported by the National Institutes of Health's National Institute of Diabetes and Digestive and Kidney Diseases, United States through grant number R01-DK093513. Michael A. Rees and Alan B. Leichtman were partially supported by grant number R18 HS-020610 from the Agency for Healthcare Research and Quality, United States.
Data Sharing Statement
The data that support the results of this study are available from the Scientific Registry of Transplant Recipients and the Alliance for Paired Kidney Donation. Restrictions apply to the availability of the data, which were under data use agreements for this study.
References
- 1.Park K., Moon J.I., Kim S.I., Kim Y.S. Exchange donor program in kidney transplantation. Transplant Proc. 1999;31:356–357. doi: 10.1016/s0041-1345(98)01659-5. [DOI] [PubMed] [Google Scholar]
- 2.Rapaport F.T. The case for a living emotionally related international kidney donor exchange registry. Transplant Proc. 1986;18(suppl 2):5–9. [PubMed] [Google Scholar]
- 3.Gentry S.E., Montgomery R.A., Segev D.L. Kidney paired donation: fundamentals, limitations, and expansions. Am J Kidney Dis. 2011;57:144–151. doi: 10.1053/j.ajkd.2010.10.005. [DOI] [PubMed] [Google Scholar]
- 4.Wallis C.B., Samy K.P., Roth A.E., Rees M.A. Kidney paired donation. Nephrol Dial Transplant. 2011;26:2091–2099. doi: 10.1093/ndt/gfr155. [DOI] [PubMed] [Google Scholar]
- 5.Roth A.E., Sönmez T., Ünver M.U. Pairwise kidney exchange. J Econ Theor. 2005;125:151–188. doi: 10.1016/j.jet.2005.04.004. [DOI] [Google Scholar]
- 6.Montgomery R.A., Gentry S.E., Marks W.H., et al. Domino paired kidney donation: a strategy to make best use of live non-directed donation. Lancet. 2006;368:419–421. doi: 10.1016/S0140-6736(06)69115-0. [DOI] [PubMed] [Google Scholar]
- 7.Roth A.E., Sönmez T., Ünver M.U., Delmonico F.L., Saidman S.L. Utilizing list exchange and nondirected donation through ‘chain’ paired kidney donations. Am J Transplant. 2006;6:2694–2705. doi: 10.1111/j.1600-6143.2006.01515.x. [DOI] [PubMed] [Google Scholar]
- 8.Gentry S.E., Montgomery R.A., Swihart B.J., Segev D.L. The roles of dominos and nonsimultaneous chains in kidney paired donation. Am J Transplant. 2009;9:1330–1336. doi: 10.1111/j.1600-6143.2006.01515.x. [DOI] [PubMed] [Google Scholar]
- 9.Ashlagi I., Gilchrist D.S., Roth A.E., Rees M.A. Nonsimultaneous chains and dominos in kidney-paired donation—revisited. Am J Transplant. 2011;11:984–994. doi: 10.1111/j.1600-6143.2011.03481.x. [DOI] [PubMed] [Google Scholar]
- 10.Rees M.A., Kopke J.E., Pelletier R.P., et al. A nonsimultaneous, extended, altruistic-donor chain. N Engl J Med. 2009;360:1096–1101. doi: 10.1056/NEJMoa0803645. [DOI] [PubMed] [Google Scholar]
- 11.Flechner S.M., Thomas A.G., Ronin M., et al. The first 9 years of kidney paired donation through the National Kidney Registry: characteristics of donors and recipients compared with National Live Donor Transplant Registries. Am J Transplant. 2018;18:2730–2738. doi: 10.1111/ajt.14744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cowan N., Gritsch H.A., Nassiri N., Sinacore J., Veale J. Broken chains and reneging: a review of 1748 kidney paired donation transplants. Am J Transplant. 2017;17:2451–2457. doi: 10.1111/ajt.14343. [DOI] [PubMed] [Google Scholar]
- 13.Segev D.L., Gentry S.E., Warren D.S., Reeb B., Montgomery R.A. Kidney paired donation and optimizing the use of live donor organs. JAMA. 2005;293:1883. doi: 10.1001/jama.293.15.1883. [DOI] [PubMed] [Google Scholar]
- 14.Roth A., Sonmez T., Unver M.U. Kidney exchange. Q J Econ. 2004;119:457–488. doi: 10.1162/0033553041382157. [DOI] [Google Scholar]
- 15.Li Y., Song P.X., Zhou Y., Leichtman A.B., Rees M.A., Kalbfleisch J.D. Optimal decisions for organ exchanges in a kidney paired donation program. Stat Biosci. 2014;6:85–104. doi: 10.1007/s12561-013-9082-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dickerson J.P., Procaccia A.D., Sandholm T. Failure-aware kidney exchange. Paper presented at: 14th ACM Conference on the Electronic Commerce; June 2013; Philadelphia, PA.Accessed April 21, 2022. https://dl.acm.org/doi/abs/10.1145/2492002.2482596
- 17.Yanhua C., Yijiang L., Kalbfleisch J.D., et al. Graph-based optimization algorithm and software on kidney exchanges. IEEE Trans Bio Med Eng. 2012;59:1985–1991. doi: 10.1109/TBME.2012.2195663. [DOI] [PubMed] [Google Scholar]
- 18.Bray M., Wang W., Song P.X., et al. Planning for uncertainty and fallbacks can increase the number of transplants in a kidney-paired donation program. Am J Transplant. 2015;15:2636–2645. doi: 10.1111/ajt.13413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Melcher M.L., Roberts J.P., Leichtman A.B., Roth A.E., Rees M.A. Utilization of deceased donor kidneys to initiate living donor chains. Am J Transplant. 2016;16:1367–1370. doi: 10.1111/ajt.13740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Haynes C., Leishman R. Allowing deceased donor-initiated kidney paired donation (KPD) chains. OPTN/UNOS Kidney Transplantation Committee. https://optn.transplant.hrsa.gov/media/2219/kidney_pcconcepts_201707.pdf
- 21.Furian L., Cornelio C., Silvestre C., et al. Deceased donor-initiated chains. Transplantation. 2019;103:2196–2200. doi: 10.1097/TP.0000000000002645. [DOI] [PubMed] [Google Scholar]
- 22.Massie A.B., Leanza J., Fahmy L.M., et al. A risk index for living donor kidney transplantation. Am J Transplant. 2016;16:2077–2084. doi: 10.1111/ajt.13709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wall A.E., Veale J.L., Melcher M.L. Advanced donation programs and deceased donor-initiated chains—2 innovations in kidney paired donation. Transplantation. 2017;101:2818–2824. doi: 10.1097/TP.0000000000001838. [DOI] [PubMed] [Google Scholar]
- 24.Wang W., Rees M.A., Leichtman A.B., et al. Deceased donors as nondirected donors in kidney paired donation. Am J Transplant. 2021;21:103–113. doi: 10.1111/ajt.16268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Turgeon N.A. Deceased donor chains—it is time for debate and consensus. Am J Transplant. 2021;21:5–6. doi: 10.1111/ajt.16362. [DOI] [PubMed] [Google Scholar]
- 26.Organ Procurement and Transplantation Network Organ procurement and transplant network policies. Organ Procurement and Transplantation Network. https://optn.transplant.hrsa.gov/media/1200/optn_policies.pdf
- 27.Zenios S.A., Woodle E.S., Ross L.F. Primum non nocere: avoiding harm to vulnerable wait list candidates in an indirect kidney exchange. Transplantation. 2001;72:648–654. doi: 10.1097/00007890-200108270-00015. [DOI] [PubMed] [Google Scholar]
- 28.Ross L.F., Zenios S. Restricting living-donor-cadaver-donor exchanges to ensure that standard blood type O wait-list candidates benefit. Transplantation. 2004;78:641–646. doi: 10.1097/01.tp.0000134522.31554.05. [DOI] [PubMed] [Google Scholar]
- 29.Ross L.F., Woodle E.S. Ethical issues in increasing living kidney donations by expanding kidney paired exchange programs. Transplantation. 2000;69:1539–1543. doi: 10.1097/00007890-200004270-00001. [DOI] [PubMed] [Google Scholar]
- 30.Organ Procurement and Transplantation Network Organ Procurement and Transplantation Network national data report. Organ Procurement and Transplantation Network. https://optn.transplant.hrsa.gov/data/view-data-reports/national-data/
- 31.Health Resources and Services Administration . Health Resources and Services Administration; Published 2018. OPTN/SRTR 2018 annual data report: kidney.https://srtr.transplant.hrsa.gov/annual_reports/2018/Kidney.aspx#KI_37_deceased_don_age_1_b64 [Google Scholar]
- 32.National Marrow Donor Program Be the match registry haplotype frequencies. National Marrow Donor Program. https://bioinformatics.bethematchclinical.org/hla-resources/haplotype-frequencies/be-the-match-registry-haplotype-frequencies/