Hinge point emergence in mammalian spinal neurulation

Significance

Spinal neural tube folding shows a transition from medial to dorsolateral neural plate bending sites (hinge points) along the embryo’s body axis. While hinge points are considered an important driving force in neural tube closure, their biomechanical origin is poorly understood. Here we use a computational model based on mouse and human embryo imaging data to show that the median hinge point emerges in simulations combining mesoderm expansion, nonneural ectoderm expansion, and neural plate adhesion to the notochord. Furthermore, dorsolateral hinge points emerge through a medial pulling force exerted by dorsal nonneural ectoderm (zippering). This indicates that spinal neural tube folding could be primarily driven by mesoderm expansion and zippering, with hinge points passively emerging in response to extrinsic forces.

Abstract

Neurulation is the process in early vertebrate embryonic development during which the neural plate folds to form the neural tube. Spinal neural tube folding in the posterior neuropore changes over time, first showing a median hinge point, then both the median hinge point and dorsolateral hinge points, followed by dorsolateral hinge points only. The biomechanical mechanism of hinge point formation in the mammalian neural tube is poorly understood. Here we employ a mechanical finite element model to study neural tube formation. The computational model mimics the mammalian neural tube using microscopy data from mouse and human embryos. While intrinsic curvature at the neural plate midline has been hypothesized to drive neural tube folding, intrinsic curvature was not sufficient for tube closure in our simulations. We achieved neural tube closure with an alternative model combining mesoderm expansion, nonneural ectoderm expansion, and neural plate adhesion to the notochord. Dorsolateral hinge points emerged in simulations with low mesoderm expansion and zippering. We propose that zippering provides the biomechanical force for dorsolateral hinge point formation in settings where the neural plate lateral sides extend above the mesoderm. Together, these results provide a perspective on the biomechanical and molecular mechanism of mammalian spinal neurulation.

Neurulation is the process in early chordate embryogenesis during which the neural tube (NT) forms. The NT is a dorsal structure extending along the rostrocaudal axis which ultimately develops into the brain and spinal cord. Failure of neurulation leads to NT defects, a group of severe neurodevelopmental disorders that affect ∼1 in 1,000 births (1). Neurulation occurs through two distinct mechanisms termed primary and secondary neurulation. In amphibians, birds, and mammals, primary neurulation (reviewed in ref. 2) occurs along most of the rostrocaudal axis, whereas secondary neurulation (involving epithelialization of condensed tail bud cells) occurs caudally in the lower sacral and coccygeal regions only. At the start of primary neurulation, dorsal midline ectoderm cells differentiate into neuroepithelial cells to form a columnar pseudostratified epithelium called the neural plate (NP) (reviewed in ref. 3). The NP lateral sides elevate and meet dorsally at the embryo midline, where they fuse to form the NT. The folding NP is bordered by nonneural ectoderm (NNE) cells, which adhere to the NP borders on the basal side and migrate medially to cover the NT at the dorsal midline (2, 4).

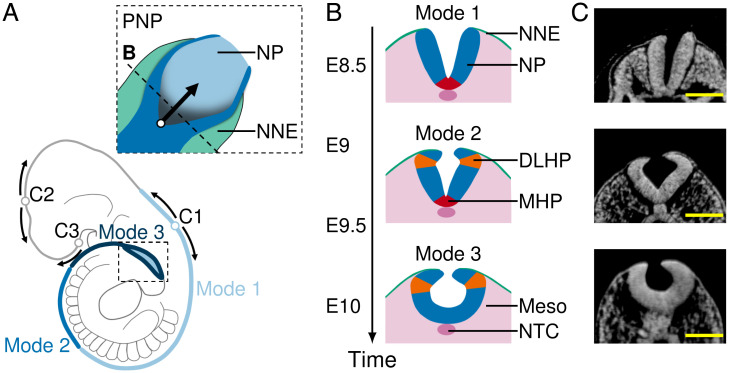
While amphibians show NT closure at all axial levels simultaneously, mammals and birds initiate closure at a few sites, with the exact closure locations differing between species (2). In mice, the NT initially closes on embryonic day (E) 8, somite stage (SS) 7, at the hindbrain/cervical boundary between somites 3 and 4 (closure 1) (5, 6). Starting from the initial closure site, NT closure progresses bidirectionally through zippering (Fig. 1A). During zippering, the NNE pulls the NP borders toward the embryo midline by forming a transitory semirosette structure at the dorsal closure site (9). The NP region caudal of the zipper is called the posterior neuropore (PNP) (2) (Fig. 1A, close-up box). Simultaneous with zippering progression, the PNP expands in caudal direction until complete closure is achieved at E10, SS30 (5).

Fig. 1.

NP morphology in the PNP at successive stages of mouse neurulation. (A) Schematic mouse embryo at E10. Dotted box, close-up of PNP (top view); empty circles, closure sites (closures 1 to 3); arrows, zippering direction; blue shades, position of folding modes 1 to 3. (B) Schematic transverse sections through the PNP at spinal neurulation modes 1 (E8.5 to E9), 2 (E9 to E9.75), and 3 (E9.75 to E10.5). Green, NNE; blue, NP; red, MHP; orange, DLHPs; pink, mesoderm (Meso) and notochord (NTC). (C) Transverse sections through the PNP at E8.5 (mode 1), E9.5 (mode 2), and E10 (mode 3). Images were derived with permission from refs. 7 and 8 under a Creative Commons Attribution license. (Scale bars: 100 µm.).

When looking at transverse cross-sections of the PNP, the folding NP shows strong curvature in two specific regions, commonly referred to as “hinge points.” Bending occurs at the ventral midline, resulting in the median hinge point (MHP), and at lateral sides near the position where the NP touches the NNE, resulting in the dorsolateral hinge points (DLHPs) (4, 10). Interestingly, the spinal NT appears to fold through different mechanisms along the rostrocaudal axis. At E8.5, when the upper spine forms, the folding NT shows an MHP but no DLHPs (mode 1). At E9.5, during midspine formation, the NT shows both an MHP and DLHPs (mode 2). When the posterior NT closes at E10, only DLHPs are present (mode 3) (Fig. 1 B and C) (10). Mouse mutants with impaired MHP formation show increased DLHPs (11), and mouse Noggin^–∕– mutants, which fail to form DLHPs, show NT closure failure in the most caudal regions (12, 13). While hinge points appear to be required for tube closure, the biomechanical and molecular mechanism of MHP and DLHP formation is poorly understood.

Hinge points are commonly thought to form through an intrinsic curvature mechanism involving apical constriction and basal widening of neuroepithelial cells. Avian and mammalian neuroepithelial cells are tightly packed in a columnar pseudostratified epithelium, such that the cells are widened at the apicobasal position of the nucleus. Neuroepithelial nuclei move along the apicobasal axis throughout the cell cycle in a process termed interkinetic nuclear migration (reviewed in ref. 14). While most neuroepithelial cells are distributed randomly throughout the cell cycle, the MHP contains an increased proportion of wedge-shaped S-phase cells with basally located nuclei. This observation led to the view that interkinetic nuclear migration is a driving force in avian (15, 16) and mammalian (17, 18) MHP formation. However, while DLHPs show an increased proportion of cells with basally located nuclei in the chick (15), no significant increase has been found in mice (18). Furthermore, disruption of actin microfilaments does not prevent hinge point formation in the mouse spinal NP, contradicting the idea that hinge points form through cell-intrinsic bending (19).

Aside from intrinsic forces of NP bending, extrinsic forces from the notochord, mesoderm, and NNE have been implicated in NT folding. During early NT folding, the notochordal plate is covered by an apical basement membrane which maintains direct contact with the NP basement membrane. The notochordal plate gives rise to the notochord, which remains in contact with the NP midline until after the NT has fully closed (20, 21). The notochord is essential for MHP formation. Notochordless embryos lack strong midline curvature and do not develop a floor plate (11, 22, 23). In addition to the notochord, mesoderm expansion has been proposed to drive NT folding in the rostral region (24, 25). NT closure at the lower spinal cord region requires the presence of NNE but can still form after mesoderm removal (26, 27).

Computational modeling allows for an isolated study of biomechanical NT folding driving forces in a defined and quantifiable setting. Previous modeling studies have focused on amphibian neurulation (28–31). Due to differences in closure progression and NP morphology, a new model is needed which is specific for mammals. Here we employ a two-dimensional (2D) finite element model to study the biomechanics of NT folding. We find that mesoderm and NNE expansion combined with NP–notochord adhesion are sufficient to simulate MHP formation and mode 1 closure. Furthermore, we find that DLHPs emerge in simulations with low mesoderm expansion and zippering.

Results

Intrinsic NP Curvature and Midline Tapering Can Promote Tube Folding.

To investigate the mechanical mechanism of NT folding, we first examined the minimal requirements to form a tube from a flat tissue. In a 2D cross-sectional plane, an epithelial sheet (in the present case, consisting of both the NP and NNE) necessarily needs to expand in width relative to the underlying tissue area to fold into a tube structure within that plane. In concordance, we modeled an expanding epithelial 2D section with spatially fixed boundaries, dubbed model I.

The initial model I configuration is a horizontal tissue of width $w_{\text{NP}}=500$ µm and apicobasal height $h_{\text{NP}}=45$ µm (Fig. 2A; simulation time t = 0). The ectoderm expands in width uniformly over space and time, whereas the apicobasal height remains constant. The simulation ends at twice the initial tissue length (1,000 µm, simulation time $t=1$). In order to mimic differential growth of the ectoderm with respect to underlying tissues, the net area under the ectoderm horizontal midline is kept at zero using a Lagrange multiplier. As deforming embryonic tissues show viscoelastic properties (32), we modeled the epithelium as a linearly viscoelastic continuum. Furthermore, as biological cells show stress relaxation in response to external forces through cytoskeletal remodeling (33), we included plastic stress relaxation in the model (Materials and Methods). For an introduction to tissue mechanics, we refer to ref. 34. Epithelial width expansion resulted in tissue outgrowth but did not lead to tube formation (Fig. 2 B, Top, and Movie S1).

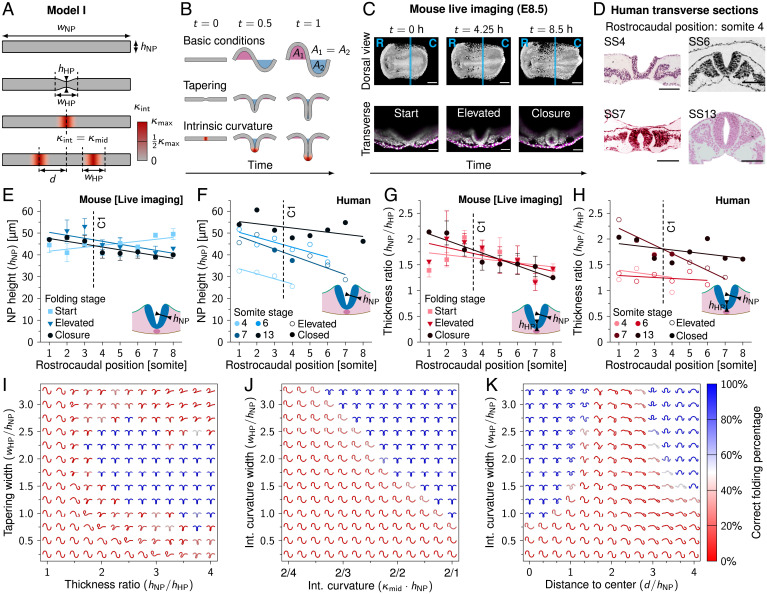
Fig. 2.

Intrinsic NP curvature and midline tapering can promote tube folding. (A) Schematic representation of model I. $w_{\text{NP}}$, NP width; $h_{\text{NP}}$, NP apicobasal height; $h_{\text{HP}}$, MHP (midline) height; $w_{\text{HP}}$, hinge point domain width; d, domain distance to center; ${\kappa }_{\text{int}}$, intrinsic tissue curvature; ${\kappa }_{\text{mid}}$, intrinsic tissue curvature at the hinge point midline; ${\kappa }_{\text{max}}$, theoretical maximum tissue curvature. (B) Model I simulations rendered between t = 0 ($w_{\text{NP}}=500$ µm) and t = 1 ($w_{\text{NP}}=1000$ µm). The area underneath the tissue horizontal midline is fixed at 0. (C) Mouse live-imaging of early NT closure at E8.5. R, rostral; C, caudal; magenta, cell membrane; white, nucleus. Cyan lines in dorsal view images indicate rostrocaudal position (somite 4.5) of transverse view. (Scale bars: 200 µm [dorsal view] and 100 µm [transverse view].) (D) Human transverse sections of early NT closure at SS4 to SS13, rostrocaudal position somite 4. Images were derived with permission from refs. 35 and 36 under a Creative Commons Attribution license. (Scale bars: 100 µm.) (E) Measured NP apicobasal height ($h_{\text{NP}}$) during NT folding progression along the rostrocaudal axis in developing mouse embryos. (F) Measured NP apicobasal height ($h_{\text{NP}}$) along the rostrocaudal axis in human embryos (SS4, SS6, SS7, and SS13). (G) Measured NP midline thickness ratio ($h_{\text{NP}}/h_{\text{HP}}$) during NT folding progression along the rostrocaudal axis in developing mouse embryos. (H) Measured NP midline thickness ratio ($h_{\text{NP}}/h_{\text{HP}}$) along the rostrocaudal axis in human embryos (SS4, SS6, SS7, and SS13). Lines in E–H represent linear least-squares fit; C1 indicates closure 1 rostrocaudal position. In E and G, error bars indicate SEM, $N=1\text{–}3$ (SI Appendix, Table S1). In F and H, open circles indicate that NP is in the process of folding; closed circles indicate that NP is closed. (I–K) NP folding simulations (t = 1) with midline tapering thickness ratio versus tapering domain width (I), intrinsic midline curvature strength versus intrinsic curvature domain width (J), and intrinsic dorsolateral curvature (${\kappa }_{\text{mid}}={\kappa }_{\text{max}}/2$) distance to center versus intrinsic curvature domain width (K). In I, simulation renderings were flipped along the y axis to point downward. Color scale represents the percentage of intermediate simulation steps in which the neural ectoderm is sufficiently symmetrical along the x axis and the neuroepithelium midline is buckled; i.e., the sum of the x coordinates of the elements on the left and right half of the neural ectoderm differ by less than 10%, and the middle element has $\left|y\right|>h_{\text{NP}}$.

To obtain realistic simulation parameters on early NT closure, we analyzed in vitro live-imaging data of three developing mouse embryos at E8.5 expressing a cell membrane and nuclear marker (Fig. 2C and Movie S2). We analyzed one of our previously published mouse embryo datasets (37) and combined this with two new ones. Parameters were measured along the rostrocaudal axis at every somite position and at three time points during folding progression: start, elevated, and closure. These time points were different for each somite position. Start refers to the time point after gastrulation where the NP has become distinguishable from the NNE. Closure is the first time point where the lateral sides of the NP touch at the dorsal midline. Elevated refers to the middle time point between start and closure. To compare mouse with human NT folding, mouse live-imaging data were complemented with stained histological sections of four human embryos (Fig. 2D). Human embryo sections were obtained from the Virtual Human Embryo Project (35) and the 3D Atlas of Human Embryology (36). Specimens included for analysis were between SS4 (the earliest stage embryo available which showed a folding NT) and SS13 (the earliest stage embryo available which showed complete NT closure between somite positions 1 and 8). Human embryo measurements were made along the rostrocaudal axis at each somite position, with each rostrocaudal position marked as elevated or closed. Mouse NP apicobasal height (measured at the middle of one of the NP lateral sides) was measured to be 44 ±5 µm (SD) across samples and rostrocaudal positions (Fig. 2E), which we rounded off to $h_{\text{NP}}=45$ µm for the simulations. The human data showed a NP apicobasal height of 30 ±3 µm (SD) in the SS4 embryo and a combined mean of 42 ±6 µm (SD) around the stage of closure 1 in the SS6/SS7 embryos (Fig. 2F). This suggests that NP apicobasal height could increase during folding in humans, reaching a similar NP apicobasal height as observed in mice around the time of closure 1.

We subsequently considered the effect of midline tapering on NP folding. Neuroepithelial cells at the NP midline have a lower apicobasal height than lateral neuroepithelial cells due to SHH signaling from the notochord (22, 23, 38). Bending energy scales with the tissue thickness cubed (39), such that tissues subject to transverse forces tend to bend at the thinnest sites. Midline tapering was present during folding in both our mouse and human data (Fig. 2 G and H). It may thus facilitate MHP formation and tube folding. We implemented midline tapering in model I using a thickness ratio given by the lateral NP height ($h_{\text{NP}}$) divided by the midline NP height ($h_{\text{HP}}$) (Fig. 2A). We modeled the neural epithelium height transitions from $h_{\text{HP}}$ to $h_{\text{NP}}$ using a smooth function covering the MHP domain width ($w_{\text{HP}}$) (Fig. 2A). We ran model I simulation for varying thickness ratios and tapering widths. Tubes with left–right symmetry formed at thickness ratios of 1.75 and higher and at tapering widths between 0.75 and 2.75 times the NP height (Fig. 2 B and I and Movie S3). As midline thinning was symmetrical along the apicobasal axis, tubes folded in both the outward and inward directions. Thus, while our simulation results suggest midline tapering could promote tube folding, an additional process is needed to ensure that the tube folds inward.

As a possible mechanism to ensure inward folding, we next considered intrinsic midline curvature. NT folding is associated with increased presence of wedge-shaped cells at the MHP (17, 18). The formation of wedge-shaped cells with narrow apical and wide basal sides is considered a driving force of NT folding (2, 17, 18). We ran model I simulations for varying levels of intrinsic midline inward curvature and MHP width values (Fig. 2 A, B, and J and Movie S4). Intrinsic curvature strength is given by ${\kappa }_{\text{int}}=1/r$, with r the radius of curvature. As the theoretical minimum radius of curvature corresponds to the tissue half-height ($h_{\text{NP}}/2$), the theoretical maximum intrinsic curvature ${\kappa }_{\text{max}}=2/h_{\text{NP}}$. We modeled intrinsically curved regions using a spatially smooth and temporally instantaneous function ranging from ${\kappa }_{\text{int}}={\kappa }_{\text{mid}}$ in the middle of the intrinsically curved domain to ${\kappa }_{\text{int}}=0$ on the lateral domain borders. Note that simulations with intrinsic curvature start out in a straight configuration; the intrinsically curved regions curve up during early simulation time steps (Fig. 2 A and B). Intrinsic midline curvature combined with NP width expansion leads to tube formation for intrinsic curvature domain widths $w_{\text{HP}}=h_{\text{NP}}$ and higher and intrinsic curvatures above ${\kappa }_{\text{mid}}={\kappa }_{\text{max}}/3.5$ (Fig. 2J). Wide intrinsically curved domains were favorable for folding and required weaker intrinsic curvature to form an NT. In contrast to midline tapering, intrinsic midline curvature was biased in the ventral direction and thus consistently led to inward folding.

As intrinsic midline curvature caused a tube shape with MHP resembling mode 1 folding (E8.5), we wondered if likewise we could simulate a tube with DLHPs resembling mode 3 (E10) using intrinsic dorsolateral curvature. To implement this, we introduced the parameter d to indicate the distance between the NP midline and the middle of the DLHP intrinsic curvature domains (Fig. 2 A, Bottom). Intrinsic dorsolateral curvature was fixed at ${\kappa }_{\text{mid}}={\kappa }_{\text{max}}/2$, and distance d was varied from 0 (hinge points overlap at the midline) to 180 µm (hinge points positioned close to NP borders). For low d, the intrinsically curved regions overlapped to form an MHP. However, when the intrinsically curved regions were shifted laterally to form separate DLHPs (at d = 75 to 120 µm), the epithelium folded into an irregular shape not resembling a tube (Fig. 2K and Movie S5). Repeating the midline tapering and intrinsic curvature simulations with an NP height that linearly increases from 30 to 45 µm over time, as roughly observed in human embryos (Fig. 2 D and F), did not alter the outcomes significantly. These results suggest that epithelium width expansion combined with intrinsic NP curvature may be sufficient for tube formation when the NP curves in the midline region but not when the NP curves in dorsolateral regions.

When the inward DLHP intrinsic curvature domains approached the NP borders (d > 120 µm), a tube shape did form, albeit consistently in the outward direction (Fig. 2K). Thus, curvature at the NP borders in the outward direction could contribute to tube folding. Such curvature has been commonly observed in birds and mammals and has previously been described as “epithelial ridging and kinking” at the NP borders as an event preceding adhesion between the NNE and NP basal sides (40).

NNE Width Increase in NT Folding.

After studying intrinsic NP curvature and midline tapering in a minimal model, we adapted the model to better represent mammalian NT folding. In the transverse plane, NP width decreases over time as a result of convergent extension movements (reviewed in ref. 41). NP width decreased throughout folding by an average of 30% in live-imaged mouse embryos (360 ±73 µm at folding start versus 251 ±42 µm [SD] at time of closure; Fig. 3A). In human embryos, we observed no significant changes in NP width during folding between SS4 and SS7 (Fig. 3B). While the reason for this observation could not be fully clarified, a possible explanation is that NP elevation is advanced already in the earliest human embryo, SS4, making it difficult to track convergent extension (Fig. 2D). Notably, NP width at human stages SS4 to SS7 (237 ±24 µm [SD]) was similar to NP width at time of closure in mice. The NP is bordered by NNE on the lateral sides, which increased in width throughout folding (48% increase from 175 ±46 µm at folding start versus 259 ±29 µm [SD] at time of closure in mice; Fig. 3C). The human embryos showed lateral folding (Fig. 2D), which made it challenging to compare the complete NNE width between embryos. In human embryos we therefore measured only the NNE portion dorsal of the somites, which markedly increased with folding progression (Fig. 3D). The NNE apicobasal height was measured at 7.2 ±1.2 µm (SD) in human embryos, which is ∼6 times shorter compared to the NP (Fig. 3E). According to linear elastic beam theory (39), this makes NNE about $6^3=216$ times less rigid in bending than the NP. After incorporating this information into model I, midline tapering (with $h_{\text{NP}}/h_{\text{MHP}}=2,\hspace{0.17em}{w}_{\text{HP}}=2h_{\text{NP}}$) and midline intrinsic curvature (${\kappa }_{\text{mid}}={\kappa }_{\text{max}},\hspace{0.17em}{w}_{\text{HP}}=2h_{\text{NP}}$) were no longer sufficient to create a tube shape (Fig. 3F). When combining midline tapering and maximum midline intrinsic curvature in the original model I, a tube formed (Fig. 3 F, first row, and Movie S6). However, the folding NP did not close after incorporating the NNE thickness profile and differential width expansion in the model, with a fixed $w_{\text{NP}}$ and only $w_{\text{NNE}}$ expanding over time (Fig. 3 F, second and third rows, and Movies S7 and S8). Even when adding maximum outward intrinsic curvature at the NP borders to promote NP elevation (${\kappa }_{\text{mid}}=-{\kappa }_{\text{max}},\hspace{0.17em}{w}_{\text{HP}}=2h_{\text{NP}},\hspace{0.17em}d=w_{\text{NP}}/2$), the NP did not close (Fig. 3 F, fourth row, and Movie S9). While in theory we could force the NP to form a tube by increasing the intrinsic curvature domain width, this is not consistent with observations from birds and mammals, which during mode 1 folding only show sharp bending at the NP midline (15, 17, 18). Together, these results suggest that intrinsic NP midline curvature and midline tapering are not sufficient for NT closure in mammals and birds. Thus, an additional or different mechanism is needed.

Fig. 3.

NNE width expansion in NT folding. (A) Measured NP width ($w_{\text{NP}}$) during NT folding progression along the rostrocaudal axis in developing mouse embryos. $N=1\text{–}3$ (SI Appendix, Table S1). (B) Measured NP width ($w_{\text{NP}}$) along the rostrocaudal axis in human embryos (SS4, SS6, SS7, and SS13). (C) Measured NNE width ($w_{\text{NNE}}$) during NT folding progression along the rostrocaudal axis in developing mouse embryos. $N=1\text{–}3$ (SI Appendix, Table S1). (D) Measured NNE width ($w_{\text{NNE}}$) along the rostrocaudal axis in human embryos (SS4, SS6, SS7, and SS13). (E) Measured NNE height ($h_{\text{NNE}}$) along the rostrocaudal axis in human embryos (SS4, SS6, SS7, and SS13). Lines in A–E represent linear least-squares fits, C1 in A–E indicates closure 1 rostrocaudal position, and error bars in A and C indicate SEM. In B, D, and E, open circles indicate that NP is in the process of folding; closed circles indicate that NP is closed. (F) Model I simulations rendered between t = 0 and t = 1. First row, midline thinning + midline intrinsic curvature; second row, previous simulation + NNE thickness profile; third row, previous simulation + differential width expansion; fourth row, previous simulation + NP border intrinsic curvature. Red, inward (midline) intrinsic curvature; blue, outward (NP border) intrinsic curvature.

Extrinsic Forces Are Sufficient for NT Closure.

As intrinsic NP curvature appeared insufficient for mouse NT closure, we next considered extrinsic forces. Mesoderm area increased by 58% during mouse NT folding ($1.9\times {10}^4\pm 0.4\times {10}^4$ µm² at folding start versus $3.0\times {10}^4\pm 0.6\times {10}^4$ µm² [SD] at time of closure) (Fig. 4A). A roughly similar trend was seen for mesoderm area in humans (measured between the NP and somite lateral border; Fig. 4B). Mesoderm has been proposed to promote NP elevation (24, 25). The NP midline maintains direct contact with the underlying notochordal plate and notochord during NT folding (20, 21), thus possibly anchoring the NP midline while the lateral sides elevate. In addition to the notochord and mesoderm, NNE has been implicated in NT folding (26, 27). The NNE expanded in width during mouse and human NT folding (Fig. 3 C and D). While the NNE appeared too thin to push the neural folds toward the midline in model I (Fig. 3F), NNE could nevertheless promote NT folding in a biomechanical model by constraining the direction of mesoderm expansion.

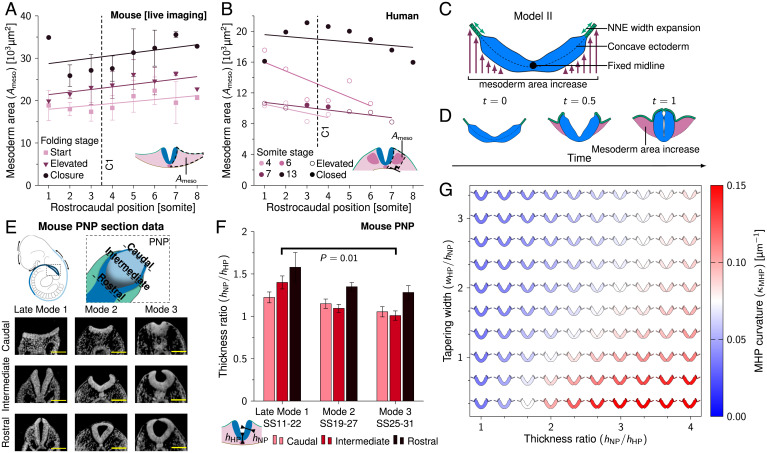
Fig. 4.

Mesoderm area increase and midline tapering promote MHP formation. (A) Measured mesoderm area ($A_{\text{meso}}$) during NT folding progression along the rostrocaudal axis in developing mouse embryos. $N=1\text{–}3$ (SI Appendix, Table S1). Error bars indicate SEM, and lines represent linear least-squares fits. (B) Measured mesoderm area ($A_{\text{meso}}$) along the rostrocaudal axis in human embryos (SS4, SS6, SS7, and SS13). Open circles indicate that NP is in the process of folding; closed circles indicate NP is closed. Lines represent linear least-squares fits. (C) Schematic representation of model II. The NP midline position is held fixed. The NNE width expands over time, and the area ventral of the ectoderm increases to simulate mesoderm expansion. The initial ectoderm configuration is concave. (D) Model II simulation rendered between t = 0 and t = 1. The pink area indicates mesoderm area increase ($1.7\times {10}^4$ µm² at t = 1). (E) Schematic drawing of the PNP and transverse sections through the PNP at late mode 1 (SS11 to SS22), mode 2 (SS19 to SS27), and mode 3 (SS25 to SS31). In the caudal images, NP is flat; in the intermediate images, NP is elevated; and in the rostral images, NP closes. Images were derived with permission from refs. 7 and 8 under a Creative Commons Attribution license. (Scale bars: 100 µm.) (F) Measured thickness ratio ($h_{\text{NP}}/h_{\text{HP}}$) during NT folding progression at modes 1 to 3 in the developing mouse PNP. For late mode 1, N = 5; for mode 2, N = 12; and for mode 3, N = 7. Error bars are SEM. Mann–Whitney u test, P = 0.01. (G) Model II simulations (t = 0.5) with midline tapering ratio versus MHP domain width. Color scale indicates the highest curvature measured in the MHP region (${\kappa }_{\text{MHP}}$).

We combined mesoderm area increase, NNE width increase, and NP–notochord adhesion into a new model (model II; Fig. 4C). Unlike model I, model II does not keep the area underneath the ectoderm fixed but rather lets it increase linearly over time to simulate mesoderm area increase. The NNE simultaneously expands in width to facilitate the increasing mesoderm area. The NP remains constant in height and width during folding progression. To simulate notochord adhesion, the NP midpoint position is held fixed. To mimic the E8.5 embryo shape during early NT closure (Fig. 2C and Movie S2), we started the simulation from a concave ectoderm shape. Furthermore, to create more realistic ectoderm behavior we added adhesion between the NNE and NP basal sides upon reaching a proximity of 3 µm. In the embryo, neuroepithelial thickening during NP formation promotes NP–NNE adhesion (42). To facilitate initial NP–NNE adhesion in the model, we included intrinsic outward curvature at the NP borders (${\kappa }_{\text{mid}}={\kappa }_{\text{max}},\hspace{0.17em}w=3h_{\text{NNE}}$). When combining mesoderm area increase and NNE width increase in model II, the NP lateral sides elevated and moved toward the embryo midline to form a tube (Fig. 4D and Movie S10). Model II shows a similar result when including NP width decrease over time (due to convergent extension), with a similar morphology of the final tube (Movie S11). Note that model II is based on external forces and thus does not rely on intrinsic NP midline curvature. This result suggests that mesoderm and NNE expansion combined with notochord adhesion are sufficient for NT closure in the concave-shaped E8.5 embryo.

Midline Tapering Enhances MHP Curvature.

In model II (Fig. 4D), the MHP emerges through mesoderm expansion and NP midline adhesion to the notochord. During folding, the PNP shows a gradual decrease in midline curvature over time until there is no distinct MHP in the mouse PNP at E10 (Fig. 1B). To understand these observed differences along the rostrocaudal axis, we studied which factors determine MHP curvature. As elastic structures tend to deform at their thinnest point, where least force is required (39), we considered midline tapering. To see how midline tapering changes over developmental time between mode 1 and mode 3 folding, we analyzed high-resolution plastic sections and high-resolution episcopic microscopy data of the mouse PNP between modes 1 and 3 (SS11 to SS31). We refer to the PNP mode 1 data (SS11 to SS22) as late mode 1 to distinguish it from the early mode 1 folding in our mouse live-imaging data (SS8), as we observed relevant morphological differences between these time points (to be discussed in DLHPs Emerge through Zippering at Sites with Low Mesoderm Expansion). Mouse embryo images were obtained from refs. 7 and 8. We took transverse sections of the PNP at the caudal (NP is flat), intermediate (NP is elevated), and rostral (NP closes) sites (Fig. 4E). These rostrocaudal positions show folding progression roughly corresponding to the time points start, elevated, and closure from the mouse live-imaging data (Fig. 2C). While late mode 1 folding showed midline tapering in the elevated PNP (thickness ratio 1.4 ±0.1 [SD]), no midline tapering was present in the elevated PNP at mode 3 (thickness ratio 1.0 ±0.1 [SD]). No significant changes in midline tapering were found at the rostral and caudal PNP. Next, we ran model II simulations for varying midline thickness ratios and midline tapering widths. We measured the curvature in the MHP region at simulation halftime $t=0.5$. Higher thickness ratios promoted midline curvature (Fig. 4G). Interestingly, simulations without midline thinning showed a rounded NP midline that looked similar to the Shh mouse mutant, which lacks floor plate development (Movie S12) (11, 38). Furthermore, midline curvature decreased with increasing tapering widths. Together, these results indicate that high NP midline thickness ratios and low tapering widths can enhance mesoderm-driven MHP curvature.

DLHPs Emerge through Zippering at Sites with Low Mesoderm Expansion.

After studying MHP formation, we sought to identify the biomechanical driving force of DLHPs. DLHPs form in the PNP at SS19 to SS30 (11). As the PNP caudal NP is flat rather than concave, we adapted model II to start out in a horizontal configuration. To obtain a simple relationship between mesoderm area increase and NNE width increase, we approximated the growing embryo as a semiellipse, introducing the linear mesoderm area increase factor α. α = 1 corresponds to the area of a semiellipse with the lateral simulation boundary separation as the lateral diameter and $w_{\text{NP}}$ as the dorsoventral diameter. The mesoderm area was increased linearly over time, and the NNE width was increased linearly over space and time to match the area and corresponding circumference of the semicircle at the end of the simulation ($t=1$). Model II simulations with $\alpha =1$ showed NP elevation, but mesoderm area expansion was not sufficient to reach NT closure (Fig. 5 A, Top, and Movie S13). When increasing mesoderm area expansion ($\alpha =1.75$, NNE width increase unchanged), the folding NP was forced to close. However, closure was initiated at the midlateral sides, rather than at the NP borders, and the resulting mesoderm area was significantly larger compared to the mesoderm area in the PNP at NT closure (Fig. 5 A, Middle, and Movie S14). As PNP closure depends on zippering (43), zippering could function to ensure closure at sites with insufficient mesoderm area expansion. Zippering is a 3D process. In our model, we mimicked the effect on 2D cross-sections by applying an effective medial force to the NP boundaries within the simulated plane, fixing them on a linear trajectory along the x axis, such that they reach the embryo midline at t = 1. In 3D, the progressing zippering front will result in effective force vectors lying mostly, but not perfectly, parallel to the modeled planar section. The perpendicular, rostral, or caudal component of the zippering forces will distort or shear the tissue slightly in rostral–caudal direction, i.e., out of the modeled plane. Considering the significant stress relaxation capabilities of developing epithelia, these transverse effects are likely to have a negligible impact on NT folding and hinge point formation. Simulating zippering (α = 1) leads to tube formation with a slit-shaped lumen characteristic of mode 1 closure (Fig. 5A, Bottom, and Movie S15). Note that also model I folds and closes similarly when augmented by zippering, as we have verified in simulations. Nevertheless, zippering requires closure 1 to be established, which we achieve with realistic thickness profiles only with model II.

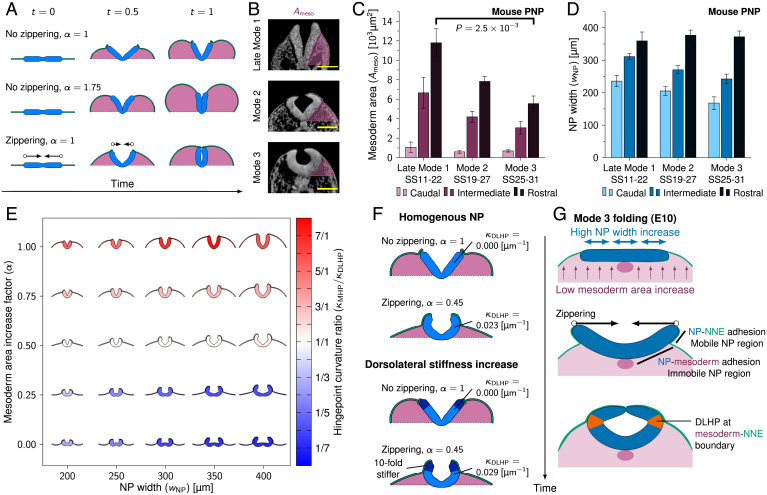
Fig. 5.

Zippering drives DLHP formation at sites with low mesoderm area increase. (A) Model II simulations with flat initial configurations rendered between t = 0 and t = 1. Arrows indicate zippering direction, and pink area indicates mesoderm area increase. (B) Transverse sections through the PNP at late mode 1, mode 2, and mode 3. Pink area indicates $A_{\text{meso}}$. Images were derived with permission from refs. 7 and 8 under a Creative Commons Attribution license. (Scale bars: 100 µm.) (C and D) Measured mesoderm area ($A_{\text{meso}}$; C) and NP width ($w_{\text{NP}}$; D) during NT folding progression at modes 1 to 3 in the developing mouse PNP. For late mode 1, N = 5; for mode 2, N = 12; and for mode 3, N = 7. Error bars indicate SEM. In C, Mann–Whitney u test is used, $P=2.5\times {10}^{-3}$. (E) NP folding simulations (model II + zippering) rendered at t = 0.7 with NP width ($w_{\text{NP}}$) versus mesoderm area increase factor (α). Color indicates the ratio of MHP curvature versus DLHP curvature. Red indicates that MHP dominates (mode 1), white indicates that both MHP and DLHPs (mode 2), and blue indicates that DLHPs dominate (mode 3). DLHP curvature was the highest curvature measured between the MHP and NP border regions at one of the NP lateral sides. (F) Model II simulations rendered at t = 0.7 with and without 10-fold dorsolateral NP stiffness increase (dark blue regions). (G) Proposed biomechanical mechanism of DLHP formation. The E10 PNP shows high NP width increase and low mesoderm area increase (Top), which causes the NP lateral sides to elevate above the mesoderm and form basal contact with the NNE (Middle). The lateral NP regions are therefore mobile and get pulled inward through zippering, resulting in DLHPs at the mesoderm–NNE boundary (Bottom).

To identify a potential biomechanical mechanism of DLHP formation, we analyzed high-resolution plastic sections and high-resolution episcopic microscopy data of the mouse PNP between late mode 1 and mode 3 (SS11 to SS31). The progression from late mode 1 (no DLHPs) to modes 2 and 3 (DLHPs) showed a strong reduction in mesoderm area lateral to the NP at the rostral PNP, with mode 3 showing over 45% reduction in mesoderm area compared to late mode 1 (Mann–Whitney u test, $P=2.5\times {10}^{-3}$) (Fig. 5 B and C). For NP width we found no significant differences between late mode 1 and modes 2 and 3, with and average width of 360 ±6 µm (SD) at the closure site in the rostral PNP (Fig. 5D). Note, however, that the late mode 1 NP width dynamics differ significantly from early mode 1 folding (somite position 1 to 8) as observed in our live-imaging data (Fig. 3A). While the NP decreased by 30% in width during early mode 1 folding to reach 251 ±42 µm (SD) at time of closure (Fig. 3A), late mode 1 folding showed a 53% increase in NP width from 236 ±38 to 360 ±6 µm (SD) between the caudal and rostral PNP, which can be considered a proxy for closure progression over time.

To test whether mesoderm expansion and NP width influence DLHP formation, we ran model II simulations with zippering for varying levels of mesoderm area expansion (α between 0 and 1) and varying NP widths ($w_{\text{NP}}$ between 200 and 400 µm). Strikingly, DLHPs emerged in simulations with decreased mesoderm expansion (Fig. 5E). Moreover, DLHPs became more visible at higher NP widths. We compared the MHP and DLHP curvature measured in the mouse PNP sections at modes 1 to 3 with the curvature in our simulations and found good agreement (SI Appendix, Fig. S1 A and B and Movies S16 and S17). Together, these results indicate that DLHPs could emerge in the late-stage PNP as a result of zippering in areas with low mesoderm expansion and high NP width.

Finally, we tested the hypothesis that DLHPs could form through a mechanical discontinuity in the folding NP, put forward when increased cell density was found in the NP region dorsal of the DLHP (18). We ran model II simulations with a Young’s modulus that linearly increased over time in the dorsolateral thirds of the NP lateral sides to 10-fold its medial value. For a model II simulation without zippering and with α = 1, this mechanical discontinuity did not induce notable morphological changes (Fig. 5 F, first and third rows). However, when applied to a setting where DLHPs do form (model II with zippering, $\alpha =0.45$), the mechanical discontinuity led to a 26% increase in dorsolateral curvature, and the point of maximum curvature occurred somewhat medial/ventral of the discontinuity (Fig. 5 F, second and fourth rows). Thus, while a NP mechanical discontinuity appears insufficient to induce DLHP formation or to substantially contribute to NT closure, a nonuniform stiffness potentially caused by increased NP dorsal cell density could enhance zippering-driven DLHP formation.

Discussion

We combined mathematical modeling and quantitative image analysis to explore the role of mechanical forces in mammalian spinal NT folding. While intrinsic NP curvature could in theory promote tube folding, we found that intrinsic curvature at the NP midline and NP borders is not sufficient for tube closure in a model adapted to measurements from our mouse live-imaging data (Fig. 3F). In contrast, a model based on notochord adhesion, mesoderm area expansion, and NNE width expansion was sufficient for MHP formation and NT closure (Fig. 4D).

Intrinsic versus Extrinsic Forces in MHP Formation.

The mammalian and avian MHP contains an increased proportion of wedge-shaped S-phase cells with basally located nuclei (15–18). These observations have led to the view that changes in cell cycle in the MHP region drive increased basal localization through interkinetic nuclear migration, which then drives cell wedging, which in turn causes NP-intrinsic bending. However, to the best of our knowledge, a direct causation between cell cycle changes and MHP curvature has not been demonstrated. In our computational model, the MHP forms as a result of mesoderm area increase, NNE width increase, and NP anchoring to the notochord (Fig. 4D), suggesting that the chain of causation may run in the other direction, i.e., that NP-external forces cause MHP curvature and cell wedging. This could in turn affect cell cycle progression and nuclear localization. Cells generally respond to compression forces from their environment by slowing down their cell cycle (reviewed in ref. 44). The cell cycle changes and basal nuclear localization observed in the MHP could thus be a result (rather than a cause) of MHP curvature. Future research should clarify this through experimentally manipulating the mesoderm in developing mouse embryos or in vitro NT folding model systems. We predict that mesoderm area increase during folding will lead to increased MHP curvature, combined with slower cell cycle progression and increased basal localization of neuroepithelial nuclei at the MHP.

Biomechanical Mechanism of DLHP Formation.

Our findings suggest that DLHPs emerge as a result of zippering in regions with low mesoderm expansion (Fig. 5). In these regions, the NP lateral-basal sides elevate above the mesoderm and adhere to the NNE. This could make the NP lateral sides more mobile than the medial NP, which is attached to the underlying mesoderm and notochord (45). Thus, while zippering pulls the NP lateral tips toward the dorsal midline, the medial NP remains attached to the underlying tissue. As a result, the NP bends at the mesoderm/NNE boundary (Fig. 5G). In this framework, DLHP formation is a passive reaction to zippering rather than a process which actively contributes to NT closure. If zippering drives DLHP formation, laser ablation at the point of zippering should reverse dorsolateral curvature, which indeed appears to have been shown in a previous study (9).

Molecular Mechanism of DLHP Formation.

Our mouse and human embryo data show that mesoderm area decreases between early and late-stage spinal NT folding, whereas NP width increases (Figs. 3 A and B, 4 A and B, and 5 B and C). This shift in the neural-to-mesodermal tissue balance drives the transition from late mode 1 (MHP) to mode 3 (DLHPs) folding in our computational model. During posterior body formation, the neural-to-mesodermal cell ratio is regulated by bipotent neuromesodermal progenitor cells which can differentiate into both paraxial (presomitic) mesoderm and neuroepithelial cells (46, 47). Termination of body axis elongation is characterized by neuromesodermal progenitor cell depletion and high neuromesodermal progenitor cell differentiation into neural tissue at the expense of paraxial mesoderm (48, 49). Neuromesodermal progenitor cell proliferation and differentiation depend on several molecular pathways, in particular, WNT, FGF, and retinoic acid signaling. Interestingly, these pathways have also been implicated in NT folding and hinge point formation. WNT and FGF signaling together drive neuromesodermal progenitor cell self-renewal as well as neuromesodermal progenitor cell differentiation toward paraxial mesoderm (50–52). Wnt3a^–∕– knockout mice show fewer mesoderm cells and more neural cells compared to wild-type embryos and appear to show early DLHPs at E9 and an early transition to mode 3 folding at E9.5 (52–54). A similar phenotype appears to be present in β-catenin conditional knockouts as well as Fgf4/Fgf8 conditional double knockout mice (55, 56). Retinoic acid counteracts WNT and FGF signaling by promoting neuromesodermal progenitor cell differentiation into neural cells (57). Raldh2^–∕– mouse embryos, which lack retinoic acid synthesis, show decreased neural cell identity and increased mesoderm tissue in the caudal lateral epiblast and appear to show a stronger MHP during early NT folding between E8 and E8.5 (58, 59). Inversely, embryos treated with retinoic acid during NT folding appear to have less mesoderm tissue and show sharper DLHPs (60).

A previous study found that BMP signaling blocks DLHP formation, with Bmp2^–∕– mutants showing premature appearance of DLHPs at SS9 (12). The mechanism through which BMP-2 exerts this effect remains unknown. Loss of BMP signaling causes ectopic neural induction and loss of mesodermal cell identity (61). Additionally, dual-SMAD inhibition promotes differentiation of human embryonic stem cells, induced pluripotent stem cells, and neuromesodermal progenitor cells into neural cells in vitro (62, 63). In line with our model, it would be interesting to study if BMP signaling blocks DLHP formation through shifting the neural-to-mesodermal cell ratio toward more mesoderm.

To conclude, our results suggest hinge point formation is not a driving force in spinal NT folding but can rather be viewed as a folding side effect. Transition from mode 1 to mode 3 folding is directly linked to a shift from mesodermal to neural tissue in our model. NT folding mutants with aberrant hinge points may therefore best be understood in the context of PNP neural/mesodermal tissue dimensions.

Materials and Methods

Computational Model.

The folding NT was modeled as an expanding transverse ectoderm cross-section in 2D. We minimized the 2D elastic energy density

$$U=\frac{1}{2}{\displaystyle {\int }_0^{w}E}h(s)\left(ϵ{(s)}^2+\frac{h{(s)}^2}{12}{(\kappa (s)-{\kappa }_0(s))}^2\right)ds$$

with the finite element method. Energy density refers to energy per unit length, where the length dimension is the rostrocaudal axis perpendicular to the simulated cross-section. The ectoderm thickness h(s) is a field that depends on the location given by the arclength parameter s as detailed in the equations in Midline thinning and NP borders below. Young’s modulus E sets the energy density scale, equally affecting all deformation modes. ϵ is the tensile Cauchy strain, κ is the curvature along the tissue centerline, and ${\kappa }_0={\kappa }_{\text{int}}+{\kappa }_{\text{p}}$ is the curvature contribution from intrinsic curvature and plastic stress relaxation. We employed third-order beam elements containing an additional energy term for transverse shear that depends on Poisson’s ratio ν. A detailed description can be found in ref. 39. A predictor–corrector method from the Newmark family was used to integrate Newton’s equations of motion in time, using a uniform homogeneous mass density ρ in the tissue. For numerical equilibration, we used a damping density $\gamma \rho$, where γ defined the viscous relaxation rate of the tissue.

Simulation parameters are listed in Table 1. The tissue was assumed to have homogeneous and uniform material properties both within and between NP and NNE. Simulations started from a horizontal configuration unless otherwise specified. A small random spatial perturbation was imposed on the ectoderm to allow for symmetry breaking through Euler buckling and to allow for independent simulation repetitions. Between 150 and 500 elements were used to discretize the ectoderm, with higher element densities applied at thin tissue regions and regions with a high width expansion. At the ectoderm end points, displacement was fixed but rotations were unconstrained (pinned boundary conditions) to reduce the number of free or unknown model parameters and to maintain controlled contact with the embryo that is not explicitly represented in the model. Apart from its outer end points, the NNE is free to move in both dorsal-ventral and lateral directions in our simulations. Its movement is governed by the mesoderm area constraint $A_{\text{meso}}(t)$ and the width expansion $w_{\text{NNE}}(t)$ (detailed in PNP simulations). Simulations were rendered using ParaView 5.5.0.

Table 1.

Model parameters

Symbol	Value	Dimension	Description
E	1 kPa	Mass/length × time2	Young’s modulus of the tissue
ν	0.5	—	Poisson’s ratio of the tissue
ρ	1 g/cm3	Mass/length3	Mass density of the tissue
K	10E	Mass/length × time2	Bulk modulus of the mesoderm
H	$0.05E$	Mass/length × time2	Kinematic hardening modulus of the tissue
${\sigma }_{\text{Y}}$	$0.005E$	Mass/length × time2	Yield stress of the tissue
γ	1,000 s–1	1/time	Viscous relaxation rate of the tissue
$l_{\text{a}}$	3 µm	Length	Spatial range of adhesion (model II)
k	3 mN/m	Mass/time2	Spring constant of adhesion (model II)
t	Variable	Time	Simulated time (value between 0 and 1 s)
$h_{\text{NP}}$	45 µm	Length	NP height (apicobasal)
$h_{\text{NNE}}$	8 µm	Length	NNE height (apicobasal)
$h_{\text{HP}}$	Variable	Length	NP (median) hinge point height (apicobasal)
$w_{\text{NP}}$	Variable	Length	NP width
$w_{\text{NNE}}$	Variable	Length	NNE width
$w_{\text{HP}}$	Variable	Length	Hinge point width
${\kappa }_{\text{int}}$	Variable	1/length	Intrinsic curvature of the ectoderm
${\kappa }_{\text{mid}}$	Variable	1/length	Intrinsic curvature of the ectoderm at the middle of the hinge point domain
${\kappa }_{\text{max}}$	2/$h_{\text{NP}}$	1/length	Theoretical maximum curvature of the ectoderm
d	Variable	Length	Distance between the middle of the hinge point domain and the NP midline
α	Variable	—	Mesoderm area increase factor

Tissue growth.

Volumetric growth of the tissue was modeled by expanding the reference length of each finite element over time according to a growth multiplier g. For model I, $g(t)=1+t$. See ref. 64 for implementation details.

Stress relaxation.

To model stress relaxation, we used a bilinear elastoplastic stress–strain relationship for the bending moment in all simulations, with linear kinematic hardening and a rate-independent associative flow rule, as developed in ref. 64. The resulting bending moment density reads

$$M=\frac{E{h}^3}{12}\{\begin{array}{ll}{\kappa }_{\text{e}}\hfill & \text{if}\hspace{1em}\mid {\kappa }_{\text{e}}\mid \le {\kappa }_{\text{Y}}\hfill \\ \text{sign}({\kappa }_{\text{e}}){\kappa }_{\text{Y}}+\frac{H}{E+H}({\kappa }_{\text{e}}-{\kappa }_{\text{Y}})\hfill & \text{if}\hspace{1em}\mid {\kappa }_{\text{e}}\mid >{\kappa }_{\text{Y}}\hfill \end{array},$$

where ${\kappa }_{\text{e}}=\kappa -{\kappa }_0$ denotes the elastic curvature and ${\kappa }_{\text{Y}}=3{\sigma }_{\text{Y}}/Eh$ is the effective curvature at the yield point, defined by the yield stress ${\sigma }_{\text{Y}}$. In order to let almost all bending stress dissipate, both the yield stress ${\sigma }_{\text{Y}}$ and the kinematic hardening modulus H were kept small (Table 1).

Midline thinning.

The height transition from the lateral NP to the NP midline was modeled using a smooth function:

$$h(x)=\frac{h_{\text{NP}}}{2}\left(\frac{h_{\text{HP}}}{h_{\text{NP}}}+\left(1-\frac{h_{\text{HP}}}{h_{\text{NP}}}\right){\sin }^2\left[\frac{\pi }{2}\min \left\{\mid \frac{x}{w_{\text{HP}}}\mid ,1\right\}\right]\right)\text{},$$

where $h_{\text{NP}}$ is the lateral NP height, $h_{\text{HP}}$ is the (median) hinge point height, and $w_{\text{HP}}$ is the hinge point domain width.

Intrinsic curvature.

Intrinsically curved domains were modeled using a smooth function with the highest intrinsic curvature in the domain center:

$${\kappa }_{\text{int}}(x)={\kappa }_{\text{mid}}{\cos }^2\left[\frac{\pi }{2}\min \left\{\mid \frac{x-d}{w_{\text{HP}}}\mid ,1\right\}\right]$$

with ${\kappa }_{\text{mid}}$ the intrinsic curvature at the HP domain center. d denotes the distance from the HP domain center to the NP midline.

Adhesion and contact.

In model II, adhesion between adjacent NP and NNE was modeled with a bilinear traction–separation law. Given a separation l between the two tissue surfaces, an adhesive force

$$f=k\{\begin{array}{ll}l\hfill & \text{if}\hspace{1em}0<l<l_{\text{a}}/2\hfill \\ l_{\text{a}}-l\hfill & \text{if}\hspace{1em}{l}_{\text{a}}/2<l<l_{\text{a}}\hfill \end{array}$$

was applied, where k is the adhesive spring constant. In the case of volumetric overlap (l < 0), a linear repulsive Hertzian contact force was applied.

NP borders.

For all simulations including both NP and NNE, NP border zones were modeled for the domain $w_{\text{NP}}/2-w_{\text{NPB}}<\left|x\right|<w_{\text{NP}}/2$ using a smooth tissue height transition:

$$h(x)=\frac{h_{\text{NNE}}}{2}+\frac{h_{\text{NP}}-h_{\text{NNE}}}{2}{\cos }^2\left[\frac{\pi }{2}\left(\frac{\left|x\right|}{w_{\text{NPB}}}-\frac{w_{\text{NP}}}{2w_{\text{NPB}}}-1\right)\right]$$

with NP border zone width $w_{\text{NPB}}=25$ µm.

Model I.

In model I, an integral constraint preserved the area underneath the ectoderm during ectoderm width expansion, using a bulk modulus K as Lagrange multiplier. Model I simulations used an NP height $h_{\text{NP}}=45$ µm and an initial epithelium width $w_{\text{NP}}=500$ µm. For simulations including NNE, the NP width was set to $w_{\text{NP}}=250$ µm. NNE width was set to $w_{\text{NP}}=125$ µm on both sides, and the NNE height was fixed at $h_{\text{NNE}}=8$ µm.

Model II.

In model II, the target value in the area constraint increased linearly with time to simulate mesoderm expansion. The mesoderm expansion to the left and the right of the tissue midline was constrained independently. The ectoderm midline was fixed at its initial coordinates to mimic NP–notochord adhesion. The NP height was set to $h_{\text{NP}}=45$ µm and the NNE height to $h_{\text{NNE}}=8$ µm. NP and NNE adhered to each other when reaching a proximity of $l_{\text{a}}=3$ µm. To promote NP–NNE adhesion, intrinsic curvature was incorporated at the NP borders (${\kappa }_{\text{mid}}=-{\kappa }_{\text{max}},\hspace{0.17em}w=3h_{\text{NNE}}$).

Closure 1 simulations.

Closure 1 (Fig. 4) was simulated using model II. The simulation started in a concave configuration defined by $y=\frac{3}{2}(w_{\text{NP}}+h_{\text{NNE}}){(x/\text{μm})}^2$. The closure 1 simulation included midline tapering with $h_{\text{NP}}/h_{\text{HP}}=2$ and $w_{\text{HP}}=2h_{\text{NP}}$ and had an initial epithelium width $w_{\text{NP}}=250$ µm. The mesoderm area increased linearly over time from $A_{\text{meso}}(t=0)=0$ µm² to $A_{\text{meso}}(t=1)=1.7\times {10}^4$ µm². The NNE started at width $w_{\text{NNE}}(t=0)=20$ µm on both sides and linearly increased over time to $w_{\text{NNE}}(t=1)=100$ µm. For the closure 1 simulation with NP convergent extension (Movie S11), NP width was decreased linearly over time from $w_{\text{NP}}(t=0)=360$ µm to $w_{\text{NP}}(t=1)=250$ µm. Mesoderm area was increased to $A_{\text{meso}}(t=1)=3\times {10}^4$ µm², and NNE width was increased to $w_{\text{NNE}}(t=1)=150$ µm.

PNP simulations.

NTF in the PNP was simulated using model II, starting out from a horizontal configuration with 100 µm NNE on both sides of the NP. PNP simulations included midline tapering with $h_{\text{NP}}/h_{\text{HP}}=1.5$ and $w_{\text{HP}}=2h_{\text{NP}}$. For the simulations in Fig. 5A, the NP width was set to $w_{\text{NP}}=350$ µm. Zippering was included by letting the NP borders converge linearly toward the midline along the x axis (while keeping NP border movement along the y axis unconstrained), reaching x = 0 at t = 1. Mesoderm area increased linearly over time, proportional to a half-ellipse:

$$A_{\text{meso}}(t)=\alpha \frac{\pi r_1{r}_2}{2}t$$

with $r_1=w_{\text{NP}}/2+w_{\text{NNE}}(0)-h_{\text{NP}}/2,\hspace{0.17em}{r}_2=w_{\text{NP}}/2$, and α the mesoderm area expansion factor. NNE width was increased linearly over time and uniformly in space on each side of the PNP to match the corresponding circumference of the half-ellipse:

$$w_{\text{NNE}}(t)=(1-t)w_{\text{NNE}}(0)+t\frac{\pi \sqrt{r_1^2+r_2^2}}{2\sqrt{2}}.$$

Note that $w_{\text{NNE}}(t)$ increases with $w_{\text{NP}}$ but is independent of α.

Microscopy Data Analysis.

Image measurements were performed in ImageJ 1.52r-1. Measurements methods are illustrated in SI Appendix, Fig. S2. NP apicobasal height was measured at the NP lateral side midpoint. NNE apicobasal height was measured between 5 and 30 µm of the NP–NNE domain border. NNE width was measured at one of the embryo lateral sides as the NNE length from the NP–NNE domain border to the border between NNE and extraembryonic tissue (mouse live-imaging data), as the NNE length dorsal of the somite (human data), or as the NNE length along the embryo area dorsolateral to the notochord (mouse PNP data). Mesoderm area was measured either as the total area of the mesoderm and its derivatives at one of the embryo lateral sides (mouse live-imaging data), between the NP and somite lateral border (human data), or by measuring the area dorsolateral to the notochord at one of the embryo lateral sides (in the mouse PNP and human data). MHP and DLHP curvature was measured in the mouse PNP data by drawing a circle through the hinge point at midapicobasal height and taking its radius (with ${\kappa }_{\text{HP}}=1/r$).

Mouse live images.

For the mouse live imaging, all animal studies were reviewed and approved by HHMI Janelia Research Campus’s IACUC which is fully accredited by AAALAC. CAG-tdTomato-2A-H2B-EGFP (CAGTAG1) mice expressing ubiquitous membrane and nuclear markers were obtained by the authors from ref. 65. Lifeact-mRFPruby mice [which visualize F-actin (66)] were obtained by the authors from ref. 67. All mice were maintained on a mixed, CD-1/129Sv/C57BL/6J background. Developing E6.5 to E8.5 mouse embryos were imaged using a light sheet microscope for adaptive imaging of mouse embryo development. Embryos were prepared, cultured, and imaged as described in ref. 37.

Mouse PNP section data.

Mouse embryo images analyzed in this study were obtained from the eMouse Atlas Project (EMAP) (8) and Deciphering the Mechanisms of Developmental Disorders (DMDD) (7). DMDD is a program funded by the Wellcome Trust with support from the Francis Crick Institute. The original data and image specifications can be found on the EMAP and DMDD websites, and usage of both data sources is licensed under a Creative Commons Attribution license. From these online databases, all wild-type embryos in the stage of PNP folding were included (data accessed 17 November 2020). An overview of mouse embryos used is given in SI Appendix, Table S2. In total, 5 mode 1 embryos (SS11 to SS22), 13 mode 2 embryos (SS19 to SS27), and 7 mode 3 embryos (SS25 to SS31) were analyzed. High-resolution episcopic microscopy data (DMDD) and high-resolution plastic section data (EMAP) were processed in Imaris 9.5.1 using an oblique slicer to obtain images perpendicular to the PNP. Resulting images were further analyzed in ImageJ 1.52r-1.

Human embryo section data.

Human embryos included in this study are historical specimens from the Carnegie collection (Silver Spring, MD) and the Boyd collection (University of Cambridge, United Kingdom). Transverse section images of historical embryo specimens were obtained from the Virtual Human Embryo Project (35) and the 3D Atlas of Human Embryology (36), both under a Creative Commons Attribution license, with permission by B. S. de Bakker for the 3D Atlas data. Specimens 3709 (SS4), 6330 (SS7), and 6344 (SS13) originated from the Carnegie collection. Specimen H712 (SS6) originated from the Boyd collection. An overview of specimen origins and section specifications is published in ref. 68.

Data Availability

All information needed to replicate the computational model is described in a technical publication (39) and in ref. 64. Please contact the corresponding author for further advice on more direct replication. The mouse live-imaging datasets used for this study are publicly available at the Image Data Resource repository (https://idr.openmicroscopy.org/webclient/?show=image-4007801) under project ID 502, dataset ID 3351 [previously published dataset (37, 69)]. The raw data is publicly available as openBIS repository at https://u.ethz.ch/Kduyc under the name NT_folding_data.

Data were used from DMDD (https://dmdd.org.uk), licensed under a Creative Commons Attribution license; EMAP (http://www.emouseatlas.org/emap/home.html), licensed under a Creative Commons Attribution license; the 3D Atlas of Human Embryology (https://www.3dembryoatlas.com/), licensed under a Creative Commons Attribution license, with additional permission from B. S. de Bakker; and the Virtual Human Embryo Project (https://virtualhumanembryo.lsuhsc.edu/), licensed under a Creative Commons Attribution license.

Change History

May 16, 2022: Due to a production error, Movies S11 and S12 appeared incorrectly; these movies have been updated.