Abstract
The nucleocapsid protein of the SARS-CoV-2 virus comprises two RNA-binding domains and three regions that are intrinsically disordered. While the structures of the RNA-binding domains have been solved using protein crystallography and NMR, current knowledge of the conformations of the full-length nucleocapsid protein is rather limited. To fill in this knowledge gap, we combined coarse-grained molecular simulations with data from small-angle X-ray scattering (SAXS) experiments using the ensemble refinement of SAXS (EROS) method. Our results show that the dimer of the full-length nucleocapsid protein exhibits large conformational fluctuations with its radius of gyration ranging from about 4 to 8 nm. The RNA-binding domains do not make direct contacts. The disordered region that links these two domains comprises a hydrophobic α-helix which makes frequent and nonspecific contacts with the RNA-binding domains. Each of the intrinsically disordered regions adopts conformations that are locally compact, yet on average, much more extended than Gaussian chains of equivalent lengths. We offer a detailed picture of the conformational ensemble of the nucleocapsid protein dimer under near-physiological conditions, which will be important for understanding the nucleocapsid assembly process.
Keywords: SAXS, Nucleocapsid, SARS-CoV-2, EROS
Graphical abstract
1. Introduction
Recent advances in cryo-EM microscopy have allowed us to structurally characterize very large proteins and their complexes [1,2], and structure prediction by AlphaFold has reached previously unseen accuracy [3]. Together with classical macromolecular crystallography and protein NMR, these advances could create an impression that most – if not all – protein structures can be rather easily solved or accurately predicted. Yet one class of proteins is outstanding in this respect, the intrinsically disordered proteins (IDPs) – especially proteins where well-folded domains are connected by long, flexible, intrinsically disordered polypeptide segments. Such proteins are usually too big for NMR analysis and too flexible for crystallographic or cryo-EM analysis [4].
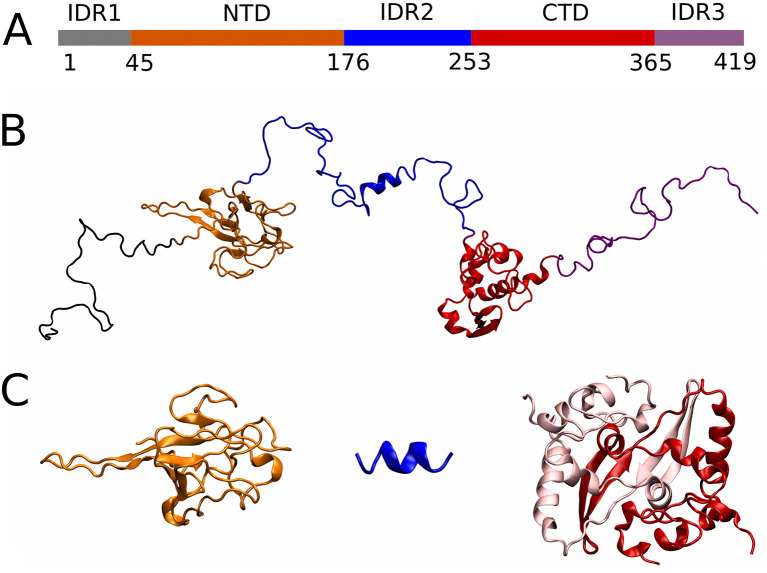
SARS-CoV-2 encodes for more than 20 proteins including 16 non-structural proteins (nsp1–16), spike glycoprotein (S), nucleocapsid protein (N), membrane protein (M), envelope protein (E) and several accessory proteins [5]. Most of these are well folded and were structurally characterized using cryo-EM or macromolecular crystallography. However, the N protein is composed of two globular domains and three intrinsically disordered regions (IDR1–3, Fig. 1 ). The structured domains are named NTD (N-terminal domain) and CTD (C-terminal domain). The NTD has a right hand-like fold composed of a β-sheet core with a large protruding central loop that resembles a finger (Fig. 1) [6]. Importantly, it binds both single-stranded and double-stranded RNA [7]. The CTD also binds RNA with a preference for viral genomic intergenic transcriptional regulatory sequences [8]. It is composed of eight helices and two β-strands and its shape reminds of the letter C (Fig. 1) [8,9]. Two C-shaped monomers form a dimer which is responsible for the dimerization of the N protein [[8], [9], [10], [11]]. As outlined above, SARS-CoV-2 nucleocapsid NTD and CTD are well structurally characterized. However, the current knowledge about conformations of the full-length N protein is more limited. Importantly, small angle X-ray scattering (SAXS) experiments have shown that the full-length N protein in solution is a dimer with a radius of gyration of 5.9 nm [12].
Fig. 1.
Domain architecture of the N protein. A) Schematic representation of the N protein domain architecture. The boundaries of the globular domains and the IDRs are indicated. B) A random conformation of a monomeric N protein, which is composed of two folded domains (NTD shown in orange and CTD shown in red) and three intrinsically disordered regions (IDR1 in gray, IDR2 in blue, and IDR3 in purple). C) Structural constrains used in our simulations; from left: the NTD (PDB entry 6YI3), a short α-helix within the IDR2 (PDB entry 7PKU), and a dimer of the CTDs (PDB entry 7DE1). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
SAXS is a powerful method to characterize macromolecules in solution [13,14]. Despite the loss of structural information due to orientational averaging of the scattering signal, SAXS provides useful information about the shapes and dimensions of macromolecules in solution. In particular, standard analysis of SAXS data permits the determination of low-resolution structures of proteins in the form of molecular envelopes, where protein shapes are represented by a set of dummy atoms [15]. However, this approach is only valid for proteins with a stable ternary structure that can be represented as a rigid body, which the N protein is certainly not. SAXS analysis of IDPs requires different approaches that are based on generating an ensemble of protein conformations [[16], [17], [18], [19], [20], [21], [22]]. Useful and appropriate tools for generating conformational ensembles of biomolecules are molecular dynamics (MD) simulations. However, despite steady developments in this field [[23], [24], [25]], all-atom MD simulations of multi-domain and partially disordered proteins are still challenging – not only because of the large sizes of such proteins but also because of the long time scales on which large conformational fluctuations occur. Coarse-grained molecular simulations, on the other hand, provide means to efficiently sample conformational ensembles of large, multi-domain and dynamic proteins and their complexes [4,20,26]. However, the predictive power of coarse-grained simulations certainly lags behind that of all-atom MD simulations. One way to overcome these challenges is to use experimental data to guide or bias coarse-grained simulations.
Recently, original data are more and more reused within the scientific community and many studies are published as open-access articles. Usually the data are deposited in open-access databases such as PDB (Protein Data Bank) or EMDB (Electron Microscopy Data Bank). SASBDB (Small Angle Scattering Biological Data Bank) and PED (Protein Ensemble Database) [27,28] are also available but not yet broadly established and their use is not mandatory (unlike PDB) by most journals. Nevertheless, professors Tengchuan Jin and Hongliang He kindly provided us with the SAXS data they recently acquired on the SARS-CoV-2 N protein [12]. Here, we combined coarse-grained simulations of the N protein dimer with the data from SAXS experiments using the ensemble refinement of SAXS (EROS) method [18]. Our results provide a detailed picture of the conformational ensemble of the SARS-CoV-2 N protein dimer.
2. Materials and methods
2.1. Coarse-grained simulations
We used the coarse-grained model for multi-domain IDPs introduced by Kim and Hummer [29]. Replica exchange Monte Carlo (REMC) simulations of the coarse-grained model were performed with replicas at 24 different temperatures T i below and above the room temperature T = 300 K. Specifically, we used T/T i = 0.45, 0.49, 0.52, 0.55, …, 1.09, 1.12, 1.15. Following the simulation methods of Kim and Hummer [29], the basic MC steps were rotations and translations of each of the rigid domains. For the flexible linkers and termini, in addition to local MC moves on each of the residue beads, crank-shaft moves were employed to enhance sampling. The REMC simulation consisted of 1.1 × 108 MC cycles, where the initial 107 MC cycles were used for equilibration and the subsequent 108 MC cycles for data collection. The protein conformations were saved every 5000 MC cycles at room temperature, T i = T, which resulted in an ensemble of N = 20,000 conformations for further analysis. Selected conformations were visualized using VMD [30].
2.2. Ensemble refinement of SAXS
We computed scattering intensity profiles of the recorded conformations using an algorithm co-developed with the EROS method [18] taking the default value of the electron density of the protein hydration shell (0.03 e/Å3). Then the ensemble-averaged scattering intensity profile was computed as
where the index k = 1, …, N labels the conformations in the ensemble, w k is the statistical weight assigned to conformation k, I k(q) denotes the scattering intensity profile of the k-th conformation, and q denotes the momentum transfer. (We use the notation q = 4πsin(θ/2)/λ, where θ is the scattering angle and λ is the X-ray wavelength). The discrepancy between the experimental SAXS data, I exp(q), and the ensemble-averaged scattering intensity profile, I sim(q), was quantified by
where i = 1, …, N q labels points in the SAXS dataset, q i are the values of momentum transfer in the SAXS dataset, and σ(q i) is the statistical error of intensity Iexp(q i). The scale factor a and the offset b result from the conditions ∂χ2/∂a = 0 and ∂χ2/∂b = 0. The offset parameter b accounts for uncertainties in the buffer subtraction procedures.
At first, all conformations in the simulation ensemble were taken to be equally relevant, which implied w k = w k (0) = 1/N for k = 1, …, N and resulted in χ2 = 1.9 (Fig. 2A). The agreement between the simulation ensemble and the experimental SAXS data was thus good but still could be improved. We therefore refined the conformational ensemble using the EROS method [18], which prevents over-fitting and keeps the refined ensemble (with weights w k) as close as possible to the reference ensemble (with weights w k (0) = 1/N). Following the original EROS method, we introduced a function F = χ2 - θS, where θ is a parameter that expresses the confidence in the reference ensemble whereas
is the relative entropy, which equals to the negative Kullback-Leiber divergence. We minimized F with respect to the set of weights w k using a steepest descent method within the log-weights formulation [31,32]. Fig. S1 shows χ2 as a function of S at F = F min for different values of θ. For large values of θ, when the relative entropy term dominates over χ2, minimizing F leads to small perturbations in the statistical weights and, thus, w k ≈ w k (0) for the majority of conformations k. Decreasing the value of θ, the value of χ2 decreases and approaches the least-χ2 fit value, under the constraints of positive and normalized weights w k. Minimization of F at θ = 0 produces the best possible agreement with experiment but also largest changes in the statistical weights, possibly as a result of over-fitting. In the L-shaped curve shown in Fig. S1 we chose a point in the elbow region, as indicated by the gray horizontal line, where the refined ensemble agrees very well with the experimental data (χ2 = 1, Fig. 2B) without undue over-fitting. The optimal weights at this value of θ are shown in Fig. S2.
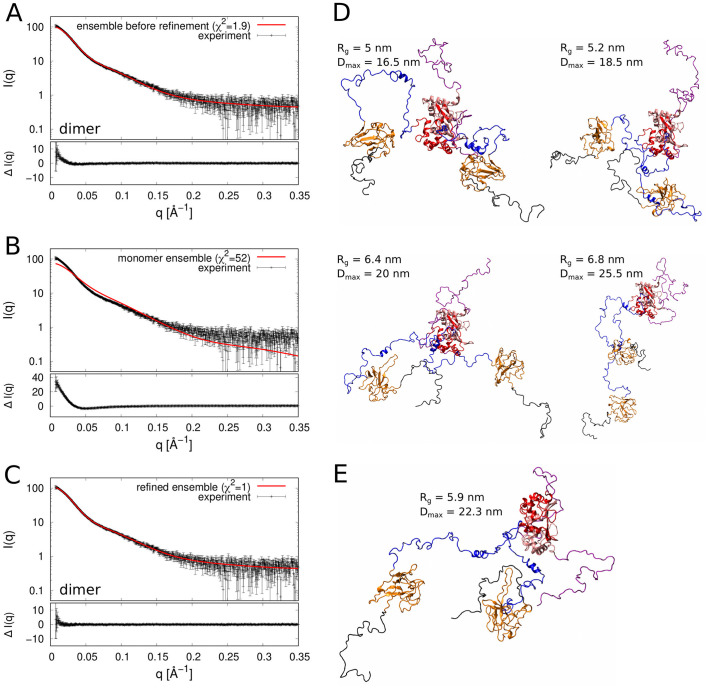
Fig. 2.
SAXS of the N protein. A) Comparison of the experimental SAXS data taken from [12] (black points with error bars) with the scattering intensity profile computed from the ensemble of the simulation structures of the N protein dimer (red line). B) Comparison of the experimental SAXS data with the scattering intensity profile computed from the ensemble of the simulation structures of the N protein monomer. C) Comparison of the experimental SAXS data with the scattering intensity profile of the refined ensemble of the dimer structures. D) Cartoon representation of four structures which jointly fit the experimental SAXS data with χ2 = 1. Their Rg and Dmax values are indicated. E) Cartoon representation of a dimer structure that best fits the experimental SAXS data (χ2 = 1.12). The colour code is as in Fig. 1. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
2.3. Contacts between residues
Each residue bead was assigned a van der Waals radius as introduced by Kim and Hummer [29]. We assumed that a pair of beads, i and j, with van der Waals radii σi and σj, respectively, were in contact if their distance r ij was smaller than 1.5 × σ ij, where σ ij = (σi + σj)/2 [33]. According to this criterion, we calculated a map of residue contacts for each conformation obtained in the REMC simulations. The relative weight of a given contact was then taken as a sum of statistical weights w k of the conformations in which this contact was present.
3. Results
To efficiently sample conformations of the nucleocapsid protein in solution, we used an implicit-solvent, coarse-grained model introduced by Kim and Hummer [29]. This model is equipped with a transferable energy function and devised to simulate conformational ensembles of large, dynamic, multi-domain proteins. It has been successfully applied to systems ranging from membrane-protein trafficking machineries [34,35] to lipid kinases in dynamic complexes with regulatory proteins [36,37] to hijacking of host protein by viruses [38,39] and to protein complexes controlling the biogenesis of autophagosomes [40]. In the framework of this model, amino acid residues are represented as spherical beads centered at the α‐carbon atoms. The interactions between the residue beads are described by amino-acid dependent pair potentials and Debye-Hückel-type electrostatics. Folded protein domains are treated as rigid bodies whereas inter-domain linkers and flexible termini (IDR1–3, Fig. 1) are represented as polymers of amino acid beads with bending, stretching and torsion potentials. Here, the rigid domains were the NTD (PDB entry 6YI3) [7], the dimer of the CTD (PDB entry 7DE1) [8] and the hydrophobic α-helix within the polypeptide segment joining the NTD and CTD (PDB entry 7PKU) [41] (Fig. 1).
We performed extensive replica exchange Monte Carlo simulations of the coarse-grained model (see Materials and methods). From the simulations we obtained an ensemble of N = 20,000 structures of the N protein dimer at room temperature (T = 300 K). We computed the scattering intensity profile for each of the simulation structures using an algorithm co-developed with the EROS method [18]. The ensemble-averaged scattering intensity profile was found to be in good agreement (χ2 = 1.9) with the SAXS data published by Zeng et al. [12] (Fig. 2A). We also performed analogous simulations of the monomeric form of the N protein (Fig. 1B), and computed the scattering intensity profile corresponding to the ensemble of the simulation structures of the N protein monomer (Fig. 2B). This scattering intensity profile is distinctly inconsistent with the experimental SAXS data (χ2 = 52), which confirms that monomers of the N protein are very unlikely to exist in solution at the concentrations used in the SAXS experiments. (To our knowledge, the N protein has never been reported to be in the monomeric form). This result illustrates how SAXS and computer simulations can be used together to determine the multimeric state of a macromolecule.
Next, we refined the conformational ensemble of the N protein dimer using the EROS approach, which employs the maximum-entropy method to minimally modify the statistical weights of the simulation structures in an attempt to match the conformational ensemble to the experimental SAXS data (see Materials and methods). The refined ensemble was very close to the original ensemble and in perfect agreement with the SAXS data (χ2 = 1, Fig. 2C). We also employed the minimum ensemble method [34] and picked out four structures of the N protein dimer that jointly fit the SAXS data perfectly well (χ2 = 1, Fig. 2D). This set of structures gives us a glimpse into conformational fluctuations of the N protein dimer. We also identified a single structure that best fits the SAXS data (χ2 = 1.12). We note that this structure (Fig. 2E) involves very few inter-domain contacts, thus it cannot be stable in solution: it represents only a single “snapshot” of the flexible N dimer.
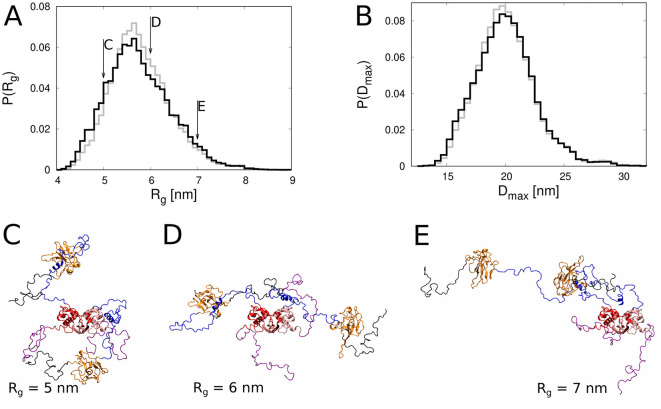
To quantify the degree of conformational fluctuations of the N protein dimer, we computed the radius of gyration (R g) and the maximum dimension (D max) of each of the simulation structures. The maximum dimension is defined as the maximum distance between any two points of the protein. The resulting histograms of R g and D max together with three representative structures are shown in Fig. 3 . We note that in the simulation ensemble (i.e. before refinement), structures with an R g between 5.3 and 6.3 nm and a D max between about 18 and 20 nm are slightly over-represented, whereas more compact structures with an R g smaller than 5 nm and a D max smaller than 18 nm are slightly under-represented. Taken together, the histograms in Fig. 3 show that the N protein dimer exhibits large conformational fluctuations with an R g ranging from about 4 to over 8 nm and a D max between 12 and 32 nm.
Fig. 3.
Analysis of the radius of gyration (Rg) and maximum dimension (Dmax) of the N protein dimer. Histograms of A) Rg and B) Dmax. The lines in gray and black correspond to the ensemble of simulation structures before and after refinement, respectively. C-E) Snapshots of selected conformations with C) Rg = 5 nm D) Rg = 6 nm and E) Rg = 7 nm, as indicated by the arrows in panel A. The colour code is as in Fig. 1.
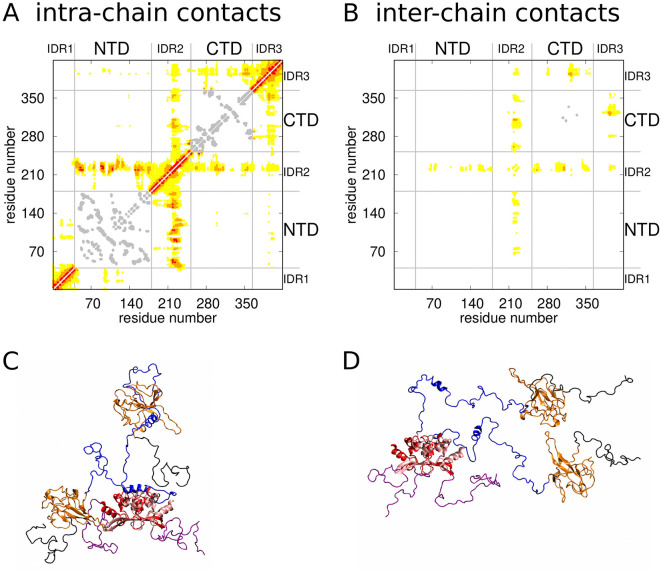
To characterize the structural ensemble of the dimer, we identified contacts between pairs of amino acid residues and the relative frequency of their occurrence. To this end, we determined contacts between pairs of amino-acid beads in each of the simulation structures using a distance criterion [33]. The relative frequency f of a given contact in the refined ensemble was then taken as a sum of statistical weights of the conformations in which this contact was present (see Materials and methods). The maps of the relative frequency of the intra- and inter-chain contacts are shown in Fig. 4A and B, respectively. The intra-chain contacts are the contacts formed within each of the polypeptide chains of the dimer. The inter-chain contacts, on the other hand, are those between the two polypeptide chains of the dimer. The points in red indicate frequent contacts with f > 0.1. The points in orange correspond to transient contacts with 0.01 < f < 0.1. The points in yellow indicate rare contacts with 0.001 < f < 0.01. Finally, the points in gray show contacts within rigid domains that do not evolve in the course of the REMC simulations.
Fig. 4.
Analysis of intra- and inter-chain contacts. A, B) Maps of intra- and inter-chain contacts. The points in red, orange and yellow represent frequent, transient and rare contacts, respectively. The points in gray indicate contacts within the folded domains (NTD and CTD) which do not change in the course of the simulations. C) Cartoon representation of a simulation structure with the largest number of contacts. The hydrophobic α-helices (blue) are bound to the NTD (orange) and CTD (red). The IDRs adopt compact conformations. D) Snapshot of a simulation structure with the smallest number of contacts. The hydrophobic α-helices are unbound and the IDRs are rather extended. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
The contact map in Fig. 4A shows that the frequent contacts can be grouped in two categories: i) contacts formed within each of the three IDRs and ii) contacts formed by either the NTD or the CTD with the hydrophobic α-helix in the IDR2. The contact map in Fig. 4B shows that there are rather few contacts between the two chains and that these contacts are mostly rare or transient.
To characterize the level of extension or compactness of the IDRs, we determined their end-to-end distances in each of the simulation structures. Fig. 5 shows the resulting histograms of the end-to-end distances. The end-to-end distances of IDR1, IDR2 and IDR3 are found to vary from 1 to 9 nm, from 1 to 13 nm, and from 0.5 to 11.5 nm, respectively. The average and root-mean-square values of the end-to-end distances are summarized in Table 1 .
Fig. 5.
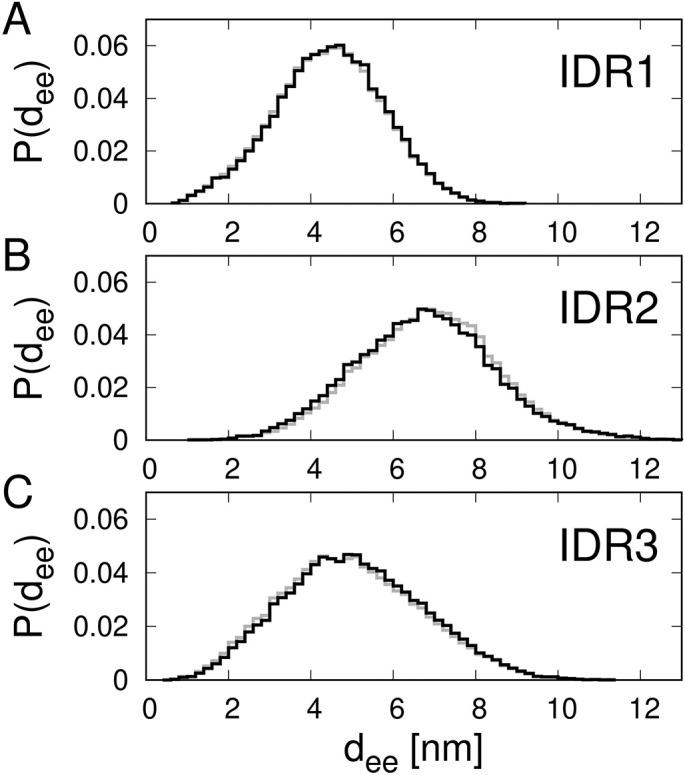
Histograms of the end-to-end distance of IDR1,2,3 (A,B,C). The lines in gray and black correspond to the ensemble of simulation structures before and after refinement, respectively.
Table 1.
Statistical properties of the end-to-end distances of the IDRs.
| IDR | Average end-to-end distance [nm] | Root-mean-square end-to-end distance [nm] | Number of amino acid residues (n) | Root-mean-square end-to-end distance of a Gaussian chain of n monomers [nm] | Ratio of the root-mean-square end-to-end distances in columns 3 and 5 |
|---|---|---|---|---|---|
| 1 | 4.32 ± 0.08 | 4.52 ± 0.07 | 40 | 2.40 | 1.88 |
| 2 | 6.77 ± 0.29 | 6.95 ± 0.25 | 71 | 3.20 | 2.17 |
| 3 | 4.87 ± 0.16 | 5.15 ± 0.15 | 55 | 2.82 | 1.83 |
It is interesting to compare the root-mean-square end-to-end distances of the IDRs with those of freely-jointed chains, which are also often called ideal chains or Gaussian chains. The root-mean-square end-to-end distance of a Gaussian chain of n beads is equal to the square root of n times the length of the bond between consecutive beads in the chain. As in the coarse-grained model for multi-domain IDPs introduced by Kim and Hummer, here we take the chain beads to be centered at the α‐carbon atoms and the length of the pseudo-bond between consecutive α‐carbon atoms to be 0.38 nm. The results presented in Table 1 show clearly that each of the three IDRs exhibits a root-mean-square end-to-end distance larger than the Gaussian chains of the corresponding length. This observation implies that although the conformations of the IDRs are locally compact (see the contact map in Fig. 4A), they are clearly more extended than those of the Gaussian chains overall. Interestingly, the N- and C-terminal tails (IDR1 and IDR3) behave somewhat more like Gaussian chains compared to the middle linker (IDR2).
4. Discussion
The thermodynamic state of an IDP is an ensemble of rapidly interconverting conformations. Important examples of IDPs are large, multi-domain proteins in which several autonomously folded domains are held together by intrinsically disordered regions [42]. Their structural analysis is difficult because of their large sizes and dynamic nature [4]. A notable example is the nucleocapsid protein of SARS-CoV-2 (Fig. 1). The question we posed in this study was about the degree of conformational fluctuations of this flexible protein complex.
We performed extensive REMC simulations of the N protein dimer and refined the resulting ensemble of conformations using the available SAXS data (Fig. 2). Our results show that the N protein dimer exhibits large conformational fluctuations in solution. Its radius of gyration varies between about 4 and 8 nm with an average of 5.9 nm (Fig. 3A). The maximum dimension exhibits large fluctuations in a range of 12 to 32 nm (Fig. 3B). The NTD does not make direct contacts with the CTD (Fig. 4); however, the hydrophobic α-helix within the IDR2 makes frequent and transient contacts with both the NTD and the CTD. Frequent contacts within each of the three IDRs indicate that these regions can adopt conformations that are locally compact. Yet, our analysis of the distances between termini of the IDRs (Fig. 5 and Table 1) shows that each of the three IDRs exhibits conformations that are more extended than Gaussian chains of corresponding lengths. Taken together, our results provide a detailed picture of the conformational ensemble of the SARS-CoV-2 N protein dimer under near-physiological conditions.
The structure and flexibility of the SARS-CoV-2 N protein is likely to be important for the assembly of the nucleocapsid. Interestingly, both the NTD and CTD can bind RNA, yet it is evident from the contact maps in Fig. 4 that there are practically no direct contacts between the NTD and the CTD. Thus our structural analysis suggests that the NTD and CTD do not directly cooperate in RNA binding. However, the hydrophobic α-helix within the IDR2 makes multiple intra- and inter-chain contacts with both the NTD and CTD. This α-helix makes most frequent contacts with the NTD of the same chain (Fig. 4A) and least frequent contacts with the NTD of the other chain in the N dimer (Fig. 4B). Frequent contacts are observed also within each of the disordered segments IDR1–3. The presence of these contacts indicates that the IDRs adopt conformations that are locally compact. It remains to be shown how IDRs influence other interesting properties of the N protein such as its ability to phase separate with RNA [[43], [44], [45], [46], [47]]. However, we note that the conformations adopted by the N protein could be modified by RNA or protein binding [41,48].
Author contributions
EB and BR planned the research, BR performed the simulations and analyzed the results, EB and BR wrote the manuscript.
Declaration of Competing Interest
The authors declare no conflicts of interests.
Acknowledgements
We thank professors Tengchuan Jin and Hongliang He from the University of Science and Technology of China for sharing their SAXS data with us. We are also grateful to Michael Downey (University of Alberta) for language corrections. The research has been supported by the Polish National Science Centre within the international CEUS-UNISONO program, grant number 2020/02/Y/NZ1/00020 (to BR), and European Regional Development Fund; OP RDE; Project: “Chemical biology for drugging undruggable targets (ChemBioDrug)” (No. CZ.02.1.01/0.0/0.0/16_019/0000729). The Academy of Sciences of the Czech Republic (RVO: 61388963) is also acknowledged. The simulations were carried out using the supercomputer resources at the Centre of Informatics – Tricity Academic Supercomputer & networK (CI TASK) in Gdańsk, Poland.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.bpc.2022.106843.
Appendix A. Supplementary data
Supplementary material: Information on ensemble refinement
References
- 1.Glaeser R.M. How good can single-particle Cryo-EM become? What remains before it approaches its physical limits? Annu. Rev. Biophys. 2019;48(48):45–61. doi: 10.1146/annurev-biophys-070317-032828. [DOI] [PubMed] [Google Scholar]
- 2.Bai X.C., McMullan G., Scheres S.H.W. How cryo-EM is revolutionizing structural biology. Trends Biochem. Sci. 2015;40(1):49–57. doi: 10.1016/j.tibs.2014.10.005. [DOI] [PubMed] [Google Scholar]
- 3.Jumper J., Evans R., Pritzel A., Green T., Figurnov M., Ronneberger O., Tunyasuvunakool K., Bates R., Zidek A., Potapenko A., Bridgland A., Meyer C., Kohl S.A.A., Ballard A.J., Cowie A., Romera-Paredes B., Nikolov S., Jain R., Adler J., Back T., Petersen S., Reiman D., Clancy E., Zielinski M., Steinegger M., Pacholska M., Berghammer T., Bodenstein S., Silver D., Vinyals O., Senior A.W., Kavukcuoglu K., Kohli P., Hassabis D. Highly accurate protein structure prediction with AlphaFold. Nature. 2021;596(7873):583–589. doi: 10.1038/s41586-021-03819-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rozycki B., Boura E. Large, dynamic, multi-protein complexes: a challenge for structural biology. J. Phys. Condens. Matter. 2014;26(46):463103. doi: 10.1088/0953-8984/26/46/463103. [DOI] [PubMed] [Google Scholar]
- 5.V'Kovski P., Kratzel A., Steiner S., Stalder H., Thiel V. Coronavirus biology and replication: implications for SARS-CoV-2. Nat. Rev. Microbiol. 2021;19(3):155–170. doi: 10.1038/s41579-020-00468-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kang S., Yang M., Hong Z., Zhang L., Huang Z., Chen X., He S., Zhou Z., Zhou Z., Chen Q., Yan Y., Zhang C., Shan H., Chen S. Crystal structure of SARS-CoV-2 nucleocapsid protein RNA binding domain reveals potential unique drug targeting sites. Acta Pharm. Sin. B. 2020;10(7):1228–1238. doi: 10.1016/j.apsb.2020.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dinesh D.C., Chalupska D., Silhan J., Koutna E., Nencka R., Veverka V., Boura E. Structural basis of RNA recognition by the SARS-CoV-2 nucleocapsid phosphoprotein. PLoS Pathog. 2020;16(12):e1009100. doi: 10.1371/journal.ppat.1009100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yang M., He S., Chen X., Huang Z., Zhou Z., Zhou Z., Chen Q., Chen S., Kang S. Structural insight into the SARS-CoV-2 nucleocapsid protein C-terminal domain reveals a novel recognition mechanism for viral transcriptional regulatory sequences. Front. Chem. 2020;8:624765. doi: 10.3389/fchem.2020.624765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhou R., Zeng R., von Brunn A., Lei J. Structural characterization of the C-terminal domain of SARS-CoV-2 nucleocapsid protein. Mol. Biomed. 2020;1(1):2. doi: 10.1186/s43556-020-00001-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Luo H., Chen J., Chen K., Shen X., Jiang H. Carboxyl terminus of severe acute respiratory syndrome coronavirus nucleocapsid protein: self-association analysis and nucleic acid binding characterization. Biochemistry. 2006;45(39):11827–11835. doi: 10.1021/bi0609319. [DOI] [PubMed] [Google Scholar]
- 11.Yu I.M., Oldham M.L., Zhang J., Chen J. Crystal structure of the severe acute respiratory syndrome (SARS) coronavirus nucleocapsid protein dimerization domain reveals evolutionary linkage between corona- and arteriviridae. J. Biol. Chem. 2006;281(25):17134–17139. doi: 10.1074/jbc.M602107200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zeng W., Liu G., Ma H., Zhao D., Yang Y., Liu M., Mohammed A., Zhao C., Yang Y., Xie J., Ding C., Ma X., Weng J., Gao Y., He H., Jin T. Biochemical characterization of SARS-CoV-2 nucleocapsid protein. Biochem. Biophys. Res. Commun. 2020;527(3):618–623. doi: 10.1016/j.bbrc.2020.04.136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Grawert T.W., Svergun D.I. Structural Modeling using solution small-angle X-ray scattering (SAXS) J. Mol. Biol. 2020;432(9):3078–3092. doi: 10.1016/j.jmb.2020.01.030. [DOI] [PubMed] [Google Scholar]
- 14.Brosey C.A., Tainer J.A. Evolving SAXS versatility: solution X-ray scattering for macromolecular architecture, functional landscapes, and integrative structural biology. Curr. Opin. Struct. Biol. 2019;58:197–213. doi: 10.1016/j.sbi.2019.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Petoukhov M.V., Svergun D.I. Global rigid body modeling of macromolecular complexes against small-angle scattering data. Biophys. J. 2005;89(2):1237–1250. doi: 10.1529/biophysj.105.064154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tria G., Mertens H.D.T., Kachala M., Svergun D.I. Advanced ensemble modelling of flexible macromolecules using X-ray solution scattering. Iucrj. 2015;2:207–217. doi: 10.1107/S205225251500202X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pelikan M., Hura G.L., Hammel M. Structure and flexibility within proteins as identified through small angle X-ray scattering. Gen. Physiol. Biophys. 2009;28(2):174–189. doi: 10.4149/gpb_2009_02_174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rozycki B., Kim Y.C., Hummer G. SAXS ensemble refinement of ESCRT-III CHMP3 conformational transitions. Structure. 2011;19(1):109–116. doi: 10.1016/j.str.2010.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Peti W., Page R., Boura E., Rozycki B. Structures of dynamic protein complexes: hybrid techniques to study MAP kinase complexes and the ESCRT system. Methods Mol. Biol. 2018;1688:375–389. doi: 10.1007/978-1-4939-7386-6_17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cordeiro T.N., Herranz-Trillo F., Urbanek A., Estana A., Cortes J., Sibille N., Bernado P. Small-angle scattering studies of intrinsically disordered proteins and their complexes. Curr. Opin. Struct. Biol. 2017;42:15–23. doi: 10.1016/j.sbi.2016.10.011. [DOI] [PubMed] [Google Scholar]
- 21.Estana A., Sibille N., Delaforge E., Vaisset M., Cortes J., Bernado P. Realistic ensemble models of intrinsically disordered proteins using a structure-encoding coil database. Structure. 2019;27(2) doi: 10.1016/j.str.2018.10.016. p. 381-+ [DOI] [PubMed] [Google Scholar]
- 22.Benayad Z., von Bulow S., Stelzl L.S., Hummer G. Simulation of FUS protein condensates with an adapted coarse-grained model. J. Chem. Theory Comput. 2021;17(1):525–537. doi: 10.1021/acs.jctc.0c01064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Huang J., Rauscher S., Nawrocki G., Ran T., Feig M., de Groot B.L., Grubmuller H., MacKerell A.D., Jr. CHARMM36m: an improved force field for folded and intrinsically disordered proteins. Nat. Methods. 2017;14(1):71–73. doi: 10.1038/nmeth.4067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Turonova B., Sikora M., Schurmann C., Hagen W.J.H., Welsch S., Blanc F.E.C., von Bulow S., Gecht M., Bagola K., Horner C., van Zandbergen G., Landry J., de Azevedo N.T.D., Mosalaganti S., Schwarz A., Covino R., Muhlebach M.D., Hummer G., Krijnse Locker J., Beck M. In situ structural analysis of SARS-CoV-2 spike reveals flexibility mediated by three hinges. Science. 2020;370(6513):203–208. doi: 10.1126/science.abd5223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pandey P.R., Rozycki B., Lipowsky R., Weikl T.R. Structural variability and concerted motions of the T cell receptor - CD3 complex. Elife. 2021;10 doi: 10.7554/eLife.67195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sieradzan A.K., Czaplewski C.R., Lubecka E.A., Lipska A.G., Karczynska A.S., Gieldon A.P., Slusarz R., Makowski M., Krupa P., Kogut M., Antoniak A., Wesolowski P.A., Augustynowicz A., Leszczynski H., Liwo J.A. Extension of the Unres package for physics-based coarse-grained simulations of proteins and protein complexes to very large systems. Biophys. J. 2021;120(3):83a–84a. [Google Scholar]
- 27.Lazar T., Martinez-Perez E., Quaglia F., Hatos A., Chemes L.B., Iserte J.A., Mendez N.A., Garrone N.A., Saldano T.E., Marchetti J., Rueda A.J.V., Bernado P., Blackledge M., Cordeiro T.N., Fagerberg E., Forman-Kay J.D., Fornasari M.S., Gibson T.J., Gomes G.W., Gradinaru C.C., Head-Gordon T., Jensen M.R., Lemke E.A., Longhi S., Marino-Buslje C., Minervini G., Mittag T., Monzon A.M., Pappu R.V., Parisi G., Ricard-Blum S., Ruff K.M., Salladini E., Skepo M., Svergun D., Vallet S.D., Varadi M., Tompa P., Tosatto S.C.E., Piovesan D. PED in 2021: a major update of the protein ensemble database for intrinsically disordered proteins. Nucleic Acids Res. 2021;49(D1):D404–D411. doi: 10.1093/nar/gkaa1021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kikhney A.G., Borges C.R., Molodenskiy D.S., Jeffries C.M., Svergun D.I. SASBDB: towards an automatically curated and validated repository for biological scattering data. Protein Sci. 2020;29(1):66–75. doi: 10.1002/pro.3731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kim Y.C., Hummer G. Coarse-grained models for simulations of multiprotein complexes: application to ubiquitin binding. J. Mol. Biol. 2008;375(5):1416–1433. doi: 10.1016/j.jmb.2007.11.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14(1) doi: 10.1016/0263-7855(96)00018-5. p. 33–8, 27–8. [DOI] [PubMed] [Google Scholar]
- 31.Kofinger J., Rozycki B., Hummer G. Inferring structural ensembles of flexible and dynamic macromolecules using Bayesian, maximum entropy, and minimal-ensemble refinement methods. Biomolecul. Simul. 2019;2022:341–352. doi: 10.1007/978-1-4939-9608-7_14. [DOI] [PubMed] [Google Scholar]
- 32.Kofinger J., Stelzl L.S., Reuter K., Allande C., Reichel K., Hummer G. Efficient ensemble refinement by reweighting. J. Chem. Theory Comput. 2019;15(5):3390–3401. doi: 10.1021/acs.jctc.8b01231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Rozycki B., Cieplak M., Czjzek M. Large conformational fluctuations of the multi-domain xylanase Z of clostridium thermocellum. J. Struct. Biol. 2015;191(1):68–75. doi: 10.1016/j.jsb.2015.05.004. [DOI] [PubMed] [Google Scholar]
- 34.Boura E., Rozycki B., Herrick D.Z., Chung H.S., Vecer J., Eaton W.A., Cafiso D.S., Hummer G., Hurley J.H. Solution structure of the ESCRT-I complex by small-angle X-ray scattering, EPR, and FRET spectroscopy. Proc. Natl. Acad. Sci. U. S. A. 2011;108(23):9437–9442. doi: 10.1073/pnas.1101763108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Boura E., Rozycki B., Chung H.S., Herrick D.Z., Canagarajah B., Cafiso D.S., Eaton W.A., Hummer G., Hurley J.H. Solution structure of the ESCRT-I and -II supercomplex: implications for membrane budding and scission. Structure. 2012;20(5):874–886. doi: 10.1016/j.str.2012.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Chalupska D., Eisenreichova A., Rozycki B., Rezabkova L., Humpolickova J., Klima M., Boura E. Structural analysis of phosphatidylinositol 4-kinase IIIbeta (PI4KB) - 14-3-3 protein complex reveals internal flexibility and explains 14-3-3 mediated protection from degradation in vitro. J. Struct. Biol. 2017;200(1):36–44. doi: 10.1016/j.jsb.2017.08.006. [DOI] [PubMed] [Google Scholar]
- 37.Chalupska D., Rozycki B., Humpolickova J., Faltova L., Klima M., Boura E. Phosphatidylinositol 4-kinase IIIbeta (PI4KB) forms highly flexible heterocomplexes that include ACBD3, 14-3-3, and Rab11 proteins. Sci. Rep. 2019;9(1):567. doi: 10.1038/s41598-018-37158-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Chalupska D., Rozycki B., Klima M., Boura E. Structural insights into acyl-coenzyme A binding domain containing 3 (ACBD3) protein hijacking by picornaviruses. Protein Sci. 2019;28(12):2073–2079. doi: 10.1002/pro.3738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Horova V., Lyoo H., Rozycki B., Chalupska D., Smola M., Humpolickova J., Strating J., van Kuppeveld F.J.M., Boura E., Klima M. Convergent evolution in the mechanisms of ACBD3 recruitment to picornavirus replication sites. PLoS Pathog. 2019;15(8) doi: 10.1371/journal.ppat.1007962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kofinger J., Ragusa M.J., Lee I.H., Hummer G., Hurley J.H. Solution structure of the Atg1 complex: implications for the architecture of the phagophore assembly site. Structure. 2015;23(5):809–818. doi: 10.1016/j.str.2015.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bessa L.M., Guseva S., Camacho-Zarco A.R., Salvi N., Maurin D., Perez L.M., Botova M., Malki A., Nanao M., Jensen M.R., Ruigrok R.W.H., Blackledge M. The intrinsically disordered SARS-CoV-2 nucleoprotein in dynamic complex with its viral partner nsp3a. Sci. Adv. 2022;8(3) doi: 10.1126/sciadv.abm4034. p. eabm4034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Dunker A.K., Oldfield C.J., Meng J.W., Romero P., Yang J.Y., Chen J.W., Vacic V., Obradovic Z., Uversky V.N. The unfoldomics decade: an update on intrinsically disordered proteins. BMC Genomics. 2008;9 doi: 10.1186/1471-2164-9-S2-S1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Cubuk J., Alston J.J., Incicco J.J., Singh S., Stuchell-Brereton M.D., Ward M.D., Zimmerman M.I., Vithani N., Griffith D., Wagoner J.A., Bowman G.R., Hall K.B., Soranno A., Holehouse A.S. The SARS-CoV-2 nucleocapsid protein is dynamic, disordered, and phase separates with RNA. Nat. Commun. 2021;12(1) doi: 10.1038/s41467-021-21953-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chen H., Cui Y., Han X.L., Hu W., Sun M., Zhang Y., Wang P.H., Song G.T., Chen W., Lou J.Z. Liquid-liquid phase separation by SARS-CoV-2 nucleocapsid protein and RNA. Cell Res. 2020;30(12):1143–1145. doi: 10.1038/s41422-020-00408-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Iserman C., Roden C.A., Boerneke M.A., Sealfon R.S.G., McLaughlin G.A., Jungreis I., Fritch E.J., Hou Y.J., Ekena J., Weidmann C.A., Theesfeld C.L., Kellis M., Troyanskaya O.G., Baric R.S., Sheahan T.P., Weeks K.M., Gladfelter A.S. Genomic RNA elements drive phase separation of the SARS-CoV-2 nucleocapsid. Mol. Cell. 2020;80(6):1078–1091 e6. doi: 10.1016/j.molcel.2020.11.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Cascarina S.M., Ross E.D. Phase separation by the SARS-CoV-2 nucleocapsid protein: consensus and open questions. J. Biol. Chem. 2022;298(3) doi: 10.1016/j.jbc.2022.101677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Dignon G.L., Zheng W.W., Best R.B., Kim Y.C., Mittal J. Relation between single-molecule properties and phase behavior of intrinsically disordered proteins. Proc. Natl. Acad. Sci. U. S. A. 2018;115(40):9929–9934. doi: 10.1073/pnas.1804177115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Chang C.K., Hsu Y.L., Chang Y.H., Chao F.A., Wu M.C., Huang Y.S., Hu C.K., Huang T.H. Multiple nucleic acid binding sites and intrinsic disorder of severe acute respiratory syndrome coronavirus nucleocapsid protein: implications for ribonucleocapsid protein packaging. J. Virol. 2009;83(5):2255–2264. doi: 10.1128/JVI.02001-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material: Information on ensemble refinement