Revisiting the Bonding Model for Gold(I) Species: The Importance of Pauli Repulsion Revealed in a Gold(I)-Cyclobutadiene Complex

Abstract

Understanding the bonding of gold(I) species has been central to the development of gold(I) catalysis. Herein, we present the synthesis and characterization of the first gold(I)-cyclobutadiene complex, accompanied with bonding analysis by state-of-the-art energy decomposition analysis methods. Analysis of possible coordination modes for the new species not only confirms established characteristics of gold(I) bonding, but also suggests that Pauli repulsion is a key yet hitherto overlooked element. Additionally, we obtain a new perspective on gold(I)-bonding by comparison of the gold(I)-cyclobutadiene to congeners stabilized by p-, d-, and f-block metals. Consequently, we refine the gold(I) bonding model, with a delicate interplay of Pauli repulsion and charge transfer as the key driving force for various coordination motifs. Pauli repulsion is similarly determined as a significant interaction in Au(I)-alkyne species, corroborating this revised understanding of Au(I) bonding.

Graphical Abstract

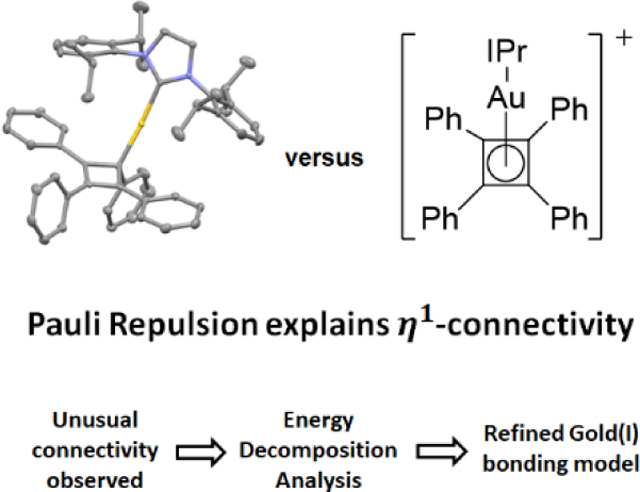
We present a novel Au(I)-cyclobutadiene complex for which reduced Pauli repulsion yields an η¹ instead of η⁴-coordination. This combined experimental and theoretical study motivates a reformulation of the Au(I)-π-ligand bonding model to include Pauli repulsion as a key element. Further analysis of Au(I)-alkynes corroborates this conclusion.

Introduction

Carbophilic Au(I) catalysts have been highly active in enabling a wide variety of transformations involving activation of C-C π-bonds, including cycloisomerization reactions of polyunsaturated species^[1] and nucleophilic additions to alkynes.^[2] As a result, homogeneous gold catalysis for alkyne activation is now part of the synthetic organic chemistry repertoire.^[3]

The high activity of Au(I) species has been rationalized by models of Au(I) bonding (Figure 1a). One important description of Au(I)-π-ligand bonding arises from the isolobal relationship between the empty 6s orbital of Au(I) and the 1s orbital of a proton,^[4] with the cationic Au(I) fragment described as a Lewis acidic “soft proton” that accepts electron density from the π-ligand.^[5] A complementary model is the Dewar-Chatt-Duncanson model,^[6] describing forward donation from the π-ligand to the metal atom and electron back-donation by the filled 5d Au orbitals to the π-ligand.^[7] Notably, computational methods have assessed the extent of back-donation from the L-Au(I) fragment to π-ligands or carbene fragments as limited due to the relativistic expansion of the 5d orbitals.^{[5, 8]} The combination of these two models consists of a net positive charge accumulation on the π-ligand in the bound complex, resulting in significant activation of the π-ligand towards nucleophilic attack.

Figure 1.

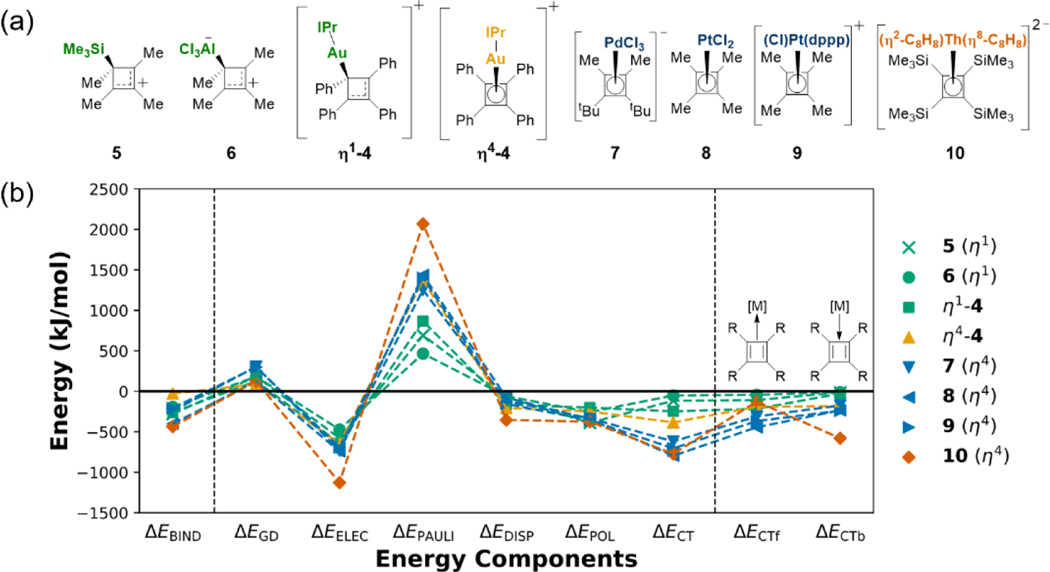
a) Established models for Au(I) bonding to π-ligands, and b) standard coordination modes for metal-cyclobutadiene complexes

In the past two decades, the aforementioned models have been applied to experimentally isolated Au(I) complexes of π-ligands, namely alkyne, alkene, allene, and arene complexes.^[9] However, no Au(I) cyclobutadiene species is known, hindering the validation of the models on this important ligand platform. Metal-cyclobutadiene complexes have been a historically significant platform for the development of metal-ligand bonding models, and a notable application of theory was the prediction of stable, η⁴-coordinated d-block cyclobutadiene complexes with significant backbonding stabilizing the cyclobutadiene fragment.^[10] This inspired much synthetic effort with the subsequent isolation of such complexes constituting important confirmation of theory.^[10a]

Consequently, we envisioned that a Au(I)-cyclobutadiene complex would be an excellent platform to reevaluate Au(I) bonding models, especially given the multiple coordination modes available to such a species. In the absence of geometrically biasing cyclobutadiene substituents that favor η²-connectivity,^[11] all structurally characterized d- and f-block cyclobutadiene complexes have been observed in η⁴-connectivity (Figure 1b).^[12] This contrasts to η¹-connectivity in cyclobutadienes stabilized by p-block metalloid Si and Al fragments lacking backbonding from filled d-orbitals.^[13] With limited backbonding from Au(I), we hypothesized that a Au(I)-cyclobutadiene could plausibly adopt η¹, η², or η⁴-coordination, with the balance of energetic interactions deciding the preferred geometry. For further insight into Au(I) bonding, the Au(I)-cyclobutadiene could be compared by theoretical methods to known congeners containing other metals, thereby contextualizing Au(I) bonding.

We therefore proposed that the synthesis of a novel Au(I)-cyclobutadiene in conjunction with modern energy decomposition analysis (EDA) methods could enable a reappraisal of Au(I) bonding.^[14] While earlier theoretical work on Au(I)-π-ligand bonding examined electrostatic contributions in conjunction with forward bonding and back-donation,^{[7, 15]} they did not consider London dispersion and Pauli repulsion, two interactions whose contributions to bonding in small molecules have recently been undergoing a reappreciation.^[16] Modern variational EDA methods explicitly incorporating these two interactions have been developed and should result in more accurate analysis.^[14]

Results and Discussion

Synthesis of Novel Au(I) Cyclobutadiene 4.

Common methods for synthesizing cyclobutadiene complexes include reductive elimination from a metallacyclopentadiene, dehalogenation of dihalocyclobutenes, and cyclobutadiene ligand transfer.^[10b] Based on observations that biphenyl-Au(III) complexes undergo reductive elimination under mild conditions to generate antiaromatic biphenylene,^[17] we hypothesized that Au(I)-cyclobutadiene could be generated similarly from the corresponding auracycle (Scheme 1).^[18] Accordingly, stannacycle 1 was synthesized by the Fagan-Nugent method,^[19] and transmetallation of 1 with (pyr)AuCl₃ smoothly yielded auracycle 2.^[18a] Subsequent ligand substitution with free N-heterocyclic carbene (NHC) IMes produced 3a. The structural connectivity of 3a was confirmed by single-crystal X-ray diffraction (XRD) (Figure 2) as a butadienyl-Au(III) species.

Scheme 1.

a) Synthesis of Au(III)-auracycles 3a and 3b, and b) synthesis of Au(I)-cyclobutadiene 4.

Figure 2.

Crystal structure of 3a.^[41] Thermal ellipsoid plots are drawn at 50% probability. Hydrogen atoms are omitted for clarity.

Chloride abstraction from 3a in CD₂Cl₂ solution with silver salts or NaBAr^F₄ produced a new species, tentatively assigned as Au(I)-cyclobutadiene based on the chemical equivalence of the four phenyl substituents by ¹H NMR analysis. However, crystal growth to establish structural connectivity was unsuccessful with product decomposing upon precipitation. Subsequently, the bulkier IPr carbene ligand was employed to synthesize auracycle 3b (Scheme 1a). Finally, chloride abstraction from 3b with AgSbF₆ produced Au(I)-cyclobutadiene 4 that was isolated as a green solid (Scheme 1b). 4 was stable as a solid for months at room temperature in a glovebox, but decomposition in solution was observed even in the presence of weak Lewis bases such as water, diethyl ether or benzene.

Single crystals were grown by layering a concentrated dichloromethane solution of 4 with pentane, and the solid-state connectivity of the gold atom to the cyclobutadiene ring was unambiguously characterized by XRD as η¹ (Figure 3), with the structure of the ring being consistent with a cyclobutenyl cation. The Au-C bond length of 4 of 2.080(4) Å is significantly shorter than that in structurally characterized η²-Au(I)-alkene (typically ranging from 2.19–2.35 Å),^[20] and -alkyne complexes (typically ranging from 2.18–2.39 Å)^{[15d, 21]} while being closer to simple Au(I)-alkyl bond length (2.039 Å for IPrAuMe).^[22] However, no significant puckering of the cyclobutadiene ring was observed (dihedral angle of 1.49°), consistent with other known aryl-substituted cyclobutenyl complexes.^[23] The two phenyl substituents vicinal to the gold atom were essentially coplanar to the cyclobutadiene ring. Bond lengths involving the cyclobutadiene ring carbons C1-C2, C1-C4, C1-C5, C3-C7 are consistent with single bonds, and C2-C3, C3-C4, C2-C6, and C4-C8 have bond orders between single and double bonds.^[24] In sum, the structural data of 4 is consistent with a bond description of a covalent single Au-C1 bond, with the positive charge of the complex delocalized over an allyl-type (C2-C3-C4) species, together with the phenyl substituents on C2 and C4 (Figure 3).

Figure 3.

Crystal structure of 4.^[41] Thermal ellipsoid plots are drawn at 50% probability. Hydrogen atoms are omitted for clarity. Selected bond lengths (Å): Au-C1, 2.080(4); C1-C2,1.543(5); C2-C3, 1.402(5); C3-C4, 1.403(5); C1-C4, 1.523(5); C1-C5, 1.529(4); C2-C6, 1.431(5); C3-C7, 1.483(5); C4-C8, 1.441(5).

As discussed above, the η¹-connectivity of 4 is in sharp contrast to known d-block cyclobutadiene species. However, the observed η¹-coordination is known for homologues stabilized by p-block metals and those stabilized formally by proton, methenium, and halonium fragments.^{[13, 23]}

A ¹H NMR spectrum of 4 in CD₂Cl₂ at room temperature was obtained, and the symmetry revealed that the four phenyl groups on the cyclobutadiene ring were chemically equivalent (Figure S9), consistent with η⁴-coordination or η¹-coordination with rapid (1,n)-Au shifts in solution. Variable-temperature NMR studies were not able to distinguish between these two scenarios (Figure S12).

We therefore turned to DFT^[25] studies using Q-Chem^[26] (see SI for computational details) for further investigation and determined that η¹-coordination was the preferred geometry in CH₂Cl₂ solution. Thus, in solution 4 must undergo either rapid (1,2)- or (1,3)-migration known to occur for other η¹-coordinated homologues.^[27] The DFT calculations suggest that only the (1,2)-shift is viable, proceeding via a stable η² intermediate being 35 kJ/mol higher in Gibbs energy than the corresponding η¹ structure (Figure 4). Localization of the transition states for this process proved difficult due to a flat PES around the η² intermediate indicating a low activation barrier. Thus, the free energy difference approximates the activation energy for the (1,2)-shift and corresponds to a short lifespan of the η² complex that cannot be resolved at the NMR time scale (t_1/2 = 0.1 μs and k = 5 ∙10⁶ 1/s based on Eyring transition state theory^[28] with transmission coefficient assumed as unity). Notably, an energetic minimum for the η⁴-coordinated 4 could not be located (see SI for detailed discussion).

Figure 4.

Reaction coordinate of the (1,2) shift of the IPr-Au(I) unit in 4. Both the η¹- and η²- coordinated structures are minima of the potential energy surface (PES). Vibrational analysis yielded slightly different thermal corrections to the Gibbs energy of η¹-4 with the Au moiety bound to adjacent carbon atoms. However, this deviation is irrelevant to the qualitative discussion of the (1,2)-shift.

At this point, we believed that further analysis was required to understand the preference of 4 for η¹-coordination over η⁴-coordination. We therefore turned to variational EDA methods to analyze the various possible coordination motifs of 4, and to compare 4 to other cyclobutadiene complexes.

Energy Decomposition Analysis on Complex η¹-4.

With XRD-obtained structural data on 4 and other reported cyclobutadiene complexes in hand, we employed the variational EDA ^{[14, 25a, 29]} scheme based on absolutely localized molecular orbitals (ALMOs) (see SI and reference^[14] for an overview of the method and references^{[14, 25a, 29]} for more details).

Herein, the binding energy between Au(I) with ancillary ligand and the cyclobutadiene fragment at a given geometry (vertical EDA) is decomposed as ΔE_BIND = ΔE_GD + ΔE_ELEC + ΔE_PAULI + ΔE_DISP + ΔE_POL + ΔE_CT, where ΔE_GD is the energy penalty for bringing the fragments into the complex geometry and ΔE_ELEC are permanent electrostatic, ΔE_PAULI repulsive Pauli (overlap of occupied orbitals from both fragments), ΔE_DISP dispersive, ΔE_POL polarization (also known as induction) and ΔE_CT charge transfer (CT) (orbital overlap between fragments forming dative bonds) contributions to the binding energy. The CT energy can then be further decomposed in unidirectional contributions ΔE_CTf/b, where the forward direction is defined as charge flow from the ligand to the metal (e.g., cyclobutadiene → IPr-Au(I)⁺) and the backward direction as CT from the metal fragment to the ligand, or forward donation and backbonding respectively. It is important to point out that the total binding energy and all EDA terms incorporate solvation effects for CH₂Cl₂ consistently^[29c] via an implicit solvation model.^[30]

To gain further insights into the characteristics of bonding for different hapticities, we first performed EDA calculations on the optimized η¹, η² and η⁴ coordinated 4. Insights into why the non-minimum η⁴-4 is unstable are critical. Therefore, we obtained an artificial structure by constraining the pyramidal arrangement of the η⁴-4 to be identical to the platinum complex η⁴-8 (see SI for detailed discussion).

The EDA results are shown in Figure 5 and reveal a correlation between the hapticity and the resulting binding energy. The η¹-4 (orange) is the most stable being over 35 kJ/mol lower in energy than the η²-4 (blue) and over 230 kJ/mol more stable than the η⁴-4 (green). Analysis of the individual EDA terms can explain this trend: The low interaction of the η⁴-4 is the result of a strong increase in Pauli repulsion induced by increasing the hapticity. This sharp increase of the repulsive Pauli interaction cannot be compensated by other attractive interactions such as an increase in CT. This high destabilization can be rationalized by: First, strong relativistic effects leading to diffuse valence 5d-orbitals fully occupied in the Au(I) oxidation state.^[5] Second, the increase of carbon atoms in close contact with the Au(I) as the hapticity increases. In contrast, permanent electrostatic, dispersion, and polarization contributions are less affected by the different coordination environments. Interestingly, CT increases substantially from η¹-4 to η⁴-4. Further analysis of the nature of CT shows that this is the result of significantly stronger backbonding of the gold moiety in the higher hapticity. Complementary occupied-virtual pair orbitals (COVPs) depict the key donor and acceptor orbitals of the CT interaction and can help understand this finding (see Figure S16): The singly occupied MOs and the lowest unoccupied MO of the isolated cyclobutadiene fragment have a π and δ symmetry, respectively. Hence, π type backbonding with the filled d-orbitals of the gold is possible in the η⁴-4, whereas the η¹-4 without cyclobutadiene-MO in corresponding symmetry is mainly stabilized through σ-forward interactions.

Figure 5.

Energy decomposition analysis (EDA) of the total binding energy (left) for 4 in different coordination motifs into additive components (middle, see text for full definitions). The dative charge-transfer (CT) energy is also separated into forward and backward contributions at right. Hatched bars correspond to structures with a fixed Au-C distance of 2.145 Å as found in the pyramidal 8 (see main text and SI for justification).

The energy contributions of the η²-4 to the binding energy are generally lower than expected based on the comparison of the η¹ and η⁴ complexes. This is due to an overall weaker interaction due to the longer Au-C equilibrium distances (see SI).

Unique Role of Au(I) Within the Periodic Table.

The isolation of a wide spectrum of cyclobutadiene complexes has previously been reported, ranging from p- (5,6),^{[13a, 13b]} to d- (7,8,9) ^[12a–c] and f- metals (10)^{[12d, 31]} as the central species. EDA results for representatives of each class of complexes, previously characterized by XRD, are shown in Figure 6a. Complexes from identical blocks of the periodic table show similar EDA fingerprints as indicated by the coloring scheme, despite differences in ancillary ligands on the metal and overall electronic charge of the complex. The η¹-coordinated main group complexes (green) have moderate Pauli repulsion and are mainly stabilized by coulombic interactions (ΔE_ELEC and ΔE_POL) with weak CT stabilization. Back-donation is negligible for η¹ structures which is in line with the COVP analysis as discussed above. The compounds with η⁴-coordinated d-metal centers (blue) experience more severe Pauli destabilization but also a stronger CT contribution, where forward bonding is more significant than back-donation. This can be rationalized by the antiaromaticity of the cyclobutadiene ring.^[32] Lastly, the f-block complex 10 (red) with a high electron count and a large ancillary ligand exhibits the highest Pauli repulsion that is mainly compensated for through strong backbonding and (permanent and induced) electrostatics.

Figure 6.

Lewis structures (a) and energy decomposition analysis (EDA) (b, see text and Figure 5 for definitions) of the investigated cyclobutadiene systems are shown with a color code according to the position of the central atom in the periodic table. Note that all geometries except for the η⁴-4 (yellow) are fully relaxed.

Interestingly, both the η¹- and η⁴-motif of 4 falls outside the trend for d-metals: η¹-4 shows a main group EDA fingerprint but with a stronger Pauli repulsion and the η⁴-4 (yellow) has a d-metal EDA fingerprint with the exception that CT is significantly weaker causing an overall weak interaction. Decomposing the CT shows that in comparison to other d-metal compounds this is mainly due to reduced forward CT. Hence, the limited electron-accepting capabilities of the Au(I) in the η⁴-4 environment make reduced Pauli repulsion a driving force for the η¹ coordination.

This observation is independent of conjugative delocalization onto the cyclobutadiene phenyl substituents of 4 (see Figure S14).

To support this classification and further gauge the effects of CT and Pauli repulsion on hapticity, we performed adiabatic EDA calculations.^{[29b, 33]} This method enables geometry optimizations with no (POL), only forward (CTf) or only backward charge transfer (CTb) allowed. The hapticities of these geometries on the POL, CTf, and CTb potential energy surface (PES) are shown in Table 1 and can be compared to the conventionally optimized geometries (FULL).

Table 1.

Hapticity after optimization on the fully relaxed, both unidirectional CT PES as well as the POL PES (adiabatic EDA). The more stabilizing direction of CT is highlighted with bold symbols. A model gold complex 4’with a less bulky carbene was employed (methyl instead of 2,6-diisopropylphenyl substituents in 4). More details are available in Table S10.

Category	FULL	POL	CTf	CTb
p-block	η 1	η 1	η 1	η 1
d-block	η 4	η 2	η 1	η 2
f-block	η 4	[a]	[a]	η 4
η1-4’	η 1	η 2	η 1	η 2
η4-4’	η 1	η 2	η 1	η 2

^[a]dissociates

Consistent with our previous results, compounds with main group central atoms always remain in η¹ hapticity and form stable adducts even without CT, confirming that these interactions are significantly controlled by favorable permanent electrostatics and polarization.

This is not the case for the remaining complexes since a structural reorganization is necessary to reduce Pauli destabilization which otherwise cannot be compensated for without CT which manifests in loosely “bound” d-complexes on the POL-PES with the shortest M-C bond length being 3 Å (see Table S10). Nevertheless, arbitrary unidirectional CT alone is also not sufficient to stabilize all complexes. Restricting 10 for example to only forward CT still leads to an overall repulsive interaction and thus induces dissociation of the strongly backbonded Th fragment. In contrast, the d-block complexes optimize to a lower η² hapticity on the charge transfer restricted CTb-PES due to the presence of partly filled d_π-orbitals which can interact with the empty π orbitals of one of the cyclobutadiene double bonds.

Hence, η² coordination can not only facilitate significant stabilization through backward CT, which is in line with the previous COVP analysis but is also accompanied by a reduction of Pauli repulsion as a consequence of decreasing the hapticity with elongated bond lengths. This highlights the delicate interplay of Pauli repulsion and CT for determining the final hapticity.

Interestingly, depending on the initial guess structure, 8 relaxes to η¹ or η⁴ connectivity on the CTf-PES where the former geometry is significantly lower in energy. In combination with the η² coordination on the CTb-PES, this bears a remarkable similarity to η⁴-4 as it also rearranges to η¹ or η² due to a limited capacity for dative bonding, with final hapticity controlled by the direction of charge flow. Concurrently, the ability to rearrange to a backbonded η² structure constitutes a key difference between the experimentally observed η¹-4 and the main group complexes analyzed as they do not possess filled d-orbitals.

Refining the Origins of Au(I) Bonding.

Considering these exceptional characteristics of Au(I) bonding, we propose to extend the established bonding model for Au(I)-π-ligand species to include the decisive effects of Pauli repulsion. Notably, our EDA results support current views (“soft proton”^[4] in combination with Dewar-Chatt-Duncanson model)^[6] on the nature of CT in Au(I) species since, depending on the electronic structure of the second ligand, significant backbonding can be observed while forward CT is still crucial for the overall electrophilic stabilization.^{[5, 15a]} The latter can be evidently influenced by the choice of ancillary ligand or by the molecular environment of the Au(I) fragment as demonstrated by changing the hapticity from η¹ to η² for example.^{[5, 8a]} However, the heretofore disregarded influence of Pauli repulsion enables deeper understanding of Au(I)-π-ligand bonding. Both (permanent and induced) electrostatics and bidirectional CT are essential for counterbalancing Pauli-induced destabilization which in turn is, due to its significance, a driving force for geometric change and thus different molecular connectivities. Recent computational investigations support our claims as they likewise unraveled the critical role of Pauli repulsion in numerous catalytic transformations^{[16a, 34]} and it being a key component for understanding specific bonding motifs (e.g. linear hydrogen bonding)^[35]. We also note that the significant role of Pauli repulsion in gold chemistry has been shown for metal-metal bonds by comparing the energetics of different closed-shell structures with varying metals.^[36] Furthermore, Che and colleagues demonstrated that reduced metallophilicity in a representative gold species is a direct consequence of increased Pauli repulsion which mainly stems from the repulsive metal-metal interaction.^[37] While not decisive for the complexes examined here, we further note that with bulkier substituents, dispersion interactions can also significantly affect structure and stability.^[38]

Application of Revised Bonding Model to Metal π-Alkyne-Complexes.

To further exemplify these new insights, we revisited models of group 11 metal alkyne η² complexes (11).^[15d] Figure 7 shows the vertical EDA results for the fully relaxed complexes andconstrained structures (hatched bars) with M-C bond lengths as found in the optimized copper complex (2.044 Å, 2.151 Å). Comparison of the results for constrained and unconstrained structures explains the small contributions for the silver adduct as those can be attributed to elongated equilibrium bond lengths (2.292 Å, 2.469 Å).

Figure 7.

Energy decomposition analysis (EDA) of the total binding energy for π-alkyne complexes 11 with the group 11 metals Cu(I), Ag(I), and Au(I) into additive components (see text and Figure 5 for definitions). Hatched bars correspond to constrained structures with M-C distances as found in the relaxed Cu(I) adduct (2.044 Å, 2.151 Å). All remaining geometries are fully relaxed.

Generally, all complexes exhibit strong permanent and induced electrostatic stabilization as reported by Frenking and colleagues.^[15a] Moreover, a strong increase in CT stabilization can be observed for the gold alkyne due to forward donation, resulting in a more partial positively charged and thus more π-activated alkyne which is in agreement with preceding studies.^{[7, 15c, 15d]} Decomposing this CT shows that back-donation is significant but limited as predicted by the Au(I) bonding model. However, the relative contribution to the total CT decreases with increasing electron count of the metal species due to lower 4d and 5d orbital energies as a consequence of smaller d-d repulsion energies.^{[8a, 39]} Additionally, backbonding appears marginally more distance-dependent than forward-bonding. Lastly, Pauli repulsion is largest for the gold complex with a 270% and 135% increase in repulsion energy in comparison to the similarly constrained copper and silver complexes, respectively. Thus, Pauli repulsion again plays an important role in decreasing the overall interaction energy which is also true for the fully relaxed species (145% and 180%).

Based on these results, we believe it essential to propose that the interplay of Pauli repulsion with other energetic contributions to the interfragment interaction is key for understanding the unique π-activation capabilities of Au(I) species and the features of gold-mediated transformations in general. As a numerical experiment to further explore our hypothesis, we investigated the η² to η¹ shift of the gold moiety in a model complex ([(H₃P)Au(C₂H₂)]⁺, see Figure S19). While the permanent electrostatic and CT stabilization decreases during the shift, this is also accompanied by a strong reduction of Pauli repulsion as expected for a lower overlap of the filled Au 5d subshell with the filled 2p orbitals of the alkyne carbons. The large Pauli repulsion component in Au(I)-alkyne bonding suggests that investigating ground state destabilization due to this factor is a promising direction for future studies investigating the high activity of Au(I) as Lewis acid. Analyzing the influence of a present nucleophile on the electron densities and EDA contributions of transition states and further intermediate structures is the subject of future studies in preparation.

Conclusion

We have synthesized a novel Au(I)-cyclobutadiene complex 4 via reductive elimination from auracycle 3b. XRD demonstrated 4 to have an η¹-connectivity between the Au atom and the cyclobutadiene ring, unusual for d-block cyclobutadiene complexes. The data was consistent with a covalent Au-C1 single bond, while combined experimental and computational analysis suggests rapid (1,2)-Au shifts in solution. As analyzed by EDA methods, the coordination geometry of 4 can be explained by weak charge transfer (CT) abilities of the Au(I) moiety in combination with large Pauli repulsion favoring the η¹-coordination mode.

The unusual bonding of Au(I) is further underlined by comparing 4 with cyclobutadiene species stabilized by coordination to p-, d- and f- block metals, revealing distinct EDA fingerprints. Complexes with p-block metals are mainly stabilized by permanent and induced electrostatics, f-block metals are strongly backbonded, and d-block metals are stabilized by forward and slightly less significant backward CT. Adiabatic EDA confirms that the interplay of CT and Pauli repulsion is key for determining the hapticity, as other d-block metals also rearrange from η⁴-coordination when CT is constrained. This further underlines the uniqueness of Au(I) bonding in η¹-4.

Consequently, we proposed a refined bonding model of Au(I)-π-ligand complexes, modifying the combined “soft proton” and Dewar-Chatt-Duncanson picture to include significant influence of Pauli repulsion. This model was then successfully corroborated with analysis of coinage metal-alkyne complexes. We envisage that consideration of Pauli repulsion could yield more insights for transition metal chemistry in general.