Simulating bidirectional peripheral neural interfaces in EIDORS

Abstract

Bioelectronic neural interfaces that deliver adaptive therapeutic stimulation in an intelligent manner must be able to sense and stimulate activity within the same nerve. Existing minimally-invasive peripheral neural interfaces can provide a read-out of the aggregate level of activity via electrical recordings of nerve activity, but these recordings are limited in terms of their specificity. Computational simulations can provide fine-grained insight into the contributions of different neural populations to the extracellular recording, but integration of the signals from individual nerve fibers requires knowledge of spread of current in the complex (heterogenous, anisotropic) extracellular space. We have developed a model which uses the open-source EIDORS package for extracellular stimulation and recording in the pelvic nerve. The pelvic nerve is the primary source of autonomic innervation to the pelvic organs, and a prime target for electrical stimulation to treat a variety of voiding disorders. We simulated recordings of spontaneous and electrically-evoked activity using biophysical models for myelinated and unmyelinated axons. As expected, stimulus thresholds depended strongly on both fibre type and electrode-fibre distance. In conclusion, EIDORS can be used to accurately simulate extracellular recording in complex, heterogenous neural geometries.

I. INTRODUCTION

The activity of the internal organs of the body are regulated via a combination of hormonal control and neural input from the autonomic nervous system. Disruptions to communication between organs and the brain are central to a wide variety of disorders, such as Crohn’s disease [1] and overactive bladder [2]–[4]. Consequently, the autonomic nervous system is being investigated as a neuromodulation target for conditions lacking clear pharmaceutical targets.

Surgically implanted peripheral neural interfaces have been developed over many years for a variety of applications (e.g. [1]–[5]). The majority of devices in current use operate in open-loop mode and require the parameters of stimulation to be configured by a clinician to achieve the desired therapeutic effect and updated periodically. Increasingly, modern neural interfaces are moving towards closed-loop control, motivated by a desire to reduce power consumption, avoid side-effects of unnecessary treatment, and to provide a more physiologically realistic neural input to restore a wider range of behaviors (e.g. [6], [7]).

In order to achieve closed-loop control, a peripheral neural interface needs to detect the activity of different populations of axons contained within the nerve. The majority of nerves being targeted for the development of electronic medicine, such as the vagus [8] and pelvic [3], [4] nerves, are mixed nerves comprised of both afferent (sensory and nocioceptive) and efferent (somatic and autonomic motor) pathways, and comprise functionally distinct subclasses that regulate different organs. Minimally invasive nerve recordings, such as those obtained with nerve cuff electrodes, generally cannot resolve activity to a single-axon level of specificity. Recorded compound action potentials [9] are an aggregate measure of various types of activity, not all of which is relevant to the pathology being treated. To address this, one approach has been to relate the Fourier spectra of the recording to levels of activities in different axon populations [10]; other signal-processing techniques to achieve conduction-velocity-selective recordings have been proposed [11].

Here we present a computational modeling approach built on open-source components for generating recordings of spontaneous and electrically-evoked nerve activity based on physiologically realistic axons and distributions of different axon classes for autonomic nerve. In such an environment, the experimenter has full control over the distributions of activity of different populations, which gives the ability to test signal-processing strategies for selectively recording different signals of interest. Our approach combines multidomain anisotropic electric field modeling using EIDORS (3.9.1, eidors.org) and biophysical modeling of individual axons in NEURON (7.7.2, Yale), as detailed below.

II. METHODS

Forward solutions for the electrode potentials observed given small unit currents entering the extracellular domain were calculated using the first-order forward solution in EIDORS. In order to validate this application of EIDORS, results from a finite element calculation were compared to the theoretical potentials for a simplified (infinite homogenous isotropic) system of four electrodes (numbered E1–E4, with a unit current I flowing from E1 to E4), as shown in Fig. 1A. The theoretical potential observed at a radius r from a monopolar point source of current I in an infinite homogenous medium is given by [12] as

$$V={\int }_{\text{inf}}^r\frac{-I}{4\pi \sigma r^2}dr=\frac{I}{4\pi \sigma r}$$ (1)

where σ is the conductivity of the medium. In this arrangement, the theoretical potential observed between E2 and E3 in this configuration with r = 1 is given by

$$V_{23}=\left(V_{12}+V_{42}\right)-\left(V_{13}+V_{43}\right)=V_{12}=\frac{I}{4\pi \sigma }.$$ (2)

Using this prediction, we can evaluate the discretisation and finite-domain errors using EIDORS. As the number of finite elements in the domain increases, the approximation error diminishes, as shown in Fig. 1B. The finite element model can be constructed with either Dirichlet (zero-voltage) or Neumann (zero-current) boundary conditions; for the sample of 184 meshes shown in Fig. 1B, the error was greater for models with Dirchlect vs. Neumann boundary conditions (1.61% vs 0.85%, p < 0.001).

Fig. 1.

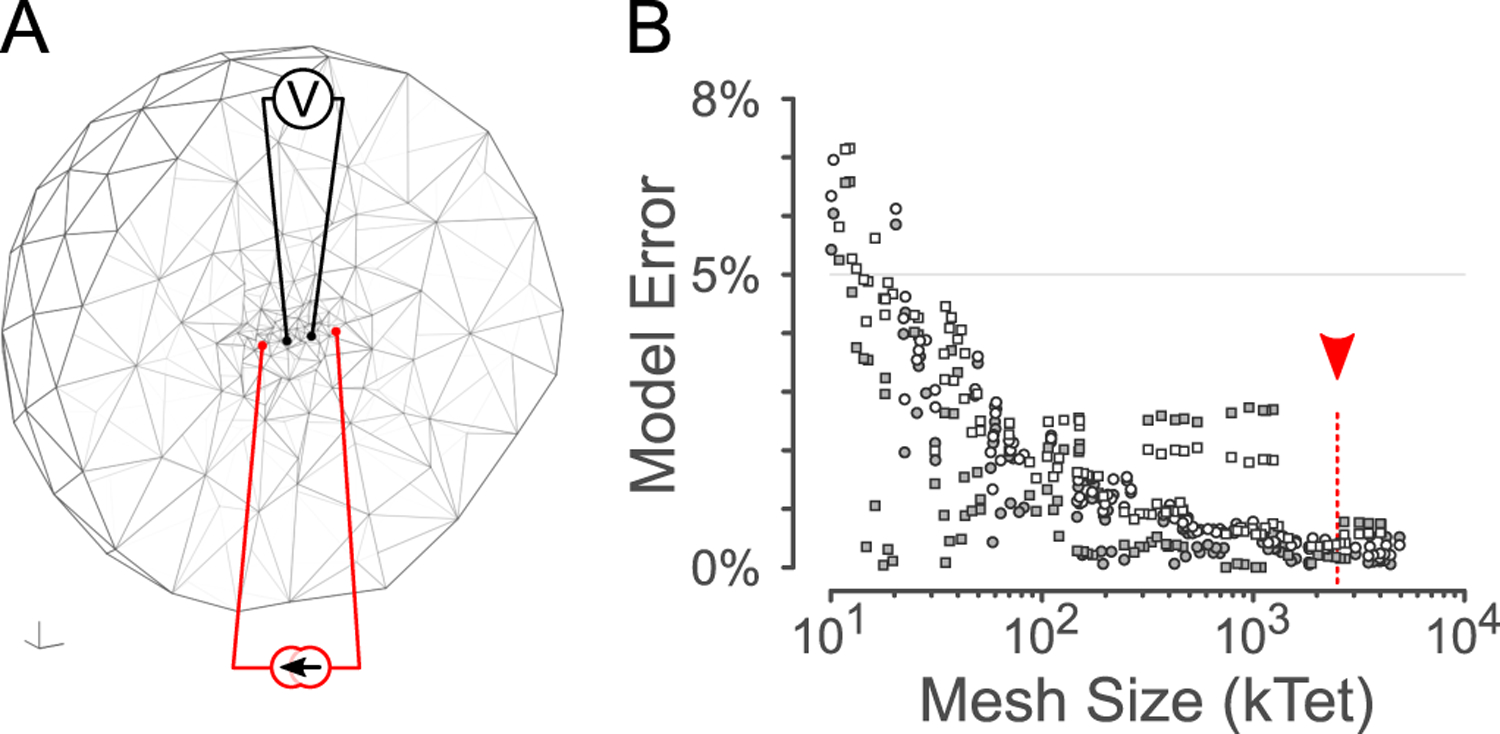
Verification of simulation error against theory. A: cross-section through a 3-D spherical forward model mesh in EIDORS for a small mesh size. B: Model error relative to mesh size for different meshes and boundary conditions. Red arrowhead: relative size of the mesh shown in Fig. 2A.

We developed an anatomically detailed model of the rat pelvic nerve, a multi-functional fasciculated nerve which connects the spinal cord (levels L6-S1) and sensory ganglia to the pelvic organs, via the pelvic ganglia. This nerve contains sensory, sympathetic, parasympathetic, and vasoconstrictor fibers which innervate the colon, lower urinary tract, and reproductive tracts ([3], [4], [13], Fig. 2A). The overall dimensions of the modeling domain, shown in Fig. 2B, were 5 × 5 × 2 mm. The conductivities of the different regions of the model are given in table 1. The model was meshed using GMSH (4.4.1), resulting in a mesh of 2.5 million elements with a minimum element quality (Baker’s τ) of 0.118 and mean element quality 0.636. EIDORS was used to calculate forward solutions for currents in each branch of the pelvic nerve, resulting in a map of the recording sensitivity $T_{\mathit{\text{elec }}}(\overrightarrow{x})$ as a function of spatial position $\overrightarrow{x}$. An example of a recording sensitivity profile is shown in Fig. 2C. This sensitivity map is a property of the recording electrode array design; larger electrodes will result in broader sensitivity peaks.

Fig. 2.

Pelvic Nerve stimulation & recording model. A: Overall modeling domain, showing fascicles(blue), electrode array (yellow), and stimulating / recording electrodes (red). Scale: 1mm. B: pelvic nerve cross-section adapted from Hulsebosch [13] showing fascicles and simulated distribution of axons of each type. C: Sensitivity relationship $T_{\mathit{\text{elec}}}(\overrightarrow{x})$ as a function of length along the center of one fascicle for each electrode.

TABLE I.

Conductivity of different regions in the model

Region	σ (S/m)	Reference
Fascicle (transverse)	0.570	[19]
Fascicle (longitudinal)	0.088	[19]
Perineurium	8.7e-4	[20]
Interstitial Fluid	0.66	[21]
Silicone	1e-12

Given a sensitivity map $T_{\mathit{\text{elec }}}(\overrightarrow{x})$, the resulting potential V_elec on the electrode surface for any spatial distribution of membrane currents $I_m(\overrightarrow{x})$ can be calculated by taking the inner product across the volume of tissue

$$V_{\mathit{\text{elec}}}=\int T_{\mathit{\text{elec}}}(\overrightarrow{x})I_m(\overrightarrow{x})d\overrightarrow{V}$$ (3)

The sensitivity map does not strongly depend on the location of the distant reference relative to the recording array; For instance, moving the reference (modeled as a 2 mm diameter disk on the simulation boundary) between the front and rear faces changed the computed sensitivity by 1.8%±1.9%.

To model nerve cuff recordings of nerve activity, distributions of axons within the pelvic nerve were modeled using the densities of myelinated and unmyelinated sensory and motor fibers adapted from Hulsebosch [13]. Extracellular potentials depend on the distribution of axon diameters and myelin thickness, as well as the population of ion channels expressed in each axon. Data on axon diameters and myelination thickness for rat pelvic nerve are not available, so this data was adapted from measurements performed on cervical rat vagus nerve sections [14] as the vagus nerve also innervates visceral organs and has a 1:4 ratio of myelinated to unmyelinated fibers [13], [14]. Membrane currents were calculated using NEURON, using the well-established MRG model [15], [16] for myelinated axons. Since there are no spatially-extended models for mammalian visceral efferent or afferent axons, we used a model for nocioceptor afferents [17] to simulate the unmyelinated axons. As axons do not normally generate spontaneous action potentials, propagating action potentials were generated in the model using a step injection of current at the end of a single axon to model spontaneous activity; each axon was simulated independently. Each axon was 6 mm long and contained between 45–1079 elements (median 523, depending on fiber diameter). To reduce modeling overhead, membrane currents from 24 unique axons of each type were modeled, based on nearest-neighbor clustering of axon diameters and g-ratios. To remove the end effects from the finite length of simulated axon, membrane currents for segments near the axon edges were replaced with stereotypical membrane currents from a segment near the center of the axon. Multiple independent simulations of axon locations and spike patterns (n=10) were conducted to generate 100 ms samples of spontaneous activity sampled at 30 kHz. The spectrum of the ongoing recordings were estimated using multi-taper spectral estimation [18] to assess the distinguishability of different axon populations within the whole-nerve recording.

Finally, in order to simulate electrically-evoked compound action potentials, we also calculated the extracellular potentials evoked by a unit stimulus current through different bipolar pairs of electrodes. These were included as a monophasic bipolar extracellular potential applied for 400 μs in the NEURON model, and the minimum amount of current required to produce a propagating action potential was determined using a logarithmic stair-step procedure. These data were used to predict stimulus recruitment curves for different axon populations within the pelvic nerve, as shown in Fig. 4.

III. RESULTS

By combining bulk electric-field modeling in EIDORS and biophysical modeling of individual axons in NEURON, we were able to simulate recordings which reveal the contributions of different populations of axons to the overall recording. Ongoing activity was simulated at population-average spike rates of 2 and 20 imp/s, generating simulated recordings of neural activity in the pelvic nerve (Fig. 3A, B) for each of the four simulated axon types. Simulations of stimulus-evoked activity (Fig. 3C) show significant summation from 0.8–29 ms and 52–77 ms post-stimulus, corresponding to the contributions of the myelinated and unmyelinated fibers with conduction velocities of 3.2–37.8 m/s and 0.12–0.23 m/s, respectively, within the range of expected values [9]. Across all simulations, the contributions of the myelinated and unmyelinated fibers were spectrally distinct (Fig. 3D–F). Below 600 Hz, the contributions of the unmyelinated fibers dominated, while the myelinated fiber signal occupied a broader range of higher frequencies.

Fig. 3.

Simulations of electrical recordings using EIDORS. A: Simulation of ongoing activity, 2 imp/s/axon spike rate. Traces show the voltage observed by each bipolar measurement pair, and the contribution of each axon type to the potential observed between E3–E4. B: 20 imp/s/axon spike rate. C: Simulation of evoked activity, stimulated at E12, showing the propagating evoked compound action potential. D–F: frequency spectra for each of A–C, average of 10 simulations, showing the contribution of each axon type.

As expected, electrical stimulation of the nerve results in recruitment of myelinated axons before unmyelinated axons, and larger-diameter fibers before smaller-diameter fibers within each axon type. Fig. 4A shows cross-sections of the nerve with axons of different diameters demonstrating the ordered recruitment of myelinated and unmyelinated axons. Fiber diameter, g-ratio, and electrode-fiber distance (Fig. 4B) combine to determine the overall efficacy of electrical stimulation. Finally, Fig. 4C shows the predicted recruitment curves for myelinated and unmyelinated axons as a function of stimulation strength. Afferent myelinated axons [16] have a lower stimulus threshold than efferent myelinated axons [15] (41 vs 74 μA and 74 vs 158 μA to recruit 50% and 95% of the axons, respectively). At a stimulus which recruits 100% of myelinated afferents (313 μA), fewer than 6% unmyelinated axons are stimulated; unmyelinated axons required currents of 625 μA and 1.38 mA to recruit 50% and 95% of the axons, respectively.

Fig. 4.

Electrical Stimulus Thresholds. A: Pelvic nerve cross-sections for myelinated (top) and unmyelinated (bottom) fibers; color corresponds to the threshold. Electrode located at the bottom of the cross-section. B: thresholds as a function of fiber diameter. C: Recruitment curves for each type of axon.

IV. CONCLUSIONS

EIDORS can be used to model bioelectric fields for stimulation and recording of peripheral nerves, for the development of advanced signal-processing techniques to isolate the activity of different axonal populations within whole nerve recordings (e.g. [10], [11]). The different populations of axons give rise to distinguishable spectral signatures within a mixed nerve such as the pelvic nerve, which importantly do not depend on implanting high-channel-count arrays. This open-source simulation environment provides a platform to explore different stimulation paradigms, electrode designs, and signal-processing strategies for the development of peripheral neural implants for bioelectronic medicine.