Abstract
This study introduces a universal correlation based on the modified version of the Arrhenius equation to estimate the solubility of anti-cancer drugs in supercritical carbon dioxide (CO2). A combination of an Arrhenius-shape term and a departure function was proposed to estimate the solubility of anti-cancer drugs in supercritical CO2. This modified Arrhenius correlation predicts the solubility of anti-cancer drugs in supercritical CO2 from pressure, temperature, and carbon dioxide density. The pre-exponential of the Arrhenius linearly relates to the temperature and carbon dioxide density, and its exponential term is an inverse function of pressure. Moreover, the departure function linearly correlates with the natural logarithm of the ratio of carbon dioxide density to the temperature. The reliability of the proposed correlation is validated using all literature data for solubility of anti-cancer drugs in supercritical CO2. Furthermore, the predictive performance of the modified Arrhenius correlation is compared with ten available empirical correlations in the literature. Our developed correlation presents the absolute average relative deviation (AARD) of 9.54% for predicting 316 experimental measurements. On the other hand, the most accurate correlation in the literature presents the AARD = 14.90% over the same database. Indeed, 56.2% accuracy improvement in the solubility prediction of the anti-cancer drugs in supercritical CO2 is the primary outcome of the current study.
Subject terms: Drug discovery, Chemistry, Chemical engineering
Introduction
Supercritical is a technical phrase to refer to operating conditions where both pressure and temperature are higher than their critical values for a given substance1. It is widely accepted that supercritical fluids (SCF) pose some valuable advantages over traditional solvents (liquid-like density, gas-like transport properties, low surface tension, and good mass transfer capacity)2. These characteristics have drawn attention to the SCFs as solvent media for supercritical extraction/purification purposes in a wide range of applications1. Carbon dioxide (CO2) is likely the most trustful supercritical fluid in energy3, food4, pharmaceutical5,6, and bioactive agent delivery7–10 applications. Indeed, the non-toxic, inflammable, and non-explosive nature of supercritical carbon dioxide (SCCO2) is responsible for these trustful applications2. Furthermore, the SCCO2 critical characteristics are mild (temperature = 31.1 °C, pressure = 73.8 bar)11, it is recyclable, simply available at low expense, and covers the real-field requirement2.
The SCCO2 has outstanding applications in pharmaceutical manufacturing processes12,13. Drug solubility in SCF is the most crucial information for the feasibility study, development, and construction of the pharmaceutical processes utilized the supercritical fluids as solvent media14. Since cancer is a leading cause of human death all around the world15–18, researchers experimentally measured the solubility of different anti-cancer drugs in supercritical CO2, including sorafenib tosylate19, sunitinib malate20, azathioprine21, busulfan22, tamoxifen23, letrozole24, tamsulosin25, capecitabine26, paclitaxel27, 5-fluorouracil27, thymidine27, and decitabine28. Unfortunately, the laboratory measurement of drug solubility in supercritical CO2 at whole ranges of pressures and temperatures is time-consuming and requires high economic expenses2.
In order to resolve these operating and economic problems, different thermodynamic-based models (known as the equation of state)29–32, intelligent paradigms14, predictive model33,34, and empirical correlations35–44 are proposed to simulate different phenomena, including estimating solids solubility in SCCO2. Sodeifian et al. compared the accuracy of the Peng-Robinson (PR), Soave–Redlich–Kwong (SRK), and available empirical correlations for predicting solubility of sorafenib tosylate19, sunitinib malate20, and azathioprine21 anti-cancer drugs in SCCO2. Performances of the PR equation of state, statistical associating fluid theory of variable range (SAFT-VR), and six empirical correlations for predicting tamsulosin solubility in supercritical CO2 have also been compared25. Generally, the estimation methods of drug solubility in the SCCO2 using the equations of state (EoS) are often mathematically complicated2, require high computations efforts2, need relatively high entry information2,45,46, provide high levels of uncertainty19, and may sometimes fail20. More precisely, they need the operating conditions, critical properties, and also drug characteristics to deliver their predictions19,20.
The least-squares support vector machines14, artificial neural networks47–50, quantitative structure–property relationships51, adaptive neuro-fuzzy inference systems52,53, wavelet transform54–57, and dynamic simulation58–60 are some of the approaches may be used for estimating the solid solubility in supercritical carbon dioxide. Utilizing these intelligent paradigms is only possible when their structure, adjusted hyper-parameters, and performed pre-processing and post-processing stages be completely available61–65. Despite an acceptable accuracy of these intelligent methods, some parts of their information are often missed to present, and it is hard or even impossible to be used by other researchers.
The empirical correlations that only need temperature, pressure, and pure SCCO2 density to predict solid solubility in supercritical carbon dioxide29–32 have attracted greater attention in this regard. In order to escape an unnecessary repetition, the mathematical expressions of these empirical correlations will be reviewed in the subsequent sections (see “Most widely used correlations for drug solubility in SCCO2”). The mathematical formulations of these empirical correlations are simple, understandable, ready to use, and their accuracy is often far better than the thermodynamic-based models19,20. Moreover, it is possible to incorporate them in an appropriate optimization algorithm to determine the operating condition that maximizes the drug solubility in SCCO2.
The current research briefly reviewed ten well-known and reliable empirical correlations for estimating solid solubility in supercritical CO235–44. After that, a universal approach based on the modified Arrhenius model is introduced to relate the anti-cancer drug solubility in SCCO2. This universal approach added a departure function to the Arrhenius-shape term to estimate the anti-cancer drug solubility in SCCO2. The predictive performance of the modified Arrhenius model and available correlations in the literature is compared using all available experimental data for solubility of anti-cancer drugs in SCCO2. 316 experimental data for solubility of sorafenib tosylate19, sunitinib malate20, azathioprine21, busulfan22, tamoxifen23, letrozole24, tamsulosin25, capecitabine26, paclitaxel27, 5-fluorouracil27, thymidine27, and decitabine28 in SCCO2 are used to perform this comparison. The results show that the modified Arrhenius model improves the previously achieved accuracy in the literature by more than 56.2%.
Materials and methods
The first part of this section presents the available experimental measurements for the solubility of anti-cancer drugs in supercritical CO2. The second part reviews the most well-known empirical models for correlating the solid solubility in SCCO2 to the independent variables (pressure, temperature, and pure supercritical CO2 density).
Anti-cancer drugs
As mentioned earlier, cancer is approved as the leading cause of human death worldwide15. Therefore, all aspects of anti-cancer drugs, including their solubility in the supercritical CO2 are an exciting research topic for both academic and manufacturing purposes. Based on our best knowledge, the solubility of only twelve anti-cancer drugs in the supercritical carbon dioxide were measured up to now. These anti-cancer drugs are sorafenib tosylate19, sunitinib malate20, azathioprine21, busulfan22, tamoxifen23, letrozole24, tamsulosin25, capecitabine26, paclitaxel27, 5-fluorouracil27, thymidine27, and decitabine28. Table 1 separately reports the range of pressure, temperature, supercritical CO2 density, and anti-cancer drug solubility for all the laboratory-scale studies. Furthermore, the numbers of available measurements in each research are also shown in this table.
Table 1.
Literature data for solubility of anti-cancer drugs in supercritical carbon dioxide.
| CO2 (1) + drug (2) | Temperature (K) | Pressure (MPa) | CO2 density (kg/m3) | Drug solubility* × 106 | No. data |
|---|---|---|---|---|---|
| Sorafenib tosylate19 | 308–338 | 12–27 | 388–914 | 0.68–12.57 | 24 |
| Sunitinib malate20 | 308–338 | 12–27 | 388–914 | 5–85.6 | 24 |
| Azathioprine21 | 308–338 | 12–27 | 388–914 | 2.7–18.3 | 24 |
| Busulfan22 | 308–338 | 12–40 | 383–971 | 32.7–865 | 32 |
| Tamoxifen23 | 308–338 | 12–40 | 383–971 | 18.8–989 | 32 |
| Letrozole24 | 318–348 | 12–36 | 319–922 | 1.6–85.1 | 20 |
| Tamsulosin25 | 308–338 | 12–27 | 384–914 | 0.18–10.13 | 24 |
| Capecitabine26 | 308–348 | 15.2–35.4 | 477–955 | 2.7–158.8 | 40 |
| Paclitaxel27 | 308–328 | 10–27.5 | 654–915 | 1.2–6.2 | 21 |
| 5-Fluorouracil27 | 308–328 | 12.5–25 | 541–901 | 3.8–14.6 | 18 |
| Thymidine27 | 308–328 | 10–30 | 325–928 | 1.2–8 | 25 |
| Decitabine28 | 308–338 | 12–40 | 383–971 | 28.4–1070 | 32 |
Most widely used correlations for drug solubility in SCCO2
The developed empirical correlations by Chrastil35, Jouyban et al.36, Kumar and Johnstone37, Garlapati and Madras38, Bian et al.39, Bartle et al.40, Méndez-Santiago and Teja41, Sodeifian et al.42, Tan et al.43, and Gordillo et al.44 are widely used to estimate drug solubility in supercritical carbon dioxide. It should be mentioned that some of these correlations were initially proposed for the prediction of the solid (not specifically drug) solubility in SCCO2. However, researchers preserved their mathematical forms, readjusted their coefficients, and modified them to be applied in the drug/SCCO2 phase equilibria modeling19,25,26,28.
The mathematical formulations of these empirical correlations are given in Table 2. It should be mentioned that excluding Eq. (1) that predicts the solubility in terms of the mass of solids per volume of the solvent (), all other considered correlations provide the solubility in terms of mole fraction unit (). Furthermore, temperature, pressure, and pure SCCO2 density are designated by , , and , respectively. Finally, the coefficients of the correlations are shown by the to notations.
Table 2.
Available empirical correlations for solute/drug solubility in supercritical carbon dioxide.
| Correlation | Formula | |
|---|---|---|
| Chrastil35 | Equation (1) | |
| Jouyban et al.36 | Equation (2) | |
| Kumar and Johnstone37 | Equation (3) | |
| Garlapati and Madras38 | Equation (4) | |
| Bian et al.39 | Equation (5) | |
| Bartle et al.40 | Equation (6) | |
| Méndez-Santiago and Teja41 | Equation (7) | |
| Sodeifian et al.42 | Equation (8) | |
| Tan et al.43 | Equation (9) | |
| Gordillo et al.44 | Equation (10) |
Excluding the pure SCCO2 density of the Eq. (3) that is in the kmol/m3 unit, the units of all other variables are in complete agreement with those unites presented in Table 1.
Results and discussion
This section presents the idea of developing the modified Arrhenius correlation, adjusts its unknown coefficients, and compares its accuracy with other available correlations. The next part of this section is devoted to the performance analysis of the modified Arrhenius correlation using different graphical methods. Finally, the modified Arrhenius correlation is employed to monitor the effect of operating conditions on the anti-cancer drug solubility in SCCO2.
Developing the modified Arrhenius correlation
The massive data processing stages are performed on the experimental values of solubility of each drug in SCCO2 to reach a general form of the proposed correlation as follows:
| 11 |
Equation (11) states that the anti-cancer drug solubility in the SCCO2 can be accurately estimated by combining an Arrhenius term and a departure function.
At this stage, it is necessary to clarify how the pre-exponential and exponential parts of the Arrhenius term are related to the influential variables. Then, the departure function incorporates to reduce the deviation between the Arrhenius term predictions and experimental measurements.
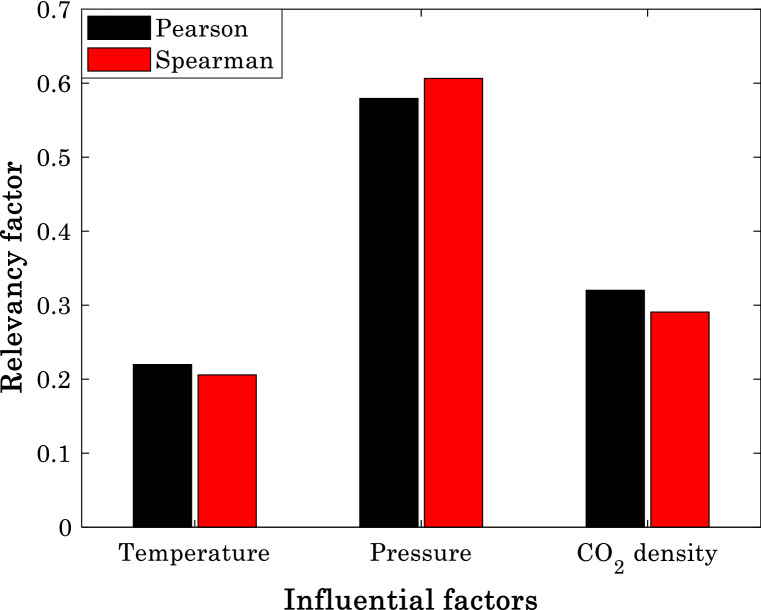
Spearman and Pearson are two well-known relevancy discovery scenarios in the field of data processing62. They introduce the relevancy between a pair of feature-response variables by a factor in the range of − 1 to + 1. The minus, zero, and positive factors correspond with indirect dependency, no-relation, and direct dependency, respectively62,66. The strength of either direct or indirect relevancy increases by increasing the magnitude of factors67. Furthermore, the higher absolute value of the Spearman than the Pearson factor confirms that the non-linear relationship is stronger than the linear one and vice versa62,66.
Figure 1 exhibits the values of relevancy factor between anti-cancer drug solubility and pressure, temperature, and pure SCCO2 density. This figure confirms that direct relationships exist between the response and all feature variables. The anti-cancer drug solubility has the strongest relationship with the pressure and weakest dependency to the temperature. Moreover, since the Pearson factors for temperature and CO2 density are higher than the Spearman ones, the linear relationship is superior to the non-linear one. The higher Spearman factor than Pearson for the pressure shows that the anti-cancer drug solubility non-linearly relates to the pressure.
Figure 1.
Relevancy between the solubility of anti-cancer drugs in supercritical CO2 and temperature, pressure, and carbon dioxide density.
These findings are in complete agreement with the mathematical form of the Arrhenius model. Indeed, the pre-exponential term can be a function of temperature and CO2 density, and the exponential term provides the non-linear relation with the pressure.
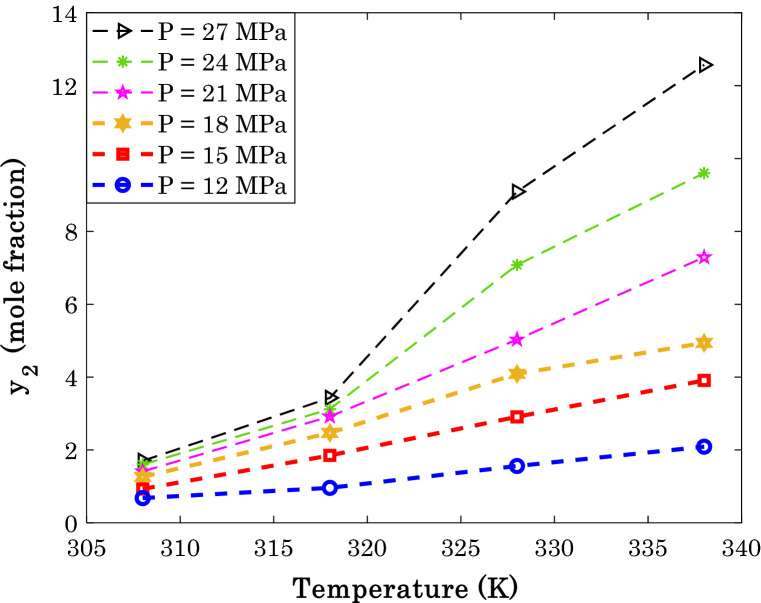
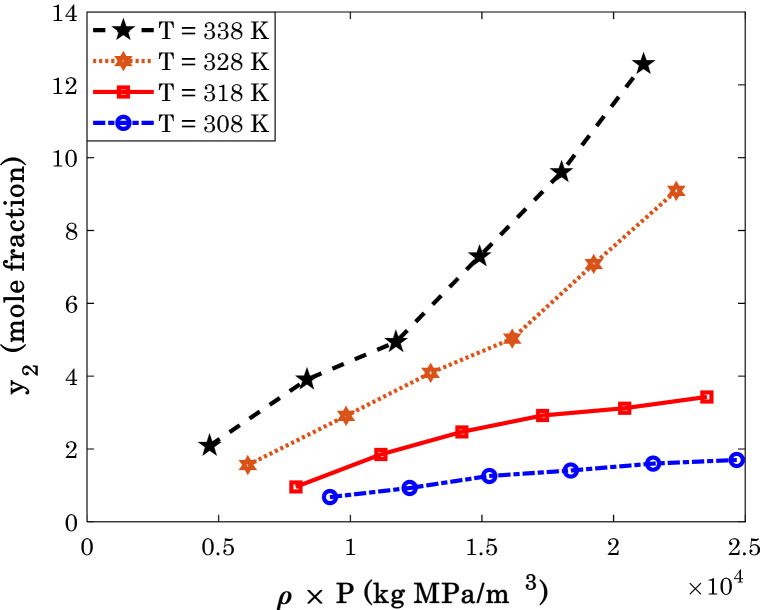
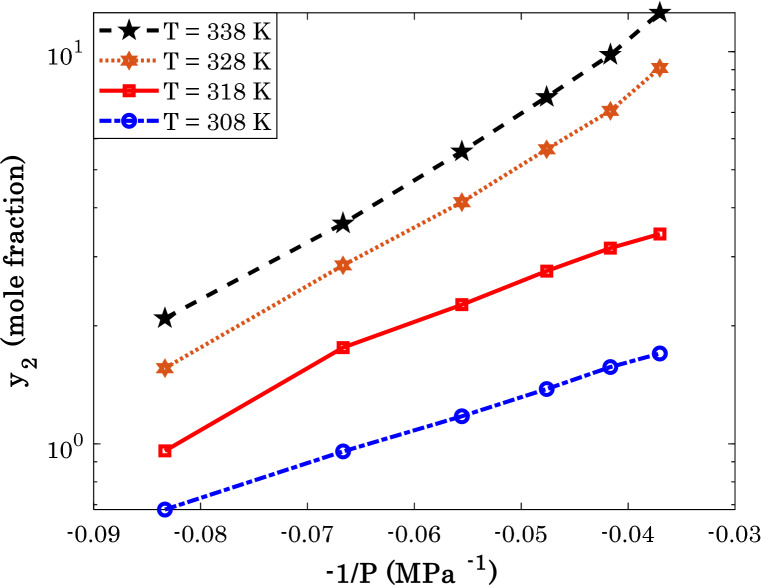
The previous findings specify the linear dependency of the anti-cancer drug solubility on temperature and CO2 density and its non-linear relationship with the pressure. Figures 2, 3 and 4 are plotted to approve these findings through visual inspection.
Figure 2.
Dependency of sorafenib tosylate solubility in the supercritical CO2 on the isobaric variation of temperature (the cartesian coordinate).
Figure 3.
The variation of sorafenib tosylate solubility in the SCCO2 by the solvent density (the cartesian coordinate).
Figure 4.
The effect of the inverse pressure on the sorafenib tosylate solubility in the SCCO2 (the semi-logarithm coordinate).
The experimental values of typical anti-cancer drug solubility in the SCCO2 as a function of temperature are shown in Fig. 2. This figure approves that the temperature dependency of the solubility of the anti-cancer drugs is almost linear. The departure function is efficiently involved in compensating for the deviation from the linear relationship.
Since the density of the pure SCCO2 changes by both pressure and temperature, it is impossible to monitor the dependency of the anti-cancer drug solubility on the CO2 density in the two-dimensional graph. Hence, Fig. 3 depicts the solubility of a typical anti-cancer drug versus the product of pressure and CO2 density. The linear dependency of the anti-cancer drug solubility on the pure SCCO2 density can be inferred from this figure. Similar to the temperature, the departure function can compensate for the deviation from the linear relationship between drug solubility and CO2 density.
The semi-logarithm presentation of typical anti-cancer drug solubility in the SCCO2 versus the inverse of pressure is shown in Fig. 4. This figure approves that the anti-cancer drug solubility in SCCO2 exponentially relates to the inverse of pressure, i.e., . The observed deviation between the exponential data and predictions of the Arrhenius term for the pressure effect is then reduced by applying the departure function.
In summary, the following Arrhenius-shape correlation68 is inferred to estimate the anti-cancer drug solubility in the SCCO2 (Eq. 12).
| 12 |
It is expected that some deviations observe between the Arrhenius term predictions and actual solubility data. However, it is possible to enhance the accuracy of the Arrhenius-shape model by diminishing the observed deviations. Therefore, a new term (i.e., departure function) adds to the Arrhenius-shape part to compensate for this deviation. The observed deviation shows the highest compatibility with the natural logarithm of the CO2 density to the temperature as follows:
| 13 |
In summary, the general form of the proposed correlation achieves by combining the Arrhenius term and departure function (Eq. 14).
| 14 |
Equation (15) presents the final form of the proposed correlation for estimating the solubility of the anti-cancer drugs in supercritical CO2.
| 15 |
The pre-exponential part of the Arrhenius term linearly combines the effect of temperature and CO2 density, while its exponential part is a function of pressure only. The departure function linearly relates to the natural logarithm of the CO2 density to the temperature ratio.
Adjusting the coefficients of the correlations
After determining the general form of the proposed correlation, it is now necessary to adjust its coefficients using an appropriate method. The differential evolution (DE) optimization algorithm69,70 is employed to adjust these unknown coefficients through a non-linear regression process. The absolute average relative deviation (AARD%) between the model predictions and actual measurements is an objective function for the optimization stage. The AARD% formula can be expressed by Eq. (16)71.
| 16 |
Table 3 presents the adjusted coefficients for estimating the solubility of different anti-cancer drugs in the SCCO2.
Table 3.
Adjusted coefficients of the proposed correlation for estimating the solubility of anti-cancer drugs in supercritical CO2.
| Drug | a1 × 10–6 | a2 × 10–6 | a3 × 10–6 | a4 | a5 × 10–6 | a6 × 10–6 |
|---|---|---|---|---|---|---|
| Sorafenib tosylate | 1.4247605573 | − 0.0500529210 | − 385.827674360 | 45.3662839688 | 0 | 0.349064452 |
| Sunitinib malate | 0.2647256734 | − 1.4200164959 | 1355.66373666 | 36.2840647550 | − 12.8796352 | 0 |
| Azathioprine | 0.9468557792 | − 0.0163521099 | − 266.098396089 | 24.1069578946 | 8.36900373 | − 4.83860672 |
| Busulfan | 60.280909168 | − 16.630567159 | − 1344.60675047 | 78.2721455261 | 76.7145899 | 0 |
| Tamoxifen | 144.11848954 | − 42.703480295 | − 1974.01401538 | 99.6434546809 | 41.05460792 | 6.14532671 |
| Letrozole | 8.7649418657 | − 2.9569956441 | 4.94014077630 | 80.8669042062 | 4.145085191 | − 0.53838515 |
| Tamsulosin | 0.7923204828 | 0.1478689559 | − 368.263373717 | 35.1646118112 | 0 | 2.51134612 |
| Capecitabine | 48.093681561 | − 12.750147899 | − 2037.79351684 | 123.522295303 | 17.1813407 | − 8.09385756 |
| Paclitaxel | 0.0068347581 | 0.0253752394 | − 6.61523852780 | 14.6087222619 | − 22.8448049 | 17.3239309 |
| 5-Fluorouracil | 0.5186887168 | − 0.1340640969 | − 1.39609503380 | 44.0728502801 | − 10.2690278 | 11.7076100 |
| Thymidine | 0.2122407854 | 0.0094685158 | − 70.3123673279 | 18.0254848942 | − 2.51330781 | 3.01138517 |
| Decitabine | 117.68771002 | − 10.092201917 | − 25,295.9332530 | 74.7951605316 | 48.3284747 | 0 |
The literature has already used some correlations (see Table 2) to estimate the anti-cancer drug solubility in SCCO2. Therefore, the researchers readjusted coefficients and apply them in the drug/SCCO2 systems. However, readjusting the coefficients of other ones are accomplished in the current study. Supplementary file presents the coefficients of the considered correlations for solubility of all anti-cancer drugs in supercritical CO2. The optimization algorithm and objective function like that utilized for the modified Arrhenius model are also employed to adjust the coefficients of the literature correlations.
Comparative analysis
This section compares the uncertainty in the predictions of the modified Arrhenius model and available correlations in the literature for solubility of anti-cancer drugs in SCCO2. The prediction uncertainty of all considered empirical correlations is measured in terms of the AARD% and reported in Table 4. First of all, it is better to clarify that the highlighted cells (gray color) are calculated in the present study, and the clean cells are those reported in the literature. As mentioned earlier, the associated coefficients for calculating this AARD% are presented in Supplementary file. The cells shown by the bold font are the smallest AARD% (the best results) obtained for estimating a specific anti-cancer drug in supercritical CO2. It is obvious that the modified Arrhenius correlation provides the most accurate results for solubility of six out of twelve anti-cancer drugs in SCCO2 (i.e., sorafenib tosylate, sunitinib malate, azathioprine, tamsulosin, 5-fluorouracil, thymidine).
Table 4.
Uncertainty of the proposed model and available correlations in the literature in terms of AARD% (the italicized cells are calculated in the current study; the bold font values show the most accurate predictions).
| Drug | Empirical correlation | |||||
|---|---|---|---|---|---|---|
| Modified Arrhenius | Chrastil35 | Jouyban et al.36 | Kumar and Johnston37 | Garlapati and Madras38 | ||
| Sorafenib tosylate | 7.91 | 13.9019 | 14.4019 | 12.7019 | 11.0019 | |
| Sunitinib malate | 3.89 | 21.2620 | 14.2020 | 38.85 | 17.1620 | |
| Azathioprine | 4.29 | 9.8821 | 10.2121 | 16.26 | 8.6221 | |
| Busulfan | 7.41 | 11.2022 | 88.70 | 7.5722 | 11.2022 | |
| Tamoxifen | 12.02 | 16.5023 | 96.87 | 11.1023 | 16.4023 | |
| Letrozole | 13.21 | 22.16 | 21.5024 | 39.42 | 7.1424 | |
| Tamsulosin | 9.27 | 22.1125 | 82.70 | 15.2025 | 24.91 | |
| Capecitabine | 11.42 | 12.2026 | 11.9026 | 10.3026 | 43.48 | |
| Paclitaxel | 9.69 | 28.90 | 80.95 | 38.89 | 11.79 | |
| 5-Fluorouracil | 8.39 | 19.48 | 69.90 | 19.48 | 22.77 | |
| Thymidine | 16.64 | 25.10 | 91.77 | 29.86 | 32.48 | |
| Decitabine | 9.11 | 15.3028 | 88.88 | 9.0428 | 15.3028 | |
| Overall | 9.54 | 17.42 | 56.51 | 18.97 | 19.64 | |
| Drug | Empirical correlation | |||||
|---|---|---|---|---|---|---|
| Bian et al.39 | Bartle et al.40 | MST41 | Sodeifian et al.42 | Tan et al.43 | Gordillo44 | |
| Sorafenib tosylate | 10.3019 | 13.7019 | 15.3019 | 10.1019 | 52.21 | 95.85 |
| Sunitinib malate | 21.0720 | 26.1120 | 24.6820 | 12.1620 | 54.69 | 91.67 |
| Azathioprine | 8.4021 | 12.2221 | 10.7021 | 8.0421 | 13.72 | 84.91 |
| Busulfan | 6.55 | 11.7022 | 10.7022 | 25.99 | 32.48 | 96.87 |
| Tamoxifen | 8.84 | 16.1023 | 16.0023 | 58.03 | 45.91 | 96.87 |
| Letrozole | 10.42 | 46.61 | 15.4024 | 26.66 | 39.20 | 95.00 |
| Tamsulosin | 14.2425 | 17.0825 | 16.9825 | 13.6425 | 29.07 | 95.83 |
| Capecitabine | 33.00 | 12.8026 | 9.9026 | 41.4726 | 9.1026 | 20.5026 |
| Paclitaxel | 15.96 | 50.09 | 55.31 | 9.26 | 18.44 | 95.23 |
| 5-Fluorouracil | 15.59 | 35.34 | 31.98 | 13.86 | 25.52 | 82.99 |
| Thymidine | 19.68 | 46.90 | 40.32 | 22.31 | 32.78 | 96.00 |
| Decitabine | 8.82 | 15.3028 | 13.3028 | 80.01 | 49.18 | 96.88 |
| Overall | 14.90 | 23.24 | 20.01 | 30.05 | 33.19 | 84.66 |
On the other hand, the derived correlation by Bian et al.39 predicts the solubility of busulfan, tamoxifen, and decitabine in supercritical CO2 with the highest accuracy. Finally, the Garlapati and Madras38, Sodeifian et al.42, and Tan et al.43 correlations provide the most accurate predictions for only one anti-cancer drug.
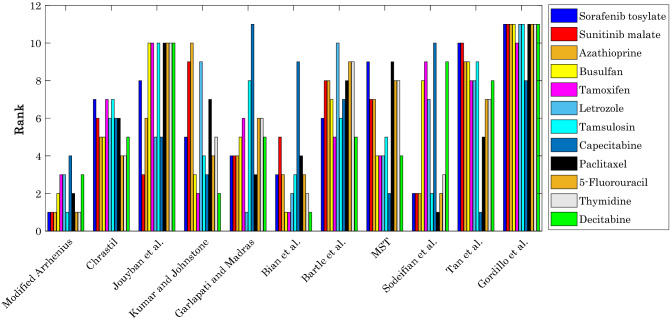
Figure 5 exhibits the results of ranking analysis on the accuracy of the modified Arrhenius model and available empirical correlations in the literature for calculating the solubility of different anti-cancer drugs in supercritical CO2. It can be readily deduced that the proposed correlation in the current study not only presents the most accurate predictions for six anti-cancer drugs, it also has two second and three third ranks. The worst accuracy of the modified Arrhenius correlation is associated with capecitabine solubility in the SCCO2 (i.e., the fourth rank). The proposed correlation by Bian et al.39 with the three first, two second, four third, one fourth, and one ninth ranks is the next reliable model for the given task. On the other hand, the proposed correlations by Gordillo44, Jouyban et al.36, and Tan et al.43 have the highest levels of uncertainty, respectively.
Figure 5.
Outcome of the ranking analysis on the accuracy of the developed correlation and those available in the literature.
Overall ranking of the correlation
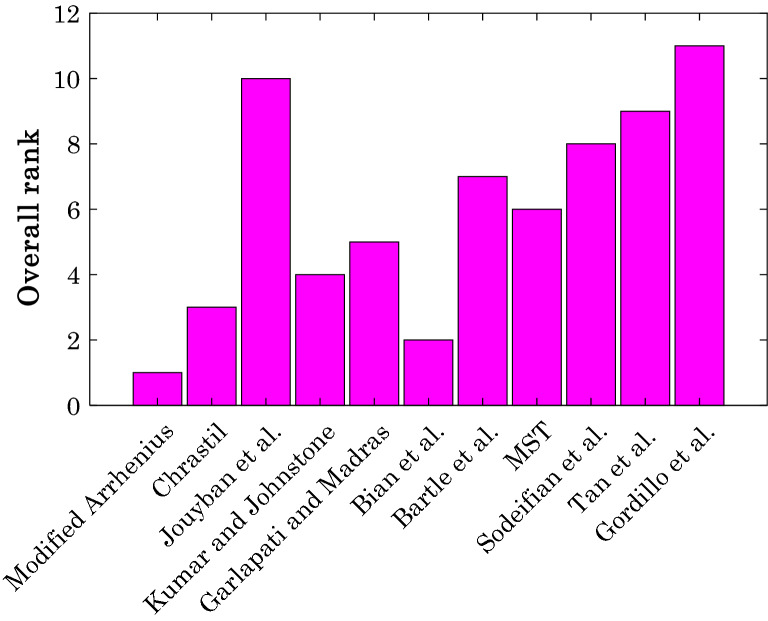
This section investigates/compares the accuracy of the modified Arrhenius model and available empirical correlation in the literature for estimating the whole of the database (solubility of all anti-cancer drugs in supercritical CO2). Hence, Fig. 6 illustrates the results of ranking analysis for the overall accuracy of the considered empirical correlations.
Figure 6.
Overall ranking of the considered correlations to predict the solubility of anti-cancer drugs in supercritical carbon dioxide.
As expected, the modified Arrhenius correlation (with the smallest overall AARD = 9.54%) takes the first ranking place for the whole of the experimental databank. The Bian et al. correlation39 with the overall AARD = 14.90% is the next accurate model for the given purpose. Generally, all available correlations in the literature have the AARD% equal to or higher than 14.9%. Indeed, the modified Arrhenius correlation improves the accuracy of available models in the literature by at least 56.2%.
Performance monitoring of the modified Arrhenius correlation
The agreement between the experimental solubility data and calculated values by the developed modified Arrhenius correlation is plotted in Fig. 7. This figure includes the solubility of all anti-cancer drugs in the supercritical carbon dioxide. Despite an infinitesimal range of the solubility data (~ 10–4), an acceptable compatibility can be observed between actual and calculated information. The modified Arrhenius correlation provides the R2 (regression coefficient, Eq. 17a72) of 0.98479 and standard error of 2.02 × 10–5 for all 316 experimental data.
| 17a |
Figure 7.
Cross-plot of the modified Arrhenius predictions versus experimental measurements for anti-cancer drug solubility in supercritical CO2.
Figure 8 investigates the performance of the modified Arrhenius correlation as a function of its relative deviation (RD) for the available database. Equation (17b) expresses the formulation of the RD index73.
| 17b |
Figure 8.
The observed relative deviations for estimating each experimental measurement of anti-cancer drug solubility in supercritical carbon dioxide.
This figure confirms that the proposed correlation has successfully correlate the experimental solubility data to its corresponding influential variables. Excluding only three experiments, all other solubility measurements are estimated with the − 0.5 < RD < 0.5.
Differentiating between outlier/valid data
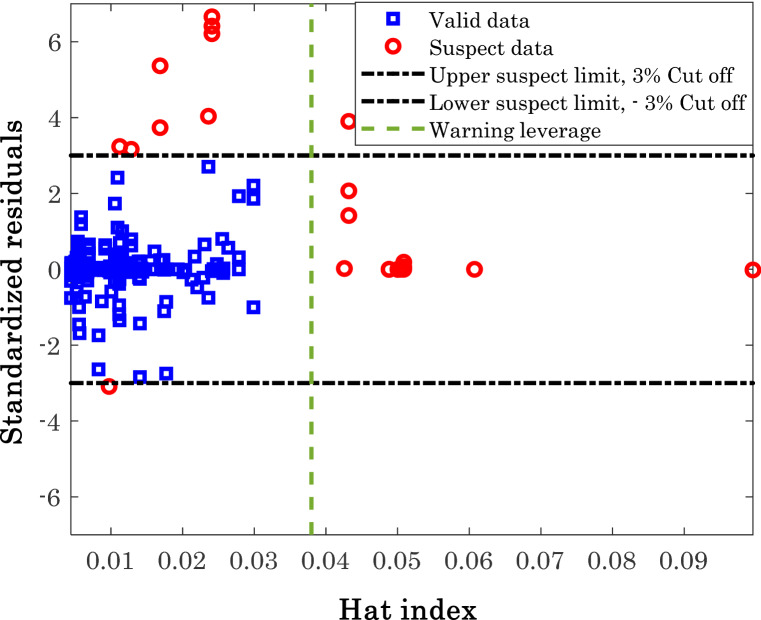
The focus of this section is concentrated on diagnosis of either valid and suspect data. The experimentally-measured information often contain noises74 and uncertainties75. The leverage method is used to conduct this analysis76. As Fig. 9 shows, the leverage method discriminates between the valid (□ symbols) and suspect (○ symbols) information by plotting the standardized residual (SR) as a function of hat index. The SR can be obtained by dividing the residual error (RE) by its standard deviation (SD). Equations (18) to (21) present the RE, average value of RE, SD, and SR formula, respectively77,78.
| 18 |
| 19 |
| 20 |
| 21 |
Figure 9.
Differentiating between valid and suspect data collected from the literature.
Applying the leverage method on the experimental databank and estimated values of anti-cancer drug solubility (Fig. 9) justifies that the major segment of the experimental data (92.72%) is valid, and only 23 datasets may be outliers.
The excellent accuracy of the modified Arrhenius correlation is previously approved using experimental data and comparison by other available models in the literature. Moreover, the current analysis confirms the validity of the experimental databank. Therefore, it can be claimed that the modified Arrhenius correlation can be readily used in the real application.
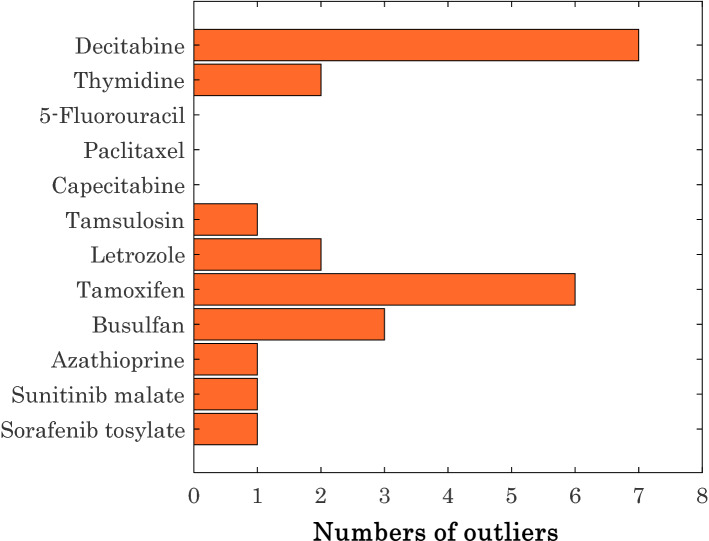
The numbers of possible outlier for each anti-cancer drug are reported in Fig. 10. It seems that the experimental solubility data for capecitabine, paclitaxel, and 5-fluorouracil with no outlier are the most reliable information. On the other hand, the solubility measurements of decitabine and tamoxifen (with seven and six outliers) in SCCO2 are the under-question experiments.
Figure 10.
Numbers of detected outliers for the considered anti-cancer drugs.
Investigating the effect of operating conditions
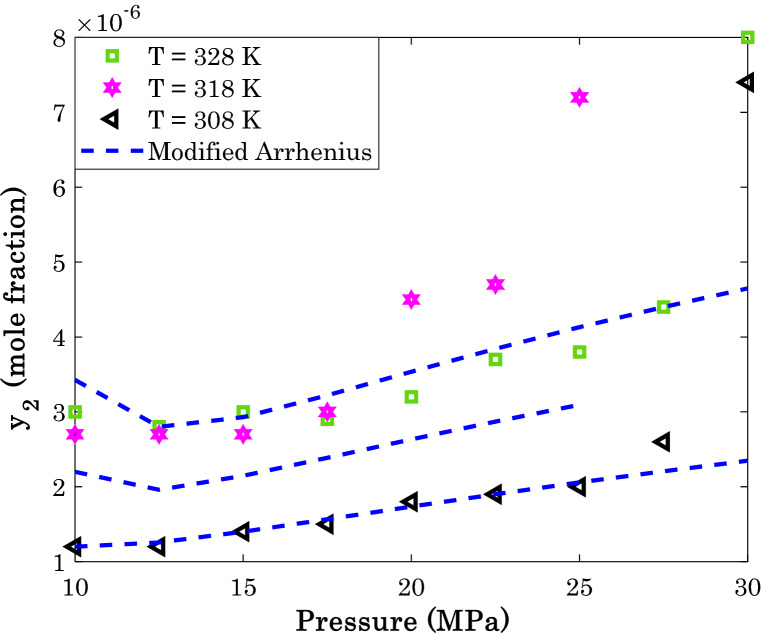
It is previously shown in Table 4 that the modified Arrhenius correlation predict sunitinib malate (AARD = 3.89%) and thymidine (AARD = 16.64%) with the highest and lowest accuracies, respectively. This section investigates the effect of pressure and temperature on the solubility of these anti-cancer drugs in the SCCO2 both experimentally and modeling.
Figure 11 explains the effect of isothermal variation of the operating pressure on the sunitinib malate in supercritical carbon dioxide, while Fig. 12 is associated with the thymidine/SCCO2 binary system.
Figure 11.
Variation of the sunitinib malate solubility in the supercritical CO2 as a function of operating pressure and temperature.
Figure 12.
The effect of pressure and temperature on the thymidine solubility in the supercritical carbon dioxide.
Excluding some scattering data in Fig. 12, generally the solubility of anti-cancer drugs in SCCO2 increase by increasing either pressure or temperature. This finding is in complete agreement of relevancy analysis (see Fig. 1). Moreover, an acceptable level of agreement exists between actual solubility data and their associated predictions by the modified Arrhenius correlation.
A relatively high scattering measurements for thymidine/SCCO2 system (especially at higher temperatures) is responsible for observed deviation between actual and modeling data. It is worth noting that this is the most accurate predictions among eleven different empirical correlations (Supplementary Information).
Investigating the effect drug type
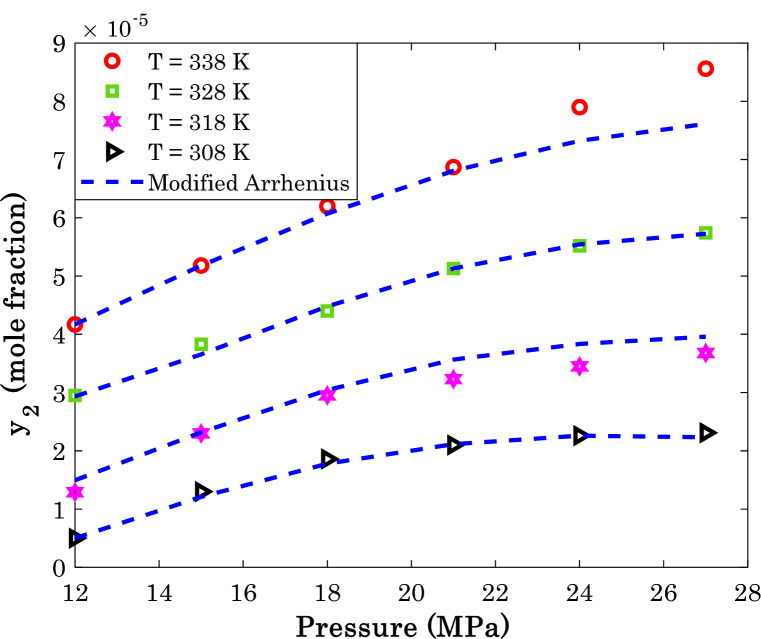
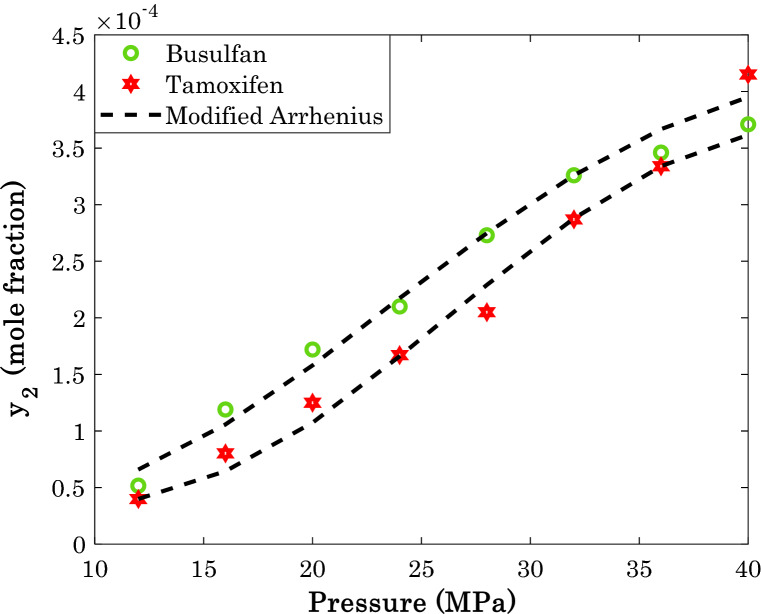
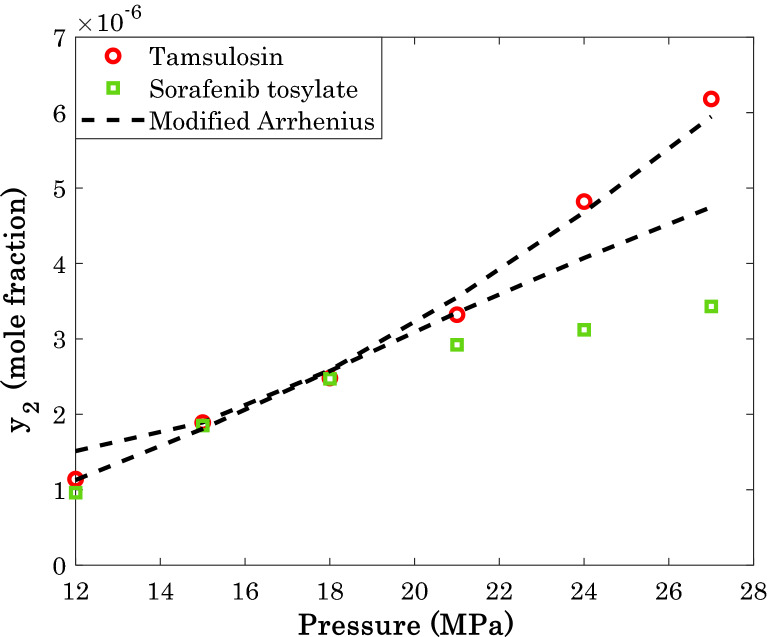
By measuring the average value of solubility of different anti-cancer drugs, it is concluded that busulfan and tamoxifen have the highest tendency for dissolution in supercritical CO2, while the sorafenib tosylate and tamsulosin show the lowest tendency.
Figures 13 and 14 present the modeling and experimental data for two high-soluble and two low-soluble anti-cancer drugs in SCCO2, respectively. The provided AARD of 7.92% (busulfan) and 7.40% (tamoxifen) for the high-soluble anti-cancer drugs by the modified Arrhenius correlation is a justification for excellent performance of the model.
Figure 13.
The highest amount of drug solubility in SCCO2 at temperature = 318 K.
Figure 14.
The smallest amount of drug solubility in SCCO2 at temperature = 318 K.
On the other hand, the proposed correlation predicts the solubility of the low-soluble anti-cancer drugs with the AARD of 8.44% (tamsulosin) and 17.92% (sorafenib tosylate).
It should be mentioned that this level of uncertainty for this ultra-low variable (anti-cancer drug solubility in SCCO2) has its own scientific and real-field merits.
Maximum achievable drug solubility in SCCO2
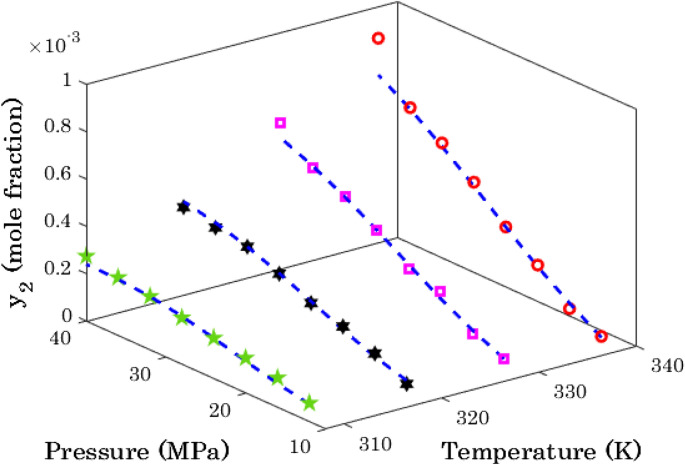
The previous analysis approved that the busulfan is the most soluble anti-cancer drug in the supercritical CO2. Therefore, for locating the operating condition that maximizes the busulfan solubility in the SCCO2, it is necessary to monitor it for all pressures and temperatures. Figure 15 exhibits the busulfan solubility in SCCO2 for all possible operating conditions from experimental and modeling perspectives.
Figure 15.
Effect of operating conditions on the busulfan solubility in SCCO2 (open circle: 338 K, open rectangle: 328 K, six pointed filled star: 318 K, four pointed filled star: 308 K, dashed lines modified Arrhenius predictions).
Like all other analyses, an excellent performance of the modified Arrhenius correlation can be justified in this analysis too. This figure also clarifies that the positive effect of pressure on the drug solubility intensifies by increasing the temperature. In other word, the slope of solubility with respect to the pressure increases by increasing temperature.
Finally, both experimental data and modeling results show that the highest busulfan solubility in the SCCO2 may be achieved at the highest allowable temperature and pressure (i.e., P = 40 bar, T = 338 K).
Conclusion
A combination of the Arrhenius-shape and departure functions is proposed to correlate the anti-cancer drug solubility in the supercritical carbon dioxide. The pre-exponential part of the Arrhenius-shape term is linearly related to the temperature and carbon dioxide density, and its exponential part inversely relates to the pressure. The departure function is directly related to the natural logarithm of the carbon dioxide density to the temperature ratio. The developed correlation outperformed all well-known literature equations for predicting the solute solubility in supercritical carbon dioxide. The modified Arrhenius correlation provided the AARD = 9.54% and R2 = 0.98479 for estimating all experimental datasets in the literature. In contrast, the most accurate correlation in the literature (i.e., Bian et al. correlation) showed the AARD = 14.90% for predicting the considered database. It is possible to improve predicting accuracy of anti-cancer drug solubility in supercritical CO2 by more than 56% using the developed correlation in this study. The relevancy analysis exhibited that anti-cancer drug solubility in supercritical CO2 increases by increasing either pressure and temperature. Furthermore, it is found that less than 7.5% of the literature data are suspect information, and the remaining 92.5% are valid measurements. The provided Supplementary Material reports the adjusted coefficients of the available empirical correlations in the literature.
Supplementary Information
Author contributions
All authors have a same contribution in this study.
Data availability
All data generated or analyzed during this study are available on reasonable request from the corresponding author.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-022-13233-x.
References
- 1.Kiran E, Debenedetti PG, Peters CJ. Supercritical Fluids: Fundamentals and Applications. Springer Science & Business Media; 2012. [Google Scholar]
- 2.Hozhabr SB, Mazloumi SH, Sargolzaei J. Correlation of solute solubility in supercritical carbon dioxide using a new empirical equation. Chem. Eng. Res. Des. 2014;92:2734–2739. doi: 10.1016/j.cherd.2014.01.026. [DOI] [Google Scholar]
- 3.Li MJ, Zhu HH, Guo JQ, Wang K, Tao WQ. The development technology and applications of supercritical CO2 power cycle in nuclear energy, solar energy and other energy industries. Appl. Therm. Eng. 2017;126:255–275. doi: 10.1016/j.applthermaleng.2017.07.173. [DOI] [Google Scholar]
- 4.Wang W, et al. Supercritical carbon dioxide applications in food processing. Food Eng. Rev. 2021;13:570–591. doi: 10.1007/s12393-020-09270-9. [DOI] [Google Scholar]
- 5.Rezaei T, et al. A universal methodology for reliable predicting the non-steroidal anti-inflammatory drug solubility in supercritical carbon dioxide. Sci. Rep. 2022;12:1–12. doi: 10.1038/s41598-021-99269-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Jiang Q, et al. Alzheimer’s disease variants with the genome-wide significance are significantly enriched in immune pathways and active in immune cells. Mol. Neurobiol. 2017;54(1):594–600. doi: 10.1007/s12035-015-9670-8. [DOI] [PubMed] [Google Scholar]
- 7.Lai WF, Wong WT. Property-tuneable microgels fabricated by using flow-focusing microfluidic geometry for bioactive agent delivery. Pharmaceutics. 2021;13:787. doi: 10.3390/pharmaceutics13060787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Obireddy SR, Lai WF. Preparation and characterization of 2-hydroxyethyl starch microparticles for co-delivery of multiple bioactive agents. Drug Deliv. 2021;28:1562–1568. doi: 10.1080/10717544.2021.1955043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yan J, et al. Chiral protein supraparticles for tumor suppression and synergistic immunotherapy: an enabling strategy for bioactive supramolecular chirality construction. Nano Lett. 2020;20(8):5844–5852. doi: 10.1021/acs.nanolett.0c01757. [DOI] [PubMed] [Google Scholar]
- 10.Hou C, et al. Recent progress in the research of Angelica sinensis (Oliv.) Diels polysaccharides: extraction, purification, structure and bioactivities. Chem. Biol. Technol. Agric. 2021;8(1):1–14. doi: 10.1186/s40538-021-00214-x. [DOI] [Google Scholar]
- 11.Lashkarbolooki M, Vaferi B, Shariati A, Zeinolabedini Hezave A. Investigating vapor-liquid equilibria of binary mixtures containing supercritical or near-critical carbon dioxide and a cyclic compound using cascade neural network. Fluid Phase Equilib. 2013;343:24–29. doi: 10.1016/j.fluid.2013.01.012. [DOI] [Google Scholar]
- 12.Bhusnure O, et al. Importance of supercritical fluid extraction techniques in. Indo Am. J. Pharm. Res. 2016;5:3785–3801. [Google Scholar]
- 13.Champeau M, Thomassin JM, Tassaing T, Jérôme C. Drug loading of polymer implants by supercritical CO2 assisted impregnation: A review. J. Control. Release. 2015;209:248–259. doi: 10.1016/j.jconrel.2015.05.002. [DOI] [PubMed] [Google Scholar]
- 14.Baghban A, Sasanipour J, Zhang Z. A new chemical structure-based model to estimate solid compound solubility in supercritical CO2. J CO2 Util. 2018;26:262–270. doi: 10.1016/j.jcou.2018.05.009. [DOI] [Google Scholar]
- 15.Bray F, Laversanne M, Weiderpass E, Soerjomataram I. The ever-increasing importance of cancer as a leading cause of premature death worldwide. Cancer. 2021;127:3029–3030. doi: 10.1002/cncr.33587. [DOI] [PubMed] [Google Scholar]
- 16.Kazemi M, et al. Pegylated multifunctional pH-responsive targeted polymeric micelles for ovarian cancer therapy: Synthesis, characterization and pharmacokinetic study. Int. J. Polym. Mater. Polym. Biomater. 2021;70:1012–1026. doi: 10.1080/00914037.2020.1776282. [DOI] [Google Scholar]
- 17.Kazemi M, et al. In vitro and in vivo evaluation of novel DTX-loaded multifunctional heparin-based polymeric micelles targeting folate receptors and endosomes. Recent Pat. Anticancer. Drug Discov. 2020;15:341–359. doi: 10.2174/1574892815666201006124604. [DOI] [PubMed] [Google Scholar]
- 18.Molani S, Madadi M, Williams DL. Investigating the effectiveness of breast cancer supplemental screening considering radiologists’ bias. MedRxiv. 2020 doi: 10.1101/2020.12.16.20248373. [DOI] [Google Scholar]
- 19.Sodeifian G, Razmimanesh F, Sajadian SA. Prediction of solubility of sunitinib malate (an anti-cancer drug) in supercritical carbon dioxide (SC–CO2): Experimental correlations and thermodynamic modeling. J. Mol. Liq. 2020;297:105998. doi: 10.1016/j.molliq.2019.111740. [DOI] [Google Scholar]
- 20.Sodeifian G, Saadati Ardestani N, Sajadian SA, Golmohammadi MR, Fazlali A. Prediction of solubility of sodium valproate in supercritical carbon dioxide: Experimental study and thermodynamic modeling. ACS Appl. Mater. Interfaces. 2020;297:111740. [Google Scholar]
- 21.Sodeifian G, Razmimanesh F, Saadati Ardestani N, Sajadian SA. Experimental data and thermodynamic modeling of solubility of Azathioprine, as an immunosuppressive and anti-cancer drug, in supercritical carbon dioxide. J. Mol. Liq. 2020;299:112179. doi: 10.1016/j.molliq.2019.112179. [DOI] [Google Scholar]
- 22.Pishnamazi M, et al. Measuring solubility of a chemotherapy-anti cancer drug (busulfan) in supercritical carbon dioxide. J. Mol. Liq. 2020;317:113954. doi: 10.1016/j.molliq.2020.113954. [DOI] [Google Scholar]
- 23.Pishnamazi M, et al. Thermodynamic modelling and experimental validation of pharmaceutical solubility in supercritical solvent. J. Mol. Liq. 2020;319:114120. doi: 10.1016/j.molliq.2020.114120. [DOI] [Google Scholar]
- 24.Sodeifian G, Sajadian SA. Solubility measurement and preparation of nanoparticles of an anticancer drug (Letrozole) using rapid expansion of supercritical solutions with solid cosolvent (RESS-SC) J. Supercrit. Fluids. 2018;133:239–252. doi: 10.1016/j.supflu.2017.10.015. [DOI] [Google Scholar]
- 25.Hazaveie SM, Sodeifian G, Sajadian SA. Measurement and thermodynamic modeling of solubility of Tamsulosin drug (anti cancer and anti-prostatic tumor activity) in supercritical carbon dioxide. J. Supercrit. Fluids. 2020;163:104875. doi: 10.1016/j.supflu.2020.104875. [DOI] [Google Scholar]
- 26.Yamini Y, et al. Solubility of capecitabine and docetaxel in supercritical carbon dioxide: Data and the best correlation. Thermochim. Acta. 2012;549:95–101. doi: 10.1016/j.tca.2012.09.010. [DOI] [Google Scholar]
- 27.Suleiman D, Antonio Estévez L, Pulido JC, García JE, Mojica C. Solubility of anti-inflammatory, anti-cancer, and anti-HIV drugs in supercritical carbon dioxide. J. Chem. Eng. Data. 2005;50:1234–1241. doi: 10.1021/je049551l. [DOI] [Google Scholar]
- 28.Pishnamazi M, et al. Experimental and thermodynamic modeling decitabine anti cancer drug solubility in supercritical carbon dioxide. Sci. Rep. 2021;11:1–8. doi: 10.1038/s41598-020-79139-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Coimbra P, Duarte CMM, De Sousa HC. Cubic equation-of-state correlation of the solubility of some anti-inflammatory drugs in supercritical carbon dioxide. Fluid Phase Equilib. 2006;239:188–199. doi: 10.1016/j.fluid.2005.11.028. [DOI] [Google Scholar]
- 30.Sodeifian G, Saadati Ardestani N, Sajadian SA, Panah HS. Measurement, correlation and thermodynamic modeling of the solubility of Ketotifen fumarate (KTF) in supercritical carbon dioxide: Evaluation of PCP-SAFT equation of state. Fluid Phase Equilib. 2018;458:102–114. doi: 10.1016/j.fluid.2017.11.016. [DOI] [Google Scholar]
- 31.Yang H, Zhong C. Modeling of the solubility of aromatic compounds in supercritical carbon dioxide-cosolvent systems using SAFT equation of state. J. Supercrit. Fluids. 2005;33:99–106. doi: 10.1016/j.supflu.2004.05.008. [DOI] [Google Scholar]
- 32.Huang Z, Kawi S, Chiew YC. Application of the perturbed Lennard-Jones chain equation of state to solute solubility in supercritical carbon dioxide. Fluid Phase Equilib. 2004;216:111–122. doi: 10.1016/j.fluid.2003.10.004. [DOI] [Google Scholar]
- 33.Yang M, et al. Predictive model for minimum chip thickness and size effect in single diamond grain grinding of zirconia ceramics under different lubricating conditions. Ceram. Int. 2019;45:14908–14920. doi: 10.1016/j.ceramint.2019.04.226. [DOI] [Google Scholar]
- 34.Chu YM, Bashir S, Ramzan M, Malik MY. Model-based comparative study of magnetohydrodynamics unsteady hybrid nanofluid flow between two infinite parallel plates with particle shape effects. Math. Methods Appl. Sci. 2022 doi: 10.1002/mma.8234. [DOI] [Google Scholar]
- 35.Aim K, Fermeglia M. Solubility of solids and liquids in supercritical fluids. Exp. Determ. Solubilities. 2005;86:491–555. [Google Scholar]
- 36.Jouyban A, et al. Solubility prediction in supercritical CO2 using minimum number of experiments. J. Pharm. Sci. 2002;91:1287–1295. doi: 10.1002/jps.10127. [DOI] [PubMed] [Google Scholar]
- 37.Kumar SK, Johnston KP. Modelling the solubility of solids in supercritical fluids with density as the independent variable. J. Supercrit. Fluids. 1988;1:15–22. doi: 10.1016/0896-8446(88)90005-8. [DOI] [Google Scholar]
- 38.Garlapati C, Madras G. New empirical expressions to correlate solubilities of solids in supercritical carbon dioxide. Thermochim. Acta. 2010;500:123–127. doi: 10.1016/j.tca.2009.12.004. [DOI] [Google Scholar]
- 39.Bian XQ, Zhang Q, Du ZM, Chen J, Jaubert JN. A five-parameter empirical model for correlating the solubility of solid compounds in supercritical carbon dioxide. Fluid Phase Equilib. 2016;411:74–80. doi: 10.1016/j.fluid.2015.12.017. [DOI] [Google Scholar]
- 40.Bartle KD, Clifford AA, Jafar SA, Shilstone GF. Solubilities of solids and liquids of low volatility in supercritical carbon dioxide. J. Phys. Chem. Ref. Data. 1991;20:713–756. doi: 10.1063/1.555893. [DOI] [Google Scholar]
- 41.Méndez-Santiago J, Teja AS. The solubility of solids in supercritical fluids. Fluid Phase Equilib. 1999;158–160:501–510. doi: 10.1016/S0378-3812(99)00154-5. [DOI] [Google Scholar]
- 42.Sodeifian G, Razmimanesh F, Sajadian SA. Solubility measurement of a chemotherapeutic agent (Imatinib mesylate) in supercritical carbon dioxide: Assessment of new empirical model. J. Supercrit. Fluids. 2019;146:89–99. doi: 10.1016/j.supflu.2019.01.006. [DOI] [Google Scholar]
- 43.Fei T, Jichu Y, Hongyao S, Jiading W. Study on the solubility of substances in supercritical fluids. J. Chem. Ind. Eng. 1989;4:402–409. [Google Scholar]
- 44.Gordillo MD, Blanco MA, Molero A, Martinez De LaOssa E. Solubility of the antibiotic Penicillin G in supercritical carbon dioxide. J. Supercrit. Fluids. 1999;15:183–190. doi: 10.1016/S0896-8446(99)00008-X. [DOI] [Google Scholar]
- 45.Gao T, et al. Dispersing mechanism and tribological performance of vegetable oil-based CNT nanofluids with different surfactants. Tribol. Int. 2019;131:51–63. doi: 10.1016/j.triboint.2018.10.025. [DOI] [Google Scholar]
- 46.Li B, et al. Grinding temperature and energy ratio coefficient in MQL grinding of high-temperature nickel-base alloy by using different vegetable oils as base oil. Chinese J. Aeronaut. 2016;29(4):1084–1095. doi: 10.1016/j.cja.2015.10.012. [DOI] [Google Scholar]
- 47.Vaferi B, Karimi M, Azizi M, Esmaeili H. Comparison between the artificial neural network, SAFT and PRSV approach in obtaining the solubility of solid aromatic compounds in supercritical carbon dioxide. J. Supercrit. Fluids. 2013;77:44–51. doi: 10.1016/j.supflu.2013.02.027. [DOI] [Google Scholar]
- 48.Lashkarbolooki M, Vaferi B, Rahimpour MR. Comparison the capability of artificial neural network (ANN) and EOS for prediction of solid solubilities in supercritical carbon dioxide. Fluid Phase Equilib. 2011;308:35–43. doi: 10.1016/j.fluid.2011.06.002. [DOI] [Google Scholar]
- 49.Cao Y, Khan A, Zabihi S, Albadarin AB. Neural simulation and experimental investigation of Chloroquine solubility in supercritical solvent. J. Mol. Liq. 2021;333:115942. doi: 10.1016/j.molliq.2021.115942. [DOI] [Google Scholar]
- 50.Zhao TH, Khan MI, Chu YM. Artificial neural networking (ANN) analysis for heat and entropy generation in flow of non-Newtonian fluid between two rotating disks. Math. Methods Appl. Sci. 2021 doi: 10.1002/mma.7310. [DOI] [Google Scholar]
- 51.Valenzuela LM, Reveco-Chilla AG, Del Valle JM. Modeling solubility in supercritical carbon dioxide using quantitative structure-property relationships. J. Supercrit. Fluids. 2014;94:113–122. doi: 10.1016/j.supflu.2014.06.022. [DOI] [Google Scholar]
- 52.Zhu H, Zhu L, Sun Z, Khan A. Machine learning based simulation of an anti-cancer drug (busulfan) solubility in supercritical carbon dioxide: ANFIS model and experimental validation. J. Mol. Liq. 2021;338:116731. doi: 10.1016/j.molliq.2021.116731. [DOI] [Google Scholar]
- 53.Zha T-H, et al. A fuzzy-based strategy to suppress the novel coronavirus (2019-NCOV) massive outbreak. Appl. Comput. Math. 2021;20:160–176. [Google Scholar]
- 54.Ashpazzadeh E, Chu Y-M, Hashemi MS, Moharrami M, Inc M. Hermite multiwavelets representation for the sparse solution of nonlinear Abel’s integral equation. Appl. Math. Comput. 2022;427:127171. [Google Scholar]
- 55.Qiao W, Li Z, Liu W, Liu E. Fastest-growing source prediction of US electricity production based on a novel hybrid model using wavelet transform. Int. J. Energy Res. 2022;46(2):1766–1788. doi: 10.1002/er.7293. [DOI] [Google Scholar]
- 56.Qiao W, Liu W, Liu EA. A combination model based on wavelet transform for predicting the difference between monthly natural gas production and consumption of US. Energy. 2021;235:121216. doi: 10.1016/j.energy.2021.121216. [DOI] [Google Scholar]
- 57.Qiao W, et al. An innovative coupled model in view of wavelet transform for predicting short-term PM10 concentration. J. Environ. Manage. 2021;289:112438. doi: 10.1016/j.jenvman.2021.112438. [DOI] [PubMed] [Google Scholar]
- 58.Rashid S, Abouelmagd EI, Khalid A, Farooq FB, Chu YM. Some recent developments on dynamical discrete fractional type inequalities in the frame of nonsingular and nonlocal kernels. Fractals. 2022;30(2):2240110. doi: 10.1142/S0218348X22401107. [DOI] [Google Scholar]
- 59.Iqbal SA, Hafez MG, Chu YM, Park C. Dynamical Analysis of nonautonomous RLC circuit with the absence and presence of Atangana-Baleanu fractional derivative. J. Appl. Anal. Comput. 2022;12(2):770–789. [Google Scholar]
- 60.Chu YM, Nazir U, Sohail M, Selim MM, Lee JR. Enhancement in thermal energy and solute particles using hybrid nanoparticles by engaging activation energy and chemical reaction over a parabolic surface via finite element approach. Fractal Fract. 2021;3(3):119. doi: 10.3390/fractalfract5030119. [DOI] [Google Scholar]
- 61.Daryayehsalameh B, Nabavi M, Vaferi B. Modeling of CO2 capture ability of [Bmim][BF4] ionic liquid using connectionist smart paradigms. Environ. Technol. Innov. 2021;22:101484. doi: 10.1016/j.eti.2021.101484. [DOI] [Google Scholar]
- 62.Jiang Y, Zhang G, Wang J, Vaferi B. Hydrogen solubility in aromatic/cyclic compounds: Prediction by different machine learning techniques. Int. J. Hydrog. Energy. 2021;46:23591–23602. doi: 10.1016/j.ijhydene.2021.04.148. [DOI] [Google Scholar]
- 63.Vaferi B, Eslamloueyan R, Ayatollahi S. Application of recurrent networks to classification of oil reservoir models in well-testing analysis. Energy Sources Part A. 2015;37:174–180. doi: 10.1080/15567036.2011.582610. [DOI] [Google Scholar]
- 64.Qiao W, Li Z, Liu W, Liu E. Fastest-growing source prediction of US electricity production based on a novel hybrid model using wavelet transform. Int. J. Energy Res. 2022;46:1766–1788. doi: 10.1002/er.7293. [DOI] [Google Scholar]
- 65.Zou Q, Xing P, Wei L, Liu B. Gene2vec: Gene subsequence embedding for prediction of mammalian N6-methyladenosine sites from mRNA. RNA. 2019;25:205–218. doi: 10.1261/rna.069112.118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Karimi M, Vaferi B, Hosseini SH, Olazar M, Rashidi S. Smart computing approach for design and scale-up of conical spouted beds with open-sided draft tubes. Particuology. 2020;55:179–190. doi: 10.1016/j.partic.2020.09.003. [DOI] [Google Scholar]
- 67.Guo S, et al. Experimental evaluation of the lubrication performance of mixtures of castor oil with other vegetable oils in MQL grinding of nickel-based alloy. J. Clean. Prod. 2017;140:1060–1076. doi: 10.1016/j.jclepro.2016.10.073. [DOI] [Google Scholar]
- 68.Drzymala J, Bednarek-Gąbka P, Kowalczuk PB. Simplified empirical and phenomenological evaluation of relation between particle size and kinetics of flotation. Powder Technol. 2020;366:112–118. doi: 10.1016/j.powtec.2020.02.041. [DOI] [Google Scholar]
- 69.Storn R, Price K. Differential evolution: A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997;11:341–359. doi: 10.1023/A:1008202821328. [DOI] [Google Scholar]
- 70.Cao Y, Kamrani E, Mirzaei S, Khandakar A, Vaferi B. Electrical efficiency of the photovoltaic/thermal collectors cooled by nanofluids: Machine learning simulation and optimization by evolutionary algorithm. Energy Rep. 2022;8:24–36. doi: 10.1016/j.egyr.2021.11.252. [DOI] [Google Scholar]
- 71.Karimi M, Vaferi B, Hosseini SH, Rasteh M. Designing an efficient artificial intelligent approach for estimation of hydrodynamic characteristics of tapered fluidized bed from its design and operating parameters. Ind. Eng. Chem. Res. 2018;57:259–267. doi: 10.1021/acs.iecr.7b02869. [DOI] [Google Scholar]
- 72.Qiao W, et al. An innovative coupled model in view of wavelet transform for predicting short-term PM10 concentration. J. Environ. Manage. 2021;289:112438. doi: 10.1016/j.jenvman.2021.112438. [DOI] [PubMed] [Google Scholar]
- 73.Mahmoodi F, Darvishi P, Vaferi B. Prediction of coefficients of the Langmuir adsorption isotherm using various artificial intelligence (AI) techniques. J. Iran. Chem. Soc. 2018;15:2747–2757. doi: 10.1007/s13738-018-1462-4. [DOI] [Google Scholar]
- 74.Salekshahrezaee Z, Leevy JL, Khoshgoftaar TM. A reconstruction error-based framework for label noise detection. J. Big Data. 2021;8:1–16. doi: 10.1186/s40537-021-00447-5. [DOI] [Google Scholar]
- 75.Molani S, Madadi M, Wilkes W. A partially observable Markov chain framework to estimate overdiagnosis risk in breast cancer screening: Incorporating uncertainty in patients adherence behaviors. Omega. 2019;89:40–53. doi: 10.1016/j.omega.2018.09.009. [DOI] [Google Scholar]
- 76.Moosavi SR, Vaferi B, Wood DA. Auto-characterization of naturally fractured reservoirs drilled by horizontal well using multi-output least squares support vector regression. Arab. J. Geosci. 2021;14:545. doi: 10.1007/s12517-021-06559-9. [DOI] [Google Scholar]
- 77.Wang J, et al. Estimating the relative crystallinity of biodegradable polylactic acid and polyglycolide polymer composites by machine learning methodologies. Polymers. 2022;14:527. doi: 10.3390/polym14030527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Karimi M, Hosin Alibak A, Seyed Alizadeh SM, Sharif M, Vaferi B. Intelligent modeling for considering the effect of bio-source type and appearance shape on the biomass heat capacity. Meas. J. Int. Meas. Confed. 2022;189:110529. doi: 10.1016/j.measurement.2021.110529. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data generated or analyzed during this study are available on reasonable request from the corresponding author.