QMugs, quantum mechanical properties of drug-like molecules

Abstract

Machine learning approaches in drug discovery, as well as in other areas of the chemical sciences, benefit from curated datasets of physical molecular properties. However, there currently is a lack of data collections featuring large bioactive molecules alongside first-principle quantum chemical information. The open-access QMugs (Quantum-Mechanical Properties of Drug-like Molecules) dataset fills this void. The QMugs collection comprises quantum mechanical properties of more than 665 k biologically and pharmacologically relevant molecules extracted from the ChEMBL database, totaling ~2 M conformers. QMugs contains optimized molecular geometries and thermodynamic data obtained via the semi-empirical method GFN2-xTB. Atomic and molecular properties are provided on both the GFN2-xTB and on the density-functional levels of theory (DFT, ωB97X-D/def2-SVP). QMugs features molecules of significantly larger size than previously-reported collections and comprises their respective quantum mechanical wave functions, including DFT density and orbital matrices. This dataset is intended to facilitate the development of models that learn from molecular data on different levels of theory while also providing insight into the corresponding relationships between molecular structure and biological activity.

Measurement(s)	Quantum Mechanics
Technology Type(s)	density functional theory

Background & Summary

Machine learning methodologies are increasingly becoming well-established tools in many chemistry-related disciplines, such as drug discovery¹, material science², and physical chemistry³. In recent years, significant progress has been made in quantum-based machine learning (QML) methods⁴, which aim to accurately and computationally inexpensively predict the governing properties of atomistic systems, such as energies and forces^5–12, dipole moments¹³, wave functions^14,15 and electron densities^16,17. Despite the success and promise surrounding the applicability of such approaches, several challenges remain for QML. Arguably, one of the most important challenges is the increasing need for curated, comprehensive datasets¹³. While several options, such as the QM9¹⁸, ANI-1¹⁹, or PubChemQC²⁰ datasets have paved the way for the development of current-generation QML methods^{5–8,21–23}, the computational cost entailed in their generation limits both the scope of the explored chemical space (e.g., molecule size, atom-type diversity), and prospective modeling applicability^13,24.

There has been a recent surge in interest in the delta-learning (Δ-learning) of chemical properties, which aims to use a machine learning model to predict a physically relevant quantity, such as those generated by density-functional theory (DFT) by utilizing information extracted with a computationally cheaper method^22,25 (e.g., semi-empirical approaches such as GFN2-xTB^26–29 and PM6³⁰). Datasets that enable this type of learning are scarce and could promote the development of accurate models at potentially a fraction of the computational cost of more precise alternatives³¹. Furthermore, datasets that provide three-dimensional conformational data, for a wide variety of chemical space, at levels of theory higher than classical force fields^32,33, could boost the performance of machine learning methods in predicting properties from ensembles as well as generative models of conformations. Relevant examples include the PubChemQC-PM6²³ and GEOM³³ datasets, which include molecules with properties computed using different semi-empirical levels of theory. Finally, there is a clear potential to open up new lines of research by combining biological annotations (e.g., from molecular databases such as ChEMBL³⁴), and additional QM-derived physical information.

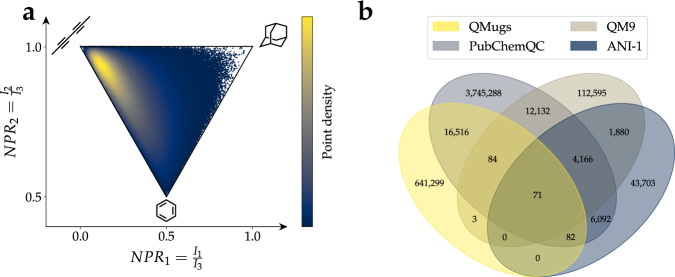
This work introduces QMugs (Quantum-Mechanical Properties of Drug-like Molecules), a data collection of over 665 k curated molecular structures extracted from the ChEMBL database, with accompanying computed quantum mechanical properties. Different levels of theory were combined in these calculations. Per compound, three conformers were generated, and their geometries were optimized using the semi-empirical GFN2-xTB method^26–29, whereas a comprehensive array of quantum properties was computed at the DFT level of theory using the ωB97X-D functional³⁵ and the def2-SVP Karlsruhe basis set³⁶. The data collection presented herein is put in the context of other sets that also feature DFT-level properties. A descriptive evaluation against the QM9¹⁸, ANI-1¹⁹, and PubchemQC²⁰ datasets is provided in Fig. 1b, as well as in Table 1. With an average of 30.6 and a maximum of 100 heavy atoms per compound (Table 1 & Fig. 2), QMugs features molecular samples that are considerably larger than those provided by other previously-reported datasets. QMugs also provides a larger number of distinct molecules than QM9 and ANI-1. Though the total number of provided molecules in QMugs is lower than that provided in PubChemQC, QMugs provides multiple conformers per molecule and therefore enables the training of QML models which can differentiate between molecular constitution and conformation. QMugs additionally provides a wide range of properties on multiple levels of theory. Furthermore, the vast majority of the included compounds (~641 k, 96.3%) were previously unreported in other DFT data collections, while also providing equivalent information at additional levels of theory, namely GFN2-xTB. QMugs provides quantum mechanical wave functions represented as local bases of atomic orbitals (i.e., DFT density and orbital matrices). Single-point properties as well as wave functions were computed with the Psi4 software suite³⁷ for all the conformers (~2.0 M) present in the database. As previously reported for the ChEMBL database³⁸, most of the considered drug-like molecules in this study fall within the rod-disk axis in the principal moments of inertia plot³⁹ (Fig. 1a).

Fig. 1.

(a) Principal-moments-of-inertia plot³⁹ for molecules in the QMugs dataset. NPR_x = x-th normalized principal moment, I_x = x-th smallest principal moment of inertia. (b) Venn diagram showing overlap between QMugs and other well-known datasets with DFT-level computed properties: QM9¹⁸, PubChemQC²⁰, and ANI-1¹⁹. Overlap was computed based on the uniqueness of the InChI representations of the contained molecules. Numbers do not add up to those reported in Table 1 because of InChI strings that occur multiple times.

Table 1.

Descriptive statistics of the dataset reported herein in the context of other DFT-level molecular datasets and the information provided by each.

Dataset	Unique compounds	Total conformations	Heavy atoms max (mean)	Method	Δ-learning possible	Wave functions
QM9	133,885	133,885	9 (8.8)	B3LYP/6–31 G(2df,p)	✗	✗
ANI-1	57,462	22,057,374	8 (7.1)	ωB97X/6–31 G(d)	✗	✗
PubChemQC	3,982,436	3,982,436	51 (14.1)	B3LYP/6–31 G(d)	✗	✓
QMugs	665,911	1,992,984	100 (30.6)	GFN2-xTB + ωB97X-D/def2-SVP	✓	✓

The number of molecules for PubChemQC corresponds to that available on the website of the project⁵⁷. Heavy atom averages are weighted by the number of conformations.

Fig. 2.

Distribution of properties for the molecules contained in the QMugs dataset.

Overall, the potential utility of the presented dataset is fourfold: (i) it will provide researchers with a dataset containing substantially larger molecules than previously reported, in order to either directly predict quantum chemical properties, or to learn a property mapping between two popular quantum mechanical levels of theory (i.e., GFN2-xTB and ωB97X-D/def2-SVP); (ii) it will facilitate the development of novel machine-learning methodologies for the generation of molecular conformations and molecular property predictions via their ensembles; (iii) it will facilitate the development of novel deep learning frameworks for the prediction of the quantum mechanical wave function in a local basis of atomic orbitals; and (iv) it will enable research towards the exploration of quantum featurization in the context of pharmacologically relevant, annotated biological data.

Methods

Molecules were extracted from the ChEMBL database³⁴ (version 27). Conformers were generated using RDKit (http://www.rdkit.org) and GFN2-xTB^26–29. DFT (ωB97X-D/def2-SVP) calculations were carried out via Psi4³⁷. A similar approach was adopted in a previous study on transition-metal complexes¹³. An overview of the data processing pipeline is given in Fig. 3, while individual steps are described in more detail in the following subsections.

Fig. 3.

Overview of the data generation process. Molecules were extracted from the ChEMBL database, standardized, and filtered, and starting conformers were generated using the RDKit software package. Metadynamics (MTD) simulations were performed using the GFN2-xTB semi-empirical method to generate three diverse conformations before final geometry optimization. Molecules that did not pass a series of geometric sanity checks were removed. DFT-level properties (ωB97X-D/def2-SVP) were computed using Psi4 software.

In chemical terminology, the term “conformation” refers to any arrangement of atoms in space, whereas “conformer” refers to a conformation that is a local minimum on the potential energy surface of the molecule⁴⁰. In the analyses that follow, the term “conformation” is loosely used to refer to both, unless explicitly mentioned otherwise.

Data extraction and SMILES processing

Single-protein targets with assay information for at least 10 compounds with unique internal identifiers were extracted from the ChEMBL database. Several activity and annotation filters were subsequently applied to these compounds (see Supporting Information for a detailed query description). This procedure resulted in 685,917 molecules with unique external identifiers (ChEMBL-IDs), represented by their Simplified Molecular Input Line Entry Specification (SMILES)⁴¹. Molecules were neutralized, and salts and solvents were removed (“washing”) using the ChEMBL Structure Pipeline package⁴². For compounds consisting of multiple separate fragments, all fragments except the one with the highest number of heavy atoms were discarded after the washing. Additionally, molecules containing fewer than 3 or more than 100 heavy atoms, as well as radical species and molecules with a net charge different from zero after the attempted neutralization, were removed. Atom types included in the QMugs dataset are hydrogen, carbon, nitrogen, oxygen, fluorine, phosphorus, sulfur, chlorine, bromine, and iodine.

Conformer generation and optimization

With the procedure described herein, a compromise between efficient molecular conformational search and practical computational expense considerations was sought. Similar to previous studies^13,43, the semiempirical GFN2-xTB method was used as a surrogate for full DFT geometry optimization, as the latter is associated with challenging computational costs when considering the size and number of molecules in the QMugs dataset.

The RDKit (http://www.rdkit.org) implementation of the Experimental-Torsion Knowledge Distance Geometry (ETKDG) method⁴⁴ was used to generate up to 100 conformers for each molecule, with a maximum of 1000 embedding attempts and an initial coordinate assignment using distance-matrix eigenvalues and default settings (boxSizeMult = 2.0, forceTol = 1e-3). Upon no successful conformer generation, it was re-attempted via random assignment of the starting coordinates. The resulting conformers were further minimized using the Merck molecular force field⁴⁵ (MMFF94s) for a maximum of 1000 iterations, with default settings (nonBondedThresh = 100.0). The lowest-energy conformer (according to the selected force field) for each structure was then used as a starting point for meta-dynamics (MTD) simulations. Stereocenters that were previously undefined in the SMILES extraction procedure were assigned in this conformer generation process.

For each generated conformer, an MTD simulation was performed with the xTB software package²⁸ for a duration of 5 ps with time steps of 1 fs, at a temperature of 300 K. The biasing root-mean-square deviation (RMSD) potential used for all MTD simulations is given by $E_{\mathrm{bias}}^{\mathrm{RMSD}}={\sum }_{i=1}^N{k}_i\exp \left(\alpha {\mathrm{\Delta }}_i^2\right)$, where N is the number of reference structures, k_i the pushing strength, Δ_i the collective variable (i.e., the RMSD between structure i and a reference structure), and α the width of the Gaussian potential used in the RMSD criterion. Simulations were carried out with α = 1.2⁻¹ and k_i = 0.2 mEh with snapshots taken every 50 fs, resulting in 100 conformations stored with their corresponding energies. To obtain conformationally diverse samples, these structures were subsequently clustered into three groups via the k-means⁴⁶ algorithm, as implemented in the scikit-learn⁴⁷ (version 0.23.1) Python package using the pairwise RMSD of the aligned structures as molecular features. The conformation with the lowest-energy value from each cluster was then selected for further processing. The three resulting conformations for each molecule were then optimized using the GFN2-xTB^26–29 method using energy and gradient convergence criteria of 5 × 10⁻⁶ Eh and 1 × 10⁻³ Eh α⁻¹, respectively, and the approximate normal coordinate rational function optimizer (ANCopt). Harmonic frequencies, entropies, enthalpies and heat capacities at 298.15 K were extracted at the end of the geometry optimization process. Structures for which vibrational frequencies with imaginary wave numbers were obtained — indicative of failure to reach energy minima — were subjected to additional optimizations until no significant ones remained, up to a maximum of 100 attempts.

Quantum mechanical calculations

Single-point electronic calculations were performed for the optimized geometries using the ωB97X-D quantum functional and the def2-SVP basis set as implemented in the open-source quantum-chemistry software suite Psi4³⁷. Single-point properties such as formation and orbital energies, dipole moments, rotational constants, partial charges, bond orders, valence numbers, as well as wave functions including α and β DFT-density matrices, orbital matrices, and the atomic-orbital-to-symmetry-orbital transformer matrix were obtained. For practical reasons, 52 structures whose DFT calculations required computational resources that exceeded empirically determined limits, or for which calculations were unsuccessful, were discarded (see Supporting Information for details).

Data Records

All computed molecular structures, as well as their corresponding properties and wave functions are accessible through the ETH Library Collection service⁴⁸.

Format specification

A summary.csv comma-separated file contains computed molecular-level properties and additional annotations. A compressed tarball file (structures.tar.gz) of ~7 gigabytes (GB) contains plain MDL structure-data files⁴⁹ (SDFs) with embedded atomic and molecular properties, grouped in sub-directories according to their respective ChEMBL identifiers. These SDFs include single-point electronic properties calculated on the GFN2-xTB and ωB97X-D/def-SVP levels of theory, as described in Table 2. A second compressed tarball file (vibspectra.tar.gz, ~3 GB) contains vibrational spectra.

Table 2.

Calculated properties as stored in the SDFs of the QMugs data collection.

Property	Symbol	Unit	Key	Δ-ML
ChEMBL identifier	—	—	CHEMBL_ID
Conformer identifier	—	—	CONF_ID
Total energy	URT	Eh	GFN2:TOTAL_ENERGY	♦
Internal atomic energy	EAtom	Eh	GFN2:ATOMIC_ENERGY
Formation energy	EForm	Eh	GFN2:FORMATION_ENERGY	♦
Total enthalpy	HRT	Eh	GFN2:TOTAL_ENTHALPY
Total free energy	GRT	Eh	GFN2:TOTAL_FREE_ENERGY
Dipole (x, y, z, total)	μ	D	GFN2:DIPOLE	♦
Quadrupole (xx, xy, yy, xz, yz, zz)	Qij	D Å	GFN2:QUADRUPOLE
Rotational constants (A, B, C)	A, B, C	cm−1	GFN2:ROT_RONSTANTS	♦
Enthalpy (vib., rot., transl., total)	ΔH	cal mol−1	GFN2:ENTHALPY
Heat capacity (vib., rot., transl., total)	CV	cal K−1 mol−1	GFN2:HEAT_CAPACITY
Entropy (vib., rot., transl., and total)	ΔS	cal K−1 mol−1	GFN2:ENTROPY
HOMO energy	EHOMO	Eh	GFN2:HOMO_ENERGY	♦
LUMO energy	ELUMO	Eh	GFN2:LUMO_ENERGY	♦
HOMO-LUMO gap	EGap	Eh	GFN2:HOMO_LUMO_GAP	♦
Fermi level	EFermi	Eh	GFN2:FERMI_LEVEL
Mulliken partial charges	δM	e	GFN2:MULLIKEN_CHARGES	♦
Covalent coordination number	Ncoord	—	GFN2:COVALENT_COORDINATION_NUMBER
Molecular dispersion coefficient	C6	a.u.	GFN2:DISPERSION_COEFFICIENT_MOLECULAR
Atomic dispersion coefficients	C6	a.u.	GFN2:DISPERSION_COEFFICIENT_ATOMIC
Molecular polarizability	α(0)	a.u.	GFN2:POLARIZABILITY_MOLECULAR
Atomic polarizabilities	α(0)	a.u.	GFN2:POLARIZABILITY_ATOMIC
Wiberg bond orders	MAB	—	GFN2:WIBERG_BOND_ORDER	♦
Total Wiberg bond orders	${\sum }_{A\left(A\ne B\right)}{M}_{AB}$	—	GFN2:TOTAL_WIBERG_BOND_ORDER	♦
Total energy	URT	Eh	DFT:TOTAL_ENERGY	♦
Total internal atomic energy	EAtom	Eh	DFT:ATOMIC_ENERGY
Formation energy	EForm	Eh	DFT:FORMATION_ENERGY	♦
Electrostatic potential	VESP	V	DFT:ESP_AT_NUCLEI
Löwdin partial charges	δL	e	DFT:LOWDIN_CHARGES
Mulliken partial charges	δM	e	DFT:MULLIKEN_CHARGES	♦
Rotational constants (A, B, C)	A, B, C	cm−1	DFT:ROT_CONSTANTS	♦
Dipole (x, y, z, total)	μ	D	DFT:DIPOLE
Exchange correlation energy	EXC	Eh	DFT:XC_ENERGY
Nuclear repulsion energy	${\widehat{V}}_{eN}$	Eh	DFT:NUCLEAR_REPULSION_ENERGY
One-electron energy	${\widehat{T}}_e$	Eh	DFT:ONE_ELECTRON_ENERGY
Two-electron energy	${\widehat{V}}_{ee}$	Eh	DFT:TWO_ELECTRON_ENERGY
HOMO energy	EHOMO	Eh	DFT:HOMO_ENERGY	♦
LUMO energy	ELUMO	Eh	DFT:LUMO_ENERGY	♦
HOMO-LUMO gap	EGap	Eh	DFT:HOMO_LUMO_GAP	♦
Mayer bond orders	MAB	—	DFT:MAYER_BOND_ORDER
Wiberg-Löwdin bond orders	WAB	—	DFT:WIBERG_LOWDIN_BOND_ORDER	♦
Total Mayer bond orders	${\sum }_{A\left(A\ne B\right)}{M}_{AB}$	—	DFT:TOTAL_MAYER_BOND_ORDER
Total Wiberg-Löwdin bond orders	${\sum }_{A\left(A\ne B\right)}{W}_{AB}$	—	DFT:TOTAL_WIBERG_LOWDIN_BOND_ORDER	♦

Abbreviations: a.u., atomic units; vib., vibrational; rot., rotational; transl., translational. Properties that enable Δ machine learning are labelled with ♦.

Wave function files (i.e., DFT density and orbital matrices) as described in Table 3, are split into 100 compressed tarballs (wfns_xx.tar.gz) of ~50 GB each for easier management and downloading. These are supplied as NumPy⁵⁰ (.npy) binary files, which can be read using the Psi4 software package. Molecules (with all conformers grouped together) were assigned at random to the tarballs to enable easy use of subsets of the QMugs dataset without having to download all the files. The assignment of ChEMBL identifiers to tarballs is described in a tarball_assignment.csv file.

Table 3.

Calculated molecular properties stored in the wave function files provided in the QMugs data collection.

Property	Symbol	Key
Alpha density matrix	Dα	matrix, Da
Beta density matrix	Dβ	matrix, Db
Alpha orbitals	Cα	matrix, Ca
Beta orbitals	Cβ	matrix, Cb
Atomic-orbital-to-symmetry-orbital transformer	CAOTOSO	matrix, aotoso
Mayer bond orders	MAB	MAYER_INDICES
Wiberg-Löwdin bond orders	WAB	WIBERG_LOWDIN_INDICES

Mayer and Wiberg-Löwdin bond orders included here represent a superset of the bond orders in the SDFs which additionally comprise bond orders for non-covalent bonds.

Technical Validation

Optimized geometry sanity checks

Four consecutive geometry checks were performed to filter out structures for which the geometry optimization procedure converged to unrealistic conformations. To determine suitable thresholds for removing a structure from our dataset, the generated geometries were compared to experimental reference values and to DFT-optimized geometries extracted from the PubChemQC dataset²⁰. Specifically, we investigated (i) the deviation of bond lengths from experimental reference values, (ii) isomorphism between the initial molecular graphs and those obtained after geometry optimization, (iii) linearity of triple bonds, and (iv) planarity of aromatic rings. Structures were removed from the dataset if they failed any of these tests. In total, 10,986 (0.55%) conformations were discarded from the dataset. Each test is briefly described in the following subsections, with further technical details reported in the Supporting Information.

Deviation of bond lengths from experimental reference values

Bond lengths in the optimized structures were compared to average experimental reference values for bonds of the same bond type (single, double, triple, or aromatic) and between the same atoms. Reference values were obtained from the Computational Chemistry Comparison and Benchmark DataBase (CCCBDB)⁵¹, and the largest absolute bond-length deviation from reference values was recorded per molecule. Bonds for which no reference value was available (0.75%) were omitted. The same analysis was carried out for molecules from the PubChemQC dataset containing the same atom types as QMugs, in order to obtain a comparable set with respect to the present atom types. The PubChemQC set (3,834,382 conformations with reference bond lengths) showed a deviation of 0.06 ± 0.04Å (median ± 1 standard deviation), whereas the QMugs dataset (2,004,003 conformations with reference bond lengths) showed a deviation of 0.07 ± 0.03Å. Based on the observed distribution of bond-length deviations from experimental reference values (Figure S1) and manual investigation of example structures, 0.2 was determined to be a suitable threshold for a conformation to be removed from the dataset, which included 6,131 (0.31%) examples.

Molecular graph isomorphism

It was investigated whether atom connectivity could be reconstructed after removing bond information from the generated SDFs. To this end, molecular graphs constructed exclusively from atom positions and types were compared to those obtained using the original atom connectivity (see Supporting Information for details). 1,568 (0.08%) conformations for which the resulting molecular graphs were non-isomorphic failed this test.

Deviation of triple bonds from linear geometry

The deviation of triple bonds from their ideal linear geometry was examined. In this investigation, ring triple bonds were not considered owing to routinely-occurring deviations from linear geometry in systems with high ring strain⁵². The largest deviation from a 180 (linear) bond angle was recorded for each molecule containing at least one non-ring triple bond. The same analysis was performed on the PubChemQC dataset²⁰. Triple-bond-containing molecules from PubchemQC and QMugs (273,320 and 165,101 samples, respectively) showed deviations of 1.38 ± 1.46° (median ± 1 standard deviation), and 1.46 ± 2.13°, respectively. Based on the observed distribution of triple bond angles from a linear geometry (Figure S2) and manual inspection of structures, a 10° deviation was identified as a suitable threshold. 1,147 (0.06%) conformations failed this test.

Deviation of aromatic rings from planar geometry

The planarity of carbon-containing aromatic rings was also investigated. For each molecule containing aromatic carbon atoms, the largest dihedral angle between the two planes spanned by each aromatic carbon atom and its three neighbors was recorded (see Supporting Information for details). The same analysis was performed on the PubChemQC dataset²⁰. Molecules from PubchemQC and QMugs (2,391,589 and 1,950,929 conformations with aromatic carbons, respectively) showed median dihedral angles ( ± 1 standard deviation) of 1.70 ± 1.85° and 2.99 ± 2.20°, respectively. Based on the observed distribution of dihedral angles from planar geometries (Figure S3) and manual inspection of structures, 2,769 (0.14%) conformations with aromatic carbon dihedral angles above 15° were discarded.

Further geometrical assessment

The changes in the molecular geometries along the applied pipeline were examined in order to evaluate the effects of the applied steps. Figure 4a shows the mean pairwise RMSD of atom positions between the conformations of each molecule at different steps along the pipeline. Conformations sampled during MTD simulations showed a mean pairwise RMSD of 2.40 ± 0.52° (median ± 1 standard deviation). The k-means clustering procedure accomplished the envisaged task of sampling conformations with higher geometric diversity (2.67 ± 0.74°). During the geometry optimization process, conformational diversity decreased (2.48 ± 0.86°). Unsurprisingly, for some molecules featuring rigid structures, conformations tended to converge toward the same energy minimum (0.09% of molecules show a mean pairwise RMSD < 0.01° between their optimized conformers).

Fig. 4.

(a) Distributions of mean pairwise RMSD of atom positions between conformations of each molecule in the QMugs dataset at different stages along the pipeline. While the k-means sampling process selects conformations that are, on average, more geometrically diverse than the average pair of structures generated by MTD simulations, geometry optimization reduces the geometrical diversity between the optimized conformers. (b) Change in atom positions during geometry optimization vs. mean pairwise RMSD of conformations before optimization. Molecules with initially more diverse conformations displayed a greater change in atom positions than those with initially less diverse conformations. (c) Distribution of RMSD of structures prior to and after optimization with the semi-empirical GFN2-xTB method, and of structures optimized with the same approach vs. with ωB97X-D/def2-SVP. The structures of three molecules with varying differences between the two methods are shown as illustrative examples (black and gray correspond to GFN2-xTB and ωB97X-D/def2-SVP-optimized structures, respectively). For illustrative purposes, the example molecules are aligned on their substructures.

The degree to which the molecular geometries changed during the final optimization step was further analyzed. Molecules with initially more diverse conformations (higher mean pairwise RMSD of pre-optimized conformations) were shown to undergo a greater chance in atom positions (mean RMSD of pre- vs. post-optimized conformations) during optimization with the GFN2-xTB method (Fig. 4b). The observed heteroscedastic behavior of these two properties indicates that while the mean RMSD of pre- vs. post-optimized conformations tends to increase with higher mean pairwise RMSD of pre-optimized conformations, its variance also increases.

Finally, the suitability of GFN2-xTB as a lower-cost surrogate for DFT-level geometry optimization (Fig. 4c) was confirmed. 500 randomly-chosen structures prior to semi-empirical geometry optimization from the QMugs dataset were further subjected to DFT-level geometry optimization (ωB97X-D/def2-SVP), discarding structures that could not be converged in 100 iterations or with the computational resources described in the Supporting Information. The RMSDs between the structures independently optimized at both levels of theory were then measured. The pairs of structures showed RMSDs of 0.47 ± 0.63° (median ± 1 standard deviation), indicating that the chosen semi-empirical method obtains similar geometries to those obtained with more expensive first-principle calculations. Large RMSDs in some example pairs (Fig. 4c) could be interpreted as indicative of convergence to distinct local minima.

For 2,067 molecules, their individual conformations have different SMILES describing two different (E)/(Z) isomers. Those structures are either α-β-unsaturated ketones, α-β-unsaturated nitriles, imine, or azo compounds, for which isomerization might be plausible^53,54. In part due to the applied “washing” procedure, 17,176 molecules can be represented with a SMILES string that is shared with at least one other ChEMBL-ID.

Validation of single-point properties

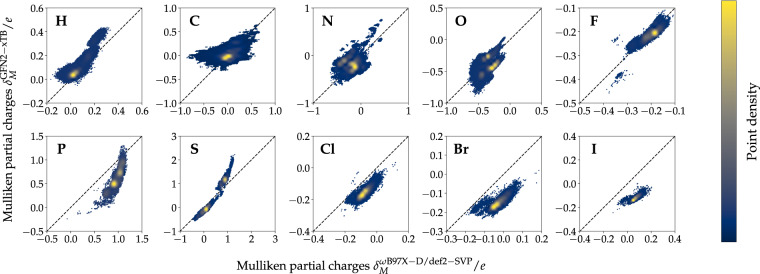
To validate the general agreement between the two methods employed in this work, the correlation between a series of single-point properties computed on both levels of theory was analyzed. Both global molecular (Fig. 5) and local atomic/bond properties (Fig. 6, 7) were considered. All single-point molecular properties showed a high degree of correlation. Formation energies E_Form (Fig. 5a), which were obtained by subtracting atomic energies E_Atom from total internal energies U_RT, show a Pearson correlation coefficient (PCC) of 0.998. Dipole moments μ and rotational constants A (excl. 22 small structures with very high rotational constants; Fig. 5b,c) displayed PCCs of 0.969 and 0.999, respectively. Orbital energies, namely the energies for highest occupied (HOMO) E_HOMO and lowest unoccupied molecular orbitals (LUMO) E_LUMO and HOMO-LUMO gap energies E_Gap showed PCCs of 0.769, 0.924 and 0.830, respectively (Fig. 5d–f). The observed PCCs for all six single-point molecular properties indicate good agreement between the two methods. Atom-type-specific partial charges for the 10 atom-types in QMugs (Fig. 6, Table S1) as well as the 15 most abundant covalent bond types (Fig. 7, Table S2) also showed high correlations between the two methods used herein. Regarding partial charges, 7 out of the 10 atom types considered in QMugs were observed to have PCCs > 0.8, with the remaining carbon, nitrogen, and oxygen atom-types resulting in lower PCCs of 0.574, 0.124, and 0.274, respectively. Regarding bond orders, 10 out of the 15 show PCCs > 0.9 and 14 out of 15 displayed PCCs > 0.75 (see Table S2 for additional metrics). Notably only carbon-fluorine bonds displayed a larger discrepancy between both levels of theory, with an observed PCC of 0.153. The observed correlations in both molecular and atomic single-point properties between GFN2-xTB and ωB97X-D/def2-SVP confirm the suitability of the former method as a computationally affordable starting point for Δ-learning of DFT-level properties.

Fig. 5.

Comparison of molecular properties computed at the two levels of theory considered herein (GFN2-xTB, ωB97X-D/def2-SVP) for the molecules contained in QMugs. The molecular formation energy E_Form E_Form in (a) was calculated by subtracting the atomic U_Atom contributions from the total molecular energies U_RT. Only the rotational constants A are shown in (c) as their B and C counterparts showed highly similar values. 22 conformations of small molecules show very large rotational constants and are not shown. RMSE and PCC for rotational constant A are 845.834 cm⁻¹ and 0.091 respectively, if those structures are included. Abbreviations: RMSE, root mean squared error; PCC, Pearson’s correlation coefficient.

Fig. 6.

Atom-type-specific partial charge correlations (GFN2-xTB, ωB97X-D/def2-SVP) for the QMugs dataset (see Table S1 in the Supporting Information for additional metrics).

Fig. 7.

Comparison of Wiberg bond orders between GFN2-xTB and ωB97X-D/def2-SVP for the 15 most frequently occurring bond types in the QMugs dataset. The latter level of theory uses Löwdin-orthogonalization. See Table S2 in the Supporting Information for additional metrics. For bond types which occurred > 1 M times in the dataset, a randomly chosen sample of 1 M bonds is plotted.

Usage Notes

All data files can be accessed via any modern web browser, and can be programmatically downloaded using the provided instructions in the archive’s readme. The provided SDFs can be processed using standard cheminformatics software (for example, RDKit, KNIME⁵⁵), and wave function files using the Psi4³⁷ software package or directly using Numpy⁵⁰.

Author contributions

Clemens Isert: Methodology, Formal Analyses, Writing. Kenneth Atz: Methodology, Formal Analyses, Writing. José Jiménez-Luna: Conceptualization, Methodology, Writing. Gisbert Schneider: Supervision, Writing.

Code availability

All analyses were supported by the Python programming language (version 3.7.7) and its scientific software stack⁵⁰. Molecular conformations were generated using RDKit (http://www.rdkit.org, version 2020.03.3) and GFN2-xTB^26–29 (version 6.3.1). All quantum mechanical calculations were carried out with Psi4³⁷ (version 1.3.2). Molecular structure visualizations were created using PyMol⁵⁶ (version 2.3.5) and ChemDraw (version 19.1.1.32). The rclone (https://rclone.org, version 1.54.0) WebDAV client was used for all data uploading purposes.

Competing interests

G.S. is a cofounder of inSili.com LLC, Zurich, and a consultant to the pharmaceutical industry.

Supplementary information

The online version contains supplementary material available at 10.1038/s41597-022-01390-7.