Dosimetric Evaluation of the Treatment Plan on Indigenous Heterogeneous Phantoms using Analytical Anisotropic Algorithm and Acuros-XB Algorithm for Different Photon Energies

Abstract

Background:

Modern radiotherapy techniques are using advanced algorithms; however, phantoms used for quality assurance have homogeneous density; accordingly, the development of heterogeneous phantom mimicking human body sites is imperative to examine variation between planned and delivered doses.

Objective:

This study aimed to analyze the accuracy of planned dose by different algorithms using indigenously developed heterogeneous thoracic phantom (HT).

Material and Methods:

In this experimental study, computed tomography (CT) of HT was done, and the density of different parts was measured. The plan was generated on CT images of HCP with 6 and 15 Megavoltage (MV) photon beams using different treatment techniques, including three-dimensional conformal radiotherapy (3D-CRT), intensity-modulated radiation therapy (IMRT), and volumetric modulated arc therapy (VMAT). Plans were delivered by the linear accelerator, and the dose was measured using the ion chamber (IC) placed in HT; planned and measured doses were compared.

Results:

Density patterns for different parts of the fabricated phantom, including rib, spine, scapula, lung, chest wall, and heart were 1.849, 1.976, 1.983, 0.173, 0.855, and 0.833 g/cc, respectively. Variation between planned and IC estimated doses with the tolerance (±5%) for all photon energies using different techniques. Acuros-XB (AXB) showed a slightly higher variation between computed and IC estimated doses using HCP compared to the analytical anisotropic algorithm (AAA).

Conclusion:

The indigenous heterogeneous phantom can accurately simulate the dosimetric scenario for different algorithms (AXB or AAA) and be also utilized for routine patient-specific QA.

Introduction

Based on the Global Cancer Observatory (GLOBOCAN) 2018, a high prevalence and rapid increment of new cancer cases estimate every year and report 18.1 million new cases and 9.6 million cancer-associated deaths worldwide [ 1 , 2 ]. Modern treatment techniques, such as intensity-modulated radiation therapy (IMRT), volumetric modulated arc therapy (VMAT), and image-guided radiation therapy (IGRT) demand rapid dose gradient around the target, advanced treatment planning, and complex delivery, leading to the high risk of maladministration of radiation doses due to small geometric miss and possible misalignment between mechanical components of the machine. Due to the anticipated increase in cancer, plan calculation and verification are necessary to ensure safe and effective delivery. The IMRT collaborative working group (CWG) supported verification of radiation dose before treatment for safe and efficient treatment [ 3 ].

The radiation therapy (RT) treatment depends on the implementation of a comprehensive quality assurance (QA) program in a routine clinical environment. An independent dose verification program conducted by Radiological Physics Centre (RPC) revealed that one-third of the participated institutions failed to obtain the prescribed tolerance after the espousal of IMRT for a decade [ 4 - 6 ]. The errors in beam input data/ beam calibration, suboptimal beam modeling, an inherent limitation of the dose calculation algorithm, and a mix of other unknown reasons may also result in the failures of IMRT/VMAT patient-specific QA [ 6 ].

Kumar et al. [ 7 ] reported two types of pre-treatment dose verification in a survey of IMRT QA in India, i.e. point dose was verified using an ion chamber (IC) in combination with slab phantom of uniform density and planner dosimetry using two-dimensional (2D) radiochromic/radiographic films, electronic portal imaging devices (EPID), and a 2D array of ICs/ semiconductor diodes. In addition, Nakamura et al. [ 8 ] highlighted the logistics and other issues, including the shortage of manpower for the standardization of IMRT QA in Japan. Pan et al. [ 9 ] demonstrated the significantly varied practice of IMRT QA in China, including the need to increase manpower, QA devices, and the linac machines.

This study aimed to compare the planned dose against the estimated doses on the indigenously fabricated heterogeneous phantom in comparison to slab phantom and Octavius phantom. Treatment plans were generated with two-dimensional (2D), three-dimensional (3D) conformal radiotherapy (3D-CRT), IMRT, and VMAT delivery techniques using different photon energies. In addition, analytical anisotropic algorithm (AAA) and Acuros-XB (AXB) algorithms were applied to all the above-mentioned techniques to verify the algorithm for the respective diagnostic and dealing technique.

Material and Methods

1. Thoracic phantom design

An experimental study was conducted using an indigenously developed heterogeneous chest phantom to analyze the accuracy of doses calculated by different dose calculation algorithms. An in-house heterogeneous phantom was fabricated in the shape of the abdomen region of the human body with a dimension of 31 × 24 ×21 cm³, using bone equivalent powder, sawdust of kail-wood, the paraffin-wax, and hydro-gel. A thoracic rib case was fabricated in the phantom to replicate a thoracic part of a patient, and a pouch of the size of a male heart was filled with hydro-gel, and later, placed in a container to pour paraffin-wax. The lung region was filled with sawdust of kail-wood. After the solidification of the wax, extra wax was removed to achieve the final shape and size. A cavity was also placed to hold the ion chamber (IC) inside the phantom; the fiducial lead markers were placed on the anterior surface and bilateral surface of the phantom. The relative electron density (RED) was estimated using Eclipse treatment planning system (TPS) version 15.5 (Varian Medical Systems, Palo Alto, USA) for artificial bone, sawdust of kail, hydro-gel, and paraffin-wax. Figure 1 shows the experimental setup of (a) indigenous phantom, (b) slab phantom, and (c) Octavius phantom on the True Beam (TB) linac.

Figure 1.

Pictorial representation of the experimental setup of (a) indigenous heterogeneous thoracic, (b) slab, and (c) Octavius phantoms on the TrueBeamlinac

2. Techniques

The computed tomography (CT) scan was executed using GE DISCOVERY (GE Medical System, WI, USA) CT scanner, and digital imaging and communications in medicine (DICOM) images were transferred to Eclipse TPS version 15.5 (Varian Medical Systems, Palo Alto, CA, USA). In eclipse, body phantom and ionization chamber (Semi-flex 3D 0.07cc chamber, PTW-Freiburg, Germany) were delineated, and plans were generated for single anteroposterior (AP) field (F), AP- PA (Posterior Anterior), and 3DCRT (3F and 5F), IMRT (5F, 7F and 9F), and VMAT plans (coplanar: single arc, double arc, and non-coplanar arc) for photon energies of 6 megavoltages (MV) _flattened beam (FB), 6 MV_FFFB (Flattening filter-free beam), and 15 MV_FB. The photon energies were triggered using TrueBeam (TB)-SVC (Varian Medical System, Palo Alto, Inc., CA, USA) linear accelerator (linac) calibrated according to the international code of practice, i.e. technical report series (TRS) number: 398 prescribed by International Atomic Energy Agency (IAEA). The dose measured in the fabricated phantom was also validated against the well-established slab and Octavius phantom.

3. Dose computation

3.1. Analytical Anisotropic Algorithm (AAA)

The AAA is a pencil-beam convolution/ superposition dose computation algorithm encoded in Eclipse TPS using a pre-defined Monte-Carlo derived kernel for handling the heterogeneity in the medium. The energy fluence of beam-let (β) is comprised of primary photons, extra-focal photons, electron contamination from the flattening filter, ionization chamber collimating jaws, and air.

The dose D_β(x,y,z) from β is computed using the convolution of Φ (fluence) and I_β(z,ρ) (energy deposition density function) with K_β(x,y,z,ρ) (scatter kernel) as shown in equation 1 [ 10 ] as follows:

$D_{\beta }\mathrm{(x,y,z)}={\varphi }_{\beta }\times I_{\beta }\mathrm{(z,\rho )}\times \int {\int }_{\beta }{K}_{\beta }(\mathrm{X\prime }-X,\mathrm{Y\prime }-Y,\mathrm{Z\prime }-Z,\rho )\mathrm{dX\prime }\mathrm{dY\prime }$ (1)

where β is energy fluence of beam-let; D_β (x,y,z) is dose deposition at a particular coordinate (x -X-axis, y- Y-axis, z- Zaxis coordinates) due to a particular beamlet.

3.2. Acuros XB (AXB)

In Eclipse, AXB implementation depends on the photon-beam source and radiation transport models. The AXB explicitly solved the Boltzmann transport equation (LBTE) using a deterministic numerical approach and discretized the LBTE’s variables into space ($\overrightarrow{r}$), angle ($\hat{\Omega }$), and energy (E). The dose is computed using the following equation [ 11 , 12 ]:

$D_i{\int }_0^{\infty }\mathrm{dE}{\int }_{\mathrm{4\pi }}d\hat{\Omega }\frac{{\sigma }_{\mathrm{ED}}^e(\overrightarrow{r},E)}{\rho \left(\overrightarrow{r}\right)}{\psi }^e(\overrightarrow{r},E,\hat{\Omega })$ (2)

where ρ is the density of the material, ${\sigma }_{\mathrm{ED}}^e(\overrightarrow{r},E)$ is macroscopic electron energy deposition cross-section, and ${\psi }^e(\overrightarrow{r},E,\hat{\Omega })$ is angular electron fluence.

4. Dose reporting and evaluation

All the treatment plans were exported to TrueBeam linac for measurements. A calibrated semi-flex 3D chamber (PTW Freiburg, Germany) of 0.07 cc volume along with a UNIDOSE-E electrometer (PTW Freiburg, Germany) was used for measuring the radiation dose. A set of three measurements was performed for each plan to avoid statistical uncertainties. The dose deposited at the depth of reference was estimated as prescribed by TRS 398 using the following equation [ 13 ]:

$D=\mathrm{MR}\times N_{\mathrm{D,\; W}}\times K_{\mathrm{Q,\; Qo}}\times K_{\mathrm{T,\; P}}\times K_S\times K_{\mathrm{pol}}$ (3)

where MR, N_D,W, and K_{Q, Qo} define electrometer reading, IC calibration factor, and beam quality correction factor, respectively. K_TP is a temperature-pressure correction factor, K_S is a saturation factor (ion recombination) for IC, and K_POL is Polarity correction for IC.

The variation between measured and planned radiation dose was estimated using the following equation:

$\mathrm{Variation(in\; percenage)}=100\times \left(\frac{D_{\mathrm{IC}}-D_{\mathrm{algorithm}}}{D_{\mathrm{algorithm}}}\right)$ (4)

where D_IC and D_algorithm are IC measured dose and dose estimated by a particular algorithm.

Results

The Hounsfield Units (HU) were estimated using the HU-tool encoded in Eclipse TPS using the region of interest of 2 × 2 cm². The relative electron density (RED) patterns estimated from the HU values of the fabricated phantom and patient CT images are listed in Table 1. The REDs for the rib, spine, scapula, lung, chest wall, and heart of the fabricated phantom were 1.849, 1.976, 1.983, 0.173, 0.855, and 0.833 g/cc, respectively.

Table 1.

The density pattern in different organs of indigenous phantom and computed tomography-image of a real patient

Organ	Density pattern in indigenous phantom (g/cc)	Density pattern in real patient computed tomography image (g/cc)
Ribs	1.849	1.810
Spine	1.976	2.015
Scapula	1.983	2.050
Lung	0.173	0.171
Chest wall	0.855	0.880
Heart	0.833	1.030

The dose computed based on different dose computation algorithms and estimated on the linac using IC were analyzed and detailed in Table 2. The percentage variation between IC estimated and algorithm computed doses on the slab phantom, Octavius phantom, and indigenous HT phantom for (a) 6 MV_FFB, (b) 6 MV_FFFB, and (c) 15 MV_FFFB is shown for various treatment setups and techniques (Figure 2).

Table 2.

The variation between Analytical Anisotropic Algorithm (AAA) and Acuros-XB (AXB) calculated and Ionising Chamber (IC) estimated doses using slab, Octavius, and indigenous phantoms

Energy	Technique	AAA									AXB
		Slab Phantom			Octavius Phantom			Indigenous HT Phantom			Slab Phantom			Octavius Phantom			Indigenous HT Phantom
		IC	TPS	% DD	IC	TPS	% DD	IC	TPS	% DD	IC	TPS	% DD	IC	TPS	% DD	IC	TPS	% DD
6FFB	1F	207.9	205.0	1.40	200.8	200.5	0.14	206.4	200.1	3.13	196.8	199.7	-1.44	197.6	200.3	-1.38	195.7	198.8	-1.58
	2F	205.1	207.4	-1.09	400.0	400.1	-0.02	201.9	200.1	0.90	197.8	198.3	-0.24	198.1	200.2	-1.06	194.6	199.1	-2.28
	3F_3DCRT	198.2	195.3	1.47	199.9	200.5	-0.29	196.5	200.1	-1.82	189.1	192.0	-1.49	196.7	200.0	-1.68	191.8	198.7	-3.47
	5F_3DCRT	192.0	189.4	1.37	198.9	200.5	-0.80	199.8	200.1	-0.15	200.2	205.1	-2.41	196.1	200.2	-2.07	190.5	198.7	-4.13
	5F_IMRT	201.4	204.7	-1.63	200.3	201.2	-0.47	171.5	177.5	-3.40	209.5	211.1	-0.74	288.4	290.5	-0.74	175.2	179.5	-2.41
	7F_IMRT	188.5	186.0	1.33	200.2	200.5	-0.17	197.5	200.4	-1.46	198.4	201.5	-1.52	201.2	202.1	-0.45	207.0	211.4	-2.08
	9F_IMRT	196.8	199.0	-1.12	201.3	202.0	-0.36	198.0	200.4	-1.18	195.2	198.7	-1.76	205.3	204.1	0.61	202.4	211.1	-4.12
	1ARC_VMAT	197.9	201.0	-1.54	193.2	196.0	-1.43	201.4	204.5	-1.52	207.6	209.7	-1.02	195.6	198.2	-1.35	211.3	216.2	-2.26
	2ARC_VMAT	205.1	208.1	-1.43	220.1	219.1	0.47	197.5	201.8	-2.13	190.8	187.2	1.92	189.4	192.4	-1.60	211.5	215.5	-1.87
	NONCO_VMAT	299.3	296.5	0.94	196.8	196.1	0.34	185.2	188.2	-1.60	172.6	170.5	1.21	211.0	209.1	0.92	191.3	193.0	-0.89
6FFFB	1F	213.2	209.5	1.75	203.6	200.6	1.48	209.5	200.2	4.66	200.1	201.1	-0.48	198.6	200.2	-0.82	197.4	198.8	-0.71
	2F	207.7	203.0	2.30	405.9	401.2	1.15	204.6	200.1	2.23	199.7	200.2	-0.23	199.1	200.5	-0.69	195.7	199.1	-1.69
	3F_3DCRT	199.7	195.0	2.39	202.5	200.6	0.95	197.6	200.1	-1.27	192.2	192.7	-0.24	197.9	199.9	-1.01	189.4	198.7	-4.70
	5F_3DCRT	191.1	189.4	0.88	201.8	200.6	0.58	199.7	200.1	-0.20	184.1	186.8	-1.46	197.2	199.9	-1.35	191.5	198.7	-3.62
	5F_IMRT	202.5	205.0	-1.22	198.2	199.1	-0.47	187.4	190.6	-1.70	190.7	192.3	-0.81	208.5	211.0	-1.20	189.1	190.6	-0.77
	7F_IMRT	197.5	199.7	-1.10	202.4	205.1	-1.35	198.2	199.2	-0.50	201.4	203.1	-0.82	195.4	197.1	-0.85	214.3	210.3	1.92
	9F_IMRT	198.4	195.7	1.38	200.6	200.5	0.05	196.5	199.7	-1.62	205.5	203.2	1.12	150.4	152.3	-1.26	203.5	210.0	-3.10
	1ARC_VMAT	201.4	199.8	0.80	187.3	188.3	-0.51	197.6	201.8	-2.10	196.7	199.8	-1.53	101.3	104.2	-2.83	210.4	214.9	-2.08
	2ARC_VMAT	213.2	217.6	-2.04	207.4	208.5	-0.53	199.8	205.2	-2.61	198.7	200.1	-0.72	189.2	190.3	-0.58	202.4	205.3	-1.40
	NONCO_VMAT	193.4	195.2	-0.91	202.1	205.0	-1.45	189.1	190.5	-0.73	185.6	187.2	-0.87	205.8	209.2	-1.64	188.4	193.5	-2.62
15FFB	1F	205.0	202.8	1.08	201.0	200.1	0.45	206.0	200.0	3.00	198.1	198.3	-0.08	198.0	199.3	-0.66	199.5	199.1	0.18
	2F	201.8	200.2	0.82	401.6	400.1	0.37	202.2	200.1	1.03	202.3	200.2	1.03	195.2	196.4	-0.61	202.1	200.1	1.00
	3F_3DCRT	199.5	197.8	0.88	200.6	200.2	0.22	204.1	200.1	2.01	191.2	190.9	0.14	197.9	199.1	-0.62	194.7	199.0	-2.16
	5F_3DCRT	197.7	194.4	1.68	200.1	200.2	-0.03	204.2	200.1	2.05	188.8	189.1	-0.14	197.5	199.3	-0.90	195.9	199.1	-1.62
	5F_IMRT	207.3	210.0	-1.27	198.7	200.5	-0.90	195.6	197.3	-0.84	207.1	210.1	-1.41	208.2	209.5	-0.64	199.4	200.1	-0.33
	7F_IMRT	198.5	200.1	-0.80	205.3	207.8	-1.23	201.1	205.6	-2.17	186.8	188.2	-0.74	205.1	207.9	-1.35	199.6	204.3	-2.30
	9F_IMRT	210.1	212.1	-0.94	205.3	207.3	-0.97	200.7	203.0	-1.15	196.7	195.4	0.68	202.7	204.2	-0.76	202.2	205.3	-1.51

AAA: Analytical Anisotropic Algorithm, AXB: Acuros-XB, IC: Ionising Chamber, HT: Heterogeneous Thoracic, TPS: Treatment planning system, DD: Depth Dose, FFB: Flattening Filter Beam, 3DCRT: 3Dimentional Conformal Radiotherapy, IMRT: Intensity-modulated radiation therapy, NONCO: Non-Coplanar, VMAT: Volumetric modulated arc therapy

Figure 2.

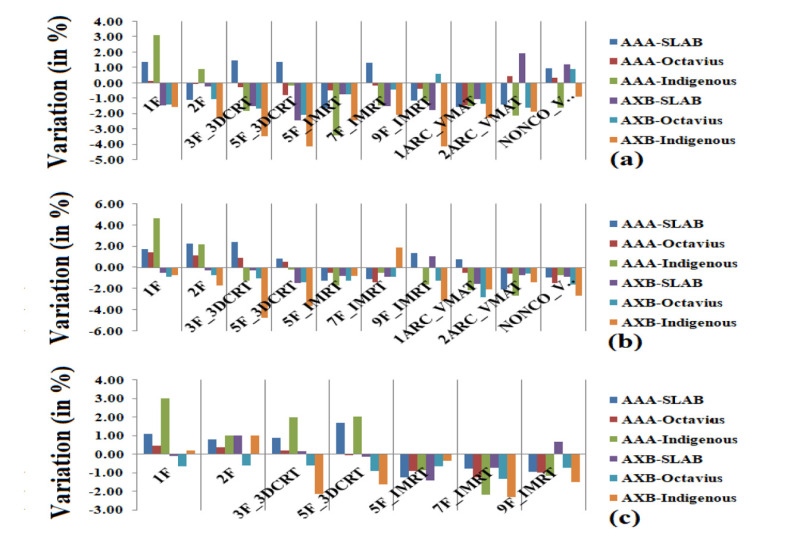
The percentage variation between IC estimated and algorithm computed doses on a slab, Octavius, and indigenous phantoms for (a) 6 MV, (b) 6 MV_flattening filter-free beam (FFFB), and (c) 15 MV_FFFB for various treatment setups and techniques

The average percentage variation between AAA computed and IC estimated doses were -0.03 ± 1.42, -0.03 ± 0.56 and -0.90 ± 1.82 for 6 MV_FFB, 0.42 ± 1.61, -0.01 ± 1.03 and -0.38 ± 2.22 for 6 MV_FFFB, and 0.21 ± 1.17, -0.30 ± 0.71 and 0.56 ± 1.95 for 15 MV_FFB using slab, Octavius and indigenous phantom, respectively. The average percentage variation between AXB computed and IC estimated doses were -0.75 ± 1.36, -0.88 ± 0.98 and -2.51 ± 1.07 for 6 MV_FFB, -0.61 ± 0.75, -1.22 ± 0.65 and -1.88 ± 1.84 for 6 MV_FFFB, and -0.08 ± 0.83, -0.79 ± 0.27 and -0.96 ± 1.26 for 15 MV_FFB using slab, Octavius and indigenous phantom, respectively.

Additionally, patient-specific QA was also executed on slab and Octavius phantom to analyze the performance of indigenous heterogenous thoracic phantom for patient-specific QA in the clinic. Patient-specific QA for a cohort of 10 patients was calculated on these phantoms, and measurement was recorded. Figure 3 illustrates the average percentage variations between IC measured and algorithm computed doses. The average percentage variations between computed and measured doses were 0.13 ± 1.91, 0.37 ± 1.22, and -0.91 ± 1.01 for AAA computations, respectively, using slab, Octavius, and indigenous phantoms. Similarly, average percentage variations between computed and measured doses were -1.18 ± 1.22, -1.56 ± 0.53, and -1.26 ± 0.98 for AXB computations, respectively, using slab, Octavius, and indigenous phantoms.

Figure 3.

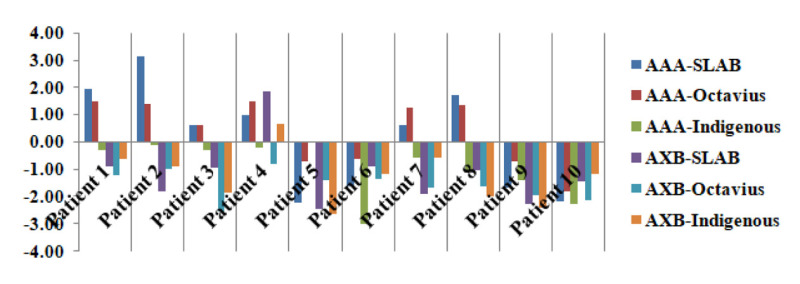
The patient specific-quality assurance (QA) results using slab, Octavius, and indigenous phantoms for thoracic cancer patient

Discussion

The present study aimed to develop a heterogeneous phantom for mimicking the thoracic region of the human. Additionally, the effect of tissue heterogeneity in the thoracic part on different dose computation engines was studied. The present study reveals that machined phantoms mimic the thoracic part of the human body in terms of size, shape, and comparable REDs for the rib, spine, scapula, lung, chest wall, and heart of the fabricated phantom to that of a real patient.

The dose verification performed indigenous HT phantom for different techniques (as mentioned in Table 2) using different photon energies were well within the prescribed tolerance, i.e. ± 5%. The AAPM TG 65 advocated accuracy within 5% in dose delivery for successful treatment outcomes [ 14 ]. The results obtained using heterogeneous phantom were comparable to the data obtained using slab and Octavius phantom, and the variations were within the limits of ± 5%, influencing the noticeable treatment outcome. Further, an indigenous HT phantom comprised of heterogeneities (varying densities) similar to the human body, is compared to slab and Octavius phantoms (uniform density). Kishore et al. [ 15 ] also reported similar results using a heterogeneous phantom compared to the uniform phantom. The accuracy of different dose computation engines is needed in a region of tissue heterogeneities due to the difference in their modeling approach. Additionally, AXB shows higher variation between computed and IC estimated doses using indigenous HT phantom compared to AAA since the contrast is in dose computation approaches utilized by these algorithms. The AXB estimation is medium sensitive and relies on its composition and characterization; the AXB establishes radiation transport in the medium. On the contrary, the AAA deals with the medium as water of various densities [ 16 , 17 ]. Kumar et al. [ 18 ] reported that AXB computation was more accurate compared to AAA in dealing with low-density mediums. Further, AXB was comparable to the gold standard Monte-Carlo algorithm [ 19 - 20 ].

Indigenous HT phantom was also validated in comparison to slab and Octavius phantoms for performing the patient-specific QA in a clinical environment. The patient-specific results were within the prescribed tolerance and comparable to data obtained using slab and Octavius phantoms. The major drawback of the present study was the uniformity of slab and Octavius phantoms in contrast to heterogeneous indigenous phantoms.

In comparison to slab and OCTAVIOUS homogeneous phantom, this study reported that the indigenous heterogeneous phantom can accurately simulate the dosimetric scenario and can be utilized for routine patient-specific QA. For resource constraints, radiotherapy centers in developing countries locally fabricate thoracic phantom that can be used for better dosimetry in thoracic cancer patients. Additionally, this phantom is highly useful for a high-dose Stereotactic Body Radiation Therapy (SBRT) treatment for thoracic cancer patients. Furthermore, an important difference is in AXB and AAA computation, which needs the correlated with clinical outcomes in the future.

Conclusion

The density pattern for indigenous HT phantom was in agreement with that of a real thoracic region of the human body. The computed and IC dose estimated using slab, OCTAVIUS, and HT phantom was within the prescribed limit (within the range of ± 5%) for different techniques and different photon energies. The patient-specific QA data were recorded using slab, OCTAVIUS, and HT phantom and were well within the prescribed limit calculated using AXB and AAA algorithms.

Authors’ Contribution

VK. Gangwar conceived the idea. Introduction and manuscript of the paper was written by VK. Gangwar, A. Agarwal, S. Prasad Mishra, OP. Gurjar and VK. Mishra. L. Kumar gathers the images and the related literature along with VK. Gangwar and also help with writing of the related works. The method implementation and experimental studies was carried out by VK. Gangwar. Results and Analysis was carried out by VK. Gangwar, OP. Gurjar, A. Agarwal and L. Kumar. The research work was proofread and supervised by S. Prasad Mishra and A. Agarwal. Clinical help was provided by S. Pandey All the authors read, modified, and approved the final version of the manuscript.

Ethical Approval

We took all measurement at Apollo medics hospital Lucknow Uttar Pradesh India, and took full permission for the same.

Conflict of Interest

None