Abstract
We present an update and revision to our 2010 review on the topic of proton-coupled electron transfer (PCET) reagent thermochemistry. Over the past decade, the data and thermochemical formalisms presented in that review have been of value to multiple fields. Concurrently, there have been advances in the thermochemical cycles and experimental methods used to measure these values. This Review (i) summarizes those advancements, (ii) corrects systematic errors in our prior review that shifted many of the absolute values in the tabulated data, (iii) provides updated tables of thermochemical values, and (iv) discusses new conclusions and opportunities from the assembled data and associated techniques. We advocate for updated thermochemical cycles that provide greater clarity and reduce experimental barriers to the calculation and measurement of Gibbs free energies for the conversion of X to XHn in PCET reactions. In particular, we demonstrate the utility and generality of reporting potentials of hydrogenation, E∘(V vs H2), in almost any solvent and how these values are connected to more widely reported bond dissociation free energies (BDFEs). The tabulated data demonstrate that E∘(V vs H2) and BDFEs are generally insensitive to the nature of the solvent and, in some cases, even to the phase (gas versus solution). This Review also presents introductions to several emerging fields in PCET thermochemistry to give readers windows into the diversity of research being performed. Some of the next frontiers in this rapidly growing field are coordination-induced bond weakening, PCET in novel solvent environments, and reactions at material interfaces.
Graphical Abstract
1. INTRODUCTION
The widespread occurrence of proton-coupled electron transfer (PCET) reactions in chemical processes has drawn broad interest from a myriad of scientific communities. PCET is involved in chemical synthesis from the bench to the industrial plant and is common in nature, biology, materials, and chemical energy processes. This review describes the Gibbs free energies—here denoted simply as free energies—of PCET half reactions for a wide range of substrates and reagents, with an emphasis on solution-phase reactivity. While PCET reactions can be broadly defined as those that involve transfers of electrons and protons (ne−/mH+), the material covered here is restricted to reactions involving equal numbers of e− and H+ (n = m, eq 1). Even with these confines this is a very broad class of reactions, from the cathodic 4e−/4H+ reduction of O2 to H2O in fuel cells (eq 2) to the 1e−/1H+ oxidation of the tyrosine residue (eq 3) that facilitates water oxidation in the photosynthetic oxygen-evolving complex. It is therefore unsurprising that there have been many previous reviews of the PCET field which cover reaction chemistry,1–3 computation and theory,4 electrochemical aspects,5 biochemical and biomimetic systems,6–9 photoinitiated reactions,10,11 organic synthesis,12,13 hydride transfer,14,15 and more.16,17
| (1) |
| (2) |
| (3) |
The thermochemistry of PCET reagents provides the foundation for understanding their reaction chemistry. Eleven years ago, our laboratory presented the first comprehensive listings of solution thermochemical values for PCET substrates.3 We are delighted that it has been widely used and that it seems to have influenced several burgeoning areas of chemistry, including photoredox (Section 3.3), N2 reduction (Section 3.6), and redox-mediated systems.
Unfortunately, we have found a few systematic mathematical errors in that review which shifted the absolute values of reported bond dissociation free energies (BDFEs), as stated in our recent correction.18 One purpose of this review is to correct the values in the 2010 review.3,19 These corrections systematically decrease previously reported BDFEs by between 1.6 and 4.8 kcal mol−1, depending on the solvent. We note that the differences between prior BDFE values in the same solvent are typically correct, just not the absolute values. Furthermore, the discussion provided in the previous review remains relevant, and we refer the reader to those sections for further context on the thermochemical values presented.3 More details on correct derivation are given in Sections 5 and 6 of the Supporting Information of our recent publication.19 More details about how the values in the updated tables were calculated are given below.
The increasing centrality of PCET thermochemistry over the past decade has greatly increased the quantity and standard of measurement methods and data. These advances have, in most cases, made previously used approximations unnecessary. Examples of approximations include the use of peak potentials from irreversible electrochemical couples in Bordwell’s early pathbreaking studies20 and Abraham parameters for estimating transfer free energies between solvents.3 Values from our previous review that employed these and other approximations are generally not recalculated in the tables below. Despite these omissions, we still report a robust compendium of experimentally determined thermochemical values for PCET half-reactions. This includes new values determined since our last review, which are largely for coordination complexes and multielectron/multiproton reductions. Efforts have been made to make this review comprehensive, but this is a challenging standard to reach given the diversity and rapid growth of the field.
In summarizing what has been learned about PCET thermochemistry over the past decade and advocating for new directions, this Review goes well beyond simply correcting and collecting values. We provide a thorough breakdown of the thermochemical cycles used (Section 2), which we hope provides a simplified analysis for newcomers and new insights to already expert practitioners. Furthermore, we demonstrate the experimental and theoretical advantages of using potentials of hydrogenation, denoted E∘(V vs H2), to describe the thermochemistry of PCET reactions. In particular, E∘(V vs H2) is shown to be effectively equivalent to more widely reported BDFEs in solution while also being far easier to measure directly (Section 2.2.2 and ref 19). In fact, we highlight a recently published method which enables direct measurement of E∘ (V vs H2) for many compounds under any buffered solvent condition amenable to electrochemical analysis (Section 2.2.3). Thermochemical cycles based on this method and future ones like it will be important to fulfilling the growing interest in measuring reaction thermodynamics in real systems where significant nonidealities exist (Section 2.3).
The higher standard of data included in this review enabled a novel analysis of the solvent dependence of free energies for ne−/nH+ PCET half reactions (Section 3.1). Over a wide range of systems, both BDFEs and E∘ (V vs H2) values are shown to be highly insensitive to solvent identity across a wide range of molecules and solvents. Importantly, this is not the case for ne−/nH+ PCET potentials measured against a pure-electron transfer reference such as ferrocene. This is because the overall thermochemical equations will involve the transfer of charged species (e− and/or H+), if a hydrogen-based reference is not used. As a result, we advocate for the use of H2(g), H•, and the reversible hydrogen electrode (RHE) as reference states for both aqueous and nonaqueous thermochemistry. We hope that this transition is expedited by expanded experimental use of H2-based reference electrodes, to more easily and more accurately determine PCET thermochemistry.19
The advantages of referencing PCET thermochemistry to H2(g) are most apparent in the connections it enables to studies in complex reaction media and related fields. We highlight the growing interest in engineering solution conditions to improve system performance, such as in the use of organic/aqueous mixtures to solubilize redox mediators for oxygen reduction21,22 and to perturb solvation environments for small-molecule activation (Section 3.1).23,24 Additionally, we provide an introduction to the many connections between PCET thermochemistry at molecules and (nano)materials (Section 3.8). This includes the measurement of hydrogen adsorption energies for gas/solid reactions by temperature-programmed desorption methods, as well as electrochemical and thermal studies of solid/solution interfaces. These highlights and others (Section 3) emphasize the centrality of PCET thermochemistry and the connections it enables.
2. THERMOCHEMICAL BACKGROUND
The free energy of the ne−/nH+ oxidation of a PCET reagent (XHn) can be described by multiple thermochemical formalisms. The simplest case, with n = 1, involves the making or breaking of only one X–H bond to give X•; and H• (H+ + e−). The “gold standard” thermochemical descriptor for such a process is the bond dissociation free energy (BDFE) of X–H (eq 4). When n > 1, the average BDFE (or free energy per H• dissociated) has typically been the preferred value for tabulation. However, most tables of X–H bond strengths instead give bond dissociation enthalpies (BDEs).This choice is in part historical as widely reported gas-phase BDEs were easier to measure and to connect with early computational approaches. When studies of solution-phase bond strengths became more common, most tried to parallel the known gas-phase values and report BDEs. Excellent resources exist for BDEs, such as Luo’s Comprehensive Handbook of Chemical Bond Energies (2007) and the iBonD Databank from Tsinghua and Nankai Universities that lists 7600 BDEs and 35 000 pKa values.25,26 However, free energies are more important for reactions in solution. This is because ΔG∘ values determine equilibrium constants and are used in both linear free energy relations and treatments derived from Marcus theory.
| (4) |
We advocate here for the use of a relatively new thermochemical parameter, the potential of hydrogenation, E∘(V vs H2), for PCET reactions that involve equal numbers of electrons and protons (eq 1). This thermochemical value is directly related to the free energy of hydrogenation, by eq 5. We prefer the intrinsic E∘(V vs H2) because it does not scale with the number of electrons transferred in a reaction. E∘(V vs H2) is the potential for a whole reaction, the addition of H2, rather than the more commonly tabulated half reactions that involve the addition of electrons, such as the potential to add protons and electrons to a reagent (eq 6). Sections 2.2.2 and 2.2.3 below describe E∘(V vs H2) in more detail, and they present the practical experimental advantages of its measurement. Sections 2.3 and 3.1 discuss the fundamental advantages of this term over electrochemical half reactions, such as allowing close comparisons across reaction conditions and reaction types.
| (5) |
| (6) |
In this section, we provide an overview of methods and thermochemical cycles used to obtain the values presented in the tables below, with a specific emphasis on the similarities between BDFE and E∘(V vs H2). In all of the equations, schemes, and tables, all species are solution phase unless otherwise noted, except for H2 and other gases (O2, N2, CO2, CO, and CH4) which here are always considered to be in the gas phase (though the use in the literature is varied27). The gas-phase standard state is 1 atm, at 298 K. For dissolved species, 1 M solutions have typically been used as the standard state, though more precise definitions are available.28 For reactions where all of the species are in the gas phase, the “solvent” is labeled “gas”.
2.1. Traditional Methods for the Measurement of BDFEs
Relative BDFEs can be accurately determined by equilibration, and this gives absolute BDFEs when the value for one of the PCET reagents is known (eq 7). Lucarini and co-workers, for instance, used this approach to determine phenol BDFEs.29 Similarly, Kreevoy et al. used equilibration to measure the relative hydride affinities of NAD+ analogues (a type of heterolytic bond strength).14,30,31
| (7) |
Solution BDFEs (BDFE(solv)) can be derived from known bond dissociation enthalpies (BDEs) but only with certain assumptions. If the BDE of X–H is known in the solution of interest, then the conversion requires the absolute entropies of XH, X•, and H• in the solvent (eq 8). The thermochemistry of H• solvation has been well estimated in various solvents, as discussed below (Table 1), but the entropies for HX and X• are almost never known experimentally. If the BDE is only known for gas-phase species, additional energies of solvation are needed to convert a BDE(g) to a BDFE(solv), which are also almost never known.
Table 1.
Key Thermodynamic Constants in Common Solvents
| solvent | TS∘(H•)a,b | ΔG∘f(H•)a,c | E∘(H+/H2)d,e | C G e |
|---|---|---|---|---|
| gas phase | 8.17f | 48.59f | -- | -- |
| water | 2.9549 | 52.849 | 0.00g | 52.850,g |
| acetone | 6.5047 | 51.947 | -- | -- |
| acetonitrile (MeCN) | 6.3747 | 52.047 | −0.02819 | 52.619 |
| benzene | 6.2348 | 52.148 | -- | -- |
| CCl4 | 6.1648 | 51.948 | -- | -- |
| chlorobenzene | 5.8348 | 52.148 | -- | -- |
| N,N-dimethylacetamide (DMA) | -- | -- | −0.7951 | -- |
| N,N-dimethylformamide (DMF) | 6.0747 | 52.347 | −0.66219 | 67.619 |
| dimethyl sulfoxide (DMSO) | 6.1649 | 52.649 | −0.6752,h | 68h |
| 1,4-dioxane | 6.2547 | 52.247 | -- | -- |
| n-hexane | 6.3047 | 51.747 | -- | -- |
| isopropanol (IPA) | -- | -- | −0.49419 | -- |
| methanol (MeOH) | 5.7149 | 51.949 | −0.50153 | 63.4 |
| toluene | 6.1047 | 52.047 | -- | -- |
| tetrahydrofuran (THF) | 6.4347 | 52.047 | −0.343i | 59.9 |
Values in kcal mol−1 at 298 K.
TS∘(H•) = T[S∘(H•(g)) + ΔSsolv∘(H•)], where H2 data are used to approximate H• solvation, and the standard state is 1 M in solution unless otherwise specified.
Adapted and expanded from ref 19.
Potentials are in V.
E∘ and CG are vs Cp2Fe+/0 unless otherwise stated.
Values involve H•(g) at 1 atm gaseous standard state from ref 42.
Value referenced to SHE.
E∘(H+/H2) in DMSO was determined from the E1/2 of a quasi-reversible wave, and therefore both it and the corresponding CG are not reported to the same level of accuracy as other values in this table.
Value is an average of those presented in refs 19, 54, and 55 with corrections for TS∘(H•) where necessary. [The value of TS∘(H·) in THF in ref 55 was corrected from unit mole fraction to 1 M standard state, giving 6.43 kcal mol−1 and E∘(H+/H2) = −0.33 V (values that were then averaged with those from the citations noted just above).] Standard state is defined by an absolute pKa scale.56
| (8) |
In practice, the conversion of BDEs to BDFEs uses the assumption that the absolute entropies for X• and XH are very similar and cancel, presumably because these species are very similar in size and polarity (eq 9).32,33
| (9) |
Bordwell, Parker, Tilset, and others have found this to be a good assumption for the organic and organometallic systems they studied.34–37 However, there may be significant deviations when X• and/or XH can engage in hydrogen bonding with the solvent.3,38 In addition, there can be large entropy terms when high-spin transition metal complexes are involved.33,39 The concerns about these assumptions emphasize the need for direct measurements of free energies to describe PCET reaction thermochemistry, especially when comparing across conditions.
2.2. Square Scheme Approaches to BDFEs and Potentials of Hydrogenation
Many BDFEs have been determined by measuring a pKa and a one-electron reduction potential (E∘), in a method which essentially parses the BDFE into the free energies for electron transfer (ET) and proton transfer (PT) (eq 10).
| (10) |
This approach was first popularized by Bordwell, although he used it to derive BDEs.34 The development of this method required the definition of an unusual free energy constant, CG. While the use of one constant makes eq 10 elegant in its simplicity, it also buries the fact that CG is a composite value that is challenging to measure (see below). As a result, widespread adoption of this approach has left the field with complex terminology that can confuse even well-versed practitioners. After all, this review is being written in part because our group made thermochemical errors when calculating CG values a decade ago. Below we describe the traditional analysis, and then, in Section 2.3, we advocate for the adoption of new terminology based on E∘(V vs H2) to make this powerful new method more accessible to the research community—intuitively and experimentally.
2.2.1. BDFE Analysis Using CG.
Division of the overall free energy for a solution-phase PCET process into the components for electron and proton transfer is best visualized using a square scheme (Scheme 1). Following this roadmap and eq 10, the overall free energy for the PCET process is calculable by adding together the appropriate E∘ and pKa values, via the bottom left (eqs 11 and 12) or top right corners. However, the resulting equation describes the transfer of e− and H+ (eq 6 where n = 1), as opposed to the desired transfer of H•. This thermochemical quandary was first solved with the advent of CG, or E∘(H+/H•), since its addition neatly converts e− plus H+ to H• (eq 13). As a result, when the CG and the E∘(X/X−) use the same reference electrode—recommended by IUPAC to be the Cp2Fe+/0 couple in organic solvents40,41—then the sum of eqs 11–13 gives the BDFE in kcal mol−1 (eq 4).
Scheme 1.
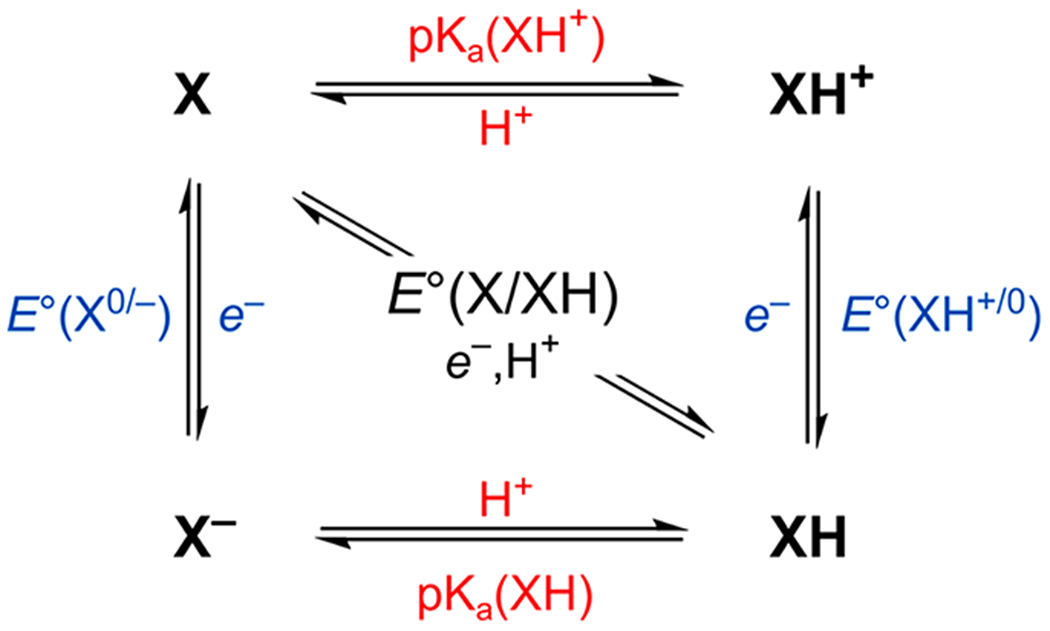
Square Scheme of PCET Thermochemistry
| (11) |
| (12) |
| (13) |
| (4a) |
However, the calculation of CG involves multiple steps.19 The first is the determination of E∘(H+/H2) against the appropriate reference electrode (eq 14). Addition of this quantity switches the reference potential to H+/H2(g) in the solvent of interest, and it changes the overall thermodynamic equation to describe the potential of hydrogenation (Section 2.2.2). Next, the well-known free energy of H2 dissociation in the gas phase is added (eq 15).42 The last step is addition of the free energy for solvating H• in the solvent of interest (eq 16). The sum of eqs 15 and 16 gives ΔG∘f(H•) (eq 17), which itself is of practical use and whose values are compiled for a range of solvents in Table 1.
| (14) |
| (15) |
| (16) |
| (17) |
In this paragraph, we describe, for the interested reader, the nuances of properly calculating ΔG∘solvation(H•). While the solvation term described by eq 16 is intractable to measure directly, the solvation of H• has been shown to be well-described by that of H2.43 Other workers have used noble gases as models for H•, and recent papers have argued the merits of both of these approaches, though values derived from the two methods differ by only 1 kcal mol−1 at 298 K.44–46 For simplicity and consistency, here we choose to use the H2 assumption for all solvents. This assumption can be broadly applied, as solvation data for H2 are available for numerous solvents.47–49 We note that calculation of ΔG∘solvation(H•) is complicated by the need to convert the standard state of H• in the solvent from the reported unit mole fraction (χ = 1) to 1 molar.19 A sign error in applying this conversion resulted in systematic errors for the BDFEs reported in our original publication, as noted in our recent correction.18 A complete and corrected walk-through of the underlying equations is provided in Sections 5 and 6 of the Supporting Information of our recently published work.19
2.2.2. Potential of Hydrogenation.
As shown in the section above, determination of the CG term needed to measure BDFEs is complex and inaccessible to the beginning practitioner. Below, we introduce a more experimentally accessible, and equally robust, thermochemical value that one necessarily calculates in the process of determining a BDFE. The addition of eqs 11, 12, and 14 (Scheme 2) gives the potential of hydrogenation, or E∘(V vs H2). In this scheme, the sum of eqs 11 and 12 gives an electrochemical potential, E∘(X/XH, vs Cp2Fe+/0), and eq 14 changes the reference state to E∘(H+/H2). Thus, E∘(V vs H2) is the electrochemical potential for an ne−/nH+ half reaction with RHE as the reference potential (see below). More generally, since a potential vs RHE is equivalent to the addition of H2(g), E∘(V vs H2) is directly related to the free energy of hydrogenation via eq 5 (repeated below). Equation 5, as noted above and discussed below, is a whole reaction, not a half reaction.
Scheme 2.
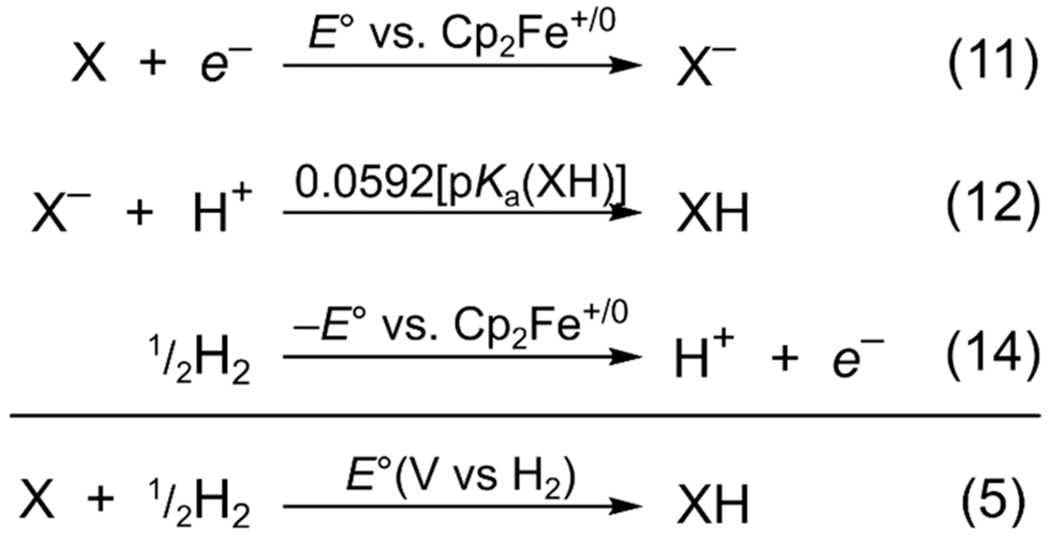
Calculation of E∘(V vs H2) from the 1e− Reduction Potential and pKa
| (5a) |
Values of E∘(V vs H2) are also easily compared with BDFEs, as they only differ by ΔG∘f(H•) in the solvent of interest (eq 18). Values of ΔG∘f(H•) are 52.2 ± 0.6 kcal mol−1 across a wide range of solvents, aqueous or nonaqueous, protic, or aprotic (Table 1). As a result, solution-phase values of E∘(V vs H2) and BDFE are effectively equivalent. In the following paragraphs (and in Sections 2.2.3 and 2.3), we discuss the practical aspects of measuring E∘(V vs H2) as well as the experimental and theoretical advantages.
| (18) |
E∘(V vs H2), in common with a BDFE, describes a complete chemical reaction without charged species or electrons (eq 5, Scheme 2). E∘(V vs H2) refers to an electrochemical whole reaction, the sum of the two half reactions, E∘(X/XH vs Cp2Fe+/0) (eq 6, or eqs 11 and 12) and E∘(H+/1/2H2 vs Cp2Fe+/0) (eq 14). Because this is the sum of two half reactions and refers to the addition of H2(g) and not electrons, E∘(V vs H2) does not involve a reference electrode. This makes E∘(V vs H2) a more universal value, in a sense using H2(g) as the specified reference state.
While we prefer to think of E∘(V vs H2) as a whole-reaction potential, it can equivalently be described as a half reaction referenced to the H+/H2 potential under the reaction conditions (eq 19). The H+/H2 potential under any conditions is called the reversible hydrogen potential, RHE. RHE is commonly used in aqueous electrochemistry to refer to the hydrogen potential when the proton is not at the standard state, i.e., when the pH differs from zero [when pH = 0, this is the standard hydrogen electrode, SHE]. Equation 19 is the same as eq 14 except that the proton is not required to be at the standard state, and therefore the potential is denoted E without a ∘. However, the H2(g) in eq 19 is constrained to be at a standard state (1 atm, 298 K) in the definition of RHE. As discussed below, using protons at the nonstandard state makes E∘(V vs H2) a much more universal and useful parameter.
| (19) |
The use of RHE in nonaqueous solvents is powerful because it has become readily measurable with the new open-circuit potential (OCP) method by Roberts and Bullock (Figure 1).57 This OCP method was originally performed under nonstandard proton activities (RHE) and extrapolated to the standard state (SHE). The robustness of this extrapolation was proved by the authors by demonstrating Nernstian shifts of the OCP with changes in buffer pKa and reagent concentrations.57 This is therefore a valuable methodology for measuring the nonaqueous equivalent of RHE in any solvent suitable for electrochemistry and SHE when the pKa scale is known.
Figure 1.
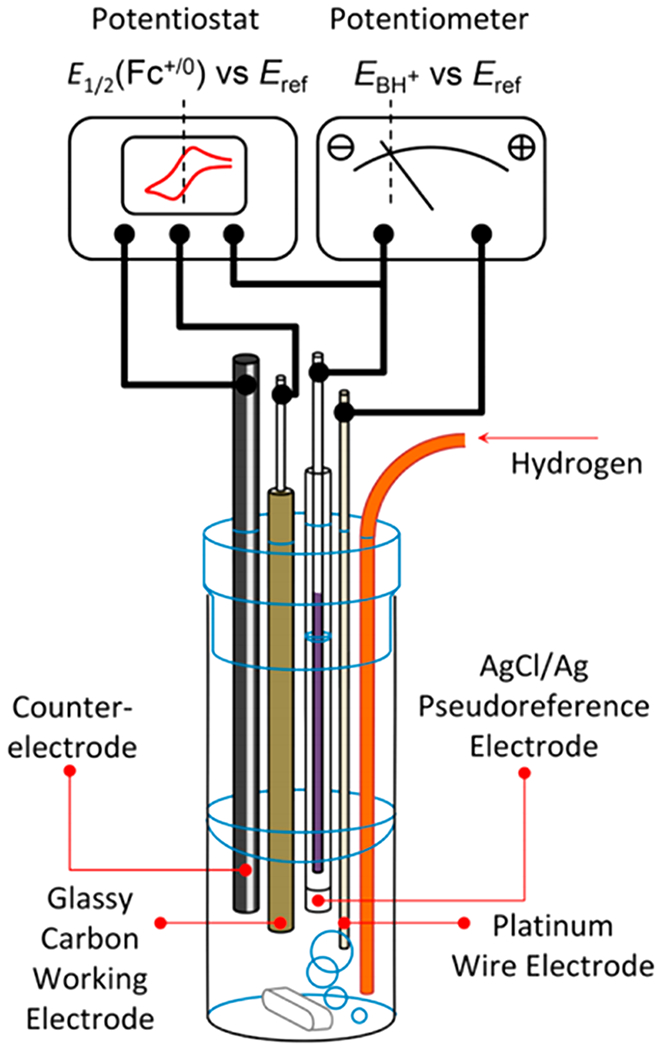
Roberts and Bullock’s schematic of the four-electrode cell configuration used for H2 open-circuit potential (OCP) measurements. The analyte solution consists of an acid:base:H2 mixture of known composition. The Ag/AgCl pseudoreference is calibrated to Cp2Fe+/0 after determination of the OCP. Potentiostat and potentiometer are shown as separate devices to illustrate the principle of the measurement. Reprinted with permission from ref 57. Copyright 2013 American Chemical Society.
For full details of the method, we refer readers to the original article.57 In brief, the OCP of a clean platinum wire electrode is measured in a buffered electrolyte solution in the presence of 1 atm of H2. This is a direct measurement of the reduction potential of the acid component of the buffer to H2 (eq 20). It is termed with the prime (′) indicating that it is specific to the buffer used and the Fc subscript indicating that the reference potential is Cp2Fe+/0.
| (20) |
Equation 20 is the nonaqueous equivalent to eq 19 in that both define RHE, but eq 20 recognizes that in nonaqueous solvents the proton is usually bound to a buffer acid. As noted above, RHE is commonly used in aqueous PCET electrochemistry and electrocatalysis, as both a physical reference electrode and a theoretical reference state. In RHE electrodes, the potential is measured with a clean Pt wire in an electrolyte sparged with 1 atm of H2, with proton activity being that of the electrolyte. This means that E∘RHE is zero and independent of changes in pH (aqueous solutions) or buffer pKa, making the reference state independent of proton activity. The great value of this reference state is developed in the next sections.
The Roberts and Bullock method requires the assumption that the Pt wire reversibly interconverts H2(g) and protons in solution at the reversible potential (RHE) on the time scale of the OCP measurements. The advantage of OCP measurements is that they allow equilibrium to be achieved over long times, from minutes to hours. Solvent or buffer adsorption to the Pt surface would have to be quite strong to inhibit this catalysis over such long time scales. This assumption is supported by the quantitatively Nernstian shifts upon changes to the solution. When Nernstian behavior is not observed, the method is not appropriate. Prior literature studies of HER on platinum electrodes indicate that the reaction occurs on the cyclic voltammetry time scale, which is much shorter than the OCP time scale.58–60 This assumption is also supported by the equivalence of E∘(V vs H2) and BDFE values measured by OCP with those measured by other methods, in different solvents and with different buffers.19,57
2.2.3. Direct Electrochemical Measurements of PCET Thermochemistry.
Direct electrochemical measurements of reversible PCET processes are often possible in aqueous solutions. Under acidic, basic, or buffered conditions, proton transfer in water is often sufficiently rapid that reversible electrochemical responses are observed for PCET redox couples such as quinone + 2e− + 2H+ → hydroquinone.61 The resulting values of E∘(X/XHn) are aqueous PCET potentials (eq 6), measured under various conditions and corrected to standard states. Many of these appear in the tables below.
Our laboratory has recently developed a direct electrochemical measurement of E∘′(X/XHn) in organic and mixed solutions using an OCP method similar to that of Roberts and Bullock’s for E∘′(HA/H2).19 This is a significant advance as cyclic voltammograms (CVs) of PCET couples are almost always irreversible in nonaqueous solvents due to the slower proton transfer rates. As a result, E1/2 values determined from these voltammograms do not provide accurate measures of the underlying PCET thermochemistry.19,62 OCP measurements have a longer time scale than CV, allowing more time for protons and other nuclei to equilibrate. The strategy of using OCP measurements, or redox potentiometry, to evaluate the thermodynamics of sluggish electroreductions has previously been explored in biochemical systems, as well as toward the measurement of molecular hydricities and nanoparticle Fermi levels.63–65
In our studies,19 the OCP of a solution containing X, XHn, an acid/base buffer, and electrolyte was measured. This directly determined the X/XHn potential vs the reference electrode used. Ferrocene was then added to calibrate the internal reference electrode, to give E∘′(X/XHn vs Cp2Fe+/0) in that buffered electrolyte (eq 21).19 When multiple hydrogens are added to X this approach gives the average free energy to add e− + H+ and, via eq 18, the average BDFE. The procedure was validated and applied to a number of X/XHn PCET couples with O–H and N–H bonds, for n = 1 or 2. When applying it, we recommend using monoprotic 1:1 buffers AH/A− because then the proton activity is simply the pKa of the acid. Keeping the AH:A− ratio at 1:1 also eliminates the need to correct for homoconjugation (the formation of AH⋯A− hydrogen-bonded adducts) in most buffers.19,66
| (21) |
| (22) |
The PCET electrochemical potential derived from OCP measurements can be combined with the measurement of E∘RHE to give E∘(V vs H2) (Scheme 3 and eqs 21 and 22, the latter being just n times eq 20). This addition requires that the two measurements be made using the same solvent, buffer, and electrolyte, and then the contributions of the buffer cancel. The resulting reaction, at the bottom of Scheme 3, and shown earlier as eq 5, is simply the potential of hydrogenation of X to XHn. This reaction is, therefore, independent of the buffer or ferrocene reference. The advantages of this approach are described in the following section.
Scheme 3.
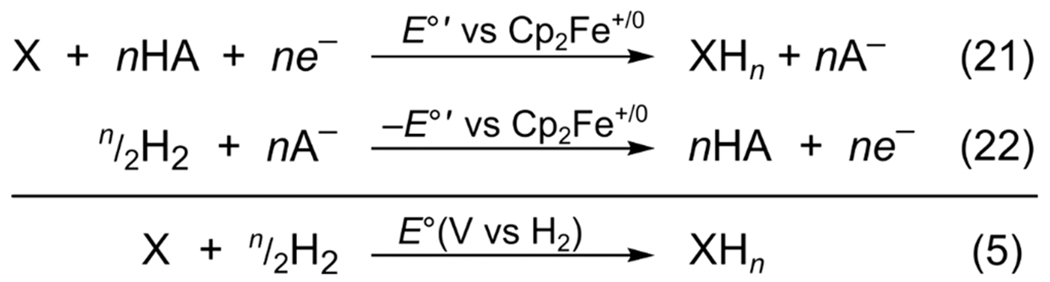
Calculation of E∘(V vs H2) Directly from E∘′(X/XHn)
Scheme 3 is thermochemically equivalent to the route to E∘(V vs H2) in Scheme 2 using pKa and E∘. However, these two methods are not experimentally equivalent because one OCP potential takes the place of two separate pKa and E∘ measurements, eqs 11 and 12. The pKa(XH) and E∘(X/X−) are often measured under different conditions from each other and from E∘(H+/H2), introducing potential systematic errors in the analysis. In particular, ion pairing with the electrolyte and homoconjugation of the buffer acid and base can shift the proton activity in organic solvents significantly from that predicted from ideal pKa measurements. The OCP approach has the dual advantages of measuring the proton and electron transfer energetics together and of providing more time for thermodynamic equilibrium to be reached. In our experience, the OCP approach outlined in Scheme 3 is the most accurate measurement of PCET thermochemistry when experimentally accessible.
2.3. Advantages of Potentials of Hydrogenation
As discussed above, values of E∘(V vs H2) are experimentally accessible. They are equivalent to proton-coupled electrochemical potentials, E∘(X/XHn vs H+/H2), and they are directly related to free energies of hydrogenation. However, potentials of hydrogenation are not commonly reported, especially for reactions in nonaqueous environments.19 Instead, common practice for electrochemists is to report proton-coupled potentials vs Cp2Fe+/0, and common practice for thermochemists is to report BDFEs (or BDEs). Below we demonstrate the advantages of instead reporting E∘(V vs H2), and we discuss how this suggested new paradigm promotes connections between the thermal and electrochemical communities.
Reporting of proton-coupled potentials as E∘(V vs H2) has significant advantages over potentials versus ferrocene or other electron-only references. Because electrochemical PCET involves the transfer of both protons and electrons, the proton activity of solution affects the measured potential. While a pure electron reference does not move with proton activity, use of E∘RHE does. As shown in Scheme 2 and Scheme 3, this removes all charged species from the overall reaction. Thus, the E∘ (V vs H2) for an ne−/nH+ couple is independent of changes in the proton activity of the solvent. This independence leads to E∘(V vs H2) having very similar values in a range of solvent conditions (Section 3.1). The solvent independence is furthered by the use of the same H2(g) reference for all measurements.
Reporting of E∘(V vs H2) instead of BDFEs allows for a direct comparison with a large database of electrochemical values without any conversions. While E∘(V vs H2) values are perhaps not as conceptually simple as BDFEs (eqs 4 and 5), they require one less step to calculate. E∘ (V vs H2) is converted to a BDFE (or an average BDFE) by addition of ΔG∘f(H•) (eq 18). This free energy has been reported in many but not all solvents (e.g., not in DMA, MeOH, and IPA (Table 1)). Still, ΔG∘f(H•) varies little with solvent and, if necessary, can be well estimated by averaging values for similar solvents.
The advantages of this approach are particularly evident for studies in mixed solvents. Thermochemical measurements of PCET reactivity have traditionally been inaccessible in mixed solvents due to the lack of established pKa scales. In fact, this is a barrier to applying a square scheme approach (Section 2.2) even in many pure solvents, as pKa scales are not ubiquitous and reagent instability can make measurements challenging. However, both issues can be solved by measuring E∘(V vs H2) via Scheme 3, as this method removes the need to measure a pKa. In Scheme 3, pKa measurement is effectively replaced by the OCP measurement of E∘RHE which is readily accessible by experiment in any medium that is amenable to electrochemical analysis (Figure 1).19,51,57,67–70
The approach in Scheme 3 should be broadly applicable to PCET reagents with O–H and N–H bonds in almost any polar medium.19 Currently, the generality of this scheme is limited by the OCP method for determining E∘′(X/XHn) (eq 21). In our experience, the method will not be successful if there is no Faradaic response for the X/XHn couple in the solution window for voltammetry. This is consistent with the understanding that electrochemical equilibria can only be reached if electrode kinetics are sufficiently fast to enable current flow.71 We therefore suspect that electrode kinetics are the main barrier to measuring E∘′(X/XHn) for PCET reactions that involve C–H bonds by the OCP method.19 Nevertheless, the promise of this methodology is significant as it greatly increases access to the direct measurement of E∘(V vs H2) using widely available electrochemical setups. Furthermore, the measurement of E∘′(X/XHn), where n > 1, is also made simple by this method as a single measurement replaces the alternative of 2n free energy measurements required by a square scheme approach. This new method has enabled a broad analysis of the solvent dependence of BDFEs and E∘(V vs H2) values (Section 3.1).
Values of E∘(V vs H2) have the additional advantage that they are readily compared to other free energies of hydrogen addition (eq 5), in solution or in the gas phase. In aqueous solution, tabulated electrochemical potentials vs RHE are equivalent to E∘ (V vs H2). There is also a long history of tabulating energies of gas-phase hydrogen addition to both molecules and materials (see Section 3.8). BDFEs can also be compared to gas-phase measurements, although the overall reaction is slightly different and a correction of ~4 kcal mol−1 must be applied to account for the free energy of solvation for H• (Table 1). For both E∘ (V vs H2) and BDFE, practical comparison of solution- and gas-phase values requires the assumption that the solvation free energies of X and XHn are very similar. This assumption is discussed in Section 3.1.1 below.
Overall, potentials of hydrogenation have the unique advantage of being universal. When solution-phase potentials are reported in this way, they not only are solvent independent but also become comparable to a broad base of previously reported thermochemical values. While we hope that E∘(V vs H2) values will be widely adopted, we recognize that a new term brings the potential of further convoluting the literature. As a result, we have striven to clearly define the relationships between E∘(V vs H2) and more established thermochemical values, such as BDFEs, in Section 2. We anticipate that using E∘(V vs H2) instead of BDFEs will facilitate communication between different fields and will spur development of the PCET field in multiple directions, such as those highlighted in the various parts of Section 3.
3. INSIGHTS AND EMERGING AREAS OF PCET THERMOCHEMISTRY
3.1. Medium Dependence
Section 2.2 of this review demonstrates that the BDFE of X–H is effectively equivalent to E∘(V vs H2). Nevertheless, in the tables below, both the BDFE and E∘(V vs H2) values are reported for each compound. This is done to emphasize the utility of E∘(V vs H2) or the free energy of H2 addition, which can be measured directly for many reagents in many solvent conditions (Section 2.3).
3.1.1. Solvent Dependence.
The assembled data in the tables below send a clear message: BDFEs and E∘(V vs H2) values are essentially independent of solvent identity, with few exceptions. In Table 2, we compile all reported substrates for which BDFEs and E∘(V vs H2) values are known in three or more solvents. When generating this list of compounds, all values from our previous review were double checked to ensure that they met the more stringent criteria for inclusion used herein (Section 4). Before application of this procedure, there were many compounds whose BDFEs seemed to have a significant solvent dependence, but afterward there was only one: 4-oxo-1-hydroxy-2,2,6,6-tetramethyl-piperidine (4-oxo-TEMPOH). The outlier BDFE for 4-oxo-TEMPOH was 61.2 kcal mol−1 in hexane, which was initially consistent with the intuition that a substrate with polar substituents might show a solvent effect between MeCN and hexane. Nevertheless, we decided to double check this value experimentally by performing an equilibration between TEMPOH (whose BDFE is reported as 63.4 kcal mol−1 in hexane) and 4-oxo-TEMPO. Interestingly, we find that the Keq for this reaction is 3.9 ± 2.0, suggesting that 4-oxo-TEMPOH is less reducing than TEMPOH and should therefore have a higher BDFE (see SI). In fact, use of the corrected BDFE removes the effect of solvent on BDFE such that the average value across hexane, CCl4, and MeCN is 65.6 ± 1.4 kcal mol−1. With this correction in mind, all substrates we know, for which data are available in three or more solvents, have BDFEs that are independent of solvent. This is a remarkable result because E∘ and pKa values often vary substantially with solvent, and yet the averages of BDFEs and E∘(V vs H2) values across a range of solvents have uncertainties similar to those of the individual values.
Table 2.
Solvent Dependence of PCET Thermochemistrya
| molecule | # of solvents | avg. E∘(V vs H2) | avg. − ΔG∘/nb | Δεc | table |
|---|---|---|---|---|---|
| TEMPOH | 4 | 0.558 ± 0.048 | 65.0 ± 1.3 | 34.8 | 5 |
| 4-oxo-TEMPOHd | 3 | 0.595 ± 0.053 | 64.6 ± 1.4 | 34.8 | 5 |
| 2,4,6-tBu3PhOH | 6 | 1.003 ± 0.028 | 75.4 ± 0.8 | 77.9 | 6 |
| 4-MeO-2,6-tBu2PhOH | 3 | 0.864 ± 0.025 | 72.0 ± 0.6 | 34.4 | 6 |
| 1,4-hydroquinone | 3 | 0.656 ± 0.011 | 67.4 ± 0.2 | 72.6 | 7 |
| 2,6-dimethyl-1,4-hydroquinone | 5 | 0.560 ± 0.012 | 65.1 ± 0.4 | 72.6 | 7 |
| O2(g) + 2H2(g) → 2H2O | 4 | 1.242 ± 0.013 | 81.0 ± 0.4e | 43.5 | 11 |
| DPPH-H | 3 | 0.929 ± 0.012 | 73.5 ± 0.4 | 34.4 | 15 |
| CO2(g) + H2(g) → CO(g) + H2O | 4 | −0.091 ± 0.016 | 50.3 ± 0.4 | 43.5 | 21 |
| CO2(g) + 4H2(g) → CH4(g) + 2H2O | 3 | 0.176 ± 0.007 | 56.4 ± 0.3 | 43.5 | 21 |
Averages and standard deviations were calculated for each molecule across the different solvent conditions listed in the tables below. Values for E∘(V vs H2) are in V; −eE∘ is the average free energy for addition.
These are averages of the average free energies to remove H• from the substrate; denoted as BDFE, BDFEavg, or −ΔG∘/n in the tables (see Section 4).
Range of solvent dielectric constants for the values being averaged, with ε values taken from ref 72.
Value in hexane redetermined by equilibration with TEMPOH. See Supporting Information for full details.
Three solvents used to calculate the avg. of −ΔG∘/n.
The explanation of the solvent constancy or medium independence of ne−/nH+ transfer reactions can be described by a new square scheme (Scheme 4). The top and bottom of the scheme are the equations for the BDFE of X–H, differing only in the solvent (S vs S′). The difference between the BDFEs in the two solvents is the difference in the transfer free energies of dissolved reagents.67 The free energy of solvation (ΔG∘solv) for H• is essentially constant across all solvents (Table 1), so all differences in BDFEs between solvents can be attributed to ΔG∘solv(XH) – ΔG∘solv(X•). Both XH and X• are of similar size and polarity, differing only by one H atom, so it is not surprising that these terms are usually similar and effectively cancel one another. One might expect significant differences because XH and X• have different capacities for hydrogen bonding, depending on the solvent, but this is not evident in the data. Even 1,4-hydroquinones, which are expected to have significantly different hydrogen bonding characteristics as compared to their corresponding quinones, show very small solvent dependencies between protic and aprotic/H-bond-accepting mediums (Table 2).
Scheme 4.
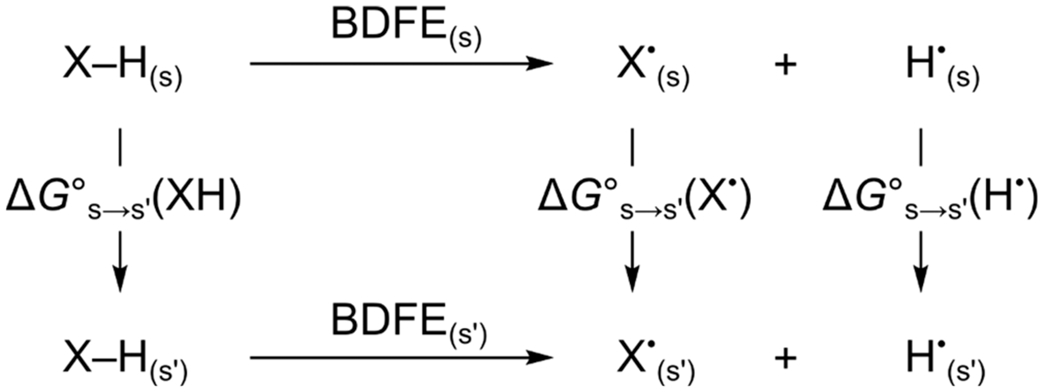
Thermochemistry of BDFE Medium Dependence
3.1.2. Phase Dependence.
A scheme similar to Scheme 4 can be used to compare gas- and solution-phase X–H BDFEs and E∘(V vs H2) values [more details on E∘(V vs H2)(g) are provided in Section 4]. If the solvation free energies of X• and XH cancel (including the entropy term for the change in standard state from 1 atm to 1 M for both reagents), the only difference between the solution- and gas-phase BDFEs is the ΔΔG∘f(H•), which is 3–4 kcal mol−1 across many solvents (Table 1). Furthermore, under these assumptions there is no expected difference between values of E∘(V vs H2) across the solution and gas phase. In Table 3, we compare aqueous and gas-phase potentials of hydrogenation, as the difference between the two values describes whether X or XHn is more favorably solubilized. For three simple alkyl and phenyl thiols, there is no significant phase dependence of the potential of hydrogenation of RS• (ΔE∘(V vs H2) = E∘(aq) – E∘(g) = 0.01 ± 0.06 V), thereby demonstrating that the free energies of solvation of RSH and RS• are very similar. However, for three alkyl hydroperoxides, ΔE∘(V vs H2) = 0.32 ± 0.09 V. This indicates significantly more favorable solvation of ROOH versus ROO•. While it makes sense for ROOH to be preferentially stabilized by being a hydrogen bond donor, this effect is often small as evidenced by the phase-independent PCET thermochemistry of PhOH and other hydrogen-bonding compounds. In general, a slight preferential solvation of XHn over X does seem to be common, although this trend shifts in a few rare cases including the reduction of H2O2 to 2H2O and that of Ph2N• → Ph2NH.
Table 3.
Phase Dependence of PCET Thermochemistrya
| reaction | E∘(V vs H2)(g) | E∘(V vs H2)(aq) | ΔE∘(V vs H2)b | table |
|---|---|---|---|---|
| PhO• + 1/2H2 → PhOH | 1.353 | 1.382 | 0.029 | 6 |
| HO• + → HO–H | 2.690 | 2.730 | 0.040 | 10 |
| O + → HO− | 1.997 | 2.134 | 0.137 | 10 |
| O•− + → HO− | 2.317 | 2.609 | 0.292 | 11 |
| HO2• + → H2O2 | 1.242 | 1.46 | 0.218 | 11 |
| H2O2 + → 2H2O | 1.823 | 1.763 | −0.06 | 11 |
| ROO• + → ROOHc | 1.25(8) | 1.57(9) | 0.32(9) | 12 |
| HN•NH–H + → H2NNH-H | 1.04 | 1.12 | 0.08 | 13 |
| PhNH• + → PhNH2 | 1.428 | 1.437 | 0.009 | 15 |
| 4-MePhNH• + → 4-MePhNH2 | 1.333 | 1.423 | 0.09 | 15 |
| 4-CF3PhNH• + → 4-CF3PhNH2 | 1.389 | 1.564 | 0.175 | 15 |
| Ph2N• + → Ph2NH | 1.320 | 1.225 | −0.095 | 15 |
| HS• + → HS–H | 1.49 | 1.56 | 0.07 | 18 |
| RS• + → RS–Hd | 1.33(1) | 1.35(1) | 0.02(1) | 18 |
| PhS• + → PhS–H | 1.16 | 1.08 | −0.08 | 18 |
| O2(g) + 2H2(g) → 2H2O | 1.185 | 1.229 | 0.044 | 11 |
| O2(g) + H2(g) → H2O2 | 0.546 | 0.695 | 0.149 | 11 |
| O2(g)/•OOH | −0.15 | −0.07 | 0.08 | 11 |
| CO2(g) + H2(g) → HCOOH | −0.225 | −0.114 | 0.111 | 21 |
| CO2(g) + H2(g) → CO(g) + H2O | −0.148 | −0.104 | 0.044 | 21 |
| CO2(g) + 4H2(g) → CH4(g) + 2H2O | 0.145 | 0.169 | 0.024 | 21 |
| N2(g) + 3H2(g) → 2NH3 | 0.057 | 0.092 | 0.035 | 13 |
For the second column, labeled (g), all of the species are gas phase. For the third column, labeled (aq), above the blank row all of the species are in aqueous solution. Values above the blank row are for reactions where there is no phase change when converting from products to reactants, for both the gas-phase and aqueous values. Reactions below the blank row involve a phase change from gaseous reactants to aqueous products for the values in the third column (labeled (aq)). This distinction is important as free energy contributions from changing standard state contribute to the phase dependence of values below the blank row (see text).
ΔE∘(V vs H2) = E∘(V vs H2)(aq) – E∘(V vs H2)(g).
Average of values for R = CH3−, CH3CH2−, and (CH3)3C−.
Average of values for R = CH3− and CH3CH2−.
Analyzing the phase dependences of reactions that involve cleaving more than one X–H bond should be done with caution. For instance, the conversion of N2(g) + 3H2(g) to 2NH3 involves the solvation of NH3 and also the entropy term for the two ammonia molecules converting from 1 atm to 1 M standard state. Nevertheless, the potentials of hydrogenation for N2 to NH3 are roughly independent of phase. Similarly, the ΔE∘(V vs H2) is <50 mV for several other complex reactions including the reduction of O2 to H2O and the hydrogenations of CO2 to both CO and CH4.
These observations of phase-independent E∘ (V vs H2) are not nearly as robust as the solvent independence described in Table 2. Nevertheless, they demonstrate that in many cases the effect of phase on PCET thermochemistry is minimal. Further study will be required to more clearly predict which compounds should be expected to demonstrate phase-dependent potentials of hydrogenation.
3.1.3. Mixed Solvent Systems.
Nontraditional solvent systems, including mixed solvents and those without established pKa scales, have been shown to be valuable for a variety of applications involving PCET reactivity. Investigators have employed various media to tune reagent activity, control reagent solubility, and separate reagents, in efforts to increase the selectivity and efficiency of their systems. The optimal medium for catalyzing PCET reactions must, among other properties, adequately solubilize the substrate and catalyst while maintaining a rapid rate of proton transfer. Organic solvents often excel at the former requirement, while aqueous solutions excel at the latter. To get the “best of both worlds”, some authors have investigated the efficacy of mixed solvent systems. Below we discuss several examples and consider the challenges that PCET in mixed solvent systems poses to thermochemical measurements.
One example comes from the work of O’Hagan and co-workers who demonstrated that changes in the reaction medium—ionic liquids with varying mole fractions of H2O—could engender faster rates of electrocatalytic hydrogen production without increasing the overpotential.69,70,73 A key to these studies was accurate measurements of overpotential and therefore of E∘′(H+/H2) in various solvents (Figure 2A), following the procedure of Roberts and Bullock discussed above.57 With increasing water content, overpotentials remained relatively constant, while catalytic currents increased by nearly 2 orders of magnitude. The rate increase correlated with the proton diffusion coefficient measured using pulsed-field-gradient NMR (Figure 2B).70 Beyond changing water content, the rates were 3–5 orders of magnitude higher in the ionic liquid/water mixtures than in MeCN:H2O mixtures. This effect was found to be related to the rate of boat/chair catalyst isomerization based on further studies which varied the chain length of substituents on the outskirts of the catalyst (Figure 2C,D).73 Later work interrogated the melding of these effects with that of solvent viscosity, to design a state-of-the-art molecular electrocatalyst for hydrogen production.74 These studies demonstrate that solvent engineering can play a valuable role in the development of advanced electrocatalysts for PCET processes.
Figure 2.
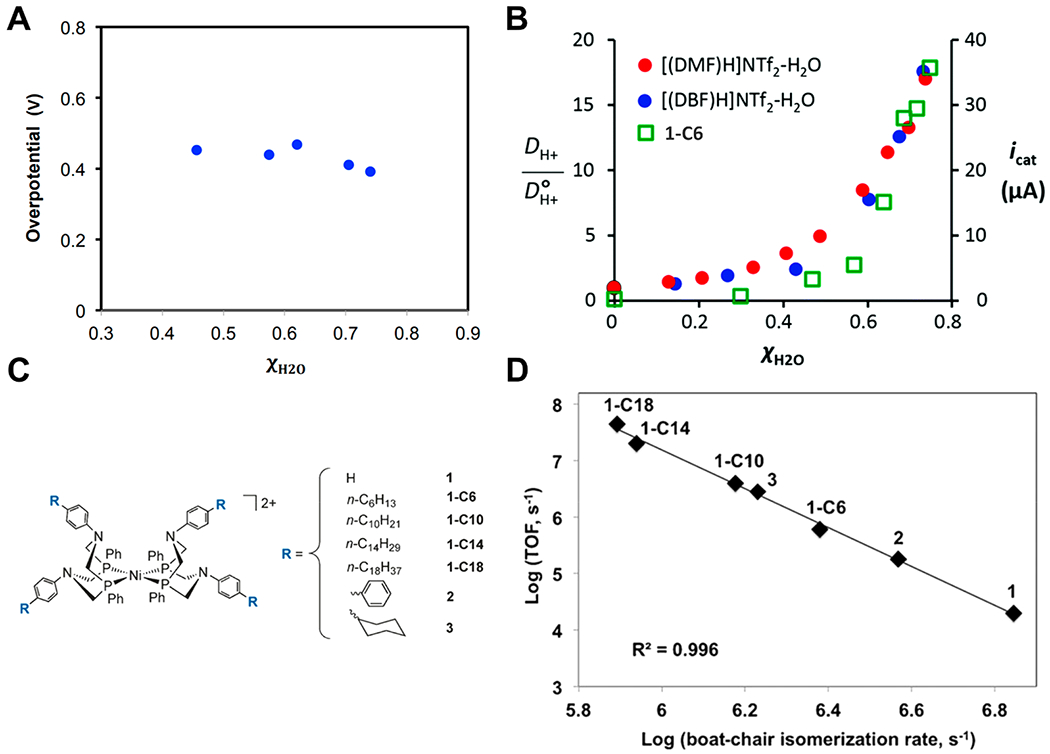
(A) Dependence of reaction overpotential on the mole fraction of H2O in a [(DMF)H]NTf2–H2O ionic liquid, where overpotential is the difference between Ecat/2 and E(H+/H2) under the reaction conditions. (B) The dependence of proton diffusion constant for two different ionic liquids (red or blue dots) and of catalytic current for 1-C6 in [(DBF)H]NTf2–H2O (green squares) on the mole fraction of H2O. (C) Structures of the nickel catalysts used and their R groups of varying steric bulk. (D) Relationship between the logarithms of boat-chair isomerization rate and turnover frequency. (A) and (B) are reprinted with permission from ref 70. Copyright 2014 Royal Society of Chemistry. (C) and (D) are reprinted (adapted) with permission from ref 73. Copyright 2016 Wiley.
Mixed-solvent systems and tailored microenvironments are of increasing interest. One high-profile study of CO2 electro-reduction with cationic iron porphyrins reported remarkable rates in DMF “in the presence of 3 M phenol”.75 This is roughly DMF and phenol in mole fraction. The authors estimated the standard potential for CO2 to CO using the Henry’s law constant for CO2 and the pKa of carbonic acid in pure DMF. Measurement of E∘′(H+/H2) in the CO2-saturated, 0.1 M H2O, mixed DMF/phenol solvent would allow for a more direct comparison of the catalytic response with the essentially solvent-independent E∘(CO2/CO vs H2) ( Table 21). These are important considerations for reporting catalyst metrics that are comparable across conditions. Other recent work has used acetonitrile with ≥5 M water (4:1 mole fraction MeCN/H2O) for the electrochemical oxidations of cyclohexene and cyclic ketones.76,77 As shown by the elegant O’Hagan studies above, OCP measurements of E∘(H+/H2) in such mixed solvent systems enable the determination of thermochemical parameters and comparisons with potentials of hydrogenation since those are almost solvent-independent. We encourage researchers to use this approach, which offers simple access to accurate overpotentials and enables quantitative analysis of effects of solvent identity on catalyst performance. Although the potentials are relatively insensitive to solvent identity (Table 2), rate constants may vary significantly. We also note that the overpotential for electrocatalysis can be different in the reaction-diffusion layer from that referenced in the bulk solution if the local environment at the electrode surface differs from the bulk solution.
Table 21.
PCET Thermochemistry of Carbon Dioxide Reductiona
| CO2(g) + H2(g) → HCOOH | solvent | E∘(V vs H2) | −ΔG∘/nb | |
|---|---|---|---|---|
| CO2/HCOOH | gas | −0.22542 | ||
| CO2/HCOOH | H2O | −0.114327 | ||
| CO2(g) + H2(g) → CO(g) + H2O | solvent | E∘(CO2/CO2•−) | E∘(V vs H2) | −ΔG∘/nb |
| CO2/CO | gas | – | −0.14842 | 45.2 |
| CO2/CO | H2O | −1.99376 | −0.10467 | 50.4 |
| CO2/CO | DMF | −2.01377,c | −0.06867 | 50.7 |
| CO2/CO | MeCN | – | –0.09267 | 49.8 |
| CO2/CO | DMA | – | –0.1051 | |
| CO2(g) + 4H2(g) → CH4(g) + 2H2O | solvent | E∘(V vs H2) | −ΔG∘/nb | |
| CO2/CH4 | gas | 0.14542 | 51.9 | |
| CO2/CH4 | H2O | 0.16967 | 56.7 | |
| CO2/CH4 | MeCN | 0.17867 | 56.5 | |
| CO2/CH4 | DMF | 0.18267 | 56.1 |
Potentials for 1e− reductions are in V vs SHE if in aqueous solution and V vs Cp2Fe+/0 if they are in organic solution. Values for E∘(V vs H2) are in V; – eE∘ is the average free energy for addition. −ΔG∘/n values are average free energies for the overall reaction in kcal mol−1.
−ΔG∘/n values are for the overall reaction shown except to form H• [rather than add H2(g)] (see Section 4) and were calculated from E∘(V vs H2) using eq 18.
Standard state converted to 1 atm of CO2 based on Henry’s Law constant reported in ref 378.
More complex media with multiple liquid phases or regions are also of increasing importance. For example, a recent U.S. Department of Energy Basic Energy Sciences report recently identified the control of these “microenvironments” as a priority research objective in solar fuels research.78 One recent study used a two-phase 1-hexanol/water mixture to electrochemically generate hydrogen peroxide, with the 2,7-disulfonylanthraquinone electrocatalyst migrating between the aqueous and organic layers.21 Selective electrochemical conversion of methane and O2 to methanol under ambient conditions was enabled by a silicon nanowire electrode that created separate anoxic and oxic environments near the electrode interface.79 In general, these studies and many related ones have not focused so much on the PCET thermochemistry, though it can play a key role.
3.2. Relationships between Proton, Electron, and Hydrogen Transfer Free Energies
The PCET square scheme for an XH reagent, as shown with a free energy surface in Figure 3, has five separate reactions and free energies: two E∘ values (for the ET steps), two pKa values (PT steps), and one BDFE (for the concerted, CPET reaction). This section describes analyses of these five parameters for a single species and then across a series of related molecules.
Figure 3.
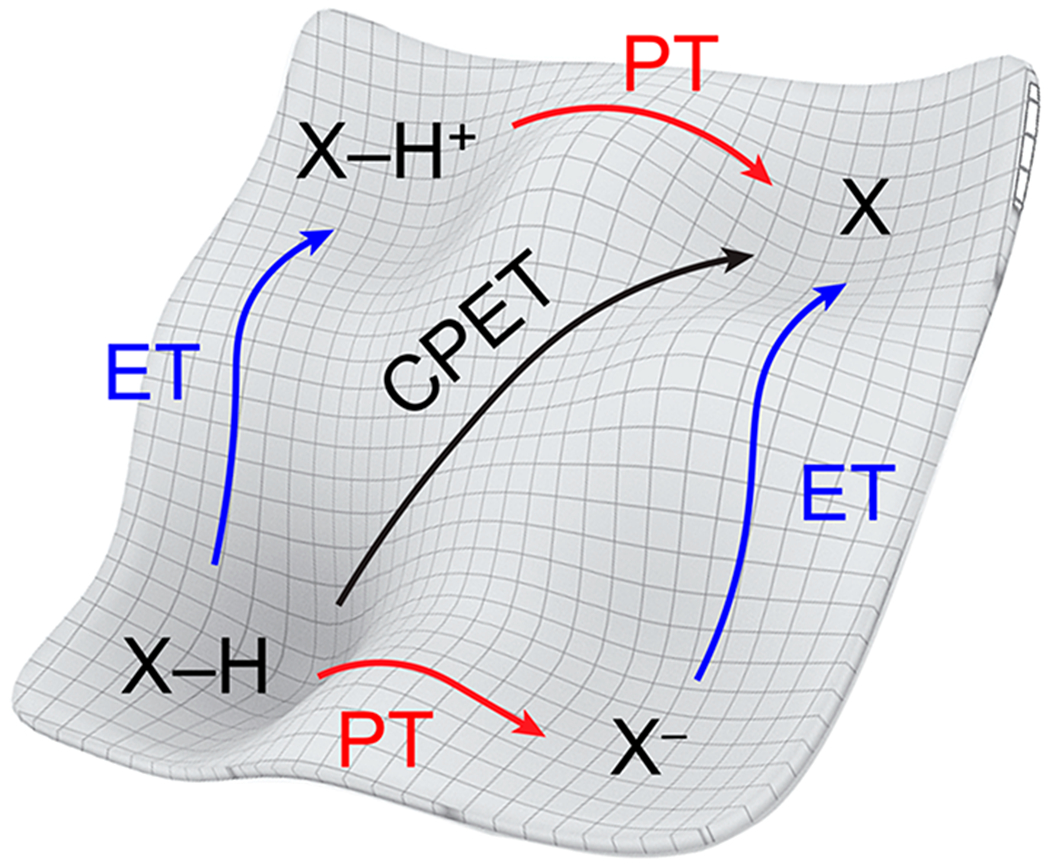
Free energy surface of the square scheme for a PCET reagent XH, showing the concerted proton–electron transfer (CPET) pathway and the stepwise paths (ET/PT and PT/ET). Each arrow is drawn over the barrier for the respective step.
3.2.1. Thermodynamic Coupling between ET and PT Free Energies.
The free energies corresponding to the ET (−FE∘), PT (2.303RTpKa), and CPET events in Figure 3 are interdependent. This is because free energy is a state function, and Hess’ Law necessitates that the free energy difference between two states is path-independent. Movement around any closed loop in Figure 3 must therefore have ΔG∘ = 0. This analysis leads to the result that, for any reagent XH, the free energy shift in E∘ upon deprotonation must equal that in pKa upon oxidation (eq 23).
| (23) |
We have called the value of this shift the thermodynamic coupling between the e− and H+ for reagent XH, and it can vary dramatically.3 When the e− and H+ “come from the same bond”, the shift can be enormous. For instance, CH4 is an extremely weak acid but upon oxidation to CH4•+ becomes highly acidic. For the hydroxylamine TEMPOH, for which the effects of e− and H+ transfer are localized to the NOH unit, the shift in E∘ upon protonation is ~2.6 V, which is equivalent to the shift in pKa of >40 units.3 As our 2010 Chem. Rev. explained in detail, such reagents where the thermodynamic coupling is large have a strong preference to react by transfer of the e− and H+ together, by concerted proton–electron transfer (CPET).3 This is because, when the coupling is large, the top left and bottom right corners of Figure 3 are typically high in energy (e.g., the CH4•+ and CH3− species), thereby disfavoring stepwise mechanisms. A common form of CPET is hydrogen atom transfer, wherein the e− and H+ are transferred together from a single site on one reagent to a single site on another. Through the lens of thermodynamic coupling, then, hydrogen atom transfer represents the case in which both reagents have large thermodynamic coupling.80
As the electron (or hole) becomes more delocalized or is farther from the site of protonation/deprotonation, the thermodynamic coupling decreases.80 For phenol in water, the ΔE∘ is 0.7 V (ΔpKa = 12 units). For metal-imidazole and related complexes, where the nitrogen atom being deprotonated is three bonds removed from the metal center undergoing formal redox change, removal of one proton raises E∘ by ca. 300 mV. Examples include 365 mV for an iron(tetraphenylporphyrin)–bis(4-methylimidazole) complex,81 340 mV for the ruthenium pyridyl–imidazole in Figure 4A,82 and 240 mV for the benzimidazole deprotonation in Figure 4B.83 Williams et al. showed that Fe, Co, and Ru complexes with multiple imidazole ligands exhibit a shift of ~300 mV per imidazole deprotonated, up to a remarkable 1.38 V shift for an iron complex with four imidazoles (Figure 4D).84,85 When the acid/base site is well separated from the redox one, the coupling becomes very small. For example, Figure 4C displays a complex in which the iron potential shifts only 20 mV upon deprotonation of the distant propionic acid side chain.86,87 When the ET and PT agents are separate molecules, then of course there is no coupling (Section 3.3 and Table 22).
Figure 4.
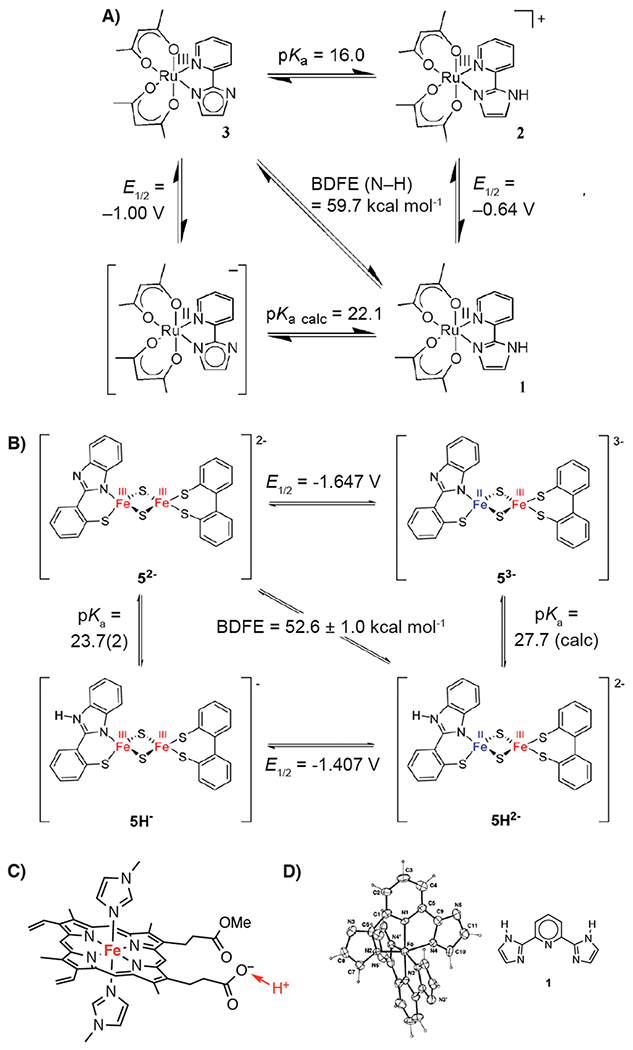
Imidazole and other complexes with an acid/base group removed from the redox-active metal center. (A) Square scheme for a ruthenium–imidazole complex showing the 0.36 V increase in the reduction potential upon protonation. Reprinted (adapted) with permission from ref 82. Copyright 2007 American Chemical Society. (B) Square scheme for a di-iron disulfido–benzimidazole complex showing a 0.240 V increase upon protonation. Reprinted with permission from ref 83. Copyright 2017 American Chemical Society. BDFEs in A and B were updated to reflect the new CG(MeCN) value. (C) An iron–protoporphyrin-IX complex that shifts 20 mV upon protonation at the carboxylate. Reprinted with permission from ref 86. Copyright 2011 American Chemical Society. (D) Drawing of the structure of the Fe(III) complex with two doubly deprotonated bis(imidazolyl)pyridine ligands, [Fe(1–2H)2]−.84,85 Reprinted with permission from ref 84. Copyright 1998 Royal Society of Chemistry.
Table 22.
PCET Thermochemistry of Oxidant/Base and Reductant/Acid Pairs in MeCNa
| oxidant | E ∘b | base | pKac | E∘(V vs H2) | BDFEeff |
|---|---|---|---|---|---|
| N(4-MeO-C6H4)3•+ | 0.16 | pyridine | 12.53 | 0.93 | 73.4 |
| N(4-MeO-C6H4)3•+ | 0.16 | 2,6-Me2-pyridine | 14.13 | 1.02 | 75.6 |
| N(4-MeO-C6H4)3•+ | 0.16 | 4-NH2-pyridine | 17.62 | 1.23 | 80.4 |
| N(4-MeO-C6H4)3•+ | 0.16 | acetate | 23.51298 | 1.58 | 88.4 |
| N(4-Me-C6H4)3•+ | 0.38379 | pyridine | 12.53 | 1.15 | 78.5 |
| N(4-Me-C6H4)3•+ | 0.38379 | 2,6-Me2-pyridine | 14.13 | 1.24 | 80.7 |
| N(4-Br-C6H4)3•+ | 0.67 | pyridine | 12.53 | 1.44 | 85.2 |
| N(4-Br-C6H4)3•+ | 0.67 | 2,6-Me2-pyridine | 14.13 | 1.53 | 87.4 |
| N(2,4-Br2-C6H4)3•+ | 1.14 | pyridine | 12.53 | 1.91 | 96.0 |
| Cp2Fe+ | 0 | pyridine | 12.53 | 0.770 | 69.8 |
| Cp2Fe+ | 0 | 2,6-Me2-pyridine | 14.13 | 0.864 | 71.9 |
| [Fe(bpy)3]3+ | 0.70379 | pyridine | 12.53 | 1.47 | 85.9 |
| [Fe(bpy)3]3+ | 0.70379 | 2,6-Me2-pyridine | 14.13 | 1.56 | 88.1 |
| *IrIII(dF(CF3)ppy)2(dtbbpy)d,e | 0.95131,e | 4-N(Me)2-pyridine | 17.95 | 2.04 | 99.1 |
| *IrIII(dF(CF3)ppy)2(dtbbpy)d,e | 0.95131,e | benzoate | 21.51298 | 2.25 | 103.9 |
| *IrIII(dF(CF3)ppy)2(bpy)d,e | 1.04131,e | 4-N(Me)2-pyridine | 17.95 | 2.13 | 101.1 |
| *IrIII(dF(CF3)ppy)2(bpy)d,e | 1.04131,e | benzoate | 21.51298 | 2.34 | 106.0 |
| reductant | E ∘b | acid | pKac | E∘(V vs H2) | BDFEeff |
|
| |||||
| *IrIII(ppy)3d,e | −2.13123,e | pTSAf | 8.6298 | −1.59 | 15.3 |
| *IrIII((dF)ppy)3d,e | −1.92123,e | pTSAf | 8.6298 | −1.38 | 20.1 |
| *IrIII(d(OMe)ppy)3d,e | −2.28123,e | NMe3H+ | 17.61380 | −1.21 | 24.1 |
| *IrIII(d(OMe)ppy)3d,e | −2.28123,e | NEt3H+ | 18.5380 | −1.16 | 25.3 |
| [Ru(bpy)3]+ | −1.71381,g | pTSAf | 8.6298 | −1.17 | 25.0 |
| [Ru(bpy)3]+ | −1.71381,g | NMe3H+ | 17.61380 | −0.64 | 37.3 |
| [Ru(bpy)3]+ | −1.71381,g | NEt3H+ | 18.5380 | −0.59 | 38.5 |
| [Ru(bpy)3]+ | −1.71381,g | benzoic acid | 21.51298 | −0.41 | 42.6 |
| [Ru(bpy)3]+ | –1.71381,g | acetic acid | 23.51298 | −0.29 | 45.3 |
| Ir(ppy)2(dtbbpy)d | −1.89133 | 2,6-Me2-pyridinium | 14.13 | −1.03 | 28.4 |
| Ir(ppy)2(dtbbpy)d | −1.89133 | NMe3H+ | 17.61380 | −0.82 | 33.1 |
| (C5Me5)2Fe | −0.51288 | pyridinium | 12.53 | 0.26 | 58.0 |
| Cp2Fe | 0 | pyridinium | 12.53 | 0.770 | 69.8 |
| Cp2Fe | 0 | acetic acid | 23.51298 | 1.420 | 84.7 |
Potentials for 1e− reductions are in V vs Cp2Fe+/0. Values for E∘(V vs H2) are in V; −eE∘ is the average free energy for addition. Uncited values of E∘(V vs H2) were calculated from other values in the row using Scheme 2 or eq 18. BDFEeff (effective BDFE; BDFEeff = 23.06E∘ox/red + 1.37pKa,HA/A− + CG; see ref 104 for more discussion) values were calculated in kcal mol−1 from E∘(V vs H2) using eq 18.
From ref 382 unless otherwise noted.
pKa of baseH+ from ref 383 unless otherwise noted.
ppy = 2-phenylpyridine; (dF)ppy = 2-(2,4-difluorophenyl)pyridine; dF(CF3)ppy = 2-(2′,4′-difluorophenyl)-5-(trifluoromethyl)pyridine; d(OMe)ppy = 4-methoxy-2-(4-methoxyphenyl)pyridine; dtbbpy = 4,4′-di-tert-butyl-2,2′-bipyridine.
Asterisk (*) denotes that the active oxidant or reductant is the excited-state complex. As such, the given potential is the reported excited-state redox potential.
p-Toluenesulfonic acid.
Reference potential adjusted from SCE to Cp2Fe+/0 using ref 287.
3.2.2. Thermodynamic Compensation between ET and PT Free Energies.
Over a series of related PCET compounds, the BDFE, pKa, and E∘ values will vary with the changes in substituents and structure. These correlations are typically analyzed with linear free energy relationships (LFERs), extra thermodynamic empirical relationships between different parameters. The most common is perhaps the Hammett equation from 193788 which relates the variation in a property of interest with the pKa values of benzoic acids with the same substituents.89 Similarly, a range of metal complex reduction potentials can be predicted fairly accurately with a set of “Lever parameters” for the metal and ligands.90,91
Typically, over a set of PCET reagents within a given chemical class, the E∘ and pKa values will vary much more than the BDFEs. This is because the pKa and E∘ are inversely correlated quantities—an electron-withdrawing substituent makes XH and XH+ more acidic but also makes XH and X− harder to oxidize. Because the BDFE correlates positively with both the pKa and E∘, these changes counterbalance one another and give a much smaller change in BDFE. This can be viewed as a thermodynamic compensation between the E∘ and pKa over the series of compounds (that is, between pKa(XH) and E∘(X•/−) or between pKa(XH+) and E∘(XH+/0)).3,92 To our knowledge, this effect was first emphasized by Pratt, DiLabio, Mulder, and Ingold in a 2004 Acc. Chem. Res. article on the relationships between toluene, aniline, and phenol BDEs and Hammett substituent constants.93 The exact extent of thermodynamic compensation in a particular series is represented by the proportionality constant γ in eq 24.
| (24) |
Within some classes of PCET compounds, the free energy changes in the E∘ and pKa are so closely balanced that the BDFE stays remarkably constant, such that γ = 1 in eq 24. Substituted toluenes, for example, show almost perfect thermodynamic compensation of this kind. p-Tolunitrile is ~10 pKa units more acidic than toluene (~14 kcal mol−1 from ΔΔG∘ = −RTΔln Keq), while the corresponding benzyl radicals differ in E∘ by ~0.7 V (~16 kcal mol−1), leaving the NCC6H4CH2–H BDFE only 2 kcal mol−1 higher than the PhCH2–H BDFE.94
Other PCET reagent classes do not show such close thermodynamic compensation. Across a series of substituted phenols in DMSO and water, for example, changes in aromatic ring substituents cause smaller changes in the free energy of deprotonation than in the free energy of the subsequent oxidation of the phenoxide (γ > 1). Therefore, electron-donating substituents generally decrease the phenolic O–H BDFE, while electron-withdrawing substituents increase the BDFE. An analysis by Dhar et al. examined the extent of compensation for different classes of organic molecules and metal complexes, as shown in graphical form in Figure 5 (where the red line indicates perfect compensation, γ = 1).92
Figure 5.
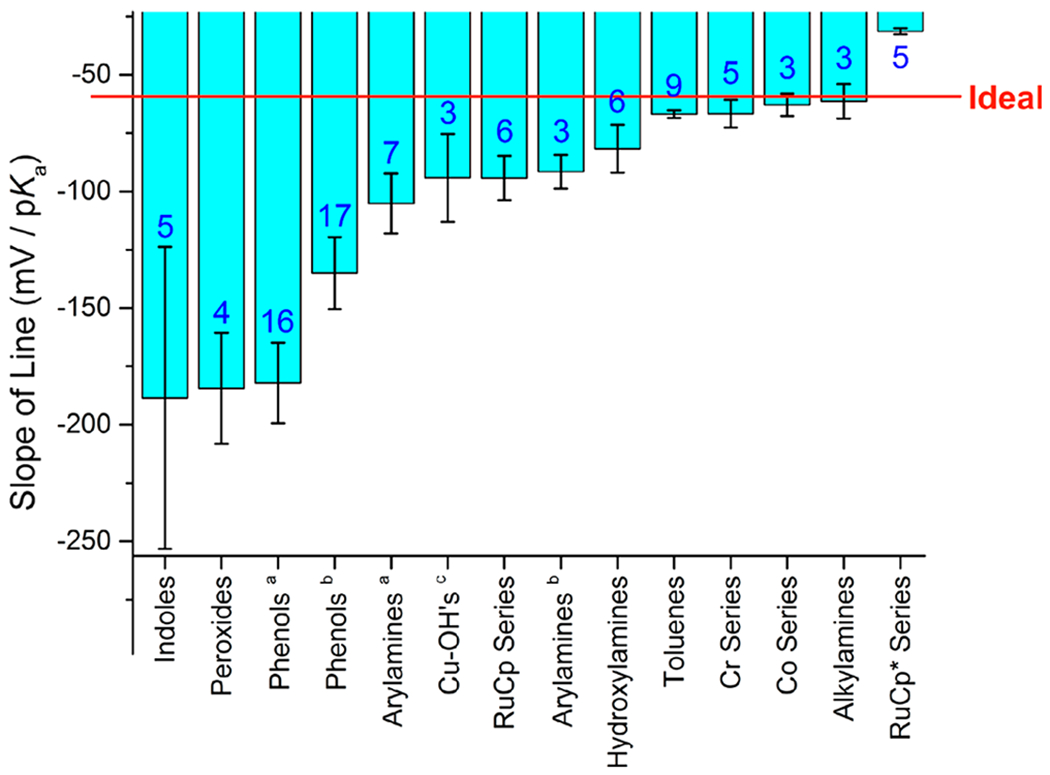
Histogram depiction of compensation between E1/2 and pKa, for compounds within different classes of PCET reagents and in different solvents. Perfect compensation of −59.2 mV/pKa is indicated by the red line. Blue numbers in the bars are the number of compounds analyzed in each class. aIn water. bIn DMSO. cRef 92. Reprinted (adapted) with permission from ref 92, Supporting Information Figure S33, with blue numbers added. Copyright 2016 American Chemical Society.
The frequent pattern that E∘ values are more sensitive than pKa values to substituent changes (γ > 1) may be due to deprotonation occurring locally at the X–H bond, while oxidation involves removal of an electron from a delocalized molecular orbital. For phenols, substituents on the aromatic ring directly interact with the redox-active π system but are more distant from the acidic OH. In contrast, the carbanion formed upon deprotonation of a toluene has much more delocalization into the aromatic ring. This rationalization is consistent with near perfect thermodynamic compensation of toluenes (γ = 1.1 in acetonitrile94) and a much larger γ for phenols (γ ≈ 3 in water). In the ruthenium complex in Figure 4A, replacement of the acac ligands in hexafluoro-acac shifts the E1/2 positive by 0.93 V, while the imidazole pKa shifts only a modest 3.2 units (giving γ = 5).82 This lack of good compensation means that the N–H BDFE increases by 17 kcal mol−1.
An important example of thermodynamic compensation is redox leveling, which occurs when a metal complex is oxidized or reduced by multiple steps, but its BDFE and E∘ (V vs H2) remain fairly constant. This effect was noticed at least as far back as 1981 by Bruce Moyer and Thomas J. Meyer (who coined the term PCET), for a RuII(H2O)/RuIII(OH)/RuIV(O) system.95 The reduction potentials and pKa values for these different complexes vary substantially, but the compensation means that the two BDFEs are very similar (the diagonal lines in the Pourbaix diagram in Figure 6 are close). This is a critical effect in the use of metal complexes or active sites for multielectron catalysis. In the tetramanganese–calcium oxygen evolving complex (OEC) in Photosystem II, for example, the four redox equivalents need to be removed at similar potentials to generate O2, as discussed by Pecoraro and Babcock.96–99 This need for redox leveling should apply to many ne−/nH+ catalytic processes, from enzymatic active sites to the surface of IrO2-catalyzing water oxidation.
Figure 6.
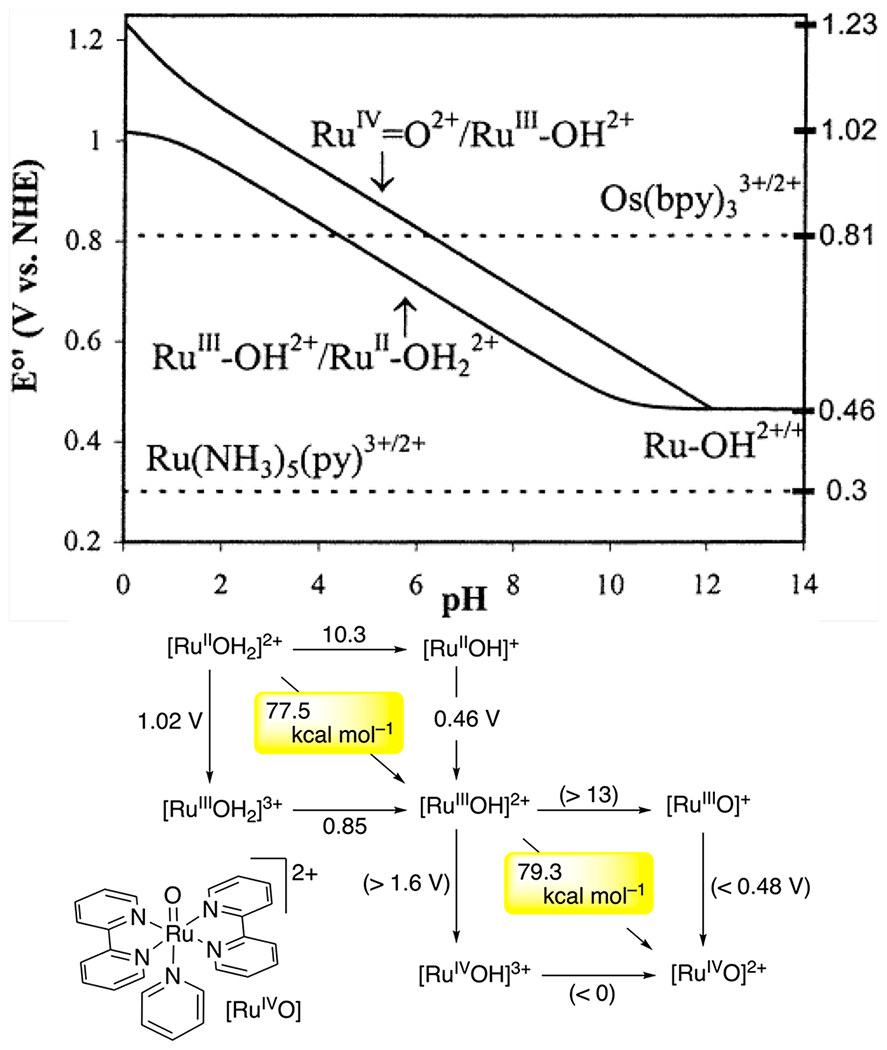
Aqueous PCET thermochemistry of [cis-(bpy)2pyRuOHx]n+ from refs 95, 100, and 101. Top: Pourbaix diagram102,103 for this system and a map of the predominant species present as a function of pH and solution potential. The pH of the inflection points corresponds to pKa values, and the slopes of the horizontal and diagonal lines indicate the stoichiometry of the redox process occurring, (59 mV)ne−/mH+. Bottom: Double square scheme showing pKa values above horizontal arrows, pure-ET E∘ values beside vertical arrows, and BDFEs along the diagonals (from eq 10). Thermochemical values are from Table 24. Reprinted (adapted) with permission from ref 3, 95, and 100 Copyright 2010, 2001, and 1981 American Chemical Society.
3.3. Oxidant–Base and Reductant–Acid Pairs for MS-CPET
In multiple-site concerted proton–electron transfer (MS-CPET), a proton and electron come from (or go to) two chemically distinct sites (Figure 7A).80,104 This has also been termed “multisite” or “orthogonal” or “bidirectional” PCET.1,2,105–109 Overall, the thermochemistry of MS-CPET is similar to that of other PCET systems.104 An “effective BDFE” can be defined for any reductant–acid (or oxidant–base) pair to express their H-atom-donating or -abstracting ability, even though no X–H bond is homolytically cleaved (respectively, formed) in the process (eq 25).
| (25) |
Figure 7.
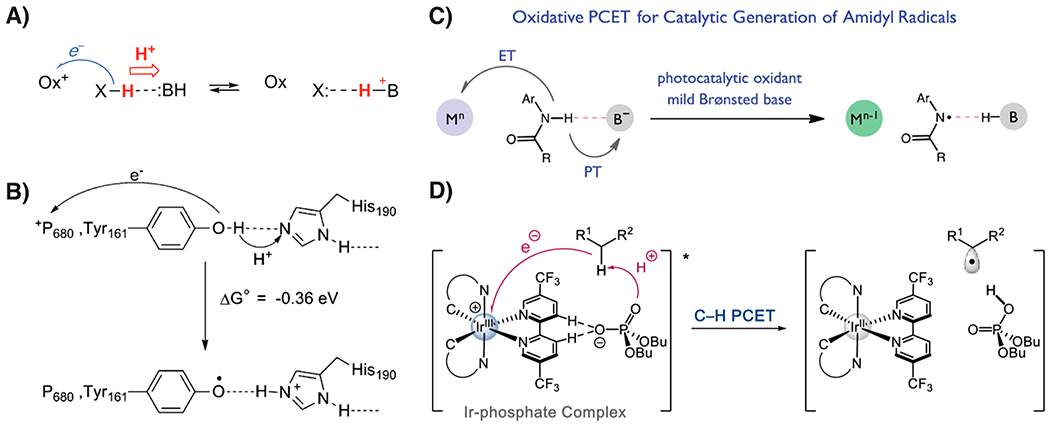
Multiple-site concerted proton–electron transfer (MS-CPET). (A) General scheme for XH oxidation or X reduction.80 (B) Schematic of tyrosine-161 oxidation in Photosystem-II by long-range ET to the oxidized chlorophyll special pair P680+ concerted with PT to histidine-190.1,8 (C) Photocatalytic MS-CPET oxidation of an amide with photooxidant Mn and base B−.109 (D) Photoinduced MS-CPET to a noncovalently bonded oxidant/base pair.110 Reprinted with permission from refs 80, 1, 109, and 110, respectively. Copyright 2018, 2007, 2016, and 2019 American Chemical Society.
Figure 7 displays several examples of MS-CPET reactions in biology and synthetic applications and highlights the diverse nature of these reactions.
3.3.1. Continuum between HAT and MS-CPET Reactions.
This section presents some of the complexities of MS-CPET reactions, including the extent of thermodynamic coupling, separation of charge, ground-state hydrogen bonding and complexation, and the possible conflation of multiple of these effects. In Photosystem-II (Figure 7B), tyrosine-161 appears to be oxidized in a CPET process in which the e− is transferred ~10 Å to the oxidized chlorophyll special pair P680+, while the H+ travels to the nearby histidine-190.1,2,8 In examples like this, the cofactors are independent of each other, and there is no thermodynamic coupling or thermodynamic compensation (Section 3.2). This leads to the point that there is a continuum between “simple” hydrogen atom transfer and MS-CPET. In this example, P680+, histidine-190, and tyrosine-161 are all in the same protein complex, yet this process most closely resembles MS-CPET.80 In C–H oxidations by cytochrome P450 enzymes, on the other hand, the proton moves to the oxygen of the ferryl group, while the electron is transferred to a hole on the other, redox-active ligand (see Section 3.7.1 below). These sites are much more thermodynamically coupled, and this process lies in between HAT and MS-CPET.
The distinctions between HAT and MS-CPET can be quite significant. When the e− and H+ start far apart, such as in MS-CPET, there can be a substantial change in the charge distribution, as opposed to a reaction that resembles the transfer of a neutral hydrogen atom. The change in charge distribution also means that electrostatic “work terms”, free energies to assemble the reactive complexes, can be important. For bimolecular electron transfer reactions, there are work terms in forming the precursor and successor complexes (wp and ws, respectively, in Scheme 5). This means that the thermochemistry of the actual unimolecular ET step, ΔG∘’, can be different from the overall thermochemistry ΔG∘ (Scheme 5a; see excellent and accessible summaries by Sutin and by Eberson111,112). For hydrogen atom transfer reactions, however, no charge is passed in the unimolecular HAT step, so ΔG∘′ = ΔG∘ (though there can be electrostatic and hydrogen bond effects on the formation of the precursor and successor complexes,113 shown in Scheme 5b).
Scheme 5. Precursor and Successor Complexes and Work Terms (w) for Electron Transfer, Hydrogen Atom Transfer, and Multiple-Site Concerted Proton– Electron Transfera.
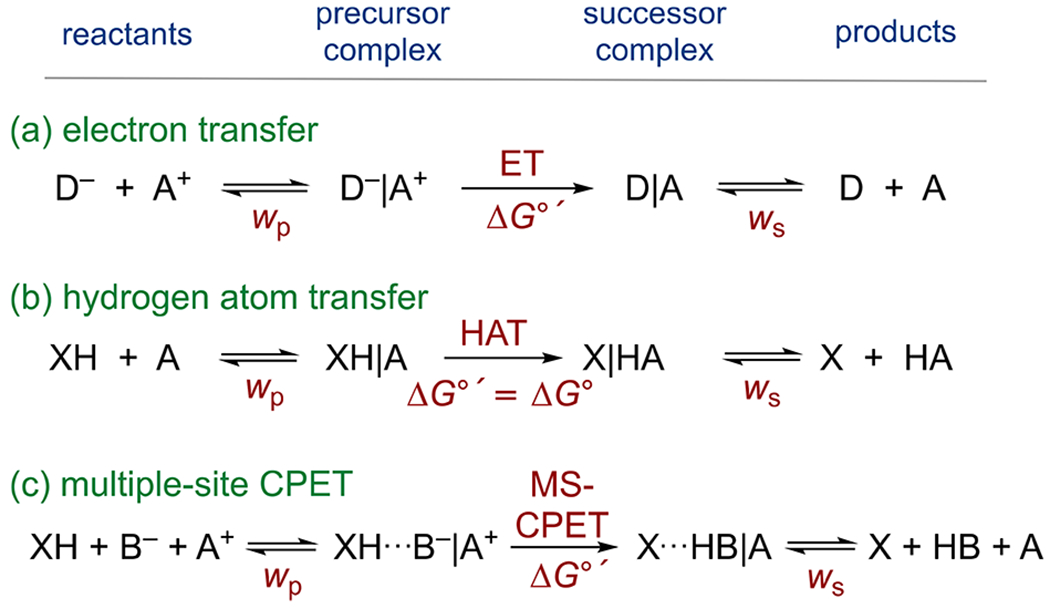
aThe overall energetics from separated reactants to separated products is ΔG∘.
Multisite processes more resemble ET in that there is a charge redistribution in the MS-CPET step (Scheme 5c). In this case, the free energy of unimolecular MS-CPET can be different from that among the separated reactants, ΔG∘′ ≠ ΔG∘, and this effect is significant when the charges are large and the medium has a low dielectric constant.109 These effects can be particularly pronounced in termolecular systems.114–116 These were (to our knowledge) first systematically pursued by Linschitz et al., for instance, quenching photoexcited 3C60 with various phenol–base pairs.114,115 A few more recent examples are from the groups of Meyer,117–120 Hammarström,121 Stanbury,122 Knowles,123 Tommos,124 Barry,125 and our laboratory,116 among others.
Another feature that is very common in CPET reactions is hydrogen bonding between the acceptor and donor molecules (Figure 7A–C). In the aforementioned Photosystem-II, for example, the tyrosine-161 donor is hydrogen bonded to the histidine-190 acceptor.1,2,8,126 In fact, most CPET reactions involve the pre-equilibrium formation of a hydrogen-bonded complex between the proton donor and acceptor.12,109,110,113,127,128 Knowles and co-workers have demonstrated that this feature can be utilized to selectively cleave strong N–H and O–H bonds in the presence of weaker C–H and S–H bonds, which do not form such favorable hydrogen bonds (Figure 7C).109
We conclude this section by highlighting a recent paper from Knowles in which a noncovalent complex formed between an iridium(III) photooxidant and phosphate base cleaves a strong C–H bond (Figure 7D). C–H MS-CPET is often difficult because there is no hydrogen bond to prealign the PT coordinate. Our group has shown in the C–H MS-CPET reactions of fluorenyl benzoates that this prealignment can be achieved through covalent attachment of the base to the C–H bond.127–129 Yet, the system from Knowles has no such prealignment, perhaps suggesting that the key lies instead in the reduced molecularity of the reaction. Regardless of the exact origin of this reactivity, these MS-CPET systems represent an exciting development in methodologies for C–H bond cleavage. We also note that such preassociation of the oxidant and base affects the basicity (and likely also the oxidizing power) of this pair and complicates the assignment of an exact BDFEeff (eq 25). Moreover, this system exemplifies the continuum between HAT and MS-CPET reactivity as a quasi-bimolecular system with intermediately coupled ET and PT events.
3.3.2. Practical Considerations for Thermal and Photoinduced MS-CPET.
While there is, in principle, an infinite number of oxidant–base and reductant–acid pairs, the number of practical combinations in typical solution chemistry is limited by the compatibility of the two reagents. In the case of oxidant–base pairs, there are often side reactions between the electron-poor oxidant and the electron-rich base. Reductant/acid pairs are also limited by incompatibility issues, including protonation of the electron-rich reductant and formation of H2 by reductant–acid pairs with effective BDFEs less than ΔG∘f(H•) or 52 kcal mol−1 (Table 1).
A number of oxidant–base and reductant–acid pairs have been studied for their chemical compatibility and stability with regard to solvent, concentration, temperature, and counterion.104 In general, low temperatures, low concentrations, and unreactive solvents and counterions increase chemical compatibility. In some cases, low-polarity solvents lead to ion pairing and high local concentrations of the components, resulting in faster decay (e.g., ref 130). In Table 22, we highlight compatible combinations, verified either by direct study of their compatibility under certain conditions104 or by their success in performing organic transformations.123,131–134 These pairs have the remarkable ability to break bonds as strong as 106 kcal mol−1 and to form bonds as weak as 15 kcal mol−1. For a discussion of reductant–acid pairs for the reduction of N2, see Section 3.6 and the more detailed review from Peters.135 MS-CPET reactions have been particularly utilized in the application of photoredox catalysis to organic synthesis.12,109,110,127,128,136 Photogenerated strong oxidants and bases give pairs with remarkably high effective BDFEs,12 and analogously the combination of a photoreductant and an acid can have a very low BDFEeff. A few representative examples are included in Table 22. Compared to thermal oxidants/reductants, the concentrations of photogenerated species are typically significantly lower and can be controlled by the incident photon influx, which can mitigate compatibility limitations.12
The field of photoinduced CPET has been growing rapidly, as summarized in excellent recent reviews by Wenger.7,11 One thermochemical challenge in photoinduced ET and PCET is the determination of the reduction potential of the thermally relaxed excited state. This issue has been discussed in great detail in the enormous area of excited-state ET reactions, notably in 1968 by Weller.137 The excited state E∘ is estimated using a thermochemical cycle with the excitation energy, which is typically taken as the low energy side of the emission spectrum, such as the lowest peak in a vibrational progression, or at 1 or 10% of the maximum emission intensity.138–140 While this issue is beyond the scope of this review, we note that readers can often find different values for the excited-state potential of a particular chromophore.
3.4. Coordination-Induced Bond Weakening
The concept of coordination-induced bond weakening first became important in organic free radical chemistry, in the search for “greener” sources of hydrogen atoms than, for example, tin-hydride reagents (e.g., Ph3SnH).141–144 This came to the fore in work by Cuerva et al. in 2006, who showed that H2O coordinated to a TiIII center had a sufficiently weak O–H bond to transfer H• to carbon radicals (Scheme 6).145–147 This was very surprising because water itself has a very large BDFE (110.6 kcal mol−1 [gas] or 115.8 kcal mol−1 [liquid], Table 10). They computed the Cp2(Cl)TiIII(HO–H) BDE to be 49.4 kcal mol−1, a weakening of 59 kcal mol−1 from the first BDE of H2O(g) computed at the same DFT level of theory.
Scheme 6. Water O–H Bond Sufficiently Weakened by Coordination to TiIII That It Can Transfer H• to an Alkyl Radicala.
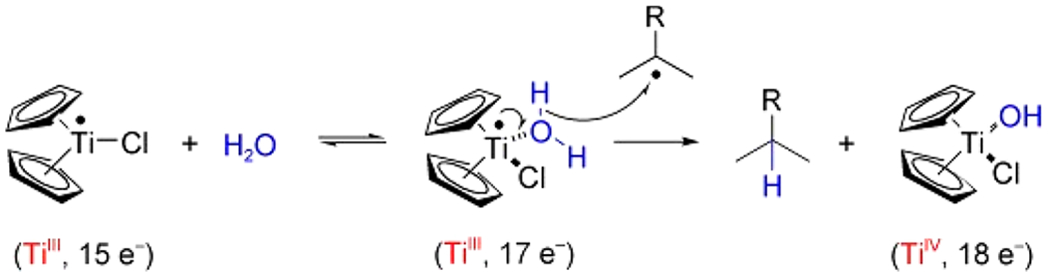
aReproduced with permission from ref 145. Copyright 2006 Wiley.
Table 10.
PCET Thermochemistry of Water and Common Alcoholsa
| compound | solvent | E∘(RO•/−) | pKa(ROH) | E∘(V vs H2) | BDFE | compound | solvent | E∘(RO•/− ) | pKa(ROH) | E∘ (V vs H2) | BDFE |
|---|---|---|---|---|---|---|---|---|---|---|---|
| HO–H | gas | -- | -- | 2.690 | 110.6325 | O–H− | H2O | -- | -- | 2.609b | 113.0 |
| HO–H | H2O | 1.90245 | 14.045 | 2.73045 | 115.8 | MeOH | gas | -- | -- | 2.075 | 96.432 |
| •O–H | gas | -- | -- | 1.997 | 94.6325 | EtOH | gas | -- | -- | 2.079 | 96.532 |
| •O–H | H2O | 1.43326 | 11.9326 | 2.13 | 102.0 | iPrOH | gas | -- | -- | 2.122 | 97.532 |
| O–H− | gas | -- | -- | 2.317 | 102.032 | tBuOH | gas | -- | -- | 2.148 | 98.132 |
Potentials for 1e− reductions are in V vs SHE if in aqueous solution. Values for E∘(V vs H2) are in V; −eE∘ is the average free energy for addition. Uncited values of E∘(V vs H2) were calculated from other values in the row using Scheme 2 or eq 18. BDFEs are in kcal mol−1 and if uncited were calculated from E∘(V vs H2) using eq 18. In many cases, the citation associated with a BDFE is for the related BDE, and the tabulated value was calculated using eq 9.
Calculated from E∘(RO•/−) = 1.902 and the pKa(•O–H) = 11.9 given above.
In a broader sense, the PCET reaction in Scheme 6 is a typical example of most PCET reactions of metal complexes, which couple redox change at the metal center with proton exchange at the ligand. The X–H BDFE on the ligand is then defined by an E∘ at the metal center and a pKa of the ligand acidic site, going through either corner of the relevant square scheme (Scheme 7A, similar to Scheme 1 for a simple X–H reagent). In general, bonds in a ligand will be weak (i) when LnM–X–H is a strong reductant and (ii) when the oxdized form LnM+–X–H is a strong acid (the left and bottom edges of Scheme 7A).
Scheme 7.
Thermochemical Schemes for X–H Bond Weakening upon Metal Coordination
The origin and amount of bond weakening can be analyzed using Scheme 7B, where BDFE′(XH) is the coordination-induced weakened X–H BDFE. The BDFE decrease is equal to the difference in the binding energy between the ligands XH and X• to LnM+. A metal center binding X•, such as a hydroxyl radical, can be further thought of as an ET from the metal followed by binding of X− (hydroxide) to the oxidized metal (LnM+). This directly relates the magnitude of bond weakening to the reducing power of the metal center. Therefore, non-reducing metal centers such as TiIV will not cause bond weakening, only reductants such as TiIII. Overall, the bond weakening is given by eq 26. From the perspective of Scheme 7B/eq 26, Cuerva’s Cp2TiCl system is very well set up for bond weakening. The binding of OH− to Cp2TiCl+ should be much stronger than the binding of water to Cp2TiCl, and electron transfer from TiIII to OH• should be very favorable.
| (26) |
Even more ideal is the case of Sm2+, which is an exceptional reductant (E∘ = −1.55 V vs SHE in water). Oxidation gives Sm3+, which is a stronger Lewis acid and therefore can bind X− strongly. We estimated the O–H BDFE for aqueous [Sm(H2O)n]2+ as 26 kcal mol−1,148 consistent with earlier estimates from Szostak and from Flowers.149,150 This is a remarkable 90 kcal mol−1bond weakening versus liquid water. The difference between the value for [Sm(H2O)n]2+ and the 73.6 kcal mol−1 O–H BDFE for [Fe(H2O)6]2+ (Table 23) is primarily due to the lower reducing power for the iron complex (FΔE∘ = 2.3 eV = 53 kcal mol−1).
Table 23.
PCET Thermochemistry of 3d-Based Transition Metal Systemsa
| compound (ML–H) | solvent | E∘(Mn–L)0/− | E∘(Mn–LH)+/0 | pKa(Mn+1LH) | pKa(Mn–LH) | E∘(V vs H2) | BDFE |
|---|---|---|---|---|---|---|---|
| FeII(H2O)62+ | H2O | [0.43] | 0.77384 | 2.2384 | 9.5384 | 0.90 | 73.6 |
| [(TPA)CuOH2]+b | H2O | – | −0.11385 | 7.26385 | – | 0.32 | 60.2 |
| MnO3(OH)− | H2O | – | 0.564386 | 7.4386 | – | 0.984 | 75.5 |
| (H2O)5CrOH2+ | H2O | – | – | – | – | >1.578 | ≥89.2387 |
| (H2O)5CrOOH2+ | H2O | – | – | – | – | 1.030 | 76.6388 |
| (Me6cyclam)Co(H2O)(OOH)2+c | H2O | – | – | – | – | 1.050 | 77.0389 |
| ([14]aneN4)Co(H2O)(OOH)2+c | H2O | – | – | – | – | 1.010 | 76.1389 |
| NiII(cyclamN-H) | H2O | – | 0.984390 | 7.1390 | – | 1.40 | 85.2 |
| (Py5)FeII(OH2)2+d | DMSO | −0.095391 | – | – | 8.1391 | 1.055e | 76.9e |
| [(LD)FeIIOH]2−f | DMSO | – | −1.79392,393 | 25.0392,393 | – | 0.360e | 60.9e |
| [(LD)MnIIOH]2−f | DMSO | <−2394 | –1.51392,393 | 28.3392,393 | [>36.6] | 0.835e | 71.9e |
| [(LD)MnIIIOH]−f | DMSO | −1.0392,393 | [−0.21] | ~15394 | 28.3392,393 | 1.3e | 84e |
| [FeIICp(η6-C6Me6)]PF6ab | DMSO | – | 1.25425 | −11.6425 | – | 1.23 | 81.0 |
| [FeIICp*(η6-C6Me6)]PF6ab | DMSO | – | 1.03425 | –8.5425 | – | 1.20 | 80.2 |
| (Py5)MnII(OH2)2+d | MeCN | 0.186395 | 0.636395 | [5.4] | 13.0395 | 0.984 | 74.7 |
| (bpy)2VV(O)(OH)+ | MeCN | – | – | – | – | 0.807 | 70.6396 |
| Py2Py(piCy)2FeIIOHg | MeCN | – | −0.028397 | 16.5397 | – | 0.977 | 74.5 |
| PhB(tBuIm)3CoIIOH | MeCN | – | −0.23398 | 25.6398 | – | 1.31 | 82.3 |
| [Mn2(OH)2(phen)4]3+ | MeCN | −0.03399,400 | – | – | 11.5399,400 | 0.68 | 67.7 |
| [Mn2(O)(OH)(phen)4]3+ | MeCN | −0.01399,400 | – | – | 14.6399,400 | 0.88 | 72.3 |
| (salpn)2(Mn2(O)(OH))h | MeCN | −0.8996 | −0.2196 | 13.496 | 24.596 | 0.61 | 66.1 |
| (LA)2(Mn2(O)(OH))i | MeCN | −0.6396 | 0.0196 | 10.896 | 20.596 | 0.68 | 67.6 |
| (LB)2(Mn2(O)(OH))j | MeCN | −0.1296 | 0.4796 | 5.096 | 13.396 | 0.79 | 70.3 |
| [(TPA)2Cu2OH]2+b | MeCN | – | –0.48385 | 24.3385 | – | 0.99 | 74.8 |
| [(TPA)2Cu2OH]3+b | MeCN | 0.76385 | – | – | 24.3385 | 2.23 | 103.3 |
| [LetCu2(OOH)]2+k | MeCN | −0.59401,k | – | – | 22.2401 | 0.75 | 69.3 |
| FeII(H2bip)3l | MeCN | – | –0.55402 | 17.5402 | – | 0.51 | 63.9 |
| FeII(H2bim)3m | MeCN | ~ − 0.8403 | −0.31403 | 17.5403 | ~26403 | 0.75 | 69.4 |
| CoII(H2bim)3m | MeCN | – | −0.53404 | 20.3404 | – | 0.70 | 68.1 |
| (TPP)FeII(MeImH)2n | MeCN | [−0.95] | −0.58581 | 20.881 | 26.981 | 0.674 | 67.6 |
| (PrbbimH)(Prbbim)Fe2S2 Reiske modelo | MeCN | −1.43405 | –1.2405 | 23.6405 | 27.9405 | 0.2 | 57 |
| (LE)Fe2S2(LF-H) (mito-NEET model)p | MeCN | −1.64783 | −1.40783 | 23.783 | [27.7] | 0.024 | 52.6 |
| [(TAML)FeIV(NHTs)]−q | MeCN | −0.07406 | – | – | 15.7406 | 0.89 | 72.5 |
| [(Cp)Co(CpNH)]+r | MeCN | −1.35407 | −1.21407 | 8.6407 | [11.0] | −0.67 | 36.5 |
| [(Cp)Co(CpNH)]2+r | MeCN | 0.52407 | – | – | 8.6407 | 1.06 | 76.4 |
| [SNS]Ni(PPh3f)s | MeCN | −0.61408 | – | – | 15.9408 | 0.36 | 60.3 |
| CpCr(CO)3H | MeCN | −0.688409 | – | [−9.5] | 13.3410 | 0.127 | 54.9 |
| CpCr(CO)2(PPh3)H | MeCN | –1.289411 | – | – | 21.8411 | 0.030 | 52.7 |
| (dppm)V(CO)4Ht | MeCN | −1.18412 | – | – | 18.8412 | −0.04 | 51.1 |
| (dppe)V(CO)4Hu | MeCN | –1.12412 | – | – | 17.6412 | –0.05 | 50.8 |
| [(TPP)FeIII(OOH)n,x,aa | THF | −1.18413,aa | – | – | 24.6413,aa | 0.61 | 66.2 |
| [(PIm)FeIII(OOH)]v,x | THF | −1.33414 | – | – | 28.6414 | 0.70 | 68.2 |
| [(F8TPP)FeIII(OOH)]w,x | THF | −1.17415 | – | – | 28.8415 | 0.87 | 72.1 |
| pipMeLGCuOHy | THF | −0.2692 | – | – | 20.092 | 1.27 | 81.2 |
| LGCuOHy | THF | –0.07492 | – | – | 18.892 | 1.382 | 83.9 |
| P3SiFeCNHz | THF | – | −1.27191 | 5.6191 | – | –0.60 | 38.3 |
| [P3SiFeCN(Me)H]+z | THF | −1.31191 | – | – | 7.1191 | −0.55 | 39.4 |
| P3SiFeCN(Me)Hz | THF | – | −1.27191 | 7.1191 | – | −0.51 | 40.3 |
| P3SiFeNN(Me)Hz | THF | −1.22191 | – | – | 8191 | −0.40 | 42.7 |
Potentials for 1e− reductions are in V vs SHE if in aqueous solution and V vs Cp2Fe+/0 if they are in organic solution. Values for E∘(V vs H2) are in V; −eE∘ is the average free energy for addition. Uncited values of E∘(V vs H2) were calculated from other values in the row using Scheme 2 or eq 18. BDFEs are in kcal mol−1 and if uncited were calculated from E∘(V vs H2) using eq 18. Values in [square brackets] have been calculated from the other values in the row using Hess’ law.
TPA = tris(2-pyridylmethyl)amine.
Me6cyclam = Me6cyclam = meso-hexamethylcyclam;[14] aneN4 = 1,4,8,11-tetraazacyclotetradecane.
Py5 = 2,6-bis(bis(2-pyridyl)methoxymethane)-pyridine.
Compared with other solvents, both E∘(V vs H2) and BDFE values in DMSO have larger uncertainties from the thermochemical constants E∘(H+/H2) and CG (see Table 1).
LD = tris[(N′-tert-butylureaylato)-N-ethyl)]aminato.
Py2Py(piCy) = 2,2′,2′-methylbispyridyl-6-(2,2′,2′-methylbis-5-cyclohexyliminopyrrol)-pyridine.
salpn = 1,3-bis(salicylideneamino)propane.
LA = 1,3-bis(3,5-dichloro-salicylideneamino)propane.
LB = 1,3-bis(3,5-dinitrosalicylideneamino)-propane.
Let = 3,5-bis(1,4-di-isopropyl-1,4,7-triazacyclononane-1-ethyl)-pyrazole. Potential determined at 0 °C.
bip = 2,2′-(tetrahydro)-pyrimidine.
bim = 2,2′-biimidazoline.
TPP = meso-tetraphenylporphyrin; MeImH = 5-methylimidazole.
PrbbimH2 = 4,4-bis(benzimidazole-2-yl)heptane.
LE = 1,1′-biphenyl-2,2′-dithiol; LF = 2-(1H-benzimidaol-2-yl)benzenthiol.
TAML = tetraamido macrocyclic ligand; NTs = tosylimido.
CpNH = 4-cyclopentadienyl-dimethylaniline.
[SNS]H3 = bis(2-mercapto-p-tolyl)amine.
dppm = bis(diphenylphosphino)methane.
dppe = bis(diphenylphosphino)ethane.
PIm = tris(2,6-difluorophenyl)(NHCOBzCH2Im)porphyrin.
F8TPP = tetrakis(2,6-difluorophenyl)-porphyrin.
Measurements done at −80 °C.
ypipMeLG = N,N′-bis(2,6-diisopropylphenyl)-2,6-N-methylpiperidinedicarboxamide; LG = N,N′-bis(2,6-diisopropylphenyl)-2,6-pyridinedicarboxamide.
P3Si = tris(2-(diisopropylphosphino)phenyl)silane.
More porphyrin derivatives of FeIII(OOH) complexes can be found in ref 413.
More analogues to these complexes, and their thermochemistry, can be found in ref 425.
Bond weakening is not limited to water ligands. Alcohols, amides, and other groups bound to Sm2+, Ti3+, and other reducing metal centers show the same effect. This has been exploited in SmI2·H2O/THF reductions in organic synthesis.151–156 Knowles applied the coordination-induced bond weakening of amides to perform catalytic conjugate aminations using a TiIII–TEMPO system, demonstrating the potential of this effect for catalyst design (Figure 8A).157 Similarly, Holland and Poli recently suggested a PCET step involving an FeII–ethanol complex with a weak O—H bond as a key intermediate in alkene cross couplings (Figure 8B).158 The concept of coordination-induced bond weakening has also been very valuable in understanding metal-mediated N2 reduction and ammonia oxidation, as discussed in Section 3.6.
Figure 8.
Catalytic applications of coordination bond weakening. (A) Knowles’ use of amide coordination bond weakening (bottom left) to enable catalytic amination. (B) Kim, Holland, and Poli’s possible mechanism for carbon radical trapping by an iron(II)-bound ethanol ligand. Reproduced with permission from refs 157 and 158, respectively. Copyright 2015 and 2019 American Chemical Society.
3.5. Kinetics of Concerted PCET Mechanisms
While this review is about PCET thermochemistry, we would be remiss not to mention its close connections to the kinetics of such reactions. These connections are increasingly evident, and they are a key reason why the thermochemistry is of continuing interest. The connections between the kinetics and thermodynamics of CPET would fill another review, so only some brief comments are given here.
3.5.1. Linear Free Energy Relationships and Marcus Theory.
Many sets of similar CPET reactions have been shown to obey linear free energy relationships (LFERs) between the kinetics and thermodynamics of PCET reactions. The most common are correlations of log(kCPET) with the BDFE or BDFEeff.3,80 These are equivalent to plots of log(kCPET) vs log(Keq) or of barrier vs driving force, ΔG‡ vs ΔG∘. The unitless slopes of such plots—the Brønsted slopes or the Brønsted α—can provide useful intuition. At low driving forces, |ΔG∘| ≪ ΔG‡, simple analyses suggest that changes in barrier should be roughly half of the changes in ΔG∘, . From one perspective, this is because the transition state in this limit is roughly halfway between reactants and products following the Hammond postulate.159,160 Similar PCET LFERs are part of the “scaling relationship” or “volcano plot” analyses of heterogeneous catalysis and electrocatalysis (Section 3.8). However, several recent papers have reported α values that differ strongly from in the low driving force regime.123,127,128
A number of laboratories, including ours, have gone beyond LFERs to apply versions of Marcus theory to CPET reactions.123,161–169 This is based on theoretical treatments of CPET built on Marcus foundations.4,6 We have found that most CPET rate constants obey the Marcus cross relation, at least to an order of magnitude or two, though there are certainly exceptions.161 Marcus theory predicts the mentioned above for CPET reactions at low driving force (|ΔG∘| ≪ 2λ) and predicts larger or smaller values of αα for uphill or downhill reactions. As −ΔG∘ approaches λ, the simple Marcus analysis predicts α → 0 and ΔG‡ → 0. When −ΔG∘ exceeds λ, Marcus famously predicted an inverted region, where reactions slow with increasing driving force (α < 0). The predictions of very small ΔG‡ have been observed for some photoinduced MS-CPET reactions, and some of us have recently reported the first example of a PCET reaction in the Marcus inverted region.170 Looking forward, we anticipate closer connections between kinetics and thermodynamics, building on advances and interactions in experiment and theory.
3.5.2. Asynchrony or Asymmetry of PCET Reactions.
As shown above, PCET reagents can have the same BDFE and E∘(V vs H2) with different contributions from the ET and PT components. This raises the interesting question: is kCPET affected only by the overall ΔG∘PCET, or is it also influenced by the relative contributions of the ET and PT components? A recent computational (DFT) paper by Srnec et al. provided evidence that an imbalance between ΔG∘ET and ΔG∘PT can give rise to an “asynchronous” CPET pathway with a transition state containing more PT or ET character.171 They suggested a connection between asynchrony and the long-known “polar effects” in organic HAT reactions, for example, that an electrophilic radical will preferentially abstract an electron-rich hydrogen.172,173 In addition to this experimental study, several experimental papers have invoked asynchronous transfers of the proton and electron to explain the apparent sensitivity of CPET rates to how the driving force is changed.92,123,128,174–177 However, current PCET theory describes these reactions with vibronic states and therefore uses the overall ΔG∘PCET without any simple mechanism to distinguish the PT and ET components.4,6 Still, differences in the driving forces for ET vs PT across a series could affect the intrinsic barriers for CPET (λ), the quantum-mechanical coupling between vibronic states, and the structure and energetics of the precursor and successor complexes. For example, Sayfutyarova, Lam, and Hammes-Schiffer found that the base pKa in a series of fluorenyl–benzoate reactions affected the rate constant by changing the ground-state structure rather than the PCET step.129 Whatever the mechanism by which the overall rate constants are affected, if kCPET can be manipulated by changing the balance between PT and ET without changing the overall ΔG∘, that could have implications for synthesis, catalysis, and enzyme mechanisms. We anticipate that this will be an active area of PCET research in the years to come.
3.6. N2 Fixation and Ammonia Oxidation
The reduction of N2 to NH3 and its reverse, the oxidation of ammonia to N2, are persistent challenges in coordination chemistry and homogeneous/heterogeneous catalysis. These 6e−/6H+ PCET processes are frequently described in 1e−/1H+ steps (even though typically the detailed ET/PT/CPET mechanism is not known). Many studies in this area have emphasized the Chatt (or distal) cycle, illustrated for the first homogeneous mononuclear N2 reduction catalyst in Scheme 8. This 6e−/6H+ process has many intermediates—Schrock and Yandulov isolated eight of the intermediates in Scheme 8.178 While the mechanism in Scheme 8 shows stepwise additions of electrons and protons, it seems likely (at least to us) that at least some of these steps in catalysis would involve concerted transfers of both particles.135 Additionally, although the emphasis of this review is the transfer of equimolar amounts of H+/e−, significant effort has been dedicated to understanding reactions that have an excess of protons, e.g., N2 to N2H5+, and we direct the readers to the following references for further details.179,180 These basic principles should be general to most mechanisms for small-molecule transformations going through multiple PCET processes.
Scheme 8. Schrock Catalyst (Top) and Proposed Intermediates along the Chatt Cycle in the Reduction of Dinitrogen through the Stepwise Addition of Protons and Electrons (Bottom)a,b.
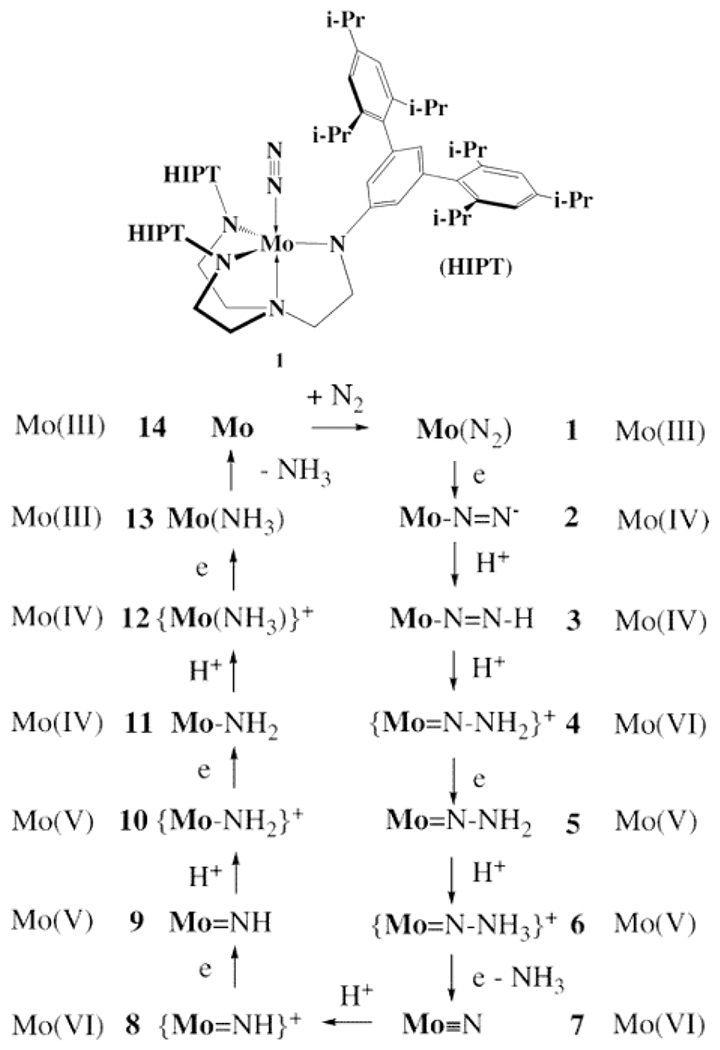
aIn the bottom portion, compounds that were not isolated are bracketed with { and }.
bReproduced with permission from ref 178. Copyright 2005 American Chemical Society.
The overall reaction 2NH3 → N2 + 6H• has a free energy per H atom (ΔG∘/n) of 53.5 kcal mol−1 in MeCN (Table 13). This value is not an average N–H BDFE because it includes the NN triple bond energy. This value does show the BDFE or BDFEeff (see Section 3.3) required for an H atom donor to give isoergic conversion of N2 to ammonia. The original Schrock catalytic system used CrCp*2 + [lutidinium] [BAr′4] (Ar′ = 3,5-(CF3)2C6H3) as the net H atom donor, which has a BDFEeff of 38.2 kcal mol−1 in MeCN.181 The catalysis was done in heptane, however, where the acid was insoluble, to minimize reductant/acid incompatibility (Section 3.3.2). Taking the MeCN BDFEeff as an estimate, the catalytic reaction had an overpotential of |38.2 – 53.5| = 15.3 kcal mol−1 per H atom, or 0.66 V. Later catalytic reactions used reductants as strong as potassium graphite with strong acids such as [(Et2OH)][BArF4] where the effective BDFE is negative (BDFEeff < −16 kcal mol−1); i. e., the reducing power of the pair is greater than that of a free H atom in solution.135 Recent studies have implicated protonated metallocenes as likely H atom donors, such as [CoCp*(Cp*H)]+ (C–H BDFE < 26 kcal mol−1).143 Often these acid/reduction combinations have competing hydrogen-evolution reaction (HER) pathways (free energy per H• of 52 kcal mol−1 in solution, Table 1), hindering the catalytic generation of ammonia.
Table 13.
PCET Thermochemistry for Nitrogen Reductiona
| HN2•/HNN-H | solvent | E∘(HNNH•+/0) | pKa(HNNH•+) | pKa(HNNH) | E∘(V vs H2)b | BDFE |
|---|---|---|---|---|---|---|
| HNN-H | gas | – | – | – | 0.17 | 52.625 |
| HNNH/HN•NH-H | solvent | E∘(HNNH2+/• | pKa(HNNH2+) | pKa(HNNH2•) | E∘(V vs H2) | BDFE |
|
| ||||||
| HN•NH-H | gas | – | – | – | −0.56 | 35.6334 |
| HN•NH-H/H2NNH-H | solvent | E∘(H2NNH2•+/0) | pKa(H2NNH2•+) | pKa(H2NNH2) | E∘(V vs H2) | BDFE |
|
| ||||||
| H2NNH-H | gas | - | - | – | 1.04 | 72.6334 |
| H2NNH-H | H2O | 0.69180 | 7.2335 | – | 1.12 | 78.5 |
| N2(g) + 3H2(g) → 2NH3 | solvent | E∘(V vs H2) | −ΔG∘/nc | |||
|
| ||||||
| N2/NH3 | gas | 0.05742 | 49.9 | |||
| N2(g)/NH3 | H2O | 0.092179 | 54.9 | |||
| N2(g)/NH3 | MeCN | 0.063179 | 53.5 | |||
| N2(g) + 2H2(g) → N2H4 | solventc | E∘(V vs H2) | −ΔG∘/nd | |||
|
| ||||||
| N2/N2H4 | gas | −0.41342,e | 39.1 | |||
| N2(g) + H2(g) → N2H2 | solventc | E∘(V vs H2) | BDFEavg | |||
|
| ||||||
| N2/N2H2 | gas | −1.07f | 23.9 | |||
Potentials for 1e− reductions are in V vs SHE if in aqueous solution and V vs Cp2Fe+/0 if they are in organic solution. Values for E∘(V vs H2) are in V; −eE∘ is the average free energy for addition. Uncited values of E∘(V vs H2) were calculated from other values in the row using Scheme 2 or eq 18. BDFEs and −ΔG∘/n values are in kcal mol−1 and if uncited were calculated from E∘(V vs H2) using eq 18. In many cases, the citation associated with a BDFE is for the related BDE, and the tabulated value was calculated using eq 9. Values in [square brackets] have been calculated from the other values in the row using Hess’ law.
E∘(V vs H2) of HN•NH-H in H2O was derived from those of N2/N2H4, N2/N2H2, and H2NNHH.
Related values in MeCN or H2O have been reported, but they include computational components or different numbers of protons and electrons and therefore are not included here.179,180
−ΔG∘/n values are average free energies for the overall reaction shown except to form H•[rather than add H2(g)]. See Section 4.
Other values of ΔH∘f of N2H4 exist,42 but a similar value was obtained from another thermochemical cycle in ref 179.
E∘(V vs H2) of N2/N2H2 in the gas phase was derived from those of H2NNH-H, HN•NH-H, and N2/N2H4.
3.6.1. N–H BDFEs of Intermediate Mononuclear Complexes.
There has been a burgeoning interest in experimentally assessing the individual N–H BDFEs in complexes pertaining to N2 fixation and NH3 oxidation. The N–H BDFEs are a good measure of the stability of the intermediates, though imperfect because the steps that include ligand substitution and N–N bond cleavage/formation have additional energy terms. While the high reactivity of some intermediates can preclude accurate assessment of relevant BDFEs, many intermediates’ N–H BDFEs have been estimated experimentally using irreversible electrochemical potentials or through reactivities with acid/reductant combinations or with PCET reagents.182–186 In addition, it has proven valuable to benchmark DFT calculations against measured BDFEs and then use the same computational approach to determine the BDFEs that were not experimentally accessible.183,184,187–190 Having these N–H BDFEs has identified at least some of the thermochemical bottlenecks to catalysis. Here, we briefly mention some estimated N–H BDFEs in intermediates along the Chatt cycle.
The first H atom addition to a metal–N2 complex forms a diazenido complex MNNH whose N–H BDFEs have been studied in molybdenum and iron complexes. The N–H BDFE of the molybdenum diazenido complex [N3NHIPT]Mo(N═NH) was found to be 40.9 kcal mol−1 from the reduction potential and an estimate of the 1e−-reduced pKa (Figure 9). Here and throughout this section, we have adjusted the originally reported BDFE or BDE values to use the revised CG’s in Table 1, and in this case the new CG(THF) = 59.9 kcal mol−1. The N–H BDFE for the putative diazenido complex P3NFeNNH was indicated to be <37 kcal mol−1, in part based on its likely disproportionation to the FeN2 and FeNNH2 complexes, even at 138 K (Figure 9).191 The PCET reactivity of the analogous P3NFe–CNHx compounds (and alkylated derivatives) were also examined as models, as they were somewhat more stable model compounds.
Figure 9.
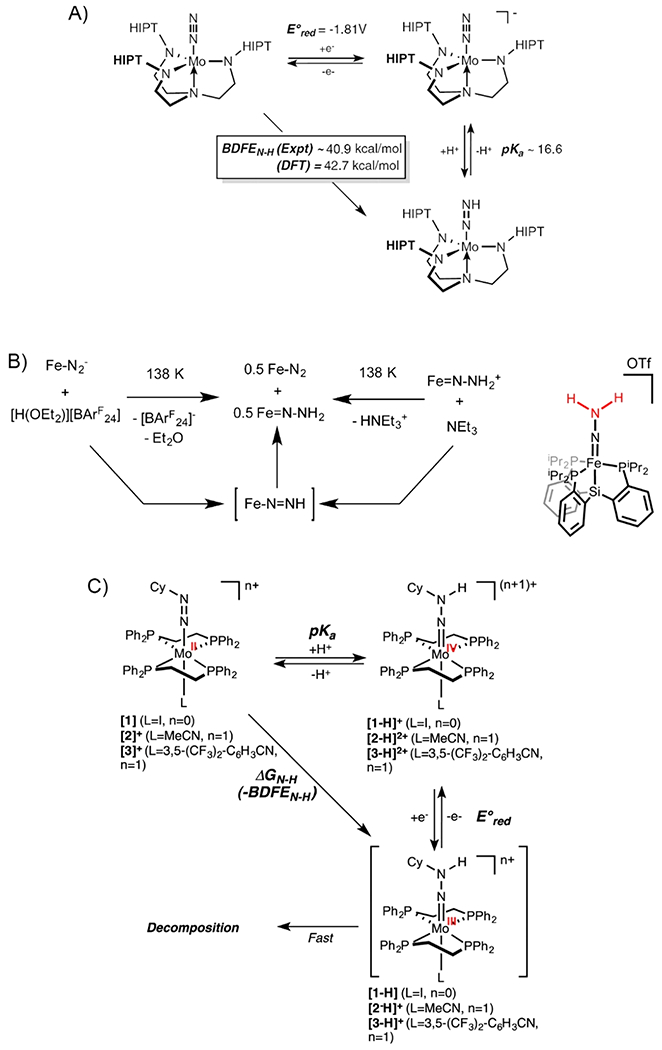
(A) Scheme for estimating a Mo-diazenido N–H BDFE (HITP = 3,5-(2,4,6-iPr3C6H2)2-C6H3); the BDFEN–H has been edited to reflect our updated CG value in THF. Reprinted (adapted) with permission from ref 192. Copyright 2017 Springer Nature. (B) Suggested generation and disproportionation of P3SiFe–N═NH to P3SiFe–N2 and P3SiFe═N–NH2; the cationic hydrazido complex is drawn at the right, showing the structure of the P3Si ligand. Reprinted with permission from ref 191. Copyright 2017 American Chemical Society. (C) Scheme for theN–H BDFEs in (dppe)2(L)Mo(═NN(Cy)H)n+. Reprinted with permission from ref 188. Copyright 2016 Royal Chemical Society.
Metal hydrazido (MNNH2) complexes also appear to have very low N–H BDFEs in molybdenum and iron complexes, similar to MNNH compounds. To achieve sufficient stability for thermochemical studies, an alkyl substituent can be placed on the distal N. Thus, the N–H BDFE of the methylated hydrazido P3SiFe[NN(Me)–H)] was estimated to be around 43 kcal mol−1 with the P3SiFe[CN(Me)–H] analogue exhibiting a similar N–H bond strength of 39 kcal mol−1.191 A series of molybdenum cyclohexylhydrazido complexes, [trans-(dppe)2(L)Mo(NN(Cy)–H)]n+ (L = I−, MeCN, or 3,5-CF3C6H3CN; Figure 9C), were found to have very weak N–H bonds, 32–39 kcal mol−1. Increasing the π-acidity of the ligand trans to the hydrazido ligand increases the N–H bond strength, presumably because it makes the Mo center less reducing and the oxidized hydrazido less acidic (see Section 3.4 above).188
In the Chatt mechanism, 3e−/3H+ reduction of a dinitrogen complex gives 1 equiv of ammonia and the formation of a nitrido complex, stabilized by M–N π bonds. Then, the PCET additions of H atoms start again, forming metal–imido (M═NH), –amido (M–NH2), and –ammine (MNH3) complexes. As with the M(N2) complexes above, the first H addition to nitride complexes appears to be the most challenging. A number of metal nitride compounds with M = Mn, Fe, Re, and Ir have been reduced by H atom donor equivalents (e.g., TEMPOH, SmI2/H2O) to give metal amides or ammonia, but the imido analogue has not been observed.132,182,183,189 Such observations suggest that the MN–H bonds are quite weak. For instance, H atom transfer reagents interconvert the unusual iridium nitride complex 3a and its amido congener 6 in Figure 10.132,182,183,189 The lack of observation of the presumed intermediate imido complex suggests that it has a weak N–H BDFE and dis-proportionates. These properties were rationalized with frontier MO theory, which postulated that lower Ir–N covalency and stronger π interactions led to the formation of the amido and nitrido complexes, respectively.
Figure 10.
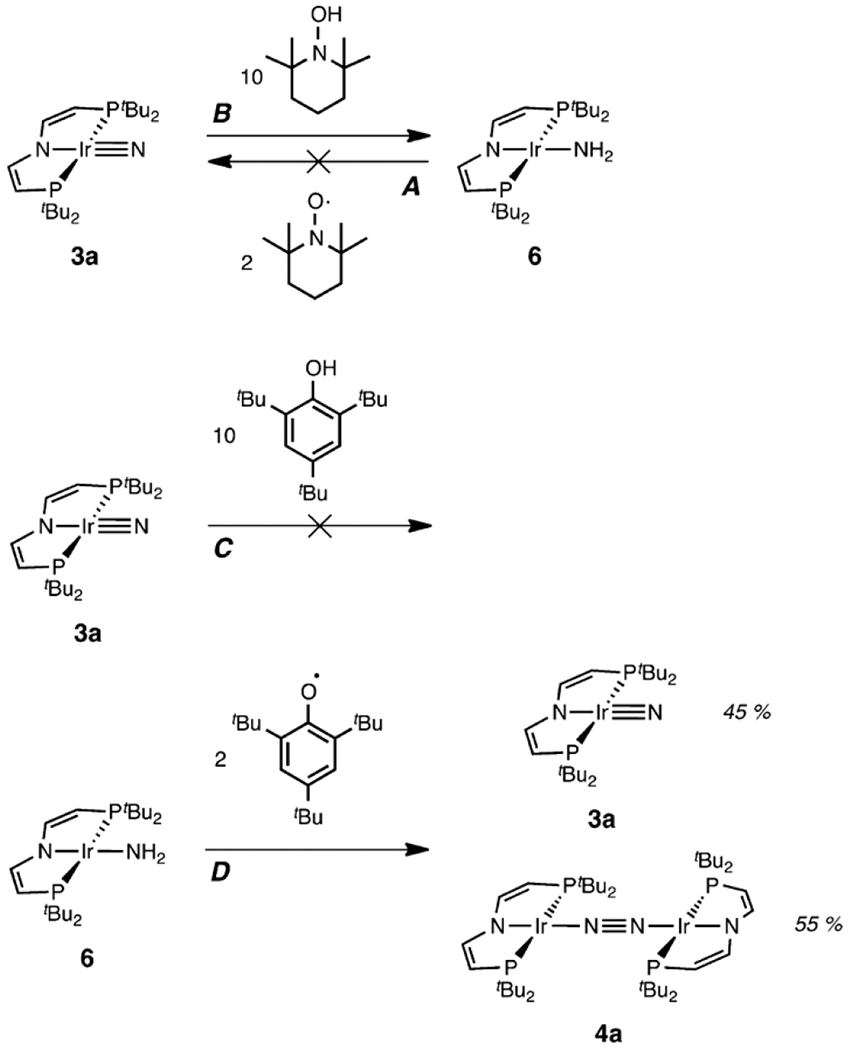
Reactions of iridium nitride and amide complexes 3a and 6 with hydrogen atom transfer reagents. Reprinted with permission from ref 183. Copyright 2015 American Chemical Society.
The oxidation of metal amine complexes to amide derivatives is similarly driven by the reduction potential of the metal and by more favorable π interactions with the higher valent metal center.184,193,194 An example of the latter is the stability of a terpyridine-Mo(II) amide following loss of H2 from the Mo(I)-amine, in which the ammonia N–H bond is significantly weakened to 40.2 kcal mol−1 upon coordination to the reducing metal center.195 Similar to the hydrazido complexes above, substituted metal amide complexes (M–RNH) feature stronger N–H BDFEs than parent amide complexes (M–NH2). Others have taken advantage of larger substituted amide BDFEs to abstract weak C–H bonds using metal imido complexes, which can subsequently do a number of transformations, including cyclizations and aminations.196–200
A recurring theme in the PCET transformations throughout the Chatt cycle is that removal of a hydrogen atom is compensated by increased M–N and N–N bonding, especially π bonding.132,182–184,189,193,194 This, together with the oxidation of the low-valent metal, are likely the primary origins of the very weak N–H bonds in these molecules. The BDFEs listed above (30–45 kcal mol−1) are much weaker than those in organic nitrogen compounds such as amines, anilines, hydrazines, and heterocycles (60–95 kcal mol−1; Tables 14 and 16). The π bonding compensation is found in simple organic compounds as well. For instance, the H–CH2CH2• bond in the ethyl radical is a remarkable 64 kcal mol−1 weaker than the similar H–CH2CH3 bond in ethane (Table 19) because the radical forms a C═C π bond upon H atom loss. This effect is also closely related to the coordination-induced bond weakening described in Section 3.4, though that was rationalized in part with changes in metal–ligand σ bonding. The very exergonic disproportionation of the ethyl radical to ethylene and ethane is an extreme example of PCET potential inversion—the second bond is weaker than the first—discussed in the Section on biological electron bifurcation (Section 3.7.2 below). The authors of this review hope that readers will see many examples of such cross-fertilization in PCET chemistry that discoveries in one area have unexpected value in a different area.
Table 14.
PCET Thermochemistry of Ammonia and Alkylamines (N–H and C–H Bonds)a
| compound | solvent | E∘(RR′NH•+/0) | pKa(RR′NH•+) | E∘(V vs H2) | BDFE |
|---|---|---|---|---|---|
| NH3 | gas | -- | -- | 2.241 | 100.342 |
| •NH2 | gas | -- | -- | 1.769 | 89.442 |
| NH | gas | -- | -- | 0.880 | 68.942 |
| MeNH2 | gas | -- | -- | 1.944 | 93.425 |
| PrNH2 | MeCN | 1.14336 | [6.1] | 1.506b | 86.7337,b |
| PrNH2 | C6H6 | -- | -- | 1.417b | 84.8337,b |
| pentylNH2 | MeCN | 1.12336 | [7.8] | 1.610b | 89.1337,b |
| pentylNH2 | C6H6 | -- | -- | 1.395b | 84.3337,b |
| Me2NH | gas | -- | -- | 1.641 | 86.425 |
| Me2NH | H2O | 1.27338 | 6.8338 | 1.67 | 91.4 |
| Et2NH | H2O | 1.36338 | 5.3338 | 1.67 | 91.4 |
| Et2NH | MeCN | 1.311b | 82.2337,b | ||
| Et2NH | C6H6 | -- | -- | 1.243b | 80.8337,b |
| pyrrolidine | H2O | 1.26338 | 5.5338 | 1.59 | 89.4 |
| piperidine | H2O | 1.34338 | 5.8338 | 1.68 | 91.6 |
| nBu2NH | C6H6 | -- | -- | 1.408b | 84.6337,b |
| nBu2NH | MeCN | -- | -- | 1.324b | 82.5337,b |
| tBuNH2 | C6H6 | -- | -- | 1.590 | 88.8337 |
| tBuNH2 | MeCN | 1.27336 | [3.7] | 1.515 | 86.9337 |
Potentials for 1e− reductions are in V vs SHE if in aqueous solution and V vs Cp2Fe+/0 if they are in organic solution. Italicized values are irreversible potentials, Ep,a or Ep,c, measured by cyclic voltammetry. Values for E∘(V vs H2) are in V; −eE∘ is the average free energy for addition. Uncited values of E∘(V vs H2) were calculated from other values in the row using Scheme 2 or eq 18. BDFEs are in kcal mol−1 and if uncited were calculated from E∘(V vs H2) using eq 18. In many cases the citation associated with a BDFE is for the related BDE, and the tabulated value was calculated using eq 9. Values in [square brackets] have been calculated from the other values in the row using Hess’ law.
The relevant bond for the BDFE and E∘(V vs H2) values is a combination of the α(C–H) and N–H bonds.337
Table 16.
Thermochemical Data for Indoles and Tryptophana
| compound | solvent | E∘(R2N•/−) | E∘(R2NH•+/0) | pKa(R2NH•+) | pKa(R2NH) | E∘ (V vs H2) | BDFE |
|---|---|---|---|---|---|---|---|
| indole | H2O | [0.52] | 1.24342 | 4.9342 | 17.0343 | 1.53 | 88.1 |
| tryptophan | H2O | [0.43] | 1.15344 | 4.7344 | 16.8343 | 1.43 | 85.7 |
| 2-CH3-indole | H2O | -- | 1.10342 | 5.7342 | -- | 1.44 | 85.9 |
| 3-CH3-indole | H2O | [0.38] | 1.07342 | 5.0342 | 16.6343 | 1.37 | 84.3 |
| 2,3-CH3-indole | H2O | -- | 0.93342 | 6.1342 | -- | 1.29 | 82.6 |
Potentials for 1e− reductions are in V vs SHE. Values for E∘(V vs H2) are in V; – eE∘ is the average free energy for addition. Uncited values of E∘(V vs H2) were calculated from other values in the row using Scheme 2 or eq 18. BDFEs are in kcal mol−1 and if uncited were calculated from E∘(V vs H2) using eq 18. Values in [square brackets] have been calculated from the other values in the row using Hess’ law.
Table 19.
PCET Thermochemistry of C–H Bonds in Selected Compoundsa
| compound | solvent | E∘(R•/−) | E∘(RH•+/0) | pKa(RH•+) | pKa(RH) | E∘ (V vs H2) | BDFE |
|---|---|---|---|---|---|---|---|
| CH4 | gas | -- | -- | -- | -- | 2.092 | 96.8362 |
| CH3CH2-H | gas | -- | -- | -- | -- | 1.923 | 92.942 |
| •CH2CH2-H | gas | –0.892 | 28.042 | ||||
| (CH3)2CH-H | gas | -- | -- | -- | -- | 1.814 | 90.4363 |
| (CH3)3C-H | gas | -- | -- | -- | -- | 1.723 | 88.3363 |
| CH2═CH-H | gas | -- | -- | -- | -- | 2.339 | 102.5364 |
| HC≡C-H | gas | -- | -- | -- | -- | 3.319 | 125.1365 |
| cyclo-C5H6b | gas | -- | -- | -- | -- | 1.069 | 73.2366 |
| cyclo-C5H6b | DMSO | −0.778367 | -- | -- | 18.0368 | 0.958c | 74.7c |
| 1,4-cyclohexadiene | gas | -- | -- | -- | -- | 0.833 | 67.8369 |
| cyclohexadienyl (•C6H7) | gas | -- | -- | -- | -- | −1.509 | 13.842,369 |
| C6H5-H | gas | -- | -- | -- | -- | 2.435 | 104.7364 |
| C6H5CH2-H | gas | -- | -- | -- | -- | 1.433 | 81.6370 |
| (CH3)6C6 | MeCN | -- | 1.11371,372 | 2.0373 | -- | 1.26 | 81.0 |
| p-(CH3)2C6H4 | MeCN | −2.094 | 1.45371,372 | [–4.3] | 53.894 | 1.2 | 80 |
| (CH3)5C6H | MeCN | -- | 1,19371,372 | 2.0373 | -- | 1.34 | 82.8 |
| 1,2,4,5-Me4C6H2 | MeCN | -- | 1.20371,372 | 3.0373 | -- | 1.41 | 84.4 |
| indene | DMSO | −0.952372 | -- | -- | 20.1372 | 0.908c | 73.6c |
| fluorene | DMSO | −1.069372 | -- | -- | 22.6372 | 0.940c | 74.3c |
| DHAd | DMSO | −1.575372 | -- | -- | 30.1372 | 0.879c | 72.9c |
| xanthene | DMSO | −1.685372 | -- | -- | 30.0372 | 0.763c | 70.2c |
| Ph3CH | DMSO | −1.486372 | -- | -- | 30.6372 | 0.998c | 75.7c |
| Ph2CH2 | DMSO | −1.54372 | -- | -- | 32.2372 | 1.04c | 76.6c |
Potentials for 1e− reductions are vs Cp2Fe+/0 in the organic solution. Italicized values are irreversible potentials, Ep,a or Ep,c, measured by cyclic voltammetry. Values for E∘(V vs H2) are in V; –eE∘ is the average free energy for addition. Uncited values of E∘(V vs H2) were calculated from other values in the row using Scheme 2 or eq 18. BDFEs are in kcal mol−1 and if uncited were calculated from E∘(V vs H2) using eq 18. In many cases the citation associated with a BDFE is for the related BDE, and the tabulated value was calculated using eq 9. Values in [square brackets] have been calculated from the other values in the row using Hess’ law.
cyclo--C5H6 = 1,3-cyclopentadiene.
Compared with other solvents, both E∘(V vs H2) and BDFE values in DMSO have larger uncertainties from the thermochemical constants E∘(H+/H2) and CG (see Table 1).
DHA = 9,10-dihydroanthracene.
3.7. Selected Biological Systems
Investigations of PCET in protein systems are older than the term “PCET” itself. The “old yellow enzyme”, a flavin-containing protein, was discovered in the 1930s and was known to carry out proton-coupled redox reactions by the late 1960s.201 Investigations of the chemistry of cytochrome P450s started in the 1940s and 1950s.202 The photosynthetic Kok cycle for water oxidation emerged in the 1970s.203 As illustrated in the tables below, the PCET chemistry of amino acid side chains and organic cofactors has long been studied, especially tyrosine, tryptophan and cysteine, quinones, flavins, and nicotinamides. Studies of these and other biochemical systems, including metalloenzymes, have provided a primary motivation for the PCET field.6,8,204–208
3.7.1. Metalloprotein Active Sites.
Biochemical PCET reactions can be especially complex because of the presence of many acid/base groups and interfacial effects, for instance, at lipid bilayers. This can lead to fractional numbers of protons being transferred with the transfer of an integer number of electrons. This is exemplified by the metalloprotein charge ladders investigated by Shaw and co-workers.209–211 These charge ladders connect the change in charge of an entire protein (ΔZ) with redox change at the active site. In small metalloproteins such as azurin, cytochrome c, and myoglobin, a one-electron transfer event at the embedded metal ion induces changes in ΔZ that are not equal to 1. For example, reduction of the Cu(II) ion in azurin results in ΔZ = −0.51, rather than −1.210 The level of charge regulation upon ET is associated with pKa changes, and thus protonation state changes, at amino acids both near and far from the metal ion via thermodynamic coupling (Section 3.2.1). In the case of copper–zinc superoxide dismutase, charge regulation is nearly perfect (ΔZ ≅ 0), which was attributed to proton transfer at the active site.209 Related information can be obtained from the pH dependence of the active site reduction potential. From a biological PCET perspective, we hope that these types of measurement become more common.
A pathbreaking example of elucidating enzymatic PCET thermochemistry is the determination of the redox and acid–base properties of highly reactive intermediates in the catalytic cycle of cytochrome P450 enzymes by Green and co-workers.212,213 Understanding the thermochemical landscape of P450s is very important because these enzymes are the primary processors of xenobiotics in many organisms including humans, and their reactivity depends on this landscape. This is a very challenging task because of the high reactivity and transient nature of the key intermediates, the so-called compound I oxidant O═FeIVporphyin•+ and its one-electron reduced compound II. The ability of these enzymes to abstract hydrogen atoms from strong C–H bonds was confusing for many years, given the very high outer-sphere oxidation potentials of the hydrocarbon substrates. Green demonstrated that reduction of compound I is a PCET or H atom transfer process, wherein the ferryl (Fe═O) is converted to a one-electron-reduced iron hydroxide Fe–OH. They have experimentally developed a double square scheme for this highly reactive system, including the pH-dependent E∘, BDFE, and pKa of compounds I and II (Figure 11), and connected the thermochemistry with enzymatic reactivity.
Figure 11.
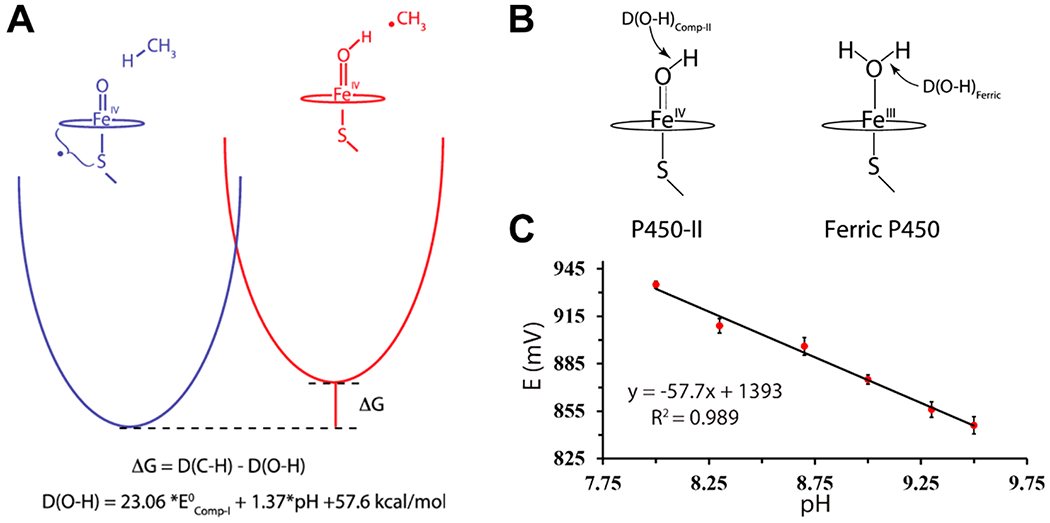
(A) Marcus-type reaction coordinate for P450 compound I abstracting a hydrogen atom from methane. (B) O–H bond strengths that define the ground-state thermodynamics of P450 catalysis, for compound II (also the red structure in part (A)) and for the ferric water-bound form of the enzyme. (C) Measured E∘′ for compound I to compound II versus pH. The 57.7 mV/pH slope demonstrates the 1e−/1H+ nature of the reduction. Reprinted with permission from ref 213. Copyright 2019 American Chemical Society.
3.7.2. Electron Bifurcation.
A fascinating and increasingly recognized area of bioenergetics is the ability of organisms to “bump up” the oxidizing or reducing power of their feedstocks using a process known as electron bifurcation (EB).214–221 Enzyme complexes that perform EB take advantage of “two-electron” redox cofactors such as quinones or flavins, which serve as the bifurcating site and direct participating electrons down either a low-potential (highly reducing) or high-potential (less reducing) branch of acceptors. The redox coupling between these two branches is ultimately what enables the negative free energy change of an exergonic redox reaction to drive a redox reaction that is ostensibly endergonic. Discussions of EB often highlight only the electron transfer steps, but the central role of quinones and flavins in biological EB raises interesting questions regarding the role of PCET in this process.
EB depends on a bifurcating site that can effectively mediate transfers of both one and two electrons. The familiar two-electron redox chemistry of quinones and flavins in protic media is a result of the inversion of their reduction potentials, a counterintuitive scenario in which the first reduction is more difficult (occurs at a more negative potential) than the second. In other words, the cofactor reduced by one electron—or, more commonly, one electron and one proton—is less stable than both the unreduced and doubly reduced cofactors. Such potential inversion is discussed in more detail at the end of this section.
Figure 12 illustrates how potential inversion of the cofactor in the bifurcating site can be used to accomplish EB. Beginning with the bifurcating site in its doubly reduced state (i.e., hydroquinone), Step 1 involves one-electron oxidation by a high-potential acceptor to transiently generate the unstable, singly reduced cofactor. The unusually negative reduction potential of this species (resulting from potential inversion) enables, in Step 2, a subsequent exergonic electron transfer to a low-potential acceptor. Notably, the reduction potential of the low-potential acceptor may be more negative than the average two-electron reduction potential of the bifurcating site. The overall EB process can be described as an “oxidatively-triggered reduction”, provided that adequate gating prevents both electrons of the reduced bifurcating site from transferring to high-potential acceptors.
Figure 12.
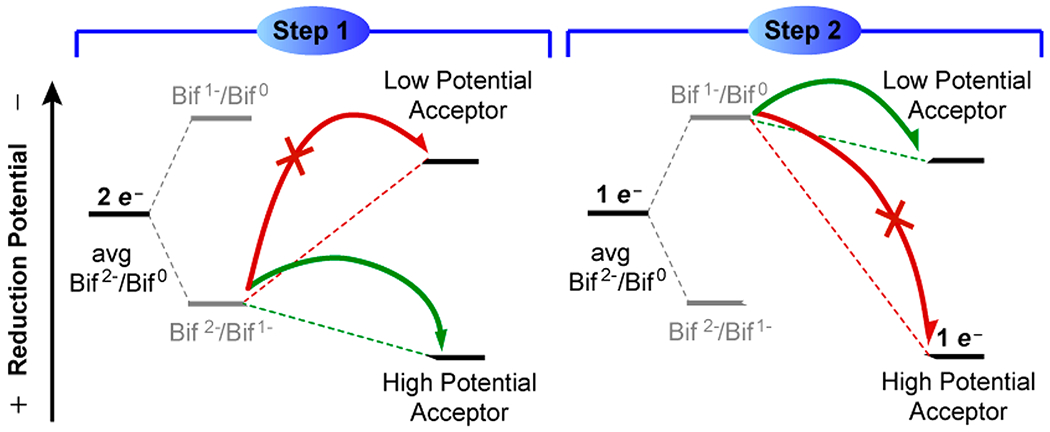
Schematic of EB: In Step 1, a high-potential acceptor oxidizes the doubly reduced bifurcating site by one electron, generating the unstable singly reduced bifurcating site, which is a potent reductant. In Step 2, this reductant can transfer an electron to a low-potential acceptor, provided that the more exergonic electron transfer to a second high-potential acceptor is prevented (gated). Here the redox steps are shown as pure electron transfers, as is common in the field, but one or both of these steps is (in our view) likely to be PCET (see below).
EB was originally proposed by Peter Mitchell to explain a curious observation in the bc1 complex of the mitochondrial electron transport chain: treatment of mitochondrial suspensions with the oxidant ferricyanide resulted in reduction of a low-potential heme center.214 It is now understood that this process, known as the Q cycle, involves redox cycling between the hydroquinone and quinone forms of coenzyme Q (Figure 13). Ubiquinol (hydroquinone form, H2Q) reacts at the Qo bifurcation site, sending its two electrons down two separate acceptor chains (Figure 13B). The first electron participates in H atom transfer to a histidine-ligated Rieske FeS cluster and subsequently reduces cytochrome c1 and cytochrome c; ubiquinol is thus oxidized to the semiquinone radical HQ•, which is a powerful reductant due to inverted reduction potentials. The second electron transfers when HQ• reduces hemes bL and bH, likely by multiple-site PCET (Section 3.3). The semiquinone reduces the series of b hemes even though they have reduction potentials more negative than that of the average 2e−/2H+ couple of the original hydroquinone. The terminal b heme ultimately rereduces ubiquinone to ubiquinol and translocates protons across the membrane, thereby generating proton motive force for ATP synthesis.
Figure 13.
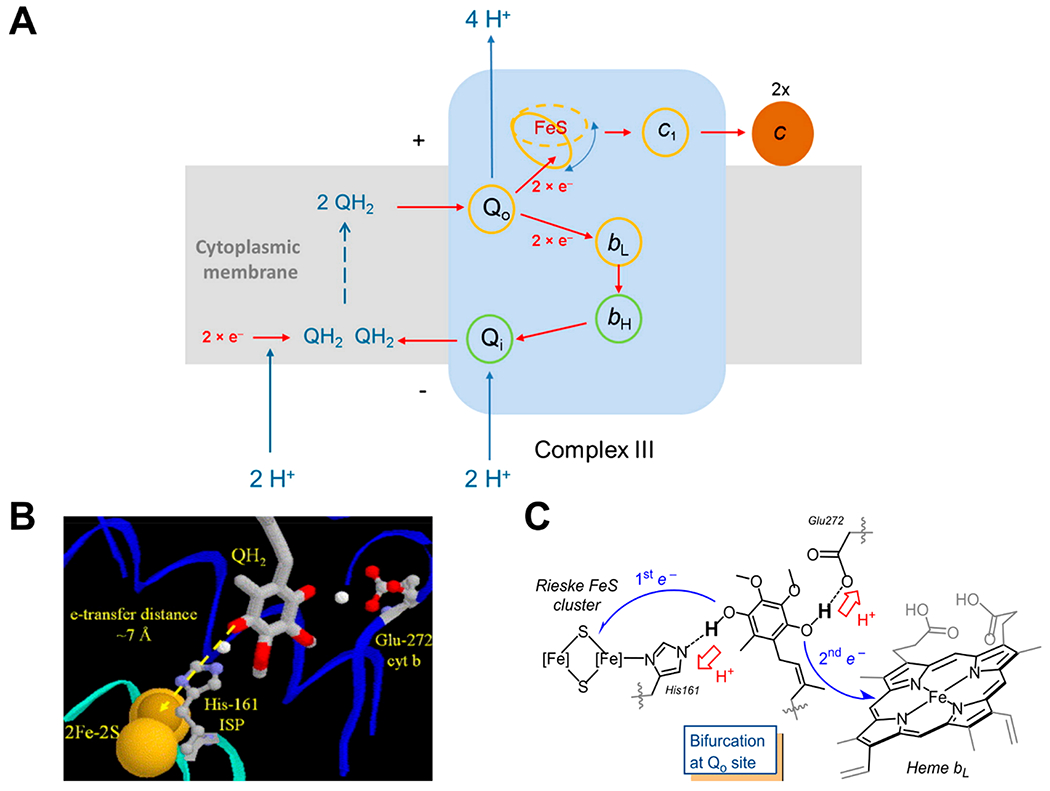
(A) Schematic of the Q-cycle in the mitochondrial bc1 complex (complex III). Qo is the bifurcation site, with the 1st e−/H+ pair moving to the FeS Rieske cluster and the 2nd redox equivalent reducing heme bL. Reprinted (adapted) with permission from ref 217. Copyright 2013 Elsevier. (B) Drawing of the active site of electron bifurcation in the Q cycle showing successive ET steps that are associated with proton transfers to nearby residues. (C) Image of the Fe2S2–His–QH2–Glu portion of a crystal structure with the QH2 modeled in, in place of an inhibitor. Reprinted with permission from ref 222. Copyright 2006 Elsevier.
In 2008, Buckel and Thauer greatly expanded the scope of EB by proposing that this process also occurs in anaerobic microorganisms, this time using flavins (another PCET reagent) as the bifurcating cofactor.215,217,223–225 Flavin-based EB was proposed to explain how, for example, methanogens generate highly reducing ferredoxins (E ≈ −500 mV) despite having access only to H2 as an electron donor (E = −414 mV at pH 7). Based on the crystal structure of a methanogenic flavin-containing EB enzyme complex, it was proposed that hydrogen-bonding interactions between a lysine residue and various redox states of the flavin cofactor modulate the reduction potential of the flavin semiquinone radical.226 Numerous questions remain about how this and other flavin-based EB enzyme complexes orchestrate two full cycles of EB per equivalent of reduced ferredoxin generated, as well as how the flavin cofactor is initially reduced.227,228 Another intriguing example of a possible EB system is that of the molybdoenzyme arsenite oxidase, which may use the 2e−/2H+ cycle between Mo(VI)-dioxo and Mo(IV)-oxo states as the active site of bifurcation.229
Ostensibly endergonic electron transfer in EB is thought to be enabled by the inversion of reduction potentials, a counterintuitive scenario in which reduction of a molecule by the first electron is more difficult than reduction by the second electron. Although it has been suggested that inverted reduction potentials may not be a strict requirement for EB cofactors,221 all known examples of biological EB take advantage of inversion. Potential inversion is rare for pure ET cofactors and typically requires a significant structural change.230 However, potential inversion is the norm for PCET reagents. For instance, while quinone dianion Q2− is a much stronger reductant than the monoanion Q•− (reduction potentials in the normal order), hydroquinone H2Q is a weaker reductant than semiquinone HQ• (inverted reduction potentials). Using BDFEs or E∘(vs H2) as measures of reducing power for this PCET reagent, HQ• has a 22 kcal mol−1 weaker O–H BDFE than H2Q(a difference of almost 1 V in E∘) ( Table 8). An extreme case of such inversion is the removal of two H atoms from ethane to make ethylene, which is discussed at the end of Section 3.6.1. In this case, the second C–H bond is 64 kcal mol−1 weaker than the first one (Table 19). In the context of EB, it seems reasonable that the larger the inversion, the larger the possible “bump up” in potential.
Table 8.
PCET Thermochemistry of Hydroquinones and Semiquinones in H2Oa
| HQ•/H2Qb | E∘(HQ•/−) | E∘(H2Q•+/0) | pKa(H2Q•+) | pKa(H2Q) | E∘(V vs H2) | BDFE | |
|---|---|---|---|---|---|---|---|
| 1,2-H2Q | 0.59 | – | – | 12309 | – | 1.30 | 82.8 |
| 1,4-H2Q | 0.36c | 1.1310 | −1.1311 | 9.85312 | – | 0.94 | 74.6 |
| 2-methyl-1,4-H2Q | 0.31c | – | – | 10.1312 | – | 0.91 | 73.8 |
| 2,3-dimethyl-1,4-H2Q | 0.28c | – | – | 10.4313 | – | 0.90 | 73.6 |
| 2,5-dimethyl-1,4-H2Q | 0.37c | – | – | 10.4313 | – | 0.98 | 75.6 |
| 2,3,5-trimethyl-1,4-H2Q | 0.20c | – | – | 10.8313 | – | 0.84 | 72.2 |
| tetramethyl-1,4-H2Q | 0.10c | – | – | 11.3313 | – | 0.77 | 70.6 |
| 2-methyl-1,4-H2NQ | – | – | – | – | – | 0.77 | 70.6 |
| 2,3-dimethyl-1,4-H2NQ | – | – | – | – | – | 0.67 | 68.1 |
| Q/HQ•b | E∘(Q•/−) | E∘(HQ•/−) | pKa(HQ•+) | pKa(HQ•) | pKa(HQ−) | E∘(V vs H2) | BDFE |
|
| |||||||
| 1,2-HQ• | 0.043 | – | – | 5314 | 0.34 | 60.6 | |
| 1,4-HQ• | 0.099315 | [0.76] | −7311 | 4.1316,317 | 11.4312 | 0.34 | 60.7 |
| 2-methyl-1,4-HQ• | 0.023315 | – | – | 4.5318 | 12d | 0.29 | 59.5 |
| 2,3-dimethyl-1,4-HQ• | −0.074315 | – | – | 4.7318 | 12.6313 | 0.20 | 57.5 |
| 2,5-dimethyl-1,4-HQ• | −0.067315 | – | – | 4.6318 | 12.5313 | 0.21 | 57.5 |
| 2,3,5-trimethyl-1,4-HQ• | −0.165315 | – | – | 5318 | 12.9313 | 0.13 | 55.8 |
| Tetramethyl-1,4-HQ• | −0.235319 | – | – | 5318 | 13.2313 | 0.06 | 54.2 |
| 2-methyl-1,4-HNQ• | −0.203319 | – | – | 4.4318 | – | 0.06 | 54.1 |
| 2,3-dimethyl-1,4-HNQ• | −0.240315 | – | – | 4.3318 | – | 0.01 | 53.1 |
Potentials for 1e− reductions are in V vs SHE. Values for E∘(V vs H2) are in V; – eE∘ is the average free energy for addition. Uncited values of E∘(V vs H2) were calculated from other values in the row using Scheme 2 oreq 18. BDFEs are in kcal mol−1 and were calculated from E∘(V vs H2) usingeq 18. Values in [square brackets] have been calculated from the other values in the row using Hess’ law.
H2Q = 1,4-dihydroxybenzene; H2NQ = 1,4-dihydroxynaphthalene; HQ = semiquinone; HNQ = seminaphthoquinone.
E∘(HQ•/−) derived from the E∘(V vs H2) of H2Q/Q (Table 7) and HQ•/Q.
A question that lies at the heart of any EB system like the Q cycle is what “gates” electron transfer, such that the second electron traverses the endergonic path rather than following the first electron down the exergonic path or short circuiting the cycle to form unwanted reactive radicals. Gating is thought to be accomplished by tightly regulating the concentrations, redox states, and binding of all of the cofactors involved. However, any discussion of PCET reactions must also consider the associated proton transfers. This begs the question, raised many years ago, whether PCET chemistry offers a key mechanism to gate EB.222,231 In the case of the Q cycle, it is believed that the initial hydroquinone forms a hydrogen bond with a nearby histidine,232 while the transient semiquinone radical can be deprotonated by a glutamate residue.231 Mutagenesis experiments have demonstrated the importance of this glutamate in determining the extent of EB short circuiting.233 PCET seems to play a critical role in EB in the Q cycle.
Based on this discussion, it seems likely to us that PCET and PCET cofactors will be found to be central to most biological EB. We believe that it is not a coincidence that the three classes of EB enzymes discussed above all involve PCET processes. Likely, nature requires PCET reagents to generate the potential inversion that enables EB. Biology also likely utilizes the proton transfer component of the PCET reactions as one of the mechanisms of gating, of directing redox flow to one pathway or another.
3.8. Materials Interfaces
An important emerging area in PCET thermochemistry is the measurement of hydrogen adsorption energies at solution/material interfaces. These may involve surface X–H bonds, intercalation of H into the bulk, and perhaps cases in between. For hydrogen on surfaces, the main topic of the discussion below, the free energy of adsorption is commonly defined as the free energy of or H• addition. These values are equivalent to E∘(V vs H2) and BDFE, respectively.
Hydrogen is ubiquitous in and on materials. Intercalation of H into metals is known to cause embrittlement and other changes in properties.234 Hydrogen (H+ + e−) is also an impurity in many semiconductor materials and is a common n-dopant in metal oxides.235–237 Pseudocapacitance, for instance with RuO2, is usually ascribed to surface and near-surface H adsorption.238–241 Transfers of hydrogen are central in many areas of heterogeneous catalysis and electrocatalysis, from hydrogenations of organic molecules to the hydrogen evolution reaction. Such processes are often analyzed using “scaling-relationship” and “volcano plot” approaches that frequently utilize the hydrogen adsorption free energy (equivalent to E∘(V vs H2)) as a thermochemical predictor.242–246 Given all of these applications, understanding the thermochemistry of H2 adsorption on materials is, and will be, an important topic.
The thermochemistry of gas-phase H2 addition to clean metal surfaces has been extensively examined by the surface science community. Studies using well-defined single crystals, epitaxially grown substrates, and nanoparticles under high-vacuum conditions have enabled measurements of surface–H bond enthalpies, with some measurements of free energies.247–249 The PCET thermochemistry of noble or less active metals can also be amenable to study in solution using electrochemical techniques (Section 3.8.1). For other materials, however, experimental measurements of hydrogen adsorption energies at solution interfaces have largely been inaccessible. Instead, these materials have been examined primarily by computations, usually assuming ideal stoichiometries and crystalline structures.243,244,246,250,251
This section shows how the thermochemical approaches developed in Section 2 can be adapted to measure PCET energies for material interfaces. An excellent introduction to these connections was recently presented by Jackson and co-workers in Figure 14, as part of their studies of well-defined active sites on graphitic carbon electrodes (Section 3.8.3 and Figure 14B).252 The close relationship between BDFEs and E∘(V vs H2) emphasized above (eq 18) provides a close connection between the molecular picture (Figure 14A) and interfacial electrochemistry such as proton and electron addition to platinum (Figure 14C). The selected experimental studies described below illustrate these analogies, and they reveal important differences between the PCET thermochemistry of molecular systems and that of material interfaces.
Figure 14.
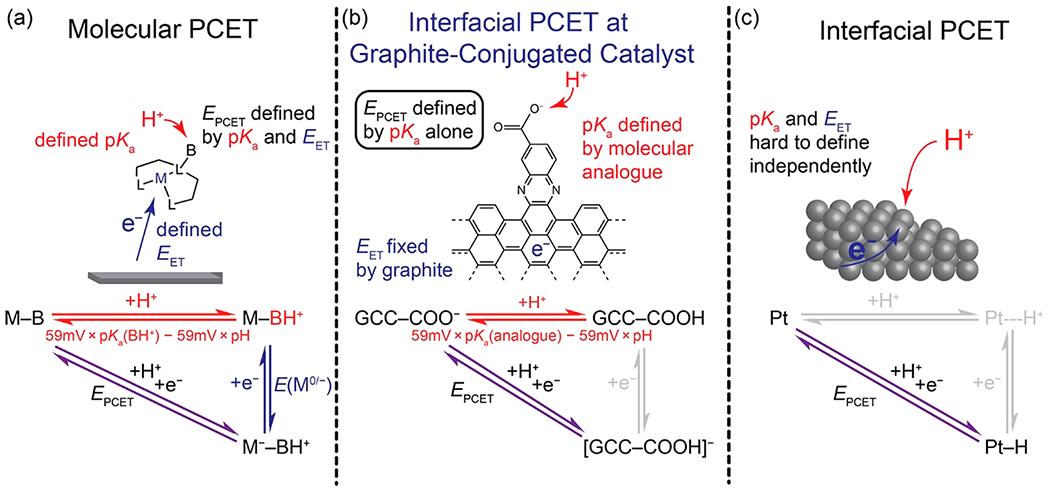
Partial square scheme representations of PCET thermochemistry for (a) a metal complex, (b) a graphite-conjugated catalyst (GCC) with a pendent carboxylate, and (c) a platinum electrode. Reprinted with permission from ref 252. Copyright 2019 American Chemical Society.
3.8.1. Volmer Reaction.
The electrosorption of a proton to a surface is known as the Volmer reaction (Figure 14C).253 This phenomenon has been well-studied on platinum surfaces and, in particular, the flat and symmetric (111) facet. Pt(111) single-crystal surfaces in contact with noninteracting aqueous electrolytes show characteristic cyclic voltammograms between the onsets of hydrogen and oxygen evolution catalysis (Figure 15).254 The reversible Faradaic feature at more positive potentials corresponds to the formation of “underpotential deposited hydrogen” (Hupd), so-called because this deposition occurs at potentials “under” (less reducing than) that needed to produce H2 (RHE). Full coverage of Hupd on Pt(111) is commonly taken to be close to one H for every surface Pt atom.255–257 These Hupd sites are distinct in both free energy and structure from the “overpotential deposited hydrogen” atoms that are active for the hydrogen evolution reaction.258 The electrochemical response for Hupd on Pt(111) moves ~59 mV per unit pH change, exactly as expected for a molecular ne−/nH+ PCET reaction. This ~59 mV, or Nernstian, shift is important because it means that the potentials to deposit Hupd are constant versus RHE (eqs 19, 20), and they can be extrapolated to give E∘ (V vs H2) at the standard state.
Figure 15.
Cyclic voltammetry of a Pt(111) electrode at different solution pH’s (scan rate: 50 mV s−1). The wave for UPD hydrogen is the shape at the left in each CV, with the pH inscribed inside. Reprinted with permission from ref 254. Copyright 2015 Elsevier.
The E∘(V vs H2) for the Volmer reaction can be converted to an average BDFE, or hydrogen adsorption free energy, using eq 18. Analyses of hydrogen electrosorption have previously explored the magnitude and distribution of surface adsorption free energies for polycrystalline and single-crystal noble metal electrodes.259–263 For Pt(111), the midpoint of the Hupd wave of ~0.1 V vs RHE in aqueous media corresponds to an average BDFE of 55 ± 2 kcal mol−1. This value is slightly larger than the free energy to form H• in water from H2 gas (Table 1)—as it must be because it is underpotential is deposited. We will return to these data in Section 3.8.4, to analyze the width of the Hupd wave.
3.8.2. Pourbaix Diagrams for Metal Oxide Materials.
The thermochemistry of bulk metal oxides and hydroxides has long been studied because of the importance of these materials and minerals. From our PCET perspective, a landmark in these studies is the Atlas of Electrochemical Equilibria in Aqueous Solutions by Marcel Pourbaix, first published in 1963.265 His diagrams, such as Figure 16 here and Figure 6 above, have proven to be a very valuable way to summarize a lot of thermochemical information. While Pourbaix’s career was primarily in corrosion science, the motivation for his original diagram (1938) was catalysis.266 The diagrams, known as pE/pH plots,267 are now used in many fields including aqueous coordination chemistry and geochemistry, and they have been conceptually extended to nonaqueous solvents.103
Figure 16.
One of the Pourbaix (E/pH) diagrams for copper. Reproduced from the Atlas of Electrochemical Equilibria in Aqueous Solutions by Marcel Pourbaix,102 with permission of the National Association of Corrosion Engineers.
Pourbaix diagrams are preponderance diagrams, essentially a map of the most thermodynamically stable (preponderant) species in each E/pH region. One of the diagrams for copper from the Atlas is shown in Figure 16 (some Pourbaix diagrams have been updated since 1963, so readers should check the current literature). The four most important species are copper metal (Cu, at the bottom, the most stable copper species under reducing conditions), solid Cu2O in the middle, and the top portion of the diagram divided between aqueous Cu2+ (in acidic, low pH conditions at the left) and solid Cu(OH)2 in the upper middle. [A separate but quite similar diagram in the Atlas involves CuO instead of Cu(OH)2; for this discussion we ignore the soluble CuII species at high pH and the soluble Cu+.] Each of the solid lines divides regions where different materials predominate. Lines (7) and (9) in the center of the diagram, for instance, separate Cu, Cu2O, and Cu(OH)2, according to eqs 27 and 28. The slopes of these lines is −59 mV/pH, following the Nernst equation for these equations and the equal numbers of protons and electrons. These diagrams show pH-independent processes as horizontal lines and nonredox protonation equilibria as vertical lines. Thus, these diagrams capture the full PCET thermochemistry of stable species as a function of pH and potential, including both materials and soluble species.
| (27) |
| (28) |
The encyclopedic detail of Pourbaix diagrams for bulk metal oxides has, so far, not been achievable for thin-film and nanoscale versions of the same minerals where material structures and stoichiometries are less well-defined. Nevertheless, electrochemical measurements of 1e−/1H+ couples for semiconducting and conducting metal oxide (nano)materials, similar to those shown in eqs 27 and 28, have been an important method for understanding their PCET thermochemistry.
Nickel oxide is a widely used p-type semiconductor. Aqueous voltammetry of calcined NiO thin films typically shows one or two well-defined Faradaic waves that have a Nernstian shift with pH (Figure 17A).268,269 These waves are usually interpreted as the PCET oxidations of Ni(OH)2, a hydrated form of nickel oxide at the surface (eqs 29 and 30; characterization of the “NiIV” material is a matter of some debate). Similar to Hupd on Pt(111), extrapolating the E1/2 values of the CV waves to pH = 0 in Figure 17A should give good estimates of the E∘(V vs H2) and related BDFE values for these two processes. To test this analogy, electrodes were charged to the NiIII(O)(OH) and NiII(OH)2 forms and separately reacted with substoichiometric amounts of either 2,4,6-tBu3PhOH or its corresponding phenoxyl radical (Scheme 9).264 Reactions did not go to completion in either case, suggesting the formation of an equilibrium state. The BDFE of 2,4,6-tBu3PhOH is 75.5 kcal mol−1, very close to that determined electrochemically for NiII(OH)2, thereby confirming that E∘(V vs H2) and the related BDFE can be determined for metal oxide materials that show Faradaic waves with Nernstian pH shifts.264
| (29) |
| (30) |
Figure 17.
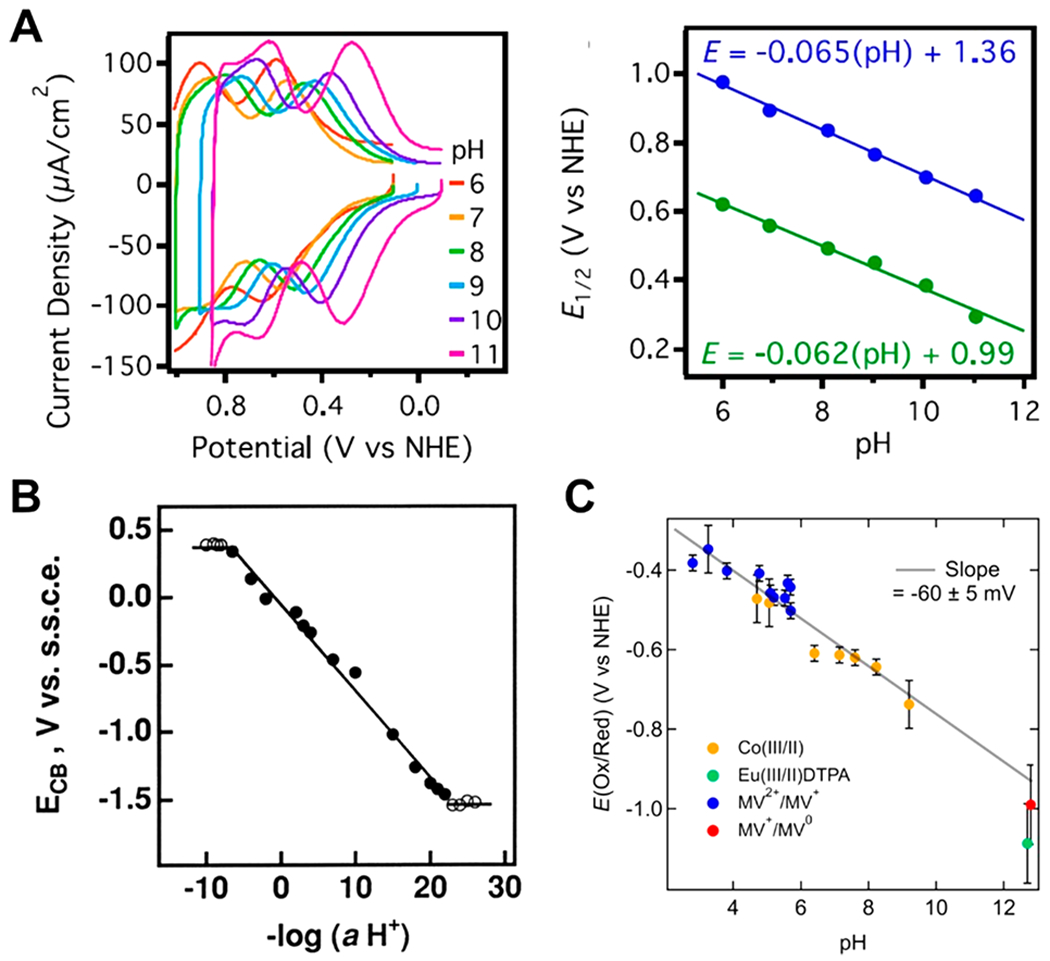
(A) NiO on FTO CVs of NiO|FTO collected in aqueous buffers and plot of E1/2 vs pH for both redox features, showing Nernstian dependences. Reprinted with permission from ref 264. Copyright 2019 American Chemical Society. (B)Dependence of reduction potential on log proton activity for a TiO2 film, with a slope of 64mV/log(aH+). Reprinted with permission from ref 275. Copyright 1999 American Chemical Society. (C) Reduction potentials of citrate-capped aqueous colloidal TiO2 nanoparticles determined by titration with various solution ET reagents.278 Reprinted with permission. Copyright 2019 Dr. Jennifer L. Peper.
Scheme 9.
(A) Electrochemical Interconversion of NiIIIOOH to NiII(OH)2 and (B) Reversible PCET between a Phenol/Phenoxyl Radical and NiIIIOOH/NiII(OH)2264
Many other materials show Nernstian shifts of their potentials with pH.270–274 One remarkable example is the demonstration by Lyon and Hupp that the conduction band of TiO2 films shifts 64 mV per factor of 10 in solution proton activity, over a range of more than 1025 (Figure 17B).275 Hupp et al. concluded that, for TiO2, SnO2, and ZnO, proton uptake accompanied electron addition to the material; in other words, these were PCET processes.275,276 A similar ~60 mV shift per pH unit was observed for equilibration of colloidal TiO2 nanoparticles with solution redox reagents,277,278 which can be extrapolated to an E∘(V vs H2) of −0.16 ± 0.03 V (Figure 17C),278 close to Lyons and Hupp’s value for TiO2 films. By analogy with the molecular thermochemistry in Section 2 and the NiO electrode study above, it seems likely that these E∘(V vs H2) potentials are best assigned 1e−/1H+ processes with a TiO–H BDFE of 49 kcal mol−1.278
Overall, many materials at aqueous interfaces show a roughly 59 mV/pH unit dependence of their electrochemical response, including metals, oxides, chalcogenides, and pnictides, at least in some forms and solution conditions.279 In the context of this review, we suggest that all of these measurements can be used to determine E∘(V vs H2) and surface–H BDFE values.
3.8.3. Square Scheme Approach.
The square scheme is a key tool for defining the PCET thermochemistry of molecules. This scheme describes the relationship between the proton and electron transfer free energies and that of the overall net hydrogen transfer reaction (Scheme 1). For molecules, the thermochemistry of the ET and PT steps can be simpler to measure than that of the overall reaction. However, in electrochemical measurements of many material interfaces, this paradigm is flipped due to strongly coupled ET and the difficulty of structurally characterizing surface acid/base sites. Seminal work by White and co-workers utilized self-assembled monolayers on noble metal electrodes to create well-defined carboxylic acid sites. The deprotonation of these sites could be driven by the potentiostat and used to measure the pK1/2 of these sites.280 More recently, Jackson and co-workers have extended this concept to well-defined active sites on graphitic carbon electrodes and defined a partial square scheme (Figure 18).252
Figure 18.
(a) Pourbaix diagram showing the pH dependence of interfacial proton-coupled electron-transfer (PCET) waves for GCC-phenazine (red), GCC-phen-NH2 (purple), GCC-phen-COOH (dark green; structure shown in (b)), GCC-phen-m-OH (olive green), and GCC-phen-o-OH (blue). The dotted line shows the computed potential of zero free charge (EPZFC). (b) Partial square scheme for interfacial PCET at GCC-phen-COOH, as an example reaction. The model reported partitions the potential for PCET (diagonal leg) into a horizontal leg, defined as the difference between the 0-field pKa of the surface site and the pH of the solution, and a vertical leg, defined as the EPZFC, of the electrode. Reprinted with permission from ref 252. Copyright 2019 American Chemical Society.
The molecularly well-defined active sites, formed using conjugated aromatic pyrazine linkages with varying acid/base sites, were examined electrochemically as a function of pH (Figure 18A).252 All of these graphite-conjugated catalysts (GCCs) exhibit a clear wave in their CVs and a Nernstian shift with pH. Based on these data and previous studies, the Faradaic features were ascribed to protonation/deprotonation of the acid/base group on the pyrazine linkage coupled to electron transfer from the external circuit, and E∘(V vs H2) and BDFE values were determined. This is perhaps surprising because conductive electrodes typically do not show such well-defined waves and because protonation of a carboxylate is not normally considered as coupled to electron transfer. We encourage interested readers to read the original papers which discuss the unique features of these systems.252,281,282
The CV waves of these GCCs surprisingly also show a Nernstian shift with the pKa of the solution-phase pyrazine analogue.252 These data revealed that the free energy for PT in the overall PCET step is well described by the pKa of the surface acid/base group (the carboxylic acid/carboxylate in Figure 18B). With the free energies for the overall PCET reaction and proton transfer component in hand, the free energy for electron transfer could also be calculated. Jackson et al. suggested that this ET free energy is defined by the potential of zero free charge (EPZFC) and can be used to complete a square scheme analogous to those described molecules (Figure 18B). The EPZFC is traditionally connected to the work function of a material and is generally considered to be extremely sensitive to surface structure.283 The possibility of connections between work functions, PCET at materials, and square schemes for molecules is exciting, and we look forward to future studies.
3.8.4. Surface Coverage, Heterogeneity, Adsorbate Interactions, and Isotherms.
While the above sections have developed many analogies between the PCET thermochemistry of interfaces and molecular systems, there are a number of key differences. Among the most significant are the contributions of surface heterogeneity and adsorbate interactions. In a molecular system, every molecule of a particular compound is by definition the same, with the same BDFE. However, surfaces essentially always have a distribution of sites and BDFEs. This is due to steps, edges, and other irregularities on a clean surface and to the presence of impurity atoms or nonstoichiometry at the surface, in other words intrinsic and extrinsic defects. Even a perfectly well-ordered, clean surface has a range of BDFEs because the adsorbates interact with each other. For example, the first Hupd atoms deposit on a clean Pt(111) surface at ca. +0.25 V vs RHE (Section 3.8.1), and they continue to deposit as the potential scans lower to values negative of RHE.256,257 A normal Faradaic feature in the CV should be roughly Gaussian with a full-width half-maximum of 90.6 mV.284,285 The >250 mV range of potentials to form a monolayer of Hupd is, therefore, indicative of interactions between surface–H species.
Our group recently explored the relationship between BDFE and surface coverage for colloidal cerium oxide nanoparticles (OLE-Ce).286 These nanoparticles were capped with oleate ligands and studied mostly in THF solution. Cerium oxide is a mixed-valence Ce4+/Ce3+ oxide. When a hydrogen atom is added, one Ce4+ is reduced to Ce3+, and one oxide is protonated to form a surface hydroxide (analogous to NiIIIOOH + H• → NiII(OH)2, Scheme 9 above). The reverse reaction defines the BDFE to remove H• from the material (Figure 19A).
Figure 19.
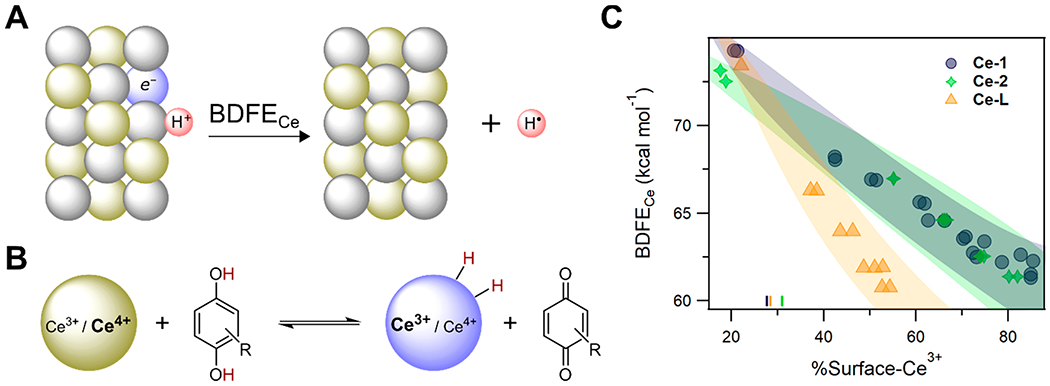
(A) Schematic of the chemical process defines the ceria–H BDFE; Ce4+: gold; Ce3+: purple; O2−: gray; H: red. (B) Equilibrium reaction of colloidal, oleate-ligated cerium oxide nanocrystals with hydroquinones and quinones. (C) Variation of CeO–H BDFEs with the % Ce3+ in the surface regions for three batches of nanocrystals, Ce-1, Ce-2, and Ce-L, with average diameters of 1.8 ± 0.2 nm, 1.9 ± 0.3 nm, and 4.0 ± 0.4 nm, respectively. Reprinted with permission from ref 286. Copyright 2021 American Chemical Society.
BDFEs of OLE-Ce were measured by equilibrating the nanoparticles with hydroquinones and quinones. Organic substrates were found to reduce surface O or oxidize surface O–H groups on OLE-Ce. Monitoring reactions by both 1H NMR (organic products) and X-ray absorption (Ce3+/Ce4+ ratio) spectroscopies demonstrated that OLE-Ce reached equilibrium states with multiple PCET reagents (Figure 19B). At equilibrium, the hydrogen atom affinities of OLE-Ce and the PCET reagent are equal, and the average redox state of OLE-Ce (% Ce3+) is stable. As a result, each equilibrium state provides a direct measure of the average surface O–H BDFE of OLE-Ce (BDFECe) at the equilibrium % Ce3+. Remarkably, BDFECe for the same batch of OLE-Ce varied by 13 kcal mol−1 (0.56 eV), depending on the % Ce3+ (Figure 19C). The magnitude of this effect is consistent across different sizes of OLE-Ce, suggesting that it is general to cerium oxide surfaces.
The range of BDFEs for OLE-Ce contrasts with the PCET thermochemistry of molecular reagents. When every molecule is the same, the thermochemical ability of an ensemble of molecules to donate H• depends only on the ratio of oxidized and reduced species, according to a modified version of the Nernst equation (eq 31). This is analogous to the acidity of a buffer solution varying with the ratio of the components. Application of eq 31 to OLE-Ce would predict a range in BDFEs of only 0.6 kcal mol−1 for the observed change in % Ce3+, one twentieth of the 13 kcal mol−1 range observed. A breakdown in this molecular analogy is not surprising, as the surface structure of OLE-Ce is not well-defined with ligands and multiple bonding environments between cerium and oxygen.
| (31) |
In the limiting case of identical surface sites and no significant interaction between the surface H’s, the free energy of binding will follow a Langmuir isotherm,253 which simply reflects Le Chatelier’s principle or the law of mass action. This isotherm is effectively equivalent to the Nernst equation (eq 31), and BDFECe∘ is defined at θ = 0.5 (eq 32). Since the Langmuir isotherm does not describe the very large range of BDFEs for OLE-Ce, a different “ΔG∘” was defined for each colloid particle sample, depending on its % Ce3+. These data could also be fit by adding a linear correction term, Cθ, to eq 32 (eq 33). This relationship is called a Frumkin isotherm, and it provides a first-order correction to interactions between surface adsorbates and/or surface heterogeneity which cause deviations from Langmuirian behavior.
| (32) |
| (33) |
The isotherm formalism has also been used to analyze the width of the CV for UPD hydrogen on platinum surfaces, such as the ~250 mV UPD peak for Pt(111) (Figure 15).262,263 As discussed above, this is broader than that predicted for a Nernstian adsorption following a Langmuir isotherm: full-width half-maximum = 90.6 mV.284,285 The difference between the observed and ideal widths suggests a spread of ca. 4 kcal mol−1 (170 meV) in the Pt–H BDFEs through the UPD wave (or a Frumkin correction of that magnitude).
We hope that this section shows the power and the complexities of applying molecular PCET thermochemical approaches to the study of materials and solution/solid interfaces. As with molecules, the PCET thermochemistry of materials is a key property and predictive of reactivity. Furthermore, the descriptions and effective equivalence of the potential of hydrogenation and BDFE, derived in Section 2, are similarly applicable to materials and enable comparisons between electrochemical and thermochemical perspectives (1 eV = 23.06 kcal mol−1; 1 kcal mol−1 = 43.36 meV). Unlike molecules, however, materials have complex surfaces that present a multitude of sites, either identical or different. We speculate, based on a few examples, that this multiplicity will often lead to a range of PCET thermochemistry for a single material surface. Such a range of thermochemistry may prove to be fundamental to the catalytic and other properties of the interface.286
3.9. Summary of Insights and Emerging Areas
Building on the thermochemical framework developed in Section 2, Sections 3.1–3.4 discuss several insights which can be derived from mining data in the tables (Section 4.2). These insights about PCET reagents are then shown to be critical to understand a wide range of PCET topics: kinetics, N2 reduction, biological PCET, and PCET at materials (Sections 3.5–3.8). Connections across these different fields are broadly enabled by the ability to measure the free energies of H binding electrochemically or chemically and the essential equivalence of E∘(V vs H2) and BDFEs. The interdisciplinary nature of this discussion emphasizes the critical importance and centrality of PCET thermochemistry to research across a range of fields.
4. GUIDE TO THE THERMOCHEMICAL TABLES
In Tables 5–24, thermochemical values are presented for numerous classes of PCET reagents including biologically relevant phenols and nicotinamides, transition metal complexes, and ne−/nH+ processes for quinones and small molecules such as N2, O2, and CO2 (Table 4). The importance of these reagent classes to the PCET field is largely discussed in our previous review.3 Although those values have been systematically adjusted to account for previous errors in our derivation of thermochemical constants, the discussion sections in that review remain relevant.3 In the decade since that review was prepared, there have been many improvements in the standard of measurement methods and in the range of data for PCET thermochemistry, as interest in the topic has grown. In light of these advances, values from our previous review which used approximations, such as peak potentials from irreversible electrochemical couples, are generally not recalculated here, in order to maintain a higher standard of data. Nevertheless, we acknowledge that in some cases better methods still do not exist, such as for the measurement of C–H bonds (Table 19) and N–H bonds in aliphatic compounds (Table 14). In those cases, we include values that do not meet the general standard with associated footnotes to alert the reader. Over the past decade, the field of PCET has also begun to focus more strongly on answering fundamental questions related to the development of clean energy technologies. In response to this interest, we have added tables on the PCET thermochemistry of O2, N2, and CO2 reduction. All values reported in the tables were determined by experiment.
Table 5.
PCET Thermochemistry of Hydroxylaminesa
| compound (ROH)b | solvent | E∘(RO•/−) | E∘(ROH•+/0) | pKa(ROH•+) | pKa(ROH) | E∘(V vs H2) | BDFE |
|---|---|---|---|---|---|---|---|
| H2NOH | H2O | 0.09290 | 1.3290 | [−6.7] | 13.7291 | 0.90 | 73.6 |
| TEMPOH | MeCN | [−1.85] | -- | -- | 41c | 0.6019 | 6619,33 |
| TEMPOH | THF | -- | -- | -- | -- | 0.5819 | 65.519 |
| TEMPOH | C6H6 | -- | -- | -- | -- | 0.508 | 63.833,g |
| TEMPOH | hexane | -- | -- | -- | -- | 0.508 | 63.4292,g |
| 4-oxo-TEMPOH | hexane | -- | -- | -- | -- | 0.412 | 61.2292,g |
| 4-oxo-TEMPOH | hexane | -- | -- | -- | -- | 0.542 | 64.2h |
| 4-oxo-TEMPOH | CCl4 | -- | -- | -- | -- | 0.594 | 65.6293,g |
| 4-oxo-TEMPOH | MeCN | -- | -- | -- | -- | 0.648 | 66.9294 |
| 4-MeO-TEMPOH | MeCN | -- | -- | -- | -- | 0.622 | 66.3294 |
| 4-OH-TEMPOH | hexane | -- | -- | -- | -- | 0.577 | 65.0292,g |
| 4-NH2-TEMPOH | hexane | -- | -- | -- | -- | 0.564 | 64.7292,g |
| 4-Cl-TEMPOH | hexane | -- | -- | -- | -- | 0.573 | 64.9292,g |
| tBu2NOH | MeCN | [−1.8]c | -- | -- | 39295,d | 0.551 | 64.7294 |
| NHPI | H2O | 1.2296 | -- | -- | 6.3297 | 1.6 | 89 |
| NHPI | MeCN | 0.30e | -- | -- | 22.9297,d | 1.69 | 90.9 |
| 4-AcO-NHPI | MeCN | -- | -- | -- | -- | 1.359 | 83.3f |
| 3-F-NHPI | MeCN | -- | -- | -- | -- | 1.346 | 83.0f |
| 4-Me-NHPI | MeCN | -- | -- | -- | -- | 1.328 | 82.6f |
| 4-MeO-NHPI | MeCN | -- | -- | -- | -- | 1.289 | 81.7f |
| 3-MeO-NHPI | MeCN | -- | -- | -- | -- | 1.315 | 82.3f |
| 3,6-(MeO)2-NHPI | MeCN | -- | -- | -- | -- | 1.281 | 81.5f |
Potentials for 1e− reductions are in V vs SHE if in aqueous solution and V vs Cp2Fe+/0 if they are in organic solution. Values for E∘(V vs H2) are in V; −eE∘ is the average free energy for addition. Uncited values of E∘(V vs H2) were calculated from other values in the row using Scheme 2 or eq 18. BDFEs are in kcal mol−1 and if uncited were calculated from E∘(V vs H2) using eq 18. Values in [square brackets] have been calculated from the other values in the row using Hess’ law.
TEMPOH = 1-hydroxy-2,2,6,6-tetramethyl-piperidine, NHPI = N-hydroxyphthalimide.
Estimated in ref 33.
Extrapolated from DMSO to MeCN using the method of Kütt and co-workers for OH acids.298
Determined at −10 °C in MeCN with respect to NHPI in ref 301. Modified relative to our value for BDFEMeCN(NHPI).
BDFE values calculated from the cited BDE.
This value was measured by our laboratory through equilibration with TEMPO• (see SI). We recommend this value (vs the prior report) because the equilibration method is a more sensitive measure of the relative BDFE (and E∘(V vs H2)). Furthermore, we discuss in Section 3.1.1 the evidence that this BDFE should change very little with solvent identity.
Table 24.
PCET thermochemistry of 4d/5d-based transition metal systems.a
| compound (ML–H) | solvent | E∘(Mn–L)0/− | E∘(Mn–LH)+/0 | pKa(Mn+1LH) | pKa(Mn–LH) | E∘(V vs H2) | BDFE |
|---|---|---|---|---|---|---|---|
| [(bpy)2pyRuIIOH2]2+ | H2O | 0.4695 | 1.0295 | 0.8595 | 10.395 | 1.07 | 77.5 |
| trans-[RuIV(tmc)(O)(OH2)]2+b | H2O | 0.80416 | -- | -- | 4.7416 | 1.08 | 77.7 |
| trans-[RuV(tmc)(O)(OH)]2+b | H2O | 0.56416 | [>0.67] | <1.0416 | 2.8416 | 0.73 | 69.5 |
| [[(bpy)2pyRuIIIOH]2+ | H2O | <0.48100 | >1.6100 | <0.0100 | >13.0100 | 1.15 | 79.3 |
| (Me6cyclam)Rh(HO)(OOH)2+c | H2O | -- | -- | -- | -- | 0.950 | 74.7389 |
| (Me6cyclam)Rh(H2O)(OOH)2+c | H2O | -- | -- | -- | -- | 0.970 | 75.2389 |
| (dipic)RuII(tpyCO2H)d | MeCN | 0.047417 | -- | -- | 18.5417 | 1.170 | 79.0 |
| (dipic)RuII(tpyPhCO2H)d | MeCN | 0.1787 | -- | -- | 20.587 | 1.41 | 84.6 |
| (acac)2RuII(pyImH)e | MeCN | −1.0082 | −0.6482 | 16.082 | [22.1] | 0.34 | 59.7 |
| (hfacac)2RuII(pyImH)e | MeCN | –0.0782 | 0.2982 | [13.2] | 19.382 | 1.10 | 77.4 |
| [RuII(dmdmp)Cl(MeBPA)]f | MeCN | −0.16418 | 0.14418 | [11.4] | 16.4418 | 0.84 | 71.3 |
| [RuII(dmdmp)(TPA)]+f | MeCN | 0.26419 | 0.52419 | [9.9] | 14.3419 | 1.14 | 78.2 |
| TpOsIII(NH2Ph)Cl2g | MeCN | −1.05420 | 0.48420 | [−3.3]420 | 22.5420 | 0.31 | 59.1 |
| [SNS]Pd(PPh3)h | MeCN | −0.58408 | -- | -- | 17.4408 | 0.48 | 63.0 |
| [SNS]Pt(PPh3)h | MeCN | –0.51408 | -- | -- | 22.2408 | 0.83 | 71.2 |
| TpMo(CO)3Hg | MeCN | –0.521421 | -- | -- | 10.7421 | 0.140 | 55.2 |
| Tp′Mo(CO)3Hi | MeCN | −0.59422 | -- | -- | 10.2422 | 0.04 | 53.0 |
| TpW(CO)3Hg | MeCN | −0.582421 | -- | -- | 14.4421 | 0.298 | 58.9 |
| (Phtpy)(PPh2Me)2MoNH3j | THF | −1.09195 | -- | -- | 3.6195 | −0.53 | 39.7 |
| (Phtpy)(PPh2Me)2MoCH2CH3j | THF | −1.35423 | -- | -- | 16.3423 | −0.04 | 51.0 |
| (teriPrP2)Mo2PHk | THF | −0.52424 | -- | -- | 3.6423 | 0.04 | 52.8 |
Potentials for 1e− reductions are in V vs SHE if in aqueous solution and V vs Cp2Fe+/0 if they are in organic solution. Values for E∘(V vs H2) are in V; – eE∘ is the average free energy for addition. Uncited values of E∘(V vs H2) were calculated from other values in the row using Scheme 2 or eq 18. BDFEs are in kcal mol−1 and if uncited were calculated from E∘(V vs H2) using eq 18. Values in [square brackets] have been calculated from the other values in the row using Hess′ law.
tmc = 1,4,8,11-tetramethyl-1,4,8,11-tetraazacyclotetradecane.
Me6cyclam = Me6cyclam = meso-hexamethylcyclam.
dipic = dipicolinic acid; tpyCO2H = 2,2′:6,2″-terpyridine-4’-carboxylic acid; tpyPhCO2H = 2,2′:6,2″-terpyridine-4′-benzoic acid.
acac = acetylacetonate; hfac = 1,1,1,5,5,5-hexafluoroacetylacetonate; pyimH = 2-(1H-imidazol-2-yl)pyridine.
dmdmp = N,N-dimethyl-6,7-dimethylpterin; TPA = tris(2-pyridylmethyl)amine; MeBPA = N-methyl-N,N-bis(pyridylmethyl)amine.
Tp = hydrotris(1-pyrazolyl)borate.
[SNS]H3 = bis(2-mercapto-p-tolyl)amine.
Tp′ = hydrotris(3,5-dimethylpyrazolyl)borate.
Phtpy = 4′-phenyl-2,2′:6,2″-terpyridine.
teriPrP2 = 1,4-bis(2-(diisopropylphosphino)phenyl)benzene.
Table 4.
Table of Thermochemical Tables
| table link | description | table link | description |
|---|---|---|---|
| Table 5 | hydroxylamines | Table 15 | arylamines and arylhydrazines |
| Table 6 | phenols | Table 16 | indoles and tryptophan |
| Table 7 | hydroquinones – overall | Table 17 | nucleosides |
| Table 8 | hydroquinones – separated | Table 18 | thiols |
| Table 9 | ascorbates | Table 19 | C–H bonds |
| Table 10 | water and alcohols | Table 20 | nicotinamides |
| Table 11 | oxygen reduction | Table 21 | carbon dioxide reduction |
| Table 12 | organic hydroperoxides | Table 22 | separated PCET pairs |
| Table 13 | nitrogen reduction | Table 23 | 3d transition metal complexes |
The Tables for each reagent class include both the E∘(V vs H2) and BDFE values, which are related via ΔG∘f(H•(solv)) (eq 18). In most cases, these values are derived by combining values from Table 1 with measurements of BDEs (eq 9), or combinations of pKa values and one-electron reduction potentials (often measured as E1/2 of reversible waves and taken as E∘ values) (Scheme 2 and eq 10). Individual E∘ and pKa values are provided in the Tables below when used to derive the overall free energy of the process. For all 1e− reduction potentials originally reported versus SCE, we use known conversions to switch the reference to Cp2Fe+/0.287,288 References are provided when values are derived from BDEs. For multivalent reagents or reactions, – FE∘ (V vs H2) and BDFE give the average free energy of the processes per or H atom transferred. In all cases, values in the Tables are presented with an associated literature reference or a footnote explaining their origin. Values presented in square brackets were calculated from other values in the same row of the Table using Hess’s law. The phase or solvent of the species in each row is denoted by the column labeled “solvent”, with the exceptions of gases and when otherwise specified in the stated reaction. H2 and other gases (O2, N2, CO2, CO, etc.) are always considered to be in the gas-phase at the 1 atm, 298 K standard state. The details of these standard states are emphasized here because that information is key to properly understanding the values below. We strongly urge all authors reporting thermochemical values to clearly report the standard states for all reagents in the reactions they examine.
Several calculations applied in the Tables warrant additional comment. In particular, we report the unusual calculation of gas-phase values for E∘(V vs H2). Although there is, of course, no electrochemical potential in the gas-phase, this value is still thermochemically robust since E∘(V vs H2) just describes the average free energy for the addition of H2, eq 5. As a result, the conversion between BDFE and E∘(V vs H2) described in eq 18 simply changes the overall reaction from the transfer of H• to that of H2. Application of this method is powerful, as it allows for a direct comparison E∘(V vs H2) values measured in the gas- and solution-phase. Such comparisons are discussed in Section 3.1.1.
For multivalent PCET processes, such as the 2e−/2H+ oxidation of hydroquinones to quinones in Table 7, the BDFEavg values are the average of the distinct BDFEs. For organic reagents, the first BDFE in XH2 is almost always stronger and describes the free energy to form HX• + H•, e.g., the semiquinone HQ• (reference289 reports a very rare exception). Conversion of HX• to the stable X product (semiquinone to quinone) is generally more favorable and therefore has a lower BDFE, Table 8. This is an inversion w 1e−/1H+ oxidation (or reduction) is easier than the first (see Section 3.7.2 above). .
Table 7.
PCET Thermochemistry of Hydroquinones to Quinonesa
| hydroquinoneb | solvent | E∘(V vs H2) | BDFEavg | hydroquinoneb | solvent | E∘(V vs H2) | BDFEavg |
|---|---|---|---|---|---|---|---|
| 1,2-H2Q | H2O | 0.820308 | 71.7 | 2,6-dimethyl-1,4-H2Q | IPA | 0.56619 | 65.1c |
| tetrachloro-1,2-H2Q | H2O | 0.83361 | 72.0 | 2,3,5-trimethyl-1,4-H2Q | H2O | 0.48761 | 64.0 |
| 4-tBu-1,2-H2Q | H2O | 0.69461 | 68.8 | tetramethyl-1,4-H2Q | H2O | 0.41661 | 62.4 |
| 3,5-tBu2-1,2-H2Q | H2O | 0.58061 | 66.2 | 2-methyl-5-isopropyl-1,4-H2Q | H2O | 0.589308 | 66.4 |
| 1,4-H2Q | H2O | 0.64361 | 67.6 | 2,5-dimethyl-3-chloro-1,4-H2Q | H2O | 0.595308 | 66.5 |
| 1,4-H2Q | MeCN | 0.66419 | 67.3 | 2-tBu-1,4-H2Q | H2O | 0.57961 | 66.2 |
| 1,4-H2Q | THF | 0.6619 | 67.2 | 2,6-tBu2–1,4-H2Q | MeCN | 0.47519 | 62.9 |
| tetrafluoro-1,4-H2Q | H2O | 0.70661 | 69.1 | 2-phenyl-1,4-H2Q | H2O | 0.63461 | 67.4 |
| 2-chloro-1,4-H2Q | H2O | 0.67661 | 68.4 | 2-methoxy-1,4-H2Q | H2O | 0.57061 | 65.9 |
| 2,6-dichloro-1,4-H2Q | H2O | 0.721308 | 69.4 | 2,5-dimethoxy-1,4-H2Q | H2O | 0.590308 | 66.4 |
| 2,5-dichloro-1,4-H2Q | H2O | 0.69961 | 68.9 | 2,6-dimethoxy-1,4-H2Q | H2O | 0.47361 | 63.7 |
| 2,3-dichloro-1,4-H2Q | H2O | 0.706308 | 69.1 | 2,6-dimethoxy-1,4-H2Q | MeCN | 0.46919 | 62.8 |
| tetrachloro-1,4-H2Q | H2O | 0.69961 | 68.9 | 1,2-H2NQ | H2O | 0.52261 | 64.8 |
| 2,3-dichloro-5,6-dicyano-1,4-H2Q | H2O | 0.88761 | 73.3 | 1,4-H2NQ | H2O | 0.37661 | 61.5 |
| bromo-1,4-H2Q | H2O | 0.715308 | 69.3 | 1,4-H2NQ | THF | 0.4619 | 62.6 |
| 2-bromo-5-methyl-1,4-H2Q | H2O | 0.656308 | 67.9 | 2-methyl-1,4-H2NQ | H2O | 0.415308 | 62.4 |
| 2-chloro-5-methyl-1,4-H2Q | H2O | 0.654308 | 67.9 | 2,3-dimethyl-1,4-H2NQ | H2O | 0.340308 | 60.6 |
| 2-methyl-1,4-H2Q | H2O | 0.59961 | 66.6 | 2,3-dichloro-1,4-H2NQ | H2O | 0.44761 | 63.1 |
| 2,3-dimethyl-1,4-H2Q | H2O | 0.55361 | 65.6 | 2,7-tBu2-1,4-H2NQ | THF | 0.41419 | 61.5 |
| 2,5-dimethyl-1,4-H2Q | H2O | 0.596308 | 66.5 | 9,10-H2AQ | H2O | 0.08961 | 54.9 |
| 2,6-dimethyl-1,4-H2Q | H2O | 0.54861 | 65.4 | 1,8-dichloro-9,10-H2AQ | H2O | 0.11561 | 55.5 |
| 2,6-dimethyl-1,4-H2Q | MeCN | 0.5519 | 64.6 | 1,8-dichloro-9,10-H2AQ | THF | 0.15019 | 56.3 |
| 2,6-dimethyl-1,4-H2Q | THF | 0.5619 | 64.9 | phenanthrenequinone | H2O | 0.40661 | 62.2 |
| 2,6-dimethyl-1,4-H2Q | DMF | 0.57819 | 65.6 | 1,10-phenanthroline-5,6-dione | H2O | 0.58461 | 66.3 |
Values for E∘(V vs H2) are in V; −eE∘ is the average free energy for addition. BDFEavg values are average free energies for the overall reaction in kcal mol−1; see Section 4. Uncited BDFEavg values were calculated from E∘(V vs H2) using eq 18.
H2Q = 1,4-dihydroxybenzene; H2NQ = 1,4-dihydroxynaphthalene; 1,4-dihydroxynaphthalene; H2AQ = 9,10-dihydroxyanthracene.
For multielectron processes in which X–H and other X–E bonds are made or broken, average free energies (−ΔG∘/n) values are given in place of BDFEs. For example, in Table 21 thermochemical values for the reduction of CO2 to CO and H2O are presented. For this reaction, and others like it, − ΔG∘/n defines the average free energy of the reverse reaction which involves breaking water O–H bonds and forming a C = O bond. Similar to a BDFE, − ΔG∘/n provides a meaningful gauge of the strength of H atom abstractors required to, thermodynamically, drive these reactions.
4.1. Estimated Uncertainties
The thermochemical data given here come from a wide variety of sources and are derived from a variety of different measurements. It is beyond the scope of this review to provide error analyses for each value presented. Instead, we encourage interested readers to critically examine the primary literature because uncertainties can vary depending on the method of measurement.
Cited values are reported per the original literature, but many values in the Tables are calculated from others. For these calculated values, determination of the correct number of significant figures is complicated by differences in units and measurement methods between input values. As a result, we have decided to typically report all BDFEs to one decimal place and all E∘ (V vs H2) values to three decimal places to eliminate ambiguity due to rounding. Only in clear cases have we reduced the number of significant figures.
While evaluation of uncertainties can be complex, we have striven to simplify this process by citing values that involve a minimal number of assumptions and including footnotes when values deviate from that standard. As a general guideline, absolute uncertainties in BDFEs are in most cases ±1 kcal mol−1 (equivalent to ±40 mV for E∘(V vs H2) for values determined from a BDFE). However, uncertainties of twice that value are more appropriate for some entries. Relative uncertainties can be much smaller because a significant proportion of the overall error is attributed to the various constants used to calculate values from available literature data.
4.2. Thermochemical Tables
Supplementary Material
Table 6.
PCET Thermochemistry of Phenolsa
| compound | solvent | E∘(RO•/−) | E∘(ROH•+/0) | pKa(ROH•+) | pKa(ROH) | E∘(V vs H2)j | BDFE |
|---|---|---|---|---|---|---|---|
| PhOH | gas | – | – | – | – | 1.353 | 79.842 |
| PhOH | H2O | 0.79302 | 1.5303 | [−2] | 10.044 | 1.38 | 84.7 |
| PhOH | C6H6 | – | – | – | – | 1.320 | 82.5c |
| 4-Me-PhOH | H2O | 0.68302 | 1.4303 | [−2] | 10.344 | 1.29 | 82.5 |
| 4-Me-PhOH | C6H6 | – | – | – | – | 1.229 | 80.4c |
| 4-MeO-PhOH | H2O | 0.54302 | 1.1303 | [0.7] | 10.144 | 1.14 | 79.0 |
| 4-MeO-PhOH | C6H6 | – | – | – | – | 1.082 | 77.1c |
| 4-NO2-PhOH | H2O | 1.22302 | – | – | 7.144 | 1.64 | 90.6 |
| 4-F-PhOH | H2O | 0.76302 | – | – | 9.944 | 1.35 | 83.8 |
| 4-Cl-PhOH | H2O | 0.80302 | – | – | 9.444 | 1.36 | 84.1 |
| 4-Br-PhOH | H2O | 0.82302 | – | – | 9.444 | 1.38 | 84.5 |
| 4-I-PhOH | H2O | 0.82302 | – | – | 9.344 | 1.37 | 84.4 |
| 4-CO2−-PhOH | H2O | 0.90302 | – | – | 9.444 | 1.46 | 86.4 |
| 4-Me(O)C-PhOH | H2O | 1.00302 | – | – | % | 1.47 | 86.8 |
| 4-CN-PhOH | H2O | 1.12302 | – | – | 7.944 | 1.59 | 89.4 |
| 4-NH2-PhOH | H2O | 0.217302 | – | – | 10.444 | 0.833 | 72.0 |
| 4-NH2-PhOH | DMSO | −1.06020,i | 20.7520 | 0.839 | 71.9 | ||
| 4-NMe2-PhOH | H2O | 0.174304 | – | – | 10.144 | 0.772 | 70.6 |
| 1-naphthol | H2O | 0.59305 | – | – | 9.3305 | 1.14 | 79.1 |
| 2-naphthol | H2O | 0.69305 | – | – | 9.6305 | 1.26 | 81.8 |
| tyrosine | H2O | 0.71302 | – | – | 10.144 | 1.31 | 83.0 |
| trolox Ce | H2O | 0.192304 | – | – | 12.1306 | 0.908 | 73.7 |
| HPMCf | C6H6 | – | – | – | – | 0.884 | 72.5c |
| TocOHg | C6H6 | – | – | – | – | 0.883 | 72.5c |
| 2,4,6-tBu3PhOH | H2O | – | – | – | – | 0.983 | 75.5d |
| 2,4,6-tBu3PhOH | MeCN | [−0.67] | – | – | 2820,h | 0.9919 | 74.8 |
| 2,4,6-tBu3PhOH | DMSO | −0.67420,i | 17.820 | 1.050 | 76.8 | ||
| 2,4,6-tBu3PhOH | C6H6 | – | – | – | – | 1.014 | 75.5b |
| 2,4,6-tBu3PhOH | CCl4 | – | – | – | – | 1.014 | 75.3b |
| 2,4,6-tBu3PhOH | THF | – | – | – | – | 0.9719 | 74.4 |
| 2,6-tBu2PhOH | C6H6 | – | – | – | – | 1.082 | 77.0c |
| 4-Me-2,6-tBu2PhOH | C6H6 | – | – | – | – | 1.004 | 75.3c |
| 4-MeO-2,6-tBu2PhOH | C6H6 | – | – | – | – | 0.887 | 72.6c |
| 4-MeO-2,6-tBu2PhOH | MeCN | – | – | – | – | 0.86819 | 72.0 |
| 4-MeO-2,6-tBu2PhOH | THF | – | – | – | – | 0.83819 | 71.3 |
Potentials for 1e− reductions are in V vs SHE if in aqueous solution and V vs Cp2Fe+/0 if they are in organic solution. Values for E∘(V vs H2) are in V; −eE∘ is the average free energy for addition. Uncited values of E∘(V vs H2) were calculated from other values in the row using Scheme 2 or eq 16. BDFEs are in kcal mol−1 and if uncited were calculated from E∘(V vs H2) using eq 18. In many cases, the citation associated with a BDFE is for the related BDE, and the tabulated value was calculated using eq 9. Values in [square brackets] have been calculated from the other values in the row using Hess’ law.
Calculated from previously estimated BDEs in ref 33 but using hydrogen enthalpy of solvation (ΔH∘solv[H2]s) values reported for C6H6 and CCl4 in ref 48.
Calculated relative to 2,4,6-tBu3PhOH by applying the difference in BDFEs reported in ref 29.
Calculated from the PCET potential reported in ref 307 and extrapolating to pH 0.
Trolox C = (±)-6-hydroxy-2,5,7,8-tetramethylchromane-2-carboxylic acid.
HPMC = 6-hydroxy-2,2,5,7,8-pentamethylchroman.
TocOH = α-tocopherol.
Extrapolated from DMSO to MeCN using the method of Kütt and co-workers.298
Calculated from the reported anodic peak potentials, assuming a 57 mV peak-to-peak separation.
Compared with other solvents, both E∘(V vs H2) and BDFE values in DMSO have larger uncertainties from the thermochemical constants E∘(H+/H2) and CG (see Table 1).
Table 9.
PCET Thermochemistry of Ascorbatesa
| compound | solvent | E∘(Asc•−/2−) | E∘(AscH•/−) | pKa(Asc•) | pKa(AscH−) | E∘(V vs H2) | BDFE |
|---|---|---|---|---|---|---|---|
| AscH−b | water | 0.015321 | 0.72322 | −0.45322,323 | 11.3321,322 | 0.684 | 68.6 |
| iAscH−c | MeCN | [−1.07] | -- | -- | 28.8324 | 0.663 | 67.3324,d |
| compound | solvent | E∘(AscH2•+/0) | E∘(AscH•/−) | pKa(AscH2) | pKa(AscH2•+) | E∘ vs H2 | BDFE |
|
| |||||||
| AscH2e | water | -- | 0.72322 | 4.0321,322 | -- | 0.96 | 74.9 |
| iAscH2f | MeCN | -- | −0.41324 | 18.3324 | -- | 0.70 | 68.2 |
| compound | solvent | E∘(Asc0/•−) | NA | pKa(Asc•) | NA | E∘(V vs H2) | BDFE |
|
| |||||||
| Asc•− | water | −0.14321 | -- | −0.45322,323 | -- | −0.17 | 49.0 |
Potentials for 1e− reductions are in V vs SHE if in aqueous solution and V vs Cp2Fe+/0 if they are in organic solution. Values for E∘(V vs H2) are in V; −eE∘ is the average free energy for addition. Uncited values of E∘(V vs H2) were calculated from other values in the row using Scheme 2 or eq 18. BDFEs are in kcal mol−1 and if uncited were calculated from E∘(V vs H2) using eq 18. Values in [square brackets] have been calculated from the other values in the row using Hess’ law.
AscH− = ascorbate.
iAcsH− = 5,6-isopropylidene ascorbate.
A quasi-reversible potential is reported in ref 324, but we prefer the use of the BDFE from equilibration with TEMPO.
AscH2 = ascorbic acid.
iAscH2 = 5,6-isopropylidene ascorbic acid.
Table 11.
PCET Thermochemistry of Dioxygen Reductiona
| HO2•/HOOH | solvent | E∘(HOOH•+/0) | E∘(HOO•/−) | pKa(HOOH•+) | pKa(HOOH) | E∘(V vs H2) | BDFE |
|---|---|---|---|---|---|---|---|
| HOOH | gas | – | – | – | – | 1.24242 | 77.2 |
| HOOH | H2O | – | [0.77] | – | 11.672 | 1.4645 | 86.5 |
| O2(g)/•OOH | solvent | E∘(HOO+/•) | E∘(O20/•−) | pKa(HO2+) | pKa(HO2•) | E∘(V vs H2) | BDFE |
|
| |||||||
| •OOH | gas | – | – | – | – | −0.15042 | 45.1 |
| •OOH | H2O | – | −0.3545 | – | 4.845 | −0.0745 | 51.2 |
| O2•−/−OO–H | solvent | E∘(HOO•/−) | E(O2•−/2−) | pKa(HO2•) | pKa(HOO−) | E∘(V vs H2) | BDFE |
|
| |||||||
| −OO–H | H2O | 0.77b | – | 4.845 | – | 1.05 | 77.1 |
| O2(g) + 2H2(g) → 2H2O | solvent | E∘(V vs H2) | −ΔG∘/nc | ||||
|
| |||||||
| O2/H2O | gas | 1.18542 | 75.9 | ||||
| O2/H2O | MeCN | 1.2467 | 80.6 | ||||
| O2/H2O | DMF | 1.2667 | 81.4 | ||||
| O2/H2O | DMA | 1.23751 | |||||
| O2/H2O | H2O | 1.229327 | 81.1 | ||||
| O2(g) + H2(g) → H2O2 | solvent | E∘(V vs H2) | −ΔG∘/nc | ||||
|
| |||||||
| O2/H2O2 | gas | 0.54642 | 61.2 | ||||
| O2/H2O2 | H2O | 0.695327 | 68.8 | ||||
| H2O2 + H2(g) → 2H2O | solvent | E∘(V vs H2) | −ΔG∘/nc | ||||
|
| |||||||
| H2O2/H2O | gas | 1.82342 | 90.6 | ||||
| H2O2/H2O | H2O | 1.76345 | 93.5 | ||||
Potentials for 1e− reductions are in V vs SHE if in aqueous solution and V vs Cp2Fe+/0 if they are in organic solution. Values for E∘(V vs H2) are in V; – eE∘ is the average free energy for addition. BDFEs and −ΔG∘/n are in kcal mol−1 and if uncited were calculated from E∘(V vs H2) using eq 18. In many cases the citation associated with a BDFE is for the related BDE, and the tabulated value was calculated using eq 9.
E∘(HOO•/−) has been calculated using the H2O2 pKa and HO2•/HOOH PCET potential in water.
−ΔG∘/n values are average free energies for the overall reaction shown except to form H• [rather than add H2(g)]. See Section 4.
Table 12.
PCET Thermochemistry of Organic Hydroperoxidesa
| ROO•/ROOH | solvent | E∘(ROO•/−) | pKa(ROOH) | E∘ (V vs H2) | BDFE |
|---|---|---|---|---|---|
| MeOOH | gas | -- | -- | 1.346 | 79.6328 |
| MeOOH | H2O | 0.94329 | 11.5330 | 1.62 | 90.2 |
| EtOOH | gas | -- | -- | 1.216 | 76.6328 |
| EtOOH | H2O | 0.91329 | 11.8330 | 1.61 | 89.9 |
| iPrOOH | H2O | 0.81329 | 12.1330 | 1.53 | 88.0 |
| tBuOOH | gas | -- | -- | 1.194 | 76.1328 |
| tBuOOH | H2O | 0.71329 | 12.8330 | 1.47 | 86.6 |
| trans-HC(O)OOH | gas | -- | -- | 1.658 | 86.8331 |
| cis-HC(O)OOH | 1.801 | 90.1331 | |||
| CH3C(O)OOH | gas | -- | -- | 1.463 | 82.3 |
| CH3C(O)OOH | H2O | 1.14b | 8.2330 | 1.63 | 90.3 |
| ROOH + H2(g) → ROH + H2O | solvent | E∘(V vs H2) | −ΔG∘/nc | ||
|
| |||||
| MeOH/MeOOH | H2O | 1.70332 | 92.0 | ||
| tBuOH/tBuOOH | H2O | 1.68332 | 91.5 | ||
| HC(O)OH/HC(O)OOH | H2O | 1.82332 | 94.8 | ||
| CH3C(O)OH/CH3C(O)OOH | H2O | 1.80332 | 94.3 | ||
Potentials for 1e− reductions are in V vs SHE. Values for E∘(V vs H2) are in V; −eE∘ is the average free energy for addition. Uncited values of E∘(V vs H2) were calculated from other values in the row using Scheme 2 or eq 18. BDFEs and −ΔG∘/n are in kcal mol−1 and if uncited were calculated from E∘(V vs H2) using eq 18. In many cases the citation associated with a BDFE is for the related BDE, and the tabulated value was calculated using eq 9.
Estimated from electron transfer kinetic data.333
−ΔG∘/n values are average free energies for the overall reaction shown except to form H• [rather than add H2(g)]. See Section 4.
Table 15.
PCET Thermochemistry of Arylamines and Arylhydrazinesa
| compound | solvent | E∘(R2N•/−) | E∘(R2NH•+/0) | pKa(R2NH•+) | pKa(R2NH) | E∘(V vs H2) | BDFEb |
|---|---|---|---|---|---|---|---|
| PhNH2 | gas | – | – | – | – | 1.428 | 81.5339 |
| PhNH2 | H2O | – | 1.02340 | 7.05340 | – | 1.44 | 85.9 |
| PhNH2 | C6H6 | 1.469 | 86.0339 | ||||
| 4-MePhNH2 | gas | 1.333 | 79.3339 | ||||
| 4-MePhNH2 | H2O | – | 0.92340 | 8.5340 | – | 1.42 | 85.5 |
| 4-MePhNH2 | C6H6 | 1.373 | 83.8339 | ||||
| 4-MeOPhNH2 | H2O | – | 0.79340 | 9.6340 | – | 1.36 | 84.1 |
| 4-CNPhNH2 | H2O | – | 1.32340 | 4340 | – | 1.56 | 88.7 |
| 4-CF3PhNH2 | gas | 1.389 | 80.6339 | ||||
| 4-CF3PhNH2 | H2O | – | 1.28340 | 4.8340 | – | 1.56 | 88.9 |
| Ph2NH | gas | 1.320 | 79.0339 | ||||
| Ph2NH | H2O | – | 1.0338 | 3.8338 | – | 1.2 | 81 |
| Ph2NH | C6H6 | 1.209 | 80.0339 | ||||
| (4-MePh)2NH | gas | 1.277 | 78.0339 | ||||
| DPPH-Hc | MeCN | 0.91719 | 73.119 | ||||
| DPPH-Hc | THF | 0.9319 | 73.519 | ||||
| DPPH-Hc | C6H6 | 0.940 | 73.8293 | ||||
| 2,4-(NO2)2C6H3NHNPh2 | DMSO | −0.292341 | – | – | 12.1341 | 1.093d | 77.8d |
| PhNHNPh2 | DMSO | −1.117341 | – | – | 24.5341 | 1.005d | 75.8d |
| PhNHNHPh | DMSO | −1.730341 | – | – | 26.2341 | 0.493d | 64.0d |
| PhNHNHPh | MeCN | 0.38719,f | 60.919,f | ||||
| DHPe | MeCN | 0.29119,f | 58.719,f |
Potentials for 1e− reductions are in V vs SHE if in aqueous solution and vs Cp2Fe+/0 if in organic solution. Values for E∘(V vs H2) are in V; −eE∘ is the average free energy for addition. Uncited values of E∘(V vs H2) were calculated from other values in the row using Scheme 2 or eq 18.
BDFEs are in kcal mol−1 and if uncited were calculated from E∘(V vs H2) using eq 18. In many cases the citation associated with a BDFE is for the related BDE, and the tabulated value was calculated using eq 9.
DPPH-H = 1,1-diphenyl-2-picrylhydrazine.
Compared with other solvents, both E∘(V vs H2) and BDFE values in DMSO have larger uncertainties from the thermochemical constants E∘(H+H2) and CG (see Table 1).
DHP = 5,10-dihydrophenazine.
E∘(V vs H2) and BDFE correspond to the average of the overall 2e−/2H+ transfer.
Table 17.
PCET Thermochemistry of Nucleosides in Watera
Table 18.
PCET Thermochemistry of Thiols
| compound | solvent | E∘(RS•/−)a | pKa(RSH) | E∘(V vs H2)a | BDFE |
|---|---|---|---|---|---|
| HS-H | gas | -- | -- | 1.49 | 83.032 |
| HS-H | H2O | 1.15348 | 7.0349 | 1.56 | 88.9 |
| MeS-H | gas | -- | -- | 1.33 | 79.2350 |
| MeS-H | H2O | 0.73 | 10.330 | 1.34 | 83.7 |
| EtS-H | gas | -- | -- | 1.32 | 79.1348 |
| EtS-H | H2O | 0.74 | 10.6b | 1.35 | 84.3 |
| tBuS-H | gas | -- | -- | 1.29 | 78.4351 |
| HOCH2CH2S-H | H2O | 0.75348 | 9.6352 | 1.31 | 83.1 |
| cysteine | H2O | 0.73353 | 8.8c | 1.25 | 81.6 |
| glutathione | H2O | 0.81354 | 9.3355 | 1.36 | 84.2 |
| PhS-H | gas | -- | -- | 1.16 | 75.3356 |
| PhS-H | H2O | 0.69357 | 6.6358 | 1.08 | 77.7 |
| PhS-H | C6H6 | -- | -- | 1.22 | 80.2356 |
| 4-MePhS-H | H2O | 0.64357 | 6.8359 | 1.04 | 76.8 |
| 4-MeOPhS-H | H2O | 0.57357 | 6.8359 | 0.97 | 75.2 |
| 4BrPhS-H | H2O | 0.71357 | 6.0359 | 1.07 | 77.4 |
Potentials for 1e− reductions are in V vs SHE if in aqueous solution. Values for E∘(V vs H2) are in V; −eE∘ is the average free energy for addition. Uncited values of E∘(V vs H2) were calculated from other values in the row using Scheme 2 or eq 18. BDFEs are in kcal mol−1 and if uncited were calculated from E∘(V vs H2) using eq 18. In many cases the citation associated with a BDFE is for the related BDE, and the tabulated value was calculated using eq 9.
Average pKa of the zwitterionic form of cysteine and HSCH2CH(CO2Et)NH2 from ref 361.
Table 20.
PCET Thermochemistry of Nicotinamides and Related Compoundsa
| compound | solvent | E∘(RH•+/0) | E∘(R+/•) | pKa(RH•+) | E∘(V vs H2) | BDFE |
|---|---|---|---|---|---|---|
| AcrH2b | MeCN | 0.475374 | −0.845374 | 0.8374 | 0.55 | 64.7 |
| AcrH2•+ | −0.77 | 34.3 | ||||
| BNAHc | MeCN | 0.406374 | −1.49374 | 4.7374 | 0.71 | 68.4 |
| BNAH•+ | −1.18 | 24.7 | ||||
| NADHd | H2O | 0.94375,e | −0.92375 | −3.5375 | 0.73 | 69.7 |
| NADH•+ | −1.13 | 26.8 |
Potentials for 1e− reductions are in V vs SHE if in aqueous solution and V vs Cp2Fe+/0 if they are in organic solution. Values for E∘(V vs H2) are in V; −eE∘ is the average free energy for addition. Uncited values of E∘(V vs H2) were calculated from other values in the row using Scheme 2 or eq 18. Uncited values of E∘(V vs H2) for the radical cations were calculated from values for the neutral species using schemes in Figure 9 of ref 3. BDFEs are in kcal mol−1 and if uncited were calculated from E∘(V vs H2) using eq 18. Values in [square brackets] have been calculated from the other values in the row using Hess’ law.
AcrH2 = 10-methyl-9,10-dihydroacridine.
BNAH = 1-benzyl-1,4-dihydronicotinamide.
NADH = 1,4-dihydronicotinamide adenine dinucleotide.
E(NADH•+/0) = 1.05 V in propanol/water.375
ACKNOWLEDGMENTS
We are grateful to the many co-workers and colleagues who have measured values and contributed in other ways to the field of PCET. We are particularly indebted to Dr. Eric Wiedner, Dr. Aaron Appel, and Dr. Morris Bullock of Pacific Northwest National Laboratory for their insights and feedback. R.G.A. and A.M.H. gratefully acknowledge support from National Science Foundation Graduate Research Fellowships. S.C.C. (F32GM1329266-02) and E.M.N. (F32GM129902) gratefully acknowledge support from U.S. National Institutes of Health Ruth L. Kirschstein Postdoctoral Fellowships. This research was primarily supported as part of the Center for Molecular Electrocatalysis (CME), an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences. This center provided primary support for C.F.W. and H.N. and substantial support for B.D.G. NIH grant 2R01GM50422 to J.M.M. provided partial support for S.C.C., G.A.P., and B.D.G. NSF grant CHE-1904813 provided partial support for R.G.A. and for the ideas in the materials section.
Biographies
Rishi Agarwal was born in Santa Clara, CA in 1994. He received his B.A. in Chemistry from Cornell University in 2016 while working with Professor Peter T. Wolczanski. He is currently a Ph.D. candidate in the laboratory of Professor James M. Mayer at Yale University studying the thermodynamics and kinetics of hydrogen transfer to molecules, nanomaterials, and metallic electrodes.
Scott Coste was born in Berkeley, CA in 1991 and received his B.S. in Chemistry in 2013 from the University of California, Irvine, working under Professor Matt Law. He completed his Ph.D. at Northwestern University in 2019 under the advisement of Professor Danna Freedman. Currently, he is a postdoctoral fellow working for Professor James Mayer at Yale University studying multisite concerted proton–electron transfer reactions with metal complexes.
Benjamin Groff was born in Lancaster, Pennsylvania in 1996. He received his B.S. in Chemistry and B.A. in Mathematics in 2018 from the University of Virginia, where he worked under the mentorship of Professor Rebecca Pompano. He is currently a Ph.D. candidate in the laboratory of Professor James Mayer at Yale University, where he is studying kinetic–thermodynamic relationships in concerted proton–electron transfer reactions and electrocatalytic dioxygen reduction.
Abigail Heuer was born in West Bend, WI in 1994. She received her B.S. in Biochemistry from the University of St. Thomas in 2015 where she worked in the laboratory of Prof. J. Thomas Ippoliti. She is currently a Ph.D. candidate in Prof. James Mayer’s lab at Yale University studying the kinetics of H atom transfer reactions at C–H bonds.
Hyunho Noh was born in Daegu, South Korea in 1992 and was raised in Tokyo, Japan. He received his B.S. in Chemistry in 2014 from the University of Illinois Urbana–Champaign, working under Prof. Mei Shen. He completed his Ph.D. at Northwestern University in 2019 under the guidance of Prof. Joseph T. Hupp and Prof. Omar K. Farha. He is currently a postdoctoral fellow at Yale University working under Prof. James M. Mayer, studying the kinetics and thermodynamics of heterogeneous electrocatalysts that undergo proton-coupled electron transfers.
Giovanny Parada was born and raised in Bogotá, Colombia in 1983. He received his B.S. and M.S. in Chemistry at the National University of Colombia working alongside Professors Luca Fadini and Marco Fidel Suarez. He moved to Sweden to complete his Ph.D. at Uppsala University under the guidance of Professors Sascha Ott and Leif Hammarstrom. On moving back to the Americas, he was a postdoctoral associate with Professor James Mayer at Yale University. Currently, he is an Assistant Professor at The College of New Jersey. His research includes photoinduced and thermal multi proton-coupled electron transfer of biomimetic model systems and nanomaterials.
Catherine Wise was born in Richmond, VA, in 1992. She received her B.S. in Chemistry from the College of William and Mary in 2015, where she worked in the laboratory of Professor William McNamara. She completed her Ph.D. at Yale University in 2020 under the guidance of Professor James Mayer, studying proton-coupled electron transfer in electrochemical systems. She is currently an Associate Program Officer with the Board on Energy and Environmental Systems at the National Academies of Sciences, Engineering, and Medicine.
Eva Nichols was born in Tucson, AZ in 1990. She received her B.S. in Chemistry from California Institute of Technology working with Professor Theodor Agapie. She completed her Ph.D. at the University of California, Berkeley, under the direction of Professor Christopher Chang and was a postdoctoral fellow with Professor James Mayer at Yale University from 2018 to 2020. She is currently an Assistant Professor at the University of British Columbia. Her research interests include molecular and interfacial electrocatalysis, reaction mechanisms, spectroscopy, and molecular models of electron bifurcation.
Jeffrey Warren was born in Spokane, WA in 1982. He has been interested in proton-coupled redox chemistry for most of his adult life. Following a B.Sc. at Washington State University (working alongside James K. Hurst), Jeff earned his Ph.D. from the University of Washington in 2010 (under the mentorship of James M. Mayer). He went on to a position as a postdoctoral fellow at the California Institute of Technology (working with Harry B. Gray). Since 2013, Jeff has been at Simon Fraser University, where he is now an Associate Professor of Chemistry.
James Mayer was born and raised in New York City. He received his A.B. from Harvard in 1978, with concurrent research at Hunter College CUNY during summers. His Ph.D. studies at Caltech were done under the guidance of Professor John Bercaw, followed by two years as a visiting scientist at DuPont. Mayer joined the faculty of the University of Washington in 1984, eventually being appointed the Alvin L. and Verla R. Kwiram Professor of Chemistry. In 2014, he moved to Yale University where he is now the Charlotte Fitch Roberts Professor of Chemistry.
Footnotes
Complete contact information is available at: https://pubs.acs.org/10.1021/acs.chemrev.1c00521
Supporting Information
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.chemrev.1c00521.
Experimental procedures and data for the determination of the BDFE of 4-oxo-TEMPO-H in hexanes (PDF)
The authors declare no competing financial interest.
Contributor Information
Rishi G. Agarwal, Department of Chemistry, Yale University, New Haven, Connecticut 06520, United States.
Scott C. Coste, Department of Chemistry, Yale University, New Haven, Connecticut 06520, United States.
Benjamin D. Groff, Department of Chemistry, Yale University, New Haven, Connecticut 06520, United States.
Abigail M. Heuer, Department of Chemistry, Yale University, New Haven, Connecticut 06520, United States.
Hyunho Noh, Department of Chemistry, Yale University, New Haven, Connecticut 06520, United States.
Giovanny A. Parada, Department of Chemistry, Yale University, New Haven, Connecticut 06520, United States; Department of Chemistry, The College of New Jersey, Ewing, New Jersey 08628, United States.
Catherine F. Wise, Department of Chemistry, Yale University, New Haven, Connecticut 06520, United States.
Eva M. Nichols, Department of Chemistry, University of British Columbia, Vancouver, BC V6T 1Z1, Canada.
Jeffrey J. Warren, Department of Chemistry, Simon Fraser University, Burnaby, BC V5A 1S6, Canada.
James M. Mayer, Department of Chemistry, Yale University, New Haven, Connecticut 06520, United States.
REFERENCES
- (1).Huynh MHV; Meyer TJ Proton-Coupled Electron Transfer. Chem. Rev 2007, 107, 5004–5064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Weinberg DR; Gagliardi CJ; Hull JF; Murphy CF; Kent CA; Westlake BC; Paul A; Ess DH; McCafferty DG; Meyer TJ Proton-Coupled Electron Transfer. Chem. Rev 2012, 112, 4016–4093. [DOI] [PubMed] [Google Scholar]
- (3).Warren JJ; Tronic TA; Mayer JM Thermochemistry of Proton-Coupled Electron Transfer Reagents and its Implications. Chem. Rev 2010, 110, 6961–7001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Hammes-Schiffer S; Stuchebrukhov A A Theory of Coupled Electron and Proton Transfer Reactions. Chem. Rev 2010, 110, 6939–6960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Costentin C; Robert M; Savéant J-M Update 1 of: Electrochemical Approach to the Mechanistic Study of Proton-Coupled Electron Transfer. Chem. Rev 2010, 110, PR1–PR40. [DOI] [PubMed] [Google Scholar]
- (6).Migliore A; Polizzi NF; Therien MJ; Beratan DN Biochemistry and Theory ofProton-Coupled Electron Transfer. Chem. Rev 2014, 114, 3381–3465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Pannwitz A; Wenger OS Recent Advances in Bioinspired Proton-Coupled Electron Transfer. Dalton Trans. 2019, 48, 5861–5868. [DOI] [PubMed] [Google Scholar]
- (8).Dempsey JL; Winkler JR; Gray HB Proton-Coupled Electron Flow in Protein Redox Machines. Chem. Rev 2010, 110, 7024–7039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Stubbe J; Nocera DG; Yee CS; Chang MCY Radical Initiation in the Class I Ribonucleotide Reductase: Long-Range Proton-Coupled Electron Transfer? Chem. Rev 2003, 103, 2167–2202. [DOI] [PubMed] [Google Scholar]
- (10).Gagliardi CJ; Westlake BC; Kent CA; Paul JJ; Papanikolas JM; Meyer TJ Integrating Proton Coupled Electron Transfer (PCET) and Excited States. Coord. Chem. Rev 2010, 254, 2459–2471. [Google Scholar]
- (11).Wenger OS Proton-Coupled Electron Transfer with Photoexcited Ruthenium(II), Rhenium(I), and Iridium(III) Complexes. Coord. Chem. Rev 2015, 282–283, 150–158. [Google Scholar]
- (12).Miller DC; Tarantino KT; Knowles RR Proton-Coupled Electron Transfer in Organic Synthesis: Fundamentals, Applications, and Opportunities. Top. Curr. Chem 2016, 374, 30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Hoffmann N Proton-Coupled Electron Transfer in Photoredox Catalytic Reactions. Eur. J. Org. Chem 2017, 2017, 1982–1992. [Google Scholar]
- (14).Wiedner ES; Chambers MB; Pitman CL; Bullock RM; Miller AJM; Appel AM Thermodynamic Hydricity of Transition Metal Hydrides. Chem. Rev 2016, 116, 8655–8692. [DOI] [PubMed] [Google Scholar]
- (15).Brereton KR; Smith NE; Hazari N; Miller AJM Thermodynamic and Kinetic Hydricity of Transition Metal Hydrides. Chem. Soc. Rev 2020, 49, 7929–7948. [DOI] [PubMed] [Google Scholar]
- (16).Hammes-Schiffer S Introduction: Proton-Coupled Electron Transfer. Chem. Rev 2010, 110, 6937–6938. [DOI] [PubMed] [Google Scholar]
- (17).Themed Collection Frontiers in Proton Coupled Electron Transfer (PCET) Chem. Commun [Online], 2019. https://pubs.rsc.org/en/journals/articlecollectionlanding?sercode=cc&themeid=555a6d40-9f26-4f28-a334-fcc83195fa53.
- (18).Agarwal RG;Wise CF;Warren JJ;Mayer JM Correction to Thermochemistry of Proton-Coupled Electron Transfer Reagents and its Implications. Chem. Rev 2021, DOI: 10.1021/acs.chemrev.1c00791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Wise CF; Agarwal RG; Mayer JM Determining Proton-Coupled Standard Potentials and X–H Bond Dissociation Free Energies in Nonaqueous Solvents Using Open-Circuit Potential Measurements. J. Am. Chem. Soc 2020, 142, 10681–10691. [DOI] [PubMed] [Google Scholar]
- (20).Bordwell FG; Cheng J Substituent Effects on the Stabilities of Phenoxyl Radicals and the Acidities of Phenoxyl Radical Cations. J. Am. Chem. Soc 1991, 113, 1736–1743. [Google Scholar]
- (21).Murray AT; Voskian S; Schreier M; Hatton TA; Surendranath Y Electrosynthesis of Hydrogen Peroxide by Phase-Transfer Catalysis. Joule 2019, 3, 2942–2954. [Google Scholar]
- (22).Gerken JB; Stahl SS High-Potential Electrocatalytic O2 Reduction with Nitroxyl/NOx Mediators: Implications for Fuel Cells and Aerobic Oxidation Catalysis. ACS Cent. Sci 2015, 1, 234–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Matsubara Y Unified Benchmarking of Electrocatalysts in Noninnocent Second Coordination Spheres for CO2 Reduction. ACS Energy Lett. 2019, 4, 1999–2004. [Google Scholar]
- (24).Nagao H; Mizukawa T; Tanaka K Carbon-Carbon Bond Formation in the Electrochemical Reduction of Carbon Dioxide Catalyzed by a Ruthenium Complex. Inorg. Chem 1994, 33, 3415–3420. [Google Scholar]
- (25).Luo Y-R Comprehensive Handbook of Chemical Bond Energies; CRC Press: Boca Raton, 2007. [Google Scholar]
- (26).Internet Bond-Energy Databank (pKa And BDE)—iBond Home Page. http://ibond.nankai.edu.cn (accessed Feb 15, 2021).
- (27).For reagents that are gases at ambient temperatures, one finds both 1 atm and 1 M standard states. Species at 1 M are 24.5 times more concentrated than those at 1 atm at 298 K (1 mol per Lvs 1 mol per 24.5 L for an ideal gas). The concentration difference alone contributes an unfavorable −TΔS∘ of RTln(24.5) = 1.84 kcal mol−1. Readers are encouraged to specify their standard states and to give the units of equilibrium constants (e.g., atm−1 vs M−1 for X + H2 ⇄ XH2 binding constants).
- (28).PCET thermochemistry can use various different standard states. Standard practice for solution-phase experimental studies is to extrapolate concentrations to the common and accessible 1 M standard state. In the absence of nonidealities such as ion pairing or homoconjugation, this treatment is equivalent to extrapolating “the properties of the solute at infinite dilution converted to a concentration of 1 M”, (a typical definition of a unit activity coefficient). Traditional thermochemical papers often use a standard state of “unit mole fraction”, which is infinite dilution extrapolated to mole fraction χ = 1 (the pure solute).
- (29).Lucarini M; Pedrielli P; Pedulli GF; Cabiddu S; Fattuoni C Bond Dissociation Energies of O–H Bonds in Substituted Phenols from Equilibration Studies. J. Org. Chem 1996, 61, 9259–9263. [Google Scholar]
- (30).Kreevoy MM; Eichinger BE; Stary FE; Katz EA; Sellstedt JH The Effect of Structure on Mercaptan Dissociation Constants. J. Org. Chem 1964, 29, 1641–1642. [Google Scholar]
- (31).Kreevoy MM; Harper ET; Duvall RE; Wilgus HS; Ditsch LT Inductive Effects on the Acid Dissociation Constants of Mercaptans. J. Am. Chem. Soc 1960, 82, 4899–4902. [Google Scholar]
- (32).Blanksby SJ; Ellison GB Bond Dissociation Energies of Organic Molecules. Acc. Chem. Res 2003, 36, 255–263. [DOI] [PubMed] [Google Scholar]
- (33).Mader EA; Manner VW; Markle TF; Wu A; Franz JA; Mayer JM Trends in Ground-State Entropies for Transition Metal Based Hydrogen Atom Transfer Reactions. J. Am. Chem. Soc 2009, 131, 4335–4345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Bordwell FG; Cheng JP; Harrelson JA Homolytic Bond Dissociation Energies in Solution from Equilibrium Acidity and Electrochemical Data. J. Am. Chem. Soc 1988, 110, 1229–1231. [Google Scholar]
- (35).Wayner DDM; Parker VD Bond Energies in Solution from Electrode Potentials and Thermochemical Cycles. A Simplified and General Approach. Acc. Chem. Res 1993, 26, 287–294. [Google Scholar]
- (36).Tilset M, The Thermodynamics of Organometallic Systems Involving Electron-Transfer Paths. In Electron Transfer In Chemistry; Balzani V, Ed.; Wiley-VCH: Weinheim, Germany, 2001; pp 677–713. [Google Scholar]
- (37).Tilset M Organometallic Electrochemistry: Thermodynamics of Metal–Ligand Bonding; Elsevier: Amsterdam, 2007; Vol. 1, pp 279–305. [Google Scholar]
- (38).Warren JJ; Mayer JM Predicting Organic Hydrogen Atom Transfer Rate Constants Using the Marcus Cross Relation. Proc. Natl. Acad. Sci. U. S. A 2010, 107, 5282–5287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Mader EA; Davidson ER; Mayer JM Large Ground-State Entropy Changes for Hydrogen Atom Transfer Reactions of Iron Complexes. J. Am. Chem. Soc 2007, 129, 5153–5166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Gritzner G; Kuta J Recommendations on Reporting Electrode Potentials in Nonaqueous Solvents. Electrochim. Acta 1984, 29, 869–873. [Google Scholar]
- (41).Noviandri I; Brown KN; Fleming DS; Gulyas PT; Lay PA ; Masters AF; Phillips L The Decamethylferrocenium/Decamethylferrocene Redox Couple: A Superior Redox Standard to the Ferrocenium/Ferrocene Redox Couple for Studying Solvent Effects on the Thermodynamics of Electron Transfer. J. Phys. Chem. B 1999, 103, 6713–6722. [Google Scholar]
- (42).Linstrom PJ; Mallard WG NIST Chemistry Webbook, NIST Standard Database Number 69. http://webbook.nist.gov/chemistry/ (accessed February 8, 2021).
- (43).Roduner E Hydrophobic Solvation, Quantum Nature, and Diffusion of Atomic Hydrogen in Liquid Water. Radiat. Phys. Chem 2005, 72, 201–206. [Google Scholar]
- (44).Serjeant EP; Dempsey B Ionisation Constants of Organic Acids in Aqueous Solution; Permagon: Oxford, 1979. [Google Scholar]
- (45).Armstrong DA; Huie RE; Koppenol WH; Lymar SV; Merényi G; Neta P; Ruscic B; Stanbury DM; Steenken S; Wardman P Standard Electrode Potentials Involving Radicals in Aqueous Solution: Inorganic Radicals (IUPAC Technical Report). Pure Appl. Chem 2015, 87, 1139. [Google Scholar]
- (46).Parker VD Homolytic Bond (H-A) Dissociation Free Energies in Solution. Applications of the Standard Potential of the (H+/H•) Couple. J. Am. Chem. Soc 1992, 114, 7458–7462. [Google Scholar]
- (47).Brunner E Solubility of Hydrogen in 10 Organic Solvents at 298.15, 323.15, and 373.15 K. J. Chem. Eng. Data 1985, 30, 269–273. [Google Scholar]
- (48).Wilhelm E; Battino R Thermodynamic Functions of the Solubilities of Gases in Liquids at 25∘. Chem. Rev 1973, 73, 1–9. [Google Scholar]
- (49).Young CL Hydrogen and Deuterium, 1st ed.; Pergamon Press: New York, 1981; Vol. 5/6, p 646. [Google Scholar]
- (50).Connelly SJ; Wiedner ES; Appel AM Predicting the Reactivity of Hydride Donors in Water: Thermodynamic Constants for Hydrogen. Dalton Trans. 2015, 44, 5933–5938. [DOI] [PubMed] [Google Scholar]
- (51).Matsubara Y Standard Electrode Potentials for Electrochemical Hydrogen Production, Carbon Dioxide Reduction, and Oxygen Reduction Reactions in N,N-Dimethylacetamide. Chem. Lett 2020, 49, 915–917. [Google Scholar]
- (52).Fourmond V; Jacques PA; Fontecave M; Artero V H2 Evolution and Molecular Electrocatalysts: Determination of Over-potentials and Effect of Homoconjugation. Inorg. Chem 2010, 49, 10338–10347. [DOI] [PubMed] [Google Scholar]
- (53).Kolthoff IM; Chantooni MK Critical Study Involving Water, Methanol, Acetonitrile, N,N-Dimethylformamide, and Dimethyl Sulfoxide of Medium Ion Activity Coefficients, γ, on the Basis of the γAsPh4+ = γPBh4− Assumption. J. Phys. Chem 1972, 76, 2024–2034. [Google Scholar]
- (54).Klug CM; O’Hagan M; Bullock RM; Appel AM; Wiedner ES Impact of Weak Agostic Interactions in Nickel Electrocatalysts for Hydrogen Oxidation. Organometallics 2017, 36, 2275–2284. [Google Scholar]
- (55).Quist DA; Ehudin MA; Schaefer AW; Schneider GL; Solomon EI; Karlin KD Ligand Identity-Induced Generation of Enhanced Oxidative Hydrogen Atom Transfer Reactivity for a CuII2(O2•−) Complex Driven by Formation of a CuII2(−OOH) Compound with a Strong O–H Bond. J. Am. Chem. Soc 2019, 141, 12682–12696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (56).Garrido G; Koort E; Ràfols C; Bosch E; Rodima T; Leito I; Rosés M Acid–Base Equilibria in Nonpolar Media. Absolute pKa Scale of Bases in Tetrahydroluran. J. Org. Chem 2006, 71, 9062–9067. [DOI] [PubMed] [Google Scholar]
- (57).Roberts JAS; Bullock RM Direct Determination of Equilibrium Potentials for Hydrogen Oxidation/Production by Open Circuit Potential Measurements in Acetonitrile. Inorg. Chem 2013, 52, 3823–3835. [DOI] [PubMed] [Google Scholar]
- (58).Ledezma-Yanez I; Díaz-Morales O; Figueiredo MC; Koper MTM Hydrogen Oxidation and Hydrogen Evolution on a Platinum Electrode in Acetonitrile. ChemElectroChem 2015, 2, 1612–1622. [Google Scholar]
- (59).Ray SK; Datta J; Kundu KK Kinetics of Hydrogen Evolution Reaction on some Noble Metal Coated Platinum Electrode Surfaces in Aqueous Acetonitrile and Dimethylformamide Solutions by Cyclic Voltammetry. Indian J. Chem 1992, 303–309. [Google Scholar]
- (60).Vojinovic V; Mentus S; Komnenic V Thermodynamic and Kinetic Behavior of Hydrogen Electrode in a Solution of 0.5 M KClO4 in Dimethyl Sulfoxide. J. Serb. Chem. Soc 2003, 68, 497–504. [Google Scholar]
- (61).Huynh MT; Anson CW; Cavell AC; Stahl SS; Hammes-Schiffer S Quinone 1e− and 2e−/2H+ Reduction Potentials: Identification and Analysis of Deviations from Systematic Scaling Relationships. J. Am. Chem. Soc 2016, 138, 15903–15910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (62).Izutsu K Electrochemistry in Nonaqueous Solutions; Second, Revised and Enlarged ed.; Wiley-VCH: 2009; pp 136–138. [Google Scholar]
- (63).Brozek CK; Hartstein KH; Gamelin DR Potentiometric Titrations for Measuring the Capacitance of Colloidal Photodoped ZnO Nanocrystals. J. Am. Chem. Soc 2016, 138, 10605–10610. [DOI] [PubMed] [Google Scholar]
- (64).Dutton PL Redox Potentiometry: Determination of Midpoint Potentials of Oxidation-Reduction Components of Biological Electron-Transfer Systems. In Methods Enzymology; Academic Press: 1978; Vol. 54, pp 411–435. [DOI] [PubMed] [Google Scholar]
- (65).Pitman CL; Brereton KR; Miller AJM Aqueous Hydricity of Late Metal Catalysts as a Continuum Tuned by Ligands and the Medium. J. Am. Chem. Soc 2016, 138, 2252–2260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (66).Izutsu K Acid-Base Dissociation Constants in Dipolar Aprotic Solvents; Blackwell Scientific: Boston, 1990; p 5. [Google Scholar]
- (67).Pegis ML; Roberts JA; Wasylenko DJ; Mader EA; Appel AM; Mayer JM Standard Reduction Potentials for Oxygen and Carbon Dioxide Couples in Acetonitrile and N,N-Dimethylformamide. Inorg. Chem 2015, 54, 11883–11888. [DOI] [PubMed] [Google Scholar]
- (68).Matsubara Y Standard Electrode Potentials for the Reduction of CO2 to CO in Acetonitrile–Water Mixtures Determined Using a Generalized Method for Proton-Coupled Electron-Transfer Reactions. ACS Energy Lett. 2017, 2, 1886–1891. [Google Scholar]
- (69).Pool DH; Stewart MP; O’Hagan M; Shaw WJ; Roberts JAS; Bullock RM; DuBois DL Acidic Ionic Liquid/Water Solution as Both Medium and Proton Source for Electrocatalytic H2 Evolution by [Ni(P2N2)2]2+ Complexes. Proc. Natl. Acad. Sci. U. S. A 2012, 109, 15634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (70).Hou J; Fang M; Cardenas AJP; Shaw WJ; Helm ML; Bullock RM; Roberts JAS; O’Hagan M Electrocatalytic H2 Production with a Turnover Frequency > 107 s−1: The Medium Provides an Increase in Rate but Not Overpotential. Energy Environ. Sci 2014, 7, 4013–4017. [Google Scholar]
- (71).Compton RG; Banks CE Understanding Voltammetry; Imperial College Press: London, 2007; Section 1.10: Electrode Processes: Kinetics vs. Thermodynamics, pp 32–34. [Google Scholar]
- (72).Lide DR CRC Handbook of Chemistry and Physics, 90th ed.; CRC Press: Boca Raton, FL, 2009; pp 6-148–6-169. [Google Scholar]
- (73).Cardenas AJP; Ginovska B; Kumar N; Hou J; Raugei S; Helm ML; Appel AM; Bullock RM; O’Hagan M Controlling Proton Delivery through Catalyst Structural Dynamics. Angew. Chem., Int. Ed 2016, 55, 13509–13513. [DOI] [PubMed] [Google Scholar]
- (74).Klug CM; Cardenas AJP; Bullock RM; O’Hagan M; Wiedner ES Reversing the Tradeoff between Rate and Overpotential in Molecular Electrocatalysts for H2 Production. ACS Catal. 2018, 8, 3286–3296. [Google Scholar]
- (75).Azcarate I; Costentin C; Robert M; Saveant JM Through-Space Charge Interaction Substituent Effects in Molecular Catalysis Leading to the Design of the Most Efficient Catalyst of CO2-to-CO Electrochemical Conversion. J. Am. Chem. Soc 2016, 138, 16639–16644. [DOI] [PubMed] [Google Scholar]
- (76).Jin K; Maalouf JH; Lazouski N; Corbin N; Yang D; Manthiram K Epoxidation of Cyclooctene Using Water as the Oxygen Atom Source at Manganese Oxide Electrocatalysts. J. Am. Chem. Soc 2019, 141, 6413–6418. [DOI] [PubMed] [Google Scholar]
- (77).Maalouf JH; Jin K; Yang D; Limaye AM; Manthiram K Kinetic Analysis of Electrochemical Lactonization of Ketones Using Water as the Oxygen Atom Source. ACS Catal. 2020, 10, 5750–5756. [Google Scholar]
- (78).Report of the Basic Energy Sciences Roundtable on Liquid Solar Fuels; National Renewable Energy Lab. (NREL): United States, 2019. https://science.osti.gov/bes/Community-Resources/Reports (accessed on January 22, 2021). [Google Scholar]
- (79).Natinsky BS; Lu S; Copeland ED; Quintana JC; Liu C Solution Catalytic Cycle of Incompatible Steps for Ambient Air Oxidation of Methane to Methanol. ACS Cent. Sci 2019, 5, 1584–1590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (80).Darcy JW; Koronkiewicz B; Parada GA; Mayer JM A Continuum of Proton-Coupled Electron Transfer Reactivity. Acc. Chem. Res 2018, 51, 2391–2399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (81).Warren JJ; Mayer JM Hydrogen Atom Transfer Reactions of Iron–Porphyrin–Imidazole Complexes as Models for Histidine-Ligated Heme Reactivity. J. Am. Chem. Soc 2008, 130, 2774–2776. [DOI] [PubMed] [Google Scholar]
- (82).Wu A; Masland J; Swartz RD; Kaminsky W; Mayer JM Synthesis and Characterization of Ruthenium Bis(β-diketonato) Pyridine-Imidazole Complexes for Hydrogen Atom Transfer. Inorg. Chem 2007, 46, 11190–11201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (83).Bergner M; Dechert S; Demeshko S; Kupper C; Mayer JM; Meyer F Model of the MitoNEET [2Fe–2S] Cluster Shows Proton Coupled Electron Transfer. J. Am. Chem. Soc 2017, 139, 701–707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (84).Carina RF; Verzegnassi L; Williams AF; Bernardinelli G Modulation of Iron Reduction Potential by Deprotonation at a Remote Site. Chem. Commun 1998, 2681–2682. [Google Scholar]
- (85).Stupka G; Gremaud L; Williams AF Control of Redox Potential by Deprotonation of Coordinated 1H-Imidazole in Complexes of 2-(1H-Imidazol-2-yl)pyridine. Helv. Chim. Acta 2005, 88, 487–495. [Google Scholar]
- (86).Warren JJ; Mayer JM Proton-Coupled Electron Transfer Reactions at a Heme-Propionate in an Iron-Protoporphyrin-IX Model Compound. J. Am. Chem. Soc 2011, 133, 8544–8551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (87).Manner VW; Mayer JM Concerted Proton–Electron Transfer in a Ruthenium Terpyridyl-benzoate System with a Large Separation between the Redox and Basic Sites. J. Am. Chem. Soc 2009, 131, 9874–9875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (88).Hammett LP The Effect of Structure upon the Reactions of Organic Compounds. Benzene Derivatives. J. Am. Chem. Soc 1937, 59, 96–103. [Google Scholar]
- (89).Anslyn EV; Dougherty DA Modern Physical Organic Chemistry; University Science: Sausalito, Calif., 2006; pp 445–471. [Google Scholar]
- (90).Lever ABP Electrochemical Parametrization of Metal Complex Redox Potentials, Using the Ruthenium(III)/Ruthenium(II) Couple to Generate a Ligand Electrochemical Series. Inorg. Chem 1990, 29, 1271–1285. [Google Scholar]
- (91).Lever ABP Electrochemical Parametrization of Rhenium Redox Couples. Inorg. Chem 1991, 30, 1980–1985. [Google Scholar]
- (92).Dhar D; Yee GM; Spaeth AD; Boyce DW; Zhang H; Dereli B; Cramer CJ; Tolman WB Perturbing the Copper(III)–Hydroxide Unit through Ligand Structural Variation. J. Am. Chem. Soc 2016, 138, 356–368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (93).Pratt DA; DiLabio GA; Mulder P; Ingold KU Bond Strengths of Toluenes, Anilines, and Phenols: To Hammett or Not. Acc. Chem. Res 2004, 37, 334–340. [DOI] [PubMed] [Google Scholar]
- (94).Sim BA; Griller D; Wayner DDM Reduction Potentials for Substituted Benzyl Radicals: pKa Values for the Corresponding Toluenes. J. Am. Chem. Soc 1989, 111, 754–755. [Google Scholar]
- (95).Moyer BA; Meyer TJ Properties of the Oxo/Aqua System (bpy)2(py)RuO2+/(bpy)2(py)Ru(OH2)2+. Inorg. Chem 1981, 20, 436–444. [Google Scholar]
- (96).Baldwin MJ; Pecoraro VL Energetics of Proton-Coupled Electron Transfer in High-Valent Mn2(μ-O)2 Systems: Models for Water Oxidation by the Oxygen-Evolving Complex of Photosystem II. J. Am. Chem. Soc 1996, 118, 11325–11326. [Google Scholar]
- (97).Caudle MT; Pecoraro VL Thermodynamic Viability of Hydrogen Atom Transfer from Water Coordinated to the Oxygen-Evolving Complex of Photosystem II. J. Am. Chem. Soc 1997, 119, 3415–3416. [Google Scholar]
- (98).Tommos C; Babcock GT Oxygen Production in Nature: A Light-Driven Metalloradical Enzyme Process. Acc. Chem. Res 1998, 31, 18–25. [Google Scholar]
- (99).Tommos C; Babcock GT Proton and Hydrogen Currents in Photosynthetic Water Oxidation. Biochim. Biophys. Acta, Bioenerg 2000, 1458, 199–219. [DOI] [PubMed] [Google Scholar]
- (100).Lebeau EL; Binstead RA; Meyer TJ Mechanistic Implications of Proton Transfer Coupled to Electron Transfer. J. Am. Chem. Soc 2001, 123, 10535–10544. [DOI] [PubMed] [Google Scholar]
- (101).Roecker L; Kutner W; Gilbert JA; Simmons M; Murray RW; Meyer TJ Instability of the Oxidation Catalysts ([(bpy)2(py)-Ru(O)]2+) and Oxo(1,10-phenanthroline)(2,2’,2”-terpyridine) Ruthenium2+ ([(trpy)(phen)Ru(O)]2+) in Basic Solution. Inorg. Chem 1985, 24, 3784–3791. [Google Scholar]
- (102).Pourbaix M Atlas of Electrochemical Equilibria in Aqueous Solutions, 2nd English ed.; National Association of Corrosion Engineers: Houston, TX, 1974. Figure 16 is from p 388. [Google Scholar]
- (103).McCarthy BD; Dempsey JL Decoding Proton-Coupled Electron Transfer with Potential-pKa Diagrams. Inorg. Chem 2017, 56, 1225–1231. [DOI] [PubMed] [Google Scholar]
- (104).Waidmann CR; Miller AJM; Ng C-WA; Scheuermann ML; Porter TR; Tronic TA; Mayer JM Using Combinations of Oxidants and Bases as PCET Reactants: Thermochemical and Practical Considerations. Energy Environ. Sci 2012, 5, 7771–7780. [Google Scholar]
- (105).Cukier RI; Nocera DG Proton-Coupled Electron Transfer. Annu. Rev. Phys. Chem 1998, 49, 337–369. [DOI] [PubMed] [Google Scholar]
- (106).Reece SY; Hodgkiss JM; Stubbe J; Nocera DG Proton-Coupled Electron Transfer: The Mechanistic Underpinning for Radical Transport and Catalysis in Biology. Philos. Trans. R. Soc., B 2006, 361, 1351–1364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (107).Irebo T; Reece SY; Sjodin M; Nocera DG; Hammarström L Proton-Coupled Electron Transfer of Tyrosine Oxidation: Buffer Dependence and Parallel Mechanisms. J. Am. Chem. Soc 2007, 129, 15462–15464. [DOI] [PubMed] [Google Scholar]
- (108).Chen J; Kuss-Petermann M; Wenger OS Distance Dependence of Bidirectional Concerted Proton-Electron Transfer in Phenol-Ru(2,2’-bipyridine)32+ Dyads. Chem. - Eur. J 2014, 20, 4098–4104. [DOI] [PubMed] [Google Scholar]
- (109).Gentry EC; Knowles RR Synthetic Applications of Proton-Coupled Electron Transfer. Acc. Chem. Res 2016, 49, 1546–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (110).Morton CM; Zhu Q; Ripberger H; Troian-Gautier L;Toa ZSD; Knowles RR; Alexanian EJ C-H Alkylation via Multisite-Proton-Coupled Electron Transfer of an Aliphatic C-H Bond. J. Am. Chem. Soc 2019, 141, 13253–13260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (111).Sutin N Theory of Electron Transfer Reactions: Insights and Hindsights. In Prog. Inorg. Chem 2007, 30, 441–498. [Google Scholar]
- (112).Eberson L Electron Transfer Reactions in Organic Chemistry. In Reactivity And Structure Concepts In Organic Chemistry [Online]; Springer Berlin: Heidelberg, 1987; pp 27–28. [Google Scholar]
- (113).Mader EA; Mayer JM The Importance of Precursor and Successor Complex Formation in a Bimolecular Proton-Electron Transfer Reaction. Inorg. Chem 2010, 49, 3685–3687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (114).Biczok L; Linschitz H Concerted Electron and Proton Movement in Quenching of Triplet C60 and Tetracene Fluorescence by Hydrogen-Bonded Phenol-Base Pairs. J. Phys. Chem 1995, 99, 1843–1845. [Google Scholar]
- (115).Biczók L; Gupta N; Linschitz H Coupled Electron-Proton Transfer in Interactions of Triplet C60 with Hydrogen-Bonded Phenols: Effects of Solvation, Deuteration, and Redox Potentials. J. Am. Chem. Soc 1997, 119, 12601–12609. [Google Scholar]
- (116).Morris WD; Mayer JM Separating Proton and Electron Transfer Effects on Three-Component Concerted Proton-Coupled Electron Transfer Reactions. J. Am. Chem. Soc 2017, 139, 10312–10319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (117).Fecenko CJ; Meyer TJ; Thorp HH Electrocatalytic Oxidation of Tyrosine by Parallel Rate-Limiting Proton Transfer and Multisite Electron-Proton Transfer. J. Am. Chem. Soc 2006, 128, 11020–11021. [DOI] [PubMed] [Google Scholar]
- (118).Fecenko CJ; Meyer TJ; Thorp HH Electrocatalytic Oxidation of Tyrosine by Parallel Rate-Limiting Proton Transfer and Multisite Electron–Proton Transfer. J. Am. Chem. Soc 2010, 132, 5323. [DOI] [PubMed] [Google Scholar]
- (119).Fecenko CJ; Thorp HH; Meyer TJ The Role of Free Energy Change in Coupled Electron–Proton Transfer. J. Am. Chem. Soc 2007, 129, 15098–15099. [DOI] [PubMed] [Google Scholar]
- (120).Gagliardi CJ; Murphy CF; Binstead RA; Thorp HH; Meyer TJ Concerted Electron–Proton Transfer (EPT) in the Oxidation of Cysteine. J. Phys. Chem. C 2015, 119, 7028–7038. [Google Scholar]
- (121).Tyburski R; Liu T; Glover SD; Hammarström L Proton-Coupled Electron Transfer Guidelines, Fair and Square. J. Am. Chem. Soc 2021, 143, 560–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (122).Song N; Stanbury DM Proton-Coupled Electron-Transfer Oxidation of Phenols by Hexachloroiridate(IV). Inorg. Chem 2008, 47, 11458–11460. [DOI] [PubMed] [Google Scholar]
- (123).Qiu G; Knowles RR Rate-Driving Force Relationships in the Multisite Proton-Coupled Electron Transfer Activation of Ketones. J. Am. Chem. Soc 2019, 141, 2721–2730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (124).Nilsen-Moe A; Reinhardt CR; Glover SD; Liang L; Hammes-Schiffer S; Hammarström L; Tommos C Proton-Coupled Electron Transfer from Tyrosine in the Interior of a de novo Protein: Mechanisms and Primary Proton Acceptor. J. Am. Chem. Soc 2020, 142, 11550–11559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (125).Pagba CV; McCaslin TG; Chi SH; Perry JW; Barry BA Proton-Coupled Electron Transfer and a Tyrosine-Histidine Pair in a Photosystem II-Inspired β-Hairpin Maquette: Kinetics on the Pico-second Time Scale. J. Phys. Chem. B 2016, 120, 1259–1272. [DOI] [PubMed] [Google Scholar]
- (126).Saito K; Shen JR; Ishida T; Ishikita H Short Hydrogen Bond between Redox-Active Tyrosine Yz and D1-His190 in the Photosystem II Crystal Structure. Biochemistry 2011, 50, 9836–9844. [DOI] [PubMed] [Google Scholar]
- (127).Markle TF; Darcy JW; Mayer JM A New Strategy to Efficiently Cleave and Form C–H Bonds Using Proton-Coupled Electron Transfer. Sci. Adv 2018, 4, No. eaat5776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (128).Darcy JW; Kolmar SS; Mayer JM Transition State Asymmetry in C-H Bond Cleavage by Proton-Coupled Electron Transfer. J. Am. Chem. Soc 2019, 141, 10777–10787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (129).Sayfutyarova ER; Lam YC; Hammes-Schiffer S Strategies for Enhancing the Rate Constant of C-H Bond Cleavage by Concerted Proton-Coupled Electron Transfer. J. Am. Chem. Soc 2019, 141, 15183–15189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (130).Eberson L; Larsson B; Maartmann-Moe K; Sæbø J; Fischer GW Electron Transfer Reactions in Organic Chemistry. Xii. Reactions of 4-Substituted Triarylaminium Radical Cations with Nucleophiles; Polar vs. Electron Transfer Pathways. Acta Chem. Scand 1987, 41b, 367–378. [Google Scholar]
- (131).Ener ME; Darcy JW; Menges FS; Mayer JM Base-Directed Photoredox Activation of C-H Bonds by PCET. J. Org. Chem 2020, 85, 7175–7180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (132).Wang D; Loose F; Chirik PJ; Knowles RR N-H Bond Formation in a Manganese(V) Nitride Yields Ammonia by Light-Driven Proton-Coupled Electron Transfer. J. Am. Chem. Soc 2019, 141, 4795–4799. [DOI] [PubMed] [Google Scholar]
- (133).Tarantino KT; Liu P; Knowles RR Catalytic Ketyl-Olefin Cyclizations Enabled by Proton-Coupled Electron Transfer. J. Am. Chem. Soc 2013, 135, 10022–10025. [DOI] [PubMed] [Google Scholar]
- (134).Choi GJ; Knowles RR Catalytic Alkene Carboaminations Enabled by Oxidative Proton-Coupled Electron Transfer. J. Am. Chem. Soc 2015, 137, 9226–9229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (135).Chalkley MJ; Drover MW; Peters JC Catalytic N2-to-NH3 (or −N2H4) Conversion by Well-Defined Molecular Coordination Complexes. Chem. Rev 2020, 120, 5582–5636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (136).Prier CK; Rankic DA; MacMillan DW Visible Light Photoredox Catalysis with Transition Metal Complexes: Applications in Organic Synthesis. Chem. Rev 2013, 113, 5322–5363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (137).Weller A Electron-Transfer and Complex Formation in the Excited State. Pure Appl. Chem 1968, 16, 115–124. [Google Scholar]
- (138).Arias-Rotondo DM; McCusker JK The Photophysics of Photoredox Catalysis: A Roadmap for Catalyst Design. Chem. Soc. Rev 2016, 45, 5803–5820. [DOI] [PubMed] [Google Scholar]
- (139).Bevernaegie R; Wehlin SAM; Elias B; Troian-Gautier L A Roadmap Towards Visible Light Mediated Electron Transfer Chemistry with Iridium(III) Complexes. Chemphotochem 2021, 5, 217–234. [Google Scholar]
- (140).Thompson DW; Ito A; Meyer TJ [Ru(bpy)3]2+* and Other Remarkable Metal-to-Ligand Charge Transfer (MLCT) Excited States. Pure Appl. Chem 2013, 85, 1257–1305. [Google Scholar]
- (141).Martínez AR; Morales LP; Ojeda ED; Rodríguez MC; Rodríguez-García I The Proven Versatility of Cp2TiCl. J. Org. Chem 2021, 86, 1311–1329. [DOI] [PubMed] [Google Scholar]
- (142).Resa S; Millán A; Fuentes N; Crovetto L; Luisa Marcos M; Lezama L; Choquesillo-Lazarte D; Blanco V; Campaña AG; Cárdenas DJ; et al. O–H and (CO)N–H Bond Weakening by Coordination to Fe(II). Dalton Trans. 2019, 48, 2179–2189. [DOI] [PubMed] [Google Scholar]
- (143).Chalkley MJ; Oyala PH; Peters JC Cp* Noninnocence Leads to a Remarkably Weak C–H Bond via Metallocene Protonation. J. Am. Chem. Soc 2019, 141, 4721–4729. [DOI] [PubMed] [Google Scholar]
- (144).van Leest NP; Epping RFJ; van Vliet KM; Lankelma M; van den Heuvel EJ; Heijtbrink N; Broersen R; de Bruin B Chapter Two - Single-Electron Elementary Steps in Homogeneous Organometallic Catalysis. In Advances in Organometallic Chemistry; Pérez PJ, Stone FGA, West R, Eds.; Academic Press: 2018; Vol. 70, pp 71–180. [Google Scholar]
- (145).Cuerva JM; Campaña AG; Justicia J; Rosales A; Oller-López JL; Robles R; Cárdenas DJ; Buñuel E; Oltra JE Water: The Ideal Hydrogen-Atom Source in Free-Radical ChemistryMediated by TiIII and Other Single-Electron-Transfer Metals? Angew. Chem., Int. Ed 2006, 45, 5522–5526. [DOI] [PubMed] [Google Scholar]
- (146).Paradas M; Campaña AG; Jiménez T; Robles R; Oltra JE; Buñuel E;Justicia J; Cárdenas DJ; Cuerva JM Understanding the Exceptional Hydrogen-Atom Donor Characteristics of Water in TiIII-Mediated Free-Radical Chemistry. J. Am. Chem. Soc 2010, 132, 12748–12756. [DOI] [PubMed] [Google Scholar]
- (147).Paradas M; Campaña AG; Marcos ML; Justicia J; Haidour A; Robles R; Cárdenas DJ; Oltra JE; Cuerva JM Unprecedented H-Atom Transfer from Water to Ketyl Radicals Mediated by Cp2TiCl. Dalton Trans. 2010, 39, 8796–8800. [DOI] [PubMed] [Google Scholar]
- (148).Kolmar SS; Mayer JM SmI2(H2O)N Reduction of Electron Rich Enamines by Proton-Coupled Electron Transfer. J. Am. Chem. Soc 2017, 139, 10687–10692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (149).Shi S; Szostak R; Szostak M Proton-Coupled Electron Transfer in the Reduction of Carbonyls Using SmI2-H2O: Implications for the Reductive Coupling of Acyl-Type Ketyl Radicals with SmI2-H2O. Org. Biomol. Chem 2016, 14, 9151–9157. [DOI] [PubMed] [Google Scholar]
- (150).Chciuk TV; Li AM; Vazquez-Lopez A; Anderson WR; Flowers RA Secondary Amides as Hydrogen Atom Transfer Promoters for Reactions of Samarium Diiodide. Org. Lett 2017, 19, 290–293. [DOI] [PubMed] [Google Scholar]
- (151).Molander GA; Harris CR Sequencing Reactions with Samarium(II) Iodide. Chem. Rev 1996, 96, 307–338. [DOI] [PubMed] [Google Scholar]
- (152).Edmonds DJ; Johnston D; Procter DJ Samarium(II)-Iodide-Mediated Cyclizations in Natural Product Synthesis. Chem. Rev 2004, 104, 3371–3404. [DOI] [PubMed] [Google Scholar]
- (153).Nicolaou KC; Ellery SP; Chen JS Samarium Diiodide Mediated Reactions in Total Synthesis. Angew. Chem., Int. Ed 2009, 48, 7140–7165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (154).Szostak M; Fazakerley NJ; Parmar D; Procter DJ Cross-Coupling Reactions Using Samarium(II) Iodide. Chem. Rev 2014, 114, 5959–6039. [DOI] [PubMed] [Google Scholar]
- (155).Hoz S Samarium Iodide Showcase: Unraveling the Mechanistic Puzzle. Acc. Chem. Res 2020, 53, 2680–2691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (156).Bartulovich CO; Flowers RA Coordination-Induced O–H Bond Weakening in Sm(II)-Water Complexes. Dalton Trans. 2019, 48, 16142–16147. [DOI] [PubMed] [Google Scholar]
- (157).Tarantino KT; Miller DC; Callon TA; Knowles RR Bond-Weakening Catalysis: Conjugate Aminations Enabled by the Soft Homolysis of Strong N–H Bonds. J. Am. Chem. Soc 2015, 137, 6440–6443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (158).Kim D; Rahaman SMW; Mercado BQ; Poli R; Holland PL Roles of Iron Complexes in Catalytic Radical Alkene Cross-Coupling: A Computational and Mechanistic Study. J. Am. Chem. Soc 2019, 141, 7473–7485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (159).Hammond GS A Correlation of Reaction Rates. J. Am. Chem. Soc 1955, 77, 334–338. [Google Scholar]
- (160).Leffler JE Parameters for the Description of Transition States. Science 1953, 117, 340–341. [DOI] [PubMed] [Google Scholar]
- (161).Mayer JM Understanding Hydrogen Atom Transfer: From Bond Strengths to Marcus Theory. Acc. Chem. Res 2011, 44, 36–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (162).Nomrowski J; Wenger OS Photoinduced PCET in Ruthenium–Phenol Systems: Thermodynamic Equivalence of Uni- and Bidirectional Reactions. Inorg. Chem 2015, 54, 3680–3687. [DOI] [PubMed] [Google Scholar]
- (163).Sjodin M; Styring S; Wolpher H; Xu Y; Sun L; Hammarström L Switching the Redox Mechanism: Models for Proton-Coupled Electron Transfer from Tyrosine and Tryptophan. J. Am. Chem. Soc 2005, 127, 3855–3863. [DOI] [PubMed] [Google Scholar]
- (164).Bourrez M; Steinmetz R; Ott S; Gloaguen F; Hammarström L Concerted Proton-Coupled Electron Transfer from a Metal-Hydride Complex. Nat. Chem 2015, 7, 140–145. [DOI] [PubMed] [Google Scholar]
- (165).Johannissen LO; Irebo T; Sjodin M; Johansson O; Hammarström L The Kinetic Effect of Internal Hydrogen Bonds on Proton-Coupled Electron Transfer from Phenols: A Theoretical Analysis with Modeling of Experimental Data. J. Phys. Chem. B 2009, 113, 16214–16225. [DOI] [PubMed] [Google Scholar]
- (166).Eisenhart TT; Howland WC; Dempsey JL Proton-Coupled Electron Transfer Reactions with Photometric Bases Reveal Free Energy Relationships for Proton Transfer. J. Phys. Chem. B 2016, 120, 7896–7905. [DOI] [PubMed] [Google Scholar]
- (167).Zhu H; Sommerhalter M; Nguy AK; Klinman JP Solvent and Temperature Probes of the Long-Range Electron-Transfer Step in Tyramine β-Monooxygenase: Demonstration of a Long-Range Proton-Coupled Electron-Transfer Mechanism. J. Am. Chem. Soc 2015, 137, 5720–5729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (168).Schneider J; Bangle RE; Swords WB; Troian-Gautier L; Meyer GJ Determination of Proton-Coupled Electron Transfer Reorganization Energies with Application to Water Oxidation Catalysts. J. Am. Chem. Soc 2019, 141, 9758–9763. [DOI] [PubMed] [Google Scholar]
- (169).Bailey WD; Dhar D; Cramblitt AC; Tolman WB Mechanistic Dichotomy in Proton-Coupled Electron-Transfer Reactions of Phenols with a Copper Superoxide Complex. J. Am. Chem. Soc 2019, 141, 5470–5480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (170).Parada GA; Goldsmith ZK; Kolmar S; Pettersson Rimgard B; Mercado BQ; Hammarström L; Hammes-Schiffer S; Mayer JM Concerted Proton-Electron Transfer Reactions in the Marcus Inverted Region. Science 2019, 364, 471–475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (171).Bim D; Maldonado-Dominguez M; Rulisek L; Srnec M Beyond the Classical Thermodynamic Contributions to Hydrogen Atom Abstraction Reactivity. Proc. Natl. Acad. Sci. U. S. A 2018, 115, E10287–E10294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (172).Tedder JM Which Factors Determine the Reactivity and Regioselectivity of Free Radical Substitution and Addition Reactions? Angew. Chem., Int. Ed. Engl 1982, 21, 401–410. [Google Scholar]
- (173).Roberts BP Polarity-Reversal Catalysis of Hydrogen-Atom Abstraction Reactions: Concepts and Applications in Organic Chemistry. Chem. Soc. Rev 1999, 28, 25–35. [Google Scholar]
- (174).Goetz MK; Anderson JS Experimental Evidence for pKa-Driven Asynchronicity in C-H Activation by a Terminal Co(III)-Oxo Complex. J. Am. Chem. Soc 2019, 141, 4051–4062. [DOI] [PubMed] [Google Scholar]
- (175).Roth JP Intrinsic and Thermodynamic Influences on Hydrogen Atom Transfer Reactions Involving Transition Metal Complexes. Ph.D. Dissertation, University of Washington, 2000; p 39. [Google Scholar]
- (176).Kotani H; Shimomura H; Ikeda K; Ishizuka T; Shiota Y; Yoshizawa K; Kojima T Mechanistic Insight into Concerted Proton-Electron Transfer of a RuIV-Oxo Complex: A Possible Oxidative Asynchronicity. J. Am. Chem. Soc 2020, 142, 16982–16989. [DOI] [PubMed] [Google Scholar]
- (177).Huang T; Rountree ES; Traywick AP; Bayoumi M; Dempsey JL Switching between Stepwise and Concerted Proton-Coupled Electron Transfer Pathways in Tungsten Hydride Activation. J. Am. Chem. Soc 2018, 140, 14655–14669. [DOI] [PubMed] [Google Scholar]
- (178).Schrock RR Catalytic Reduction of Dinitrogen to Ammonia at a Single Molybdenum Center. Acc. Chem. Res 2005, 38, 955–962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (179).Lindley BM; Appel AM; Krogh-Jespersen K; Mayer JM; Miller AJM Evaluating the Thermodynamics of Electrocatalytic N2 Reduction in Acetonitrile. ACS Energy Lett. 2016, 1, 698–704. [Google Scholar]
- (180).Stanbury DM Oxidation of Hydrazine in Aqueous Solution. Prog. Inorg. Chem 2007, 511–561. [Google Scholar]
- (181).Yandulov DV; Schrock RR Catalytic Reduction of Dinitrogen to Ammonia at a Single Molybdenum Center. Science 2003, 301, 76. [DOI] [PubMed] [Google Scholar]
- (182).Scepaniak JJ; Young JA; Bontchev RP; Smith JM Formation of Ammonia from an Iron Nitrido Complex. Angew. Chem. Int. Ed 2009, 48, 3158–3160. [DOI] [PubMed] [Google Scholar]
- (183).Scheibel MG; Abbenseth J; Kinauer M; Heinemann FW; Würtele C; de Bruin B; Schneider S Homolytic N–H Activation of Ammonia: Hydrogen Transfer of Parent Iridium Ammine, Amide, Imide, and Nitride Species. Inorg. Chem 2015, 54, 9290–9302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (184).Bezdek MJ; Chirik PJ Interconversion of Molybdenum Imido and Amido Complexes by Proton-Coupled Electron Transfer. Angew. Chem., Int. Ed 2018, 57, 2224–2228. [DOI] [PubMed] [Google Scholar]
- (185).Margulieux GW; Kim S; Chirik PJ Determination of the N–H Bond Dissociation Free Energy in a Pyridine(diimine)-molybdenum Complex Prepared by Proton-Coupled Electron Transfer. Inorg. Chem 2020, 59, 15394–15401. [DOI] [PubMed] [Google Scholar]
- (186).Yandulov DV; Schrock RR Studies Relevant to Catalytic Reduction of Dinitrogen to Ammonia by Molybdenum Triamidoamine Complexes. Inorg. Chem 2005, 44, 1103–1117. [DOI] [PubMed] [Google Scholar]
- (187).Matson BD; Peters JC Fe-Mediated HER vs N2RR: Exploring Factors That Contribute to Selectivity in P3EFe(N2) (E = B, Si, C) Catalyst Model Systems. ACS Catal 2018, 8, 1448–1455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (188).Bezdek MJ; Chirik PJ Thermodynamics of N–H Bond Formation in Bis(phosphine) Molybdenum(II) Diazenides and the Influence of the Trans Ligand. Dalton Trans. 2016, 45, 15922–15930. [DOI] [PubMed] [Google Scholar]
- (189).Bruch QJ; Connor GP; Chen C-H; Holland PL; Mayer JM; Hasanayn F; Miller AJM Dinitrogen Reduction to Ammonium at Rhenium Utilizing Light and Proton-Coupled Electron Transfer. J. Am. Chem. Soc 2019, 141, 20198–20208. [DOI] [PubMed] [Google Scholar]
- (190).Pappas I; Chirik PJ Catalytic Proton Coupled Electron Transfer from Metal Hydrides to Titanocene Amides, Hydrazides and Imides: Determination of Thermodynamic Parameters Relevant to Nitrogen Fixation. J. Am. Chem. Soc 2016, 138, 13379–13389. [DOI] [PubMed] [Google Scholar]
- (191).Rittle J; Peters JC N–H Bond Dissociation Enthalpies and Facile H Atom Transfers for Early Intermediates of Fe–N2 and Fe–CN Reductions. J. Am. Chem. Soc 2017, 139, 3161–3170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (192).Bezdek MJ; Pappas I; Chirik PJ Determining and Understanding N-H Bond Strengths in Synthetic Nitrogen Fixation Cycles. In Nitrogen Fixation; Nishibayashi Y, Ed.; Springer International Publishing: Cham, 2017; pp 1–21. [Google Scholar]
- (193).Nurdin L; Yang Y; Neate PGN; Piers WE; Maron L; Neidig ML; Lin J-B; Gelfand BS Activation of Ammonia and Hydrazine by Electron Rich Fe(II) Complexes Supported by a Dianionic Pentadentate Ligand Platform through a Common Terminal Fe(III) Amido Intermediate. Chem. Sci 2021, 12, 2231–2241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (194).Dunn PL; Cook BJ; Johnson SI; Appel AM; Bullock RM Oxidation of Ammonia with Molecular Complexes. J. Am. Chem. Soc 2020, 142, 17845–17858. [DOI] [PubMed] [Google Scholar]
- (195).Bezdek MJ; Guo S; Chirik PJ Coordination-Induced Weakening of Ammonia, Water, and Hydrazine X–H Bonds in a Molybdenum Complex. Science 2016, 354, 730. [DOI] [PubMed] [Google Scholar]
- (196).Eckert NA; Vaddadi S; Stoian S; Lachicotte RJ; Cundari TR; Holland PL Coordination-Number Dependence of Reactivity in an Imidoiron(III) Complex. Angew. Chem. Int. Ed 2006, 45, 6868–6871. [DOI] [PubMed] [Google Scholar]
- (197).Baek Y; Betley TA Catalytic C–H Amination Mediated by Dipyrrin Cobalt Imidos. J. Am. Chem. Soc 2019, 141, 7797–7806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (198).Wilding MJT; Iovan DA; Betley TA High-Spin Iron Imido Complexes Competent for C–H Bond Amination. J. Am. Chem. Soc 2017, 139, 12043–12049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (199).Wiese S; McAfee JL; Pahls DR; McMullin CL; Cundari TR; Warren TH C–H Functionalization Reactivity of a Nickel–Imide. J. Am. Chem. Soc 2012, 134, 10114–10121. [DOI] [PubMed] [Google Scholar]
- (200).Zhang L; Liu Y; Deng L Three-Coordinate Cobalt(IV) and Cobalt(V) Imido Complexes with N-Heterocyclic Carbene Ligation: Synthesis, Structure, and their Distinct Reactivity in C–H Bond Amination. J. Am. Chem. Soc 2014, 136, 15525–15528. [DOI] [PubMed] [Google Scholar]
- (201).Williams RE; Bruce NC ‘New Uses for an Old Enzyme’-The Old Yellow Enzyme Family of Flavoenzymes. Microbiology 2002, 148, 1607–1614. [DOI] [PubMed] [Google Scholar]
- (202).Estabrook RW A Passion for P450s (Rememberances of the Early History of Research on Cytochrome P450). Drug Metab. Dispos 2003, 31, 1461–1473. [DOI] [PubMed] [Google Scholar]
- (203).McEvoy JP; Brudvig GW Water-Splitting Chemistry of Photosystem II. Chem. Rev 2006, 106, 4455–4483. [DOI] [PubMed] [Google Scholar]
- (204).Siegbahn PE; Blomberg MR Quantum Chemical Studies of Proton-Coupled Electron Transfer in Metalloenzymes. Chem. Rev 2010, 110, 7040–7061. [DOI] [PubMed] [Google Scholar]
- (205).Warren JJ; Mayer JM Moving Protons and Electrons in Biomimetic Systems. Biochemistry 2015, 54, 1863–1878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (206).Klinman JP; Kohen A Hydrogen Tunneling Links Protein Dynamics to Enzyme Catalysis. Annu. Rev. Biochem 2013, 82, 471–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (207).Layfield JP; Hammes-Schiffer S Hydrogen Tunneling in Enzymes and Biomimetic Models. Chem. Rev 2014, 114, 3466–3494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (208).Vinyard DJ; Brudvig GW Progress Toward a Molecular Mechanism of Water Oxidation in Photosystem II. Annu. Rev. Phys. Chem 2017, 68, 101–116. [DOI] [PubMed] [Google Scholar]
- (209).Zhang AY; Koone JC; Dashnaw CM; Zahler CT; Shaw AF Complete Charge Regulation by a Redox Enzyme Upon Single Electron Transfer. Angew. Chem. Int. Ed 2020, 59, 10989–10995. [DOI] [PubMed] [Google Scholar]
- (210).Zahler CT; Zhou H; Abdolvahabi A; Holden RL; Rasouli S; Tao P; Shaw BF Direct Measurement of Charge Regulation in Metalloprotein Electron Transfer. Angew. Chem. Int. Ed 2018, 57, 5364–5368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (211).Zahler CT; Shaw BF What Are We Missing by Not Measuring the Net Charge of Proteins? Chem. - Eur. J 2019, 25, 7581–7590. [DOI] [PubMed] [Google Scholar]
- (212).Yosca TH; Rittle J; Krest CM; Onderko EL; Silakov A; Calixto JC; Behan RK; Green MT Iron(IV)hydroxide pKa and the Role of Thiolate Ligation in C-H Bond Activation by Cytochrome P450. Science 2013, 342, 825–829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (213).Mittra K; Green MT Reduction Potentials of P450 Compounds I And II: Insight into the Thermodynamics of C-H Bond Activation. J. Am. Chem. Soc 2019, 141, 5504–5510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (214).Mitchell P The Protonmotive Q Cycle: A General Formulation. FEBS Lett. 1975, 59, 137–139. [DOI] [PubMed] [Google Scholar]
- (215).Thauer RK; Kaster AK; Seedorf H; Buckel W; Hedderich R Methanogenic Archaea: Ecologically Relevant Differences in Energy Conservation. Nat. Rev. Microbiol 2008, 6, 579–591. [DOI] [PubMed] [Google Scholar]
- (216).Nitschke W; Russell MJ Redox Bifurcations: Mechanisms and Importance to Life Now, and at its Origin: A Widespread Means of Energy Conversion in Biology Unfolds. BioEssays 2012, 34, 106–9. [DOI] [PubMed] [Google Scholar]
- (217).Buckel W; Thauer RK Energy Conservation via Electron Bifurcating Ferredoxin Reduction and Proton/Na+ Translocating Ferredoxin Oxidation. Biochim. Biophys. Acta, Bioenerg 2013, 1827, 94–113. [DOI] [PubMed] [Google Scholar]
- (218).Yuly JL; Lubner CE; Zhang P; Beratan DN; Peters JW Electron Bifurcation: Progress and Grand Challenges. Chem. Commun 2019, 55, 11823–11832. [DOI] [PubMed] [Google Scholar]
- (219).Zhang P; Yuly JL; Lubner CE; Mulder DW; King PW; Peters JW; Beratan DN Electron Bifurcation: Thermodynamics and Kinetics of Two-Electron Brokering in Biological Redox Chemistry. Acc. Chem. Res 2017, 50, 2410–2417. [DOI] [PubMed] [Google Scholar]
- (220).Peters JW; Beratan DN; Bothner B; Dyer RB; Harwood AS; Heiden ZM; Hille R; Jones AK; King PW; Lu Y; et al. A New Era for Electron Bifurcation. Curr. Opin. Chem. Biol 2018, 47, 32–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (221).Yuly JL; Zhang P; Lubner CE; Peters JW; Beratan DN Universal Free-Energy Landscape Produces Efficient and Reversible Electron Bifurcation. Proc. Natl. Acad. Sci U. S. A 2020, 117, 21045–21051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (222).Crofts AR; Lhee S; Crofts SB; Cheng J; Rose S Proton Pumping in the bc1 Complex: A New Gating Mechanism that Prevents Short Circuits. Biochim. Biophys. Acta, Bioenerg 2006, 1757, 1019-1034. [DOI] [PubMed] [Google Scholar]
- (223).Li F; Hinderberger J; Seedorf H; Zhang J; Buckel W; Thauer RK Coupled Ferredoxin and Crotonyl Coenzyme A (CoA) Reduction with NADH Catalyzed by the Butyryl-CoA Dehydrogenase/Etf Complex From Clostridium kluyveri. J. Bacteriol 2008, 190, 843–850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (224).Herrmann G; Jayamani E; Mai G; Buckel W Energy Conservation via Electron-Transferring Flavoprotein in Anaerobic Bacteria. J. Bacteriol 2008, 190, 784–791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (225).Buckel W; Thauer RK Flavin-Based Electron Bifurcation, a New Mechanism of Biological Energy Coupling. Chem. Rev 2018, 118, 3862–3886. [DOI] [PubMed] [Google Scholar]
- (226).Wagner T; Koch J; Ermler U; Shima S Methanogenic Heterodisulfide Reductase (HdrABC-MvhAGD) Uses Two Non-cubane [4Fe-4S] Clusters for Reduction. Science 2017, 357, 699–703. [DOI] [PubMed] [Google Scholar]
- (227).Kaster AK; Moll J; Parey K; Thauer RK Coupling of Ferredoxin and Heterodisulfide Reduction via Electron Bifurcation in Hydrogenotrophic Methanogenic Archaea. Proc. Natl. Acad. Sci. U. S. A 2011, 108, 2981–2986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (228).Schut GJ; Mohamed-Raseek N; Tokmina-Lukaszewska M; Mulder DW; Nguyen DMN; Lipscomb GL; Hoben JP; Patterson A; Lubner CE; King PW; et al. The Catalytic Mechanism of Electron-Bifurcating Electron Transfer Flavoproteins (ETFs) Involves an Intermediary Complex with NAD+. J. Biol. Chem 2019, 294, 3271–3283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (229).Hoke KR; Cobb N; Armstrong FA; Hille R Electrochemical Studies of Arsenite Oxidase: An Unusual Example of a Highly Cooperative Two-Electron Molybdenum Center. Biochemistry 2004, 43, 1667–1674. [DOI] [PubMed] [Google Scholar]
- (230).Evans DH One-Electron and Two-Electron Transfers in Electrochemistry and Homogeneous Solution Reactions. Chem. Rev 2008, 108, 2113–2144. [DOI] [PubMed] [Google Scholar]
- (231).Crofts AR Proton-Coupled Electron Transfer at the Qo-Site of the bc1 Complex Controls the Rate of Ubihydroquinone Oxidation. Biochim. Biophys. Acta, Bioenerg 2004, 1655, 77–92. [DOI] [PubMed] [Google Scholar]
- (232).Iwaki M; Yakovlev G; Hirst J; Osyczka A; Dutton PL; Marshall D; Rich PR Direct Observation of Redox-Linked Histidine Protonation Changes in the Iron-Sulfur Protein of the Cytochrome bc1 Complex by ATR-FTIR Spectroscopy. Biochemistry 2005, 44, 4230–4237. [DOI] [PubMed] [Google Scholar]
- (233).Crofts AR; Hong S; Ugulava N; Barquera B; Gennis R; Guergova-Kuras M; Berry EA Pathways for Proton Release During Ubihydroquinone Oxidation by the bc1 Complex. Proc. Natl. Acad. Sci. U.S.A 1999, 96, 10021–10026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (234).Kirchheim R; Pundt A 25 - Hydrogen in Metals. In Physical Metallurgy, 5th ed.; Laughlin DE, Hono K, Eds.; Elsevier: Oxford, 2014; pp 2597–2705. [Google Scholar]
- (235).Janotti A; Van de Walle CG Fundamentals of Zinc Oxide as a Semiconductor. Rep. Prog. Phys 2009, 72, 126501. [Google Scholar]
- (236).Van de Walle CG; Neugebauer J Universal Alignment of Hydrogen Levels in Semiconductors, Insulators and Solutions. Nature 2003, 423, 626–628. [DOI] [PubMed] [Google Scholar]
- (237).Van de Walle CG; Neugebauer J Hydrogen in Semiconductors. Annu. Rev. Mater. Res 2006, 36, 179–198. [Google Scholar]
- (238).Conway BE Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications; Springer Science & Business Media: New York, 1999; pp 221–257. [Google Scholar]
- (239).Conway BE; Gileadi E Kinetic Theory of Pseudo-Capacitance and Electrode Reactions at Appreciable Surface Coverage. Trans. Faraday Soc 1962, 58, 2493–2509. [Google Scholar]
- (240).Fleischmann S; Mitchell JB; Wang R; Zhan C; Jiang D.-e.; Presser V; Augustyn V Pseudocapacitance: From Fundamental Understanding to High Power Energy Storage Materials. Chem. Rev 2020, 120, 6738–6782. [DOI] [PubMed] [Google Scholar]
- (241).Costentin C; Porter TR; Saveant JM How Do Pseudocapacitors Store Energy? Theoretical Analysis and Experimental Illustration. ACS Appl. Mater. Interfaces 2017, 9, 8649–8658. [DOI] [PubMed] [Google Scholar]
- (242).Koper MTM Thermodynamic Theory of Multi-Electron Transfer Reactions: Implications for Electrocatalysis. J. Electroanal. Chem 2011, 660, 254–260. [Google Scholar]
- (243).Seh ZW; Kibsgaard J; Dickens CF; Chorkendorff I; Nørskov JK; Jaramillo TF Combining Theory and Experiment in Electrocatalysis: Insights into Materials Design. Science 2017, 355, No. eaad4998. [DOI] [PubMed] [Google Scholar]
- (244).Nørskov JK; Bligaard T; Logadottir A; Kitchin JR; Chen JG; Pandelov S; Stimming U Trends in the Exchange Current for Hydrogen Evolution. J. Electrochem. Soc 2005, 152, J23. [Google Scholar]
- (245).Quaino P; Juarez F; Santos E; Schmickler W Volcano Plots in Hydrogen Electrocatalysis – Uses and Abuses. Beilstein J. Nanotechnol 2014, 5, 846–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (246).Schmickler W; Trasatti S Comment On “Trends in the Exchange Current for Hydrogen Evolution” [J. Electrochem. Soc., 152, J23 (2005)]. J. Electrochem. Soc 2006, 153, L31. [Google Scholar]
- (247).Campbell CT; Sellers JRV Enthalpies and Entropies of Adsorption on Well-Defined Oxide Surfaces: Experimental Measurements. Chem. Rev 2013, 113, 4106–4135. [DOI] [PubMed] [Google Scholar]
- (248).Silbaugh TL; Campbell CT Energies of Formation Reactions Measured for Adsorbates on Late Transition Metal Surfaces. J. Phys. Chem. C 2016, 120, 25161–25172. [Google Scholar]
- (249).García-Diéguez M; Hibbitts DD; Iglesia E Hydrogen Chemisorption Isotherms on Platinum Particles at Catalytic Temperatures: Langmuir and Two-Dimensional Gas Models Revisited. J. Phys. Chem. C 2019, 123, 8447–8462. [Google Scholar]
- (250).Paier J; Penschke C; Sauer J Oxygen Defects and Surface Chemistry of Ceria: Quantum Chemical Studies Compared to Experiment. Chem. Rev 2013, 113, 3949–3985. [DOI] [PubMed] [Google Scholar]
- (251).Sauer J Molecular Models in ab Initio Studies of Solids and Surfaces: From Ionic Crystals and Semiconductors to Catalysts. Chem. Rev 1989, 89, 199–255. [Google Scholar]
- (252).Jackson MN; Pegis ML; Surendranath Y Graphite-Conjugated Acids Reveal a Molecular Framework for Proton-Coupled Electron Transfer at Electrode Surfaces. ACS Cent. Sci 2019, 5, 831–841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (253).Gileadi E Electrosorption; Springer: Boston, MA, 1967; pp 1–18. [Google Scholar]
- (254).Rizo R; Sitta E; Herrero E; Climent V; Feliu JM Towards the Understanding of the Interfacial pH Scale at Pt(111) Electrodes. Electrochim. Acta 2015, 162, 138–145. [Google Scholar]
- (255).Fearon J; Watson GW Hydrogen Adsorption and Diffusion on Pt {111} and PtSn {111}. J. Mater. Chem 2006, 16, 1989–1996. [Google Scholar]
- (256).Karlberg GS; Jaramillo TF; Skúlason E; Rossmeisl J; Bligaard T; Nørskov JK Cyclic Voltammograms for H on Pt(111) and Pt(100) from First Principles. Phys. Rev. Lett 2007, 99, 126101. [DOI] [PubMed] [Google Scholar]
- (257).Asiri HA; Anderson AB Using Gibbs Energies to Calculate the Pt(111) Hupd Cyclic Voltammogram. J. Phys. Chem. C 2013, 117, 17509–17513. [Google Scholar]
- (258).Lindgren P; Kastlunger G; Peterson AA A Challenge to the G ~ 0 Interpretation of Hydrogen Evolution. ACS Catal. 2020, 10, 121–128. [Google Scholar]
- (259).Jerkiewicz G; Zolfaghari A Determination of the Energy of the Metal–Underpotential-Deposited Hydrogen Bond for Rhodium Electrodes. J. Phys. Chem 1996, 100, 8454–8461. [Google Scholar]
- (260).Jerkiewicz G Hydrogen Sorption At/In Electrodes. Prog. Surf. Sci 1998, 57, 137–186. [Google Scholar]
- (261).Marković NM; Schmidt TJ; Grgur BN; Gasteiger HA; Behm RJ; Ross PN Effect of Temperature on Surface Processes at the Pt(111)–Liquid Interface: Hydrogen Adsorption, Oxide Formation, and CO Oxidation. J. Phys. Chem. B 1999, 103, 8568–8577. [Google Scholar]
- (262).Lasia A Modeling of Hydrogen Upd Isotherms. J. Electroanal. Chem 2004, 562, 23–31. [Google Scholar]
- (263).Kowalczyk P; Savard S; Lasia A Determination of the Adsorption Energy Distribution Function of Upd Hydrogen on Monocrystalline Platinum. J. Electroanal. Chem 2004, 574, 41–47. [Google Scholar]
- (264).Wise CF; Mayer JM Electrochemically Determined O–H Bond Dissociation Free Energies of NiO Electrodes Predict Proton-Coupled Electron Transfer Reactivity. J. Am. Chem. Soc 2019, 141, 14971–14975. [DOI] [PubMed] [Google Scholar]
- (265).Pourbaix M Atlas D’équilibres Électrochimiques; Gauthier-Villars: Paris, 1963; p 644. [Google Scholar]
- (266).Pourbaix M Thermodynamics and Corrosion. Corros. Sci 1990, 30, 963–988. [Google Scholar]
- (267).Stumm W; Morgan JJ Aquatic Chemistry: Chemical Equilibria and Rates in Natural Waters, 3rd ed.; Wiley-Interscience: New York, 1995; Section 8.4, pp 455–464. [Google Scholar]
- (268).Boschloo G; Hagfeldt A Spectroelectrochemistry of Nano-structured NiO. J. Phys. Chem. B 2001, 105, 3039–3044. [Google Scholar]
- (269).Liu Q; Chen Q; Zhang Q; Xiao Y; Zhong X; Dong G; Delplancke-Ogletree M-P; Terryn H; Baert K; Reniers F; et al. In Situ Electrochromic Efficiency of a Nickel Oxide Thin Film: Origin of Electrochemical Process and Electrochromic Degradation. J. Mater. Chem. C 2018, 6, 646–653. [Google Scholar]
- (270).Manjakkal L; Szwagierczak D; Dahiya R Metal Oxides Based Electrochemical pH Sensors: Current Progress and Future Perspectives. Prog. Mater. Sci 2020, 109, 100635. [Google Scholar]
- (271).Brown ES; Peczonczyk SL; Wang Z; Maldonado S Photoelectrochemical Properties of CH3-Terminated P-Type GaP(111)A. J. Phys. Chem. C 2014, 118, 11593–11600. [Google Scholar]
- (272).Finlayson MF; Wheeler BL; Kakuta N; Park KH; Bard AJ; Campion A; Fox MA; Webber SE; White JM Determination of Flat-Band Position of Cadmium Sulfide Crystals, Films, and Powders by Photocurrent and Impedance Techniques, Photoredox Reaction Mediated by Intragap States. J. Phys. Chem 1985, 89, 5676–5681. [Google Scholar]
- (273).Stoerzinger KA; Rao RR; Wang XR; Hong WT; Rouleau CM; Shao-Horn Y The Role of Ru Redox in pH-Dependent Oxygen Evolution on Rutile Ruthenium Dioxide Surfaces. Chem. 2017, 2, 668–675. [Google Scholar]
- (274).Gambardella AA; Bjorge NS; Alspaugh VK; Murray RW Voltammetry of Diffusing 2 nm Iridium Oxide Nanoparticles. J. Phys. Chem. C 2011, 115, 21659–21665. [Google Scholar]
- (275).Lyon LA; Hupp JT Energetics of the Nanocrystalline Titanium Dioxide/Aqueous Solution Interface: Approximate Conduction Band Edge Variations Between H0 = − 10 And H− = + 26. J. Phys. Chem. B 1999, 103, 4623–4628. [Google Scholar]
- (276).Lemon BI; Hupp JT Electrochemical Quartz Crystal Microbalance Studies of Electron Addition at Nanocrystalline Tin Oxide/Water and Zinc Oxide/Water Interfaces: Evidence for Band-Edge-Determining Proton Uptake. J. Phys. Chem. B 1997, 101, 2426–2429. [Google Scholar]
- (277).Koelle U; Moser J; Graetzel M Dynamics of Interfacial Charge-Transfer Reactions in Semiconductor Dispersions. Reduction of Cobaltoceniumdicarboxylate in Colloidal Titania. Inorg. Chem 1985, 24, 2253–2258. [Google Scholar]
- (278).Peper JL Studies of Titanium Dioxide Nanoparticles: Thermodynamics and Reactivity. Ph.D. Dissertation, Yale University, New Haven, CT, 2019; Chapter 4, pp 45–81. Figure 17 is from p 55. [Google Scholar]
- (279).Nozik AJ Photoelectrochemistry: Applications to Solar Energy Conversion. Annu. Rev. Phys. Chem 1978, 29, 189–222. [Google Scholar]
- (280).White HS; Peterson JD; Cui Q; Stevenson KJ Voltammetric Measurement of Interfacial Acid/Base Reactions. J. Phys. Chem. B 1998, 102, 2930–2934. [Google Scholar]; The pK1/2 is defined in this paper as the pH at which half of the surface acid groups are deprotonated when the electrode potential is at the point of zero charge.
- (281).Jackson MN; Surendranath Y Molecular Control of Heterogeneous Electrocatalysis through Graphite Conjugation. Acc. Chem. Res 2019, 52, 3432–3441. [DOI] [PubMed] [Google Scholar]
- (282).Warburton RE; Hutchison P; Jackson MN; Pegis ML; Surendranath Y; Hammes-Schiffer S Interfacial Field-Driven Proton-Coupled Electron Transfer at Graphite-Conjugated Organic Acids. J. Am. Chem. Soc 2020, 142, 20855–20864. [DOI] [PubMed] [Google Scholar]
- (283).Koene L; Sluyters-Rehbach M; Sluyters JH The Relation between Electrical Double Layer Data and Electronic Work Functions for Amalgams. J. Electroanal. Chem 1995, 396, 569–581. [Google Scholar]
- (284).Bard AJ; Faulkner LR Electrochemical Methods: Fundamentals and Applications, 2nd ed.; John Wiley & Sons: NY, 2001; p 591 for the CV of an ideal Nernstian reaction following a Langmuir isotherm. [Google Scholar]
- (285).Eckermann AL; Feld DJ; Shaw JA; Meade TJ Electrochemistry of Redox-Active Self-Assembled Monolayers. Coord. Chem. Rev 2010, 254, 1769–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (286).Agarwal RG; Kim H-J; Mayer JM Nanoparticle O–H Bond Dissociation Free Energies from Equilibrium Measurements of Cerium Oxide Colloids. J. Am. Chem. Soc 2021, 143, 2896–2907. [DOI] [PubMed] [Google Scholar]
- (287).Pavlishchuk VV; Addison AW Conversion Constants for Redox Potentials Measured Versus Different Reference Electrodes in Acetonitrile Solutions at 25°C. Inorg. Chim. Acta 2000, 298, 97–102. [Google Scholar]
- (288).Aranzaes JR; Daniel M-C; Astruc D Metallocenes as References for the Determination of Redox Potentials by Cyclic Voltammetry — Permethylated Iron and Cobalt Sandwich Complexes, Inhibition by Polyamine Dendrimers, and the Role of Hydroxy-Containing Ferrocenes. Can. J. Chem 2006, 84, 288–299. [Google Scholar]
- (289).Carter SM; Sia A; Shaw MJ; Heyduk AF Isolation and Characterization ofa Neutral Imino-Semiquinone Radical. J. Am. Chem. Soc 2008, 130, 5838–5839. [DOI] [PubMed] [Google Scholar]
- (290).Lind J; Merenyi G Kinetic and Thermodynamic Properties of the Aminoxyl (NH2O*) Radical. J. Phys. Chem. A 2006, 110, 192–197. [DOI] [PubMed] [Google Scholar]
- (291).Bonner FT; Wang NY Reduction of Nitric Oxide by Hydroxylamine. 1. Kinetics and Mechanism. Inorg. Chem 1986, 25, 1858–1862. [Google Scholar]
- (292).Malievskii AD; Koroteev SV; Shapiro AB Kinetics and Thermodynamics of Hydrogen Atom Exchange Reactions in Sterically Hindered Hydroxylamine-Nitroxyl Radical Systems. Kinet. Catal 2005, 46, 812–820. [Google Scholar]
- (293).Mahoney LR; Mendenhall GD; Ingold KU Calorimetric and Equilibrium Studies on Some Stable Nitroxide and Iminoxy Radicals. Approximate Oxygen-Hydrogen Bond Dissociation Energies in Hydroxylamines and Oximes. J. Am. Chem. Soc 1973, 95, 8610–8614. [Google Scholar]
- (294).Wu A; Mader EA; Datta A; Hrovat DA; Borden WT; Mayer JM Nitroxyl Radical Plus Hydroxylamine Pseudo Self-Exchange Reactions: Tunneling in Hydrogen Atom Transfer. J. Am. Chem. Soc 2009, 131, 11985–11997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (295).Bordwell FG; Liu W-Z Solvent Effects on Homolytic Bond Dissociation Energies of HydroxylicAcids. J. Am. Chem. Soc 1996, 118, 10819–10823. [Google Scholar]
- (296).Xu F; Deussen HJW; Lopez B; Lam L; Li K Enzymatic and Electrochemical Oxidation of N-Hydroxy Compounds: Redox Potential, Electron-Transfer Kinetics, and Radical Stability. Eur. J. Biochem 2001, 268, 4169–4176. [DOI] [PubMed] [Google Scholar]
- (297).Koppel I; Koppel J; Leito J; Pihl V; Grehn L; Ragnarsson U The Acidity of Substituted 1-Hydroxybenzotriazoles in Water and Dimethyl Sulfoxide. J. Chem. Res 1993, 11, 3008–3028. [Google Scholar]
- (298).Kutt A; Leito I; Kaljurand I; Soovali L; Vlasov VM; Yagupolskii LM; Koppel IA A Comprehensive Self-Consistent Spectrophotometric Acidity Scale of Neutral Bronsted Acids in Acetonitrile. J. Org. Chem 2006, 71, 2829–2838. [DOI] [PubMed] [Google Scholar]
- (299).Gorgy K; Lepretre JC; Saint-Aman E; Einhorn C; Einhorn J; Marcadal C; Pierre JL Electrocatalytic Oxidation of Alcohols Using Substituted N-Hydroxyphthalimides as Catalysts. Electrochim. Acta 1998, 44, 385–393. [Google Scholar]
- (300).Kishioka S. y.; Yamada A Electro-Oxidation of N-Hydroxy Imides for Redox Mediator in Acetonitrile Containing Lutidine as a Base. Electrochim. Acta 2006, 51, 4582–4588. [Google Scholar]
- (301).Annunziatini C; Gerini MF; Lanzalunga O; Lucarini M Aerobic Oxidation of Benzyl Alcohols Catalyzed by Aryl Substituted N-Hydroxyphthalimides. Possible Involvement of a Charge-Transfer Complex. J. Org. Chem 2004, 69, 3431–3438. [DOI] [PubMed] [Google Scholar]
- (302).Lind J; Shen X; Eriksen TE; Merenyi G The One-Electron Reduction Potential of 4-Substituted Phenoxyl Radicals in Water. J. Am. Chem. Soc 1990, 112, 479–482. [Google Scholar]
- (303).Kimura M; Kaneko Y Kinetics of Electron-Transfer Reactions of para-Substituted Phenols p-C6H4(X)OH with [Fe(phen)3]3+(phen = 1,10-phenanthroline) and with [IrCl6]2− in Aqueous Acidic Solutions: Correlation between the Hammett Constant of X and the One-Electron Redox Potential of p-6H4(X)OH. J. Chem. Soc. Dalton Trans 1984, 431–343. [Google Scholar]
- (304).Steenken S; Neta P One-Electron Redox Potentials of Phenols. Hydroxy- and Aminophenols and Related Compounds of Biological Interest. J. Phys. Chem 1982, 86, 3661–3667. [Google Scholar]
- (305).Das TN; Neta P Reduction Potentials of Naphthoxyl and Pyridoxyl Radicals in Aqueous Solutions. J. Phys. Chem. A 1998, 102, 7081–7085. [Google Scholar]
- (306).Bernhard K; Geimer J; Canle-Lopez M; Reynisson J; Beckert D; Gleiter R; Steenken S Photo- and Radiation-Chemical Formation and Electrophilic and Electron Transfer Reactivities of Enolether Radical Cations in Aqueous Solution. Chem. - Eur. J 2001, 7, 4640–4650. [DOI] [PubMed] [Google Scholar]
- (307).Costentin C; Louault C; Robert M; Saveant JM Evidence for Concerted Proton-Electron Transfer in the Electrochemical Oxidation of Phenols with Water as Proton Acceptor. Tri-tert-butylphenol. J. Am. Chem. Soc 2008, 130, 15817–15819. [DOI] [PubMed] [Google Scholar]
- (308).Clark WM Oxidation Reduction Potentials of Organic Systems; Williams and Wilkins: Baltimore, 1960; pp 362–374. [Google Scholar]
- (309).Harada H An Investigation of the Stability Constant of the 2,3-Dihydroxy-benzoic Acid Complex with Copper(II). Bull. Chem. Soc. Jpn 1971, 44, 3459–3460. [Google Scholar]
- (310).Bailey SI; Ritchie IM; Hewgill FR The Construction and Use of Potential–pH Diagrams in Organic Oxidation–Reduction Reactions. J. Chem. Soc., Perkin Trans 2 1983, 645–652. [Google Scholar]
- (311).Laviron E Electrochemical Reactions with Protonations at Equilibrium: Part X. The Kinetics of the p-Benzoquinone/Hydro-quinone Couple on a Platinum Electrode. J. Electroanal. Chem. Interfacial Electrochem 1984, 164, 213–227. [Google Scholar]
- (312).Baxendale JH; Hardy HR The Ionization Constants of Some Hydroquinones. Trans. Faraday Soc 1953, 49, 1140–1144. [Google Scholar]
- (313).Bishop CA; Tong LKJ Equilibria of Substituted Semiquinones at High pH. J. Am. Chem. Soc 1965, 87, 501–505. [Google Scholar]
- (314).Steenken S; O’Neill P Oxidative Demethoxylation of Methoxylated Phenols and Hydroxybenzoic Acids by the Hydroxyl Radical. An in Situ Electron Spin Resonance, Conductometric Pulse Radiolysis and Product Analysis Study. J. Phys. Chem 1977, 81, 505–508. [Google Scholar]
- (315).Ilan YA; Czapski G; Meisel D The One-Electron Transfer Redox Potentials of Free Radicals. I. The Oxygen/Superoxide System. Biochim. Biophys. Acta, Bioenerg 1976, 430, 209–224. [DOI] [PubMed] [Google Scholar]
- (316).Adams GE; Michael BD Pulse Radiolysis of Benzoquinone and Hydroquinone. Semiquinone Formation by Water Elimination from Trihydroxy-Cyclohexadienyl Radicals. Trans. Faraday Soc 1967, 63, 1171–1180. [Google Scholar]
- (317).Rao PS; Hayon E Ionization Constants and Spectral Characteristics of Some Semiquinone Radicals in Aqueous Solution. J. Phys. Chem 1973, 77, 2274–2276. [Google Scholar]
- (318).Patel KB; Willson RL Semiquinone Free Radicals and Oxygen. Pulse Radiolysis Study of One Electron Transfer Equilibria. J. Chem. Soc., Faraday Trans. 1 1973, 69, 814–825. [Google Scholar]
- (319).Meisel D; Czapski G One-Electron Transfer Equilibriums and Redox Potentials of Radicals Studied by Pulse Radiolysis. J. Phys. Chem 1975, 79, 1503–1509. [Google Scholar]
- (320).Youngblood MP Kinetics of Electron-Transfer Reactions of Hydroquinones and Ascorbic Acid with 1-Phenyl-3-pyrazolidone Radicals. J. Am. Chem. Soc 1989, 111, 1843–1849. [Google Scholar]
- (321).Creutz C Complexities of Ascorbate as a Reducing Agent. Inorg. Chem 1981, 20, 4449–4452. [Google Scholar]
- (322).Williams NH; Yandell JK Outer-Sphere Electron-Transfer Reactions of Ascorbate Anions. Aust. J. Chem 1982, 35, 1133–1144. [Google Scholar]
- (323).Laroff GP; Fessenden RW; Schuler RH The Electron Spin Resonance Spectra of Radical Intermediates in the Oxidation of Ascorbic Acid and Related Substances. J. Am. Chem. Soc 1972, 94, 9062–9073. [DOI] [PubMed] [Google Scholar]
- (324).Warren JJ; Mayer JM Surprisingly Long-Lived Ascorbyl Radicals in Acetonitrile: Concerted Proton-Electron Transfer Reactions and Thermochemistry. J. Am. Chem. Soc 2008, 130, 7546–7547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (325).Ruscic B; Wagner AF; Harding LB; Asher RL; Feller D; Dixon DA; Peterson KA; Song Y; Qian X; Ng C-Y; et al. Onthe Enthalpy of Formation of Hydroxyl Radical and Gas-Phase Bond Dissociation Energies of Water and Hydroxyl. J. Phys. Chem. A 2002, 106, 2727–2747. [Google Scholar]
- (326).Sawyer DT Oxygen Chemistry; Oxford University Press: New York, 1991; p 223. [Google Scholar]
- (327).Bratsch SG Standard Electrode Potentials and Temperature Coefficients in Water at 298.15 K. J. Phys. Chem. Ref. Data 1989, 18, 1–21. [Google Scholar]
- (328).Blanksby SJ; Ramond TM; Davico GE; Nimlos MR; Kato S; Bierbaum VM; Lineberger WC; Ellison GB; Okumura M Negative-Ion Photoelectron Spectroscopy, Gas-Phase Acidity, and Thermochemistry of the Peroxyl Radicals CH3OO and CH3CH2OO. J. Am. Chem. Soc 2001, 123, 9585–9596. [DOI] [PubMed] [Google Scholar]
- (329).Das TN; Dhanasekaran T; Alfassi ZB; Neta P Reduction Potential of the tert-Butylperoxyl Radical in Aqueous Solutions. J. Phys. Chem. A 1998, 102, 280–284. [Google Scholar]
- (330).Everett AJ; Minkoff GJ The Dissociation Constants of Some Alkyl and Acyl Hydroperoxides. Trans. Faraday Soc 1953, 49, 410–414. [Google Scholar]
- (331).Villano SM; Eyet N; Wren SW; Ellison GB; Bierbaum VM; Lineberger WC Photoelectron Spectroscopy and Thermochemistry of the Peroxyformate Anion. J. Phys. Chem. A 2010, 114, 191–200. [DOI] [PubMed] [Google Scholar]
- (332).Merényi G; Lind J; Engman L One- and Two-Electron Reduction Potentials of Peroxyl Radicals and Related Species. J. Chem. Soc., Perkin Trans 2 1994, 2551–2553. [Google Scholar]
- (333).Jonsson M Thermochemical Properties of Peroxides and Peroxyl Radicals. J. Phys. Chem 1996, 100, 6814–6818. [Google Scholar]
- (334).Ruscic B; Berkowitz J Photoionization Mass Spectrometric Study of N2H2 and N2H3: N–H, N = N Bond Energies and Proton Affinity of N2. J. Chem. Phys 1991, 95, 4378–4384. [Google Scholar]
- (335).Buxton GV; Stuart CR Radiation Chemistry of Aqueous Solutions of Hydrazine at Elevated Temperatures. Part 1.—Oxygen-Free Solutions. J. Chem. Soc., Faraday Trans 1996, 92, 1519–1525. [Google Scholar]
- (336).Bourdelande JL; Gallardo I; Guirado G Inductive vs Solvation Effects in Primary Alkyl Amines: Determination of the Standard Potentials. J. Am. Chem. Soc 2007, 129, 2817–2821. [DOI] [PubMed] [Google Scholar]
- (337).Lalevee J; Allonas X; Fouassier JP N-H and α(C-H) Bond Dissociation Enthalpies of Aliphatic Amines. J. Am. Chem. Soc 2002, 124, 9613–9621. [DOI] [PubMed] [Google Scholar]
- (338).Jonsson M; Wayner DDM; Lusztyk J Redox and Acidity Properties of Alkyl- and Arylamine Radical Cations and the Corresponding Aminyl Radicals. J. Phys. Chem 1996, 100, 17539–17543. [Google Scholar]
- (339).MacFaul PA; Wayner DD; Ingold KU Measurement of N-H Bond Strengths in Aromatic Amines by Photoacoustic Calorimetry. J. Org. Chem 1997, 62, 3413–3414. [DOI] [PubMed] [Google Scholar]
- (340).Jonsson M; Lind J; Eriksen TE; Merényi G Redox and Acidity Properties of 4-Substituted Aniline Radical Cations in Water. J. Am. Chem. Soc 1994, 116, 1423–1427. [Google Scholar]
- (341).Zhao Y; Bordwell FG; Cheng JP; Wang D Equilibrium Acidities and Homolytic Bond Dissociation Energies (BDEs) of the Acidic H-N Bonds in Hydrazines and Hydrazides. J. Am. Chem. Soc 1997, 119, 9125–9129. [Google Scholar]
- (342).Merenyi G; Lind J; Shen X Electron Transfer from Indoles, Phenol, and Sulfite (SO32−) to Chlorine Dioxide (ClO2•). J. Phys. Chem 1988, 92, 134–137. [Google Scholar]
- (343).Remers WA Properties and Reactions of Indoles. In Chemistry of Heterocyclic Compounds: Indoles, Part 1; Houlihan WJ, Ed.; Wiley-Interscience: New York, 1971; Vol. 25, p 14. [Google Scholar]
- (344).Harriman A Further Comments on the Redox Potentials of Tryptophan and Tyrosine. J. Phys. Chem 1987, 91, 6102–6104. [Google Scholar]
- (345).Steenken S; Jovanovic SV How Easily Oxidizable is DNA? One-Electron Reduction Potentials of Adenosine and Guanosine Radicals in Aqueous Solution. J. Am. Chem. Soc 1997, 119, 617–618. [Google Scholar]
- (346).Candeias LP; Steenken S Structure and Acid-Base Properties of One-Electron-Oxidized Deoxyguanosine, Guanosine, and 1-Methylguanosine. J. Am. Chem. Soc 1989, 111, 1094–1099. [Google Scholar]
- (347).Steenken S Purine Bases, Nucleosides, and Nucleotides: Aqueous Solution Redox Chemistry and Transformation Reactions of their Radical Cations and e− and OH Adducts. Chem. Rev 1989, 89, 503–520. [Google Scholar]
- (348).Surdhar P; Armstrong DA Redox Potentials of Some Sulfur-Containing Radicals. J. Phys. Chem 1986, 90, 5915–5917. [Google Scholar]
- (349).Chen KY; Morris JC Kinetics of Oxidation of Aqueous Sulfide by Oxygen. Environ. Sci. Technol 1972, 6, 529–537. [Google Scholar]
- (350).Berkowitz J; Ellison GB; Gutman D Three Methods to Measure RH Bond Energies. J. Phys. Chem 1994, 98, 2744–2765. [Google Scholar]
- (351).Reed DR; Hare MC; Fattahi A; Chung G; Gordon MS; Kass SR α,2-, α,3-, and α,4-Dehydrophenol Radical Anions: Formation, Reactivity, and Energetics Leading to the Heats of Formation of α,2-, α,3-, and α,4-Oxocyclohexadienylidene. J. Am. Chem. Soc 2003, 125, 4643–4651. [DOI] [PubMed] [Google Scholar]
- (352).Jencks WP; Salvesen K Equilibrium Deuterium Isotope Effects on the Ionization of Thiol Acids. J. Am. Chem. Soc 1971, 93, 4433–4436. [Google Scholar]
- (353).Prütz WA; Butler J; Land EJ; Swallow AJ Unpaired Electron Migration between Aromatic and Sulfur Peptide Units. Free Radical Res. Commun 1986, 2, 69–75. [DOI] [PubMed] [Google Scholar]
- (354).Madej E; Wardman P The Oxidizing Power of the Glutathione Thiyl Radical as Measured by its Electrode Potential at Physiological pH. Arch. Biochem. Biophys 2007, 462, 94–102. [DOI] [PubMed] [Google Scholar]
- (355).Tajc SG; Tolbert BS; Basavappa R; Miller BL Direct Determination of Thiol pKa by Isothermal Titration Microcalorimetry. J. Am. Chem. Soc 2004, 126, 10508–10509. [DOI] [PubMed] [Google Scholar]
- (356).Borges dos Santos RM; Muralha VSF; Correia CF; Guedes RC; Costa Cabral BJ; Martinho Simões JA S–H Bond Dissociation Enthalpies in Thiophenols: A Time-Resolved Photoacoustic Calorimetry and Quantum Chemistry Study. J. Phys. Chem. A 2002, 106, 9883–9889. [Google Scholar]
- (357).Armstrong DA; Sun Q; Schuler RH Reduction Potentials and Kinetics of Electron Transfer Reactions of Phenylthiyl Radicals: Comparisons with Phenoxyl Radicals. J. Phys. Chem 1996, 100, 9892–9899. [Google Scholar]
- (358).De Maria P; Fini A; Hall FM Thermodynamic Acidity Constants of ortho-Substituted Benzenethiols. J. Chem. Soc., Perkin Trans 2 1974, 1443–1445. [Google Scholar]
- (359).Bordwell FG; Hughes DL Thiol Acidities and Thiolate Ion Reactivities Toward Butyl Chloride in Dimethyl Sulfoxide Solution. The Question of Curvature in Brønsted Plots. J. Org. Chem 1982, 47, 3224–3232. [Google Scholar]
- (360).Guthrie JP Hydration of Thioesters. Evaluation of the Free-Energy Changes for the Addition of Water to Some Thioesters, Rate-Equilibrium Correlations over Very Wide Ranges in Equilibrium Constants, and a New Mechanistic Criterion. J. Am. Chem. Soc 1978, 100, 5892–5904. [Google Scholar]
- (361).Benesch RE; Benesch R The Acid Strength of the -SH Group in Cysteine and Related Compounds. J. Am. Chem. Soc 1955, 77, 5877–5881. [Google Scholar]
- (362).Ruscic B; Litorja M; Asher RL Ionization Energy of Methylene Revisited: Improved Values for the Enthalpy of Formation of CH2 and the Bond Dissociation Energy of CH3 via Simultaneous Solution of the Local Thermochemical Network. J. Phys. Chem. A 1999, 103, 8625–8633. [Google Scholar]
- (363).Seakins PW; Pilling MJ; Niiranen JT; Gutman D; Krasnoperov LN Kinetics and Thermochemistry of R + HBr ⇄ RH + Br Reactions: Determinations of the Heat of Formation of Ethyl, Isopropyl, Sec-Butyl and Tert-Butyl Radicals. J. Phys. Chem 1992, 96, 9847–9855. [Google Scholar]
- (364).Ervin KM; DeTuri VF Anchoring the Gas-Phase Acidity Scale. J. Phys. Chem. A 2002, 106, 9947–9956. [Google Scholar]
- (365).Mordaunt DH; Ashfold MNR Near Ultraviolet Photolysis of C2H2: A Precise Determination of D0(HCC–H). J. Chem. Phys 1994, 101, 2630–2631. [Google Scholar]
- (366).Roy K; Braun-Unkhoff M; Frank P; Just T Kinetics of the Cyclopentadiene Decay and the Recombination of Cyclopentadienyl Radicals with H-Atoms: Enthalpy of Formation of the Cyclopentadienyl Radical. Int. J. Chem. Kinet 2001, 33, 821–833. [Google Scholar]
- (367).Bordwell FG Equilibrium Acidities of Carbon Acids. In Physical Organic Chemistry–3; Fruchier A, Ed.; Pergamon: 1977; pp 963–968. [Google Scholar]
- (368).Bordwell FG Equilibrium Acidities in Dimethyl Sulfoxide Solution. Acc. Chem. Res 1988, 21, 456–463. [Google Scholar]
- (369).Tsang W Thermodynamic and Kinetic Properties of the Cyclohexadienyl Radical. J. Phys. Chem 1986, 90, 1152–1155. [Google Scholar]
- (370).Ellison GB; Davico GE; Bierbaum VM; DePuy CH Thermochemistry of the Benzyl and Allyl Radicals and Ions. Int. J. Mass Spectrom. Ion Processes 1996, 156, 109–131. [Google Scholar]
- (371).Miller LL; Nordblom GD; Mayeda EA Simple, Comprehensive Correlation of Organic Oxidation and Ionization Potentials. J. Org. Chem 1972, 37, 916–918. [Google Scholar]
- (372).Knochel P; Molander GA Comprehensive Organic Synthesis, 2nd ed.; Elsevier: Amsterdam, Netherlands, 2014. [Google Scholar]
- (373).Schlesener CJ; Amatore C; Kochi JK Marcus Theory in Organic Chemistry. Mechanisms of Electron and Proton Transfers from Aromatics and their Cation Radicals. J. Phys. Chem 1986, 90, 3747–3756. [Google Scholar]
- (374).Anne A; Hapiot P; Moiroux J; Neta P; Saveant JM Dynamics of Proton Transfer from Cation Radicals. Kinetic and Thermodynamic Acidities of Cation Radicals of NADH Analogs. J. Am. Chem. Soc 1992, 114, 4694–4701. [Google Scholar]
- (375).Carlson BW; Miller LL; Neta P; Grodkowski J Oxidation of NADH Involving Rate-Limiting One-Electron Transfer. J. Am. Chem. Soc 1984, 106, 7233–7239. [Google Scholar]
- (376).Matsubara Y; Grills DC; Kuwahara Y Thermodynamic Aspects of Electrocatalytic CO2 Reduction in Acetonitrile and with an Ionic Liquid as Solvent or Electrolyte. ACS Catal. 2015, 5, 6440–6452. [Google Scholar]
- (377).Costentin C; Robert M; Savéant J-M Catalysis of the Electrochemical Reduction of Carbon Dioxide. Chem. Soc. Rev 2013, 42, 2423–2436. [DOI] [PubMed] [Google Scholar]
- (378).Costentin C; Drouet S; Robert M; Savéant J-M A Local Proton Source Enhances CO2 Electroreduction to CO by a Molecular Fe Catalyst. Science 2012, 338, 90. [DOI] [PubMed] [Google Scholar]
- (379).Rhile IJ; Markle TF; Nagao H; DiPasquale AG; Lam OP; Lockwood MA; Rotter K; Mayer JM Concerted Proton-Electron Transfer in the Oxidation of Hydrogen-Bonded Phenols. J. Am. Chem. Soc 2006, 128, 6075–6088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (380).Kaljurand I; Lilleorg R; Murumaa A; Mishima M; Burk P; Koppel I; Koppel IA; Leito I The Basicity of Substituted N,N-Dimethylanilines in Solution and in the Gas Phase. J. Phys. Org. Chem 2013, 26, 171–181. [Google Scholar]
- (381).Kalyanasundaram K Photophysics, Photochemistry and Solar Energy Conversion with Tris(bipyridyl)ruthenium(II) and its Analogues. Coord. Chem. Rev 1982, 46, 159–244. [Google Scholar]
- (382).Connelly NG; Geiger WE Chemical Redox Agents for Organometallic Chemistry. Chem. Rev 1996, 96, 877–910. [DOI] [PubMed] [Google Scholar]
- (383).Kaljurand I; Kutt A; Soovali L; Rodima T; Maemets V; Leito I; Koppel IA Extension of the Self-Consistent Spectrophotometric Basicity Scale in Acetonitrile to a Full Span of 28 pKa Units: Unification of Different Basicity Scales. J. Org. Chem 2005, 70, 1019–1028. [DOI] [PubMed] [Google Scholar]
- (384).Richens DT The Chemistry of Aqua Ions: Synthesis, Structure, and Reactivity; John Wiley and Sons: New York, 1997; Chapter 8: Group 8 Elements: Iron, Ruthenium and Osmium, pp 363–438. [Google Scholar]
- (385).VanNatta PE; Ramirez DA; Velarde AR; Ali G; Kieber-Emmons MT Exceptionally High O–H Bond Dissociation Free Energy of a Dicopper(II) μ-Hydroxo Complex and Insights into the Geometric and Electronic Structure Origins Thereof. J. Am. Chem. Soc 2020, 142, 16292–16312. [DOI] [PubMed] [Google Scholar]
- (386).Gardner KA; Kuehnert LL; Mayer JM Hydrogen Atom Abstraction by Permanganate: Oxidations of Arylalkanes in Organic Solvents. Inorg. Chem 1997, 36, 2069–2078. [DOI] [PubMed] [Google Scholar]
- (387).Bakac A Hydrogen Atom Abstraction by Metal–Oxo and Metal–Superoxo Complexes: Kinetics and Thermodynamics. J. Am. Chem. Soc 2000, 122, 1092–1097. [Google Scholar]
- (388).Bakac A Kinetics and Thermodynamics of Hydrogen Atom Transfer to Superoxometal Complexes. J. Am. Chem. Soc 1997, 119, 10726–10731. [Google Scholar]
- (389).Szajna-Fuller E; Bakac A Thermodynamics of Oxygen Activation by Macrocyclic Complexes of Rhodium. Inorg. Chem 2007, 46, 10907–10912. [DOI] [PubMed] [Google Scholar]
- (390).De Santis G; Fabbrizzi L; Poggi A; Taglietti A Nickel(III)-Promoted Deprotonation of an Amide Group of Cyclam. Characterization of the Violet Transient through Stopped-Flow Spectrophotometric Techniques and Determination of the pKa Value. Inorg. Chem 1994, 33, 134–139. [Google Scholar]
- (391).Goldsmith CR; Stack TDP Hydrogen Atom Abstraction by a Mononuclear Ferric Hydroxide Complex: Insights into the Reactivity of Lipoxygenase. Inorg. Chem 2006, 45, 6048–6055. [DOI] [PubMed] [Google Scholar]
- (392).Gupta R; MacBeth CE; Young VG; Borovik AS Isolation of Monomeric MnIII/II–OH and MnIII–O Complexes from Water: Evaluation of O–H Bond Dissociation Energies. J. Am. Chem. Soc 2002, 124, 1136–1137. [DOI] [PubMed] [Google Scholar]
- (393).Gupta R; Borovik AS Monomeric MnIII/II and FeIII/II Complexes with Terminal Hydroxo and Oxo Ligands: Probing Reactivity via O–H Bond Dissociation Energies. J. Am. Chem. Soc 2003, 125, 13234–13242. [DOI] [PubMed] [Google Scholar]
- (394).Parsell TH; Yang M-Y; Borovik AS C–H Bond Cleavage with Reductants: Re-investigating the Reactivity of Monomeric MnIII/IV–Oxo Complexes and the Role of Oxo Ligand Basicity. J. Am. Chem. Soc 2009, 131, 2762–2763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (395).Goldsmith CR; Cole AP; Stack TDP C–H Activation by a Mononuclear Manganese(III) Hydroxide Complex: Synthesis and Characterization of a Manganese-Lipoxygenase Mimic? J. Am. Chem. Soc 2005, 127, 9904–9912. [DOI] [PubMed] [Google Scholar]
- (396).Waidmann CR; Zhou X; Tsai EA; Kaminsky W; Hrovat DA; Borden WT; Mayer JM Slow Hydrogen Atom Transfer Reactions of Oxo- and Hydroxo-Vanadium Compounds: The Importance of Intrinsic Barriers. J. Am. Chem. Soc 2009, 131, 4729–4743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (397).Drummond MJ; Ford CL; Gray DL; Popescu CV; Fout AR Radical Rebound Hydroxylation Versus H-Atom Transfer in Non-Heme Iron(III)-Hydroxo Complexes: Reactivity and Structural Differentiation. J. Am. Chem. Soc 2019, 141, 6639–6650. [DOI] [PubMed] [Google Scholar]
- (398).Goetz MK; Hill EA; Filatov AS; Anderson JS Isolation of a Terminal Co(III)-Oxo Complex. J. Am. Chem. Soc 2018, 140, 13176–13180. [DOI] [PubMed] [Google Scholar]
- (399).Lockwood MA; Wang K; Mayer JM Oxidation of Toluene by [(phen)2Mn(μ-O)2Mn(phen)2]4+ via Initial Hydride Abstraction. J. Am. Chem. Soc 1999, 121, 11894–11895. [Google Scholar]
- (400).Larsen AS; Wang K; Lockwood MA; Rice GL; Won T-J; Lovell S; Sadílek M; Tureček F; Mayer JM Hydrocarbon Oxidation by Bis-μ-oxo Manganese Dimers: Electron Transfer, Hydride Transfer, and Hydrogen Atom Transfer Mechanisms. J. Am. Chem. Soc 2002, 124, 10112–10123. [DOI] [PubMed] [Google Scholar]
- (401).Kindermann N; Günes C-J; Dechert S; Meyer F Hydrogen Atom Abstraction Thermodynamics of a μ-1,2-Superoxo Dicopper(II) Complex. J. Am. Chem. Soc 2017, 139, 9831–9834. [DOI] [PubMed] [Google Scholar]
- (402).Roth JP; Yoder JC; Won T-J; Mayer JM Application of the Marcus Cross Relation to Hydrogen Atom Transfer Reactions. Science 2001, 294, 2524. [DOI] [PubMed] [Google Scholar]
- (403).Roth JP; Lovell S; Mayer JM Intrinsic Barriers for Electron and Hydrogen Atom Transfer Reactions of Biomimetic Iron Complexes. J. Am. Chem. Soc 2000, 122, 5486–5498. [Google Scholar]
- (404).Manner VW; Lindsay AD; Mader EA; Harvey JN; Mayer JM Spin-Forbidden Hydrogen Atom Transfer Reactions in a Cobalt Biimidazoline System. Chem. Sci 2012, 3, 230–243. [Google Scholar]
- (405).Albers A; Demeshko S; Dechert S; Saouma CT; Mayer JM; Meyer F Fast Proton-Coupled Electron Transfer Observed for a High-Fidelity Structural and Functional [2Fe–2S] Rieske Model. J. Am. Chem. Soc 2014, 136, 3946–3954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (406).Lu X; Li X-X; Seo MS; Lee Y-M; Clémancey M; Maldivi P; Latour J-M; Sarangi R; Fukuzumi S; Nam W A Mononuclear Nonheme Iron(IV)–Amido Complex Relevant for the Compound II Chemistry of Cytochrome P450. J. Am. Chem. Soc 2019, 141, 80–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (407).Chalkley MJ; Garrido-Barros P; Peters JC A Molecular Mediator for Reductive Concerted Proton-Electron Transfers via Electrocatalysis. Science 2020, 369, 850. [DOI] [PubMed] [Google Scholar]
- (408).Charette BJ; Ziller JW; Heyduk AF Metal-Ion Influence on Ligand-Centered Hydrogen-Atom Transfer. Inorg. Chem 2021, 60, 1579–1589. [DOI] [PubMed] [Google Scholar]
- (409).Tilset M; Parker VD Solution Homolytic Bond Dissociation Energies of Organotransition-Metal Hydrides. J. Am. Chem. Soc 1989, 111, 6711–6717. [Google Scholar]
- (410).Jordan RF; Norton JR Kinetic and Thermodynamic Acidity of Hydrido Transition-Metal Complexes. 1. Periodic Trends in Group VI Complexes and Substituent Effects in Osmium Complexes. J. Am. Chem. Soc 1982, 104, 1255–1263. [Google Scholar]
- (411).Parker VD; Handoo KL; Roness F; Tilset M Electrode Potentials and the Thermodynamics of Isodesmic Reactions. J. Am. Chem. Soc 1991, 113, 7493–7498. [Google Scholar]
- (412).Choi J; Pulling ME; Smith DM; Norton JR Unusually Weak Metal–Hydrogen Bonds in HV(CO)4(P–P) and Their Effectiveness as H• Donors. J. Am. Chem. Soc 2008, 130, 4250–4252. [DOI] [PubMed] [Google Scholar]
- (413).Mondal P; Ishigami I; Gérard E; Lim C; Yeh S-R; de Visser S; Wijeratne GB Proton-Coupled Electron Transfer Reactivities of Electronically Divergent Heme Superoxide Intermediates: A Kinetic, Thermodynamic, and Theoretical Study. Chem. Sci 2021, 12, 8872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (414).Kim H; Rogler PJ; Sharma SK; Schaefer AW; Solomon AI; Karlin KD Ferric Heme Superoxide Reductive Transformations to Ferric Heme (Hydro)Peroxide Species: Spectroscopic Characterization and Thermodynamic Implications for H-Atom Transfer (HAT). Angew. Chem., Int. Ed 2021, 60, 5907–5912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (415).Kim H; Rogler PJ; Sharma SK; Schaefer AW; Solomon EI; Karlin KD Heme-FeIII Superoxide, Peroxide and Hydroperoxide Thermodynamic Relationships: FeIII-O2•–Complex H-Atom Abstraction Reactivity. J. Am. Chem. Soc 2020, 142, 3104–3116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (416).Lam WWY; Man W-L; Leung C-F; Wong C-Y; Lau T-C Solvent Effects on the Oxidation of RuIV=O to O = RuVI=O by MnO4−. Hydrogen-Atom Versus Oxygen-Atom Transfer. J. Am. Chem. Soc 2007, 129, 13646–13652. [DOI] [PubMed] [Google Scholar]
- (417).Manner VW; DiPasquale AG; Mayer JM Facile Concerted Proton–Electron Transfers in a Ruthenium Terpyridine-4’-carboxylate Complex with a Long Distance between the Redox and Basic Sites. J. Am. Chem. Soc 2008, 130, 7210–7211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (418).Mitome H; Ishizuka T; Kotani H; Shiota Y; Yoshizawa K; Kojima T Mechanistic Insights into C–H Oxidations by Ruthenium-(III)-Pterin Complexes: Impact of Basicity of the Pterin Ligand and Electron Acceptability of the Metal Center on the Transition States. J. Am. Chem. Soc 2016, 138, 9508–9520. [DOI] [PubMed] [Google Scholar]
- (419).Miyazaki S; Kojima T; Mayer JM; Fukuzumi S Proton-Coupled Electron Transfer of Ruthenium(III)–Pterin Complexes: A Mechanistic Insight. J. Am. Chem. Soc 2009, 131, 11615–11624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (420).Soper JD; Mayer JM Slow Hydrogen Atom Self-Exchange between Os(IV) Anilide and Os(III) Aniline Complexes: Relationships with Electron and Proton Transfer Self-Exchange. J. Am. Chem. Soc 2003, 125, 12217–12229. [DOI] [PubMed] [Google Scholar]
- (421).Skagestad V; Tilset M Thermodynamics of Heterolytic and Homolytic Metal-Hydrogen Bond Cleavage Reactions of 18-Electron and 17-Electron Group 6 Hydridotris(pyrazolyl)borate Metal Hydrides. J. Am. Chem. Soc 1993, 115, 5077–5083. [Google Scholar]
- (422).Protasiewicz JD; Theopold KH A Direct Comparison of the Rates of Degenerate Transfer of Electrons, Protons, and Hydrogen Atoms between Metal Complexes. J. Am. Chem. Soc 1993, 115, 5559–5569. [Google Scholar]
- (423).Bezdek MJ; Chirik PJ Proton-Coupled Electron Transfer to a Molybdenum Ethylene Complex Yields a β-Agostic Ethyl: Structure, Dynamics andMechanism. J. Am. Chem. Soc 2018, 140, 13817–13826. [DOI] [PubMed] [Google Scholar]
- (424).Buss JA; Hirahara M; Ueda Y; Agapie T Molecular Mimics of Heterogeneous Metal Phosphides: Thermochemistry, Hydride-Proton Isomerism, and HER Reactivity. Angew. Chem., Int. Ed 2018, 57, 16329–16333. [DOI] [PubMed] [Google Scholar]
- (425).Trujillo HA; Casado CM; Ruiz J; Astruc D Thermodynamics of C–H Activation in Multiple Oxidation States: Comparison of Benzylic C–H Acidities and C–H Bond Dissociation Energies in the Isostructural 16-20-Electron Complexes [Fex(η5-C5R5)(η6-arene)]n, x = 0-IV, R = H or Me, n = −1 to +3. J. J. Am. Chem. Soc 1999, 121, 5674–5686. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


