Precision Bayesian phase I-II dose-finding based on utilities tailored to prognostic subgroups

Abstract

A Bayesian phase I-II design is presented that optimizes the dose of a new agent within predefined prognostic subgroups. The design is motivated by a trial to evaluate targeted agents for treating metastatic clear cell renal carcinoma, where a prognostic risk score defined by clinical variables and biomarkers is well established. Two clinical outcomes are used for dose-finding, time-to-toxicity during a prespecified follow-up period, and efficacy characterized by ordinal disease status evaluated at the end of follow-up. A joint probability model is constructed for these outcomes as functions of dose and subgroup. The model performs adaptive clustering of adjacent subgroups having similar dose-outcome distributions to facilitate borrowing information across subgroups. To quantify toxicity-efficacy risk-benefit trade-offs that may differ between subgroups, the objective function is based on outcome utilities elicited separately for each subgroup. In the context of the renal cancer trial, a design is constructed and a simulation study is presented to evaluate the design’s reliability, safety, and robustness, and to compare it to designs that either ignore subgroups or run a separate trial within each subgroup.

1 |. INTRODUCTION

In many medical settings, multiple prognostic factors are used to define patient prognostic risk subgroups that are expected to have different treatment effects. Such risk subgroups often are used by physicians to guide their therapeutic decisions. As a motivating example, we consider a phase I-II trial in metastatic clear cell renal cell carcinoma (mRCC). Patients with mRCC often are classified by their International Metastatic Renal-Cell Carcinoma Database Consortium (IMDC) prognostic risk scores. IMDC scores are defined based on a combination of clinical variables and biomarkers, including anemia, thrombocytosis, neutrophilia, hypercalcemia, Karnofsky performance status, and time from diagnosis to treatment.¹ It is well established that IMDC risk scores are informative in predicting treatment outcomes for patients with mRCC. IMDC risk score is recommended by the National Comprehensive Cancer Network (NCCN) guidelines to guide treatment selection for mRCC, and it is used very commonly by oncologists. For example, Heng et al¹ formed three prognostic subgroups of mRCC patients using IMDC risk scores: favorable (IMDC = 0), intermediate (IMDC = 1 or 2), and poor (IMDC ≥ 3), and reported that these subgroups had substantially different overall survival time distributions following first-line VEGF-targeted treatment. Motzer et al² combined the intermediate and poor subgroups and compared the combination of immune checkpoint inhibitors nivolumab plus ipilimumab (N+I) to sunitinib within each of the favorable and intermediate/poor subgroups.

In this article, we develop a Bayesian phase I-II clinical trial design that optimizes prognostic subgroup-specific doses based on time-to-toxicity and ordinal efficacy outcomes. Our motivating application is a trial of sitravatinib, a tyrosine kinase inhibitor, combined with fixed doses of N+I, in patients with mRCC. The five doses of sitravatinib considered are 20, 40, 60, 80, and 120 mg, hereafter denoted by d₁, … , d₅. While targeted treatments can achieve durable responses in mRCC patients, the magnitudes of their effects often vary due to substantial prognostic heterogeneity, as shown in Heng et al¹ and Motzer et al.² The study reported by Motzer et al² found that the effects of N+I on objective response, defined by RECIST, vary with IMDC risk subgroups. Consequently, it may be anticipated that the effects of sitravatinib dose, combined with N+I, also may vary with IMDC subgroups. Despite the established prognostic value of IMDC prognostic risk score, however, to date it has not been used explicitly in a dose-finding clinical trial design. The goal of our proposed design is to make decisions, including optimal dose selection and identification of excessively toxic or inefficacious doses, that may differ between prognostic risk subgroups.

Currently, there is a limited literature on phase I-II designs for finding subgroup-specific doses. For phase I trials based on toxicity, O’Quigley and Conaway,³ Iasonos and O’Quigley,⁴ and Horton et al⁵ considered the problem of finding the maximum-tolerated doses (MTD) for heterogeneous patient populations. Horton et al⁵ developed a two-stage design where a rule-based allocation under a shifted version of the continual reassessment model is used in each stage to find subgroup specific MTDs based on a binary toxicity outcome. However, there is a need for dose-finding designs that can handle more complex studies involving complex clinical outcomes and heterogeneous groups of patients, as in our motivating trial.

To provide a basis for subgroup-specific decision making, we build a Bayesian hierarchical model for regression of clinical outcomes on dose d and subgroup g. Our motivating trial has two co-primary patient outcomes, the time Y_T to severe toxicity over a 12-week follow-up period after the initiation of treatment, and disease severity, Y_E, evaluated as an ordinal categorical variable at the end of this follow up period. The possible values of Y_E are progressive disease (PD), stable disease (SD), partial response (PR), and complete response (CR), a very common ordinal response categorization in oncology. The regression model for [Y_T, Y_E |d, g] assumes additive dose and subgroup effects for each outcome. In general, we denote ordinal risk subgroups by {1, 2, … , G}, with g = 1 the lowest and g = G the highest risk. The mRCC trial accounts for three IMDC risk subgroups: favorable, intermediate, and poor, denoted by g = 1, 2, and 3. Our model exploits the prognostic subgroups established in previous studies, and avoids the task of attempting to identify new patient subgroups from baseline covariates, since this would be very difficult to do reliably given the limited sample size and sequentially adaptive decision making in a phase I-II trial. To improve the accuracy of subgroup-specific decisions, the model and design allow adaptive clustering of adjacent subgroups based on intermediate data during a trial. This may be especially useful in settings with sparse subgroups. While we will develop the design in the context of the mRCC trial, the model and method can be applied generally to design phase I-II trials with time-to-toxicity and ordinal efficacy outcomes, and ordinal prognostic subgroups.

Many clinical trial designs that base decisions on elicited utilities of multiple clinical outcomes have been proposed, including Thall and Nguyen⁶ for phase I-II dose-finding, Lee et al⁷ for two-cycle phase I-II dose-finding, Murray et al⁸ and Murray et al⁹ for randomized treatment comparisons, and Lin et al¹⁰ for a basket trial to jointly optimize dose and schedule. While these designs provide coherent decision making frameworks for homogeneous patient populations, assuming that one utility function U(y) is appropriate for all patients may be less useful for prognostic subgroup-specific decision making. For example, in mRCC subjective risk-benefit trade-offs of clinical outcomes can vary substantially with IMDC score, and even produce opposite conclusions.¹¹ mRCC patients with favorable risk often prefer less intensive treatments with low risks of toxicity, while mRCC patients with poor risk may prefer more potent treatment combinations with a higher risk of toxicity,¹² in order to increase the probability of a substantive anti-disease effect. This implies that the mRCC subgroups should have different outcome utility functions. This likely is also the case in other diseases where prognostic level affects risk-benefit trade-offs. To address this, we extend the usual utility-based approach by eliciting subgroup-specific utility functions and using these as a basis for making subgroup-specific decisions.

Section 2 presents the probability model. Section 3 describes and illustrates how the subgroup-specific utility function is constructed, and Section 4 presents the design. In Section 5, a simulation study is presented to evaluate the design’s operating characteristics (OCs) and robustness, and compare it to the two designs that either make the same decisions for all subgroups or run a separate trial for each subgroup. The simulations show that the proposed design produces much more accurate subgroup-specific decisions compared to these two more conventional approaches. We close with a brief discussion in Section 6.

2 |. PROBABILITY MODEL

2.1 |. Sampling and frailty models

For interim sample size n(t) ≤ N_max at trial time t in days, index patients in order of enrollment by i = 1, … , n(t), with trial entry times 0 ≤ e₁ ≤ e₂ ≤ · · · ≤ e_n(t). Subgroups are predefined using prognostic scores, and treatment effects of a study drug in adjacent subgroups may be either similar or significantly different. At the time of each patient’s enrollment, their prognostic risk score is evaluated and the patient is classified into one of the G ordinal risk subgroups. Let g_i ∈ {1, … , G} denote the subgroup of the ith patient. In practice, the prevalences of the subgroup will differ from 1∕G, and the numbers of patients enrolled in the subgroups will differ accordingly.

Given fixed follow-up time C, for patient i severe toxicity is monitored continuously until e_i + C. The toxicity event occurs at trial time e_i + Y_i,T, with Y_i,T < C if it is observed. Let $Y_{i,\text{T}}^o$ denote the observed time from e_i to toxicity Y_i,T or right-censoring, with binary indicator δ_i,T = 1 if $Y_{i,\text{T}}^o=Y_{i,\text{T}}$ and δ_i,T = 0 otherwise. At trial time t > e_i, if Y_i,T ≤ min(t − e_i, C), then $Y_{i,\text{T}}^o=Y_{i,\text{T}}$ is the observed time of toxicity, and δ_i,T = 1. If Y_i,T > min(t − e_i, C), then $Y_{i,\text{T}}^o$ is the time of independent right censoring with δ_i,T = 0. In particular, the event of $Y_{i,\text{T}}^o\le C$ and δ_i,T = 0 implies that no toxicity has occurred up to time t. Ordinal disease status Y_i,E is observed at time e_i + C, and we define δ_i,E = 1 at any t ≥ e_i + C. For t < e_i + C, Y_i,E is not observed and δ_i,E = 0. Denote the ordinal disease status outcome of patient i at time e_i + C by Y_i,E, taking on values in {0, 1, … , K − 1}. For example, disease severity levels {PD, SD, PR, CR}, are represented by Y_i,E = 0, 1, 2, 3 and K = 4. Disease status is evaluated independently of (Y_i,T, δ_i,T).

For the dose-outcome model, we denote the doses standardized to have mean 0 and variance 1 by {d₁, … , d_M}. In the renal cancer trial, given the raw doses {20, 40, 60, 80, 120} mg/day of oral sitravatinib, the standardized doses are {−1.144, −0.624, −0.104, 0.416, 1.456}, with M = 5. For each patient i = 1, … , n(t), denote the dose by d_[i], subgroup by g_i, and the latent frailty vector by ${\mathit{\gamma }}_i=\left({\gamma }_{i,\text{T}},{\gamma }_{i,\text{E}}\right)\in {ℝ}^2$. We assume conditional independence of Y_i,T and Y_i,E given γ_i, specify marginal models, and obtain a joint distribution by averaging over the distribution of γ_i.

For the toxicity event time Y_i,T, if patient i in prognostic subgroup g_i is treated with dose d_[i], we assume a proportional hazards (PH) model with conditional hazard function

$$h_{\text{T}}\left(t|g_i,d_{[i]},{\mathit{\alpha }}_T,{\gamma }_{i,\text{T}}\right)=h_{0\text{T}}(t)\exp \left\{{\eta }_{\mathrm{T}}\left(d_{[i]}\right)+{\alpha }_{\text{T},g_i}+{\gamma }_{i,\text{T}}\right\},$$ (1)

where h_0T(t) is a baseline hazard function and α_T = (α_T,1, … , α_T,G) are the prognostic subgroup effects on the risk of toxicity. In (1), the regression function η_T(d_[i]) accounts for dose effects on toxicity, and ${\alpha }_{\text{T},g_i}$ is the additive effect of subgroup g_i. We will give a parametric model for η_T(d_m) below. We fix α_T,1 = 0 to avoid identifiability problems with h_0T. To ensure that the toxicity hazard is non-decreasing in the ordinal risk subgroups, we impose the ordering constraint α_T,1 ≤ · · · ≤ α_T,G. The survival function of [Y_{i, T}|g_i, d_[i]] is

$$S_{\text{T}}\left(t|g_i,d_{[i]},{\mathit{\alpha }}_T,{\gamma }_{i,\text{T}}\right)=\exp \left\{-{\int }_0^t{h}_{\text{T}}\left(v|g_i,d_{[i]},{\mathit{\alpha }}_T,{\gamma }_{i,\text{T}}\right)dv\right\}.$$

We assume a multinomial probit model for ordinal disease status Y_i,E. Denote subgroup-specific cutoffs u_g,0 < u_g,1 < … < u_g,K for each g. The conditional marginals are

$$\begin{gathered} {\pi }_k(g_i,d_{[i]},{\alpha }_{\text{E},g_i},{\gamma }_{i,\text{E}},\mathit{u})=\text{P}(Y_{i,\text{E}}=k|g_i,d_{[i]},{\mathit{\alpha }}_E,{\gamma }_{i,\text{E}},\mathit{u}) \\ =\mathrm{\Phi }(u_{g_i,k+1}|{\eta }_{\text{E}}(d_{[i]})+{\alpha }_{\text{E},g_i}+{\gamma }_{i,\text{E}},{\sigma }_{\pi }^2)-\mathrm{\Phi }(u_{{\text{g}}_i,k}|{\eta }_{\text{E}}(d_{[i]})+{\alpha }_{\text{E},g_i}+{\gamma }_{i,\text{E}},{\sigma }_{\pi }^2), \end{gathered}$$ (2)

for k = 0, … , K − 1, where α_E = (α_E,1, … , α_E,G) is the vector of prognostic subgroup effects on Y_i,E and ${\sigma }_{\pi }^2$ is a fixed hyperparameter. In (2), Φ(·|a, b²) denotes the cumulative distribution function of a normal distribution with mean a and variance b². We let u_g,k, k = 2, … , K − 1 be random, while fixing u_g,1 = 0 for all g to ensure identifiablilty. We set u_g,0 = −∞ and u_g,K = ∞ for all g, so ${\sum }_{k=0}^{K-1}\text{P}(Y_{i,\text{E}}=k|g_i,d_{[i]},{\gamma }_{i,\text{T}})=1$. The function η_E quantifies the dose effect on Y_E. Subgroup effects are accounted for through u_g,k and α_E,g, and various patterns in the relationships between subgroup and the efficacy outcome can be accommodated flexibly. We assume α_E,1 ≥ · · · ≥ α_E,G to ensure that the probability of PD is non-decreasing in subgroups. No restriction by g is imposed on u_g,k for k = 2, … , K − 1, and under the model P(Y_i,E ≤ k|g_i, d_[i],𝛾_i,T) is not necessarily stochastically increasing in subgroups for k > 0. If desired, stochastic ordering of the distribution of Y_E in g can be imposed by requiring u_1,k − α_E,1 ≥ · · · ≥ u_G,k − α_E,G for all k.

We model the relationship between Y_i,j and d_[i] through the regression function

$${\eta }_j(d_{[i]})=\frac{{\beta }_{j3}}{1+\exp \left\{-{\beta }_{j1}\times \left(10\times d_{[i]}-{\beta }_{j2}\right)\right\}}$$ (3)

that appears in the linear component of each marginal, j = E, T. Dose is multiplied by 10 to stabilize numerical computations. We assume 𝛽_j,1, ${\beta }_{j,3}\in {ℝ}^{+}$ and ${\beta }_{j,2}\in ℝ$, so that η_j(d), P(Y_T ≤ C_T|g, d, γ), and P(Y_E ≥ k|g, d, γ) each increases in d. The functional form in (3) may take many different shapes, including an “S” shape that allows the probabilities to plateau at some dose, with η_j → 0 as d → −∞, while η_j → β_j3 as d → ∞.

Let θ denote the vector of all model parameters and $\tilde{\mathit{\theta }}$ the vector of all fixed hyperparameters, which we will specify below. The joint likelihood of all observable outcomes of patient i, conditional on the latent frailty vector γ_i, subgroup g_i, dose d_[i], and model parameters, is the product likelihood given by

$$\begin{gathered} p(y_{i,\text{T}}^o,y_{i,\text{E}},{\delta }_{i,\text{T}},{\delta }_{i,\text{E}}|g_i,d_{[i]},{\mathit{\gamma }}_i,\mathit{\theta },\tilde{\mathit{\theta }})=p(y_{i,\text{T}}^o,{\delta }_{i,\text{T}}|g_i,d_{[i]},{\mathit{\gamma }}_i,\mathit{\theta },\tilde{\mathit{\theta }})\times {\left\{p(y_{i,\text{E}}|g_i,d_{[i]},{\mathit{\gamma }}_i,\mathit{\theta },\tilde{\mathit{\theta }})\right\}}^{{\delta }_{i,\text{E}}} \\ ={\left\{h_{i,\text{T}}(y_{i,\text{T}}^o|g_i,d_{[i]},{\gamma }_{i,\text{T}})\right\}}^{{\delta }_{i,\text{T}}}{S}_{\text{T}}(y_{i,\text{T}}^o|g_i,d_{[i]},{\gamma }_{i,\text{T}}) \\ \times {\left\{{\pi }_{y_{i,\text{E}}}(g_i,d_{[i]},{\gamma }_{i,\text{E}})\right\}}^{{\delta }_{i,\text{E}}}. \end{gathered}$$ (4)

We assume ${\mathit{\gamma }}_i|\mathrm{\Omega }\stackrel{iid}{~}{\text{N}}_2(\mathbf{0},\mathrm{\Omega })$ with random Ω. We include γ_i,1, … , γ_i,n(t) in the model to account for between-patient heterogeneity not explained by d_[i] and g_i, with correlations among the γ_i,j’s inducing dependence between Y_i,E and Y_i,T. Frailty models have been used widely for multivariate failure time data in a wide variety of settings, including competing risks,¹³ and a phase I-II design with a complex 5-variate time-to-event outcome.¹⁴ The joint distribution of Y_i = (Y_i,T, Y_i,E) is obtained by integrating over the frailty distribution,

$$p({\mathit{y}}_i|g_i,d_{[i]},\mathit{\theta },\tilde{\mathit{\theta }})={\int }_{{ℝ}^2}p({\mathit{y}}_i|g_i,d_{[i]},{\mathit{\gamma }}_i,\mathit{\theta },\tilde{\mathit{\theta }})\times p\left({\mathit{\gamma }}_i|\mathrm{\Omega }\right)d{\mathit{\gamma }}_i.$$

2.2 |. Subgroup clustering and posterior computation

To reduce notation, temporarily suppress patient index, i. We allow the possibility of adaptively combining prognostic subgroups that have similar subgroup effects on Y, based on the observed trial data, by introducing latent cluster membership indicators for the subgroups, z = (z₁, … , z_G). To account for risk subgroup ordinality, the model allows only adjacent subgroups to be combined. Each set of one or more combined subgroups is a cluster, and the R ≤ G clusters are indexed consecutively by r = 1, … , R. For example, if G = 3, the four possible configurations of z = (z₁, z₂, z₃) are (1, 1, 1), (1, 1, 2), (1, 2, 2), and (1, 2, 3) which define, respectively, R = 1, 2, 2, and 3 clusters. The case with z = (1, 1, 2) is that where subgroups 1 and 2 are combined and subgroup 3 is distinct, and the clusters are {1,2} indexed by r = 1 and the singleton {3} indexed by r = 2. To implement the clustering, we set z₁ = 1 and assume P(z_g = z_g−1|z_g−1) = ξ_g and P(z_g = z_g−1 + 1|z_g−1) = 1 − ξ_g for subgroups g = 2, … ,G, so the prior of z is

$$p(\mathit{z}|\mathit{\xi })=\prod _{g=2}^G{\xi }_g^{\text{I}(z_g=z_{g-1})}{(1-{\xi }_g)}^{1-\text{I}(z_g=z_{g-1})},$$ (5)

where I(A) = 1 if A is true and 0 otherwise. Under this model, subgroup g may join the cluster to which subgroup g − 1 belongs with probability ξ_g, so z_g = z_g−1, and with the remaining probability, 1 − ξ_g, subgroup g may start a new cluster, z_g = z_g−1 + 1. This ensures non-decreasing ordering of cluster membership indicators, z_g ≤ z_g+1, and subgroup g cannot be in the cluster to which subgroup g − 2 belongs if subgroup g − 1 is not in the cluster. The cluster membership indicator z_G of the highest risk subgroup is R, and both R and z are random. If the subgroups are not ordinal, the ordering constraint on z_g is not imposed and any model-based clustering approach, such as using a Gaussian mixture model, can be assumed as a prior for z, e.g., Chapple and Thall (2018).¹⁵

We assume that subgroup effects are identical within each cluster. To formalize this, we introduce cluster-specific parameters ${\alpha }_{\text{T},r}^{\star }$ and ${\alpha }_{\text{E},r}^{\star }$ for clusters r = 1, … , R, denoting ${\mathit{\alpha }}_j^{\star }=({\alpha }_{j,1}^{\star },\dots ,{\alpha }_{j,R}^{\star })$ for j = T or E, and let ${\alpha }_{j,g}={\alpha }_{j,z_g}^{\star }$. A cluster-specific cutoff vector ${\mathit{u}}_r^{\star }$ is defined similarly, with each $u_{r,k}^{\star }$ the same for all subgroups in cluster r. The probabilities $\text{P}(Y_{\text{T}}\le t|g,d,{\mathit{\alpha }}_T^{\star },\mathit{\gamma })$ and $\text{P}(Y_{\text{E}}=k|g,d,{\mathit{\alpha }}_E^{\star },\mathit{\gamma })$ do not change with g in each cluster.

We next specify priors for ${\mathit{\alpha }}_j^{\star }$ and u^⋆. Given z, we assume normal distributions with order constrains on $\{{\alpha }_{j,z}^{\star }\}$, given by

$$\begin{gathered} p({\alpha }_{\text{T},2}^{\star },\dots ,{\alpha }_{\text{T},R}^{\star }|\mathit{z},{\overline{\mathit{\alpha }}}_{\text{T}},{\mathit{v}}_{\text{T}}^2)\propto \prod _{r=2}^R\exp \{-{({\alpha }_{\text{T},r}^{\star }-{\overline{\alpha }}_{\text{T},r}^{\star })}^2/(2v_{\text{T}r}^2)\}1({\alpha }_{\text{T},r}^{\star }>{\alpha }_{\text{T},r-1}^{\star }), \\ p({\alpha }_{\text{E},1}^{\star },\dots ,{\alpha }_{\text{E},R}^{\star }|\mathit{z},{\overline{\mathit{\alpha }}}_{\text{E}},{\mathit{v}}_{\text{E}}^2)\propto \prod _{r=1}^R\exp \{-{({\alpha }_{\text{E},r}^{\star }-{\overline{\alpha }}_{\text{E},r}^{\star })}^2/(2v_{\text{E}r}^2)\}1({\alpha }_{\text{E},r}^{\star }<{\alpha }_{\text{E},r-1}^{\star }), \end{gathered}$$ (6)

where ${\alpha }_{\text{T},1}^{\star }=0$ and ${\alpha }_{\text{E},0}^{\star }=\infty$, and ${\overline{\mathit{\alpha }}}_j^{\star }=({\overline{\alpha }}_{j,1}^{\star },\dots ,{\overline{\alpha }}_{j,R}^{\star })$ and ${\mathit{v}}_j^2=(v_{j,1}^2,\dots ,v_{j,R}^2)$ are fixed hyperparameters. Due to the ordering on $\{{\alpha }_{j,r}^{\star }\}$, higher risk subgroups have larger probabilities of toxicity and PD. For k = 2, … , K − 1 and r = 1, … , R, we let $u_{r,k}^{\star }=u_{r,k-1}^{\star }+{\rho }_{r,k}$, and assume ${\rho }_{r,k}\stackrel{indep}{~}\text{Ga}\left({\rho }_{r-1,k}{\kappa }_{r,k},{\kappa }_{r,k}\right)$ with prior mean ρ_r−1,k and prior variance ρ_r−1,k/κ_r,k, and fix ρ_0,k and κ_r,k. The distributions of z in (5), ${\mathit{\alpha }}_j^{\star }$ in (6), and u^⋆ jointly define the distributions of α_j and u. In the posterior computations, z, ${\mathit{\alpha }}_j^{\star }$ and u^⋆ are included as a parameter subvector of θ instead of α_j and u.

Clustering is done to borrow strength by combining subgroups having similar effect distributions. However, optimal doses still are chosen for subgroups using their respective utilities and the distributions of α_j,g and u_g. Doses are not chosen for clusters. In clinical practice, physicians often cluster prognostic subgroups in an ad hoc manner to simplify their decision making. In contrast, our adaptive clustering algorithm is a Bayesian statistical methodology that forms subgroup clusters based on data.

We specify priors for the model parameters h_0T(t), β = {β_j,ℓ,j = T or E, and ℓ = 1, 2, 3}, and Ω as follows. For h_0T, we assume a constant hazard over (0, C) and let $h_{0\text{T}}~\mathrm{Log}-\text{N}({\overline{h}}_{0\text{T}},v_h^2)$, since previous studies indicate that it is reasonable to assume a constant hazard during the follow-up period.^2,16,17 If a hazard that varies over time is more appropriate, other models such as a Weibull or piecewise exponential distribution can be used. To ensure that relationships of doses with the outcomes are monotonically increasing, we assume normal or truncated normal distributions for β_j,ℓ, j = T,E and ℓ = 1, 2, 3, accordingly. We assume β_j,1 and β_j,3 have normal distributions truncated below at 0, $p({\beta }_{j,\ell }|{\overline{\beta }}_{j,\ell },{\tau }_{j,\ell }^2)\propto \exp \left\{-{({\beta }_{j,\ell }-{\overline{\beta }}_{j,\ell })}^2/(2{\tau }_{j,\ell }^2)\right\}$ for β_j,ℓ > 0, ℓ = 1,3. We assume normal prior distributions $\text{N}({\overline{\beta }}_{j,2},{\tau }_{j,2}^2)$ for β_j,2, j = E, T. To complete the prior specification of γ_i, we let Ω|ν, Ω⁰ ~ inv-Wishart(ν, Ω⁰) for fixed ν > 1 and 2 × 2 positive definite hyperparameter matrix Ω⁰.

Collecting terms, θ = (h_T0, β, α^⋆, z, ρ, Ω) denotes the vector of all model parameters, where β = {β_j,ℓ,j = T,E,ℓ = 1, 2, 3}, ${\mathit{\alpha }}^{\star }=\{{\alpha }_{j,r}^{\star },j=T,E,r=1,\dots ,R\}$, and ρ = {ρ_r,k, r = 1, … , R, k = 2, … , K − 1}. For j = E, T, ℓ = 1, 2, 3, r = 1, … , G, and k = 2, … , K − 1, we denote $\overline{\mathit{\beta }}=\{{\overline{\beta }}_{j,\ell }\}$, ${\mathit{\tau }}^2=\{{\tau }_{j,\ell }^2\}$, ξ = (ξ₂, … , ξ_G), ${\overline{\mathit{\alpha }}}^{\star }=\{{\overline{\alpha }}_{j,r}^{\star }\}$, ${\mathit{v}}^2=\{v_{j,r}^2\}$, ρ₀ = {ρ_0,k}, and κ = {κ_r,k}, so the vector of all fixed hyperparameters is $\tilde{\mathit{\theta }}=({\overline{h}}_{\text{T}0},v_h^2,\overline{\mathit{\beta }},{\mathit{\tau }}^2,\mathit{\xi },{\overline{\mathit{\alpha }}}^{\star },{\mathit{v}}^2,{\mathit{\rho }}_0,\mathit{\kappa },v,{\mathrm{\Omega }}^0)$. For the mRCC trial design, we established $\tilde{\mathit{\theta }}$ by using data from the phase 3 CheckMate 214 trial described by Motzer et al,² and elicited prior probabilities from the clinical investigators. In the CheckMate 214 trial, patients were categorized into favorable, intermediate, and poor risk subgroups by their IMDC risk status, and randomly assigned to one of two treatments including a combination of nivolumab and ipilimumab. Table 1 of Motzer et al² reports P(Y_E = k) for g = 1 and g > 1 when no sitravatinib is given, that is, η_j = 0 under our model in (3). Using the historical data and elicited probabilities, we fit our model to pseudo data simulated from the elicited probabilities or the historical data, and used posterior means to determine location hyper-parameters. We calibrated dispersion hyper-parameters to reflect prior uncertainty, and examined the calibrated $\tilde{\mathit{\theta }}$ with pseudo data simulated under various settings. Details of prior calibration are given in Supplementary Section 2.

TABLE 1.

Simulation results

		d 1	d 2	d 3	d 4	d 5	d 1	d 2	d 3	d 4	d 5
ztrue = (1, 2, 3)		Scenario 1					Scenario 2
U true	g = 1	56.89	51.38	47.69	43.81	39.46	34.34	35.57	34.21	32.38	32.45
	g = 2	58.17	53.25	51.91	49.83	47.67	35.85	38.94	40.73	40.27	41.70
	g = 3	39.85	35.41	33.63	32.13	30.50	34.59	38.40	41.17	41.94	43.86
$p_{\mathrm{T}}^{\text{true}}$	g = 1	0.05	0.20	0.35	0.50	0.65	0.25	0.35	0.50	0.60	0.65
	g = 2	0.07	0.28	0.47	0.64	0.79	0.32	0.44	0.61	0.71	0.76
	g = 3	0.11	0.39	0.61	0.78	0.90	0.38	0.51	0.68	0.78	0.82
${\pi }_0^{\text{true}}$	g = 1	0.16	0.16	0.12	0.09	0.07	0.50	0.37	0.25	0.20	0.16
	g = 2	0.25	0.25	0.20	0.16	0.12	0.57	0.43	0.31	0.25	0.20
	g = 3	0.57	0.56	0.50	0.43	0.37	0.63	0.50	0.37	0.31	0.25
$p_m^{\text{sel}}(g)$
D-Sub	g = 1	0.84	0.06	0.03	0.01	0.03	0.00	0.02	0.03	0.00	0.02
	g = 2	0.85	0.07	0.04	0.01	0.02	0.01	0.02	0.01	0.00	0.00
	g = 3	0.13	0.01	0.00	0.00	0.00	0.00	0.01	0.00	0.00	0.00
D-Comb	all g	0.75	0.04	0.02	0.00	0.01	0.00	0.00	0.00	0.00	0.00
D-Sep	g = 1	0.62	0.14	0.10	0.02	0.10	0.05	0.02	0.06	0.03	0.07
	g = 2	0.83	0.06	0.06	0.01	0.02	0.02	0.02	0.01	0.00	0.00
	g = 3	0.10	0.03	0.04	0.02	0.02	0.08	0.03	0.05	0.01	0.01
$p_m^{\text{unacc}}(g)$
D-Sub	g = 1	0.06	0.07	0.32	0.55	0.62	0.99	0.97	0.95	0.97	0.97
	g = 2	0.02	0.05	0.54	0.92	0.95	0.98	0.96	0.99	1.00	1.00
	g = 3	0.86	0.91	0.99	1.00	1.00	1.00	0.99	1.00	1.00	1.00
D-Comb	all g	0.18	0.23	0.74	0.96	0.97	1.00	1.00	1.00	1.00	1.00
D-Sep	g = 1	0.06	0.06	0.20	0.43	0.51	0.94	0.92	0.86	0.89	0.89
	g = 2	0.03	0.07	0.57	0.91	0.94	0.97	0.96	0.99	1.00	1.00
	g = 3	0.86	0.89	0.92	0.97	0.98	0.88	0.90	0.94	0.99	0.99
$n_m^{\text{ptrt}}(g)$
D-Sub	g = 1	7.35	7.19	5.31	3.80	3.43	1.87	2.66	2.90	2.16	2.04
	g = 2	25.71	23.94	13.13	4.55	3.31	8.90	8.53	4.60	1.76	1.16
	g = 3	3.88	3.06	1.30	0.30	0.08	1.67	1.81	0.66	0.16	0.05
D-Comb	g = 1	9.68	8.43	3.90	1.41	1.07	2.44	2.08	1.27	0.54	0.45
	g = 2	24.76	22.25	10.07	3.69	2.72	6.21	5.63	3.35	1.50	1.16
	g = 3	7.06	6.25	2.80	1.05	0.78	1.66	1.52	0.99	0.44	0.34
D-Sep	g = 1	6.96	6.93	5.82	4.36	3.89	7.49	7.11	5.14	3.31	2.88
	g = 2	25.85	23.47	12.53	5.22	3.81	11.74	10.01	5.66	2.49	1.86
	g = 3	6.96	6.09	3.66	1.75	1.34	7.09	5.52	2.94	1.53	1.15
		d 1	d 2	d 3	d 4	d 5	d 1	d 2	d 3	d 4	d 5
ztrue = (1, 2, 3)		Scenario 3					Scenario 4
U true	g = 1	59.95	64.84	72.19	64.57	58.12	54.07	48.75	48.63	40.37	36.04
	g = 2	64.96	70.83	79.05	74.63	70.18	56.47	54.15	55.52	49.64	46.55
	g = 3	56.53	63.35	73.50	65.89	60.18	51.47	52.05	54.98	50.88	48.50
$p_{\mathrm{T}}^{\text{true}}$	g = 1	0.05	0.08	0.10	0.35	0.50	0.05	0.25	0.30	0.50	0.60
	g = 2	0.05	0.08	0.10	0.35	0.50	0.05	0.25	0.30	0.50	0.60
	g = 3	0.13	0.20	0.25	0.69	0.85	0.05	0.25	0.30	0.50	0.60
${\pi }_0^{\text{true}}$	g = 1	0.16	0.09	0.03	0.02	0.02	0.16	0.12	0.09	0.09	0.09
	g = 2	0.16	0.09	0.03	0.02	0.02	0.16	0.12	0.09	0.09	0.09
	g = 3	0.31	0.20	0.09	0.07	0.07	0.41	0.34	0.29	0.29	0.29
$p_m^{\text{sel}}(g)$
D-Sub	g = 1	0.01	0.04	0.87	0.05	0.03	0.74	0.13	0.13	0.00	0.00
	g = 2	0.00	0.02	0.85	0.08	0.05	0.60	0.16	0.19	0.01	0.04
	g = 3	0.02	0.04	0.85	0.04	0.01	0.44	0.14	0.22	0.01	0.05
D-Comb	all g	0.01	0.03	0.86	0.07	0.04	0.65	0.13	0.17	0.02	0.03
D-Sep	g = 1	0.06	0.11	0.47	0.14	0.21	0.64	0.16	0.12	0.02	0.05
	g = 2	0.01	0.04	0.70	0.14	0.12	0.64	0.12	0.16	0.03	0.05
	g = 3	0.09	0.13	0.59	0.11	0.08	0.14	0.09	0.20	0.09	0.41
$p_m^{\text{unacc}}(g)$
D-Sub	g = 1	0.01	0.00	0.00	0.10	0.26	0.01	0.01	0.07	0.32	0.47
	g = 2	0.00	0.00	0.00	0.15	0.37	0.01	0.01	0.08	0.40	0.57
	g = 3	0.08	0.05	0.06	0.74	0.92	0.17	0.20	0.34	0.73	0.82
D-Comb	all g	0.00	0.00	0.01	0.31	0.60	0.01	0.02	0.11	0.39	0.55
D-Sep	g = 1	0.02	0.01	0.01	0.12	0.20	0.05	0.05	0.14	0.36	0.46
	g = 2	0.00	0.00	0.01	0.14	0.28	0.00	0.03	0.11	0.37	0.52
	g = 3	0.03	0.03	0.07	0.65	0.81	0.23	0.22	0.23	0.38	0.46
$n_m^{\text{ptrt}}(g)$
D-Sub	g = 1	5.83	6.02	5.86	5.22	4.73	6.49	6.49	5.91	4.64	4.10
	g = 2	15.86	15.87	15.86	13.17	11.08	18.29	17.82	15.72	10.87	8.97
	g = 3	5.14	5.45	5.40	2.33	1.32	5.49	5.20	4.02	1.95	1.43
D-Comb	g = 1	6.66	6.56	6.27	4.59	3.60	7.17	6.74	5.98	4.11	3.51
	g = 2	16.93	16.97	16.61	12.33	9.10	18.88	17.62	15.17	11.15	9.16
	g = 3	4.74	4.80	4.60	3.52	2.62	5.28	5.04	4.20	3.03	2.64
D-Sep	g = 1	5.95	6.01	5.88	5.27	4.90	6.87	6.74	5.80	4.50	4.04
	g = 2	15.97	15.63	15.28	13.26	11.79	18.55	17.23	15.28	11.19	9.63
	g = 3	5.14	5.19	4.79	2.78	2.04	4.71	4.70	4.21	3.33	3.01
		d 1	d 2	d 3	d 4	d 5	d 1	d 2	d 3	d 4	d 5
ztrue = (1, 2, 3)		Scenario 5					Scenario 6
U true	g = 1	57.64	48.14	47.08	49.66	52.30	57.62	55.12	53.76	63.17	56.94
	g = 2	65.44	59.25	58.92	63.74	67.67	52.93	46.64	44.45	52.85	42.68
	g = 3	70.05	65.27	64.67	70.81	75.03	55.65	50.80	48.84	59.80	51.27
$p_{\mathrm{T}}^{\text{true}}$	g = 1	0.03	0.28	0.30	0.35	0.38	0.03	0.10	0.13	0.15	0.30
	g = 2	0.03	0.28	0.30	0.35	0.38	0.13	0.38	0.46	0.52	0.80
	g = 3	0.03	0.28	0.30	0.35	0.38	0.13	0.37	0.46	0.52	0.80
${\pi }_0^{\text{true}}$	g = 1	0.12	0.12	0.12	0.07	0.04	0.16	0.16	0.16	0.05	0.05
	g = 2	0.16	0.16	0.16	0.09	0.06	0.20	0.20	0.20	0.07	0.07
	g = 3	0.16	0.16	0.16	0.09	0.05	0.20	0.20	0.20	0.07	0.07
$p_m^{\text{sel}}(g)$
D-Sub	g = 1	0.64	0.01	0.00	0.01	0.34	0.21	0.02	0.03	0.26	0.49
	g = 2	0.28	0.01	0.00	0.02	0.68	0.77	0.03	0.03	0.14	0.03
	g = 3	0.15	0.01	0.00	0.02	0.81	0.69	0.02	0.04	0.12	0.02
D-Comb	all g	0.27	0.01	0.01	0.02	0.70	0.60	0.01	0.03	0.22	0.11
D-Sep	g = 1	0.50	0.04	0.03	0.03	0.39	0.09	0.05	0.06	0.22	0.58
	g = 2	0.24	0.02	0.01	0.03	0.70	0.77	0.03	0.03	0.12	0.03
	g = 3	0.10	0.04	0.04	0.05	0.77	0.45	0.09	0.11	0.17	0.17
$p_m^{\text{unacc}}(g)$
D-Sub	g = 1	0.00	0.01	0.02	0.02	0.03	0.00	0.00	0.01	0.02	0.03
	g = 2	0.00	0.01	0.03	0.04	0.05	0.01	0.10	0.46	0.75	0.92
	g = 3	0.02	0.04	0.06	0.08	0.09	0.11	0.23	0.59	0.84	0.96
D-Comb	all g	0.00	0.02	0.03	0.04	0.05	0.03	0.08	0.28	0.54	0.77
D-Sep	g = 1	0.02	0.04	0.10	0.13	0.16	0.06	0.05	0.03	0.03	0.05
	g = 2	0.00	0.02	0.04	0.06	0.07	0.03	0.14	0.49	0.77	0.91
	g = 3	0.00	0.02	0.07	0.12	0.15	0.04	0.11	0.33	0.59	0.77
$n_m^{\text{ptrt}}(g)$
D-Sub	g = 1	5.63	5.64	5.48	5.40	5.41	5.59	5.58	5.53	5.40	5.29
	g = 2	15.55	15.00	14.28	13.50	13.44	24.17	20.77	13.62	7.98	4.87
	g = 3	4.58	4.31	3.93	3.63	3.56	6.91	5.73	3.22	1.49	0.65
D-Comb	g = 1	6.15	5.66	5.33	5.23	5.22	8.31	7.16	5.32	3.69	2.54
	g = 2	15.97	15.02	13.89	13.59	13.50	21.86	18.73	13.79	9.32	6.48
	g = 3	4.41	4.27	4.06	3.96	3.75	6.29	5.34	3.87	2.72	1.86
D-Sep	g = 1	6.36	6.19	5.50	5.05	4.87	5.73	5.79	5.54	5.52	5.42
	g = 2	16.10	15.14	14.17	13.37	13.22	25.84	20.59	12.58	7.08	4.46
	g = 3	4.47	4.47	4.00	3.55	3.51	5.64	5.23	4.00	2.72	2.20
		d 1	d 2	d 3	d 4	d 5	d 1	d 2	d 3	d 4	d 5
ztrue = (1, 2, 3)		Scenario 7					Scenario 8
U true	g = 1	39.68	42.13	46.41	50.73	54.11	46.93	53.95	46.36	40.27	36.10
	g = 2	40.33	43.08	48.81	55.18	60.06	48.04	55.63	52.02	47.72	44.74
	g = 3	40.83	43.79	50.06	57.99	63.55	48.90	57.16	55.02	51.73	49.26
$p_{\mathrm{T}}^{\text{true}}$	g = 1	0.03	0.05	0.10	0.20	0.25	0.05	0.05	0.30	0.45	0.55
	g = 2	0.03	0.05	0.10	0.20	0.25	0.05	0.05	0.30	0.45	0.55
	g = 3	0.03	0.05	0.10	0.20	0.25	0.05	0.05	0.30	0.45	0.55
${\pi }_0^{\text{true}}$	g = 1	0.54	0.46	0.31	0.16	0.09	0.31	0.16	0.12	0.12	0.12
	g = 2	0.54	0.46	0.31	0.16	0.09	0.31	0.16	0.12	0.12	0.12
	g = 3	0.54	0.46	0.31	0.16	0.09	0.31	0.16	0.12	0.12	0.12
$p_m^{\text{sel}}(g)$
D-Sub	g = 1	0.00	0.00	0.05	0.17	0.76	0.08	0.82	0.09	0.00	0.00
	g = 2	0.00	0.00	0.04	0.11	0.84	0.04	0.76	0.17	0.00	0.03
	g = 3	0.00	0.00	0.02	0.10	0.82	0.03	0.68	0.21	0.01	0.05
D-Comb	all g	0.00	0.00	0.03	0.12	0.82	0.06	0.74	0.15	0.00	0.03
D-Sep	g = 1	0.01	0.01	0.07	0.14	0.72	0.26	0.40	0.17	0.02	0.08
	g = 2	0.00	0.00	0.05	0.12	0.82	0.08	0.64	0.17	0.02	0.09
	g = 3	0.00	0.00	0.04	0.09	0.86	0.05	0.25	0.20	0.09	0.41
$p_m^{\text{unacc}}(g)$
D-Sub	g = 1	0.98	0.97	0.58	0.03	0.02	0.27	0.02	0.05	0.29	0.38
	g = 2	0.66	0.54	0.15	0.02	0.02	0.04	0.00	0.07	0.38	0.49
	g = 3	0.77	0.68	0.23	0.06	0.05	0.08	0.02	0.12	0.51	0.60
D-Comb	all g	0.90	0.85	0.34	0.03	0.03	0.10	0.02	0.12	0.41	0.51
D-Sep	g = 1	0.93	0.88	0.52	0.13	0.07	0.28	0.18	0.20	0.37	0.42
	g = 2	0.62	0.54	0.17	0.02	0.03	0.04	0.01	0.10	0.32	0.42
	g = 3	0.44	0.35	0.11	0.04	0.04	0.04	0.02	0.09	0.26	0.33
$n_m^{\text{ptrt}}(g)$
D-Sub	g = 1	1.46	2.27	5.18	8.93	9.25	5.43	6.53	6.20	4.92	4.49
	g = 2	8.96	10.19	15.49	18.37	18.43	17.46	18.00	15.96	11.21	9.69
	g = 3	1.65	2.47	4.21	5.49	5.49	4.87	5.50	4.49	2.55	2.07
D-Comb	g = 1	2.32	2.64	5.72	8.36	8.19	6.46	7.05	5.78	4.23	3.62
	g = 2	6.03	7.24	14.84	21.34	21.28	17.20	18.49	15.36	10.72	9.57
	g = 3	1.70	2.05	4.23	5.95	6.04	4.95	5.09	4.32	3.10	2.69
D-Sep	g = 1	5.18	5.36	5.56	5.92	5.88	6.35	6.61	5.79	4.71	4.41
	g = 2	9.97	10.90	15.42	17.65	17.53	17.23	17.40	15.29	11.42	10.39
	g = 3	3.96	4.12	4.10	3.98	3.84	4.51	4.60	4.17	3.52	3.21

Note: p^unacc(g, d_m) = P(declare dose d_m unacceptable for subgroup g), p^sel(g, d_m) = P(select dose d_m as optimal for subgroup g), and $n_m^{\text{ptrt}}$ = mean number of patients in subgroup g treated at dose d_m. Values for true unacceptable and true optimal doses are given in italics and bold, respectively. ${\overline{\zeta }}_{\text{PD}}(g)$ = 0.20,0.35, and 0.35 for g− = 1, 2, 3 and ${\overline{\zeta }}_{\text{T}}(g)=0.40$ for all subgroups.

Given $\tilde{\mathit{\theta }}$ and interim data ${\mathcal{D}}_{n(t)}$ at trial time t, the joint posterior of θ and the patient specific random effects γ = {γ_i, i = 1, … , n(t)} is

$$p(\mathit{\theta },\mathit{\gamma }|{\mathcal{D}}_{n(t)},\tilde{\mathit{\theta }})\propto \left\{\prod _{i=1}^{n(t)}p(y_{i,\text{T}}^o,y_{i,\text{E}},{\delta }_{i,\text{T}},{\delta }_{i,\text{E}}|d_{[i]},{\mathit{\gamma }}_i,\mathit{\theta },\tilde{\mathit{\theta }})\right\}p(\mathit{\theta },\mathit{\gamma }|\tilde{\mathit{\theta }}),$$ (7)

Where $p(y_{i,\text{T}}^0,y_{i,\text{E}},{\delta }_{i,\text{T}},{\delta }_{i,\text{E}}|d_{[i]},{\mathit{\gamma }}_i,\mathit{\theta },\tilde{\mathit{\theta }})$ is specified in (4). We use Markov chain Monte Carlo (MCMC) simulation to generate posterior samples of (θ, γ). Since z is a subvector of θ, its posterior is obtained as a marginal of the posterior of (θ, γ), which in turn provides a posterior on R, the clusters, and the cluster-specific subgroup effects α^⋆. Computational details are given in Supplementary Section 1. A computer program “Dose-finding-subgroup” for implementing the proposed design is available from https://users.soe.ucsc.edu/~juheelee/.

3 |. SUBGROUP-SPECIFIC UTILITY FUNCTION

Our utility function is constructed to accommodate the possibility that clinicians may be more willing to accept a higher risk of toxicity if disease status is likely to be improved for patients in a poor risk subgroup, and they also consider an early occurrence of toxicity less desirable for patients in more favorable risk subgroups. To construct a utility function that allows risk-benefit preferences between Y_T and Y_E to differ between subgroups in this way, we elicited G subgroup-specific utility functions, U_g(Y), g = 1, … , G. Denote the utility of Y_j in subgroup g by U_j,g(Y_j), for j = E, T. For each g, we first establish U_T,g(y_T) for 0 ≤ y_T, then establish U_E,g(y_E) for y_E = 0, 1, … , K − 1, scaled to have values on the same numerical domain as those of U_T,g(y_T), and finally define U_g(Y) = U_T,g(Y_T) + U_E,g(Y_E).

We begin by eliciting the numerical utility, U_T,max, of not observing toxicity during the follow up period [0, C], and define

$$U_{\text{T},g}\left(Y_{\text{T}}\right)=\{\begin{array}{lll}{U}_{\text{T},\max }{\left(\frac{Y_{\text{T}}}{C}\right)}^{a_g}\hfill & \text{if}\hfill & Y_{\text{T}}<C,\hfill \\ U_{\text{T},\max }\hfill & \text{if}\hfill & Y_{\text{T}}\ge C.\hfill \end{array}$$

The shape parameter a_g > 0 is determined during the utility elicitation process by showing several plots of U_T,g(y) as a function of y on the interval [0, C] to the physician(s) providing the utility for a set of candidate a_g values. The function U_T,g(y) increases continuously with y over the follow-up period [0, C] to its maximum value U_T,max for all Y_T ≥ C.

For the motivating mRCC trial, based on the clinicians’ experiences and preferences, we elicited U_T,max = 140 and U_T,g(Y_T) = 70 at Y_T = 70 days for g = 1 (good prognosis), at Y_T = 42 days for g = 2 (intermediate prognosis), and at Y_T = 28 days for g = 3 (poor prognosis). The resulting shape parameters are a₁ = 3.80, a₂ = 1.00, and a₃ = 0.63, and the functions {U_T,g, g = 1, 2, 3} are illustrated in Figure 1A. The figure shows that an early occurrence of toxicity has a lower utility compared to a later occurrence within each subgroup. Also, toxicity-vs-no toxicity utility differences are largest for subgroup 1. Thus, a dose with a high toxicity probability is less likely to be optimal for subgroup 1 than for the other subgroups, even when the dose has good efficacy.

FIGURE 1.

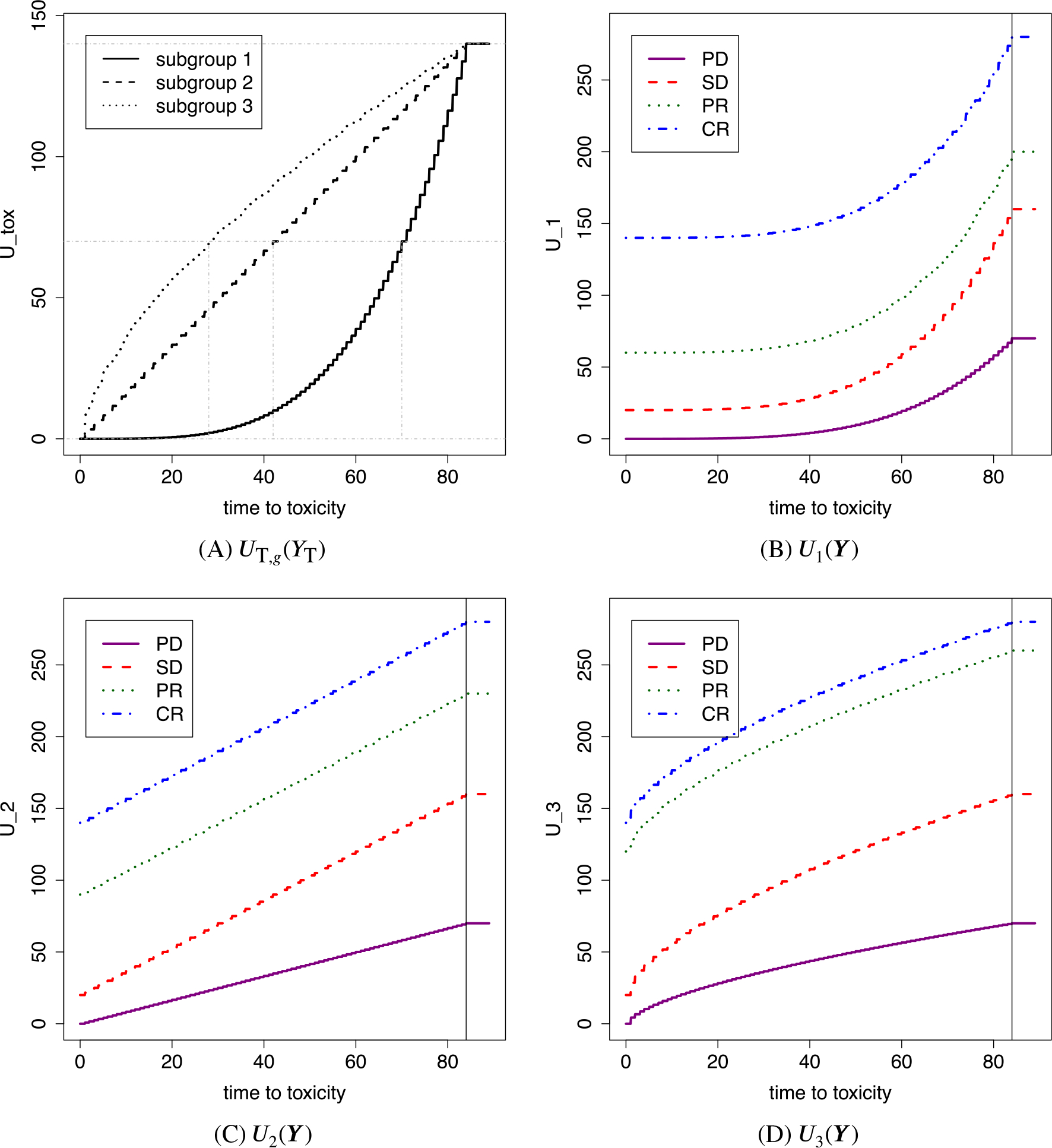
Illustration of subgroup-specific utilities U_g. A, The utility of toxicity for subgroup g, U_T,g(Y_T), $Y_{\text{T}}\in {ℝ}^{+}$. B-D, The utilities of a bivariate outcome, U_g(Y) with Y = (Y_T, Y_E), for subgroups 1, 2, and 3, respectively. Y_E = 0, 1, 2, and 3 represent PD, SD, PR, and CR, respectively

We incorporate Y_E into the total utility U_g as follows: If Y_E = 0 (PD), we define U_g(Y) = U_T,g(Y_T)∕2, and for Y_E = 1, 2, or 3, we define U_g(Y) = U_T,g(Y_T) + U_E,g(Y_E). Thus, having PD reduces the total utility by half of U_T,g, while the better efficacy outcomes, SD, PR, and CR, each increase the utility additively. We fix U_E,g(1) = 20 and U_E,g(3) = 140 for all g and set U_E,1(2) = 60, U_E,2(2) = 90, and U_E,3(2) = 120. The numerical value of U_E,g(2) is the preference of PR relative to SD and CR in subgroup g, and a larger value of U_E,g(2) makes a higher dose more desirable. The maximum utility 280 is achieved if a toxicity event does not occur during the follow-up period and CR is observed, that is, Y_T > C and Y_E = 3. Outcomes with Y_T < 1 and Y_E = 0 are assigned the minimum utility, 0. Figure 1B-D illustrates the utility functions. The relative preferences of the outcomes in subgroup g is determined jointly by a_g and U_E,g(2). Absolute numerical values of U_g are of little importance, whereas the relative sizes of U_g(Y) over different Y values within each subgroup are most relevant for optimal dose selection in that subgroup. The elicited utility should reflect experts’ experience treating the disease of the study. For example, whereas more potent therapies are preferable in IMDC poor risk mRCC, patients with poor prognosis metastatic triple negative breast cancer may be treated with less intensive therapies to preserve quality of life.¹⁸ Thus, elicited subgroup-specific utilities for breast cancer patients can be very different from those for mRCC patients. A detailed discussion of how subgroup-specific utilities may be elicited is given in Supplementary Section 2.

The design uses posterior predictive (PP) mean utilities as optimality criteria for dose selection. Given data ${\mathcal{D}}_{n(t)}$ at trial time t, the PP mean utility of giving dose d_m to a future patient in subgroup g is

$$\begin{gathered} u_g(d_m|{\mathcal{D}}_{n(t)})={\int }_0^{\infty }\sum _{y_{\text{E}}=0}^{K-1}{U}_g(\mathit{y})p(\mathit{y}|g,d_m,{\mathcal{D}}_{n(t)})d{y}_{\text{T}} \\ ={\int }_{\mathit{\theta }}{\int }_{\gamma }{\int }_0^{\infty }\sum _{y_{\text{E}}=0}^{K-1}{U}_g(\mathit{y})p(\mathit{y}|g,d_m,\mathit{\gamma },\mathit{\theta })p(\mathit{\gamma },\mathit{\theta }|{\mathcal{D}}_{n(t)})d{y}_{\text{T}}d\mathit{\gamma }d\mathit{\theta }. \end{gathered}$$ (8)

We compute $u_g\left(d_m|x,{\mathcal{D}}_{n(t)}\right)$ using the empirical posterior sample mean of θ values simulated from $p\left(\mathit{\theta }|{\mathcal{D}}_{n(t)},\tilde{\mathit{\theta }}\right)$. Computational details are given in Supplementary Section 1.

4 |. TRIAL DESIGN

Since lower doses carry a higher risk of PD, and higher doses carry a higher risk of toxicity, we identify acceptable doses by imposing the following subgroup-specific safety conditions. In each subgroup, we will restrict optimal dose selection and treatment assignment to the set of acceptable doses. The first safety constraint is that an untried dose may not be skipped when escalating, with this rule applied separately in each subgroup. If $d_{m_g^{\max }}(t)$ is the highest dose that has been administered by trial time t in subgroup g, then the search for the optimal dose and the treatment assignment are constrained to ${\mathcal{A}}^{\text{Tried}}(g,t)=\left\{d_1,\dots ,d_{\min \left\{m_g^{\max }(t)+1,M\right\}}\right\}$. We monitor both toxicity and efficacy as follows. Recalling that (Y_E = 0) = PD, for each pair (g, d_m), we denote the probabilities of observing PD or severe toxicity during the full 9-week (84-day) follow-up period in subgroup g by

$${\zeta }_{\text{E}}\left(g,d_m,\mathit{\theta }\right)=\mathrm{Pr}\left(Y_{\text{E}}=0|g,d_m,\mathit{\theta }\right),$$

$${\zeta }_{\text{T}}\left(g,d_m,\mathit{\theta }\right)=\mathrm{Pr}\left(Y_{\text{T}}\le C|g,d_m,\mathit{\theta }\right).$$

For each outcome and subgroup g, let ${\overline{\zeta }}_j(g)$ be an elicited fixed upper limit on ζ_j(g, d_m, θ), and let p^⋆ be a fixed cut-off probability. A dose d_m is unacceptable for subgroup g if

$$\text{P}\left\{{\zeta }_j\left(g,d_m,\mathit{\theta }\right)>{\overline{\zeta }}_j(g)\text{for}j=E\text{or}T|{\mathcal{D}}_{n(t)}\right\}>p^{\star }.$$ (9)

Expression (9) says that the probability of PD or toxicity in subgroup g is unacceptably high with d_m. In this case, d_m is not administered to any new patients enrolled in that subgroup. The set of acceptable doses at time t for subgroup g that do not satisfy (9) is denoted by ${\mathcal{A}}^{\mathrm{Accp}}(g,t)$. For the mRCC trial, elicited values were ${\overline{\zeta }}_{\text{T}}(x)=0.40$ for all g, and ${\overline{\zeta }}_{\text{E}}(g)=0.20,0.35$ and 0.35 for the three subgroups. The upper limit ${\overline{\zeta }}_{\text{E}}(g)$ for the probability of PD was set based on the historical data on nivolumab and ipilimuma in Motzer et al,² so adding sitravatinib to the combination should not be permitted to have worse safety. To obtain a design with high probabilities of stopping a truly unsafe or inefficacious dose, while still having high probabilities of selecting the best safe and efficacious dose, we investigated decision probability cutoffs 0.80 and 0.85 by simulation, and chose p^⋆ = 0.85.

For the mRCC trial, the first patient enrolled in each subgroup is treated at d₂, chosen by physicians. For all subsequent patients in each subgroup, the dose acceptability rules first are applied. At trial time t, the safety and efficacy constraints together define the set of acceptable doses $\mathcal{A}(g,t)={\mathcal{A}}^{\text{Tried}}(g,t)\cap {\mathcal{A}}^{\text{Accp}}(g,t)\subseteq \left\{d_1,\dots ,d_M\right\}$ based on interim data ${\mathcal{D}}_{n(t)}$. Since the efficacy outcomes are observed only at e_i + C, we define ${\mathcal{A}}^{\mathrm{Accp}}(g,t)$ based on toxicity only to produce reliable decisions of acceptability until at least 20 patients have been fully followed up to 84 days. Subject to the acceptability rules during trial conduct, patients are adaptively randomized among $d_m\in \mathcal{A}(g,t)$. A patient in subgroup g is assigned to dose $d_m\in \mathcal{A}(g,t)$ with probability proportional to 1∕{n_g,m(t) + 1}, where n_g,m(t) is the number of patients in subgroup g treated at dose d_m up to time t. This implies that a new patient tends to be treated at a dose that is acceptable but less explored. If $\mathcal{A}(g,t)=\varnothing$, then no patients in subgroup g are enrolled. If $\mathcal{A}(g,t)=\varnothing$ for all g, then the trial is terminated and no dose is selected, denoted by d_sel(g) = None for all g. If the trial is not terminated early, subgroup-specific final optimal actions are taken at time $T_{\max }=e_{N_{\max }}+C$. We first identify $\mathcal{A}\left(g,T_{\max }\right)$, and let d_sel(g) = None if $\mathcal{A}\left(g,T_{\max }\right)=\varnothing$. Otherwise, the optimal dose selected for subgroup g is

$$d_{\text{sel}}(g)=\underset{d_m\in \mathcal{A}\left(g,T_{\max }\right)}{argmax}u\left(d_m|g,{\mathcal{D}}_{N_{\max }}\right).$$

5 |. SIMULATION STUDY

5.1 |. Simulation design

To evaluate the design’s performance, we simulated the mRCC trial under eight scenarios. For all scenarios, three subgroups, five doses, and four categorical efficacy outcomes were assumed, that is, G = 3, M = 5, and K = 4. We simulated each g_i from a multinomial distribution with probability vector p_g = (0.23, 0.60, 0.17), to reflect the historical data in Motzer et al.² With N_max = 120, we expect 27.6, 72.0, and 20.4 patients, on average, for the three subgroups. Thus, learning about the dose-outcome distributions for subgroups 1 and 3 may be challenging due to their relatively small sample sizes. For each scenario, we first specified the true latent clustering of the three predefined subgroups, $z^{\text{true}}=(z_1^{\text{true}},z_2^{\text{true}},z_3^{\text{true}})$. We specified the covariance matrix Ω^true for the frailty vectors, and simulated frailties ${\gamma }_i^{\text{true}}\stackrel{iid}{~}{\text{N}}_2\left(\mathbf{0},{\mathrm{\Omega }}^{\text{true}}\right)$. To simulate Y_i,T, we specified marginal probabilities of toxicity occurring during the follow-up period $\text{P}(Y_{i,\text{T}}<C|g_i,d_m,{\gamma }_i^{\text{true}})$, for g_i, d_[i] ∈ {d₁, … ,d₅} and ${\mathit{\gamma }}_i^{\text{true}}$. We simulated Y_i,E from {0, … , K − 1} with probabilities $({\pi }_{i,0}^{\text{true}},\dots ,{\pi }_{i,(K-1)}^{\text{true}})$ conditional on g_i, d_[i] and ${\mathit{\gamma }}_i^{\text{true}}$. Additional details are given in Supplementary Section 4. Table 1 gives the assumed true probabilities of observing severe toxicity during the follow-up period and of observing PD, given the frailty equals zero,

$$\begin{gathered} p_{\text{T}}^{\text{true}}\left(g,d_m\right)=1-\exp \left[-C\left\{h_{0\text{T}}^{\text{true}}\left(d_m\right)+{\alpha }_{\text{T},z_g}^{\star ,\text{true}}\right\}\right],\text{and} \\ {\pi }_k^{\text{true}}\left(g,d_m\right)=\mathrm{\Phi }\left(u_{z_g^{\text{true}},k+1}^{\star ,\text{true}}|{\eta }_{\text{E}}^{\text{true}}\left(d_m\right)+{\alpha }_{\text{E},z_g^{\text{true}}}^{\star ,\text{true}},{\sigma }_{\pi }^{2,\text{true}}\right)-\mathrm{\Phi }\left(u_{z_{\text{g}}^{\text{true}},k}^{\star \text{,true}}|{\eta }_{\text{E}}^{\text{true}}\left(d_m\right)+{\alpha }_{\text{E},z_{\text{g}}^{\text{true}}}^{\star \text{,true}},{\sigma }_{\pi }^{2,\text{true}}\right), \end{gathered}$$

with k = 0 for each scenario. Also, the table gives the expected utility, U^true(g, d_m), under the truth after scaling to have maximum utility 100 for the best outcome. Truly unacceptable doses are given in italics, and truly optimal doses are given in bold. Recall that the elicited thresholds are ${\overline{\zeta }}_{\text{T}}(g)=0.40$ for all g, and ${\overline{\zeta }}_{\text{PD}}(g)=0.20,0.35,0.35$ for g = 1, 2, 3. Supplementary Table 5 illustrates ${\pi }_k^{\text{true}}\left(g,d_m\right)$ for all k, d_m, and g. The simulation truth is different from the assumed model, since the assumed true dose-outcome relationships are arbitrarily specified, and do not follow the regression model assumed for the design. Either $p_{\text{T}}^{\text{true}}\left(g,d_m\right)$ or ${\pi }_k^{\text{true}}\left(g,d_m\right)$ may remain unchanged for multiple doses, as in Scenarios 3, 4, and 8. For some scenarios, the subgroups in different clusters have different distributions for one outcome, but the same distribution for the other outcome, as in Scenarios 4 and 5, while the model assumes that both distributions vary with subgroup clusters. The simulation truth also is very different from the historical data used to calibrate the prior’s location hyperparameters in Supplementary Section 2. Possibly due to the weakly informative prior in Section 2.2, as will be shown below, the design performs well in a range of different simulation scenarios.

With G = 3, four configurations of z^true are possible due to the constraint of subgroup ordinality. Scenarios 1 and 2 have z^true = (1, 2, 3), Scenarios 3 and 4 have z^true = (1, 1, 2), Scenarios 5 and 6 have z^true = (1, 2, 2), and Scenarios 7 and 8 have z^true = (1, 1, 1). Due to potential subgroup effects and the subgroup-specific utility function, the pattern of the true expected utilities in doses varies with subgroups in all scenarios, including Scenarios 7 and 8. In Scenario 1, dose 1 is optimal for subgroups 1 and 2, but no dose is acceptable for subgroup 3 due to excessive probabilities of toxicity or PD. In Scenario 2, no dose is acceptable for any subgroup. In Scenarios 3, 7, and 8, the optimal dose is the same for all subgroups, but in Scenario 3 the true dose acceptability changes with subgroup. In Scenarios 4 to 6, the optimal dose varies with subgroup. For example, in Scenario 4, dose 1 is optimal for subgroups 1 and 2, whereas dose 3 is optimal for subgroup 3. In Scenarios 4 and 5, a higher risk subgroup has a higher optimal dose. In Scenario 6, subgroup 1 has dose 4 as optimal, but dose 1 is optimal in subgroups 2 and 3 due to a large increase in the severe toxicity probabilities.

We call the proposed design “D-Sub”, and considered two comparators, “D-Comb,” which ignores patient subgroups, and “D-Sep,” which runs a separate trial for each subgroup. Both D-comb and D-Sep still are more sophisticated than most phase I-II designs used in practice, such as designs based on two binary outcomes, which would be very impractical for conduct of the mRCC trial due to the 84-day evaluation period.

For D-Comb, we assumed the same model developed for D-Sub, but removed all subgroup-specific factors from the model, so the hazard function was h_T(t|d_[i], 𝛾_i,T) = h_0T(t) exp{η_T(d_[i]) + 𝛾_i,T} and the disease status distribution was ${\pi }_k(d_{[i]},{\gamma }_{i,\text{E}})=\mathrm{\Phi }(u_{k+1}|{\eta }_{\text{E}}(d_{[i]})+{\alpha }_{\text{E}}+{\gamma }_{i,\text{E}},{\sigma }_{\pi }^2)-\mathrm{\Phi }(u_{g_i,k}|{\eta }_{\text{E}}(d_{[i]})+{\alpha }_{\text{E}}+{\gamma }_{i,\text{E}},{\sigma }_{\pi }^2)$. For dose acceptability, we used the upper limits ζ_T = 0.40 and ζ_E = 0.30, elicited for D-Comb. We used U₂(Y) as the common utility function since subgroup 2 has the highest prevalence. Under D-Comb, if a dose is identified as unacceptable, no patient will be treated at that dose regardless of the patient’s subgroup, and if all doses are identified as unacceptable, the trial is terminated. A dose selected as optimal is recommended for all subgroups.

For the D-Sep design, we removed all subgroup specific-factors and kept the remaining parts of the model unchanged, as done for D-Comb. Under D-Sep, trials are run separately in the three subgroups, and no information is borrowed across trials. For each g, we used the same upper limits ${\overline{\zeta }}_j(g)$ and U_g(Y) used for D-Sub, and let N_max = 28, 72, and 20 for the three subgroups.

We evaluated each of the three designs using the following criteria. In subgroup g,

• p^unacc(g, d_m) = probability of identifying an unacceptable dose d_m with a truly excessive probability of either severe toxicity or PD.

• p^sel(g, d_m) = probability of selecting the truly optimal dose d_m.

• n^ptrt(g, d_m) = mean number of patients in subgroup g treated at d_m.

Thus, p^unacc(g, d_m) and p^sel(g, d_m) vary with g under D-Sub and D-Sep, but they are the same for all g under D-Comb. For each simulated trial, b = 1, … , B under each design, we denote by d_sel,b(g) the dose selected as optimal for subgroup g. We let w_b,m(g) = 1 if dose d_m is identified as unacceptable for subgroup g in simulated trial b, or 0 if not, and the number of patients treated in trial b is denoted by N_b. For each scenario and design, we summarized simulation results by the following simulation sample proportions:

$$p^{\text{unacc}}(g,d_m)=\frac{1}{B}\sum _{b=1}^B{w}_{b,m}(g),p^{\text{sel}}(g,d_m)=\frac{1}{B}\sum _{b=1}^B\text{I}(d_{\text{sel},b}(g)=d_m),$$

$$n^{\text{ptrt}}(g,d_m)=\sum _{b=1}^B\sum _{i=1}^{N_b}\text{I}(d_{b,[i]}=d_m\text{and}{g}_{b,[i]}=g)/\sum _{b=1}^B\sum _{i=1}^{N_b}\text{I}(g_{b,[i]}=g).$$

5.2 |. Simulation results

Simulation results are summarized in Table 1. A total of R = 1000 trials with N_max = 120 were simulated under each scenario. Overall, for each subgroup, the D-Sub design reliably identifies doses that are either unsafe or have low efficacy, and selects subgroup-specific optimal acceptable doses. Large p^unacc(g, d_m) is achieved for d_m with unacceptably large $p_{\text{T}}^{\text{true}}\left(g,d_m\right)$ or ${\pi }_0^{\text{true}}\left(g,d_m\right)$. When either of $p_{\text{T}}^{\text{true}}\left(g,d_m\right)$ or ${\pi }_0^{\text{true}}\left(g,d_m\right)$ is clearly greater than its threshold ${\overline{\zeta }}_j(g)$, p^unacc(g, d_m) is particularly high. We also observe that p^unacc(g, d_m) tends to be larger for higher risk subgroups even with the same $p_{\text{T}}^{\text{true}}\left(g,d_m\right)$ or ${\pi }_0^{\text{true}}\left(g,d_m\right)$, possibly due to the order constraint on ${\alpha }_{j,z}^{\star }$. For example, in Scenario 4, $p_{\text{T}}^{\text{true}}\left(g,d_5\right)=0.60$ in all g, and p^unacc(g, d₅) = 0.45, 0.57, and 0.81 for the three subgroups, respectively. When all doses are unacceptable, for example, subgroup 3 in Scenario 1 or all subgroups in Scenario 2, p^unacc(g, d_m) is especially high for all m, possibly because the model borrows information across doses through η_j and across subgroups through ${\alpha }_{j,z}^{\star }$ and thus improves reliability. The D-Sub design is likely to selectively identify unacceptable doses even for scenarios where only some of doses are unacceptable, as in Scenarios 3, 4, and 6 to 8. When all doses are truly unacceptable for all subgroups, as in Scenario 2, trials are stopped and it is concluded that there is no optimal dose with high probability. In Scenario 2, the design identifies all doses as unacceptable, and stops accrual of patients or selects no dose 98%, 96%, and 99% of the time for the three subgroups, respectively. If all doses are truly unacceptable for some subgroups only, trials are continued but accrual is likely to be stopped in those subgroups. For example, in Scenario 1, accrual in subgroup 3 is stopped or no dose is selected for that subgroup 86% of the time, but accrual of patients in subgroups 1 and 2 is continued and dose 1 is correctly selected as the optimal 84% and 85% of the time, respectively. For cases where at least one dose is acceptable for a subgroup, p^sel(g, d_m) tends to be large for the true optimal doses. In most cases, p^sel(g, d_m) is at least 0.60 for the true optimal doses. This indicates that the design performs very well in subgroup-specific optimal dose selection. For example, p^sel(g, d_m) = 0.86, 0.83, and 0.85 for the subgroups, respectively, for the true optimal dose d₂ in Scenario 3. In Scenario 5 where the true optimal dose varies greatly by subgroup, p^sel(g, d_m) corresponding to the true optimal dose is 0.65, 0.66, and 0.80 for the subgroups, respectively. In some other cases where the optimal dose varies by subgroups, p^sel(g, d_m) is not very large, especially for a sparse subgroup. Specifically, subgroup 1 in Scenario 6 has p^sel(1, d₄) = 0.26 for its true optimal dose d₄. Rather, the design more often selects d₅ as optimal, p^sel(1, d₅) = 0.47. However, given that the difference in the true expected utility between doses 4 and 5 is small, 6.23, the design often tends to select the largest dose as optimal. On the other hand, p^sel(g, d_m) = 0.76 and 0.68 are obtained for subgroups 2 and 3, respectively, for their true optimal dose d₁. Subgroup 3 in Scenario 4 is a similar case.

The mean numbers n^ptrt(g, d_m) of patients in subgroup g treated at d_m show that the design is very safe in that it reliably identifies unacceptable doses during the trial and assigns fewer patients to truly unacceptable doses. In Scenarios 3, 4, and 6 to 8, fewer patients were treated at unacceptable doses, and more patients were treated at truly acceptable doses. Recall that the true probabilities of observing events during the follow-up period, $p_{\text{T}}^{\text{true}}\left(g,d_m\right)$, and ${\pi }_k^{\text{true}}\left(g,d_m\right)$, are arbitrarily specified for the doses, whereas the design assumes regression models for the dose-outcome relationships. Thus, in terms of all criteria, D-Sub is robust in that it performs well in a variety of scenarios not based on the underlying model.

Probabilities of identifying unacceptable doses and of dose selection under the comparators, D-Comb and D-Sep, also are summarized in Table 1. D-Sub has greatly superior performance compared to the two comparators in most scenarios. D-Comb failed severely when optimal decisions should differ between subgroups. For example, in Scenario 1, D-Comb assigned patients in subgroup 3 to a dose although no dose is acceptable for subgroup 3, and selected d₁ as optimal for subgroup 3, although d₁ is clearly unacceptable for subgroup 3 due to its unacceptably large probability of PD. D-Comb also identified d₁ and d₂, which are acceptable for subgroups 1 and 2 but not acceptable for subgroup 3, as unacceptable only 18% and 22% of the time, respectively. The corresponding p^unacc(g, d_m) values for d₁ and d₂ under D-Sub are 6% and 6% for subgroup 1, 2% and 4% for subgroup 2, and 87% and 92% for subgroup 3, respectively. In Scenario 5, d₁ is the true optimal dose for subgroup 1 with U^true(1, d₁) = 57.64, followed by U^true(1, d₅) = 52.30. D-Sub selected d₁ as optimal 65% of the time for subgroup 1, but D-Comb selected d₁ only 27% of the time. In Scenario 6, D-Comb performs very poorly, selecting d₁, which is the true optimal dose for subgroups 1 and 2, but not for subgroup 3, as an optimal dose for subgroup 3 more often than its true optimal dose d₄. When there is no subgroup effect, as in Scenarios 7 and 8, D-Sub and D-Comb perform similarly. In Scenarios 7 and 8, due to the subgroup-specific utilities, the patterns of U^true(g, d_m) differ by subgroups. In Scenario 8, d^opt(g) = 2 for all g, but the difference between U^true(g, d₂) and U^true(g, d₃) is greater for subgroup 1. Consequently, D-Sub selected d₂ as optimal more often for subgroup 1 (83%) than for subgroups 2 (76%) and 3 (70%). In contrast, D-Comb selected d₂ as optimal for all subgroups 74% of the time.

D-Sep has very poor performance for subgroups 1 and 3 for most scenarios, due to their low prevalences and the fact that D-Sep does not borrow strength between subgroups. In Scenario 2, where all doses clearly are unacceptable, D-Sep stopped trials with no dose was selected as optimal 78% and 82% of the time for subgroups 1 and 3, respectively, while D-Sub was much safer in that it correctly selected no dose 94% and 100% of the time for those subgroups. When the true optimal doses are middle doses, as in Scenarios 3 and 8, p^sel(g, d_m) values for D-Sep are very small for the true optimal doses, especially in subgroups 1 and 3. For example, in Scenario 8, D-Sep obtained p^sel(g, d_m) = 39% and 23% for the true optimal dose d₂ for subgroups 1 and 3, respectively, compared to 83% and 70% for these subgroups with D-Sub. In Scenario 1, where subgroup-specific decision making is critical, D-Sep behaves more reasonably than D-Comb but is much less reliable than D-Sub. Under D-Sep, trials were terminated or no dose was selected as optimal for subgroup 3 79% of the time, but D-Sep selected d₁ as optimal, for subgroups 1 and 2, 61% and 84% of the time, respectively. Figures 2 and 3 compare the performance metrics of D-Sub, D-Comb, and D-Sep. The figures show histograms of between-design differences in p^sel(g, d_m) for the truly optimal doses, p^unacc(g, d_m) for all doses, and n^ptrt(g, d_m) for the truly unacceptable doses. Positive differences in p^sel(g, d_m) and p^unacc(g, d_m), and negative differences in n^ptrt(g, d_m), correspond to superior performance by D-Sub. The figures show that, overall, D-Sub is greatly superior to both D-Comb and D-Sep in terms of both dose selection and safety.

FIGURE 2.

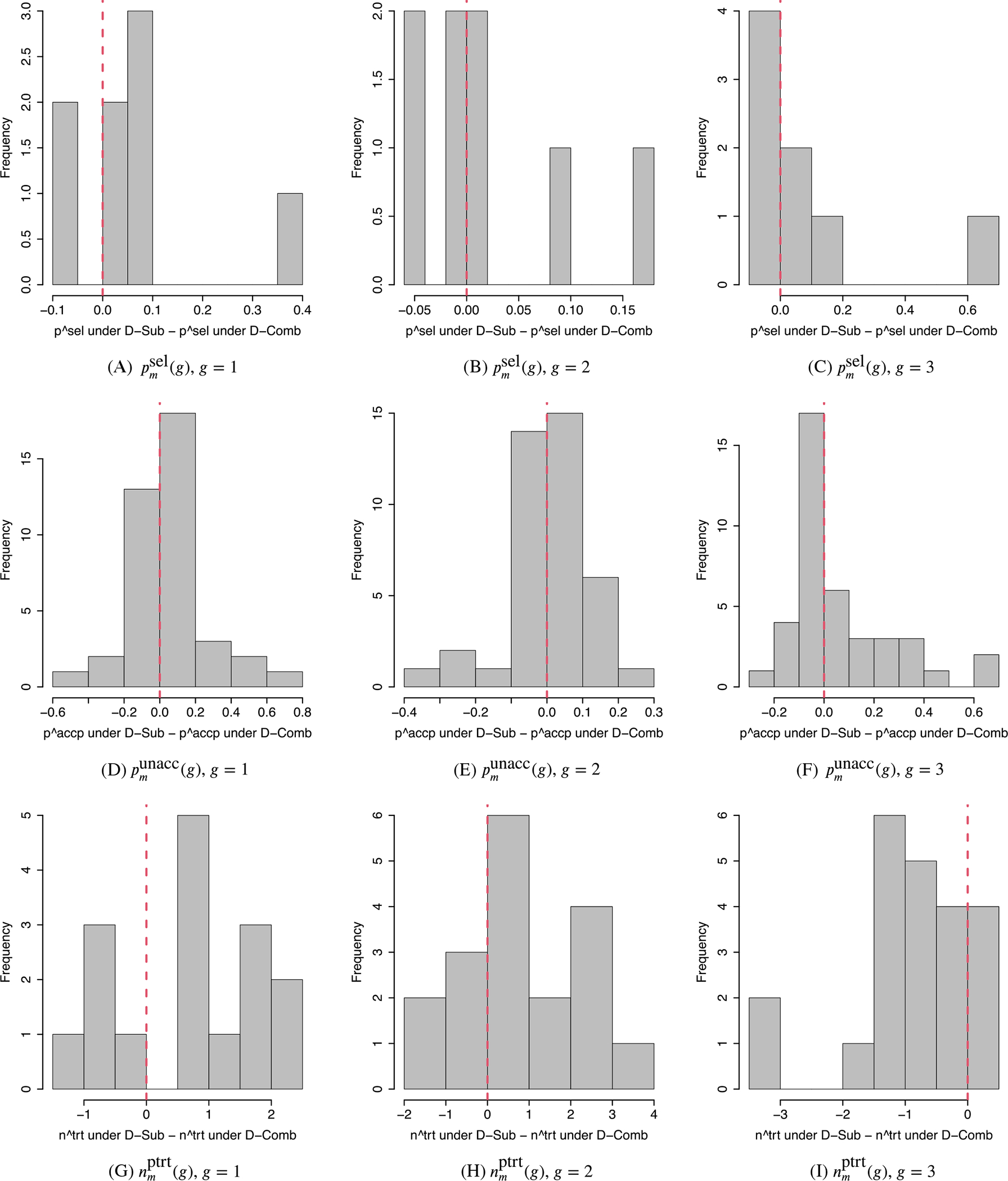
Comparison between D-Sub and D-Comb. A-C, Histograms of differences in $p_m^{\text{sel}}(g)$ between D-Sub and D-Comb. D-F, Histograms of differences in $p_m^{\text{unacc}}(g)$ between D-Sub and D-Comb for the truly unacceptable doses and those between D-Comb and D-Sub for the truly acceptable doses. G-I, Histograms of differences in $n_m^{\text{ptrt}}(g)$ between D-Sub and D-Comb for the truly unacceptable doses. The left, middle, and right columns are for subgroups g = 1 (favorable), g = 2 (intermediate), and g = 3 (poor). A positive value indicates better performance of D-Sub than D-Comb in Panels A-F, and a worse performance in Panels G-I

FIGURE 3.

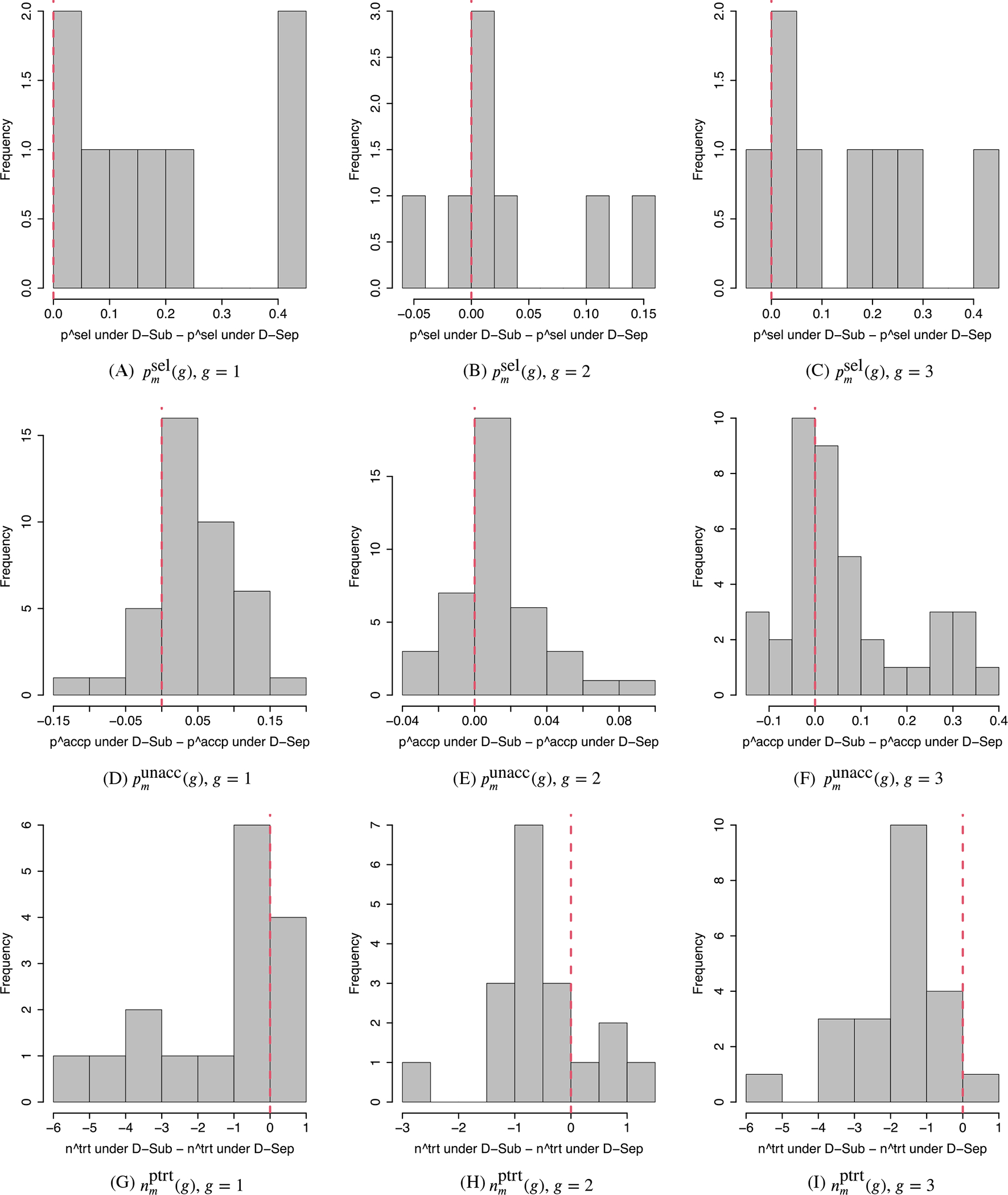
Comparison between D-Sub and D-Sep. A-C, Histograms of differences in $p_m^{\text{sel}}(g)$ between the D-Sub and D-Sep designs. D-F, Histograms of differences in $p_m^{\text{unacc}}(g)$ between D-Sub and D-Sep for the truly unacceptable doses and those between D-Sep and D-Sub for the truly acceptable doses. G-I, Histograms of differences in $n_m^{\text{ptrt}}(g)$ between D-Sub and D-Sep for the truly unacceptable doses. The left, middle, and right columns are for subgroups g = 1 (favorable), g = 2 (intermediate), and g = 3 (poor). A positive value indicates better performance of D-Sub than D-Sep in Panels A-F, and a worse performance in Panels G-I

We performed additional simulations to examine the performance of D-Sub under several different scenarios and relative to the comparators. We also examined how D-Sub’s performance is affected by different specifications of certain design and model parameters, including p_g, U_g(Y), $h_{0\text{T}}^{\text{true}}$ and N_max. We first examined the designs’ performances in the easier case where the subgroup proportions are equal, using p_g = (1∕3, 1∕3, 1∕3) with N_max = 120. Supplementary Table 6 summarizes the results under all scenarios for all three designs, D-Sub, D-Comb, and D-Sep. As expected, the performances of D-Sub and D-Sep are improved for subgroups 1 and 3 in most scenarios, since they have larger subsample sizes. D-Sub performs very similarly for subgroup 2, but D-Sep performs worse for this subgroup. D-Comb performs similarly, except in Scenarios 1 and 8 where decisions vary with subgroups. We also evaluated a more conventional utility based design by assuming that all subgroups have the same utility, using U₂(Y) for all three subgroups. The results are summarized in Supplementary Table 7. Using four selected scenarios, Scenarios 1, 3, 5, and 7, we further examined the robustness of D-Sub by changing the assumption on $h_{0\text{T}}^{\text{true}}$ and varying N_max. We assumed $h_{0\text{T}}^{\text{true}}$ to be either increasing or decreasing by using Weibull distributions to simulate Y_i,T. Recall that D-Sub assumes a constant hazard. Supplementary Table 8 shows that D-Sub performs reasonably well under all the three evaluation criteria, even when the assumption on h_0T is violated. We also studied D-Sub’s performance, assuming different maximum numbers of patients, N_max = 60 and N_max = 180, and compared it to those of D-Comb and D-Sep. The results are summarized in Supplementary Tables 9 and 10. For each N_max, D-Sub has superior performance than the comparators by a large margin. As expected, the performance of D-Sub improves with larger N_max over the range 60, 120, 180. In contrast, when truly optimal doses or dose acceptability vary between subgroups, as in Scenarios 1 and 5, the performance of D-Comb does not improve, even with N_max = 120. This strongly suggests that ignoring subgroups is a very bad idea in settings where they have truly different dose-outcome distributions.

We compared D-Sub to four comparators, “D-w/o clustering,” “D-w/o frailty,” “D-diff AR,” and “D-linear tox,” where each simplifies the model or method used for D-Sub in a particular way. We used all scenarios for the comparison to D-w/o clustering, and four scenarios, Scenarios 1, 3, 5, and 7, for the comparison to the others. Comparison of D-Sub to these designs provides an empirical justification for using a complex model for D-Sub. A version of D-Sub that does not induce clustering of subgroups is “D-w/o clustering.” For D-w/o clustering, z = (1, 2, 3) is fixed and the subgroups have their own subgroup effects with the ordering constraint, α_j,g < α_j,g′, g < g′. Everything else is the same as in the model for D-Sub. Supplementary Table 11 provides a summary of the simulation results. To facilitate comparison, the table also includes the results for D-Sub. D-Sub and D-w/o clustering perform very similarly in many scenarios, but the performance of D-w/o clustering is sometimes much worse, especially for small subgroups, for example, subgroups 1 and 3 in Scenarios 4 and 5. For D-w/o frailty, the patient-specific random effects γ are removed, while the remaining model elements are the same as for D-Sub. The model for D-w/o frailty thus assumes that there is no between-patient heterogeneity beyond subgroups, and that the two outcomes of each patient are independent. Supplementary Table 12 shows that D-w/o frailty has much worse p^unacc(g, d_m) and n^ptrt(g, d_m) for dose that are truly unacceptable within some subgroups, while it is comparable to D-Sub for p^sel(g, d_m). This may be due to the fact that variability between patients is not properly accommodated for by the model of D-w/o frailty. D-diff AR uses the same probability model as used for D-Sub, but it uses a different adaptive randomization method based on posterior expected utilities. Specifically, a patient in subgroup g is assigned to dose $d_m\in \mathcal{A}(g,t)$ with probability proportional to $u_g\left(d_m|x,{\mathcal{D}}_{n(t)}\right)$. The results, summarized in Supplementary Table 14, show that the change in the design’s performance with this different AR method is very small. D-linear tox assumes a simpler linear regression model for the toxicity hazard, ${\eta }_{\text{T}}^{\prime }\left(d_m\right)={\beta }_{\text{T}}^{\prime }{d}_m$, while the remaining model components are the same as in the model of D-Sub. We assumed a normal distribution truncated below at 0 as a prior for ${\beta }_{\text{T}}^{\prime }$. The results, summarized in Supplementary Table 14, show that the performance of D-linear tox is similar to that of D-Sub for Scenario 1, but D-linear tox shows an inferior performance in the other three scenarios.

6 |. DISCUSSION

We have presented a phase I-II clinical trial design in a setting where the patient population has multiple prognostic subgroups. The design was applied and evaluated for a trial in metastatic renal cancer. The design adaptively clusters patient risk subgroups with adjacent subgroups when there is no subgroup effect, and efficiently borrows information across subgroups and across doses. In a departure from established utility-based designs, subgroup-specific utilities are formulated to reflect risk-benefit trade-offs between efficacy and toxicity that vary with subgroups. Our simulations show that the design performs quite well under a wide variety of dose-outcome scenarios, and that incorporating all data while accounting for heterogeneity between patients significantly benefits correct decision making. The simulations also showed that the proposed design compares very favorably to both a design that ignores subgroups and a design that runs a separate trial within each subgroup.

DATA AVAILABILITY STATEMENT

The data used in this article are computer simulated. The codes that simulate datasets are available from one of the authors’ homepage.