Chromatographic separation of active polymer–like worm mixtures by contour length and activity

Abstract

The convective transport rate of polymers through confined geometries depends on their size, allowing for size-based separation of polymer mixtures (chromatography). Here, we investigate whether mixtures of active polymers can be separated in a similar manner based on their activity. We use thin, living Tubifex tubifex worms as a model system for active polymers and study the transport of these worms by an imposed flow through a channel filled with a hexagonal pillar array. The transport rate through the channel depends strongly on the degree of activity, an effect that we assign to the different distribution of conformations sampled by the worms depending on their activity. Our results demonstrate a unique way to sort mixtures of active polymers based on their activity and provide a versatile and convenient experimental system to investigate the hydrodynamics of active polymers.

A unique way to sort mixtures of active polymers on the basis of their length and activity is demonstrated.

INTRODUCTION

Active matter consists of interacting agents that can extract energy from their environment and convert it into a mechanical force (1). Their collective dynamics exist at every scale of life, from motor-driven mechanics of actin filaments and myosin motors in a cell, up to crowds of people (2, 3). This new class of matter exhibits singular and complex dynamics that are purely due to their activity. Recently, it has been demonstrated that an assembly of active entities can be used to harvest energy to power micromotors (4), for self-cleaning of polluted water (5), or even achieve more complicated tasks such as carrying a load or navigating through an obstacle course (6, 7). In these situations, the efficiency in accomplishing a task is related to the level of activity, which directly affects the mechanical stress that can be developed. Motility of biological agents also plays an important role in medicine, being, for instance, not only a major contributing factor to pathogenicity and colonization of bacteria (8, 9) but also predominant in the success rate of fertilization with sperm (10). Since the level of activity is an essential parameter in determining the unique collective properties, many strategies have been developed to sort self-propelled organisms with different activities, for instance, using wall geometries and obstacles (11–16) or external forces such as centrifugation (17).

So far, this research has focused mostly on point-like particles (18–24), and much less is known about active polymers (25). The term “active polymers” has been used to describe a wide variety of systems, including synthetic colloidal systems that can be assembled and pushed out of equilibrium (26, 27) and dynamic self-assembling polymers and filaments encountered in biological systems (28). Here, we will use the term “active polymer” to refer to a chain-like structure of which the segments exhibit active motion. There have been theoretical and few experimental investigations on these active polymers that have shed new light on their rheology (26, 29–32), aggregation (33, 34), dynamics in crowded environment (35, 36), but also their potential to emerge as mechano-functional robotics (37). These results have already shown that the physics of active polymers differs fundamentally from that of point-like active particles.

The hydrodynamic properties of active polymers remain largely unexplored. In research on conventional polymers, hydrodynamics is commonly applied to separate polymer mixtures (38–40). In the most basic approach, polymer mixtures are pumped through a narrow channel, and the Poiseuille flow-velocity profile combined with the diffusive motion of the polymers across the flow profile as they travel through the column ensures that polymers with larger radius of gyration have a lower net transport rate (41). In a more sophisticated approach, the flow channel is filled with a periodic array of pillars (42–45), and if the pillar spacing is comparable to the polymer size, this leads to an efficient separation based on size (slalom chromatography) (46–48). Here, we investigate how active worms behave under convective flow through periodic spaces and to what extent the separation phenomena characteristic for conventional polymers may also occur for active polymers.

We study the hydrodynamic flow of active worms and worm mixtures through a periodic space with a spatial period comparable to the size of the active worms. The worms have adjustable activity and are sufficiently large that we can observe them with a camera, so we can fully characterize their conformational dynamics as they flow through periodic pillar arrays. Surprisingly, we find that the transport rate of the active worms is determined not only by their size but also by their activity.

RESULTS

An experimental model for active polymers

Recently, Tubifex tubifex has been introduced as a promising experimental model for active polymers (32, 34, 37). The anatomy of the T. tubifex worm consists of many segments, similar to how polymers are composed of multiple repeating units (49). The worms live in water and are approximately 300 μm thick and 10 to 40 mm long, depending on their age. The motion of the worms is purely active, and their passive thermal diffusion is negligible (34). To investigate the potential role of stimuli-induced motion of the worms in the pillar array, we determined to what extent the worms “reel away” from the pillar upon contact: We tracked the worms with high resolution while they were in the pillar array and recorded the radial velocity component of the end points of the worms with respect to the pillar center during the periods before and after pillar contact. In case of perfect “elastic collisions,” the radial velocity distribution should be symmetric around v = 0, as is indeed the case (fig. S1), indicating that the pillars do not cause stimuli-induced response.

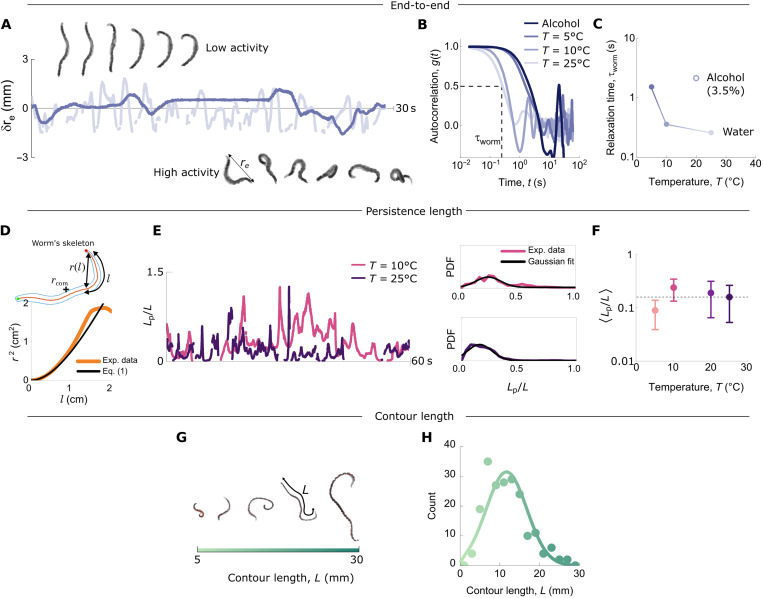
We quantify the dynamics and the length of the worms by evaluating their typical polymer characteristics (Fig. 1). The shape fluctuations of individual worms placed in water outside the channel and without water current are quantified using filament tracking, similar to the tracking analysis of conformationally fluctuating biopolymers (50). We also analyze quantities such as the persistence length L_p by least-squares fitting snapshots of a worm’s contour using (51)

$$r{(l)}^2=3 L_{\mathrm{p}}l(1-\frac{1.5 L_{\mathrm{p}}}{l}(1-e^{-\frac{l}{1.5L_{\mathrm{p}}}}))$$ (1)

the radius of gyration

$${R_{\mathrm{g}}}^2=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{({\overrightarrow{r}}_i-{\overrightarrow{r}}_{\text{com}})}^2$$ (2)

with r_com the position of the center of mass of the worm, the worm’s contour length L, and the time-dependent end-to-end distance r_e(t) (49, 52). From the fluctuations in the latter (Fig. 1A), we determine a characteristic time τ_worm, which we use to quantify activity (32). Specifically, τ_worm of an individual worm is defined as the half-decay time of the autocorrelation function

$$g(\mathrm{\tau })=\frac{⟨\mathrm{\delta }{r}_{\mathrm{e}}(t)\mathrm{\delta }{r}_{\mathrm{e}}(t+\mathrm{\tau })⟩}{⟨\mathrm{\delta }{r}_{\mathrm{e}}{(t)}^2⟩}$$ (3)

where δr_e(t) is the time-dependent variation in the end-to-end distance

$$\mathrm{\delta }{r}_{\mathrm{e}}(t)=r_{\mathrm{e}}(t)-⟨r_{\mathrm{e}}⟩$$ (4)

and 〈…〉 indicates time average (Fig. 1B).

Fig. 1. Active worm characterization.

(A) Sequence of images of a single worm at a low level of activity (T = 5°C) compared with the same worm at a high level of activity (T = 25°C). The fluctuating end-to-end distance δr_e highlights the effect of the temperature on the activity [results from (32)]. (B) Autocorrelation function of δr_e (Eq. 3) at the different temperature T = 5°, 10°, and 25°C and in the presence of alcohol shown in (A), with the same color code. From this, the characteristic time τ_worm of a single worm was determined as indicated by the dotted lines and reported in (C) as a function of the temperature and in the presence of alcohol. (D) Persistence length L_p of a worm at a given temperature T and time t, determined by fitting the dependence of the end-to-end distance r(l) with the contour length l (Eq. 1). (E) Persistence length over 60 s for 3000 consecutive conformations (the shape is tracked at a frame rate of 50 fps). The corresponding probability distribution function is shown for two temperatures. From the latter, we extracted the persistence length (F) as a function of temperature by fitting a Gaussian distribution. Error bars are 1σ. (G) The contour length L of a T. tubifex worm increases with its age. (H) A typical distribution of contour lengths from the same batch of worms. The solid curve is a fit to a Gaussian distribution.

The activity of the worms can be tuned continuously by two different methods: (i) reducing the activity by placing the worms temporarily in a 3 to 5% ethanol solution before the experiment and (ii) changing the temperature of the water in the experimental setup (32). The characteristic times τ_worm are reported in Fig. 1C as function of the temperature and in the presence of alcohol: The lower the temperature (or in the presence of alcohol), the less active the worm is and the larger the characteristic time τ_worm. In contrast to the activity, the persistence length and the radius of gyration are much less affected by the temperature (Fig. 1, D to F, and figs. S2 and S3). To investigate the effect of the pillar array and the imposed flow on the activity, we performed experiments in which the same set of worms was tracked inside and outside the pillar array and in the presence and absence of imposed flow. The results (fig. S4) show that the pillar array and the flow have no significant influence on the activity.

Method (i) has the advantage that we can study mixtures of worms with different activities (by mixing normal and intoxicated worms), whereas in the second, the activity of all worms is modified simultaneously. Method (ii) has the advantage that the activity level is constant, whereas with the first, the activity of the worms fed with alcohol slowly increases back to normal level when they are in fresh water as they recover. This process takes place on a time scale of about 10 min, so we ensure that each experiment is completed in much less than this time. Thus, we can control both the contour length and activity of the active worms and, hence, investigate the effect of these parameters on their behavior in a hydrodynamic flow.

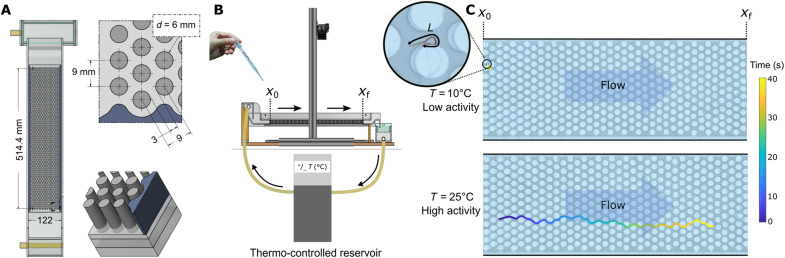
To optimize the efficiency in size-exclusion separation, different geometries to pack the column have been investigated (44, 53). Most recent studies on pillar-array chromatography with conventional polymers use hexagonal ordered pillar arrays as they appear to be the most efficient method (42, 44, 45). Inspired by these methods, we designed a scaled-up version of the classical pillar-array hydrodynamic chromatography experiments, in which an imposed flow makes the worms travel through a hexagonal pillar array. We tune the activity level by tuning the temperature of the water using a thermo-controlled reservoir (see Materials and Methods). Figure 2 (A and B) shows the hexagonal pillar array and its dimensions.

Fig. 2. Hydrodynamic pillar array experiment with active polymer–like worms.

(A) Top view of the channel with hexagonal pillar array. The design is based on conventional (hydrodynamic) chromatography experiments (41). The dimensions of the channel are 51 cm by 12 cm by 1.5 cm. The diameter of the pillars is D_pillar = 6 mm, and the interpillar distance is D_int = 3 mm. (B) Schematic of the experimental setup. The worms enter the channel at coordinate x₀, travel through the pillar array due to the imposed flow (in the direction of the arrows), and are finally flushed out at x_f. The temperature T of the surrounding medium (distilled water) is regulated by a thermo-controlled reservoir. Motion of the transported worms along the whole channel is recorded using a camera placed on the top of the experiment. (C) Trajectories in the channel for the same worms at two different temperatures (top, T = 10°C and bottom, 25°C) in time (color gradient). The continuous line shows the tracked paths along the channel at the two different temperatures for the same amount of time (40 s); decreasing temperature increases the elution time.

The worms enter the pillar array on the left at the position x₀, travel through the array with the help of the imposed flow Q = 0.2 liter/s, and are finally flushed out at x_f. In Fig. 2C, we show a typical trajectory of a worm after 40 s during its passage through the pillar array for two different levels of activity (low activity level at T = 10^∘C in Fig. 2C, top, and higher activity level at T = 25^∘C in Fig. 2C, bottom). The difference between the two levels of activity is clearly visible. In the remainder and in analogy with the chromatography techniques, the time spent by the worm in the channel is referred as “elution time.”

Effect of size and activity on the elution time

To quantify the effect of contour length and activity level on the active-polymer flow through the pillar array, we performed experiments where we systematically varied these parameters. We measured the elution times with the method described in Fig. 2. The main results of these experiments are shown in Fig. 3.

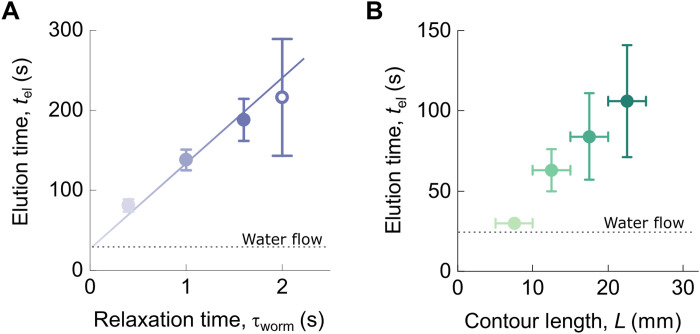
Fig. 3. Activity and contour-length dependence of the elution time of the active worms.

(A) Elution time of the active worms plotted against the relaxation time τ_worm of a single worm at four levels of activity. The colored line indicates a linear relationship. The elution time t_el was measured for four different levels of activity (T = 5°, 10°, 25°C and in the presence of alcohol, open symbol). For all the temperatures, the contour length of the worms was kept constant (L = 15 ± 5 mm), and the elution time was averaged on six trajectories. (B) The elution time was measured on 13 worms from the same batch, varying in their contour length, and each worm averaged over six passages in the channel for T = 20°C. The contour lengths are binned on the x axis. Horizontal dashed lines represent the imposed flow rate in the channel. Error bars represent 1σ.

In the first experiment, we investigated the effect of the activity level on the elution time (Fig. 3A). We performed experiments on worms with similar contour lengths (in the range 15 ± 5 mm) and imposed different temperatures T = 5°, 10°, and 25°C to vary the activity level. To obtain better statistics, we averaged the elution times of the same worm over six passages through the pillar array for a given temperature. These measurements confirm the above observation that the elution time decreases with the activity level. Converting imposed temperature to the individual characteristic time τ_worm of the worms (measured independently; Fig. 1C), we obtain the result of Fig. 3A. We find that the elution time shows an approximately linear dependence on the characteristic time of the worm: The higher the activity level the active polymer, the shorter the elution time. In contrast, there is no correlation between the elution time and the persistence length L_p (fig. S5). This makes it possible to sort mixtures of active polymer–like entities based on their individual level of activity, as we will demonstrate below.

In the second experiment, we investigated the effect of the contour length while keeping the activity level (i.e., the water temperature) at a fixed value. We selected 13 worms of different lengths L∈ [5 to 30] mm from the same batch of worms (Fig. 1D) and determined the elution time of each worm in a similar fashion as above, with the elution time of a worm of a given contour length averaged over six passages through the channel. We find that the elution time shows a linear dependence and increases with the worm’s contour length. This is generally observed for large polymers such as DNA in slalom chromatography techniques (46–48, 54, 55); the larger the polymer, the more difficult for them to turn around the obstacles, consequently delaying their elution through the pillar array.

The question remains why worms with a lower level of activity are eluted much later than highly active worms. Since the activity has negligible effect on the radius of gyration and the average end-to-end distance of the worms (fig. S3), these properties cannot explain the activity-dependent elution time. To investigate the effect of activity on the elution time in more detail, we observed the conformations taken by the worm while transported in the pillar array. Close-up photos of low- and high-activity worms are shown in Fig. 4A. We find that for a worm with a high activity level, a wider range of conformations is sampled than for a low level of activity (Fig. 4B), with the highly active worms exhibiting “curling” and “knotting” conformations that help them circumvent the pillars. Decreasing the level of activity by decreasing the temperature or exposing the worm to alcohol lowers the probability of adopting these conformations.

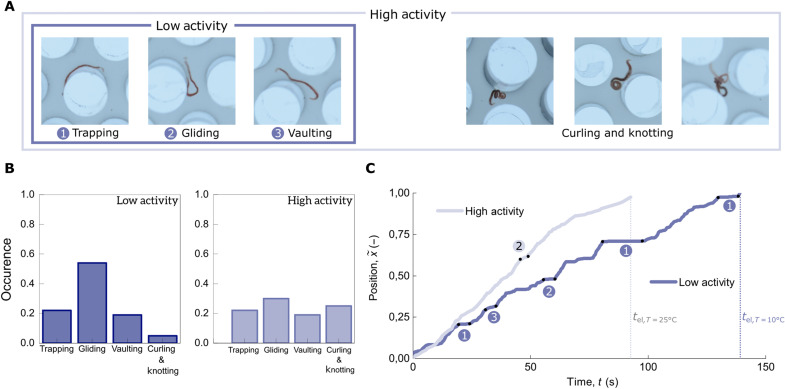
Fig. 4. Effect of active-worm conformations on the transport through a pillar array.

(A) Photographs showing the typical conformations at a high level of activity (T = 25°C, light blue) and restricted to fewer conformations at low activity (i.e., low temperature or in the presence of alcohol, dark blue). (B) Conformation statistics. The worm conformations have been measured along the elution in the channel for two different levels of activity. (C) Tracked position of the active worm along the length of the channel $\tilde{x}=\frac{x}{(x_{\mathrm{f}}-x_0)}$ for two different levels of activity as a function of time. Conformations of the active worms influence the elution time in the channel. At low level of activity, modes (1 to 3) are dominant, which increases the elution time.

We qualitatively observe dominant conformations that have been previously reported in numerical simulations on the transport of inactive semiflexible polymers (56). During their transport, the active polymers can wrap around the pillars (“trapping” mode) as shown in photo (1) of Fig. 4A and so get trapped for a certain period of time. This is highlighted in Fig. 4C, where we have tracked the position x of worms with different activity levels as they travel through the pillar-array channel. The plateaus seen in the trace of the low-activity worm show that it gets trapped more often and longer than the high-activity worm. Other conformations such as (2) “gliding” and (3) “vaulting” (see Fig. 4) may also contribute to the increased elution time for low-activity worms. In all these trapping modes, it then depends on the end-to-end fluctuations of the polymer shape how long it takes to escape from the trapped state: When increasing the activity level, the relaxation time of the worm τ_worm decreases and, consequently, so does the elution time (Fig. 3A).

Separating a mixture of high- and low-activity worms

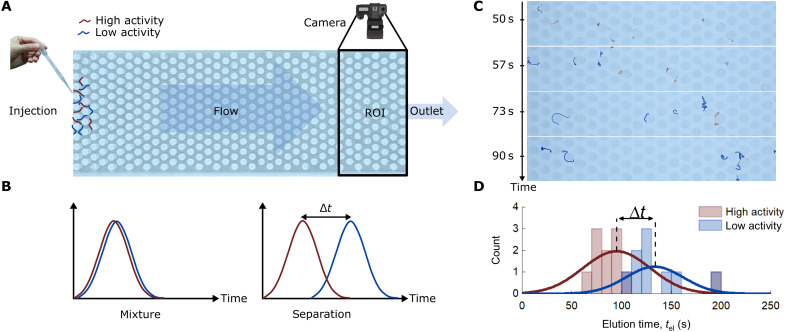
We finally apply our findings to perform a chromatography-type experiment in which we try to separate a mixture of 50% high-activity and 50% low-activity worms. Low-activity worms were prepared by exposing them, before injection, to a solution of 5% ethanol, which also contained a small amount of methylene blue as dye. The mixture is then composed of blue-colored low-activity worms and red high-activity worms, which can be distinguished by their color.

The hydrodynamic separation experiment is performed with the setup described in Fig. 5A. The mixture is injected at the entrance of the channel x₀, and we record videos of the region of interest (ROI) at the exit of the channel. On the basis of the observed dependence of the elution time on the activity (Fig. 3B), it should be possible to separate the high- and low-activity populations, as shown schematically in Fig. 5B, with a delay time Δt between the two populations. In Fig. 5C, we show a sequence of photos of the ROI for a typical experiment (conducted at T = 20°C), where the first worms arrive at the end of the channel about 50 s after injection at the entrance. From these images, we can see that the high-activity (red) worms arrive first at the exit x_f of the channel, followed by the low-activity (blue) worms. This is quantitatively shown in the distribution plot in Fig. 5, where the time delay Δt ≈ 40 s between the averaged elution times of the two populations allows for efficient separation based on the activity. These results demonstrate the potential of hydrodynamic techniques to efficiently sort mixtures of active polymers according to their activity level.

Fig. 5. Hydrodynamics separation of a low- and high-active worms mixture.

(A) A solution of ∼50/50 high-activity and low-activity worms (the latter prepared by exposing them to 5% of alcohol) is injected at the start of the channel. Low-activity worms are dyed blue to distinguish them from the high-activity worms (red). The last part of the channel is video-recorded [region of interest (ROI)] with a camera, so the worms can be identified and followed in time. (B) Initially injected at t = 0 at the entrance of the channel, the principle of the method relies on the time separation of the two populations. (C) Temporal sequence of images of the ROI showing the separation of the worms based on their activity: The arrival time of the low-activity worms (blue) is delayed with respect to the high-activity worms (red). The blue color of the low-active worms has been artificially enhanced. (D) Resulting elution time for the mixture containing the worms with two levels of activity. At the end of the channel, the high- and low-activity populations are separated by an average delay time Δt ≈ 38 s. The solid curves are Gaussian fits.

DISCUSSION

The results presented here can be extended in many directions. As in conventional chromatography, the separation can be improved by increasing the length of the channel. Furthermore, it is known from slalom chromatography that the elution time strongly depends on the flow rate and the particle size (48). Experiments by Hirabayashi et al. (46) have shown that the order in which DNA fragments are eluted depends on the diameter of the packing material. In our experiments, the contour length of the smallest worm is comparable to the diameter of the pillars (Fig. 2), and the flow is kept constant. In future work, it might be interesting to investigate in what order the worms are eluted for different relative lengths (D_pillar/L). Likewise, the separation of the worms could possibly also be enhanced by examining the effect of the flow rate. For instance, we find that the relaxation time of the end-to-end fluctuations increases because of the confinement by the pillars (fig. S6) and even more so in combination with the imposed flow, as is to be expected since the confinement by the pillars hinders the end-to-end distance fluctuations, as does the flow pushing the worms against the pillars. This effect is not specific to T. tubifex but can be expected for any active polymer. This result connects to the broader question of interaction between an active filament and a fluid, an actively investigated topic (57, 58). Last, the conformations sampled by the active worms play an important role in the transport through the pillar array (and for the hydrodynamic properties in general). We hope that our experimental results will stimulate theoretical work and simulations to obtain quantitative models for these conformations and their dynamics, beyond the current models and works already performed on conventional polymers (56, 59–62).

To conclude, active polymer-like worms constitute an interesting and versatile experimental model to study the separation of active polymers. Our research shows that flow through a structured space makes it possible to sort active polymers by length and activity, providing a reliable method by which this can be done. Our results suggest that the activity dependence of the travel time through the array originates from a difference in conformations sampled by the high-activity and low-activity polymers and from the difference in the time scale of the conformational fluctuations. However, the active worms can adopt many complex conformations, of which we still need a better understanding of their effect on the elution time.

MATERIALS AND METHODS

T. tubifex worms

All batches of T. tubifex worms studied were purchased from Aquarium Rainer, javastraat 106 h, 1053 HL Amsterdam, the Netherlands, and provided by the company Ichtyo Trophic. The worms are initially extracted from their natural environment and kept in an aquarium for 1 week to rinse off any trace of pollutant, sludge, or their own waste and then stored at 4°C. We collected them at this step. After the experiment (∼1 hour), the worms were put back in their natural living environment.

Chromatography-inspired channel

The design of the channel is inspired by hexagonal pillar arrays used in analytical chemistry to sort large conventional polymers and described, e.g., in (42). We scaled up the technique to the size of our Tubifex worms. The interpillar distance is 3 mm, the diameter of the pillar is 6 mm, and the pillars are 15 mm high. The channel length is 514.4 mm (67 rows of pillars), and the width is 122 mm (alternately 11 or 12 rows of pillars). The hexagonal arrays were designed by laser cutting holes in transparent acrylic perspex sheet, in which we placed the pillars that consist of cylinders made from the same material. The whole setup is mounted on a light-emitting diode panel providing a uniform light background. To control the temperature of the living medium (water), thermo-controlled water flow through the channel was provided by a circulating bath thermostat (Thermo Fisher Scientific, HAAKE A 25). The difference in the water level between the left and the right parts of the channel results in the imposed flow Q = 0.2 liter/s. The worms are picked up at the very end of the channel, where a mesh prevents them from being reinjected in the closed water circuit. At a height of ∼1 m above the channel, a standard camera (Nikon D5300) equipped with an objective (AF-S DX Zoom-Nikkor 18–55 mm f/3.5–5.6G ED II) allows us to visualize and track the worms during their elution.

Image analyses

A homemade routine developed in Matlab allowed us to accurately characterize the shape of the worms and track its trajectory while eluted in the channel. We used the following protocol:

(i) The original sequence of images (initially recorded at 50 fps) was converted in an 8-bit gray level (0 to 255).

(ii) A threshold was applied to differentiate the active polymer–like filament from the remaining background. Gray levels exceeding the threshold were assigned a value of 1 (black), and the remaining levels a value of 0 (white).

(iii) For the shape’s fluctuation, the resulting cluster of pixels covering the worm’s shape was finally thinned to a 1-pixel-wide line using a skeletonization routine that erodes pixels by iteration. The (eventual) residual neighbor–less pixels were eliminated using a simple algorithm to exclude nonconnected pixels.

(iv) The center of mass if followed over time by using tracking methods similar to IDL (63).

Supplementary Materials

This PDF file includes:

Figs. S1 to S6