Abstract
In this paper, we present and evaluate a novel Bayesian regime-switching zero-inflated multilevel Poisson (RS-ZIMLP) regression model for forecasting alcohol use dynamics. The model partitions individuals’ data into two phases, known as regimes, with: (1) a zero-inflation regime that is used to accommodate high instances of zeros (non-drinking); (2) a multilevel Poisson regression regime in which variations in individuals’ log transformed average rates of alcohol use are captured by means of an autoregressive process with exogenous predictors and a person-specific intercept. The times at which individuals are in each regime are unknown, but may be estimated from the data. We assume that the regime indicator follows a first-order Markov process as related to exogenous predictors of interest. The forecast performance of the proposed model was evaluated using a Monte Carlo simulation study, and further demonstrated using substance use and spatial covariate data from the Colorado Online Twin Study (CoTwins). Results showed that the proposed model yielded better forecast performance compared to a baseline model which predicted all cases as non-drinking and a reduced ZIMLP model without the RS structure, as indicated by higher AUC (the area under the receiver operating characteristic (ROC) curve) scores, and lower mean absolute errors (MAEs) and root-mean-square errors (RMSEs). The improvements in forecast performance were even more pronounced when we limited the comparisons to participants who showed at least one instance of transition to drinking.
Keywords: Bayesian zero-inflated Poisson model, forecast, intensive longitudinal data, regime-switching, spatial data, substance use
1. Introduction
Intensive longitudinal methods have become increasingly popular in the study of substance use (Litt, Cooney, & Morse, 1998; Wray, Merrill, & Monti, 2014), where more nuanced changes in substance use dynamics can now be investigated based on intensively collected data. Recent advances in data collection tools such as increasing access to and use of wearable sensors to collect ambulatory assessments (Russell, Almeida, & Maggs, 2017; Russell & Odgers, 2020; Wilhelm, Grossman, & Muller, 2012) have led to renewed interest and growth in modeling innovations for studying change processes in social and behavioral sciences (Chow, 2019; Li et al., 2019; Lu, Chow, Sherwood, & Zhu, 2015). When it comes to forecasting, many machine learning (ML) models offer excellent forecasting results in large-sample cross-sectional or longitudinal panel data with a limited number of measurement occasions (see, e.g., Orrù, Monaro, Conversano, Gemignani, & Sartori, 2020; Yarkoni & Westfall, 2017), but these methods may be limited in predicting moment-to-moment time dependencies in the data. Even though advanced ML methods such as recurrent neural networks (RNNs) exist and can be used to account for linear, nonlinear, and nonparametric temporal relationships in the data, the statistical properties of these (often highly over-parameterized) methods are not well understood, and decisions on model structures and tuning parameters are data-driven and can be arbitrary at times. As such, mappings to theories can be prohibitive or even impossible (Sánchez-Sánchez, García-González, & Coronell, 2019). Furthermore, myriad flexible, often non-parametric tools also exist in the statistical and econometric literature for forecasting future values of time series data, particularly those with very small units of analysis (e.g., n = 1 or < 10; Harvey, 2001; Helske, 2017; Shen, 2010; West & Harrison, 1997). However, these methods often do not integrate modeling features that can simultaneously capture characteristics of intraindividual changes and interindividual differences, particularly when intermittent transitions through distinct patterns of dynamics (e.g., different phases of a change process) are observed. Other issues that warrant close attention include the implications of forecasting in the presence of missingness, and the importance of quantifying the uncertainty around prediction results in making decisions.
We propose in this article a novel regime-switching zero-inflated multilevel Poisson (RS-ZIMLP) regression model with autoregressive (AR) relations to forecast alcohol use in early adolescence. The proposed RS-ZIMLP model uses a mixture of a Poisson process and a degenerate point mass at zero (Lambert, 1992) to capture the zero inflation (ZI; i.e., prominence of non-drinking responses) in early adolescent drinking data and associated dynamics. Such high instances of zero responses, if unaccounted for, are known to yield biased estimates and inferential results (Chow, Witkiewitz, Grasman, & Maisto, 2015; Lambert, 1992; Lu, Chow, Ram, & Cole, 2019; Maisto et al., 2017). Compared to previous longitudinal extensions of the zero-inflated Poisson (ZIP) regression model, which already allow for over-time dependencies (e.g., AR relations) in the Poisson process (e.g., Berry & West, 2020; Hall, 2000; Lee, Wang, Scott, Yau, & McLachlan, 2006; Min & Agresti, 2005; Neelon, O’Malley, & Normand, 2010; Yau & Lee, 2001; models with AR relations: Lee et al., 2006; Maisto et al., 2017), the proposed model is unique in the inclusion of a first-order Markov process to capture within-individual transitions between the ZI and Poisson process with AR relations. Consistent with conventions in the econometric literature, such transitions between two distinct patterns of data are referred to as regime switches (Kim, Nelson, et al., 1999). Thus, whereas other ZIP models with AR relations typically assume that the probability of being in a particular regime is linked instantaneously to other person- and/or time-specific covariates, the first-order Markov process instills some over-time regularity in each individual’s probability of being in a regime as dependent on the individual’s previous regime. This regularity may still change as a function of other person- and/or time-varying covariates, but in the absence of other covariate information or at zero values of mean-centered covariates, its inclusion allows the “prototypical” individuals to transition between regimes over time, as opposed to staying statically within a regime. In the context of our motivating example, this means that adolescents who engage in drinking and other substance use may occasionally switch to prolonged periods of sustained abstinence. Conversely, those who usually abstain from alcohol use may also transition abruptly to the drinking regime. Forecasting the moments and possible determinants of such transitions may allow identification and prevention of escalation to subsequent problematic substance use (Howard, Patrick, & Maggs, 2015; Russell et al., 2017).
The proposed model also extends earlier work on regime-switching (RS) dynamic models with ZI (Chow et al., 2015; Lu et al., 2019) to the framework of multilevel ZIP by incorporating a person-specific intercept into the Poisson process with AR relations. Finally, another key innovation of the present article resides in the use of spatial covariates derived from Global Positioning System (GPS) data in our motivating empirical example to forecast within-person variations in alcohol use while in the drinking regime, as well as transitions between the ZI and drinking regime1. The proposed model is presented and evaluated in a Bayesian framework, which provides more modeling flexibility, and allows for quantification of the uncertainty associated with the estimation and forecast results.
The rest of the paper is organized as follows. We first introduce the empirical data example that motivates our development and use of the proposed model for forecasting purposes. Then we review the standard ZIP model and introduce the proposed RS-ZIMLP model. This is followed by the descriptions of Bayesian estimation and forecast details. The estimation and forecast performance (including forecast uncertainty) are then evaluated using a simulation study and an empirical illustration based on our empirical data. Finally, we discuss the results and the limitations of the proposed approach and highlight some future directions.
2. Motivating Example
The motivating example was inspired by the Colorado Online Twin Study (CoTwins) in which participants were asked to report alcohol use weekly and carry GPS-enabled smartphones to track their locations over two years. Figure 1 shows the trajectories of alcohol use for four randomly selected participants. The four trajectories represent different patterns of alcohol use and amounts of missingness across participants. For instance, the trajectory in the upper-left panel displays frequent transitions between drinking and ZI regimes, whereas the trajectory in the upper-right panel displays an extensive period of abstinence and abrupt transitions to heavy drinking. The two trajectories in the two lower panels display overall abstinence and occasional alcohol use. Compared to previous studies involving individuals with alcohol use disorders (e.g., Chow et al., 2015; Maisto et al., 2017), there was, as expected, an even greater extent of inflation in zero responses. Even in this relatively young sample with ages ranging from 14 to 17 at the time of enrollment, there were already some transitions between ZI and drinking regimes in varying amounts, as well as considerable individual differences in such dynamics. Our proposed model was motivated by our goal to simultaneously address the ZI and capture the underlying mechanism of transitioning between ZI and drinking regimes as well as gradual changes in the drinking regime over time.
Figure 1:

The trajectories of alcohol use for four randomly selected participants. The weekly alcohol use was measured as the total number of drinks consumed in the past week (see how alcohol use values were coded in the Data Descriptions subsection).
In the following part, we will start with the standard ZIP model proposed by Lambert (1992) and then describe our proposed RS-ZIMLP model. The ZIP model assumes that the count data are from a mixture of a Poisson distribution and a degenerate distribution at zero. Specifically, the responses of N individuals, Y1,…, YN, are independent and
| (1) |
where the mean of the Poisson distribution, λi (i = 1,…, N), and the probability, pi, are modeled by
| (2) |
| (3) |
where xi and zi are person-specific covariates with corresponding coefficients β and α, respectively.
The model presented above can be extended to allow for repeated measures of the response variable. Let Yi,t represent the tth (t = 1,…,Ti) observation of the ith person and
| (4) |
where λi,t and pi,t are now predicted by person- and time-specific covariates, xi,t and zi,t, respectively, as defined below.
| (5) |
| (6) |
In our proposed RS-ZIMLP model, we extend Equation 5 to account for autocorrelation in the time series data. Specifically, ηi,t defined as ηi,t = log(λi,t), is assumed to follow a multilevel AR process of lag order 1 with exogenous predictors, formulated as
| (7) |
| (8) |
The level-1 model as defined in Equation 7 is an AR-X model, where the AR parameter, ϕ1, controls the dependence between the process’s current (e.g., ηi,t) and previous (e.g., ηi,t–1) values. It is also referred to as the “inertia” of a dynamic process in the literature on affective dynamics (Kuppens, Allen, & Sheeber, 2010). Specifically, the AR(1) process is stationary if and only if ∣ϕ1∣ < 1 (Hamilton, 1994; Lütkepohl, 2005), and within such range, a high positive value of ϕ1 reflects a construct’s resistance to change (i.e., inertia). Person- and time-specific covariates are collected in xi,t–1, which is a nx-dimensional vector, with corresponding coefficients β. The person-specific intercept, ϕ0,i, reflects individual i’s baseline around which the process of interest (i.e., the log means of the Poisson distribution) fluctuates when all xi,t–1 equal 0. The innovation term (also called process noise), is denoted as ϵi,t, which reflects unmeasured sources that affect the dynamics of ηi,t, following a normal distribution with zero mean and variance . The initial condition, ηi,1, follows a normal distribution with a mean of μη1 and a variance of . The level-2 model is defined in Equation 8. In Equation 8, the person-specific intercept is predicted by person-specific covariates in the ng-dimensional vector, gi, with the first entry being unity to define an intercept term and γ being the corresponding regression coefficients. Parameter vi is the random effect, which follows a normal distribution with zero mean and variance , and represents individual i’s deviations in the values of ϕ0,i not accounted for by the exogenous variables, gi.
The proposed model also extends Equation 6 to incorporate the time dependency in switches between the ZI and Poisson processes by specifying the probability of being in a certain regime to be dependent on the previous regime. That is, a first-order Markov transition model with multinomial logistic regression is used as:
| (9) |
with the probability of the initial regime at time 1 specified as:
| (10) |
where Si,t is a latent (i.e., unknown) person- and time-specific regime indicator; r and s are indices for the regime at time t and t – 1, which take on the value of 0 or 1, corresponding to the ZI and Poisson process, respectively. The RS model is defined in Equation 9, where the log-odds of RS dependencies are predicted by person- and time-specific covariates in the nz-dimensional vector, zi,t–1, with the first entry being unity to define an intercept term and αrs being the corresponding regression coefficients. Note that for identification purposes, one of the two terms in the denominator of Equation 9 has to be designated as the reference level. For instance, in the present study, we set staying in the same regime as the reference level by fixing all elements in α00 and α11 to 0 given that exploring determinants that help predict transitions between regimes are of more interest to us. Initial regime probabilities are defined in Equation 10, where the log-odds of being in regime 1 are predicted by person-specific covariates in the nh-dimensional vector, hi, with the first entry being unity to define an intercept term and π being the corresponding regression coefficients. Under situations with high probabilities of staying within the same regimes, these initial regimes can play a non-trivial role in characterizing the overall probabilities of being in a certain regime.
Following these model specifications, conditional on the value of the previous regime,
| (11) |
and
| (12) |
where λi,t, p1s,i,t, λi,1 and p1,i,1 follow the specifications in Equations 7 - 10. Accordingly, conditional on Si,t–1, the probability distribution of Yi,t can be written as
| (13) |
Finally, missingness may occur in both dependent variables and covariates. The missingness in dependent variables can be automatically imputed based on the model specified above, which is analogous to a Bayesian full-information likelihood approach and is known to work adequately under specific missing data mechanisms (e.g., missing at random (MAR); Little & Rubin, 1987). However, to handle missingness in covariates, it is necessary to specify models for covariates. In the present study, we assumed an AR(1) process for each person- and time-specific covariate in xi,t and zi,t such that
| (14) |
where xj,i,t and zj,i,t are the jth covariates for person i at time t in Equations 7 and 9, respectively; ϕxj and ϕzj denote the AR parameters; and ζxj,i,t and ζzj,i,t are process noises following a normal distribution with a zero mean and variance of and , respectively. Note that all covariates are assumed to be scaled within-person and across time points to zero mean and unit variance in this study, therefore no intercept parameters are included in this part of the model. In addition, no cross-regressions between covariates were allowed for reasons of parsimony.
3. Bayesian Estimation and Forecast
In this section, we first discuss the Bayesian modeling framework for the proposed RS-ZIMLP model, including prior probability distribution specifications, followed by descriptions of the general estimation procedures. We then discuss how forecast performance is evaluated in the proposed Bayesian framework using six performance measures.
3.1. Modeling Framework
Suppose that stores the dependent variable and covariates for individual i at time t; and ω is a collection of model parameters. Then, conditional on the value of Si,t and , the probability distribution function of can be written as
| (15) |
Instead of solving the above high-dimensional integral analytically, we implement model fitting in a Bayesian framework using Markov chain Monte Carlo (MCMC) methods to perform numerical integration. In this section, we focus on the Poisson process (i.e., when Si,t = 1), while the distribution of Si,t will be discussed in the Measures of Forecast Performance section.
First, f(ηi,t∣ηi,t–1, xi,t–1, ϕ0,i, ω) and f(ϕ0,i∣gi, ω) jointly represent the multilevel AR-X model for ηi,t as presented in Equations 7 and 8. Second, represents the joint model for the dependent variable and time-varying covariates, which is specified as:
| (16) |
where P(Yi,t = y∣Si,t, ηi,t) represents the model for the dependent variable as presented in Equations 11 - 12, and f(xi,t∣xi,t–1, ω) and f(zi,t∣zi,t–1, ω) represent models for covariates as presented in Equation 14.
3.2. Prior Specifications
In a Bayesian model, prior probability distributions need to be specified for all unknown model parameters — including parameters in the Poisson and ZI component of the model and models for covariates. Specifically, we assigned standard normal distributions (i.e., N(0, 1)) to all AR parameters (i.e., ϕ1 in Equation 7, ϕxj and ϕzj in Equation 14), where the variance of the prior distribution was set to a relatively small value (i.e., 1) given the aforementioned permissible range of the AR coefficient for a stationary AR(1) process. In terms of regression coefficients (i.e., β in Equation 7, γ in Equation 8, α01 and α10 in Equation 9, π in Equation 10), we assigned normal distributions with zero means and variances of 100 (i.e., N(0, 100)), which were relatively diffuse priors. Note that parameters in α00 and α11 were fixed to 0 due to the reason described above, so no priors needed to be specified for these parameters. The inverse-Gamma distributions, IG(0.001, 0.001), were assigned to all variance parameters (i.e., in Equation 7, in Equation 8, and in Equation 14). The IG distributions with relatively small shape and rate parameters (e.g., 0.001) would yield positive values with a relatively large range and thus can be regarded as noninformative priors. Note that these priors are conjugate in the sense that the conditional posterior distributions and prior distributions are in the same family, and they were selected mainly for simplicity and computational efficiency reasons. Lastly, in terms of initial conditions in AR processes defined in Equations 7 and 14 — ηi,1, xj,i,1, and zj,i,1, we fixed their distributions to N(0, 100). Generally speaking, these prior and initial condition specifications would not introduce much information into the estimation process and were used in our simulation study. However, in the empirical illustration, we assigned weakly informative priors to certain parameters based on the expected range of the data (see descriptions in the Empirical Study section).
3.3. MCMC Estimation Procedures
We fit the proposed model using the default MCMC algorithms in the statistical software “Just Another Gibbs Sampler” (JAGS; Plummer et al., 2003). These MCMC algorithms are designed to sample representative values from the posterior distribution. More specifically, they perform iterative sampling by drawing samples from approximate conditional distributions for each parameter, and the approximation to the parameters’ true posterior distributions improves as the number of samples increases. With complex multiple-parameter models, JAGS uses slice sampling (Neal, 2003) in a Gibbs-sampling scheme (Geman & Geman, 1984) to sample from the parameters’ posteriors, allowing for flexibly in sampling from distributions with arbitrary shapes. We check the sampling quality by computing two diagnostic statistics (Gelman et al., 2013): (1) the effective sample size (ESS), which describes how many posterior draws in the MCMC procedure can be regarded as independent, and (2) , which describes the ratio of the overall variance of posterior samples across chains to the within-chain variance, and can be indicative for convergence problems. Fitting models in JAGS yields posterior distributions for each model parameter, from which we can obtain point and standard error estimates by calculating the distributions’ means/medians, and standard deviations, respectively.
One way to forecast values of future observed data in JAGS before the data become available is to insert missing values at the time locations to be forecast. For instance, a forecast for t* = 50 may be obtained by passing observed data from up to t <= 49 to JAGS, with missing values inserted for all variables at t = 50. Our code, which is freely accessible at https://github.com/yanlingli1/Bayesianforecast-RSZIMLP, demonstrates how missing values are iteratively inserted for the dependent variable and covariates at time t*, with observed data provided only up to time t* – 1 to yield one-step ahead forecast values for the dependent variable and associated covariates. For forecasting purposes in the current study, we generally stop updating the model parameters before the forecast window to emulate real-world forecasting scenarios in which forecasts may have to performed using a model with parameters “frozen” at particular pre-estimated values.
3.4. Measures of Forecast Performance
The predictive estimates of are computed using data from up to time t – 1 (i.e., one-step ahead forecast). Let represent all information that is known up to time t – 1 for individual i, then two elements are of interest in forecasting — the posterior predictive distribution of Yi,t (i.e., ) and the posterior predictive distribution of the regime indicator variable, Si,t (i.e., ). As mentioned earlier, we use MCMC methods to obtain samples from these posterior predictive distributions and calculate pertinent summary statistics accordingly. For instance, the probability of being in regime 1 at time t conditional on the observed data up to time t – 1 (i.e, ) can be obtained by calculating the empirical proportion of posterior samples of Si,t with values equal to 1.
Suppose that M iterations after the burn-in phase are implemented in the MCMC procedure, and the posterior sample in the mth iteration drawn from the posterior predictive distribution of Yi,t is denoted as . To evaluate forecast accuracy and uncertainty, we calculate, for each iteration, the average mean absolute error (MAE), root-mean-square error (RMSE), prediction accuracy (ACC), recall (also called sensitivity), precision (also called positive predictive value), and the area under the receiver operating characteristic (ROC) curve (AUC; see, e.g., Bradley, 1997; Hanley & McNeil, 1982) across individuals and the last K time points we seek to forecast.
Among these measures, MAE and RMSE evaluate the forecast performance related to the values of the dependent variable (e.g., alcohol use). Let yi,t (t = Ti – K + 1, Ti – K + 2, … , Ti) be the actual value of the last K observations for individual i, then the the MAE and RMSE at the mth iteration are defined as
| (17) |
| (18) |
ACC, recall, precision, and AUC evaluate the classification performance. Specifically, let if the predictive probability of Yi,t being positive (i.e., ) is greater than a decision threshold at the mth iteration, otherwise, . For each iteration, the predictive probability can be obtained as according to Equation 13, where and are the mth samples drawn from the posterior predictive distributions of λi,t and p1s,i,t, respectively.
Let TP(m), TN(m), FP(m), and FN(m) refer to the number of true positive cases (i.e., when yi,t > 0), true negative cases (i.e., when yi,t = 0), false positive cases (i.e., when yi,t = 0), and false negative cases (i.e., when yi,t > 0), respectively, across individuals and the last K time points, at the mth iteration. Then ACC, recall, precision, and AUC at the mth iteration are defined as follows.
| (19) |
| (20) |
| (21) |
In the context of alcohol use, a higher recall score is desired because it reflects the ability to correctly identify drinking instances (true positives). For instance, a recall of 1 means that all drinking instances are predicted as drinking. The recall score can be increased by lowering the decision threshold, but doing so also reduces the precision score such that more non-drinking instances will be labeled as drinking. Therefore, we also evaluate the ROC curve which displays true positive rates versus false positive rates at different classification thresholds, and thus is useful in the case of imbalanced data. The AUC score measures the area underneath the ROC curve, which ranges from 0 to 1, with 0.5 representing a random guess and a value closer to 1 indicating better capacity to distinguish between positive and negative cases. For each iteration, we can obtain the predictive probability of Yi,t being positive as described above, and then obtain the AUC score, denoted as AUC(m).
Using MCMC procedures, we can obtain a posterior distribution of each performance measure and then inspect its corresponding characteristics. Specifically, we calculate the means of these distributions to obtain point estimates for the above measures and standard deviations and quantiles to quantify the uncertainty in these measures.
4. Simulation Study
4.1. Simulation Designs
The goal of the simulation study was to investigate the forecast performance of the proposed model with different percentages of zeros in the data set. We considered two conditions — the moderate ZI condition where the percentage of zeros in the observations within each person was 50% on average, and the high ZI condition for which the percentage was 70% on average. The sample size was set as N = 200 persons and T = 60 time points to mirror the number of participants and the median time series length in the empirical study. For each condition, we ran 500 Monte Carlo replications, and for each replication, we ran two chains, each with 25000 iterations in total and a burn-in of 5000 (discarded) iterations. The prior settings were identical to those described in the Prior Specifications section.
Complete data were first simulated based on the model presented in Equations 7 - 10, and 14. For simplicity purposes, we did not include person-specific covariates in Equations 8 and 10 and only specified one person- and time-specific covariate in Equations 7 and 9, respectively. The true values of model parameters under the moderate ZI condition were set as follows. The AR parameters, including ϕ1 in Equation 7 and ϕx1 and ϕz1 in Equation 14, we set to 0.3, 0.9, and 0.6, respectively, based on estimation results from fitting AR models in previous studies (e.g., Chow & Zhang, 2013; Li, Wood, Ji, Chow, & Oravecz, 2021; You, Hunter, Chen, & Chow, 2019). The standard deviation parameters, including σϵ in Equation 7, σv in Equation 8, and σx1 and σz1 in Equation 14, were set to 0.5. In terms of the intercept parameters, the population mean of the random intercepts (γ0 in Equation 8) was set to 2 to distinguish between the ZI and Poisson process; the log odds in the initial regime model (π0 in Equation 10) was set to −2, assuming that the initial time point was mostly in the ZI regime; the intercepts α01,0 and α10,0 in Equation 9 were both set to −2.5, assuming that individuals were more likely to stay in a certain regime. Finally, the covariate coefficients, including β1 in Equation 7 and α01,1 and α10,1 in Equation 9, were set to 0.5, 0.2, and 0.2, respectively. The true values under the high ZI condition were identical to those under the moderate ZI condition, except that α10,0 was set to −3.5 to decrease the probability of switching to regime 1, thus increasing the percentage of zeros in the data.
Missingness in the dependent variable and two time-varying covariates was generated based on the missing data mechanism specified below.
| (22) |
where R was the missing indicator (1 = missing) and the probability of missingness was dependent on fully observed variables, c1,i,t - c4,i,t, simulated from a uniform distribution, U[−3, 3], thus yielding an MAR condition and missing rates of 30% for the dependent variable and covariates, which mirrored the proportion of missingness in the empirical data.
Then we applied the proposed model to the simulated data to forecast the last observation of each individual. The data generation code and JAGS scripts for model fitting can be accessed via the link provided before. The calculation of the above performance measures involved saving all posterior samples for each replication. Given the constraints of computational resources, we obtained the point estimates of these measures for each replication, and then calculated the means across replications to measure forecast accuracy, and standard deviations and quantiles to measure forecast uncertainty. In addition, to evaluate other estimation properties of the proposed approach, we calculated biases, standard errors (i.e., standard deviations of the posterior distributions of the parameters), and coverage rates (i.e., the percentage of replications in which the credible intervals contained the true values) of all parameters presented above across 500 replications.
4.2. Simulation Results
As mentioned before, we used ESS and to check the sampling efficiency and convergence issues. No replications indicated problems with convergence – was below 1.1 for all parameters in all replications. The ESS was generally good (i.e., greater than 800) for most parameters, except for the AR parameter (i.e., ϕ1) in the multilevel AR-X model, for which the average ESS across replications was around 300 and 200 under the moderate ZI and high ZI condition, respectively. The lower ESS under the high ZI condition indicated that the low ESS with the AR parameter was likely due to the large proportion of zeros and relatedly, limited data from the AR process to estimate this parameter well. Even so, the ESS can be deemed acceptable, especially when the forecast performance was of greater interest in the present study.
The estimation results are summarized in Table 1. We found that with both conditions, most parameters were recovered accurately as indicated by their biases and coverage rates, except that the AR parameter, ϕ1, had slightly larger biases (e.g., −0.04) and lower coverage rates. By comparing the estimated and true latent regime indicators for all individuals from time 1 to Ti – 1 in one simulation replication, we found that 98% of the regime indicators were correctly recovered.
Table 1:
Comparison of Estimation Performance Based on 500 Replications
| Moderate ZI | High ZI | ||||||
|---|---|---|---|---|---|---|---|
| True | Bias | SE | CR(%) | Bias | SE | CR(%) | |
| Parameters in the Poisson Process (see Equations 7-8) | |||||||
| γ 0 | 2 | 0.00 | 0.04 | 96 | 0.00 | 0.04 | 95 |
| ϕ 1 | 0.3 | −0.04 | 0.02 | 62 | −0.04 | 0.03 | 72 |
| β 1 | 0.5 | 0.02 | 0.02 | 86 | 0.02 | 0.03 | 89 |
| σv | 0.5 | 0.00 | 0.03 | 96 | 0.00 | 0.04 | 96 |
| σϵ | 0.5 | 0.00 | 0.01 | 94 | 0.00 | 0.01 | 95 |
| Parameters in the Initial Regime Model (see Equation 10) | |||||||
| π 0 | −2 | 0.24 | 0.26 | 81 | 0.15 | 0.25 | 90 |
| Parameters in the RS Model (see Equation 9) | |||||||
| α 01,0 | −2.5 | 0.00 | 0.06 | 97 | 0.00 | 0.08 | 94 |
| α 01,1 | 0.2 | 0.00 | 0.05 | 96 | 0.00 | 0.07 | 94 |
| α 10,0 | −2.5 | −0.01 | 0.05 | 96 | |||
| −3.5 | −0.02 | 0.07 | 95 | ||||
| α 10,1 | 0.2 | 0.00 | 0.05 | 95 | 0.00 | 0.06 | 96 |
| Parameters in the Covariate Model (see Equation 14) | |||||||
| ϕ x 1 | 0.6 | 0.00 | 0.01 | 93 | 0.00 | 0.01 | 93 |
| σ x 1 | 0.5 | 0.00 | 0.00 | 93 | 0.00 | 0.00 | 93 |
| ϕ z 1 | 0.9 | 0.00 | 0.00 | 95 | 0.00 | 0.00 | 95 |
| σ z 1 | 0.5 | 0.00 | 0.00 | 95 | 0.00 | 0.00 | 95 |
Note. True: true values; Bias: estimates minus true values; SE: standard errors estimated by standard deviations of the posterior distributions; Bias and SE were averaged across 500 replications, respectively; CR(%): percentages of replications in which the credible intervals contained the true values.
The forecast results are summarized in Table 2 and displayed in Figure 2. Under both conditions, the proposed model yielded good forecast performance as indicated by mean AUC scores higher than 0.9, as well as mean ACC, recall, and precision scores close to 0.9, under the decision threshold of 0.5. The comparison between conditions showed better forecast accuracy under the high ZI condition than the moderate ZI condition, as indicated by notably higher ACC and AUC scores, as well as lower MAEs and RMSEs. This was expected as higher instances of staying within a particular regime — in our case, the ZI regime — generally ease forecast complexity in most scenarios. However, the comparable recall and precision values across the two conditions provided some reassurance of the performance of the proposed estimation procedures in successfully detecting positive cases (e.g., drinking) despite the presence of high instances of ZI.
Table 2:
Comparison of Forecast Performance Based on 500 Replications
| Moderate ZI | High ZI | |||||
|---|---|---|---|---|---|---|
| Mean | SD | 95% CI | Mean | SD | 95% CI | |
| ACC* | .87 | .02 | [.82, .91] | .93 | .02 | [.89, .96] |
| recall* | .86 | .04 | [.79, .92] | .86 | .05 | [.76, .94] |
| precision* | .88 | .03 | [.81, .94] | .88 | .05 | [.78, .96] |
| AUC | .91 | .02 | [.87, .95] | .94 | .02 | [.89, .98] |
| MAE | 3.22 | 0.44 | [2.47, 4.14] | 1.78 | 0.33 | [1.20, 2.44] |
| RMSE | 6.84 | 1.42 | [4.90, 9.96] | 5.03 | 1.33 | [3.09, 8.09] |
Note. The calculation of ACC, recall, and precision was based on a threshold of 0.5. The Mean, SD, and 95% CI represented the means, standard deviations, and 95% credible intervals of these measures across 500 replications.
Figure 2:
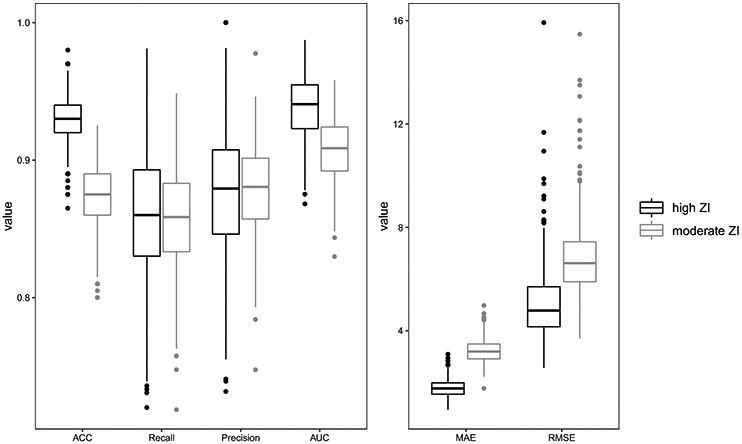
Comparisons of forecast accuracy and uncertainty under the high ZI (black) and moderate ZI (grey) condition in the simulation study. Performance measures considered included ACC, recall, precision, AUC (the left plot), MAE and RMSE (the right plot). The calculation of ACC, recall, and precision was based on a threshold of 0.5.
In terms of forecast uncertainty, the standard deviations of ACC and AUC scores were identical between two conditions; the high ZI condition showed slightly higher levels of forecast uncertainty on recall and precision scores and lower levels of forecast uncertainty on MAEs and RMSEs. In sum, our simulation results showed that improved forecast accuracy can be attained within the context of the RS-ZIMLP model with increased instances of replications in each regime. The simulation study further validated the capacity of the proposed model and estimation procedures in detecting positive cases (e.g., drinking) even with high instances of ZI, and clarified whether and in what ways classification-based performance indices such as ACC, AUC, recall, and precision might provide supplemental formation concerning forecast utility relative to discrepancy-based measures such as MAEs and RMSEs.
5. Empirical Study
5.1. Data Descriptions
The empirical data used in this study were part of the CoTwins, an intensive longitudinal study of adolescent twins recruited from Colorado Department of Health birth records. Twins were initially recruited at ages 14-17 and followed from 2015 to 2018. Throughout the study, in each week, participants were asked to report whether they used substances and if so, what substances they used in the past week. If the participants chose a certain type of substance (i.e., alcohol, marijuana, cigarettes), they would be directed to answer the frequency and quantity of substance use during that week. The responses ranged from 1 to 7 in terms of the frequency (i.e., number of days they drank alcohol in the past week) of all types of substance use.
In terms of quantity, the quantity of alcohol use was measured by the number of drinks per day (i.e., “on those days that you drank alcohol, how many drinks2 did you usually have each day?”). Part of a drink was coded as 0.5 and re-coded as 1 in our analysis so that the dependent variable took integer values, as consonant with properties of count data. In a similar vein, the rest of the options, ranging from one drink to 20 drinks, were re-coded as 2 to 40 to reflect the original scale. Note that the option “more than 20 drinks” was also coded as 40. The quantity of marijuana use was measured by the number of times per day they used enough to feel the effects, which ranged from 0 to 5 times. Note that zero responses on marijuana use indicated that the participants never had enough to feel the effects and the option “more than 5 times” was coded as 5. The quantity of cigarette use was measured by the number of cigarettes per day as well as the number of times per day they used e-cigarettes, which ranged from 0.5 to 30 (more than 30 cigarettes was coded as 30), and 1 to 10 (more than 10 times was coded as 10), respectively.
5.2. Forecasting With Spatial Information From GPS Data
Technological advances in the past decades now allow physical location data from smartphones with GPS capabilities to serve as measures of environmental context. As postulated by the Ecological Systems Theory (Bronfenbrenner, 1992), and consistent with findings from empirical studies, adolescents’ pathways to alcohol use and abuse are associated with social contextual factors such as proximity to alcohol outlets (Byrnes et al., 2016, 2017). While the causal nature of such associations are far from clear, identifying such a correlation is the first step in evaluating the utility of GPS for measuring environmental influences. Therefore, we conducted exploratory analyses using the spatial measures described below to help enhance our understanding of when, how, and why some adolescents transition into and sustain regular use of alcohol.
The spatial measures used in this study included shared space and time spent with twin siblings, as well as time spent near certain landmarks, such as bars, mental health services, and gyms — all measures were aggregated to a weekly level to mirror the time scale of the substance use data (see definitions and calculations below). We hypothesized that shared space and time spent with twin siblings might be an interpersonal factor that protects against alcohol use (Maisto et al., 2017) in that adolescents who had stronger social relationships with their twin siblings might be more likely to stay within the drinking regime and also less likely to switch from the ZI to the drinking regime. The time spent near certain landmarks were also hypothesized to be associated with alcohol use because it might reflect individuals’ activities and social contacts. Specifically, although it is unlikely that adolescents drink alcohol in bars, proximity to bars (e.g., within a radius of 100 meters) could be an indicator of social contacts (Reboussin, Song, & Wolfson, 2011) and perceptions of use as normative (Pasch, Hearst, Nelson, Forsyth, & Lytle, 2009). Time spent near bars was thus hypothesized to be positively associated with alcohol use. Based on previous studies on the comorbidity between mental health disorders and alcohol use (Jane-Llopis & Matytsina, 2006), we assumed that time spent near mental health services would serve as an indicator for mental health problems, and thus, would be positively associated with alcohol use. In contrast, time spent near gyms might indicate good maintenance of physical and mental health, and was thus hypothesized to be negatively associated with alcohol use.
5.2.1. Calculation of Spatial Measures From GPS data
The location (GPS) data were collected using participants’ own smartphones. With iOS devices, the protocol was that location was reported every time participants moved a significant distance (i.e., 500 meters); with Android devices, a location was to be reported every five minutes. Prior to extracting the spatial measures of interest, some data processing steps were needed. Specifically, records with less than 20 valid data points within a week were excluded from the data set because these unusually low numbers of GPS points lacked sufficient variability to reflect the mobility trajectories of the participants over the course of a week and likely reflected missing data instead of a true mobility trace. In addition, data points representing long-distance travels and other atypical travel trajectories were excluded from the data set because these points were extreme outliers that would bias estimation of the spatial and mobility patterns of the individuals. For outlier detection purposes, we used an R package, Density-Based Spatial Clustering of Applications with Noise (dbscan; Hahsler, Piekenbrock, & Doran, 2019), to identify clusters and outlying points based on a density-based clustering algorithm (Ester, Kriegel, Sander, Xu, et al., 1996).
Using the pre-processed GPS data, we derived the following person- and time-varying spatial measures via a Python package, gps2space (Zhou, Li, Bodovski, Chi, & Chow, 2021; Zhou, Li, Chi, et al., 2021). Users are referred to the documentation (https://gps2space.readthedocs.io/en/latest/) of this package, which provides the step-by-step guide to calculating the key spatial measures.
Activity Space and Shared Space.
In this study, an individual’s daily activity space was defined as the area of the minimum bounding geometry enclosing all the non-missing latitude and longitude coordinates for that individual over the entire day. The buffer method was used in this study to build such the bounding geometry from coordinates, which required selection of a pre-defined buffer size that determined the smallest size of the bounding geometry thought to reflect meaningful, quantifiable distance given the accuracy of the GPS devices. In our case, we set the buffer to 1,000 meters based on previous studies (e.g., James et al., 2014; Perchoux, Chaix, Brondeel, & Kestens, 2016). The daily shared space was then defined as the proportion of overlapping areas of daily activity spaces between a participant and his/her twin sibling. We then aggregated it to a weekly measure by averaging daily shared spaces over the course of a week.
Time Spent With Twin Siblings Over the Week.
The shared space calculated above simply captured general physical proximity in terms of overlap in activity spaces, therefore it was not a direct validation that two twin members were actually at the same location at a particular time point. Rather, what this measure provided was some information concerning similarity in everyday routines between twin members. To approximate the time spent together with twin siblings, we first built hourly buffer-based activity spaces with a buffer size of 100 meters for each twin pair and considered them to be together if their activity spaces overlapped. This yielded a dummy variable with 1 representing being together over the course of an hour. We then aggregated it to a weekly measure by calculating the proportion of 1’s over each week, thus yielding proportions ranging from 0 to 1, which were regarded as the approximation to the time spent together with twin siblings over the week.
Time Spent Near Landmarks Over the Week.
The landmarks considered in this study included bars, mental health services, and gyms. For each pair of GPS coordinates, each participant’s distance from a particular landmark (e.g., distance from gyms) was computed as the Euclidean distance from the coordinates recorded from participants’ devices to the coordinates of the nearest landmark (e.g., the nearest gym)3. Participants were considered to be at that landmark if the Euclidean distance was less than 100 meters, thus yielding a dummy variable with 1 representing being at the landmark at a particular time point. Similar to the calculation of time spent with twin siblings, we aggregated it to a weekly measure by calculating the proportion of 1’s over each week and regarded it as the approximation to the time spent near a specific landmark over the week.
5.3. Data Analytic Plans
The above person- and time-specific spatial measures were scaled within-person and across time points to zero mean and unit variance, and then merged with the weekly substance use data. All substance use measures were calculated as the product of frequency (e.g., number of days they drank alcohol in the past week) and quantity (e.g., number of drinks per day), as defined above. In particular, cigarette use was calculated as the sum of cigarettes and e-cigarettes. Both marijuana and cigarette use were first log transformed and then scaled within-person and across time points to zero mean and unit variance.
Our final data set were built based on the following selection criteria: 1) participants should have both substance use and GPS data over the same time period; 2) the total number of time points for each participant should be no less than 8. That is, participants should have at least 8 weeks’ data; 3) the missing rate for each variable should be less than 90% for each participant. As a result, the sample size was reduced from 670 to 402, with the number of weeks for each participant ranging from 8 to 95. Participants’ ages at the initial time point ranged from 14 to 20, and 41% of the participants were males. For each variable considered in the present study, the median of the missing rates across participants was 35% for substance use measures, 4% for shared space, 1% for time spent near landmarks, and 10% for time spent with twin siblings, respectively. Note that in reality, participants might not provide one response per week, thus yielding irregularly spaced data. Thus, we blocked the data at equally spaced time windows (i.e., weeks) and inserted missingness in weeks with no responses, which inevitably generated a large proportion of missingness. However, previous studies have shown that reasonable inferential results could be obtained from fitting dynamical systems models with large proportions of missingness (e.g., more than 50% missingness; see, e.g., Jacobson, Chow, & Newman, 2019; Ji et al., 2020). We also discussed other possible ways of handling missing data in the Discussion section.
With all these measures, we adapted Equations 7 - 9 to build the following RS-ZIMLP model for forecasting adolescent alcohol use.
| (23) |
| (24) |
| (25) |
| (26) |
Briefly, substance use measures (Mar = marijuana use; Cig = cigarette use) at time t – 1 were included in the AR-X model as predictors of levels of alcohol use at time t in the drinking regime; gender (0 = female; 1 = male) and baseline age (centered by subtracting the minimum baseline age so that 0 corresponded to age 14) were included in the level-2 model to explain individual differences in the average levels of alcohol use such that γ0 represented the average alcohol use for females at age 14 with average levels of marijuana and cigarette use across participants; The person-specific covariates in Equation 25 represented the average levels of spatial measures (Bar = time spent near bars; Menth = time spent near mental health services; Gym = time spent near gyms; SS = shared space; Together = time spent with twin siblings) across the entire study span (except for the last 5 observations since they were used to evaluate forecast performance in this study) for each person, hypothesized to be associated with initial regime probabilities. In contrast, the person- and time-specific covariates in Equation 26, which by definition represented time-varying within-person deviations from average levels of spatial measures, were assumed to explain log-odds of RS dependencies, under the assumption that the GPS data collected during week t would help forecast the transition probability in this week. We expected greater shared space and time spent with twin siblings and longer time spent near gyms than usual to increase adolescents’ log odds of transitioning to the ZI regime and reduce the log odds of transitioning to the drinking regime. We expected longer time spent near bars and mental health services than usual to assume the reversed roles.
Given the high proportion of non-drinking instances in the empirical data, a reasonable baseline model would be a model that always posited non-drinking for all participants and time points. We refer to this as the “Null Model”. As an alternative comparison, we also fitted a ZIMLP model without the RS structure, whose ZI component was defined as an ordinary logistic model shown below.
| (27) |
Here, the person- and time-specific covariates were assumed to explain log-odds of being in the drinking regime.
We then applied both models to forecast the last 5 observations of alcohol use for each individual, following the one-step ahead forecast procedure described before. The number of chains, number of (burn-in) iterations, and prior settings were almost identical to those adopted in the simulation study, except that a more informative prior (i.e., N(2, 5)) was assigned to γ0 because eγ0 reflected the overall baseline around which the levels of alcohol use fluctuated in the drinking regime and thus was assumed to be higher than zero. The mean of the prior distribution of γ0 was thus specified as the empirical log mean of alcohol use when participants used alcohol, and a small variance (i.e., 5) was specified so that eγ0 would not take extremely low or high values.
5.4. Empirical Results
We first fitted the full RS-ZIMLP model presented in Equations 23 - 26 and found that none of the person-specific spatial measures covariates, shown in Equation 25, were credibly linked to initial regime probabilities. That is, all of the credible intervals of the coefficients linking initial regime probabilities to these covariates (i.e., π1 - π5) contained 0, therefore in the final RS-ZIMLP model, we removed these covariates and only estimated the intercept, π0, in Equation 25. The time-varying spatial covariates in Equations 26 and 27 were kept in the final ZIMLP model to explore the associations between these spatial measures and the probability of being in the drinking regime, and were also kept in the final RS-ZIMLP model to explore associations between spatial measures and transition probabilities, as well as facilitate forecasts. In addition, both ZIMLP and RS-ZIMLP models yielded low ESSs and higher than 1.1 for the AR parameters. The non-convergence might be due to the large proportion of missingness and instances of staying long in the drinking regime being so rare (e.g., the median of the proportions of zero responses was 83% across participants) and thus information on the AR process was limited. Hence, we reduced the multilevel AR-X model to a random intercept-only model with covariates by removing ϕ1(ηi,t–1 – ϕ0,i) and ϵi,t on the right-hand side of Equation 23. The following descriptions were based on this reduced model.
On an Intel i7-8700, 64GB RAM, Windows 10 computer, it took about 8 hours and 36 hours to run the ZIMLP and RS-ZIMLP model, respectively. The diagnostic criteria for adequate sampling were set as ESS greater than 800 and below 1.1. Results showed that ESS was greater than 800 for 78% and 76% of the parameters with the ZIMLP and RS-ZIMLP model, respectively. Parameters with low ESS included γ0, γ1, γ2, σv, and the ESS reached a minimum of 200 for these parameters, which can be deemed acceptable. The was below 1.1 for all parameters with both models.
We first compared the forecast performances of the different candidate models considered based on all participants in the data set (N = 402) and a subset of participants who consumed alcohol at least once during the study (N = 142). Here, the calculation of ACC, recall, and precision scores was based on a threshold of 0.3 for both ZIMLP and RS-ZIMLP models. Table 3 shows forecast performance based on the full sample size. Both the ZIMLP and RS-ZIMLP models yielded satisfactory classification performance in terms of distinguishing between positive cases (drinking) and negative cases (non-drinking), as indicated by their respective AUC scores, which were both greater than 0.9. The RS-ZIMLP model yielded better classification performance than the ZIMLP model as indicated by its higher AUC score, and its ROC curve that was further away from the diagonal line, as shown in Figure 3a. Under the threshold of 0.3, the RS-ZIMLP model yielded higher ACC, recall, and precision scores than the other two models. As mentioned before, one could modify the threshold to obtain different values for these measures. Hence, caution need to be exercised when comparing forecast performance based on these measures. Due to the large proportion of zeros, the null model also yielded good accuracy (i.e., 0.87) but the recall score was merely 0. Finally, the comparisons of the means and standard deviations of MAEs and RMSEs showed that the RS-ZIMLP model yielded slightly better forecast accuracy than the other two models and comparable forecast uncertainty to the ZIMLP model.
Table 3:
Comparison of Forecast Performance Based on Empirical Data (N = 402)
| Null Model | ZIMLP | RS-ZIMLP | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | 95% CI | Mean | SD | 95% CI | Mean | SD | 95% CI | |
| ACC* | 0.87 | - | - | 0.84 | 0.01 | [0.83, 0.85] | 0.91 | 0.00 | [0.90, 0.92] |
| recall* | 0.00 | - | - | 0.73 | 0.02 | [0.70, 0.75] | 0.77 | 0.03 | [0.72, 0.82] |
| precision* | - | - | - | 0.46 | 0.01 | [0.44, 0.48] | 0.71 | 0.02 | [0.68, 0.75] |
| AUC | - | - | - | 0.90 | 0.00 | [0.89, 0.91] | 0.93 | 0.01 | [0.92, 0.94] |
| MAE | 1.57 | - | - | 1.72 | 2.31 | [1.39, 4.13] | 1.27 | 1.21 | [0.96, 3.40] |
| RMSE | 5.82 | - | - | 5.11 | 9.17 | [3.24, 34.67] | 4.53 | 9.97 | [2.85, 40.45] |
Note. The forecast performance was evaluated based on all participants (N = 402) in the empirical study. The calculation of ACC, recall, and precision was based on a threshold of 0.3 for both ZIMLP and RS-ZIMLP models. The Mean, SD, and 95% CI represented the means, standard deviations, and 95% credible intervals of the posterior distributions of these measures.
Figure 3:
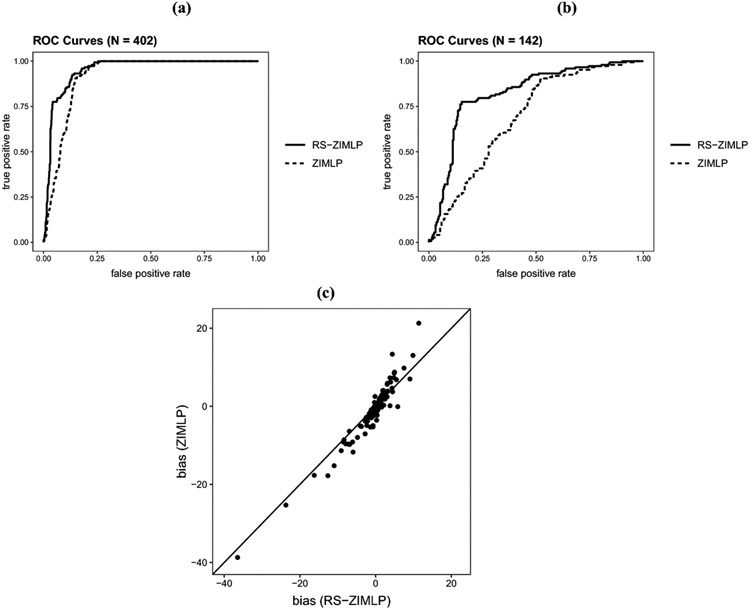
(a) ROC curves for the ZIMLP model (dashed line) and RS-ZIMLP model (solid line) generated based on all participants (N = 402). (b) ROC curves for the ZIMLP model (dashed line) and RS-ZIMLP model (solid line) generated based on participants who consumed alcohol at least once during the study (N = 142). (c) Comparison of the forecast biases (predicted values minus actual values) for all participants (N = 402) with the ZIMLP model (y-axis) and the RS-ZIMLP model (x-axis).
A substantial proportion (i.e., 65%) of the participants in the current sample never reported consuming any alcohol during the entire study span. These participants did not provide helpful information concerning possible timing and determinants of transition to drinking, so we then conducted a closer inspection of participants who consumed alcohol at least once during the study (i.e., N = 142). The forecast performance for this subset of participants can be found in Table 4. We can see that for this particular subset of participants, the differences in forecast performance across candidate models were substantial. Specifically, the AUC score with the RS-ZIMLP model was reduced to 0.82, which was still satisfactory, whereas the AUC score with the ZIMLP model decreased to 0.69 (see also Figure 3b for the comparison of ROC curves). The recall and precision did not change, indicating no false identification of non-drinking participants (N = 260) as drinking within the forecast window. Since many instances of zeros were removed, the ACC of the null model was reduced to 0.66. Finally, comparisons of the means and standard deviations of MAEs and RMSEs showed that the RS-ZIMLP model yielded notably better forecast accuracy than the other two models and slightly less forecast uncertainty.
Table 4:
Comparison of Forecast Performance Based on Empirical Data (N = 142)
| Null Model | ZIMLP | RS-ZIMLP | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | 95% CI | Mean | SD | 95% CI | Mean | SD | 95% CI | |
| ACC* | 0.66 | - | - | 0.62 | 0.01 | [0.60, 0.64] | 0.82 | 0.01 | [0.80, 0.85] |
| recall* | 0.00 | - | - | 0.73 | 0.02 | [0.69, 0.76] | 0.77 | 0.03 | [0.72, 0.83] |
| precision* | - | - | - | 0.46 | 0.01 | [0.45, 0.48] | 0.71 | 0.02 | [0.68, 0.75] |
| AUC | - | - | - | 0.69 | 0.01 | [0.66, 0.71] | 0.82 | 0.01 | [0.79, 0.85] |
| MAE | 4.24 | - | - | 4.67 | 0.60 | [3.87, 6.27] | 3.44 | 0.47 | [2.69, 4.54] |
| RMSE | 9.57 | - | - | 8.41 | 4.96 | [5.78, 22.97] | 7.45 | 2.89 | [5.29, 15.97] |
Note. The forecast performance was evaluated based on participants who consumed alcohol at least once during the study (N = 142). The calculation of ACC, recall, and precision was based on a threshold of 0.3 for both ZIMLP and RS-ZIMLP models. The Mean, SD, and 95% CI represented the means, standard deviations, and 95% credible intervals of the posterior distributions of these measures.
To help clarify the respective strengths and limitations of the candidate models in forecasting and explaining individuals’ drinking dynamics, we inspected the parameter estimates corresponding to the ZIMLP and RS-ZIMLP model, as summarized in Table 5. The two models yielded similar results in terms of parameters in the Poisson process. Specifically, in terms of alcohol use dynamics in the drinking regime, we found that cigarette use in the previous week was positively associated with alcohol use in the current week (e.g., β2 = 0.10, 95% CI = [0.02, 0.18]), indicating that higher levels of cigarette use tended to predict more alcohol use in the following week. Such credible relationship was not found between marijuana and alcohol use. We also found substantial individual differences in participants’ average levels of alcohol use while in the drinking regime, as indicated by the large random effect standard deviation (e.g., σv = 3.96) with its corresponding credible interval being relatively narrow (e.g., 95% CI = [3.46, 4.38]). In addition, older adolescents were found to have higher average levels of alcohol use (e.g., γ2 = 1.17, 95% CI = [0.78, 1.55]). No credible gender difference was found in adolescents’ average levels of alcohol use. This lack of credible gender difference in average alcohol use was consistent with the finding from the Substance Abuse and Mental Health Services Administration (SAMHSA)’s National Survey on Drug Use and Health (NSDUH; SAMHSA, 2008), which indicated that males only started to demonstrate higher levels of alcohol use than females as they moved into young adulthood. The majority of participants in the present study were in the stage of middle adolescence (i.e., ages 14 to 17), and we did not find consistent evidence for gender differences at this age span.
Table 5:
Parameter Estimates for Empirical Data
| Parameter | ZIMLP |
RS-ZIMLP |
|||||
|---|---|---|---|---|---|---|---|
| Est | SE | 95% CI | Est | SE | 95% CI | ||
| Parameters in the Poisson Process (see Equations 23-24) | |||||||
| Fixed Effects | |||||||
| Intercept, γ0 | −3.97 | 0.33 | [−4.62, −3.32] | −3.23 | 0.30 | [−4.12, −2.75] | |
| Gender, γ1 | −1.02 | 0.53 | [−2.08, 0.01] | −0.95 | 0.49 | [−1.91, 0.02] | |
| Age, γ2 | 1.23 | 0.20 | [0.83, 1.61] | 1.17 | 0.19 | [0.78, 1.55] | |
| Marijuana use, β1 | 0.01 | 0.04 | [−0.06, 0.09] | 0.01 | 0.03 | [−0.06, 0.08] | |
| Cigarette use, β2 | 0.12 | 0.04 | [0.04, 0.21] | 0.10 | 0.04 | [0.02, 0.18] | |
| Random Effects | |||||||
| SD, σv | 4.23 | 0.27 | [3.73, 4.78] | 3.96 | 0.24 | [3.46, 4.38] | |
| Parameters in the Regime-defining Model (see Equation 27) | |||||||
| Intercept, α0 | −0.70 | 0.04 | [−0.78, −0.61] | ||||
| Bar, α1 | 0.03 | 0.04 | [−0.04, 0.11] | ||||
| Menth, α2 | −0.03 | 0.04 | [−0.11, 0.04] | ||||
| Gym, α3 | −0.08 | 0.04 | [−0.16, 0.00] | ||||
| SS, α4 | −0.07 | 0.04 | [−0.15, 0.02] | ||||
| Together, α5 | −0.12 | 0.05 | [−0.22, −0.03] | ||||
| Parameters in the Initial Regime Model (see Equation 25) | |||||||
| Intercept, π0 | −1.76 | 0.22 | [−2.20, −1.32] | ||||
| Parameters in the RS Model (see Equation 26) | |||||||
| ZI → drinking, Intercept, α10,0 | −1.60 | 0.06 | [−1.72, −1.48] | ||||
| ZI → drinking, Bar, α10,1 | 0.01 | 0.06 | [−0.12, 0.12] | ||||
| ZI → drinking, Menth, α10,2 | 0.04 | 0.06 | [−0.08, 0.15] | ||||
| ZI → drinking, Gym, α10,3 | −0.11 | 0.06 | [−0.24, 0.02] | ||||
| ZI → drinking, SS, α10,4 | 0.00 | 0.07 | [−0.14, 0.14] | ||||
| ZI → drinking, Together, α10,5 | 0.01 | 0.07 | [−0.12, 0.16] | ||||
| drinking → ZI, Intercept, α01,0 | −0.44 | 0.07 | [−0.58, −0.30] | ||||
| drinking → ZI, Bar, α01,1 | −0.08 | 0.08 | [−0.24, 0.07] | ||||
| drinking → ZI, Menth, α01,2 | 0.06 | 0.07 | [−0.08, 0.21] | ||||
| drinking → ZI, Gym, α01,3 | 0.12 | 0.08 | [−0.03, 0.28] | ||||
| drinking → ZI, SS, α01,4 | 0.12 | 0.09 | [−0.06, 0.28] | ||||
| drinking → ZI, Together, α01,5 | 0.18 | 0.09 | [0.01, 0.36] | ||||
| Parameters in the Covariate Model (see Equation 14) | |||||||
| Marijuana use | |||||||
| ϕ x 1 | 0.12 | 0.01 | [0.10, 0.14] | 0.12 | 0.01 | [0.09, 0.14] | |
| σ x 1 | 0.46 | 0.00 | [0.45, 0.46] | 0.46 | 0.00 | [0.45, 0.46] | |
| Cigarette use | |||||||
| ϕ x 2 | 0.25 | 0.01 | [0.23, 0.27] | 0.25 | 0.01 | [0.23, 0.27] | |
| σ x 2 | 0.45 | 0.00 | [0.44, 0.45] | 0.45 | 0.00 | [0.44, 0.45] | |
| Time spent at bars | |||||||
| ϕ z 1 | 0.11 | 0.01 | [0.09, 0.12] | 0.11 | 0.01 | [0.09, 0.12] | |
| σ z 1 | 0.98 | 0.01 | [0.97, 0.99] | 0.98 | 0.01 | [0.97, 0.99] | |
| Time spent at mental health services | |||||||
| ϕ z 2 | 0.03 | 0.01 | [0.02, 0.05] | 0.03 | 0.01 | [0.02, 0.05] | |
| σ z 2 | 0.97 | 0.01 | [0.96, 0.98] | 0.97 | 0.01 | [0.96, 0.98] | |
| Time spent at gyms | |||||||
| ϕ z 3 | 0.09 | 0.01 | [0.08, 0.11] | 0.09 | 0.01 | [0.08, 0.11] | |
| σ z 3 | 0.98 | 0.01 | [0.97, 0.99] | 0.98 | 0.01 | [0.97, 0.99] | |
| Shared space with twin siblings | |||||||
| ϕ z 4 | 0.32 | 0.01 | [0.31, 0.33] | 0.32 | 0.01 | [0.31, 0.33] | |
| σ z 4 | 0.86 | 0.00 | [0.85, 0.87] | 0.86 | 0.00 | [0.85, 0.87] | |
| Time spent with twin siblings | |||||||
| ϕ z 5 | 0.29 | 0.01 | [0.27, 0.31] | 0.29 | 0.01 | [0.27, 0.31] | |
| σ z 5 | 0.94 | 0.01 | [0.93, 0.95] | 0.94 | 0.01 | [0.93, 0.95] | |
Results from both ZIMLP and RS-ZIMLP models suggested that time spent with twin siblings could be a protective factor against alcohol use, but in slightly different ways. Specifically, results from the ZIMLP model showed that individuals were less likely to be in the drinking regime during the weeks when they spent more time with their twin siblings than usual (α5=−0.12, 95% CI = [−0.22, −0.03]). The RS-ZIMLP model provided more nuanced clarifications of the mechanisms for this predictor’s protective roles: individuals were more likely to transition from the drinking regime (regime 1) to the ZI regime (regime 0) during the weeks when they spent more time with their twin siblings than usual (α01,5 = 0.18, 95% CI = [0.01, 0.36]). Thus, whereas spending more time with twin siblings did not appear to help prevent individuals to transition from non-drinking to drinking, doing so was associated with increased probability of returning to non-drinking following a drinking episode.
Results for covariate model parameters are also summarized in Table 5. Briefly, for each covariate considered in the final model, the current measurement was positively associated with the previous measurement, indicating that if individuals spent much time near these landmarks or had a large proportion of shared space or spent time mostly with their twin siblings in the current week, it is likely that they would continue doing so in the following week.
In terms of individual forecast performance, we compared the biases (i.e., predicted values minus actual values) for all individuals between the two models in Figure 3c. Recall that one drink was coded as 2 in the data set, so a bias of −10 means 5 drinks less than the actual value. The two models yielded similar predictive results for most individuals, as indicated by a large proportion of points around the diagonal line. Most biases were close to 0, indicating overall satisfactory forecast accuracy with both models. However, both models failed to capture heavy drinking, as reflected by instances with higher negative bias values.
To further evaluate the individual forecast performance of the proposed model, we plotted observed alcohol use (blue lines), imputed/forecast alcohol use (red lines), uncertainty in imputation/forecast (red error bars), the estimated/predictive probability of drinking alcohol (shaded areas) for three participants in Figure 4. These plots helped highlight circumstances in which the proposed RS-ZIMLP model yielded reasonable (e.g., participants 1 and 2) as compared to inadequate (e.g, participant 3) forecast performance. Note that missing entries in the alcohol use variable were imputed in the model fitting process, so there were also error bars indicating uncertainty in imputation before the forecast window. In both participants 1 and 2, the actual amounts of alcohol use fell within the credible intervals of the predicted alcohol use values. In contrast, participant 3’s heavy observed alcohol use during the forecast window was not enclosed within the credible intervals of the participant’s predicted alcohol use (see Figure 4c). Thus, even though the RS-ZIMLP model was reasonable at forecasting instances of zero to moderate drinking, it fell short in predicting instances of heavy alcohol use. Despite this, we have verified post-hoc that in the forecast window, most heavy drinking instances occurred immediately after non-drinking instances. It is challenging to capture such sudden and sharp shifts without sufficient contextual information before the shifts, such as information from other person- and time-specific covariates that align closer in time with the corresponding sudden shifts in alcohol use (e.g., spatial, social, and other interpersonal covariate information from yesterday, as opposed to one week earlier) may be helpful. In the present study, the covariates investigated were inadequate at predicting the transition from non-drinking to drinking, and to a lesser degree, the reverse transition from drinking to non-drinking. That is, none of the covariates were characterized by coefficients that were credibly different from 0 in predicting the transition from non-drinking to drinking, although one covariate, time spent with twin siblings, did have a coefficient that was credibly different from 0 in predicting the transition from drinking to non-drinking.
Figure 4:
Plots of observed alcohol use (blue thick lines), imputed/forecast alcohol use (red thin lines) with uncertainty (red error bars), and estimated/predictive probability of drinking alcohol (shaded area) for three participants to show the forecast performance with different trajectory patterns. The time period between the two black vertical lines was the forecast window. The left y-axis represented the observed and forecast value of alcohol use (see how alcohol use values were coded in the Data Descriptions subsection), whereas the right y-axis represented the probability of drinking alcohol, whose scale was different from the left y-axis.
6. Discussion
In this paper, we proposed a Bayesian RS-ZIMLP model to forecast count time series data with excess zeros. Our proposed model is innovative by incorporating time dependencies between observations in both the Poisson and ZI component of the ZIP model. In particular, we added an RS structure to the ZI component to capture the underlying mechanism of transitioning between the ZI regime and the Poisson process in the change process. The simulation results suggested satisfactory estimation and forecast performance with the proposed model with different levels of ZI in the data, and slightly better forecast accuracy and less forecast uncertainty under the high ZI condition. The proposed model was applied to data collected from CoTwins to forecast adolescent alcohol use. Compared with the null model and the ZIMLP model, a set of performance measures (e.g., AUC, MAE and RMSE) indicated that the proposed model yielded more accurate representation of time dependencies in alcohol use and thus higher forecast accuracy. Such improvement in forecast performance was even more pronounced when we limited the comparisons to participants who consumed alcohol at least once during the study. The investigation of individual forecast performance showed that the proposed model was good at forecasting non-drinking and moderate drinking, but not sudden shifts to heavy drinking.
Spatial measures derived from GPS data, including time spent near certain landmarks, shared space and time spent with twin siblings were included in the RS model to explain within-individual transitions between the ZI and drinking regimes. Results showed that individuals were more likely to transition from the drinking regime to the ZI regime during the weeks when they spent more time with their twin siblings than usual. In addition, none of the person-specific, time-invariant spatial measures helped explain substantial between-person differences in initial regime probabilities. Our findings suggested that spatial measures did in fact provide valuable contextual information to help clarify individuals’ alcohol use dynamics, but more at the within- than between-individual level, particularly in explaining individuals’ probabilities of transitioning from drinking to non-drinking in comparison to the probabilities of transitioning from non-drinking to drinking.
Despite the promise shown by the application of the proposed model to ILD and GPS data, there are several limitations to the current work. First, the adolescent alcohol use data were highly imbalanced, with a large proportion of zero responses, thus the corresponding classification performance showed a moderately high false negative rate, as indicated by a recall of 0.77 (see Tables 3 and 4). Certainly, the recall score could be increased by lowering the threshold, but doing so would lead to lower precision as well. Second, results showed that the proposed model could not capture heavy drinking well, which might be due to the lack of time-varying covariates from a prior week that would be predictive of alcohol use at the subsequent week. Third, inclusion of the AR structure might help better capture instances of heavy drinking, but it was removed from the empirical data analysis due to convergence issues probably caused by the large proportion of missingness as well as the insufficient length of non-zero time series. An alternative would be to fix the AR parameter at 1 to yield a random walk while in the drinking regime. Fourth, no cross-validation was conducted to prevent over-fitting in the empirical illustration. Several cross-validation approaches could be considered or adapted for forecasting with longitudinal data (see, e.g., Cudeck & Browne, 1983; De Jong, 1988; Gelfand, Dey, & Chang, 1992; MacCallum, Roznowski, Mar, & Reith, 1994; Piironen & Vehtari, 2017; Vehtari, Gelman, & Gabry, 2017). Finally, the calculation of shared space depended on an arbitrarily chosen buffer distance (i.e., 1000 meters in this study). A more thorough sensitivity check to evaluate the robustness of our modeling conclusions with variations in this buffer distance is warranted.
Several extensions are worth pursuing in future studies. From a substantive perspective, several other spatial measures can be derived from the GPS data to facilitate forecasts of alcohol use. For instance, with home and school addresses, individuals’ distances from homes and schools may help predict the extent and instances of alcohol use. In addition, spatial and other temporal (e.g., self-report ecological momentary assessments (EMAs)) data can be more strategically integrated with each other to help pinpoint the roles of some of the contextual factors considered in this study. For instance, in this study, time spent with twin siblings was defined as the proportion of instances where the twins’ hourly activity spaces overlapped with each other, but it was not directly validated whether the twin siblings were actually spending time together at particular time points. In this case, drawing information from other sources to pinpoint when and where exactly individuals were spending time with their family members can help increase the accuracy of the proposed forecasting approach. Incorporating additional sources of geospatial data to help distinguish urban from suburban areas, as well as other between-individual and between-neighborhood differences in alcohol use tendency may also help improve forecast accuracy.
From a methodological perspective, several modeling extensions are possible and may help enrich our investigation of adolescent alcohol use dynamics. First, one possibility is to incorporate missing data models into the current modeling framework to represent the missing mechanisms associated with alcohol use and covariates. Non-ignorable missingness (Little & Rubin, 1987) is a legitimate concern in the context of our empirical example because adolescents might actively avoid responding to the EMA survey when they were engaging in drinking-related activities. In these cases, missingness in the EMA might be meaningfully informed by other passive data sources, such as GPS data and related spatial measures. We did not pursue such missing data modeling possibilities in the present article, however, a more thorough examination of the robustness of our modeling results to variations in missing data assumptions and models is imperative in future studies. Second, it should be noted that in the present study, we blocked the data at the weekly level to yield equally spaced data, which allowed us to fit discrete-time models but inevitably generated a large proportion of missingness. However, the unequally spaced measurement occasions can be readily accounted for by fitting a continuous-time model (e.g., a first-order stochastic differential equation (SDE) model Arminger, 1986; Lu et al., 2019; Oravecz, Tuerlinckx, & Vandekerckhove, 2011) to the original data set. Parameters in continuous-time models are invariant to changes in the measurement interval and can be transformed to the corresponding discrete-time parameters according to the time interval (Kuiper & Ryan, 2018; Oud & Jansen, 2000; Voelkle, Oud, Davidov, & Schmidt, 2012).
Third, given the less satisfying forecasts of heavy drinking, we may consider three regimes — for instance, abstinence, light drinking, and heavy drinking — to explore under what circumstances one may be more likely to transition from abstinence to light/heavy drinking, and from light drinking to heavy drinking, and vice versa. The nonlinear associations (either regime-based or overall associations) between alcohol use and social contexts would also be an interesting future direction. Fourth, moving beyond a univariate framework, it is also possible to evaluate and forecast alcohol use by including reciprocal linkages between twin members via a bivariate RS-ZIMLP model. We did not pursue this option because of design-related discrepancies in the measurement windows of some twin pairs’ EMAs, which entailed excessive missingness in the data when a bivariate RS-ZIMLP was pursued in our model exploration phase. Another complication that needs to be resolved is the potentially large number of regimes that may have to be included in the bivariate model to accommodate the twin members’ possible asynchronous transitions into and out of the drinking regime. Fifth, a negative binomial regression model may be considered as an overdispersed alternative to the Poisson regression model to allow for greater variability in the data set. Finally, it would be interesting to compare zero-inflated models with other techniques that could be applied to work around the imbalance issue, such as extensions of resampling strategies (e.g., synthetic minority oversampling technique (SMOTE); Chawla, Bowyer, Hall, & Kegelmeyer, 2002) and cost-sensitive learning approaches (e.g., Elkan, 2001) for time series forecasting tasks (see, e.g., Cao, Li, Woon, & Ng, 2013; Geng & Luo, 2019; Moniz, Branco, & Torgo, 2017; Roychoudhury, Ghalwash, & Obradovic, 2017).
In conclusion, we presented, evaluated, and demonstrated a Bayesian approach for forecasting intensively measured adolescent alcohol use in the context of a novel Bayesian RS-ZIMLP model. Forecasting with ILD is very much an emerging area of research in social and behavioral sciences, complicated further by challenges to perform timely model formulation, estimation, inference, and parameter updates in a manner that is helpful for real-world prevention and intervention purposes. As a field, we are far from accomplishing such efficacious forecasts. Nevertheless, having useful models and approaches for performing and evaluating forecast results is a much needed first step toward achieving these long-term goals.
Acknowledgments
Funding for this study was provided by the NIH Intensive Longitudinal Health Behavior Cooperative Agreement Program under U24AA027684 and U01DA046413 (SV/NF), National Science Foundation grants BCS-1052736, IGE-1806874, and SES-1823633, the Eunice Kennedy Shriver National Institute of Child Health and Human Development under P2C HD041025, and the Pennsylvania State University Quantitative Social Sciences Initiative and UL TR000127 from the National Center for Advancing Translational Sciences. Part of the computations for this research were performed on the Pennsylvania State University’s Institute for Computational and Data Sciences’ Roar supercomputer.
Footnotes
Publisher's Disclaimer: This AM is a PDF file of the manuscript accepted for publication after peer review, when applicable, but does not reflect post-acceptance improvements, or any corrections. Use of this AM is subject to the publisher's embargo period and AM terms of use. Under no circumstances may this AM be shared or distributed under a Creative Commons or other form of open access license, nor may it be reformatted or enhanced, whether by the Author or third parties. See here for Springer Nature's terms of use for AM versions of subscription articles: https://www.springernature.com/gp/open-research/policies/accepted-manuscript-terms
Note that in this article, the “ZI regime” and “drinking regime” were used in the context of alcohol use to correspond to the ZI and Poisson process in the ZIP model, respectively.
One “drink” is equal to 1 can or bottle of beer, a glass of wine, or a shot of hard liquor.
It should be noted that these Euclidean distances were crude measures and did not measure the actual road distances that the participants had to travel (by walking or transportation) to the landmarks. Future research could consider road network-based distance measures.
References
- Arminger G (1986). Linear stochastic differential equation models for panel data with unobserved variables. Sociological Methodology, 16, 187–212. [Google Scholar]
- Berry LR, & West M (2020). Bayesian forecasting of many count-valued time series. Journal of Business & Economic Statistics, 38 (4), 872–887. [Google Scholar]
- Bradley AP (1997). The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognition, 30 (7), 1145–1159. [Google Scholar]
- Bronfenbrenner U (1992). Ecological systems theory. Jessica Kingsley Publishers. [Google Scholar]
- Byrnes HF, Miller BA, Morrison CN, Wiebe DJ, Remer LG, & Wiehe SE (2016). Brief report: Using global positioning system (GPS) enabled cell phones to examine adolescent travel patterns and time in proximity to alcohol outlets. Journal of Adolescence, 50, 65–68. [DOI] [PubMed] [Google Scholar]
- Byrnes HF, Miller BA, Morrison CN, Wiebe DJ, Woychik M, & Wiehe SE (2017). Association of environmental indicators with teen alcohol use and problem behavior: Teens’ observations vs. objectively-measured indicators. Health & Place, 43, 151–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao H, Li X-L, Woon DY-K, & Ng S-K (2013). Integrated oversampling for imbalanced time series classification. IEEE Transactions on Knowledge and Data Engineering, 25 (12), 2809–2822. [Google Scholar]
- Chawla NV, Bowyer KW, Hall LO, & Kegelmeyer WP (2002). SMOTE: synthetic minority over-sampling technique. Journal of Artificial Intelligence Research, 16, 321–357. [Google Scholar]
- Chow S-M (2019). Practical tools and guidelines for exploring and fitting linear and nonlinear dynamical systems models. Multivariate Behavioral Research, 54 (5), 690–718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chow S-M, Witkiewitz K, Grasman RPPP, & Maisto SA (2015). The cusp catastrophe model as cross-sectional and longitudinal mixture structural equation models. Psychological Methods, 20, 142–164. doi: 10.1037/a0038962 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chow S-M, & Zhang G (2013). Nonlinear regime-switching state-space (RSSS) models. Psychometrika: Application Reviews and Case Studies, 78 (4), 740–768. [DOI] [PubMed] [Google Scholar]
- Cudeck R, & Browne MW (1983). Cross-validation of covariance structures. Multivariate Behavior Research, 18, 147–167. [DOI] [PubMed] [Google Scholar]
- De Jong P (1988). A cross-validation filter for time series models. Biometrika, 75, 594–600. [Google Scholar]
- Elkan C (2001). The foundations of cost-sensitive learning. In International Joint Conference on Artificial Intelligence (Vol. 17, pp. 973–978). [Google Scholar]
- Ester M, Kriegel H-P, Sander J, Xu X, (1996). A density-based algorithm for discovering clusters in large spatial databases with noise. In Kdd (Vol. 96, pp. 226–231). [Google Scholar]
- Gelfand AE, Dey DK, & Chang H (1992). Model determination using predictive distributions with implementation via sampling-based methods. In Bayesian Statistics 4 (p. 147–159). Oxford University Press. [Google Scholar]
- Gelman A, Carlin JB, Stern HS, Dunson DB, Vehtari A, & Rubin DB (2013). Bayesian data analysis. CRC press. [Google Scholar]
- Geman S, & Geman D (1984). Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI-6(6), 721–741. [DOI] [PubMed] [Google Scholar]
- Geng Y, & Luo X (2019). Cost-sensitive convolutional neural networks for imbalanced time series classification. Intelligent Data Analysis, 23 (2), 357–370. [Google Scholar]
- Hahsler M, Piekenbrock M, & Doran D (2019). dbscan: Fast density-based clustering with R. Journal of Statistical Software, 25, 409–416. [Google Scholar]
- Hall DB (2000). Zero-inflated Poisson and binomial regression with random effects: a case study. Biometrics, 56 (4), 1030–1039. [DOI] [PubMed] [Google Scholar]
- Hamilton JD (1994). Time series analysis (Vol. 2). Princeton New Jersey. [Google Scholar]
- Hanley JA, & McNeil BJ (1982). The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology, 143 (1), 29–36. [DOI] [PubMed] [Google Scholar]
- Harvey AC (2001). Forecasting, structural time series models and the Kalman filter. Cambridge: Cambridge University Press. [Google Scholar]
- Helske J (2017). KFAS: Exponential family state space models in R. Journal of Statistical Software, 78 (10), 1–39. doi: 10.18637/jss.v078.i10 [DOI] [Google Scholar]
- Howard AL, Patrick ME, & Maggs JL (2015). College student affect and heavy drinking: Variable associations across days, semesters, and people. Psychology of Addictive Behaviors, 29 (2), 430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobson NC, Chow S-M, & Newman MG (2019). The differential time-varying effect model (DTVEM): Identifying optimal time lags in intensive longitudinal data. Behavioral Research Methods, 51 (1), 295–315. doi: 10.3758/s13428-018-1101-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- James P, Berrigan D, Hart JE, Hipp JA, Hoehner CM, Kerr J, … Laden F (2014). Effects of buffer size and shape on associations between the built environment and energy balance. Health & Place, 27, 162–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jane-Llopis E, & Matytsina I (2006). Mental health and alcohol, drugs and tobacco: a review of the comorbidity between mental disorders and the use of alcohol, tobacco and illicit drugs. Drug and Alcohol Review, 25 (6), 515–536. [DOI] [PubMed] [Google Scholar]
- Ji L, Chen M, Oravecz Z, Cummings EM, Lu Z-H, & Chow S-M (2020). A Bayesian vector autoregressive model with nonignorable missingness in dependent variables and covariates: Development, evaluation, and application to family processes. Structural Equation Modeling: A Multidisciplinary Journal, 27 (3), 442–467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim C-J, Nelson CR, (1999). State-space models with regime switching: classical and Gibbs-sampling approaches with applications. MIT Press Books, 1 . [Google Scholar]
- Kuiper RM, & Ryan O (2018). Drawing conclusions from cross-lagged relationships: Re-considering the role of the time-interval. Structural Equation Modeling: A Multidisciplinary Journal, 25 (5), 809–823. [Google Scholar]
- Kuppens P, Allen NB, & Sheeber LB (2010). Emotional inertia and psychological maladjustment. Psychological Science, 21 (7), 984–991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lambert D (1992). Zero-inflated poisson regression, with an application to defects in manufacturing. Technometrics, 34 (1), 1–14. [Google Scholar]
- Lee AH, Wang K, Scott JA, Yau KK, & McLachlan GJ (2006). Multi-level zero-inflated Poisson regression modelling of correlated count data with excess zeros. Statistical Methods in Medical Research, 15 (1), 47–61. [DOI] [PubMed] [Google Scholar]
- Li Y, Ji L, Oravecz Z, Brick TR, Hunter MD, & Chow S-M (2019). dynr.mi: An R program for multiple imputation in dynamic modeling. International Journal of Computer, Electrical, Automation, Control and Information Engineering, 13 (5), 302 – 311. Retrieved from http://waset.org/Publications?p=149 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Wood J, Ji L, Chow S-M, & Oravecz Z (2021). Fitting multilevel vector autoregressive models in Stan, JAGS, and Mplus. Structural Equation Modeling: A Multidisciplinary Journal, 1–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Litt MD, Cooney NL, & Morse P (1998). Ecological momentary assessment (EMA) with treated alcoholics: methodological problems and potential solutions. Health Psychology, 17 (1), 48. [DOI] [PubMed] [Google Scholar]
- Little RJA, & Rubin DB (1987). Statistical analysis with missing data. New York, N.Y.: Wiley. [Google Scholar]
- Lu Z-H, Chow S-M, Ram N, & Cole PM (2019). Zero-inflated regime-switching stochastic differential equation models for highly unbalanced multivariate, multi-subject time-series data. Psychometrika, 84 (2), 611–645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu Z-H, Chow S-M, Sherwood A, & Zhu H (2015). Bayesian analysis of ambulatory cardiovascular dynamics with application to irregularly spaced sparse data. Annals of Applied Statistics, 9, 1601–1620. doi: 10.1214/15-AOAS846 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lütkepohl H (2005). Introduction to multiple time series analysis (2nd ed.). New York, NY: Springer-Verlag. [Google Scholar]
- MacCallum RC, Roznowski M, Mar CM, & Reith JV (1994). Alternative strategies for cross-validation of covariance structure models. Multivariate Behavioral Research, 29 (1), 1–32. [DOI] [PubMed] [Google Scholar]
- Maisto SA, Xie FC, Witkiewitz K, Ewart CK, Connors GJ, Zhu H, … Chow S-M (2017). How chronic self-regulatory stress, poor anger regulation, and momentary affect undermine treatment for alcohol use disorder: Integrating social action theory and the dynamic model of relapse. Journal of Social and Clinical Psychology, 36, 238–263. doi: 10.1521/jscp.2017.36.3.238 [DOI] [Google Scholar]
- Min Y, & Agresti A (2005). Random effect models for repeated measures of zero-inflated count data. Statistical Modelling, 5 (1), 1–19. [Google Scholar]
- Moniz N, Branco P, & Torgo L (2017). Resampling strategies for imbalanced time series forecasting. International Journal of Data Science and Analytics, 3 (3), 161–181. [Google Scholar]
- Neal RM (2003). Slice sampling. Annals of Statistics, 31 (3), 705–741. [Google Scholar]
- Neelon BH, O’Malley AJ, & Normand S-LT (2010). A Bayesian model for repeated measures zero-inflated count data with application to outpatient psychiatric service use. Statistical Modelling, 10 (4), 421–439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oravecz Z, Tuerlinckx F, & Vandekerckhove J (2011). A hierarchical latent stochastic differential equation model for affective dynamics. Psychological Methods, 16 (4), 468. [DOI] [PubMed] [Google Scholar]
- Orrù G, Monaro M, Conversano C, Gemignani A, & Sartori G (2020). Machine learning in psychometrics and psychological research. Frontiers in Psychology, 10, 2970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oud JH, & Jansen RA (2000). Continuous time state space modeling of panel data by means of SEM. Psychometrika, 65 (2), 199–215. [Google Scholar]
- Pasch KE, Hearst MO, Nelson MC, Forsyth A, & Lytle LA (2009). Alcohol outlets and youth alcohol use: Exposure in suburban areas. Health & Place, 15 (2), 642–646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perchoux C, Chaix B, Brondeel R, & Kestens Y (2016). Residential buffer, perceived neighborhood, and individual activity space: New refinements in the definition of exposure areas–the RECORD Cohort Study. Health & Place, 40, 116–122. [DOI] [PubMed] [Google Scholar]
- Piironen J, & Vehtari A (2017). Comparison of Bayesian predictive methods for model selection. Statistics and Computing, 27 (3), 711–735. Retrieved from 10.1007/s11222-016-9649-y doi: 10.1007/s11222-016-9649-y [DOI] [Google Scholar]
- Plummer M, et al. (2003). JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling. In Proceedings of the 3rd International Workshop on Distributed Statistical Computing (Vol. 124, p. 1–10). [Google Scholar]
- Reboussin BA, Song E-Y, & Wolfson M (2011). The impact of alcohol outlet density on the geographic clustering of underage drinking behaviors within census tracts. Alcoholism: Clinical and Experimental Research, 35 (8), 1541–1549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roychoudhury S, Ghalwash M, & Obradovic Z (2017). Cost sensitive time-series classification. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases (pp. 495–511). [Google Scholar]
- Russell MA, Almeida DM, & Maggs JL (2017). Stressor-related drinking and future alcohol problems among university students. Psychology of Addictive Behaviors, 31 (6), 676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell MA, & Odgers CL (2020). Adolescents’ subjective social status predicts day-to-day mental health and future substance use. Journal of Research on Adolescence, 30, 532–544. [DOI] [PubMed] [Google Scholar]
- Sánchez-Sánchez PA, García-González JR, & Coronell LHP (2019). Encountered problems of time series with neural networks: Models and architectures. In Recent trends in artificial neural networks-from training to prediction. IntechOpen. [Google Scholar]
- Shen H (2010). Exponentially weighted methods for forecasting intraday time series with multiple seasonal cycles: Comments. International Journal of Forecasting, 26, 653–654. [Google Scholar]
- Substance Abuse and Mental Health Services Administration, Office of Applied Studies. (2008). Results from the 2007 National Survey on Drug Use and Health: National Findings (DHHS Publication No. SMA 08–4343, NSDUH Series H-34). Rockville, MD: Substance Abuse and Mental Health Services Administration. [Google Scholar]
- Vehtari A, Gelman A, & Gabry J (2017). Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Statistics and Computing, 27 (5), 1413–1432. [Google Scholar]
- Voelkle MC, Oud JH, Davidov E, & Schmidt P (2012). An SEM approach to continuous time modeling of panel data: relating authoritarianism and anomia. Psychological Methods, 17 (2), 176. [DOI] [PubMed] [Google Scholar]
- West M, & Harrison J (1997). Bayesian forecasting and dynamic models (2nd ed.). New York, NY: Springer-Verlag. [Google Scholar]
- Wilhelm FH, Grossman P, & Muller MI (2012). Bridging the gap between the laboratory and the real world: Integrative ambulatory psychophysiology. In Handbook of research methods for studying daily life (p. 210–234). New York, NY: Guilford. [Google Scholar]
- Wray TB, Merrill JE, & Monti PM (2014). Using ecological momentary assessment (EMA) to assess situation-level predictors of alcohol use and alcohol-related consequences. Alcohol Research: Current Reviews, 36 (1), 19. [PMC free article] [PubMed] [Google Scholar]
- Yarkoni T, & Westfall J (2017). Choosing prediction over explanation in psychology: Lessons from machine learning. Perspectives on Psychological Science, 12 (6), 1100–1122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yau KK, & Lee AH (2001). Zero-inflated Poisson regression with random effects to evaluate an occupational injury prevention programme. Statistics in Medicine, 20 (19), 2907–2920. [DOI] [PubMed] [Google Scholar]
- You D, Hunter M, Chen M, & Chow S-M (2019). A diagnostic procedure for detecting outliers in linear state-space models. Multivariate Behavioral Research, 1–25. Retrieved from 10.1080/00273171.2019.1627659 (PMID: 31264463) doi: 10.1080/00273171.2019.1627659 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou S, Li Y, Bodovski Y, Chi G, & Chow S-M (2021). GPS2space: An open-source Python library for spatial data building and spatial measure extraction. Retrieved from https://github.com/shuai-zhou/gps2space doi: 10.5281/zenodo.4672651 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou S, Li Y, Chi G, Yin J, Oravecz Z, Bodovski Y, … Chow S-M (2021). GPS2space: An open-source Python library for spatial measure extraction from GPS data. Journal of Behavioral Data Science. doi: 10.35566/jbds/v1n2/p5 [DOI] [PMC free article] [PubMed] [Google Scholar]



