Beyond Standard Pipeline and p < 0.05 in Pathway Enrichment Analyses

Abstract

A standard pathway/gene-set enrichment analysis, the over-representation analysis, is based on four values: the size of two gene-sets, size of their overlap, and size of the gene universe from which the gene-sets are chosen. The standard result of such an analysis is based on the p-value of a statistical test. We supplement this standard pipeline by six cautions: (1) any p-value threshold to distinguish enriched gene-sets from not-enriched ones is to certain degree arbitrary; (2) genes in a gene-set may be correlated, which potentially overcount the gene-set size; (3) any attempt to impose multiple testing correction will increase the false negative rate; (4) gene-sets in a gene-set database may be correlated, potentially overcount the factor for multiple testing correction; (5) the discrete nature of the data make it possible that a minimum change in counts may lead to a quantum change in the p-value threshold-based conclusion; (6) the two gene-sets may not be chosen from the universe of all human genes, but in fact from a subset of that universe, or even two different subsets of all genes. Careful reconsideration of these issues can have an impact on an enrichment analysis conclusion. Part of our cautions mirror the call from statistician that reaching conclusion from data is not a simple matter of p-value smaller than 0.05, but a thoughtful process with due diligences.

Introduction

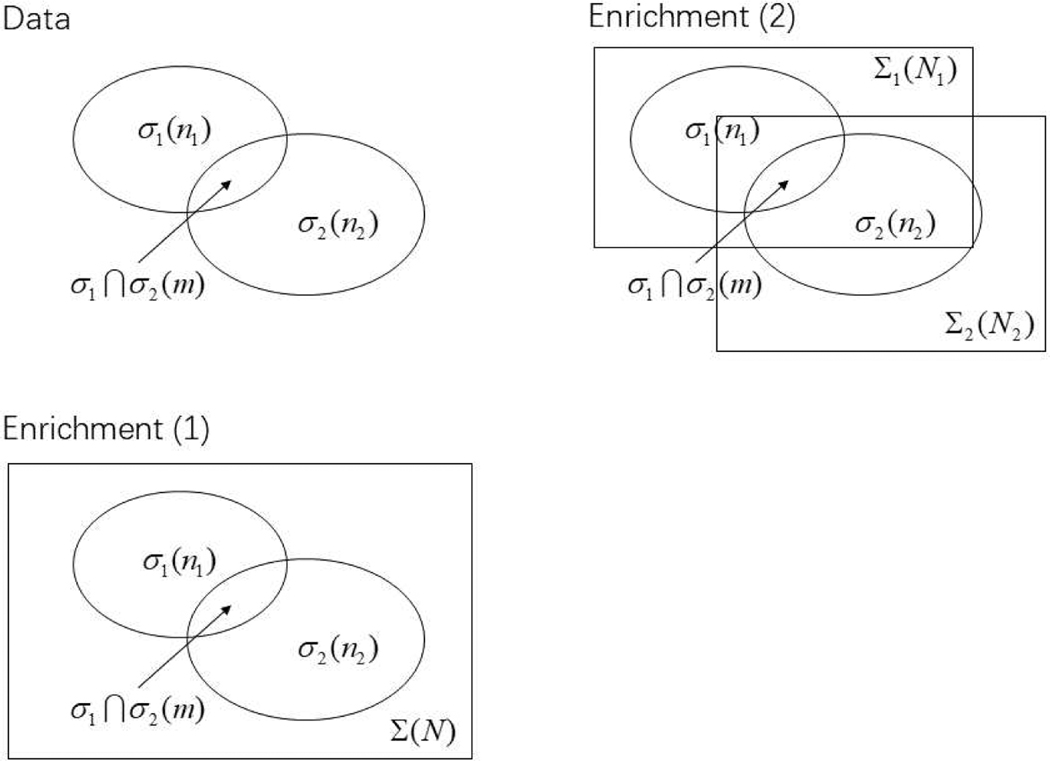
Bioinformatic enrichment analysis is essential in dealing omics data (Huang et al., 2009a; Mooney and Wilmot, 2015; Reimand et al., 2019; Maleki, 2019). The premise of the standard enrichment analysis is very simple, and can be summarized by the Venn diagram in Fig.1. First, the data as drawn at the top of Fig.1 includes a collection of genes σ₁ of interest to you (size is n₁), another collection of genes σ₂ which can be a pathway, those labeled with a specific gene ontology term, etc. (size is n₂), and an intersect σ₁ ∩ σ₂ for genes common in both sets (size is m genes). Both σ₁ and σ₂ can be conveniently called a gene set (Li et al., 2015). Secondly, as shown at the bottom of Fig.1, a space of all genes Σ is outlined. The question asked in one version of the enrichment analysis is: are the two gene-set genes overlap more than by chance?

Figure 1:

Illustration of the over-representation (enrichment) analysis, where only the set membership information is used. The first gene set is σ₁ with n₁ genes, and the second gene set is σ₂ has n₂ genes. The number of genes belonging to both gene-sets is m. The implied assumption is that all these genes are sampled from a gene pool/universe Σ with N genes (“enrichment(1)”). Another possibility is that the genes in σ₁ is sampled from Σ₁ with N₁ genes, whereas σ₂ is sampled from Σ₂ with N₂ genes (“enrichment(2)”).

This enrichment analysis is also called over-representation analysis in (Khatri et al., 2012) in the following sense. Suppose both σ₁ and σ₂ are randomly sampled from the universe of N genes. In this null model, if we partition the gene universe into σ₁ and non-σ₁ (can be called the complement ${\sigma }_1^c$), the σ₂ genes should appear in the two partitions with uniform probability. Similarly, if we partition the gene universe in σ₂ and ${\sigma }_2^c,{\sigma }_1$ genes appear in both with uniform probability in the null model.

When no more information besides the set membership is available (for example, genes in the gene set is not ranked in an order), the standard approach of enrichment analysis is to carry out a statistical test on a 2-by-2 count table with these four elements: m, n₁ −m, n₂ −m, N − n₁ − n₂ + m (Goeman and Bühlmann, 2007), essentially comparing the two probabilities m/n₁ and (n₂ −m)/(N −n₁). The test can be Fisher’s exact test (hypergeometric test) (Fury et al., 2006), chi-square test, binomial test, z test (on standardized m), etc. They are mostly equivalent with each other (Khatri et al., 2005;Rivals et al., 2007).

To list a few major bioinformatic enrichment analysis sites, we have, for example, DAVID (david.ncifcrf.gov), GeneMANIA (genemania.org), Ingenuity Pathway Analysis (www.qiagenbioinformatics.com/products/ingenuity-pathway-analysis/), GeneGo/Thomson Reuters/Clarivate’s MetaCore (portal.genego.com), Enrichr (http://amp.pharm.mssm.edu/Enrichr/), g:Profiler (http://biit.cs.ut.ee/gprofiler/), nextBio (https://www.nextbio.com/)), WebGestalt (http://www.webgestalt.org), etc.

Most enrichment analysis programs provide result by a p-value (the probability that we observe m or more overlapping genes under the null hypothesis that there is no enrichment), and a odds-ratio (m(n₂ − m)/[(n₁ − m)(N − n₁ − n₂ + m], which is roughly the ratio of the two probabilities of σ₂ elements within σ₁ and that outside). Users of such a program would be on their own to decide which enrichment results they believe to make biological sense, often guided by a statistical “gold standard” that the p-value should be smaller than 0.05 in a family-wise context (e.g., using Bonferroni correction or false-discovery rate (FDR), which can be represented by a q-value (Storey and Tibshirani, 2003)).

However, more and more statisticians realized that using only p-value (or q-value, for that matter), and using a single prefixed threshold value, to separate “worthwhile” results and those of “insignificance”, to distinguish publishable and unpublishable, leads to problems (Wasserstein and Lazar, 2016; Wasserstein et al., 2019). A phrase “beyond p < 0.05” is coined to advocate the practices of avoiding binary claim but accept uncertainty in an analysis and to be thoughtful on all aspects of the procedure. What does “beyond p < 0.05” mean to enrichment analysis and specifically to the over-representation analysis? Although one may consider it as a negative step as it takes away a statistical guidance from the users, we actually treat it positively, as we take advice from the mainstream statisticians to be less robotic and to be more thoughtful in running this enrichment analysis.

One might ask why can’t we just plug in the count numbers n₁, n₂,m, N and getting a test result automatically from an over-representation analysis? Here we list six reasons (some old and some new) to caution on an autopilot mode during the over-representation analysis:

1. To echo the call from the field of statistics, any threshold for p-value, be it 0.05, 0.01, 0.005 without multiple testing correction, 0.01 after multiple testing correction, or alternatively, any threshold for q-value, be it 0.05, 0.01, etc. is to certain degree arbitrary. These threshold values are historically set for convenience only, or reflect specific cost on making false positive claims.

2. The assumption of independence of genes in the reference gene-set may be violated. Two or more genes may tend to co-appear in many gene-sets more frequently than by chance. This will cause count values to be inflated (i.e., the true number of independent genes is less than the apparent count number).

3. Any attempt to control the false positive rate by imposing multiple testing correction will automatically reduce the statistical power (lowering the sensitivity, increasing the false negative rate, missing more true signal calls). In other words, the more we might be confident of the involvement of some pathway in a disease through enrichment analysis, the less likely we will find other truly involved pathways. There is always a false-positives and false-negatives trade-off, and an implied cost values for two types of error.

4. Different gene-sets/pathways in a gene-set database may not be independent, which may inflate the number of gene-sets (that value is used in multiple testing). If one does not intend to impose multiple testing, this point is less relevant.

5. Theoretically, the p-value is supposed to be a continuous function of the data. However, the count data in an over-representation analysis is discrete. A consequence of the discrete nature of the data is that even if there is a minimal change in the count (as small as ± 1), one may move across the p-value threshold line, changing to an opposite conclusion. It is a problem in particular when the n₁, n₂, m values are small. Another way to describe the situation is that over-representation analysis may not be robust.

6. One of the assumptions in over-representation analysis of omics data is that N is the total number of (human) genes, because our gene-set is either obtained from a genomic study and pathway genes are selected from the pool of all genes. We also assume that the two gene-sets are sampled from the same gene universe. In reality, both assumptions may not be true. For example, a pathway may only have a chance to randomly sample genes that are exclusively expressed in embryo development, but not expressed in adult cells; or genes in a pathway should only be limited those expressed in brain, but not in other tissues; etc. We may need to change the assumption to that σ₁ genes are sampled from N₁ ≤ N genes, and σ₂ genes sampled from N₂ ≤ N genes (see Fig.1). The p-value calculation is then changed also (Swaminathan and Fury, 2012).

An example of genes genetically associated with Alzheimer’s disease

To illustrate an over-representation analysis, we look at genes that are genetically associated with the Alzheimer’s disease (AD). We do not claim general representation of this particular dataset, only that it happened to be a gene list we worked on. Based on the compilation in (Freudenberg-Hua et al., 2018) through literature search, combined with two new large scale studies in 2019 (Jansen et al, 2019; Kunkle et al, 2019), we compile a list of 61 AD genes. This n₁ = 61 AD gene list includes both late-onset AD (LOAD) genes and autosomal dominant AD (ADAD) genes (which are often referred to as early-onset AD (EOAD) genes, but the term may not be precise without an exact early/late definition). LOAD genes are obtained through genome-wide association studies (GWAS), as well as from candidate gene studies. EOAD genes are obtained from family studies. In the case of GWAS, a genetic association signal may appear between two genes in an intergenic region. We mostly follow the choice in other publications to pick one gene out of the two, except for one locus where both genes are kept.

We produce three more AD gene lists: “n₁ = 58 list” is the n₁ = 61 list subtracting the three ADAD genes (APP, PSEN1, PSEN2); “n₁ = 48” list is the n₁ = 61 list subtracting all genes where the associated allele is rare than 0.01 (including the above mentioned ADAD genes: APP, PSEN1, and PSEN2); “n = 47 list” is n₁ = 61 list subtracting all genes where the associated effect size is weak: odds-ratio (OR) being between 0.9 and 1.1. Since rare alleles tend to have strong ORs, the last list keeps all rare variants (genes) but throws away some common variants.

While σ₁ is one of our four AD gene lists, σ₂ is any one of the gene-sets in the MSigDB database (software.broadinstitute.org/gsea/msigdb/) which includes some well established pathways manually curated by other databases, and gene-ontology categories. Table 1 shows all σ₂ in MSigDB where the Fisher’s test p-value is significant at 0.05 level under Bonferroni multiple testing correction (i.e., p-value smaller than 0.05/N_gs for MSigDB where N_gs is the number of gene-sets within a MSigDB major collection). For example, for the H gene-set collection which contains some well defined and well studied “hallmark” biological processes, N_gs = 50; whereas for C5 gene-set collection which groups genes by gene ontology annotations, N_gs = 5917. We also calculate the q-value (Storey and Tibshirani, 2003), another family-wise significance measure based on FDR. We list also those σ₂’s where q-value < 0.05 but p-value > 0.05/N_gs, except for C5 (which is listed in the supplement material).

Table 1:

Enrichment results of Alzheimer’s disease (AD) genes using MSigDB gene-sets. The initial AD gene list consists of 61 genes, and those gene-sets with Fisher’s test p-value smaller than 0.05/N_gs, where N_gs is the number of gene-sets within each major collections (h,c2,··· c7), are marked with “Y” under n₁ = 61 column. Those with q-value smaller than 0.05 are marked by Y^q. “pv(corr)” is Bonferonni-corrected p-value which is Fisher’s p-value multiplied by N_gs.“qv” is the q-value. “overlap” is defined as $m/\sqrt{n_1{n}_2}$ which measure the proportion of overlapping genes in the geometric mean of the two gene lists. Three other AD gene lists are used for the same enrichment analysis: n₁ = 58 removes the three autosomal dominant AD (ADAD) genes (APP, PSEN1, PSEN2); n₁ = 48 removes all genes where the associated variant allele is rare (minor allele frequency < 0.01); n₁ = 47 removes all genes where the odds-ratio (OR) of the associated variant is known to be within (0.9, 1.1). A gene-set is marked as “Y*” if p-value is smaller than 0.05/N_allgs where N_allgs = 17484 is the total number of gene-sets in MSigDB. Due to space limitation, gene-sets in gone-ontology collection (c5) are not listed if 0.01 < q-value < 0.05 and p-vale > 0.05/N_gs: 75 for n₁ = 61 AD gene list; 3 for n₁ = 58 list; 17 for n₁ = 48 list; and 39 for n₁ = 47 list.

gene-set	n 1	n 2	m	pv	pv(corr)	qv	overlap	change n1
								61	58	48	47
H: hallmark (Ngs=50)
myogenesis	61	200	7	4.9e-6	2.4e-4	2.4e-4	6.3 %	Y	Y	Y	Y
apoptosis	47	161	4	8.1e-4	4.1e-2		4.6 %				Y
C2: known & curated (Ngs=4762), incl. REACTOME
signaling by NOTCH2/3/4	61	12	4	5.8e-8	2.7e-4	9.1e-5	14.8 %	Y*			Y
nuclear signaling by ERBB4	61	38	5	1.7e-7	8.2e-4	2.1e-4	10.4 %	Y*			Y*
activated NOTCH1 transmits sig. nucleus	61	26	4	1.7e-6	8.0e-3	1.6e-3	10.0 %	Y*			Yq
regulated proteolysis of P75NTR	61	10	3	4.3e-6	2.1e-2	3.5e-3	12.1 %	Y			Y*
signaling by ERBB4	61	87	5	1.1e-5	0.053	6.6e-3	6.9 %	Yq			Y*
nrif signals cell death from the nucleus	61	14	3	1.3e-5	0.062	7.8e-3	10.0 %	Yq			Y
signaling by NOTCH 1	61	68	4	8.2e-5	0.39	0.04	6.2 %	Yq			Y
metastasis down	47	149	5	4.2e-5	0.2	0.025	6%				Yq
C3: motif based (Ngs =836)
STAT6_02	61	251	7	2.1e-5	1.8e-2	0.02	5.7%	Y	Y	Y
C5: gene ontology (GO) (Ngs=5917)
reg. amyloid precursor prot. catabolic proc.	61	11	5	2e-10	1.0e-6	1.0e-6	19.3 %	Y*	Y*	Y*	Y*
membrane protein proteolysis	61	35	5	1.1e-7	6.7e-4	3.3e-4	10.8 %	Y*		Yq	Yq
NOTCH receptor processing	61	16	4	2.1e-7	1.2e-3	4.1e-4	12.8 %	Y*			Yq
cell surface	61	726	13	7.2e-7	4.3e-3	9.8e-4	6.2 %	Y*	Yq	Yq	Y
membrane protein ectodomain proteolysis	61	22	4	8.3e-7	4.9e-3	9.8e-4	10.9 %	Y*
positive reg. cell death	61	602	11	4.8e-6	2.9e-2	4.8e-3	5.7%	Y		Yq	Yq
protein lipid complex	61	40	4	9.9e-6	0.059	8.4e-3	8.1 %	Yq	Y	Y	Y*
beta amyloid metabolic process	61	14	3	1.3e-5	0.077	8.7e-3	10.3 %	Yq			Y
humoral immune response	61	157	6	1.5e-5	0.088	8.7e-3	6.1 %	Yq			Yq
reg. cell death	61	1458	16	1.9e-5	0.11	8.7e-3	5.4%	Yq			Yq
reg. incl. body assembly	61	16	3	2e-5	0.12	8.7e-3	9.6%	Yq	Yq	Yq	Yq
reg. neuron death	61	249	7	2e-5	0.12	8.7e-3	5.7%	Yq		Yq	Yq
cell leading edge	61	345	8	2e-5	0.12	8.7e-3	5.5 %	Yq			Y*
reg. cell, amide metabolic proc.	61	346	8	2.1e-5	0.12	8.7e-3	5.5%	Yq		Yq	Yq
membrane protein intra-domain proteolysis	61	17	3	2.4e-5	0.14	9.6e-3	9.3 %	Yq
positive reg. catalytic act.	61	1495	16	2.6e-5	0.15	9.6e-3	5.3%	Yq			Yq
C7: immunologic expression signature (Ngs = 4872)
CD8 αα vs αβ CD161 high tcell up	61	193	8	2.7e-7	1.3e-3	7.7e-4	7.4 %	Y*	Y*	Yq
early thymic progenitor vs dn3 thymoc. up	61	197	8	3.2e-7	1.5e-3	7.7e-4	7.3 %	Y*	Y	Y*
lps vs heatshock and lps stim mef up	61	194	7	4.0e-6	2.0e-2	6.5e-3	6.4 %	Y	Y*	Yq
ID3 K0 vs WT CD8 t-cell down	58	196	6	3.9e-5	0.19	0.038	5.6%		Yq
untreated vs IL2-treated t-cell up	58	192	6	3.4e-5	0.17	0.038	5.7%		Yq

When we change the σ₁ gene-set from the n₁ = 61 list to the other three shorter AD-gene lists, the “0.05-level-family-wise-significant” σ₂’s may be different. If there are new σ₂ gene-sets which are significant at the same level, these are added to Table 1. On the other hand, if a σ₂ remains significant at the same level in one of the three shorter lists, it is label as a Y letter. Another more extreme version of Bonferroni correction is to require p-value less than 0.05/N_allgs where N_allgs=17484 is the total number of gene-sets in MSigDB. If a σ₂ is significant at this definition, it is marked by Y*.

There are several observations from Table 1. The first is that, counterintuitively, even when n₁, n₂, m might be small (e.g. m can be as small as 3), the Fisher’s test p-value can still manage to reach a family-wise significance. The “secret” is that another number, the total number of human genes (N), enters the data used in the test. N is large (N ∼ 20000 and for MSigDB, N =18028), but ironically, it is not part of the observational data in a particular study. Our intuition that small count tables cannot lead to a very significant test result would have been correct if N were not large. This will lead us to question the use of N, as addressed in the point-#6.

Another related observation is that if we look at the number of genes shared in common between σ₁ (AD gene list) and σ₂ (a gene set in MSigDB) (m), as a percentage of some average of the two list sizes (we use the geometric mean of the two list size: $\sqrt{n_1{n}_2}$), the shared proportion is only between 5.7% – 14.8% (with the exception of “regulation of amyloid precursor protein catabolic process” gene-ontology (GO) gene-set, which has a proportion of 19.3%). Would one consider a proportion of 10% overlapping genes between two gene-sets to be a large proportion?

Thirdly, by using AD gene list with various sizes, we highlight the issue that both σ₁ and σ₂ lists to be compared for common elements can be tentative, incomplete, with false positive, misses. The question is whether these minor changes may have an impact on the enrichment result. Indeed, by even removing just three genes from n₁ = 61 to n₁ = 58, many family-wise significant gene-sets are no longer significant (see Table 1). This is our issue No.5.

We will not go deep into pathway enrichment for data from GWAS because there is a nontrivial hierarchical structure of data: signal is observed at the unit of single nucleotide bases, while unit of pathway is genes. The enrichment runs in Table 1 are all carried out at the gene unit level. Even without the multi-level complication, our AD gene list can be used to illustrate the six points mentioned early, to be discussed in the next four sections.

Any threshold on test p-value (or q-value) can not be universally justified (points #1 and #3)

One of the main “beyond p < 0.05” point from statisticians is that any p-value threshold in making decision is in some sense arbitrary (Wasserstein and Lazar, 2016; Wasserstein et al., 2019), at least cannot be argued to be fixed in all circumstances. In our n₁ = 61 AD genes list, using single-test p-value thresholds of 0.05, 0.01, 0.005 (Benjamin and Berger, 2019; Johnson, 2019), 0.001 (Colquhoun, 2017) lead to 1428, 543, 417, and 151 gene-sets. This argument on the arbitrariness applies equally to multiple-testing-corrected threshold. Family-wise Bonferroni corrected p-value of 0.05 (0.01) and q-value threshold of 0.05 (0.01) lead to 17 (13) and 105 (28) gene-sets. It seems that result with individual-test p-value threshold of 0.001 is similar to those using family-wise thresholds.

One commonly practiced “go beyond p-value or q-value < 0.05” approach is to use the candidate gene-sets which are known to be associated with the AD in other studies, then check their respective p- or q-values. For example, using rare allele burden, we found AD is linked to innate immune system genes (Freudenberg-Hua et al., 2016). In MSigDB gene-sets, the (REACTOME) INNATE_IMMUNE_SYSTEM and GO_INNATE_IMMUNE_RESPONSE gene sets have single-test p-value of 0.013 (empirical p-value by simulation to be 0.009 and proportion of overlap is $m/\sqrt{n_1{n}_2}=4/\sqrt{61\cdot 268}=3.1\text{\%}$) and 0.015 (empirical p-value also close to 0.009 and $6/\sqrt{61\cdot 594}=3.2\text{\%}$ overlap). Interestingly, there are 13 gene-ontology gene-sets with q-value smaller than 0.05 (p-value in the range of 10⁻⁵ ∼ 10⁻⁴, overlapping in 0.4 ∼ 0.6 range). This points to a stronger evidence associating AD with immune system in general and adaptive immune system. With our AD gene list, the innate immune system connection may or may not be claimed, depending on our choice of threshold.

The difference between using single-test p-value threshold and family-wise q-value threshold raises another question on the balance of two different errors (type-I/false-positive and type-II/false-negative). Tightening the threshold by using a small p-value threshold will reduce the false positives (simply because less number of gene-sets will pass the threshold). But on the other hand, it makes it more difficult to find a pathway truly linked to AD. It is easy to show that reducing one type of error leads to an increase of another type of error. Statistical power is rarely considered in data analysis stage because, as a property of the model (e.g., with an assumed odds-ratio value), it cannot be calculated from the real data. If missing a true signal is of concern, one should think about the consequence of using multiple testing correction.

Violation of independence assumption (points #2 and #4)

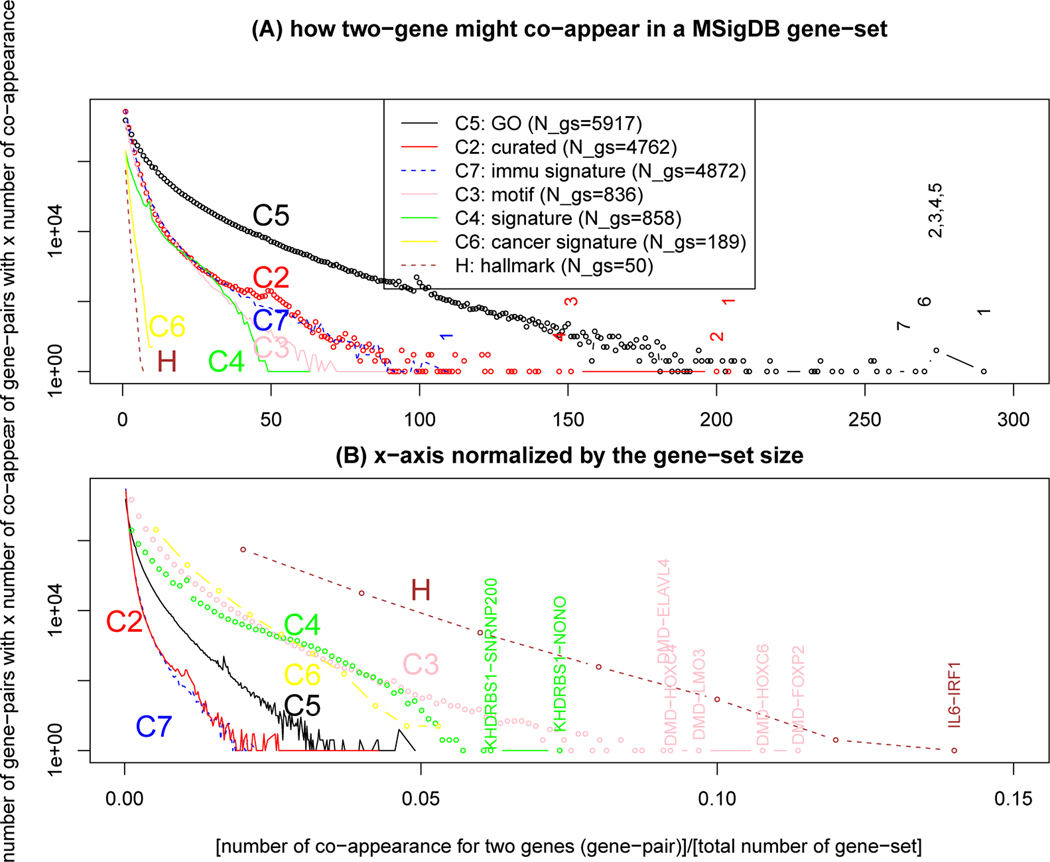
In the Fisher’s test, n₁, n₂, m are all assumed to be counts of independent genes. If some genes are not independent, these counts may not be correct. Intuitively, we may think that genes that produce proteins to be part of a protein complex are positively correlated. Fig.2 shows the distribution of co-appearance of a pair of genes for 7 major collections of gene-sets in MSigDB. The C5 (Gene Ontology) collection in particular is full of gene-pairs that co-appear in many gene-sets such “gene propagation” is also observed in (Bauer, 2017)), with the maximum of 290 times for RPS27A and UBA52. The UBA52 (or UBA80) gene codes a ubiquitin protein which is often fused with the ribosomal protein coded by RPS27A (or RPL40) (Han et al., 2012), which explains why there is a correlation between the two genes. To deal with the potentially correlated genes, a simple step is to check all genes in σ₁ among the most correlated gene pairs in gene-set database. In our case, AD genes do not appear in the highly correlated gene pairs, so the effect of gene-gene co-appearance on our enrichment result is expected to be small.

Figure 2:

Distribution of co-appearance of two-genes (a gene-pair). (A) The x axis is the number of times a gene-pair co-appear in gene-sets within a major collection of MSigDB (H, C2-C7); the y-axis is how many gene-pairs with this number of co-appearance. Some gene-sets with the highest number of co-appearence within a given collection are marked: C5 (black): 1. RPS27A-UBA52, 2.CALM2-CALM3, 3. CALM1-CALM3, 4. BMP4-CTNNB1, 5. CALM1-CALM2, 6. BMP4-TGFB1, 7.IL1B-TNF; C2 (red): 1.PIK3CA-PIK3R1, 2.MAPK1-MAPK3, 3. MAP2K1-MAPK3, 4.GRB2-SOS1; C7 (blue): 1. IFIT2-IFIT3. (B) The x axis is normalized by the total number of gene-sets in a MSigDB collection. These gene-sets are highlighted with the highest normalized number of co-appearence: H (brown): IL6-IRF1, C3 (pink): DMD-FOXP2, DMD-HOXC6, DMD-LMO3, DMD-HOXC4, DMD-ELAVL4; C4 (green): KHDRBS1-NONO, KHDRBS1-SNRNP200.

There is another type of correlation which is between two gene-sets (Simillion et al., 2017; Maleki and Kusalik, 2019). This correlation can be measured by a self-enrichment analysis, i.e., enrichment of genes in one gene-set in the second gene-set. If we use our previous defined measure of overlap between two lists $\alpha \equiv m/\sqrt{n_1{n}_2}$ there are 185 gene-set pairs that have α ≥ 0.9 for the Gene Ontology (C5) collection. Note that our use of geometric mean $\sqrt{n_1{n}_2}$ instead of arithmetic mean in Sørensen-Dice coefficient 2m/(n₁ + n₂) may alleviate an imbalanced situation when one list is much larger than the other; similar argument also applies to the Jaccard similarity index m/(n₁ + n₂ − m). The top ten pairs are: leukocyte_activation vs lymphocyte_act., positive_regulation_of_nuclear_division vs pos. reg. mitotic_nucl_div., chromosome_segregation vs nuclear chro. seg., sodium_independent_organic_anion transport vs sod.ind. org. ani. transmembranetransp. activity, dnatemplatedtranscriptionelongation vs transc._elong._from_rna_polymerase_ii_promoter, regulation_of_lyase_activity vs reg._adenylate_cyclase_act., phospholipid_metabolic_process vs glycerophospholipid_metabolic_proc., body_morphogenesis vs head_morphog., regulation_of_phospholipase_activity vs positive_reg._phosph._act., amino_acid_activation vs ligase_act._forming_carbon_oxygen_bonds (where the first gene-set is always larger than the second, and the number of overlapping genes m is equal to the size of the shorter list, with the exception of one pair).

A consequence of correlation between gene-sets (point #4) is that the multiple testing correction on single-test p-value to obtain the family-wise p-value is overdone. Adjustment of the number of correlated tests has been discussed in (e.g) (Leek and Storey, 2008; Stevens et al., 2017; Carvajal-Rodríguez, 2017), and in the special application of multiple testing correction in GWAS has been addressed in (Galwey, 2009; Derringer, 2018). Another solution is to clean the gene-set database to combine or reorganize correlated gene-sets (Vivar et al., 2013; Stoney et al., 2018).

Whether it’s correlation between genes or between gene-sets, a generic approach to find out the “effective number of units” can be similar to the approach of dimension reduction by principal component analysis (PCA). A correlation matrix between the units can be constructed, and the eigenvalues of the matrix can be determined and ranked. We can determine how many dimensions are needed to explain a fixed (e.g. 90) percentage of the variance. That dimension is the effective number of dimension.

For example, using the similarity matrix $s_{ij}=m_{ij}/\sqrt{n_i{n}_j}(i\ne j)$, and s_ij = 1(i = j) between 50 gene-sets in H/MSigDB, 95% of variance explained with 47 gene-sets (or 0.94 of the total 50 gene-sets). The 0.94 is very close to 0.95, indicating the reduction of effective number of gene-sets is small. For C2/MSigDB (curated gene-sets), on the other hand, 3909 (or 0.821 of the total 4762 gene-sets) is enough to explain 95% of the variance. Finally, for C5/MSigDB (Gene Ontology based gene-sets), 4277 (or 0.723 of the total 5917 gene-sets) is enough to explain 95% of the variance, both indicating a reduction of the effective number of gene-sets. For genes within H/MSigDB, it can also be shown that there is almost no reduction of the effective number of genes. Similar concept when the unit is individual sample has been discussed in (e.g.) (Kang et al., 2010; Yang et al., 2011; Lenth, 2012; Berger et al., 2013).

Discrete nature of count data and robustness of enrichment test (point #5)

The p-value as a function of the count data p = f(n₁, n₂, m|N) (total number of genes N is a given number and is not part of the observed data), is a function on a discrete space. Even a minimal possible change of the data, i.e., n₁ → n₁ ± 1 or n₂ → n₂ ± 1 or m → m ± 1 could move the test result across the threshold of significance at a specific level. We have already argued that any given threshold for p-value can be re-adjusted, our new point is that even if that threshold is fixed, a test result may not be robust against small changes in the data due to the nature of the data, A similar discussion can be found in (Schmid et al., 2016).

Using our AD gene list for example: there are many reasons that we may not be sure that our collection of AD genes is complete or most appropriate. GWAS mainly detects common variants instead of rare variants (Li et al., 2014), even though the latter tend to have a stronger effect on phenotype. GWAS or even exome sequencing in a population design is unlikely to detect causing genes if there is a genetic heterogeneity. When our AD gene list n₁ = 61 is reduced by 3 genes (APP, PSEN1, and PSEN2), the number of gene-sets in MSigDB with q-value < 0.05 is reduced from 105 to 14. Similarly, the number of q < 0.05 gene-sets for common-variant AD gene list n₁ = 48 is 30, and that for the stronger-signal AD gene list n₁ = 47 is 64, both very different from 105.

Even when n₁ and n₂ are fixed, there could still be mistakes in m caused by various factors, such as one of the gene name was mistaken for another, two genes that do not have the same name but may have the same biological effect, etc. Fig.3 shows the −log₁₀(p-value) for n₁ = 61 and actual n₂’s for gene-sets in MSigDB C5 collection (marked by numbers for the values of m) as well as simulated n₂’s (dashed lines). We might call the discrete stripes in Fig.3 “m-lines”,

Figure 3:

The discrete nature of “m-lines”. Enrichment test p-values (minus log with base 10) of 61 Alzheimer’s disease genes in all MSigDB C5 (Gene Ontology) gene-sets, as a function of gene-set size (n₂). Each point represents a gene-set in C5. The number on a point indicates the number of overlapping genes (m) between AD gene list and that gene-set. The family-wise p-value thresholds based on 0.01, 0.05, 0.2 (after Bonferroni correction using the number of gene-sets in C5 only) are shown at horizontal lines. The effect of m → m − 1 for the best results (in Table 1) is marked by the arrows.

Fig.3 illustrates what would happen to the six Bonferroni-correction-wise significant C5 gene-sets listed in Table 1 if m → m − 1 (but n₁ and n₂ remain the same), by the downward arrows. Three of them would cross the pre-set significance threshold and the evidence for their enrichment is not robust against one less m value. The effect is more severe when m is small. This provides some justification for filtering enrichment test results by requiring a relatively larger value for m, besides the p-value. On the other hand, the situation of small m might be of biological interest because it points to a more narrowed list of candidate genes. But to prove the link between the two gene-sets in this situation is harder by statistics alone.

A recent paper shows that equivalent pathways from different databases may lead to very different over-representation enrichment results (Mubeen et al., 2019). As worrisome as this result may be, it corroborates our point that enrichment analysis may not be robust with respect to minor changes in the gene-sets, either the first or the second one.

Do we really sample genes from the pool of all genes? (point #6)

Let’s first examine the important of N, the number of all genes from which we pick genes σ₁ and σ₂. The count table to contrast the proportion of σ₂ genes in two conditions can be approximated as (columns 1, 2 for the number of σ₂ genes and non-σ₂ genes, and rows 1,2 for be within σ₁ and outside), if m ≪ n₁,n₂ ≪ N):

$$\left(\begin{array}{cc}m& n_1-m\\ n_2-m& N-n_1-n_2+m\end{array}\right)\approx \left(\begin{array}{cc}m& n_1\\ n_2& N\end{array}\right).$$ (1)

The χ² test statistic of Eq.(1) is approximately (see, e.g., (Suh and Li, 2007)):

$$X^2=N\frac{{\left(m\left(N-n_1-n_2+m\right)-\left(n_1-m\right)\left(n_2-m\right)\right)}^2}{n_1{n}_2\left(N-n_1\right)\left(N-n_2\right)}\approx N\frac{n_1{\left(\frac{m}{n_1}-\frac{n_2}{N}\right)}^2}{n_2}\approx N\frac{n_2{\left(\frac{m}{n_2}-\frac{n_1}{N}\right)}^2}{n_1}.$$ (2)

When n₁, n₂, m are fixed, increasing N will increase the χ² statistics in two ways: one is to make (e.g.) σ₂ a more rare set, thus the difference between two proportions within the bracket is larger; another is to linear increase the statistics. Clearly, increasing N will make p-value smaller.

If N is so important for the enrichment test result, whereas it is not part of the count data, why should we trust the N value given to us? It is not that we do not think the total number of human genes to be around 20000 (Li, 2011); we question the assumption that in construct a gene set, whether all human genes have a chance to be sampled under the null model. Our questioning is not unreasonable, as the same point was also made in, e.g., (Tilford and Siemers, 2009; Tipney and Hunter, 2010). For example, some human genes are only expressed in early embryo development, and these would not have a role in housekeeping cell functions, thus not considered in a housekeeping gene-set. If we consider AD a brain disease, only genes expressed in brain should be a potential candidate, whereas those not expressed genes are not.

An analysis of Allen Brain Atlas (www.brain-map.org) a brain expression database, shows that 84% of human genes are expressed in at least one of the brain regions (Negi and Guda, 2017). If we require that a AD gene has to be expressed in brain, the size of the gene pool is no longer N=20000, but N = 20000 × 0.84 ≈ 16000. The Human Protein Atlas (www.proteinatlas.org) (Uhlén et al., 2015) lists 13000 ∼ 14000 proteins expressed in various regions of human brain. If in the future, certain brain regions can be shown to be unrelated to AD etiology, the gene pool size where σ₁ and σ₂ are sampled from can be further reduced. All these will result in a lower N value to be used in evaluating enrichment.

Fig.4 shows how enrichment results (single-Fisher’s-test p-value) would alter if both gene sets are sampled from only a percentage of the N=18028 genes. We only use those gene-sets that are significant at 0.05 level for n₁ = 61 set after Bonferroni correction. At the percentage around 80% (x-axis), which is roughly the proportion for brain-expressed genes among all human genes, some previously family-wise significant (at 0.05 level) gene-sets may not be significant at the same level anymore.

Figure 4:

The potential impact of reduced size of gene pool/universe N. The x-axis is the hypothesized proportion of all human genes (a total N = 18028 protein-coding genes is listed in MSigDB) used in the Fisher’s test; y-axis is the potential change of results in Table 1 with that proportion.

The issue on the size of gene universe can also be addressed for σ₁ and σ₂ gene-sets separately. If under the null model, σ₁ genes are sampled from a gene universe with N₁ genes, and σ₂ genes are sampled from a different gene universe with N₂ genes (see Fig.1), it can be shown that the p-value in this two-gene-universe situation is (Swaminathan and Fury, 2012):

$$p=\sum _{j=m}^{\min \left(n_1,n_2\right)}\frac{C\left(M,j\right)}{C\left(N_1,n_1\right)C\left(N_2,n_2\right)}\sum _{i=0}^{\min \left(n_1-j,M-j\right)}C\left(M-j,i\right)C\left(N_1-M,n_1-j-i\right)C\left(N_2-j-i,n_2-j\right)$$ (3)

where M is the size of intersect between the two gene universes/pools, C(N,n) ≡ N!/(n!(N − n)!) (n ≤ N) is the number of choices of choosing n objects from a pool of N objects.

The effect of N₁, N₂, M on two-gene-univse enrichment p-value is more complicated. In Fig.5, the −log₁₀(p-value) is colored coded as a function of N₁ (x-axis), N₂ (y-axis) and M (size of a circle). Generally speaking, reducing N₁ and N₂ will make the test result less significant (as in Fig.4). A new information from the two-gene-universe formula is that the smaller the overlap M between N₁ and N₂, the more significant the test. Interestingly, when Σ₂ is completely within Σ₁ so that N₂ = M, the test p-value is completely determined by N₁.

Figure 5:

Enrichment p-value obtained from Eq.(3) for two-gene-universe situation. The rainbow color marks the −log₁₀(p-value) with the most significant ones labeled as red squares. The x-axis (y-axis) is N₁ (N₂, and size of the circle is proportional to M, all randomly sampled. The n₁ = 30, n₂ = 90, m = 3 are fixed for illustration purpose only.

Summaries and possible recommendations

Let us go through the six points beyond the standard pipeline again:

1. Choices of p-value or q-value threshold: Nobody says that you must use the threshold of 0.05, or 0.01, or any other given value. If we want to be more confidence on association call to a pathway, we use a more stringent threshold value (e.g. 0.005 or 0.001). If we are more interested in discovering previously unknown relevance of some pathways, a more relaxed threshold can be used. Besides p-value, it could be a good idea to examine the $m/\sqrt{n_1{n}_2}$ value, which is a measure of the level of overlapping.

2. Non-independence of genes: Remember that your n₁, n₂, N, and even m might be actually smaller if there is a positive correlation (i.e., a tendency for co-appearance of two genes in gene-sets). In reality, this is perhaps less a problem, and one can introduce weights or discount factors to reduce the artifact.

3. Carrying out a multiple testing correction or not: See # 1.

4. Non-independence of gene-sets: See # 2 and # 3. Again it might not be a major issue (perhaps with an exception to the Gene Ontology based gene-set collection such as C5/MSigDB). Generic solutions exist such as the eigenvalue of the correlation matrix, if it is a concern of yours.

5. Robustness against small changes in the counts: It might be worth checking how a small adjustment of n₁, n₂, or m might change the p-value, in particular when m is small.

6. Re-thinking about the total number of genes: Because N is such an important factor causing many pathway enrichment analysis to be significant, we should re-examine the assumption that all genes have a chance to be selected in your gene-set, and have a chance to be in another gene-set to be compared to. Even if there is no better way to estimate N, reducing it by (e.g.) 20% to see its impact on your result.