Implementation of an Alternative Method for Assessing Competing Risks: Restricted Mean Time Lost

Abstract

In clinical and epidemiologic studies, hazard ratios are often applied to compare treatment effects between 2 groups for survival data. For competing-risks data, the corresponding quantities of interest are cause-specific hazard ratios and subdistribution hazard ratios. However, they both have some limitations related to model assumptions and clinical interpretation. Therefore, we recommend restricted mean time lost (RMTL) as an alternative measure that is easy to interpret in a competing-risks framework. Based on the difference in RMTL (RMTLd), we propose a new estimator, hypothetical test, and sample-size formula. Simulation results show that estimation of the RMTLd is accurate and that the RMTLd test has robust statistical performance (both type I error and statistical power). The results of 3 example analyses also verify the performance of the RMTLd test. From the perspectives of clinical interpretation, application conditions, and statistical performance, we recommend that the RMTLd be reported along with the hazard ratio in analyses of competing-risks data and that the RMTLd even be regarded as the primary outcome when the proportional hazards assumption fails.

Abbreviations:

cHR

cause-specific hazard ratio

CI

confidence interval

CIF

cumulative incidence function

COVID-19

coronavirus disease 2019

CSH

cause-specific hazard function

HR

hazard ratio

RMTL

restricted mean time lost

RMTLd

difference in restricted mean time lost

SDH

subdistribution hazard function

sHR

subdistribution hazard ratio

Clinical trials of treatments and preventative measures for coronavirus disease 2019 (COVID-19) have received global attention. In published and ongoing randomized trials for COVID-19 treatments, the time-to-event endpoint of interest, such as the time to clinical improvement (or recovery), has been the most commonly used primary outcome (1). The corresponding method used has been the Kaplan-Meier method, and the effect size has been the hazard ratio (HR). However, patients may die of COVID-19 before improvement (or recovery), so competing-risks problems occur (2); that is, the occurrence of the event of interest (improvement or recovery) may be precluded by a competing event (death). At this time, the commonly applied single-event survival analysis techniques may lead to biased results, with subjects who experience a competing event being censored (3, 4). Therefore, competing-risks analysis should be applied in such situations.

There are 2 widely used approaches to competing-risks analysis based on hazards (5). One is based on a cause-specific hazard function (CSH), which refers to the instantaneous rate of occurrence of a specific event among the individuals who are still event-free; its corresponding statistical test is the log-rank test, and the statistical measure—that is, the cause-specific hazard ratio (cHR)—can be estimated through a cause-specific Cox regression model. The other approach is the subdistribution hazard function (SDH), which refers to the instantaneous rate of the event of interest in subjects who have not yet experienced the given event. The statistical test is the Gray test, and the estimated effect of one group relative to another—that is, the subdistribution hazard ratio (sHR)—can be calculated using the Fine-Gray model. Meanwhile, the clinical or epidemiologic interests in this approach are characterized by the cumulative incidence function (CIF), the probability of one event of interest occurring by a particular time in the presence of other events, which reflects the risk of the cause of interest without ignoring the presence of other competing events.

In the clinical analysis of competing-risks data, the estimations and statistical tests based on the cHR and sHR still have some limitations. First, the HR (both the cHR and the sHR) should be described as a relative rate, not as a relative risk (6). Without the assumption of independence of competing events, the cHR cannot be linked to the comparison of CIFs for an event between 2 groups (7), which means that cHR > 1 does not necessarily imply CIF₁ > CIF₀; that is, even if the hazard due to a main cause in a control group is always higher than that in a treatment group, the risk of the main cause in the control group is not necessarily always higher than that in the treated group. Although the sHR can affect the comparison of CIFs—that is, sHR > 1 can indicate that CIF₁ > CIF₀ and vice versa—it reflects the relative change in the instantaneous rates of occurrence of a given type of event in subjects who have not yet experienced that event between 2 groups. Researchers may find it difficult to interpret the results when individuals who had a competing event are retained in the risk set (8). Second, both the cause-specific Cox model and the Fine-Gray model depend on an assumption of the proportionality of the CSH and the SDH; as a consequence, researchers in many published survival analyses report only a single cHR or sHR, which is an average of specific HRs at different time points. However, if the above assumption is violated, a single HR is difficult to interpret because the true HR varies over time. Third, because of the semiparametric nature of the 2 regression models, the “relative” hazard rates cHR and sHR are not interchangeable with the “absolute” hazard rate without baseline hazards, which may make their clinical interpretation difficult to conceptualize.

Considering the above limitations, especially the problem of clinical interpretation, some researchers recommended an alternative statistic (9–11): restricted mean time lost (RMTL). RMTL can be estimated as the area under the CIF curve up to a specified time point and interpreted as the mean amount of time lost due to a specific cause during a predefined time window. Thus, compared with that of HRs, the clinical interpretation of the RMTL, which is based on a time scale, can easily be understood by physicians and patients (12–14). The difference in RMTL (RMTLd) is used to qualify the treatment effect and is also directly associated with comparisons of CIFs.

Although Anderson (9) and Zhao et al. (10) introduced the concept of RMTL, neither of them discussed the corresponding estimation and hypothetical test based on the RMTLd. Lyu et al. (11) presented a statistical inference framework and sample-size estimator based on the RMTLd, but it seemed to be relatively conservative on the basis of simulations. Therefore, in this article, we introduce a new RMTLd-based statistical inference framework and sample-size formula and demonstrate its performance through simulation and illustrative examples.

METHODS

Without loss of generality, only 1 event of interest (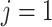) and 1 competing event (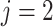) are assumed. T is defined as the observed time (time to event or censoring time).

Estimation of the RMTLd

The nonparametric estimation of the CIF is

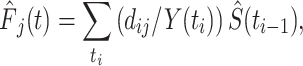where is the ith ordered event time, 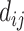is the number of events of cause j that occur at time 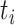, 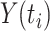is the number of subjects at risk at time 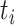, and is the event-free survival probability. Tau (τ) is the chosen time point, and τ ≤ T. For simplicity, we denote the RMTL of the event of interest to be 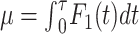; then, the nonparametric estimation of is given by

which can be interpreted as the mean amount of time lost due to a specific cause within the τ year window. The variance in 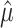can be estimated based on the derivation of the martingale approximation (15) (for the detailed process, see Web Appendix 1, available at https://doi.org/10.1093/aje/kwab235):

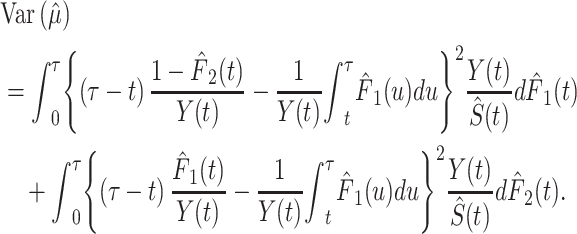Let 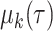be the RMTL of the event of interest in group ; then, denotes the estimated RMTL, and 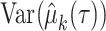corresponds to the variance in 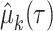. Then, the RMTLd between 2 groups is , and the corresponding variance is 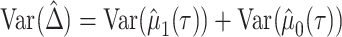. In large samples, the 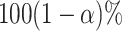confidence interval (CI) of the RMTLd is estimated as

where is the upper 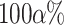quantile of the standard normal distribution.

Hypothetical test

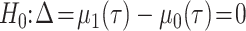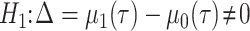The null and alternative hypotheses of the RMTLd test are and , respectively. Under the null hypothesis , the RMTLd test statistic can be computed as

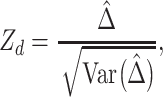which asymptotically follows a standard normal distribution.

Sample size

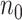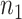Suppose and are the required sample sizes in the control group and the treatment group, respectively, and that is the ratio of sample sizes. Assume we test the null hypothesis with statistical power 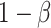at a 2-sided significance level 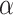. Under alternative hypothesis , we then have

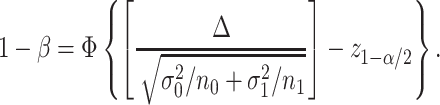Hence, the total sample size (for the detailed derivation, see Web Appendix 2) is

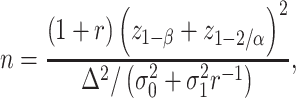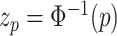is the inverse standard normal distribution function at probability 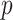, and the population variance of group k can be estimated as 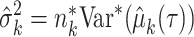, where 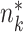and 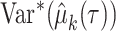can be obtained through a pilot study or previous study.

Simulation setup

In the simulation setup, we assessed the performance of the estimation of the RMTLd, the RMTLd test, and the RMTLd-based sample size under 6 different scenarios: 1) no difference between groups (Figure 1A); 2) a proportional SDH with sHR ≈ 0.905 (Figure 1B); 3) a proportional SDH with sHR ≈ 0.741 (Figure 1C); 4) an early difference between groups (Figure 1D); 5) a late difference with curves separated at t = 1 year (Figure 1E); and 6) a late difference with curves separated at t = 2 years (Figure 1F).

Figure 1.

Scenarios considered in a simulation study comparing the statistical performance of the Gray test and the RMTLd test. A) No difference in the event of interest between groups; B) a proportional subdistribution hazard function with a small difference; C) a proportional subdistribution hazard function with a large difference; D) an early difference; E) a late difference with a large difference; F) a late difference with a small difference. RMTLd, difference in restricted mean time lost.

Let the type of interest and competing events be generated through the binomial distributions 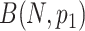and , where N is defined as the sample size of each group and 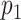is the maximum cumulative incidence of events of interest, which is set to 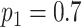. 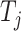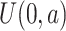The parameter settings of failure time () correspond to the event of interest and the competing event, respectively, under different situations (shown in Web Table 1), and the censoring times of the 2 groups are based on the uniform distributions and 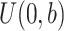, respectively. Next, define the observed time 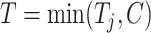and the event indicator 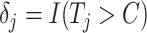. The censoring rates are required to be similar between the 2 groups and can be set at approximately 0%, 15%, 30%, or 45% by changing the settings of a and b. For the sample size, we consider both a balanced design (n₀ = n₁ = 300, 500, 1,000) and an unbalanced design (n₀ = 300, n₁ = 500; n₀ = 500, n₁ = 1,000). For all scenarios, a nominal level 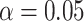is applied, and the specific time point τ is selected as the minimum of the maximum follow-up time of the 2 groups (16). All simulations are performed using 10,000 replications.

To evaluate the performance of the RMTLd estimation, we determined the true RMTLd at 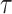 = 4 years with a total sample size of n = 1,000,000 (n₀ = n₁ = 500,000) under the different scenarios. The true RMTLd’s between groups for the event of interest under the 6 scenarios shown in Figure 1 (scenarios A–F) are 0.00004, −0.3935, −0.5141, −0.2986, −0.3517, and −0.1729 years, respectively, over a period of 4 years. Then, according to the above settings, we sampled from this large sample to calculate the mean relative bias, the root mean squared error, the relative standard error, and the coverage of the RMTLd (17) to measure the performance of the estimation of the RMTLd.

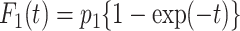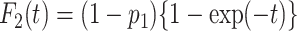Meanwhile, we compared the type I error and statistical power of the Gray test and proposed the RMTLd test to evaluate the performance of the RMTLd test. To evaluate the type I error rate, the CIFs of the events of interest and competing events were assumed to be and , respectively, so the failure time in both groups was generated from 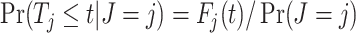, given the event type 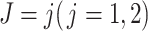, as shown in Figure 1A.

To assess the statistical power, we considered several situations (Figures 1B–1F). In the first situation, the proportional SDH assumption was met: Failure times were generated from the CIFs (18) 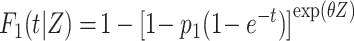and 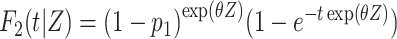, where 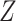is the group indicator (Z = 0 and Z = 1 for the control group and the treatment group, respectively). Meanwhile, we considered 2 scenarios, sHR ≈ 0.905 and sHR ≈ 0.741, corresponding to Figure 1B and Figure 1C, respectively. In the second situation, the proportional SDH assumption was violated: Both the early difference (Figure 1D) and the late difference (Figures 1E and 1F) in the CIFs were considered. The failure time was generated on the basis of CIFs with piecewise Weibull distributions 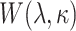(where 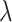and 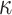are the scale parameter and the shape parameter, respectively): 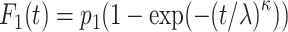and 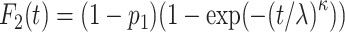(19). The specific parameter settings of all scenarios are presented in Web Table 1.

To evaluate the performance of the proposed sample-size estimation, we set 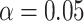and 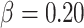(the targeted power was 80%) and generated the necessary parameters by averaging over each simulation to calculate the RMTLd-based sample sizes under different situations (Figures 1B–1F). Next, we simulated the observed power of the Gray test and the RMTLd test based on the calculated sample sizes through 10,000 simulations.

RESULTS

Estimation of the RMTLd

The results for the performance criterion of the estimation of the RMTLd are summarized in Table 1 and Table 2. Considering that the true RMTLd in scenario A is approximately equal to 0, we replaced the mean relative bias with bias to assess the performance (20). In summary, the estimation of RMTLd has a small bias (or mean relative bias) under all scenarios, and the root mean squared error decreases with increasing sample size and decreasing censoring. Meanwhile, the relative standard error is approximately equal to 1, and the coverage falls within a reasonable range.

Table 1.

Estimation of the Difference in Restricted Mean Time Lost Under the Proportional Subdistribution Hazard Function

	Scenario
	Scenario A				Scenario B				Scenario C
(n 0 , n 1 ) a and CR, %	Bias b ( )	RMSE	RSE c	Coverage d	MRB b ( )	RMSE	RSE c	Coverage d	MRB b ( 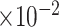)	RMSE	RSE c	Coverage d
(300, 300)
0	−0.0437	0.1289	1.0012	0.9503	0.2837	0.1324	0.9887	0.9441	−0.1210	0.1291	1.0023	0.9509
15	0.1275	0.1372	0.9945	0.9487	−0.2349	0.1378	1.0004	0.9526	0.0310	0.1365	0.9959	0.9469
30	−0.1657	0.1543	0.9819	0.9456	−1.4239	0.1543	0.9852	0.9471	−2.6107	0.1502	0.9927	0.9476
(500, 500)
0	−0.1462	0.1003	0.9977	0.9477	−0.2314	0.1018	0.9969	0.9469	−0.1333	0.1020	0.9837	0.9432
15	0.1584	0.1049	1.0080	0.9537	−0.2476	0.1064	1.0044	0.9519	−0.4303	0.1059	0.9954	0.9482
30	−0.0464	0.1180	0.9985	0.9503	−1.9034	0.1196	0.9894	0.9508	−2.0862	0.1186	0.9763	0.9462
(1,000, 1,000)
0	0.0463	0.0718	0.9865	0.9484	0.1519	0.0716	1.0029	0.9493	0.0659	0.0708	1.0030	0.9540
15	−0.0825	0.0744	1.0055	0.9499	−0.6177	0.0746	1.0140	0.9516	−0.4003	0.0738	1.0108	0.9491
30	0.1286	0.0850	0.9846	0.9449	−1.3734	0.0855	0.9820	0.9459	−1.7447	0.0827	0.9949	0.9470
(300, 500)
0	0.2184	0.1162	0.9943	0.9499	−0.4228	0.1164	1.0036	0.9501	−0.4984	0.1159	0.9989	0.9475
15	−0.0496	0.1229	0.9923	0.9472	−0.2165	0.1236	0.9952	0.9495	−0.1835	0.1220	0.9982	0.9490
30	0.4669	0.1366	0.9935	0.9477	−1.7534	0.1380	0.9861	0.9455	−2.4770	0.1376	0.9750	0.9439
(500, 1,000)
0	−0.0903	0.0861	1.0072	0.9505	0.0500	0.0866	1.0107	0.9503	0.2498	0.0872	0.9952	0.9451
15	−0.0614	0.0904	1.0133	0.9527	−0.4181	0.0931	0.9914	0.9493	−0.4221	0.0911	1.0038	0.9506
30	0.1896	0.1043	0.9799	0.9467	−1.7623	0.1029	0.9960	0.9480	−2.1686	0.1023	0.9897	0.9444

Abbreviations: CR, censoring rate, MRB, mean relative bias; RMSE, root mean squared error; RMTLd, difference in restricted mean time lost; RSE, relative standard error.

^a 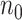and 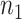are the required sample sizes in the control group and the treatment group, respectively.

^b Mean bias relative to the true RMTLd. The true RMTLd’s under scenarios A–C were 0.00004, −0.3935, and − 0.5141 years during 4 years, respectively.

^c Average model standard error/empirical standard error.

^d The reasonable coverage (0.9457, 0.9543) was based on 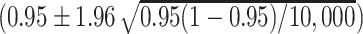(20).

Table 2.

Estimation of the Difference in Restricted Mean Time Lost Under the Nonproportional Subdistribution Hazard Function

	Scenario
	Scenario D				Scenario E				Scenario F
(n 0 , n 1 ) a and CR, %	MRB b ( )	RMSE	RSE c	Coverage d	MRB b ( )	RMSE	RSE c	Coverage d	MRB b ( )	RMSE	RSE c	Coverage d
(300, 300)
0	0.2004	0.1032	1.0206	0.9528	−0.4009	0.1062	1.0071	0.9523	−0.0479	0.1085	0.9898	0.9444
15	0.6546	0.1120	0.9962	0.9477	−0.2764	0.1119	0.9967	0.9487	0.7193	0.1112	1.0107	0.9512
30	0.2601	0.1182	1.0034	0.9512	−0.4848	0.1170	1.0055	0.9519	−0.4682	0.1182	1.0061	0.9486
(500, 500)
0	−0.2143	0.0818	0.9985	0.9493	0.0281	0.0835	0.9931	0.9485	0.1572	0.0836	0.9954	0.9488
15	0.6183	0.0861	1.0050	0.9517	−0.2761	0.0857	1.0089	0.9516	0.2146	0.0865	1.0068	0.9513
30	0.7100	0.0928	0.9910	0.9471	−0.0503	0.0912	0.9992	0.9499	0.6477	0.0930	0.9912	0.9479
(1,000, 1,000)
0	−0.0850	0.0576	1.0033	0.9511	−0.0996	0.0591	0.9915	0.9453	−0.0263	0.0588	1.0011	0.9502
15	0.0271	0.0610	1.0038	0.9527	−0.2364	0.0612	0.9999	0.9526	0.1664	0.0617	0.9985	0.9483
30	0.4661	0.0655	0.9927	0.9486	0.2138	0.0645	1.0000	0.9483	0.0847	0.0656	0.9946	0.9493
(300, 500)
0	−0.3262	0.0968	1.0032	0.9490	−0.0204	0.0953	0.9964	0.9480	0.3601	0.0959	0.9937	0.9492
15	−0.0674	0.1018	1.0084	0.9505	−0.5680	0.0988	1.0065	0.9521	0.0784	0.1001	0.9986	0.9502
30	−0.2966	0.1096	0.9932	0.9467	0.9197	0.1063	0.9905	0.9462	1.3494	0.1063	0.9980	0.9498
(500, 1,000)
0	0.0673	0.0737	0.9992	0.9510	0.1859	0.0705	1.0091	0.9498	−0.3422	0.0712	1.0010	0.9494
15	0.3837	0.0791	0.9824	0.9463	−0.5905	0.0751	0.9924	0.9489	0.5657	0.0749	0.9992	0.9490
30	0.4481	0.0822	1.0033	0.9487	0.2771	0.0787	1.0031	0.9507	0.4813	0.0793	1.0029	0.9518

Abbreviations: CR, censoring rate; MRB, mean relative bias; RMSE, root mean squared error; RMTLd, difference in restricted mean time lost; RSE, relative standard error.

^a and 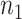are the required sample sizes in the control group and the treatment group, respectively.

^b Mean bias relative to the true RMTLd. The true RMTLd’s under scenarios D–F were −0.2986, −0.3517, and − 0.1729 years during 4 years, respectively.

^c Average model standard error/empirical standard error.

^d The reasonable coverage (0.9457, 0.9543) was based on (20).

Hypothetical test

For each of the 6 hypothetical scenarios shown in Figure 1, the type I error rate and statistical power results are summarized in Table 3. The type I error rates in Table 3 show that both the proposed RMTLd test and the Gray test have well-controlled error rates. Under the proportional SDH assumption (scenarios B and C), the RMTLd test has power similar to that of the Gray test. In the early difference scenario (scenario D), the RMTLd test provides significantly greater power than the Gray test. Meanwhile, as the censoring rate increases, the power of the 2 tests increases. This tendency may be interpreted as follows: Because of high censoring, the number of patients in the later part of the CIF curve may be small, resulting in increased variability in the shape of the curve. The results for the late difference situations (scenarios E and F) show that the power of the 2 tests increases as the sample size increases and when the difference is larger and that the RMTLd test provides higher (or much higher) values than the Gray test. According to the above findings, the RMTLd test has relatively robust performance in different situations.

Table 3.

Type I Error and Statistical Power of the Gray Test and the RMTLd Test in a Simulation of Statistical Performance

	Scenario
	Type I Error b		Statistical Power
	Scenario A		Scenario B		Scenario C		Scenario D		Scenario E		Scenario F
(n 0 , n 1 ) a and CR, %	Gray Test	RMTLd Test	Gray Test	RMTLd Test	Gray Test	RMTLd Test	Gray Test	RMTLd Test	Gray Test	RMTLd Test	Gray Test	RMTLd Test
(300, 300)
0	0.0497	0.0500	0.2343	0.2482	0.9468	0.9609	0.2236	0.6842	0.8706	0.9326	0.4714	0.4575
15	0.0538	0.0531	0.2413	0.2366	0.9528	0.9486	0.3770	0.6812	0.8698	0.9039	0.4207	0.4056
30	0.0501	0.0505	0.2226	0.2187	0.9412	0.9398	0.5604	0.6960	0.8487	0.8541	0.3487	0.3372
45	0.0506	0.0504	0.1954	0.1969	0.9065	0.9074	0.7910	0.8464	0.7376	0.7281	0.1892	0.1952
(500, 500)
0	0.0504	0.0500	0.3497	0.3700	0.9945	0.9965	0.3374	0.8340	0.9441	0.9931	0.6222	0.6807
15	0.0532	0.0525	0.3636	0.3472	0.9967	0.9961	0.5574	0.8344	0.9625	0.9870	0.5830	0.6224
30	0.0477	0.0487	0.3453	0.3381	0.9959	0.9952	0.7739	0.8507	0.9677	0.9776	0.4963	0.5293
45	0.0505	0.0510	0.3057	0.3039	0.9864	0.9867	0.9466	0.9674	0.9166	0.9218	0.2934	0.3249
(1,000, 1,000)
0	0.0490	0.0505	0.6009	0.6087	1.0000	1.0000	0.5820	0.9694	0.9775	1.0000	0.8172	0.9411
15	0.0474	0.0485	0.6185	0.5901	1.0000	1.0000	0.8459	0.9681	0.9922	0.9999	0.8221	0.9109
30	0.0542	0.0528	0.6036	0.5866	1.0000	1.0000	0.9690	0.9731	0.9991	0.9999	0.7786	0.8488
45	0.0477	0.0482	0.5353	0.5336	1.0000	1.0000	0.9989	0.9995	0.9972	0.9981	0.5136	0.5950
(300, 500)
0	0.0500	0.0513	0.2889	0.2957	0.9769	0.9837	0.2788	0.7277	0.8917	0.9697	0.5390	0.5509
15	0.0515	0.0518	0.2954	0.2823	0.9839	0.9820	0.4642	0.7295	0.9096	0.9521	0.4853	0.4811
30	0.0491	0.0523	0.2841	0.2715	0.9767	0.9753	0.6658	0.7444	0.9071	0.9171	0.3947	0.3963
45	0.0501	0.0524	0.2461	0.2390	0.9567	0.9539	0.8825	0.8982	0.8133	0.8150	0.2167	0.2345
(500, 1,000)
0	0.0511	0.0527	0.4577	0.4645	0.9996	0.9997	0.4374	0.8891	0.9373	0.9990	0.7010	0.8115
15	0.0469	0.0478	0.4684	0.4406	0.9997	0.9996	0.6877	0.8822	0.9733	0.9982	0.6841	0.7533
30	0.0526	0.0530	0.4517	0.4346	0.9995	0.9993	0.8794	0.9018	0.9904	0.9959	0.5912	0.6491
45	0.0516	0.0507	0.3901	0.3795	0.9990	0.9985	0.9838	0.9845	0.9647	0.9732	0.3430	0.4128

Abbreviations: CR, censoring rate; RMTLd, difference in restricted mean time lost.

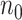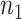^a and are the required sample sizes in the control group and the treatment group, respectively.

^b The reasonable range (0.0457, 0.0543) was based on the formula 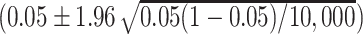(26).

Sample size

For each scenario (Figures 1B–1F), 10,000 simulations were performed to evaluate the observed power of the Gray test and the RMTLd test under the RMTLd-based sample size; the results are shown in Table 4. Under the proportional subdistribution hazards scenarios (scenarios B and C), the power of the RMTLd test and the Gray test is approximately equal to the predefined level of 80%. In the early difference scenario (scenario D), the power of the RMTLd test is larger than the prespecified level, while that of the Gray test is much lower than 80%. In the late difference scenarios (scenarios E and F), the observed power of the RMTLd test is close to 80% but that of the Gray test has an obvious decrease with a smaller difference (scenario F).

Table 4.

Observed Statistical Power of the Gray-Based and RMTLd-Based Sample-Size Formulas Based on the Same Sample Setting in a Simulation^a

	Scenario
	Scenario B			Scenario C			Scenario D			Scenario E			Scenario F
CR, %	No.	Gray Test	RMTLd Test	No.	Gray Test	RMTLd Test	No.	Gray Test	RMTLd Test	No.	Gray Test	RMTLd Test	No.	Gray Test	RMTLd Test
0	3,180	0.7903	0.7885	370	0.7976	0.8380	1,074	0.3567	0.8453	400	0.7470	0.7966	1,308	0.7001	0.8009
15	3,258	0.8282	0.7958	376	0.8238	0.8226	1,060	0.5827	0.8472	438	0.7648	0.7808	1,444	0.7174	0.7898
30	3,348	0.8251	0.8102	372	0.7987	0.7943	980	0.7639	0.8477	496	0.7867	0.7778	1720	0.7114	0.7832
45	3,600	0.7818	0.7798	428	0.7825	0.7833	566	0.7667	0.8300	650	0.7650	0.7618	3,286	0.7134	0.8125

Abbreviations: CR, censoring rate; RMTLd, difference in restricted mean time lost.

^a Sample sizes were calculated on the basis of the RMTLd test. The chosen time point τ was the shortest maximum follow-up time of the 2 groups, and the prespecified power was 80%.

In summary, the sample size based on the RMTLd can obtain a nominal power of approximately 80%, except in the early difference scenario. Therefore, the validity of the RMTLd-based sample size should be acceptable.

Illustrative examples

Example 1.

Data on 599 Chinese-American patients with cervical cancer diagnosed between 1988 and 2008 were obtained from the Surveillance, Epidemiology, and End Results (SEER) database of the US National Cancer Institute to assess the association between surgical factors and survival. In our analysis, death from cervical cancer was defined as the event of interest, while death from other causes was defined as a competing event (21, 22). The rate of the event of interest in the nonsurgery group (n = 101) was 29.70%, while the rate was 5.82% in the surgery group (n = 498). The corresponding censoring rates were 38.61% and 81.73%, respectively. Figure 2A shows the CIF curve of the event of interest, and Table 5 shows the statistical results of different tests.

Figure 2.

Cumulative incidence function of the event of interest in example 1 (A) and example 2 (B). The restricted time point was chosen as 25.667 years in example 1 and 16.238 years in example 2.

Table 5.

Statistical Results of Hazard-Based and RMTL-Based Analyses for 3 Illustrative Examples

	Example
	Example 1 (τ1= 25.667 years)					Example 2 (τ2= 16.238 years)					Example 3 (τ3= 28 days)
	Comparison		Ratio/ Difference c	95% CI	P Value d	Comparison		Ratio/ Difference c	95% CI	P Value d	Comparison		Ratio/ Difference c	95% CI	P Value d
Test	Nonsurgery a , b	Surgery a				Mismatch a , b	Match a				Placebo a , b	Remdesivir a
cHR			0.132	0.079, 0.220	<0.001			0.828	0.684, 1.002	0.051			1.326	1.145, 1.539	<0.001
sHR			0.158	0.095, 0.262	<0.001			0.835	0.692, 1.008	0.064			1.305	1.130, 1.506	<0.001
RMTLd	7.485	1.346	−6.139	−8.400, −3.878	<0.001	4.661	3.638	−1.023	−1.755, −0.291	0.006	10.859	13.286	2.427	1.242, 3.612	<0.001

Abbreviations: cHR, cause-specific hazard ratio; CI, confidence interval; RMTL, restricted mean time lost; RMTLd, difference in restricted mean time lost; sHR, subdistribution hazard ratio.

^a Because of the semiparametric nature of the cause-specific Cox and Fine-Gray regression models, neither the cause-specific hazard function nor the subdistribution hazard function could be obtained in any group, which resulted in empty cells for those functions.

^b Reference group for calculation of the cHR, sHR, and RMTLd.

^c The cHR and sHR are related to the corresponding ratio, while the RMTLd is related to the difference.

^d P values for the cHR, sHR, and RMTLd were calculated by means of the log-rank test, the Gray test, and the RMTLd test, respectively.

The CSH-based results suggested a positive association between surgery and death from cervical cancer (cHR = 0.132, 95% CI: 0.079, 0.220), and the assumption of the proportionality of the CSH was satisfied (P = 0.596). Meanwhile, the SDH-based method showed a positive association between surgery and the event of interest (sHR = 0.158, 95% CI: 0.095, 0.262). A test of the proportional SDH assumption yielded a result of P = 0.230. Because of the semiparametric nature of the regression model, neither the CSH nor the SDH could be obtained in any group, resulting in empty cells in Table 5.

Next, we let 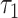= 25.667 years, which corresponds to the shortest maximum follow-up time between the 2 groups. Table 5 shows that the RMTL of the nonsurgery group was 7.485 years, while that of the surgery group was 1.346 years. The results can be interpreted as follows: During 25.667 (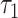) years of follow-up, the mean years of life lost due to death from cervical cancer among patients in the nonsurgery and surgery groups was 7.485 years and 1.346 years, respectively. The RMTLd test results also favored the surgery group (RMTLd = −6.139, 95% CI: −8.400, −3.878), and the RMTLd of −6.139 years (the RMTL of the surgery group minus the RMTL of the nonsurgery group) indicated that the patients without surgery lost an additional 6.139 years of life due to cervical cancer within 25.667 () years of follow-up. Thus, the RMTLd-based results provided a more acceptable conception of the time scale.

Example 2.

The cases of 2,279 patients with acute lymphocytic leukemia who received allogeneic bone transplants from a human leukocyte antigen (HLA)-identical sibling donor were recorded by the European Group for Blood and Marrow Transplantation (23). We studied the association between donor-recipient sex match and survival, so a total of 2,279 patients were grouped into sex-mismatched (n = 545) and sex-matched (n = 1,734) groups. Death after transplantation was documented as the event of interest, and relapse from transplantation was a competing event. The proportions of the event of interest in the mismatched and matched groups were 26.61% and 22.38%, and the censoring rates were 56.88% and 61.48%, respectively.

The results based on the CSH showed no significant difference between the 2 groups (cHR = 0.828, 95% CI: 0.684, 1.002), and the proportional CSH assumption was violated (P = 0.001). The result based on the SDH also indicated no statistically significant difference (sHR = 0.835, 95% CI: 0.692, 1.008), and the proportional SDH assumption was not satisfied (P = 0.004). Regarding the above results, the true cHR and sHR may vary with time rather than be constant (cHR = 0.828 and sHR = 0.835), which makes clinical interpretation difficult.

Unlike the above CSH-based and SDH-based tests, the RMTLd test detected a difference between the 2 groups and showed a positive association in the matched group over 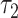= 16.238 years of follow-up (RMTLd = −1.023, 95% CI: −1.755, −0.291), and the RMTLd indicated that the sex-mismatched patients lost an additional 1.023 years of life on average during the 16.238 years. This significant result of the RMTL test was not unexpected, because this example (Figure 2B) corresponds to simulation scenario F (Figure 1F), and it demonstrated that the RMTLd test had higher power than the Gray test, as shown in Table 3.

Example 3.

Adaptive COVID-19 Treatment Trial 1 is a placebo-controlled trial designed to assess remdesivir use in patients hospitalized with COVID-19 (2, 24). The data were reconstructed (for the detailed process, see Web Appendix 3) because the original data were not publicly available (2); the event of interest was defined as recovery, and the corresponding competing event was death. In the trial, 541 patients were assigned to the remdesivir group and 521 were assigned to the placebo group. The proportions of recovered patients in the remdesivir and control groups were 70.98% and 63.92%, respectively, and the censoring rates were 17.56% and 20.92%, respectively. Figure 3A shows the CIF curve of recovery between groups.

Figure 3.

Cumulative incidence function of the event of interest in example 3 (A) and sample sizes based on the subdistribution hazard ratio (sHR) and the difference in restricted mean time lost (RMTLd) (B). The restricted time points were chosen from 14–28 days when calculating RMTLd-based sample sizes.

The results based on the CSH and SDH (Table 5) showed significant differences, and the proportional CSH assumption was satisfied (P = 0.056), while the SDH assumption was violated (P = 0.002). In regard to the RMTL, we note that different from the event of interest in example 1 (in which death from cervical cancer was a negative outcome), the event of interest in this example (i.e., recovery) was a positive outcome. Thus, a larger RMTL indicated better therapy. From Table 5, the RMTLs of the placebo and remdesivir groups were 10.859 days and 13.286 days, respectively, which can be interpreted to indicate that over the 28 () days of follow-up, the patients in the placebo group had 10.859 postrecovery days, on average, while the patients in the remdesivir group had 13.286 days. In other words, the patients in the placebo and remdesivir groups had been recovered for an average of 10.859 days and 13.286 days by day 28, respectively. The RMTLd of 2.427 days (95% CI: 1.242, 3.612) favored the remdesivir group and showed that the patients in the remdesivir group recovered 2.427 days earlier than those in the placebo group during the 28-day period.

Meanwhile, because of the clinical significance of COVID-19 research, we set equal to 28 days and reestimated that the sample sizes based on the sHR (25) and the RMTLd were 658 and 517, respectively. Moreover, based on different time points, we calculated the RMTLd-based sample sizes. As Figure 3B shows, the RMTLd-based sample sizes were always smaller than the sHR-based sample sizes.

DISCUSSION

The presence of competing risks makes treatment effect assessment in clinical trials and epidemiologic studies with time-to-event endpoints more cumbersome. The commonly reported quantitative measures are the cHR and sHR, where the former might be used to study the etiology of diseases from biological mechanisms and the latter might be more suitable for predicting an individual’s risk of a specific outcome (7).

However, based on our examples, there are still some limitations to the above 2 indicators based on the HR. First, as a “relative” measure, HRs (both the cHR and the sHR) cannot be easily understood when a baseline hazard (e.g., of a control group) is lacking, even though the proportional CSH and SDH assumptions were satisfied in example 1. Moreover, the cHR = 0.132 and sHR = 0.158 in example 1 cannot be directly interpreted, as the “risk” of death from cervical cancer decreased by 86.8% or 84.2%, respectively, for the surgery group; rather, this result should be understood as an 86.8% or 84.2% decrease, respectively, in the “hazard” of death from cervical cancer, which is difficult to interpret clinically (2, 6). Furthermore, because the proportional hazards assumptions were violated in example 2, the CSH and SDH curves of the 2 groups in Web Figure 1 (obtained through the nonparametric technique) have a late difference, showing that the cHRs and sHRs may vary over time. Therefore, a weighted average HR alone may fail to quantify and interpret the treatment effect.

As an alternative statistic, some researchers (9–11) developed the RMTL, which corresponds to the area under the CIF curve. Thus, the RMTL can easily be implemented and interpreted on a time scale. Meanwhile, as an “absolute” measure, the RMTLd can be used to supplement the cHR and sHR to evaluate the treatment effect. Moreover, the RMTLd-based test does not require any model assumptions.

Based on the RMTLd, we introduced a new statistical inference framework and sample-size estimator. From our simulation results, the performance of the estimation of the RMTLd and the RMTLd test is acceptable and robust. However, notably, the simulation results of 45% censoring are not shown in Table 1 and Table 2 because we set the true RMTLd at t = 4 years; that is, the final follow-up time should be equal to or greater than 4 years for the generation of survival data, which is violated with 45% censoring (for more discussion, see Web Table 2, Web Table 3, and Web Figure 2). In summary, the proposed RMTLd is accurate, and the RMTLd test has well-controlled type I error rates and has power similar to (or even larger than) that of the Gray test. Meanwhile, the results of the sample-size simulation showed that the power of the RMTLd-based sample size can approximately achieve the predefined level of power, and we also calculated the RMTLd-based and sHR-based sample sizes in examples 1 and 2 (regardless of the clinical significance, shown in Web Figure 3), which also indicates that the proposed sample-size formula is effective and suitable. Thus, for clinical trials and epidemiologic studies, the RMTLd test may be the most robust approach for competing risks.

However, there were still some limitations in this study: 1) the time point τ was simply restricted to be the shortest maximum follow-up time of the 2 groups, whereas from a practical perspective, τ can be chosen according to scientific clinical or epidemiologic knowledge (e.g., 28 days based on COVID-19 studies); and 2) the results of the statistical tests in the examples were applied to illustrate the analysis and interpret the outcomes, but they did not offer any clinically relevant conclusions.

In summary, in competing-risks analysis, we recommend the RMTLd as a supplement to the cHR or sHR in the measurement of treatment effects when the proportional hazard assumptions are satisfied. When the assumptions are violated, the RMTLd could be selected as an alternative statistic for summarizing and interpreting the treatment effect.