Abstract
The coordination of one and two aflatoxin B1 (AFB1, a potent carcinogen) molecules with chlorophyll a (chl a) was studied at a theoretical level. Calculations were performed using the M06-2X method in conjunction with the 6-311G(d,p) basis set, in both gas and water phases. The molecular electrostatic potential map shows the chemical activity of various sites of the AFB1 and chl a molecules. The energy difference between molecular orbitals of AFB1 and chl a allowed for the establishment of an intermolecular interaction. A charge transfer from AFB1 to the central cation of chl a was shown. The energies of the optimized structures for chl a show two configurations, unfolded and folded, with a difference of 15.41 kcal/mol. Chl a appeared axially coordinated to the plane (α-down or β-up) of the porphyrin moiety, either with the oxygen atom of the ketonic group, or with the oxygen atom of the lactone moiety of AFB1. The complexes of maximum stability were chl a 1-α-E-AFB1 and chl a 2-β-E-AFB1, at −36.4 and −39.2 kcal/mol, respectively. Additionally, with two AFB1 molecules were chl a 1-D-2AFB1 and chl a 2-E-2AFB1, at −60.0 and −64.8 kcal/mol, respectively. Finally, biosorbents containing chlorophyll could improve AFB1 adsorption.
Keywords: chlorophyll a, aflatoxin B1, intermolecular interactions, molecular modeling, density functional theory, M06-2X functional
1. Introduction
Several fungi, such as Aspergillus flavus, A. parasiticus, A. nomius, and A. psudotamarii, can produce toxic secondary metabolites recognized as mycotoxins [1,2]. Among the toxins produced by these fungi, aflatoxin B1 (AFB1) (Figure 1a) exhibits the most potent mutagenic and carcinogenic potential. Consequently, it has been categorized as a human Group 1 carcinogen by the International Agency of Research on Cancer [3]. In addition, several outbreaks of human aflatoxicosis have been reported in emergent countries [4,5,6,7]. Therefore, investigation of dietary agents that selectively bind AFB1 in the gastrointestinal tract and reduce their bioavailability must be considered essential.
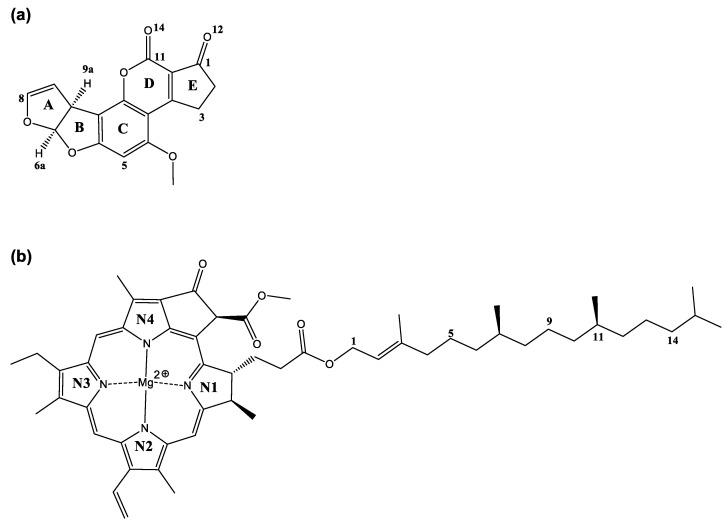
Figure 1.
Structures of (a) aflatoxin B1 and (b) chlorophyll a (chl a).
Chlorophylls are among the most abundant pigments in nature; this class of compounds contains four linked pyrrole rings and a hydrophobic side chain of phytol. Chlorophyll a (chl a) (Figure 1b) and chlorophyll b (chl b) are the two most significant chlorophylls present in higher plants, green algae, and some prochlorophytes. These molecules differ in that there is an aldehyde group in chl b instead of a methyl group, present in chl a, located at the pyrrole ring N3. It is important to note that many studies have shown that chlorophylls have significant anticarcinogenic activity against a wide range of potential human carcinogens, including AFB1 [8,9,10,11]. Therefore, different mechanisms responsible for cancer-preventative activity have been proposed, including antioxidant activity [12,13], modulation of detoxification pathways [14], induction of apoptosis [15], and carcinogen trapping [16,17,18,19,20]. However, the mechanisms involved in the anticarcinogenic action of chlorophylls and their potential for human chemoprevention against AFB1 are poorly understood. Furthermore, chlorophyllin (chl), a water-soluble derivative of chlorophyll, could also create strong non-covalent complexes with carcinogens. Using molecular modeling and experimental studies, it has been determined that chl–AFB1 interactions are extremely energetically favorable (up to −20 kcal/mol), involving both electrostatic attractions and van der Waals interactions [21,22].
As a part of our research, we have previously performed important studies contributing to the understanding of AFB1, summarized as follows: (a) A mass spectrometry/mass spectrometry study on the degradation of AFB1 in maize with aqueous citric acid [23]. (b) In addition to several theoretical calculations, applying density functional theory, confirming that the active site corresponds to the carbonylic functionality of the lactonic moiety [24]. The performance of quantum mechanical calculations to explain the chemical behavior of the lactone ring of AFB1 hydrolyzed under acidic conditions, suggesting the deletion of its carcinogenic properties. (c) A theoretical study [25] of 8-chloro-9-hydroxy-AFB1, carried out by DFT, determining the structural, electronic, and spectroscopic properties of this reaction product of AFB1, allowing for its theoretical characterization. (d) A theoretical study [26] related to the adsorption process of B-aflatoxins using a vegetable specimen Pyracantha koidzumii (Hayata); the interaction of AFB1 with the functional groups present in the biosorbent was investigated. (e) In a recent publication [27], several in vitro experiments were conducted to evaluate the effectiveness of lettuce and field horsetail as biosorbents for the removal of aflatoxin AFB1. In conclusion, several physicochemical interactions with chlorophylls are involved in the adsorption process [17,22,28,29].
Considering the previously disclosed information, the goal of this work is to provide novel knowledge related to the interaction between AFB1 and chl a using theoretical calculations employing density functional theory (DFT). In other words, appropriate interactions between AFB1 and chl a were achieved. As a result, a careful in silico study was performed using geometry optimization, molecular electrostatic potential maps, and the highest occupied molecular orbital–lowest unoccupied molecular orbital gap, explaining the progress of several chl a–AFB1 complexes.
2. Results
2.1. DFT Optimized Structures
Determination of Most Stable Conformer between chl a 1 and chl a 2
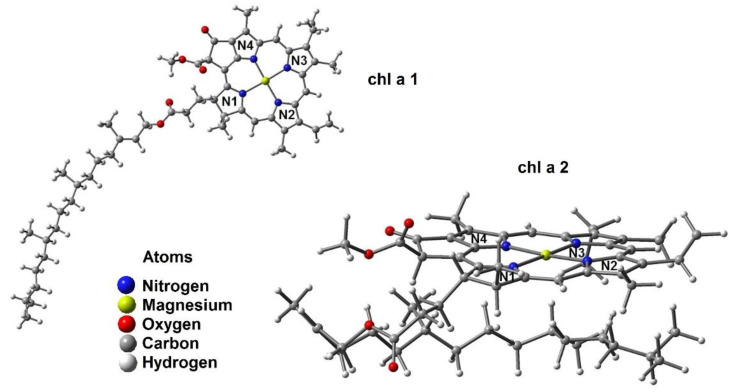
Figure 1 shows the chemical structures of AFB1 and chl a with appropriate nomenclature; this will make this section easier to comprehend. The energies of the corresponding optimized structures for chl a show two different configurations, as shown in Figure 2. In the first instance, there is a phytol moiety on the N1 ring in an unfolded form (chl a 1) [30,31] with −2934.13 Hartrees. On the other hand, there is a phytol chain with a folded structure (chl a 2) and −2934.15 Hartrees, meaning that conformer chl a 2 is the most stable, with a difference of 15.41 kcal/mol (Figure 2). This, may be due to weak hydrogen bond interactions [32] between the lone pair of electrons at the nitrogen atoms and nearby hydrogens atoms of the phytol moiety, resulting in the following data: C5H2–N4: 2.86 Å, C11H–N3: 2.9 Å, and C14H2–N2: 2.63 Å. After searching in the literature, we found that Alvarado-González et al. [30] and Schulte et al. [31] reported this more stable conformation (chl a 2). In preceding works by Kobayashi and Reimers [33] and Chen and Cai [34], it was stated that if a methyl group replaces the phytol chain, non-significant consequences can be expected; however, in this work, the bulky chain plays an important role in the stereo structure adopted by the chlorophyll. Therefore, this moiety should not be underestimated.
Figure 2.
Optimized geometry of the more stable conformers: chl a 1 and chl a 2.
AFB1, the most stable conformer, displayed an energy value of −1106.22 Hartrees. In general, the molecule is planar, but with the A ring perpendicular to the plane.
In general, the optimized structure calculations were established in the gas phase.
2.2. Structural and Energetic Parameters from Optimized Conformers
2.2.1. Atomic Charges of chl a 1, chl a 2, AFB1, and Their Complexes
Atomic charge is not a physically obvious parameter; its value depends on the scheme by which the electron density of a molecule is partitioned. Additionally, a natural charge results from natural population analysis (NPA), converting a wave function’s molecular orbitals from delocalized to localized, maintaining all information contained in the wave function [35]. Moreover, NPA has been recommended to overcome problems associated with other schemes of charge [36].
Related to the above commentary, Table S1 displays the atomic charges of chl a 1, chl a 2, and their corresponding complexes, considering one and two molecules of AFB1. Accordingly, Figure S1 displays the atomic charges of AFB1. Theoretical calculations showed that the most negative charge in the complexes is generally localized on N1 (−0.737–796 e−), except for chl a 1-α-E-AFB1 (−0.698 e−). However, for the uncoordinated chl a 1 and chl a 2, higher values were obtained: −0.792 and −0.796 e–, respectively.
The nitrogen atoms, N2, N3, and N4, for chl a 1 and 2, exhibit similar charge values: For the chl a 1 complex with one AFB1, −0.724 e− for N2, −0.731 e− for N3, and −0.703 e− for N4; for the chl a 2 complex with one AFB1, −0.719 e− for N2, −0.745 e− for N3, and −0.695 e− for N4. For chl a 1 with two AFB1 molecules, the charges are −0.718 e− for N2, −0.732 e− for N3, and −0.667 e− for N4. For chl a 2 with two AFB1 molecules, the charges are −0.698 e− for N2, −0.7185 e− for N3, and −0.671 e− for N4.
Concerning AFB1, the most negative charge is located on the oxygen atoms of the carbonyl groups, showing similar charge values of −0.534 and −0.533 e–. Meanwhile, the major hydrogen acidity atoms corresponded to H9a > H9 > H8 > H6a, 0.242, 0.236, 0.201, and 0.183 e–, respectively.
On the other hand, for all the target molecules, the site with higher positive charge is located on the Mg2+ ion (1.749–1.766 e−). In particular, the obtained data are as follows: chl a 1, 1.758 e–; chl a 1 complexes with one AFB1, 1.757–1.760 e−; chl a 1 complexes with two AFB1, 1.753 e−; chl a 2, 1.762 e−; chl a 2 complexes with one AFB1 molecule, 1.760–1.766 e−; for chl a 2 complexes with two AFB1, 1.749–1.756 e−.
2.2.2. Bond Distance (Å) of Optimized Geometries
Table 1 shows the bond distances for chl a 1, chl a 2, and their complexes. The distances were taken between the magnesium ion and the oxygen or nitrogen atom.
Table 1.
Bond distances, in Å, of optimized geometries.
| Molecule | Mg–O1 | Mg–N1 | Mg–N2 | Mg–N3 | Mg–N4 |
|---|---|---|---|---|---|
| chl a 2 | - | 2.131 | 2.013 | 2.061 | 2.001 |
| chl a 1 | - | 2.133 | 2.015 | 2.063 | 2.002 |
| chl a 1-α-D-AFB1 | 2.101 | 2.176 | 2.032 | 2.087 | 2.033 |
| chl a 1-α-E-AFB1 | 2.106 | 2.183 | 2.037 | 2.076 | 2.036 |
| chl a 1-β-D-AFB1 | 2.124 | 2.157 | 2.025 | 2.098 | 2.041 |
| chl a 1-β-E-AFB1 | 2.111 | 2.160 | 2.023 | 2.092 | 2.050 |
| chl a 2-α-D-AFB1 | 2.123 | 2.178 | 2.058 | 2.099 | 2.030 |
| chl a 2-α-E-AFB1 | 2.080 | 2.170 | 2.045 | 2.088 | 2.020 |
| chl a 2-β-E-AFB1 | 2.120 | 2.172 | 2.028 | 2.099 | 2.056 |
| chl a 2-β-E-AFB1 | 2.119 | 2.151 | 2.057 | 2.101 | 2.016 |
| chl a 1-D-2AFB1 | 2.230 | 2.135 | 2.043 | 2.084 | 2.024 |
| 2.428 * | |||||
| chl a 1-E-2AFB1 | 2.228 | 2.113 | 2.025 | 2.114 | 2.030 |
| 2.351 * | |||||
| chl a 2-D-2AFB1 | 2.285 | 2.128 | 2.054 | 2.084 | 2.019 |
| 2.167 * | |||||
| chl a 2-E-2AFB1 | 2.251 | 2.149 | 2.027 | 2.092 | 2.028 |
| 2.186 * |
E= oxygen atom of carbonyl group on ring E, D = oxygen atom of lactone group on ring D, * AFB1 molecule is α-located.
Once the optimized conformers were established, and the charges of all atoms were acquired, the subsequent strategy was to recognize the reactive sites in the target molecules. Accordingly, in Figure S2, the obtained electrostatic potential maps for AFB1, chl a 1, and chl a 2 are displayed; in the case of AFB1, the electrostatic potential [37] is more reactive (negative, red color) around the oxygen atoms localized on D and E rings, indicating that these positions may perform electrophilic attacks, and highlighting that, as in previous studies, the D ring (lactone moiety) is the active site [24].
Regarding the chlorophyll conformers, the light red color of the oxygen atoms of both the ketonic and the ester carbonyl groups positioned on the N4 ring is indicative of a negative area. An interesting zone around the magnesium ion (positive, blue color) reveals that this position may be subject to a nucleophilic attack [21,34]. Since the porphyrinic moiety is planar, the magnesium ion could display two axial nucleophilic interactions. Thus, the results are congruent with the data on atomic charges.
2.2.3. Molecular Orbitals: HOMO–LUMO for chl a 1, chl a 2, and AFB1
The highest occupied, and the lowest unoccupied, molecular orbitals were determined to reveal the stability of the studied molecules, as show in Figure S3. Only the HOMO for AFB1 and the LUMO for chl a 1 and chl a 2 were considered due to their corresponding nucleophilic and electrophilic character. The HOMO for AFB1, −7.604 eV, is mainly located at the oxygen atoms on rings D and E, with significant contributions by the aromatic system ring C. Thus, these rings must be considered as the interaction sites when AFB1 acts as an electron-donor specie, interacting with a cationic center [38] (Figure S3). The LUMO for chl a 2, −2.295 eV, and chl a 1, −2.126 eV, is located on the double bonds of the porphyrin system (π bonds and lone-electron-pair N atoms), according to Alvarado-González et al. [30] and Bechaieb et al. [39]. The energy gap is smaller between the HOMO of AFB1 and LUMO of chl a 2; therefore, they could accomplish a better interaction than chl a 1 with the HOMO of AFB1 (Figure S3). This assumption is made since the gap (ELUMO − EHOMO) in the interaction of chl a 2–AFB1 has a value of 5.309 eV, and the gap for chl a 1–AFB1 shows a value of 5.477 eV, confirming that the chl a 2–AFB1 complex is the most stable. Considering the maximum hardness principle [40,41], which asserts that the systems tend to be hard when they show significant gap energy, the AFB1 molecule is hard, showing a gap of 6.324 eV. Chl a 1 and chl a 2 have gap values of 3.799 and 3.824 eV, respectively. Thus, the chlorophyll molecule is soft. Nevertheless, the interaction between AFB1–HOMO and chl a–LUMO is favored.
Finally, the frontier electron density can be used to predict the most reactive position in a π electron system. Hence, considering, that HOMO–LUMO and its property (energy) is very useful to estimate the chemical reactivity of molecules, the interactions between the vacant orbital (LUMO of chl a 2) and the electron pair (HOMO of AFB1) displayed small energy separation. It can also be assumed that with the overlapping between the orbitals of two target molecules, the stability is improved. In addition, as shown in Figure S3, the site and sharpness of some lobes display noticeable changes, but not intensely.
2.3. Geometry of Unfolded and Folded Chlorophyll with One AFB1 Molecule
2.3.1. Frontal View of Unfolded and Folded Chlorophyll
Unfolded (Figure 3a) corresponds to the phytol chain in an extended form. In contrast, folded (Figure 3b) corresponds to the phytol chain positioned under the plane of a porphyrin moiety. In addition, Figure 3 shows the axial possibilities of coordination, α implies AFB1 placed under the chain and, consequently, β is positioned on the up side [42].
Figure 3.
(a) Unfolded and (b) folded chl a.
2.3.2. Geometry of Unfolded Chlorophyll with One AFB1 Molecule
In the computed ground state of chl a, the Mg2+ ion could be axially coordinated by β and α to the oxygen atom of the ketone group, ring E, or with the oxygen atom of the carbonylic lactone group, ring D, such that C1=O12 or C11=O14, respectively. Therefore, it was considered appropriate to carry out these axial interactions, employing both chl a 1 and chl a 2, conformers, as shown in Figures S4 and S5. These interactions were proposed since Mg2+ yields more stable complexes with oxygen atom donors than with nitrogen atom donors, and considering that the coordination number of Mg2+ in porphyrins could be five or six [43,44].
The first offered interaction of chl a 1 is with the oxygen molecule (C=O) on ring D, and the Mg–O distance in the optimized geometry is 2.101 Å, as shown in Figure S4a and Table 1. The distance to the oxygen (C=O) on ring E is 2.106 Å, as shown in Figure S4b and Table 1. Similar data were reported by Heimdal et al. (2.18 Å) [45], Rutkowska et al. (2.19 Å) [43], and Timkovich et al. (2.10 Å) [46] for complexes of Mg2+–H2O, and 1.9–2.3 Å for Mg–RNA complexes [47]. The smaller value for chl a 1-α-D–AFB1 is explained considering a minor steric hindrance. This effect plays an important role, because in the chl a 1-α-D–AFB1 complex, the C11=O14 of AFB1 is α-located, with a small section between N1 and N4, as shown in Figure 1 and Figure S4a. Related to C1=O12, in the chl a 1-α-E–AFB1 complex, the AFB1 is α-positioned, again with a small section between N1 and N4, as shown in Figure 1 and Figure S4b. This confirms that the D ring (lactone moiety) is the most active site, which is in agreement with data from the literature [24].
On the other hand, in the chl a 1-β-D–AFB1 complex, the Mg–O distance has a value of 2.124 Å, as shown in Figure S4c and Table 1. For the chl a 1-β-E–AFB1 complex, this value is 2.111 Å, as show in Figure S4d and Table 1.
In the complex with the higher-energy value (chl a 1–AFB1), the Mg–N interatomic distances are longer in comparison to uncoordinated chl a 1 (see Table 1). This behavior must be due to a saturated bond in the N1 ring. It has been reported that the Mg–N bond can be elongated to 0.02–0.04 Å by neutral ligands [45]. In this work, the resulting distance order for all complexes was N1 > N3 > N2 > N4, in agreement with previous reports [48,49,50]. The Mg2+–AFB1 complex caused small but noticeable changes in the geometry of the porphyrin moiety of chl a 1 due to a change in the coordination number (4 to 5) of the Mg2+ ion. It is important to note that in chl a 1-α-D–AFB1, the substituents on N2 (vinyl) and N3 (methyl) change their configuration. Additionally, for chl a 1-α-E–AFB1, chl a 1-β-D–AFB1, and chl a 1-β-E–AFB1, a change in configuration is also perceived for the vinyl group on N2.
In general, the Mg2+ ion coordinated with the nitrogen atoms yielded a square-based pyramid geometry with the Mg2+ located out-of-plane due to the coordination number (5), in agreement with literature data [35,47,48,49,50,51,52,53,54,55,56]. A displacement of the Mg2+ ion toward the axial ligand was perceived from 0.57 to 0.68 Å; according to Heimdal et al. [45] and Zucchelli et al., this displacement was 0.43–0.54 Å [52]. In addition, AFB1 caused a relatively strong polarization of the chlorophyll molecule [54,57,58].
2.3.3. Geometry of Unfolded Chlorophyll with Two AFB1 Molecules
Since six is the common coordination number of the magnesium ion [43] and satisfies its coordination sphere, it was proposed as the coordination number of chlorophyll (chl a 1 and chl a 2) with two AFB1 molecules. Accordingly, the β and α coordinations with C1=O12 or C11=O14 (rings E and D) were also considered, as shown in Figures S6 and S7, respectively. Additionally, the magnesium atom exhibits a coordination number of five, the water molecule being the fifth axial ligand [44,55].
Thus, for the interaction between oxygen in ring E and chl a 1 (chl a 1-E–2AFB1 complex), the corresponding Mg–O distances for β and α interactions were 2.228 and 2.351 Å, as shown in Figure S6a and Table 1. For the analog interactions with the oxygen in ring D (chl a 1-D–2AFB1 complex), the Mg–O distances were 2.230 and 2.428 Å for β and α interactions, respectively, as shown in Figure S6b and Table 1. These values agree with those reported by Ben Fredj et al. (2.24 Å) [44], Rutkowska et al. (2.26 Å) [43], and the values between 2.210 and 2.267 Å reported by Ghosh et al. [56].
The previously mentioned values are smaller in both complexes due to steric hindrance with N2 and N3 rings. Hence, it is convenient to highlight that, for the chl a 1-D–2AFB1 complex, the AFB1 molecule is more internally situated, in comparison to the chl a 1-E–2AFB1 complex, generating more steric hindrance and consequently larger bond distances.
Regarding the Mg–N interatomic distances, they were longer in both previously mentioned complexes in comparison with that in the uncoordinated chl a 1. This is shown in Table 1. Moreover, the previous order established for the distances of Mg–N, N1 > N3 > N2 > N4, is also maintained in these complexes [48,49,50]. Consequently, the Mg2+–2AFB1 complex achieved small but noticeable changes in the configuration of the vinylic group on N2. It is important to highlight that the Mg2+ ion satisfies their coordination sphere, displaying an octahedral geometry due to the acquired coordination number of six, setting the magnesium ion in a plane [51,52,53,56,59]. Thus, the Mg–N bond distances decreased [44].
2.3.4. Geometry of Folded Chlorophyll with One AFB1 Molecule
For the chl a 2–AFB1 complex, axial attacks on the Mg2+ ion by oxygen atoms (C1=O12 or C11=O14) were considered. The first displayed interaction was with the oxygen on ring D; the Mg–O distance in the optimized geometry was 2.123 Å (Figure S5a, Table 1). The distance to the oxygen on ring E is 2.080 Å (Figure S5b, Table 1); similar data were reported by Heimdal et al. (2.18 Å) [45], Rutkowska et al. (2.19 Å) [43], and Timkovich et al. (2.10 Å) [46]. The minor value for chl a 2-α-E–AFB1 is due to a steric hindrance, since the AFB1 molecule is located under N1 and N4. For the chl a 2-α-D–AFB1 complex, the AFB1 molecule is under N1, and ring A of AFB1 is located under N3.
On the other hand, for the chl a 2-β-E–AFB1 complex, the Mg–O distance has a value of 2.120 Å (Figure S5c, Table 1), and that for the chl a 2-β-D–AFB1 complex was 2.119 Å (Figure S5d, Table 1). Again, the most active site is the D ring [24].
Moreover, in the higher-energy chl a 2–AFB1 complex, the Mg–N interatomic distances are longer than in uncoordinated chl a 2 (Table 1) due to the saturated bond on the N1 ring, as previously reported (0.02 to 0.04 Å) [45]. In this work, the resulting distance order for all complexes was N1 > N3 > N2 > N4, in agreement with previous reports [48,49,50]. Additionally, the Mg2+–AFB1 complex caused small but noticeable changes in the geometry of the porphyrin moiety of chl a 2-α-D–AFB1, chl a 2-α-E–AFB1, and chl a 2-β-E–AFB1, which was due to a change in the coordination number (four to five) of the Mg2+ ion. As in the case of chl a 1, comparable changes in configuration for the substituents were perceived, and for chl a 2-β-D–AFB1, a change was observed in the methyl substituent on N3. As previously shown for chl a 1, the complexes also yielded a square-based pyramid geometry [35,47,48,49,50,51,52,53,54,55,56]. A displacement of the Mg2+ ion toward the axial ligand was perceived from 0.57 to 0.68 Å [45]; according to Zucchelli et al., this displacement was 0.43–0.54 Å [52]. Additionally, the AFB1 caused a comparatively robust polarization in the chlorophyll molecule [54,57,58].
2.3.5. Geometry of Folded Chlorophyll with Two AFB1 Molecules
For the β and α interactions with the oxygen on ring E of the chl a 2-E–2AFB1 complex, the Mg–O distances were 2.251 and 2.186 Å, respectively (Figure S7a, Table 1). In addition, for the interactions with the oxygen on ring D of the chl a 2-D–2AFB1 complex, the corresponding Mg–O distances were 2.285 and 2.167 Å (Figure S7b, Table 1). These values are in agreement with those reported by Ben Fredj et al. (2.24 Å) [44], Rutkowska et al. (2.26 Å) [43], and the 2.210 to 2.267 Å reported by Ghosh et al. [56]. The α values are shorter in both complexes due to steric hindrance.
In addition, Mg–N interatomic distances are slightly longer than those of chl a, as shown in Table 1. This is due to the saturated bond on the N1 ring, which was 2.131 Å and 2.128 Å for chl a and complex chl a 2-D–2AFB1, respectively. The other Mg–N bonds exhibited elongation from 0.02 to 0.04 Å [45,46,47,48]; the previous order established for the distances of Mg–N, N1 > N3 > N2 > N4, is also maintained in this complex type [48,49,50]. Additionally, the Mg2+–AFB1 complex yielded changes in the configuration of substituents on N2; the Mg2+ ion satisfied its coordination sphere, showing an octahedral geometry [51,52,53,56,59], and the Mg–N bond distances decreased when the magnesium atom came into the plane [44].
2.4. Interaction Energy of the Complexes in Gas Phase
2.4.1. Considering the Coupling of One AFB1 Molecule with chl a 1 and chl a 2
In chl a 1, considering both α and β configurations, the chl a 1-α-E–AFB1 complex was more stable, at −36.4 kcal/mol, as shown in Table S2, with differences between 0.7 and 4.3 kcal/mol in comparison with the other complexes. In view of the energy differences between the carbonyl groups in these four complexes, the observed energy values were 0.9–3.6 kcal/mol. When AFB1 is β-oriented, the energetic difference between C1=O12 and C11=O14 is not significant. However, if it is α-oriented, important energy differences are perceived due to steric hindrance in the phytol chain.
Regarding the four chl a 2 complexes, chl a 2-β-E–AFB1, with a value of −39.2 kcal/mol, was more stable, as shown in Table S2. It had a range of 2.7–6.4 kcal/mol in comparison to the other related complexes. In addition, a difference was detected between the carbonyl groups in the complexes. Thus, when the configuration of AFB1 is α, the difference is 2.7 kcal/mol. However, if AFB1 is β-oriented, the difference is 0.4 kcal/mol. In general, considering the eight interactions, chl a 2-β-E–AFB1, with a value of −39.2 kcal/mol, was the most stable of all.
2.4.2. Considering the Coupling of Two AFB1 Molecules with chl a 1 and chl a 2
Table S2 summarizes the energy of interaction values of the corresponding double coupling. Regarding the energy interactions between chl a 1-E–2AFB1 and chl a 1-D–2AFB1, the second was more stable, at −62.3 kcal/mol. The difference between them was 2.2 kcal/mol. Comparing chl a 2-E–2AFB1 and chl a 2-D–2AFB1 complexes, the first was more stable (−64.8 kcal/mol), with a difference between them of 6.7 kcal/mol.
Concerning the four double complexes, the chl a 1 double coupling had energy value differences of 11.2 and 20.1 kcal/mol for D and E, respectively, compared to the chl a 2 analogs.
2.5. Interaction Energy of the Complexes in Water as a Solvent
In general, in the presence of water (ε = 78.4) as a solvent, the observed values in Tables S2 and S3 implicate that the complexes’ stabilities diminish. However, the same tendency is exhibited in both evaluations. For example, as can be seen in Table S2, the chl a 2-β-E–AFB1 complex presents an interaction energy of −39.2 kcal/mol in the gas phase. The same molecule showed a value of −27.9 kcal/mol in the solvent (Table S3); in other words, this complex is the most stable under both conditions (gas vs. solvent). The above may be because water exerts an effect as a coordination agent, causing the Mg2+ ion to adopt a different geometry to the square-based pyramid, or that water molecules solvate the AFB1 or chl a [51,60,61]. Regarding the chl a–H2O complex, Kobayashi and Reimers reported interaction energy values of −15.3, −14.9, and −15.1 kcal/mol, determined using MP2, DFT ωB97XD, and PBE-D3 methods, respectively [34]. According to the latter points and the obtained results, the solvent molecules could display an interaction with chl a.
On the other hand, double complexes also displayed more stability in the gas phase (−64.8 to −58.0 kcal/mol) compared to water (−49.0 to −45.9 kcal/mol). This could be because water solvates the AFB1 molecule, preserving the octahedral geometry of chl a [51,52,53,56,59]. The diaxial complex (chl a–2H2O) is unstable, in agreement with Fredj and Ruiz-López [60]; consequently, the water will not be able to displace the AFB1 molecules in the coordination with the magnesium ion.
2.6. Weak Hydrogen Bond Interactions between the Ester Functions of chl a 1 and chl a 2 with AFB1
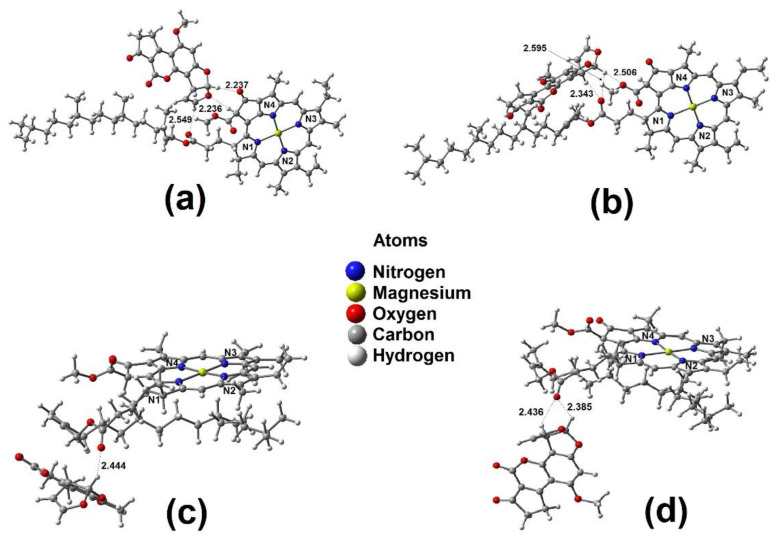
All points made in the previous paragraphs are correlated, and mainly consider interactions with the magnesium ion. In this section, the occurrence of weak hydrogen bond interactions [33] between the ester functions of chl a 1 and chl a 2 with AFB1 are discussed and displayed in Table S3 and Figure 4a–d. It is important to remember that the numeration of several atoms is shown in Figure 1.
Figure 4.
Optimized geometry of (a) chl a 1–AFB1a (three hydrogen bond interactions), (b) chl a 1–AFB1b (three hydrogen bond interactions); (c) chl a 2–AFB1c (one hydrogen bond interaction), and (d) chl a 2–AFB1d (two hydrogen bond interactions).
2.6.1. Chl a 1–AFB1a (Three Hydrogen Bond Interactions)
The chl a 1–AFB1a complex (Figure 4a) shows three interactions: H8 of AFB1 and the oxygen of the ester carbonyl group of the phytol chain; O7 (furane) of AFB1 and the double α-hydrogen atom to both ketonic and ester groups in chl a 1; H6a of AFB1 with ketonic oxygen near N4. These have corresponding bond lengths of 2.237, 2.237, and 2.549 Å.
2.6.2. Chl a 1–AFB1b (Three Hydrogen Bond Interactions)
As can be seen in Figure 4b, the chl a 1-AFB1b complex shows three weak hydrogen bonds: H6a atom of AFB1, proceeding as a bifurcated donor, has interactions with both oxygens of the ester groups of chl a, and the corresponding bond lengths are 2.506 Å and 2.595 Å. The carbonylic oxygen of the acetate group in the phytol chain acts as a bifurcated acceptor with H6a and H9a of the AFB1, exhibiting bond lengths of 2,343Å and 2,595 Å.
The chl a 1-AFB1a interactions are more stable than the chl a 1-AFB1b interactions, with a difference between them of 1.4 kcal/mol. Nevertheless, reverse behavior is shown in solvent conditions, at 1.1 kcal/mol.
2.6.3. Chl a 2–AFB1c (One Hydrogen Bond Interaction)
Chl a 2–AFB1c (Figure 4c) displays only one weak hydrogen bond between hydrogen H6a of AFB1 and the phytol acetate’s carbonylic oxygen; the resulting bond length is 2.444 Å.
2.6.4. Chl a 2–AFB1d (Two Hydrogen Bond Interactions)
Figure 4d presents two weak hydrogen interactions for chl a 2–AFB1, between hydrogen atoms H6a and H9a and the carbonylic oxygen of the phytol acetate. This oxygen atom acts as a bifurcated acceptor, displaying bond lengths of 2.385 Å and 2.436 Å. The chl a 2–AFB1c interactions are more stable than the chl a 1–AFB1d interactions, with a difference between them of 9.2 kcal/mol in the gas phase and 8.6 kcal/mol under solvent conditions. These four complexes show interaction energies lower than the previous complexes. In addition, the chl a 2–AFB1 interactions are more stable than in chl a 1–AFB1. The intermolecular hydrogen bonding interactions are less strong with the solvent effect.
The chl a 2–AFB1c interactions are more stable than in chl a 1–AFB1d. The differences between them are 9.2 kcal/mol in the gas phase and 8.6 kcal/mol under solvent conditions.
2.7. Docking Studies for chl a 1– and chl a 2–AFB1 Complexes
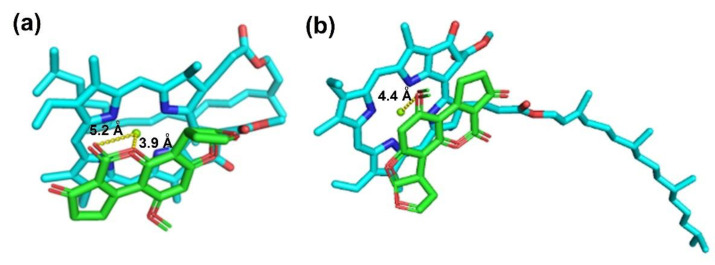
The docking studies were performed employing chl a 1 and chl a 2 as receptors and AFB1 as a ligand. Figure 5 shows that the binding mode between chl a 2 and AFB1 show similar behavior to that previously discussed. Chl a 2– and chl a 1–AFB1 complexes display similar ΔG values, at −6.99 and −6.61 kcal/mol, respectively. Thus, as shown in Figure 5a for chl a 2, the Mg2+ ion interacts with the lactonic group (ring D) of the AFB1 molecule, revealing Mg–O distances with values of 5.2 and 3.9 Å, respectively. For chl a 1, as shown in Figure 5b, the Mg2+ ion interacts with the oxygen of the methoxy group on ring C, with an Mg–O distance of 4.4 Å. These results implicate that the conformation of chl a 2 is preferred (−2934.15 Hartrees). This was reinforced with the HOMO–LUMO data, in agreement with the smaller energy gap.
Figure 5.
Interaction between chlorophyll and AFB1 obtained by docking studies; (a) chl a 2–AFB1 complex, (b) chl a 1–AFB1 complex.
2.8. Molecular Dynamics (MD) Simulations for chl a 2
MD simulations employ Newton’s law to evaluate the motions of complex systems, thus reproducing the behavior of the biological environment, including water molecules. Specifically, they show the changes in conformational states, which are very important in understanding the recognition pattern of macromolecule–ligand complexes. In this sense, MD simulations are used to identify the motions that can be modeled using this methodology [62]. To perform MD simulations, chl a 2 was selected as a starting molecule because it is the most stable conformation (−2934.15 Hartrees) in comparison with unfolded conformer chl a 1 [31,32].
Figure S8 shows the root-mean-square deviation (RMSD) and radius of gyration of chl a 2 obtained from 50 ns of MD simulations. The RMSD values represent the stability of the simulation and allow for the estimation of the equilibration timescale of the simulation. Thus, in Figure S8a, it is possible observe that RMSD varies from 2.1 to 6.6 without reaching confluence, indicating that chl a 2 presents conformational changes along the entire simulation [63]. In addition, it is possible to perceive a variability in radius of gyration values (Figure S8b). The radius of gyration is a measure of the compactness of a ligand; in this case, the values can be deduced in folding and unfolding processes [64]. As can be seen, these changes in values are representative of folding and unfolding processes of chl a 2.
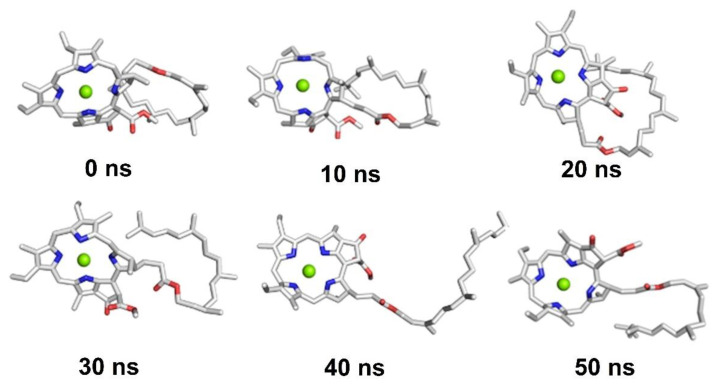
Figure 6 shows snapshots of every 10 ns of MD simulation of chl a 2. As can be seen, chl a 2 displays a conformational change during the entire simulation. Interestingly, at 40 ns of simulation, chl a 2 be disposed to acquire an unfolded conformation, and at 50 ns, chl a 2 begins to returns to its folded conformation. Thus, with this result, it is possible to propose and verify that chl a 2, the most stable conformer, can exist in both conformational states, changing from folded to unfolded. Consequently, with a longer simulation, chl a 2 could adopt its initial stable conformation.
Figure 6.
Snapshots for 50 ns of MD simulation of chl a 2.
2.9. Correlation between Experimental and Theoretical Findings
According to previous results [27], the biosorbents (lettuce, field horsetail, and Formosa firethorn) [26] tested in an in vitro study displayed excellent biosorption of AFB1, employing 0.1% w/v doses (95, 71, and 60% for lettuce, field horsetail, and Formosa firethorn, respectively). It is important to highlight the case of the lettuce, which showed a higher quantity of chl (5.10 mg/g sorbent) in comparison to field horsetail and Formosa firethorn (1.32 and 3.14 mg/g sorbent, respectively). Moreover, it is worth noting that lettuce possesses more chl a (from 1.6- to 3.8-fold) than Formosa firethorn and field horsetail.
In addition, in terms of point of zero charge and zeta potential studies, it was determined that all biomaterials were negatively charged at their surface, agreeing with the molecular electrostatic potential surface data of this study. Regarding chlorophyll, this negative area was identified on the oxygen atoms of both the ketonic carbonyl and the ester carbonyl groups, positioned on the N4 ring. On the other hand, an important zone around the magnesium ion reveals that this site may be subject to a nucleophilic attack [21,35]. Therefore, for AFB1, the electrostatic potential is more reactive around the oxygen atoms localized on the D and E rings, accomplishing a nucleophilic attack. Furthermore, according to the atomic charge data in Table S1 for chl a 1 and chl a 2, and their complexes, oxygen and nitrogen atoms possess negative charges, and the magnesium atom retains a positive charge, confirming the nucleophilic attack from oxygen atoms of AFB1 to chl a 1 and to chl a 2. Complementarily, the HOMO–LUMO data show that the D and E rings are considered as the interaction sites with a cationic center (magnesium ion) [38], supporting the maximum hardness principle [40,41]. Consequently, the anticarcinogenic activity should be improved if a large quantity of chlorophyll is present in the biosorbents.
3. Materials and Methods
3.1. Quantum Chemical Calculations
Density functional theory [65,66] calculations were carried out using the Gaussian09 (Version 09, Gaussian, Inc., Wallingford CT, UK, 2013) [67] and Spartan’06 (Version 06, Wavefunction, Inc., Irvine CA, USA) [68] software. All the structures considered in the study, shown in Figure 1, were constructed using the graphical interface of Spartan ‘06 and Gaussview5 (Version 05, Gaussian, Inc., Wallingford CT, UK, 2013) [69] programs. Geometry optimizations and frequency analysis for the complexes and the individual fragments were carried out using the hybrid meta-generalized gradient approximation functional M06-2X [70]. It was efficacious to obtain configurations with all the real frequencies at this level. The choice of the M06-2X functional was based on the fact that it has been demonstrated as appropriate to perform modeling of these kinds of molecules [71,72], and the use of basis set 6-311G(d,p) [73]. Default convergence criteria were employed in each software package. The geometries of all the different configurations of chl a, and their complexes with AFB1, were fully optimized in the gas phase. The results confirm that the calculated geometry is at a minimum (all the normal modes are positive). The molecular electrostatic potential (MEP) map is habitually used as a predictive and interpretative tool in chemistry; creating a reactivity map displaying the molecular regions makes electrophilic and nucleophilic interactions more likely [74]. MEP maps can be obtained by mapping electrostatic potential onto the total electron density with a color code [75]. MEP contour maps provide a simple way to predict how different geometries could interact [76]. This property was determined using the DFT (M06-2X/6-311G(d,p) method. The HOMO–LUMO gap is a typical quantity used to describe the stability of certain molecules [77]. In this study, the corresponding calculations were based on a complete chl a model containing 135 atoms (chl a), as described in Figure 1. This model includes the whole structure of chl a, incorporating the phytol chain, not considered in several preceding studies on chl a.
The solvent effect was also calculated using the self-consistent reaction field (SCRF) method and the Tomasi’s polarizable continuum model (PCM), using water as a medium (dielectric value ε= 78.4) [78,79]. Natural bond orbital (NBO) was used for the electron natural population analysis in the Gaussian09 program. Natural population analysis (NPA) was used to compare differences rather than determining absolute atomic charges [80]. An atomic charge is not a physically obvious parameter; its value depends on the scheme by which the electron density of a molecule is partitioned. Additionally, a natural charge results from NPA in order to convert a wave function’s delocalized molecular orbitals into localized ones. This is performed to maintain all the information contained in the wave function [36]. The solvent effect and atomic charge were calculated at the same level of theory for all the molecules involved in the present study.
3.2. Docking Studies
The three-dimensional (3D) structure of chl a 1, chl a 2, and AFB1 were obtained as previously described. For this, chl a 1 and chl a 2 were employed as macromolecules, and AFB1 as a ligand. Docking studies were performed employing Autodock 4.2 [81]. A rectangular lattice (126 × 126 × 126) was superimposed on the entire macromolecule to achieve a blind docking procedure. All docking simulations were conducted using the hybrid Lamarckian genetic algorithm with an initial population of 100 randomly placed individuals and a maximum of 107 energy evaluations. All other parameters were maintained at their default settings. The resulting docked orientations were clustered together, within a root-mean-square deviation (RMSD) of 0.5. Conformations with the lowest free energy binding (ΔG) and the highest frequency were selected employing Autodock tools [82]. The images were created using PyMol.
3.3. Molecular Dynamics Simulations
For the molecular dynamics (MD) simulations, chl a 2 was submitted to MD employing the NAMD 2.6 software [83]. The parameters and topology for chl a 2 were obtained employing the online SwissParam server (http:// www.swissparam.ch/ accessed on 6 April 2022). Hydrogen atoms were added with the psfgen command within the VMD program [84], and the structure was minimized using the steepest descent algorithm for 2000 steps using the CHARMM27 force field [85]. The resulting structure was immersed in water (10 Å TIP3 water model), and the charge was neutralized using 2 Cl− ions. The particle mesh Ewald method [86] and periodic boundary conditions were applied to complete the electrostatic calculations. Additionally, Nose–Hoover Langevin piston pressure control was used, and maintained the temperature at 310 K [87]. The SHAKE method was used to provide an integration time step of 2 fs while keeping all bonds connected to the hydrogen atoms rigid [88]. The equilibration protocol involved 1500 minimization steps, followed by 30 ps of MD at 0 K for the water and ions while freezing the entire protein. Once the minimization of the entire system was achieved, the temperature was increased from 10 to 310 K over 30 ps to ensure that it would continue to modify its volume with 30 ps of NTP dynamics [88]. As a final step, the NTV dynamics continued for 50 ns. The trajectory of the system was stored every 1 ps, and the simulations were analyzed by capturing several snapshots every 1 ns. The snapshots and RMSD were obtained using the carma program [89]. The RMSD was analyzed to determine whether the protein had undergone a conformational change, because this value reflects the distance between pairs of the same atoms, represented by d, with respect to time. All the computational work was performed using pmemd cuda on an Intel Core i7–980x 3.33 Ghz Linux workstation with 12 Gb of RAM, 2 NVIDIA Geforce GTX530 video cards, and 1 NVIDIA Geforce GTX580 video card.
4. Conclusions
The M06-2X density functional led to the qualitative and quantitative description of chemical interactions among chl a 1 and chl a 2 with one and two AFB1 molecules. To our knowledge, chl a 2 alludes to a novel conformation. The obtained results revealed that the interaction sites of chl a 1 and chl a 2 are explained using molecular electrostatic potential surface, molecular orbitals (HOMO and LUMO), and charge calculations; these properties were conveniently employed for the characterization and successful description of the preferred interaction sites, affording a well-founded explanation on behalf of the coordination of chl a 1 and chl a 2 with one and two AFB1 molecules. When the interaction between one AFB1 molecule and the chlorophyll molecule is β-oriented, the corresponding coordination product appeared more stable. However, when the interaction was between two AFB1 molecules and chl a, the chl a 2-E–2AFB1 interaction was the most stable. An energetic interaction difference with chl a was also found when comparing the oxygen’s carbonyl groups between the D and E rings. The acquired energy interactions between chl a 1 and chl a 2, and the aflatoxin, considering water as the solvent, are lower than those shown in the gas phase. This is probably because chl a 1 and chl a 2 undergo a greater interaction with the medium than with AFB1. These findings were supported by results achieved from the docking studies, with the interaction between chl a 2 and one AFB1 molecule being the most stable. This is because the folded conformation is preferred. In addition, regarding molecular dynamics simulations, chl a 2 shows conformational changes along the entire simulation, meaning that it probably exists in folding and unfolding conformational equilibrium processes. Finally, considering all the calculated complexes (folded and unfolded α and β configurations and the involved carbonyl groups), the complexes with two AFB1 molecules were more stable than those with only one AFB1. Thus, it is important to highlight that, in general, biosorbents containing chlorophyll could improve AFB1 adsorption.
Acknowledgments
The authors acknowledge UNAM-PAPIIT for the financial support for this research through the Grants IN212421 and IN207920. The authors are grateful to Dirección General de Cómputo y de Tecnologías de Información y Comunicación (DGTIC-UNAM) for the use of the Supercomputer MIZTLI-LANCAD-UNAM-DGTIC-400. Additionally, thanks to Moises Hernandez Duarte for his technical assistance.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/ijms23116068/s1.
Author Contributions
Conceptualization, J.M. and M.I.N.-V.; methodology, A.V.-D., G.T.-I. and J.M.A.-H.; software, M.H.-R. and M.I.N.-V.; formal analysis, J.M. and M.I.N.-V.; investigation, A.V.-D., G.T.-I. and J.M.A.-H.; data curation, M.H.-R. and J.M.A.-H.; writing—original draft preparation, J.M. and M.I.N.-V.; writing—review and editing, M.I.N.-V. and R.M.R.; visualization, M.I.N.-V. and A.M.-A.; supervision, M.I.N.-V., R.M.R. and A.M.-A. All authors have read and agreed to the published version of the manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data reported in this study are available upon request to atlanta126@gmail.com or nicovain@yahoo.com.mx.
Conflicts of Interest
The authors declare no conflict of interest.
Funding Statement
National Autonomous University of Mexico: PAPIIT IN212421 and IN207920. The APC was funded by University of Arkansas, Department of Poultry Science, Fayetteville, USA.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Asao T., Buchi G., Abdel-Kader M., Chang S.B., Wick E.L., Wogan G. Aflatoxins b and g. J. Am. Chem. Soc. 1963;85:1706–1707. doi: 10.1021/ja00894a050. [DOI] [PubMed] [Google Scholar]
- 2.Feibelman T.P., Cotty P.J., Doster M., Michailides T. A morphologically distinct strain of Aspergillus nomius. Mycologia. 1998;90:618–623. doi: 10.1080/00275514.1998.12026951. [DOI] [Google Scholar]
- 3.Ostry V., Malir F., Toman J., Grosse Y. Mycotoxins as human carcinogens-the IARC Monographs classification. Mycotoxin Res. 2017;33:65–73. doi: 10.1007/s12550-016-0265-7. [DOI] [PubMed] [Google Scholar]
- 4.Probst C., Njapau H., Cotty P.J. Outbreak of an acute aflatoxicosis in Kenya in 2004: Identification of the causal agent. Appl. Environ. Microbiol. 2007;73:2762–2764. doi: 10.1128/AEM.02370-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Azziz-Baumgartner E., Lindblade K., Gieseker K., Rogers H.S., Kieszak S., Njapau H., Schleicher R., McCoy L.F., Misore A., DeCock K., et al. Case-control study of an acute aflatoxicosis outbreak, Kenya, 2004. Environ. Health Perspect. 2005;113:1779–1783. doi: 10.1289/ehp.8384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lewis L., Onsongo M., Njapau H., Schurz-Rogers H., Luber G., Kieszak S., Nyamongo J., Backer L., Dahiye A.M., Misore A., et al. Aflatoxin contamination of commercial maize products during an outbreak of acute aflatoxicosis in eastern and central Kenya. Environ. Health Perspect. 2005;113:1763–1767. doi: 10.1289/ehp.7998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kamala A., Shirima C., Jani B., Bakari M., Sillo H., Rusibamayila N., De Saeger S., Kimanya M., Gong Y., Simba A. Outbreak of an acute aflatoxicosis in Tanzania during 2016. World Mycotoxin J. 2018;11:311–320. doi: 10.3920/WMJ2018.2344. [DOI] [Google Scholar]
- 8.Negishi T., Arimoto S., Nishizaki C., Hayatsu H. Inhibitory effect of chlorophyll on the genotoxicity of 3-amino-1-methyl-5H-pyrido [4,3-b indole (Trp-P-2) Carcinogenesis. 1989;10:145–149. doi: 10.1093/carcin/10.1.145. [DOI] [PubMed] [Google Scholar]
- 9.Kimm S. Antimutagenic activity of chlorophyll to direct-and indirect-acting mutagens and its contents in vegetables. Korean J. Biochem. 1982;14:1–8. [Google Scholar]
- 10.Barale R., Zucconi D., Bertani R., Loprieno N. Vegetables inhibit, in vivo, the mutagenicity of nitrite combined with nitrosable compounds. Mutat. Res. 1983;120:145–150. doi: 10.1016/0165-7992(83)90156-2. [DOI] [PubMed] [Google Scholar]
- 11.Lai C.-N., Butler M.A., Matney T.S. Antimutagenic activities of common vegetables and their chlorophyll content. Mutat. Res./Gen. Toxicol. 1980;77:245–250. doi: 10.1016/0165-1218(80)90057-9. [DOI] [Google Scholar]
- 12.Endo Y., Usuki R., Kaneda T. Antioxidant effects of chlorophyll and pheophytin on the autoxidation of oils in the dark. II. The mechanism of antioxidative action of chlorophyll. J. Am. Oil Chem. Soc. 1985;62:1387–1390. doi: 10.1007/BF02545965. [DOI] [Google Scholar]
- 13.Endo Y., Usuki R., Kaneda T. Antioxidant effects of chlorophyll and pheophytin on the autoxidation of oils in the dark. I. Comparison of the inhibitory effects. J. Am. Oil Chem. Soc. 1985;62:1375–1378. doi: 10.1007/BF02545962. [DOI] [Google Scholar]
- 14.Fahey J.W., Stephenson K.K., Dinkova-Kostova A.T., Egner P.A., Kensler T.W., Talalay P. Chlorophyll, chlorophyllin and related tetrapyrroles are significant inducers of mammalian phase 2 cytoprotective genes. Carcinogenesis. 2005;26:1247–1255. doi: 10.1093/carcin/bgi068. [DOI] [PubMed] [Google Scholar]
- 15.Chan J.Y.-W., Tang P.M.-K., Hon P.-M., Au S.W.-N., Tsui S.K.-W., Waye M.M.-Y., Kong S.-K., Mak T.C.-W., Fung K.-P. Pheophorbide a, a major antitumor component purified from Scutellaria barbata, induces apoptosis in human hepatocellular carcinoma cells. Planta Med. 2006;72:28–33. doi: 10.1055/s-2005-873149. [DOI] [PubMed] [Google Scholar]
- 16.Jubert C., Mata J., Bench G., Dashwood R., Pereira C., Tracewell W., Turteltaub K., Williams D., Bailey G. Effects of chlorophyll and chlorophyllin on low-dose aflatoxin B1 pharmacokinetics in human volunteers. Cancer Prev. Res. 2009;2:1015–1022. doi: 10.1158/1940-6207.CAPR-09-0099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Simonich M.T., Egner P.A., Roebuck B.D., Orner G.A., Jubert C., Pereira C., Groopman J.D., Kensler T.W., Dashwood R.H., Williams D.E., et al. Natural chlorophyll inhibits aflatoxin B 1-induced multi-organ carcinogenesis in the rat. Carcinogenesis. 2007;8:1294–1302. doi: 10.1093/carcin/bgm027. [DOI] [PubMed] [Google Scholar]
- 18.Newmark H.L. A hypothesis for dietary components as blocking agents of chemical carcinogenesis: Plant phenolics and pyrrole pigments. Nutr. Cancer. 1984;6:58–70. doi: 10.1080/01635588509513807. [DOI] [PubMed] [Google Scholar]
- 19.Simonich M.T., McQuistan T., Jubert C., Pereira C., Hendricks J.D., Schimerlik M., Zhu B., Dashwood R.H., Williams D.E., Bailey G.S. Low-dose dietary chlorophyll inhibits multi-organ carcinogenesis in the rainbow trout. Food Chem. Toxicol. 2008;46:1014–1024. doi: 10.1016/j.fct.2007.10.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Dashwood R., Negishi T., Hayatsu H., Breinholt V., Hendricks J., Bailey G. Chemopreventive properties of chlorophylls towards aflatoxin B1: A review of the antimutagenicity and anticarcinogenicity data in rainbow trout. Mutat. Res. 1998;399:245–253. doi: 10.1016/S0027-5107(97)00259-5. [DOI] [PubMed] [Google Scholar]
- 21.Huq F., Yunos N. A molecular modelling analysis of the toxicity of Aflatoxin B1 and its modulation by chlorophyllin. Int. J. Pure Appl. Chem. 2007;2:371–376. [Google Scholar]
- 22.Breinholt V., Schimerlik M., Dashwood R., Bailey G. Mechanisms of chlorophyllin anticarcinogenesis against aflatoxin B1: Complex formation with the carcinogen. Chem. Res. Toxicol. 1995;8:506–514. doi: 10.1021/tx00046a004. [DOI] [PubMed] [Google Scholar]
- 23.Méndez-Albores A., Nicolás-Vázquez M.I., Miranda-Ruvalcaba R., Moreno-Martínez E. Mass spectrometry/mass spectrometry study on the degradation of B-aflatoxins in maize with aqueous citric acid. Am. J. Agric. Biol. Sci. 2008;3:482–489. [Google Scholar]
- 24.Nicolas-Vazquez I., Mendez-Albores A., Moreno-Martınez E., Miranda R., Castro M. Role of lactone ring in structural, electronic, and reactivity properties of aflatoxin B1: A theoretical study. Arch. Environ. Contam. Toxicol. 2010;59:393–406. doi: 10.1007/s00244-010-9501-x. [DOI] [PubMed] [Google Scholar]
- 25.Escobedo-González R., Méndez-Albores A., Villarreal-Barajas T., Aceves-Hernández J.M., Miranda-Ruvalcaba R., Nicolás-Vázquez I. A theoretical study of 8-Chloro-9-hydroxy-Aflatoxin B1, the conversion product of aflatoxin B1 by neutral electrolyzed water. Toxins. 2016;8:225. doi: 10.3390/toxins8070225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Méndez-Albores A., Escobedo-González R., Aceves-Hernández J.M., García-Casillas P., Nicolás-Vázquez M.I., Miranda-Ruvalcaba R. A theoretical study of the adsorption process of B-aflatoxins using Pyracantha koidzumii (Hayata) Rehder biomasses. Toxins. 2020;12:283. doi: 10.3390/toxins12050283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nava-Ramírez M.J., Salazar A.M., Sordo M., López-Coello C., Téllez-Isaías G., Méndez-Albores A., Vázquez-Durán A. Ability of low contents of biosorbents to bind the food carcinogen aflatoxin B1 in vitro. Food Chem. 2021;345:128863. doi: 10.1016/j.foodchem.2020.128863. [DOI] [PubMed] [Google Scholar]
- 28.Vázquez-Durán A., Nava-Ramírez M.D.J., Hernández-Patlán D., Solís-Cruz B., Hernández-Gómez V., Téllez-Isaías G., Méndez-Albores A. Potential of kale and lettuce residues as natural adsorbents of the carcinogen aflatoxin B1 in a dynamic gastrointestinal tract-simulated model. Toxins. 2021;13:771. doi: 10.3390/toxins13110771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hayashi T., Schimerlik M., Bailey G. Mechanisms of chlorophyllin anticarcinogenesis: Dose–responsive inhibition of aflatoxin uptake and biodistribution following oral co-administration in rainbow trout. Toxicol. Appl. Pharmacol. 1999;158:132–140. doi: 10.1006/taap.1999.8695. [DOI] [PubMed] [Google Scholar]
- 30.Alvarado-González M., Flores-Holguín N., Glossman-Mitnik D. Computational nanochemistry study of the molecular structure and properties of chlorophyll a. Int. J. Photoenergy. 2013;2013:1–8. doi: 10.1155/2013/424620. [DOI] [PubMed] [Google Scholar]
- 31.Schulte T., Hiller R.G., Hofmann E. X-ray structures of the peridinin-chlorophyll-protein reconstituted with different chlorophylls. FEBS Lett. 2010;584:973–978. doi: 10.1016/j.febslet.2010.01.041. [DOI] [PubMed] [Google Scholar]
- 32.Desiraju G., Steiner T. The Weak Hydrogen Bond, in Structural Chemistry and Biology. Oxford University Press; New York, NY, USA: 2001. p. 506. [Google Scholar]
- 33.Kobayashi R., Reimers J.R. Free energies for the coordination of ligands to the magnesium of chlorophyll-a in solvents. Mol. Phys. 2015;113:1648–1654. doi: 10.1080/00268976.2014.1003620. [DOI] [Google Scholar]
- 34.Chen M., Cai Z.-L. Theoretical study on the thermodynamics properties of chlorophyll d-peptides coordinating ligand. Biochim. Biophys. Acta. 2007;1767:603–609. doi: 10.1016/j.bbabio.2007.01.006. [DOI] [PubMed] [Google Scholar]
- 35.Reed A.E., Weinstock R.B., Weinhold F.A. Natural population analysis. J. Chem. Phys. 1985;83:735–746. doi: 10.1063/1.449486. [DOI] [Google Scholar]
- 36.Gross K.C., Seybold P.G., Peralta-Inga Z., Murray J.S., Politzer P. Comparison of quantum chemical parameters and Hammett constants in correlating pKa values of substituted anilines. J. Org. Chem. 2001;66:6919–6925. doi: 10.1021/jo010234g. [DOI] [PubMed] [Google Scholar]
- 37.Politzer P., Murray J.S. The fundamental nature and role of the electrostatic potential in atoms and molecules. Theor Chim Acta. 2002;108:134–142. doi: 10.1007/s00214-002-0363-9. [DOI] [Google Scholar]
- 38.Nicolás I., Vilchis M., Aragón N., Miranda R., Hojer G., Castro M. Theoretical study of the structure and antimicrobial activity of horminone. Int. J. Quantum Chem. 2003;93:411–421. doi: 10.1002/qua.10581. [DOI] [Google Scholar]
- 39.Bechaieb R., Lakhdar Z., Gérard H. DFT and TD-DFT studies of Mg-substitution in chlorophyll by Cr(II), Fe(II) and Ni(II) Chem. Africa. 2018;1:79–86. doi: 10.1007/s42250-018-0003-y. [DOI] [Google Scholar]
- 40.Chattaraj P.K., Sakar U., Roy D.R. Electrophilicity index. Chem. Rev. 2006;106:2065–2091. doi: 10.1021/cr040109f. [DOI] [PubMed] [Google Scholar]
- 41.Pearson R.G. The principle of maximum hardness. Acc. Chem. Res. 1993;26:250–255. doi: 10.1021/ar00029a004. [DOI] [Google Scholar]
- 42.Eliel E.L., Wilen S.H., Monder L.N. Stereochemistry of Organic Compounds. John Wiley & Sons, Inc.; New York, NY, USA: 1994. pp. 698–718. [Google Scholar]
- 43.Rutkowska-Zbik D., Witko M., Fiedor L. Ligation of water to magnesium chelates of biological importance. J. Mol. Model. 2013;19:4661–4667. doi: 10.1007/s00894-012-1459-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ben Fredj A., Ben Lakhdar Z., Ruiz-López M.F. Six-coordination in chlorophylls: The fundamental role of dispersion energy. Chem. Phys. Lett. 2009;472:243–247. doi: 10.1016/j.cplett.2009.03.025. [DOI] [Google Scholar]
- 45.Heimdal J., Jensen K.P., Devarajan A., Ryde U. The role of axial ligands for the structure and function of chlorophylls. J. Biol. Inorg. Chem. 2007;2:49–61. doi: 10.1007/s00775-006-0164-z. [DOI] [PubMed] [Google Scholar]
- 46.Timkovich R., Tulinsky A. Structure of aquomagnesium tetraphenylporphyrin. J. Am. Chem. Soc. 1969;71:4430–4432. doi: 10.1021/ja01044a018. [DOI] [Google Scholar]
- 47.Leonarski F., D’ascenzo L., Auffinger P. Nucleobase carbonyl groups are poor Mg2+ inner-sphere binder but excellent monovalent ion binders—A critical PDB survey. RNA. 2019;25:173–192. doi: 10.1261/rna.068437.118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Bechaieb R., Fredj A.B., Akacha A.B., Gérard H. Interactions of copper (II) and zinc (II) with chlorophyll: Insights from Density Functional Theory studies. New J. Chem. 2016;40:4543–4549. doi: 10.1039/C5NJ03244J. [DOI] [Google Scholar]
- 49.Ben Fredj A. Theoretical study of the dimerization of chlorophyll(a) and its hydrates: Implication for chlorophyll (a) aggregation. Helv. Chim. Acta. 2016;99:1–13. doi: 10.1002/hlca.201500027. [DOI] [Google Scholar]
- 50.Sharma Yamijala S.R.K.C., Periyasamy G., Pati S.K. Computational studies on structural and excited-state properties of modified chlorophyll f with various axial ligands. J. Phys. Chem. A. 2011;115:12298–12306. doi: 10.1021/jp2041235. [DOI] [PubMed] [Google Scholar]
- 51.Borah K.D., Bhuyan J. Magnesium porphyrins with relevance to chlorophylls. Dalton Trans. 2017;46:6497–6509. doi: 10.1039/C7DT00823F. [DOI] [PubMed] [Google Scholar]
- 52.Zucchelli G., Brogioli D., Casazza A.P., Garlaschi F.M., Jennings R.C. Chlorophyll ring deformation modulates Qy electronic energy in chlorophyll-protein complexes and generates spectral forms. Biophys. J. 2007;93:2240–2254. doi: 10.1529/biophysj.107.104554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Saito K., Suzuki T., Ishikita H. Absorption-energy calculations of chlorophyll a and b with an explicit solvent model. J. Photochem. Photobiol. A Chem. 2018;358:422–431. doi: 10.1016/j.jphotochem.2017.10.003. [DOI] [Google Scholar]
- 54.Huheey J.E. Inorganic Chemistry: Principles of Structure and Reactivity. 3rd ed. Harper & Row, Publishers; New York, NY, USA: 1983. p. 506. [Google Scholar]
- 55.Balaban T.S., Fromme P., Holzwarth A.R., Kraub N., Plokhorenko V.I. Relevance of diastereotopic ligation of magnesium atoms of chlorophylls in photosystem I. Biochim. Biophys. Acta Bioenerg. 2002;1556:197–207. doi: 10.1016/S0005-2728(02)00363-8. [DOI] [PubMed] [Google Scholar]
- 56.Ghosh A., Mobin S.M., Fröhlich R., Butcher R.J., Maity D.K., Ravikanth M. Effect of five membered versus six membered meso-substituents on structure and electronic properties of Mg(II) porphyrins: A combined experimental and theoretical study. Inorg. Chem. 2010;49:8287–8297. doi: 10.1021/ic1008522. [DOI] [PubMed] [Google Scholar]
- 57.Jing Z., Liu C., Qi R., Ren P. Many-body effect determines the selectivity for Ca2+ and Mg2+ in proteins. Proc. Natl. Acad. Sci. USA. 2018;115:E7495–E7501. doi: 10.1073/pnas.1805049115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Stevens M.J., Rempe S.L.B. Ion-specific effects in carboxylate binding sites. J. Phys. Chem. B. 2016;120:12519–12530. doi: 10.1021/acs.jpcb.6b10641. [DOI] [PubMed] [Google Scholar]
- 59.Chen X., Pu H., Fang Y., Wang X., Zhao S., Lin Y., Zhang M., Dai H.E., Gong W., Liu L. Crystal structure of the catalytic subunit of magnesium chelatase. Nat. Plants. 2015;1:15125. doi: 10.1038/nplants.2015.125. [DOI] [PubMed] [Google Scholar]
- 60.Fredj A.B., Ruiz-López M.F. Theoretical study of chlorophyll a hydrates formation in aqueous solvents. J. Phys. Chem. B. 2010;114:681–687. doi: 10.1021/jp909380t. [DOI] [PubMed] [Google Scholar]
- 61.Agostiano A., Cosma P., Monica M.D. Spectrocopic and electrochemical characterization of chlorophyll a in different water + organic solvent mixtures. J. Electroanal. Chem. 1990;98:311–324. doi: 10.1016/0022-0728(90)87475-Y. [DOI] [Google Scholar]
- 62.Hernández-Rodríguez M., Rosales-Hernández M.C., Mendieta-Wejebe J.E., Martínez-Archundia M., Basurto J.C. Current tolos and methods in molecualr dynamics (MD) simulations for the drug design. Curr. Med. Chem. 2016;23:3909–3924. doi: 10.2174/0929867323666160530144742. [DOI] [PubMed] [Google Scholar]
- 63.Grossfield A., Zuckerman D.M. Quantifying uncertainty and sampling quality in biomolecular simulations. Annu. Rep. Comput. Chem. 2009;5:23–48. doi: 10.1016/S1574-1400(09)00502-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Vincenzi M., Costantini S., Scala S., Tesauro D., Accardo A., Leone M., Colonna G., Guillon J., Portella L., Trotta A.M., et al. Conformational ensembles explored dynamically from disordered peptides targeting chemokine receptor CXCR4. Int. J. Mol. Sci. 2015;16:12159–12173. doi: 10.3390/ijms160612159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Parr R.G. Density-Functional Theory of Atoms and Molecules. Oxford University Press; New York, NY, USA: 1989. p. 333. [Google Scholar]
- 66.Kohn W., Becke A.D., Parr R.G. Density functional theory of electronic structure. J. Phys. Chem. 1996;100:12974–12980. doi: 10.1021/jp960669l. [DOI] [Google Scholar]
- 67.Frisch M.J., Trucks G.W., Schlegel H.B., Scuseria G.E., Robb M.A., Cheeseman J.R., Scalmani G., Barone V. Gaussian 09. Gaussian, Inc.; Wallingford, UK: 2013. Revision E.01. [Google Scholar]
- 68.Deppmeier B.J., Driessen A.J., Hehre T.S., Hehre W.J., Johnson J.A., Klunzinger P.E., Leonard J.M., Pham I., Pietro W.J., Jianguo Y., et al. Spartan 06 for Windows. Wave Function Inc; Irvine, CA, USA: 2006. [Google Scholar]
- 69.Frisch A., Nielsen A.B., Holder A.J. Gaussview Users Manual. Gaussian Inc; Pittsburgh, PA, USA: 2000. [Google Scholar]
- 70.Zhao Y., Truhlar D.G. The Mo6 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functional sans systematic testing of four Mo6-class functionals and 12 other functionals. Theor. Chem. Acc. 2008;120:215–241. [Google Scholar]
- 71.Torrent-Sucarrat M., Navarro S., Cossío F.P., Anglada J.M., Luis J.M. Relevance of the DFT method to study expanded porphyrins with different topologies. J. Comput. Chem. 2017;38:2819–2828. doi: 10.1002/jcc.25074. [DOI] [PubMed] [Google Scholar]
- 72.Jaramillo P., Coutinho K., Costa Cabral B.J., Canuto S. Ionization of chlorophyll-c2 in liquid metanol. Chem. Phys. Lett. 2012;546:67–73. doi: 10.1016/j.cplett.2012.07.040. [DOI] [Google Scholar]
- 73.Krishnan R., Binkley J.S., Seeger R., Pople J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. Chem. Phys. Lett. 1980;72:650–654. doi: 10.1063/1.438955. [DOI] [Google Scholar]
- 74.Huczyński A., Janczak J., Łowicki D., Brzezinski B. Monensin A acid complexes as a model of electrogenic transport of sodium cation. Biochim. Biophys. Acta. 2012;1818:2108–2119. doi: 10.1016/j.bbamem.2012.04.017. [DOI] [PubMed] [Google Scholar]
- 75.Alam M.J., Ahmad S. Anharmonic vibrational studies of L-aspartic acid using HF and DFT calculations. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2012;96:992–1004. doi: 10.1016/j.saa.2012.07.135. [DOI] [PubMed] [Google Scholar]
- 76.Ramalingam S., Babu P.D.S., Periandy S., Fereyduni E. Vibrational investigation, molecular orbital studies and molecular electrostatic potential map analysis on 3-chlorobenzoic acid using hybrid computational calculations. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2011;4:210–220. doi: 10.1016/j.saa.2011.09.030. [DOI] [PubMed] [Google Scholar]
- 77.Karelson M., Lobanov V.S., Katritzky A.R. Quantum-chemical descriptors in QSAR/QSPR studies. Chem. Rev. 1996;96:1027–1044. doi: 10.1021/cr950202r. [DOI] [PubMed] [Google Scholar]
- 78.Miertus S., Scrocco E., Tomasi J. Electrostatic interactions of a solvent with a continuum. A direct utilization of AB initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981;55:117–129. doi: 10.1016/0301-0104(81)85090-2. [DOI] [Google Scholar]
- 79.Cammi R., Tomasi J. Remarks on the use of the apparent surface charges (ASC) methods in solvation problems: Iterative versus matrix-inversion procedures and the renormalization of the apparent charges. J. Comp. Chem. 1995;16:1449–1458. doi: 10.1002/jcc.540161202. [DOI] [Google Scholar]
- 80.Rubarani P., Gangadharana S., Sampath K. First order hyperpolarizabilities, NPA and Fukui functions of cyclohexanone by density functional theory method. Acta Phys. Pol. A. 2015;127:748–752. [Google Scholar]
- 81.Morris G.M., Huey R., Lindstrom W., Sanner M.F., Belew R.K., Goodsell D.S., Olson A.J. AutoDock4, AutoDock-Tools4, Automated docking with selective receptor flexibility. J. Comput. Chem. 2009;30:2785–2791. doi: 10.1002/jcc.21256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Ramírez-Durán L.A., Rosales-Hernández M.C., Hernández-Rodríguez M., Mendieta-Wejebe J.E., Trujillo-Ferrara J., Correa-Basurto J. Mapping myeloperoxidase to identify its promiscuity properties using docking and molecular dynamics simulations. Curr. Pharm. Des. 2013;19:2204–2215. doi: 10.2174/1381612811319120008. [DOI] [PubMed] [Google Scholar]
- 83.Phillips J.C., Braun R., Wang W., Gumbart J., Tajkhorshid E., Villa E., Chipot C., Skeel R.D., Kal L., Schulten K. Scalable molecular dynamics with NAMD. J. Comp. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Humphrey W., Dalke A., Schulten K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 85.Zhu X., Lopez P.E.M., MacKerell A.D. Recent developments and applications of the CHARMM force fields. WIREs. 2012;2:167–185. doi: 10.1002/wcms.74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Batcho P.F., Case D.A., Schlick T. Optimized particle-mesh Ewald/multiple-time step integration for molecular dynamics simulation. J. Chem. Phys. 2001;115:4003–4041. doi: 10.1063/1.1389854. [DOI] [Google Scholar]
- 87.Martyna G.J., Tobias D.J., Klein M.L. Constant pressure molecular-dynamics algorithms. J. Chem. Phys. 1994;101:4177–4189. doi: 10.1063/1.467468. [DOI] [Google Scholar]
- 88.Miyamoto S., Kollman P.A. SETTLE: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992;13:952–962. doi: 10.1002/jcc.540130805. [DOI] [Google Scholar]
- 89.Glykos N.M. Carma: A molecular dynamics analysis program. J. Comput. Chem. 2006;27:1765–1768. doi: 10.1002/jcc.20482. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data reported in this study are available upon request to atlanta126@gmail.com or nicovain@yahoo.com.mx.