Surface Characterization of Colloidal Silica Nanoparticles by Second Harmonic Scattering: Quantifying the Surface Potential and Interfacial Water Order

Abstract

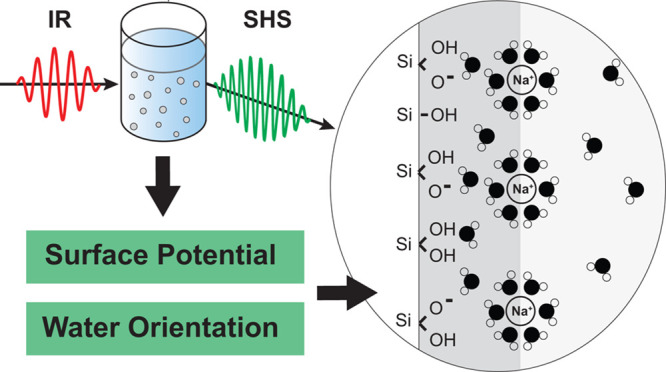
The microscopic description of the interface of colloidal particles in solution is essential to understand and predict the stability of these systems, as well as their chemical and electrochemical reactivity. However, this description often relies on the use of simplified electrostatic mean field models for the structure of the interface, which give only theoretical estimates of surface potential values and do not provide properties related to the local microscopic structure, such as the orientation of interfacial water molecules. Here we apply polarimetric angle-resolved second harmonic scattering (AR-SHS) to 300 nm diameter SiO₂ colloidal suspensions to experimentally determine both surface potential and interfacial water orientation as a function of pH and NaCl concentration. The surface potential values and interfacial water orientation change significantly over the studied pH and salt concentration range, whereas zeta-potential (ζ) values remain constant. By comparing the surface and ζ-potentials, we find a layer of hydrated condensed ions present in the high pH case, and for NaCl concentrations ≥1 mM. For milder pH ranges (pH < 11), as well as for salt concentrations <1 mM, no charge condensation layer is observed. These findings are used to compute the surface charge densities using the Gouy–Chapman and Gouy–Chapman–Stern models. Furthermore, by using the AR-SHS data, we are able to determine the preferred water orientation in the layer directly in contact with the silica interface. Molecular dynamics simulations confirm the experimental trends and allow deciphering of the contributions of water layers to the total response.

Introduction

The surface chemistry of silica is key to a large number of applications, both in research and in industrial processes. In the past few decades, colloidal suspensions of SiO₂ particles have been extensively used for separation, heterogeneous catalysis, and as major components of ceramics and coatings. Colloidal silica is also widely used in the food, health care and pharmaceutical industries, as well as in the production of microelectronics components.¹ The microscopic characterization of colloidal particle interfaces with liquids is of fundamental interest to understand the stability of these systems and their chemical and electrochemical reactivity. In contact with water or another fluid, a solid surface usually develops a charged layer at its surface that is compensated by a distribution of counterions in the surrounding solution. This so-called “electrical double layer” (EDL) has been first put forth by Helmholtz in the 1850s and since then, many different mean field models have been proposed to describe the structure of a solid/electrolyte interface. In such models, the often complex chemical nature of the interface with its different structures and nonuniformity is reduced to a uniformly charged interface, the aqueous phase is represented by a uniform dielectric, and the ions are represented as point charges. The most frequently used model was originally proposed by Gouy and Chapman. In their model a charged interface is in contact with an aqueous solution in which the counterion distribution decays exponentially along the surface normal. This layer is usually referred to as the diffuse double layer (DDL). Stern suggested a modification for high charge densities, comprised of the formation of a condensed layer, or Stern layer, of potentially hydrated counterions close to the surface.²⁻⁴ However, in reality, the structure and chemistry of this electrical double layer is more complex and the electrostatic environment will depend on the local chemical nature of the surface, of the type of ions, their solvation shells and the solvent in the first few atomic dimensions adjacent to the interface.⁴⁻⁹ As many of the mentioned ingredients are challenging to determine experimentally, the microscopic description of a relatively simple interface such as SiO₂/aqueous solution remains elusive.

When considering a colloidal suspension, two parameters are most often reported, as they give an information on the stability of the suspension. These quantities, namely surface charge density and ζ-potential, can be measured with relatively simple experimental techniques. The first quantity is usually determined by potentiometric titrations,¹⁰ assuming that all the charges in the system are confined to an outer smooth surface of the particle, which means such a measurement gives, at best, an upper limit for the surface charge. The second one is obtained by measuring the electrophoretic mobility. The ζ-potential is then calculated from the mobility, assuming a sufficiently thin double layer, and it is defined as the potential at the plane of shear, where the liquid velocity is zero. This plane is likely at some distance outside the particle and includes both the particle plus a 0.3–1 nm thick layer of stationary solvent and ions that can move with the particle in an electric field.¹¹⁻¹⁴ However, the ζ-potential only provides an empirical indication of the stability of colloidal suspensions. Direct information on the surface electrostatics is obtained via the surface potential, which in contrast to the ζ-potential, is not a trivial quantity to access experimentally.¹⁵ The surface potential can be computed from applying the constant capacitor model (CC), the Gouy–Chapman (GC) or the Gouy–Chapman–Stern (GCS) models to titration and ζ-potential data¹⁶ or to nonlinear optics data. Indeed, for planar SiO₂/water interfaces, surface-sensitive techniques such as SHG and sum frequency generation (SFG) have shown to provide insight into the structure of the SiO₂ double layer and water orientation at the interface,^9,17−24 as well as values for surface potential as developed by Eisenthal and co-workers.²⁵⁻³⁰ For colloidal solutions, the so-called “Eisenthal-chi3 method” can be used to estimate values for surface potential;^18,31 however, this method is bound to the use of a model such as the CC, GC, or the GCS one, and does not provide a unique solution for the surface potential, as the number of unknowns in the expression exceeds the number of independently available observables. Information about the potential drop in the EDL can be obtained by X-ray photoelectron spectroscopy (XPS).³² Brown et al. have shown that surface potential values of colloidal SiO₂ particles can be obtained through XPS of a liquid microjet,³³⁻³⁵ using the charge divided energy difference between the binding energy of the Si 2p photoelectrons in the presence of salt and the extrapolated binding energy of the Si 2p photoelectrons at the point of zero charge. However, this measurement requires the use of synchrotron facilities and has some intrinsic limitations due to the relatively low signal-to-noise level. The colloid size needs to be small (ca. 10 nm diameter), and the salt concentration high, ∼>50 mM.

Our laboratory has recently reported an alternative way to determine the average surface potential of colloidal particles in solution using polarimetric angle-resolved nonresonant second harmonic scattering (AR-SHS) measurements.³⁶⁻³⁹ AR-SHS does not require any information on the specific structure of the interface, and only assumes exponential decay of the electrostatic potential several nanometers away from the interface. In this all-optical approach taking advantage of nonlinear light scattering theory, the nonresonantly scattered second harmonic (SH) light that is emitted from the particle interface and the EDL contains enough information to determine the surface potential quantitatively. Additionally, because of the symmetry properties of second harmonic experiments, AR-SHS also provides another essential parameter of interfaces: molecular orientation of water molecules at the interface. These two elements together greatly contribute to the microscopic description of colloid/solvent interfaces.

Here, we apply polarimetric AR-SHS to 300 nm diameter SiO₂ colloids suspended in aqueous solution and extract both surface potential and interfacial molecular orientation. Polarimetric AR-SHS experiments are performed as a function of pH and NaCl concentration. The surface potential values, as well as the interfacial water orientation, vary drastically over the studied pH and salt concentration range, in contrast to the ζ-potential values, which do not change much in magnitude. Comparing the surface and ζ-potentials, we find that for high pH cases, as well as for salt concentrations ≥1 mM, there is a (Stern) layer of condensed charges, forming a capacitor with respect to the surface and causing preferential orientation of interfacial water molecules with their hydrogens facing the particle surface. On the other hand, for pH values below 11, as well as below 1 mM salt concentration, there is no such layer, and the interfacial water is preferentially oriented with the oxygen atom facing the particle surface. These findings are compared to results from molecular dynamics (MD) simulations that consider the orientation of water on a single crystalline quartz surface and agree with the experimental results.

Materials and Methods

A. Chemicals

Sodium hydroxide (NaOH, > 99.99% trace metals basis, Sigma-Aldrich) and sodium chloride (NaCl, > 99.999%, Sigma-Aldrich) were used as received. SiO₂ colloids (300 nm diameter) were purchased in powder form from Bangs Laboratories, Inc. Colloidal particles were washed as described in the sample preparation section.

B. Sample Preparation

All procedures described hereafter used ultrapure water (Milli Q, Millipore, Inc., electrical resistance of 18.2 MΩ × cm). First, 50 mg of SiO₂ colloidal particles were dispersed in 1 mL of ultrapure water, sonicated for 10 min, and then diluted to 10 mL with ultrapure water and sonicated again for 3 min. The solution was then centrifuged for 10 min at 7800 rpm (5430R, Eppendorf) in order to precipitate the colloidal particles. Then 9 mL of the supernatant were removed, and the pellet was resuspended in the same volume of Milli Q water by vortexing, followed by ultrasonication (35 kHz, 400 W, Bandelin) for 3–5 min. This procedure was repeated twice to ensure proper washing of the SiO₂ particles and removal of any additional ions in solution coming from the synthetic procedure. The conductivity of the washed particles was measured as described in section C to ensure that the initial ionic strength of the particle solution was as low as possible (below 2 μS/cm for a sample in ultrapure water and in equilibrium with atmospheric CO₂). Particles were further diluted to 0.1% wt. solutions (corresponding to ca. 3.5 × 10¹⁰ particles/mL). The pH and/or ionic strength of the solution were adjusted using 0.1 or 0.01 M stock solutions of NaOH and NaCl. The solutions were used without further filtering and measured on the same day. Corresponding water references at the same pH/ionic strength where prepared for each SiO₂ sample. All preparation steps and measurements were performed at room temperature, 23 °C.

C. Sample Characterization

The particle size distribution was determined by dynamic light scattering (DLS) and the ζ-potential was measured by electrophoretic measurements (Zetasizer Nano ZS, Malvern). The SiO₂ colloids had a mean hydrodynamic diameter of ∼300 nm with a narrow distribution (for most samples, polydispersity index (PDI) < 0.1). Average radii and ζ-potentials are tabulated in parts D of Figures 1 and 2. Values for size and ζ-potential are averages of 3 measurements. pH was measured using a pH-meter (HI 5522 pH/ISE/EC bench meter and HI 1330 pH electrode, Hanna Instruments) calibrated with the appropriate buffer solutions. Conductivity values were measured to ensure that the proper amount of salt had been added to the sample. Conductivity values were obtained by two different means: using a conductivity meter (HI 5522 pH/ISE/EC bench meter and HI 76312 conductivity electrode, Hanna Instruments) calibrated with the appropriate buffer solutions, as well as from the ζ- potential measurements (Zetasizer Nano ZS, Malvern). Average ionic strengths in solution were calculated by the following formula:

where c is the concentration of ions in solution, κ is the specific conductance, Λ_m is the equivalent (molar) ionic conductivity, λ_i is the equivalent ionic conductivities of the cations and anions, and υ_i refers to the number of moles of cations and anions.

Figure 1.

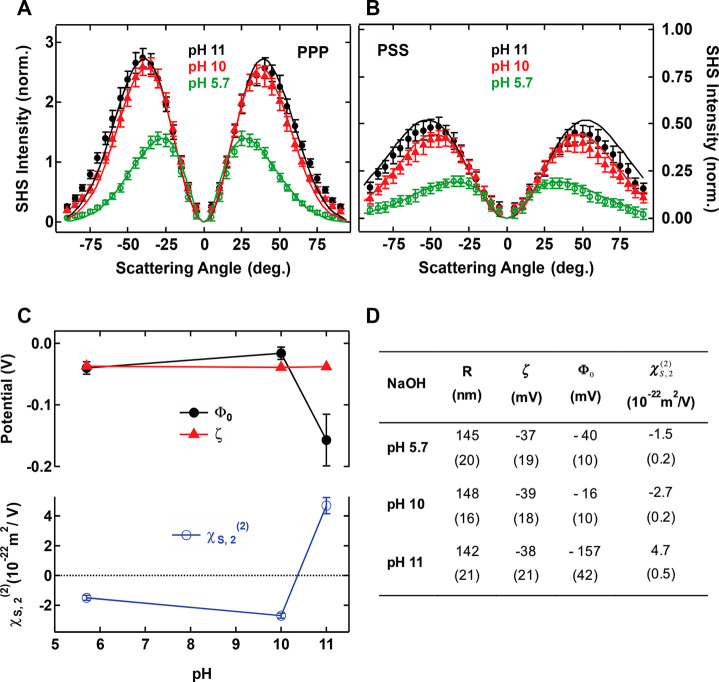
AR-SHS patterns for silica particles in aqueous solution. SH scattering patterns of 300 nm diameter SiO₂ particles as a function of pH in (A) PPP polarization combination and (B) PSS polarization combination. Black plain dots: pH 11. Red plain triangles: pH 10. Green open circles: pH 5.7. pH was adjusted through NaOH addition. The particle density was kept constant for each sample and equal to 3.5 × 10¹⁰ particles/mL. All measurements were performed at T = 23 °C. All the parameters used for the fits, including ionic concentrations, are summarized in Table S2. Error bars represent the standard deviation from 30 measurements. Solid lines represent the fit to the data points using the AR-SHS model. (C, top) Surface potential Φ₀ and zeta-potential ζ. (C, bottom) Surface susceptibility χ_S,2⁽²⁾ as a function of pH. The values are extracted from the fit of data of parts A and B, where error bars represent error on the values as estimated from fitting the data ± standard deviation. (D) Table summarizing the radius R, ζ-potential ζ, surface potential Φ₀ and the surface susceptibility χ_S,2 for different pH conditions. Numbers in brackets pertain to measurement errors as detailed in the Materials and Methods.

Figure 2.

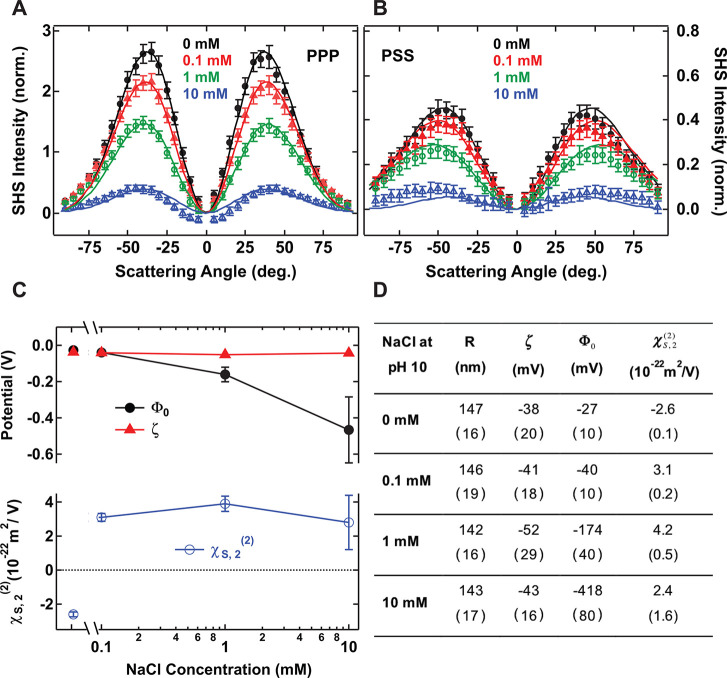
Scattering patterns of 300 nm diameter SiO₂ particles in a pH 10 solution as a function of NaCl concentration in (A) PPP polarization combination and (B) PSS polarization combination. Black plain dots: 0 mM NaCl. Red plain triangles: 0.1 mM NaCl. Green open circles: 1 mM NaCl. Blue open triangles: 10 mM NaCl. pH was adjusted through NaOH addition. The particle density was kept constant for each sample and equal to 3.5 × 10¹⁰ particles/ml. All measurements were performed at T = 23 °C. All the parameters used for the fits are summarized in Table S3. Error bars represent the standard deviation from 30 measurements. Solid lines represent the fit to the data points using the AR-SHS model. (C, top) Semilog plot of surface potential Φ₀ and ζ-potential ζ. (C, bottom) Surface susceptibility χ_S,2⁽²⁾ as a function of NaCl concentration for fixed pH = 10. The values are extracted from the fit of data in parts A and B. Error bars represent error on the values as estimated from fitting the data ± standard deviation. (D) Table summarizing the radius R, ζ-potential ζ, surface potential Φ₀, and the surface susceptibility χ_S,2 for different salt conditions. Numbers in brackets pertain to measurement errors as detailed in the Materials and Methods.

Below theoretical concentrations of 0.1 mM, the ionic molar conductivity at infinite dilution was used, whereas for higher theoretical concentrations the ionic molar conductivity, obtained through the Debye–Hückel–Onsager equation, was used. For samples diluted in ultrapure water (no added ionic strength), average conductivity was assumed to be due solely to protons and bicarbonate ions coming from the dissociation of carbonic acid in water, as the volumes of solution were small enough to always be in equilibrium with atmospheric CO₂ (confirmed by pH measurements, pH 5.7). The measured conductivity values were in agreement with the pH of a water solution fully saturated with carbonic acid. This measurement was used in order to determine the value of the ionic strength to be used in the fitting procedure for the sample in ultrapure water.

D. AR-SHS Measurements

Second harmonic scattering measurements were performed on the same SHS setup as described in ref (38). Briefly, 190 fs laser pulses at a center wavelength of 1028 nm with a repetition rate of 200 kHz and average power of 60 mW were focused into a cylindrical glass sample cell (4.2 mm inner diameter, high precision cylindrical glass cuvettes, LS instruments). The input- (output-) polarization was controlled by a Glan Taylor polarizer (GT10-B, Thorlabs) and a zero-order half wave plate (WPH05M-1030), and another Glan Taylor polarizer (GT10-A, Thorlabs), respectively. The beam waist was about 2w₀ ∼ 36 μm; the corresponding Rayleigh length was ∼0.94 mm. The scattered SH light was collected, collimated with a plano-convex lens (f = 5 cm), polarization analyzed, and filtered (ET525/50, Chroma) before being focused into a gated photomultiplier tube (H7421–40, Hamamatsu). The acceptance angle was set to 2.4° for scattering patterns. Patterns were obtained in steps of 5° from θ = −90° to θ = 90° with 0° being the forward direction of the fundamental. Data points were acquired using 30 × 1 s acquisition time with a gate width of 10 ns. To correct for incoherent hyper-Rayleigh scattering (HRS) from the solvent phase, both the SHS response from the sample solution and the HRS response from a solution of identical ionic strength but without nanoparticles are collected. The measured data, which is a relative quantity, needs to be related to absolute quantities for the parameters required in these expressions: the second order hyperpolarizability β⁽²⁾, the third order hyperpolarizability β⁽³⁾, number of contributing molecules, ionic strength, radius of the particle, temperature, and refractive indices. Indeed, the detector counts in a certain polarization combination cannot be linked directly to an absolute magnitude of the β⁽²⁾ component. We thus employ a normalization scheme that uses water as a reference, which has the advantage that the β⁽²⁾ and β⁽³⁾ values for uncorrelated water are known, so that the calibrated SSS response of water can be used to correct for differences in the beam profile on a day-to-day basis. The HRS is subtracted from the SHS and the obtained difference is then normalized to the isotropic SSS intensity of pure water:

This normalization does not affect the value of χ_S,2⁽²⁾, or Φ₀. The fitting procedure is described in details elsewhere.^37,38 We note here that the errors we report for surface potential and surface susceptibility are the numerical errors on the fitting procedure. The total error may include other sources, such as the variations in the experimentally determined parameters (the radius, the number density, in some cases the ionic strength) and an estimation for such error on the values of surface potential and surface susceptibility for samples of oil droplets in water is given in ref (38).

E. Molecular Dynamics

To support findings obtained by AR-SHS measurements, we also carried out realistic all-atom molecular dynamics simulations. Investigating the water orientation at SiO₂/water interface, we prepared a simulation setup consisting of two SiO₂ slabs (55 Å × 39.82 Å) modeled as quartz surfaces with (101) crystal face that were separated by a ∼55 Å thick aqueous NaCl solution. The obtained results are averaged over both identical solid/liquid interfaces present in the system.

The recently developed force field for quartz (101) surfaces⁴⁰ allowing simulations over the wide range of pH values (at pH equal to the point of zero charge (∼2.5–4) and higher) has been applied and improved to adopt the electronic continuum correction, ECC (also known as model with scaled charges to 75% of their nominal values).⁴¹ The latter accounts for usually missed solvent polarization effects in nonpolarizable force fields, which can significantly influence interactions of charged species including charged surfaces. A general approach how to apply ECC to the modeling of solid/liquid interfaces has been described previously for TiO₂ systems,⁴² while a study dedicated to “ECC-quartz” force field is currently under preparation. Note that the only modifications to the original force field⁴⁰ are modified partial charges of surface atoms, while all other parameters remain the same. Compatible ECC models were also used for Na⁺ and Cl^– ions,⁴³ while the rigid SPC/E model of water was employed as the solvent.⁴⁴ The charge scaling introduced by ECC significantly improves the interactions of multivalent ions (divalent, trivalent, ...) while its effect on monovalent ions is minor. We confirmed that the results presented here with ECC for NaCl are very similar to those we obtained with the original force field for quartz (101).⁴⁰ Number of surface atoms (apart from removed silanol hydrogens to design a surface charge) and water molecules was the same in all simulations, and only number of Na⁺ and Cl^– ions was varied to compensate a negative surface charge and yield a specific bulk ionic concentration. All the simulations were 50 ns long after 5 ns equilibration of prepared structures. Other simulations settings were similar to those used in our previous studies.^40,42

To probe the pH and ionic concentration effects on the water orientation at the interface, we performed two sets of simulations. In the first set, we varied a surface charge of quartz (101) surfaces via the deprotonation of selected surface silanols as described previously.⁴⁰ The bulk ionic concentration in these simulations was approximately constant (0.1–0.15 M). In the second set, we compared four different ionic concentrations ranging from 0.05 to 0.31 M at the one selected surface charge density (−0.06 C/m²). While experiments could be performed only up to 1 mM NaCl concentration, computer simulations of a limited sample of 3745 water molecules and dozens of ions face the opposite limitations–already just one ion pair in the bulk region of our box generates a concentration ∼0.02 M, and we are therefore restricted to higher bulk concentrations. We were however able to approach the ultimate limit of low bulk concentration of the salt by modeling a system with just the number of Na⁺ counterions needed to compensate the negative surface charge and no Cl^– in the system. Such a system mimics the effect of added NaOH to pure water, with all the OH^– groups attached to the surface. We admit that this setup is a bit unrealistic, as any Na⁺ outside of the interfacial region makes the interfacial charge unbalanced, but it represents successfully the salt solution close to infinite dilution.

Experimental Results

Before describing the results, we briefly summarize some of the important aspects of the AR-SHS model; more details can be found elsewhere.^36,37 In a nonresonant AR-SHS experiment, the fundamental frequency of a laser beam interacts with a liquid dispersion containing particles. In regions where the centrosymmetry of the material is broken—typically at the interface between the particles and the liquid—SH photons at half the wavelength of the fundamental beam will be generated. These photons are then collected as a function of the scattering angle (θ), defined as the angle between the sum of the incoming k-vectors of the fundamental beam and the k-vector of the scattered SH light. Under nonresonant conditions, the second-order polarization depends on the electron density in the medium,⁴⁵ which implies that the SH response is of the same order of magnitude for every noncentrosymmetric molecule in the sample. However, since the SH intensity scales quadratically with the number density, in most cases the majority of the SH signal intensity is due to water molecules at the interface, as the number of noncentrosymmetrically distributed surface groups is much smaller than the number of noncentrosymmetrically distributed water molecules.²⁶ In an aqueous solution, the nonresonant SHS signal then arises from the net orientational order of water molecules along the surface normal. Two types of interactions will contribute to this orientational order of water: The orientational order induced by electrostatic field interactions, either at the surface or in the bulk (present in the effective third order particle susceptibility, denoted as Γ^(3)’), and the orientational order induced by all other (chemical) interactions confined to the particle surface plane (represented by the second-order particle surface susceptibility Γ⁽²⁾ that contains the surface susceptibility χ_S⁽²⁾). A third type of effect could be in principle considered, such as a reactant/product gradient along the surface normal; however, such an effect would be mostly noticeable outside of equilibrium conditions and/or during a chemical reaction, which is outside the scope of the present paper. The scattered intensity of the second harmonic can thus be given as

1

where is R the particle radius, θ is the scattering angle, and Φ₀ is the surface potential. χ^(3)′ is the effective third order surface susceptibility, which includes the contributions of the water molecules oriented by the electric field as well as the water bulk susceptibility. The scattered intensity for the two independent polarization combinations PPP and PSS (the first letter refers to the polarization state of the SH beam and the second and third letter refer to that of the fundamental beam; P is parallel to the detector plane³⁸) can be expressed as

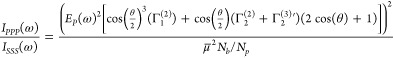2

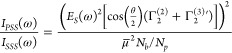3

where 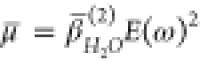, N_P is the density of particles, and N_b is the density of bulk water (3.34 × 10²⁸ molecules/m³). By definition, Γ^(3)’is directly related to the surface potential Φ₀, and χ_S⁽²⁾ contains information about interfacial oriented water, limited to the water molecules that experience an orientational change due to chemical interactions with the silica surface.³⁷ χ_S is a tensor element with 81 components, but in the case of a particle interface that can be considered isotropic in the lateral dimensions of the interface, this number reduces to four components, χ_S,1⁽²⁾, χ_S,2, χ_S,3⁽²⁾, and χ_S,4. Assuming nonresonant interactions and an orientationally broad water distribution⁴⁶ χ_S,1⁽²⁾ vanishes and χ_S,2 = χ_S,3⁽²⁾ = χ_S,4 (a definition for those terms is provided in Table S1).^37,47 By fitting polarimetric AR-SHS patterns in two different polarization combinations as described by eqs 2 and 3, and knowing the radius of the particle as well as the ionic strength of the solution, unique values for both Φ₀ and χ_S,2⁽²⁾ can be extracted (see ref (38) for more details). Note that all patterns are normalized with respect to the water SSS pattern, which does not influence the value of χ_S,2 or Φ₀, as detailed in the Materials and Methods. This ensures a comparison to other samples and experiments, and it corrects for any change in the experimental geometry (such as small variations in beam alignment or sample position). We also note that the model assumes an exponential decay in the diffuse double layer,³⁷ which is a common term for all models.⁴⁸ For the convention on the sign of χ_S,2⁽²⁾, we use the following: Negative for water molecules with O atoms pointing toward the surface (dipole moment pointing away from the surface) and positive for water molecules with H atoms toward the surface (dipole moment pointing toward the surface). This sign convention arises from a comparison to imaginary values obtained from SFG studies.⁴⁹

Parts A and B of Figure 1 show AR-SHS scattering patterns obtained for solutions of 300 nm diameter SiO₂ particles at different pH values. The pH was adjusted through addition of NaOH and no additional salt was added to the solutions. Increasing pH promotes deprotonation of the silanol groups at the surface, leading to a larger negative surface charge density of the SiO₂ particles. The solid lines are fits to eqs 2 and 3, and the values for all experimental parameters used for the fits are summarized in the Supporting Information. The normalized SHS intensity directly relates to the number of oriented water molecules at the interface. Parts A and B of Figure 1 show an increasing normalized SHS intensity with increasing pH. The obtained values of both Φ₀ and χ_S,2⁽²⁾ from the fits of PPP and PSS patterns are plotted in Figure 1C as a function of pH. Figure 1C also shows ζ-potential values measured by electrophoretic light scattering from the same samples. All values are summarized in Figure 1D for easier comparison. The negative valued ζ-potentials are almost unchanged from pH 5.7 to 11 (∼-38 mV). For these particles, the isoelectric point (ζ = 0 mV) is reached at pH = 3, as given by electrokinetic measurements. The surface potential has the same sign as the ζ-potential. However, contrarily to the ζ-potential, the obtained surface potential values vary as a function of pH showing two distinct behaviors: one where the ζ and Φ₀- potentials are very close in magnitude (pH 5.7 and 10) and one where they deviate significantly. This behavior is also shown in the obtained χ_S,2 values: pH 11 shows positive values of χ_S,2⁽²⁾, corresponding to water hydrogen atoms oriented toward the surface, while milder pHs (5.7 and 10) show negative values of χ_S,2, corresponding to water hydrogen atoms oriented away from the surface, and oxygen atoms facing the surface.

We also performed similar measurements at constant pH while varying the ionic strength. Parts A and B of Figure 2 show SHS scattering patterns for solutions of 300 nm diameter SiO₂ particles at pH 10, where different amounts of NaCl were added. In this case, the surface charge density is mainly expected to be set by the presence of NaOH and to a minor extent by the additional Na⁺ ions, which can facilitate the deprotonation of surface silanol groups through electrostatic screening and stabilization of the SiO^– group.⁵⁰ On the basis of values of surface charge densities measured for a fixed pH and different NaCl concentrations,⁵⁰ this latter effect can be estimated to ∼10% of the total deprotonation and will depend on the range of salt concentration and the size of the particles, as well as the nature of the cation.^30,51 It can be seen that the normalized SHS intensity decreases with increasing salt concentration, indicative of a decrease in the amount of ordered water molecules around the surface of the SiO₂ particles. Figure 2C shows the obtained fit values for the surface potential and the second-order susceptibility element representative of the molecular orientation of interfacial water. The measured ζ-potential values are also plotted. All values are summarized in Figure 2D. For the two lowest salt concentrations both potentials are similar in magnitude. For 1 and 10 mM NaCl, however, the magnitude of the surface potential becomes much higher than the ζ-potential. Another interesting observation is that the sign of χ_S,2⁽²⁾ changes when salt is added. In the case where no salt is added at a fixed pH of 10, a negative sign of χ_S,2 indicates a situation where water molecules are mostly oriented with their hydrogen atoms away from the surface. With the addition of NaCl, and even for the smallest quantity (0.1 mM), the sign of this parameter is inverted and points to a shift in the water orientation, where the hydrogen atoms are oriented toward the surface.

Simulation Results

Computer simulations provide molecular details of the interface and help the experiment in deciphering the contribution of oriented water molecules at a given distance from the surface to the nonlinear optics signal (i.e., χ_S, 2⁽²⁾ or Φ₀). Because a model of ∼300 nm diameter colloidal SiO₂ is not available, we utilized our model of the flat (101) quartz surface (see Materials and Methods). The flat geometry is well justified by the large size of the colloidal particles, and the terminations by silanol groups are similar in both cases,⁵² though more defects must be expected for amorphous and spherical particles. The density of silanol groups for perfect (101) quartz (5.8 OH/nm² for neutral surface, 5.1 OH/nm² for −0.12 C/m² negative surface⁴⁰) is close to the value 4.9 OH/nm² reported for amorphous silica.⁵³

The signal of each layer is proportional to the “dipole concentration” given by a product of the number density of water molecules, water dipole orientation (the cosine of the angle between the water dipole vector and z-axis with positive values indicating hydrogens facing the solid surface, i.e. as in the experiment), and the dipole moment of SPC/E water model, which equals 2.35 D (1 D = 3.336 × 10^–30 Cm). The running integral of the dipole concentration provides an indicator for the buildup of the total SHS intensity. Indeed, the SHS intensity is by definition given as the square of the absolute value (magnitude) of the summed nonlinear second order and third order polarization (emitted at the second harmonic frequency). We then assume that the sum of the dipoles in a certain volume is proportional to the second order and third order polarization (emitted at the second harmonic frequency), and as such the SHS intensity is proportional to the square of the running integral of the dipole concentration.⁵⁴ The interfacial plane at z = 0 corresponds to the average position of surface silicon atoms. MD simulations were carried out for surface charge densities 0, −0.03, −0.06, and −0.12 C/m². Using surface titration experiments we can link these simulations to pH ∼ 4, 8.5, 9.4, and 10.1, respectively, which allows us to compare simulation and experimental data, though the simulation and experimental conditions cannot be matched exactly due to differences in surface geometry. A simulation of the quartz surface in pure water is also added for comparison.

The results obtained from the molecular dynamics simulations are summarized in Figure 3. The left-hand panels (A, B, C) display effects of changing surface charge density, while the right-hand panels (E, F) display effects of changing the ionic strength at fixed surface charge density. Figure 3A shows the axial density profile of water oxygens, i.e., the laterally averaged density of water as a function of distance from the quartz (101) surface. The axial density of water is nearly independent of the surface charge (shown in Figure 3A) and salt concentration (not shown). The positions of the first two clearly evident water layers are z ∼ 3.5 Å and z ∼ 6 Å, and are invariable. Figure 3B shows the dipole concentration as a function of distance for different surface charge densities. A positive value indicates water molecule with hydrogens facing the surface, while a negative value indicate a reversed molecular orientation with oxygens facing the surface. These features can thus be used to connect to the sign of χ_S,2⁽²⁾. It can be seen that the curves for low charge density are more negative, while increasing the charge density brings them up to positive values. Figure 3C shows the running integral of the dipole concentration, which reaches a plateau away from the interface, where the average orientation of water molecules is zero (isotropic). This plateau value is an indicator of the total SH intensity and increases with surface charge density. Figure 3E shows the ionic strength dependence of the interfacial dipole orientation for a fixed surface charge density of −0.06 C/m², and for the salt concentration range used in the simulations (0.05 to 0.31 M NaCl). The water orientation with hydrogens facing the surface is less pronounced at higher concentrations, leading also to decreasing plateau values of the running integral of the dipole concentration (Figure 3F) with salt concentration.

Figure 3.

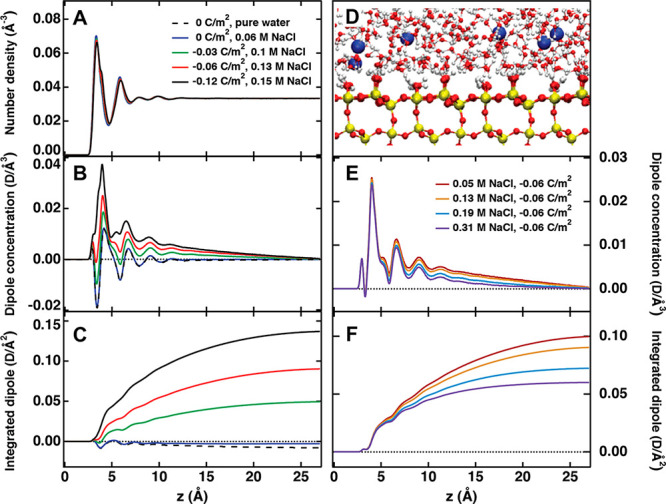
(A) Number density of water, (B) dipole concentration, and (C) integrated dipole as a function of distance z from the quartz (101) surface for different surface charge densities at similar bulk ionic concentration. (D) Snapshot of the quartz (101) surface at 0.34 M and −0.12 C/m². (E) Dipole concentration and (F) integrated dipole as a function of distance from the quartz (101) surface for different bulk ionic concentrations at the same surface charge density of −0.06 C/m².

Discussion

Surface Potential and Water Orientation under Low Ionic Strength Conditions

In mild pH cases (5.7 and 10) and low ionic strength (<1 mM), the values of the surface potential are very close to the ζ-potential values. Negative values of the ζ-potential are found for colloidal SiO₂ surfaces^50,55,56 as expected from the negative surface charge densities.^10,57,58 As mentioned in the introduction, the slip plane where the ζ-potential is measured is considered to be located in the first few water layers away from the surface plane where the surface potential is measured. Therefore, with both values being very similar, it is highly unlikely that there is any buildup of counterions close to or at the surface. This means there is no charge condensation or Stern layer formed. By charge condensation layer, we refer to a packed layer of ions that is at some distance away from the interface, also known as an outer-sphere complex. We note here the specific case of direct counterion adsorption, also referred to as an inner-sphere complex, which would lead to (partial) surface charge neutralization. This surface charge neutralization effectively decreases the electric field extending in the solution and therefore results in a reduction of the surface potential. However, this effect is expected to be small for small concentrations of counterions in solution.

The negative values of χ_S, 2⁽²⁾ are indicative of a net dipole moment pointing away from the surface, with water molecules mainly oriented with their oxygen atom toward the surface. This water orientation in low ionic strength conditions can be rationalized by considering the hydrogen bonding between the silanol groups and the oxygen atom of water. This is illustrated in Figure 4A.

Figure 4.

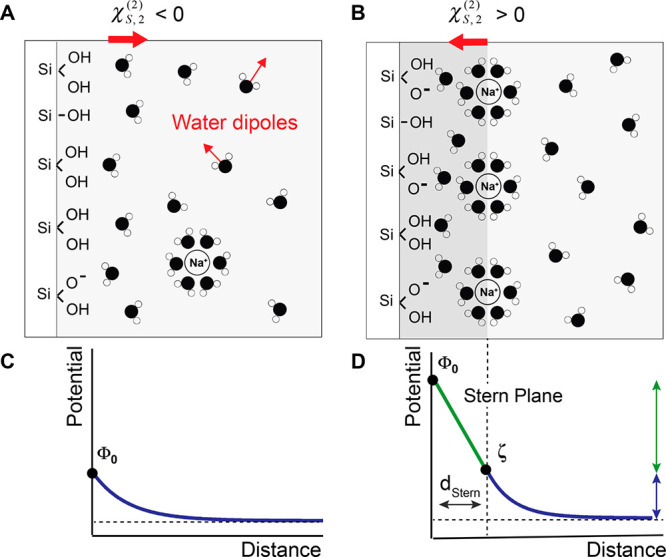
Schematic view of a SiO₂/water interface for (A) Low surface charge density and low Na⁺ concentration and (B) High surface charge density and high concentration of Na⁺ ions. In both cases the surface keeps a majority of silanol groups protonated and is overall negatively charged. (A) Water molecules are preferably oriented with their oxygen toward the surface. The net water dipole summed over all water molecules is then oriented away from the surface (red arrow). (B) Water molecules are preferably oriented with their hydrogens toward the surface. The net water dipole is oriented toward the surface (red arrow). The potential decay profile in the Gouy–Chapman (C) or Gouy–Chapman–Stern models (D). In the first case, the ionic strength in solution is low and the surface potential decays exponentially with distance. At higher ionic strengths, the GCS approximation is considered, where the potential decay profile integrates two components: a steep decay associated with the strong electric field in the charge condensation layer, known in the model as the Stern layer, and a more gradual one at larger distances from the interface. We approximate here the potential at the Stern plane to be equal to the ζ-potential.

Having established that there is no significant accumulation of counterions at the interface, for this particular case, the simplest model that describes the relation between surface charge and surface potential is given by the spherical Gouy–Chapman model. Ohshima derived an approximate analytical solution for the potential distribution around a sphere with arbitrary potential,⁴⁸ where the surface charge density is related to the surface potential by

4

where σ₀^GC is the surface charge density in the spherical Gouy–Chapman model, R the particle radius, ε_r the relative permittivity of the solvent (water), ε₀ the permittivity of vacuum, κ the Debye parameter, e the elementary electric charge, z the valence of ions, k_B the Boltzmann constant, and T the temperature. Knowing Φ₀, we can compute σ₀, and the expected degree of deprotonation. Table 1 shows the values for σ₀^GC as a function of pH and NaCl concentration, as well as the corresponding percentage of surface deprotonation.

Table 1. σ₀^GC and Percentage of Deprotonation as a Function of pH and Salt Concentration.

NaOH	σ0GC (mC/m2)	% deprotonation	[NaCl], pH = 10 (mM)	σ0GC (mC/m2)	% deprotonation
pH 5.7	–0.35	0.04	0	–0.77	0.10
pH 10	–0.45	0.06	0.1	–1.63	0.21

Table 1 shows that the surface charge densities for the low ionic strength regime range from −0.35 to +1.63 mC/m², which correspond approximately to 0.04–0.2% deprotonation, assuming a silanol density of 4.9 OH/nm² as reported by Zhuravlev,⁵³ who showed that this value is a constant for a fully hydroxylated amorphous surface and does not depend on the type of silica. These surface charge densities values are in the range of reported values in the literature for salt free and low salt dispersions^59,60 and agree with the notion that the majority of the silanol groups remain protonated.^61,62 Thus, in mild pH conditions and low ionic strength, only a very small fraction of the silanol groups are deprotonated, and the dominant orientation of water dipoles in the first layer away from the surface is due to hydrogen bonding between the protonated silanol groups and the oxygen atoms of water.

Surface Potential and Water Orientation in Higher Ionic Strength Conditions

In higher pH conditions (pH 11) and with increasing amounts of NaCl (≥1 mM), we observe a much higher magnitude for the surface potential than the ζ-potential. The distance between the slip plane and the surface plane is 1–3 water molecules.¹² The differences ∥Φ₀ – ζ∥ of 119 mV (pH 11), 122 mV (1 mM NaCl), and 375 mV (10 mM NaCl) means that the electrostatic field in this thin layer must be on the order of 10⁸–10⁹ V/m. This large electrostatic field indicates the presence of a condensed layer of charges.¹²

This hypothesis is further supported by the fact that higher values of surface potential are found for both pH 11 and for pH 10 + 1 mM NaCl and above, which correspond to a similar concentration of sodium ions (respectively 1 mM and 1.1 mM Na⁺). Such a charge condensation layer of positive counterions close to the negative surface influences water orientation. Positive values of χ_S,2⁽²⁾ here indicate a net dipole moment with the hydrogens pointing toward the surface, thus effectively interpreted as a net flip in the surface water orientation with respect to the low ionic strength situation (Figures 1C and 2C). This flip in water orientation is illustrated in Figure 4B and arises from the formation of a charge condensation layer composed of hydrated sodium ions. As the hydration shells of the Na⁺ ions overlap with the surface hydration layer, the Na⁺ ions disrupt the hydrogen bonding between the silanol groups and the water molecules and a water layer with a net dipole moment facing the surface results.

Having determined experimentally that here we are dealing with a Stern layer, we can compute the charge density on the slip plane, σ_d, assuming that the slip plane and the outer Stern layer coincide, using eq 4 and replacing Φ₀ by ζ and σ₀^GC by σ_d. Values for σ_d are shown in Table 2. Approximating the surface of the particle and the Stern layer as two plates of a spherical capacitor, it is also possible to use the equation describing a spherical capacitor to relate the potential drop in the Stern layer (Φ_drop = Φ₀–ζ) to the surface charge density at the surface, σ₀^GCS:

5

where σ₀^GCS is the surface charge density in the presence of a charge condensation layer, R is the radius of the particle, ε₀ is the vacuum permittivity, and d_Stern is the thickness of the capacitor. Contrary to the GC case, which assumes the permittivity of bulk water because of the small electric fields generated at the interface, in the GCS case the higher electric fields will orient the water dipoles and therefore change the dielectric constant of the first few layers adjacent to the interface. Therefore, we use here ε_SW as the dielectric constant at the silica/water interface (ε_SW = 43).⁶³ Assuming a Stern layer thickness range of 0.3 < d_Stern < 0.9 nm (between one and three water molecules) one obtains a range of values for σ₀, summarized in Table 2.

Table 2. Table Showing σ_d, σ₀^GCS and % Deprotonation as a Function of pH and Salt Concentration.

NaOH	σd (mC/m2)	σ0GCS (mC/m2)		% deprot.
pH 11	–3.2	dStern= 0.3 nm	–151	19.2
		dStern= 0.9 nm	–50.3	6.4

[NaCl], pH = 10	σd (mC/m2)	σ0GCS (mC/m2)		% deprot.
1 mM	–5.0	dStern = 0.3 nm	–155	19.7
		dStern = 0.9 nm	–51.6	6.6
10 mM	–11.5	dStern = 0.3 nm	–476	60.6
		dStern = 0.9 nm	–159	20.2

Table 2 shows that the computed surface charge densities range from −50 to −476 mC/m² depending on the choice of the Stern layer thickness. These values correspond to deprotonation degrees between 6 and 61%. While the deprotonation value for [NaCl] = 10 mM seems high for d_Stern = 0.3 nm (maximum 25% deprotonation is expected at pH 10 and 0.1 M NaCl),⁵⁰ all the other results are comparable to surface charge densities that have been measured by potentiometric titrations for SiO₂ particles in similar conditions,^10,35,57,64 keeping in mind that these values are strongly size-dependent below 30 nm diameter.^65,66 Interestingly, one can see that surface charge densities in both pH 11 case and the 1 mM NaCl case at pH 10 are very similar, which is a direct result of the similar surface potential values obtained by AR-SHS (Figures 1C,D and 2C,D). Considering nearly the same concentrations of ions at these two conditions (1 mM Na⁺,OH^– at pH 11 vs 0.1 mM of Na⁺,OH^– + 1 mM Na⁺,Cl^– at pH 10), this indicates that the ionic strength and the interfacial presence of Na⁺ ions, is here the main element in setting the magnitude of the surface potential.

While both base and salt treatment show a similar increase in the surface potential value, similar surface charge densities for a given value of d_Stern and similar orientation of the surface water molecules indicating the presence of a charge condensation layer, the SH intensity change as a function of the ionic strength does show some differences, which has implications on the thickness of this charge condensation layer. In the case of the basic treatment, the surface charge becomes increasingly more negative with increasing NaOH addition. This higher surface charge density is then compensated by screening by the Na⁺ cations, which additionally participate in orienting the water molecules with their hydrogens facing the surface (Figure 4B). For a higher surface charge density, we can thus expect a larger number of water molecules to be oriented with their hydrogen facing the surface to counterbalance for the presence of deprotonated silanols. The increase in SH signal intensity as a function of pH (Figure 1A,B) thus reflects the electric-field induced polarization of the water molecules at the interface as previously described for flat surfaces.^25,67 In the case of salt addition at fixed pH, we observe a decrease in SH intensity (Figure 2A,B) that physically corresponds to a decrease in the number of the oriented water molecules. Such a decrease in ordered water is then indicative of more efficient screening of the surface charge by more concentrated salt solution and shrinking of the diffuse layer. This decrease in the amount of ordered water is already visible between 0 mM NaCl at pH 10 and 0.1 mM NaCl at pH 10, while it is not noticeable between pH 10 and 11 when no salt is added. This indicates that the thickness of the charge condensation layer will be dependent on the nature of the added compound (NaOH/NaCl), most likely because of modifications of the surface charge density. Additional information that can be extracted from the AR-SHS plots is the relative variation of the thickness of the charge condensation layer and of the surface charge density. From eq 5, a decrease in the thickness would directly result in a decrease of the magnitude of the surface potential. However, since we observe an effective increase in magnitude of surface potential with increasing salt concentration, this implies that, in this range of salt concentrations, the increase in magnitude of surface charge density must be larger than the decrease in the charge condensation thickness. Note that at higher salt concentration (>10 mM), the opposite behavior has been observed:⁵⁰ While the surface charge density still increases with increasing salt concentration, the decrease in the thickness of the charge condensation layer overall dominates, thus resulting in a decrease of the surface potential with increasing salt concentration. In our case, due to the limited range of stability of our colloidal suspensions, we could not explore salt concentration ranges above 10 mM. It is also important to note that Brown et al.⁵⁰ use particles below 10 nm diameter, and as the surface charge density is strongly size-dependent for particles below 30 nm diameter,^65,66 we can expect a different relative variation of the surface charge density and the charge condensation layer thickness for different sizes of particles, which could imply a different dependence of the surface potential on the salt concentration. Further measurements are thus needed to test the size dependence of the surface potential at various ionic strengths. Similarly, the surface charge density as well as the pK_a of different silanol groups is expected to change depending on the preparation of the surface prior to the experiment,^25,61,68 which could be additional factors playing a role in the observed trends for the surface potential.

One last observation that can be made on the basis of the AR-SHS results is that the transition between the low ionic strength regime, where ∥Φ₀∥ ≈ ∥ζ∥ and the high ionic strength regime, where ∥Φ₀∥ ≫ ∥ζ∥, occurs for electrolyte concentrations between 10^–4 and 10^–3 M, while it is generally considered for flat surfaces (as for example metal electrodes) that the GC model can be used up to electrolyte concentrations of 10^–3–10^–2 M.^12,69,70

Comparison of AR-SHS Experiment and MD Simulation

We turn now to the discussion of the results obtained through simulations. Despite the fact that simulation results for one selected crystal face of quartz surface are used when comparing to experimental data of spherical silica nanoparticles, the trends observed in simulations are in line with experimental findings. The lowest charge densities and salt concentrations studied experimentally are not reachable with the MD simulations (see Materials and Methods for details), but we still can discuss the experimental trends in the presence of only NaOH or for very small salt concentrations with the help of the molecular picture of this model interface. Figure 3A shows that there is interface induced water layering as witnessed by the two peaks at ∼3.5 and 6 Å. The orientational first peak in Figure 3B can be easily connected to χ_S,2⁽²⁾, as by definition χ_S,2 contains the orientational order induced by all chemical interactions confined to the particle surface plane. The first peak in Figure 3B for surface charge densities σ = 0 and −0.03 C/m² is negative, in agreement with negative χ_S,2⁽²⁾ observed experimentally at pH 5.7. The negative signal at low pH is further supported by simulations of neutral quartz surface (σ = 0 C/m²), where even the integrated dipole is very slightly negative, both for 0.06 M NaCl solution (represented by only 4 ion pairs in the simulated system) and even more for pure water (which is the limiting case of low salt concentration for neutral surfaces). The first peak for σ = −0.06 C/m² is close to zero and does not predict the negative χ_S,2 seen experimentally at pH 10 in absence of salt, but the concentration dependence of the second peak easily explains the positive χ_S,2⁽²⁾ at larger concentrations. Finally, based on the positive first peak at σ = −0.12 C/m², we predict that at very high pH values, even in the absence of salt, χ_S,2 should be positive, in agreement with Figure 1C for pH 11. Figure 3C also agrees with the measured SH intensity shown in Figure 1A,B, where increasing pH (and thus more negative surface charge density) leads to an increase in the total SH intensity, indicative of a larger number of overall oriented molecules.

Parts E and F of Figure 3 capture, as much as possible using our MD setup, the experimental drop in overall SHS intensity with salt concentration (Figure 2A,B), indicative of more efficient charge screening and less overall oriented water. Figure 3E shows that for higher charge densities (pH) the magnitude and sign of the first peak for a given pH is insensitive to the salt concentration. The second peak (∼6 Å) and the water orientation further out displays however a decreasing magnitude with increasing salt concentration. This behavior is also shown in the curves in Figure 3F, which overlap in the first peak but start to deviate at the second peak and gain less signal at distances of ∼6–20 Å for higher salt concentrations. In this high concentration range (>10 mM), the weakening of the orientation with hydrogens facing the solid with increase in concentration also agrees with the drop in susceptibility measured experimentally from 1 to 10 mM (see Figure 2C,D). These effects were observed for all simulated ionic concentrations and surface charge densities.

Simulations evidence Na⁺ (a strong sorbent) adsorbing as an inner-sphere complex at height ∼3.5 Å, i.e., in the location of the first water layer, and also as outer-sphere complex at distances around 5.5 Å, i.e., close to the position of the second water layer (not shown). With increasing pH and salt concentration, the surface attains more negative charge. While less negative surface charge can be easily compensated by a few Na⁺ ions, at more negative surfaces the compensation of the surface charge is partly hindered by repulsion among numerous adsorbed Na⁺ ions, leading to formation of the condensed layer further from the surface and more negative surface potential, as deduced from the SHS data.

Conclusions

Nonlinear light scattering theory can be used to derive expressions for surface potential of colloidal suspensions Φ₀ and interfacial water ordering in terms of the second-order susceptibility χ_S,2⁽²⁾. This system of two variables can be solved by nonresonant polarimetric AR-SHS measurements in two different polarization combinations. Φ₀ and χ_S,2 are obtained from analytical expressions and therefore do not assume any model for the distribution of ions at the interface. In this work, we report AR-SHS patterns for 300 nm diameter SiO₂ colloidal suspensions as a function of pH and NaCl concentration, and we support these data by MD simulations of the crystal quartz (101) surface interacting with aqueous solutions. By combining the knowledge of the parameters χ_S,2⁽²⁾ and Φ₀ with ζ, which is obtained through electrokinetic measurements, we are able to establish a description of the interface that does not rely on a specific model for the charge distribution at the interface. Between pH values close to neutral and 10, as well as at low salt concentration (<1 mM), our data indicate the presence of a diffuse double layer where the surface potential is very close to the ζ-potential, and where the most favorable orientation for the interfacial water molecules is the one with the oxygen atom facing the silanol terminated surface. At higher pH or ionic strength (pH 11 or ≥1 mM salt), we observe an increase in surface potential, while the ζ-potential changes very little, indicative of the formation of a charge condensation layer. Furthermore, values of χ_S,2 indicate that interfacial water adjusts its orientation following counterion adsorption, in this case favoring hydrogen atoms facing the surface. Surface charge densities estimated through the GC or GCS model using the measured surface potential values agree with reported values in the literature. This validates our experimental approach where the surface potential values can be extracted without assuming any model for the structure of the electrical double layer. The experimental trends are nicely supported by molecular simulations, which observe that the orientation of interfacial water increases with pH and decreases with NaCl concentration, in accord with the intensity of the AR-SHS signal. The flipping of the dipolar orientation of water molecules closest the surface from orientations away from the surface (prevailing orientation due to termination of the surface by protonated silanols) at low pH to orientation toward the surface at high pH (induced by negative surface charge and the presence of Na⁺ counterions), can be directly linked to the trends observed for the pH dependence of the surface susceptibility.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.9b05482.

• Table of the shorthand notation for independent tensor components and tables of parameters used for the surface potential fittings (PDF)

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry virtual special issue “Hai-Lung Dai Festschrift”.