Abstract
Despite a growing literature on the impacts of the COVID-19 pandemic, scant evidence currently exists on its impacts on air quality. We offer an early assessment with cross-national evidence on the causal impacts of COVID-19 on air pollution. We assemble a rich database consisting of daily, sub-national level data of air quality for 164 countries before and after the COVID-19 lockdowns and we analyze it using a Regression Discontinuity Design approach. We find the global concentration of NO2 and PM2.5 to decrease by 5 percent and 4 percent, respectively, using data-driven optimal bandwidth selection. These results are consistent across measures of air quality and data sources and robust to various model specifications and placebo tests. We also find that mobility restrictions following the lockdowns are a possible explanation for improved air quality.
Keywords: COVID-19, Air pollution, Mobility restriction, RDD
1. Introduction
It has by now become clear that the COVID-19 pandemic is not only a global health emergency but has also led to a major global economic downturn. An emerging body of economic literature has examined the negative impacts of COVID-19 on a range of outcomes, but scant evidence currently exists on the impacts of the COVID-19 crisis on air quality.1 Given the linkage of air pollution to heart and lung damage and other diseases (Brunekreef and Holgate, 2002; Liu et al., 2019), understanding how air quality is affected during the COVID-19 pandemic provides important empirical evidence for health policies, as well as post-pandemic economic policies that involve trade-offs between economic gains and environmental losses.
The few existing studies focus on country-specific case studies rather than investigate the impacts of the pandemic on the global scale and have yet to offer conclusive evidence. Employing a difference-in-difference model that compares Chinese cities with and without the pandemic-induced lockdown policies, He et al. (2020) find that city lockdowns led to considerable improvement in air quality as measured by Air Quality Index (AQI) and PM2.5. This result is consistent with Brodeur et al. (2020) findings for the United States that ‘safer-at-home’ policies decreased PM2.5 emissions. However, using a similar difference-in-difference approach, Almond et al. (2020) show that COVID-19 had ambiguous impacts and might even decrease air quality in Hubei, the province at the center of the outbreak in China. To our knowledge, Lenzen et al. (2020) and Venter et al. (2020) are the only exceptions that examine the pandemic impacts on global air quality. Using an input-output model for 38 regions around the word, Lenzen et al. (2020) find the pandemic to reduce greenhouse gas, PM2.5, and air pollutants by 4.6 percent, 3.8 percent and 2.9 percent of the global annual totals, respectively. Comparing air quality during the pandemic with that in previous years, Venter et al. (2020) analyze station-based air quality data in 34 countries and find concentration of NO2 and PM2.5 to decrease by approximately 60 percent and 31 percent.2
We add several new contributions to the emerging literature on the pandemic impacts on air pollution. We offer global estimates for the causal impacts of COVID-19 on air quality in 164 countries using a Regression Discontinuity Design (RDD) approach in a short window of time before and after each country implemented its lockdown policies. Since the lockdown policy—as most society-wide regulations—cannot be randomized across countries, the RDD offers us the most rigorous evaluation model that is available. We also provide estimates for several different measures of air quality, including NO2 and PM2.5 (for our main analysis) and O3, PM10, and SO2 (for robustness checks). These various indicators help strengthen the estimation results.
Finally, we combine a variety of real-time data sources for richer analysis. We obtain daily data on air pollution at the more disaggregated, sub-national level from satellite data and station-based data. We combine these data with the Oxford COVID-19 Government Response Tracker, a unique database on government policy responsiveness to COVID-19. We supplement our analysis with data from other sources including the National Oceanic and Atmospheric Administration, Google Community Mobility Reports, World Bank World Development Indicators, WHO Global Ambient Air Quality Database, and Economist Intelligence Unit.
The rich database that we assemble allows us to address a key challenge in cross-country analysis, which is to construct comparable lockdown dates for different countries. Indeed, the term ‘lockdown’ can refer to anything from mandatory quarantines to bans on events and gatherings, businesses closures, or non-mandatory stay-at-home recommendations. Some governments immediately respond to the outbreak by implementing a complete (regional or national) lockdown (e.g., China, Italy), while some implement a gradual lockdown in a staggering manner for different locations (e.g., the United States).
We find strong evidence for reduced air pollution after the lockdowns, with more reduction for a larger window of time around the lockdown dates. In particular, the global decreases in NO2 and PM2.5 hover around 5 percent and 4 percent using the optimal bandwidths of 62 and 88 days after the lockdowns, respectively. We perform various placebo tests and robustness tests using falsified lockdown dates, different indicators of air quality and government policy indexes, alternative bandwidth specifications, functional forms, and inclusion of different covariates.3 Our findings suggest that mobility restrictions following the lockdowns can be a channel that explains the improvement in air quality.
2. Data
To examine the relationship between COVID-19 and air quality, we use two measures of air pollution, namely fine particulate matter PM2.5 (mass concentration of particles with diameters ≤2.5 μm) and nitrogen dioxide NO2. PM2.5 is a common cause for adverse health outcomes such as chronic obstructive pulmonary disease and lower respiratory infection causing death of nearly three million people globally (Gakidou et al., 2017). At the same time, NO2 is the leading source of childhood asthma in urban areas (Achakulwisut et al., 2019).
We obtain high-resolution global NO2 data from the Sentinel-5P/TROPOMI (S5P) instrument of the European Union’s Copernicus programme. As an alternative air-quality measure, we use daily station-based air quality index (AQI) from the World Air Quality Index (WAQI) project. However, given certain limitations with station-based data (such as slower reporting and likely non-random locations), the satellite data are our preferred data for analysis. Finally, we obtain sub-national data on daily rainfall and temperature from the National Center for Environmental Prediction (NCEP) at the National Oceanic and Atmospheric Administration (NOAA).
We subsequently merge the air pollution data with the government stringency data from the Oxford University’s COVID-19 Government Response Tracker (OxCGRT), which contains information on various lockdown measures, such as school and workplace closings, travel restrictions, bans on public gatherings, and stay-at-home requirements (Hale et al., 2020). The OxCGRT data measure government stringency responses on a scale of 0–100.
To explore a potential channel through which COVID-19 affects air quality, we collect data on global mobility from Google Community Mobility Reports (GCMR). The GCMR provide daily mobility data in different categories on Google Maps users across 132 countries. We provide a more detailed description of the data sources and the summary statistics of the main variables in Appendix B, Table B1.
3. Empirical model
We first employ for analysis the following fixed-effects panel data model
| (1) |
The coefficient of interest in Equation (1) is , which measures how the air quality () in country i and date t changes in response to the stringency of government COVID-19 policies (). Because varies by country and date, this fixed-effects model allows for the inclusion of country fixed effects () and time fixed effects () to absorb the effects of unobservable time-invariant country or time characteristics. is a vector of observed time-varying control variables such as daily temperature and rainfall.
Yet, Equation (1) yields an inconsistent estimate of if omitted variables exist that correlate with both air quality and government policies. Since is positive only after the lockdown date, Equation (1) does not address the fact that unobserved pre-COVID-19 time-varying country characteristics, such as governance quality and public preferences for protecting the environment, can differ. Another challenge in this context is that air pollution is positively associated with the number of COVID-19 cases (Cicala et al., 2020; Cole et al., 2020; Isphording and Pestel, 2020), which can lead to governments implementing more stringent lockdown. Failure to control for possible reverse causality would result in biased estimates of the effects of the lockdown.
We propose two strategies in this paper to identify the causal effects of COVID-19 on air quality. First, we use a flexible event study framework to help mitigate concerns about the common trends. Specifically, we decompose the estimated effects of lockdown () into coefficients up to 100 days prior to and following the lockdown date. This will provide a descriptive test for whether the lockdowns are correlated with differential trends before and after the lockdowns. Second, we apply a more rigorous econometric technique by taking advantage of the pandemic-induced lockdowns as an exogenous policy shock and applying a Regression Discontinuity Design in Time (RDiT) approach. In this approach, the observations immediately before the lockdown dates provide the counterfactual outcomes for those observations immediately after the lockdown dates because the lockdown (treatment) status is randomized in a small neighborhood of the lockdowns. This approach is built on the standard Regression Discontinuity Design (RDD) (see, e.g., Hahn et al. (2001)) but the running variable is the days from the lockdown dates. It has been widely used in the literature to study changes in air quality caused by a specific event (Davis, 2008; Auffhammer and Kellogg, 2011; Chen and Whalley, 2012). We estimate the following reduced form
| (2) |
where (treatment variable) is a dummy variable that equals 1 after the lockdowns and 0 otherwise, and is the parameter of interest. denotes a function of the running variable (number of days from the lockdown dates). Similar to Equation (1), and respectively denote the country fixed effects and the time fixed effects, and denotes the error term. For comparison and robustness checks, we use different functional forms of the running variable to estimate Equation (2). These include (i) the linear model (), (ii) the linear model with the interaction term of the running variable and the treatment variable (∗), (iii) the quadratic model (, and (iv) the quadratic model with the interaction term of the running variable and the treatment variable (∗).4 Since our estimates might be sensitive to bandwidth choices, we employ Imbens and Kalyanaraman (2012)’s data-driven selection procedures to obtain the optimal bandwidths.
As discussed earlier, a key challenge with estimating Equation (2) is to identify lockdown dates that are comparable across different countries, which likely implement lockdowns with various degrees of strictness. For example, business activities and travels can continue to varying extents after the lockdown dates, or while all schools are shut down, universities operate on a different schedule for different countries. Furthermore, there can be multiple lockdown dates even within the same country where regions/states impose different lockdown dates (with different levels of intensity). To address this issue, the OxCGRT provides a unique composite measure which combines indicators on different aspects of lockdown policies regarding school, workplace, public transportation, and public events into a general index (Appendix B, Table B2). By using a range of different indicators, this stringency index accounts for any indicator that may be over- or mis-interpreted, thus allows for a better and more systematic comparison across countries (Hale et al., 2020).
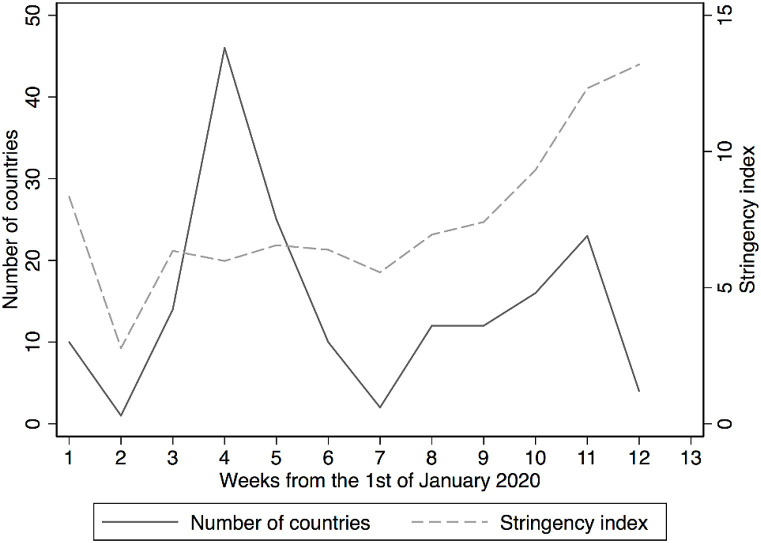
For each country, we define the lockdown date as the first day on which the stringency index becomes positive. Using our constructed measure, Figure A1 (Appendix A) shows that most countries introduced lockdowns somewhere between the last week of January and the first week of February 2020, and countries that implemented lockdown policies later tend to have more stringent responses.5
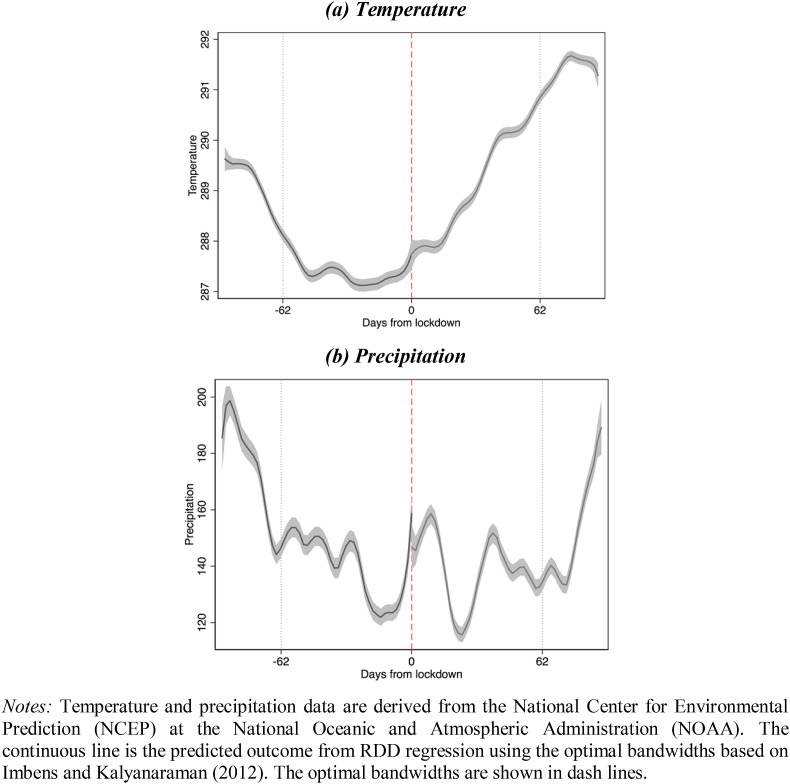
To validate the RDD identifying assumptions, we present two types of tests. First, we conduct a discontinuity test in the covariates, namely temperature and precipitation, around the lockdown dates. The results, presented in Table A1 (Appendix A), show no discontinuity at the cut-off date. This finding is further confirmed by Figure A2 (Appendix A). Second, another concern with the RD-in-time approach is serial correlation (Hausman and Rapson, 2018). To address this issue, we follow previous studies and cluster the standard errors on both the location and time dimensions (Auffhammer and Kellogg, 2011; Anderson, 2014). Furthermore, we conduct a robustness check by including the lagged dependent variable in the regressions and find consistent results with our main findings (see Table A2, Appendix A).
4. Results
4.1. Main findings
We present in Table 1 the estimation results for Equation (1) using data at the sub-national level (columns 1 and 2) and the country level (columns 3 and 4). Our preferred results are columns (2) and (4), which control for daily temperature and precipitation (humidity for station-based data).6 But we also show the estimates without these control variables in columns (1) and (3) for comparison and robustness checks. The estimation results are strongly statistically significant in our preferred models (columns 2 and 4) and point to reduced air pollution where government policies are more stringent. Overall, our findings suggest that global air quality improved in response to COVID-19-induced lockdown policies.
Table 1.
Government response to COVID-19 and air pollution.
| ADM1/City level |
Country level |
|||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Panel A: Air quality is measured by NO2(satellite data) | ||||
| Stringency index | −0.032∗∗∗ (0.003) |
−0.012∗∗∗ (0.003) |
−0.040∗∗∗ (0.004) |
−0.033∗∗∗ (0.004) |
| Controls | No | Yes | No | Yes |
| Country and time FE | Yes | Yes | Yes | Yes |
| Observations | 250,838 | 248,120 | 14,850 | 14,712 |
| Panel B: Air quality is measured by PM2.5(station-based data) | ||||
| Stringency index | −0.164∗∗∗ (0.016) |
−0.129∗∗∗ (0.016) |
−0.175∗∗∗ (0.011) |
−0.148∗∗∗ (0.011) |
| Controls | No | Yes | No | Yes |
| Country and time FE | Yes | Yes | Yes | Yes |
| Observations | 81,478 | 75,048 | 12,784 | 11,986 |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of panel model. Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. Control variables are daily temperature and rainfall (humidity for station-based data).
Column (2) indicates that a one-point increase in the stringency index is associated with a 0.012 mol/km2 (mole per square kilometer) decrease in NO2 (Panel A). The corresponding figure for station-based data is a 0.129 μg/m3 (micogram per cubic meter) decrease in PM2.5 (Panel B). Estimates at the country level (column 4) are similar to those at the sub-national level (column 2). However, as discussed earlier, the estimates based on Equation (1) are likely biased since they do not properly account for the unobservables that may correlate with both the stringency index and air quality.
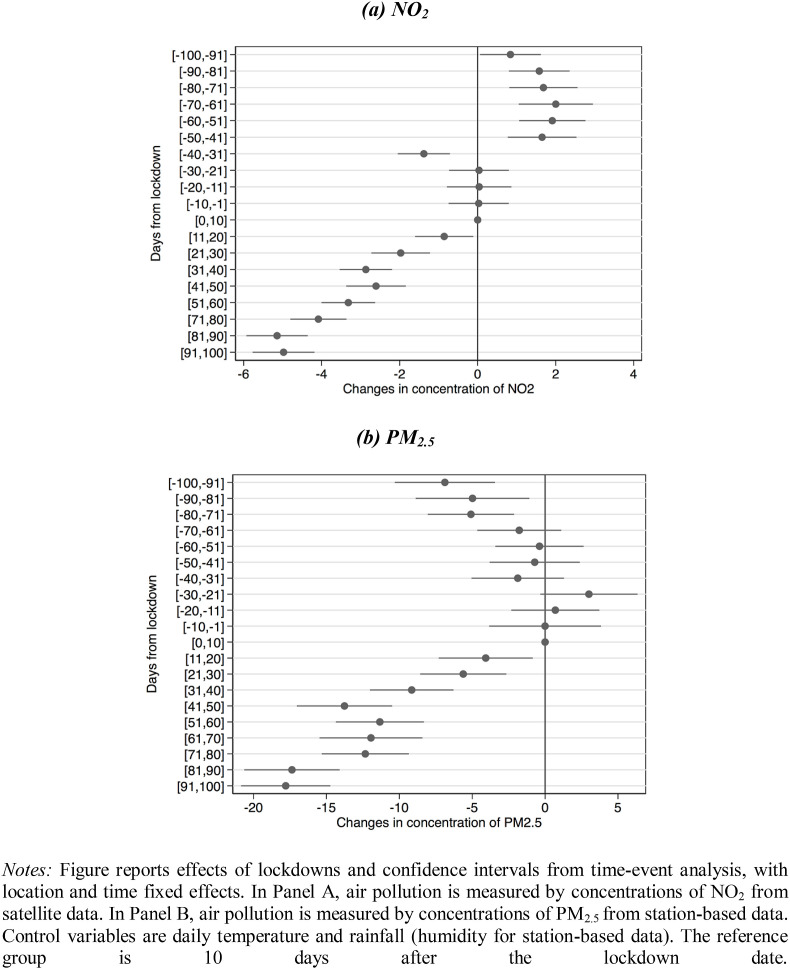
To address this issue, we conduct time-event analysis by regressing air quality on a full set of control variables and location and time fixed effects, and a series of “event time” indicators. These indicator variables are in groups of 10 days for days ranging from −100 to +100 before and after the lockdown dates. Fig. 1 plots these results, which confirm our previous finding that concentrations of air pollution are significantly lower after the lockdown dates (Panels A and B), and the impacts are more pronounced for satellite data (Panel A).
Fig. 1.
Event study analysis. Notes: Figure reports effects of lockdowns and confidence intervals from time-event analysis, with location and time fixed effects. In Panel A, air pollution is measured by concentrations of NO2 from satellite data. In Panel B, air pollution is measured by concentrations of PM2.5 from station-based data. Control variables are daily temperature and rainfall (humidity for station-based data). The reference group is 10 days after the lockdown date.
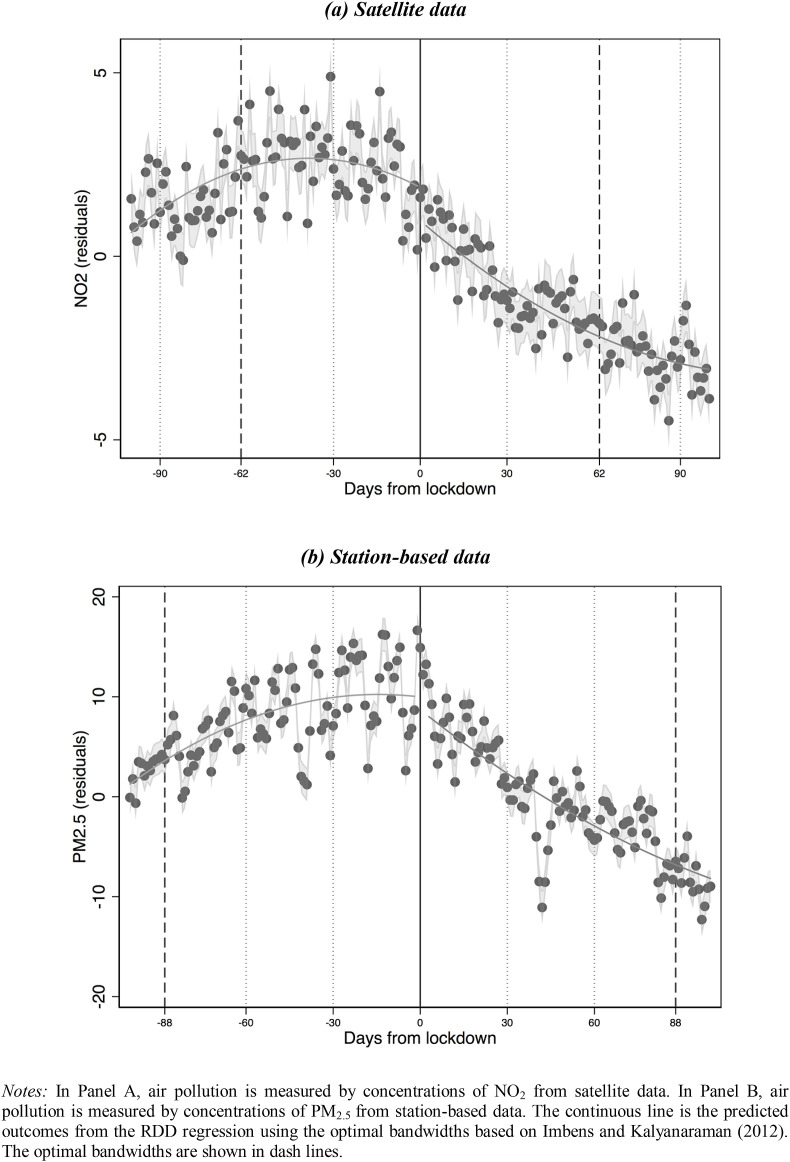
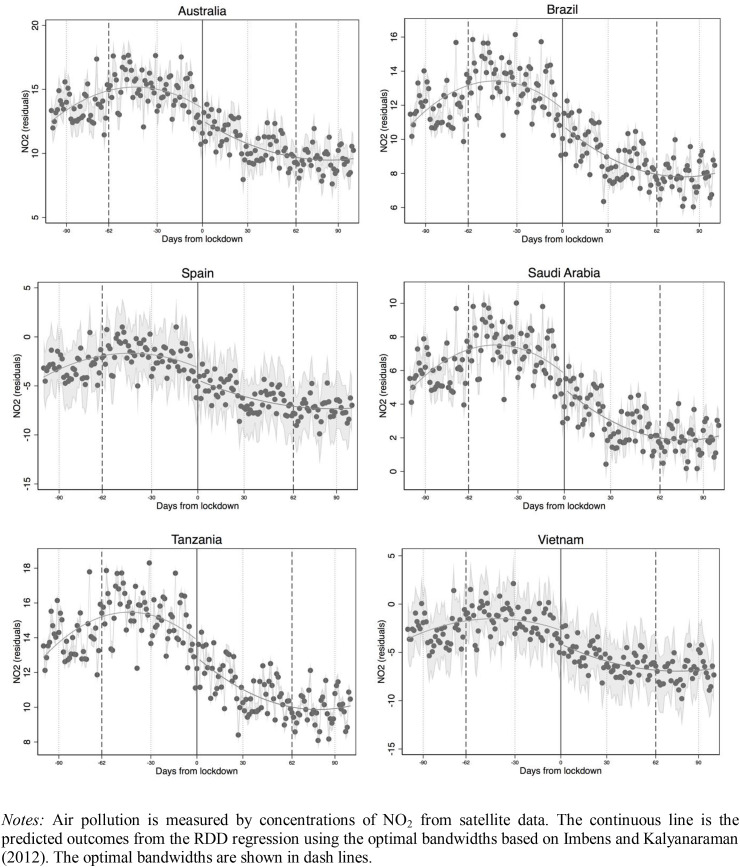
We subsequently present the main estimation results using our preferred identification – the RD-in-time model. We start first with showing in Fig. 2 the prima facie evidence of the impacts of lockdowns on air quality. The figure plots the residuals from a data-driven RDD regression of air pollution, measured by NO2 (Panel A) and PM2.5 (Panel B), on daily temperature and rainfall against the days before and after the lockdown dates. A negative jump at the lockdown (cut-off) dates suggests reduced air pollution after the lockdowns. The downward sloping trend for air pollution in Fig. 2 also suggests that the reduction in air pollution becomes stronger as the lockdowns go into effect for a longer period. This is understandable, since a short period of time may not be sufficient to detect the changes in air quality.7
Fig. 2.
COVID-19 lockdowns and air pollution. Notes: In Panel A, air pollution is measured by concentrations of NO2 from satellite data. In Panel B, air pollution is measured by concentrations of PM2.5 from station-based data. The continuous line is the predicted outcomes from the RDD regression using the optimal bandwidths based on Imbens and Kalyanaraman (2012). The optimal bandwidths are shown in dash lines.
We report the estimation results for Equation (2) in Table 2 , which shows estimates using two data samples: the satellite data (Panel A) and the station-based data (Panel B). Our preferred models are, again, those that control for weather conditions (columns 2, 4, and 6). We use the optimal data-driven bandwidth selection procedures proposed by Imbens and Kalyanaraman (2012).8 The estimation results using the satellite data, our main data for analysis, show that air quality improves after the lockdowns, and the results are strongly statistically significant at the 5 percent level or less (Panel A). The estimates are qualitatively similar whether we include the control variables.
Table 2.
COVID-19 lockdowns and air pollution.
| Panel A: Satellite air pollution | ||||||
| Air quality: |
Optimal bandwidth |
Optimal bandwidth +10 days |
Optimal bandwidth −10 days |
|||
| NO2 |
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
| Model 1: Linear model | ||||||
| Lockdown = 1 | −1.251∗∗∗ (0.326) |
−1.260∗∗∗ (0.321) |
−1.482∗∗∗ (0.314) |
−1.512∗∗∗ (0.310) |
−0.898∗∗ (0.354) |
−0.918∗∗∗ (0.348) |
| Model 2: Linear interaction model | ||||||
| Lockdown = 1 | −1.227∗∗∗ (0.324) |
−1.230∗∗∗ (0.319) |
−1.462∗∗∗ (0.312) |
−1.494∗∗∗ (0.307) |
−0.865∗∗ (0.352) |
−0.871∗∗ (0.346) |
| Model 3: Quadratic model | ||||||
| Lockdown = 1 | −1.242∗∗∗ (0.325) |
−1.251∗∗∗ (0.320) |
−1.480∗∗∗ (0.313) |
−1.520∗∗∗ (0.307) |
−0.877∗∗ (0.353) |
−0.888∗∗ (0.346) |
| Model 4: Quadratic interaction model | ||||||
| Lockdown = 1 |
−1.227∗∗∗ (0.326) |
−1.235∗∗∗ (0.321) |
−1.470∗∗∗ (0.314) |
−1.508∗∗∗ (0.309) |
−0.863∗∗ (0.353) |
−0.874∗∗ (0.347) |
| Means before lockdowns | 23.281 | 23.281 | 23.281 | 23.281 | 23.281 | 23.281 |
| Controls | No | Yes | No | Yes | No | Yes |
| Country and time FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations |
260,007 |
257,339 |
303,316 |
300,266 |
216,917 |
214,775 |
| Panel B: Station-based air pollution | ||||||
| Air quality: |
Optimal bandwidth |
Optimal bandwidth +10 days |
Optimal bandwidth −10 days |
|||
| PM2.5 |
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
| Model 1: Linear model | ||||||
| Lockdown = 1 | −4.406∗∗∗ (1.107) |
−2.525∗∗ (1.257) |
−4.790∗∗∗ (1.105) |
−2.713∗∗ (1.235) |
−3.954∗∗∗ (1.181) |
−1.998 (1.314) |
| Model 2: Linear interaction model | ||||||
| Lockdown = 1 | −3.830∗∗∗ (1.067) |
−2.049∗ (1.225) |
−4.149∗∗∗ (1.049) |
−2.284∗ (1.196) |
−3.433∗∗∗ (1.136) |
−1.584 (1.280) |
| Model 3: Quadratic model | ||||||
| Lockdown = 1 | −3.976∗∗∗ (1.078) |
−2.133∗ (1.240) |
−4.303∗∗∗ (1.063) |
−2.396∗∗ (1.211) |
−3.568∗∗∗ (1.148) |
−1.662 (1.297) |
| Model 4: Quadratic interaction model | ||||||
| Lockdown = 1 |
−3.805∗∗∗ (1.059) |
−2.035∗ (1.217) |
−4.143∗∗∗ (1.047) |
−2.231∗ (1.188) |
−3.375∗∗∗ (1.128) |
−1.599 (1.269) |
| Means before lockdowns | 64.824 | 64.824 | 64.824 | 64.824 | 64.824 | 64.824 |
| Controls | No | Yes | No | Yes | No | Yes |
| Country and time FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 90,938 | 79,200 | 100,869 | 89,117 | 80,962 | 69,238 |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of RDD using the optimal bandwidths based on Imbens and Kalyanaraman (2012). The optimal bandwidths are 62 and 88 days for satellite and station-based data, respectively. Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. Model 1 uses running variable in linear form, Model 2 includes interaction of running variable and treatment variable, Model 3 includes quadratic term of running variable, Model 4 includes interactions of running variable (linear and quadratic terms) with treatment variable. Control variables are daily temperature and rainfall (humidity for station-based data).
Specifically, the estimated coefficient on the lockdown variable is negative and statistically significant at the 1 percent level using the linear model (Panel A, column 2), indicating that the lockdown leads to a 1.260-mol/km2 decrease in the global concentration of NO2 using the optimal bandwidth of 62 days. This translates into a 5.4-percent decrease compared to an average value of NO2 of 23.281 mol/km2 before the lockdowns. Using different functional forms (models 2 to 4) results in similar estimates. Finally, we present the results using different bandwidth lengths (±10 days from the optimal bandwidth) and find consistent impacts of the lockdowns on NO2. The decreases in concentration of NO2 are roughly 6.5 percent for 72 days (Panel A, column 4) and 3.9 percent for 52 days (Panel A, column 6) after the lockdowns.
We turn next to the alternative station-based data. Using the optimal bandwidth of 88 days, we find that the global decrease in PM2.5 hovers around 3.1 to 3.9 percent depending on the functional form that we employ (Panel B, column 2). These results are consistent with the global reduction of 4 percent in PM2.5 estimated by Lenzen et al. (2020). But estimates become statistically insignificant for the narrower bandwidth of 78 days.9
We now perform a set of placebo tests to check the robustness of our results, as reported in Table 3 . First, we falsely assume the cut-off date to be 5, 10, 15, 30, and 45 days prior to the lockdown dates. Regardless of measures of air pollution, the treatment effects are not statistically significant (Panels A to E). Second, we use the lockdown dates of several countries as placebo tests, which is motivated by the fact that the shutdown of a large trading economy partner may have spill-over effects on local industrial activity, and thereby affecting air pollution. We select China and India given their large economies and trade resources. Again, the statistically insignificant results lend support to our main specification (Panels F to G). Finally, following Barreca et al. (2011), we also conduct a “donut” RDD by systematically removing observations 5 and 10 days near the lockdown dates. This approach allows us to address potential anticipation effects around the lockdown dates (i.e., there is non-random sorting around the threshold). The results, presented in Table A4 (Appendix A), rule out this concern.
Table 3.
Placebo test.
| Dependent variable: | NO2 |
PM2.5 |
|---|---|---|
| (1) | (2) | |
| Panel A: 5 days prior to lockdown date | ||
| Lockdown = 1 | −1.193∗ (0.656) |
−1.257 (2.479) |
| Observations | 256,246 | 79,098 |
| Panel B: 10 days prior to lockdown date | ||
| Lockdown = 1 | −0.894 (0.593) |
0.517 (2.442) |
| Observations | 255,785 | 78,918 |
| Panel C: 15 days prior to lockdown date | ||
| Lockdown = 1 | −0.300 (0.555) |
2.714 (2.505) |
| Observations | 254,805 | 78,415 |
| Panel D: 30 days prior to lockdown date | ||
| Lockdown = 1 | 0.043 (0.449) |
2.719 (3.603) |
| Observations | 253,870 | 76,384 |
| Panel E: 45 days prior to lockdown date | ||
| Lockdown = 1 | 0.533 (0.763) |
−0.751 (1.798) |
| Observations | 252,852 | 71,773 |
| Panel F: China lockdown date | ||
| Lockdown = 1 | 0.489 (0.623) |
−1.429 (1.474) |
| Observations | 252,003 | 78,463 |
| Panel G: India lockdown date | ||
| Lockdown = 1 | −0.049 (0.450) |
−1.811 (1.107) |
| Observations |
252,306 |
78,594 |
| Means before lockdowns | 23.281 | 64.824 |
| Controls | Yes | Yes |
| Country and time FE | Yes | Yes |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of RDD using the optimal bandwidths based on Imbens and Kalyanaraman (2012). The optimal bandwidths are 62 and 88 days for satellite and station-based data, respectively. Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. Control variables are daily temperature and rainfall (humidity for station-based data).
4.2. Further robustness tests and heterogeneity analysis
We conduct a battery of robustness tests on the estimation results. These include employing different procedures for selecting the optimal bandwidth, higher-degree polynomials of the running variable, adding different covariates to the regressions (i.e. such as GDP per capita in constant 2010 USD, population density, log of energy consumption per capita, the number of motor vehicles per 1000 inhabitants, and the share of electricity generated by coal power), using wider time bandwidths (i.e., weekly indicators) and different versions of the stringency index, controlling for potentially differential time trends across countries, and converting the air quality variables into the logarithmic form. The estimation results, which are presented in Appendix A, Table A10, Table A11, Table A12, Table A13, Table A6, Table A7, Table A8, Table A9 and discussed in detail in Appendix C, remain robust.
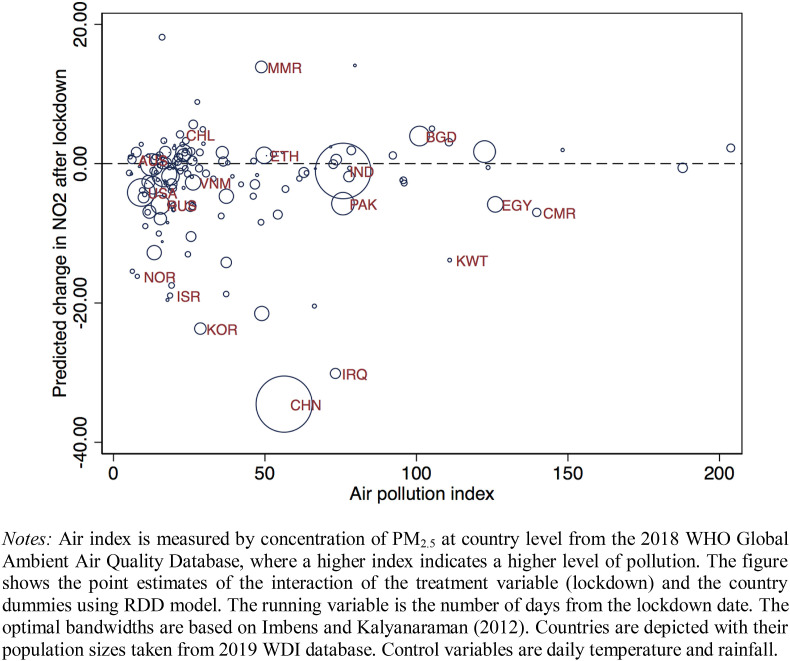
We further examine whether the impacts of lockdowns differ by country characteristics. Estimation results, shown in Table A14 (Appendix A), suggest that after the lockdowns i) countries near the equator have a higher concentration of NO2, ii) countries with strong institutions do not perform better in terms of air quality, iii) countries with a larger share of trade or manufacturing have more reduced air pollution, and iv) countries with an initially lower level of air pollution (i.e., the 1st quintile) have more reduced air pollution compared to those with initially higher levels of air pollution. Several countries with a large population size that recorded higher air quality stand out, including China, Iraq, Norway, Russia, South Korea, and the United States (see Figure A5; Appendix A).
4.3. Stringent policies and mobility restriction
Once we established the causal impacts of COVID-19 on air pollution, we shift our attention to the role of mobility restrictions as a potential mechanism. Since one main source of air pollution comes from traffic mobility (Viard and Fu, 2015), more stringent policies can result in less mobility, thereby improving air quality. We directly test this hypothesis, using data from the Google Community Mobility Reports. Since mobility data were not available before the lockdown date, we are unable to apply the more rigorous RDD approach. We thus present in Table 4 the estimation results using the fixed-effects model in Equation (1), which show that human mobility has declined significantly where government policies are more stringent.10 In particular, a higher stringency index is associated with less mobility in both ‘essential services’ (e.g., grocery and pharma, workplace) and ‘non-essential services’ (retail and recreation, parks), but more mobility in the ‘residential’ category.
Table 4.
Stringency index and mobility restriction.
| Mobility changes | Retail and recreation |
Grocery and pharmacy |
Park |
Transit |
Workplaces |
Residential |
|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |
| Panel A: Sub-national level | ||||||
| Stringency index | −0.820∗∗∗ (0.014) |
−0.392∗∗∗ (0.020) |
−0.587∗∗∗ (0.012) |
−0.772∗∗∗ (0.012) |
−0.624∗∗∗ (0.013) |
0.292∗∗∗ (0.004) |
| Controls | Yes | Yes | Yes | Yes | Yes | Yes |
| Country and time FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 377,883 | 364,427 | 225,097 | 258,844 | 471,734 | 267,863 |
| Panel B: Country level | ||||||
| Stringency index | −0.766∗∗∗ (0.005) |
−0.481∗∗∗ (0.005) |
−0.539∗∗∗ (0.007) |
−0.789∗∗∗ (0.004) |
−0.596∗∗∗ (0.005) |
0.285∗∗∗ (0.002) |
| Controls | Yes | Yes | Yes | Yes | Yes | Yes |
| Country and time FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 13,284 | 13,284 | 13,284 | 13,284 | 13,284 | 13,238 |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of panel model. Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. Control variables are daily temperature and rainfall.
5. Conclusion
We offer an early study that provides cross-national evidence on the causal impacts of COVID-19 on air pollution. We assemble a rich database from various sources, which we analyze with RDD and panel data models. We find the COVID-19-induced lockdowns to result in significant decreases in global air pollution. Results of placebo tests reassure that our findings are not driven by confounding factors. We also find heterogeneous impacts for different country characteristics, and we identify reduced mobility, especially nonessential individual movements, as a potential channel that can help improve air quality on a global scale. A promising direction for future research is to identify ways to maintain these beneficial impacts on air quality (e.g., through reduced mobility) when the economy returns to pre-COVID-19 conditions.
Footnotes
We would like to thank the editor Nicholas Rivers, two anonymous reviewer, Dean Jolliffe, and Paolo Verme for helpful discussions on earlier versions. Dang would also like to thank the UK Department of International Development for additional funding assistance through a Knowledge for Change (KCP) grant for the World Development Report 2021 “Data for Better Lives”. Trinh acknowledges support from the World Bank Young Fellows Program in Forced Displacement.
For example, studied topics include unemployment (Fairlie et al., 2020), household consumption (Baker et al., 2020), gender inequality (Dang and Nguyen, 2020), and individual income (loss) and behaviour changes (Akesson et al., 2020).
A recent study applies time series analysis to historical data to predict the impacts of pandemic on air pollution (Smith et al., 2020). Other studies examine instead the related impacts on health outcomes caused by the pandemic-induced changes in air quality (Cicala et al., 2020; Cole et al., 2020; Isphording and Pes,tel, 2020).
We also find some limited evidence that countries with a higher share of trade and manufacturing in the economy have more reduced air pollution after the lockdowns, as do countries with an initially lower level of air pollution. But the opposite result holds for countries near the equator (see Appendix C).
We offer additional results using high-order polynomial terms in Table A6 (Appendix A); however, controlling for high-order polynomials in RDD analysis may lead to noisy estimates (Gelman and Imbens, 2019).
Although the OxCGRT data provides a systematic comparison across different countries, it is still possible that not all business activities and travel cease exactly by the time of our constructed lockdown dates. In that case, a better approach is to employ the fuzzy RDD model rather than the sharp RDD model where the treatment variable can assume the value of 0 for for some countries. However, we do not have such additional information for in our case and have to uniformly define as 1 after the lockdown date for each country. But we offer a multi-layered approach to ensure that estimation results are robust. First, the estimates using Equation (1) above provide the first set of evidence over the (correlational) relationship between air quality and the government stringency index. Second, examining the outcomes over several different time bandwidths helps average out any lingering impacts after the lockdowns and provides comparisons. The subsequent estimates remain (qualitatively) similar, indicating that they are robust to this concern. Third, estimates also remain robust to different ways to aggregate data (such as using weekly air quality data instead of daily air quality data) and different versions of the stringency index (such as probing more deeply into its different components). Finally, we also offer a battery of other additional robustness tests in Section 4.2.
Precipitation from the station-based data is not used due to its low frequency.
We replicate the graphical analysis in Fig. 2 for several countries from different regions. The results (Appendix A; Figure A3) confirm our expectation that the lockdowns result in significant reduction of air pollution.
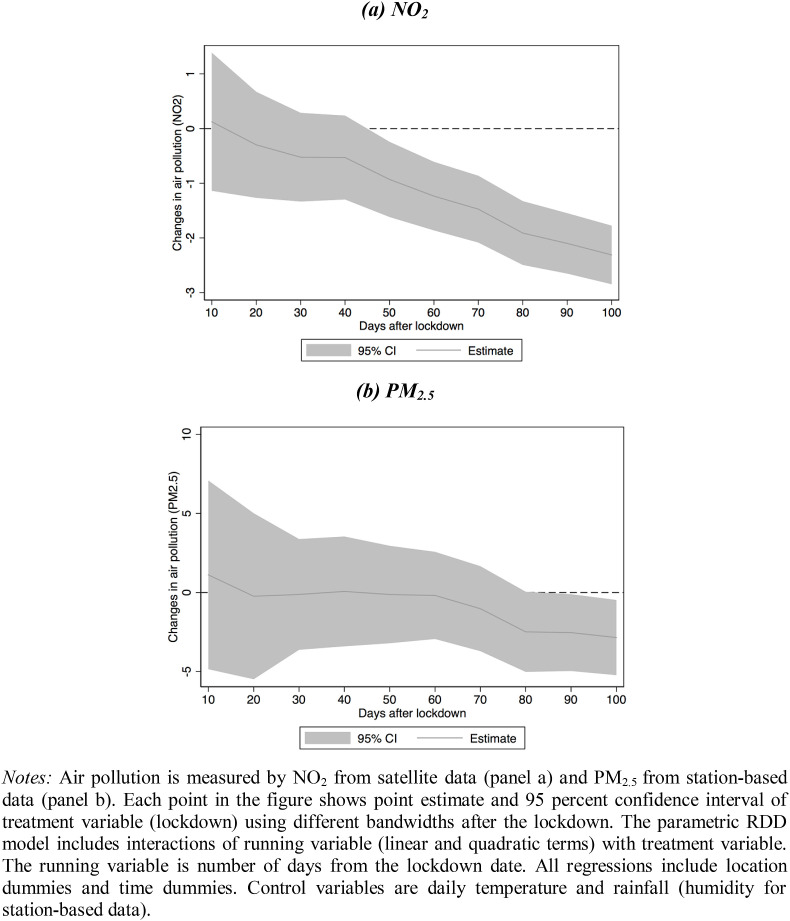
We also plot the estimated impacts of lockdowns for other bandwidths that range from 0 to 100 days. The estimation results, shown in Figure A4 (Appendix A), indicate that the lockdown impacts become much weaker for bandwidths of up to 50 and 80 days for satellite and station-based data, respectively.
Using different measures of air pollution available from the station-based data yields a similar conclusion (Table A3, Appendix A). An exception is the indicator O3 which is found to be positively associated with the lockdowns. A possible explanation for the increase in concentration of O3 is warmer weather during this period (Tobías et al., 2020).
The Google Community Mobility Reports starts collecting data on mobility data from February 15th, 2020. We estimate that about 109 countries (out of 164) have already implemented lockdowns based on the stringency index. The estimation results obtained by the panel data model (Table 1) are qualitatively similar to those obtained by the RDD approach (Table 2), suggesting that applying this model can provide some qualitative evidence on the mechanism of impacts.
The data have recently been used to study changes in air quality caused by COVID-19 in some health and environmental studies (see, e.g., Chen et al. (2020) and Zambrano-Monserrate et al. (2020)).
In some countries, the ADM1 refers to province level while for others, it refers to state/region level. The administrative data are available at https://gadm.org/about.html.
For more details, see: https://atmosphere.copernicus.eu/flawed-estimates-effects-lockdown-measures-air-quality-derived-satellite-observations?q=flawed-estimates-effects-lockdown-measures-air-quality-satellite-observations.
We apply the user-written program “rdbwselect” provided by Calonico et al. (2014) to estimate the cross-validation functions that determine our bandwidths.
Another index is Legacy stringency index; however, it is not recommended by the OxCGRT team (Hale et al., 2020).
Appendix A. Additional Figures and Tables
Fig. A1.
Number of countries that introduced lockdowns and average policy stringency index.
Fig. A2.
COVID-19 lockdowns and temperature/precipitation.
Fig. A3.
COVID-19 lockdowns and air pollution – Country-specific case studies.
Fig. A4.
COVID-19 lockdowns and air pollution – Alternative bandwidths.
Fig. A5.
Air pollution reduction by country.
Table A1.
Lockdown impacts on weather conditions.
| Dependent variable: | Temperature |
Rainfall |
|---|---|---|
| (1) | (2) | |
| Lockdown = 1 | 0.752 (0.742) |
−0.002 (0.014) |
| Controls | Yes | Yes |
| Country and time FE | Yes | Yes |
| Observations | 425,624 | 425,624 |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of RDD. Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. The optimal bandwidths are calculated based on Imbens and Kalyanaraman (2012). Control variable in columns (1) and (2) is daily rainfall and temperature, respectively.
Table A2.
COVID-19 lockdowns and air pollution – Lagged dependent variable estimation.
| Bandwidth | Air pollution: NO2 |
Air pollution: PM2.5 |
||||
|---|---|---|---|---|---|---|
| Optimal bandwidth | Optimal bandwidth +10 days | Optimal bandwidth −10 days | Optimal bandwidth | Optimal bandwidth +10 days | Optimal bandwidth −10 days | |
| Lockdown = 1 | −0.421∗∗∗ (0.125) |
−0.552∗∗∗ (0.121) |
−0.208∗ (0.115) |
−0.639∗∗ (0.311) |
−0.586∗∗ (0.286) |
−0.520 (0.332) |
| Lagged dependent variable | 0.646∗∗∗ (0.026) |
0.648∗∗∗ (0.025) |
0.628∗∗∗ (0.027) |
0.707∗∗∗ (0.013) |
0.719∗∗∗ (0.013) |
0.696∗∗∗ (0.014) |
| Means before lockdowns | 23.281 | 23.281 | 23.281 | 64.824 | 64.824 | 64.824 |
| Controls | Yes | Yes | Yes | Yes | Yes | Yes |
| Country and time FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 209,825 | 245,188 | 174,500 | 76,939 | 86,714 | 67,043 |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of RDD using the optimal bandwidths based on Imbens and Kalyanaraman (2012). Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. Control variables are daily temperature and rainfall (humidity for station-based data).
Table A3.
COVID-19 lockdowns and air pollution – Other parameters of pollution.
| Bandwidths | (1) |
(2) |
(3) |
|---|---|---|---|
| Optimal bandwidth | Optimal bandwidth +10 days | Optimal bandwidth −10 days | |
| Panel A: Air quality is measured by PM10 | |||
| Lockdown = 1 | −1.644∗∗ (0.739) |
−1.958∗∗∗ (0.676) |
−1.621∗∗ (0.722) |
| Means before lockdowns | 30.655 | 30.655 | 30.655 |
| Observations | 83,886 | 92,890 | 74,209 |
| Panel B: Air quality is measured by NO2 | |||
| Lockdown = 1 | −1.062∗∗∗ (0.349) |
−1.387∗∗∗ (0.326) |
−0.706∗ (0.374) |
| Means before lockdowns | 12.880 | 12.880 | 12.880 |
| Observations | 65,473 | 75,076 | 55,942 |
| Panel C: Air quality is measured by O3 | |||
| Lockdown = 1 | 1.182∗∗∗ (0.360) |
1.554∗∗∗ (0.337) |
1.084∗∗∗ (0.356) |
| Means before lockdowns | 14.543 | 14.543 | 14.543 |
| Observations | 51,809 | 60,682 | 42,850 |
| Panel D: Air quality is measured by SO2 | |||
| Lockdown = 1 | −0.364∗ (0.209) |
−0.453∗∗ (0.189) |
−0.355 (0.230) |
| Means before lockdowns | 4.643 | 4.643 | 4.643 |
| Observations |
49,795 |
57,880 |
41,729 |
| Controls | Yes | Yes | Yes |
| Country and time FE | Yes | Yes | Yes |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of RDD using the optimal bandwidths based on Imbens and Kalyanaraman (2012). The optimal bandwidths are 95, 76, 66 and 69 days for PM10, NO2, O3, and SO2, respectively. Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. Control variables are daily temperature and humidity.
Table A4.
COVID-19 lockdowns and air pollution – “Donut” RDD.
| Bandwidth | Air pollution: NO2 |
Air pollution: PM2.5 |
||||
|---|---|---|---|---|---|---|
| Optimal bandwidth | Optimal bandwidth +10 days | Optimal bandwidth −10 days | Optimal bandwidth | Optimal bandwidth +10 days | Optimal bandwidth −10 days | |
| Panel A: Excluding observations 5 days near the lockdown date | ||||||
| Lockdown = 1 | −1.641∗∗∗ (0.393) |
−1.955∗∗∗ (0.367) |
−1.215∗∗∗ (0.434) |
−3.781∗∗∗ (1.211) |
−3.841∗∗∗ (1.167) |
−3.486∗∗∗ (1.298) |
| Observations | 234,913 | 277,840 | 192,349 | 73,810 | 83,727 | 63,848 |
| Panel B: Excluding observations 10 days near the lockdown date | ||||||
| Lockdown = 1 | −2.120∗∗∗ (0.489) |
−2.408∗∗∗ (0.436) |
−1.554∗∗∗ (0.557) |
−3.948∗∗ (1.620) |
−4.079∗∗∗ (1.487) |
−3.615∗∗ (1.605) |
| Observations |
214,381 |
257,308 |
171,817 |
69,467 |
79,384 |
59,505 |
| Means before lockdowns | 23.281 | 23.281 | 23.281 | 64.824 | 64.824 | 64.824 |
| Controls | Yes | Yes | Yes | Yes | Yes | Yes |
| Country and time FE | Yes | Yes | Yes | Yes | Yes | Yes |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of “Donut” RDD using the optimal bandwidths based on Imbens and Kalyanaraman (2012). Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. Control variables are daily temperature and rainfall (humidity for station-based data).
Table A5.
COVID-19 lockdowns and air pollution – Alternative Optimal bandwidths.
| Optimal bandwidth calculation method | Satellite NO2 |
Station-based PM2.5 |
||
|---|---|---|---|---|
| CCT (Calonico, Cattaneo, and Titiunik) | Cross-valid (Lee and Lemieux) | CCT (Calonico, Cattaneo, and Titiunik) | Cross-valid (Lee and Lemieux) | |
| Lockdown = 1 | −1.125∗∗∗ (0.305) |
−1.224∗∗∗ (0.325) |
−0.558 (1.010) |
−3.827∗∗∗ (1.191) |
| Optimal bandwidth | [-58, 76] | [-60, 60] | [-74, 109] | [-77, 77] |
| Means before lockdowns | 23.281 | 23.281 | 64.824 | 64.824 |
| Controls | Yes | Yes | Yes | Yes |
| Country and time FE | Yes | Yes | Yes | Yes |
| Observations | 285,467 | 255,628 | 94,784 | 79,963 |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of RDD using the optimal bandwidths based on Calonico et al. (2014) and Lee and Lemieux (2010). Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. Control variables are daily temperature and rainfall (humidity for station-based data).
Table A6.
COVID-19 lockdowns and air pollution – Alternative functional forms.
| Panel A: Satellite air pollution | ||||||
| Air quality: |
Optimal bandwidth |
Optimal bandwidth +10 days |
Optimal bandwidth −10 days |
|||
| NO2 |
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
| Model 1: Cubic interaction model | ||||||
| Lockdown = 1 | −0.487∗∗ (0.241) |
0.377 (0.305) |
−0.631∗∗∗ (0.220) |
−0.571∗∗∗ (0.221) |
−0.338 (0.264) |
−0.294 (0.264) |
| Model 2: Quartic interaction model | ||||||
| Lockdown = 1 | −1.058∗∗∗ (0.184) |
−1.242∗∗∗ (0.233) |
−1.193∗∗∗ (0.173) |
−1.032∗∗∗ (0.173) |
−0.939∗∗∗ (0.200) |
−0.832∗∗∗ (0.200) |
| Model 3: Quintic interaction model | ||||||
| Lockdown = 1 |
−0.710∗∗∗ (0.217) |
−0.191 (0.275) |
−0.851∗∗∗ (0.199) |
−0.754∗∗∗ (0.199) |
−0.534∗∗ (0.239) |
−0.469∗∗ (0.239) |
| Means before lockdowns | 23.281 | 23.281 | 23.281 | 23.281 | 23.281 | 23.281 |
| Controls | No | Yes | No | Yes | No | Yes |
| Country and time FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations |
260,007 |
257,339 |
303,316 |
300,266 |
216,917 |
214,775 |
| Panel B: Station-based air pollution | ||||||
| Air quality: |
Optimal bandwidth |
Optimal bandwidth +10 days |
Optimal bandwidth −10 days |
|||
| PM2.5 |
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
| Model 1: Cubic interaction model | ||||||
| Lockdown = 1 | −1.155∗∗ (0.579) |
−0.427 (0.621) |
−1.883∗∗∗ (0.548) |
−1.001∗ (0.592) |
0.320 (0.620) |
0.869 (0.659) |
| Model 2: Quartic interaction model | ||||||
| Lockdown = 1 | −3.819∗∗∗ (0.436) |
−2.021∗∗∗ (0.479) |
−4.156∗∗∗ (0.411) |
−2.233∗∗∗ (0.452) |
−3.386∗∗∗ (0.463) |
−1.573∗∗∗ (0.506) |
| Model 3: Quintic interaction model | ||||||
| Lockdown = 1 |
−2.236∗∗∗ (0.521) |
−1.056∗ (0.565) |
−2.875∗∗∗ (0.493) |
−1.605∗∗∗ (0.538) |
−0.695 (0.557) |
0.451 (0.600) |
| Means before lockdowns | 64.824 | 64.824 | 64.824 | 64.824 | 64.824 | 64.824 |
| Controls | No | Yes | No | Yes | No | Yes |
| Country and time FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 90,938 | 79,200 | 100,869 | 89,117 | 80,962 | 69,238 |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of RDD using the optimal bandwidths based on Imbens and Kalyanaraman (2012). The optimal bandwidths are 62 and 88 days for satellite and station-based data, respectively. Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. Control variables are daily temperature and rainfall (humidity for station-based data).
Table A7.
COVID-19 lockdowns and air pollution – RDD with additional covariates.
| Bandwidth | Air pollution: NO2 |
Air pollution: PM2.5 |
||||
|---|---|---|---|---|---|---|
| Optimal bandwidth | Optimal bandwidth +10 days | Optimal bandwidth −10 days | Optimal bandwidth | Optimal bandwidth +10 days | Optimal bandwidth −10 days | |
| Panel A: Controlling for pre-pandemic characteristics | ||||||
| Lockdown = 1 | −2.017∗∗∗ (0.599) |
−2.418∗∗∗ (0.502) |
−1.427∗∗ (0.609) |
−3.190∗∗ (1.524) |
−3.249∗∗ (1.437) |
−2.589∗ (1.565) |
| Country FE | No | No | No | No | No | No |
| Time FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Means before lockdowns | 23.281 | 23.281 | 23.281 | 64.824 | 64.824 | 64.824 |
| Observations | 185,307 | 215,912 | 154,577 | 73,693 | 82,986 | 64,434 |
| Panel B: Controlling for country fixed-effects | ||||||
| Lockdown = 1 | −1.235∗∗∗ (0.321) |
−1.508∗∗∗ (0.309) |
−0.874∗∗ (0.347) |
−2.035∗ (1.217) |
−2.231∗ (1.188) |
−1.599 (1.269) |
| Country FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Time FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Means before lockdowns | 23.281 | 23.281 | 23.281 | 64.824 | 64.824 | 64.824 |
| Observations | 257,339 | 300,266 | 214,775 | 79,200 | 89,117 | 69,238 |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of RDD using the optimal bandwidths based on Imbens and Kalyanaraman (2012). The optimal bandwidths are 62 and 88 days for satellite and station-based data, respectively. Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. Control variables in Panel A are daily temperature and rainfall (humidity for station-based data), log of GDP per capita (constant 2010 USD), population density, log of energy consumption per capita, motor vehicles per 1000 inhabitants, and share of electricity generated by coal power. Control variables in Panel B are daily temperature and rainfall (humidity for station-based data).
Table A8.
COVID-19 lockdowns and air pollution - Weekly data.
| Panel A: Satellite air pollution | ||||||
| Air quality: |
Optimal bandwidth |
Optimal bandwidth +2 weeks |
Optimal bandwidth −2 weeks |
|||
| NO2 |
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
| Model 1: Linear model | ||||||
| Lockdown = 1 | −1.033∗∗∗ (0.354) |
−1.004∗∗∗ (0.348) |
−1.549∗∗∗ (0.236) |
−1.559∗∗∗ (0.322) |
−0.629 (0.413) |
−0.617 (0.406) |
| Model 2: Linear interaction model | ||||||
| Lockdown = 1 | −0.986∗∗∗ (0.352) |
−0.938∗∗∗ (0.346) |
−1.507∗∗∗ (0.324) |
−1.513∗∗∗ (0.319) |
−0.567 (0.410) |
−0.525 (0.403) |
| Model 3: Quadratic model | ||||||
| Lockdown = 1 | −1.018∗∗∗ (0.352) |
−0.985∗∗∗ (0.347) |
−1.550∗∗∗ (0.325) |
−1.573∗∗∗ (0.320) |
−0.599 (0.411) |
−0.571 (0.404) |
| Model 4: Quadratic interaction model | ||||||
| Lockdown = 1 |
−0.989∗∗∗ (0.358) |
−0.950∗∗∗ (0.352) |
−1.541∗∗∗ (0.329) |
−1.561∗∗∗ (0.323) |
−0.584 (0.420) |
−0.566 (0.412) |
| Means before lockdowns | 23.281 | 23.281 | 23.281 | 23.281 | 23.281 | 23.281 |
| Controls | No | Yes | No | Yes | No | Yes |
| Country and time FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations |
260,007 |
257,339 |
320,328 |
317,121 |
199,439 |
197,492 |
| Panel B: Station-based air pollution | ||||||
| Air quality: |
Optimal bandwidth |
Optimal bandwidth +2 weeks |
Optimal bandwidth −2 weeks |
|||
| PM2.5 |
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
| Model 1: Linear model | ||||||
| Lockdown = 1 | −4.145∗∗∗ (1.158) |
−2.445∗ (1.339) |
−4.677∗∗∗ (1.120) |
−2.833∗∗ (1.265) |
−3.027∗∗ (1.292) |
−1.295 (1.443) |
| Model 2: Linear interaction model | ||||||
| Lockdown = 1 | −3.387∗∗∗ (1.117) |
−1.842 (1.302) |
−3.945∗∗∗ (1.063) |
−2.302∗ (1.217) |
−2.314∗ (1.244) |
−0.806 (1.402) |
| Model 3: Quadratic model | ||||||
| Lockdown = 1 | −3.663∗∗∗ (1.127) |
−2.006 (1.317) |
−4.261∗∗∗ (1.078) |
−2.513∗∗ (1.233) |
−2.572∗∗ (1.254) |
−0.964 (1.418) |
| Model 4: Quadratic interaction model | ||||||
| Lockdown = 1 |
−3.320∗∗∗ (1.104) |
−1.726 (1.287) |
−3.936∗∗∗ (1.058) |
−2.172∗ (1.209) |
−2.141∗ (1.238) |
−0.623 (1.381) |
| Means before lockdowns | 64.824 | 64.824 | 64.824 | 64.824 | 64.824 | 64.824 |
| Controls | No | Yes | No | Yes | No | Yes |
| Country and time FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 90,938 | 79,200 | 104,531 | 92,778 | 76,962 | 65,308 |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of RDD using the optimal bandwidths based on Imbens and Kalyanaraman (2012). Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. Model 1 uses running variable in linear form, Model 2 includes interaction of running variable and treatment variable, Model 3 includes quadratic term of running variable, Model 4 includes interactions of running variable (linear and quadratic terms) with treatment variable. Control variables are daily temperature and rainfall (humidity for station-based data).
Table A9.
COVID-19 lockdowns and air pollution – ‘Regular’ stringency index.
| Bandwidth | Air pollution: NO2 |
Air pollution: PM2.5 |
||||
|---|---|---|---|---|---|---|
| Optimal bandwidth | Optimal bandwidth +10 days | Optimal bandwidth −10 days | Optimal bandwidth | Optimal bandwidth +10 days | Optimal bandwidth −10 days | |
| Lockdown = 1 | −1.260∗∗∗ (0.321) |
−1.512∗∗∗ (0.310) |
−0.918∗∗∗ (0.348) |
−2.525∗∗ (1.257) |
−2.713∗∗ (1.235) |
−1.998 (1.314) |
| Means before lockdowns | 23.281 | 23.281 | 23.281 | 64.824 | 64.824 | 64.824 |
| Controls | Yes | Yes | Yes | Yes | Yes | Yes |
| Country and time FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 257,339 | 300,266 | 214,775 | 79,200 | 89,117 | 69,238 |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of RDD using the optimal bandwidths based on Imbens and Kalyanaraman (2012). Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. Control variables are daily temperature and rainfall (humidity for station-based data). The ‘regular’ index returns null values if there are insufficient data to calculate the index while the ‘display’ version extrapolates to smooth over the last seven days of the index based on the most recent complete data. Our main analysis uses the ‘display’ version.
Table A10.
Stringency index and air pollution – Principal Component Analysis.
| Bandwidth | Air pollution: NO2 |
Air pollution: PM2.5 |
||||
|---|---|---|---|---|---|---|
| Optimal bandwidth | Optimal bandwidth +10 days | Optimal bandwidth −10 days | Optimal bandwidth | Optimal bandwidth +10 days | Optimal bandwidth −10 days | |
| Lockdown = 1 | −0.331∗∗ (0.160) |
−0.601∗∗∗ (0.146) |
−0.088 (0.178) |
−2.570∗∗∗ (0.462) |
−3.115∗∗∗ (0.429) |
−1.401∗∗∗ (0.486) |
| Means before lockdowns | 23.281 | 23.281 | 23.281 | 64.824 | 64.824 | 64.824 |
| Controls | Yes | Yes | Yes | Yes | Yes | Yes |
| Country and time FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 260,241 | 300,811 | 218,404 | 79,623 | 89,384 | 69,921 |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of RDD using the optimal bandwidths based on Imbens and Kalyanaraman (2012). Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. Control variables are daily temperature and rainfall (humidity for station-based data). Stringency index is constructed using Principal Component Analysis. For all dimensions of stringency index, see Table B2 (Appendix B).
Table A11.
Stringency index and air pollution – Alternative stringency indexes.
| Bandwidth | Air pollution: NO2 |
||
|---|---|---|---|
| Optimal bandwidth | Optimal bandwidth +10 days | Optimal bandwidth −10 days | |
| Panel A: Government response index | |||
| Lockdown = 1 | −1.360∗∗∗ (0.328) |
−1.850∗∗∗ (0.316) |
−1.237∗∗∗ (0.356) |
| Observations | 256,082 | 299,211 | 213,210 |
| Panel B: Containment and health index | |||
| Lockdown = 1 | −1.444∗∗∗ (0.328) |
−1.943∗∗∗ (0.316) |
−1.334∗∗∗ (0.356) |
| Observations | 256,078 | 299,181 | 213,353 |
| Panel C: Economic support index | |||
| Lockdown = 1 | 0.499∗ (0.255) |
0.558∗∗ (0.245) |
0.342 (0.285) |
| Observations |
249,421 |
281,210 |
213,744 |
| Means before lockdowns | 23.281 | 23.281 | 23.281 |
| Controls | Yes | Yes | Yes |
| Country and time FE | Yes | Yes | Yes |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of RDD using the optimal bandwidths based on Imbens and Kalyanaraman (2012). Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. All indexed are taken from “display” version of OxCGRT which will extrapolate to smooth over the last seven days of the index based on the most recent complete data. All regressions include country dummies and week dummies. Control variables are daily temperature and rainfall.
Table A12.
COVID-19 lockdowns and air pollution – Country linear time trend.
| Bandwidth | Air pollution: NO2 |
Air pollution: PM2.5 |
||||
|---|---|---|---|---|---|---|
| Optimal bandwidth | Optimal bandwidth +10 days | Optimal bandwidth −10 days | Optimal bandwidth | Optimal bandwidth +10 days | Optimal bandwidth −10 days | |
| Model 1: Linear model | ||||||
| Lockdown = 1 | −1.176∗∗∗ (0.330) |
−1.510∗∗∗ (0.313) |
−0.953∗∗∗ (0.352) |
−2.877∗∗ (1.244) |
−2.941∗∗ (1.242) |
−2.357∗ (1.301) |
| Model 2: Linear interaction model | ||||||
| Lockdown = 1 | −1.133∗∗∗ (0.328) |
−1.488∗∗∗ (0.310) |
−0.901∗∗ (0.350) |
−2.386∗ (1.218) |
−2.515∗∗ (1.203) |
−1.941 (1.271) |
| Model 3: Linear interaction model | ||||||
| Lockdown = 1 | −1.158∗∗∗ (0.329) |
−1.516∗∗∗ (0.310) |
−0.919∗∗∗ (0.350) |
−2.469∗∗ (1.231) |
−2.629∗∗ (1.216) |
−2.018 (1.286) |
| Model 4: Quadratic interaction model | ||||||
| Lockdown = 1 |
−1.137∗∗∗ (0.330) |
−1.501∗∗∗ (0.312) |
−0.903∗∗ (0.351) |
−2.376∗ (1.212) |
−2.465∗∗ (1.196) |
−1.963 (1.262) |
| Means before lockdowns | 23.281 | 23.281 | 23.281 | 64.824 | 64.824 | 64.824 |
| Controls | Yes | Yes | Yes | Yes | Yes | Yes |
| Country and time FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Country linear time trend | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 257,339 | 300,266 | 214,775 | 79,200 | 89,117 | 69,238 |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of RDD using the optimal bandwidths based on Imbens and Kalyanaraman (2012). The optimal bandwidths are 62 and 88 days for satellite and station-based data, respectively. Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. Model 1 uses running variable in linear form, Model 2 includes interaction of running variable and treatment variable, Model 3 includes quadratic term of running variable, Model 4 includes interactions of running variable (linear and quadratic terms) with treatment variable. Control variables are daily temperature and rainfall (humidity for station-based data).
Table A13.
COVID-19 lockdowns and air pollution – Air pollution in log form.
| Bandwidth | Air pollution: NO2 |
Air pollution: PM2.5 |
||||
|---|---|---|---|---|---|---|
| Optimal bandwidth | Optimal bandwidth +10 days | Optimal bandwidth −10 days | Optimal bandwidth | Optimal bandwidth +10 days | Optimal bandwidth −10 days | |
| Model 1: Linear model | ||||||
| Lockdown = 1 | −0.035∗∗∗ (0.011) |
−0.044∗∗∗ (0.010) |
−0.026∗∗ (0.012) |
−0.054∗∗∗ (0.019) |
−0.042∗∗ (0.018) |
−0.051∗∗∗ (0.019) |
| Model 2: Linear interaction model | ||||||
| Lockdown = 1 | −0.034∗∗∗ (0.011) |
−0.043∗∗∗ (0.010) |
−0.023∗∗ (0.012) |
−0.050∗∗∗ (0.019) |
−0.038∗∗ (0.018) |
−0.048∗∗ (0.019) |
| Model 3: Linear interaction model | ||||||
| Lockdown = 1 | −0.035∗∗∗ (0.011) |
−0.044∗∗∗ (0.010) |
−0.024∗∗ (0.012) |
−0.051∗∗∗ (0.019) |
−0.039∗∗ (0.018) |
−0.049∗∗ (0.019) |
| Model 4: Quadratic interaction model | ||||||
| Lockdown = 1 |
−0.033∗∗∗ (0.011) |
−0.043∗∗∗ (0.010) |
−0.023∗∗ (0.012) |
−0.050∗∗∗ (0.019) |
−0.037∗∗ (0.018) |
−0.048∗∗ (0.019) |
| Means before lockdowns | 23.281 | 23.281 | 23.281 | 64.824 | 64.824 | 64.824 |
| Controls | Yes | Yes | Yes | Yes | Yes | Yes |
| Country and time FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 254,477 | 297,076 | 212,387 | 79,200 | 89,117 | 69,238 |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of RDD using the optimal bandwidths based on Imbens and Kalyanaraman (2012). The optimal bandwidths are 62 and 88 days for satellite and station-based data, respectively. Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. Model 1 uses running variable in linear form, Model 2 includes interaction of running variable and treatment variable, Model 3 includes quadratic term of running variable, Model 4 includes interactions of running variable (linear and quadratic terms) with treatment variable. Control variables are daily temperature and rainfall (humidity for station-based data).
Table A14.
Heterogeneity analysis.
| Air quality: NO2 | Optimal bandwidth |
Optimal bandwidth +10 days |
Optimal bandwidth −10 days |
|---|---|---|---|
| (1) | (2) | (3) | |
| Panel A: Location | |||
| Lockdown∗Countries near equator | 3.543∗∗∗ (0.308) |
3.785∗∗∗ (0.279) |
3.106∗∗∗ (0.327) |
| Observations | 257,339 | 300,266 | 214,775 |
| Panel B: Democracy | |||
| Reference: Authoritarian | |||
| Lockdown∗Hybrid regime | 1.432∗∗ (0.572) |
1.328∗∗ (0.546) |
1.284∗∗ (0.589) |
| Lockdown∗Partial democracy | 1.197∗∗ (0.557) |
1.513∗∗∗ (0.518) |
0.877 (0.589) |
| Lockdown∗Full democracy | 0.469 (0.855) |
−0.015 (0.851) |
−0.264 (0.916) |
| Observations | 233,029 | 271,501 | 194,642 |
| Panel C: Share of trade | |||
| Lockdown∗Trade | −0.034∗∗∗ (0.012) |
−0.033∗∗∗ (0.010) |
−0.039∗∗∗ (0.014) |
| Observations | 199,787 | 232,666 | 167,163 |
| Panel D: Share of manufacturing | |||
| Lockdown∗Manufacturing | −0.439∗∗∗ (0.052) |
−0.454∗∗∗ (0.050) |
−0.482∗∗∗ (0.056) |
| Observations | 172,872 | 201,016 | 144,775 |
| Panel E: Air pollution index | |||
| Reference: 1st quintile | |||
| Lockdown∗2nd quintile | 1.005∗∗ (0.511) |
0.978∗ (0.510) |
0.772 (0.567) |
| Lockdown∗3rd quintile | 1.602∗∗∗ (0.476) |
1.826∗∗∗ (0.466) |
1.575∗∗∗ (0.538) |
| Lockdown∗4th quintile | −0.716 (0.619) |
−1.134∗ (0.606) |
−0.811 (0.666) |
| Lockdown∗5th quintile |
−0.577 (0.663) |
−0.643 (0.636) |
−0.755 (0.726) |
| Observations | 254,146 | 296,573 | 212,140 |
| Means before lockdowns | 23.281 | 23.281 | 23.281 |
| Controls | Yes | Yes | Yes |
| Country and time FE | Yes | Yes | Yes |
Notes: ∗∗∗p < 0.01, ∗∗p < 0.05, ∗p < 0.1. Results of RDD using the optimal bandwidths based on Imbens and Kalyanaraman (2012). The optimal bandwidths are 62 and 88 days for satellite and station-based data, respectively. Clustered standard errors in parentheses are robust to within-day and within-country serial correlation. Control variables are daily temperature and rainfall (humidity for station-based data).
Appendix B. Data Sources
To examine the relationship between COVID-19 and air quality, we use two measures of air pollution, namely fine particulate matter PM2.5 (mass concentration of particles with diameters ≤2.5 μm) and nitrogen dioxide NO2. While other pollutants are available in our dataset, we select the PM2.5 and NO2 given their direct link to human health. PM2.5 is a common cause for adverse health outcomes such as chronic obstructive pulmonary disease (COPD) and lower respiratory infection (LRI) causing death of nearly three million people globally (Gakidou et al., 2017). At the same time, NO2 is the leading source of childhood asthma in urban areas globally (Achakulwisut et al., 2019). In this study, we collect data on these measures from October 1st, 2019 to June 1st, 2020. We also use other pollutants, such as PM10, SO2 and O3, for robustness checks.
The NO2 data are derived from images of pollution-monitoring satellites released by the National Aeronautics and Space Administration (NASA) and European Space Agency (ESA). In particular, we use data from the Sentinel-5P/TROPOMI (S5P) instrument of the European Union’s Copernicus programme. The Copernicus S5P provides daily global coverage of atmospheric parameters at high resolution (i.e., a pixel size of about 5.5 km × 3.5 km after August 6th, 2019).11 We then use Google Earth Engine to process and average air quality data at the sub-national level using administrative areas from Database of Global Administrative Areas (GADM). In particular, we measure air pollution at the first-order administrative division (ADM1).12 While the Copernicus S5P records a wide range of pollutants including NO2 and others (O3, SO2, CO, CH4, and aerosols), we focus on NO2 because this is a noxious gas emitted by motor vehicles, power plants, and industrial facilities (see, e.g., Dutheil et al. (2020)). Among other pollutants, NO2 is also a particularly well-suited data to analysis of emission because it has a short lifetime; this implies that molecules of NO2 stay fairly close to their sources and thus offer an appropriate measure of changes in emissions.
A potential concern of using satellite air quality, however, is cloud cover. This can bias results by obscuring the sensor’s view of the lower atmosphere. Concentrations of NO2 in the atmosphere are also highly variable in space and time due to factors such as varying traffic flows on weekdays versus weekends and changes in weather conditions. Therefore, we follow suggestions from the Copernicus program and perform a cloud masking which excludes results from pixels with >10 percent cloud fraction.13 We also average data over weekly periods as a robustness test. Finally, we include data on daily rainfall and temperature to control for weather conditions, which are derived from the National Center for Environmental Prediction (NCEP) at the National Oceanic and Atmospheric Administration (NOAA). The global dataset provides four 6-h daily records of temperature and precipitation at the resolution of approximately 25 km. We extract the weather data at the sub-national level using a similar process as with the air pollution data.
As an alternative measure of air quality, we use daily station-based air quality index (AQI) from the World Air Quality Index (WAQI) project. The AQI provides accurate and reliable information on different air pollutant species from more than 12,000 ground-based air quality monitoring stations (primarily located at/near the US embassies and consulates) situated in 1000 major cities in more than 100 countries from 2014 to present. However, there are certain limitations with station-based data. One is that station-based data are often reported more slowly, and not in a ‘real-time’ fashion as satellite data. Another limitation is the locations of air quality monitoring stations are likely not random, so they may not provide representative data on an area’s air quality. Consequently, the satellite data are our preferred data for analysis.
We subsequently match the air pollution data with the government stringency data from the Oxford COVID-19 Government Response Tracker (OxCGRT). The OxCGRT is a novel country-level dataset published by the Blavatnik School of Government at the University of Oxford, which contains information on various lockdown measures, such as school and workplace closings, travel restrictions, bans on public gatherings, and stay-at-home requirements (Hale et al., 2020). It measures government stringency responses on a scale of 0–100. We provide a description of the index components in Table B2 (Appendix B).
To explore a potential channel through which COVID-19 affects air quality, we collect data on mobility from Google Community Mobility Reports. The Google Community Mobility Reports provide daily data on Google Maps users who have opted-in to the ‘location history’ in their Google accounts settings across 132 countries. The reports calculate changes in movement compared to a baseline, which is the median value for the corresponding day of the week from January to present. The purpose of travel has been assigned to one of the following categories: retail and recreation, groceries and pharmacies, parks, transit stations, workplaces, and residential. In our analysis, we expect that the lockdowns will lead to reduced mobility of all categories, except for the residential category. We also examine data from several additional sources for robustness checks. The data sources are listed in Table B1 (Appendix B).
Table B1.
Data sources and summary statistics.
| Variable | Descriptions | Mean | Standard deviation | Min | Max |
|---|---|---|---|---|---|
| Oxford COVID-19 Government Response Tracker (OxCGRT) | |||||
| Source: Blavatnik School of Government at the University of Oxford (https://covidtracker.bsg.ox.ac.uk/) | |||||
| Stringency index | Government responses to COVID-19 (Score between 0 and 100) | 44.751 | 35.254 | 0 | 100 |
| Government response index | 41.404 | 31.499 | 0 | 96.15 | |
| Containment and health index | 44.148 | 33.202 | 0 | 100 | |
| Economic support index | 26.331 | 32.501 | 0 | 100 | |
| Satellite air quality (daily) | |||||
| Source: European Union’s Copernicus programme (https://sentinels.copernicus.eu/web/sentinel/missions/sentinel-5p) | |||||
| NO2 | Nitrogen dioxide | 20.458 | 26.334 | −43.400 | 886 |
| Satellite weather data (daily) | |||||
| Source: National Oceanic and Atmospheric Administration (NOAA) (https://www.ncep.noaa.gov) | |||||
| Rainfall | Average rainfall (m) | 0.0002 | 0.0003 | 0.000 | 0.015 |
| Temperature | Average temperature (K) | 289.715 | 10.399 | 232.625 | 313.183 |
| Station-based data (daily) | |||||
| Source: World Air Quality Index (WAQI) project (https://waqi.info/) | |||||
| PM2.5 | Particles with a diameter of 2.5 μm or less | 56.291 | 43.799 | 1 | 999 |
| PM10 | Particles with a diameter of 10 μm or less | 27.338 | 25.403 | 1 | 999 |
| NO2 | Nitrogen dioxide | 10.118 | 8.442 | 0 | 500 |
| SO2 | Sulfur dioxide | 4.126 | 7.895 | 0 | 500 |
| O3 | Ozone | 19.459 | 12.670 | 0 | 500 |
| Humidity | Average humidity (percent) | 69.084 | 19.276 | 0 | 122 |
| Temperature | Average temperature (°C) | 14.393 | 9.200 | −67.7 | 93.3 |
| Mobility rates | |||||
| Source: Google Community Mobility Reports (https://www.google.com/covid19/mobility/) | |||||
| Retail & Recreation | Changes in people’s mobility (percent) in different categories | −22.801 | 28.661 | −100 | 313 |
| Grocery & pharmacy | −6.118 | 21.645 | −100 | 345 | |
| Park | −2.925 | 51.956 | −100 | 616 | |
| Transit | −27.151 | 30.046 | −100 | 497 | |
| Workplaces | −23.812 | 21.033 | −94 | 258 | |
| Residential | 10.669 | 9.177 | −25 | 56 | |
| Other control variables (Table A7) | |||||
| Source: World Bank World Development Indicators (https://databank.worldbank.org/source/world-development-indicators) | |||||
| Energy consumption | Energy consumption per capita (kWh) | 24,620 | 25,452 | 706.246 | 215,883 |
| Vehicles | Number of motor vehicles per 1000 inhabitants | 200.713 | 217.914 | 1.000 | 797 |
| GDP | GDP per capita (in constant 2010 USD) | 13,260 | 17,763 | 208.075 | 111062 |
| Population density | People per sq. km of land area | 164.668 | 586.711 | 0.137 | 20480 |
| CO2 emissions | CO2 emissions (kg per 2010 US$ of GDP) | 0.516 | 0.374 | 0.056 | 2.004 |
| Electricity | Electricity production from coal sources (percent of total) | 19.917 | 24.166 | 0.000 | 96.360 |
| Other control variables (Table A14) | |||||
| Democracy index | 2019 Economist Intelligence Unit Report (https://www.eiu.com/topic/democracy-index) | 54.714 | 20.579 | 13.200 | 98.700 |
| Air index | 2018 WHO Global Ambient Air Quality Database (https://www.who.int/airpollution/data) | 36.234 | 31.953 | 4.071 | 203.744 |
| Manufacturing | Share of manufacturing in GDP (2019 World Development Indicators database) | 12.937 | 5.892 | 1.686 | 30.838 |
| Trade | Share of trade in GDP (2019 World Development Indicators database) | 90.162 | 54.906 | 26.722 | 381.517 |
Table B2.
Stringency index components.
| Number | Components | Description |
|---|---|---|
| 1 | School closing | Record closings of schools and universities |
| 2 | Workplace closing | Record closings of workplaces |
| 3 | Cancel public events | Record cancelling public events |
| 4 | Restrictions on gatherings | Record the cut-off size for bans on private gatherings |
| 5 | Close public transport | Record closing of public transport |
| 6 | Stay at home requirements | Record orders to “shelter-in- place” and otherwise confine to home |
| 7 | Restrictions on internal movement | Record restrictions on internal movement |
| 8 | International travel controls | Record restrictions on international travel |
| 9 | Public info campaigns | Record presence of public info campaigns |
Notes: Each component is measured by an ordinal scale. The stringency index is measured by the OxCGRT team as simple averages of the individual component indicators. Each component is measured by an ordinal scale (e.g. 0 – no measures, 1 – recommended closing, 2 – require partial closing, 3 – require closing all levels). It is then rescaled by maximum value to create a score between 0 and 100. These scores are then averaged to get the stringency index.
Appendix C. Further robustness checks and heterogeneity analysis
Further robustness checks
To further check the robustness of our findings, we conduct a battery of tests on the estimation results. These include employing different methods of calculating the optimal bandwidth, higher-degree polynomials of the running variable, adding different covariates to the regressions, using wider time bandwidths and different thresholds and versions of the stringency index, controlling for potentially differential time trends across countries, and converting the air quality variables into logarithmic form.
First, our main analysis applies the optimal bandwidth choice rule of Imbens and Kalyanaraman (2012) to select the optimal bandwidth to minimize mean-squared error. In Table A5 (Appendix A), we report the results using alternative methods including CCT (Calonico et al., 2014) and Cross-valid (Lee and Lemieux, 2010).14 We find consistent impacts of the lockdowns on NO2 using the satellite data and PM2.5 using the alternative station-based data. We also check the robustness of our results by using high-order polynomial of the running variable. Our results are generally consistent, as presented in Table A6 (Appendix A). Still, we note that controlling for high-order polynomials in regression discontinuity analysis may lead to noisy estimates of the impact of lockdown (Gelman and Imbens, 2019).
Second, our estimation results are rather similar whether we control for weather conditions in our RDD regressions. For further checks, we include additional covariates to control for the pre-pandemic country characteristics, namely country’s log of GDP per capita (in constant 2010 USD), population density, log of energy consumption per capita, the number of motor vehicles per 1000 inhabitants, and the share of electricity generated by coal power. These country characteristics come from the World Development Indicators (WDI) database in the latest year when data is available. We present the estimation results in panel A of Table A7 (Appendix A) and we also provide the main results with country fixed effects in Panel B for comparison purpose. Our main findings remain robust to the inclusion of additional covariates.
Third, a potential issue with daily air pollution data is that these data can substantially vary from one day to another because of variations in emission and changes in weather conditions. Therefore, we replicate our RDD approach using a weekly indicator. We employ the optimal bandwidths selection and find that the results are generally consistent with the main findings in Table 2 (see Table A8, Appendix A).
Fourth, we use alternative measures of stringency index taken from the OxCGRT dataset. There are two versions of the stringency index: (i) a “regular” version which returns null values if there are insufficient data to calculate the index, and (ii) a “display” version which extrapolates to smooth over the last seven days of the index based on the most recent complete data. We use the latter indicator for our main analysis, but we also find consistent results using the “regular” version (Appendix A, Table A9).
Fifth, the stringency index in the OxCGRT dataset is calculated using a simple additive unweighted approach. It is thus possible that some dimensions with higher weights will be underestimated in the index. To address this issue, we create a new index based on the Principal Component Analysis (PCA) method for all the dimensions of stringency index. Table A10 in Appendix A shows rather similar estimation results for our own index, except for the optimal bandwidth −10 days (column 3).
Sixth, we further explore other indexes that are available from the OxCGRT dataset. They include: (i) Government response index, (ii) Containment and health index, and (iii) Economic support index.15 Compared to our main measure, the government response index and the containment and health index include two additional dimensions: testing policy and contact tracing. Still, we find a consistent impact of the lockdowns on air pollution when using these indexes, except for the economic support index (Appendix A, Table A11). However, the economic support index only includes income support programs and debt relief programs, so it does not fully capture the overall responsiveness of the government.
We also check whether our results are driven by differential time trends across countries. We include in the regressions the interaction terms of country dummies with linear time trends. The results, presented in Table A12 (Appendix A), are generally consistent with our main findings. Finally, our findings also remain consistent when we use the logarithmic form of the air quality variable (Appendix A, Table A13).
Heterogeneity analysis
Having shown that changes in air quality are driven by COVID-19, it is useful to understand whether the impacts of lockdowns differ by certain country characteristics. In particular, the impacts of lockdowns can vary according to a country’s geographic location. For example, cities near the deserts are often affected by sand and dust storms, which can strongly impact air quality. We thus interact a dummy variable indicating whether a country is near the equator with the treatment variable. The results presented in panel A of Table A14 (Appendix A) show that countries near the equator have a higher concentration of NO2 after the lockdowns.
A country’s institution may also affect the impacts of lockdowns. A large body of economic literature has shown the important role of institutions and culture in shaping economic development (e.g. Gorodnichenko and Roland, 2017; Acemoglu et al., 2019). Consequently, we use the democracy index from the 2019 report of the Economist Intelligence Unit. We expect that countries with strong institutions likely implement stringent policies during the time of COVID-19, and therefore have a better performance in terms of air quality. The results in panel B of Table A14 (Appendix A), however, provide little support for this argument. In contrast, partial democratic countries and countries with hybrid regime appear to have less reduced air pollution after the lockdowns than authoritarian countries.
Another useful heterogeneity analysis is whether countries with a high level of openness have more reduced air pollution after the lockdowns. Whether trade is good or bad for the environment has been a topic of debate in the literature. While evidence exists on the beneficial effects of trade on the environment (e.g. Antweiler et al., 2001; Frankel and Rose, 2005), other studies show that trade openness could in fact lead to higher emissions (Managi et al., 2009; Li et al., 2015). To answer this question, we interact a country’s share of manufacturing and share of trade in its GDP (from the 2019 World Development Indicators (WDI) database) with the treatment variable. The estimation results, presented in panels C and D of Table A14 (Appendix A), show that countries with a larger share of trade or manufacturing have more reduced air pollution after the lockdowns.
Finally, we examine whether countries with existing lower levels of air pollution may reduce air pollution more. We use the WHO Global Ambient Air Quality Database that summarizes concentration of PM2.5 at the country level in 2018. We then split our sample into five quintiles and interact each with our treatment variable. The results in panel E indicate that countries with an initially lower level of air pollution (i.e., the 1st quintile) have more reduced air pollution compared to those with initially higher levels of air pollution. For further illustration, we interact our treatment variable with the country dummies and plot the estimated interaction terms against countries’ initial level of air quality in Figure A5 (Appendix A). We highlight a country’s population size by drawing a bubble graph, where the size of a country’s circle is proportionate to its population size. Figure A5 shows countries bunching to the left of the graph and below the zero (no change) line, confirming that countries with better air quality before the pandemic tend to have higher reduction of NO2. Several countries with a large population size that improved air quality stand out, including China, Iraq, Norway, Russia, South Korea, and the United States.
References
- Achakulwisut P., Brauer M., Hystad P., Anenberg S.C. Global, national, and urban burdens of paediatric asthma incidence attributable to ambient NO2 pollution: estimates from global datasets. Lancet Planetary Health. 2019;3(4):e166–e178. doi: 10.1016/S2542-5196(19)30046-4. [DOI] [PubMed] [Google Scholar]
- Akesson J., Ashworth-Hayes S., Hahn R., Metcalfe R.D., Rasooly I. National Bureau of Economic Research; 2020. Fatalism, Beliefs, and Behaviors during the COVID-19 Pandemic (No. W27245) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almond D., Du X., Zhang S. National Bureau of Economic Research; 2020. Did COVID-19 Improve Air Quality Near Hubei? (No. W27086) [Google Scholar]
- Anderson M.L. Subways, strikes, and slowdowns: the impacts of public transit on traffic congestion. Am. Econ. Rev. 2014;104(9):2763–2796. [Google Scholar]
- Auffhammer M., Kellogg R. Clearing the air? The effects of gasoline content regulation on air quality. Am. Econ. Rev. 2011;101(6):2687–2722. [Google Scholar]
- Baker S.R., Farrokhnia R.A., Meyer S., Pagel M., Yannelis C. National Bureau of Economic Research; 2020. How Does Household Spending Respond to an Epidemic? Consumption during the 2020 Covid-19 Pandemic (No. W26949) [Google Scholar]
- Barreca A.I., Guldi M., Lindo J.M., Waddell G.R. Saving babies? Revisiting the effect of very low birth weight classification. Q. J. Econ. 2011;126(4):2117–2123. doi: 10.1093/qje/qjr042. [DOI] [PubMed] [Google Scholar]
- Brodeur A., Cook N., Wright T. 2020. On the Effects of COVID-19 Safer-At-Home Policies on Social Distancing, Car Crashes and Pollution. (No. 13255). IZA Discussion Paper. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunekreef B., Holgate S.T. Air pollution and health. Lancet. 2002;360(9341):1233–1242. doi: 10.1016/S0140-6736(02)11274-8. [DOI] [PubMed] [Google Scholar]
- Calonico S., Cattaneo M.D., Titiunik R. Robust nonparametric confidence intervals for regression-discontinuity designs. Econometrica. 2014;82(6):2295–2326. [Google Scholar]
- Chen Y., Whalley A. Green infrastructure: the effects of urban rail transit on air quality. Am. Econ. J. Econ. Pol. 2012;4(1):58–97. [Google Scholar]
- Cicala S., Holland S.P., Mansur E.T., Muller N.Z., Yates A.J. National Bureau of Economic Research; 2020. Expected Health Effects of Reduced Air Pollution from COVID-19 Social Distancing (No. W27135) [Google Scholar]
- Cole M., Ozgen C., Strobl E. 2020. Air Pollution Exposure and COVID-19 (No. 13367) (IZA Discussion Paper) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dang H.A.H., Nguyen C.V. World Development; 2020. Gender Inequality during the COVID-19 Pandemic: Income, Expenditure, Savings, and Job Loss; p. 105296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis L.W. The effect of driving restrictions on air quality in Mexico City. J. Polit. Econ. 2008;116(1):38–81. [Google Scholar]
- Fairlie R.W., Couch K., Xu H. National Bureau of Economic Research; 2020. The Impacts of COVID-19 on Minority Unemployment: First Evidence from April 2020 CPS Microdata (No. W27246) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gakidou E., Afshin A., Abajobir A.A., Abate K.H., Abbafati C., Abbas K.M., Abu-Raddad L.J. Global, regional, and national comparative risk assessment of 84 behavioural, environmental and occupational, and metabolic risks or clusters of risks, 1990–2016: a systematic analysis for the Global Burden of Disease Study 2016. Lancet. 2017;390(10100):1345–1422. doi: 10.1016/S0140-6736(17)32366-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman A., Imbens G. Why high-order polynomials should not be used in regression discontinuity designs. J. Bus. Econ. Stat. 2019;37(3):447–456. [Google Scholar]
- Hahn J., Todd P., Van der Klaauw W. Identification and estimation of treatment effects with a regression-discontinuity design. Econometrica. 2001;69(1):201–209. [Google Scholar]
- Hale T., Petherick A., Phillips T., Webster S. 2020. Variation in Government Responses to COVID-19 (No. 31) (Blavatnik School of Government working paper) [Google Scholar]
- Hausman C., Rapson D.S. Regression discontinuity in time: considerations for empirical applications. Ann. Rev. Resour. Econ. 2018;10:533–552. [Google Scholar]
- He G., Pan Y., Tanaka T. The short-term impacts of COVID-19 lockdown on urban air pollution in China. Nat. Sustain. 2020 doi: 10.1038/s41893-020-0581-y. [DOI] [Google Scholar]
- Imbens G., Kalyanaraman K. Optimal bandwidth choice for the regression discontinuity estimator. Rev. Econ. Stud. 2012;79(3):933–959. [Google Scholar]
- Isphording I.E., Pestel N. 2020. Pandemic Meets Pollution: Poor Air Quality Increases Deaths by COVID-19. (No. 13418) (IZA Discussion Paper) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee D.S., Lemieux T. Regression discontinuity designs in economics. J. Econ. Lit. 2010;48(2):281–355. [Google Scholar]
- Lenzen M., Li M., Malik A., Pomponi F., Sun Y.Y., Wiedmann T., et al. Global socio-economic losses and environmental gains from the Coronavirus pandemic. PloS One. 2020;15(7) doi: 10.1371/journal.pone.0235654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C., Chen R., Sera F., Vicedo-Cabrera A.M., Guo Y., Tong S.,, et al. Ambient particulate air pollution and daily mortality in 652 cities. N. Engl. J. Med. 2019;381(8):705–715. doi: 10.1056/NEJMoa1817364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith L.V., Tarui N., Yamagata T. University of Hawaii at Manoa, Department of Economics; 2020. Assessing the Impact of COVID-19 on Global Fossil Fuel Consumption and CO2 Emissions (No. 202016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tobías A., Carnerero C., Reche C., Massagué J., Via M., Minguillón M.C., Alastuey A., Querol X. Changes in air quality during the lockdown in Barcelona (Spain) one month into the SARS-CoV-2 epidemic. Sci. Total Environ. 2020:138540. doi: 10.1016/j.scitotenv.2020.138540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venter Z.S., Aunan K., Chowdhury S., Lelieveld J. Proceedings of the National Academy of Sciences. 2020. COVID-19 lockdowns cause global air pollution declines; p. 202006853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viard V.B., Fu S. The effect of Beijing’s driving restrictions on pollution and economic activity. J. Publ. Econ. 2015;125:98–115. [Google Scholar]
References
- Chen K., Wang M., Huang C., Kinney P.L., Anastas P.T. Air pollution reduction and mortality benefit during the COVID-19 outbreak in China. Lancet Planetary Health. 2020;4(6):e210–e212. doi: 10.1016/S2542-5196(20)30107-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dutheil F., Baker J.S., Navel V. COVID-19 as a factor influencing air pollution? Environ. Pollut. 2020;263:114466. doi: 10.1016/j.envpol.2020.114466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zambrano-Monserrate M.A., Ruano M.A., Sanchez-Alcalde L. Indirect effects of COVID-19 on the environment. Sci. Total Environ. 2020:138813. doi: 10.1016/j.scitotenv.2020.138813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Acemoglu D., Naidu S., Restrepo P., Robinson J.A. Democracy does cause growth. J. Polit. Econ. 2019;127(1):47–100. [Google Scholar]
- Antweiler W., Copeland B.R., Taylor M.S. Is free trade good for the environment? Am. Econ. Rev. 2001;91(4):877–908. [Google Scholar]
- Frankel J.A., Rose A.K. Is trade good or bad for the environment? Sorting out the causality. Rev. Econ. Stat. 2005;87(1):85–91. [Google Scholar]
- Gorodnichenko Y., Roland G. Culture, institutions, and the wealth of nations. Rev. Econ. Stat. 2017;99(3):402–416. [Google Scholar]
- Li Z., Xu N., Yuan J. New evidence on trade-environment linkage via air visibility. Econ. Lett. 2015;128:72–74. [Google Scholar]
- Managi S., Hibiki A., Tsurumi T. Does trade openness improve environmental quality? J. Environ. Econ. Manag. 2009;58(3):346–363. [Google Scholar]