Abstract
Non-carious cervical lesions (NCCLs) are saucer-shaped abrasions of a tooth. NCCLs can form due to various etiologies, including toothbrushing wear, acid erosion, and mechanical stress. Owing to this complex interplay, the mechanism of NCCLs in tooth abrasion has not been established. This study aims to develop a numerical method using a computational toothbrush to simulate NCCLs. The forces acting on the teeth and the amount of abrasion generated were evaluated. The discrete element method using in-house code, connected particle model, and Archard wear model were applied for brushing. In the toothbrush model, 42 acrylic tufts were fixed into a toothbrush head. The teeth models with enamel properties comprised four flat plates and two grooves to simulate the anterior teeth and NCCLs. The brushing speed and depth for one cycle were established as simulation parameters. The force applied within the ununiform plane was concentrated on several bristles as the toothbrush passed through the interproximal space. The brushing force (depth) had a greater effect on tooth abrasion than the brushing speed. Toothbrushing abrasion was mainly concentrated in the interproximal space. Therefore, forceful tooth brushing can cause NCCLs from the interproximal space to the cervical area of the tooth.
Keywords: toothbrush, abrasion, discrete element method, connected particle model, non-carious cervical lesion
1. Introduction
Modern manual toothbrushes comprise several components including bristles, a handle, and a head, which holds the bristles and tufts. These standard toothbrushes are widely considered essential for oral health care. If dental plaque, mainly bacterial biofilm, is not properly controlled by toothbrushing, it may cause gingivitis and dental caries, and in severe cases, periodontitis and tooth loss [1,2,3,4,5]. To ensure proper oral hygiene, the mechanical action of toothbrushing is the most common method used for plaque removal [6,7]. Using toothbrushes, however, most people are able to remove less than half of the total plaque present [2,3,8]. Furthermore, traumatic toothbrushing or ‘improper toothbrushing’ may lead to dental and/or gingival abrasion and gingival recession [9,10,11,12].
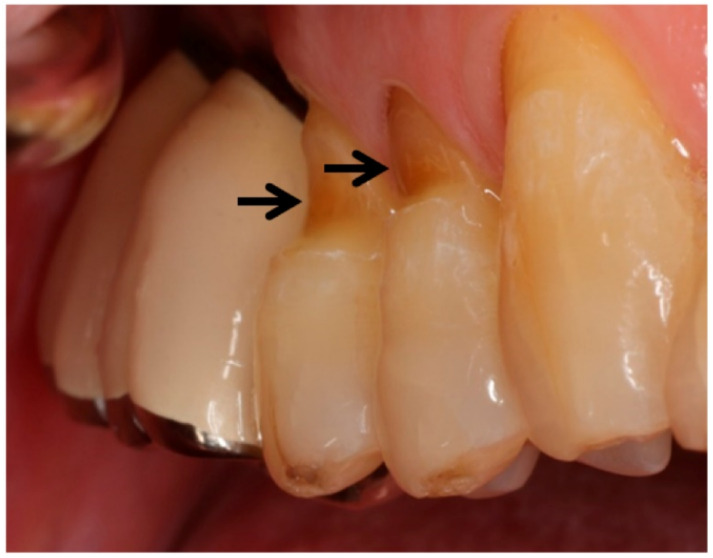
A non-carious cervical lesion (NCCL) is a saucer-shaped abrasion of a tooth near the cemento-enamel junction (Figure 1). Several studies have shown that the prevalence of tooth abrasion in adults aged 20 to 70 increases from 3% to 17%, respectively [9,10]. Approximately 60% of those with dental erosion also have dentin hypersensitivity as a result of eroded enamel and dentin loss [9,11].
Figure 1.
Clinical case of non-carious cervical lesions of teeth (indicated by arrows) caused by traumatic toothbrushing.
Clinically, NCCLs vary in size and shape, ranging from mild depressions to wedge-shaped or cup-shaped lesions [13]. The formation of NCCLs is attributed to etiologies such as tensile stress [14,15,16], compressive stress [17,18], acid erosion [19,20], stress corrosion [21], abfraction [18,22], occlusal forces, and friction (toothbrush/toothpaste wear) [23,24]. The aforementioned etiologies have varying influences on the shape of NCCLs, (e.g., wedge-, cup-, and smooth-shaped) [24]. The complex interplay of these varying mechanisms complicates the consideration of all NCCLs as a single mechanism.
Generally, three types of occlusal stresses are applied to teeth during mastication and parafunction: tensile, compressive, and shear stresses. The tensile stresses created on the teeth during occlusal loading can contribute to cervical erosive lesions [14,25]. According to certain studies, demineralization of the cervical region is caused by the low pH condition and the piezoelectric effect even under compressive stress, which are concentrated in the cervical region of the tooth [26,27]. Accordingly, tooth fracture may be attributed to such compressive stress. Considering that teeth make contact approximately one million times a year under occlusal stresses with several proteolytic enzymes in the saliva, NCCLs caused by periodic stress cannot be disregarded [28,29]. Numerous studies have investigated brushing abrasion, which is regarded as a common cause of NCCLs. In a recent study, NCCLs were reproduced using common commercial toothpaste and toothbrushes, albeit in vitro [24]. Subjects with good oral hygiene are more prone to NCCLs, and patients who brush their teeth twice daily have a statistically significantly higher incidence of NCCL than those who brush less frequently [30,31]. Therefore, toothbrushing abrasion significantly affects the occurrence of NCCLs.
Dental abrasion might be the result of several factors, one being the interaction between the force applied during toothbrushing and the chemical composition of the toothpaste used [6,9]. Other factors associated with the existence of abrasion and the effectiveness of plaque removal relate to the design of the toothbrush, brush material (length, number of bristles in a tuft, toothbrush head shape and diameter, number and arrangement of tufts, angle between the head and handle and handle design) and the frequency of toothbrush replacement [6,32].
Several theoretical and finite element studies have investigated the bending of single bristles [1,33]. These studies involved both general-purpose toothbrushes and industrial brushes. To date, however, only a limited number of numerical and theoretical studies have been conducted on toothbrushes [34,35]. In part, this is a result of the challenge associated with observing the multiple points of contact between tuft bristles and teeth. Whereas the finite element method can be used to analyze how individual bristles become deformed on teeth contact, it is nearly impossible to analyze the contact between multiple bristles or tufts. In our novel approach, we applied the discrete element method (DEM) to the connected particle model to analyze the multiple bristle-tuft contact points. The DEM is a numerical analysis method typically used in powder analysis, but it can also be used to investigate problems involving multiple contacts [36,37,38].
As mentioned above, NCCLs are closely associated with dental abrasion. However, there are no numerical tools for the analysis of toothbrushing abrasion. Therefore, this study aims to determine the feasibility of a numerical tool for the analysis of abrasion-related lesions and compare the effects of brushing force and brushing speed using the DEM. To the best of the authors’ knowledge, this is the first numerical study to analyze abrasion along tooth surfaces caused by multiple points of contact with bristles.
2. Materials and Methods
2.1. Computational Model
To simulate the NCCL caused by actual brushing, we need a computational model for the toothbrush and teeth. In addition, a model to calculate the amount of abrasion generated on the tooth by the toothbrush is required.
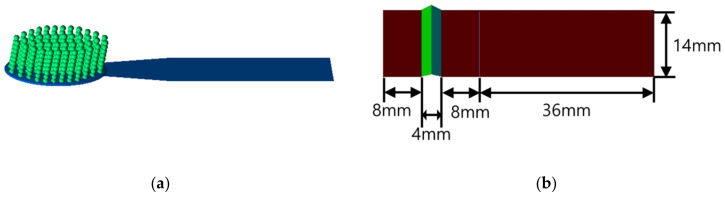
A computational toothbrush model should have multiple bristles reflecting the shape and material properties of an actual toothbrush. The bristles should be able to bend according to the theory of solid mechanics. In addition, both collisions between bristles and collisions with teeth should be considered. It is nearly impossible to consider both bending and contact in conventional numerical techniques, such as the finite element method. Hence, the bristles are described as connected particles using the DEM, as shown in Figure 2a. In other words, the vertically connected particles depict one bristle or tuft and are bent according to the theory of solid mechanics. A connected particle model based on DEM (numerical technique) was performed using in-house code.
Figure 2.
Computational model for (a) toothbrush and (b) tooth.
The tooth model consisting of a few planes shown in Figure 2b should also reflect the shape and material properties of the actual tooth. Therefore, two teeth colored brown and an interproximal area colored green are modeled in Figure 2b. The amount of tooth deformation is negligible compared to the toothbrush deformation. Because this is a feasibility study, we model a relatively simple tooth shape.
There is no way to directly “measure” the amount of abrasion on a tooth in a computational model. A portion of the tooth model is not actually removed as much as it is worn out. In other words, the tooth model does not change, and the amount of abrasion is “calculated” through the Archard wear model.
2.1.1. Toothbrush Model
The toothbrush head comprised multiple bristles implanted into the tuft holes. The bristles were typically composed of acrylic or nylon 6/12 filaments and possessed diameters in the range of 0.0375–0.0625 mm. A toothbrush generally possessed 42 tufts with approximately 40 filaments per tuft. To decrease the simulation time, we defined 40 filaments as one beam. The toothbrush had 42 beams; each beam had a diameter of 1.8 mm and a length of 10.8 mm. Each beam was created using eight particles that were 1.8 mm in diameter, and two of these particles were clamped in a similar manner to those in a real toothbrush (Figure 2a).
2.1.2. Tooth Model
The area of the toothbrush head was 27.5 × 10.2 mm. The tooth model used in this study was two flat plates (corresponding to two labial sides of the anterior teeth) connected by a single groove (corresponding to the interproximal space); this model differed from the general shape of a tooth. Because the labial and buccal sides of actual teeth are not flat, it is difficult to determine the vertical and horizontal forces acting on the teeth. For this reason, the four anterior teeth (maxillary and mandibular) and interproximal space were simplified using two planes and one groove, respectively (Figure 2b). The right-hand side of the teeth was 36 mm longer than the left-hand side. An additional plate was attached to the right-hand side of each tooth to reduce the effects of changes in the brushing direction. All teeth measurements were conducted on the planes except for the plate attached to the right-hand side.
The total brushstroke was defined as one forward and one backward movement along the direction parallel to the gingiva, i.e., perpendicular to the interproximal space of the teeth (scrub method). Some previous studies had reported that horizontal brushing is significantly related to NCCL [24,39]. Therefore, in this study, the movement of brushing was purposely simulated in the horizontal direction. The total distance of the two strokes, L, is equal to twice the reciprocal of the tooth model’s length, which is 56 mm.
The material properties of the tooth and toothbrush come from enamel and acrylic (Table 1), respectively, and were obtained by averaging the existing values in the literature [40,41].
Table 1.
Material properties.
| Material | Acrylic Brush | Tooth Enamel | Unit | |
|---|---|---|---|---|
| Elastic modulus | 3.4 | 60.0 | GPa | |
| Density | 1185 | 3000 | kg/m3 | |
| Hardness | 0.22 | 0.92 | GPa | |
| Poisson’s ratio | 0.3 | 0.3 | ||
| Coefficient of friction | Acrylic | 0.18 | 0.18 | |
| Enamel | 0.18 | N/A | ||
2.1.3. Abrasion Model Using Archard Wear Model
The Archard and Oka wear models are mainly used for modeling wear based on particle contact [42,43,44]. The classical Archard model simulates wear by friction, whereas the Oka model imitates wear due to impact. In addition, the Archard model has been utilized in several studies on tooth attrition and orthopedic implants and is thus used in the present study [45,46,47].
The Archard wear model can be described as follows:
| (1) |
where Q denotes the total volume of wear produced on the tooth surface, K represents the Archard wear constant, W denotes the total normal load, L is the sliding distance, and H denotes the hardness of the material.
By applying this equation to the DEM, we obtain
| (2) |
where t denotes the time, Fn is the normal force acting on the tooth surface, and δt represents the overlap along the tangential direction. These terms can be easily obtained using the DEM.
When the sphere (the tip of the toothbrush) comes into contact with the plane (the tooth surface), the normal component of the contact force is calculated: where is the contact force due to the overlap between the sphere and the plane, and is the unit vector for normal direction. is the relative velocity between the particle and the plane at the point of contact. The sliding distance at the contact point during the time interval dt can be expressed as , where is the tangential component of .
When the bristle stiffness of the toothbrush is increased, the force of the bristle tips pressing against the tooth surface increases, that is, Fn increases. Therefore, slightly reducing the stiffness of toothbrush bristles leads to reduced wear of the teeth. However, if the bristle stiffness is lowered and the bristle is excessively bent, the wear distance of the tooth corresponding to δt may increase, and wear may increase [9,48]. Therefore, the relationship between bristle stiffness and abrasion (wear) should be considered from a complex viewpoint.
2.2. Discrete Element Method (DEM)
The DEM is based on Newtonian mechanics, wherein the forces acting on each particle are numerically integrated to obtain the velocity and angular velocity. Accordingly, the position of each particle is determined via numerical integration. The forces include body (gravity) and surface (contact) forces on the particles.
When particles collide, the contact force on the particle surface is divided into two components: the normal and tangential forces. These forces act along the normal and tangential directions. In the DEM, the contact force is typically calculated using a spring-mass system.
2.2.1. Normal Force
The normal force using a Hertz–Mindlin spring is expressed as follows:
| (3) |
| (4) |
| (5) |
where E* denotes the equivalent elastic modulus, R* signifies the equivalent radius, δn denotes the normal overlap between particles, m* indicates the equivalent mass, vn denotes the relative velocity along the normal direction between contacting particles, and e represents the coefficient of restitution.
2.2.2. Tangential Force
The tangential force is expressed as
| (6) |
| (7) |
where G* denotes the equivalent shear modulus, δt represents the tangential overlap between particles, and vt denotes the relative velocity along the tangential direction between the contacting particles. Further details were adopted from the existing literature [48,49,50,51].
2.3. Connected Particle Model
To analyze the multiple points of contact with bristle-tufts, a coupled DEM and connected particle model was proposed [38,51,52,53,54,55,56]. Two models are typically used to connect particles to act as one fiber: the bonded particle model and the worm-like chain (WLC) model [39,51,53,54,55,56]. In this study, the WLC model, which is primarily used for deoxyribonucleic acid analysis, was selected [54].
As depicted in Figure 3, in the WLC model, the particles are connected by beam elements. The position and angle of each particle determine the force acting on this beam element. The forces acting on the beam were divided into stretching, bending, and torsion forces.
Figure 3.
Schematic of worm-like chain (WLC) model used as a connected particle model.
The stretching force maintains the connection between the particles and the axial beam deformation. The stretching free energy was calculated according to Hooke’s law as follows:
| (8) |
where ks denotes the stretching stiffness, N indicates the total number of particles in the beam, li represents the distance between the ith and (i − 1)th particles, and l0 represents the equilibrium distance between adjacent particles.
The bending free energy can also be derived using the particle position of the beam as follows:
| (9) |
where kB denotes the bending stiffness, I represents the areal moment of inertia, and denotes the unit distance vector between adjacent particles.
Similarly, the torsional free energy can be derived using the shear strain of the beam:
| (10) |
where kT denotes the torsional stiffness, γi represents the shear strain, and γ0 denotes the equilibrium shear strain.
Each force can easily be obtained by differentiating the free energy derived in Equations (8)–(10). Further details were adopted from the existing literature [55,56].
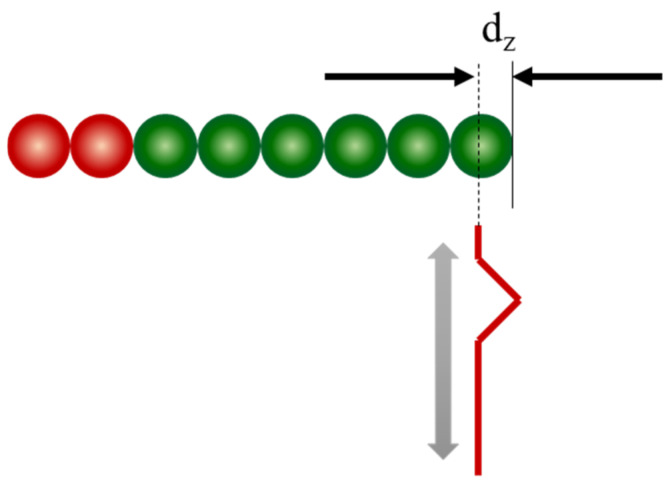
The brushing speed indicates how fast a person brushes, whereas the brushing depth indicates how forcefully the toothbrush presses against the surface of a tooth. These parameters were selected for the simulation. The brushing depth was determined as the depth at which the initial position of the bristle-tip particles descended below the tooth surface (Figure 4). In this study, three brushing depths, dz, were selected based on the radius of the bristles (r, r/2, and r/4). The brushing speeds were 0.05, 0.10, and 0.15 m/s. The diameter of the bristles was 1.8 mm, corresponding to an r value of 0.9 mm.
Figure 4.
Schematic of brushing depth.
2.4. Model Validation
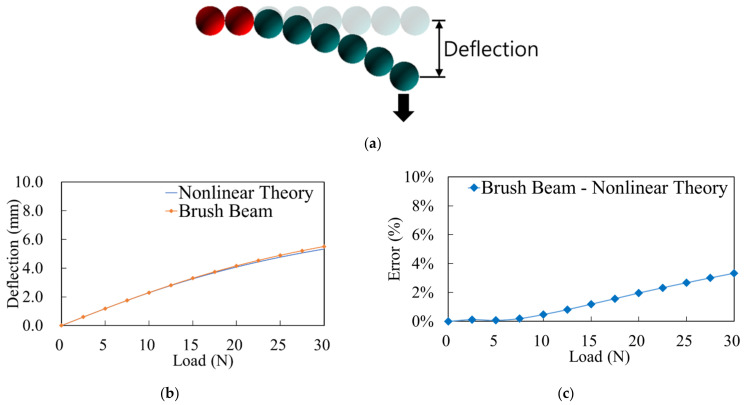
The DEM used for considering multiple contact points was not validated in this study, but it may be found in numerous previous studies. However, the WLC model is validated using the cantilever beam deflection test, as this is the first time that it has been applied to toothbrushes (Figure 5a).
Figure 5.
Comparison between nonlinear theory and discrete element method (DEM) results; (a) cantilever beam deflection represented by the WLC model; (b) deflection; (c) estimated error.
As depicted in Figure 5b,c, the overall trend of the brush beam is in good agreement with that of the nonlinear theoretical equation. Even at 30 N, which is the greatest applied force considered in this study, the error of 3.3% (approximate) is negligible.
3. Results
3.1. Dynamic Behavior of Toothbrush
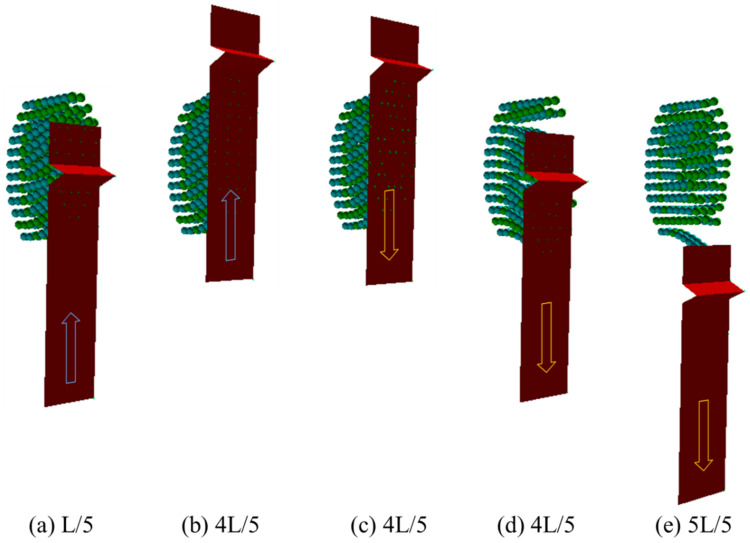
As shown in Figure 6, when the toothbrush moves forward, the bristles are deflected backward and vice versa. In addition, some bristles are bunched together while others are spread apart in the spaces between the teeth (i.e., interproximal space). The arrangement of the bristles was quite complex as they were located in the interproximal space at the positions of L/5 (Figure 6a) and 4L/5 (Figure 6d). When the bristles pass through the interproximal space, they are bent and forcefully released, thereby hitting the side surface of the teeth. Accordingly, considerable abrasion is highly likely to occur in this section, which is strongly affected by the movement of the bristles.
Figure 6.
Dynamic behavior of toothbrush at the given positions in the case of dz = r and V = 0.05 m/s [57].
3.2. Contour Plots of Forces Acting on the Toothbrush
During the brushing process, the bristles or tufts exert an impact on the plaque, removing it from the surface of the teeth; however, they also promote abrasion. Therefore, it is important to analyze the force exerted on the tooth surface by the bristles. In this study, the force acting on the tip of the bristles was considered by dividing this force into the normal force acting in the direction perpendicular to the surface and the tangential force acting along the direction in contact with the surface, as shown in Figure 7a,b. The bristles were located in the interproximal space at the positions of L/5 and 4L/5. The maximum magnitude of the normal and contact force in the interproximal space, approximately 0.05 N, was 10 times greater than the average force magnitude, approximately 0.005 N.
Figure 7.
Contour plots of forces acting on toothbrush for (a) various toothbrush penetration depths at fixed toothbrush speeds (V = 0.1 m/s) and (b) various toothbrush speeds at fixed toothbrush penetration depths (dz = r) [57].
3.3. Abrasion Distribution on the Surface of Teeth
The amount of wear was calculated using the Archard wear model. Because chemical and biological erosions were not considered in this study, the amount of wear corresponds directly to the amount of abrasion. Figure 8 illustrates the spatial distribution of the amount of abrasion that occurs over one cycle of toothbrushing according to varied brushing speeds and depths.
Figure 8.
Abrasion distribution on tooth surfaces under various conditions.
4. Discussion
Many studies have been conducted to investigate the relationship between the stiffness of bristles and plaque removal/abrasion [9,48,58,59]. Although tooth enamel and dentin exhibit high hardness, they inevitably encounter problems due to abrasion. Contrary to the general belief, when a manual toothbrush with various bristle stiffnesses was tested in terms of abrasion on eroded and mechanically sound human dentin, it was found that bristles with a soft stiffness exhibited high dentin abrasion [9]. In addition, high abrasion occurs when soft bristles are applied to normal and demineralized human enamel [48]. Conversely, when the stiffness of a toothbrush increases, damage to the gingival tissue, (i.e., gingival recession) occurs while plaque removal increases [58,59]. Without abrasive toothpaste or abrasive powder, the number of gingival recessions caused by hard brushes increases by about four times that of those caused by soft brushes [59]. On the other hand, the plaque score using the hard brush increases by 20% in comparison with using the soft brush [58]. Using the Quigley–Hein index modified by Turesky, (i.e., the plaque index), it has been demonstrated that the plaque removal rate differs among three types of manual toothbrushes [6]. Similarly, an attempt was previously made to analyze the effects of the load and toothpaste on the vibration characteristics of powered toothbrushes using the noncontact technique of scanning-laser vibrometry [60]. Several studies have also experimentally observed the effect of bristle stiffness and bristle-tip geometry on the behavior of abrasive particles in toothpaste [61,62]. Compared to soft brushes, hard brushes may act as a barrier to prevent particles from escaping, so the abrasive particles stay on the toothbrush longer. In addition, the direction of the brush, the number of filaments in the tuft, and the spacing of the tufts affect the entry and exit of particles. Nevertheless, these studies were conducted based on experimentation. Although not mentioned directly in other papers, it is possible that bristles wear may be related to NCCL. If the bristle length made of the same material is shortened by wear, the stiffness increases, leading to the occurrence of NCCL.
In general, plaque removal is mainly performed by toothbrushing. However, traumatic or improper toothbrushing can bring forth dental abrasion that may lead to NCCLs [9,10,11]. So far, proper toothbrushing mechanisms or the exact causes of NCCLs have not been established. To overcome this limitation, it is important to understand the operating mechanisms of toothbrushing considering parameters such as the brushing speed and the force applied by the toothbrush bristles on the teeth. Therefore, numerical studies are essential for this purpose.
In the first step of the toothbrushing simulation, the deformation of the model was validated. Because the bristles have three deformation modes, bending, tension, and torsion, three validations are needed. However, because the tension and torsion errors observed in previous studies were relatively negligible considering connected particle models and given that the major force generated during brushing is bending, the developed model was validated only for bending [37,53]. The bending of a bristle or tuft during brushing can be expressed by the deflection of a cantilever in solid mechanics [1]. Therefore, we used one beam composed of eight particles to describe one tuft, as illustrated in Figure 5a, and compared the results of these simulations with those obtained via theoretical solid mechanics calculations. The error between these two methods is depicted in Figure 5b,c. The measured error at the maximum force, 30 N, was 3.3%. Considering that the force applied to teeth is generally less than 10 N, it can be confirmed that the deflection of the toothbrush bristles will have a negligible error in the general brushing force [9].
In the second step, the spatial distribution of the normal and tangential forces was analyzed, as they are directly related to the amount of abrasion or plaque removal. Figure 7a,b show the instantaneous normal and tangential forces applied to the teeth, respectively. Figure 7a depicts the results obtained by setting the brushing speed to 0.1 m/s and brushing depth to three values: r (radius of the bristles), r/2, and r/4. At position L/5 where the bristles were in the interproximal space during the forward stroke, the normal and tangential forces exhibited neither a clear difference nor a tendency to increase or decrease. The normal and tangential forces both increased, however, as the brushing depth decreased (from dz = r to dz = r/4) at position 4L/5, when the toothbrush was in the interproximal space during the backward stroke. In particular, the forces were concentrated on a few specific bristles rather than the overall bristles. Figure 7b depicts the results obtained at a toothbrush penetration depth of dz = r at three brushing speeds of 0.05, 0.10, and 0.15 m/s. Similar to Figure 7a, the forces in Figure 7b are generally concentrated on a few specific bristles. While the relationship between the magnitude of the force and speed is unclear at position L/5, the magnitude of the force decreased as the speed increased at position 4L/5.
Overall, at position L/5, the normal and tangential forces were less affected by the brushing speed and depth, while at position 4L/5, they were affected considerably. The tangential force exhibited a greater overall value in comparison with that of the normal force. The magnitude of the forces changed considerably when the brushing speed was fixed and brushing depth was varied, compared with the case in which the brushing depth was fixed and brushing speed was varied. This shows that the brushing depth had a greater effect on the force magnitude than the brushing speed.
Lastly, as depicted in Figure 8, the amount of abrasion increases as the brushing speed decreases and brushing depth increases. In particular, the abrasion becomes severe on both sides of the interproximal space under these conditions as the bristles impact the side of the tooth, as shown in the red box in Figure 8. Therefore, it is inferred that the NCCL associated with dental abrasion initiates from the side (interproximal space) and spreads to the center (tooth area). As explained in the previous section, the effect of the brushing depth is larger than that of the brushing speed; therefore, the difference between dz = r and dz = r/4 is larger than that between the speed settings of 0.05 and 0.15 m/s. Overall, the abrasion exhibits a top-bottom symmetrical distribution. This is because the arrangement of the bristles is symmetrical and the arrangement of the anterior teeth of the maxilla and mandible are perfectly identical, thereby yielding nearly identical shapes with a symmetrical distribution.
As mentioned earlier, we modeled the scrub method in this study. Therefore, all results are only applicable for the scrub method, and results for other methods, such as the Bass and Roll methods, may differ [3].
In previous studies, the implementation of numerical approaches for the analysis of brushing abrasion was inhibited by the complexity of simultaneously analyzing deformation and multiple points of contact [33,34,35,63]. Conventional approaches based on the finite element method allowed for the accurate observation of the deformation mechanism of bristles. However, the analysis of the multiple points of contact with the bristles was not possible [33,37,39]. We simulated the toothbrushing process based on DEM, accounting for multiple points of contact.
A limitation of this study is that we used a flat tooth model and treated the filaments tuft of the toothbrush as one tuft. Therefore, it is essential to improve the tooth model and toothbrush model to a more detailed one in the future.
5. Conclusions
This study was the first to successfully implement a novel three-dimensional DEM analysis on a computational toothbrush model that allowed the numerical analysis of the extent of toothbrushing abrasion such as NCCLs. The force applied during toothbrushing (the depth of brushing) has a greater effect on tooth abrasion than the speed of brushing. In addition, toothbrushing abrasion was concentrated in the interdental space. Therefore, forceful toothbrushing in our daily lives can cause NCCLs to develop from the interproximal space to the cervical area of a tooth. Accordingly, as a next strategy, we plan to analyze wear by modeling and applying each bristle to real human teeth. In the future, it would be meaningful to investigate the relationship between tooth wear and interdental embrasures by applying the DEM model in a multi-centered clinical trial with a large number of patients.
Author Contributions
Conceptualization, J.N., D.H.N., S.-M.H. and J.P.; methodology, J.N., D.H.N. and J.P.; software, J.N., D.H.N. and S.L.; validation, J.N., D.H.N. and S.L.; formal analysis, J.N. and J.P.; investigation, J.N., S.-M.H. and J.P.; resources, S.-M.H. and J.P.; data curation, J.N. and D.H.N.; writing—original draft preparation, D.H.N. and J.P.; writing—review and editing, S.-M.H. and J.P.; visualization, J.N. and S.L.; supervision, S.-M.H. and J.P.; project administration, S.-M.H. and J.P.; funding acquisition, S.-M.H. and J.P. All authors have read and agreed to the published version of the manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Funding Statement
This research was funded by the National Research Foundation of Korea (NRF), grant number NRF-2018R1A2B 2004207; the Ministry of Science and ICT (MSIT), Korea, based on the Grand Information Technology Research Center support program; supervised by the Institute for Information and Communications Technology Planning and Evaluation (IITP), grant number IITP-2021-2020-0-01612; and the Fund of Research Institute of Clinical Medicine of Jeonbuk National University-Biomedical Research Institute of Jeonbuk National University Hospital.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Rawls H.R., Mkwayi-Tulloch N.J., Krull M.E. A Mathematical Model for Predicting Toothbrush Stiffness. Dent. Mater. 1990;6:111–117. doi: 10.1016/S0109-5641(05)80040-5. [DOI] [PubMed] [Google Scholar]
- 2.Bay I., Kardel K.M., Skougaard M.R. Quantitative Evaluation of the Plaque-Removing Ability of Different Types of Toothbrushes. J. Periodontol. 1967;38:526–533. doi: 10.1902/jop.1967.38.6_part1.526. [DOI] [PubMed] [Google Scholar]
- 3.Gibson J.A., Wade A.B. Plaque Removal by the Bass and Roll Brushing Techniques. J. Periodontol. 1977;48:456–459. doi: 10.1902/jop.1977.48.8.456. [DOI] [PubMed] [Google Scholar]
- 4.Pitchika V., Pink C., Völzke H., Welk A., Kocher T., Holtfreter B. Long-term Impact of Powered Toothbrush on Oral Health: 11-year Cohort Study. J. Clin. Periodontol. 2019;46:713–722. doi: 10.1111/jcpe.13126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Van Der Weijden G.A., Hioe K.P.K. A Systematic Review of the Effectiveness of Self-Performed Mechanical Plaque Removal in Adults with Gingivitis using a Manual Toothbrush. J. Clin. Periodontol. 2005;32:214–228. doi: 10.1111/j.1600-051X.2005.00795.x. [DOI] [PubMed] [Google Scholar]
- 6.Tirapelli C., de Carvalho J.F., Ribas J.P., Panzeri H. Dental Plaque Removal Efficacy of Three Toothbrushes with Different Designs: A Comparative Analysis. Oral Health Prev. Dent. 2006;4:105–111. [PubMed] [Google Scholar]
- 7.Axelsson P., Lindhe J. Effect of Controlled Oral Hygiene Procedures on Caries and Periodontal Disease in Adults. Results after 6 Years. J. Clin. Periodontol. 1981;8:239–248. doi: 10.1111/j.1600-051X.1981.tb02035.x. [DOI] [PubMed] [Google Scholar]
- 8.Slot D.E., Wiggelinkhuizen L., Rosema N.A., Van der Weijden G.A. The Efficacy of Manual Toothbrushes Following a Brushing Exercise: A Systematic Review. Int. J. Dent. Hyg. 2012;10:187–197. doi: 10.1111/j.1601-5037.2012.00557.x. [DOI] [PubMed] [Google Scholar]
- 9.Bizhang M., Riemer K., Arnold W.H., Domin J., Zimmer S. Influence of Bristle Stiffness of Manual Toothbrushes on Eroded and Sound Human Dentin-An In Vitro Study. PLoS ONE. 2016;11:e0153250. doi: 10.1371/journal.pone.0153250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Van’t Spijker A.V., Rodriguez J.M., Kreulen C.M., Bronkhorst E.M., Bartlett D.W., Creugers N.H.J. Prevalence of Tooth Wear in Adults. Int. J. Prosthodont. 2009;22:35–42. [PubMed] [Google Scholar]
- 11.West N.X. Dentine Hypersensitivity: Preventive and Therapeutic Approaches to Treatment. Periodontol. 2000. 2008;48:31–41. doi: 10.1111/j.1600-0757.2008.00262.x. [DOI] [PubMed] [Google Scholar]
- 12.Litonjua L.A., Andreana S., Bush P.J., Cohen R.E. Toothbrushing and Gingival Recession. Int. Dent. J. 2003;53:67–72. doi: 10.1111/j.1875-595X.2003.tb00661.x. [DOI] [PubMed] [Google Scholar]
- 13.Yoshizaki K.T., Francisconi-dos-Rios L.F., Sobral M.A.P., Aranha A.C.C., Mendes F.M., Scaramucci T. Clinical Features and Factors Associated with Non-carious Cervical Lesions and Dentin Hypersensitivity. J. Oral Rehabil. 2017;44:112–118. doi: 10.1111/joor.12469. [DOI] [PubMed] [Google Scholar]
- 14.Lee W.C., Eakle W.S. Possible Role of Tensile Stress in the Etiology of Cervical Erosive Lesions of Teeth. J. Prosthet. Dent. 1984;52:374–380. doi: 10.1016/0022-3913(84)90448-7. [DOI] [PubMed] [Google Scholar]
- 15.Lee W.C., Eakle W.S. Stress-Induced Cervical Lesions: Review of Advances in the Past 10 Years. J. Prosthet. Dent. 1996;75:487–494. doi: 10.1016/S0022-3913(96)90451-5. [DOI] [PubMed] [Google Scholar]
- 16.McCoy G. The Etiology of Gingival Erosion. J. Oral. Implantol. 1982;10:361–362. [PubMed] [Google Scholar]
- 17.Nalla R.K., Kinney J.H., Marshall S.J., Ritchie R.O. On the in Vitro Fatigue Behavior of Human Dentin: Effect of Mean Stress. J. Dent. Res. 2004;83:211–215. doi: 10.1177/154405910408300305. [DOI] [PubMed] [Google Scholar]
- 18.Grippo J.O. Abfractions: A New Classification of Hard Tissue Lesions of Teeth. J. Esthet. Restor. Dent. 1991;3:14–19. doi: 10.1111/j.1708-8240.1991.tb00799.x. [DOI] [PubMed] [Google Scholar]
- 19.Staninec M., Nalla R.K., Hilton J.F., Ritchie R.O., Watanabe L.G., Nonomura G., Marshall G.W., Marshall S.J. Dentin Erosion Simulation by Cantilever Beam Fatigue and pH Change. J. Dent. Res. 2005;84:371–375. doi: 10.1177/154405910508400415. [DOI] [PubMed] [Google Scholar]
- 20.Addy M., Hunter M.L. Can Tooth Brushing Damage Your Health? Effects on Oral and Dental Tissues. Int. Dent. J. 2003;53:177–186. doi: 10.1111/j.1875-595X.2003.tb00768.x. [DOI] [PubMed] [Google Scholar]
- 21.Grippo J.O., Simring M., Schreiner S. Attrition, Abrasion, Corrosion and Abfraction Revisited: A New Perspective on Tooth Surface Lesions. J. Am. Dent. Assoc. 2004;135:1109–1118. doi: 10.14219/jada.archive.2004.0369. [DOI] [PubMed] [Google Scholar]
- 22.Palamara J.E.A., Palamara D., Messer H.H., Tyas M.J. Tooth Morphology and Characteristics of Non-Carious Cervical Lesions. J. Dent. 2006;34:185–194. doi: 10.1016/j.jdent.2005.05.005. [DOI] [PubMed] [Google Scholar]
- 23.Grippo J.O., Simring M., Coleman T.A. Abfraction, Abrasion, Biocorrosion, and the Enigma of Noncarious Cervical Lesions: A 20-Year Perspective. J. Esthet. Restor. Dent. 2012;24:10–23. doi: 10.1111/j.1708-8240.2011.00487.x. [DOI] [PubMed] [Google Scholar]
- 24.Dzakovich J.J., Oslak R.R. In Vitro Reproduction of Noncarious Cervical Lesions. J. Prosthet. Dent. 2008;100:1–10. doi: 10.1016/S0022-3913(08)00084-X. [DOI] [PubMed] [Google Scholar]
- 25.Wood I., Jawad Z., Paisley C., Brunton P. Non-Carious Cervical Tooth Surface Loss: A Literature Review. J. Dent. 2008;36:759–766. doi: 10.1016/j.jdent.2008.06.004. [DOI] [PubMed] [Google Scholar]
- 26.Mishra P., Palamara J., Tyas M., Burrow M. Effect of Loading and pH on the Subsurface Demineralization of Dentin Beams. Calcif. Tissue. Int. 2006;79:273–277. doi: 10.1007/s00223-006-0050-2. [DOI] [PubMed] [Google Scholar]
- 27.Mishra P., Palamara J.E.A., Tyas M.J., Burrow M.F. Effect of Static Loading of Dentin Beams at various pH Levels. Calcif. Tissue. Int. 2006;79:416–421. doi: 10.1007/s00223-005-0271-9. [DOI] [PubMed] [Google Scholar]
- 28.Anusavice K.J. Phillips’ Science of Dental Materials. 11th ed. Elsevier; St. Louis, MO, USA: 2003. [Google Scholar]
- 29.Schlueter N., Hardt M., Klimek J., Ganss C. Influence of the Digestive Enzymes Trypsin and Pepsin in Vitro on the Progression of Erosion in Dentine. Arch. Oral Biol. 2010;55:294–299. doi: 10.1016/j.archoralbio.2010.02.003. [DOI] [PubMed] [Google Scholar]
- 30.Radentz W.H., Barnes G.P., Cutright D.E. A Survey of Factors Possibly Associated with Cervical Abrasion of Tooth Surfaces. J. Periodontol. 1976;47:148–154. doi: 10.1902/jop.1976.47.3.148. [DOI] [PubMed] [Google Scholar]
- 31.Levitch L.C., Bader J.D., Shugars D.A., Heymann H.O. Non-Carious Cervical Lesions. J. Dent. 1994;22:195–207. doi: 10.1016/0300-5712(94)90107-4. [DOI] [PubMed] [Google Scholar]
- 32.Beatty C.F., Fallon P.A., Marshall D.D. Comparative Analysis of the Plaque Removal Ability of 0.007 and 0.008 Toothbrush Bristles. Clin. Prev. Dent. 1990;12:22–27. [PubMed] [Google Scholar]
- 33.Ito R., Terai A., Hayashi S., Kaneko K. Movement Analyses of Toothbrush Bristles by Non-Linear Finite Element Method. J. Jpn. Soc. Periodontol. 1994;36:188–196. doi: 10.2329/perio.36.188. [DOI] [Google Scholar]
- 34.Vanegas-Useche L.V., Abdel-Wahab M.M., Parker G.A. Dynamic Finite Element Model of Oscillatory Brushes. Finite Elem. Anal. Des. 2011;47:771–783. doi: 10.1016/j.finel.2011.02.008. [DOI] [Google Scholar]
- 35.Holopainen R., Salonen E. Modelling the Cleaning Performance of Rotating Brush in Duct Cleaning. Energy Build. 2002;34:845–852. doi: 10.1016/S0378-7788(02)00101-9. [DOI] [Google Scholar]
- 36.Park J., Kang N. Applications of Fiber Models Based on Discrete Element Method to String Vibration. J. Mech. Sci. Technol. 2009;23:372–380. doi: 10.1007/s12206-008-0921-8. [DOI] [Google Scholar]
- 37.Nguyen D.H., Kang N., Park J. Validation of Partially Flexible Rod Model Based on Discrete Element Method Using Beam Deflection and Vibration. Powder Technol. 2013;237:147–152. doi: 10.1016/j.powtec.2013.01.038. [DOI] [Google Scholar]
- 38.Guo Y., Wassgren C., Hancock B., Ketterhagen W., Curtis J. Validation and Time Step Determination of Discrete Element Modeling of Flexible Fibers. Powder Technol. 2013;249:386–395. doi: 10.1016/j.powtec.2013.09.007. [DOI] [Google Scholar]
- 39.Haralur S.B., Alqahtani A.S., AlMazni M.S., Alqahtani M.K. Association of Non-Carious Cervical Lesions with Oral Hygiene Habits and Dynamic Occlusal Parameters. Diagnostics. 2019;9:43. doi: 10.3390/diagnostics9020043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Archangelo C.M., Rocha E.P., Anchieta R.B., Martin M., Freitas A.C., Ko C.C., Cattaneo P.M. Influence of Buccal Cusp Reduction When Using Porcelain Laminate Veneers in Premolars. A Comparative Study Using 3-D Finite Element Analysis. J. Prosthodont. Res. 2011;55:221–227. doi: 10.1016/j.jpor.2011.02.005. [DOI] [PubMed] [Google Scholar]
- 41.Negreiros W.A.d., Regis R.R., Pontes K.M.d.F., Silva A.M.d., Silva Junior F.I.d. Effect of Restoration Technique on Stress Distribution in Extensively Destroyed Premolars: A Finite Element Analysis Study. RGO Rev. Gaúcha Odontol. 2017;65:20–24. doi: 10.1590/1981-863720170001000033062. [DOI] [Google Scholar]
- 42.Archard J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953;24:981–988. doi: 10.1063/1.1721448. [DOI] [Google Scholar]
- 43.Oka Y.I., Okamura K., Yoshida T. Practical Estimation of Erosion Damage Caused by Solid Particle Impact. Part 1: Effects of Impact Parameters on a Predictive Equation. Wear. 2005;259:95–101. doi: 10.1016/j.wear.2005.01.039. [DOI] [Google Scholar]
- 44.Oka Y.I., Yoshida T. Practical Estimation of Erosion Damage Caused by Solid Particle Impact. Part 2: Mechanical Properties of Materials Directly Associated with Erosion Damage. Wear. 2005;259:102–109. doi: 10.1016/j.wear.2005.01.040. [DOI] [Google Scholar]
- 45.Borrero-Lopez O., Pajares A., Constantino P.J., Lawn B.R. A Model for Predicting Wear Rates in Tooth Enamel. J. Mech. Behav. Biomed. Mater. 2014;37:226–234. doi: 10.1016/j.jmbbm.2014.05.023. [DOI] [PubMed] [Google Scholar]
- 46.Lewis R., Dwyer-Joyce R.S. Wear of Human Teeth: A Tribological Perspective. Proc. Inst. Mech. Eng. J. 2005;219:1–18. doi: 10.1243/1350650053295394. [DOI] [Google Scholar]
- 47.Liu F., Fisher J., In J.Z., Affatato S., editors. Wear of Orthopaedic Implants and Artificial Joints. Woodhead Publishing; Sawston, UK: 2012. pp. 403–418. [Google Scholar]
- 48.AlShehab A.H., AlHazoom A.A., Alowa M.H., AlAli H.A., Abdulmohsen A.A., Farooq I. Effect of Bristle Stiffness of Manual Toothbrushes on Normal and Demineralized Human Enamel-An In Vitro Profilometric Study. Int. J. Dent. Hyg. 2018;16:e128–e132. doi: 10.1111/idh.12332. [DOI] [PubMed] [Google Scholar]
- 49.Cundall P.A., Strack O.D.L. A Discrete Numerical Model for Granular Assemblies. Géotechnique. 1979;29:47–65. doi: 10.1680/geot.1979.29.1.47. [DOI] [Google Scholar]
- 50.Yeom S.B., Ha E.S., Kim M.S., Jeong S.H., Hwang S.J., Choi D.H. Application of the Discrete Element Method for Manufacturing Process Simulation in the Pharmaceutical Industry. Pharmaceutics. 2019;11:414. doi: 10.3390/pharmaceutics11080414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Lee S., Park J. Standardized Friction Experiment for Parameter Determination of Discrete Element Method and Its Validation Using Angle of Repose and Hopper Discharge. Multiscale Sci. Eng. 2019;1:247–255. doi: 10.1007/s42493-019-00020-6. [DOI] [Google Scholar]
- 52.Lee S., Park J. Discrete Element Method of the Dynamic Behavior of Flaky Particles Using the Rigid Plate Model. Multiscale Sci. Eng. 2020;2:63–68. doi: 10.1007/s42493-020-00036-3. [DOI] [Google Scholar]
- 53.Nam J., Lyu J., Park J. Packing Structure Analysis of Flexible Rod Particles in Terms of Aspect Ratio, Bending Stiffness, and Surface Energy. Powder Technol. 2019;357:232–239. doi: 10.1016/j.powtec.2019.08.094. [DOI] [Google Scholar]
- 54.Xiao S., Liang H., Wales D.J. The Contribution of Backbone Electrostatic Repulsion to DNA Mechanical Properties Is Length-Scale-Dependent. J. Phys. Chem. Lett. 2019;10:4829–4835. doi: 10.1021/acs.jpclett.9b01960. [DOI] [PubMed] [Google Scholar]
- 55.Gauger E., Stark H. Numerical Study of a Microscopic Artificial Swimmer. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;74:021907. doi: 10.1103/PhysRevE.74.021907. [DOI] [PubMed] [Google Scholar]
- 56.Liu Y., Pérez T., Li W., Gunton J.D., Green A. Statistical Mechanics of Helical Wormlike Chain Model. J. Chem. Phys. 2011;134:065107. doi: 10.1063/1.3548885. [DOI] [PubMed] [Google Scholar]
- 57.Nguyen D.H. Master’s Thesis. Kumoh National Institute of Technology; Gumi, Gyeongbuk, Korea: 2012. Modeling the dynamics of toothbrush using discrete element method. [Google Scholar]
- 58.Elliott J.R., Bowers G.M., Clemmer B.A., Rovelstad G.H. A Comparison of Selected Oral Hygiene Devices in Dental Plaque Removal. J. Periodontol. 1972;43:217–220. doi: 10.1902/jop.1972.43.4.217. [DOI] [PubMed] [Google Scholar]
- 59.Niemi M.L., Sandholm L., Ainamo J. Frequency of Gingival Lesions After Standardized Brushing as Related to Stiffness of Toothbrush and Abrasiveness of Dentifrice. J. Clin. Periodontol. 1984;11:254–261. doi: 10.1111/j.1600-051X.1984.tb02215.x. [DOI] [PubMed] [Google Scholar]
- 60.Lea S.C., Khan A., Patanwala H.S., Landini G., Walmsley A.D. The Effects of Load and Toothpaste on Powered Toothbrush Vibrations. J. Dent. 2007;35:350–354. doi: 10.1016/j.jdent.2006.11.006. [DOI] [PubMed] [Google Scholar]
- 61.Lewis R., Barber S.C., Dwyer-Joyce R.S. Particle Motion and Stain Removal During Simulated Abrasive Tooth Cleaning. Wear. 2007;263:188–197. doi: 10.1016/j.wear.2006.12.023. [DOI] [Google Scholar]
- 62.Lewis R., Dwyer-Joyce R.S., Pickles M.J. Interaction Between Toothbrushes and Toothpaste Abrasive Particles in Simulated Tooth Cleaning. Wear. 2004;257:368–376. doi: 10.1016/j.wear.2004.01.015. [DOI] [Google Scholar]
- 63.Gujar A.N., Shivamurthy P.G., Sabrish S. Effect of 125-150 Hz Vibrational Frequency Electric Toothbrush on Teeth and Supporting Structures: A Finite Element Method Study. J. Contemp. Dent. Pract. 2021;22:1150–1159. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.