Abstract
The purpose of this paper is to demonstrate and evaluate the use of Bayesian dynamic borrowing (Viele et al, in Pharm Stat 13:41-54, 2014) as a means of systematically utilizing historical information with specific applications to large-scale educational assessments. Dynamic borrowing via Bayesian hierarchical models is a special case of a general framework of historical borrowing where the degree of borrowing depends on the heterogeneity among historical data and current data. A joint prior distribution over the historical and current data sets is specified with the degree of heterogeneity across the data sets controlled by the variance of the joint distribution. We apply Bayesian dynamic borrowing to both single-level and multilevel models and compare this approach to other historical borrowing methods such as complete pooling, Bayesian synthesis, and power priors. Two case studies using data from the Program for International Student Assessment reveal the utility of Bayesian dynamic borrowing in terms of predictive accuracy. This is followed by two simulation studies that reveal the utility of Bayesian dynamic borrowing over simple pooling and power priors in cases where the historical data is heterogeneous compared to the current data based on bias, mean squared error, and predictive accuracy. In cases of homogeneous historical data, Bayesian dynamic borrowing performs similarly to data pooling, Bayesian synthesis, and power priors. In contrast, for heterogeneous historical data, Bayesian dynamic borrowing performed at least as well, if not better, than other methods of borrowing with respect to mean squared error, percent bias, and leave-one-out cross-validation.
Supplementary Information
The online version contains supplementary material available at 10.1007/s11336-022-09869-3.
Keywords: Bayesian dynamic borrowing, power priors, multilevel modeling, large-scale assessments
The elicitation of substantive prior information is a difficult problem for subject-area researchers wishing to use Bayesian statistical methods (O’Hagan et al., 2006). In the absence of a history of cumulative inquiry on a particular problem, researchers will typically rely on software default settings that presume non-informative or weakly informative prior distributions for model parameters. One area in which a wealth of historical information exists that can be leveraged to elicit informative priors for substantive research concerns the analysis large-scale educational assessments (LSAs) (see, e.g., Rutkowski, Von Davier, & Rutkowski, 2013).
In the setting of LSAs such as the OECD Program for International Student Assessment (PISA) (OECD, 2002), different assessment cycles are often several years apart (e.g., every three years for PISA). Considering PISA in particular, on the one hand, the target group has always been in-school 15-year-old students, and many variables of policy importance have been repeatedly measured across cycles such that borrowing across cycles may improve the precision of parameter estimates, particularly when cycles are relatively homogeneous. On the other hand, due to time differences, historical large-scale educational assessment data may likely differ from the new data due to technology advancement (e.g., computer-based assessments versus paper-based assessments), changes in student knowledge structure, or unexpected societal/population changes over the past years, such as the current coronavirus pandemic. These need to be accounted for in historical borrowing to control bias.
To make use of historical information while accounting for the potential endogenous and exogenous changes across assessment cycles, this paper extends the method of Bayesian dynamic borrowing (BDB) (Viele et al., 2014), originally introduced and applied to clinical trial data, to the context of LSAs through dynamically incorporating historical LSA data with current LSA data. The basic idea is that when the effects of interest in the historical studies are similar to the effects of interest in the new study, the amount of borrowing will be strong and thus the precision of parameter estimates can be improved. When the effects of interest in the historical studies differ greatly from the effects of interest in the new study, the amount of borrowing will be weak and thus the bias due to borrowing can be controlled. Thus, an attractive feature of BDB is that a researcher can account for the fact that not all historical data, even from the same survey program, are of equivalent design or quality. In the case of PISA specifically, the assessment underwent relatively important design changes, and as such, are not perfectly commensurate with earlier cycles of PISA. BDB priors automatically adjust borrowing strength based on the heterogeneity between the historical data sets and the current data through joint prior distributions of historical and current parameters. Also, the hyperpriors of the joint prior distributions can be systematically adjusted to reflect the analysts’ degree of confidence in the importance, quality, or comparability of sources of prior data.
It is important to note that a crucial feature of LSAs such as PISA is that they are usually generated from a multistage sampling design. For example, the sampling framework for PISA (OECD, 2019) utilizes a two-stage stratified design (see, e.g., Kaplan & Kuger, 2016) for all cycles and most countries. These designs must be accounted for in any statistical modeling effort—Bayesian or otherwise—and certainly they must be addressed when borrowing information from historical data sources of similar design to inform current analyses. More often than not, the proper analytic tool to address substantive questions from large-scale assessments is multilevel modeling (Raudenbush & Bryk, 2002).
For ease of communication in this paper, and to fix terminology, we will use the term hierarchical model in the fully Bayesian sense. That is, Bayesian hierarchical models treat all parameters as random variables described in terms of prior probability distributions, which in turn are described by hyperparameters and hyperprior distributions (Gelman, Carlin, Stern, Vehtari, & Rubin, 2014; Kaplan, 2014). We will then use the term multilevel linear model (e.g., Raudenbush & Bryk, 2002) to describe a specific Bayesian hierarchical model applicable to substantive problems using large-scale assessments with multilevel structures (e.g., students nested in schools with covariates at each level). For the methods described in this paper, the parameters that control the amount of dynamic borrowing, as well as the parameters of the multilevel models, are all contained within the general framework of Bayesian hierarchical models.
The purpose of this paper is to demonstrate and evaluate BDB through hierarchical models (Viele et al., 2014) as a means incorporating historical data with specific reference to LSAs. BDB is dynamic in the sense that prior distributions can vary depending on the heterogeneity between the historical data sets and the current data set of interest. Through jointly modeling of parameters from the historical data sets and the current data set, prior strength depends on the similarity between the historical data and the current data. In contrast, static borrowing refers to borrowing based on historical information only (Viele et al., 2014) and thus prior strength does not automatically vary based on the similarity between the historical data and the current data. For example, with static borrowing, fixed prior strength might be based on a researcher’s judgment about how similar the historical information and current information would be, but this prior strength would not automatically be adjusted based on the heterogeneity between historical data and current data to supplement the researcher’s judgment. On the other hand, with dynamic borrowing, a hyperprior might be specified to indicate the researcher’s judgment regarding the similarity between the historical data and the current data, and also the heterogeneity between the historical data and the current data is accounted for by the joint prior.
The significance of this paper is threefold. First, as noted earlier, LSAs have been in operation for decades, and a wealth of historical information is available that can be used to systematically inform present analyses. For example, as of this writing, PISA has seven cycles of data going back to 2000. The PISA assessment program is the most policy-relevant international large-scale assessment in operation and also very expensive, and so it is important that novel approaches to data analysis that can leverage the information across assessments continue to be developed. As an aside however, BDB is not only applicable to PISA or other comparable LSAs; applications to other types of data collection strategies are possible, and these are highlighted in the Conclusions section. Second, we have observed that although Bayesian methods are increasingly being used in educational research (see, e.g., Kaplan & Park, 2013; Kaplan, 2016), to the best of our knowledge, BDB has never been applied in the context of LSAs wherein it is common for educational outcomes to be modeled as a function of many covariates at both the individual and school level. We note that although a few studies investigated the use of covariates in historical borrowing (e.g., O’Malley, Normand, & Kuntz, 2002; Hobbs, Carlin, & Sargent, 2012), these studies were mostly situated in clinical trial contexts, and furthermore, the extension of BDB to multilevel data structures with covariates had not been evaluated. In the case of BDB, although Viele et al. (2014) examined BDB for estimating the control rate in clinical trials, they pointed out that “the use of covariates in formal borrowing of historical data has seemingly limited investigation/discussion in the literature, revealing a potential research gap” (Viele et al., 2014 p. 16).Thus, this paper fills a gap in the literature by implementing BDB in large-scale assessments and evaluating the method under the multilevel context with various individual-level and group-level covariates through both real data and simulation studies. Third, an important policy use of LSAs is prediction, and to the best of our knowledge historical borrowing methods generally, and BDB specifically, have not been evaluated in terms of their utility in providing accurate predictions. We examine this issue by evaluating the use of historical borrowing methods in terms of point-wise predictive accuracy using the leave-one-out cross-validation approach (see Vehtari, Gelman, & Gabry 2017; Vehtari, Gabry, Yao, & Gelman 2019).
The organization of this paper is as follows. In the next section, we situate our paper within the broader literature on historical borrowing with a particular focus on four methods that have been studied in other contexts—namely (a) complete pooling, (b) power priors, (c) Bayesian synthesis of prior information, and (d) Bayesian dynamic borrowing, the latter being the main focus of this study. As a baseline for comparison, we also examine the case where historical data are ignored altogether, namely no historical borrowing. Then, we introduce the basic ideas of BDB. We fix notation and concepts by demonstrating BDB with single-level linear models. This is followed by our extension and implementation of BDB to multilevel data commonly encountered in large-scale educational assessments. We motivate our discussion with reference to PISA but we argue that these methods can be applied to other LSAs that follow multistage sampling designs such as TIMSS (e.g., Martin, Mullis, & Hooper 2016) or NAEP (e.g., US Department of Education, 2019) and also to single-level or multilevel multi-cycle surveys in general.
We then present two case studies using data from PISA 2018 as the current data of interest with borrowing from PISA 2003 through PISA 2015. We specify a single-level model in Case Study 1 and a multilevel model in Case Study 2 to examine the impact of selected predictors on mathematics achievement. This is followed by two detailed simulation studies, one using a single-level model and the other using a multilevel model, wherein we examine the behavior of BDB under different sample sizes, priors, and degrees of heterogeneity of historical data compared to the current data. Despite large-scale assessments usually having a multilevel data structure, we include the evaluation of dynamic borrowing in single-level models for potential applications to other research areas. We then conclude with a summary of practical conditions under which borrowing information from historical data provides optimal results for current analyses.
Review of Methods for Historical Borrowing
Our paper is situated within the framework of historical borrowing, which has long been applied in the clinical trials field (e.g., Pocock, 1976; Hobbs, Carlin, Mandrekar, & Sargent 2011; Hobbs et al., 2012; Schmidli et al., 2014; Viele et al., 2014). The basic idea is that so-called “standard care” control groups from previous trials can be incorporated into a current study to increase the precision of parameter estimates and also possibly reduce the number of individuals assigned to the control group, thereby lowering cost. However, one of the major challenges for historical borrowing is to decide precisely how to borrow information from historical controls. Specifically, the difficulty with historical borrowing lies in how to determine the similarity between historical studies and the current study and thus determine the amount of borrowing.
This paper focuses specifically on dynamic borrowing using Bayesian hierarchical models as described in Viele et al. (2014), which will be elaborated later in this paper, but it should be noted that this kind of borrowing is not the only method in which historical data can be directly incorporated into current analyses. We review a selected set of methods next.
Data Pooling: Integrative Data Analysis
A general framework for combining information from previous studies and which has gained popularity in the social and behavioral sciences is referred to as integrative data analysis (IDA) (Curran & Hussong, 2009, see also; Bainter & Curran, 2015); also referred to in the clinical trails literature as individual participant data or mega-analysis (see, e.g., Sung et al., 2014; Tierney et al., 2015). Integrative data analysis is a static borrowing procedure that was developed, in part, to motivate the psychology community (and developmental psychologists in particular) to consider pooling multiple sources of data in their studies. Under the assumption that the data sets to be integrated are from comparable populations, and items are either identical or can be placed on the same scale via item response theory methods, the IDA framework advocates the pooling of the data. Data pooling is straightforward to implement and applicable to multilevel settings such as LSAs. Therefore, we include complete pooling of historical data sets as one kind of static borrowing scenario and compare it to BDB.
Bayesian Synthesis
An approach advocated by Marcoulides (2017) and referred to as Bayesian synthesis represents classical Bayesian updating and pools information from historical data sources through the sequential specification of priors from previous analyses. In other words, the posterior results of an analysis from one data set serve as the priors for another analysis, and the posterior results from that analysis serves as the priors for the subsequent analysis, and so on until a final posterior distribution is obtained. Marcoulides (2017) refers to this as augmented data-dependent priors. According to Marcoulides (2017), assuming that the data sets are exchangeable, in the sense that the labels of the data sets can be permuted without changing the impact of the sequence of priors, then Bayesian synthesis has been shown through simulation studies to provide estimates that recover the true population parameter, particularly in large samples. For this paper, we examine a special case of Bayesian synthesis whereby the average parameter estimates across the historical cycles are used as informative priors for the current cycle of data.
Power Priors
Finally, a method that is popular in the biomedical sciences and beyond is referred to as the power prior. The power prior can trace its current formulation to the work of Ibrahim and Chen (2000) and Chen, Ibrahim, and Shao (2000). More recently, Ibrahim, Chen, Gwon, and Chen (2015) provided a discussion of theory and applications of the power prior to problems in various areas including human genetics, environmental science, clinical trials, and psychology. The intention of the power prior is to provide a systematic method of eliciting informative priors using historical data (see Ibrahim et al., 2015, for a detailed literature review).
Following Ibrahim and Chen (2000), let denote the current data set and denote a single historical data set, where , , and , are the sample size, outcome, and predictors in the current data. Similar notation holds for the historical data set. The power prior distribution for a (possibly vector-valued) parameter of interest in the current study is
| 1 |
where is the initial prior elicited before the historical data are observed, is a hyperparameter for the initial prior, and is a scalar prior parameter that is used to weight the historical data relative to the probability of the current data. More specifically, the hyperparameter controls the impact of on the entire prior and controls the influence of the historical data on . That is, the parameter serves as a relative precision parameter for the historical data. Notice that when , the prior does not depend on the historical data and when , the power prior distribution (1) is simply the posterior distribution from the previous study. Furthermore, the power prior in (1) can be easily extended to multiple historical data sets. Let H represent the number of historical data sets, such as the past cycles of PISA. Then,
| 2 |
Traditional power priors are inherently static insofar as the current data are not directly incorporated into the power prior itself. Hobbs et al. (2011, 2012) proposed dynamic borrowing versions of power priors, referred to as commensurate priors, where the coefficient used to downweight the historical data is viewed as random and estimated based on a measure of the agreement between the current and historical data. Specifically, Hobbs et al. (2011) proposed commensurate priors where the prior mean for the current parameters of interest is conditional on the historical population mean and the prior precision , referred to as commensurability parameter, reflects the commensurability between the current and historical parameters (equation 4 in their paper). Hobbs et al. (2011) evaluated the commensurate priors in a scenario of borrowing one historical trial to analyze a single-arm trial. However, as discussed in Hobbs et al. (2012), the commensurate prior models in Hobbs et al. (2011) had the problems that diffuse priors could actually become undesirably informative and that the historical likelihood was considered as a component of the prior rather than data. Therefore, Hobbs et al. (2012) proposed modified commensurate priors that incorporated historical data as part of the likelihood for the current parameter estimation and had empirical and fully Bayesian modifications for estimating the commensurate parameter . They also extended the method to general and generalized linear mixed regression models in the context of two successive clinical trials. The modified commensurate prior models in Hobbs et al. (2012) were compared to several meta-analytic models where priors for the historical parameters and current parameters were jointly modeled, but historical data was not incorporated in the likelihood of the current parameter estimation and thus the priors were not commensurate or dynamic. Commensurate priors in Hobbs et al. (2012) were shown to provide more bias reductions compared to several meta-analytic approaches they evaluated. The bias reduction was larger when there was only one historical study compared to when there were two and three historical studies.
A relatively recent dynamic version of the power prior was considered by Liu (2018), in which the power prior parameter is a continuous function of the p-value used to test the null hypothesis that the current data are equivalent to the historical data. Even more recently, Thompson et al. (2021) demonstrated another type of dynamic power prior where the power parameter is determined based on similarity between part of the current data available at an interim look and the historical outcome data. Then, a new measure of similarity between the current (interim) and prior data is proposed with a pre-specified clinical similarity region deemed appropriate by clinicians. Note that these dynamic power prior methods are specific to the clinical research area. Extension of these methods to other contexts such as large-scale assessments requires considering specific characteristics of data/model (e.g., data/model type, timeline of data collection, etc.) and the availability of collaborative resources (e.g., subject experts) in those areas and is beyond on the scope of this study.
Considering that the literature on dynamic power priors is sparse and applies specifically to clinical trials only, in this paper, we compare BDB with the traditional power prior as it has been much widely implemented beyond clinical trials and into fields such as genetics, health care, psychology, environmental health, engineering, economics, and business (Ibrahim et al., 2015).
Regarding the comparisons among different borrowing methods, a recent review and tutorial by Du et al. (2020) provided insights into the use of the methods discussed in the context of comparing two independent or matched group means. Du et al. (2020) examined the behavior of four methods of data synthesis: (a) meta-analysis, in which results at the individual study level are aggregated and summarized, (b) integrative data analysis, which, as described above, combines data from multiple studies into a single large data set for analysis, (c) data fusion based on augmented data-dependent priors (AUDP) (see Marcoulides 2017), where each studies information is sequentially included in the analysis and the contribution of each study is summarized, and (d) data fusion using aggregated data-dependent priors (AGDP), where parameter estimates from a set of studies are aggregated (such as calculating the mean) and then used as hyperparameters for a focal study.1
Utilizing real data for the purposes of the tutorial, and examining a number of different data structures, including multilevel data similar to large-scale assessment data structures, Du et al. (2020) recommend avoiding AGDP because of the wide credible intervals they found in the case study and the sensitivity of the results to the choice of the focal study. If raw data are available, Du et al. (2020) recommend the use of IDA or AUDP. If only effect sizes are available, Du et al. (2020) recommend meta-analysis or AUDP. In conclusion, Du et al. (2020) advise researchers to carefully choose the method that aligns most closely to their research questions.
For the present study, we build on Du et al. (2020) in following ways. First, our focus is specifically on Bayesian dynamic borrowing that Du et al. (2020) did not study. Second, we compare BDB with data pooling (IDA), Bayesian synthesis in the form of Du et al.’s 2020 AGDP, and power priors because these methods are quite popular and it is not known a priori whether they will perform the same, better, or worse than BDB. Third, in addition to common ways to evaluate statistical methods (e.g., bias, MSE), we examine these historical borrowing methods in terms of predictive performance, which we believe has not been examined before in this context. Finally, we examine these methods in the context of meaningful case studies, but also, as recommended by Du et al. (2020), we supplement our case studies with simulation studies to provide a controlled evaluation of the methods.
Bayesian Dynamic Borrowing
As noted earlier, the focus of this paper is specifically on Bayesian dynamic borrowing with comparisons to integrative data analysis, Bayesian synthesis, and power priors. Viele et al. (2014) proposed the idea of Bayesian dynamic borrowing, which incorporates heterogeneity between the historical data and the current data into the specification of the prior such that there would be strong borrowing when the historical data and the current data agree with each other and weak borrowing when there are large discrepancies between the historical and current data. Particularly, Viele et al. (2014) evaluated BDB in the context of case–control clinical trials and compared it to no borrowing, pooling, single-arm trial, test-then-pool, and power priors under different heterogeneity conditions for estimating a single parameter of interest, the control proportion. Overall, BDB performed as well as pooling under homogeneous conditions and better than pooling and closer to no borrowing under heterogeneous conditions. Variations were observed when different BDB hyperpriors were used.
Unique Features of BDB
Bayesian dynamic borrowing as proposed in Viele et al. (2014) and extended and evaluated in this paper, differs from the borrowing methods discussed in the previous section in several important ways. The key difference is that BDB incorporates the heterogeneity between the historical data and the current data through the specification of a hierarchical prior. First, similar to data pooling, BDB makes use of all of the data, but focuses attention on the joint prior distribution of the parameters of interest. In this sense, BDB does not pool all of the observations into one data set, but rather incorporates data similarity directly into the joint prior distribution.
Second, unlike traditional power priors that are based on historical data only, dynamic borrowing accounts for the agreement between the historical data and the current data. Unlike commensurate priors where current prior mean is conditional on historical population mean obtained based on historical data (Hobbs et al., 2011; 2012), BDB priors jointly model both historical parameters and current parameters, which follow the same prior mean. But consistent with Hobbs et al. (2012), BDB allows historical data contributing to the current likelihood estimation. Evaluating commensurate priors to the context of large-scale assessments would warrant for further research.
Third, dynamic borrowing differs from Bayesian synthesis insofar as priors are not just based on historical data, which does not directly or simultaneously account for heterogeneity of the historical and current data sets. Rather, dynamic borrowing utilizes all data simultaneously and the assessment of heterogeneity across the data sets is controlled by the variance of the joint distribution of the model parameters across all of the data sets.
Our paper contributes to the literature on historical borrowing by extending and demonstrating the use of BDB described in Viele et al. (2014) to higher-dimensional multilevel data structures with many covariates. We believe BDB is relatively intuitive and easy to implement in large-scale assessments and education research areas. In addition, we compare BDB to the case of no borrowing and to complete pooling, all within two substantively meaningful case studies and two large simulation studies. Finally, we focus not only on typical measures of bias and mean squared error, but also on predictive criteria using cross-validation measures.
Bayesian Dynamic Borrowing for Single-Level Linear Models
Expanding on the notation in Viele et al. (2014) for single-level linear models, let be a vector of regression coefficients of interest. In our case study below, contains the coefficients relating mathematics achievement scores to a set of student-level demographic and contextual variables. Let H denote the number of available historical cycles of data , for example, past cycles of PISA, and be the parameters of interest in each historical data set, where it is assumed that there are at least some (if not many) variables that are measured across cycles - a not unreasonable assumption in large-scale assessments. Furthermore, let be the parameters of interest in the current data set . Note that can be a scalar. Then, dynamic borrowing follows a Bayesian hierarchical structure and can be specified as follows:
| 3 |
and is an () covariance matrix written as
| 4 |
where allows for variances and covariances among parameters within cycles. For this paper, we simplify the covariance structure in (4) and assume
| 5 |
Finally, for a fully Bayesian hierarchical model, we need to place priors on and . We choose the following conjugate priors
| 6 |
and the elements of are
| 7 |
where and are the shape and scale parameters, respectively, of the IG (inverse-Gamma) distribution. Common choices for and in (7) are or (assuming ) , where is set to a low number (see, e.g., Gelman, 2006). Note that other priors for can be used, such as the half-Cauchy, half-normal, or half-t distributions (see, e.g., Gelman, 2006). It is important to point out that (3) and (4) assume that the regression coefficients across cycles are generated from a population with common means and covariance matrices. This is akin to invoking an exchangeability assumption across the cycles of data; and although this assumption might be difficult to maintain, it can be relaxed by allowing the regression coefficients and the elements of the precision matrices to have cycle-specific prior distributions.
The key parameter for dynamic borrowing is the variance of the joint prior distribution, , such that when historical data is consistent with the new data, the posterior distribution will be more heavily weighted toward a small and thus there will be extensive borrowing from the historical information. When historical data and the new data differ greatly, the posterior distribution will be more heavily weighted toward a large and thus there will be minimal borrowing.
Bayesian Dynamic Borrowing For Multilevel Linear Models
In the previous section, we considered the single-level linear model which allows BDB to be applied to models commonly used in less complex data collection situations. However, BDB can be applied to more complex data collection situation such as multistage sampling designs found in large-scale educational assessments. Specifically, large-scale educational assessments almost always derive from some form of multistage sampling and this must be accounted for in any substantive analysis. The most common approach to analyzing data from these designs is multilevel modeling (Gelman & Hill, 2007; Raudenbush & Bryk, 2002). We begin by first specifying a Bayesian multilevel linear model with individual-level and group-level predictors for the current data. It is useful for our purposes to represent this model in matrix notation (e.g., Jackman, 2009; Gelman & Hill, 2007) with superscripts representing the historical and current data. The multilevel model for the current data can be written in the form of a fully Bayesian hierarchical model (see Gelman et al., 2014, p. 389) as
| 8 |
| 9 |
| 10 |
where is an matrix of individual-level predictors with one’s in the first column and n as the number of individuals in total; is a column vector of individual-level regression coefficients that vary across G schools ; is a matrix of group-level predictors (; is a column vector of Q group-level regression coefficients. Finally, we assign a normal prior distribution to the parameter matrix , with mean and covariance matrix . The coefficients in could be modeled as function of predictors, if so desired.
Prior distributions are also required for , , and . For the current data, consider the following priors:
| 11 |
| 12 |
| 13 |
where and are the location and scale parameters of the half-Cauchy distribution, and are positive definite scale matrices, and and are the degrees-of-freedom for and , respectively, for the IW (inverse-Wishart) distributions.
Extending our notation for BDB to multilevel models, we will again use superscripts to denote the current and historical data sets. Let represent the p individual level regression coefficients for each of the H historical cycles of data and the current individual-level coefficient, . The joint distribution of is assumed to be multivariate normal with mean and precision matrix —viz.
| 14 |
where ).
The covariance matrix of the individual-level coefficients, , is specified as being block diagonal,
| 15 |
where the elements of contain the variances and covariances of the individual-level coefficients within each historical data set. We assume that the off-diagonal elements of are null matrices. The elements of are individually given IW priors,
| 16 |
The joint distribution of school-level coefficients is assumed to be multivariate normal with mean and covariance matrix —viz.
| 17 |
where ).
The covariance matrix of school-level coefficients, , under dynamic borrowing can be specified as
| 18 |
where the off-diagonal elements of are null matrices, and where could be diagonal with elements given a prior such as IG. Here again, we assume that the regression coefficients across cycles are generated from a population with common means and precision matrices. However, as with the single-level case, this assumption can be relaxed allowing the regression coefficients and elements of the precision matrices to have cycle-specific prior distributions.
Case Studies
For illustration purposes, we apply BDB to US data from the PISA (OECD, 2019). Launched in 2000 by the Organization for Economic Cooperation and Development, PISA is a triennial international survey that aims to evaluate education systems worldwide by testing the skills and knowledge of in-school 15-year-old students. In 2018, 600,000 students, statistically representative of 32 million 15-year-old students in 79 countries and economies, took an internationally agreed-upon two-hour test. Students were assessed in science, mathematics, reading, collaborative problem solving, and financial literacy.
Sample, Variables, and Model
For the purposes of demonstrating BDB in both the single-level and multilevel settings, we utilized a set of variables at the student and the school level that were measured in PISA from 2003 to 2018. The total observed sample size for the US PISA data from cycles 2003 to 2018 is 31,823 and the observed sample size per cycle ranges from 4838 to 5611. Note that we did not use data from the first cycle of PISA as this initial cycle was qualitatively different from the subsequent cycles. The major domain of assessment starting in 2003 was mathematics. We acknowledge that mathematics was not the major domain of assessment in PISA 2018; however, we did not include any “domain specific” variables in our model, but instead we used items and scales that were “domain general,” appearing across all cycles of PISA.
The student-level variables chosen for both the single-level and multilevel case studies were
PV1MATH: The outcome of interest. The first plausible value of the PISA 2018 mathematics assessment is used.
FEMALE: A dummy variable representing gender (, ).
PARED: A derived variable representing the highest educational level (in estimated years of schooling) of either parent.
HOMEPOS: A summary index of all household and possession items, including cultural possessions and educational resources at home.
IMMIG: A derived index of immigrant background (IMMIG) with the following categories: (1) native students (those students who had at least one parent born in the country), (2) second-generation students (those born in the country of assessment but whose parents were born in another country), and (3) first-generation students (those students born outside the country of assessment and whose parents were also born in another country). Students with missing responses for either the student or for both parents were assigned missing values for this variable.
The school-level variables chosen for the multilevel case study were
TCSHORT: An index of principle-reported teacher shortage in the school derived from four items in response to the question “Is your school’s capacity to provide instruction hindered by any of the following issues?”: (a) A lack of qualified science teachers, (b) A lack of qualified mathematics teachers, (c) A lack of qualified <test language> teachers, and (d) A lack of qualified teachers of other subjects.
STRATIO: An index obtained by dividing the number of enrolled students (captured by the size of the school) by the total number of teachers.2
Missing data was addressed by performing two-level multiple imputation for each cycle of PISA separately using the Blimp software program (Enders, Keller, & Levy, 2018; Keller & Enders, 2019). For simplicity, we used the first imputed data set for our analyses.3 Descriptive statistics for the full US samples across all cycles of PISA used in this study can be found in Table 1, where we observed a moderate degree of heterogeneity across the cycles and would therefore expect there to be somewhat less borrowing using BDB.
Table 1.
Descriptive statistics for all PISA cycles (full US sample).
| Statistics | Cycle | PV1MATH | Female | Lang | PARED | HOMEPOS | IMMIG | TCSHORT | STRATIO |
|---|---|---|---|---|---|---|---|---|---|
| Mean or Proportion | 2003 | 481.86 | 0.50 | 0.91 | 13.47 | 0.31 | 0.87 | 0.13 | 15.80 |
| 2006 | 471.05 | 0.50 | 0.88 | 13.49 | 0.18 | 0.84 | 0 | 16.23 | |
| 2009 | 482.94 | 0.50 | 0.86 | 13.49 | 0.04 | 0.81 | 0.45 | 16.32 | |
| 2012 | 481.98 | 0.49 | 0.86 | 13.58 | 0.18 | 0.79 | 0.41 | 17.17 | |
| 2015 | 468.74 | 0.50 | 0.82 | 13.54 | 0.19 | 0.77 | 0.24 | 16.32 | |
| 2018 | 474.30 | 0.50 | 0.86 | 14.03 | 0.02 | 0.79 | 0.15 | 17.58 | |
| SD | 2003 | 93.64 | 0.50 | 0.28 | 2.55 | 1.01 | 0.34 | 0.91 | 5.62 |
| 2006 | 87.64 | 0.50 | 0.32 | 2.48 | 0.96 | 0.37 | 0.96 | 4.73 | |
| 2009 | 89.35 | 0.50 | 0.34 | 2.56 | 0.95 | 0.40 | 0.82 | 5.24 | |
| 2012 | 89.84 | 0.50 | 0.35 | 2.66 | 1.11 | 0.41 | 0.93 | 10.26 | |
| 2015 | 88.74 | 0.50 | 0.39 | 2.81 | 1.11 | 0.42 | 1.08 | 4.87 | |
| 2018 | 91.67 | 0.50 | 0.35 | 2.49 | 1.15 | 0.40 | 1.01 | 10.08 | |
| Percent Missing | 2003 | 0 | 0 | 0.03 | 0.03 | 0.01 | 0.03 | 0.01 | 0.07 |
| 2006 | 0 | 0 | 0.03 | 0.01 | 0.01 | 0.03 | 0.01 | 0.17 | |
| 2009 | 0 | 0 | 0.02 | 0.02 | 0.01 | 0.02 | 0.01 | 0.12 | |
| 2012 | 0 | 0 | 0.02 | 0.02 | 0.01 | 0.03 | 0.01 | 0.04 | |
| 2015 | 0 | 0 | 0.01 | 0.02 | 0.01 | 0.04 | 0 | 0.11 | |
| 2018 | 0 | 0 | 0.01 | 0.02 | 0.01 | 0.03 | 0.02 | 0.10 |
For the single-level case study setting, a Bayesian single-level linear model was fit using the PISA 2018 data with math achievement as the outcome, and gender, parent education, home procession index, and immigration status as predictors. For the multilevel case study setting, which is consistent with the PISA design, a Bayesian multilevel linear model was fit using the PISA 2018 data with math achievement as the outcome, gender, parent education, home procession index, and immigration status as the individual-level predictors, and teacher shortage index and student–teacher ratio as the school-level predictors. The intercept and the slope of gender were allowed to be random, while the rest of the slopes were fixed. An interaction of gender and teacher shortage index was also evaluated. As there were only 6 to 10 of private schools in the US sample of PISA cycles 2003 to 2018 and there might be more heterogeneity among private schools, we conducted the multilevel analyses on the public schools only.
As the scales of variables included in the models vary greatly, all the variables are standardized first and their z-scores were used in the estimation. Then, all the parameters were converted back to their original scales after the estimation.
Sample Size
For both the single-level and multilevel settings, we evaluated the performance of different priors using the US full sample first, and then on a small subsample of 500 students. For the subsamples, a random sample of 25 schools with at least 20 students per school was selected from each cycle first, and then 20 students from each of those schools were randomly selected for the historical cycles and the current cycle.
Choice of Priors
For the single-level setting, we evaluated the performance of dynamic priors, which incorporate the potential heterogeneity between historical data and current data through a joint prior distribution as indicated in (3), and compared it to regular priors with predetermined prior values and strength. Specifically, for dynamic priors, we varied the IG prior for , as indicated in (7), at IG(.001, .001), IG(1, 1), and IG(1, .001), to facilitate different degrees of borrowing. The same series of inverse-gamma priors were also examined in Viele et al. (2014).4 For power priors, we vary the a parameter using values of .25, .50, and .75. For regular/static informative priors, the average values of estimated coefficients from historical data were used as the prior mean and average values of prior variances of historical coefficients were used as the prior variances. Again, note that this is similar to Bayesian updating, though not incorporating sequential updating as in Bayesian synthesis. For comparison purposes, two extreme kinds of borrowing, complete pooling (pooling historical data directly for analysis—i.e., IDA) and no borrowing (using non-informative priors on the current data) were also evaluated. We specified a weakly informative prior for the standard deviation of the error term, and a non-informative prior for the mean coefficients across all cycles () in BDB and the coefficients of the current cycle () in the non-informative prior conditions after data standardization.
Similar to the single-level case study above, we assessed the performance of dynamic priors and compared it to regular priors with predetermined prior values and strength in the multilevel setting. Specifically, for dynamic priors, we varied the IG prior for at IG(1, 1), IG(1, .1) and IG(1, .001) to allow for different degrees of borrowing for coefficients. Moreover, the precision matrix of the random intercept and random slope has an Wishart distribution prior,5 W where takes on the values 2 (weak borrowing) or 20 (strong borrowing) and is the baseline covariance matrix where is a diagonal matrix whose diagonal elements are distributed as half-Cauchy(0,1) and (Lewandowski, Kurowicka, & Joe, 2009).6 For regular/static informative priors, the average values of estimated coefficients from historical data were used as the prior mean and average values of prior variances of historical coefficients were used as the prior variances. Again, for comparison purposes, two extreme kinds of borrowing, complete pooling and no borrowing of the historical data sets were also examined. Similar to the single-level case, we specified a weakly informative prior for the standard deviation of the individual-level error term, and a non-informative prior for the school-level coefficients across all cycles () in BDB and the mean school-level coefficients in the current cycle () in the non-informative prior conditions after data standardization.
Evaluation of Bayesian Historical Borrowing
For our case studies, we adopted two statistical measures to compare the impact of different priors, namely the total effective sample size (TESS) and the leave-one-out cross-validation information criterion (LOOIC). These two measures can help with understanding how much information different priors borrow as well as gauging the accuracy of predictions, respectively, for models with different priors.
Total Effective Sample Size
Effective sample size is a way to evaluate how much information is contained in the priors for Bayesian historical borrowing, and can be used to inform one’s interpretation of inferences regarding the impact of the prior information on obtaining the final results. However, identifying an equivalent number of observations to reflect the information included in the prior probability distribution is not straightforward (Morita, Thall, & Müller, 2008). Neuenschwander, Capkun-Niggli, Branson, and Spiegelhalter (2010) proposed a simplified version of approximate prior effective sample size, assuming that information is directly proportional to precision (i.e., inverse of variance). Specifically, Neuenschwander et al. (2010) used the ratio of the variance under complete pooling and the variance under a certain prior multiplied by the total number of historical observations (equation 9 in their paper), providing an approximate effective sample size that a prior can add to the current data.
In Bayesian dynamic borrowing, because a joint prior distribution is specified among historical data and current data, we care more about the total effective sample size (TESS) that is used for estimating the parameter(s) of interest. Therefore, we propose an approximate TESS that is used to quantify the total number of effective observations through both prior information and current data. Similar to what Neuenschwander et al. (2010) proposed, we use the posterior variance of a parameter estimate under complete pooling divided by the posterior variance of the parameter of the same effect under a certain kind of historical borrowing, multiplying by the total number of observations for both historical and current data.
Leave-One-Out Cross-Validation Information Criterion (LOOIC)
In addition to the TESS mentioned above, we add to the extant literature by examining the predictive performance of Bayesian historical borrowing methods using the Leave-One-Out Cross-Validation Information Criterion (LOOIC). Leave-one-out-cross-validation (LOOCV) is a special case of k-fold cross-validation (k-fold CV) when , with n indicating the number of observations. In k-fold CV, a sample is split into k groups (folds) and each fold is taken to be the validation set with the remaining folds serving as the training set. For LOOCV, each observation serves as the validation set with the remaining observations serving as the training set. For each observation, the expected log point-wise predictive density (ELPD) is calculated and serves as a measure of predictive accuracy for n data points taken one at a time (see Vehtari et al., 2017).7 An information criterion referred to as the LOOIC can then be obtained as function of the estimated ELPD. Among a set of competing models, the one with the smallest LOOIC is considered the best from an out-of-sample point-wise predictive point of view. For this paper, students are left out one at a time for both single-level and multilevel scenarios. We obtain the Bayesian LOOIC provided by the loo software program (Vehtari et al., 2019), available in R (R Core Team, 2019).
Results of Case Study 1: Single-Level Model
Throughout this paper, we use the R program rstan (Stan Development Team, 2020). All software code for the case studies and subsequent simulation studies are available in the supplementary material. We generated four chains, with 20,000 iterations and a thinning interval of 10 across all the methods and sample size conditions within the single-level case study. The posterior means and standard deviations of coefficients for the single-level case study are listed in Table 2.
Table 2.
Posterior Means and Standard Deviations (SD) of Coefficients for Case Study 1 (Single-Level Model).
| Cycle | Method | Intercept | FEMALE | PARED | HOMEPOS | IMMIG | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | ||
| 2003 | BLR non inf | 416.89 | 6.74 | 9.49 | 2.24 | 3.62 | 0.49 | 33.54 | 1.23 | 12.08 | 3.52 |
| 2006 | BLR non inf | 387.85 | 6.88 | 12.86 | 2.20 | 6.61 | 0.49 | 25.91 | 1.22 | 8.04 | 3.15 |
| 2009 | BLR non inf | 417.92 | 6.88 | 17.22 | 2.29 | 5.17 | 0.51 | 27.71 | 1.27 | 3.85 | 3.00 |
| 2012 | BLR non inf | 408.43 | 6.90 | 8.58 | 2.34 | 5.62 | 0.52 | 21.17 | 1.17 | 5.65 | 3.12 |
| 2015 | BLR non inf | 405.80 | 5.93 | 8.87 | 2.19 | 4.72 | 0.46 | 19.61 | 1.07 | 0.23 | 2.78 |
| 2018 | BLR non inf | 426.29 | 7.64 | 7.21 | 2.42 | 4.68 | 0.54 | 25.02 | 1.14 | 18.29 | 3.15 |
| BLR inf | 419.55 | 5.13 | 9.51 | 1.68 | 4.66 | 0.35 | 25.14 | 0.79 | 7.75 | 2.12 | |
| BLR pooling | 411.46 | 2.78 | 10.57 | 0.96 | 5.00 | 0.21 | 25.00 | 0.46 | 0.34 | 1.25 | |
| BDB IG(1,1) | 426.52 | 7.40 | 7.24 | 2.36 | 4.66 | 0.53 | 25.03 | 1.11 | 18.22 | 3.07 | |
| BDB IG(1,.1) | 426.23 | 7.24 | 7.11 | 2.39 | 4.67 | 0.51 | 25.01 | 1.11 | 18.09 | 3.05 | |
| BDB IG(1,.001) | 425.41 | 6.58 | 8.05 | 2.15 | 4.68 | 0.46 | 25.03 | 1.08 | 16.62 | 3.04 | |
| PP (.25) | 416.67 | 4.55 | 9.51 | 1.56 | 4.87 | 0.33 | 25.15 | 0.77 | 5.74 | 2.04 | |
| PP (.50) | 413.72 | 3.71 | 10.10 | 1.25 | 4.94 | 0.27 | 25.07 | 0.63 | 2.20 | 1.63 | |
| PP (.75) | 412.12 | 3.14 | 10.37 | 1.08 | 4.99 | 0.23 | 25.02 | 0.54 | 0.57 | 1.45 | |
BLR non inf: Bayesian linear regression with non-informative prior; BLR inf: Bayesian linear regression with informative prior; BDB: Bayesian dynamic borrowing; IG: inverse-gamma prior for the variance of the joint prior distribution, which determines the degree of borrowing; PP: power prior.
In addition to the estimates under different prior conditions for the cycle of interest (i.e., 2018), we also included BLR with non-informative priors for the historical cycles in Table 2. A comparison of BLR non-informative estimates of the historical cycles with the BLR non-informative estimates of the current cycle indicated that the effects of interest in historical cycles were quite heterogeneous from those in the current cycle but the degree of heterogeneity varied across different coefficients. For the cycle of interest in this paper (i.e., 2018), estimates are relatively consistent across different prior conditions, except for immigration status, where BLR with non-informative prior and BDB priors are similar but different from other prior conditions. The similarity of BLR with non-informative priors and BDB results confirm that historical cycles are heterogeneous from the current cycles regarding the effect of immigration status.
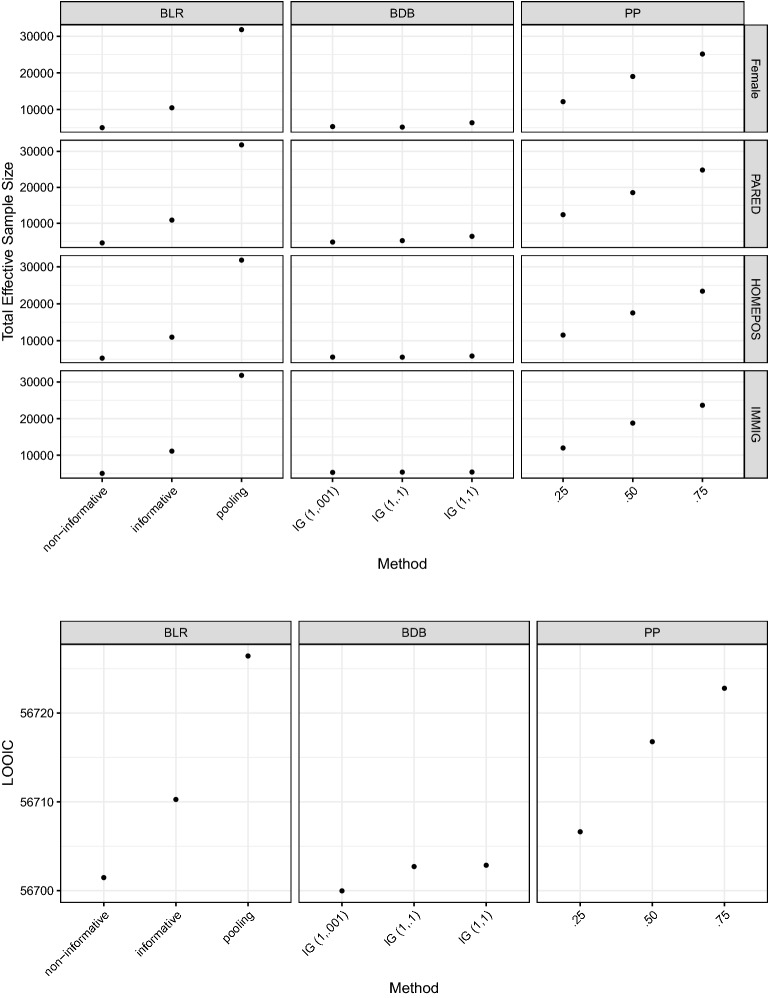
The total effective sample size and LOOIC results for the single-level case study with the full US sample are illustrated in Fig. 1. The upper panels present the results in terms of the total effective sample size and the lower panels present the results in terms of LOOIC. We presented results for a subset of BDB prior conditions with different degrees of borrowing and results for other values of the inverse-gamma prior under BDB can be found in the supplementary material.
Fig. 1.
Total effective sample size (upper panel), and LOOIC (lower panel) for single-level case study (full US sample). The horizontal axis represents the methods used under Bayesian linear regression (BLR), the priors used under Bayesian dynamic borrowing (BDB), and the a parameter used for power priors (PP).
For the total effective sample size, results indicate that complete pooling provides the largest number of effective observations as expected because all observations across six cycles were used. This is followed by BLR with informative priors, and BDB across all priors. The results for the power priors closely track those of BLR insofar as smaller values of (.25) result in TESS values close to that of the BLR non-informative condition while larger values of (.75) result in larger TESS values close to that of the complete pooling. BLR with non-informative priors provides the smallest total effective sample sizes as expected because only the current cycle’s observations were used. For BDB priors, the total effective sample sizes are close to BLR with non-informative priors, which indicates that the historical cycles are quite heterogeneous compared to the current cycle and thus BDB priors evaluated in this paper yield relatively weak borrowing.
The LOOIC results shown in the lower panel of Fig. 1 show that complete pooling performs worse compared to other prior conditions. BDB priors provide similar LOOIC values (differences < 10) compared to BLR non-informative. Moreover, the LOOIC results of BDB are relatively insensitive to the choice of priors that control the borrowing, meaning that for this example, conclusions regarding predictive performance do not depend on the priors that control borrowing. Also, power priors are uniformly higher than BDB with respect to LOOIC, indicating slightly poorer predictive performance, though the real differences are small. Overall, similar patterns of LOOIC results were observed for the small sample size condition except LOOIC results are closer across different borrowing methods.
A small sample size case study with a random sample of for each cycle was also conducted to evaluate the impact of sample size on the performance of different prior models. The analysis revealed that the performance of all of these methods was nearly identical to the full sample results. The relevant figures can be found in the supplementary material.
Results of Case Study 2: Multilevel Model
For the multilevel case study, all conditions and methods were estimated using four chains, varying the number of iterations to ensure convergence, and using a thinning interval of 10 throughout. The first half of the posterior samples were warm-up and discarded, and the second half were used for summarizing the results. For the full US sample, in most cases the iterations converged with 50,000 or 75,000 iterations; otherwise, we reran the estimation procedure with 120,000 iterations per chain. All the methods and conditions reached convergence with , which indicated that the between- and within-chain estimates mostly agreed with each other and chains were mixed well. Other criteria such as trace plots, posterior density plots, and auto-correlation plots were also examined and they demonstrated reasonable convergence.
The posterior means and standard deviations of individual-level coefficients, school-level coefficients, and variation parameters based on the multilevel model for Case Study 2 are presented in Tables 3, 4 and 5. Similar to single-level Case Study 1, the BLR estimates with non-informative prior for historical cycles are also included in those tables, which indicates that the effects of interest in the historical cycles are quite different from those in the current cycle, but with different degrees of heterogeneity across different coefficients. As Table 3 shows, individual-level coefficient estimates with different prior choices are relatively close except for gender and immigration status, where BLR non-informative and BDB with relatively non-information hyper-priors are close, while pooling and power priors are close. As Table 4 shows, school-level coefficient estimates with different prior choices are relatively close for teacher shortage, but different for student–teacher ratio and the interaction of gender and teacher shortage, where again BLR with non-informative priors and BDB with non-informative hyper-priors are close. Variation estimates in Table 5 include individual-level standard deviation (level-1 SD), school-level variances (level-2 Var.) of random intercept and random slope of gender, and covariance (level-2 Covar.) between random intercept and random slope of gender. Individual-level variation estimates across different priors are similar, but school-level variation estimates vary with different prior choices. Results for the small sample with are similar to those for the full US sample in Tables 3, 4 and 5 and are included in the supplemental material.
Table 3.
Posterior means and standard deviations (SD) of individual-level coefficients for case study 2 (multilevel model).
| Cycle | Method | Intercept | FEMALE | PARED | HOMEPOS | IMMIG | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | ||
| 2003 | BLR non inf | 451.06 | 11.53 | 9.77 | 2.59 | 2.56 | 0.54 | 26.36 | 1.39 | 3.52 | 4.15 |
| 2006 | BLR non inf | 421.04 | 13.19 | 12.50 | 2.15 | 4.53 | 0.49 | 18.35 | 1.26 | 2.48 | 3.50 |
| 2009 | BLR non inf | 456.17 | 12.78 | 16.23 | 2.49 | 3.25 | 0.49 | 19.42 | 1.33 | 3.13 | 3.26 |
| 2012 | BLR non inf | 433.41 | 9.61 | 12.24 | 2.54 | 3.95 | 0.53 | 15.17 | 1.21 | 10.14 | 3.46 |
| 2015 | BLR non inf | 422.29 | 12.09 | 9.40 | 2.28 | 3.32 | 0.47 | 15.00 | 1.11 | 0.67 | 3.10 |
| 2018 | BLR non inf | 435.74 | 9.92 | 7.82 | 2.57 | 3.29 | 0.57 | 19.55 | 1.26 | 11.39 | 3.54 |
| BLR inf | 435.28 | 7.69 | 10.40 | 1.74 | 3.33 | 0.38 | 19.62 | 0.89 | 6.05 | 2.54 | |
| BLR pooling | 434.32 | 4.33 | 11.28 | 0.96 | 3.49 | 0.21 | 18.54 | 0.51 | 1.89 | 1.41 | |
| BDB IG(1,1) W2 | 435.93 | 9.72 | 7.78 | 2.44 | 3.27 | 0.55 | 19.48 | 1.19 | 11.29 | 3.46 | |
| BDB IG(1,.1) W2 | 436.17 | 9.55 | 7.79 | 2.46 | 3.25 | 0.55 | 19.42 | 1.19 | 11.08 | 3.42 | |
| BDB IG(1,.001) W2 | 437.26 | 8.53 | 8.78 | 2.21 | 3.28 | 0.48 | 19.36 | 1.13 | 9.39 | 3.26 | |
| BDB IG(1,1) W20 | 435.90 | 9.92 | 7.82 | 2.46 | 3.26 | 0.55 | 19.42 | 1.21 | 11.26 | 3.47 | |
| BDB IG(1,.1) W20 | 436.01 | 9.86 | 7.80 | 2.44 | 3.26 | 0.55 | 19.41 | 1.19 | 11.16 | 3.46 | |
| BDB IG(1,.001) W20 | 437.39 | 8.50 | 8.82 | 2.16 | 3.28 | 0.47 | 19.34 | 1.14 | 9.34 | 3.26 | |
| PP (.25) | 426.05 | 5.74 | 10.02 | 1.64 | 4.02 | 0.36 | 20.91 | 0.84 | 3.87 | 2.28 | |
| PP (.5) | 430.96 | 4.98 | 10.71 | 1.28 | 3.71 | 0.28 | 19.58 | 0.66 | 2.61 | 1.87 | |
| PP (.75) | 433.14 | 4.48 | 11.07 | 1.09 | 3.56 | 0.24 | 18.92 | 0.56 | 2.14 | 1.59 | |
BLR non inf: Bayesian linear regression with non-informative prior; BLR inf: Bayesian linear regression with informative prior; BDB: Bayesian dynamic borrowing; IG: inverse-gamma prior for level-1 variance of the joint prior distribution, which determines the degree of level-1 borrowing; W2: Wishart prior with weak borrowing for level-2 precision matrix (results were converted back the covariance matrix); W20: Wishart prior with strong borrowing for level-2 precision matrix (results were converted back the covariance matrix); PP: power priors.
Table 4.
Posterior means and standard deviations (SD) of school-level coefficients for case study 2 (multilevel model).
| Cycle | Method | TCSHORT | STRATIO | FEMALE:TCSHORT | |||
|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | Mean | SD | ||
| 2003 | BLR non inf | 12.50 | 3.35 | 0.76 | 0.52 | 0.09 | 2.80 |
| 2006 | BLR non inf | 0.89 | 3.41 | 0.24 | 0.65 | 2.87 | 2.27 |
| 2009 | BLR non inf | 16.28 | 4.07 | 1.27 | 0.61 | 0.15 | 2.64 |
| 2012 | BLR non inf | 13.15 | 3.61 | 0.06 | 0.31 | 0.93 | 2.45 |
| 2015 | BLR non inf | 5.68 | 2.94 | 0.03 | 0.60 | 1.31 | 2.09 |
| 2018 | BLR non inf | 8.40 | 3.18 | 0.33 | 0.29 | 1.85 | 2.52 |
| BLR inf | 9.19 | 2.29 | 0.15 | 0.25 | 0.76 | 1.74 | |
| BLR pooling | 9.60 | 1.39 | 0.11 | 0.18 | 0.08 | 0.96 | |
| BDB IG(1,1) W2 | 8.43 | 3.16 | 0.34 | 0.29 | 1.80 | 2.40 | |
| BDB IG(1,.1) W2 | 8.80 | 3.49 | 0.32 | 0.28 | 1.79 | 2.36 | |
| BDB IG(1,.001) W2 | 8.63 | 2.48 | 0.17 | 0.26 | 0.96 | 1.91 | |
| BDB IG(1,1) W20 | 8.41 | 3.22 | 0.34 | 0.29 | 1.78 | 2.40 | |
| BDB IG(1,.1) W20 | 8.42 | 3.14 | 0.34 | 0.29 | 1.81 | 2.37 | |
| BDB IG(1,.001) W20 | 8.66 | 2.51 | 0.17 | 0.26 | 0.97 | 1.93 | |
| PP (.25) | 9.11 | 1.49 | 0.02 | 0.16 | 0.81 | 1.65 | |
| PP (.5) | 9.39 | 1.40 | 0.06 | 0.17 | 0.29 | 1.28 | |
| PP (.75) | 9.54 | 1.38 | 0.09 | 0.17 | 0.06 | 1.09 | |
BLR non inf: Bayesian linear regression with non-informative priors; BLR inf: Bayesian linear regression with informative priors; BDB: Bayesian dynamic borrowing; IG: inverse-gamma prior for level-1 variance of the joint prior distribution, which determines the degree of level-1 borrowing; W2: Wishart prior with weak borrowing for level-2 precision matrix (results were converted back the covariance matrix); W20: Wishart prior with strong borrowing for level-2 precision matrix (results were converted back the covariance matrix); PP: power priors.
Table 5.
Posterior means of variation parameters for case study 2 (multilevel model).
| Cycle | Method | Level-1 SD | Level-2 Var.-Intercept | Level-2 Covar. | Level-2 Var.-FEMALE |
|---|---|---|---|---|---|
| 2003 | BLR non inf | 77.12 | 1069.02 | 35.54 | 10.40 |
| 2006 | BLR non inf | 76.42 | 1185.44 | 16.86 | 7.98 |
| 2009 | BLR non inf | 73.83 | 1358.10 | 3.57 | 10.67 |
| 2012 | BLR non inf | 74.35 | 1221.41 | 11.83 | 4.43 |
| 2015 | BLR non inf | 78.41 | 1152.04 | 55.28 | 18.66 |
| 2018 | BLR non inf | 79.21 | 949.58 | 39.44 | 37.80 |
| BLR inf | 79.22 | 951.49 | 36.50 | 34.35 | |
| BLR pooling | 76.56 | 1255.06 | 73.36 | 16.36 | |
| BDB IG(1,1) W2 | 76.48 | 972.51 | 42.84 | 10.16 | |
| BDB IG(1,.1) W2 | 76.48 | 974.05 | 40.97 | 9.71 | |
| BDB IG(1,.001) W2 | 76.48 | 971.30 | 42.69 | 9.82 | |
| BDB IG(1,1) W20 | 76.47 | 1016.67 | 57.70 | 15.22 | |
| BDB IG(1,.1) W20 | 76.47 | 1015.61 | 59.58 | 15.66 | |
| BDB IG(1,.001) W20 | 76.46 | 1011.85 | 57.25 | 14.68 | |
| PP (.25) | 79.88 | 618.45 | 14.61 | 6.33 | |
| PP (.5) | 77.99 | 974.91 | 26.88 | 5.70 | |
| PP (.75) | 77.08 | 1151.31 | 49.57 | 9.43 |
BLR non inf: Bayesian linear regression with non-informative priors; BLR inf: Bayesian linear regression with informative priors; BDB: Bayesian dynamic borrowing; IG: inverse-gamma prior for level-1 variance of the joint prior distribution, which determines the degree of level-1 borrowing; W2: Wishart prior with weak borrowing for level-2 precision matrix (results were converted back the covariance matrix); W20: Wishart prior with strong borrowing for level-2 precision matrix (results were converted back the covariance matrix); PP: power priors.
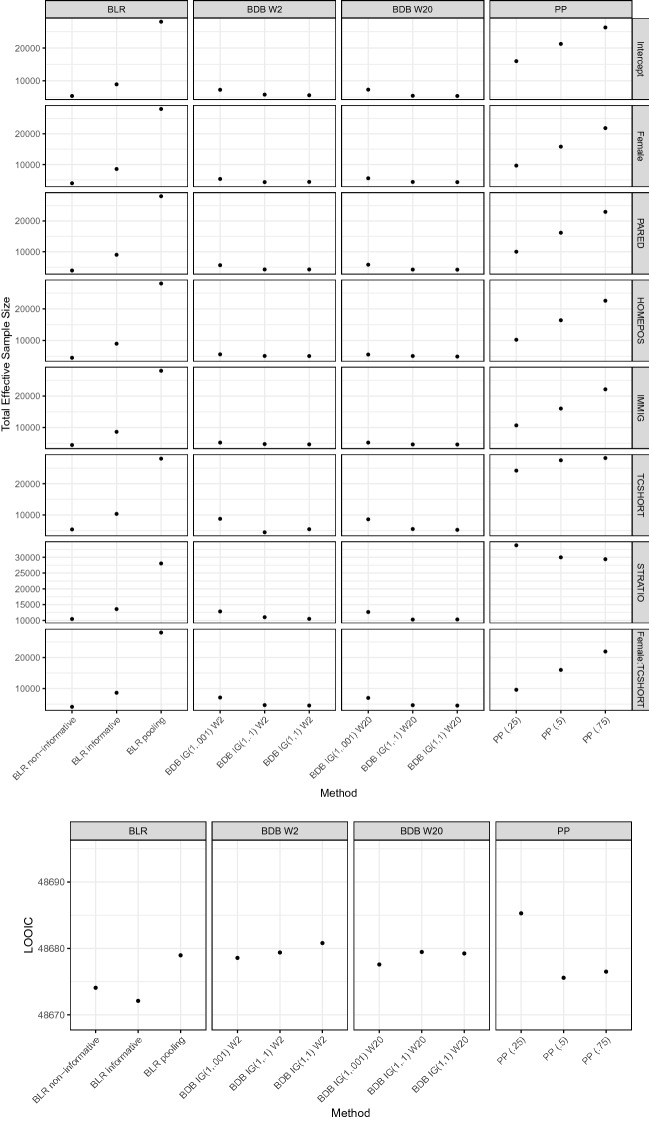
The total effective sample size and LOOIC results for the multilevel case study are illustrated in Figure 2 for the full sample with the upper panel showing the total effective sample size and the lower panel presenting the LOOIC results. Similar to the single-level case study, for the full US sample, complete pooling provides the largest effective sample size, followed by BLR with informative priors, and BDB. Again, BLR with non-informative priors yields the smallest total effective sample size, as expected. BDB and BLR with non-informative priors provide similar total effective sample sizes, which indicates again that historical cycles are heterogeneous compared to the current cycle. We also observe that power priors track the TESS results for BLR for some, but not all, variables. The TESS and LOOIC results for the small sample size condition (N=500) are in the supplementary material, which are mostly similar to the results for the full US sample, except that the informative prior provides the highest TESS, which may be related with this particular small sample.
Fig. 2.
Total effective sample size (upper panel), and LOOIC (lower panel) for multilevel case study (full US sample). The horizontal axis represents the methods used under Bayesian linear regression (BLR), the priors used under Bayesian dynamic borrowing (BDB) under weak (Wishart Prior W2) or strong (Wishart Prior W20) borrowing at level-2, and the a parameter used for power priors (PP).
Compared to the single-level case study, there are smaller differences in LOOIC across prior conditions in the multilevel case study. BDB priors yield comparable performance as other prior conditions (differences < 10 for LOOIC). LOOIC values for BDB and PP are relatively close. Thus for this case study, predictive performance does not seem to depend on the choice of borrowing method. Results for track the full sample size results very closely and are available in the supplementary material.
Simulation Studies
The results of the empirical example suggest that the cycles of PISA from 2003 to 2018 are relatively heterogeneous in terms of the effects we evaluated such that BDB borrows less due to data heterogeneity and provides estimates similar to Bayesian linear regression with non-informative priors. In order to study the performance of different methods of Bayesian historical borrowing under different levels of heterogeneity among data sets as well as varying levels of sample size, two comprehensive simulation studies were conducted: one for the implementation of historical borrowing in a Bayesian single-level linear model and the other for incorporating historical borrowing in a Bayesian multilevel linear model. We considered the framework of a “calibrated Bayesian” analysis (Dawid, 1982; Little, 2006, 2011), namely studying the frequentist properties of the historical borrowing methods.
Software Implementation for Simulation Studies
For the single-level simulation study, we used four chains, with 20,000 iterations and a thinning interval of 10. Additionally, we replicated every method and condition 1,000 times. All parameters converged with . For the multilevel simulation study, we fit the model with 30,000 iterations (where the first 15,000 were used as warm-up iterations and discarded) for each of the four chains and thinning interval being 10. We ran 500 replications, out of which the model converged well for at least 496 replications. The replications with were discarded.
Design of Simulation Study 1
For the first simulation study focusing on a Bayesian single-level model, we evaluated the impact of sample size, heterogeneity between historical data and current data, and prior choice on parameter estimation. To mimic real large-scale assessment data, the data sets used in Simulation Study 1 were based on the US samples from the PISA 2003 to PISA 2018 cycles. For illustration purposes, PISA 2003 to PISA 2015 were treated as five historical cycles and PISA 2018 was treated as the current cycle. The sample size N per cycle varied at 100 and 2000. For the historical cycles, a random sample was selected from the US samples of the PISA 2003–2015 cycles, respectively, with sample sizes of 100 or 2000 in each cycle. The evaluation of relatively smaller sample sizes such as 100 is intended to shed some light on subgroup analyses or data analyses for smaller countries in the context of large-scale assessments. An intermediate sample size condition of was also studied and the results are essentially the same as for the and cases. The results for can be found in the supplementary material. The selected variables included the math achievement score, gender, parent education, home procession, and immigration status.
To evaluate the impact of heterogeneity between historical data and current data in a controlled setting, a spectrum of current data that differed from the historical data with varying degrees of heterogeneity was generated. A Bayesian linear model was fit on each of the historical data sets with math achievement as the outcome, and gender, parent education, home procession, and immigration status as predictors to obtain the historical estimates for the effects of interest. For the current data, predictor values were obtained from the US sample of the PISA 2018 cycle, while the outcome, math achievement score, was generated with the average historical intercept as the intercept and ten different kinds of slopes, denoted as Condition 1 to Condition 10, to cover a wide range of potential heterogeneity conditions in practice. The generating intercept was kept the same across ten conditions to keep a reasonable scale of the generated math outcome variable. In terms of the generating slopes, for Condition 5, the average slopes from five historical cycles were used as the slopes for generating the outcome variable in the current data. In this scenario, the effects of interest in the current data are the same as the average effects of interests in the historical cycles, and thus represent the homogeneous case. Under this condition, complete pooling or a very strong prior based on historical data would be expected to yield better results in terms of bias and mean squared error. In Conditions 1 to 4 and Conditions 6 to 9, the outcomes were generated using the slopes that were 80 less, 50 less, 20 less, 10 less, 10 more, 20 more, 50 more and 80 more of the average historical slopes, respectively, to reflect different degrees of heterogeneity in the effects of interest across historical data and current data. For Condition 10, coefficients with the opposite sign of the average historical slopes were used, which was the most heterogeneous case among all the conditions we evaluated. In this scenario, no borrowing or a flat prior would be expected to produce results with smaller bias and mean squared error.
Regarding the choice of priors, we evaluated the same priors as in the single-level case study, which include regular non-informative prior, informative prior (based on average of historical coefficients), complete pooling, dynamic borrowing with IG(1, 1), IG(1, .1), and IG(1, .001) on in (7), and power priors with varying at .25, .5 and .75.
Results of Simulation Study 1
Figure 3 presents the log mean square error (log MSE) (upper left), percent bias (upper right), total effective sample size (lower left), and LOOIC (lower right) for sample size of 100.
Fig. 3.
Log MSE (FIG. 3a, upper left), percent bias (FIG. 3b, upper right), total effective sample size (FIG. 3c, lower left), and LOOIC (FIG. 3d, lower right) for Simulation Study 1 (). The horizontal axis represents heterogeneity conditions. Each line within the figures represents methods examined under Bayesian linear regression (BLR), the priors used under Bayesian dynamic borrowing (BDB), and the a parameter used for power priors (PP).
We preferred to take the log of the mean square error values to more clearly show the differences among the various methods and conditions. The columns display the results broken down by method (Bayesian linear regression, Bayesian dynamic borrowing, and power priors under different hyperparameter settings). The horizontal axis represents the conditions of heterogeneity between the current and past cycles of PISA described in the Design section.
The results for log MSE show generally that as the heterogeneity between the current and previous cycles increases (e.g., conditions 1 - 4 and 6 - 10), the log MSE also increases. We note that the behavior of the log MSE across methods is relatively similar, but does differ across predictors. As expected, BLR under complete pooling performs better under relatively homogeneous conditions.
Percent bias as shown in the upper right of Figure 3 follows the same pattern as log MSE. For the relatively homogeneous conditions (e.g., conditions 4 to 6), BLR pooling, power prior (), and BDB (IG[1, .001]) record the smallest percent bias across all variables. However, as cycles become more heterogeneous, the bias under BLR pooling and power prior () dramatically increases compared to BDB across all priors. We thus find that when the current cycle differs from past cycles, borrowing from historical cycles produces a greater percent bias for BLR and PP compared to BDB.
With respect to total effective sample size (TESS) in the lower left of Figure 3 for the sample size 100 condition, we see, as expected, that BLR under complete pooling uses all of the information in the data. BDB, by comparison, uses considerably less information on average and the information provided by different BDB priors vary. For example, as illustrated in Figure 3c, BDB under IG (1, .001) has a larger total effective sample size overall compared to the other IG priors, and this particular prior borrows more under the homogeneous conditions and borrows less under the heterogeneous conditions compared to the other BDB priors. We find, also as expected, that PP falls between BLR under complete pooling and BLR under no borrowing regardless of the value.
The results for LOOIC with sample size 100 are shown in lower right of Figure 3. We find that for conditions with heterogeneity above , there is a marked increase in LOOIC values for BLR and PP, whereas almost all BDB priors and informative BLR are unaffected by greater degrees of heterogeneity. As before, this suggests that BDB shows superior predictive performance compared to BLR and PP regardless of the level of heterogeneity between the current cycle and historical cycles.
Figure 4 shows the results for sample size 2000. Here, we see generally the same pattern of results as observed for sample size = 100 for log MSE, percent bias, TESS, and LOOIC. We note that as the sample size increases, there is much less variability across conditions and across methods, as would be expected from Bayesian theory. When moving to cases, we see that the relative patterns for TESS still hold for BLR and PP but the total effective sample size for BDB remains mostly constant across BDB priors and heterogeneity conditions.
Fig. 4.
Log MSE (FIG. 4a, upper left), Percent bias (FIG. 4b, upper right), Total Effective sample size (FIG. 4c, lower left), and LOOIC (FIG. 4d, lower right) for Simulation Study 1 (). The horizontal axis represents heterogeneity conditions. Each line within the figures represents methods examined under Bayesian linear regression (BLR), the priors used under Bayesian dynamic borrowing (BDB) for weak (W2) or strong (W20) borrowing, and the a parameter used for power priors (PP).
Our conclusion for the single-level simulation study is that BDB generally performs at least as well as BLR and PP, particularly for relatively homogeneous cases; and in heterogeneous cases BDB performs better, at least with respect to percent bias and point-wise predictive accuracy as measured by the LOOIC.
Design of Simulation Study 2
Simulation Study 2 was conducted to evaluate the performance of Bayesian dynamic borrowing in multilevel settings. Simulation conditions included number of schools, school size, heterogeneity of historical information, and prior choice. Data generation in Simulation Study 2 was also based on the US samples of the PISA 2003–2018. Let G denote the number of schools and let n denote sample size per school. We examined three different sample sizes: (1) , ; (2) , , and (3) , . For the data sets of historical cycles, a random sample stratified by schools was selected from the US samples of the PISA 2003–2015 cycles, respectively, with one of the sample size scenarios mentioned above for each cycle. The selected variables included math achievement score, gender, parent education, home procession, immigration status, teacher shortage index, and student–teacher ratio. We only display results for the , condition. The remaining conditions are available in the supplementary material.
Similar to Simulation Study 1, a spectrum of current data that differed from the historical data with varying degrees was generated to evaluate the impact of heterogeneity between historical data and current data. A Bayesian multilevel linear model was fit on each of the historical cycles with math achievement as the outcome, gender, parent education, home procession, and immigration status as student-level predictors, and teacher shortage and student–teacher ratio as the school-level predictors. The intercept was allowed to be random, while the slopes were fixed. Fixed effect and random effect estimates from the historical cycles were obtained and used to generate the current cycle’s data. That is, for the current cycle, predictor values were sampled from the US sample of PISA 2018 cycle, while the outcome, math achievement score, was generated with the average historical intercept as the intercept and ten different kinds of fixed slopes and random effects, denoted as Condition 1 to Condition 10, similar to those in Simulation Study 1. For Condition 5, the average fixed level-1 slopes and average level-2 variance from five historical cycles were used to generate the outcome variable in the current data. In Conditions 1 to 4 and Conditions 6 to 9, the outcomes were generated using the fixed slopes and level-2 variance that were 80 less, 50 less, 20 less, 10 less, 10 more, 20 more, 50 more and 80 more of the average historical slopes and level-2 variance, respectively, to reflect different degrees of heterogeneity. For Condition 10, coefficients with the opposite sign of the average historical slopes and level-2 variance were used.
With regard to prior choice, similar to the multilevel case study, we assessed the performance of dynamic priors and compared it to regular non-informative prior, informative prior (based on average of historical coefficients), complete pooling, and power priors. Specifically, for dynamic priors, we varied the IG prior for at IG(1, 1), IG(1, .1), and IG(1, .001). Results for intermediate prior conditions are available in the supplementary material. The precision matrix of the random intercept has a Wishart distribution W where takes 1 (weak borrowing) or 20 (strong borrowing) and is the baseline precision where is a diagonal matrix whose diagonal elements are distributed as and . For power priors, again, we varied at .25, .50, and .75.
Results of Simulation Study 2
For simulation study 2, we present the results only for the case of 30 schools with 20 students in each school. The results for the other school/student conditions are virtually identical to the 30/20 case and are available in the supplementary material. Figure 5 shows the log MSE (upper left), percent bias (upper right), TESS (lower left), and LOOIC (lower right) for different combinations of numbers of schools and numbers of students per school respectively. The columns break the results into four groups of methods: BLR, BDB with weak borrowing on random effects, BDB with strong borrowing on random effects, and PP.
Fig. 5.
Log MSE (Figure. 5a, upper left), Percent bias (Figure. 5b, upper right), Total Effective sample size (Figure. 5c, lower left), and LOOIC (Figure. 5d, lower right) for Simulation Study 2 (; 30 Schools, 20 Students Each). The horizontal axis represents heterogeneity conditions. Each line within the figures represents methods examined under Bayesian linear regression (BLR), the priors used under Bayesian dynamic borrowing (BDB), and the a parameter used for power priors (PP).
These figures basically show similar patterns to the single-level simulation study, though it must be noted that we find some variations across methods as they pertain to different level-1 and level-2 predictors. Most methods, however, show smaller log MSE (Figure 5a) on coefficient estimates when there is more homogeneity between the current cycle and historical cycles. The non-informative prior method is stable across different heterogeneity conditions, while BLR pooling performs better in the homogeneous conditions (e.g., condition 5) and worse in the heterogeneity conditions (e.g., condition 10); BDB is mostly stable across conditions and the prior of the precision matrix has little effect on the estimation of coefficients. Stronger borrowing in coefficients like IG(1, 0.001) generally leads to smaller log MSE with BDB because the variance of the estimator is reduced, even at the price of possibly greater bias. In addition, BDB is much better than all other methods for student-level standard deviation estimates, and strong borrowing of the precision matrix works better for estimating school-level variances.
The MSE can be decomposed into squared bias and variance, which are described by bias and TESS respectively (Figures 5b and 5c). BDB shows much smaller biases in estimates than other borrowing methods except condition 9 where even non-informative priors leads to large bias, while pooling and PP are seriously biased under all heterogeneous conditions. Moreover, BDB shows the smallest bias in the student-level standard deviation, and strong borrowing of the precision matrix results in smaller bias in the school-level variance than weak borrowing. According to TESS, BDB usually uses much less information than pooling and PP regardless of specific priors used, implying that BDB estimators may generally have large variances compared to complete pooling. Finally, the LOOIC results in Figure 5d confirm that BDB is preferable to other borrowing methods in its stability across all conditions.
Conclusions
Bayesian dynamic borrowing incorporates information from previous relevant data sources while taking into account the heterogeneity of those data sources with respect to the current data. While it has attracted more attention in the clinical research area in recent years, it has not been studied or applied in large-scale assessments or other educational research areas. The purpose of this paper was to extend the method Bayesian dynamic borrowing from the typical one-parameter of interest scenario in clinical trials to multilevel models with covariates with specific applications to large-scale educational assessments and evaluate its performance in two comprehensive case studies and two simulation studies. In addition, we compared BDB with several commonly used methods, including Bayesian linear regression with and without pooling of the historical and current data and power priors. Though not all the popular historical borrowing methods were included for comparison, this paper may be viewed as a first step of extending BDB to large-scale assessments and education/psychology areas. Comparison with more recent methods is warranted for further research.
To summarize, our case studies showed that BDB performed at least as well, and in some cases better, than other methods of borrowing historical information in terms of predictive accuracy as measured by the LOOIC. As historical effects of interest were relatively heterogeneous from the current effect of interest, BDB borrowed less compared to other prior conditions indicated by the total effective sample sizes (TESS).
With respect to our simulation studies, which were designed to mimic the structure of PISA, we found that BDB also performed at least as well, if not better, than other methods of borrowing with respect to MSE, percent bias, and LOOIC. Also, we found that BDB generally borrows more (TESS is larger) when the historical effects of interest are close to the current effect of interest and borrows less (TESS is smaller) when they are different. Again, this result holds for both the single-level and multilevel cases and across the sample size conditions.
An important outcome of our study is the finding that historical borrowing methods, including BDB, do not perform identically across variables in a model. As alluded to in the introduction, this may be due to exogenous changes in society as a whole or endogenous changes to the technology of the assessment that have occurred over time impacting some, but perhaps not all, of the variables in the model. It is important, therefore, to determine if methods of historical borrowing can account for these possible changes over cycles of data collection. It is noteworthy that BDB appears overall to be the most stable across conditions of heterogeneity and across cycles. In any real data setting, we would advocate a comparison of borrowing methods to ascertain differences in the amount of borrowing over effects of interest.
It is important to point out some limitations of this study as they pertain specifically to application of these methods to LSAs. First, we did not account for the psychometric methods used to obtain achievement scores—particularly the implementation of plausible value methodology (Mislevy, 1991; Mislevy, Beaton, Kaplan, & Sheehan, 1992; von Davier, 2013). It would be necessary to extend BDB to handle plausible values, and one approach advocated by Zhou and Reiter (2010) for Bayesian inference with multiply imputed data would be to combine draws from the posterior distributions from each completed data set and use the combined draws to summarize the posterior distribution. With respect to Bayesian historical borrowing, the draws from the analysis of each plausible value would be combined and summarized. It is also the case that the approach by Zhou and Reiter (2010) could, in principle, be used to handle missing data across cycles of the assessments used for borrowing. Admittedly, this approach to handling plausible values and/or missing data would add additional computational intensity and we leave this topic for future research.
Second, we did not account for the sampling weights which are a feature of large-scale assessments. The problem of sample weighting in Bayesian models generally has been discussed in Gelman (2007), who declared at the time “Survey weighting is a mess” (pg. 153). Since then, and with the advent of Stan (Stan Development Team, 2020), it is possible to incorporate weights directly into the calculation of the likelihood. Another approach advocated by Gelman (2007) would be multilevel regression with post-stratification (Gelman & Thomas, 1997). Both approaches would require considerable future research on how to properly choose weights or post-stratification adjustment cells from historical data on which to adjust parameter estimates, and is beyond the scope of this paper.
Third, we recognize that as with any other case study and simulation study, the results are not generalizable to all possible situations that investigators may encounter. Nevertheless, our study can serve as a framework for examining the sensitivity of results to different choices of borrowing methods. In particular, should different borrowing methods yield roughly the same findings, then it might serve as evidence that the historical cycles of data are relatively heterogeneous, whereas if the results are noticeably different, this might suggest a greater degree of borrowing from homogeneous data sets and with BDB perhaps yielding more accurate results, particularly when the focus is cross-validation. We would encourage such sensitivity analyses in practice.
Finally, though not a limitation per se, the methods that we described in this paper are computationally intensive, even in a high-throughput/high-speed computing environment that utilizes state-of-the-art MCMC algorithms. The computing time committed to Bayesian dynamic borrowing is, of course, a function of the number of historical cycles of data, the sample size, and the dimensionality of the parameter space.
Other Applications of BDB
Bayesian dynamic borrowing can be applied to other data collection and analysis plans beyond those described in this paper. In addition to clinical trial situations from which these methods originally derived, Bayesian dynamic borrowing can be applied to any situation in which one wishes to utilize comparable historical data. For example, the Early Childhood Longitudinal Study (NCES, 2018) was conducted twice, once with a cohort of kindergarten children in 1998 and then again with a cohort of kindergarten children in 2011. Investigators interested in growth and development in the academic and non-academic outcomes among the 2011 cohort can utilize information from the 1998 cohort via BDB.
We noted earlier that BDB, and other borrowing methods, have focused on applications to clinical trials and that Viele et al. (2014) alluded to extending BDB to the situation of multiple covariates. Although the focus of attention in this paper was to large-scale educational assessments, it is clear that BDB could be applied to clustered randomized designs where, in non-experimental settings, covariates would be required to aid in achieving balance between treatment and control groups.
To conclude, our results show that Bayesian dynamic borrowing is a prudent choice for combining information across studies, particularly when the degree of heterogeneity is either unknown or known to be extreme relative to the current data. Having demonstrated the utility of Bayesian dynamic borrowing for single and multilevel models, it will be important to examine the applicability of our method to larger classes of statistical models.
Supplementary Information
Below is the link to the electronic supplementary material.
Acknowledgements
The research reported in this paper was supported by the Institute of Education Sciences, US Department of Education, through Grant R305D190053 to The University of Wisconsin – Madison. The opinions expressed are those of the authors and do not represent the views of the Institute or the US Department of Education. The authors are grateful to Merve Sarac for valuable research assistance. This research was performed using the computing resources and assistance of the UW-Madison Center For High Throughput Computing (CHTC) in the Department of Computer Sciences. The CHTC is supported by UW-Madison, the Advanced Computing Initiative, the Wisconsin Alumni Research Foundation, the Wisconsin Institutes for Discovery, and the National Science Foundation, and is an active member of the Open Science Grid, which is supported by the National Science Foundation and the US Department of Energy’s Office of Science.
Footnotes
The use of the term data fusion by Du et al. (2020) should not be confused with the use of the term by Rässler (2002) or Rubin (1986) which focuses on the creation of synthetic data sets using a variety of different matching algorithms.
The size of the school is obtained in PISA by the derived variable SCHSIZE which is based on the enrollment data provided by the school principal, summing the number of girls and boys in a school. This variable is available in all cycles of PISA.
We recognize that it would be optimal to use all multiply imputed data sets, but extending Bayesian historical borrowing to multiply imputed data sets is beyond the scope of this paper.
Intermediate values of the inverse-gamma priors were also examined and the full set of results are provided in the supplementary material.
Note that we utilized the Wishart prior for the level-2 precision matrix in both the case studies and the simulation studies as it demonstrated better convergence properties. We then scaled the results back to a covariance matrix.
The LKJ correlation prior is suitable as a prior distribution for correlation matrices. Its density satisfies , so leads to a uniform prior over all possible correlation matrices while leads to a prior that places more mass near the identity matrix (Lewandowski et al., 2009).
Specifically, Pareto-smoothed importance sampling LOO (PSIS-LOO) is implemented in the loo software to account for the known instability in the loo weights (Vehtari et al., 2017)
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Bainter SA, Curran PJ. Advantages of Integrative Data Analysis for Developmental Research. Journal of Cognition and Development. 2015;16(1):1–10. doi: 10.1080/15248372.2013.871721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen MH, Ibrahim JG, Shao Q-M. Power prior distributions for generalized linear models. Journal of Statistical Planning and Inference. 2000;84:121–137. doi: 10.1016/S0378-3758(99)00140-8. [DOI] [Google Scholar]
- Curran PJ, Hussong AM. Integrative data analysis: The simultaneous analysis of multiple data sets. Psychological Methods. 2009;14:81–100. doi: 10.1037/a0015914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawid AP. The well-calibrated Bayesian. Journal of the American Statistical Association. 1982;77:605–610. doi: 10.1080/01621459.1982.10477856. [DOI] [Google Scholar]
- Du H, Bradbury TN, Lavner JA, Meltzer AL, McNulty JK, Neff LA, Karney BR. A comparison of Bayesian synthesis approaches for studies comparing two means: A tutorial. Research Synthesis Methods. 2020;11:36–65. doi: 10.1002/jrsm.1365. [DOI] [PubMed] [Google Scholar]
- Enders CK, Keller BT, Levy R. A fully conditional specification approach to multilevel imputation of categorical and continuous variables. Psychological Methods. 2018;23(2):298–317. doi: 10.1037/met0000148. [DOI] [PubMed] [Google Scholar]
- Gelman A. Prior distributions for variance parameters in hierarchical models. Bayesian Analysis. 2006;1:515–533. doi: 10.1214/06-BA117A. [DOI] [Google Scholar]
- Gelman A. Struggles with Survey Weighting and Regression Modeling. Statistical Science. 2007;22(2):153–164. [Google Scholar]
- Gelman A, Carlin JB, Stern DB, Dunson HS, Vehtari A, Rubin DB. Bayesian Data Analysis. 3. London, UK: Chapman & Hall; 2014. [Google Scholar]
- Gelman A, Hill J. Data analysis using regression and multilevel/hierarchical models. Cambridge: Cambridge University Press; 2007. [Google Scholar]
- Gelman A, Thomas L. Poststratification into many categories using hierarchical logistic regression. Survey Methodology. 1997;23:127–135. [Google Scholar]
- Hobbs BP, Carlin BP, Mandrekar SJ, Sargent DJ. Hierarchical commensurate and power prior models for adaptive incorporation of historical information in clinical trials. Biometrics. 2011;67:1047–1056. doi: 10.1111/j.1541-0420.2011.01564.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hobbs BP, Carlin BP, Sargent DJ. Commensurate priors for incorporating historical information in clinical trials using general and generalized linear models. Bayesian Analysis. 2012;7(2):1–36. doi: 10.1214/12-BA722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ibrahim JG, Chen MH. Power prior distributions for regression models. Statistical Science. 2000;15:46–60. [Google Scholar]
- Ibrahim JG, Chen MH, Gwon Y, Chen F. The power prior: theory and applications. Statistics in Medicine. 2015;34:3724–3749. doi: 10.1002/sim.6728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackman S. Bayesian analysis for the social sciences. New York: John Wiley & Sons; 2009. [Google Scholar]
- Kaplan D. Bayesian statistics for the social sciences. New York: Guilford Press; 2014. [Google Scholar]
- Kaplan, D. (2016). Causal inference with large-scale assessments in education from a Bayesian perspective: A review and synthesis. Large-Scale Assessments in Education,4, 10.1186/s40536-016-0022-6 [DOI] [PMC free article] [PubMed]
- Kaplan D, Kuger S. The methodology of PISA: Past, present, and future. In: Kuger S, Klieme E, Jude N, Kaplan D, editors. Assessing contexts of learning world-wide - Extended context assessment frameworks. Dordrecht: Springer; 2016. [Google Scholar]
- Kaplan D, Park S. Analyzing international large-scale assessment data within a Bayesian framework. In: Rutkowski L, Von Davier M, Rutkowski D, editors. A handbook of international large-scale assessment: Background, technical issues, and methods of data analysis. London: Chapman Hall/CRC Press; 2013. [Google Scholar]
- Keller, B. T., & Enders, C. K. (2019). Blimp user’s guide (version 2.1).
- Lewandowski D, Kurowicka D, Joe H. Generating random correlation matrices based on vines and extended onion method. Journal of Multivariate Analysis. 2009;100:1989–2001. doi: 10.1016/j.jmva.2009.04.008. [DOI] [Google Scholar]
- Little RJ. Calibrated Bayes: A Bayes/frequentist roadmap. The American Statistician. 2006;60:213–223. doi: 10.1198/000313006X117837. [DOI] [Google Scholar]
- Little RJ. Calibrated Bayes, for statistics in general, and missing data in particular. Statistical Science. 2011;26:162–174. doi: 10.1214/10-STS318. [DOI] [Google Scholar]
- Liu GF. A dynamic power prior for borrowing historical data in noninferiority trials with binary endpoint. Pharmaceutical Statistics. 2018;17:61–73. doi: 10.1002/pst.1836. [DOI] [PubMed] [Google Scholar]
- Marcoulides, K. M. (2017). A Bayesian synthesis approach to data fusion using augmented data-dependent priors (Unpublished doctoral dissertation). Arizona State University.
- Martin MO, Mullis I, Hooper M. Methods and procedures in TMISS 2015. Chestnut Hill, MA: TIMSS and PIRLS International Study Center, Boston College; 2016. [Google Scholar]
- Mislevy RJ. Randomization-based inference about latent variables from complex samples. Psychometrika. 1991;56:177–196. doi: 10.1007/BF02294457. [DOI] [Google Scholar]
- Mislevy RJ, Beaton AE, Kaplan B, Sheehan KM. Estimating population characteristics from sparse matrix samples of item responses. Journal of Educational Measurement. 1992;29:133–161. doi: 10.1111/j.1745-3984.1992.tb00371.x. [DOI] [Google Scholar]
- Morita S, Thall PF, Müller P. Determining the effective sample size of a parametric prior. Biometrics. 2008;64:595–602. doi: 10.1111/j.1541-0420.2007.00888.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- NCES. (2018). Early Childhood Longitudinal Program (ECLS) - Overview. National Center for Education Statistics, Institute of Education Sciences, U.S. Dept. of Education, Washington, DC. https://nces.ed.gov/ecls/.
- Neuenschwander B, Capkun-Niggli G, Branson M, Spiegelhalter DJ. Summarizing historical information on controls in clinical trials. Clinical Trials. 2010;7(1):5–18. doi: 10.1177/1740774509356002. [DOI] [PubMed] [Google Scholar]
- OECD. (2002). PISA 2000 technical report. Paris: Organization for Economic Cooperation and Development.
- OECD. (2019). PISA 2018 Results: (Volumes I-IV): What students know and can do. 10.1787/5f07c754-en.
- O’Hagan A, Buck CE, Daneshkhah A, Eiser JR, Garthwaite PH, Jenkinson DJ, Rakow T. Uncertain judgements: Eliciting experts’ probabilities. West Sussex, England: Wiley; 2006. [Google Scholar]
- O’Malley J, Normand S, Kuntz R. Sample size calculation for a historically controlled clinical trial with adjustment for covariates. Journal of Biopharmaceutical. 2002;12(2):227–247. doi: 10.1081/BIP-120015745. [DOI] [PubMed] [Google Scholar]
- Pocock SJ. The combination of randomized and historical controls in clincial trials. Journal of Chronic Diseases. 1976;29:175–188. doi: 10.1016/0021-9681(76)90044-8. [DOI] [PubMed] [Google Scholar]
- R Core Team. (2019). R: A language and environment for statistical computing [Computer software manual. Vienna, Austria. https://www.R-project.org/.
- Rässler S. Statistical matching: A frequentist theory, practical applications, and alternative Bayesian approaches. New York: Springer; 2002. [Google Scholar]
- Raudenbush SW, Bryk AS. Hierarchical linear models: Applications and data analysis methods. 2. Thousands Oaks, CA: Sage Publications; 2002. [Google Scholar]
- Rubin DB. Statistical matching using file concatenation with adjusted weights and multiple imputation. Journal of Business and Economic Statistics. 1986;4:87–95. [Google Scholar]
- Rutkowski L, Von Davier M, Rutkowski D. Handbook of international large-scale assessment: Background, technical issues, and methods of data analysis. Boca Raton: Chapman Hall/CRC; 2013. [Google Scholar]
- Schmidli H, Gsteiger S, Roychoudhury S, O’Hagan A, Spiegelhalter D, Neuenschwander B. Robust meta-analytic-predictive priors in clinical trials with historical control information. Biometrics. 2014;70(4):1023–1032. doi: 10.1111/biom.12242. [DOI] [PubMed] [Google Scholar]
- Stan Development Team. (2020). RStan: the R interface to Stan. http://mc-stan.org/. R package version 2.21.2.
- Sung YJ, Schwander K, Arnett DK, Kardia SLR, Rankinen T, Bouchard C, Rao D. An empirical comparison of meta-analysis and mega-analysis of individual participant data for identifying gene-environment interactions. Genetic Epidemiology. 2014;38:369–378. doi: 10.1002/gepi.21800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson L, Chu J, Xu J, Li X, Nair R, Tiwari R. Dynamic borrowing from a single prior data source using the conditional power prior. Journal of Biopharmaceutical Statistics. 2021;31(4):403–424. doi: 10.1080/10543406.2021.1895190. [DOI] [PubMed] [Google Scholar]
- Tierney, J., Vale, C., Riley, R., Smith, C. T., Stewart, L., Clarke, M., & Rovers, M. (2015). Individual participant data (ipd) meta-analyses of randomised controlled trials: Guidance on their use. PLoS Medicine12(7), 10.1371/journal.pmed.1001855. [DOI] [PMC free article] [PubMed]
- US Department of Education. (2019). NAEP: Nations Report Card. https://nces.ed.gov/nationsreportcard/. Accessed Nov. 16, 2019.
- Vehtari, A., Gabry, J., Yao, Y., & Gelman, A. (2019). loo: Efficient leave-one-out cross-validation and WAIC for Bayesian models. https://CRAN.R-project.org/package=loo R package version 2.1.0.
- Vehtari A, Gelman A, Gabry J. Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Statistics and Computing. 2017;27:1413–1432. doi: 10.1007/s11222-016-9696-4. [DOI] [Google Scholar]
- Viele K, Berry S, Neuenschwander B, Amzal B, Chen F, Enas N, Thompson L. Use of historical control data for assessing treatment effects in clinical trials. Pharmaceutical Statistics. 2014;13:41–54. doi: 10.1002/pst.1589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Davier M. Imputing proficiency data under planned missingness in population models. In: Rutkowski L, von Davier M, Rutkowski D, editors. Handbook of international large-scale assessment: Background, technical issues, and methods of data analysis. Boca Raton: Chapman Hall/CRC; 2013. [Google Scholar]
- Zhou X, Reiter JP. A note on Bayesian inference after multiple imputation. The American Statistician. 2010;64:159–163. doi: 10.1198/tast.2010.09109. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.