Frontiers in Multiscale Modeling of Photoreceptor Proteins

Abstract

This perspective article highlights the challenges in the theoretical description of photoreceptor proteins using multiscale modeling, as discussed at the CECAM workshop in Tel Aviv, Israel. The participants have identified grand challenges and discussed the development of new tools to address them. Recent progress in understanding representative proteins such as green fluorescent protein, photoactive yellow protein, phytochrome, and rhodopsin is presented, along with methodological developments.

INTRODUCTION

Photoreceptor proteins are light-sensitive proteins involved in sensing and response to light in a variety of organisms (1). In nature, these proteins fulfill important biological functions, such as regulation of circadian rhythms, phototaxis and light-oriented growth in plants. Photoreceptor proteins absorb light through small organic chromophores embedded within the protein matrix. The chromophore typically absorbs light at a specific wavelength and uses this radiant energy to trigger the protein response, which ultimately leads to completing a biological function. From a biotechnology viewpoint, these proteins represent potential candidates for use as efficient biological light converters. They have already been successfully utilized in a number of technological applications (2,3). For example, the green fluorescent protein and its derivatives are used to visualize spatial and temporal information in cells with molecular-level resolution (4,5) More recently, photoreceptor proteins have been used in the field of optogenetics, which allows light activation of specific cells in living organisms (6). In this context, they have been successfully aiding researchers investigating biological conditions such as depression, Parkinson’s disease, sleep disorders, and schizophrenia. Despite the ground-breaking nature of this utilization in life science and other disciplines, our understanding of photoreceptors’ function at molecular level is still incomplete. These gaps in knowledge, which hinder the development of new technologies, can be filled with the help of computer simulations of photoreceptors using multiscale modeling (7).

Due to the large size of the photoreceptor proteins, the hybrid quantum mechanics/molecular mechanics (QM/MM) embedding has been the main tool used to model them. QM/MM allows one to accurately model the chromophore and surrounding environment while remaining computational feasible (8–11). In this scheme, the protein environment is treated with classical force fields, and the chemically active part of the chromophore and its local environment is treated with more expensive quantum methods. Hence, the first step in using this multiscale approach is to determine how to appropriately partition the QM and MM regions. An additional challenge is to identify an appropriate QM method and force field parameters, if any exist at all. The QM/MM embedding has been widely applied to many families of photoreceptors involving retinal proteins (12), green fluorescent proteins (13,14), photoactive yellow protein (15), phytochromes (16), and flavin binding proteins (17,18) (Fig. 1).

Fig. 1.

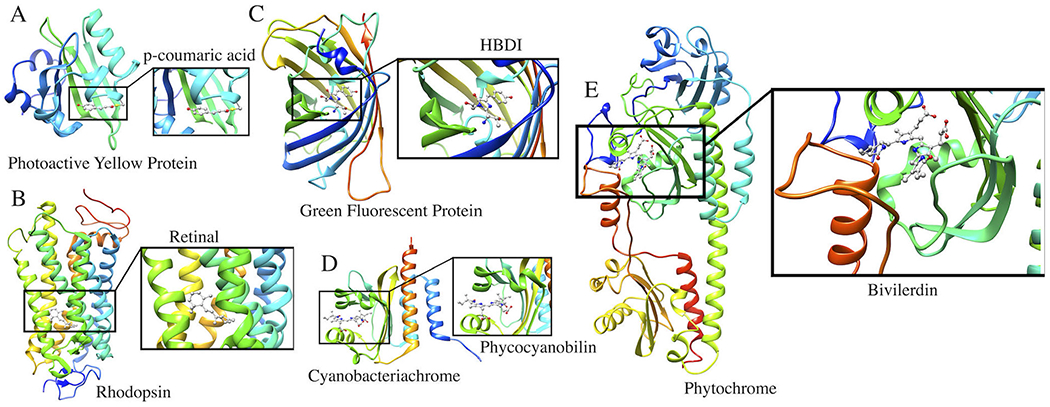
Photoreceptor proteins discussed in this perspective article. (A) Photoactive Yellow Protein with p-coumaric acid as a chromophore; (B) Rhodopsin with a retinal chromophore; (C) Green Fluorescent Protein with a HBDI chromophore; (D) Cyanobacteriochrome with phycocyanobilin as a chromophore; (E) Phytochrome with a Biliverdin chromophore.

Furthermore, the photocycle of typical photoreceptor proteins involves multiple competing processes (19,20) illustrated in Fig. 2. Photoexcitation promotes the chromophore into an electronically excited state characterized by a different electron distribution than in the ground state. Different electron distributions result in different bonding patterns and, consequently, different shapes of the potential energy surfaces (PES). Ensuing excited-state dynamics often entails isomerization, conformational changes, proton and electron transfer, as well as breaking and forming bonds. The relaxation pathways include fluorescence, internal conversion and intersystem crossing. The function of natural and engineered photoactive proteins is determined by the interplay between these processes, which entail coupled electronic and nuclear dynamics. Understanding these quantum processes, which unfold in systems with many degrees of freedom and coupled to the environment, is of great fundamental and practical importance. Thus, a theoretical modeling sufficiently accurate to describe property changes (13,18) is a key tool for deriving mechanistic insights. Theory is instrumental for understanding these fascinating species and for the design of novel motifs for practical applications. However, in order to be useful, the theory should be able to describe multiple interacting electronic states, include the effect of the environment, and be able to provide not only accurate energies, but also nuclear gradients, interstate properties (i.e., non-adiabatic and spin-orbit couplings), as well as other properties relevant for spectroscopy. Furthermore, for a complete description of the photocycle, one needs to be able to execute dynamical simulations including electronic transitions between multiple states. The main challenge here lies in the electronic structure theory and software: despite tremendous progress (20), much more needs to be done in terms of devising more robust and more versatile electronic structure models for excited states and implementing them in efficient and practical software (21).

Fig. 2.

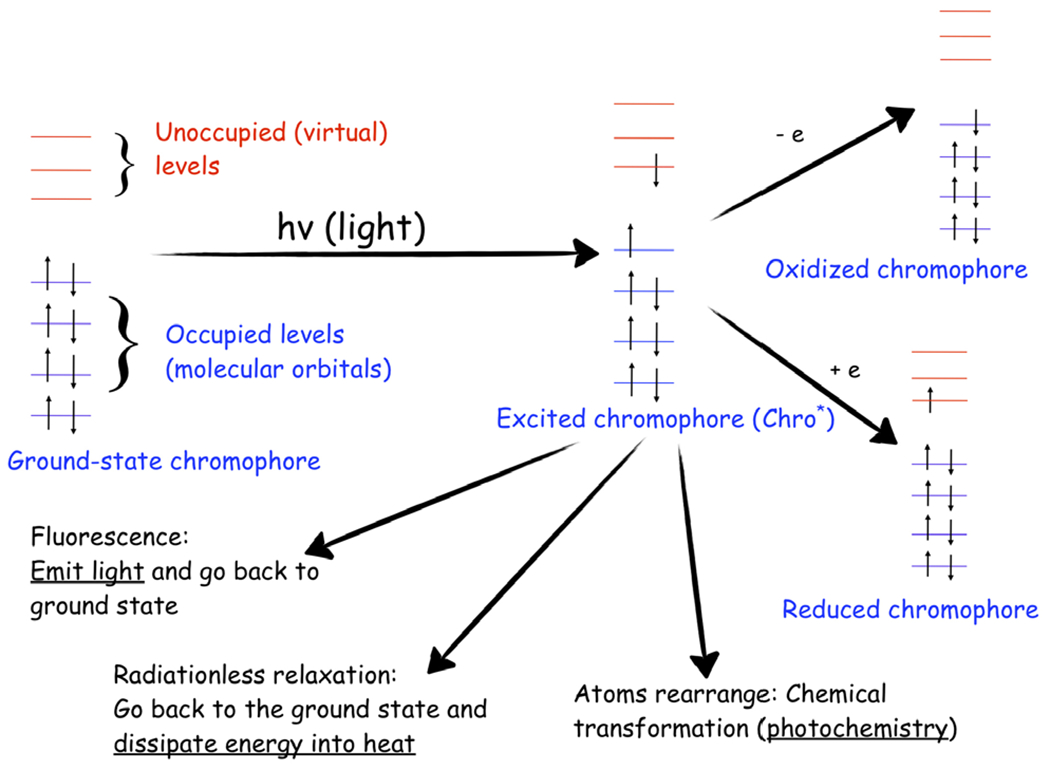
Excited-state processes in photoreceptor proteins. The photocycle of a chromophore, an acting core of a photoreceptor, involves various competing processes: fluorescence, radiationless relaxation, intersystem crossing (not shown), excited-state chemical transformations, and electron transfer. Reproduced with permission from Ref. (19).

In September 2019, leading experts in the field of computational modeling of photoreceptor proteins met for a Centre of Europeen de Calcul Atomique et Moleculaire (CECAM) meeting which took place in Tel Aviv (Israel). During this CECAM workshop titled “Frontiers in Multiscale Modelling of Photoreceptors,” the participants identified the challenges currently facing the field and discussed the development of new tools to address them. Many specific points were examined in detail including how to determine the correct protonation states of the chromophore within the protein, the effects of electronic polarization on the chromophore and resulting absorption spectra, QM/MM protocols for partitioning systems and sampling, and the computational software used in these types of simulations. In the following, we present several contributions that were presented at the CECAM workshop Tel Aviv. The contributions are organized in three categories: (1) challenges in modeling of photoactive proteins, (2) application of multiscale methods to photoactive proteins, and (3) methodological development and software updates.

CHALLENGES IN MODELING OF PHOTOACTIVE PROTEINS

Lessons from recent computational studies of GFP

To illustrate some of the persisting challenges in modeling of photoactive proteins, we consider a recent study (22) on the influence of the first chromophore-forming residue (in position 65) on brightness, photobleaching and oxidative photoconversion of fluorescent proteins from the GFP family. The goal of modeling was to explain stark differences in brightness and photostability of EGFP, EYFP, and their mutants with reciprocally substituted chromophore residues, EGFP-T65G and EYFP-G65T. The key quantities responsible for fluorescent quantum yield, extinction coefficients and bleaching yield are the rates of radiationless and radiative relaxation of the photoexcited proteins. Their first-principle modeling would have required quantum-dynamical simulations of the photoexcited proteins using on-the-fly generated ab initio PESs and couplings computed using high level of theory (e.g., equation-of-motion coupled cluster methods (23,24)), which is currently impractical. Instead, the authors (22) carried out classical molecular dynamics simulations on the ground and electronically excited states. To study excited-state state dynamics, the force field parameters of the chromophores were modified to fit the results of electronic structure calculations, most importantly, the change in the torsional potential along the phenolate twist (see Fig. 3) and the changes in partial charges.

Fig. 3.

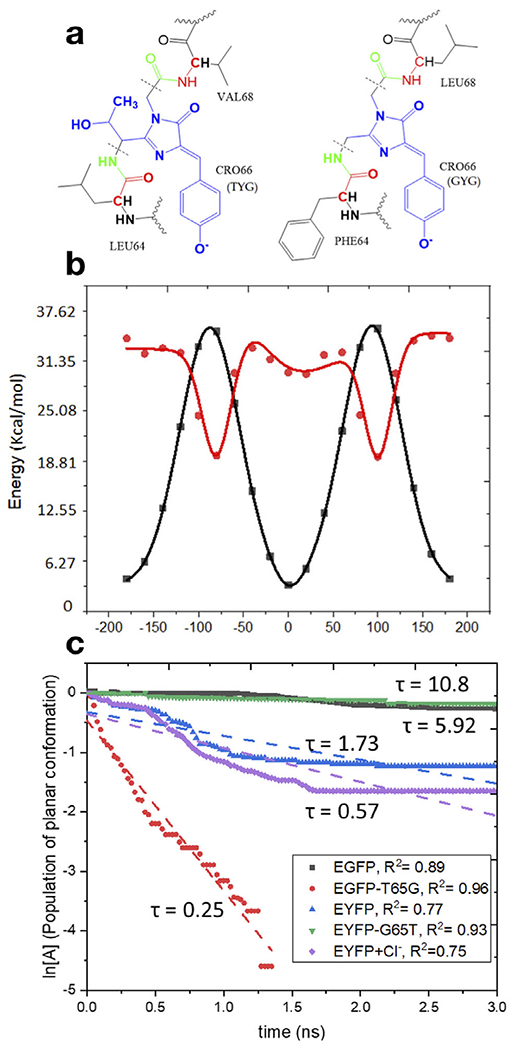
Top: Structures of the model proteins with the TYG (EGFP, YFP-G65T) (left) and GYG (YFP, EGFP-T65G) (right) chromophores and the definition of the QM/MM partitioning (the QM part is shown in blue and the MM part in black). The key difference between the TYG and GYG chromophores is the -C(OH)CH₃ tail in the latter. Bottom left: Potential energy along torsional angle φ (phenolate flip) in the ground and excited states. Bottom right: First-order kinetics of the chromophore’s twisting in the excited state in four model proteins. Reproduced with permission from Ref. (22).

The rate of twisting along torsional coordinate φ was used as a proxy for the rate of radiationless relaxation. To evaluate brightness and the rate of radiative relaxation, the authors computed excitation energies and oscillator strengths by the QM/MM protocol with high-level electronic structure (25) using the snapshots from the molecular dynamics trajectories. Despite the simplicity of this approach, the calculations were able to pinpoint the role of residue 65 on the photochemical properties of the proteins. The absence of the -C(OH)CH₃ tail in the GYG chromophore affects hydrogen bond pattern and results in an increased flexibility, which facilitates radiationless relaxation leading to the reduced fluorescence quantum yield in the T65G mutant. The computed lifetimes (see Fig. 3) were in a reasonable agreement with experiment. Although not conjugated with the π-system of the chromophore, the -C(OH)CH₃ tail also affects its electronic properties. The GYG chromophore also has larger oscillator strength as compared to TYG, which leads to a shorter radiative lifetime (i.e., a faster rate of fluorescence). The faster fluorescence rate partially compensates for the loss of quantum efficiency due to radiationless relaxation. The shorter excited-state lifetime of the GYG chromophore is responsible for its increased photostability. One important aspect left out in this study (22) was the effect of mutation 65 on the rate of photoexcited electron transfer, one of the main bleaching channels (19,26). To evaluate the rates of electron transfer, one needs to compute Gibbs free energies and couplings, which requires extensive sampling using QM/MM PESs of reduced and oxidized forms (as was done, for example, in Ref. (26)). Presently, such calculations are rather labor-intensive and also computationally expensive, which precludes their large-scale applications. This study (22) illustrates the need for devising faster electronic structure codes for excited-state treatments and more robust and automated protocols for QM/MM simulations.

Challenges in modeling bioluminescent systems

Other systems that are related to photoreceptor proteins are the bioluminescent systems. The most studied bioluminescent system is the one responsible for the light emission in fireflies. The emitting light in fireflies arises from the electronic relaxation of oxyluciferin, an organic compound produced by the oxidation of the D-luciferin substrate inside an enzyme called luciferase. As the fireflies’ bioluminescent system is already used as a marker in biology (27), one needs to understand what are the key chemical and physical factors responsible for the emitted light color. To gain insight into the mechanism of the light emission, joint experimental and theoretical studies have been performed.

Theoretical studies of such systems require the use of QM/MM methods. Taking into account the surrounding protein at the MM level is essential for understanding the influence of the enzyme on the color modulation.

The increase in computational capability of modern computers has enabled studies of larger systems, such as the firefly oxyluciferin, which is also surrounded by thousands of atoms from protein and/or solvent. The first QM/MM study of this system, published in 2010 (28), has showed that the protein surrounding modulates the color of the emitter. This first study was based on second-order multi-configurational perturbation theory enabled by the interface between two programs: MOLCAS (29), for the QM calculation describing the emitter molecule, and TINKER (30), for the MM part describing the protein and solvent environment by an additive QM/MM scheme with Electrostatic Potential Fitted (ESPF) (31) method. The calculations revealed that hydrogen-bonding network in the cavity was very important and explained how a single mutation of one residue, even far from the light emitter, could dramatically change the hydrogen bond network and, therefore, the color of the light emission. This study (and a later work (32)) demonstrated that increasing the number of hydrogen bonds involving the phenolate oxygen of the benzothiazole moiety induces a blue shift of the emitted light, whereas increasing the number of hydrogen bonds around the other side of the molecule induces a red shift. This finding can easily be rationalized by looking at molecular orbitals involved in the electronic transition responsible for the emission: the transition has a HOMO-LUMO character and results in a negative charge transfer from the thiazolone moiety to the benzothiazole moiety. Hydrogen bonding stabilizing the HOMO does not stabilize the LUMO and increases the HOMO-LUMO gap, leading to a blue shift (Fig. 4).

Fig. 4.

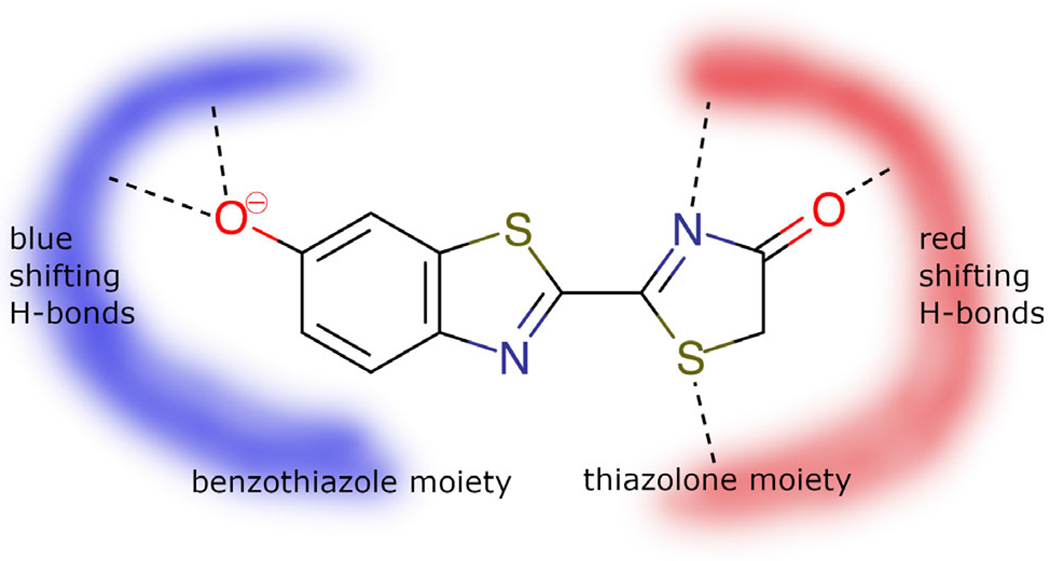
Oxyluciferin and the hydrogen-bonding networks responsible for blue- or red-shifted emission.

These studies of color modulation by protein surrounding give hope to the computational community, opening a door for fruitful collaboration with experimentalists. Computation of the light emission of modified emitters and the analysis of factors responsible for the color are also very promising (33,34). Theoretical studies impart complementary insights into the experimental findings, advancing our understanding of such complex phenomena. Yet, all computational studies carried out in the last decade also point out to the persistent challenges. For instance, the calculations are contingent on the availability of crystallographic structures of the protein. Only few structures have the ligands inside the cavity. Some have missing loops that can be important for the correct description of the protein environment (32). Models are constructed based on hypotheses. This is the case for all systems involving excited states in proteins. The discussion at the CECAM meeting in Tel Aviv high-lighted the need for robust protocols for comparing theoretical and experimental results.

Protonation states and the nature of the emitter are additional challenges shared among photoreceptor proteins. The nature of the emitter depends on the pH and the “local” pH inside the cavity is not an experimentally measurable. Joint experimental and computational studies of solvated emitters and of analogous systems in which the key reactions like the keto-enol tautomerization of the thiazolone moiety or the deprotonation of the phenolate group are blocked show that the experimental observations can be reproduced by protocols, which take into account dynamics of the protein, and that the use of analogues helps to better understand the nature of the light emitter (35-37). Nevertheless, accounting for fluctuating protonation states of the protein residues still needs to be improved.

APPLICATION OF MULTISCALE METHODS TO PHOTOACTIVE PROTEINS

Hybrid QM/MM simulations have been instrumental for gaining molecular level insights into the mechanism of light energy conversion and subsequent reactions. These simulations can be used to elucidate reaction pathways directly or in tandem with complementary spectroscopic studies. Often, these studies go hand in hand with new methodological developments and aid the derivation of new unifying concepts, advancing our understanding of these light-triggered proteins. In the following, we present state-of-the-art studies on four different photoreceptor proteins: photoactive yellow protein (PYP), the Green Fluorescent Protein (GFP), Phytochrome, and Rhodopsin.

Resonance interactions of ionic chromophores play a key role in biological photoreception

The charge of the protein-bound chromophores depends on their protonation state, which can be controlled by pH and structural modifications of the protein. Electronic properties of ionic (i.e., charged) chromophores are efficiently modulated by interactions with the protein. Such tuning is typically linked to the charge transfer, occurring in the chromophore upon photoexcitation, and electrostatic interactions with the protein (38-42). In the S₀ state, the charge is typically localized on the protonated (or deprotonated) moiety of the chromophore whereas in the excited state, the charge is often translocated to the opposite end of the conjugated π-system, leading to a considerable charge transfer character of the S₀-S₁ transition. The electrostatic environment of the protein interacts with these two different charge distributions and thus modulates the S₀-S₁ energy gap. Moreover, charge separation at highly twisted geometries enables electrostatic control of the energies of conical intersections (CoIns) and saddle points mediating photochemical or thermal isomerization (42,43). Although the protein–chromophore interactions are not limited to electrostatic effects (44-46), treating the protein and solvent as a collection of point charges remains a popular approach which, in practice, is often capable of reproducing experimentally observed protein effects quatitatively (47–49).

In the photoactive yellow protein (PYP) photoreceptor, the anionic p-coumaric-acid thioester (pCT⁻) chromophore is profoundly affected by hydrogen bonding (50) and electrostatic interactions (43). In the native protein environment, pCT⁻ photoisomerizes around its central double bond (DB) (51,52). In addition, computational studies suggested that pCT⁻ may undergo rotation around its central single bond (SB) (43). Properties of the pCT⁻ chromophore are rationalized by invoking chemical resonance (13,50) in addition to considering the S₀-S₁ charge transfer. Four resonance forms with the negative charge either on the phenolic or carbonyl groups (Fig. 5) are stabilized depending on the charge localization by hydrogen bonds that pCT⁻ forms with the protein (53). Naturally, the contributions of the resonance structures depend on the difference in their energies (54). The extent of the resonance structure mixing in the S₀ wave function is reflected by the difference in the length of the SB and DB at the S₀ optimized geometry (the bond length alternation, BLA). The larger the energy difference, the larger the BLA and vice versa. Accordingly, the pCT⁻ chromophore tuned by the interactions with water molecules shows an increased BLA when hydrogen bonds are formed with the phenolic group and a decreased BLA when a hydrogen bond is formed with the carbonyl group (53). The extent of the resonance mixing determines the S₀-S₁ excitation energy and amount of charge transfer, as demonstrated by the linear correlation plots of these properties (Fig. 6).

Fig. 5.

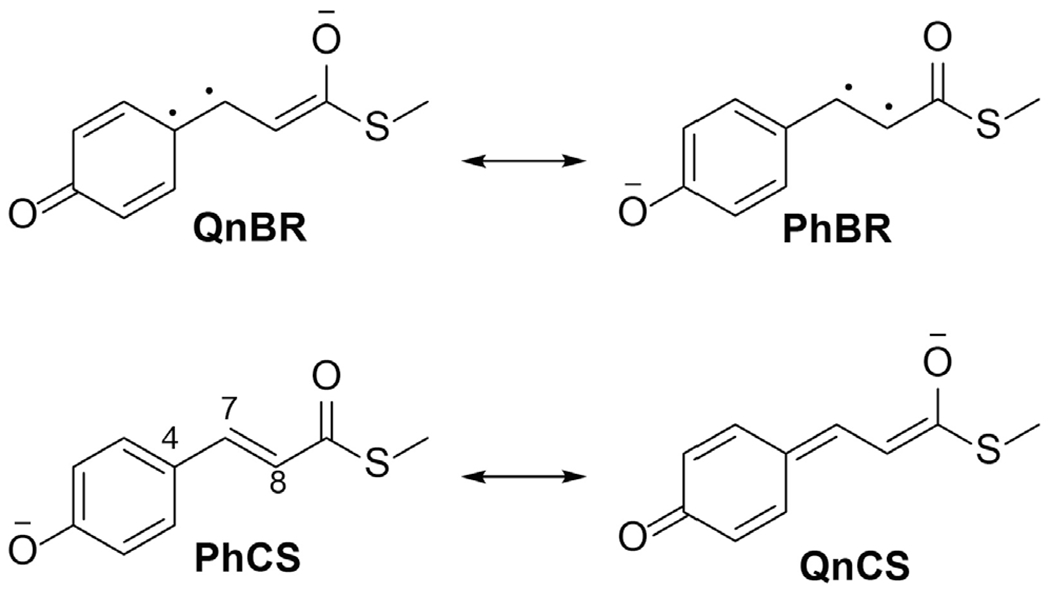
Resonance structures explaining the interdependent properties of the anionic pCT- chromophore of PYP derived in Ref. (53). C4-C7 and C7=C8 are the central single bond (SB) and double bond (DB), respectively.

Fig. 6.

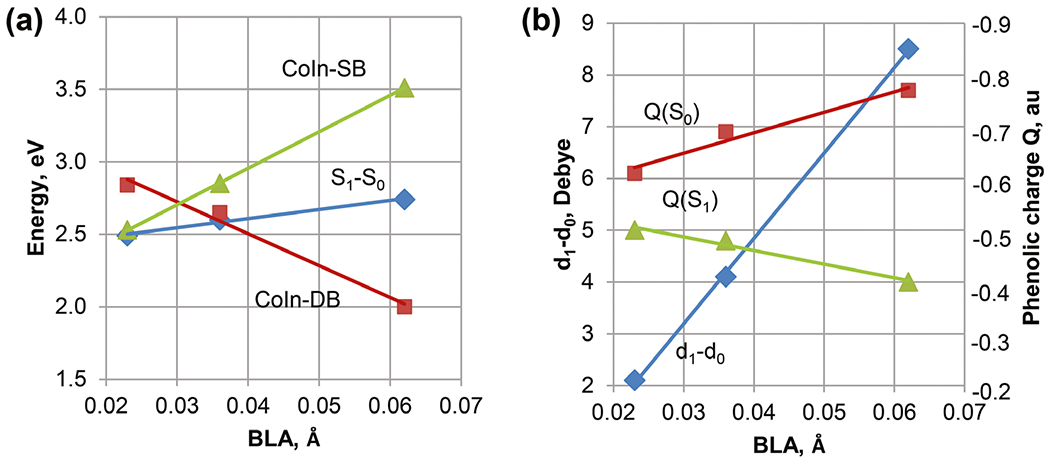
The linear correlation plots summarize the XMCQDPT2/cc-pVDZ results for the pCT- chromophore interacting with water molecules (53). Panels a and b show correlations for the energies and charge transfer, respectively. The bond length alternation (BLA) value corresponds to the difference in the length of the C4-C7 and C7=C8 bonds at the geometries fully optimized in the S₀ state.

Twisting around a central bond increases contributions of the resonance forms with the twisted bond being a single bond (in the S₀ state) and localizing diradicaloid (in the S₁ state), which also determines the localization of the molecular charge. At the geometry 90° twisted around the SB, the negative charge is localized on the carbonyl fragment in the S₁ state and on the phenolate fragment in the S₀ state. In contrast, the DB twist increases the negative charge on the phenolate in the S₁ state and on the carbonyl in the S₀ state (43,50,53). This opposite charge localization in the S₀ and S₁ states enables efficient stabilization of the SB-twisted and DB-twisted CoIns by the carbonyl and phenolic hydrogen bonds, respectively (43). Notably, the energies of the SB and DB CoIns show linear correlations with the BLA (Fig. 6a); the signs of the energy correlations are determined by the charge localization and charge transfer (Fig. 6b).

As suggested by the linear correlations, any property presented in Fig. 6 can be regarded as a descriptor (46) characterizing tuning of the pCT⁻ chromophore by interactions with its environment in the protein or solvent. The increased mixing of the resonance structures reduces the BLA and charge transfer character, shifts the absorption maximum to the red and activates the SB twist in the S₁ state. In contrast, the reduced mixing of the resonance structures increases the BLA and charge transfer character, blue shifts the absorption maximum and favors DB isomerization. In accord with these dependences derived from computational studies, recently published theoretical analysis of systematically tuned GFP variants (54) has suggested employing the difference in the energies of the resonance forms as a linear scale for analyzing and predicting optical properties. Among the chromophore properties obtained computationally, the BLA is a convenient descriptor, because it is derived from the S₀ state geometry optimization. In fact, models examining electrostatic tuning of biological chromophores by their protein environment highlight correlations among properties (42), and, in particular, the correlation between the BLA and excitation energy (38-40,55,56). The correlations of photochemical properties strongly suggest that the theory of resonance is generally applicable to rationalizing the tuning mechanism of photoreceptor proteins.

Modeling photochemical reactions

Studies of chemical reactions occurring with chromophores or molecular groups in chromophore-containing pockets in the ground and excited electronic states constitute an important field of the photoreceptor protein research. Application of methods of multiscale modeling is an essential step in computational simulations of these reactions.

To illustrate the approaches, we consider the reaction of the recovery of the fluorescence state of the reversibly photoswitchable protein Dreiklang (57). The unique properties of this protein from the GFP family are due to a reversible hydration/dehydration reaction at the imidazolinone ring of the chromophore. Recovery of the fluorescent state, which is associated with a chemical reaction of chromophore dehydration, is an important part of the photocycle of this protein.

In Fig. 7, a model system composed of the protein surrounded by solvent water molecules is shown in the left panel. The dark balls specify the atoms of the hydrated chromophore, and the side chains of the critical amino acid residues Arg96 and Glu222. The corresponding molecular groups are assigned to the quantum subsystem (QM part) shown in the right panel in the figure. The remaining molecular groups are included to the molecular mechanics (MM) subsystem.

Fig. 7.

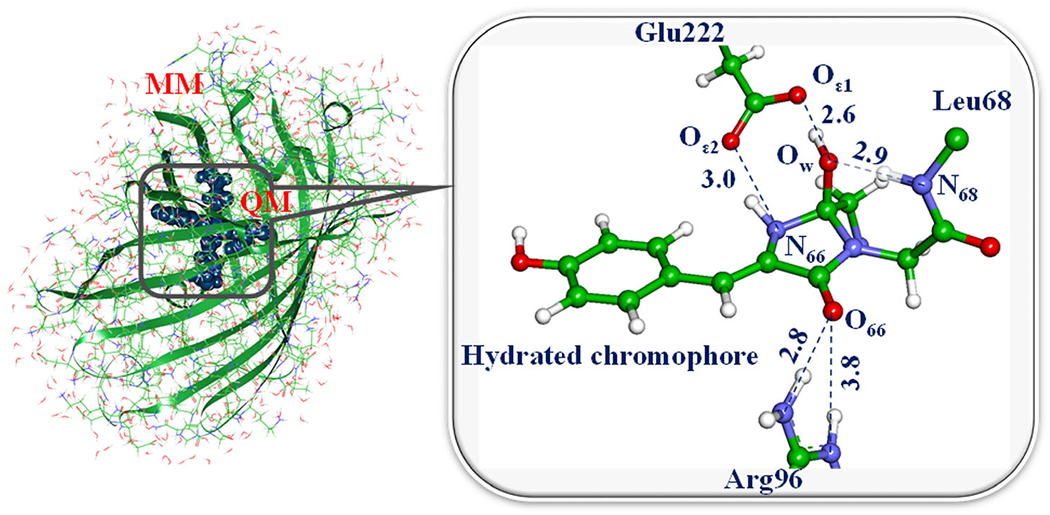
Left: a model system for simulations of the recovery reaction of the fluorescent state in Dreiklang. Right: a part of the system selected for QM/MM calculations of the reaction energy profile.

In QM/MM calculations, energies and forces in the QM part are computed using conventional quantum chemistry methods, while the MM subsystem is described by force field parameters. Usually, the electrostatic embedding scheme is applied to relate the QM and MM parts, assuming contributions of the partial charges from all MM atoms to the one-electron QM Hamiltonian.

The first step of the dehydration reaction in Dreiklang is a proton transfer from the nitrogen atom N₆₈ to the oxygen atom O_W, leading to the cleavage of the bond between the hydroxyl and the imidazolinone ring and formation of the water molecule. To compute the energy profile for this step, a series of QM/MM constrained minimizations along the assumed reaction coordinate (here, the N₆₈–H distance) should be carried out. When the saddle point on the energy surface is located using the conventional transition-state search, calculations of harmonic vibrational frequencies should confirm that single imaginary frequency (here, 810i cm⁻¹) characterizes the obtained structure. The computed energy difference between the levels of the reactant and the transition state allows one to estimate the activation energy (here, about 25 kcal mol⁻¹), which is consistent with the measured rate constant of the reaction of thermal recovery of the fluorescent state in Dreiklang.

In a similar fashion, a full cycle of chemical transformations in the chromophore maturation in the wild-type GFP (58) as well as reactions of the photo-induced decomposition of the GFP chromophore upon photobleaching of the protein is considered (59). Also, we can describe the competing reactions of covalent binding of the biliverdin chromophore to cysteine residues in the bacterial phytochrome domains upon assembly a prospective variant of the near-infrared fluorescent protein miRFP670 (60).

The primary goal of all these simulations is to establish mechanisms of chemical transformations in the chromophore-containing pockets.

pKa calculations of phytochromes with Poisson–Boltzmann electrostatics

The accurate determination of pKa values of amino acid residues buried in a protein environment remains a challenging task (61). Burying titratable moieties in proteins usually leads to an increase of the pKa value of acidic groups and the decrease of the pKa value of basic groups, as compared to the respective values in aqueous solution. However, depending on the concrete microscopic description of the protein environment, unusual titration may occur as a result of specific charge–charge interactions which can shift the pKa values of titratable groups in any direction (62). This effect is often significant at active sites, where perturbed pKa values of specific groups are of biological relevance (63).

Specifically, photoactivation of photoreceptor proteins is often coupled with protonation changes of the chromophore and/or key residues of the protein matrix (64-67). These protonation changes, in turn, facilitate proton transfer reactions involved in signal transduction and functional activation (68). Thus, the precise determination of the protonation states of chromophores and titratable amino acids in their vicinity constitutes a major step in computational modeling of photoreceptors proteins.

Various approaches for computing pKa values in proteins have been developed over the past six decades starting from the pioneering work of Tanford and Kirkwood (69). Since pKa shifts originate from electrostatics, much of the effort has been directed toward the accurate description of electrostatic interactions using either microscopic or macroscopic models, or even a combination of both (61). For example, approaches based on the combination of electrostatic energy computations based on the solution of the Poisson–Boltzmann equation (PBE) with classical molecular dynamics (MD) simulations have been used in different proteins for predicting pKa values (70). This hybrid approach enables taking into account protein flexibility, hydrogen bond network rearrangements, side-chain reorientations, and water molecules inside protein cavities.

To illustrate this methodology, here we focus on the photoactivation process of the Agp2 phytochrome structure. This process is initiated by a double-bond isomerization of the biliverdin (BV) chromophore, which is covalently bound to the protein matrix, thereby triggering conformational changes and proton transfer reactions between the protein and the cofactor. Importantly, the BV molecule contains six titratable sites, two propionic side chains (pscB and pscC) and four pyrrole rings (A, B, C and D) (see Fig. 8b) Furthermore, two conserved histidine residues are in direct contact with the tetrapyrrole chromophore. Interestingly, spectroscopic data indicate that the propionic side chain at ring C (pscC) of the BV molecule of the Agp2 phytochrome is protonated in the Pfr and Meta-F states and remains protonated even up to pH of 11 (71). Proton release is observed to take place at the step from Meta-F to Pr state, when the photoreceptor becomes activated (72). Recently, it has been demonstrated that the pscC deprotonation of BV chromophore is essential for triggering a secondary structure change (73). In the case of prototypical phytochromes, it has been spectroscopically observed that one of the inner pyrrole rings transiently loses a proton during the transition from Meta-R to Pfr states (67,74). These experimental results highlight the importance of considering the bilin chromophore as a titratable site for computational modeling.

Fig. 8.

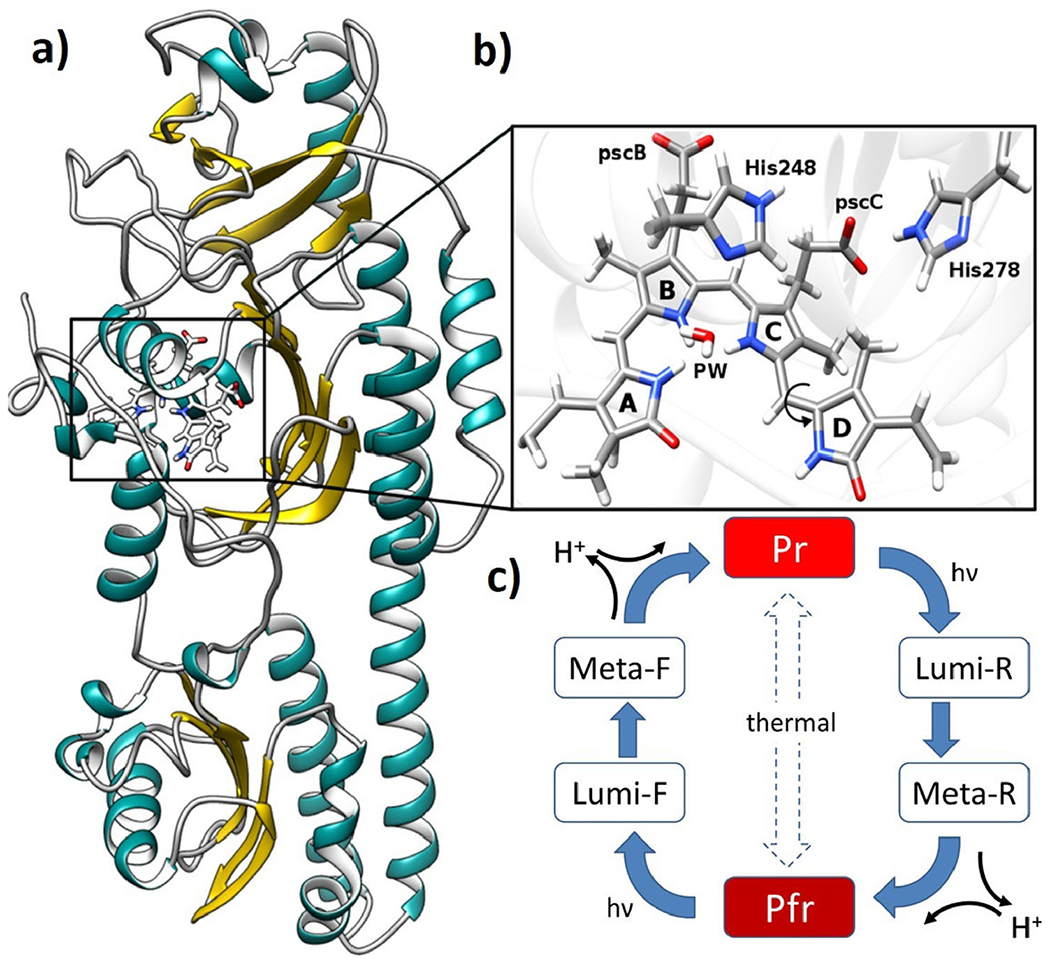
a) crystal structure of Agp2 phytochrome in Pfr state, b) BV chromophore, pyrrole water (PW) and histidines located in the chromophore binding pocket. c) generic phytochrome photocycle with the red light-absorbing parent state (Pr) and far-red light-absorbing parent state (Pfr).

Since pKa calculations rely upon an accurate description of protein’s electrostatic field, the derivation of atomic partial charges is an essential step in modeling (75). This is true, in particular, for many prosthetic groups such as bilin molecules, which were not included in the standard parametrization protocols of classical protein force fields like CHARMM (76), AMBER (77), or GROMOS (78). Such atomic partial charges can be generated from the electrostatic potential of the molecule computed using quantum chemical approaches and employing the two-stage restrained electrostatic potential (RESP) method (79).

Predicted pKa values of proteins are highly sensitive to the atomic arrangement of the input structure (80). This fact may have serious consequences when trying to gain mechanistic insights out of these calculations, since the crystal structure represents the protein arrangement at the pH in which it was crystallized and not necessarily the active conformation. In the case of Agp2 phytochrome, the pH at which the protein was crystallized was estimated to lie between 5.5 and 9 (81). Since variations in pH can alter the protonation states of titratable groups including the bilin chromophore, slight conformational changes, such as propionic side-chain reorientations (pscB and pscC) or rearrangements in the hydrogen bond network can be expected in the crystalline state. These minor structural distortions may significantly affect the computed pKa values.

In order to sample a wider conformational space and, thereby, account for protein flexibility, Monte Carlo (MC) or MD simulations are carried out considering different discrete protonation patterns. (82) These approaches have been applied successfully on different proteins even using very short MD simulations (20 ns). (70) For example, the pKa calculation of the pscC of Agp2 in the Pfr state requires at least three MD trajectories: one trajectory with deprotonated pscC and two trajectories with singly protonated pscC. On each 20 ns long trajectory, time frames are extracted every 100 ps and used as input for electrostatic energy computations performed by solving the linearized Poisson–Boltzmann equation using the BV atomic partial charges derived in the previous step. An equilibrium pKa value of the pscC can be then obtained by averaging the results of electrostatic energy computations for each of the three MD simulations weighted by their respective Boltzmann factor. (38) The pKa values of the pscC in the Pfr state obtained with this methodology are predicted within the range between 4.5 and 9.6 units, which is in perfect agreement with experimental spectroscopic data suggesting a protonation of the of the carboxylic group. Furthermore, Meyer et al. (38) showed that the root mean square deviations (RMSD) between measured and computed pKa values of 194 titratable residues in 13 proteins can be improved from 0.96 to 0.79 (in pH units) if energy minimizations with weaker electrostatic interactions (ϵ = 4) of the structures extracted from MD simulations are preformed prior to electrostatic calculations.

In a similar fashion, this methodology can be applied to determine the protonation state of histidine residues located in the chromophore binding pocket. His248 and His278 (Fig. 8b) are highly conserved residues that are involved in the proton transfer events in the chromophore binding pocket. There have been some efforts to determine precisely protonation states of both histidines. Velazquez et al. (83) identified one of these histidines as the key residue controlling pH-dependent equilibria in the Cph1 phytochrome, suggesting a pKa below 6.0. Additionally, Takiden et al. (84) performed electrostatic energy calculations in combination with MD simulations in the Agp1 phytochrome for determining the most likely protonation states of both histidines. The pKa values obtained for both histidines were below 7.0, indicating that both histidines are deprotonated. These results are in agreement with previous PROPKA calculations (67,85).

Crystal structures are often dehydrated, which means that functional water molecules may be missing. Therefore, some proteins require the inclusion of additional internal water molecules for the electrostatic energy calculations. This can be achieved implicitly by filling the volume occupied by water molecules with a dielectric medium with a dielectric constant ϵ = 80 (42). Indeed (86), applied a new cavity algorithm to 20 titratable groups introduced as point mutations in Staphylococcal nuclease (SNase) variants for which crystal structures and pKa values are available. This methodology led to a better agreement between computed and measured pKa values in a set of nine mutants, as reflected by an RMSD of 2.04 for pKa obtained with a cavity algorithm compared to 8.8 predicted using standard approach.

In summary, since photoactivation of photoreceptor proteins is often coupled to proton-transfer events between the chromophore and the key residues of the protein matrix, precise determination of their protonation states becomes a crucial step in computational modeling. In this respect, the combination of electrostatic energy calculations with classical MD simulations extended by proper description of protein hydration offers an efficient and reliable approach for investigating pKa shifts of chromophores and amino acid residues of photoreceptor proteins.

Investigation of the photoproduct color tuning in the cyanobacteriochrome Slr1393g3

Cyanobacteriochromes (CBCRs) were recently discovered and categorized as a subfamily of phytochrome photoreceptor proteins. They are distinct from the typical phytochrome due to their compact size, because they only require one domain for chromophore incorporation and complete photochemistry, whereas three domains are required in case of canonical phytochromes (87). Like all the representatives of this superfamily, they are photochromic, meaning they have two stable forms that can be interconverted into each other by light of different wavelength. What makes CBCRs special is the variability of their absorption maxima, in contrast to the canonical phytochromes that absorb in red or far-red. Therefore, it is of high interest to understand the molecular regulation of the absorption in these proteins. One measure for this quantity is the difference in the positions of the lowest energy absorption maxima between the thermodynamically stable dark state and the photoproduct state. To investigate this, application of multiscale modeling is the natural choice as it allows to determine the excited states of the chromophore, which is described with quantum mechanics, and to explicitly include the effect of the apo-protein, which is treated via molecular mechanics.

One example of a CBCR is the cyanobacteriochrome Slr1393g3, in which the absorption is shifted from the red in the dark form Pr to the green in the photoproduct form Pg as shown in Fig. 9. For this protein, crystal structures of both forms are available (88). In addition, a hybrid form Ph was reported, in which the tetrapyrrolic phycocyanobilin (PCB) chromophore is found in Pr conformation, but its protein environment is in the Pg form. First insights into the absorption of the chromophore inside the protein for these forms could already be gained by calculations on optimized structures (88).

Fig. 9.

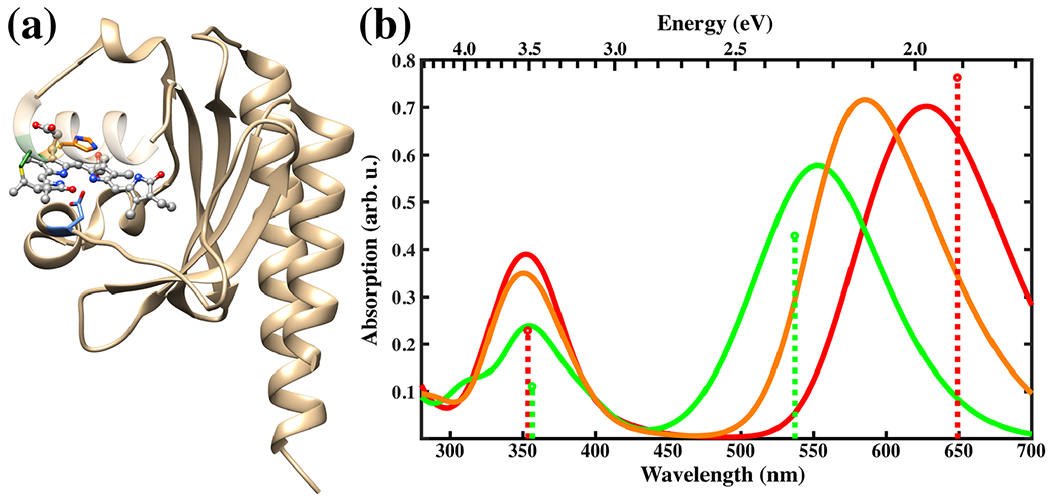
Left: Slr1393g3 protein structure in the Pr form. The PCB chromophore is shown in gray in the balls and sticks representation and the colors of selected sidechains are: CYS-528 in green, HIS-529 in orange and ASP-498 in blue. Right: Absorption spectra for the Pr (red), Pg (green) and Ph (orange) forms calculated with sTD-DFT based on CAM-B3LYP ground state calculations with a QM region consisting of PCB and the sidechains shown on the left. The spectra are based on 100 snapshots from a DFTB2+D/AMBER trajectory taken every 10 ps. The sticks represent the positions and relative absorption maxima for the Pr and Pg forms extracted from measured spectra (89).

For a systematic study of the absorption in the Pr and Pg forms, a benchmark study was conducted (90). One focus was on the efficient description of the chromophore in the ground state. For this purpose, semiempirical methods were employed to optimize the PCB structures of both forms in the ground state and the resulting geometries were compared with higher level ab initio calculations. It was found that DFTB2+D is the best performing method for this purpose. In addition, DFTB2+D/AMBER MD simulations were realized to extract snapshots for excited-state calculations, for which a variety of semiempirical and ab initio methods were benchmarked. Furthermore, methods based on ab initio time-dependent density functional theory were included. The semiempirical methods ZINDO/S and sTD-DFT as well as the ab initio method RI-ADC(2) turned out to perform the best.

The photoproduct tuning was studied systematically, using DFTB2+D/AMBER for sampling of 100 snapshots via a 1 ns trajectory and focusing on the three aforementioned methods for the excited-state calculations (91). It was found that the electrostatic interactions of the protein with the chromophore induce similar shifts in absorption for both forms. In contrast to this, wavefunction analysis showed that the length of the conjugated system decreases when going from the Pr to the Pg form explaining the unusual blue shift observed in this protein. In particular, the tilt of the D-ring is correlated with the energy of the lowest excited state (S1), which is responsible for the absorption in the visible range.

In conclusion, the computational studies lead to a molecular-level understanding of the photoproduct tuning in the CBCR Slr1393 supporting the trapped-twist mechanism proposed by Lagarias and coworkers for this class of red/green CBCRs (92). On the technical note, we established a computational protocol for spectrum simulations, including QM/MM partitioning and benchmarking of approaches for efficient sampling. We expect that the derived protocol is applicable to further phytochrome-like photoreceptors.

Application of constant-pH molecular dynamics simulations to sensory rhodopsin

QM/MM models of photoactive proteins most often are based on a particularly drastic assumption: each and every titratable amino acid keeps a user-defined protonation state which is determined according to chemical intuition and/or (semi-) empirical titration procedures (93-95). However, this assumption no longer holds if the property of interest is experimentally found to be pH-dependent. Essentially, the protein is a poly-acid with a very large number of interacting titrating sites. Accordingly, even a slight pH shift may induce numerous protonation changes, leading to structural reorganization and modified electrostatic interactions, eventually altering the property. The recently designed protocol based on Constant-pH MD followed by thousands of QM/MM calculations (CpHMD-then-QM/MM) is specifically meant to study how pH can tune the photophysical and photochemical properties of a chromophore embedded in an extended (macro-)molecular environment (96). In a nutshell, it entails: (1) extracting thousands of statistically independent structures from MD trajectories that are sampling both the conformation and the protonation state spaces of the protein (97) and (2) averaging the desired property obtained from the QM/MM calculations. The CpHMD-then-QM/MM protocol has been successfully applied to the elucidation of the molecular origin of the pH-dependent absorption spectrum of Anabaena Sensory Rhodopsin (ASR) (98), a transmembrane protein featuring the retinal chromophore in either the all-trans or 13-cis conformations (99,100). Both the tiny pH=3 to pH=5 red shift and the small pH=5 to pH=7 blue shift have been reproduced and their molecular origin analyzed.

Here, we want to stress out that the number of populated protonation microstates is always large. In the case of ASR, assuming only aspartic acid (9 residues), glutamic acid (5 residues) and histidine (4 residues) can titrate between pH=3 and pH=8, the maximum number of microstates is 2⁹×2⁵×3⁴=1327104! Even if most of them are not significantly populated at a given pH, it must be realized that hundreds or thousands of microstates can still co-exist (Table 1).

Table 1.

N: number of populated microstates at three different pH values (40 ns long CpHMD trajectories, ASR with 13-cis retinal) (98) #1 to #8: probabilities of the 8 most probable protonation microstates. Note that proton positions are considered indistinguishable in protonated ASP and GLU residues, as well as in deprotonated HIS.

pH	N	1	2	3	4	5	6	7	8
3.5	492	0.31	0.13	0.08	0.06	0.05	0.04	0.03	0.02
5.5	3600	0.03	0.03	0.03	0.02	0.01	0.01	0.01	0.01
7.5	1161	0.08	0.07	0.06	0.06	0.05	0.04	0.03	0.03

Whereas pH=3.5 can be characterized by a few important protonation microstates, it is no longer the case for pH=5.5 and pH=7.5. Accordingly, the ASR absorption spectrum must be calculated as the weighted average of all the most important microstates (Eq. 1). The weight (w_i) of a given microstate is pH-dependent: it can be evaluated by the number of structures featuring its proton distribution and extracted from a particular CpHMD trajectory, relatively to the total number of structures.

$${\lambda }_{\max }=\sum _i{w}_i{\lambda }_{\max }^i$$ (1)

In Equation (1), ${\lambda }_{\max }^i$ represents the maximum absorption wavelength of a given protonation microstate, as calculated as an average of all the corresponding structures. Because the number of populated microstates is usually large, it is possible that the most abundant one is characterized by a maximum absorption ${\lambda }_{\max }^i$ that differs significantly from the overall λ_max. An example of this effect is presented in Fig. 10. In Eq. (1), both λ_max and the 8 first ${\lambda }_{\max }^i$ are reported together for the same 3 pH values.

Fig. 10.

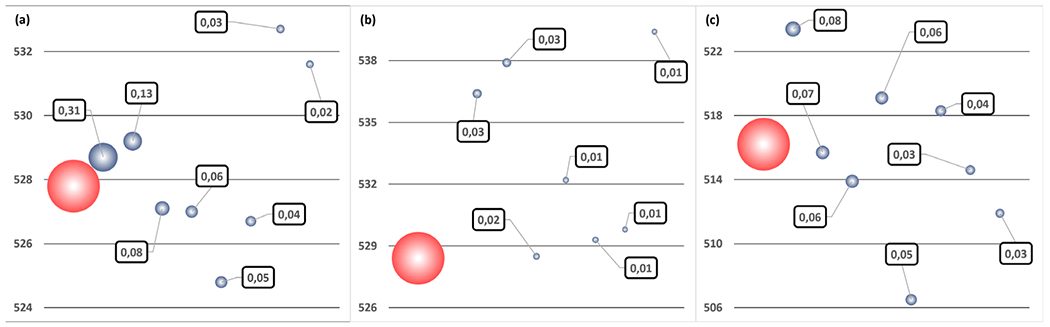
pH 3.5 (a), 5.5 (b), 7.5 (c) maximum absorption wavelength (in red) and the 8 most populated protonation microstate individual contributions (in gray). Wavelengths are given in nm. Bubble surfaces are proportional to microstate weights (squared labels), relatively to the complete ensemble.

At pH=3.5, only a few ASP and GLU residues have the potential to be titrated. This translates to a dominant contribution (31%), whose ${\lambda }_{\max }^i$ is in good agreement with the corresponding λ_max. At neutral pH, the most populated microstate features a ${\lambda }_{\max }^i$ value, which is 7 nm red-shifted. However, its occurrence is low (8%) and is balanced by other contributions, which are closer to λ_max. Accordingly, this is the perfect example where the most abundant protonation microstate is not a good representative of the average. Finally, at the intermediate pH=5.5 value, most of the ASP, GLU and HIS residues are titrating, resulting in a huge number of populated microstates, that is, to very low individual probabilities. In this case, it is virtually impossible to manually pick a protonation microstate whose ${\lambda }_{\max }^i$ would be close to λ_max.

METHODOLOGICAL DEVELOPMENT AND SOFTWARE UPDATES

Progress in algorithm and software developments is tightly coupled to the success of multiscale modeling in application to photoreceptor proteins. As a result, higher accuracy can be achieved and larger systems can be studied. In this section, seven contributions are presented, which aim at exploiting data-driven approaches in QM/MM methodologies, characterization of intricate hydrogen-bonding networks in large macromolecular systems, the development of new sampling algorithms for the characterization ground- and excited-state dynamics of biological chromophores, and the implementation of user-friendly software interfaces for efficient and automated modeling of complex biological systems, such as rhodopsin, using multiscale methods.

Extending the capabilities of QM/MM by a data-driven approach

Naturally, the essential purpose of applying any multiscale modeling technique is to reduce the associated computational cost. As explained earlier, QM/MM has been the most straightforward approach for studying photoreceptor and related proteins in this respect, as it does not suffer from any limitations from the a priori selected potential models as in conventional force fields. As a matter of fact, describing photoactive systems requires one to adopt excited-state calculations, and applying QM/MM is often very costly. One possible remedy against this cost issue could be to employ computationally more economic approaches for the QM part, such as semiempirical techniques. However, matching the reliability of high-level theories such as CASPT2 or EOMCCSD with semiempirical models is a daunting task, even after intensive re-parametrizing efforts. Thus, somehow constructing the PES in an explicit manner based on data from high-level quantum chemical theories is a desirable path. It can also be quite useful for studying protein mutation effects, as the constructed surface can often be simply re-used with the protein mutation without any further quantum chemical calculations, whereas directly using QM/MM for mutants necessitates repeating costly QM calculations. The weakest link in explicitly constructing PES is the reliability. When an analytic form of a surface is employed with parametric fitting to high-level computational data, the region of high fidelity is rather limited. This is especially troublesome for treating photo-induced processes, as the molecular system after photon absorption tends to possess a large amount of vibrational energy such that the chromophore and potentially its neighboring units can wander around an ample configurational space.

As a practical alternative of direct QM/MM calculations without assuming an intrinsically limited analytic form of the surface, using the interpolation mechanics/molecular mechanics (IM/MM) technique can be considered. The interpolation technique was originally designed for describing gas phase reaction dynamics (101), and it was recently extended for describing excited-state surface hopping dynamics of chromophore-embedded protein systems such as GFP (102). Of course, the interpolation itself depends on a relatively large data set with energies, gradients, and Hessians at multiple configurations. For example, for describing the GFP chromophore, a data set with more than 1000 configurations were needed for a reliability. This burden also increases with more flexible chromophore units. Even for the relatively flexible chromophore in the photoactive yellow protein (PYP) with multiple torsional degrees of freedom, an interpolated PES with high fidelity can still be constructed (Fig. 11).

Fig. 11.

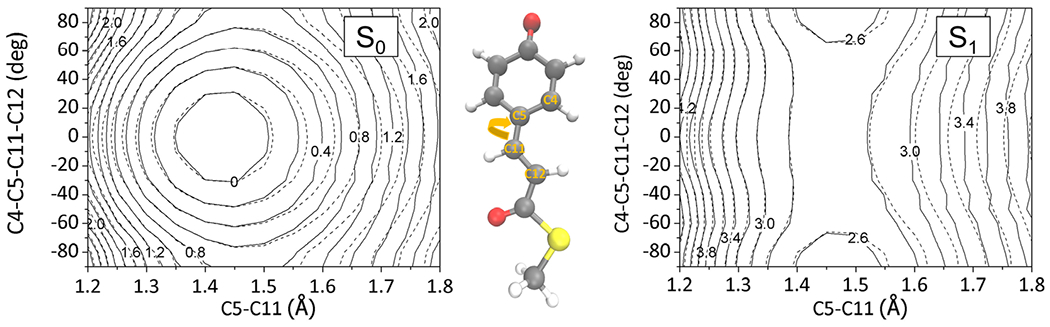
Reliability of interpolated PES: contour maps of the interpolated S₀ and S₁ state surfaces (solid lines) of the PYP chromophore in comparison with the reference quantum chemical data (dashed lines). Energy values are denoted in eV units. The contours were drawn by varying a torsional angle and its coupled bond length around the S₀-optimized geometry as denoted with the molecular structure. The interpolation data points were sampled in an iterative manner by adopting excited-state molecular dynamics simulations. The size of the interpolation data set was 2100.

Interpolation-based PES is an example of data-driven surfaces. The question then is: how to expedite the data collection processes and how to filter out more important data from a large set. This is an important milestone for generalizing the technique, and there are on-going improvements toward this goal (103). We note that commonly used Shepard interpolation scheme, based on Euclidean distances in the configurational space, may not be the most reliable approach. Machine-learning algorithms, which are fashionable these days, may contribute significantly in these efforts in the future.

Long-distance proton transfers via dynamic hydrogen-bond networks

In protein environments, the transfer of protons across long distances is thought to occur via hydrogen-bond paths composed of protein groups and water molecules. Such hydrogen-bond paths could be sampled transiently, as the protein changes conformation along its reaction cycle; moreover, changes in protonation states during the proton-transfer reaction are likely to couple to changes in local protein and water dynamics. Prominent examples here are retinal proteins, for which changes in the retinal isomeric state are coupled with the rearrangements of internal water molecules (104–106), and photosystem II, in which dynamic water molecules establish proton-conduction path (107).

The dynamic nature of the water-mediated proton-transfer paths and the complexity of the bio-systems bring about the challenge of how to identify and characterize hydrogen-bond paths between putative proton-transfer groups. We have thus designed and implemented Bridge (108), a suite of Python graph-based algorithms, which enable efficient analyses of water-mediated hydrogen bond networks. Bridge computes two-dimensional graphs of the hydrogen bonds of the bio-system, and then queries the graphs to identify, for example, all hydrogen-bonded paths starting from a proton-donor group, or all hydrogen-bonded paths between proton donor and acceptor groups (108).

Particularly important for long-distance proton transfers is to identify, in an ensemble of protein conformations, those events characterized by a continuous connection between the proton donor and acceptor group—such conformations could, for example, be used as starting point for quantum mechanical computations to find out whether the energetics of proton transfer along that path is compatible with experiments (108).

To illustrate the usefulness of Bridge with identifying hydrogen-bond paths in complex bio-systems, we present the network of protein–water hydrogen bonds in a dimer of chimera channel-rhodopsin, C1C2 (Fig. 12A). The extracellular halves of the two protein monomers participate in a remarkable network of hydrogen bonds that included some 48 charged and polar protein groups, and numerous water molecules (Fig. 12A). An unexpected observation from the Bridge graph-based analyses of C1C2 was that the two retinal Schiff bases can bridge transiently via continuous hydrogen-bond paths of 12-13 hydrogen bonds (108). This long-distance network between the two retinals is rapidly perturbed by mutations that alter H bonding (108).

Fig. 12.

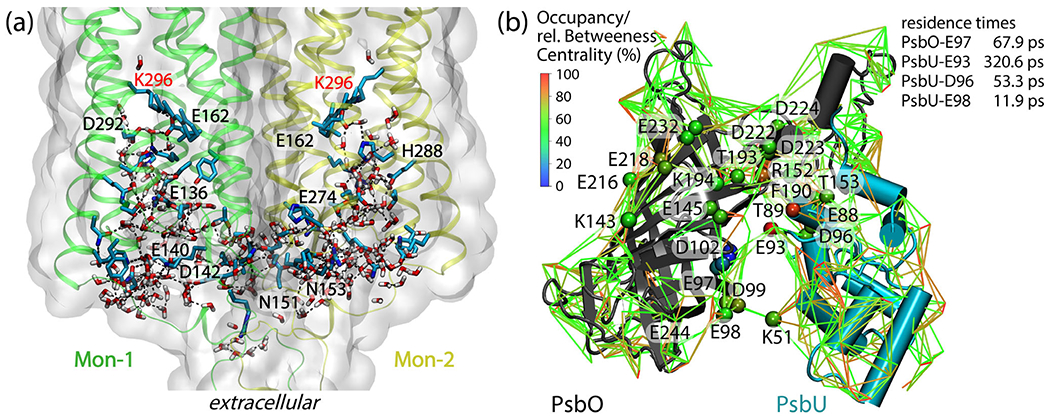
Dynamic hydrogen-bond networks in complex bio-systems. (a)t Extensive protein–water hydrogen-bond network in the extracellular halves of monomers Mon-1 and Mon-2 of the C1C2 dimer. The protein is shown as ribbons and molecular surfaces, and selected protein groups are shown as bonds with carbon atoms colored cyan, nitrogen—blue, and oxygen—red. For clarity, we label only protein groups part of a shortest-distance path that connects the two retinal Schiff bases. The molecular graphics and the path analyses are based on ref. (108). (b): Protein–water hydrogen-bond network at the surface of the soluble PsbO and PsbU subunits of photosystem II. Lines inter-connect charged and polar sidechains via hydrogen-bonded water bridges; for clarity, we display water bridges that are present during at least 50% of a simulation of the PsbO-PsbU complex in aqueous solution. Cα of amino acid residues are colored according to relative betweenness centrality values. Lines are color-coded, according to occupancy values. The image and the centrality computations are based on Ref. (109)

Once we computed a protein’s graph of hydrogen bonds, we can use centrality measures to identify protein groups that are common to hydrogen-bond paths of particular interest for the functioning of that protein (110). With betweenness centrality, for example, we evaluate how often a protein group participates in short-distance paths that connect any two other protein groups (110). Such an analysis revealed that, on the surface of photosystem II, there is a carboxylate group (PsbU-E93 in (Fig. 12B)) central to a dense network of protein–water hydrogen bonds surrounding the putative proton-binding site PsbO-D102 (109,111). Although most of the waters participating in the hydrogen-bond network are very dynamic (109) and visit the surface of the protein just shortly, for picoseconds or less, close to PsbU-E93 waters can stay for as long as 320.6 ± 0.6 ps (109).

Pursuant to the considerations above, we suggest that graph-based analyses of protein hydrogen-bond networks provide valuable tools to analyze efficiently large data sets, arising from numerical simulations of complex bio-systems, to identify long-distance hydrogen-bond paths that could conduct protons, explore the response to mutations, and to predict protein groups with central role in long-distance connection networks of a protein.

Toward efficient sampling of photoactivation mechanisms with path-based methods

Even with the computational cost efficiency of multiscale modeling techniques, such as hybrid QM/MM simulations, sampling the key steps of a photocycle can still be a daunting task. The pathway from the dark state to the signaling state, and back, is typically comprised of several somewhat activated processes—for example, electron transfers, proton transfers and conformational changes—which occur rarely in affordable simulation timescales. Enhanced sampling techniques are commonly used to tackle such challenges in protein systems. However, these schemes traditionally require the definition of a sensible reaction coordinate and/or stable states, both of which are not trivial to formulate and often unknown in photoreceptors. The application of more robust sampling techniques, not subject to numerous trials and errors, is vital to resolve intricate photoactivation mechanisms.

A possible solution toward increasing sampling efficiency and making free energy calculations and dynamics simulations more affordable is offered by path-based methods. In these schemes, the handling of a high-dimensional reaction coordinate, composed of several collective variables (CVs), is simplified by the introduction of an optimizable curve that connects two known states in the space of the CVs. Then, the progress along this path CV can effectively be used as a reaction coordinate. Examples of this kind of methods can be found in Refs (112-114). The benefits are three-fold: (1) free energy calculations along adaptive paths are not subject to the exponential increase in cost with the dimensionality of the reaction coordinate, and can reach a linear performance scaling (115); (2) with the diminished penalty for dimensionality, one can introduce more candidate CVs in a single attempt to increase the chance of success; and (3) with the directionality provided by the path, the sampling is focused into the transition region of interest. Furthermore, most standard biasing methods (e.g., umbrella sampling (116) or metadynamics (117)) and algorithmic extensions can be employed either along the path (118), or in the direction perpendicular to it in order to find alternative mechanisms (119). In Fig. 13, we show an illustrative example of an adaptive path-CV capturing a transition channel on the Müller–Brown (120) potential energy surface.

Fig. 13.

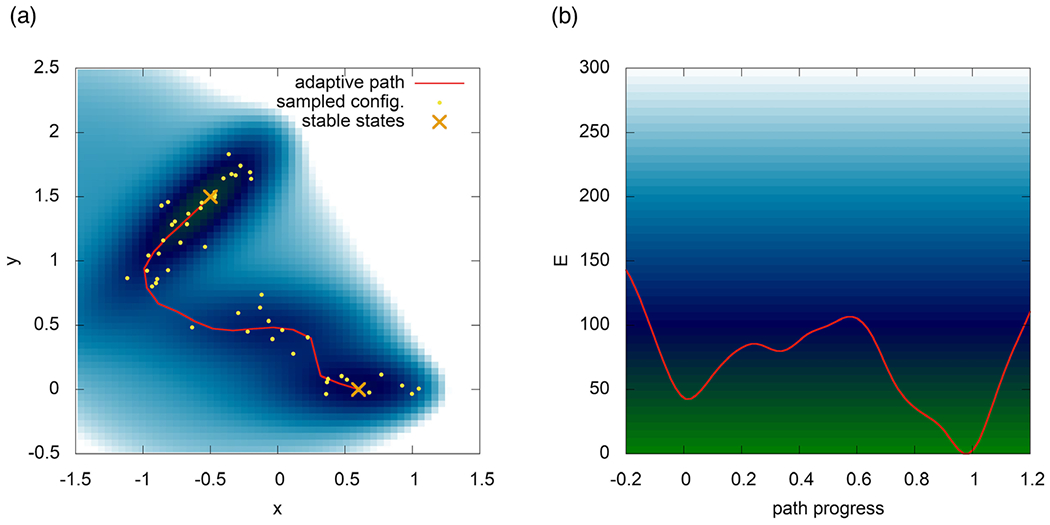
An adaptive path-CV captures the transition channel on the Müller–Brown (120) potential energy surface.

Path CVs have been successfully used in blue-light using flavin (BLUF) photoreceptors, to efficiently extract mechanistic details and free energies (121,122). Other path-based methods that do not require biasing, such as transition path sampling (TPS) (123), have also been used in PYP photoreceptors (124), and similar principles have been applied to rhodopsin by tracking the time evolution of an excited-state population (125).

Path-based methods still require two stable state definitions—for example, the dark and light states—as well as a set of, even if many, somewhat correct CVs. In cases where these aspects are unknown or debated, a new generation of data-driven and machine-learning-based sampling methods holds the key to speed up the exploration of photoactivation mechanisms. CVs can be discovered with novel combinations of clustering, time-lagged-independent component analysis, slow-mode separation, autoencoder-based dimensionality reduction and many more techniques (126–130). Cutting-edge advances in deep learning also yield free energy differences without the need for reaction coordinates, by mapping atomic configurations to a reference latent representation (131).

FDET-based simulation of vertical excitation energies of chromophores embedded in proteins

Frozen-Density Embedding Theory (FDET) (132,133)-based multi-level simulations provide an alternative to conventional QM/MM simulations (both polarizable or not). In FDET, the total energy functional is expressed as a functional depending on two independent variables: N_A-electron wavefunction (embedded wavefunction Ψ_A) and a user-chosen density ρ_B(r) associated with the environment. Ψ_A is thus obtained from the constrained minimization of the Hohenberg–Kohn density functional for the energy of the total system (Fig. 14). We refer the reader to Ref. (133) for the FDET definitions and formulas for the energy and the embedding potential applicable to variational methods for ground state and Refs. (134,135) for FDET extensions. These are omitted here for the sake of brevity. Compared to QM/MM, setting up a FDET simulations involves similar steps: (1) selecting the subsystem to be treated at the quantum mechanics level, (2) choosing the suitable method for the quantum part, (3) generating the embedding potential, (4) solving the “embedded QM problem,” (5) evaluating the properties. The most important differences between FDET-based and QM/MM simulations concern steps (1), (3) and (5). Concerning (1), the commonly used system-independent approximations for the non-Coulombic components of the FDET embedding potential given in eq. (44) in Ref. (133) are adequate only for weakly overlapping Ψ_A and ρ_B. Thus, the applicability of FDET with such approximations is limited to models where the chromophores are not covalently bound to the protein. Concerning (3), generating the FDET embedding potential involves choosing an electron density ρ_B(r) for the environment of the quantum part. This step corresponds to choosing parameters for atom-centered potentials in QM/MM describing the interactions with the environment. Concerning (5), in FDET the non-Coulombic interactions with the environment are taken into account in a self-consistent manner in both the energy and the embedding potential. This results in the dependence of the FDET embedding potential on Ψ_A. For electronic excitations, this numerically inconvenient feature of FDET can be efficiently treated by linearized FDET (134) or by performing additional iterations (see interface E in Fig. 16).

Fig. 14.

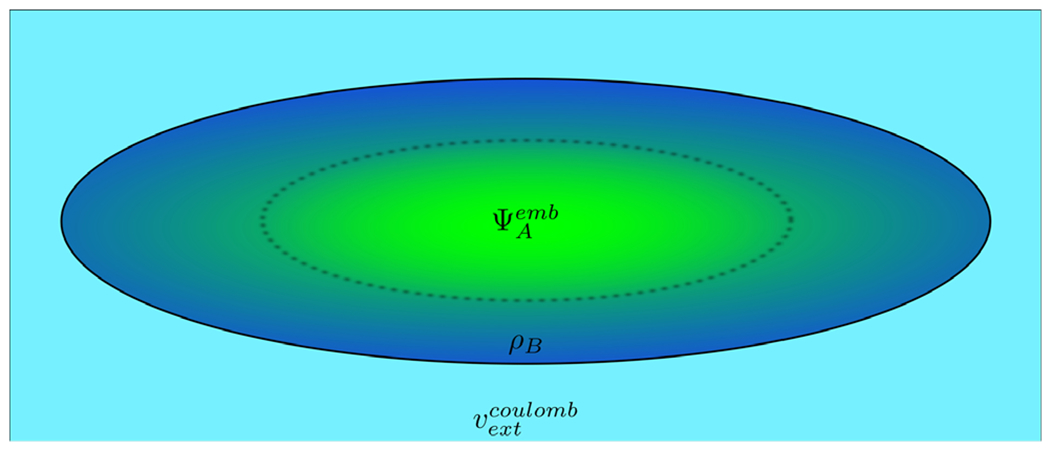
Scheme of the FDET model of a chromophore embedded in a protein. Different colors represent regions in 3D space which are described using different descriptors: embedded Ψ_A for the chromophore (green) and density ρ_B(r) for its nearest neighbors (dark blue). Note that these regions can overlap. If needed, the long range effects on the embedded wavefunction can be accounted for by means of a Coulombic potential v_ext^Coulomb.

Fig. 16.

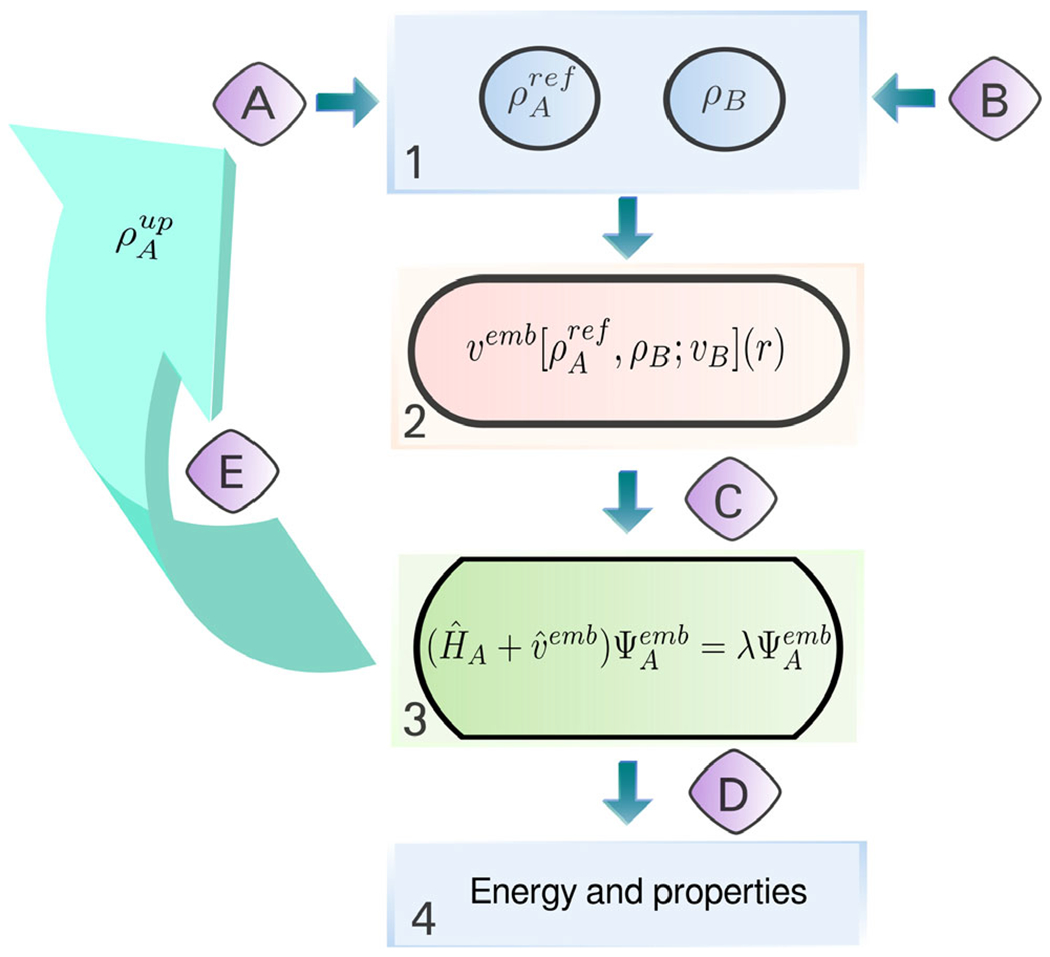
General workflow of a FDET-based simulation. The main steps, given in square boxes, can be performed using various standard quantum chemistry codes: 1—generation of ρ_A(r) and ρ_B(r) in real space, 2—generation of the embedding potential in real space, 3—obtaining embedded N_A-electron wavefunction (variational or not) from a user-chosen quantum chemistry method and code; 4—a posteriori evaluation of the FDET energy components which depend on the method used in step 3 and other properties. Interfacing is performed by subroutines indicated with capital letters: A—generation of initial N_A-electron density ρ_A ^ref(r); B—generation of ρ_B(r) (superposition of atomic or molecular densities, statistical ensemble averaging, pre-polarization, freeze-and-thaw optimization, etc.); C—generation of the embedding potential in atomic basis set representation (it can include an additional electrostatic field component as shown in Fig. 14); D—extracting quantities obtained in step 2 for step 3; E—iterative update of the embedding potential for verification of the linearization approximation (optional).

The representation of not only the Coulomb part but also all quantum effects in the FDET embedding potential (not as a posteriori energy contributor to the energy, which is usually done in QM/MM methods) makes FDET-based methods especially suitable for evaluation of changes in the properties evaluated as expectation values of the embedded wavefunction. The total FDET energy given in Eq. (30) in Ref. (133) includes a term depending solely on α_B(r). For practical applications targeting the energy of the total system, this term must be approximated as well. The essence of multi-level modeling is that this energy contribution is approximated using some simpler method. This offers a large number of possibilities for practical realizations. In this perspective, we focus on such practical applications of FDET where the explicit evaluation of this contribution to the total energy is not needed. This concerns studies targeting the environment-induced shifts of observables evaluated as expectation values for a given α_B(r).

Turning back to the choice of ρ_B(r), the simplest protocol consists in using the electron density evaluated as a ground state density of the environment without the embedded species (level 0). If the environment does not comprise molecules which are hydrogen-bonded one to another, this protocol can be simplified even further by means of generating α_B(r) as a superposition of densities of individual molecules (132,136). We recommend level 0 as the starting point for any large-scale FDET-based simulation. Benchmark studies on model systems indicate its great usefulness for modeling excitation shifts exceeding 0.1 eV (137) (MAE on 351 excitations is about 0.04 eV, see Ref. (138) and Fig. 15). Hydrogen-bonding-induced shifts of excitation energies in organic chromophores lie usually in the range of −1.5 to 1.5 eV. More sophisticated protocols to generate α_B(r) take into account such effects as (1) mutual polarization of different parts of the environment (136), (2) implicit or explicit treatment of electronic polarization of α_B(r) by the chromophore (139), (3) fluctuations of the structure of the environment (140,141). We refer the reader also to the work by Neugebauer and collaborators (142,143) on different protocols to generate α_B(r) and their effect on the observables obtained from the embedded wavefunctions for chromophores embedded in proteins. We rather see going beyond level 0 as a possible option decided on the case-by-case basis. The user should be given the possibility to estimate these effects using smaller model systems to determine if going beyond level 0 is needed in large-scale simulations. Fig. 16 shows a flow diagram indicating essential steps and tools available for setting up and performing large-scale FDET-based computations of electronic excitations for a chromophore embedded in a protein environment. Our previous report on chromophores embedded in proteins (41) used the LR-TDDFT strategy for excited states. The tools presented in Fig. 16 allow the user to: (1) use methods going beyond LR-TDDFT if the nature of the excited states requires it and (2) more flexible and controllable choices for α_B(r) if going beyond level 0 is desired.

Fig. 15.

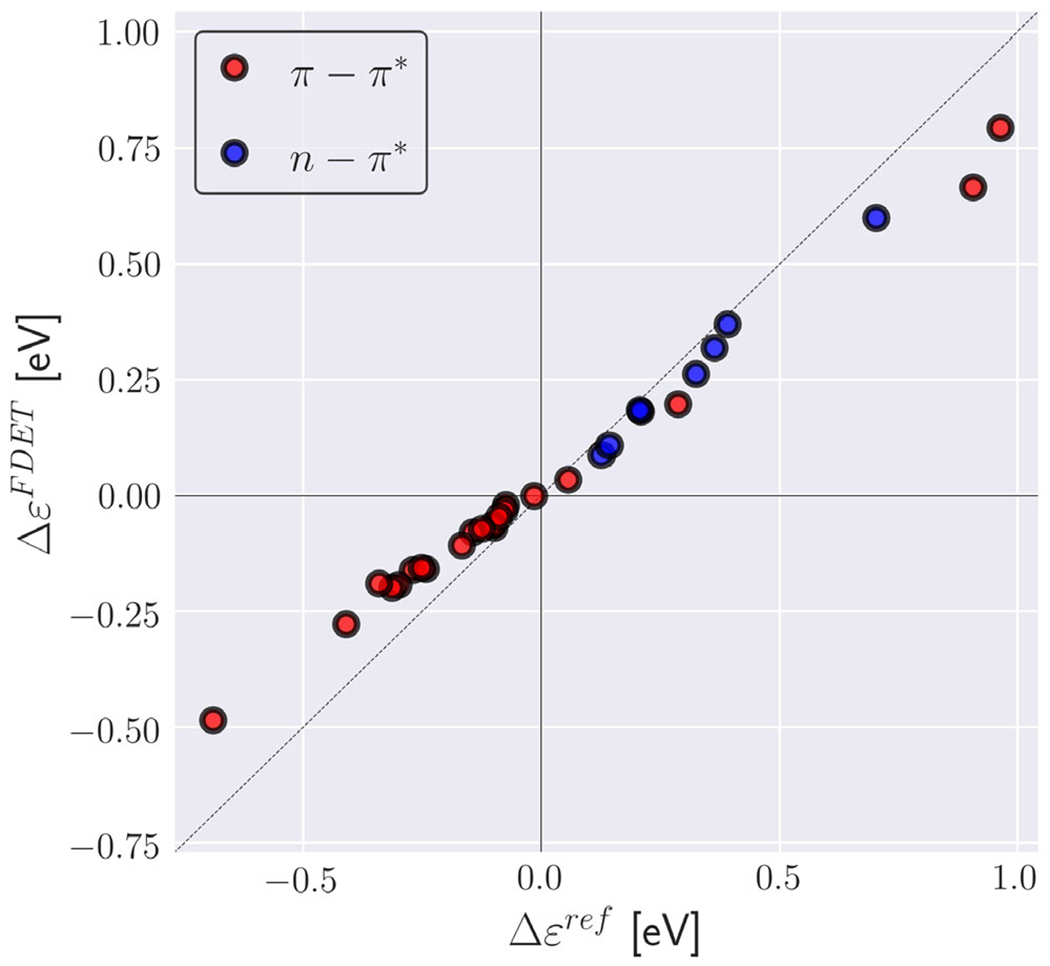
Environment-induced shifts of the lowest vertical excitation energy for organic chromophores in hydrogen-bonded environments (XH-27 dataset from Ref. (144)). Reference shifts (Δϵ^ref) are taken Ref. (144) (excitation energy shifts obtained from ADC(2) calculations for the whole clusters). FDET shifts (Δϵ^FDET) are obtained from embedded ADC (2) calculations as described in Ref. (144) except the reduction of the number of centers in the basis sets used for Ψ_A and ρ_B (monomer expansion is used here).

Polarizable embedding as a tool to address photoreceptor proteins

Photoreceptor proteins are activated by their interaction with light. In order to understand the working mechanisms of photoreceptors at an atomistic level, at least a partial quantum mechanical description is needed. This, unfortunately, is significantly hampered by the fact that the size of photoreceptor proteins in their natural environments quickly becomes out of reach for conventional quantum chemistry methods. Thus, in order to gain atomistic insight into the functioning, and eventually to be able to define rational design strategies of novel photoreceptor proteins, development of suitable quantum chemistry methods is of significant importance.

The polarizable embedding (PE) model (145) is a fragment-based classical embedding approach belonging to the class of QM/MM models, that is, a central part of the system in question is described at the level of quantum chemistry whereas the remaining part of the system—the environment—is described effectively by a classical embedding potential. For photoreceptor proteins, the part treated using quantum chemistry would typically be chosen as the chromophoric part of the protein. In the PE model, the environment is divided into a number of fragments, and the permanent charge distribution of each fragment is modeled by a multicenter multipole expansion. In addition, distributed dipole–dipole polarizabilities are assigned to each of the fragments thus introducing an explicit account of polarization in the environment. A similar strategy is utilized in the effective fragment potential (EFP) approach (146-149) One of the strengths of the PE model is exactly this account of environment polarization in addition to the possibility to calculate the fragment multipole moments and polarizabilities based on separate quantum chemistry calculations, that is, the model does not rely on the use of a predefined force field. The PE model is thus generally applicable to any kind of environment ranging from simple solvents to highly heterogeneous systems like a protein matrix. For the latter, and other biological environments as well, the fragmentation of the environment becomes more involved since covalent bonds need to be broken in order to define the fragments making up the environment. For this, we have found the method of molecular fractionation with conjugate caps to be very efficient (150,151). Fig. 17 contains an illustration of the PE model indicating the part of the system treated using either quantum chemistry or by multipoles and polarizabilities.

Fig. 17.

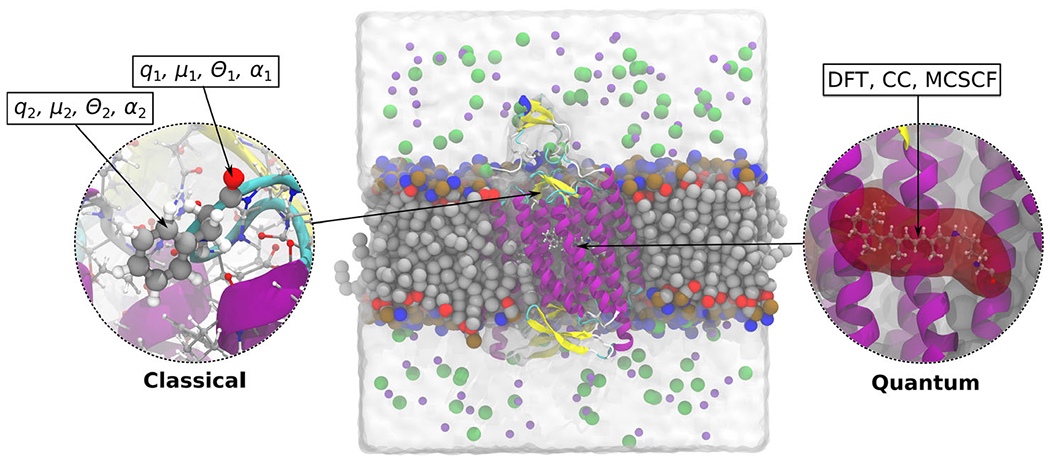
Illustration of the PE model applied on the membrane-embedded C1C2 channelrhodopsin. The active part, a protonated retinylidene Schiff base, is modeled using DFT/WFT, while the effect from the chromophores environment is modeled classically using atom-centered multipoles and polarizabilities.

The PE model has been designed for calculation of spectroscopic properties and excited states in particular. Thus, the model is centered around a formulation building on quantum chemical response theory. Both linear and non-linear properties, such as one-, two- and three-photon absorption processes, may be described based on the PE model. In addition, the PE model has been formulated within both time-dependent density functional theory (TD-DFT) as well as correlated wave function approaches, such as coupled cluster (CC) and multi-configurational self-consistent field (MCSCF), and can thus be used to describe situations where TD-DFT is known to possess problems for example in relation to excited states dominated by double excitations. For a recent discussion of the capabilities of the PE model, we refer to Refs. (152,153)

Through applications, we have generally found the PE model to represent a rather robust computational procedure providing results in close agreement with full quantum chemistry-based calculations. However, care should be taken when considering especially negatively charged molecules (chromophores) or excited states of even partial Rydberg character (154). In such situations, PE-based calculations may suffer from electron spill-out errors meaning that electron density from the part of the system treated using quantum chemistry is leaking into the environment, thereby leading to an over-stabilization of the ground and especially the excited states (155). In order to address such issues, we recently formulated the polarizable density embedding (PDE) approach (156). In this model, the fragments in the environment are described by their full charge densities, replacing the multipoles, while still keeping the atom-centered polarizabilities to efficiently account for polarization effects. Importantly, the PDE model contains, in addition, a term in the embedding operator that accounts for Pauli repulsion, thereby preventing electron spill-out (155).

Both the PE and PDE models are available through the Polarizable Embedding library (PElib) and are currently interfaced to a number of electronic structure programs—for details, we refer to a recent tutorial paper on the use of the PE model (152).

Toward automated population dynamics simulations of light-responsive proteins (11)

At the molecular level, light sensitivity is controlled by two photoreceptor properties: (1) activation quantum efficiency and (2) dark noise (125) A complete theory of light sensitivity in biological photoreceptors must therefore describe the relationship between each property and the photoreceptor electronic and molecular structure. Years ago, we reported (42) on the theory of dark noise in a specific family of biological photoreceptors (i.e., light-responsive proteins): type II (animal) rhodopsins (12) However, even when limiting our interest to such rhodopsin family, a theory of quantum efficiency has not yet been established. As a consequence, we still ignore, for instance, the mechanism enabling rod cell rhodopsin, the vertebrate retina most sensitive dim-light photoreceptor, to utilize almost 70% of the absorbed photons for visual transduction. Reveling such a mechanism will impact not only our understanding of light sensitivity, but also the design of rhodopsin mutants leading to controllable receptor responses with obvious implications in biology/medicine, (157,158) optogenetics (159,160) as well as in the emerging field of synthetic biology (161)

As for the case of rhodopsin dark noise, to be of biological interest the validity of a quantum efficiency theory/mechanism has to assess not only for a single photoreceptor but for an entire array of related photoreceptors. When this investigation has to be carried out computationally, it is necessary to construct a full array of photoreceptor models of the same class or, in the case of proteins, homologues or/and mutants. There is another reason for focusing on arrays of models. Rarely chemists and biologists are interested in properties of a specific molecular system but, rather, in trends. In fact, trends are not only more significant for predictions and applications but are less affected by systematic errors in the property calculation. This also applies to the prediction of light sensitivity.

The discussion above indicates that the investigation of light sensitivity in rhodopsins (or, actually, any other biological photoreceptor) poses a formidable computational chemistry challenge. On one hand, it is apparent that the complexity of the unavoidable atomistic and multiscale (QM/MM) photoreceptor models (a seven α-helices transmembrane protein incorporating a light-responsive retinal chromophore, see Fig. 18A) and of the protocol for building them limits the number of models, possibly a few tens, that can be built manually for each given investigation. Therefore, one has to employ an effective automated QM/MM model building protocol if one plans to study hundreds of mutants as it seems necessary for either establishing/simulating a trend, a general mechanism or a mechanistic spectrum. A second issue originates from the fact that the property to be calculated, that is, the quantum efficiency of the rhodopsin (Rh) activation requires the simulation of the light-triggered dynamics of a sizable molecular population. For Rh, this corresponds to the dynamics of the light-triggered photoisomerization of the retinal chromophore from its dark (i.e., equilibrium) form containing the 11-cis stereoisomer (rPSB11) to its transient bathorhodopsin (bathoRh) primary photoproduct (see Fig. 19A) containing a distorted form of the all-trans stereoisomer (rPSBAT) as illustrated in Fig. 19B. Thus, the quantum efficiency can be defined as the fraction of photoexcited Rh molecules that after absorption of a photon successfully form bathoRh. Such fraction is indicated with the symbol Φ_cis-trans.

Fig. 18.

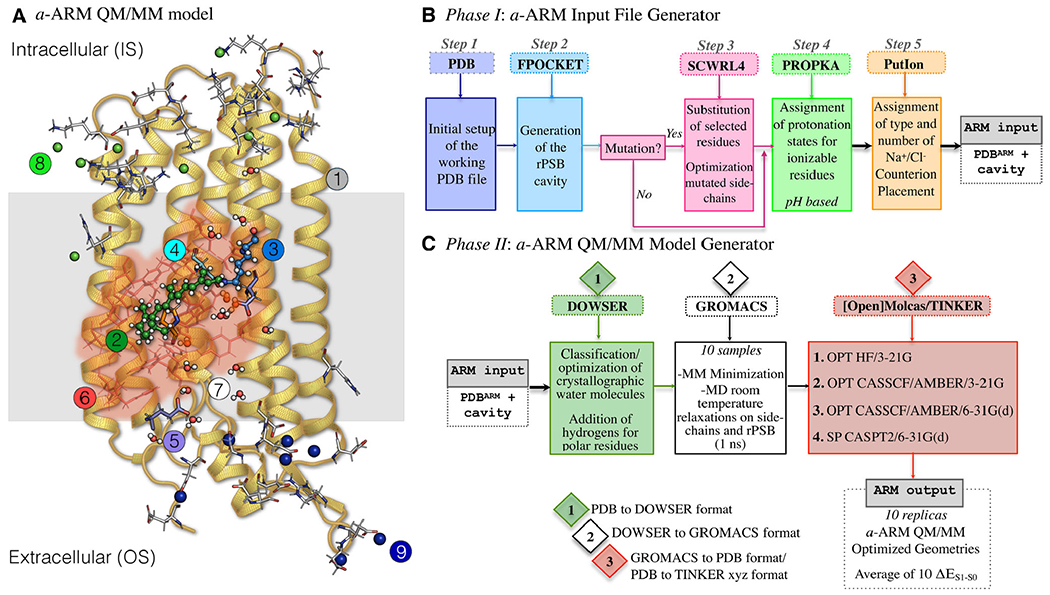
Structure of the a-ARM rhodopsin model building protocol. (A) General scheme of a QM/MM model generated by a-ARM for a Type I rhodopsin. This is composed of: (1) environment subsystem (gold cartoon), (2) retinal chromophore (green tubes), (3) Lys side-chain covalently linked to the retinal chromophore (blue tubes), (4) main counter-ion MC (cyan tubes), (5) residues with non-standard protonation states, (6) residues of the chromophore cavity subsystem (red tubes), (7) water molecules, and external (8) Cl⁻ (green balls) and (9) Na⁺ (blue balls) counterions. The external extracellular (OS) and intracellular (IS) charged residues are shown in frame representation. (right) General workflow of the a-ARM rhodopsin model building protocol for the generation of QM/MM models of wild-type and mutant rhodopsins. The a-ARM protocol comprises two phases: (B) input file preparation phase and (C) QM/MM model generator phase.

Fig. 19.

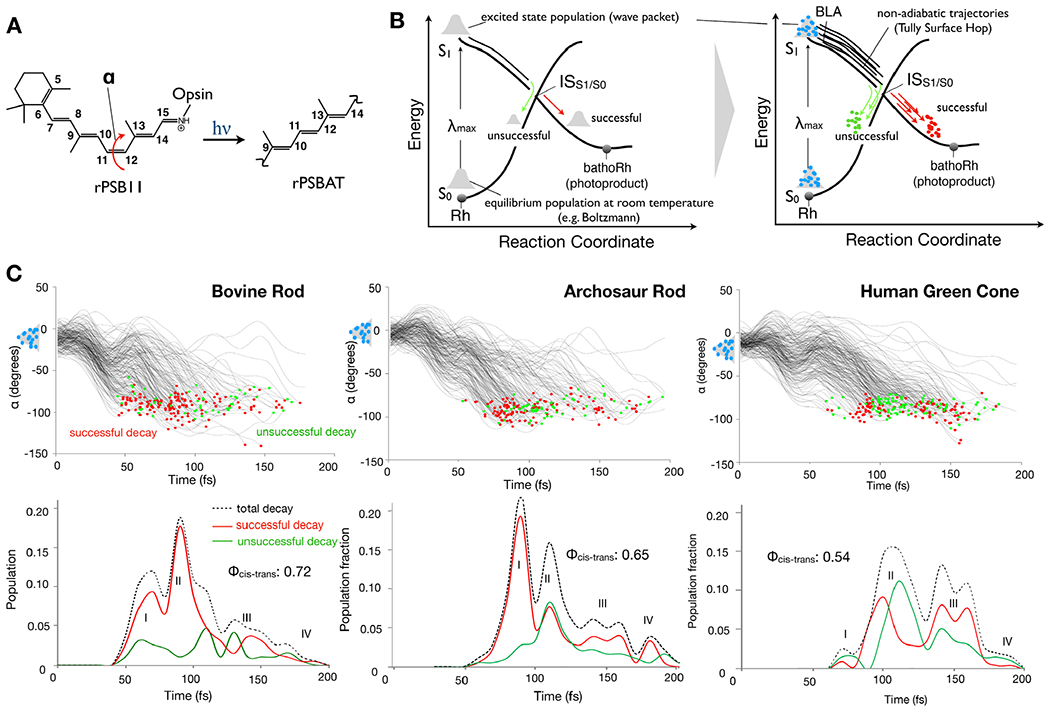
Rhodopsin population dynamics. (A) 11-cis retinal chromophore (rPSB11 for Type II rhodopsins such as Rh) photoisomerization and isomerizing torsional angle α (C10-C11-C12-C13 dihedral angle). (B) Schematic representation of the light-triggered ultrafast population dynamics of Rh. IS_S1/S0 (48,162) stands for intersection space between the ground state (S₀) and the first singlet excited state (S₁) representing collectively the points of decay (hop) to the ground state (S₀). The reaction coordinate is complex but it is mainly driven by the α angle. The diagram on the right represents a non-adiabatic trajectory calculation where the initial vibrational wave-packet (or population) is represented by a collection of initial conditions (structures and velocities) indicated by light-blue circles and one trajectory is propagated from each initial condition point. (C) The time progression of α along a set of 200 non-adiabatic trajectories simulating the S₁ population dynamics of bovine rhodopsin at room temperature is given in the top-left panel. The bottom-left panel gives the statistic of successful and unsuccessful hops as a function of time. The computed quantum efficiency value is also given. The circles represent decay from S₁ to S₀ with a red circle representing successful decays leading to the photoproduct while green circles lead to the reactant. Center. Same results for a model reconstructed from an amino acid sequence obtained via phylogenetic analysis and ancestral sequence reconstruction techniques (163,164). Right. Same data for the opsin from a human green cone receptor cell.

In this section, we report on the prospective systematic investigation of the Φ_cis-trans, and therefore of light sensitivities of an entire arrays (say hundreds) of rhodopsins. While this is still an unpractical research endeavor, we show that the basic technology necessary to do so is rapidly becoming available. Such technology is based on two paradigms: (1) the automatic building of rhodopsin QM/MM models (see Fig. 18B and C) and (2) the use of such models for the automated generation of room temperature (actually, any temperature) Boltzmann distributions providing the initial conditions (geometries and velocities) for successive quantum-classical (non-adiabatic) trajectory calculations (see Fig 19B). The resulting trajectory bundle corresponds to a simulation of the light-triggered population dynamics describing the rhodopsin photoisomerization and necessary for Φ_cis-trans calculations (Fig. 19C for three different cases).

Automatic building of QM/MM models of rhodopsins

A specialized protocol for the automated construction of QM/MM models of rhodopsins, which uses [Open]Molcas (165) as the electronic structure calculation engine, has been introduced. This is the Automatic Rhodopsin Modeling (a-ARM) protocol designed to produce congruous and reproducible monomeric, gas phase and globally uncharged models of rhodopsins based on electrostatic embedding and the hydrogen-link-atom frontier between the QM and MM subsystems (166,167) Although a-ARM currently only constructs rhodopsin-like models (see the model structure in Fig. 18A), it provides a template for future development and generation of an automatic QM/MM building strategy for other, more general systems. The building protocol is illustrated and detailed in Fig. 18B and C.

a-ARM has already been benchmarked for several rhodopsins from different organisms that display different functions. In fact, members of the rhodopsin family are found in diverse organisms and, thus, constitute an exceptionally widespread class of light-responsive proteins, driving fundamental functions in vertebrates, invertebrates and microorganisms (12,168,169) a-ARM has been shown to be able to generate models suitable for the prediction of trends in spectroscopic properties, i.e., maximum absorption (${\mathrm{\lambda }}_{\max }^a$) and emission (${\mathrm{\lambda }}_{\max }^f$) wavelengths, of wild-type rhodopsin-like photoreceptors and their variants, with an error bar of 3.0 kcal mol⁻¹ (0.13 eV) (166,167) (See Fig. 20A and B). These two critical wavelengths are approximately calculated and expressed in terms of vertical excitation energies (ΔE_S1-S0) from S₀ and S₁ energy minima respectively.

Fig. 20.

Benchmarking of a-ARM. (A) Computed excitation energies ΔE_S1-S0 in both kcal mol⁻¹ (left axis) and eV (right axis) for various rhodopsins. The employed protein structures where obtained from X-ray crystallography (left panel) or through comparative modeling (center panel). Two sets of variants for bovine rhodopsin (Rh) and bacteriorhodopsin (bR) are also reported (right panel). The computed data were obtained using the a-ARM_default (blue up-turned triangles) and a-ARM_customized (gold squares). Experimental data, as energy difference corresponding to the wavelength of the absorption maxima, are also reported (red down-turned triangles). (B) Differences between computed and experimental excitation energies ΔΔE ^Exp_S1-S0 in both kcal mol⁻¹ (left axis) and eV (right axis).

As reported in Fig. 20, the employed protein structures used as template for the model constructions where obtained from X-ray crystallography (left panel) or through comparative modeling (center panel). Two sets of variants for bovine rhodopsins (Rh) and bacteriorhodopsin (bR) are also reported (right panels). The computed data were obtained using the a-ARM_default (167,170) (blue up-turned triangles) and a-ARM_customized (167) (yellow squares). Experimental data, as energy difference corresponding to the wavelength of the absorption maxima, are also reported (red down-turned triangles). All computed data are within a 3.0 kcal mol⁻¹ (0.13 eV) error, apart from a number of outliers that were corrected using a-ARM_customized which required the semiautomatic selection of, for instance, the conformation of a residue side chain or a change in the ionization state of an ionizable residue. Further details can be found in ref. (170)

Population dynamics during the light-triggered isomerization of homologue rhodopsins

Rod rhodopsin is the light-sensitive G-protein-coupled receptor responsible for dim-light vision in vertebrates. As anticipated above and illustrated in Fig. 19A and B, its activation is driven by a vibrationally coherent 11-cis to all-trans double-bond photoisomerization of the retinal chromophore which occurs with a 67% quantum efficiency triggers the receptor photocycle and, ultimately, visual transduction (9) From the above discussion, the first step in investigating such a mechanistic problem must be the construction of the QM/MM model of the photoreceptor capable to describe its spectroscopic and photochemical properties and, most importantly, which could allow to calculate Φ_cis-trans. The fraction of successful trajectories with respect to the total provides the Φ_cis-trans value (13) Of course, the trajectories require initial conditions (nuclear positions and velocities) consistent with a Boltzmann distribution. In the near future, we hope to be able to implement an automated initial condition generator as well as an automated way to start the required number of trajectories (few hundreds at least) directly in the a-ARM QM/MM model generator so that to automate the full procedure of computing Φ_cis-trans. The use of the constantly increasing number of CPU cores available either locally or at regional, national or international computer centers, would make such a research possible even for hundreds of rhodopsins hopefully representing different organisms and mutants. We are convinced that soon in the future studying systematically Φ_cis-trans in many diverse organisms will lead to new and fundamental knowledge on how proteins control photochemical reactions in general and what are the mechanistic spectrum achievable. Most importantly, we hope to “extract” from these calculations the general mechanistic rules, which must be based on factors such as the steric and electrostatic interactions between protein and chromophore, controlling the mechanistic spectrum and, most importantly, the Φ_cis-trans.

In Fig. 19C, we report, as demonstrative examples, the comparison between the population dynamics of three different Type II rhodopsin proteins all corresponding to visual pigments (one ancestral to indicate that the proposed calculations can also be applied to studies attempting to reconstruct the evolution of biological photoreceptors (163)). The result of each calculation is described in terms of progression along the α coordinate spanning the potential energy surface connecting the S₁ vertical excitation region to a decay region in the vicinity of IS_S1/S0, where the decay occurs at geometries where α is comprised between 60 and 120 degrees on timescales and the timescale goes from 30 to 180 fs. All results shown are based on automatically constructed α-ARM models and 200 trajectory simulations.

Unifying computational protocols for multiscale modeling of photoreceptor proteins

Computational protocols for multiscale modeling of photoreceptor proteins involve a large number of computer programs and protocols that are highly specialized for a particular modeling technique and scale of modeling (171) The new platform VIKING (Scandinavian Online Kit for Nanoscale Modelling, viking-suite.com) integrates a number of these tools in a single easy-to-use multiscale platform, which provides tools for setting up simulations, data analysis and visualization (172) VIKING alleviates the need for specialized know-how, which is traditionally required for each individual modeling technique, and also provides a standardized workflow, making the elaborate work of integrating multiple methods in a single study significantly more tractable and reproducible. The primary goal of VIKING is to deliver a set of standard protocols, which researchers can use to study complex functioning of biomolecular systems, such as photoreceptors. Furthermore, VIKING has been developed as a platform where new methods and protocols could be implemented with ease, once they become available to the broad research community.

VIKING lowers the entry barrier and time investment for computational studies of biomolecular processes occurring on sub-atomic to macromolecular scales and beyond. By making it easy to set up multiscale molecular models and employ a range of industry standard tools, VIKING provides a rapid workflow and illustrates simulation results in a 3D web viewer.

VIKING serves the purpose of a computational microscope, that is, a unique instrument for researchers. In particular, it provides a computational workflow for intuitive linking of existing modeling software, which so far existed as stand-alone programs. VIKING utilizes the established programs as engines to obtain scientific data and provides unique algorithms that are able to set up all the needed files for computations; earlier the process was often tedious even for experienced users. VIKING algorithms take the user through a carefully thought workflow (VIKING wizard, see Fig. 21). This VIKING wizard is relying on a unique approach as it integrates more than 15 years of research experience in computational biophysics, which allow the system to provide protocol templates to address practically any possible simulation that involves spatial scales ranging from electronic to the macromolecular assemblies. The simulation protocols include justified combination of simulation parameters that throughout decades were shown to be optimal for different types of biophysical simulations.

Fig. 21.

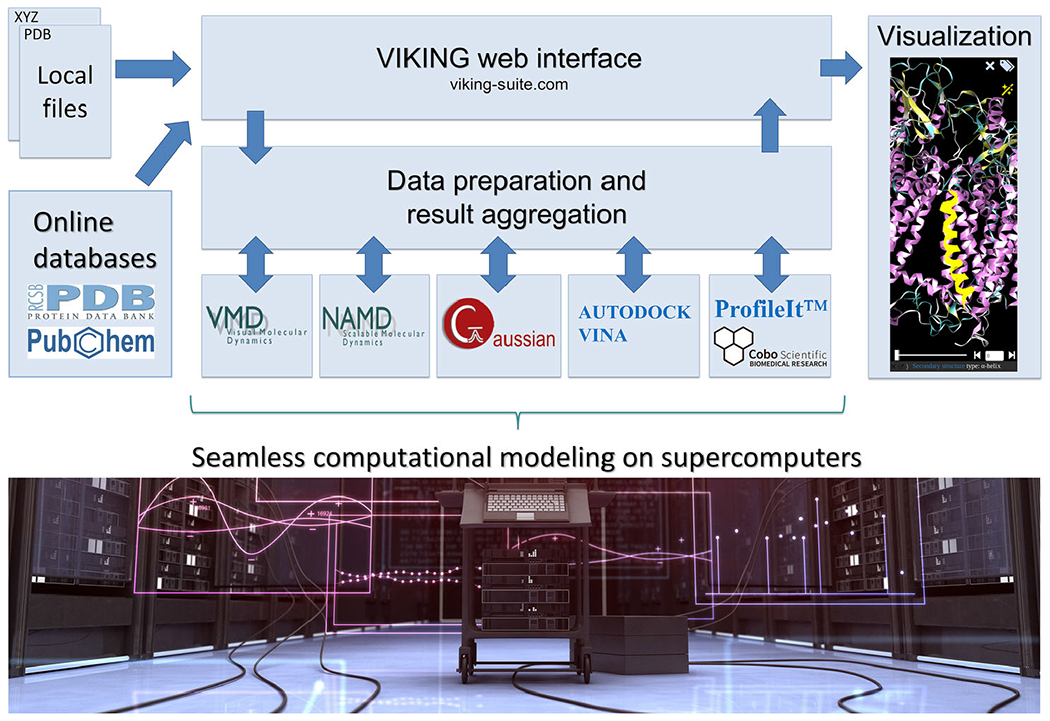
Concept and workflow of VIKING. Computational tasks are configured in the web interface by supplying the input data (structures, potentials, input field values etc), from the local computer or an online database. The simulation is then performed on a supercomputer (Stampede2, Marconi and Abacus 2.0 are currently supported), the results are aggregated and represented visually in the web browser. Supercomputer photograph courtesy of iStockphoto LP. Copyright 2012.

VIKING wizard addresses all the key questions that one has to answer to prepare needed input for simulations (provide a structure for the simulation, define temperature, pressure, level of theory, etc.); many technical parameters for simulations are then automatically determined by a complex algorithm based on the input provided by the user. This permits unexperienced users, unaware of the algorithmic backgrounds, not to worry about the technicalities. The automatic determination of simulation parameters relies on those simulation protocols that have been shown appropriate for a given simulation through decades of research experience. For example, classical MD simulations of biomolecules are handled through the MM potentials. In MD simulations, a complex molecular assembly is modeled by a set of interacting particles, whose evolution in time and space is calculated by numerical integration of Newton’s second law. In most cases, the parameters for numerical solutions of the Newton’s equation are standard, and the protocol for its solution in the case of a multimillion molecule can be automatized. MD simulations of biological systems in VIKING interface to some popular programs, currently NAMD (173), AMBER (174), MBN Explorer (175), and GROMACS (176). Interface to selected quantum chemical (QC) codes, for example, Gaussian (177), GAMESS (178), DALTON, (179) ORCA (180), and Firefly (181), or the spin dynamics code MolSpin, enables studying electronic processes in molecular systems and chemical reactions, which is important in the context of photoreceptive proteins. The capabilities can be further extended by enabling interfaces with other QC packages with the state-of-the-art methods for excited states, such as Q-Chem (25), Turbomole (182), and Molpro (183). Naturally, VIKING permits linking MD and QC simulations such that input for one calculation type can be used for another calculation. The multiscale nature of VIKING goes well beyond linking of MD and QC, as it provides the key framework to link any possible scale ranging from electronic to the scale of protein complexes. VIKING effectively prepares parameters for simulation on one scale from other complete simulations and thereby permits programs to exchange data in the most efficient way. VIKING handles the relevant chunks of data from one program into special file formats that permit effective communication between the codes on the dedicated VIKING server.

VIKING aspires to become the first tool to enable streaming support of biomedical data from supercomputers. High-performance computing (HPC) increasingly opens new frontiers for diverse research areas as well as for industrial applications; in this respect, computational investigations of photoreceptors are just one example. A traditional area of research, extensively using HPC, is computational biophysics, where MD and QC are typically employed to study the workings of complex biomolecular machineries in the minute detail. While the increasing HPC power enables researchers to study ever more complex molecular systems, the amount of data produced is becoming a serious challenge of its own—both in terms of storage and processing but also in terms of visual exploration; researchers need large data storage arrays, a fast network connection to the supercomputer and powerful computer workstations with large amounts of memory to explore and analyze the resulting datasets. VIKING is designed as powerful web-based visualization toolkit for atomistic simulations, which eventually will allow the user to visually explore results using any PC, without the need to download the data in full. Through invention of a unique specialized file format for storing simulation results, the VIKING toolkit will stream the compressed atomic coordinates from a server during “playback” of a simulation to the web browser on a client PC, which can then use the data to generate an animated visual representation of the studied molecular structure on the fly.

In summary, we envision that VIKING will become a versatile and convenient platform to (1) alleviate the growing logistic challenges when working with large-scale simulation data, (2) support broader adoption of biophysical simulations through easy-to-use and modern web-based tools and (3) enable direct sharing of simulation data through the web to any target audience.

CONCLUSION

Since its foundation more than 40 years ago, multiscale modeling has become a mature and vital research method. It has found wide application in the field of photoreceptor proteins. The hybrid QM/MM method is an essential tool for addressing electronic properties of biological chromophores, such as those present in biological photoreceptors. Despite the immense knowledge and experience collected over the last decades, numerous challenges still remain in the field. The high computational demand associated with these hybrid techniques, the large degree of freedom of the protein matrix and environment, the lack of structural and chemical information, and the complex nature of the electronic structure, significantly limits their applicability and presents the opportunity for future development. Practical applications of QM/MM approaches to various photoactive proteins, such as GFP, PYP, phytochrome, rhodopsin, and luciferase, clearly illustrate the urgent need for devising faster electronic structure codes for excited-state description, comprehensible protocols for transparent handling of structural data input and user-friendly software for the analysis and evaluation of computational output, as well as more robust and automated protocols for QM/MM simulations. These challenges and the progress in method developments were presented and thoroughly discussed at the CECAM meeting in Tel Aviv.

The participants introduced several conceptual and technical strategies for reducing the computational cost of QM/MM approaches. For instance, the exploration of potential energy surfaces of ground and excited states of chromophores in proteins can be more efficiently performed by combining QM/MM methodology with data-driven approaches, such as those based on interpolation schemes. The implementation of these data-driven approaches provides opportunities for further improvements with machine-learning techniques. High computational demand can be also overcome by rational simplification of the system under study. This simple approach has been shown to be effective for the anionic p-coumaric-acid thioester chromophore of PYP, for which linear correlations were found between excitation energies and charge transfer nature and BLA resulting from the combination of a set of resonance structures.

Many contributions highlighted the relevance of conformational sampling when computing molecular properties. The computational cost of any QM/MM calculation, however, increases enormously upon exploration of the conformational space, which is, for biological systems, still being commonly performed at a classical level. Thus, development and implementation of efficient and accurate hybrid QM/MM sampling techniques are urgently needed. The computational cost of studying reaction mechanisms can be drastically reduced, for example, by using path-based methods, which replaces the high-dimensional space of reaction coordinates by an optimizable curve in the collective variable space connecting two known states. Although the definition of adequate collective variables is not trivial, several cutting-edge methods based on clustering techniques are currently under development.

The complexity of the protein environment usually makes the computation of any ground-or excited-state property of biological chromophores demanding. Here, the fine tuning of protein electrostatics by protonation states of titratable amino acids and the dynamics of hydrogen bond networks should be adequately described. Whereas the protonation states of titratable side chain can be accurately predicted by Poisson–Boltzmann-based approaches combined with molecular dynamics simulations or in the form of constant-pH MD simulations, the analysis of the intricate hydrogen bond network is possible with the help of Bridge, a newly developed tool.

Finally, two strategies for user-friendly automation of multiscale modeling protocols of photoreceptor proteins were presented: the Automatic Rhodopsin Modeling (α-ARM), which is able to successfully reproduce and predict excited-state properties of rhodopsin-like photoreceptor. Further, the VIKING project offers a general online platform interfacing various quantum chemical codes and molecular dynamics packages for multiscale modeling of complex biological systems.

The rapid growth of high-performance computing technologies, including the emergence of new and potent mathematical algorithms and their implementations in more user-friendly and automated codes, will certainly support the development and implementation of multiscale modeling methods toward higher accuracy and expand their applicability to larger and more complex dynamical biological systems.

Abbreviations:

ARM

Automatic Rhodopsin Modeling

BLA

Bond Length Alternation

BLUF

Blue-light Using Flavin

BV

Biliverdin

CBCRS

Cyanobacteriochromes

CC

Coupled Cluster

CECAM

Centre of Europeen de Calcul Atomique et Moleculaire

CoIns

Conical intersections

CpHMD

Constant-pH Molecular Dynamics

CVS

Collective Variables

DB

Double Bond

EFP

Effective Fragment Potential

EGFP

Enhanced Green Fluorescent Protein

EGFP-T65G

EGFP with a Mutation on Residue 65 Changing Threonine to Glycine

ESPF

Electrostatic Potential Fitted

EYFP

Enhanced Yellow Fluorescent Protein

EYFP-G65T

EYFP with a Mutation on Residue 65 changing Glycine to Threonine

FDET

Frozen-Density Embedding Theory

GFP

Green Fluorescent Protein

GYG

Glycine–Tyrosine–Glycine Chromophore

HOMO

Highest Occupied Molecular Orbital

HPC

High-Performance Computing

LUMO

Lowest Unoccupied Molecular Orbital

MAE

Mean Average Error

MC

Monte Carlo

MCSCF

Multi-configurational Self-consistent Field

MD

Molecular Dynamics

MM

Molecular Mechanics

PBE

Poisson–Boltzmann equation

PCB

Phycocyanobilin

pCT⁻

p-coumaric Acid Thioester

PE

Polarizable Embedding

PES

Potential Energy Surface

Pfr

Far-red Light-Absorbing State

Pg

Green Light-Absorbing State

Pr

Red light-Absorbing State

pscB

Propionic Side Chain on ring B of BV

PYP

Photoactive Yellow Protein

QC

Quantum Chemical

QM

Quantum Mechanics

QM/MM

Quantum mechanics/Molecular mechanics

RESP

Restraint Electrostatic Potential

Rh

Rhodopsin

S₀

Singlet Ground State

S₁

First Excited Singlet State

SB

Single Bond

TD-DFT

Time-dependent Density Functional Theory

TPS

Transition Path Sampling

TYG

Threonine–Tyrosine–Glycine Chromophore

Biographies

AUTHOR BIOGRAPHIES

Maria-Andrea Mroginski studied physics at the Universidad Nacional del Nordeste in Argentina. As DAAD scholar, she performed her PhD simultaneously at the Max Planck Institute für Strahlenchemie (Germany) and at the University of the La Plata (Argentina) on Resonance Raman spectra of various compound via experimental and computational approaches under the guidance of Prof. Hildebrandt, Dr. Mark and Dr. Della-Vedova. After a Postdoc in Portugal, she became 2004 junior group leader at the TU-Berlin and later, 2009, junior professor for molecular modeling at the same institution. 2015 she was appointed to a W2-professor position in biomolecular modeling at TU-Berlin.

Igor Schapiro has studied Chemistry at the University of Duisburg-Essen. He obtained a Ph.D. under the supervision of Prof. Volker Buss. At the postdoctoral stage, he worked with Prof. Massimo Olivucci at Bowling Green State University, with Prof. Frank Neese at the Max Planck Institute for Chemical Energy Conversion in Mülheim, and with Prof. Stefan Haacke at the Institute of Physics and Chemistry of Materials of Strasbourg. In 2015, he became Senior Lecturer and in 2020 Associate Professor at the Institute of Chemistry at The Hebrew University of Jerusalem. His research focuses on the Computational Photochemistry and the method development.