Clustering Initiated Multiphase Active Contours and Robust Separation of Nuclei Groups for Tissue Segmentation

Abstract

Computer assisted or automated histological grading of tissue biopsies for clinical cancer care is a long-studied but challenging problem. It requires sophisticated algorithms for image segmentation, tissue architecture characterization, global texture feature extraction, and high-dimensional clustering and classification algorithms. Currently there are no automatic image-based grading systems for quantitative pathology of cancer tissues. We describe a novel approach for tissue segmentation using fuzzy spatial clustering, vector-based multiphase level set active contours and nuclei detection using an iterative kernel voting scheme that is robust even in the case of clumped touching nuclei. Early results show that we can reach a 91% detection rate compared to manual ground truth of cell nuclei centers across a range of prostate cancer grades.

1. Introduction

The availability of high resolution multispectral multimodal imaging of tissue biopsies provides a new opportunity to develop improved tissue segmentation algorithms for computer-aided diagnostic classification of histopathological images in a clinical setting. Typical histopathology imagery are RGB-color based on scanning hematoxylin and eosin stained (prostate) tissue and imaged at 40× optical magnification using a rapid whole slide scanner. Quantitative Gleason grading of prostate cancer tissue patches approaching expert levels can be achieved using a combination of low level image texture features and high level graph-based tissue architecture features [2]. A multiresolution approach using global texture features including first- and second-order statistics combined with a Gabor filter set was able to achieve over 90% overall accuracy in distinguishing between cancerous and benign tissue, and nearly 77% in distinguishing between two complex grades of cancer (Gleason grade 3 and 4 adenocarcinoma). However, the architectural features of gland structures including spatial distribution of cell nuclei and the arrangement of glands were manually determined [2]. Recently, semi-automated image segmentation algorithms requiring prior probability estimates for the lumen structures and pixel-wise classification was developed to facilitate the extraction of spatial arrangement information [5]. In this paper, we develop a fully automatic robust image segmentation algorithm for histopathology imagery using a three step process including fuzzy spatial clustering for class initialization, tissue class refinement using vector-based multiphase level sets to accurately extract lumen area, epithelial cytoplasm and epithelial nuclei regions [5], followed by detection of nuclei centers even within merged groups using iterative voting and oriented kernels.

2. Fuzzy C-means with Spatial Constraint

A modified version of the fuzzy c-means (FCM) algorithm is used to initialize the level set segmentation refinement process. FCM minimizes the sum of similarity measures objective function J(U, V) given by

$$J(U,V)=\sum _{i=1}^C\sum _{j=1}^N{u}_{ij}^m{\left|\right|x_j-v_i\left|\right|}^2$$ (1)

where X = {x₁, x₂, …, x_N} denotes the set of data (pixel feature vectors), V = {v₁, v₂, …, v_C} represents the prototypes, known as the clusters centers, U = [u_ij] is the partition matrix which satisfies the condition, ${\sum }_i^C{u}_{ij}=1\forall j$, and m is a fuzzifier which indicates the fuzziness of membership for each point. The FCM algorithm is an iterative process for minimizing the membership distance between each point and the prototypes. However, the objective function Eq. 1 does not explicitly include any spatial information. Incorporating spatial information provides more robustness and efficiency to the fuzzy c-means algorithm by adding a second term to the FCM objective function [3],

$$J_M(U,V)=\sum _{i=1}^C\sum _{j=1}^N{u}_{ij}^m{\left|\right|x_j-v_i\left|\right|}^2+\alpha \sum _{i=1}^C\sum _{j=1}^N{u}_{ij}^m{e}^{-{\sum }_{k\in \mathrm{\Omega }}{u}_{ik}^m}$$ (2)

where Ω is a set of neighbors. The parameter α is a weight that controls the influence of the second term. The objective function (2) has two components. The first component is the same as FCM, the second is a penalty term. This component reaches a minimum when the membership value of neighbors in a particular cluster is large. The optimization of (2) with respect to U is solved by using Lagrange multipliers and the membership function update equation is,

$$u_{ij}=\frac{1}{{\sum }_{p=1}^C{\left(\frac{{\left|\right|x_j-v_i\left|\right|}^2+\alpha e^{-{\sum }_{k\in \mathrm{\Omega }}{u}_{ik}^m}}{{\left|\right|x_j-v_p\left|\right|}^2+\alpha e^{-{\sum }_{k\in \mathrm{\Omega }}{u}_{pk}^m}}\right)}^{\frac{1}{m-1}}}$$ (3)

The neighboring membership values (u_pk) influence u_ij to follow the neighborhood behavior. For instance if a given point has a high membership value to a particular cluster and its spatial neighbors have a small membership values to this cluster, the penalty term plays the role to force the point to belong to the same cluster as its neighbors. The weight α controls the importance of the regularization term. The prototype update equation is the same as standard FCM. The spatial constraint FCM (SCFCM) algorithm consists in the same steps as the original fuzzy c-means algorithm.

3. Multiphase Vector-based Active Contours

A single level set has two-phases and provides a binary partition of a scalar image by minimizing an energy functional composed of grayscale intensity variations and the interface length between boundaries [1]. Histopathology imagery are typically color which requires a vector-based level set formulation, and have four classes (lumen, cytoplasm, nuclei, other) which requires either multiple level sets (one per class) or multiple phases [8]. We propose combining both approaches to develop a multiphase vector-based active contour segmentation algorithm. Multiphase level sets usually minimize a reduced or weak, minimal partition Mumford-Shah functional [4],

$$F_n(\mathbf{c},\mathrm{\Phi })=\underset{\text{Energy}\text{Term}}{\underbrace{\sum _{1\le i\le n=2^m}{\lambda }_i{\int }_{\mathrm{\Omega }}{(u_0-c_i)}^2{\chi }_{i}d\mathbf{x}}}+\underset{\text{Length}\text{Term}}{\underbrace{\sum _{1\le i\le n=2^m}{\mu }_i{\int }_{\mathrm{\Omega }}\mid \nabla {\chi }_i\mid }}$$ (4)

where, n is the total number of classes associated with m level set functions, u₀ is the gray-level image being segmented, Φ is a vector of level set functions, c is a vector of mean gray-level values (i.e., c_i = mean(u₀) in the class i), χ_i is the characteristic function for each class i represented by the associated Heaviside functions H(φ_i), and (λ_i, μ_i) are constants associated with each energy and length term of the functional F_n(c, Φ). In order to simplify computation of the length term in the reduced Mumford-Shah energy functional, we replace the measure of the characteristic functions by the sum of the length of the zero-level sets of φ_i, Σ_1≤i≤n μ_i ∫_Ω |∇H(φ_i)|. Instead of an unweighted total length, this approximation weights some edges more than others, but is faster to compute and still leads to satisfactory segmentation results.

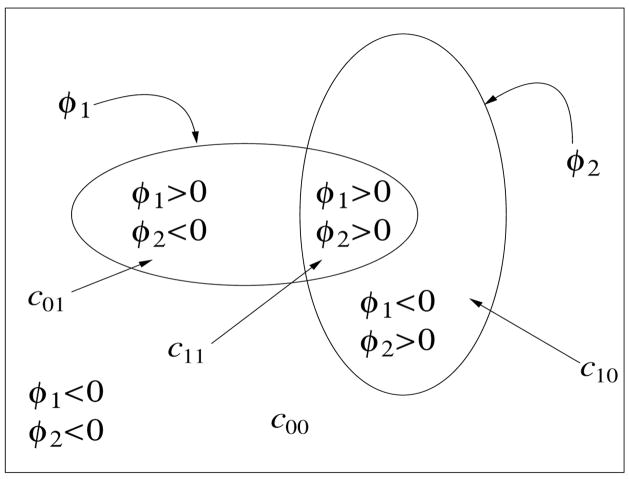
Using multiple phases the number of level sets grows only logarithmically with the number of classes instead of linearly and also has the advantage of avoiding vacuums and overlaps in the final multiclass segmentation. Usually two- or three-level set multiphase segmentations (four to eight classes) is often sufficient for histopathology imagery. Let us consider the two level set case (i.e., m = 2) that partitions a domain Ω into at most four classes as illustrated in Fig. 1. Let c = (c₀₀, c₀₁, c₁₀, c₁₁) represent a vector of average color-intensity values corresponding to each class/region with Φ = (φ₁, φ₂) being the two level set functions. The energy functional F_n(c, Φ) can thus be written as,

Figure 1.

A four-phase level set partitioning, with two level set functions φ₁ and φ₂, for segmenting a grey level image u₀. c = (c₀₀, c₀₁, c₁₀, c₁₁) represents the average gray-level values for various phases. H(φ₁) and H(φ₂) are the Heaviside functions associated with the level set functions.

$$F_n(\mathbf{c},\mathrm{\Phi })={\lambda }_1{\int }_{\mathrm{\Omega }}{\mid u_0-c_{00}\mid }^2(1-H({\phi }_1))(1-H({\phi }_2))d\mathbf{x}+{\lambda }_2{\int }_{\mathrm{\Omega }}{\mid u_0-c_{01}\mid }^2(1-H({\phi }_1))H({\phi }_2)d\mathbf{x}+{\lambda }_3{\int }_{\mathrm{\Omega }}{\mid u_0-c_{10}\mid }^{2}H({\phi }_1)(1-H({\phi }_2))d\mathbf{x}+{\lambda }_4{\int }_{\mathrm{\Omega }}{\mid u_0-c_{11}\mid }^{2}H({\phi }_1)H({\phi }_2)d\mathbf{x}+{\mu }_1{\int }_{\mathrm{\Omega }}\mid \nabla H({\phi }_1)\mid d\mathbf{x}+{\mu }_2{\int }_{\mathrm{\Omega }}\mid \nabla H({\phi }_2)\mid d\mathbf{x}$$ (5)

The Euler-Lagrange equations obtained by minimizing Eq. 5 is used to embed (c, Φ) in a dynamical system [8],

$$\begin{array}{l}\frac{\partial {\phi }_1}{\partial t}=\delta ({\phi }_1)\left\{{\mu }_1\text{div}(\frac{\nabla {\phi }_1}{\mid \nabla {\phi }_1\mid })-(\{{\lambda }_1{\mid u_0-c_{11}\mid }^2-{\lambda }_3{\mid u_0-c_{01}\mid }^2\}H({\phi }_2)+\{{\lambda }_2{\mid u_0-c_{10}\mid }^2-{\lambda }_4{\mid u_0-c_{00}\mid }^2\}\{1-H({\phi }_2)\})\right\},\\ \frac{\partial {\phi }_2}{\partial t}=\delta ({\phi }_2)\left\{{\mu }_2\text{div}(\frac{\nabla {\phi }_2}{\mid \nabla {\phi }_2\mid })-(\{{\lambda }_1{\mid u_0-c_{11}\mid }^2-{\lambda }_2{\mid u_0-c_{10}\mid }^2\}H({\phi }_1)+\{{\lambda }_3{\mid u_0-c_{01}\mid }^2-{\lambda }_4{\mid u_0-c_{00}\mid }^2\}\{1-H({\phi }_1)\})\right\}\end{array}$$ (6)

where, c_ij are the mean regional color intensities for each corresponding phase and δ(φ_k) = H′(φ_k) is the Dirac delta function. For numerical stability of the delta function, Chan and Vese propose using a regularized Heaviside function, $H_{2,\epsilon }(x)=\frac{1}{2}\left[1+\frac{2}{\pi }\left\{{\mathit{tan}}^{-1}(\frac{x}{\epsilon })\right\}\right]$ with ${\delta }_{\epsilon }(x)=\frac{1}{\pi }\frac{\epsilon }{{\pi }^2+{\epsilon }^2}$ The motivation for using a multiphase, rather than a two-phase, level set framework is to accurately detect adjacent regions that meet at a junction (i.e., the triple junction in [8]).

4. Nucleus Center Detection

The shape and organization of glandular and nuclear structures within a histological image is related to tissue type and can be used in classifying Gleason grades. Graphs describing the spatial arrangement of nuclei (i.e. Delaunay triangulation of nuclei centers) along with other spatial features can be used for Gleason grading [2]. The algorithm described in this section is based on a recent Hough transform-like approach for detecting centers of individual cell nuclei based on the segmented nucleus clusters (see previous section). We extend the iterative voting using oriented kernels method developed by Parvin, et al [6] and refined by Schmitt and Hasse [7] to incorporate an improved shaping function for more robust segmentation of touching nuclei in densely clustered regions.

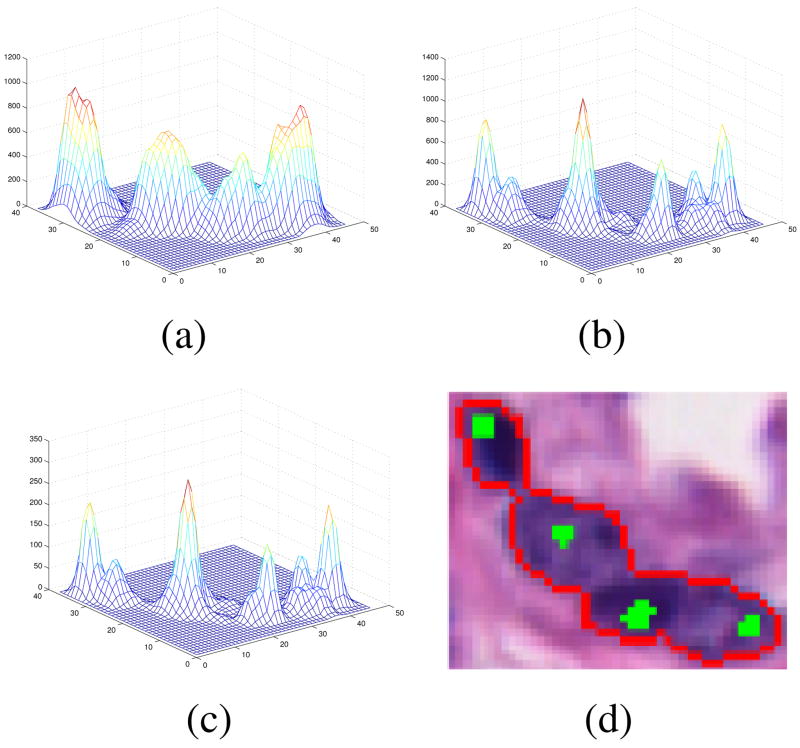
The approach detects nuclei centers from incomplete or merged boundary information through voting and perceptual grouping. A series of cone-shaped kernels (Fig. 2) is applied that vote iteratively along the radial or tangential directions [6]. The iterative process refines the center of mass at each iteration and terminates after convergence to a focal response. At each iteration, for each location along the contour, the voting kernel is aligned along the maximum response in the voting space. The shape of the kernel is refined and focused within the iterative process, which we have improved for better noise immunity and to handle closely grouped nuclei. Fig. 3 shows evolution of the voting landscape V(i, j) and the resulting centers for a small group of nuclei.

Figure 2.

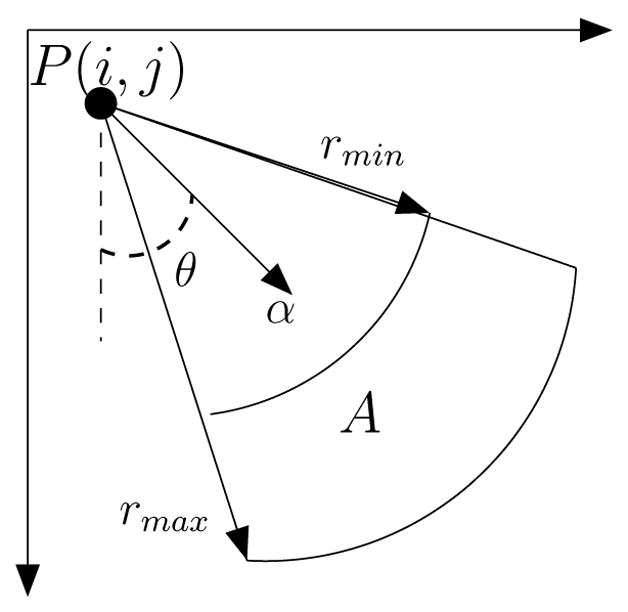
Cone shaped kernel and the voting area A.

Figure 3.

Evolution of the voting landscape V(i, j) for a nucleus cluster image. (a) iteration=1, (b) iteration=5, (c) iteration=10, (d) nucleus contours (red) and centers (green) superimposed on the original image.

5. Results and Discussion

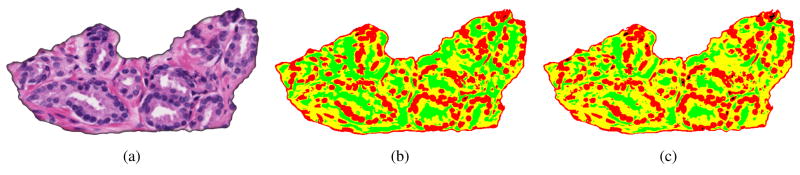
We used 8 images for testing¹, two per class: Benign Epithelium, Benign Stroma, Grade 3 and Grade 4. Performance was evaluated by measuring the detection and localization accuracy of extracted nuclei centers compared to ground truth provided by histopathology experts. Fig. 4 shows a reduced resolution Grade 4 image, with initial regions from SCFCM segmentation and the final four class segmentation using the multiphase vector Chan and Vese level-set algorithm. Once the cell nuclei regions are segmented their centers are estimated using the improved iterative voting scheme which also provides an accurate measure of tissue cell count. A number of more general nuclei or point matching statistics are measured to evaluate the quality of the automatically detected (DT) nuclei centers compared to the ground truth (GT). A one-to-one match is where each detected nucleus corresponds exactly to one ground truth point. A many-to-one match (ie fragmentation/over-segmentation) means that multiple detected nuclei centers are close enough to be matched to one ground truth point (ie nuclei center). A one-to-many match (ie merge/under-segmentation) is the opposite case where one detected center corresponds to multiple ground truth points often corresponding to a cluster. False negatives (FN) are missed nuclei. False detections or false positives (FP) are those detected centers which do not match to any nearby ground truth point. Table 1 shows the results for 8 images compared to the number and spatial distribution of nuclei in the ground truth (GT). The different error statistics are related as,

Figure 4.

Example of segmentation (a) original Grade 3 image (812 b s50 p1.tif) (b) initial segmentation with SCFCM (c) final segmentation using level sets.

Table 1.

Detailed statistics comparing automatic nuclei center detection accuracy compared to ground truth.

Category	#GT	#DT	#TP	#Match 1-to-1	#Match 1-to-Many GT	#Match Many-to-1 GT	#FN	#FP
Benign Epithelium	281	245	222	199(71%)	65(23%)	15(5%)	2(1%)	3(1%)
Benign Stroma	286	382	234	224(78%)	44(15%)	7(2%)	11(4%)	59(20%)
Grade 3	553	601	463	427(77%)	83(15%)	22(4%)	21(4%)	8(1%)
Grade 4	1425	1361	1225	1140(80%)	234(16%)	47(3%)	4(0%)	10(1%)

$$\#(\text{TP})=\#(1-to-1)+\#(\text{Fragmented})+\#(\text{Merged}\text{clusters})$$ (7)

$$\#(\text{GT})=\#(1-to-1)+\#(\text{Many}-to-1)+\#(1-to-\text{Many})+\#(\text{FN})$$ (8)

$$\text{Recall}=\frac{\#(\text{TP})}{\#(\text{GT})}\text{Precision}=\frac{\#(\text{TP})}{\#(\text{DT})}$$ (9)

Table 2 shows the overall performance using the quality measures Recall and Precision. Surprisingly, Grade 4 images have the best percentage of recall and precision even though they contain the largest number of epithelial nuclei compared to the other histological imagery.

Table 2.

Recall and precision rates for nuclei detection in different cancer grade images.

Category	Recall	Precision
Benign Epithelium	79%	91%
Benign Stroma	82%	61%
Grade 3	84%	77%
Grade 4	86%	90%

6 Conclusions

We have developed a promising, fully automatic approach for segmenting and counting epithelial nuclei in histopathology imagery, one of the most difficult tasks for automated prostate gland cancer grading. It is interesting to note that the proposed algorithm performs best for the complex Grade 4 cases where the density and number of clustered nuclei in Grade 4 images is highest. This is likely due to the salient spectral color and distinct boundaries between epithelial nuclei and surrounding epithelial cytoplasm regions reflecting morphological changes in late stage cancer tissue. In future work we will incorporate an incremental learning process to achieve higher overall detection rates.