On-scalp magnetocorticography with optically pumped magnetometers: Simulated performance in resolving simultaneous sources

Abstract

Currently, the gold standard for high-resolution mapping of cortical electrophysiological activity is invasive electrocorticography (ECoG), a procedure that carries with it the risk of serious morbidity and mortality. Due to these risks, the use of ECoG is largely limited to pre-surgical mapping in intractable epilepsy. Nevertheless, many seminal studies in neuroscience have utilized ECoG to explore domains such as visual perception, attention, auditory processing, and sensorimotor behavior. Studies such as these, occurring in patients with epilepsy rather than healthy controls, may lack generalizability, and are limited by the placement of the electrode arrays over the presumed seizure focus. This manuscript explores the use of optically pumped magnetometers (OPMs) to create a non-invasive alternative to ECoG, which we refer to as magnetocorticography. Because prior ECoG studies reveal that most cognitive processes are driven by multiple, simultaneous independent neuronal assemblies, we characterize the ability of a theoretical 56-channel dense OPM array to resolve simultaneous independent sources, and compare it to currently available SQUID devices, as well as OPM arrays with inter-sensor spacings more typical of other systems in development. Our evaluation of this theoretical system assesses many potential sources of error, including errors of sensor calibration and position. In addition, we investigate the influence of geometrical and anatomical factors on array performance. Our simulations reveal the potential of high-density, on-scalp OPM MEG devices to localize electrophysiological brain responses at unprecedented resolution for a non-invasive device.

1. Introduction

Although other invasive electrophysiological approaches such as microarrays (Truccolo et al., 2011) and stereotactic EEG exist (Nagahama et al., 2018), the gold standard for high-resolution mapping of the cortex is invasive electrocorticography (ECoG). Because of the high risks of morbidity and mortality (Rolston et al., 2015), ECoG is generally only used in situations such as pre-surgical planning for epilepsy. Despite this, many seminal studies have utilized ECoG in patients with epilepsy to also investigate basic neurocognitive processes. Due to the prevalence of temporal lobe epilepsy, the auditory and language systems have been studied extensively using ECoG. A study of language processing revealed that even a relatively simple word recognition task activated seven areas encompassed by standard subdural grids, with up to four areas simultaneously active (Zheng et al., 2021). While one ECoG study revealed distinct neuronal populations performing high frequency amplitude and low frequency phase tracking of auditory speech (Zion Golumbic et al., 2013), another identified distinct areas for expressive and receptive speech (Towle et al., 2008). ECoG has also been used to investigate other domains. A study of visual processing revealed a complex interplay between phase and frequency across cortical sites (Miller et al., 2010). During imagined movement, ECoG revealed distinct neuronal populations generating alpha and beta rhythms in sensorimotor cortex (Stolk et al., 2019). Without ECoG, research has shown that even the simplest appearing processes in the cortex may consist of many simultaneous subprocesses; for example, the N100 auditory evoked potential consists of at least six underlying simultaneous components (Naatanen and Picton, 1987). Studies investigating correlation structure of traditional and microarray ECoG have found that independent signals can be detected at sub-millimeter resolution (Maier et al., 2010; Bullock and McClune, 1989), and that correlations between electrodes are largely due to the spatial extent of local field potentials (Rogers et al., 2019). Taken together, these studies suggest that ECoG can resolve multiple, closely spaced, simultaneous independent sources.

While MEG is a unique modality for measuring electrophysiological activity of the brain with both high temporal resolution (greater than 100 Hz), and moderate (5–10 mm) spatial resolution, whole-head MEG systems are not capable of distinguishing among closely spaced independent sources of similar amplitude. To understand why that is the case, factors affecting the spatial resolution of MEG systems need to be considered. Traditional SQUID based MEG systems require a fixed helmet with substantial thermal insulation, which inevitably creates a gap between the scalp and the sensor and imposes a fixed inter-sensor distance. Besides sensor array geometry, other factors affecting the spatial resolution are the inherent sensor noise, the accuracy of the forward model, the signal-to-noise ratio (SNR) of the measurements, the presence of interfering sources, and the cortical geometry (including cortical surface orientation) apart from any co-registration issues.

Technological progress in recent years have led to the development of magnetic field sensors called optically pumped magnetometers (OPMs), which have the potential to overcome the limitations of the current SQUID based MEG devices. OPMs measure magnetic field changes by measuring the transmission of laser light through a gas of alkali metal atoms (such as Rubidium, ⁸⁷Rb). Fluctuations in the magnetic field affect the transparency of the vapor, which results in changes in the amount of light at the photodetector site. OPMs can be placed directly on the scalp, thereby decreasing the distance between the sensors and the cortical sources. This arrangement allows sampling of higher spatial frequencies of cortical activity, dramatically improving SNR, and thus improving spatial resolution (Boto et al., 2016; Borna et al., 2020). In addition, decreasing the distance between adjacent sensors can also improve the ability of MEG to resolve and accurately discriminate among multiple independent sources. OPM systems have additional advantages including the lack of need for cryogens and the ability to construct wearable systems that can move with the participant (Boto et al., 2018). Most work developing OPM MEG arrays has focused on whole-head systems to replace traditional SQUID MEG. In contrast, a system designed to accurately discriminate among multiple, closely spaced simultaneous sources would need to evaluate activity for a restricted region of the cortex, but at greater spatial resolution (analogous to ECoG grids). While a whole head array at this density may not be currently feasible, OPM arrays sampling a portion of the cortex at high density are presently achievable and are thus the focus of this investigation.

Prior authors have simulated various aspects of OPM array performance and their comparison to commercial SQUID MEG arrays. The simplest simulation involves measuring signal to noise; simulating a single dipole predicts a ten-fold increase in SNR for an on-scalp whole head system compared to a traditional axial gradiometer SQUID MEG system (Iivanainen et al., 2017). Correlation of the simulated time course for a source with its reconstructed time course is another convenient measure of source reconstruction accuracy. For cortical sources, correlations between simulated and reconstructed sources were greater than 0.9 everywhere on the cortical surface for an OPM array, with lower correlations observed for an axial gradiometer SQUID system (Boto et al., 2016). Additionally, the simulated OPM system exhibited less signal leakage into neighboring dipole locations (Boto et al., 2016). Another metric involves correlating source topographies to determine localization accuracy. Using this metric, average peak position errors were similar between radial OPM magnetometers (5.1 mm), SQUID magnetometers (7.9 mm) and SQUID planar gradiometers (5.2 mm) (Iivanainen et al., 2017). Another OPM simulation study showed that errors in the position of sensors (i.e., 2–6 mm) result in large (7.5–20%) errors in the reconstructed topography of the lead fields, i.e., fields generated by each source at the location of each sensor. Likewise, errors in the orientation of the sensor sensitive axis (5–15°) also result in large (4.8–14.7%) errors in the reconstructed topography (Zetter et al., 2018). Another straightforward metric is to measure the distance between the location of a simulated dipole source and the peak of the linearly constrained minimum variance (LCMV) beamformer source reconstruction. One study calculated this distance to be 7.9 mm for an array of OPM magnetometers, while mean errors of 10.7 mm and 11.4 mm were calculated for SQUID magnetometers or a combined magnetometer/planar gradiometer SQUID system, respectively (Zetter et al., 2018). Fewer simulations have investigated the performance of systems using multiple simultaneous sources. In the presence of five interference sources, the correlation between reconstructed and simulated time courses for a source of interest was found to be 0.7 for an OPM system and around 0.5 for an axial gradiometer SQUID system (Boto et al., 2016). These same simulations showed that the improvement in correlation relies strongly on accurate lead field estimation (Boto et al., 2016). Another simulation in the same report showed that an OPM system could differentiate two dipoles with orthogonal time series that were 2.5 mm apart, while a SQUID system could only resolve sources 6.5 mm apart (Boto et al., 2016). Importantly, while this report did utilize multiple simultaneous sources, the authors did not investigation how the discrimination of sources was affected by sensor array characteristics or calibration errors. In interpreting these studies, it should be noted that metrics related to source localization accuracy of beamformers are dependent on signal to noise and may vary between recovered sources in an image.

The purpose of this study is the evaluation of a proposed OPM sensor array designed specifically for magnetocorticography (MCoG), and its comparison with existing magnetoencephalography (MEG) instruments, with a focus on the discrimination of simultaneous sources. This simulation study differs from and extends previous work in several ways. First, our simulations are based on a spatially dense OPM sensor array that, like ECoG, is optimized for resolving activity within a small patch of cortex, while most previous work has focused on whole head OPM arrays with more widely spaced sensors. One study has simulated high density whole head OPM arrays but does not comprehensively address errors inherent in OPM systems (Boto et al., 2016). Furthermore, whole brain arrays with high resolution are not currently feasible; one study determined that 500 sensors would be required to spatially discriminate sources at 6 mm (Tierney et al., 2020). Nevertheless, given that we focus this investigation on the cortical area directly under the array, a dense whole-head array would be expected to have similar performance for cortical sources. The second novel contribution of this study is that we focus on differentiating simultaneous independent sources instead of focusing on single sources, as has been the focus of most prior studies. We will quantify performance in part by defining an independent source resolution metric (ISR) as a measure of the ability of a sensor array to discriminate source activity at biologically plausible intervals. Third, unlike the work of previous investigators, we recognize that a crucial factor limiting the resolution of independent sources is the presence of interfering source activity. While prior investigators have considered single or few (Boto et al., 2016; Brookes et al., 2021) interfering sources, we have developed a brain noise model to which sensor noise and test sources can be superposed. This model is validated by comparison with task-free brain activity measured with existing MEG sensor arrays. Lastly, we assess the effect of factors involved in the design of a sensor array, including the gap between the array and the scalp, and errors in the known positions and orientations of the sensors, as well as errors attributable to phenomena such as crosstalk and perturbation of the true sensor axis.

2. Methods

The purpose of the simulations is to characterize the performance of a densely packed array of OPMs that can be developed using existing technology. Because commercially available MEG systems currently in use utilize traditional low-temperature SQUID systems, we include the simulated performance of a SQUID MEG system for comparison purposes. Thus, simulations are based on SQUID and OPM sensors currently used in the National Institutes of Mental Health MEG Core Facility: a CTF 275 whole head MEG system (CTF MEG, Coquitlam, B.C., Canada) and FieldLine V2 OPM sensors (FieldLine, Inc., Boulder, CO). While other commercially available sensors exist, potentially with the advantage of multiple axes of sensitivity, we focus on a sensor offering closed loop mode on a single axis to avoid nonlinearity and reductions in sensitivity inherent in a multi-axis sensor. Because we are not attempting to fully characterize the SQUID system, we evaluate it “as built” rather than assessing performance in the presence of errors.

2.1. Noise model

The ability of a magnetometer sensor array to resolve multiple independent sources is limited by the presence of interfering neural sources (the brain noise), sensor noise, sensor geometry, and cortical geometry. In this section we describe the methods used for noise simulation. Sensor noise for both SQUID and OPM sensors was simulated using a Gaussian random sample generator with zero mean and standard deviation equal to the specified root mean square (RMS) noise. We assumed a noise density of 5 fT/√Hz for the SQUID sensors and 10 fT/√Hz for the OPM sensors. Brain noise was generated by an empirical model. We present our final model and brief description of our validation here and present the full verification of the model in the Supplemental Materials. All simulations were performed using in-house code developed in C (distributed as part of the SAM suite https://github.com/nih-megcore/SAMsrcV5), with python used for visualization. Realistic brain noise was simulated by 2000 dipoles randomly located within a hemispherical shell ranging from 60 to 80 mm in radius. Because most MEG signals are generated by cortical pyramidal cells, we constrained sources to a spherical shell rather than the full volume. The 20 mm shell thickness was chosen to capture the depth below the skull of most sources, given gyrification of the cortex. The amplitude of noise sources ranged from Q_min = 1.0 pA-m/√Hz to Q_max = 1.0 nA-m/√Hz, according to the following power law, where p = 6.

$$Q_i={(i/N)}^p\left(Q_{max}-Q_{min}\right)+Q_{min}$$

All brain noise dipole sources had a random orientation in the plane tangential to the surface of the sphere. In addition, we assume coupling among brain noise sources. This is modeled by applying a modulus parameter of M = 10 such that every group of 10 consecutive dipoles had the same time series (scaled by the previously defined random noise amplitude). In order to verify that our model approximated ongoing brain activity, we placed a single simulated test source in a source localized resting state dataset, as well as in the noise shell of our simulated geometry. We compared noise density, width of the beamformer reconstruction of the test source, and the eigenvalue spectra from real and simulated data.

2.2. Geometry and simulation characteristics

The simulation geometry is shown in Fig. 1. The origin was established as the center of the hemispherical shell containing the simulated brain noise sources. For the OPM system (Fig. 1A), the OPM sensors are arranged in a rectangular array 7 sensors wide and 8 sensors long to achieve a roughly square array, given the 13 × 15 mm footprint of the commercial OPM sensors. As a baseline, all simulations use a 13 × 15mm spacing of the sensors, although as detailed later, we explore the effects of varying this density. Published values for scalp to cortex distance are approximately 15 mm for the motor cortex (Lu et al., 2019). Adding extra distance for a cap or other device holding the array, as well as to compensate for the standoff of the ⁸⁷Rb cell within the fixture containing them (on the order of 4–5 mm), we set the OPM array at a radius of 102 mm (22 mm above the brain noise shell). For simulations using the CTF-275 MEG system (Fig. 1B), we used sensor positions derived from our system at NIH, which has 272 functional sensors. The maximum z-coordinate for the CTF array was approximately 110 mm. This would place the apex of the CTF array approximately 30 mm above the noise shell. Note that this would represent a best-case-scenario where the head was as high as possible into the MEG helmet; the majority of the sensors would be substantially further away from the sources.

Fig. 1.

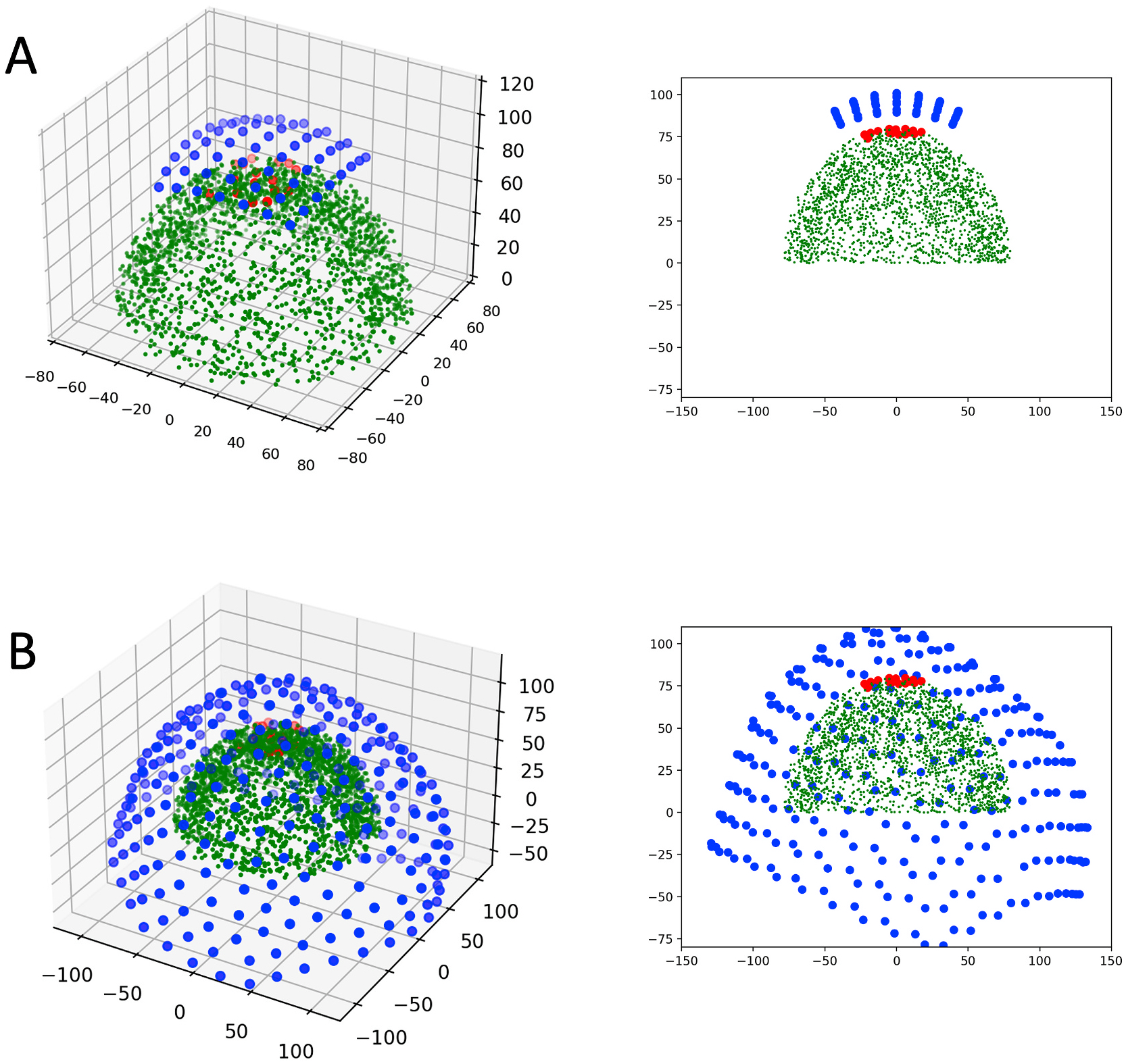
Illustration of the simulation geometry for the A) magnetocorticography array simulation and the B) CTF-275 simulation. Left panes illustrate the geometry in 3D while the right panes illustrate a projection onto the y-z plane. Scattered green dots represent the noise sources, while test sources and sensors are depicted in red and blue, respectively. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

The array of test source dipoles were randomly positioned within a 50 × 50 mm square, projected onto a spherical surface within or on the outer surface of the noise shell. As introduced in the last section, brain noise sources occupied a hemispherical shell with radius ranging between 60 and 80 mm. The simulated test dipoles were assigned random orientations in a plane parallel to a plane tangential to the sphere.

The duration of all simulations was 300 s. The sample rate for the OPM sensor simulations was 175 Hz, twice the bandwidth limit of the sensors (approximately 350 Hz), while a typical sampling frequency of 600 Hz was used for the CTF simulations. Each test dipole was assigned a unique random time series, scaled by a source magnitude of 25 nA-m RMS (similar to the 22 nA-m sources utilized in (Zetter et al., 2018)), unless otherwise stated. The magnetic field observed at each sensor was simulated by summation of brain noise, sensor noise, and the test dipole sources. The field generated by dipole sources was calculated assuming a spherical homogeneously conducting space using the Sarvas equation (Sarvas, 1987). Note that because we are assuming a sphere of activity, only tangentially directed source currents contribute to the magnetic field external to the spherical conductor.

2.3. Array calibration errors

In order to understand the performance of both idealized OPM arrays and realistic OPM arrays, we simulated various potential errors that may occur at the sensor level. These include crosstalk, angular errors to the sensitive axis, and gain error, each of which we will explain in turn. OPM sensors make use of three orthogonal onboard field nulling coil pairs to establish zero field in the ⁸⁷Rb cell, to keep the sensor in a domain of relative linearity. When operated in closed loop, the field produced by these nulling coils is dynamically altered to maintain zero field throughout a recording. While closed-loop operation will ensure a linear response, the field produced by a nulling coil on one sensor may also influence the field at neighboring sensors. This phenomenon is known as crosstalk, and it is important to understand its effects on data quality. While crosstalk cannot be eliminated, it can be mitigated in part using self-shielding nulling coils (Nardelli et al., 2019) and calibrating measured data using the inverse of the measured crosstalk matrix. We examined the effects of crosstalk ranging from 1 to 10% on the measured signal. In this simulation, sensors at the minimum distance on the array experience the full percentage effect of crosstalk, while the effect is reduced according to the inverse of the distance cubed for sensors at further distances.

In addition to crosstalk arising from closed-loop operation, there is also modulation crosstalk. The sensing axis of each OPM is established by applying high-frequency modulation to the z-axis Helmholtz coils in the sensor and demodulating that signal to measure the opacity of the ⁸⁷Rb vapor to the probe laser. Crosstalk between the z-axis coils of adjacent OPM sensors due to this modulation can perturb the sensing axis, contributing to inaccuracies in the measured signal. We explored the effects of orientation error, which we also refer to as angular error, from 1 to 4°, by giving each sensor a fixed angular offset from the ideal axis of the sensor, at a random angle in the tangential plane. While this is also a phenomenon due to crosstalk, it is static throughout the measurement provided that the sensors do not move relative to one another Sensors may also differ in their precise gain values. We modeled errors in sensor gain by scaling the observed signal by the sensor by a random percentage up to the maximum gain error specified. We explored the effects of gain errors up to 10%.

2.4. Perturbations to array and simulation geometry

The second group of potential issues affecting reconstructed signals involve the geometry of the array. While ideally, the OPM sensors would rest on the surface of the scalp, this may be impractical due to concerns with sensor temperature (the vapor cell is maintained at an internal temperature of approximately 150°C; see (Shah et al., 2007)). While custom 3D printed head casts would conform to a participant’s head, a fixed helmet which can be used on many different participants may result in gaps between the scalp and the face of the sensor. We simulated the effect of scalp-sensor gap up to 12 mm to account for this scenario. Flexible caps conforming to the participants head can be used as an alternative to head casts and helmets; however, this may result in inaccuracies in the precise localization of sensors (Hill et al., 2020). Finally, we examined the spacing of sensors. For our default sensor spacing, we assumed sensor housings of 15 × 13mm (same as FieldLine OPM sensors), and that sensors were placed immediately adjacent to one another. To investigate the effect of using densely packed arrays vs. arrays resembling whole head coverage, we simulated array spacings ranging from 10 × 8mm to 20 × 18mm (including 13×11, 14×12, 15×13, 16×14, and 17 × 15mm). Although the current footprint of the FieldLine v2 sensors is 15 × 13mm, we extrapolated to smaller spacings to more comprehensively show the dependence of SNR and ISR on sensor spacing.

In addition to these intrinsic OPM characteristics, we also examined other factors that affect the recorded signal, namely the number and magnitude of test sources and the cortical depth at which they are located. To explore the relative performance of OPM compared to SQUID MEG systems in resolving independent sources, we located the test dipoles in a 50 mm square area and varied their number from 2 to 128, and their magnitude from 5 nA-m to 30 nA-m. Given that our noise model utilized a 20 mm thick shell of noise sources, we can model the effects of cortical depth by varying the location of the test sources from the outer radius to the inner radius. While the thickness of the grey matter ribbon is considerably less than 20 mm, gyral folding should result in deeper sources of interest. The response of the array to sources at varying cortical depth will be in part due to the increased distance between sources and sensors, decreasing the spatial frequencies captured. In addition, the response will be influenced by the noise sources between the test dipoles and the sensors.

2.5. Source reconstruction

For each iteration of array and dipole arrangement, the reconstructed time series for each test source was obtained using a linearly constrained minimum variance (LCMV) scalar beamformer. The beamformer requires the calculation of the covariance matrix of the (simulated) measurements, C = m(t)m(t)^T, and the lead-field matrix. The lead field matrix L_r is the field generated by a unit dipole at position r in the two orthogonal directions tangential to the sphere. The elements b_r are the forward solution vector components for each dipole location. (Note that for a realistic head model, the matrix L would have three columns corresponding to the cardinal directions x, y and z).

$${\text{L}}_{\text{r}}=\left[\begin{array}{ll}{b}_{11}\hfill & b_{12}\hfill \\ b_{21}\hfill & b_{22}\hfill \\ ⋮\hfill & ⋮\hfill \\ b_{M1}\hfill & b_{M2}\hfill \end{array}\right]$$

The scalar beamformer proceeds in two steps. First, the dipole source orientation is estimated by solving the generalized eigensystem of the ratio of projected source power to projected noise power.

$$L^T{C}^{-2}L{e}_k={\lambda }_k{L}^T{C}^{-1}L{e}_{k}k=1,2$$

In the preceding equation, λ_k and e_k are the eigenvalues and eigenvectors, respectively. Next, the forward solution for the source is computed for the projection of the eigenvector corresponding to the maximum SNR (largest eigenvalue) with the lead field:

$$b_{\text{r}}=L_{\text{r}}{e}_{max}$$

Lastly, the scalar beamformer coefficients giving maximum SNR are:

$$w_{\text{r}}=\frac{C^{-1}{b}_{\text{r}}}{b_{\text{r}}^T{C}^{-1}{b}_{\text{r}}}$$

Thus, the estimated source time series and projected noise become:

$${\text{S}}_{\text{r}}(t)=w_{\text{r}}^{T}m(t)and{N}_{\text{r}}=\sqrt{w_{\text{r}}^T{\sigma }^2{W}_{\text{r}}}$$

respectively, where σ² is the sensor noise variance. In addition to beamformer estimates of the source time series at the known location of each test source, we computed images from the signal-to-noise ratio (source power divided by the projected noise), at each 1 mm voxel in a 60 × 60 mm grid according to the following equation:

$$SN{R}_{\text{r}}=\frac{w_{\text{r}}^{T}C{w}_{\text{r}}}{w_{\text{r}}^T{\sigma }^2{W}_{\text{r}}}$$

All software was written in-house as part of a larger suite of imaging analysis tools.

2.6. Test metrics

Several metrics were used to evaluate the simulated arrays. In order to provide a measure of how well different sensor arrays can discriminate between simultaneous sources, we calculated a metric we refer to as Independent Source Resolution (ISR). For each test source, we computed the correlation between the simulated and reconstructed time courses, which is a measure of the fidelity of reconstruction of the sources. In addition, to measure the effects of signal leakage, we calculated the correlation between the simulated time course of one test source with the reconstructed time courses of all other test sources. Thus, a correlation matrix can be formed, with each element being the correlation between the simulated time course (along one axis of the matrix) and the reconstructed time course (along the other axis of the matrix). The ISR is then defined as the mean on-diagonal correlation minus the mean off-diagonal correlation. The use of correlations between reconstructed and true test sources has been used previously to investigate the reconstruction of a source given brain inference (Boto et al., 2016). Our particular implementation is novel, as we utilized a much larger number of simultaneous sources, allowing richer characterization of array performance.

The ISR calculation, as well as the correlations used to derive the ISR are presented in several ways. First, for each test array we calculated the mean ISR and SNR across all test sources for 25 different source configurations (by incrementing the initialization seed of the random number generator). Next, for a single configuration of test sources we plotted the full correlation matrix, where, in an ideal scenario, each of the simulated dipole sources would be reproduced with high fidelity with no leakage of signal (and thus the correlation matrix would resemble an identity matrix). In addition, the correlation values between test dipole pairs were plotted against the physical distance between them. Correlation will be reduced as test sources are further apart, and the degree of decay of the correlation with distance can be used to infer how well individual sources can be resolved.

While these metrics are continuous, it may be useful to define an acceptable threshold for source discriminability. Boto et al. (Boto et al., 2016) suggest that any two sources displaying shared variance under 50%, corresponding to a correlation coefficient of 1/√2 = 0.7, are discriminable. Using the concept of shared variance, we would define a more stringent threshold, and propose that any two sources sharing less than 10% variance can be differentiated, corresponding to a correlation coefficient of 0.32 (i.e indicating acceptable leakage). In addition, we would suggest that an accurate reconstruction of a source should show at least 80% shared variance with the true source, corresponding to a correlation coefficient of at least .89 (indicating acceptable reconstruction accuracy). Thus, a desirable ISR would be greater than 0.57, although it remains useful to consider reconstruction accuracy and leakage separately.

Because our time courses for each test dipole are reconstructed at the a priori known location of the test source, a source whose reconstruction is shifted in space will exhibit potentially artifactually lower SNR. To assess how different array characteristics affect the accuracy of source localization, we also calculated and plotted two-dimensional images on the spherical surface containing the test sources (again for a single configuration of test sources). As with the reconstructed time courses, these images were constructed using an LCMV beamformer, and we plot projected source power divided by projected sensor noise power (SNR).

Finally, it should be noted that in a real system, multiple inaccuracies will be present simultaneously, further degrading performance, although we would expect these errors to add linearly rather than to interact. In addition, as the SNR of signals increases, the beamformer will more closely approximate a point source, leading to reduced output SNR if the measurement vector and forward model do not agree (Vrba, 2002). We would expect this phenomenon to also be independent of other influences on ISR and SNR.

3. Results

3.1. Baseline performance of the CTF and OPM array

In Fig. 2, we show simulation results for the CTF MEG array and the theoretical OPM array under ideal conditions – no crosstalk or other sensor calibration errors, superficial sources, and minimum scalp to cortex distance. The OPM array clearly outperforms the CTF array in the resolution of 16 independent 25 nA-m (ISR_OPM = 0.91, ISR_CTF = 0.63). Correlation matrices clearly show few off-diagonal correlations, indicating less signal leakage for the OPM array. The enhanced resolution of sources is also evident in the beamformer images, as is the increased signal to noise, with a maximal SNR of 65.81 in the OPM image compared to a maximum SNR of 7.39 in the CTF image.

Fig. 2.

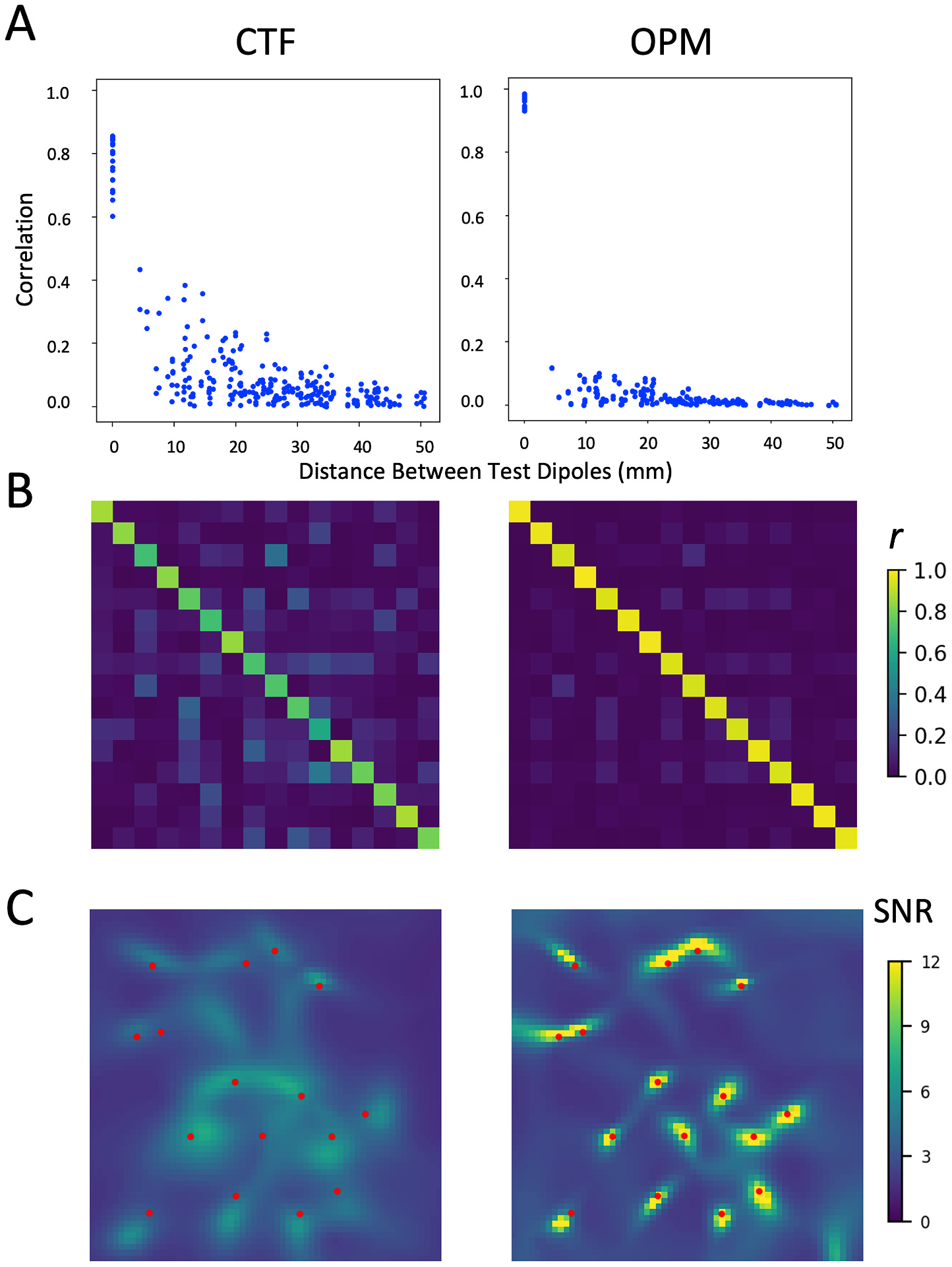
Comparison of the CTF and idealized OPM system with no calibration errors. Metrics shown are A) correlation between source time series plotted as a function of the distance between sources, B) correlation between source time series shown in matrix form, and C) LCMV beamformer image of the test source area. True test source locations are marked in red. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

3.2. Errors of sensor calibration: crosstalk, sensitive axis error, and gain error

The simulated effects of crosstalk are shown in Fig. 3. Given that crosstalk is one of the most widely discussed issues with OPM sensors, we expected it to have a significant effect on all parameters we measured. In contrast, we found that crosstalk related to closed-loop operation only had a relatively minimal impact on ISR and the ability to differentiate simultaneous independent sources (Fig. 3 B and C). As is evident in Fig. 3 A, ISR for the OPM array remained well above that found for the CTF array, although SNR did decrease markedly as a function of crosstalk magnitude. In the reconstructed source images calculated using the simulated data (Fig. 3 D), all sources were visible and properly localized at crosstalk magnitudes of up to ten percent.

Fig. 3.

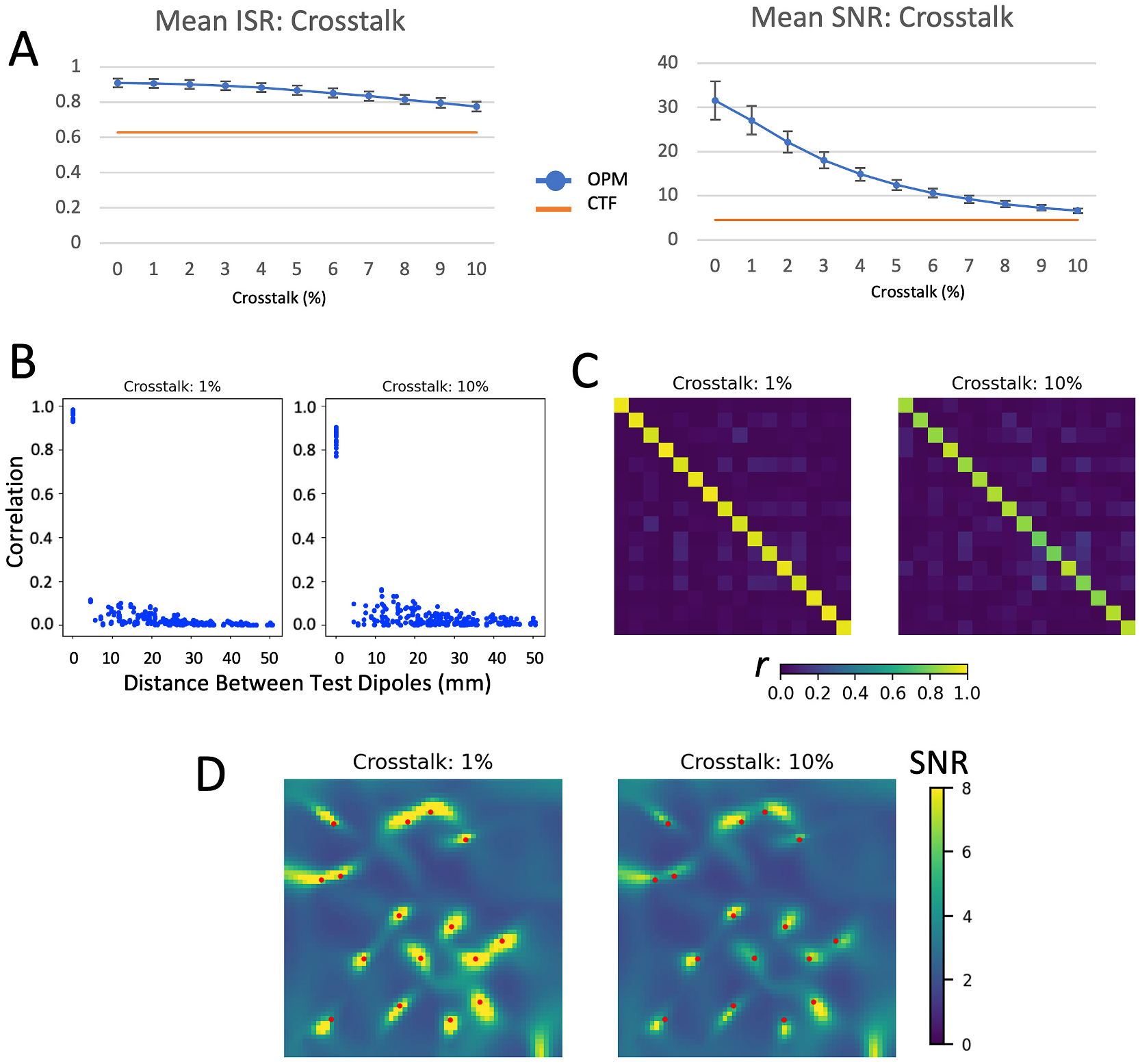
Effects of crosstalk on evaluation metrics. A) mean ISR and SNR for varying degrees of crosstalk across 25 different random sets of 16 test dipoles for crosstalk values between 0 and 10%. B) Correlation between source time series plotted as a function of the distance between sources, C) correlation between source time series shown in matrix form, and D) LCMV beamformer images of the test source area for 1% and 10% crosstalk.

In contrast to crosstalk induced errors resulting from closed-loop operation, angular error in the sensitive axis of the sensor, introduced by modulation crosstalk, had a profound effect for the proposed OPM array on all examined metrics, as shown in Fig. 4. Mean ISR was reduced to unacceptable levels between 2 and 3 degrees of error (ISR_OPM for angular error of 3° = 0.51), while SNR levels of the OPM array were reduced below the SNR of the CTF array at around 3 degrees of error (See Fig. 4 A). The primary driver of the reduction in ISR was due to a sharp decrease in the correlation between each source’s measured and simulated time courses (Fig. 4 B and C). These reductions were due in part to a mis-localization of the sources due to the axis error. The ISR is calculated from the recovered signal at the location of each test dipole; if the test dipole position is shifted due to errors in the geometry of the sensors, the ISR would appear more reduced than if the recovered source time course from the shifted location was utilized. As is evident in Fig. 4 D, even a one degree perturbation in the sensitive axis results in shifts of the peak locations of the recovered sources.

Fig. 4.

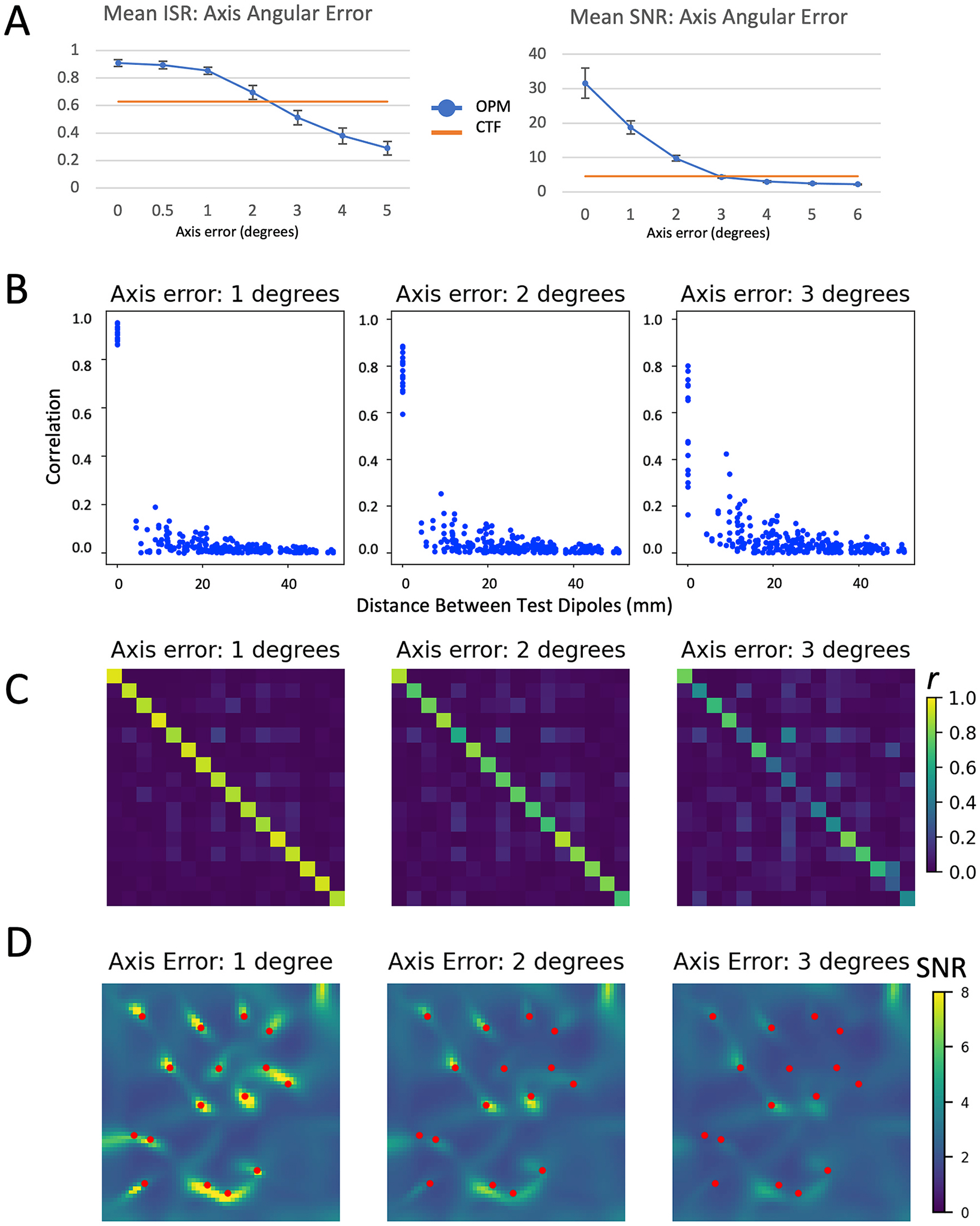
Effects of angular error in the OPM sensitive access on evaluation metrics. Figure legend for individual panels as in Fig. 3; mean ISR and SNR is shown for angular error between 0 and 5°, other evaluation metrics (correlation [C] and LCMV beamformer images [D]) are shown for angular error of 1, 2, and 3°.

Similarly, errors in gain (shown in Fig. 5) resulted in dramatic reductions in both ISR and SNR. ISR for the OPM array was reduced to levels simulated for the CTF array between 4 and 5% gain error, while SNR was reduced dramatically to below that simulated for the CTF array between 3 and 4% gain error (See Fig. 5 A). As with axis errors, rather than inducing signal leakage between independent sources, errors in gain reduced the fidelity of the reconstructed time series (see Fig. 5 B and C). Gain errors of 5% resulted in images without distinct sources visible (Fig. 5 D).

Fig. 5.

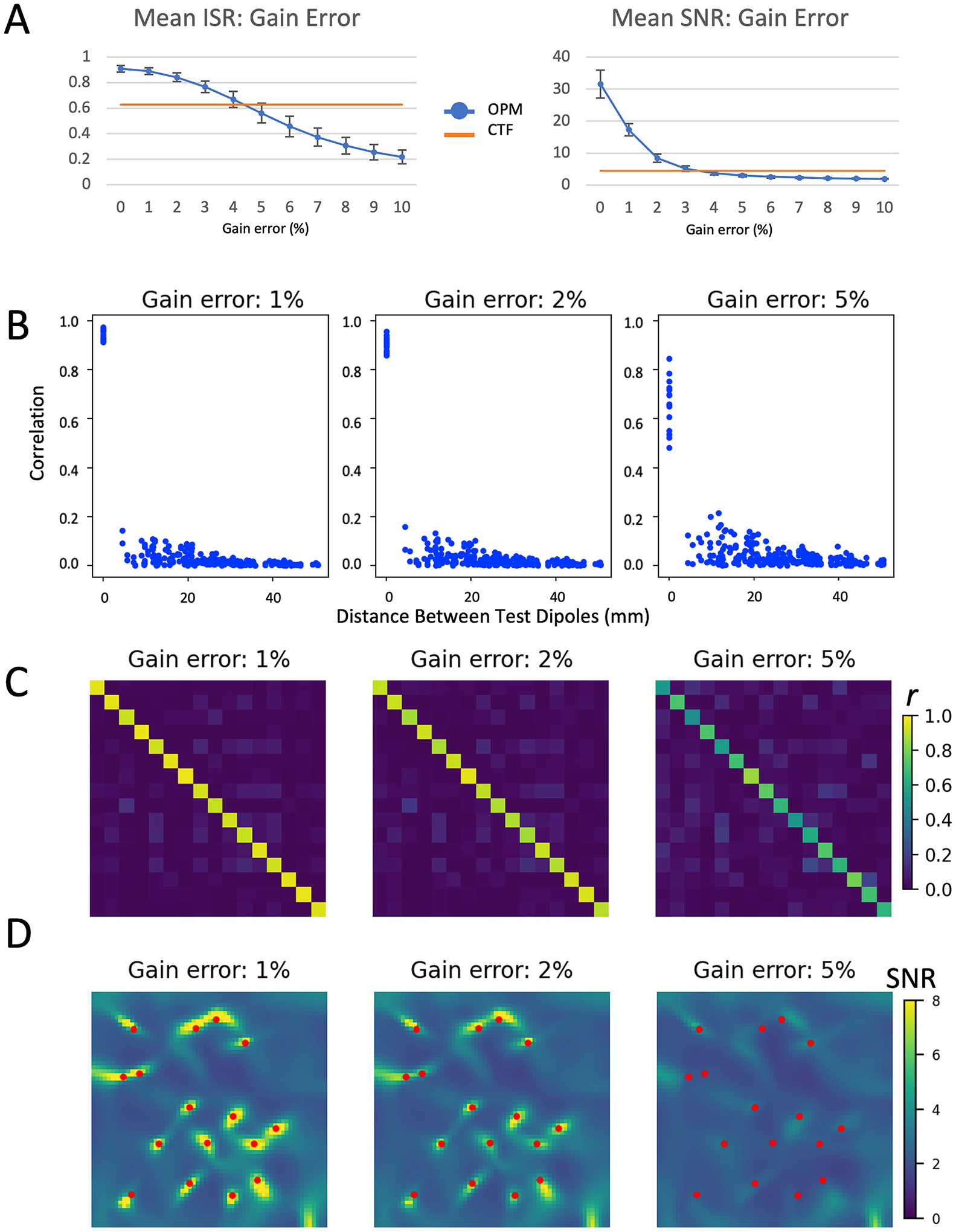
Effects of gain error on evaluation metrics. Figure legend for individual panels as in Fig. 3; mean ISR and SNR is shown for gin errors between 0 and 10%; other metrics (correlation [C] and LCMV beamformer images [D]) are shown for 1, 2, and 5% gain error.

3.3. Effects of sensor and array geometry: scalp-to-array gap and sensor position errors

Even for gaps of up to 12 mm, scalp-to-array gap had relatively low impact on the ability to accurately reconstruct source time series (See Fig. 6 A–C; for a 12 mm gap ISR = 0.71). Although ISR remained relatively high, the array with a large gap showed greater signal leakage, leading to a reduction in spatial resolution. Examining the reconstructed source maps (Fig. 6 D), it was readily apparent that sources appeared much less compact, and more diffuse, like the spread in activation observed for the CTF system. Nevertheless, both ISR and SNR remained above that observed for the CTF system. It should be noted that this is in part a demonstration of the on-scalp OPM array to capture the high spatial frequencies present in our test dipole array.

Fig. 6.

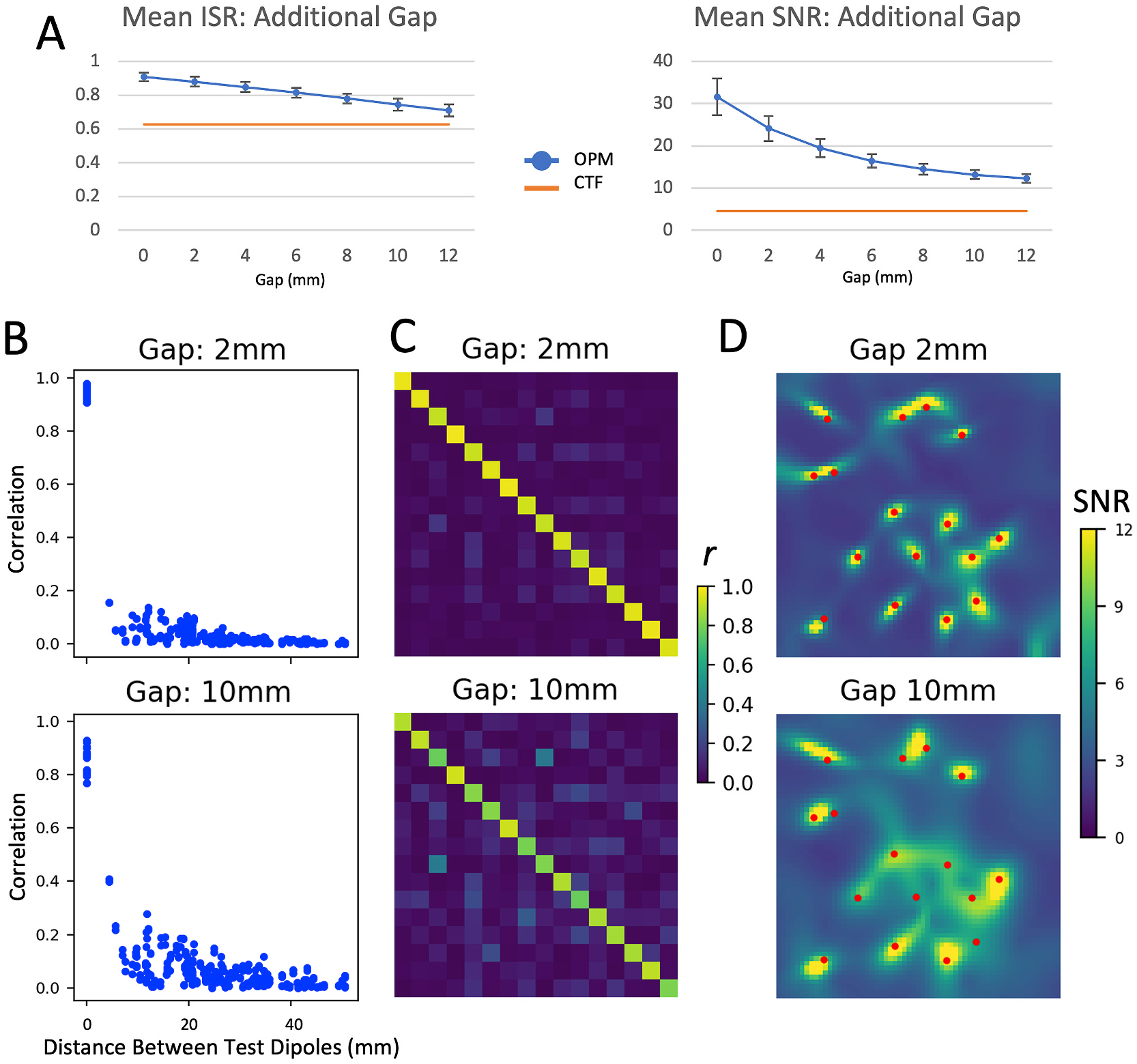
Effects of an additional gap between the OPM sensor and the test sources. Figure legend for individual panels as in Fig. 3; mean ISR and SNR is shown for additional gaps between 0 and 12 mm; other metrics (correlation [C] and LCMV beamformer images [D]) are shown for gaps of 2 mm and 10 mm.

Sensor position errors additionally had a profound effect on the ability of the theoretical array to discriminate independent sources (Fig. 7). Similar to errors in the sensitive axis of the sensors, this is partially due to mis-localization of sources. Even deviations of 0.5 mm of the location of the sensors was enough to severely degrade the reconstructed signals and render images of the test dipoles nearly indistinguishable from noise sources (Fig. 7 D).

Fig. 7.

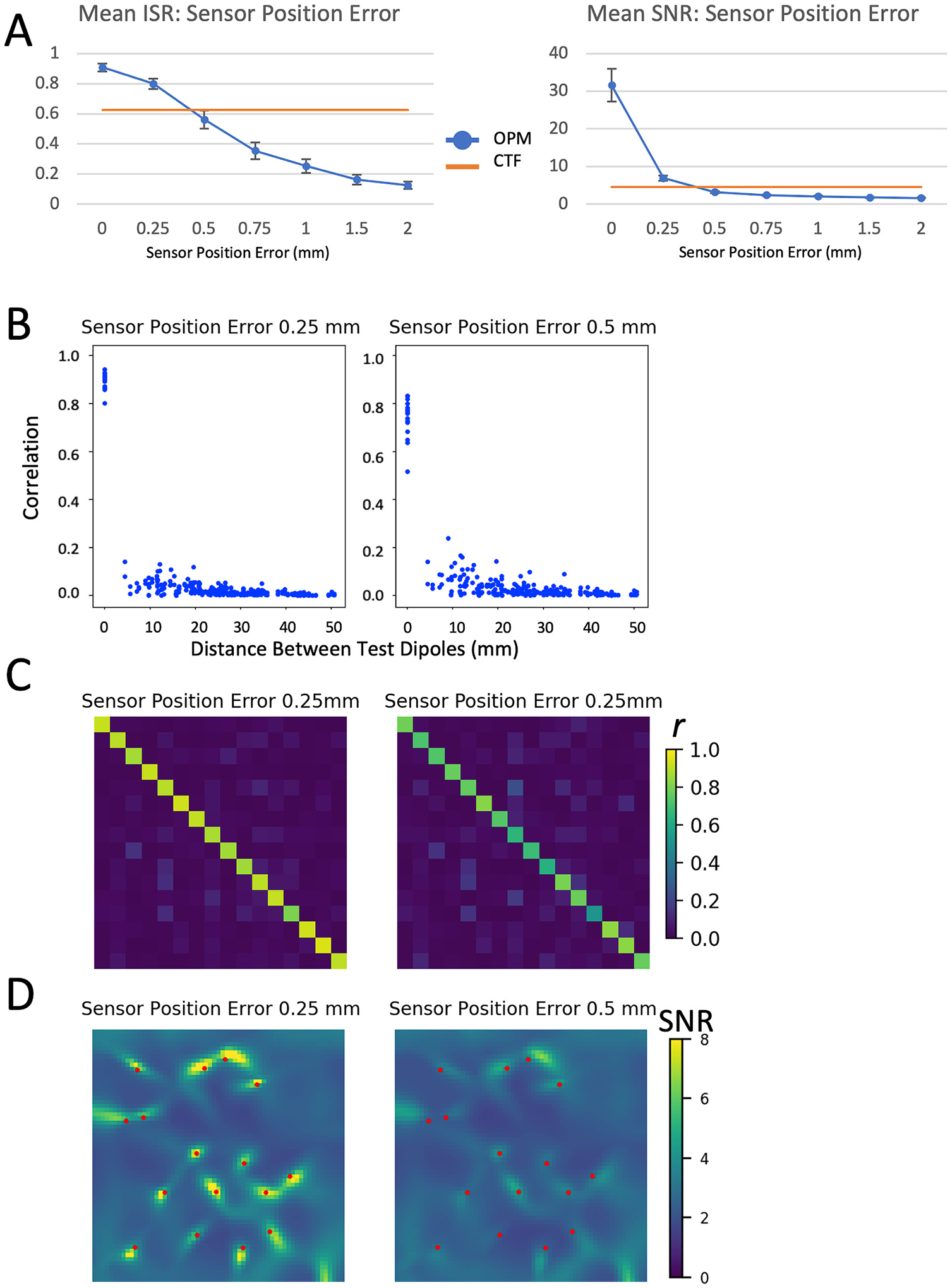
Effects of error in sensor positions. Figure legend for individual panels as in Fig. 3; mean ISR and SNR is shown for position errors between 0 and 2 mm; other metrics (correlation [C] and LCMV beamformer images [D]) are shown for position errors of 0.25 mm and 0.5 mm.

In order to fully demonstrate the effects of sensor spacing, we evaluated the results using both 16 and 32 simulated sources. As the spacing between sensors increased, the profile of the spatial reconstruction of the sensors broadened. When 32 test sources were evaluated, mean SNR increased as sensors were spread further apart due to the overlap of source reconstructions (Fig. 8). However, when 16 test sources were evaluated, mean SNR at source locations decreased due to mislocalization of source peaks. ISR remained relatively high for all configurations of the OPM array, dropping to that of the CTF system only for 32 sources and the maximum sensor spacing (20 × 18mm).

Fig. 8.

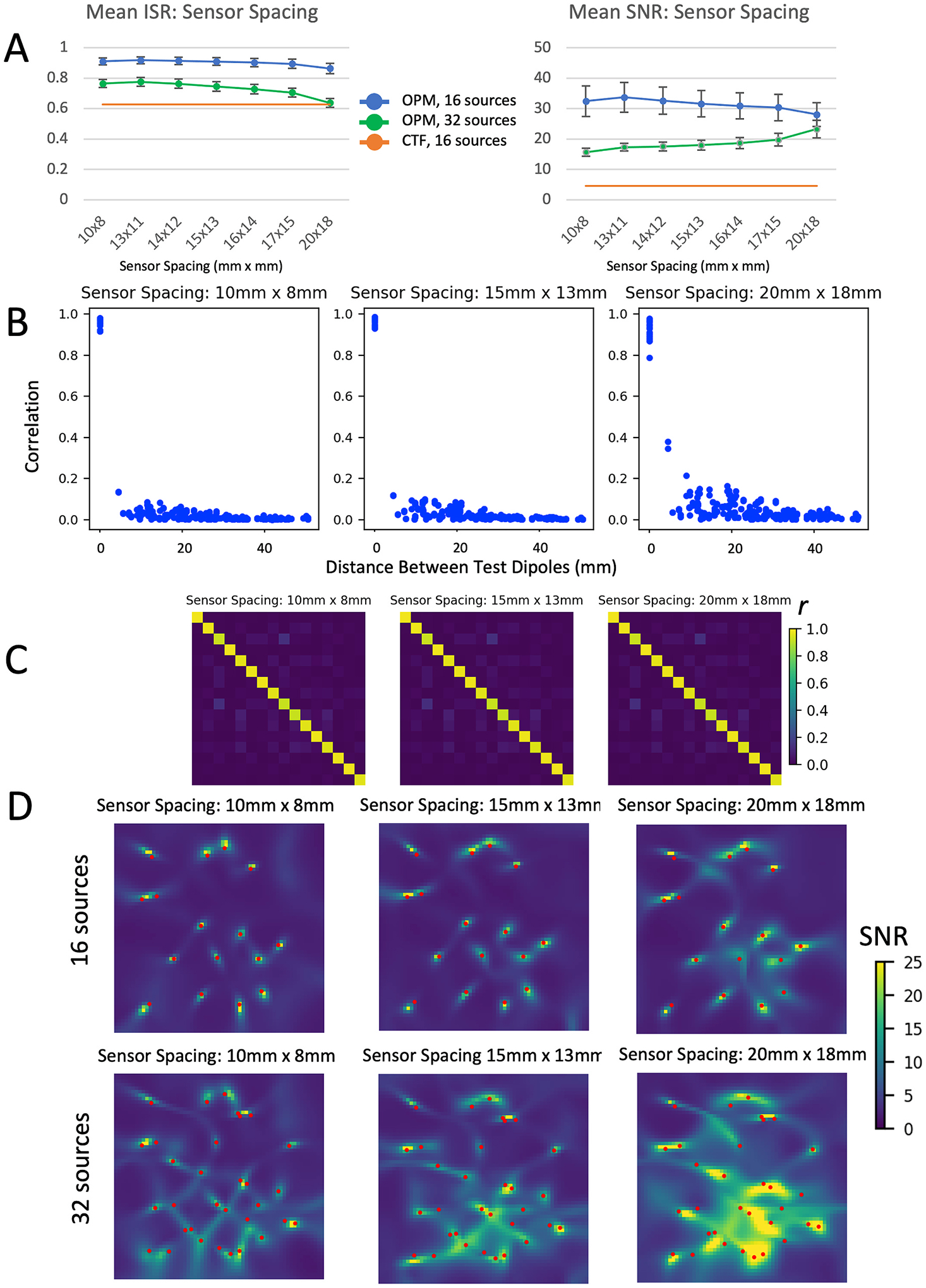
Effects of spacing between individual OPM sensors. A) mean ISR and SNR for different sensor spacings across 25 different random sets of both 16 (blue data points) and 32 test dipoles (green data points). Because commercially available sensors have rectangular rather than square faces, spacings are not symmetric, and range from 10 mm × 8 mm (not currently possible with any commercially available sensor) to 20 mm × 18 mm. B) Correlation between source time series plotted as a function of the distance between sources, C) correlation between source time series shown in matrix form, and D) LCMV beamformer images of the test source area are shown for spacings 10 mm × 8 mm, 15 mm × 13 mm, and 20 mm × 18 mm. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

3.4. Performance of OPM and SQUID systems: number, magnitude, and depth of test dipoles

The final set of parameters we assessed were aspects of the test dipoles themselves: their number, magnitude, and depth. A comparison of the CTF array and the theoretical OPM array at distinguishing multiple sources is shown in Fig. 9. The theoretical OPM array was capable of accurately discriminating among 32 dipolar sources (ISR_OPM = 0.75). In addition, although the ISR was below our threshold for 64 sources (ISR_OPM = 0.53), examining the plot of correlation vs. distance between test dipoles shows that sources at separations of at least 10 mm could be reasonably distinguished. In contrast, the CTF system struggled to resolve more than 16 sources (For N = 32, ISR_CTF = 0.43).

Fig. 9.

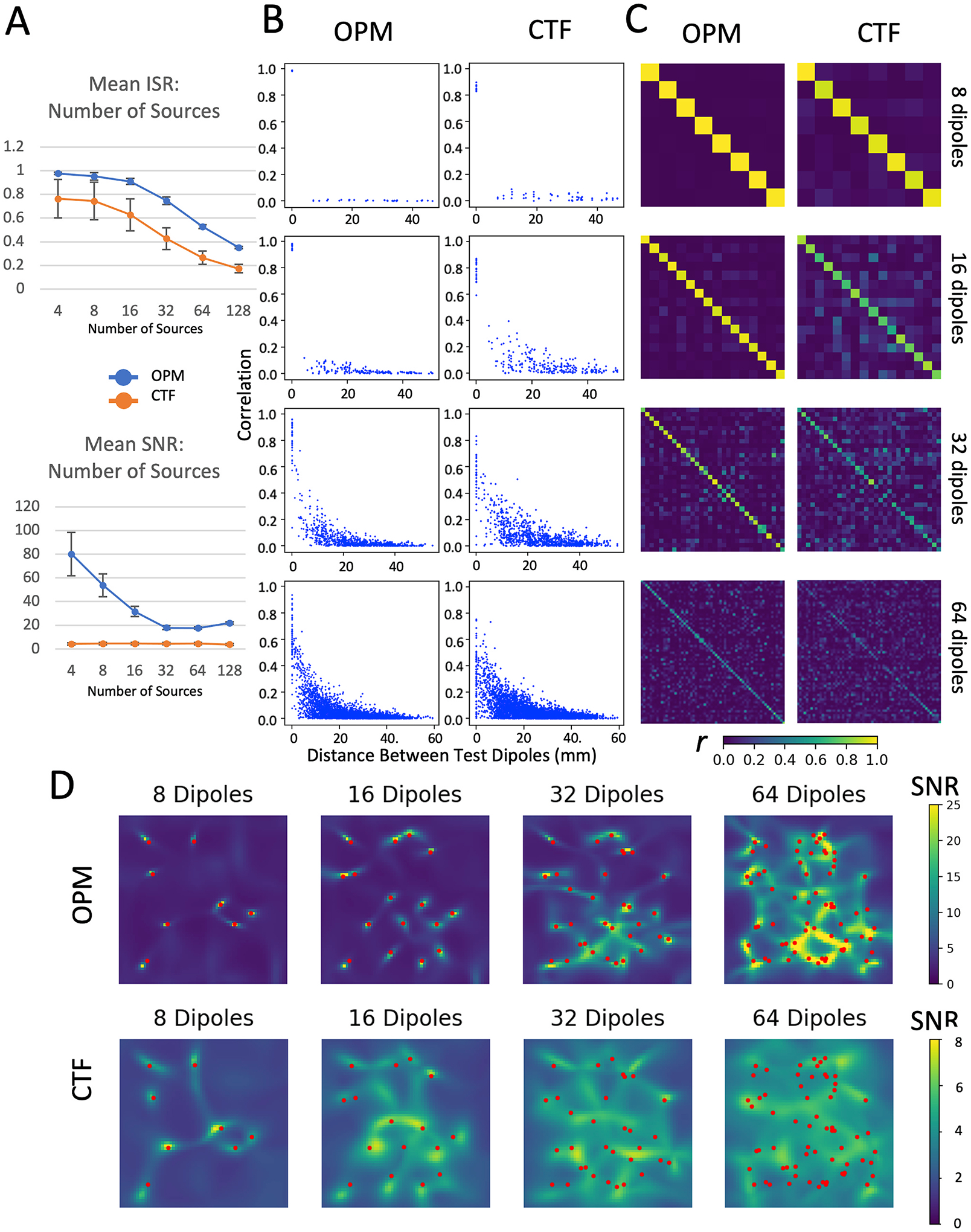
Effects of the number of tests sources. A) mean ISR and SNR across 25 different random sets of 4–128 test dipoles, shown for both CTF (orange markers) and the theoretical OPM system (blue markers). B) Correlation between source time series plotted as a function of the distance between sources, C) correlation between source time series shown in matrix form, and D) LCMV beamformer images of the test source area are shown for both the CTF and theoretical OPM systems, for 8, 16, 32, and 64 test dipoles.

When test dipole magnitude was reduced, the OPM system was able to distinguish 16 sources at the lowest magnitude tested (5 n-Am; ISR_OPM = 0.59, see Fig. 10). In contrast, the CTF system had difficulty distinguishing sources and accurately localizing them at source strengths below 15 n-Am (10 n-Am; ISR_CTF = 0.55). When the test dipole strength was increased, the ISR observed for the theoretical OPM system approached ISR = 1 for 16 independent test dipole sources, with SNR increasing as well. In contrast, for the CTF system, the maximal ISR of approximately 0.62 was achieved for a 20 nA-m source, and further increases in source strength did not increase ISR. Likewise, SNR peaked close to 5 for a source strength of 15 nA-m, then slowly decreased as source strength increased. Further examination showed that reconstructed source power increased with dipole magnitude, but the projected noise power in the area of each source also increased and became more focal. It is unclear if this is a true property of the system or a product of our simulation parameters and geometry.

Fig. 10.

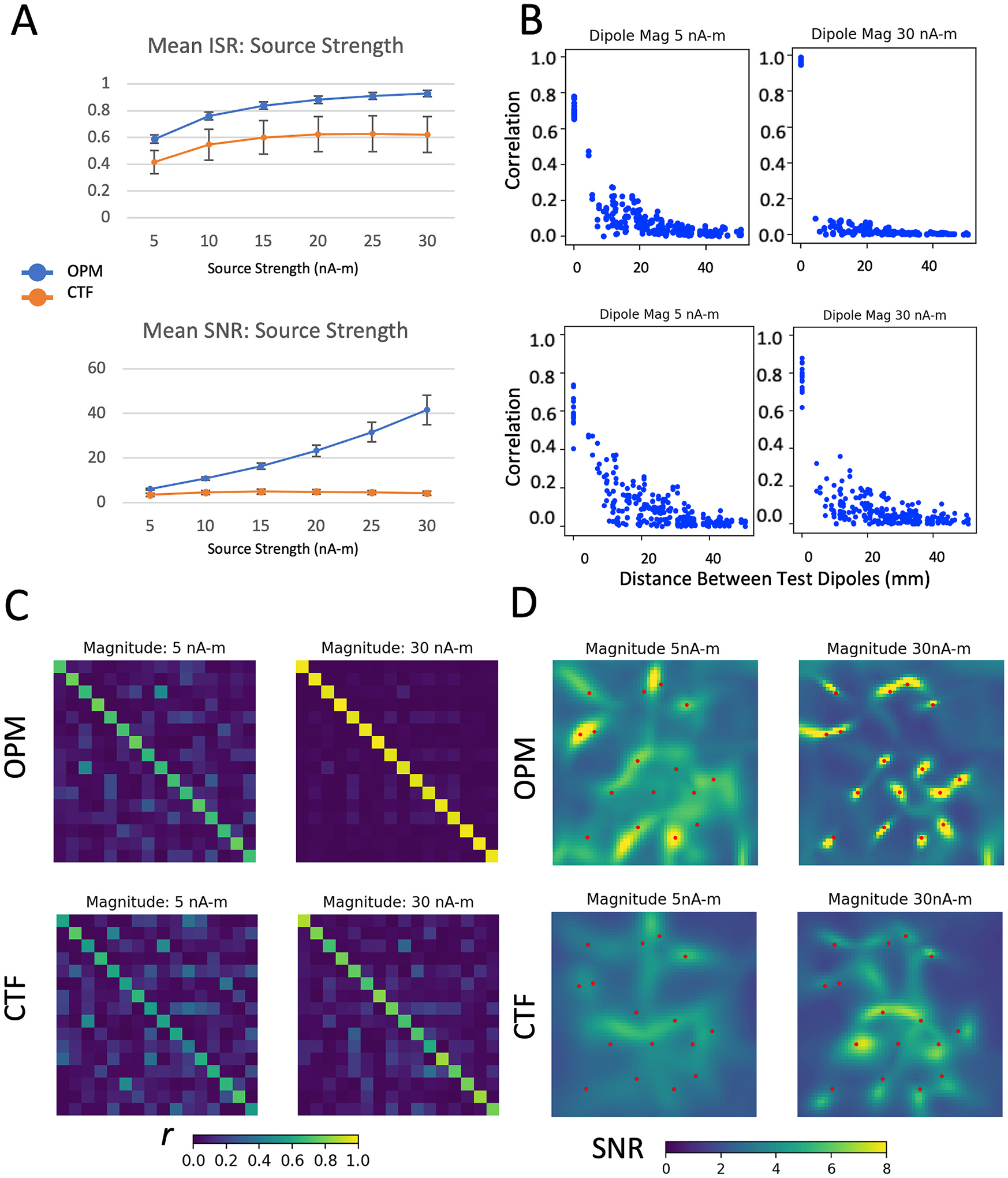
Effects of the strength of the test dipoles on evaluation metrics. A) mean ISR and SNR across 25 different random sets of test dipoles ranging in magnitude from 5 nA-m to 30 nA-m, shown for both CTF (orange markers) and the theoretical OPM system (blue markers). B) Correlation between source time series plotted as a function of the distance between sources, C) correlation between source time series shown in matrix form, and D) LCMV beamformer images of the test source area are shown for both the CTF and theoretical OPM systems, for 5 and 30 nA-m dipole strengths.

Finally, we examined the effect of cortical depth of sources in the noise shell (Fig. 11). While cortical depth had a profound effect on both the ISR and SNR of the theoretical OPM array, the ISR value was greater for the OPM array than the CTF array for all cortical depths (although within the margin of error for the deepest sources, Fig. 11 A). SNR remained higher for the OPM array at all depths, although deeper sources were poorly localized (Fig. 11 A and D). For the OPM array, cortical depth decreased the correlation between each test source and its reconstructed time series and increased the correlation with the remaining test dipoles. In contrast, for the CTF array, while the within-dipole correlation also decreased, the correlation between sources was relatively unaffected (Fig. 11 B and C).

Fig. 11.

Effects of the depth of the test dipoles inside the hemispherical noise shell, representing a simulation of cortical depth. A) mean ISR and SNR across 25 different random sets of test dipoles ranging in depth from 0 mm to 20 mm, shown for both CTF (orange markers) and the theoretical OPM system (blue markers). B) Correlation between source time series plotted as a function of the distance between sources, C) correlation between source time series shown in matrix form, and D) LCMV beamformer images of the test source area are shown for both the CTF and theoretical OPM systems, for cortical depths of 4 mm and 16 mm.

4. Discussion

In this manuscript, we evaluated an OPM array designed specifically for magnetocorticography and compared its performance in discriminating multiple independent sources with an existing SQUID MEG instrument. We assessed the effects sensor calibration issues, including crosstalk, angular errors in the sensitive axis of the sensors, and errors in sensor gain. We also evaluated errors in the presumed location of the sensors, the effect of the gap between the sensors and the scalp, and the effect of sensor spacing. Finally, we assessed the performance of our array in discriminating sources when we altered the number, strength, and depth of test dipoles.

Overall, we found that crosstalk due to closed-loop operation affected source reconstruction less than we expected. Even with 10% crosstalk for nearest neighbor sensors, the OPM array had superior ISR and SNR compared to the CTF system. This is an important finding, given that crosstalk will be exacerbated as sensors are placed closer to one another, which is required for high-resolution applications. In Boto et al. (Boto et al., 2018), crosstalk was measured in an array of sensors 3–5 cm apart and was on the order of 3%. The sensors developed by FieldLine incorporate self-shielded zeroing coils, which reduces crosstalk from 8% to 0.5% for sensors that are immediately adjacent to one another (Nardelli et al., 2019).

In contrast, the OPM system was highly sensitive to angular errors in the sensing axis of the sensor, as well as errors in gain introduced in part due to modulation crosstalk. Angular errors of 3% or gain errors of 5% resulted in unacceptable reductions in ISR. Similarly, we showed that the positions of sensors must be known to a high degree of accuracy, with errors no larger than 0.25 mm, consistent with prior published results (Zetter et al., 2018; Iivanainen et al., 2019). One caveat to this is that it may be difficult to calibrate and localize sensors with this degree of accuracy, given inherent noise in the system and factors such as crosstalk and gain errors (Duque-Munoz et al., 2019), as well as the influence of ambient transverse fields (Iivanainen et al., 2019). While authors have experimented with data-driven methods to determine orientation offsets, only angular errors above 4° can be rejected in the best case (Duque-Munoz et al., 2019). These results indicate that flexible sensor array designs (similar to EEG caps) where sensors may move relative to each other during a recording, are likely unsuitable as modulation crosstalk would be expected to change.

Provided that the position of sensors is known, however, there is some flexibility in the sensor-to-scalp distance and the spacing of sensors. While minimum gaps between the sensors and the scalp, and between adjacent sensors results in the highest separability of simultaneous sources, gaps of 15–18 mm between the ⁸⁷Rb cells and sensor-to-scalp gaps of up to about 8 mm offer acceptable resolution, provided SNR is sufficient given the location and strength of sources. This is advantageous given that space for heat mitigation strategies such as airflow around the sensors may be required to for long duration measurements.

Given its higher signal to noise ratio, the OPM system outperforms the CTF SQUID system for test dipoles of every evaluated magnitude, although the difference in performance is most evident for the stronger dipoles. This is partially a consequence of the reduced sensitivity of OPM sensors (10 vs. 5 fT/√Hz). Similarly, examining depth of test sources within the noise shell, the OPM system does not substantially outperform the CTF system for the deepest sources in terms of ISR, although SNR of the OPM system remains greater than that observed for the CTF system. This is consistent with prior simulation work, showing that the advantage of OPM systems compared to SQUID systems becomes smaller as the depth in the brain increases (Boto et al., 2019). This is in part a consequence of the greater head coverage of the CTF array. We also examined the number of simultaneous sources. Conceptualizing brain activity during a task as a finite number of discrete sources is an oversimplification, but is a useful model, particularly for sensory tasks. As the number of sources increases, the reconstruction problem becomes underdetermined; our 56 channel array cannot mathematically provide a unique solution in the presence of more than 56 sources. The OPM array nevertheless performs quite well in comparison to the CTF array, which cannot differentiate 32 sources (ISR_OPM = 0.75, ISR_CTF = 0.43)

The broader ramifications of the enhanced ability of OPM systems to discriminate simultaneous sources is readily apparent. Functional magnetic resonance imaging (fMRI), with the advent of ultra-high field scanners, has enabled the mapping of retinotopic (Olman et al., 2010), somatotopic (Martuzzi et al., 2014), and tonotopic (Norman-Haignere et al., 2013) representations. While somatotopic finger mapping has been performed using MEG, alternating stimulation between digits is required for precise localization, so that only one source is presumed active at a time (Jamali and Ross, 2013). Likewise, retinotopic maps, for instance of stimulus orientation, can also be reconstructed with conventional MEG, although with greater difficulty. One study, for instance, mapped three ranges of stimulus eccentricities, although only in V1, and mapping of the upper visual field and sulcal sources was unsuccessful (Nasiotis et al., 2017). Hierarchical visual processing in the visual system necessarily results in multiple simultaneous sources that may be possible to visualize using a dense on-scalp OPM array. Tonotopic maps have also been investigated using MEG (Falet et al., 2021), although subjects were highly heterogeneous and not all participants exhibited a gradient in receptive field from low to high frequency tones. In addition to sensory mapping, ultra-high field MRI has enabled laminar-specific imaging (Huber et al., 2018). There is evidence that the frequency of cortical oscillations may be layer specific (Sun and Dan, 2009), suggesting that the laminar specificity of MEG signals could be inferred indirectly. While Bayesian modeling has been used to differentiate MEG signals arising from deep or superficial cortical layers (Bonaiuto et al., 2018; Pinotsis and Miller, 2020), true layer-specific MEG imaging remains unattainable. Work using dense OPM arrays, however, could potentially enable a new frontier in the study of cortical lamina. In addition to the ECoG studies discussed in the introduction, other studies using EcoG revealed distinctive activation patterns for motor movements (Aoki et al., 1999), and successfully decoded hand movement and force (Flint et al., 2020), suggesting a clear application for a dense OPM array in brain computer interface. Likewise, EcoG recordings have been used to decode human speech, which may suggest another application for OPM arrays (Pasley et al., 2012; Kellis et al., 2010). Of course, a magnetocorticography array with similar resolution to EcoG has an obvious application to characterizing the seizure onset zone in epilepsy. Small studies have performed assessment of interictal activity using OPM arrays (Mellor et al., 2021; Vivekananda et al., 2020). Given the demonstration of these comparatively sparse arrays to localize spike activity, our dense array would be expected to perform quite well, at least for superficial cortical spikes. Commonly used ECoG arrays have an electrode spacing of approximately 10 mm, with spatial resolution probably in the millimeter range (Wilson et al., 2006). Depth electrodes, frequently utilized in presurgical planning, are thought to measure local field potentials within a sphere of radius 0.5–3 mm surrounding the electrode tip (Logothetis, 2003). Although spatial resolution is not straightforward to measure, given that it depends on both source number (Fig. 9) and source strength (Fig. 10), it is likely that our system would achieve millimeter resolution. Nevertheless, we do not explicitly model a comparison between ECoG and our OPM array, so definitive conclusions cannot be drawn.

There are several important limitations to this work. Regarding the sensor array, the relatively small size of the array restricts the field of view, and sources outside that field of view will add noise to the measurements. Although the most obvious solution would be to sample the entire brain with a high density array, this is not currently feasible in practice, although this option has been addressed in simulation studies (Boto et al., 2016). In addition to sources outside the field of view there is also aliasing from higher spatial frequency information, although our dense array would suffer less from this problem than arrays with larger sensor spacings (Tierney et al., 2020). As for simulation methods, we used a spherical simulation rather than a realistic head model. While this is an approximation, it simplified our geometry and ensured that our results were not confounded by individual cortical folding patterns. Our use of a finite number of equal magnitude sources is also an approximation of actual brain behavior but may nonetheless be relevant especially in the case of epileptic spike generation as well as simple sensory tasks. Our empirically derived model of brain noise may not accurately reflect underlying generators of ongoing brain activity; nevertheless, our inclusion of brain noise represents a strength of this analysis. We should also note that we specifically simulate the behavior of FieldLine sensors, which have a single axis of sensitivity and closed-loop operation for improved linearity. There are currently commercially available biaxial and triaxial OPM sensors, but these do not operate in closed-loop mode, making nonlinear response a potential limitation. In addition, increasing to two or three sensitive axes results in a reduction of the overall sensitivity of the sensor. Thus, we confined our investigation to single axis sensors, although it may be of interest to repeat these simulations for multi-axis sensors. Recent studies showed that the inclusion of triaxial sensors in an array enhanced uniformity of coverage (Boto et al., 2022) and improved the rejection of external interference and movement artifacts, although increasing the density of single axis OPMs produced better rejection of internal sources (Brookes et al., 2021). Triaxial sensors operating in closed loop with high sensitivity may represent a significant improvement over the currently simulated array, once such sensors are commercially available. Likewise, hybrid arrays of OPMs and EEG electrodes have also been proposed in the literature (Beltrachini et al., 2021), although we do not explore such configurations here.

In this manuscript, we demonstrated the ability of a theoretical OPM magnetocorticography array to resolve multiple independent sources to a degree currently achievable only using invasive ECoG. We simulated most effects which could be expected to degrade performance of an OPM array and demonstrated that OPM arrays remain superior to conventional SQUID MEG for a range of potential calibration errors or other experimental issues. These results should serve to convince the reader that OPM sensors permit the design of arrays that can achieve unprecedented resolution in a non-invasively, potentially transforming the field of human neuroscience.

5. Citation diversity statement

As proposed in (Zurn et al., 2020), we include a statement of gender diversity in our reference list. The gender balance of papers cited within this work was quantified using a manual gender determination from authors’ publicly available pronouns. From the 42 references included in this work, the distribution of genders for the first and last authors were as follows: 71.4–76.2% were MM (N = 30–32), 7.1% were MW (N = 3), 14.3–16.7% were WM (N = 6–8) and 2.4% were WW (N = 3). The gender of the first authors of 2 references were not identifiable based on public information. To account for that, we report the breakdown for MM and WM in range format.