Remote Dose Imaging from Cherenkov Light using Spatially-Resolved CT Calibration in Breast Radiotherapy

Abstract

Purpose:

Imaging Cherenkov light during radiotherapy allows the visualization and recording of frame-by-frame relative maps of the dose being delivered to the tissue at each control point used throughout treatment, providing one of the most complete real-time means of treatment quality assurance. In non-turbid media, the intensity of Cherenkov light is linear with surface dose deposited, however the emission from patient tissue is well-known to be reduced by absorbing tissue components such as hemoglobin, fat, water and melanin, and diffused by the scattering components of tissue. Earlier studies have shown that bulk correction could be achieved by using the patient planning CT scan for attenuation correction.

Methods:

In this study, CT maps were used for correction of spatial variations in emissivity. Testing was completed on Cherenkov images from radiotherapy treatments of post-lumpectomy breast cancer patients (n=13), combined with spatial renderings of the patient radiodensity (CT number) from their planning CT scan.

Results:

The correction technique was shown to provide a pixel-by-pixel correction that suppressed many of the inter- and intra-patient differences in the Cherenkov light emitted per unit dose. This correction was established from a calibration curve that correlated Cherenkov light intensity to surface-rendered CT number ($R_{6\mathrm{M}\mathrm{V}}^2$=0.70 and $R_{10\mathrm{M}\mathrm{V}}^2$=0.72). The corrected Cherenkov intensity per unit dose standard error was reduced by nearly half (from ~30% to ~17%).

Conclusions:

This approach provides evidence that the planning CT scan can mitigate some of the tissue-specific attenuation in Cherenkov images, allowing them to be translated into near surface dose images.

INTRODUCTION

Cherenkov imaging techniques developed over the last decade can provide an efficient and consistent means of imaging patients during their radiotherapy treatments [1], [2], creating a platform for dynamic monitoring of the treatment on the patient’s skin. Because Cherenkov light is only generated in the regions where the beam is actively depositing dose, it serves as a real-time, video-rate monitoring system for accurate beam shape on the patient [3], [4]. The approach could be used to track deviations from planned setup occurring during treatment, and provide a method for continuous improvement in the quality of delivery [2]. It is possible that more studies across different institutions [5] or studies of incident rates [6] might utilize a non-contact imaging tool such as Cherenkov imaging if additional information such as quantitative dose could be derived from the images.

In radiotherapy, MV x-rays interact with tissue to produce Cherenkov radiation via the Compton-scattered MeV secondary electrons, which are ultimately the dominant source of dose deposition. The characteristic broadband spectrum of Cherenkov emission follows a wavelength-dependent intensity relationship I = 1/λ² from approximately 280 nm to 1500 nm [7], although the in vivo absorbers in tissue such as blood absorbs most wavelengths shorter than 600 nm. The remaining red and near-infrared weighted signal is very low-intensity, and is only observable using a very sensitive camera, ideally with a single-photon detection capability per unit frame rate. Because the clinical linac x-ray delivery is pulsed, time-gating techniques have been optimized around the resulting pulsed Cherenkov emission to maximize the detected signal-to-background ratio [8] and enable online background subtraction.

The Cherenkov imaging signal attenuation in tissue largely comes from variable amounts of adipose and fibroglandular tissue, and this attenuation is further complicated by collagen, blood, and skin pigmentation variations [9]. So, while the Cherenkov images still correctly track beam shape frame-by-frame, the local intensities within the imaged light are non-linear with delivered dose. The adipose tissue is more translucent, while higher blood/collagen content areas such as fibroglandular tissue or areola skew the emissivity lower. While experimental methods have been demonstrated to correct Cherenkov emission for tissue optical properties, such as spatial frequency domain imaging [10], technical constraints and the need of additional expensive or time-consuming imaging setups will likely prevent wider clinical use. Furthermore, tissue optical property correction has been carried out in numerous studies usually involving probes, external source lighting, or chromometers [11]–[14]. The technique presented here, however, requires only the patient CT scan, which will always be available from the planning stage of treatment. Therefore we consider these methods to be among the least time-consuming.

Earlier work showed that the average tissue CT number from the treatment planning scan could be utilized as a surrogate for optical property correction [15] in breast treatment imaging, but this was limited to area-averaged data, and did not show value in correcting the spatial homogeneity of dose within the images. In this study presented here, we investigate the findings found in [15] further, and demonstrate the first illustration of how the full CT scan can be used to correct the Cherenkov intensity images for the tissue-specific attenuation across the breast. This work presents an updated tissue correction methodology which yields a quantitatively better result.

Extracting dose information from the tissue remotely offers advantages and disadvantages as compared to currently-utilized dosimeters. Even with established tissue optical property corrections observed Cherenkov intensity in tissue differs from dose by more than the clinically accepted 3%/3mm threshold. Other dosimeters such as OSLD/TLD and scintillators are linear with dose, however, they require time to place, time to process/read/anneal, and adhering dosimeters can be irritating to the skin for patients with erythema. This work seeks to improve upon existing tissue optical property corrections, to update findings first presented in Imaging radiation dose in breast radiotherapy by x-ray CT calibration of Cherenkov light [15], which now allow for the determination of correction factors for each pixel in the Cherenkov image, and to address lack of Cherenkov intensity linearity with dose in tissue.

MATERIALS AND METHODS

All imaging was completed as described in an approved Institutional Review Board (IRB) protocol, where patients provided informed consent, and were treated in their clinically prescribed fractionated radiotherapy. Images were acquired using an intensified CMOS camera (C-Dose Research, DoseOptics LLC, Lebanon, NH) spectral sensitivity highest in 400 nm – 800 nm [16], mounted at IEC 61217 spatial coordinates of (−1288, 1066, −687) mm from a 2100 C-Series Clinac linear accelerator isocenter (Varian Medical Systems, Palo Alto, CA), and all treatment planning was completed in the associated ECLIPSE treatment planning software. Once mounted, distance and focusing were optimized for whole-breast radiotherapy imaging. Real-time background subtraction was implemented in software to isolate the Cherenkov signal from ambient background room light images. This was carried out by imaging Cherenkov and background light together over one exposure (roughly 20 radiation pulses over 50 milliseconds) then subtracting a scaled background image gathered after a short gate delay.

In this cohort, n = 13 patients were treated for post-resected malignant neoplasms of the right breast, for which radiation treatments are traditionally delivered in two, opposing, 6 MV tangent beams at gantry angles Right Posterior Oblique (RPO) and Left Anterior Oblique (LAO). The oblique positioning of the mounted camera created an optimized viewing for both entrance and exit beams. Depending on the size, depth and location of the resected tumor, adding a 10 MV beam at each 6 MV gantry angle is common (n=5 in this patient cohort). CT planning scans are taken for each patient on a GE Medical Systems scanner, 120 kVp, 512 × 512 pixel resolution, pixel spacing 0.98 mm, slice thickness 2.5 mm. For additional information regarding patient clinical setup, please see Imaging radiation dose in breast radiotherapy by x-ray CT calibration of Cherenkov light, Hachadorian et. al [15], Figure 1.

Figure 1:

In (a) and (b) the axial and coronal views (respectively) reflect a primarily adipose breast composition (low CT number) with interior scattered fibroglandular tissue (higher CT number). In (c) the coronal view is shown with the sampled region outlined in purple. In (d), the CT slices are rendered into an isosurface using the slice and pixel spacing DICOM information provided with the scan and displayed with the surface normal generated at each vertex. In (e) the average superficial tissue CT# from the region sampled in (c) is averaged and displayed over the surface. The isosurface is projected to the same view as the Cherenkov image (f), and surface is co-registered to the background image. The intensity mask from the Cherenkov image is applied to spatial CT image.

A method for creating a 2D image of isosurface CT# that matched the Cherenkov image was developed in MATLAB (Natick, MA). Extracting the isosurface CT# map consisted of five main steps: (1) reading the CT scan and generating a 3D patient isosurface based upon a simple threshold value, (2) computing the surface normal vectors at each isosurface vertex, (3) taking surface normal slopes and sampling inward (opposite-sign slope of each vector component) at 1 mm steps down to a 5 mm depth (skipping first sample to prevent partial volume averaging), and (4) calculating the mean sampled CT#, and assigning this mean CT# to the appropriate spatial vertex of the isosurface. Finally (5), the 3D CT# isosurface was oriented to the perspective of the Cherenkov camera position in the treatment room, and a snapshot is taken to be co-registered to the Cherenkov images. For the snapshot projection used, positional coordinates were exported from C-Dose Research software (DoseOptics LLC). In Figure 1a, the axial view of a sample patient (Patient 30), show a predominantly adipose breast with some, dense areolar tissue (Fig. 1b coronal view), and in Fig. 1c, the magenta contour illustrates the first 5 mm, which were sampled for the surface rendering. The depth of 0.5 cm was used because the majority of Cherenkov light comes from the superficial 5 mm of tissue, and the frequency of sampling was refined until superficial flibroglandular content could be appropriately visualized. Figure 1d shows the surface volume and surface normal vectors rendered with the appropriate pixel spacing and slice thickness using the info preserved in the scan. Reversing the slope of each normal vector provides the sampling direction at the designated pixel. Figure 1e depicts the final total volume with the average CT# value assigned to the appropriate isosurface pixel. This rendering is masked using the same intensity threshold as used on the cumulative Cherenkov image (Figure 1f) from one fraction of treatment, reflecting the radiation field boundary. Once masked, the spatial surface CT’s (Figure 1e) represent the final input for the calibration (discussed later) and are shown in Figure 2 for all patients. With these aligned images, each pixel from the Cherenkov image is supplemented with a corresponding spatial surface pixel representing CT#. Statistics were computed using 20 randomly sampled ROI’s from the image, including ROI’s from regions attenuated heavily by blood, darker pigment or scar tissue, including the coefficient of variation (COV), or the standard deviation over the mean (σ/μ). Statistics from uncorrected images and corrected images were compared. Further, the uncorrected and corrected Cherenkov images were sampled with respect to the co-registered dose image, and these data were plotted and the linear regression R² was reported.

Figure 2:

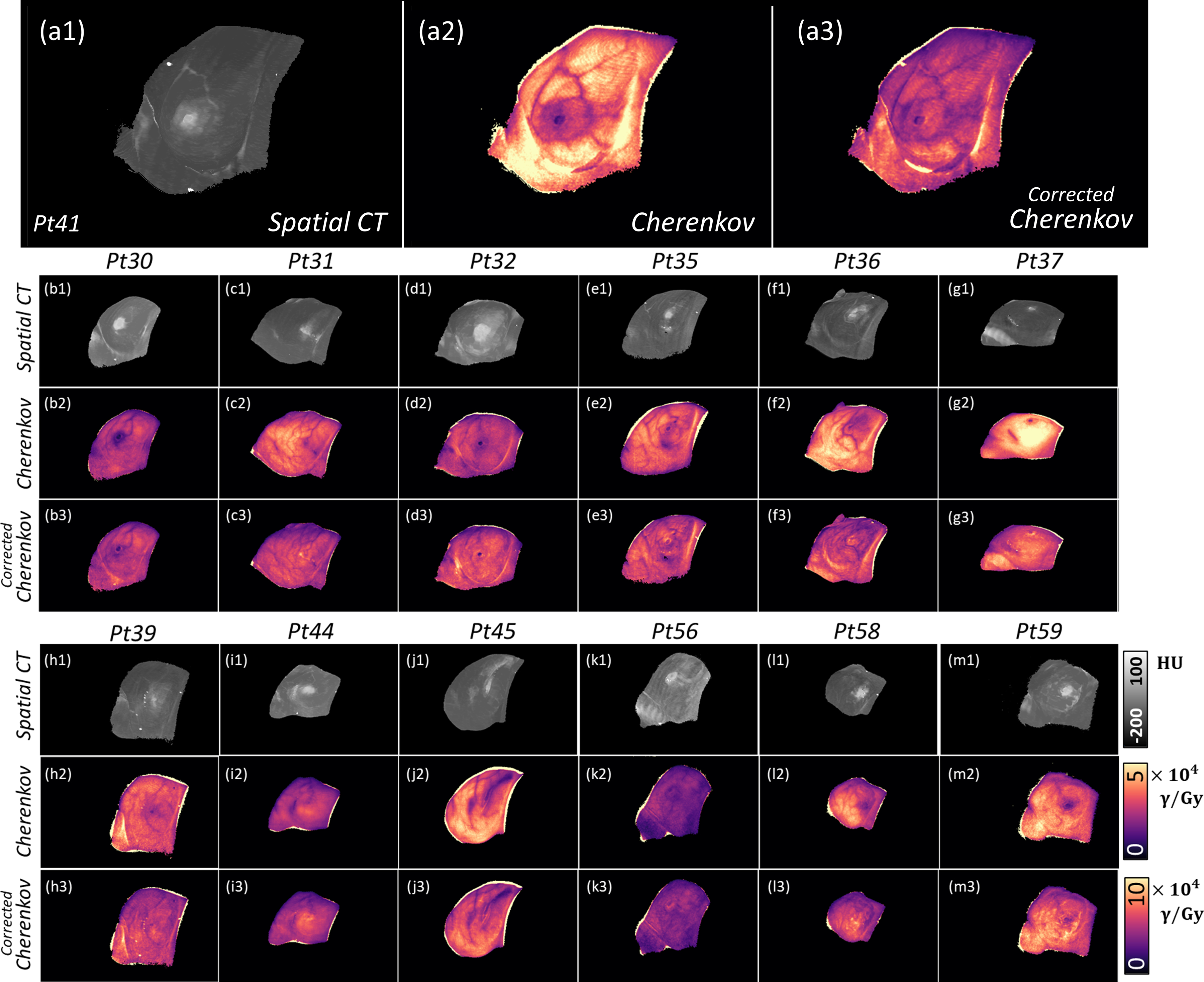
The spatial surface CT is shown from −200 to 100 HU in gray for each patient analyzed in this study (a1, b1, etc.). In the next row, Cherenkov images are shown (dose-normalized) and uncorrected. The final row gives the corrected Cherenkov image, after implementing the correction delineated in Equation 1 using the model in Figure 5. (All HU maps, uncorrected Cherenkov images, and corrected Cherenkov images correspond to the same, respective color bar.)

Images are corrected using a model fit by two summed exponentials. The models for calibration were generated using randomly-sampled ROI’s across Spatial CT and Cherenkov image types to capture both relatively unattenuated areas, as well as attenuated areas from vasculature, areolar pigmentation, and surgical scars. Compiling all data into two models for 6 MV and 10 MV beam energies, elucidated two separate summed exponential relationship between the observed Cherenkov light per unit dose (γ/Gy) deposited and the CT#.

RESULTS

In Figure 2, the spatial CT map is shown for each patient, followed by a sample, dose-normalized Cherenkov image from the first fraction imaged. In the final row, the corrected images have a more qualitative intensity consistency with dose. Note that in most cases, it can be seen that the previous variations in attenuation between dense tissue regions, such as the nipple, are markedly improved with spatial CT correction, as the surface CT image serves as an image complement to the Cherenkov image.

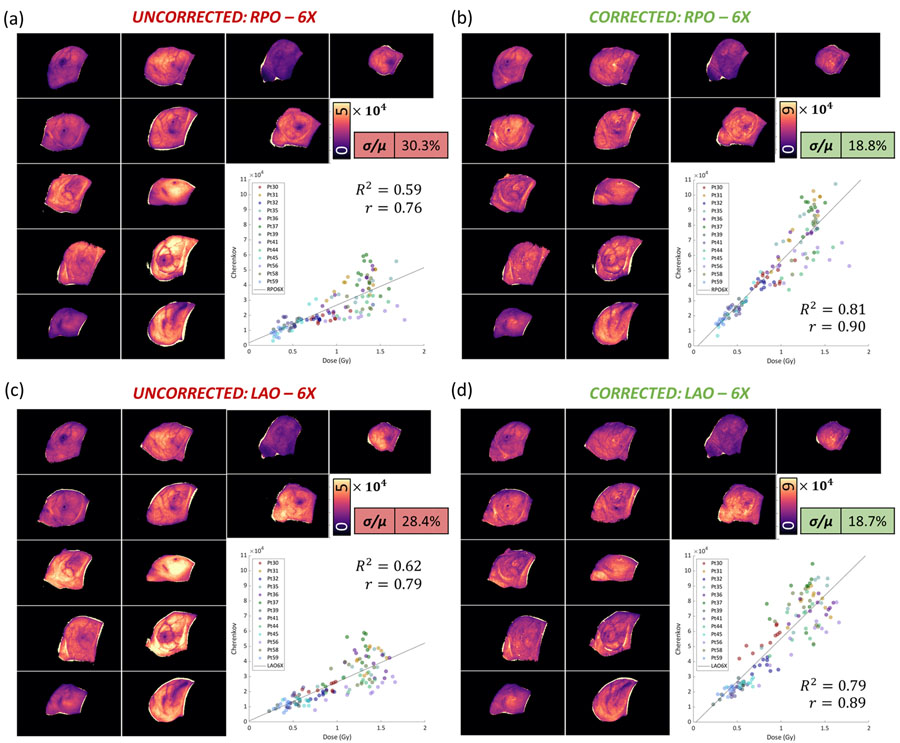
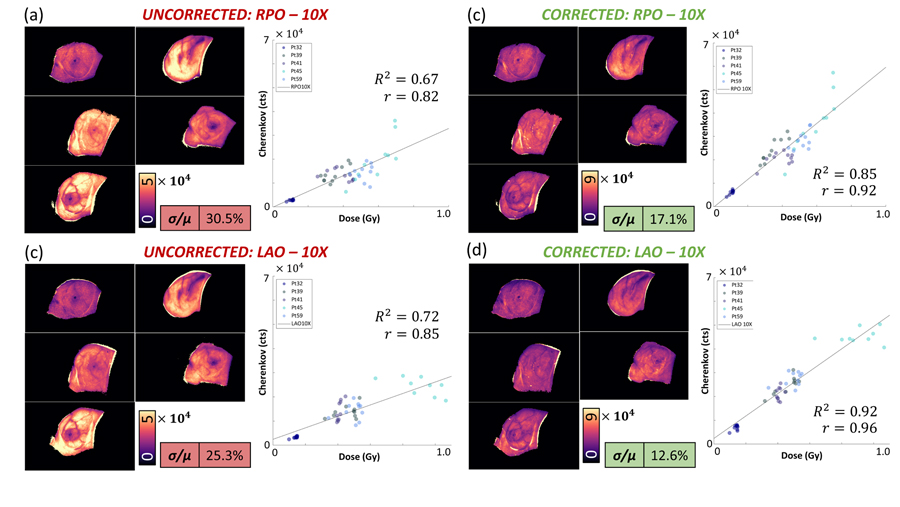
Next, to examine the improvement of the quality, Figure 3 compares the uncorrected dose-normalized images from RPO-6MV beams and LAO-6MV beams to corrected images. In the uncorrected images, units are in Cherenkov photons per unit dose (Gy). The intensity variability is reflected quantitatively in the standard deviation over the mean, which shows that the coefficient of variation (COV), or standard deviation over the mean (σ/μ) was reduced in RPO-6MV beams by 11.5% (from 30.3% to 18.8%), in LAO-6MV beams by 9.7% (from 28.4% to 18.7%). In Figure 4, the RPO-10MV beam COV was reduced by 13.4% (from 30.5% to 17.1%) and in LAO-10MV beams by 12.7% (from 25.3% to 12.6%). The first day of imaging for each patient was selected, and twenty ROI’s were used to compute twenty mean intensities, which were plotted in each respective quadrant of Figure 3 and Figure 4. The linear regression for uncorrected Cherenkov intensities with respect to dose for entrance (RPO) 6MV beams was weaker (R² = 0.59) than for the corrected beams (R² = 0.81). Similarly, for exit (LAO) 6 MV beams, uncorrected beams yield an R² = 0.62 and corrected beams yield an R² = 0.79. For entrance 10MV beams, in Figure 4, uncorrected R² = 0.67 and corrected R² = 0.85, and exit (LAO) uncorrected R² = 0.72 to corrected R² = 0.92.

Figure 3:

Dose-Normalized images are organized into pre-CT correction (a), (c), and post-CT correction (b), (d), images for the 13-patient cohort. All thirteen patients were treated with 6 MV beams. In short, the qualitative disparity is evident from patient-to-patient moreso in the images not corrected by CT. The quantitative result is shown using the COV (σ/μ) is improved, as well as the strength of the linear regression.

Figure 4:

Dose-Normalized images are organized into pre-CT correction and post-CT correction images for the 5-patient cohort receiving 10 MV treatments. Similar to that which was shown for 6 MV beams, the corrected images are much more qualitatively similar, and the statistics are notably improved.

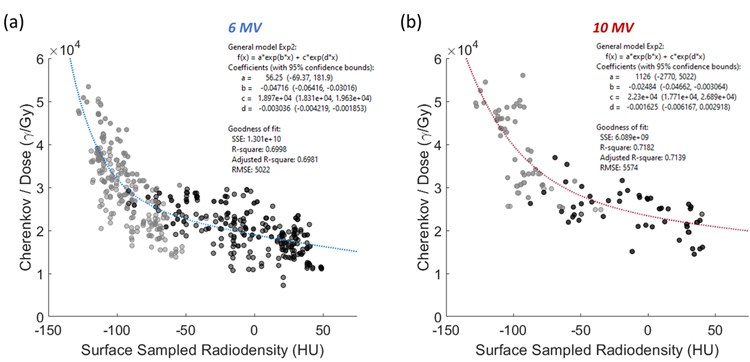
The model illustrated in Figure 5 is used to perform a correction over the local tissue differences observed for one patient, following, where I_uncorr,D(E) represents the dose-normalized, uncorrected Cherenkov image, c(HU(x,y), E) represents the matrix of correction factors which were generated using a patient-specific spatial CT map HU(x,y), and the constants A, b, C, and d are generated from the summed exponential relationships fit for both models relating CT# and Cherenkov light emitted per unit Gy, and can be found in Figure 5. The numerator of the correction factor image c(HU(x,y), E) is gathered by extrapolating back to the −135 HU crossing, an arbitrary correction endpoint chosen at a very low CT# where human breast tissue is unlikely to extend beyond. In Figure 5(a), the relationship between Cherenkov light emitted per unit dose and the isosurface CT# is fit using the summed exponential. All data points in Fig. 5 shown in dark gray indicate regions sampled from absorbing features, such as localized vasculature, areola or surgical scar. Light gray points are sampled from surrounding regions which avoided highly-attenuating features. Twenty separate points were sampled from each of the thirteen patients (ten from unattenuated regions, and ten from attenuated regions) such that each patient was equally represented in the calibration. In Figure 5(a) for 6 MV beams, the goodness of fit for the relationship shown was R² = 0.70. In Figure 5(b), the same qualitative relationship holds for 10 MV image data, though only half the patients in our 13-patient cohort were treated with 10 MV beams, whereas all 13 which were treated with 6 MV beams. For 10 MV data, the fit had R² = 0.72. Provided additional factors which further sway the Cherenkov light to dose linearity, the R² values for each curve reflect a reasonable fit.

Figure 5:

In (a), the relationship between the CT# and the amount of Cherenkov light emitted per unit dose (for both 6 MV entrance and exit beams combined) is modeled using a summed exponential with an R² of roughly 0.70. Recall that Cherenkov data has been dose normalized to render each image independent of incident beam energy. The darker gray points are representative of areas that were sampled in regions of substantial Cherenkov light attenuation, and the lighter gray points represent ROIs averaged from regions in the surrounding tissue, outside of any localized absorbing features. In (b), the same is shown for 10 MV data with a linear regression fit of R² = 0.72.

DISCUSSION

Dose-normalization of Cherenkov light is an important step which involves simply dividing the Cherenkov intensity pixel-by-pixel by the corresponding values of the surface dose image such that the light emitted for a fixed/consistent dose quantity can be observed. Thus, these dose-normalized Cherenkov images were used to analyze the coefficient of variation (COV, standard deviation over the mean σ/μ) spatially over each patients’ image first imaged fraction. This approach enabled the visualization of the variability existing within each image, and also across the patient image cohort for amount of light emitted per Gy of dose deposited. Without tissue variations in attenuation, the images would all have the same linear response to dose and would look the same with homogeneous values. As can be seen qualitatively from Figure 2, in nearly all cases, regions of increased CT number are accompanied by regions of reduced Cherenkov intensity, indicating that CT number is correlated with Cherenkov attenuation. In the corrected images, it is apparent that these image intensities are much closer to one another. Thus, the spatial CT-correction information improved the homogeneity of response with dose, both within the images and between images. Importantly, the variability observed in the amount of light produced per dose (Cherenkov/Gy) delivered is substantially reduced using the described Spatial CT correction methodology proposed here.

The variability is not eliminated entirely, however, and the remaining variations could be due to a number of factors including: (1) Attenuation due to skin color, (2) development of erythema skin changes over the course of fractionated treatment, (3) variable geometries from the tissue curvature, or (4) discrepancies in dose from what was planned [17], [18]. While all of these have been examined in previous studies, the approach used in this study to use the whole data set average trend to provide the global calibration to each pixel was found to be reasonably robust and practical.

Upon examination of these results, we expect that substantial corrective success can be attributed to accounting for subsurface fibroglandular and adipose tissue variety. While there are other factors, such as skin tone, we expect that these play a comparatively minor role. For example, the local catchment area is largely Caucasian, and all patients in this study had similar skin tone by coincidence. Furthermore, while variations in erythema typically happen after a few weeks of radiotherapy, only the first image from each patient was utilized, thereby minimizing accounting for developing erythemic effects. Thus, it was expected that the range of possible variations above would be small percentage variations in the Cherenkov/Dose intensity as compared to variation contributed by subsurface, fibro-adipose content. The major advantage of monitoring dose using Cherenkov light is to ensure consistency and verify the treatment was executed exactly as planned. Patient shifts, changes in anatomy, and breathing motion all play a role in varying delivered dose from the expected treatment plan, and this first order approach to imaging dose could have significant value.

Interestingly, the relationship between Cherenkov light intensity and CT# was shown to be linear in our previous study which studied the same cohort [15], where the implemented sampling technique involved a gross averaging of the superficial tissue radiodensity (HU) directly from the TPS. In this study, where CT information was rendered spatially, the number of regions which can be preferentially and locally sampled is much larger. Despite a new, non-linear fit emerging, the goodness of fit is roughly equivalent to that what was found previously. We estimate this relationship to be more accurate, and more representative of the way Cherenkov light behaves and is absorbed in patient breast tissues, which may then be considered for more accurate dose prediction.

A more accurate model of light transport could be applied in future work, to examine ways to verify the accuracy of calibration. Monte Carlo simulations are typically considered the most accurate computational tool to generate treatment dose values, and these could be used for Cherenkov intensity predictions as well, if the tissue optical properties are well-characterized [19]. Future studies examining of the origins of CT number and radiographic density based upon known physiological values could also be useful. While the methods presented in this study may feasibly present the most efficient, non-invasive, and accurate means of establishing whole-field corrections to Cherenkov images, creating a meaningful reporter of absolute dose at the conclusion of each fraction of treatment, there is still much work to go in terms of reducing this error to the point of clinical acceptance, i.e. 3%. While many factors influence the linearity between Cherenkov light emission and dose, tissue optical properties remains the most influential [20]. We propose that patient specific optimization of sampling depth could further reduce this error, as well as incorporation of a superficial tissue optical property correction which focuses on correction for melanin content, inflammation or blood content, or erythema-related radiation burn.

CONCLUSIONS

The spatial CT correction methods presented in this study for tissue optical properties provided a useful way to suppress some of the differences in Cherenkov intensity which are negatively correlated to blood volume or tissue type. Introducing a correction methodology from the CT scans, using a summed-exponential weighting with tissue depth at each pixel location, reduced the variability seen by roughly 14%, depending upon the beam energy and entrance/exit beam. The linear relationship between Cherenkov light and dose increased significantly between uncorrected and corrected images, thereby moving Cherenkov imaging closer to achieving absolute dosimetry by remote camera photography. In future work, skin pigmentation may be corrected for using a reflected light images, as examined in several earlier studies [21]. Implementation of this approach into a regular correction should reduce observed differences between patients (inter-patient), and the spatial differences across the treatment field of a single patient (intra-patient).