Comparing Global and Spatial Composite Measures of Neighborhood Socioeconomic Status Across US Counties

Abstract

Area-level neighborhood socioeconomic status (NSES) is often measured without consideration of spatial autocorrelation and variation. In this paper, we compared a non-spatial NSES measure to a spatial NSES measure for counties in the USA using principal component analysis and geographically weighted principal component analysis (GWPCA), respectively. We assessed spatial variation in the loadings using a Monte Carlo randomization test. The results indicated that there was statistically significant variation (p = 0.004) in the loadings of the spatial index. The variability of the census variables explained by the spatial index ranged from 60 to 90%. We found that the first geographically weighted principal component explained the most variability in the census variables in counties in the Northeast and the West, and the least variability in counties in the Midwest. We also tested the two measures by assessing the associations with county-level diabetes prevalence using data from the CDC’s US Diabetes Surveillance System. While associations of the two NSES measures with diabetes did not differ for this application, the descriptive results suggest that it might be important to consider a spatial index over a global index when constructing national county measures of NSES. The spatial approach may be useful in identifying what factors drive the socioeconomic status of a county and how they vary across counties. Furthermore, we offer suggestions on how a GWPCA–based NSES index may be replicated for smaller geographic scopes.

Introduction

Neighborhood socioeconomic status (NSES) is a complex interplay of social domains including employment, income, education, housing, and social bonds [1]. The associations of NSES with health outcomes, including diabetes, cardiovascular disease, AIDS, and cancer, have been widely researched [2–8]. One goal of The Diabetes Location, Environmental Attributes, and Disparities (LEAD) Network is to understand the impact of various mediators on the known relationship between NSES and diabetes onset across three different study populations to inform policies that might mitigate regional differences in diabetes incidence [9]. To address this and other LEAD Network goals, describing NSES is crucial.

Instead of relying on a single variable, many researchers create composite indices to characterize NSES by aggregating variables across multiple socioeconomic domains [10–13]. Because composite indices allow for inclusion of multiple dimensions, they provide a more informative and robust measure of NSES than a single variable [14]. The LEAD Network similarly opted to describe NSES using an index, leading to the investigation described herein.

Data used to construct measures of NSES often vary spatially. Spatial data pose unique challenges as they violate the classical statistical assumptions of independence and identical distributions due to spatial heterogeneity (geographic variation) and spatial autocorrelation (interaction and interdependence of processes between locations) [15]. These violations may be particularly significant if standard regression methods, which rely on assumptions of independence, are used and the residual spatial autocorrelation is unaccounted for. Subsequently, the standard errors of measures of associations may be impacted, contributing to incorrect inference. This can be further exacerbated when the inference informs policy decisions.

Although NSES is thought to vary geographically, the construction of key national NSES measures in the US, such as the Social Vulnerability Index (SVI) [16] and the Area Deprivation Index (ADI) [17], has not considered the spatial nature of data. Socioeconomic processes are not constant over space and are often interrelated because geographic boundaries are arbitrary, and neighborhood spillover effects—the phenomenon of a geographic area sharing similar characteristics with neighboring areas—are common [18]. Myint argued that when studying socioeconomic factors in urban systems, their “spatial distributions, patterns, associated functional characteristics, and centrality” may differ notably [19]. For example, owning a car in a rural area might have different impact on a measure of NSES than owning a car in a highly urban, walkable area such as New York City. Therefore, using an approach that includes geographic information in the construction of an areal-level composite index could allow researchers and policy makers to evaluate the possible spatial patterns in NSES across geographies, in turn developing a more accurate understanding of NSES in relation to health.

Many approaches to developing composite indices assume observations are independent and thus their applications do not consider the impact of spatial heterogeneity on the results [20]. One method, principal component analysis (PCA), originally developed by Pearson [21] and Hotelling [22], is a dimension reduction method that transforms variables into a linear combination of uncorrelated components. To address potential spatial heterogeneity in the NSES data, we explored a geographically weighted PCA (GWPCA) in the construction of a national measure. GWPCA is an adaptation of PCA incorporating spatial characteristics into the computation of the PCA. In GWPCA, a localized PCA is computed at each location, allowing for the results to vary over space [23].

In this paper, we developed two national NSES composite indices for the contiguous US using a non-spatial method (PCA) and a spatial method (GWPCA) with a goal of examining whether the index from the spatial method varied significantly from the index constructed using the non-spatial method. We also compared the previously established [24] association between each of the two county-level NSES measures and diabetes prevalence in the USA using the CDC’s US Diabetes Surveillance System data.

Methods

Data

Census Data

We chose the county as the spatial context of interest as it is the smallest geographic unit for which software implementation was available. While tract or zip-code level measures are common in the literature particularly as proxies for individual-level NSES, county-level NSES indices [25, 26] are not without utility as aggregated national geographic health outcome data can often only be made available at the county level.

We obtained 20 neighborhood SES variables for the 3109 counties in the contiguous US from the 2000 US Census, consistent with the exposure period for the LEAD Network data. Based on examples from the literature, we selected variables that align with 7 common socioeconomic and demographic domains, listed in Table 1. Since the chosen census variables had different measurement units, we used z-score transformation to make them more comparable and to ensure they had equal variances prior to running PCA and GWPCA. These transformations are notable as data reduction methods can lead to biased results when including variables with larger variances [27].

Table 1.

List of 20 neighborhood census variables and their respective domains used in the original PCA. Variables in bold are those that met inclusion criteria post-PCA

Domain	Census variable
Education	% Males and females with less than a HS education
Employment	% Males and females unemployed
	% Males no longer in work force
Housing	% Rented
	% Vacant
	% Crowded
	% Renter or owner costs in excess of 50% of income
	Median household value
Occupation	% Males in management
	% Males in professional occupations
	% Females in management
	% Females in professional occupations
Poverty	% Population with income below poverty level
	% Female headed households with dependent children
	% Households earning under $30,000/year
	% Households on public assistance
	% Occupied households with no vehicle
Racial Composition	% Residents who were non-Hispanic blacks
Residential Stability	% In same residence since 1995
	% Residents 65 years and above

Data for Outcome Analysis

We used 2005 county-level diagnosed diabetes counts from the CDC’s US Diabetes Surveillance System [28] as the outcome. The data were estimated from the CDC’s National Health Interview Survey. Adult respondents aged 20 years and above who answered “yes” (excluding women who had gestational diabetes) to whether they had been told by a healthcare professional that they had diabetes [28] were included in the estimated diagnosed diabetes counts.

To account for differing populations across counties, we included county-level 2005 population estimates of persons older than 20 years from the US Census Bureau as the offset in the analyses [28]. Additionally, we included county-level measures of access to food establishments [29], physical activity establishments [30], healthcare establishments [31], and rurality [32] as covariates. We defined access to food as density of supermarkets per 100,000 population and density of fast-food restaurants per 100,000 population; access to physical activity as density of physical activity establishments per 100,000 population; and access to healthcare establishments as density of clinics per 100,000 population and density of pharmacies per 100,000 population. We aggregated tract-level counts of supermarkets, fast-food, physical activity establishments, clinics, and pharmacies for the year 2000 obtained from the Retail Environment and Cardiovascular Disease [33] (RECVD) dataset to the county level. Rurality for the counties in 2000 was measured using the Index of Relative Rurality [34] (IRR) and race (% non-Hispanic Black) was obtained from the US Census.

Principal Component Analysis

We used PCA to generate a non-spatial NSES index using the z-score transformed census variables. Despite their transformations, the census variables were highly skewed, so we used a robust PCA method capable of handling outliers available in the pcaMethods [35] package in R (version 4.03) which transforms variables into a linear combination of uncorrelated components by successively maximizing the variability of the original variables. Details can be found in Jollife & Cadima’s review [20].

For each variable considered, we assessed the loadings in the first component of the PCA to determine the variable’s importance (or correlation) in the index. We then re-ran the PCA using only variables that had loadings greater than 0.2 [10]. As the primary purpose of the study was to create a single index, we only retained the first component. We then computed the non-spatial NSES index scores for each county as follows:

$$Non-spatialNSESScor{e}_i=l_1{x}_{1,i}+l_2{x}_{2,i}+...,{+l}_k{x}_{k,i}$$ 1

where l_k is the loading of the k^th variable and x_k,i is the value of the z-transformed variable k in county i. In the non-spatial PCA, the loadings of the variables in each county are the same, and the spatial nature of the data is not incorporated, as seen in Eq. (1). We re-scaled the scores to be between 0 and 100 and mapped them for visual inspection using ArcGIS (version 10.5). Higher scores indicate relatively lower NSES positions while lower scores indicate relatively higher NSES positions.

Geographically Weighted Principal Component Analysis

To construct a spatial composite NSES index, we used robust GWPCA. GWPCA geographically weights the variance–covariance structure of a PCA using a moving window approach to find localized components [23]. To generate the weights, we used a Gaussian distance-decay–based kernel function given by:

$$w_{\mathit{ij}}=exp\left[\frac{-1}{2},{\left(\frac{d_{\mathit{ij}}}{h}\right)}^2\right]$$

where d_ij is the Euclidean distance between the geographical centroids of county $i$ and county $j$, and $h$ is the kernel bandwidth. This allows the weights to gradually decay as the distance between counties increases. Further details can be found in Harris et al. [23]. Because we had no prior knowledge of the possible value of $h$, we chose an automatic and cross-validated bandwidth selection method available within the R-package (version 4.03) GWmodel [36] used for conducting the GWPCA. We used robust GWPCA because the estimation of the weights can be sensitive to outliers in the data. Harris and colleagues [37] developed an extension of the GWPCA bandwidth selection procedure which is robust to the influence of outlier observations [37].

GWPCA results in each county have its own set of principal components, allowing the loadings for each variable to vary across counties. The spatial NSES index scores were calculated as follows:

$$SpatialNSESScor{e}_i=l_{1,i}{x}_{1,i}+l_{2,i}{x}_{2,i}+...,{+l}_{k,i}{x}_{k,i}$$ 2

where l_k,i is the first principal component loading of the k^th variable in county i, and x_k,i is the value of the z-transformed variable k in county i. In contrast to the non-spatial NSES score (1) where each variable has one loading (l_k), the spatial NSES score (2) allows the loading to vary by both variable and county. We re-scaled the scores to be between 0 and 100 and mapped the scores in ArcGIS (version 10.5). Additionally, we mapped the percentage variability of the census variables explained by the geographically weighted first component. We tested for spatial autocorrelation in the percentage variability explained using a Moran’s I test.

Furthermore, we ran a Monte Carlo randomization test to test the null hypothesis that the loadings do not vary across space. In this test, paired sample locations from the dataset were successively randomized followed by applications of GWPCA. For each random sample, we calculated the standard deviation of the local loadings and compared them to the standard deviation of the actual local loadings. The p-value for the hypothesis test was estimated by:

$$\widehat{p}=\frac{1+{\sum }_{j=1}^{n}I({\mathit{sd}}_{sim,j}\ge {\mathit{sd}}_{\mathit{actual}})}{n+1}$$

where the indicator function is 1 if the standard deviation of the random sample is greater than or equal to the actual standard deviation and 0 otherwise, and $n$ is the total number of Monte Carlo simulations run. We assessed the hypothesis test using an alpha level of 0.05 and ran 499 simulations.

Outcome Analysis

To assess potential differences in the associations between NSES and diagnosed diabetes counts when using PCA and GWPCA indices of NSES, we modeled their relationships with the 2005 county-level diabetes counts from the CDC’s US Diabetes Surveillance System. We fitted univariate negative binomial regression models for each of the derived NSES exposures, six built environment variables (density per 100,000 population of supermarkets, density of fast-food restaurants, density of physical activity establishments, density of clinics, density of pharmacies, and the IRR). We then fitted multivariable negative binomial models for each NSES exposure, adjusting for built environment variables. We re-fitted the models using only covariates that showed a statistically significant association at the alpha = 0.05 level in full models. In all models, we used the estimated population size aged 20 + as the offset. We categorized the spatial NSES scores, non-spatial NSES scores, and race into three groups, low (scores ≤ 1st quartile), medium (scores > 1st quartile and < 3rd quartile), and high (scores ≥ 3rd quartile): low represents counties with relatively higher NSES positions and high represents counties with relatively lower NSES positions. We also categorized density measures as low (densities ≤ 1st quartile) and high (densities > 1st quartile).

Results

Principal Component Analysis

We ran the PCA using all 20 census variables in Table 1. The loadings for 9 variables (bolded in Table 1) were greater than 0.2 and met inclusion criteria [10]for the index. The loadings for these 9 variables and the variability explained by the first non-spatial principal component are shown in Table 2; only a single value for the loadings for each variable is estimated because this PCA is fitted across all counties jointly. At the county-level, the first component explained 54.8% of the variability of the census variables and the first three components explained a total of 68.9% of the total variability (data not shown). In the first component, % population with income below poverty level had the largest loading (0.451), suggesting that its correlation with the non-spatial NSES measure (i.e., the first principal component) was the strongest among the 9 variables. We also observed that loadings for median household value and % females with management occupations were in the opposite direction to the others, suggesting that as these values increase, the NSES score decreases, indicating less disadvantage.

Table 2.

Loadings for the first principal component from non-spatial PCA across 3109 counties in the USA

Variable	PC1
% Population with income below poverty level	0.451
% Households with income less than $30 k/year	0.385
% Households on public assistance	0.325
Median household value	− 0.207
% Males and females unemployed	0.312
% Males not in workforce	0.358
% Occupied households with no vehicle	0.282
% Population with less than a HS education	0.383
% Females with management occupations	− 0.22
Variability explained by component	0.548

Figure 1a shows a map of the re-scaled scores from the non-spatial PCA for the first principal component, with higher scores representing relatively lower county-level socioeconomic positions. The observed patterns suggest that Southern counties of the USA have higher NSES scores relative to the rest of the country (reflecting poorer NSES), while the counties in the Midwest and northeast corridor have relatively lower NSES scores, reflecting better NSES. It is notable that there are exceptions to these generalities: some California and Midwestern counties have lower values for the first principal component than surrounding counties; this may be a function of the lack of spatial correlation in the PCA.

Fig. 1.

Map of county-level scores from: a first non-spatial principal component and b first geographically weighted principal component. The boundaries defined are US state boundaries

Geographically Weighted Principal Components Analysis

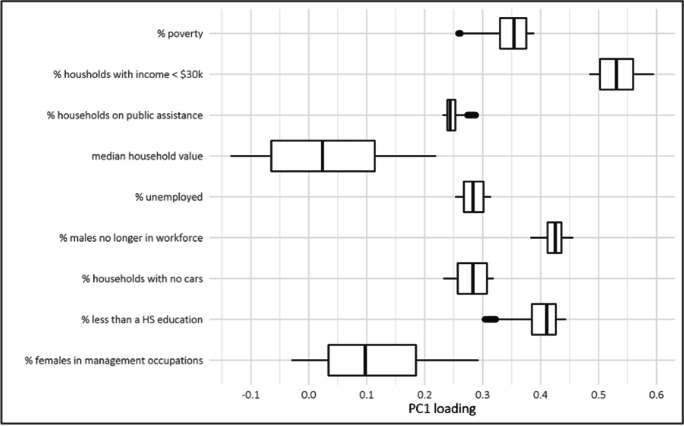
The distribution of the loadings of the 9 census variables from the first component of the GWPCA across the 3109 counties is shown in Fig. 2. The loadings for each variable varied across counties. Variables such as % of females in management occupations and median household values showed the largest variability, spanning negative and positive values, whereas % of households on public assistance and % of males no longer in the workforce had little variability in loadings. These results suggest that median household value and % of females in management occupations are characteristics of both higher and lower socioeconomic status neighborhoods.

Fig. 2.

Boxplots showing the distribution of the 2000 county-level loadings of the first geographically weighted principal component across the 3109 counties in the USA

Figure 1b shows a map of the geographically weighted first principal component. Like Fig. 1a, areas in the Southern USA consist of counties of relatively lower socioeconomic position, and the Midwest and Northeast consist of counties of higher socioeconomic position, based on the geographically weighted PCA. Though the trends for the non-spatial and spatial PCA results are similar, there are differences between the scores derived from them. The differences between the absolute scores from the two approaches ranged from 0 to 27.8 (data not shown). In general, scores from the GWPCA–derived index appear to have fewer counties with the highest NSES scores (indicating worse NSES) compared to the PCA–derived index. Furthermore, the GWPCA appears to provide a smoother picture of the NSES scores due to the incorporation of the spatial variation in the model.

Because the GWPCA essentially fits a PCA at each county, it is more difficult to describe the percentage of variation explained as there are 3109 different values. Thus, we mapped the total variance explained by the first component from the GWPCA (Fig. 3), which ranged from 60 to 90% across US counties, suggesting that the 9 census variables differentially explain the variation in the NSES variables. The Moran’s I test rejected the null hypothesis that there is no spatial autocorrelation in the variability explained by the first geographically weighted component at the 0.05 alpha level. We observed similarities in the percentage variability explained across Census regions in Fig. 3. In counties in the Northeast and the West, the first GWPC explained the largest amount of variability in the data (71–90%), while in counties in the Midwest, the first GWPC explained the least (60–70%). The proportion of variation in the first component explained by the GWPCA is uniformly higher across all counties relative to the non-spatial PCA, from which the first component explained 54.8% of the variability in the 9 census variables.

Fig. 3.

A map of county-level variability explained by the first geographically weighted principal component. The boundaries defined are the US boundaries for the 4 regions

The Monte Carlo randomization test rejected the null hypothesis (estimated $\widehat{p}$= 0.004) as seen in Fig. 4, suggesting that the loadings of the variables varied significantly across the counties; thus, incorporating the spatial variation contributes significantly to the PCA.

Fig. 4.

Distribution of local eigenvalues from Monte Carlo randomization test

Outcome Analysis

Table 3 summarizes the results of fitting negative binomial regression models assessing the association between each of the two measures of NSES and diabetes. We found that diabetes prevalence increases from relatively lower quartiles of NSES to higher quartiles of NSES regardless of whether a non-spatial (1.12 to 1.19) or spatial measure (1.12 to 1.18) of NSES is used, with similar variability around the parameter estimates with the non-spatial NSES and spatial NSES. The relationships remained unchanged when adjusting for built-environment variables in the multivariable models.

Table 3.

County-level associations between diabetes counts from the CDC’s Diabetes Surveillance program and NSES and county characteristics

	Univariate models		Multivariable models
			Non-spatial NSES		Spatial NSES
Variable	Estimate	95% CI	Estimate	95% CI	Estimate	95% CI
Non-spatial NSES
Med vs. low	1.12	(1.11, 1.14)	1.10	(1.08, 1.11)
High vs. low	1.19	(1.17, 1.20)	1.13	(1.12, 1.15)
Spatial NSES
Med vs. low	1.11	(1.09, 1.13)			1.09	(1.07, 1.10)
High vs. low	1.18	(1.16, 1.19)			1.12	(1.10, 1.14)
Density of supermarkets (high vs. low)	1.07	(1.05,1.08)	1.02	(1.01, 1.04)	1.02	(1.00, 1.04)
Density of fast-food establishments (high vs. low)	0.97	(0.96, 0.99)
Density of physical activity establishments (high vs. low)	0.95	(0.93, 0.96)
Density of clinics (high vs. low)	0.97	(0.96, 0.99)
Density of pharmacies (high vs. low)	1.08	(1.07, 1.10)	1.05	(1.04, 1.06)	1.06	(1.04, 1.07)
Index of rurality	1.26	(1.19, 1.33)	1.14	(1.08, 1.21)	1.17	(1.09, 1.25)
% Non-Hispanic Black
Med vs. low	0.96	(0.94, 0.97)	0.97	(0.96, 0.98)	0.97	(0.96, 0.99)
High vs. low	1.06	(1.04, 1.07)	1.04	(1.03, 1.06)	1.05	(1.03, 1.07)

Discussion

We developed both non-spatial and spatial NSES indices for US counties, the latter accounting for potential non-stationarity of socioeconomic processes across geographic space and spillover effects from neighboring counties, with a goal of informing ongoing research for the Diabetes LEAD Network. We constructed these county-level non-spatial and spatial NSES measures using PCA and GWPCA, respectively, on 9 census variables. The spatial NSES index differentially explained the variability in the census variables across counties. The Monte Carlo randomization test indicated that variables have a different impact on NSES across counties, and that drivers of NSES may be different across regions. We further found there is an association between NSES and prevalent diabetes among participants in the CDC’s US Diabetes Surveillance System cohort, and that the magnitude of this association is similar regardless of whether NSES is described using a spatial or a non-spatial approach, despite the exploratory results indicating that the spatial model is more appropriate.

These results observed herein are consistent with what we expect from Tobler’s First Law of Geography, which states that a geographic area inherits the characteristics of its neighbors [18]. Similar to what other studies [25, 38] have shown, we found that NSES was relatively poorer in the Southern USA compared to other regions, which have important policy implications in that policy makers could focus efforts to improve social and economic indicators in these areas. Note that these geographic trends emerged regardless of whether we included the spatial component or not; however, when examining specific counties, there may be more nuanced differences between the spatial and non-spatial approaches.

While the GWPCA provided a “smoother” NSES measure, the variations in loadings, as well as in the variation in the percentage of the variability explained by the first component, suggest the potential for measurement invariance, whereby the variables that define the measure of NSES interact with a county’s socioeconomic status differently across the USA. In particular, the regional differences observed in the variability explained by the first component hint that different sets of variables may influence a county’s NSES in different regions of the USA. Formal examination of differential item functioning in NSES is a subject of future work by the LEAD Network.

In addition to our findings suggesting there is spatial heterogeneity in NSES across the counties in the USA, we also observed the well-described relationship between NSES and diabetes prevalence [39], though the magnitude of this relationship did not differ substantively when using the spatial or non-spatial approaches. While it is difficult to reconcile the statistical findings of the benefit of using GWPCA with the application suggesting that the GWPCA does not provide an index that is differentially related to diabetes, this is context dependent, and it is possible that with other data, these results could differ. It is also possible that the scores from the non-spatial NSES and the spatial NSES were highly correlated because of the large sample size, hence leading to similar results in the exposure analysis. Furthermore, use of the first principal component only may have resulted in loss of information that could impact the results. Thus, researchers could still consider geographically weighted approaches when developing indices that have a spatial component particularly as an exploratory tool.

Epidemiological studies have highlighted how several health outcomes vary substantially across geographic space. Specifically, socioeconomic features of a neighborhood are of particular interest to researchers as they have been shown to be determinants of many disease outcomes [40]. Indeed, in our own collaborations in the Diabetes LEAD Network, we have interest in better understanding factors that impact the association between NSES and diabetes onset. However, challenges remain when trying to understand mechanisms linking NSES to various health outcomes along the causal pathway. A first step in better understanding the impact of neighborhood social and economic measures on health outcomes is investigating valid and reliable NSES measures that summarize the collective impact of several variables within these domains. Most area-level NSES constructs in the literature [4, 10, 12] are non-spatial in nature and do not capture the spatial dimensions of neighborhood social and economic processes. Our work suggests that incorporating the spatial component into these measures better explains variability in the variables comprising NSES.

Others have also found that measures of NSES have some spatial component. Andrews and colleagues [25] recently used Moran’s I to detect spatial clustering in a county-level measure of neighborhood deprivation in the USA. Similar to what we observe in Fig. 3, their results suggested the presence of spatial autocorrelation in the NSES scores. Andrews et al. [25] used the z-score sum of 10 socioeconomic variables, while we used PCA and GWPCA. Additionally, the individual variables chosen in their work differed from ours. Our study can be viewed as an extension of the work by Andrews et al., as we added the dimension of the spatially varying correlation between the index and the indicators in the index using GWPCA.

While to our knowledge GWPCA specifically has not been used as a tool in NSES studies in the USA, it has been used to derive a deprivation index for wards in Kolkata, India [18] and a social, health, and environmental composite index for counties in France [41], as well as in other contexts in environmental research [42]. Although the geography and variables analyzed in these studies differed from those in our study, the findings were similar with significant geographic non-stationarity identified in the loadings across space. Messer et al. [10] also informally assessed spatial variation in the loadings of their neighborhood deprivation index across their 8 study sites, which included cities and counties, by stratifying a non-spatial PCA. While the loadings did not vary across site, the variability explained by the first principal component varied from 51 to 73%, similar to what we observed in the GWPCA. However, the overall results are not directly comparable, as Messer et al. [10] used a non-spatial approach that does not account for potential neighboring effects, and the geographic unit of interest was the census tract, while in our study it is the county. It is possible that the tract is too small of a geographic scale to observe noticeable heterogeneity in loadings across space. Finally, Messer et al. [10] only assessed the loadings at 8 sites relevant to their study, while we assessed it for the entire contiguous US.

There are limitations with our analysis that must be noted. Like any index that uses only the first principal component, our index suffers from the inability to explain all the variability in the original data. As a result, there is some loss of information which could potentially bias the results when the index is used in outcome analyses. To overcome this limitation, researchers can use more than one principal component, although interpretability of the components may become challenging. Additionally, because we are not using all possible census variables in our index because of their relatively low loadings in the original PCA, it is possible that we excluded relevant dimensions of NSES. This is a limitation common to other NSES indices. GWPCA is also a computationally intensive method, making it infeasible to run at geographic units smaller than county for the entire US.

The use of county can be viewed as both a strength and a limitation. Many national health databases such as BRFSS, CDC Wonder, and County Health Rankings only make their data available at the county level. When analyzing data from these county-level sources, exposures and covariates are then often measured at the same geographic level. Hence, in those circumstances, our GWPCA measure can be useful. However, from a policy perspective, counties may not always be the appropriate geographic scale at which to assess NSES, as differing county sizes and resources may impact NSES differently [43]. While running GWPCA on the entire contiguous US at finer scales is not computationally feasible which makes creating a national tract-level GWPCA–based NSES index challenging, researchers could create measures that are at finer scales (such as block, zip code, or tract level) for smaller geographic areas (such as within a state) to better reflect NSES, so as to avoid losing the neighborhood to neighborhood variability in NSES.

Furthermore, it is possible that the effects of socio-spatial and residential segregation [43] could be masked with a measure such as the GWPCA measure where spatial spillover effects are considered. For example, there may be instances of wealthier counties surrounded by poorer counties. However, from what we observed in the analysis, while the PCA and GWPCA did have different loadings, the scores of the measures were correlated. Furthermore, the scores still contained the information in the individual original socioeconomic census variables, which might limit the masking of such socio-spatial segregation effects. Any segregation effects observed in those original census variables should theoretically be reflected in the index measures. Further studies could be performed that harness the benefits of a spatial measure of socioeconomic status and combine it with socio-segregation data.

Our study also has several strengths, including that it is, to our knowledge, one of the first to use a GWPCA to derive a NSES index for US counties. This approach may be useful as an exploratory tool in identifying what factors drive the socioeconomic status of a county, and how they may vary across counties. The results suggest there is clustering in the trends of the loadings for each variable in the NSES index. Therefore, it may be beneficial to work across county lines to develop and implement policies that improve the socioeconomic status of their counties collectively. This spatial NSES index may provide lawmakers with guidance on which specific domains of NSES to allocate resources, particularly when used as an exposure in outcome models, such as for the LEAD Network.

We demonstrated that NSES is a complex and dynamic measure that varies across US counties, with some similarities within regions, and that geography is an important factor when computing an NSES index. Future work may extend these results to examine the impact of the socioeconomic variables on NSES across regions by formally examining measurement invariance and to examine the impact of NSES on outcomes to inform policy changes.

Funding

Centers for Disease Control and Prevention (R01DK124400).